Abstract
We describe a new fluorescence imaging methodology in which the image contrast is derived from the fluorescence lifetime at each point in a two-dimensional image and not the local concentration and/or intensity of the fluorophore. In the present apparatus, lifetime images are created from a series of images obtained with a gain-modulated image intensifier. The frequency of gain modulation is at the light-modulation frequency (or a harmonic thereof), resulting in homodyne phase-sensitive images. These stationary phase-sensitive images are collected using a slow-scan CCD camera. A series of such images, obtained with various phase shifts of the gain-modulation signal, is used to determine the phase angle and/or modulation of the emission at each pixel, which is in essence the phase or modulation lifetime image. An advantage of this method is that pixel-to-pixel scanning is not required to obtain the images, as the information from all pixels is obtained at the same time. The method has been experimentally verified by creating lifetime images of standard fluorophores with known lifetimes, ranging from 1 to 10 ns. As an example of biochemical imaging we created lifetime images of Yt-base when quenched by acrylamide, as a model for a fluorophore in distinct environments that affect its decay time. Additionally, we describe a faster imaging procedure that allows images in which a specific decay time is suppressed to be calculated, allowing rapid visualization of unique features and/or regions with distinct decay times. The concepts and methodologies of fluorescence lifetime imaging (FLIM) have numerous potential applications in the biosciences. Fluorescence lifetimes are known to be sensitive to numerous chemical and physical factors such as pH, oxygen, temperature, cations, polarity, and binding to macromolecules. Hence the FLIM method allows chemical or physical imaging of macroscopic and microscopic samples.
The phenomenon of fluorescence is widely utilized for research in the biosciences (1-8). These applications have been focused on two divergent disciplines, time-resolved fluorescence and fluorescence microscopy. In the former one takes advantage of the high information content of the time-dependent fluorescence decays to uncover details about the structure and dynamics of macromolecules (4). Such measurements are performed almost exclusively using picosecond laser sources coupled with high-speed photodetectors. Due to the expense and complexity, time-resolved measurements are performed mostly as single-sample (single-pixel) measurements. Some parallel measurements have been reported, but only for a linear array detector and for wavelength rather than spatial resolution (9). In contrast, fluorescence microscopy, in combination with dyes, stains, fluorophores, or fluorophore-labeled antibodies, is most often used to determine the localization (intensity) of the species of interest, usually of proteins or other macromolecules (6-8). The acquisition of two-dimensional fluorescence images is preferentially accomplished with low-speed accumulating detectors (10), which are not capable of quantifying picosecond–nanosecond fluorescence decays. Consequently, the high information content of time-resolved fluorescence is not usually available for studies of microscopic biological samples. This is particularly disadvantageous when one considers the sensitivity of fluorescence decay times to chemical and environmental factors of interest, such as local pH, cation concentration, oxygen, and polarity.
In the present report we combine measurements of fluorescence lifetimes with 2D imaging, to create images in which the lifetimes are determined at each pixel and the lifetimes are used to create contrast in the images. There have been reports of lifetime measurements at specific locations in microscopic samples (11,12), and in some cases the lifetime measurements have been raster scanned to create crude lifetime images (13,14). Importantly, our approach is unique in that the information on the lifetime at each pixel is obtained simultaneously, so that the temporal resolution of the lifetime image will be ultimately limited by the light source, 2D detector and optics, rather than by the time needed to sequentially measure the lifetimes at each pixel. As presently configured, calculation of the lifetime image requires the combination of several stationary phase-sensitive images of the sample. However, these could be acquired rapidly (seconds or less) using automated and refined procedures, so that the lifetime imaging could potentially be accomplished in real time. Alternatively, by calculating the difference between two phase-sensitive images at different detector phase angles, one can rapidly compute images in which regions with decay times larger or smaller than the desired value can be suppressed, resulting in visualization of regions of distinct environments.
The concept of fluorescence lifetime imaging (FLIM)3 is illustrated in Fig. 1. Suppose that the sample is composed of two regions, each with an equal intensity of the steady-state fluorescence. Assume further that the lifetime of the probe in the central region of the object (τ2) is severalfold longer than that in the outer region (τ1). The longer lifetime in the central region could be due to the presence of a chemical species, binding of the probe to a macromolecule, or other environmental factors. The intensities of the central and outer regions could be equally due to dye exclusion or other mechanisms. Observation of the intensity image (Fig. 1b) will not reveal the different environments in regions 1 and 2. However, if the lifetimes were measured in these regions then the distinct environments would be detected. The FILM method allows image contrast to be based on the local decay times, which can be presented on a gray or color scale (Fig. 1c) or as a 3D surface in which the height represents the local decay times (Fig. 1d).
FIG. 1.
Intuitive presentation of the concept of fluorescence lifetime imaging (FLIM). The object is assumed to have two regions that display the same fluorescence intensity (I1 = I2) but different decay times, τ2 > τ1. (a) Object; (b) steady-state image; (c) gray-scale or color lifetime image; (d) lifetime surface.
It is interesting to note that the concept of FLIM is an optical analog of magnetic resonance imaging (MRI). In MRI, one measures the proton relaxation times at each location, and the numerical value of the relaxation time is used to create contrast in the calculated image. Furthermore, the local chemical composition of the tissue determines the proton relaxation times and not the proton concentration. The contrast in FLIM is determined by similar principles. The local environment determines the fluorescence lifetime, which is then used to calculate an image that is independent of probe concentration.
Since the concept of FLIM is new, one may question its potential uses. The usefulness of FLIM is derived from the known sensitivity of fluorophores to their local environment, the wealth of knowledge concerning factors and/or substances that alter fluorescence lifetimes, and the independence of the lifetime from the fluorophore concentration. More specifically, the fluorescence lifetimes of probes can be altered by oxygen (15-17), pH (18-20), calcium (21), energy transfer (22-24), and a variety of other factors and/or quenchers (25-29). To date, most fluorescence sensors such as the Ca2+ indicators are characterized only in terms of intensity changes (30-34), but it appears likely that FLIM will stimulate studies to identify other probes that display suitable changes in lifetime in response to specific environmental factors. It will also be of interest to examine lifetime images of stained chromosomes (35), where the local G–C/A–T ratios may affect the decay times of the stains (36). Such imaging could rely on the wealth of knowledge of the fluorescent properties of dye–DNA complexes (37). One can also imagine imaging of free versus protein-bound NADH in cells, recovered from the 0.5- and 1.5-ns lifetimes of free and bound NADH, respectively (38).
It is important to recognize that FLIM does not require the probe to display shifts in absorption or emission, such as those that occur in the most widely used Ca2+ indicator, Fura-2 (30). Furthermore, fluorescence lifetimes are mostly independent of the probe concentration, at least for the low concentrations and/or thin samples used for microscopy. These two factors suggest that given a suitable fluorophore, the lifetime image can be a chemical image of the chosen species. Hence, there appears to be numerous immediate and potential applications of FLIM to the biological sciences.
CREATION OF LIFETIME IMAGES
In this section we describe our present methodology for measuring fluorescence lifetime images. The basic idea is to perform high-frequency gain modulation of an image intensifier to preserve the decay time information. In our present apparatus we modulate the gain at the same frequency as the light-modulation frequency, or at some harmonic of the laser repetition rate. More specifically, we are using the image intensifier as a 2D phase-sensitive detector, in which the signal intensity at each position (r) depends on the phase angle difference between the emission and the gain modulation of the detector. This results in a constant intensity which is proportional to the concentration of the fluorophore (C) at location r(C(r)), to the cosine of the phase angle difference, to the extent of modulation of the detector (mD), and to the modulation of the emission at each location (m(r)):
| (1) |
In this expression θD is the phase of the gain modulation, and θ(r) is the phase angle of the fluorescence. A value of θD = 0 results in maximum intensity for a zero lifetime, i.e., scattered light. Our procedure is analogous to the method of phase-sensitive or phase-resolved fluorescence (39,40). However, these earlier measurements of phase-sensitive fluorescence were performed electronically on the heterodyne low-frequency cross-correlation signal, whereas our present homodyne measurements are performed electro-optically on the high-frequency modulated emission. It is interesting to note that homodyne detection at the light-modulation frequency is analogous to that used by Veselova and co-workers (41,42), who first reported homodyne phase-sensitive detection of fluorescence, in this case electronically. The phase angle of the fluorophore is related to the apparent phase lifetime τθ and the modulation frequency (ω in rad/s) by
| (2) |
It is not possible to calculate the lifetime from a single phase-sensitive intensity. However, the phase of the emission can be determined by examination of the detector phase angle dependence of the emission, which is easily accomplished by a series of electronic delays in the gain-modulation signal or by optical delays in the modulated excitation. The phase-sensitive images can also be used to compute the modulation at each pixel (m(r)). The modulation is related to the modulation lifetime τm(r) by
| (3) |
The desired information is thus obtained by varying θD (Eq. [1]), which in turn allows determination of θ(r) or m(r). In our apparatus we collect a series of phase-sensitive images, in which θD is varied over 360° or more. The phase-sensitive intensities at each pixel are used to determine the phase at each pixel, resulting in the phase angle or lifetime images. This procedure is illustrated schematically in Fig. 2. The object is illuminated with intensity-modulated light. A gain-modulated image intensifier and a CCD camera are used to obtain a series of phase-sensitive images. In these images, the phase-sensitive intensity for each region is expected to vary as the cosine of the phase angle difference (Eq. [1]). Also, the modulation of the image is expected to depend on the lifetime in each region according to Eq. [3], as well as on the cosine of the phase angle difference (Eq. [1]).
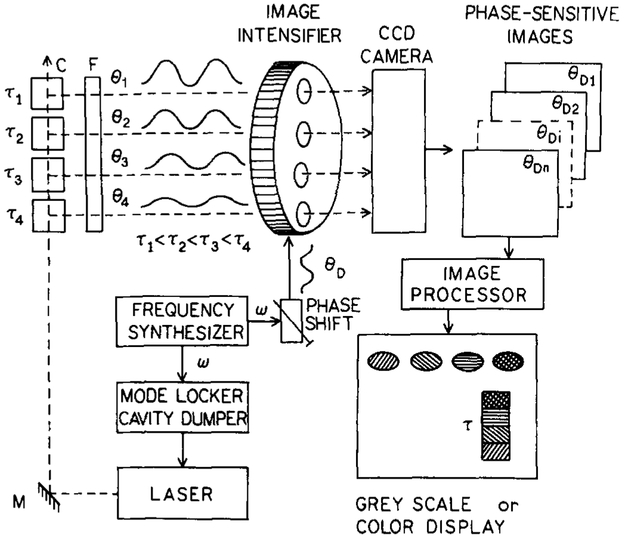
FIG. 2.
Schematic diagram of a FLIM experiment. The “object” consists of a row of four cuvettes and has regions with different decay times, τ1 to τ4. This object is illuminated with intensity-modulated light. The spatially varying emission is detected with a phase-sensitive image intensifier, which is imaged onto a CCD camera. The laser system is a cavity-dumped dye laser, which is synchronously pumped by a mode-locked and frequency-doubled NdYAG laser.
The data sets for FLIM are rather large (512 × 512 pixels, and 520 kbyte storage for each image), which can result in time-consuming data storage, retrieval, and processing. In order to allow rapid calculation, we developed an algorithm to calculate the phase and modulation images that uses each image one time, and only one image is in memory at any given time. This algorithm (called CCDFT) is described in Appendix 1. In order to test this algorithm we examined the dependence of the phase-sensitive intensities on the detector phase angle. For this analysis we used an average intensity from the central illuminated spot consisting of approximately 5 by 10 pixels. These intensities were fit to Eq. [1] (using a program called Cosine) and used to recover the phase and modulation of the emission. We note that all the phase angles and modulations (θ(r) and m(r)) initially contain shifts and amplitude changes due to instrumental factors. In the present report all detector phase angles are given as instrumental values , where θI is a phase shift intrinsic to the apparatus and the value required to give the correct phase angle for the reference sample. Similarly, the apparent modulation of the image is “normalized” so the modulation of the standard matches the expected value.
INSTRUMENTATION FOR FLIM
A detailed description of the FLIM apparatus is given elsewhere (43). The light source is a picosecond dye laser system, consisting of a mode-locked Antares NdYAG, which synchronously pumps the cavity-dumped dye lasers containing either rhodamine 6G or pyridine 1. The pulse repetition rate was varied from 3.81 to 76.2 MHz, yielding similar results, and we used either the fundamental or higher harmonics of the pulse train (44-46).
The detector was a CCD camera from Photometrics (Series 200) with a thermoelectrically cooled PM-512 CCD. The gated image intensifier (Varo 510-5772-310) was positioned between the target and the CCD camera. The intensifier gain was modulated by a radiofrequency signal applied between the photocathode and microchannel plate (MCP) input surface. This signal was capacitively isolated from the high voltage across the intensifier. A favorable feature of the Varo intensifier is that it could be gain-modulated using only the 10-dBm output of the frequency synthesizer (43). Phase delays were introduced into this gating signal using calibrated coaxial cables.
The target consisted of rows of cuvettes, each containing scatterers, standard fluorophores, or fluorophores with environment-sensitive lifetimes (Fig. 2). The laser passed through the center of the cuvettes. For calculations of the FLIM images we assumed that one of the cuvettes contained a lifetime standard of known phase and modulation. For FLIM of the standards, DMSS was taken as the standard with τ = 40 ps (48). For FLIM of acrylamide-quenched Yt-base, the unquenched sample was taken as the standard with τ = 4.56 ns. The phase and modulation of the other cuvettes were calculated using this reference, as described previously (47).
EXPERIMENTAL METHODS
Lifetimes recovered from the FLIM measurements were compared with those obtained using standard frequency-domain (FD) measurements and instrumentation (49-51). For the FLIM measurements polarizers were not used to eliminate the effects of Brownian rotation, which are most probably insignificant for these decay times and viscosities. The standard fluorophores (POPOP, perylene, and 9-cyanoanthracene) were dissolved in air-equilibrated cyclohexane. The reference fluorophore DMSS was dissolved in methanol. Yt-base was dissolved in water and is known to be collisionally quenched by acrylamide (52). The solutions were not purged with inert gas.
RESULTS
FLIM of Lifetime Standards
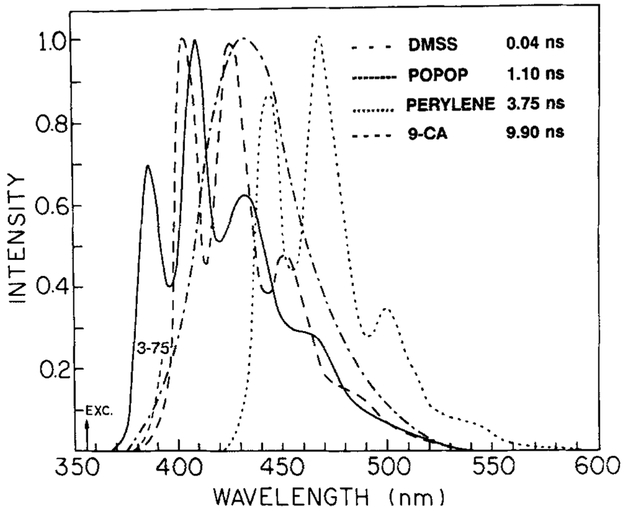
Since the technique of FLIM is new, it is necessary to test objects with known lifetimes. These control measurements are important because we are currently using homodyne detection, which is less robust than heterodyne detection with regard to rejection of harmonic and/or nonlinear effects. Hence, we imaged rows of cuvettes, each containing a different fluorophore with a different lifetime. This approach has the advantage of allowing comparison of the FLIM results with the standard frequency-domain lifetime measurements (49-51) of the same samples. We used four fluorophores with known lifetimes, these being a styrene derivative (DMSS) with a 40-ps lifetime in methanol (48) and POPOP (1.10 ns), perylene (3.75 ns), and 9-cyanoanthracene (9-CA, 9.90 ns), all dissolved in air-equilibrated cyclohexane. The emission spectra are shown in Fig. 3. These spectra overlap nearly completely on the wavelength scale, which was deliberately chosen in order to emphasize that the samples were being distinguished on the basis of the lifetimes. The lifetimes of these fluorophores result in phase shifts of 0.7, 18.9, 49.1, and 71.7° at 49.335 MHz as measured on the FD instrument (Table 1). The pulse repetition rate was 3.81 MHz, but the 49.53-MHz measurement frequency is determined by the frequency applied to the image intensifier. In a number of experiments we used pulse repetition rates ranging from 3.81 to 76.2 MHz, and we found no changes in the phase angle or modulation, as expected for a harmonic content FD measurement.
FIG. 3.
Emission spectra of standard fluorophores used for FLIM. The emission was observed through a Corning 3-75 filter. Excitation was at 355 nm.
TABLE 1.
Phase and Modulation Data for the Standard Fluorophoresa at 49.53 MHz
| Compound | Methodb | Phase |
Modulation |
||
|---|---|---|---|---|---|
| θ (degrees) | τθ (ns)c | m | τm (ns)c | ||
| DMSS | FD | 0.7 | 0.04 | 1.0 | 0.04 |
| Cosined | ⟨0.7⟩ ± 4.7 | 0 to 0.30 | ⟨1.0⟩ ± 0.09 | 0 to 1.27 | |
| CCDFTd | ⟨0.7⟩ ± 1.0 | 0.04 ± 0.04 | ⟨1.0⟩ ± 0.02 | 0 to 0.65 | |
| POPOP | FD | 18.9 | 1.10 | 0.946 | 1.10 |
| Cosine | 15.4 ± 4.2 | 0.89 ± 0.25 | 0.994 ± 0.07 | 0.35 (0 to 1.33) | |
| CCDFT | 16.6 ± 0.5 | 0.95 ± 0.05 | 0.928 ± 0.02 | 1.29 ± 0.10 | |
| Perylene | FD | 49.1 | 3.70 | 0.645 | 3.80 |
| Cosine | 48.3 ± 3.9 | 3.61 ± 0.45 | 0.797 ± 0.06 | 2.44 ± 0.45 | |
| CCDFT | 49.0 ± 0.5 | 3.68 ± 0.05 | 0.691 ± 0.06 | 3.36 ± 0.10 | |
| 9-CA | FD | 71.7 | 9.70 | 0.303 | 10.1 |
| Cosine | 77.7 ± 3.2 | 14.7 ± 4.2 | 0.383 ± 0.02 | 7.75 ± 0.5 | |
| CCDFT | 78.5 ± 0.5 | 14.7 ± 0.50 | 0.309 ± 0.01 | 9.90 ± 0.4 | |
Excitation wavelength, 355 nm; Corning 3-75 emission filter; 25°C.
FD, standard frequency-domain measurements at 49.335 MHz; Cosine, fit of the averaged phase-sensitive intensities, measured at 49.53 MHz, to Eq. [1]; CCDFT, pixel-by-pixel values as calculated from the algorithm in Appendix 1.
The uncertainty ranges of τθ and τm are not symmetrical, and average values are shown. For the cosine method the uncertainties were from the usual assumptions in a least-squares fit. For the CCDFT calculations the uncertainties in the standard value represent the standard deviations of about 120 pixels (6 × 20 pixels) from the central region of the illuminated spot.
The angle brackets indicate that these values were used as reference values.
The primary information for FLIM is presented in Fig. 4, which shows the phase-sensitive images of the illuminated cuvettes. One notes that both the absolute and relative intensities of the illuminated spots vary with the detector phase angle. These phase-sensitive intensities were used to compute the phase angles, modulation, and apparent lifetimes (Table 1). These values are in good agreement with those obtained from the standard FD measurements.
FIG. 4.
Phase-sensitive images of standard fluorophores at 49.53 MHz.
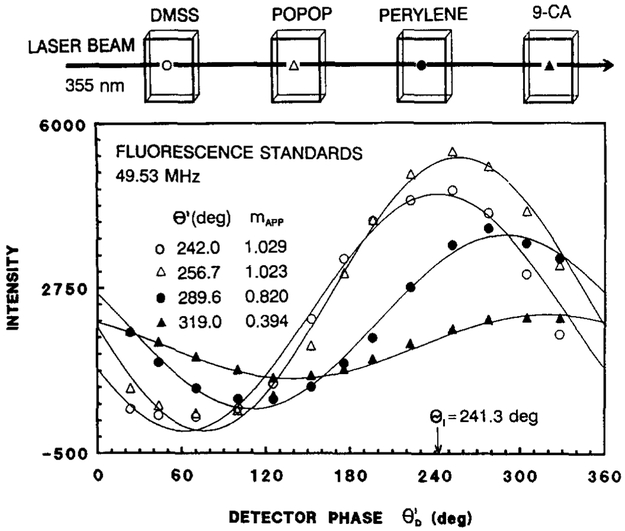
It is somewhat difficult to see the phase differences between the cuvettes in the phase-sensitive images (Fig. 4). However, the relative phase angles are easily visualized by a plot of the averaged phase-sensitive intensity versus detector phase angle (Fig. 5). For this figure we used an average phase-sensitive intensity obtained for approximately 5 by 10 pixels, using the same spatial window for all data files. The phase angle of the fluorescence sample can be determined from the phase shift relative to the reference. Inspection of this figure reveals that the phase-sensitive intensities of the fluorophores are delayed in phase relative to the 40-ps reference, and that the phase shift increases and the modulation decreases in the order DMSS, POPOP, perylene, 9-CA. Also, the phase angles are larger, and the modulations smaller, at higher frequencies (below). These phase angles and modulations are in good agreement with those observed from the direct FD measurements (Table 1). These results suggest that the FLIM apparatus is providing a reliable measure of the fluorescence phase angle and modulation.
FIG. 5.
Phase-sensitive intensities of standard fluorophores at various detector phase angles.
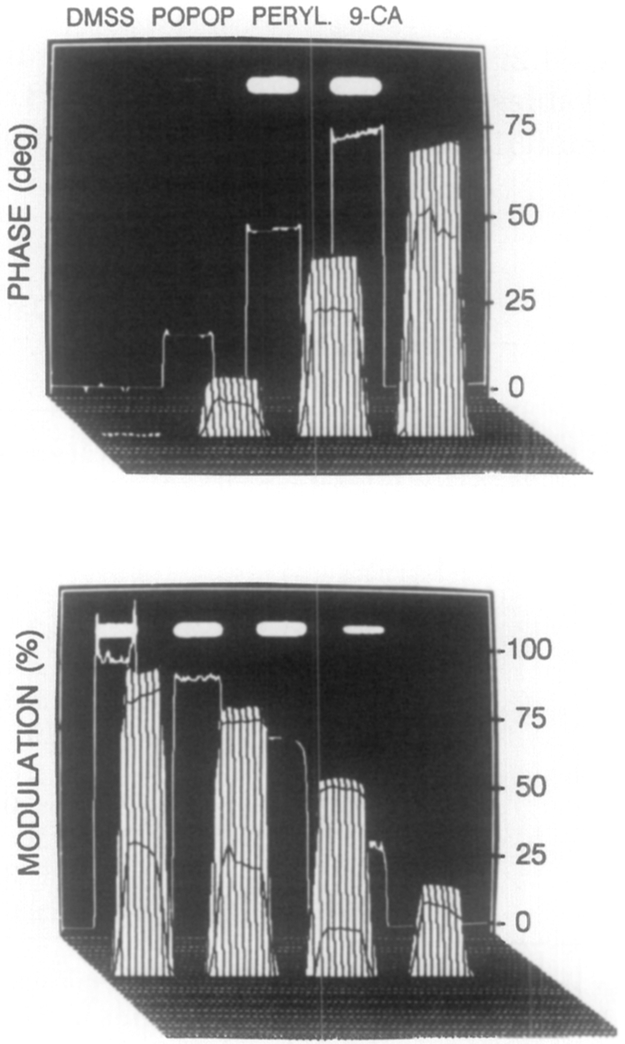
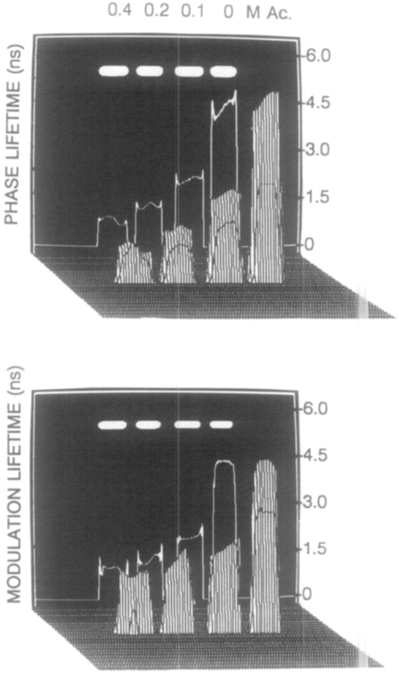
The phase-sensitive images (Fig. 4) were used to calculate the phase (Fig. 6, top) and modulation images (Fig. 6, bottom), using the algorithm described in Appendix 1. Only those pixels with phase-sensitive intensities higher than 250 (about 5% of the maximum intensity) were used to compute the phase and modulation images. For reasons that we do not presently understand, elimination of these low intensity values from the computation appears to improve the agreement between the phase and modulation values obtained from the FLIM apparatus, and those found from the FD measurements or the Cosine fits. Also, for these images we displayed the phase and modulation only for regions of the image where the stationary intensity was 5% or greater of the peak intensity in the steady-state intensity image. One notes that the phase angles increase (left to right) and the modulation decreases, as expected for the increasing lifetimes of the standards.
FIG. 6.
Phase angle (top) and modulation (bottom) of the standards observed at 49.53 MHz.
Once the phase angle and/or modulation images are available they can be subjected to any manner of image processing. For instance, the phase and modulation lifetime image is simply a numerical conversion of the phase and modulation image using Eqs. [2] and [3], respectively. The phase lifetime image of the standards at 49.53 MHz is shown in Fig. 7 (top). The lifetimes recovered from this image are in good agreement with those obtained from the FD measurements and from fitting the phase-sensitive intensities (Fig. 5 and Table 1). Any desired range of phase angles or lifetimes can be chosen as the basis for contrast, and pseudo-3D projections are possible. Figure 7 (bottom) shows the modulation lifetime image at 49.53 MHz. Agreement between these two methods suggests that both the phase and the modulation images can be used in parallel. Average or composite images of phase and modulation lifetimes may allow one to increase the robustness of the method. For instance, the modulation data may be more reliable for lifetime measurements in regions where the lifetime-modulation frequency product, , is large. Conversely, the phase angle images may be more reliable for measurement in short decay time regions of the image, where the modulation lifetimes are less reliable. In Fig. 7 we chose to compute lifetimes only where the intensity was 5% or higher than the peak intensity of the steady-state intensity image (with no gain modulation). The lack of random noise down to the 5% limit suggests that lifetime imaging can be accomplished over a 20-fold range of intensities. This will be valuable in fluorescence microscopy in that one cannot force the probe concentration and/or intensity to be equal in all regions of a cell or microscopic specimen. Further refinements in the FLIM methodology may further expand the dynamic range for the local intensities.
FIG. 7.
Phase and modulation lifetime images of the standards observed at 49.53 MHz.
In order to further test our FLIM apparatus, the standards were examined with two different modulation frequencies, 34.29 and 64.77 MHz. These results, summarized in Tables 2 and 3, are shown in Fig. 8. Reliable phase and modulation lifetimes were obtained for all substances and frequencies, indicating that the FLIM apparatus is usable over a wide range of frequencies. Importantly, the phase angles increase and the modulations decrease with increasing modulation frequency, but the phase and modulation lifetimes remain constant as expected for single exponential decays. Of course, the lifetimes are not reliable in the frequency range where the measurements are expected to fail, such as for small amounts of demodulation for DMSS at all three frequencies and for 9-CA at 64.77 MHz, where the expected phase shift is 75.5°.
TABLE 2.
Phase and Modulation Data for the Standard Fluorophoresa at 34.29 MHz
| Compound | Methodb | Phase |
Modulation |
||
|---|---|---|---|---|---|
| θ (degrees) | τθ (ns)c | m | τm (ns)c | ||
| DMSS | FD | 0.5 | 0.04 | ~1.0 | 0.04 |
| Cosined | ⟨0.5⟩ ± 4.8 | 0 to 0.43 | ⟨1.0⟩ ± 0.1 | 0 to 2.25 | |
| CCDFTd | ⟨0.5⟩ ± 0.5 | 0 to 0.08 | ⟨1.0⟩ ± 0.01 | 0 to 0.35 | |
| POPOP | FD | 13.3 | 1.10 | 0.973 | 1.10 |
| Cosine | 12.4 ± 4.6 | 1.02 ± 0.40 | 1.00 ± 0.10 | 0 to 2.22 | |
| CCDFT | 11.2 ± 0.1 | 0.92 ± 0.05 | 0.966 ± 0.003 | 1.15 ± 0.1c | |
| Perylene | FD | 38.9 | 3.75 | 0.771 | 3.85 |
| Cosine | 39.0 ± 3.4 | 3.76 ± 0.50 | 0.905 ± 0.080 | 2.18 ± 1.20 | |
| CCDFT | 37.9 ± 0.1 | 3.59 ± 0.10 | 0.767 ± 0.006 | 3.88 ± 0.2 | |
| 9-CA | FD | 64.8 | 9.90 | 0.412 | 10.31 |
| Cosine | 64.3 ± 3.2 | 9.05 ± 1.40 | 0.506 ± 0.04 | 7.92 ± 0.85 | |
| CCDFT | 62.6 ± 0.3 | 8.81 ± 0.2 | 0.416 ± 0.004 | 10.93 ± 0.5 | |
Excitation wavelength, 355 nm; Corning 3-75 emission filter; 25°C.
FD, standard frequency-domain measurements at 34.155 MHz; Cosine, fit of the averaged phase-sensitive intensities, measured at 34.29 MHz, to Eq. [1]; CCDFT, pixel-by-pixel values as calculated from the algorithm in Appendix 1.
See Table 1, footnote c.
The angle brackets indicate that these values were used as reference values.
TABLE 3.
Phase and Modulation Data for the Standard Fluorophoresa at 64.77 MHz
| Compound | Methodb | Phase |
Modulation |
||
|---|---|---|---|---|---|
| θ (degrees) | τθ (ns)c | m | τm (ns)c | ||
| DMSS | FD | 0.9 | 0.04 | 1.0 | 0.04 |
| Cosined | ⟨0.9⟩ ± 4.3 | 0 to 0.22 | ⟨1.0⟩ ± 0.10 | 0 to 1.19 | |
| CCDFTd | ⟨0.9⟩ ± 1.8 | 0.08 ± 0.07 | ⟨1.0⟩ ± 0.015 | 0 to 1.10 | |
| POPOP | FD | 24.1 | 1.10 | 0.912 | 1.10 |
| Cosine | 18.7 ± 4.0 | 0.83 ± 0.20 | 0.955 ± 0.07 | 0 to 1.29 | |
| CCDFT | 20.5 ± 1.5 | 0.92 ± 0.07 | 0.855 ± 0.06 | 1.5 ± 0.4 | |
| Perylene | FD | 55.7 | 3.62 | 0.543 | 3.82 |
| Cosine | 49.8 ± 3.4 | 2.91 ± 0.35 | 0.695 ± 0.05 | 2.54 ± 0.40 | |
| CCDFT | 50.1 ± 1.5 | 2.94 ± 0.20 | 0.535 ± 0.015 | 3.89 ± 0.30 | |
| 9-CA | FD | 75.5 | 9.54 | 0.236 | 10.16 |
| Cosine | 68.2 ± 3.3 | 6.15 ± 1.10 | 0.335 ± 0.02 | 6.81 ± 0.50 | |
| CCDFT | 68.7 ± 3.0 | 6.35 ± 1.10 | 0.254 ± 0.02 | 9.40 ± 0.60 | |
Excitation wavelength, 355 nm; Corning 3-75 emission filter; 25°C.
FD, standard frequency-domain measurements at 64.515 MHz; Cosine, fit of the averaged phase-sensitive intensities, measured at 66.77 MHz, to Eq. [1]; CCDFT, pixel-by-pixel values as calculated from the algorithm in Appendix 1.
See Table 1, footnote c.
The angle brackets indicate that these values were used as reference values.
FIG. 8.
Phase angle (top) and modulation images (bottom) of the standards observed at 34.28 MHz (left) and 64.77 (right).
FLIM of Yt-base Dynamically Quenched by Acrylamide
In a biological specimen fluorophores often exist in several environments, each with different decay times. FLIM will allow imaging of such microenvironmental factors in cells. For instance, a t-RNA can exist in folded or extended conformations, depending upon the presence of divalent cations such as Mg2+ (52-54). t-RNAPhe contains a naturally occurring fluorophore, Yt-base, whose lifetime depends upon the t-RNA conformation and the presence of covalently linked acceptors (54). To illustrate the possibility of conformation imaging we examined Yt-base in the presence of the collisional quencher acrylamide (55). Various acrylamide concentrations were chosen to obtain decay times near 4.5, 2.15, 1.4, and 0.9 ns (Table 4). These samples can be considered to represent any fluorophore that is sensitive to its local environment, or that is in environments of differing accessibility to a quencher.
TABLE 4.
Phase, Modulation, and Lifetime of Yt-base with Acrylamidea
| [Ac] (m) | Methodb | Phase |
Modulation |
||
|---|---|---|---|---|---|
| θ (degrees) | τθ (ns)c | m | τm (ns)c | ||
| 0.0 | FD | 65.5 | 4.38 | 0.394 | 4.65 |
| Cosined | ⟨65.5⟩ ± 3.4 | 4.38 ± 0.71 | ⟨0.394⟩ ± 0.02 | 4.65 ± 0.28 | |
| CCDFTd | ⟨65.5⟩ ± 3.0 | 4.35 ± 0.45 | ⟨0.394⟩ ± 0.03 | 4.64 ± 0.45 | |
| 0.1 | FD | 46.1 | 2.08 | 0.668 | 2.22 |
| Cosine | 47.1 ± 2.3 | 2.14 ± 0.17 | 0.720 ± 0.03 | 1.92 ± 0.17 | |
| CCDFT | 46.7 ± 2.0 | 2.10 ± 0.15 | 0.699 ± 0.04 | 2.06 ± 0.30 | |
| 0.2 | FD | 34.3 | 1.36 | 0.8 | 1.5 |
| Cosine | 34.6 ± 2.0 | 1.37 ± 0.10 | 0.858 ± 0.03 | 1.19 ± 0.16 | |
| CCDFT | 33.1 ± 2.0 | 1.29 ± 0.20 | 0.844 ± 0.04 | 1.26 ± 0.30 | |
| 0.4 | FD | 22.3 | 0.82 | 0.884 | 1.06 |
| Cosine | 24.6 ± 3.4 | 0.91 ± 0.15 | 0.892 ± 0.04 | 1.01 ± 0.22 | |
| CCDFT | 23.5 ± 2.0 | 0.85 ± 0.10 | 0.902 ± 0.04 | 0.94 ± 0.30 | |
Excitation wavelength, 345 nm; Corning 3-75 emission filter; near 25°C (room temperature).
FD, standard frequency-domain measurements at 79.695 MHz; Cosine, fit to Eq. [1] at 80.01 MHz; CCDFT, pixel-by-pixel fit using the algorithm in Appendix 1 at 80.01 MHz.
See Table 1, footnote c.
The angle brackets indicate that these values were used as reference values.
Phase-sensitive images of the Yt-base samples are shown in Fig. 9. The concentration of Yt-base in these samples was adjusted to yield nearly the same intensity for all acrylamide concentrations. Nonetheless, the different lifetimes of Yt-base result in distinct phase-sensitive images (Fig. 9). For instance, the phase-sensitive intensity of the sample with 0 m acrylamide is highest for , but the sample with 0.4 m acrylamide is highest for . The dependence of the phase-sensitive intensity on θD is more readily seen in Fig. 10, which shows the averaged phase-sensitive intensity versus detector phase. As can be seen from fits to Eq. [1], the phase angles are in good agreement with the expected values, assuming an unquenched lifetime of 4.38 ns (Table 4). Note that the detector phase angles () in Figs. 9 and 10 are arbitrary values and are not corrected for instrumental shifts.
FIG. 9.
Phase-sensitive images of acrylamide-quenched Yt-base for various detector phase angles.
FIG. 10.
Phase-sensitive intensities of Yt-base in the presence of 0.4 (○), 0.2 (Δ), 0.1 (●), and 0.0 m acrylamide (▲).
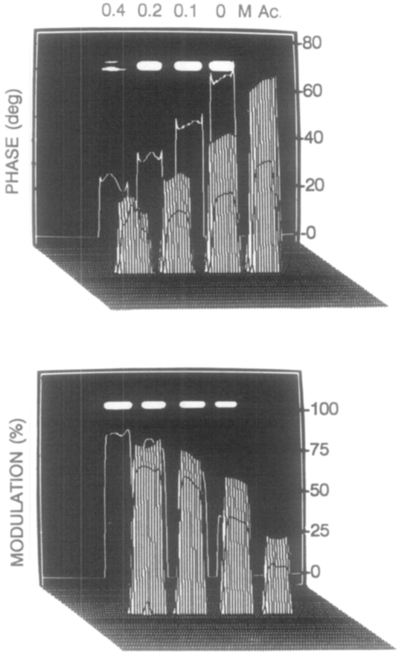
The phase-sensitive images in Fig. 9 were used to compute the phase angle and modulation images (Fig. 11). The phase angles increase and the modulations decrease with decreasing amounts of acrylamide. These images can be transformed to phase and modulation lifetime images (Fig. 12), in which the phase and modulation lifetime both increase as the quencher concentration decreases.
FIG. 11.
Phase and modulation images of Yt-base with acrylamide quenching.
FIG. 12.
Phase and modulation lifetimes images of Yt-base with various concentrations of acrylamide.
Phase-Suppression Images of Acrylamide-Quenched Yt-base
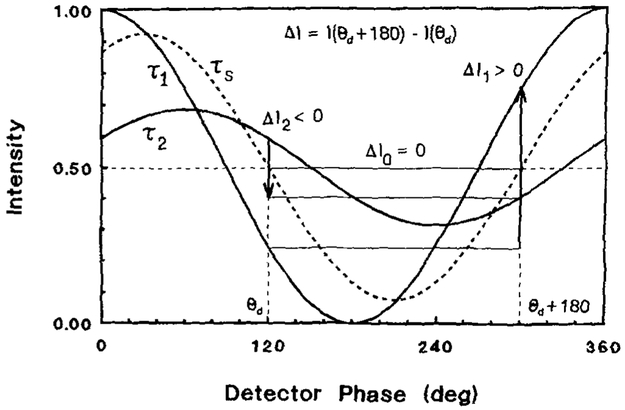
A unique property of FLIM, as described in this paper, is the ability to suppress the emission for any desired lifetime. Suppression of any given decay time can be accomplished by taking the difference of two phase-sensitive images obtained for detector phase angles of θD and θD + Δ. In the difference image ΔI = I(θD + Δ) – I(θD) components with a phase angle of θs = θD + Δ/2 ± n 180° have an amplitude of zero. This concept is shown schematically in Fig. 13 for Δ = 180°. Components with a phase angle of θs = θD + Δ/2 ± n180° have an amplitude of zero. Components with lifetimes larger than the suppressed lifetime appear as negative regions in the images, and components with shorter lifetimes have positive intensity. This relationship is reversed if one calculates I(θD) – I(θD + Δ), as is described in more detail in Appendix 2.
FIG. 13.
Intuitive description of phase suppression. In a difference image with ΔI(θD + 180°) – I(θD), a component with θ = θD is completely suppressed. Components with longer lifetimes (phase angles) appear as negative spots, and those with shorter lifetimes (phase angles) appear to be positive.
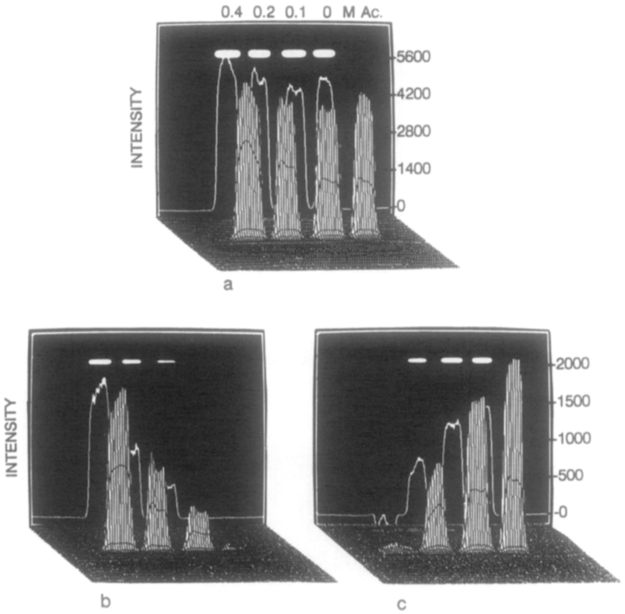
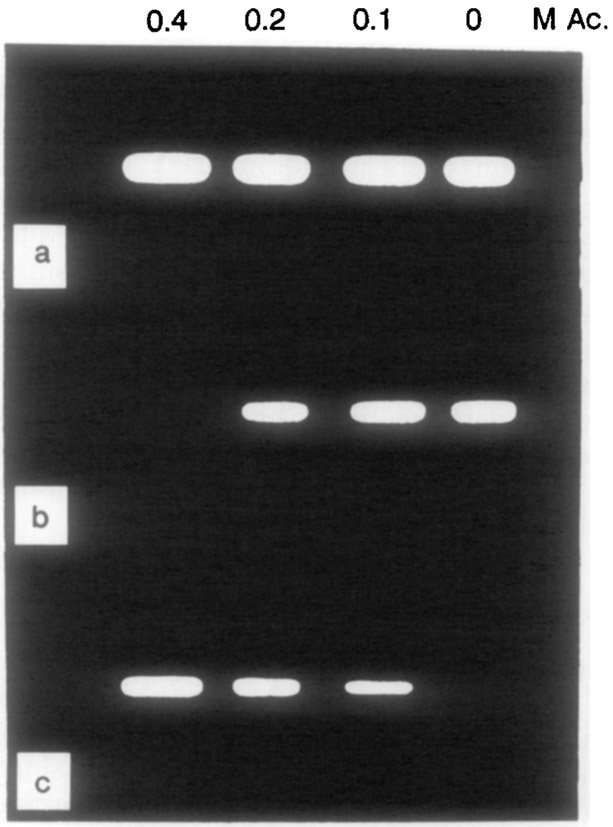
The use of difference images to suppress the emission of acrylamide-quenched Yt-base is shown in Fig. 14. Figure 14a shows a positive nonprocessed phase-sensitive image, in which all samples appear with nonzero intensity. Figures 14b and 14c show difference images, in which only the positive regions are shown as distinct from the background. In these gray-scale images, the negative regions were assigned a zero (background) intensity. In Fig. 14b, the region with an unquenched Yt-base lifetime longer than 3.53 ns is suppressed (τs = 3.53 ns), revealing only the quenched regions of the image. Similarly, in Fig. 14c, the region with a lifetime shorter than 0.94 ns is suppressed (τs = 0.94 ns), revealing three positive images for less quenched Yt-base. This imaging method, when applied to fluorophores in a heterogenous environment, will allow imaging based on a variety of factors, such as oxygen or chloride concentration, binding of a probe to a macromolecule, or exposure to solvent.
FIG. 14.
Phase-suppression images of Yt-base quenched by acrylamide. In the phase-sensitive image (a) the detector phase was 203.2°. The difference images were calculated using (b) I(48.1°) – I(338.9°), τs = 3.53 ns and (c) I(268.3°) – I(48.1°), τs = 0.94 ns.
These phase-suppression images are presented in an alternative manner in Fig. 15. In this figure, the zero and negative regions of the images are dark, and the positive regions of the phase-suppression images are shown with a gray-to-white scale. Such a presentation allows regions with lifetimes greater or less than the suppressed lifetime to be rapidly visualized. It should be noted that phase-suppression images require only simple difference calculation between two images obtained at the appropriate detector phase angles. Hence, phase-suppression images may be acquired, computed, and displayed in nearly real time with modest computational hardware.
FIG. 15.
Gray-scale suppression images of acrylamide-quenched Yt-base. (a) Phase-sensitive image with . (b) Difference image with τs = 0.9 ns using I(268.3°) – I(48.1°). (c) Difference image with τs = 3.5 ns using I(48.1°) – I(338.9°).
DISCUSSION
It is of interest to consider our present FLIM apparatus in terms of previous attempts to create lifetime images. Such images have been previously created using pixel-by-pixel scanning and time-correlated single-photon counting (13). Such measurements require considerable amounts of time, and it may not be practical to create high-resolution and/or real-time images. Such scanning lifetime measurements were extended to the frequency domain using a phase-resolved image dissection tube (14). This method is promising, but it suffers from the disadvantage of requiring pixel-by-pixel scanning and does not allow for image accumulation and averaging prior to read out as is possible with our slow-scan CCD detection.
Other laboratories have created contrast based on the decay times using on-gating of the long-lived delayed fluorescence or phosphorescence. These applications included on-gating of delayed luminescence from stained fingerprints (56), from immunophosphor conjugates (57), and to image phosphorescence from a porphyrin probe in the absence of oxygen (58) and from unidentified emitters (59). However, these methods provide information only on the presence of the delayed emission and have not been used to create contrast based on the local lifetime. Hence, on-gating of delayed emission does not appear to have the contrast opportunities that we envision for FLIM, particularly lifetime-based contrast and the selective observation of either short or long components in the decay, depending upon the detector phase angles used in a difference image. The FLIM methodology can be of use even in the distant field of aerodynamics, where oxygen quenching has been used to monitor local oxygen flow and pressure (60,61). We note that our method is distinct from the τMAP (62) and related (63) methods, which use position-sensitive detectors followed by lifetime determination of the detected pulses. Such methods require low light levels so that decay times can be measured at one or few pixels at a time. In essence, these methods are random pixel-by-pixel scanning methods in which the lowest intensity determines the probability of detecting a photon at each pixel.
The instrumentation for FLIM is in its infancy. The present configuration is just one of many possible configurations and improved instrumentation may appear. One can conceive of other schemes for 2D gain modulation, such as the use of a grid-gatable MCP photomultiplier tube (PMT) or image intensifier (64). Also, there are many opportunities to speed up and/or automate data acquisition and display. More importantly, it may be possible to develop data acquisition algorithms that allow for heterodyne detection and suppressed harmonic distortion and that make the measurements more robust in a variety of experimental situations.
It should be noted that the apparatus required for FLIM is a modestly straightforward extension of that already in use in fluorescence microscopy. Slow-scan CCD cameras are in use, as are laser sources. The image intensifier is commercially available, and is easily gain-modulated with low voltages. Phase angle or lifetime image files are easily rewritten in the format of the image-processing software packages, so that these powerful image-manipulation programs remain available after collection and processing of the lifetime images.
And finally, fluorescence lifetime imaging provides a new opportunity for the use of fluorescence in cell biology. This is because the lifetimes of probes can be sensitive to a variety of factors or chemicals, many of which are of interest for studies of intracellular chemistry and physiology. An advantage of FLIM is the insensitivity of lifetime measurements to local probe concentration and photobleaching. At present the selection of fluorophores for FLIM is not straightforward, because most sensing measurements do not rely on lifetimes and these probe characteristics are often unknown. However, one can expect this situation to change rapidly as the available sensors are tested. It should be noted that it may be easier to obtain lifetime probes for pH, Na+, Na+, K+, Ca2+, etc., rather than probes that displays spectral shifts in response to calcium (30) such as the widely used Fura-2. This removal of the dual-wavelength restriction may result in the rapid introduction of many FLIM probes. Furthermore, elimination of the requirement that a sensor display a spectral shift may result in the availability of probes that can be excited at longer wavelengths, where the laser light sources are less expensive and autofluorescence, photobleaching, and photodamage are minimal. Since the fluorescence lifetime is an absolute rather than a relative quantity, calibration may be less problematic.
It should also be noted that the FLIM measurements avoid a difficult problem in quantitative microscopy. Ratiometric imaging requires the overlap of the images observed at two emission wavelengths. These images may be different due to incomplete color correction of the optical elements. Since the FLIM measurement provides the equivalent information at a single wavelength, image registration is no longer a problem. Second, dynamic information may be obtained directly from the time-dependent intensity decays. For instance, excimer formation in membranes has been used to estimate microviscosity using wavelength–ratio methods (65,66). The use of FLIM would allow the rate of excimer fluorescence to be measured at a single wavelength using the monomer decay kinetics. Furthermore, the use of time-dependent donor decays would allow imaging based on energy transfer, i.e., proximity imaging, without the need to measure both the donor and the acceptor. That is, the donor decay times will be characteristic of the presence of a nearby acceptor, independent of the local concentration of the donor.
In conclusion, FLIM offers new opportunities for chemical imaging of cellular systems. Of course, much additional work is needed to realize this potential.
ACKNOWLEDGMENTS
The authors acknowledge support from grants from the National Science Foundation (DIR-8710401 and DMB-8804931, Center for Fluorescence Spectroscopy and Institutional grants) and support from the Medical Biotechnology Center and Graduate School at the University of Maryland, without whom these experiments could not have been accomplished.
Abbreviations used:
- Ac
acrylamide
- CCD
charge coupled device
- DMSS
4-dimethylamino-ω-methylsulfonyl-trans-styrene
- FD
frequency domain
- FLIM
fluorescence lifetime imaging
- 9-CA
9-cyanoanthracene
- POPOP
p-bis[2-(5-phenyloxazazolyl)] benzene
- Yt-base
4,9-dihyro-4,6-dimethyl-9-oxo-1H-imidazo-1,2a-purine
- MRI
magnetic resonance imaging
- MCP
microchannel plate
- FT
Fourier transform
APPENDIX 1
Calculation of Phase Angle and Amplitude Images
The task is to use a set of images taken at different detector phase angles and generate three images. The first of these desired images is of the phase of the fluorescence (θ(r) in Eq. [1]). The second is an image of the modulated amplitude of the fluorescence at the particular detector modulation frequency (i.e., the ac component or m(r) in Eq. [1]). The third is an image of the steady-state or dc component of the fluorescence.
For an ideal set of data this task would simply require a numerical Fourier transform for each of 262,144 pixels in the images. However, the statistically valid use of a numerical Fourier transform requires an odd number (>2) of images at detector-modulation phase angles equally spaced within each period of the primary modulation frequency. For the numerical integration of the Fourier transform to have a reasonable precision the number of data images must be significantly larger than 3. The method of inducing the detector phase shifts using electronic delay cables precludes easily satisfying these requirements. Because of these requirements we did not use a classical numerical Fourier transform.
We transformed the data images into the desired images by performing a least-squares fit for each of the 262,144 pixels in the images. These fits could be performed with a fitting function of the form of Eq. [1]. However, use of Eq. [1] requires a significant amount of computer time since it is a nonlinear equation in the fitting parameters m(r) and θ(r). Estimating nonlinear parameters by least squares requires an iterative solution of a system of simultaneous equations. These simultaneous equations must be reevaluated from the data images for each step of the iterative process. Thus, the use of Eq. [1] will require a large amount of computer time and memory. We therefore used an alternative form of Eq. [1], i.e.,
| (A1) |
The advantage of Eq. [A1] is that it is a linear equation, and thus the parameter estimation process requires only a single iteration. This means that each phase-sensitive image can be processed completely before the next image is considered. Thus, the use of Eq. [Al] means that the analysis program needs to process each pixel only once.
Once the values of a0(r), a1(r), and b1(r) are determined for a particular pixel then the corresponding values of the fluorescence phase (θA(r)) and modulated amplitude (mA(r)) are determined by the equations
| (A2) |
| (A3) |
These arbitrary (A) phase angles and modulations are transformed to absolute values by use of the known phase and/or modulation of one of the cuvettes in the image, as discussed in the text. The process of evaluating a0(r), a1(r), and b1(r) for each pixel simply involves the solution of a standard matrix equation Ax = B (Eqs. [A4] - [A6]) for x by Cramer’s rule. In this matrix equation, A is a Hessian matrix:
| (A4) |
| (A5) |
| (A6) |
The subscript i in Eqs. A4, A5, and A6 refers to one of the N data images at a particular detector phase shift. We find that a reasonable number of images is about 10, so that the determined parameters are almost orthogonal. Ten is also enough to smooth out the consequences of the experimental uncertainties that are contained in the data images.
Matrix A is not dependent on the individual pixel values within the data images, only on the detector phase used to obtain the individual data images. Only vector B needs to be reevaluated for each pixel to evaluate a0(r), a1(r), and b1(r) at each pixel. Consequently, we actually process each of the pixels of a data image in parallel by transforming the data into three, as yet unmentioned, images that correspond to the individual elements of the B vector. These three images are then transformed into images that correspond to a0(r), a1(r), and b1(r) by Cramer’s rule. These latter three images are then transformed into images of the fluorescence phase (with Eq. [A2]) and amplitude (with Eq. [A3]). The phase image is subsequently transformed into a lifetime image by Eq. [2], and a modulation lifetime image is obtained using Eq. [3].
The method that we have outlined is algebraically identical to a numerical Fourier transform if we have a large and odd number of data images equally spaced in time (or phase) within each period. If these requirements are met the method that we have outlined provides the phase and amplitude images with the highest probability of being correct based on the data. If these requirements are not met the numerical Fourier transform will not necessarily provide the images with the highest probability of being correct.
The method that we have outlined retains most of the orthogonal properties of Fourier transforms. The off-diagonal elements of the A matrix will approach zero as the number of data images increases. The off-diagonal elements of the A matrix are exactly zero when the requirements for a classical Fourier transform are satisfied. When these off-diagonal elements are zero the determined parameters are orthogonal by definition. A consequence of this near orthogonality is that the parameters can, to a first approximation, be determined independently. This means that we can correctly determine the properties of the primary Fourier component by this method without needing to consider, or evaluate the higher order Fourier components that might be present in the data.
In more recent experiments and computations we have found it desirable to eliminate low-intensity pixels from the computation, which removes some artifactual structure in the FLIM images. Nonetheless, the procedure outlined in Eqs. [A1]-[A6] is still advantageous by avoidance of nonlinear least-squares computations. Furthermore, if one image (or pixel) is removed, the classical Fourier transform method will not work.
APPENDIX 2
Phase-Suppression Imaging
Suppose two phase-sensitive images are collected with detector phase angles of θD and θD + Δ. According to Eq. [1] the phase-sensitive intensities are given by
| (A7) |
| (A8) |
The difference (I2 – I1) phase-sensitive image is given by
| (A9) |
Using cos(α – β) = cos α cos β + sin α sin β, one obtains
| (A10) |
The intensity in the difference image is zero when
| (A11) |
In this expression we have defined θs to be the phase angle at which ΔI = 0. Rearrangement yields
| (A12) |
Using 1 – cos α = 2 sin2(α/2) and sin(α) = 2 sin(α/2) cos (α/2) yields
| (A13) |
| (A14) |
The suppressed lifetime is given by
| (A15) |
REFERENCES
- 1.Dewey TG (Ed.). (1991) Biophysical and Biochemical Aspects of Fluorescence Spectroscopy, Plenum Press, New York. [Google Scholar]
- 2.Jameson DM, and Reinhart G (1989) Fluorescent Biomolecules, Plenum Press, New York. [Google Scholar]
- 3.Lakowicz JR (1983) Principles of Fluorescence Spectroscopy, Plenum Press, New York. [Google Scholar]
- 4.Lakowicz JR (Ed.). (1990) Time-Resolved Laser Spectroscopy in Biochemistry, II, SPIE Press, Billingham, WA. [Google Scholar]
- 5.Demchenko AP (1986) Ultraviolet Spectroscopy of Proteins, Springer-Verlag, Berlin. [Google Scholar]
- 6.Wang Y, and Taylor DL (Eds.). (1989) Fluorescence Microscopy of Living Cells in Culture. Part A. Fluorescent Analogs, Labeling Cells, and Basic Microscopy, Academic Press, New York. [PubMed] [Google Scholar]
- 7.Taylor DL, and Wang Y (Eds.). (1989) Fluorescence Microscopy of Living Cells in Culture. Part B. Quantitative Analogs, Microscopy—Imaging and Spectroscopy, Academic Press, New York. [Google Scholar]
- 8.Inoué S (1986) Video Microscopy, Plenum Press, New York. [Google Scholar]
- 9.Gratton E, Feddersen B,, and vandeVen M (1990) Proc. SPIE 1204, 21–25. [Google Scholar]
- 10.Hiraoka Y, Sedat JW, and Agard DA (1987) Science 23, 36–41. [DOI] [PubMed] [Google Scholar]
- 11.Keating SM, and Wensel TG (1990) Proc. SPIE 1204, 42–48. [Google Scholar]
- 12.Arndt-Jovin DJ, Latt SA, Striker G, and Jovin TM (1979) J. Histochem. Cytochem 27(1), 87–95. [DOI] [PubMed] [Google Scholar]
- 13.Wang SF, Kitajima S, Uchida T, Coleman DM, and Minami S (1990) Appl. Spectrosc 44(1), 25–30. [Google Scholar]
- 14.Wang XF, Uchida T, and Minami S (1989) Appl. Spectrosc 43(5), 840–845. [Google Scholar]
- 15.Kautsky H (1930) Trans. Faraday Soc 35, 216–219. [Google Scholar]
- 16.Lakowicz JR, Joshi NB, Johnson ML, Szmacinski H, and Gryczynski I (1987) J. Biol. Chem 262, 10,907–10,910. [PubMed] [Google Scholar]
- 17.Lakowicz JR, and Weber G (1973) Biochemistry 12, 4161–4170. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Laws JR, and Brand L (1979) J. Phys. Chem 83, 795–802. [Google Scholar]
- 19.Gafni A, and Brand L (1978) Chem. Phys. Lett 58, 346–350. [Google Scholar]
- 20.Jameson DM, and Weber G (1981) J. Phys. Chem 85, 95. [Google Scholar]
- 21.Miyoshi N, Hara K, Shiro K, Nakanishi K, and Fukuda M (1991) Photochem. Photobiol 53, 415–418. [DOI] [PubMed] [Google Scholar]
- 22.Förster Th. (1948) Ann. Phys. (Leipzig) 2, 55–75. [Google Scholar]
- 23.Stryer L (1978) Annu. Rev. Biochem 47, 819–846. [DOI] [PubMed] [Google Scholar]
- 24.Steinberg IZ (1971) Ann. Rev. Biochem 40, 83–114. [DOI] [PubMed] [Google Scholar]
- 25.Eftink MR, and Ghiron C (1981) Anal. Biochem 114, 199–227. [DOI] [PubMed] [Google Scholar]
- 26.Lehrer SS (1971) Biochemistry 10, 3254–3263. [DOI] [PubMed] [Google Scholar]
- 27.Ware WR, Watt D, and Holmes JD (1974) J. Am. Chem. Soc 96, 7853–7860. [Google Scholar]
- 28.Leto TL, Roseman MA, and Holloway PW (1980) Biochemistry 19, 1911–1916. [DOI] [PubMed] [Google Scholar]
- 29.Thulborn KR, and Sawyer WH (1978) Biochim. Biophys. Acta 511, 125–140. [DOI] [PubMed] [Google Scholar]
- 30.Grynkiewicz G, Poenie M, and Tsien RY (1985) J. Biol. Chem 260(6), 3440–3450. [PubMed] [Google Scholar]
- 31.Tsien RY (1989) Methods Cell Biol. 30, 127–155. [DOI] [PubMed] [Google Scholar]
- 32.Tsien RY, and Pozzan T (1989) in Methods in Enzymology (Fleischer S, and Fleischer B, Eds.), Vol. 172, pp. 230–263, Academic Press, San Diego. [DOI] [PubMed] [Google Scholar]
- 33.Tsien RY (1980) Biochemistry 19, 2396–2404. [DOI] [PubMed] [Google Scholar]
- 34.Rogers J, Hesketh TR, Smith GA, Beaven MA, Metcalfe JC, Johnson P, and Garland PB (1983) Fed. Eur. Biochem. Soc 161(1), 21–27. [DOI] [PubMed] [Google Scholar]
- 35.Weisblum B, and de Haseth PL (1971) Proc. Natl. Acad. Sci. USA 69(3), 629–632. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Arndt-Jovin D, Latt SA, Striker G, and Jovin TM (1979) J. Histochem. Cytochem 27(1), 87–95. [DOI] [PubMed] [Google Scholar]
- 37.Steiner RF, and Kubota Y (1983) in Fluorescent Dye–Nucleic Acid Complexes: Excited States of Biopolymers, pp. 203–254, Plenum Press, New York. [Google Scholar]
- 38.Scott TG, Spencer RD, Leonard NJ, and Weber G (1970) J. Am. Chem. Soc 92, 687–695. [Google Scholar]
- 39.Lakowicz JR, and Cherek HC (1981) J. Biochem. Biophys. Methods 5, 19–35. [DOI] [PubMed] [Google Scholar]
- 40.Lakowicz JR, and Cherek HC (1981) J. Biol. Chem 256, 6348–6353. [PubMed] [Google Scholar]
- 41.Veselova TV, Cherkasov AS, and Shirokov VI (1970) Opt. Spectrosc 29, 617–618. [Google Scholar]
- 42.Veselova TV, and Shirokov VI (1972) Akad. Nauk SSSR Bull. Phys. Sci 36(5), 925–928. [Google Scholar]
- 43.Lakowicz JR, and Berndt KW (1991) Rev. Sci. Instrum 67, 1727–1734. [Google Scholar]
- 44.Berndt K, Dürr H, and Palme D (1982) Opt. Commun 42(6), 419–422. [Google Scholar]
- 45.Gratton E, and Delgado RL (1979) Rev. Sci. Instrum 50, 789–790. [DOI] [PubMed] [Google Scholar]
- 46.DeStasio G, Zema N, Antonangeli F, Savoia A, Parasassi T, and Rosato N (1991) Rev. Sci. Instrum 62(6), 1670–1671. [Google Scholar]
- 47.Lakowicz JR, Cherek H, and Balter A (1981) J. Biochem. Biophys. Methods 5, 131–146. [DOI] [PubMed] [Google Scholar]
- 48.Gryczynski I, and Lakowicz JR, (1991) unpublished observation. [Google Scholar]
- 49.Lakowicz JR, and Maliwal BP (1985) Biophys. Chem 21, 61–78. [DOI] [PubMed] [Google Scholar]
- 50.Lakowicz JR, Laczko G, and Gryczynski I (1986) Rev. Sci. Instrum 57, 2499–2506. [Google Scholar]
- 51.Laczko G, Lakowicz JR, Gryczynski I, Gryczynski Z, and Malak H (1990) Rev. Sci. Instrum 61, 2331–2337. [Google Scholar]
- 52.Rigler R, and Wintermeyer W (1983) Ann. Rev. Biophys. Bioeng 12, 475–505. [DOI] [PubMed] [Google Scholar]
- 53.Beardsley K, Tao T, and Cantor CR (1970) Biochemistry 9, 3524–3532. [DOI] [PubMed] [Google Scholar]
- 54.Tao T, Nelson JH, and Cantor CR (1970) Biochemistry 9(18), 3514–3524. [DOI] [PubMed] [Google Scholar]
- 55.Gryczynski I, Johnson ML, and Lakowicz JR (1988) Biophys. Chem 31, 269–274. [DOI] [PubMed] [Google Scholar]
- 56.Mitchell KE, and Menzel ER (1989) SPIE 1054, 191–195. [Google Scholar]
- 57.Tanke HJ, Runia R, van der Geest R, Bonnet J, and Slats J (1988) in Cytometry, Supplement 2, Abstract for the XIIIth International Meeting of the Society for Analytical Cytology, September 4–9, 1988, p. 94. [Google Scholar]
- 58.Rumsey WL, Vanderkooi JM, and Wilson DF (1988) Science 241, 1649–1651. [DOI] [PubMed] [Google Scholar]
- 59.Jovin TM, Marriott G, Clegg RM, and Arndt-Jovin DJ (1989) Ber. Bunsenges. Phys. Chem 93, 387–391. [Google Scholar]
- 60.Peterson JI, and Fitzgerald RV (1980) Rev. Sci. Instrum 51(50), 670–671. [Google Scholar]
- 61.Kavandi J, Callis J, Gouterman M, Khalil G, Wright D, Green E, Burns D, and McLachlan B (1990) Rev. Sci. Instrum 61(11), 3340–3347. [Google Scholar]
- 62.Hamamatsu (1990) Tentative Specification Sheet: The 2-D Measurement and Analysis System of Photoluminescence Intensity and Lifetime, Catalogue ETV-188-01, April. [Google Scholar]
- 63.Morgan CG, Mitchell AC, and Murray JG (1990) Proc. SPIE 1204, 798–807. [Google Scholar]
- 64.Berndt KW, and Lakowicz JR (1990) Rev. Sci. Instrum 61(10), 2557–2565. [Google Scholar]
- 65.Sassaroli M, Vauhkonen D, Perry D, and Eisinger J (1990) Biophys. J 57, 281–290. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Vauhkonen M, Sassaroli M, Somerhaiju P, and Eisinger J (1990) Biophys. J 57, 291–300. [DOI] [PMC free article] [PubMed] [Google Scholar]