Modeling of Contaminant Biodegradation and Compound-Specific Isotope Fractionation in Chemostats at Low Dilution Rates

Abstract

We present a framework to model microbial transformations in chemostats and retentostats under transient or quasi-steady state conditions. The model accounts for transformation-induced isotope fractionation and mass-transfer across the cell membrane. It also verifies that the isotope fractionation ϵ can be evaluated as the difference of substrate-specific isotope ratios between inflow and outflow. We explicitly considered that the dropwise feeding of substrate into the reactor at very low dilution rates leads to transient behavior of concentrations and transformation rates and use this information to validate conditions under which a quasi-steady state treatment is justified. We demonstrate the practicality of the code by modeling a chemostat experiment of atrazine degradation at low dilution/growth rates by the strain Arthrobacter aurescens TC1. Our results shed light on the interplay of processes that control biodegradation and isotope fractionation of contaminants at low (μg/L) concentration levels. With the help of the model, an estimate of the mass-transfer coefficient of atrazine through the cell membrane was achieved (0.0025s^–1).

Introduction

Organic chemicals such as pesticides, pharmaceuticals, or personal-care products are ubiquitously used and have increasingly been detected in surface water and groundwater.^1,2 Even though the concentrations are low (submicrograms-per-liter), levels are still high enough to be of potential concern.³ For instance, atrazine concentrations investigated in this study are, although low (20–50 μg/L), still above threshold values for drinking water worldwide (0.1 μg/L).^4,5 These trace organics have received increased attention as micropollutants.⁶ While many micropollutants are biodegradable at high concentrations, their microbial degradation is observed to decrease at trace levels, down to a threshold at which natural attenuation appears to diminish.⁷ The question whether the reason is physiological adaptation of microorganisms (i.e., down-regulation of catabolic enzymes in response to substrate scarcity⁸), or bioavailability limitation of substrate (i.e., rate-limiting mass transfer into microbial cells when enzyme kinetics is no longer zero-order^9,10) has been a long-standing debate. An answer to this question may offer a new perspective on the behavior of microorganisms at low concentrations.

Until now, it has been difficult to observe the onset of mass-transfer limitations directly. Even though the concept of bioavailability limitations is well-established,¹⁰ so far it is uncertain at which exact concentrations such a mass-transfer restriction comes into play, and how this relates to physiological adaptation. Recently, isotope fractionation has been brought forward as a new opportunity to accomplish precisely such a direct detection of mass transfer limitations.¹¹⁻¹³ Basically, the isotope ratio of a micropollutant changes during a biochemical reaction since molecules with heavy isotopes are transformed at a slightly different rate than those with light isotopes.¹⁴⁻¹⁶ These changes, however, can only be observed if there is a rapid exchange of molecules within the cell interior at the enzyme level (bioavailable) with those outside the cell (bulk) where samples are taken for analysis. The exchange rate between bioavailable and bulk domains is described by a linear model in which the mass-transfer coefficient of the cell membrane is included.^9,10,13 In the presence of mass transfer limitations (i.e., when mass transfer coefficients are small), the slow exchange rate of isotopologues between these domains generates pools of different isotopic ratios across the exchanging interface (i.e., the cell membrane). At the scale of a cell, this means molecules diffuse into or out of the cell at a rate much slower than the rate at which the enzymatic isotope effect occurs. The phenomenon has been usually referred to as masking of isotopic signatures meaning that the measured isotopic fractionation at bulk domain is notably different than the actual, transformation-induced isotopic fractionation occurring at bioavailable domain (i.e., the cell interior).^12,13 As such, carbon and nitrogen isotope signatures provide direct evidence of mass-transfer limitations and have the potential to be used to quantify associated mass-transfer coefficients.

Previous studies examined such mass-transfer effects at relatively high concentration levels where bacteria were cultivated at sufficiently high substrate concentrations and then suddenly exposed to a low substrate concentration.^11,12 The drawback was that cells could not adapt to a specific concentration in batch experiments, obstructing the interpretation of measured concentrations and isotope ratios. Thus, to assess the degree of influence that mass-transfer limitations exert at steady low concentrations, an experimental system is required that continuously maintains the contaminant concentration at a low and environmentally relevant level for a reasonably long time so that cells have enough time to adapt to low-energy conditions. This was beyond the reach of previously conducted batch experiments involving atrazine.¹⁴

A solution is offered by chemostats and retentostats that run at very low dilution rates. Here, substrate is continuously added and residual substrate and cells are continuously washed out from the bioreactor. Such chemostats are operated in a way that the essential growth rate equals the dilution rate so that biomass and residual concentrations remain constant within the reactor. While chemostat experiments have a long tradition in bioengineering,^17,18 few studies have used them to study isotope fractionation.^19,20 To our knowledge all preceding isotope studies in chemostat have measured isotope fractionation by taking the difference between substrate and product. This is particularly true for studies on photosynthesis which were run on nitrate limitation so that although mass transfer of carbon dioxide was addressed, bicarbonate was always present in great excess and was never the limiting substrate.^21,22 In contrast, none has determined isotope fractionation by relating isotope ratios of the same substrate from the feed and the outflow of a reactor. In an experimental study submitted along with this contribution²³ we therefore set out to study degradation of atrazine by the strain Arthrobacter aurescens TC1 in a chemostat at very low dilution rates (and thus low concentration levels) with the aim to pinpoint the onset of mass transfer limitation by compound-specific isotope analysis (CSIA).

Application of CSIA can unravel the underlying dynamics if validated by a chemostat model that is able to account for the mechanisms of mass transfer and transformation-based isotopic fractionation at low dilution rates. Furthermore, the model allows the delineation of the interactions between these processes in a traceable manner and thus provides a platform to critically evaluate the experimental setup, guide the experimental approach, precheck possible pitfalls, and assist in quantification of the results. The first aspect is the usual concern associated with chemostats running at very low dilution rates where a dropwise input may create discontinuities in substrate levels and result in adverse consequences. For instance, too-slow drip feeds may create “feast and famine” conditions for microorganisms preventing adaptation to a certain condition.²⁴ As a consequence, the typical analyses of chemostats, which are based on the assumption of constant inflow conditions,²⁵ do not accurately resolve the change of concentrations and isotopic values in waiting times between two subsequent droplets. To overcome this issue, we present a chemostat/retentostat model that considers the transient behavior under rapid changes of boundary conditions (here addressed by a periodic inlet). The model then enabled us to illustrate the extent of influence that inlet discontinuities may have on the steady-state observations. The second aspect is the new way in which degradation-associated isotope fractionation is evaluated in chemostats. Isotope fractionation has so far been calculated as a function of remaining substrate in batch experiments according to the Rayleigh equation.^26,27 In chemostats, however, the substrate continuously enters and leaves the reactor, and the observed isotope fractionation must thus be derived from the difference between isotopic ratios of the same compound in inlet and outlet. This is again different from previous approaches which also considered the substrate in the inlet, but determined isotope fractionation by comparison to the product in the outlet. Using the model, we were able to confirm the validity of the experimental approach in the companion paper.²³ The third aspect is the inclusion of mass transfer across the cells’ membrane (i.e., between the monitored bulk solution and the cell interior⁹) into the chemostat equations. It is worth noting that due to high stirring speeds in chemostat the effects of incomplete mixing in the bulk phase are negligible so that the transfer through the cell membrane remains as the only physical barrier. The model offers a platform to describe mass transfer through the cell wall and to derive tentative quantitative estimates on mass-transfer coefficients. The fourth and final aspect is related to sensitivity and error propagation analyses of the model in order to understand the relationships between the uncertainty of input parameters and model estimates. Global sensitivity analysis further contributes to our understanding of how the variation in the model estimates can be apportioned to the variation in the input parameters. The model was then applied to the experimental study of atrazine degradation by Arthrobacter aurescens TC1 at low concentrations, detailed in the companion paper.²³

The overall aim of this contribution is to introduce a comprehensive modeling tool in order to quantitatively analyze the interactions between the following processes: (1) mass transfer through the cell membrane, (2) enzymatic transformation, and (3) transformation-induced compound-specific isotope fractionation in chemostats/retentostats with (4) periodic input of substrate.

Materials and Methods

Model Equations

We consider the concentrations of light and heavy isotopologues of a substrate (^lS and ^hS [ML^–3]), and the biomass concentration (X[ML^–3]) as dynamic state variables. Note that the dimensions of all variables are introduced by bracketed variables T, M, and L, respectively, referring to the units of time, mass, and length. The turnover of substrate is described by Monod kinetics²⁸ with competitive inhibition among the isotopologues, and is coupled to the input and output of substrate through the inflow and the outflow of the reactor, respectively. Biomass growth is assumed proportional to the substrate turnover via a yield factor. This leads to the following system of ordinary differential equations:

1a

1b

1c

where r_D[T^–1] is the dilution rate coefficient (flow rate divided by the reactor volume), q_max[T^–1] denotes the maximum specific conversion rate, K_m[ML^–3] is the half-saturation constant, m[T^–1] is the maintenance term, α[−] indicates the isotopic fractionation factor, Y[−] is the yield coefficient, and f[−] denotes the fraction of biomass filtered at the outflow, ranging between zero (biomass leaves the system at the reactor current concentration; chemostat) and one (complete filtration of biomass thus no biomass discharges from the outlet; perfect retentostat). The maximum specific growth rate μ_max[T^–1] is related to q_max by μ_max = Y(q_max – m).^29,30

The chemostat equations accounting for the mass-transfer through the cell membrane are modified such that the concentrations outside the cells (S) differ from the concentrations inside the cells (S_bio). Thus, S and S_bio are referred to as the substrate concentrations in the bulk and bioavailable phases, respectively.^9,31,32 A linear-driving force model with the mass-transfer coefficient k_tr[T^–1] was assumed to control the exchange between these two phases. Including such mass-transfer limitations, eqs 1a to 1c change as follows:

2a

2b

2c

2d

2e

in which the observable isotope fractionation in the bulk phase is affected by the transformations inside the cell and the mass transfer between bulk and bioavailable phases. The initial concentrations for the substrate and biomass are indicated by S_ini[ML^–3] and X_ini[ML^–3]. The isotope ratio of the heavy and the light isotopologues of the substrate is evaluated in the common δ^hS[‰] notation:

3

typically expressed in parts per thousand, where R is the reference isotope ratio of VPDB (Vienna Pee Dee Belemnite). The model is presented in a general form and in principle can be applied to any stable isotope element. In this study, we examined the carbon isotope effects of atrazine and thus ^hS and ^lS are respectively replaced by ¹³S and ¹²S, representing the concentrations of substrate isotopologues containing heavy (¹³C) and light (¹²C) carbon isotopes. As a result, the δ¹³C notation replaces δ^hS and represents the observed isotopic signatures of carbon.

Model Solution

We solved the above systems of ordinary differential equations, ODE, (eqs 1a to 1c and eqs 2a to 2e) with the MATLAB ODE suite (e.g., the ode15s solver).^33,34 To avoid unintended numerical instabilities, the input pulses were smoothed using forth-order analytical expressions.³⁵ For smoothing the pulses, the user can choose the time period over which the pulse is smoothed, which may be interpreted as the mixing time in the system depending on agitation, droplet size, and reactor volume. A higher numerical stability is achieved when the smoothing intervals are larger. However, the smoothing interval should be substantially smaller than the interval between the pulses in order to avoid flattening the periodicity of the incoming droplets. Increasing the smoothing intervals will negate the very purpose of examining the droplet effect, as extreme smoothing would in principle be identical to having a continues feed (averaging the droplet volume over the time period and resulting in a constant feed). The smoothing type can be chosen between the following two polynomial spike functions:

4a

4b

producing either a smoothed pulses with a constant area underneath (in case of eq 4a) or a pulse that is set to reach to a specific peak height (in case of eq 4b). t[T] denotes the time variable which varies between zero and the time until the next droplet, s[T] denotes the length of the smoothing interval. Although both approaches are available in the model, we used the first smoothing function eq 4a as the other expression overestimates the introduction of mass into the system. We also skipped the maintenance term in the chemostat model since its effect on isotope signatures was found to be negligible (discussed in more details in Ehrl et al.²³). According to Pirt,³⁰ μ_max = Yq_max when m is small enough to be treated as zero. The forthcoming sensitivity and uncertainty analyses then considers μ_max as an input parameter instead of q_max. The parameter values are taken from the companion paper of Ehrl et al.²³ for degradation of atrazine by the strain Arthrobacter aurescens TC1 in chemostat, and are listed in Table 1.

Table 1. Model Solution. Model Parameter Values Taken from Ehrl et al.²³.

reactor volume (V)	2000 mL
dilution rate (rD)	0.009 hr–1
average droplet size (Vd)	0.1 mL
average time between droplets (td)	20 s
atrazine concentration at the inlet (Sin)	30 000 μg/L
maximum specific conversion rate (qmax)	6.01 hr–1
half-saturation constant (Km)	237 μg/L
yield factor (Y)	0.018
isotopic fractionation factor (α)	0.9946
initial atrazine concentration in reactor (Sini)	65 μg/L
initial concentration of biomass in reactor (Xini)	550 μg/L
fraction of biomass retained from chemostat outflow (f)	0

Model Accuracy and Stability

The model is validated by comparing the results with the experiment²³ and its accuracy is evaluated through the comparison with the analytical model of Thullner et al.¹³ Although eqs 1 and 2 are written in a general perspective and include essential terms such as maintenance energy, additional processes can still be introduced within the existing potentials of the model. For instance, the model allows introducing degradation mechanisms other than Monod (or Michaelis–Menten) kinetics, for example, at very small concentration levels ([S] ≪ K_m) using a first-order kinetics might describe the system behavior more effectively, or in cases where the concentrations of both reaction partners (electron donor and acceptor) become rate-limiting, a dual Monod kinetics can be introduced. A similar flexibility holds for changing the mechanism controlling the rate of exchange across the cell membrane, which is currently expressed by a linear term and can be substituted by more sophisticated nonlinear expressions.

Use of MATLAB ODE suite as the internal solver increased model stability on handling relatively stiff problems. However, it should be noted that the model can still turn out numerically unstable if the smoothing interval of droplet is not sufficiently large with respect to the time period between droplets. As a rule of thumb, the smoothing interval should be around 15% of the period between droplets, that is, the time between each input cycle.

Results and Discussion

Model Results

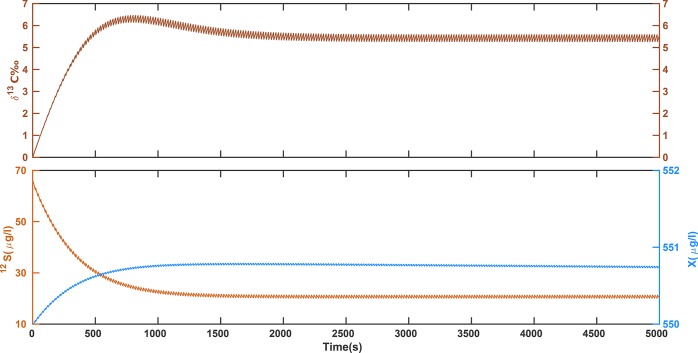
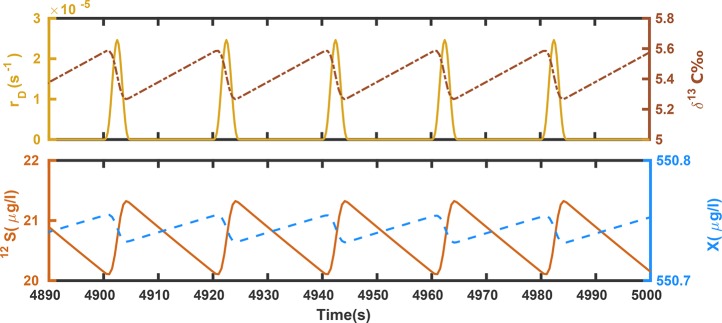
Regarding the first question—the effect of discontinuities—Figures 1 and 2 show that the model is well capable of capturing the transient behavior caused by drip-feeding of substrate (as it is perceived in the chemostats at very low dilution rates). The results confirm that the effects from a discontinuous input on concentrations and isotope compositions are small at the given dilution rate. Figure 2 displays the same data as Figure 1 over a short time period when dynamic steady state has been reached, and magnifies the recurrent fluctuations for better recognition of details. Under dynamic steady-state conditions the periodic input of droplets causes concentrations to fluctuate by 3% at most, which justifies the steady-state treatment adopted in the companion paper.²³

Figure 1.

Solution of eqs 1a to 1c (in the absence of mass-transfer limitations across the cell membrane) for the following set of parameters: S_in = 30 000 μg/L, μ_max = 0.11hr^–1, K_m = 237 μg/L, Y = 0.018, α = 0.9946, S_ini = 65 μg/L, X_ini = 550 μg/L, and r_D = 0.009 hr^–1. For better illustration of the droplet spikes, the dilution rates together with the changes of concentration, biomass, and δ¹³C at steady-state are shown over a short time span (100 s) in Figure 2. Although the concentrations of the substrate isotopologues decrease monotonically, the slight shift of timing between the light and heavy isotopologues cause a nonmonotonic behavior of the isotope ratios. As a result, the values of δ¹³C exceed slightly above the final value between times 500 and 1000 s.

Figure 2.

Solution of eqs 1a to 1c at steady-state. The figure is a close-up snapshot of the last 100 s in Figure 1 at which the system has reached steady-state. Based on size of droplet (0.1 mL), volume of chemostat (2 L), and the dilution rate (r_D = 0.009 hr^–1) the droplet frequency is calculated as one drop per every 20 s. The smoothing interval is assumed 5 s. For this setup, the results at steady-state are averaged as δ¹³C = 5.4 ± 0.2‰, ¹²S = 20.66 ± 0.6 μg/L, X = 550.74 ± 0.01 μg/L.

To address the second aspect, the evaluation of isotope fractionation from the inlet and the outlet of chemostat: the model was provided with the actual, enzymatic, intrinsic isotopic fractionation for degradation of atrazine by strain Arthrobacter aurescens TC1 ϵ¹³C = α–1 = −5.4‰ as input parameter (see Table 1). This value had been determined in batch experiments with bacterial cultures degrading atrazine at high (mg/L) concentrations^14,31 and with pure enzyme in the absence of bacterial cells.¹⁶ In all of these cases, mass-transfer limitations are either absent or insignificant. Therefore, in the absence of a mass-transfer term (solving eqs 1a to 1c), the model should predict that the carbon isotope signatures δ¹³C inside the chemostat differs from that in the inflow by almost the same enrichment factor ϵ¹³C of batch studies (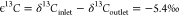). Figure 1 shows the simulated time series of concentrations and δ-values for this case where the concentration inside the cells equals the concentration in the bulk solution (eqs 1a to 1c). As shown, the obtained δ¹³C values at steady-state eventually approach the actual fractionation coefficient reported from the batch experiments (δ¹³C = 5.4‰),^14,16 validating the method of calculating the evaluation of ϵ¹³C between the inlet and the outlet of chemostat experiments. ϵ¹³C has been traditionally determined as the difference between isotope values of an infinitely large reservoir of bicarbonate in the chemostat and the biomass formed.^21,22 The approach clearly does not work for our experiments for the following reasons. In previous studies, bicarbonate was present in excess and nitrate was the limiting source for growth whereas in our experiments the carbon-containing substrate (atrazine) is the limiting source and required to be depleted in order to mimic the environmentally related conditions. Hence, the only way to determine epsilon is to measure it as the difference between atrazine in inflow and outflow (as theoretically derived by Hayes³⁶). In addition, the flow-through rate in a chemostat must be reasonably slower than the rate of degradation in order to be able to identify and measure the substrate decay, and to prevent overwriting the enzymatic isotope fractionation by isotope ratios of the inflow. Solving eqs 1a and 1b at steady-state and assuming that 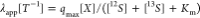is the apparent first-order decay coefficient, the following equation can be derived:

5

which is analogous to eq (8) in Farquhar et al.³⁷ (see also the derivation in “Materials and Methods” of Ehrl et al.²³). Thus, the difference between inflow and outflow would be expected to approach ϵ¹³C under realistic, sufficiently small dilution rates as it is also confirmed by the model.

Regarding the third aspect—in order to assess how observable isotope fractionation is influenced by mass-transfer limitations—we applied the model to the experimental data obtained in chemostat experiments of our companion paper.²³ At high dilution rates (>0.018 hr^–1) and at high bulk concentrations (>100 μg/L), the measured difference between isotopic ratios in the inlet and the outlet perfectly matched the isotope fractionation from batch experiments, similar to our model predictions in the absence of the mass transfer limiting term (see above). In contrast, Ehrl et al.²³ observed lower isotope fractionation with decreasing chemostat dilution rates. At a dilution rate of 0.009 hr^–1 an isotopic fractionation of ϵ¹³C = −2.2‰ was measured which was noticeably smaller in magnitude than the previously reported values for this reaction. This revealed the importance of mass transfer through the cell membrane under low-energy conditions. To reproduce a dilution rate of 0.009hr^–1 in our model, a periodic input of every 20 s was assumed with droplets of approximately 0.1 mL into a chemostat with 2 L volume. Figure 3 shows the concentration and isotope time-series for this case (solution of eqs 2a to 2e). By solving eqs 2a to 2e, in which mass-transfer mechanisms are taken into account, the model was able to reproduce smaller δ¹³C values in the outlet (and, hence, smaller apparent isotope fractionation ϵ¹³C) when the exchange rate through the cell membrane was slowed by assigning low values of the mass-transfer coefficient k_tr. In order to determine the value of k_tr in the experiment, we used a trial and error fitting procedure. In this procedure, the value of k_tr is constrained such that the late-time δ¹³C-values (at steady-state) equal the value observed in the experiment. At the dilution rate of 0.009 hr^–1 using k_tr value of 0.0025 s^–1, we achieved an apparent isotopic enrichment value of ϵ¹³C = −2.2‰ which corresponds well to the reported value in Ehrl et al.²³Figure 3 shows the concentration and isotope time-series for this case (solution of eqs 2a to 2e). Here, the simulated concentrations inside the cell S_bio were found to be only about 40% of the concentrations S outside the cell. Boosting the exchange rate between bulk and bioavailable domains through gradually increasing the value of the mass-transfer coefficient k_tr in the model increased the late-time δ¹³C-values and eventually reached the value of the actual, transformation-induced, intrinsic isotopic fractionation coefficient ϵ¹³C = −5.4‰ (identical to the late-time δ¹³C-value in Figure 1).

Figure 3.

Solution of eqs 2a to 2e (in the presence of mass-transfer limitations across the cell membrane) for the set of parameter values in Figure 1 and k_tr = 0.0025s^–1. Note that due to mass-transfer limitations the observed δ¹³C = 2.2‰ at steady-state notably reduced from 5.4% in Figure 1. It is worth mentioning that inside cells (i.e., at the bioavailable domain) the δ¹³C is equal to the expected value of 5.4‰ (data not shown).

The evaluation of the forth aspect—sensitivity of model estimates to the input parameters (Table 1)—is detailed as follows.

Sensitivity and Uncertainty Analyses

Uncertainty Propagation Analyses

A Monte Carlo simulation was used to propagate the uncertainty originating from experimental and analytical variability of the parameters k_tr, K_m, μ_max, and S_in onto concentrations and isotopic signatures. In order to reduce the total runtime of the Monte Carlo simulations, we reduced the walltime needed for simulating a single scenario to 7.5 s on a quad-cores Intel Core i5–4590 CPU at 3.30 GHz with 16GB RAM by optimizing the code and performing parallel computations.

Eqs 2a to 2e were solved for 50 000 randomly generated sets of parameters, which took about 105 h walltime. In each realization, the parameters of eqs 2a to 2e were perturbed at random, scaled to the experimentally obtained standard error. Mean values and standard deviations were calculated from repeated replicates (237 ± 57 μg/L for K_m, 0.11 ± 0.02 hr^–1 for μ_max, and 30 000 ± 600 μg/L for S_in). In case of k_tr, since the value is not experimentally determined, a relative standard error of 20% was presumed (0.0025 ± 0.0005s^–1). All parameters were drawn from normal distributions and no correlation was assumed between the input parameters.

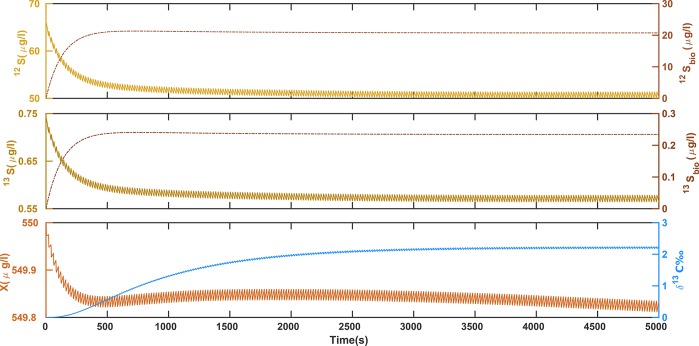
The Monte Carlo simulations showed probability distributions of the model outputs (δ¹³C, ¹²S, ¹³S, ¹²S_bio, ¹³S_bio, and X) as the result of the input parameter variabilities. Figure 4 shows the 16–84% probability range of model outcomes which corresponds to ±1 standard deviation of a normal distribution. Table 2 lists the average and standard deviation of all model predictions at late time. There is a small offset between the mean output of the ensemble calculation and a single run using the mean input parameter values which can be attributed to the nonlinear dependence of model outputs on the parameters. Figure 4 shows that the parameter uncertainty translates into a large uncertainty of model predictions, with coefficients of variation (also known as relative standard deviations) between 20% and 33% for solute concentrations and δ-values. Among all model predictions, biomass (X) was clearly the least affected by uncertainties.

Figure 4.

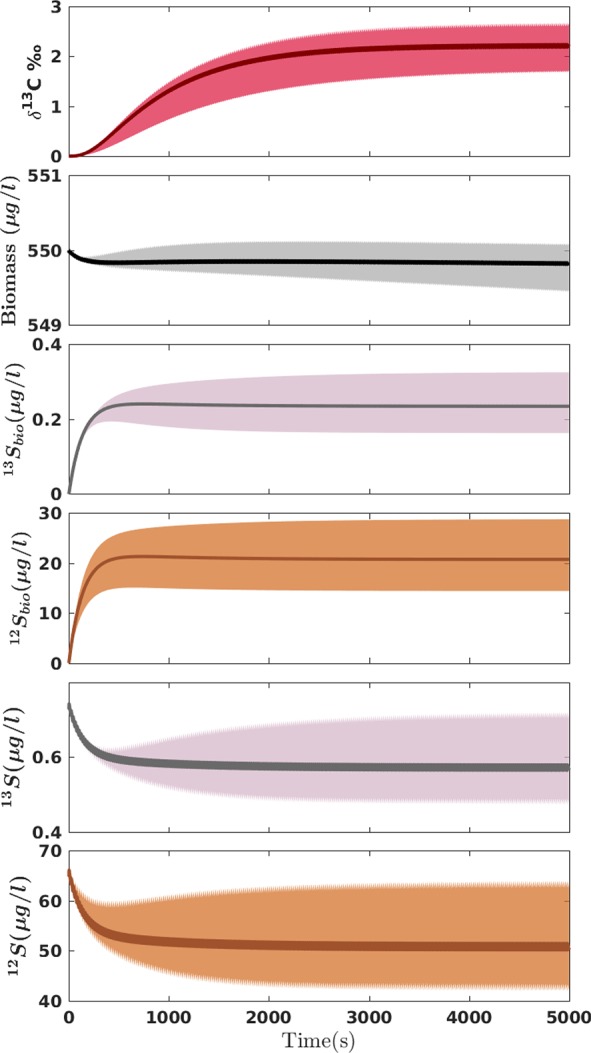
Uncertainty analysis using a Monte Carlo simulation. The 68% confidence intervals are shown for all the output parameters, from top to bottom, isotopic signature, biomass concentration, bioavailable, and bulk substrate concentrations (for both heavy and light isotopologues respectively). Note that the perturbations resulting from the periodic inlet are more visible at the profiles for bulk concentrations and δ¹³C-values.

Table 2. Uncertainty Analysis^a.

	δ13C‰	12S (μg/L)	13S (μg/L)	12Sbio (μg/L)	13Sbio (μg/L)	X (μg/L)
model run with mean input parameters	2.21	50.72	0.57	20.75	0.23	549.82
Monte Carlo simulations	2.17 ± 0.47	52.89 ± 10.25	0.59 ± 0.12	21.60 ± 7.18	0.24 ± 0.08	549.77 ± 0.31

^aThe estimated average and standard error of output parameters calculated from Monte Carlo analyses of 50 000 randomly generated sample scenarios based on the error variability of input parameters (K_m = 237 ± 57 μg/L, μ_max = 0.11 ± 0.02hr^–1, S_in = 30 000 ± 600 μg/L, and k_tr = 0.0025 ± 0.0005s^–1).

The 95% confidence interval of δ¹³C ≈ 2.17 ± 0.92‰ does not cover the value of δ¹³C = 5.4‰ expected from the isotope fractionation of the reaction.^14,16 This clearly illustrates the ability of the model to pinpoint the limitations of mass transfer across the cell membrane as the origin of masked isotope fractionation in chemostats at low dilution rates. As a result, the observed isotopic signatures (δ¹³C) are noticeably smaller than the expected transformation-induced isotopic signatures. Sources of uncertainty exist that are not addressed by the Monte Carlo simulations, for example, the error in measuring the dilution rate or the uncertainties associated with the size of droplets. The error propagation of these factors is assumed to be insignificant and is partly lumped into the uncertainty of the inlet concentration (S_in).

Local Sensitivity Analysis

A tornado diagram is used here to depict the local sensitivity of the simulated δ¹³C-value at steady state with respect to the changes in the input parameters: k_tr, K_m, μ_max, S_in, and the time between droplets 1/r_D. To compare the relative importance of the above input parameters, we varied the value of one input parameter at a time by 20% while keeping all the other input parameters at their base values. As expected, the results (depicted in Figure 5) show a strong sensitivity toward the mass-transfer coefficient k_tr in the chemostat model accounting for mass-transfer limitations eqs 2a to 2e. The modeled isotope signatures show a similar but weaker sensitivity to S_in and K_m whereas variations of μ_max and 1/r_D inversely influence the values of δ¹³C noting the absolute sensitivity to μ_max is on par with that to k_tr. The results clearly indicate that the impact of physiological parameters (K_m and μ_max) are as significant as that of the physically motivated parameter (k_tr).

Figure 5.

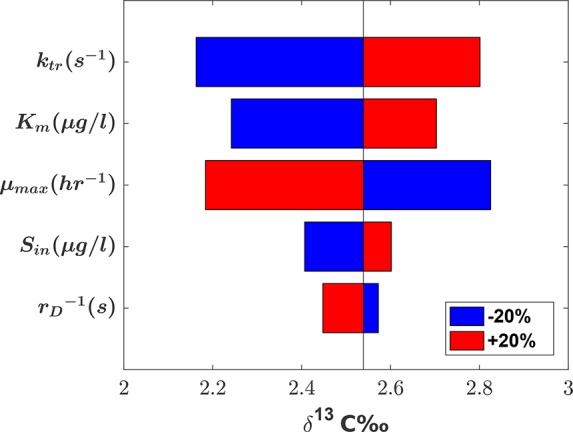
Local sensitivity analysis. Tornado plot showing the sensitivity of the observed δ¹³C values to the input variables k_tr, K_m, μ_max, S_in, and the inlet periodic time (1/r_D) when mass-transfer limitations across the cell membrane are present eqs 2a to 2e.

A similar sensitivity analysis was performed with the model neglecting mass-transfer limitations, eqs 1a to 1c. Unlike the previous model, the simulated late-time δ¹³C-values showed no sensitivity to the changes of the input parameters K_m, μ_max, S_in and 1/r_D (data not shown). This implies that in the presence of mass transfer limitations, the sensitivity of the observed δ¹³C-values even to other input parameters (e.g., K_m and μ_max) is affected by the magnitude of the mass-transfer coefficient k_tr.

Global Sensitivity Analysis

We used the variance-based analysis of Sobol³⁸ for global sensitivity analysis (GSA). The benefit of a global over a local sensitivity analysis is that it accounts for the entire range of all parameter values rather than focusing on one parameter value at a time. As such, GSA offers a more robust solution in elucidating the impact of an individual parameter considering that all other parameters are also uncertain. To this end, a quasi Monte Carlo method (here, a Latin hypercube sequencing sampler) was employed to generate 60 000 sample scenarios that uniformly covered the space of input parameters. The first-order index (FO_i) and the total-order index (TO_i) were then calculated similar to Pianosi et al.³⁹ and Sobol and Levitan.⁴⁰ FO_i indicates the effect of an individual parameter variation alone on an output variable, whereas TO_i includes also the effects caused by the interactions of that parameter with all other parameters.

The pie charts in Figure 6 demonstrate the sensitivity of output variables: δ¹³C-values, biomass (X), bioavailable (S_bio) and bulk concentrations (S) to the input parameters S_in, μ_max, K_m, and k_tr. The GSA confirms the relatively equal sensitivity of the δ¹³C-values to K_m, μ_max and k_tr as previously estimated from the local sensitivity analysis (Figure 5). Bulk concentration showed a relatively high sensitivity of about 50% to the k_tr values which is in the range of the combined sensitivity to all other input parameters. Among the model predictions, bulk concentrations are affected the most by mass transfer followed by δ¹³C-values at the second place. To our surprise, the bioavailable concentrations showed no sensitivity to mass-transfer effects. The variation of K_m showed a predominant effect on the variation of all predicted quantities except biomass. In fact, biomass showed no sensitivity to variation of any input parameter. This might be due to the reason that in all scenarios the biomass concentration hardly changed with time (see Figure 4).

Figure 6.

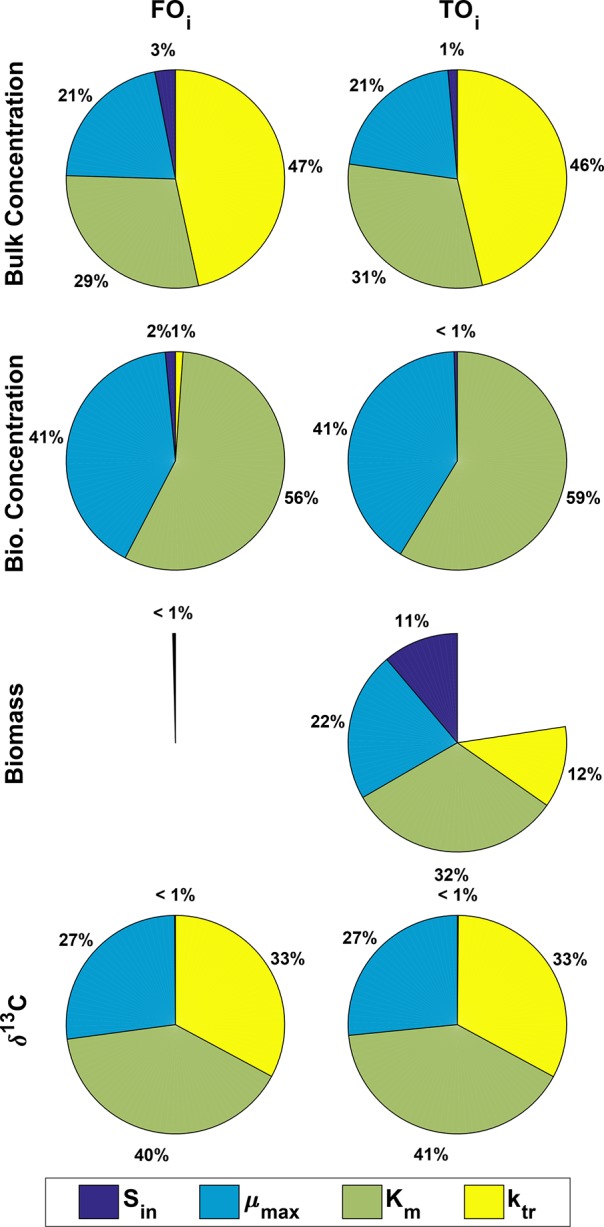
Global sensitivity analysis. The pie charts show the contributions of variability in the parameters k_tr, K_m, μ_max, and S_in to the steady-state δ¹³C-values, X, S_bio, and S (Table 3) for the case where mass transfer is limited across the cell membrane eqs 2a to 2e.

The TO_i pie charts provide a measure on the importance of interactions (of any order) between the input parameters. As shown in Table 3, the total order indices TO_i and the first-order indices FO_i were almost identical, indicating that the interactions between parameters did not impose any significant effect on variability of the model predictions except for biomass (X). We extended our GSA for another 60 000 sample scenarios to the total amount of 120 000 scenarios to check the consistency of the results and to see whether the sensitivity indices can be improved. Similar indices as those listed in Table 3 were calculated for all model outputs except for the biomass (data not shown). The inconsistency between biomass indices (obtained from 60 000 and 120 000 sample scenarios) indicates that the calculated sensitivity indices for biomass are possibly incorrect. This might have been caused by numerical errors originating mainly from the negligible change of biomass with time.

Table 3. Global Sensitivity Analysis^a.

	FOi				TOi
	δ13C	X	Sbio	S	δ13C	X	Sbio	S
Sin	0.0014	0	0.0152	0.0377	0	0.01119	0.0049	0.0165
μmax	0.2706	0	0.4153	0.2663	0.2658	0.2217	0.4108	0.2559
Km	0.4010	0	0.5737	0.3584	0.4052	0.3194	0.5914	0.3690
ktr	0.3294	0	0.0114	0.5780	0.3276	0.1208	0	0.5531

^aThe first-order index (FO_i) and the total-order index (TO_i) of the output parameters (δ¹³C-values, X, S_bio, and S) in respect to the input parameters (S_in, μ_max, K_m, and k_tr). The higher the value, the more impact the input variability exerts on the variance of the output parameter. Note that both heavy and light isotopologues showed a similar sensitivity trend in bulk and bioavailable domains.

Temporal Dynamics of Biomass Growth

The model accounts for the temporal dynamics of biomass growth and washout in the chemostat system eqs 1c and 2e. We assumed standard Monod kinetics²⁸ in which biomass growth is proportional to the turnover rate. Growth depends only on the concentration of a single substrate, indicating that all other compounds required for growth are available in excess. The only removal term is described by washout via outflow. This is a reasonable assumption for a chemostat system, in which the loss due to washout is considerably greater than the biomass death rate. Maintenance terms are also not considered since the energy demand for maintenance is constant under quasi steady-state conditions. Hence, the maintenance effect is conveniently assumed to be subsumed in the yield factor (for an explicit treatment of maintenance energy see the Supporting Information of Ehrl et al.²³). Furthermore, we did not consider a prescribed carrying capacity, or maximum biomass concentration, since the simulated biomass concentration remained fairly low as a result of limited supply of substrate and continuous washout of cells. Such an assumption is not valid for a model of a perfect retentostat where washout of biomass is prohibited and as a result biomass growth must be balanced by the maintenance energy requirement, biomass decay, or reaching the maximum carrying capacity.

In Figure 3, the biomass decreases at late times while substrate concentrations reach steady state. This can be explained by the initial biomass concentration being higher than the steady-state biomass which is controlled by the balance between bacterial growth and dilution rate. Here, a high initial biomass concentration mimics the conditions of an inoculum at high concentration levels.

Comparison with the Analytical Model of Thullner et al. (2008)

We compared our model to the analytical model of Thullner et al.¹³ which estimates the observed isotopic fractionation factor α under steady-state conditions in relation to the intrinsic isotropic fractionation of the enzymatic reaction α°,

6

where T = (a/k_tr – S/K_m – 1) is a dimensionless term and a = μ_max/K_m is the specific affinity of the microorganism promoting the enzymatic reaction. For an arbitrary case of k_tr = 0.002s^–1, K_m = 50 μg/L, μ_max = 0.027 hr^–1, Y = 0.036, S_ini = 65 μg/L, X_ini = 1000 μg/L, α° = 0.994 and r_D = 2.5× 10^–6s^–1, the observed δ¹³C at steady-state was calculated by our model to about 2.64‰. Using eq 5, the apparent fractionation factor α was calculated as 0.99738 which yields the observed δ¹³C = 2.62‰. This means that the two models estimated similar observed vs expected isotopic signatures. It is worth noting that unlike the analytical model,¹³ the presented numerical model can determine the observed isotopic signatures also under transient conditions.

Implications for Natural Systems

The model validated the approach of isotope fractionation measurements between the outflow and the inflow of a chemostat where a steady, low, and environmentally related concentration of a micropollutant is maintained for a time long enough to allow the adaptation of bacterial cultures. The model elucidates the role of mass-transfer limitations across the cell membrane in regulating the observed vs expected compound-specific isotopic signatures in chemostats. In addition, our results confirm that slow mass transfer across the cell membrane can mask the true isotope fractionation of a chemical transformation. So far the differences between observed isotopic signatures from laboratory and field were attributed to other factors, such as leakage from other contaminant sources or hydrologically driven mechanisms (e.g., by transverse dispersion at plume fringes⁴¹). As shown here, such differences in isotope fractionation can also stem from bioavailability limitations and may even originate from mass-transfer limitations across the cell membrane. The effect from bioavailability limitations is much more pronounced at low concentrations, and therefore is of high relevance for many micropollutants of which concentrations typically do not exceed micrograms-per-liter. Recognition and understanding of the interplay of bioavailability limitations with other existing processes thus enhance the overall interpretation of isotope signatures under field conditions.

Under the influence of other processes the isotopic signatures show no dependency on enzymatic reaction rates. Thus, one way to identify the masking of isotope signatures as the result of mass-transfer through a cell membrane is to focus on the fact that isotopic signatures are highly sensitive to enzymatic transformation rates in the presence of mass-transfer limitations (see the sensitivity of δ¹³C to μ_max in the presence of k_tr). Therefore, two strains with different metabolic activities when feeding on a single substrate must exhibit different isotopic signatures under mass-transfer limitations, assuming both have an identical isotopic fractionation factor and similar cell membrane characteristics.

Potential Model Applications

The presented model improves the mechanistic understanding of contaminant degradation in microbial ecosystems. While the model in its current form is only applied to fully mixed reactors, it can be easily coupled to solute transport equations⁴²⁻⁴⁴ contributing to the development of models that more realistically describe fixed-bed reactors and natural subsurface systems.

A practical aspect of our model is its capacity to calculate the membrane permeability of a specific cell in conjugation with chemostat/batch experiments. The differences between the observed isotopic signatures (δ¹³C) in batch and chemostat experiments are linked to mass-transfer limitations through the cell membrane which is widely referred to as membrane permeability. The formulation on how to obtain the value of membrane permeability P_app[LT^–1] and the diffusion coefficient through the membrane D_mem[L²T^–1] from the mass-transfer limiting coefficient k_tr[T^–1] is presented and discussed by Ehrl et al.²³ According to the model results, atrazine permeation through the cell wall of Arthrobacter aurescens TC1 was approximated as P_app = 3.5 × 10^–5ms^–1 and D_mem = 1.9 × 10^–16m²s^–1, which are close to the values reported for a typical range of small organic molecules.⁴⁵⁻⁴⁷ While different techniques are used in pharmaceutical studies to determine the membrane permeability, the present model provides an alternative way of estimating it.

Sensitivity analysis of the model enables users to inspect the influence of different physical and physiological parameters on the observable isotopic signature before performing the experiments. The results provide clarity into the specific features influencing isotopic signatures in chemo- and retentostats. The modeling framework used in this study allows for a delineation of features such as (i) biodegradation dynamics of a contaminant, (ii) metabolic activity of the microbial degrader, (iii) the role of bioavailability limitations and typical mass-transfer restrictions through a cell’s membrane, and (iv) whether the interplay between these mechanisms is responsible for observing uncommon isotopic signatures at low concentration levels. As shown above, these results have relevant implications for both theory building and practical application.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.est.8b02498.

• MATLAB source codes for solving eqs 1a to (1c); solving eqs 2a to 2e; smoothing the inlet pulses eqs 4a and 4b (PDF)

The authors declare no competing financial interest.