Neurologically Motivated Coupling Functions in Models of Motor Coordination

Abstract

We present an analysis of two Haken–Kelso–Bunz (HKB) oscillators coupled by a neurologically motivated function. We study the effect of time delay and weighted self-feedback and mutual feedback on the synchronization behavior of the model. We focus on identifying parameter regimes supporting experimentally observed decrease in oscillation amplitude and loss of anti-phase stability that has inspired the development of the HKB model. We show that a combination of cross-talk and nonlinearity in the coupling, along with physiologically relevant time delay, is able to quantitatively account for both drop in oscillation amplitude and loss of anti-phase stability in a frequency dependent manner. Furthermore, we demonstrate that the transition between discrete and rhythmic movements could be captured by this model. To this end, we carry out theoretical and numerical analysis of the emergence of in-phase and anti-phase oscillations.

1. Introduction

Intrapersonal and interpersonal motor coordination are active research topics in variety of fields including robotics and human-machine interaction [12, 35], cognitive psychology [47], and neuroscience [55]. Motor coordination has also been studied from a dynamical systems point of view for over 30 years since the seminal paper [23] introducing the Haken–Kelso–Bunz (HKB) model, which comprises a system of nonlinearly coupled hybrid Van der Pol–Rayleigh oscillators. This model qualitatively captures experimental results demonstrating a transition between in-phase and anti-phase dynamics as a result of increase in pacing of driving frequency [22, 30]. Furthermore, the hybrid Van der Pol–Rayleigh oscillator quantitatively accounts for the linear dependence between frequency and amplitude of movement [27, 29]. At present, the HKB model is a basis of various experimental paradigms such as human-dynamic clamp [12], the mirror game with a virtual player [61], and Chronos—a computer platform to study movement coordination in human ensembles [1]. Another, more recent, contribution to the field has been made by the introduction of the Jirsa–Kelso excitator model [28] that could be mapped, using a suitable change of variables, to the classical FitzHugh–Nagumo model [13].

The importance of perceptual-motor delays has been acknowledged in the original HKB model paper [23], and their role was later discussed in [36]. However, to date, there have been very few mathematical modeling studies considering time delays in motor coordination. An investigation of the excitator model with time delay has been carried out in [2], and a model of relative phase dynamics with time delay can be found in [53, 54]. Recently, we presented the first systematic analysis of the HKB model with delays. The specific model formulation was motivated by a study that used numerical simulations of the HKB model with delays to interpret changes in coordination patterns in patients with schizophrenia [58]. In [50] we demonstrated the experimentally relevant role time delays play in shaping the properties of movement coordination dynamics. Specifically, in [50] we showed that introduction of time delays increases the size of parameter regions of bistability between in-phase and anti-phase periodic solutions, thus making the model more robust in terms of reproducing the experimentally observed transition between these two modes of coordination [22, 30]. We also proposed a plausible dynamic mechanism explaining why the anti-phase solutions are experimentally less stable in comparison to the in-phase solutions. In the current paper, we analyze effects of different coupling functions on the coordination dynamics described by the HKB model.

The HKB model [23] consisting of two coupled nonlinear oscillators i and j is given by

$${\ddot{x}}_i\left(t\right)+{\omega }^2{x}_i\left(t\right)-\gamma {\dot{x}}_i\left(t\right)+\alpha x_i^2\left(t\right){\dot{x}}_i\left(t\right)+\beta {\dot{x}}_i^3\left(t\right)=I_{i,j}\left(t,\tau \right),$$ (1.1)

where ${\ddot{x}}_i(t)$ denotes acceleration, ${\dot{x}}_i(t)$ velocity, and x_i(t) position of the moving end-effector. The term I_i,j (t, τ) denotes an arbitrary coupling function, and α, β, and γ are parameters that govern the intrinsic dynamics of an oscillator, while ω could be interpreted (under the appropriate assumptions) as a pacing frequency, represented by the natural frequency of each of the oscillators in the model [23, 50]. Throughout the paper we fix the intrinsic parameter of both oscillators at experimentally validated parameter values, namely, α = 12.457, β = 0.007095, and γ = 0.641 [29].

We compare the original phenomenological coupling function, F_i,j (t, τ), introduced in [23], extended by adding time delays in [58], and analyzed in [50], which has the form

$$F_{i,j}\left(t,\tau \right)=\left({\dot{x}}_i\left(t\right)-{\dot{x}}_j\left(t-{\tau }_j\right)\right)\left(a+b{\left(x_i\left(t\right)-x_j\left(t-{\tau }_j\right)\right)}^2\right),$$ (1.2)

with the neurologically motivated coupling, G_i,j(t, τ₁, τ₂), proposed in [2], given by

$$\begin{array}{l}{G}_{i,j}\left(t,{\tau }_1,{\tau }_2\right)=\epsilon (\left(x_i\left(t\right)-\left(1-r\right)x_i\left(t-{\tau }_1\right)-r{x}_j\left(t-{\tau }_2\right)\right)\\ -\frac{\delta }{3}{\left(x_i\left(t\right)-\left(1-r\right)x_i\left(t-{\tau }_1\right)-r{x}_j\left(t-{\tau }_2\right)\right)}^3).\end{array}$$ (1.3)

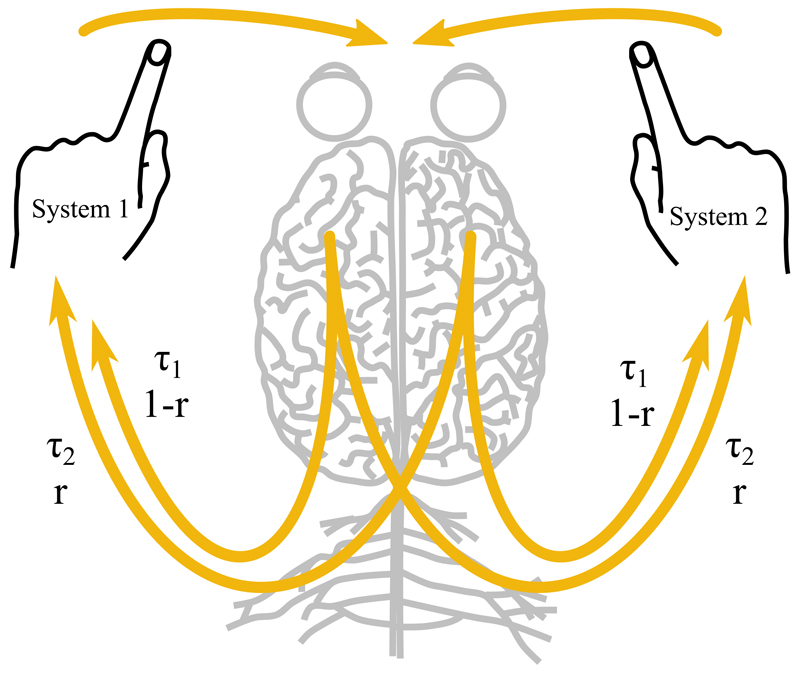
In (1.2) and (1.3) time delays τ arise due to the physiology of the neuromuscular system. The function F in (1.2) has two abstract coupling strength parameters a and b. The coupling parameters of function G given in (1.3) have the following interpretations: ϵ is the strength of coupling, r ∈ [0, 1] is the degree of cross-talk in the neuromuscular system, and δ controls the degree of nonlinearity in the coupling. The latter parameter was set in [2] to the value δ = 1. In our study δ is a free parameter, as we will demonstrate that it controls the stability of the in-phase and anti-phase solutions. A schematic representation of the ideas motivating (1.3) is illustrated in Figure 1.

Figure 1.

Schematic representation of (1.1) with the coupling function (1.3). The yellow arrows represent mixed and self-coupling on the sensory (vision and proprioception), processing (brain), and execution (spinal cord, motor neurones, and muscles) levels. The time delays in the coupling (1.3) are due to the physiology of the neuromuscular system.

We show that the HKB model with a neurologically motivated coupling, (1.3), allows for quantitative description of the experimental findings [22, 30]—in contrast to the phenomenological coupling, (1.2), which provides only qualitative description. Specifically, we analyze the onset of coordination patterns in the model, corresponding to transition from discrete to oscillatory motion, as the parameter ω increases from 0. We further investigate how the solutions of the HKB model with neurologically motivated coupling depend on the coupling parameters and time delays. In contrast to earlier studies, which focused on the phase-approximation dynamics in the HKB model for weak coupling [18, 32], here we follow [50] and use bifurcation analysis and numerical continuation to systematically investigate the behavior of the HKB model in the full four-dimensional state space for a range of coupling parameters. The bifurcation diagrams were computed using the numerical continuation package DDE-Biftool (v3.1.1) [48] using MATLAB; for simulations we used the MATLAB dde23 solver with default settings.

2. Results

Throughout the analysis we assume that τ_i = τ_j in (1.2) and that τ₁ = τ₂ in (1.3); and we denote it by τ. The simplified model with phenomenological coupling (1.2) has the form

$$\begin{array}{l}{\dot{x}}_i\left(t\right)=y_i\left(t\right),\\ {\dot{y}}_i\left(t\right)=-\left(y_i\left(t\right)\left(\alpha x_i^2\left(t\right)+\beta y_i^2\left(t\right)-\gamma \right)+{\omega }^2{x}_i\left(t\right)\right)\\ +(y_i\left(t\right)-y_j\left(t-\tau \right))(a+b{(x_i(t)-x_j(t-\tau ))}^2),\end{array}$$ (2.1)

and the model with neurologically motivated coupling (1.3) reads

$$\begin{array}{l}{\dot{x}}_i(t)=y_i(t),\\ {\dot{y}}_i(t)=-(y_i(\alpha x_i^2(t)+\beta y_i^2(t)-\gamma )+{\omega }^2{x}_i(t))\\ +ϵ((x_i(t)-(1-r)x_i(t-\tau )-r{x}_j(t-\tau ))\\ -\frac{\delta }{3}{(x_i(t)-(1-r)x_i(t-\tau )-r{x}_j(t-\tau ))}^3).\end{array}$$ (2.2)

Our main interests are the in-phase and anti-phase periodic solutions of systems (2.1) and (2.2) and in particular their stability and coexistence. The two types of solutions are illustrated in Figure 2. Figure 2(a) shows an example of the in-phase solution; due to overlap only one time trace is visible for both oscillators. Figure 2(b) shows an example of the anti-phase solution; the time traces of the two oscillators are reflected along x_1,2 = 0 or y_1,2 = 0; the phases differ by π. The in-phase solutions are restricted to a hyperplane x₁ = x₂, y₁ = y₂ and the anti-phase solutions are restricted to a hyperplane x₁ = −x₂, y₁ = −y₂ of the phase space (x₁, x₂, y₁, y₂); compare Figure 2(c)–(d), where the time traces are shown in the (x₁, x₂, t) and (y₁, y₂, t) subspaces, respectively.

Figure 2.

In-phase and anti-phase periodic solutions of (2.2) represented as time traces. (a) shows in-phase solution; left axis for x₁ and x₂; right axis for y₁ and y₂. For the in-phase solution the variables overlap x₁ = x₂ and y₁ = y₂. (b) shows anti-phase solution. For the anti-phase solution x₁ = −x₂ and y₁ = −y₂. For the chosen parameter values the anti-phase solution is unstable. (c) shows the solutions in the (x₁, x₂, t)-space. The in-phase and anti-phase solutions lie on perpendicular planes. (d) shows the solutions in the (y₁, y₂, t)-space. Blue indicates in-phase solutions, and red indicates anti-phase solutions. In all panels, α = 12.457, β = 0.007095, γ = 0.641, δ = 1, r = 1, ϵ = 1, ω = 2 [Hz], and τ = 0.14.

We start by comparing how the stability and amplitude of the in-phase and anti-phase periodic solutions depend on the parameter ω, type of coupling, and time delay τ. Figure 3 depicts the bifurcation diagrams of systems (2.1) and (2.2) in parameter ω. Panels (a1)–(a4) illustrate solutions of the system (2.1) with phenomenological coupling (note that similar computations have been presented in [50]; they are included here for the sake of completeness and comparison). Panels (b1)–(b4) and (c1)–(c4) illustrate solutions of the system (2.2) with neurological coupling for cross-talk parameter values r = 1 and r = 0.5, respectively. The cases of linear coupling, corresponding to the parameter values b = 0 and δ = 0, are illustrated in rows (a1)–(c1) and (a1)–(c2), while the nonlinear coupling cases, represented by the parameter setting b = 1 and δ = 1, are illustrated in panels (a3)–(c3) and (a4)–(c4). A two-parameter bifurcation analysis of the system (2.1) in the coupling parameters a and b is presented in Appendix A, Figure 11. Panels (a1)–(c1) and (a3)–(c3) correspond to the no-delay cases (τ = 0), whereas, the nonzero time-delay cases, for τ = 0.14, are shown in panels (a2)–(c2) and (a4)–(c4). In the figure we use delay τ = 0.14[s], which is the same as in [50].

Figure 3.

Influence of the coupling on the stability of in-phase and anti-phase periodic solutions. Bifurcation diagrams of the in-phase and anti-phase periodic solutions in the parameter ω. Panels (a1)–(a4) for the system (2.1) with phenomenological coupling. Panels (b1)–(b4) and (c1)–(c4) for system (2.2) with neurologically motivated coupling; without (r = 1) and with (r = 0.5) self-coupling, respectively. Row (a1)–(c1) for linear coupling, b = 0 and δ = 0, with delay τ = 0 and row (a2)–(c2) for linear coupling and τ = 0.14. Row (a3)–(c3) for nonlinear coupling b = 1 and δ = 1 with delay τ = 0 and row (a4)–(c4) for nonlinear coupling and τ = 0.14. Blue curves for the in-phase periodic solutions; red curves for the anti-phase periodic solutions; grey curves ((b3)–(c3) and (b4)–(c4)) for the steady states. Thick curves for stable and thin for unstable solutions. Bifurcation points labels: ● Hopf bifurcation, * torus bifurcation, × branching point or saddle node of limit cycles, ▲ bifurcation involving connecting orbit (homo- or heteroclinic). Grey rectangles indicate regions shown in the insets. In all panels, α = 12.457, β = 0.007095, and γ = 0.641.

Figure 11.

Two parameter bifurcation diagrams of periodic solutions of (2.1) in the a, b-plane for different combinations of intrinsic frequencies ω and time delays τ_1,2. In (a) τ_1,2 = 0 and ω = 1.3[Hz], (b) τ_1,2 = 0 and ω = 3[Hz], (c) τ_1,2 = 0.14[s] and ω = 1.3[Hz], and (d) τ_1,2 = 0.14[s] and ω = 3[Hz]. Blue areas indicate stable in-phase solutions, and red areas indicate stable anti-phase solutions. Bistability is indicated in purple. Enlargements in the bottom left corner of each panel show regions of bistability around a = 0 and b = 0. Thick black lines are lines of Hopf bifurcations, thin black lines are lines of branching points, and dashed black lines are lines of torus bifurcations. We show only parts of the bifurcation lines that bound regions of stable periodic solutions. Red-dashed line indicates part of the boundary of the region of anti-phase solution where growing amplitude caused computed stability information to be unreliable. Top left and right insets in each panel show 1D bifurcation diagrams in a for b = 1 and in b for a = 5; thick lines indicate stable solutions, and thin lines indicate unstable solutions; grey lines shown in the insets are unstable steady states ‖x_i‖ = 0. In all panels, α = 12.457, β = 0.007095, and γ = 0.641.

Figure 3 indicates that the in-phase and anti-phase periodic solutions arise either via a bifurcation involving a connecting orbit (homoclinic or heteroclinic, as we show in the next section) or via the Hopf bifurcation of a steady state, labeled as ▲ and ●, respectively. The in-phase and anti-phase periodic solutions gain or lose stability via torus bifurcation (∗), saddle-node of periodic orbits bifurcation, or at a branching point, both marked with (×). Both the saddle-node of periodic orbits bifurcation and branching point are characterized by a single real Floquet multiplier crossing the unit circle at 1. Distinction between the two bifurcations could be based on the corresponding one-parameter bifurcation diagram. In the case of a saddle-node of periodic orbits we observe that stable and unstable periodic solutions collide and disappear (see, e.g., insets in Figure 3(b3)–(b4)), while in the case of a branching point we observe the appearance of an additional branch of periodic solutions. For the sake of clarity in Figure 3 we only show the bifurcation points at which the solutions emerge or change stability. The only exceptions are the homoclinic bifurcations of the anti-phase solutions shown in the insets in panels (b3)–(b4) and (c3)–(c4) (for δ = 1, nonlinear coupling) that are included in order to illustrate the connection with the onset of the anti-phase solutions shown in the insets in panels (b1)–(b2) and (c1)–(c2) in the case of δ = 0, i.e., linear coupling.

Overall, Figure 3 demonstrates the discrepancy between the behavior of the model (2.1) and experimental observations. Concurrently, it shows that the behavior of the model (2.2), even for arbitrary parameter values, has the potential to quantitatively describe experimental observations. In particular, the model with phenomenologically motivated coupling, (2.1), for τ = 0 is monostable for 0 < ω ≤ 6[Hz]; see panels (a1) and (a3). The stable in-phase and anti-phase periodic solutions, for the parameter values in Figure 3, coexist (as observed experimentally) only if the time delay τ > 0 (see also Figure 11(a)–(b), which shows that the bistability of the system (2.1) with τ = 0 can be observed only in a very small part of the (a, b)-plane). Importantly, the system (2.2) with a neurologically motivated coupling function supports bistability. Furthermore, Figure 3 columns (b)–(c) show that only for the model (2.2) with the neurologically motivated coupling the amplitudes of the in-phase and anti-phase are similar in magnitude and monotonic for ω ∈ [0.5, 6][Hz]. The inverse amplitude-frequency relation and similar amplitude of in-phase and anti-phase solutions are typical features of oscillatory movements observed experimentally in various movement tasks with nonconstrained amplitude [5, 29]. These observations provide justification and motivate further investigation of neurologically motivated coupling, thus supporting the need to consider physiological and perceptual delays in order to accurately and quantitatively model experimentally observed transitions between the in-phase and anti-phase coordination patterns [2, 7, 23, 34, 38].

2.1. Connecting orbits and periodic solutions

In this section, we investigate the emergence of periodic solutions in the system (2.2) via connecting orbits. In Figure 3 columns (b)–(c) we show that in all the cases the in-phase (blue) periodic solutions of the system (2.2) arise at ω = 0 in a heteroclinic bifurcation and gain stability at ω > 0 at a branching point. Meanwhile the anti-phase (red) periodic solutions arise at ω > 0 in a heteroclinic bifurcation for the linear coupling (δ = 0; see Figure 3(b1)–(b2) and (c1)–(c2)) or via Hopf bifurcation (δ = 1; see Figure 3(b3)–(b4) and (c3)–(c4)) for the nonlinear coupling and later undergoes homoclinic bifurcation. To investigate the role of connecting orbits in the onset of the in-phase and anti-phase periodic solutions in more detail, we combine a theoretical analysis of the equilibrium state of system (2.2) and a numerical bifurcation analysis of the periodic solutions in the case τ = 0. The observed heteroclinic bifurcation appears to be similar to transitions involving connecting orbits described in [6].

Figure 4 illustrates the mechanism of emergence of the periodic solutions of (2.2) with linear coupling, δ = 0, and no delay, τ = 0. Panel (a) shows the bifurcation diagram of the system (2.2) in ω using the same parameters' values as in Figure 3(b1). Panels (b)–(f) show representative phase portraits of the system (2.2) at the values of ω indicated by the corresponding labels in panel (a). Panels (b) and (e) show the hyperplanes (x₁ = x₂, y₁ = y₂) and (x₁ = −x₂, y₁ = −y₂), respectively, while panels (c)–(d) and (f) show the phase space (x₁, x₂, y₁) of the model.

Figure 4.

Mechanisms of emergence of the in-phase and anti-phase periodic solutions. (a) Bifurcation diagram of the in-phase and anti-phase periodic solutions of (2.2) in the parameter ω for the linear coupling, δ = 0, and τ = 0, r = 1, ϵ = 1; the same parameters' values as in Figure 3(b1). Colors and symbols are as in Figure 3; additionally, the purple curve indicates periodic orbit with phase that changes from in-phase to anti-phase and grey ■ indicates transition involving family of nonisolated equilibria. Panels (b)–(f) show phase portraits for increasing values of ω. (b) Phase plane (x₁ = x₂, y₁ = y₂) at ω = 0; gray arrows indicate direction of the flow, green x-nullclines, dark green y-nullcline, and dashed blue curves indicate family of the heteroclinic orbits connecting the unstable and stable nonisolated equilibria. (c) Phase space (x₁, x₂, y₁) at ω = 0.2249[Hz]. (d) ω = 0.2250[Hz]. (e) Phase plane (x₁ = −x₂, y₁ = −y₂) at $\omega =1/(\sqrt{2}\pi );$ dashed red curves indicate family of the heteroclinic orbits. (f) ω = 0.2252[Hz]. The insets show the full shape of nullclines of the system (2.2) reduced to the in-phase plane (blue axis box) and anti-phase plane (red axis box). In all panels, α = 12.457 β = 0.007095, and γ = 0.641.

In Figure 4(b) we demonstrate that an unstable in-phase periodic orbit emerges from a family of heteroclinic orbits (blue area with dashed curves) that connects unstable (thin grey) and stable (thick grey) branches of a family of nonisolated equilibria of the dynamics of system (2.2) restricted to the in-phase hyperplane. The existence of the family of nonisolated equilibria and their stability can be inferred as follows; for δ = 0, the system (2.2) takes the form

$$\begin{array}{l}{\dot{x}}_i(t)=y_i(t),\\ {\dot{y}}_i(t)=-(y_i(t)(\alpha x_i{(t)}^2+\beta y_i{(t)}^2-\gamma )+{\omega }^2{x}_i(t))\\ +ϵ(x_i(t)-(1-r)x_i(t-\tau )-r{x}_j(t-\tau )).\end{array}$$ (2.3)

The steady state is determined by equating the right-hand side of (2.3) to 0 (recall that for steady state we have x_i(t − τ) = x_i(t)), which leads to the system of linear equations

$$\begin{array}{r}{y}_i=0,\\ -{\omega }^2{x}_i+ϵr(x_i-x_j)=0.\end{array}$$ (2.4)

For ω = 0 the solutions of the system satisfy the following conditions: y_i = 0, x_i = x_j. Therefore, the steady state of the system consists of a family of nonisolated fixed points defined by the line

$$L=\{(x_1,x_2,y_1,y_2)\in {ℝ}^4|x_1=x_2,y_1=0,y_2=0\}.$$

We investigate this case further by considering the dynamics with zero delay (τ = 0; to simplify notation we also omit the dependence on time in equations). We focus only on the dynamics defined on the in-phase plane,

$$P=\{(x_1,x_2,y_1,y_2)\in {ℝ}^4|x_1=x_2,y_1=y_2\},$$ (2.5)

which for ω = 0 can be described as

$$\begin{array}{l}\dot{x}=y,\\ \dot{y}=-y(\alpha x^2+\beta y^2-\gamma ).\end{array}$$ (2.6)

The Jacobian matrix of system (2.6) at the nonisolated family of equilibria (y = 0) is given by

$$J=\left[\begin{array}{cc}0& 1\\ 0& -(\alpha x^2-\gamma )\end{array}\right],$$

which has the eigenvalues

$${\lambda }_1=0,{\lambda }_2=\gamma -\alpha x^2.$$

For α, γ > 0 (including the choice α = 12.457 and γ = 0.641), the nonisolated equilibrium on y = 0 has a stable direction if $x\in (\infty ,-\sqrt{\frac{\gamma }{\alpha }})\cup (\sqrt{\frac{\gamma }{\alpha },\infty })$ and an unstable direction if $x\in (-\sqrt{\frac{\gamma }{\alpha }},\sqrt{\frac{\gamma }{\alpha }}).$

The nullclines of this system are given by

$$\begin{array}{l}x\text{-nullcline}:y=0,\\ y\text{-nullcline}:y=0\cup \frac{\alpha }{\gamma }{x}^2+\frac{\beta }{\gamma }{y}^2=1.\end{array}$$

The x-nullcline and the y = 0 branch of the y-nullcline overlap. The self-intersection point of the y-nullcline, i.e., the intersection points between the line y = 0 and the ellipse (α/γ)x² + β/γ)y² = 1, are located at $x=\pm \sqrt{\gamma /\alpha },$ at which the family of nonisolated equilibria changes its stability. The nullclines are shown in the inset in Figure 4(b).

Figure 4(c), ω = 0.2249[Hz], shows in-phase periodic solution (thick blue) and two phase-locked periodic solutions (purple) that appear at the branching point where the in-phase periodic solution gains stability. Panel (d), ω = 0.2250[Hz], shows further that the phase-locked periodic solutions disappear at the points of intersection of the nullclines of system (2.3) and contract to the anti-phase plane. For $\omega =1/\left(\sqrt{2}\pi \right),$ Figure 4(e), the stable anti-phase periodic solution emerges in the same fashion as the in-phase periodic solutions at ω = 0.

For ω > 0 the solutions (2.4) of the system (2.3) satisfy the following conditions: y₁ = y₂ = 0, x₁ + x₂ = 0, (2ϵr − ω²)(x₁ − x₂) = 0 (we added and subtracted the last two equations of (2.4)). Therefore, the steady state of the system either is the trivial equilibrium (0, 0, 0, 0) for (2ϵr − ω²) ≠ 0, or it consists of a family of nonisolated fixed points defined by the line

$$L=\{(x_1,x_2,y_1,y_2)\in {ℝ}^4|x_1+x_2=0,y_1=0,y_2=0\}$$

for (2ϵr − ω²) = 0. This equation defines a boundary for the region of existence of the anti-phase solution in the parameter space (ϵ, r, ω). To further investigate the dynamics before and after this transition, we again consider the dynamics of the system (2.3) for τ = 0. We proceed analogously to the in-phase case and focus only on the dynamics restricted to the anti-phase plane:

$$P=\{(x_1,x_2,y_1,y_2)\in {ℝ}^4|x_1=-x_2,y_1=-y_2\}.$$ (2.7)

The reduced system (2.3) takes the following form:

$$\begin{array}{l}\dot{x}=y,\\ \dot{y}=-(y(\alpha x^2+\beta y^2-\gamma )+{\omega }^{2}x)+ϵ(x-(1-r)x+rx).\end{array}$$

The linearization of system (2.8) at the equilibrium (x, y) = (0, 0) has the following Jacobean:

$$J_0=\left[\begin{array}{cc}0& 1\\ -{\omega }^2& \gamma \end{array}\right]$$ (2.8)

with eigenvalues

$${\lambda }_0=\frac{\gamma \mp \sqrt{{\gamma }^2+4(2ϵr-{\omega }^2)}}{2}.$$ (2.9)

Hence, depending on the sign of (2ϵr − ω²), we can distinguish three different cases:

• ω² < 2ϵr. The trivial equilibrium (0, 0) is of saddle type, and no limit cycle exists in the anti-phase plane.

• ω² = 2ϵr. In this case, there is no flow through the line y = 0, which consists of a family of nonisolated equilibria.

• ω² > 2ϵr. For γ > 0 (as in our setting γ = 0.641) the trivial equilibrium (0, 0) of (2.6) is unstable and surrounded by a stable limit cycle. (Note that for γ < 0 the equilibrium would be stable.)

The stability of the case ω² = 2ϵr restricted to the anti-phase hyperplane is similar to the ω = 0 case restricted to the in-phase hyperplane. Furthermore, this analysis can be extended to the system (2.1) for τ = 0.

Finally, Figure 4(f), ω = 0.2252[Hz], shows coexistence of the stable in-phase and anti-phase periodic solutions for $\omega >1/(\sqrt{2}\pi )$. We conjecture that the results for τ = 0 can be extended to τ > 0. We base the conjecture on two observations. First, the models for τ = 0 and τ > 0 have the same steady states, although their stability might differ. Second, as the continuation parameter ω approaches ω = 0 (for the in-phase solutions) or $\omega =1/(\sqrt{2}\pi )$ (for the anti-phase solutions) the period of the oscillatory solutions of the system (2.3) with τ > 0 increases exponentially, which is consistent with existence of a connecting orbit.

Figure 5 shows a sequence of phase portraits of the system (2.2) restricted to the anti-phase hyperplane that illustrate the bifurcations of the anti-phase periodic solutions shown in the inset in Figure 3(b3) for τ = 0, δ = 1, r = 1, ϵ = 1. In panel (a) there are two stable equilibria (large grey dots) and a saddle point at (x, y) = (0, 0). As the parameter ω increases, a pair of anti-phase periodic solutions (stable and unstable) surrounding the three equilibria appears in a saddle-node bifurcation of limit cycles, panel (b). Next, the unstable periodic orbit and the saddle point connect and become a double homoclinic orbit, panel (c). In panel (d), the homoclinic orbit breaks into two small unstable anti-phase periodic orbits surrounding two stable nodes. These two small unstable periodic orbits shrink and disappear in a Hopf bifurcation as ω increases. After the Hopf bifurcation the three unstable steady states (two nodes and one saddle) are surrounded by a single stable anti-phase periodic solution, panel (e). As the parameter ω increases further, the system undergoes a pitchfork bifurcation, where the two unstable nodes merge with the saddle point. After the pitchfork bifurcation, the single unstable focus point at the origin (0, 0) is surrounded by a stable anti-phase periodic solution.

Figure 5.

Sequence of phase portraits of the system (2.2) restricted to the anti-phase hyperplane that illustrate the bifurcations of the anti-phase periodic solutions shown in the inset in Figure 3(b3). Colors and symbols are as in Figure 4. Additionally, grey dots indicate equilibria (large - stable, small - unstable); black curves are stable and unstable manifolds of the saddle point; thin red curve with arrows indicates double homoclinic orbit. In all panels, τ = 0, δ = 1, r = 1, ϵ = 1, α = 12.457, β = 0.007095, and γ = 0.641.

2.2. Influence of coupling parameters and time delay on the stability of in-phase and anti-phase oscillations

We proceed by investigating the stability of in-phase and anti-phase coordination patterns and its dependence on the coupling parameters and time delay. We compute two-parameter continuations of the bifurcations of in-phase and anti-phase periodic solutions of system (2.2) in order to study the effect of time delay and coupling parameters on the regions of bistability and monostability in the parameter space. Our aim is to identify the regions in parameter space that support the experimentally observed transition from bistable dynamics of in-phase and anti-phase periodic regimes to monostable in-phase oscillations.

2.2.1. The influence of time delay

To explore the influence of time delay on the stability, we perform a two-parameter numerical continuation of the bifurcations of in-phase and anti-phase periodic solutions in the time delay τ, the coupling strength ϵ, and the degree of nonlinearity δ.

Figure 6 shows two-parameter bifurcation diagrams of the in-phase and anti-phase periodic solutions of the system (2.2). Panel (a) depicts the bifurcation diagram in the (τ, ϵ)-plane for δ = 0, which illustrates the dependence of stability on the time delay and coupling strength in the linear coupling case, while panel (b) shows the bifurcation diagram in the (τ, δ)-plane illustrating the dependence of stability of periodic solutions on the time delay and degree of nonlinearity of the coupling function for ϵ = 1. The other parameters are ω = 1[Hz] and r = 1. The different stability regions of the periodic solutions are bounded by curves representing the loci of torus and branching point bifurcations in the parameter plane. For the sake of clarity, we only show parts of the curves that bound the regions of stable solutions.

Figure 6.

Influence of time-delay on stability of the in-phase and anti-phase oscillations. Two parameter bifurcation diagrams of the stability of in-phase and anti-phase oscillations of system (2.2) in the (τ, ϵ)-plane for δ = 0 (a); and in the (τ, δ)-plane for ϵ = 1 (b). The labels, I and A, and colors (blue and red) indicate, respectively, the existence of stable in-phase and anti-phase oscillations in the corresponding region; IA (pink) indicates regions where the two kinds of solutions coexist. The dashed/thin curves represent, respectively, the loci of torus and branching point bifurcations of periodic solutions. In all panels, α = 12.457, β = 0.007095, γ = 0.641, ω = 1[Hz], and r = 1.

The bifurcation diagrams presented in Figure 6 demonstrate that for sufficiently small time delay, in-phase and anti-phase periodic regimes coexist for wide ranges of the coupling parameters ϵ and δ. For larger values of τ, torus or branching point bifurcation leads to the emergence of regions of monostable in-phase or anti-phase coordination patterns. As the time delay increases, the regions of bistability and monostability alternate. It can also be noticed that the bifurcations of in-phase and anti-phase coordination patterns alternate in the range of τ. Analysis of effects of time delay on the dynamics of system (2.1) can be found in [50].

2.2.2. The influence of coupling parameters

The bifurcation analysis in (τ, ϵ) and (τ, δ) parameter planes, presented in the section above, shows that for sufficiently small time delay, the dynamics of the system (2.2) at frequency ω = 1[Hz] exhibits bistable in-phase and anti-phase oscillations. The next step is to identify the ranges of the coupling parameters that support the transition from bistable dynamics to the monostable in-phase periodic regime as the frequency ω increases [23, 50].

Degree of coupling nonlinearity

First, we consider the effects of the degree of coupling nonlinearity on the stability. To this end, we perform two-parameter continuation of the bifurcations of in-phase and anti-phase periodic solutions in the parameter δ and frequency ω. Figure 7 presents the two-parameter bifurcation diagrams of the stability of in-phase and anti-phase oscillations in the (ω, δ)-plane for δ ≥ 0. Panels (a), (c) and (b), (d) show a comparison between two values of the time delays τ = 0.08[s] and τ = 0.14[s] (representing the range 70–150[ms] that have been measured experimentally in human responses to continuous stimuli [33]). Furthermore, the value of time delay τ = 0.08[s] is consistent with the most recent estimates of the delays within the neuromuscular system [60]. Figure 7 illustrates also how the bifurcation diagrams change for different levels of cross-talk. Specifically, (a)–(b) show bifurcation diagrams for r = 1 representing pure mutual (no self) feedback (corresponding to a moving effector that is influenced only by the position of the other effector), and panels (c)–(d) show show bifurcation diagrams for r = 0.5 representing equal self- and mutual feedback (corresponding to a moving effector being equally influenced by the feedback of its own and the other effector positions) [2]. The range of frequency is 0 < ω < 6[Hz] and corresponds to the experimentally explored pacing frequency range [5, 7, 29, 34].

Figure 7.

Influence of coupling nonlinearity on stability of the in-phase and anti-phase oscillations. Two parameter bifurcation diagrams of the stability of in-phase and anti-phase oscillations of system (2.2) in the (ω, δ) plane for τ = 0.08, 0.14, r = 1, 0.5, ϵ = 1, α = 12.457, β = 0.007095, and γ = 0.641. The labels, I and A, and colors (blue and red) indicate, respectively, the existence of stable in-phase and anti-phase oscillations in the corresponding region; IA (pink) indicates regions where the two kinds of solutions coexist. The solid black curves represent the loci of branching point bifurcation.

The bifurcation diagrams in Figure 7 demonstrate that bistable regimes of in-phase and anti-phase oscillations exist for a range of values of the frequency parameter ω in the regions labeled as IA. As the parameter ω increases, the anti-phase periodic solutions lose stability via a branching point bifurcation. Panels (a), (c) for τ = 0.08[s] show sizeable ranges of the (ω, τ) parameter space, where the dynamics of system (2.2) supports the experimental observations, i.e., transition from bistable to monostable coordination patterns. Furthermore, panels (a) and (c) show that increasing the degree of nonlinearity δ increases the frequency at which the anti-phase periodic solution loses its stability and the transition in coordination pattern takes place. On the other hand, for longer delays τ = 0.14[s], in panels (b) and (d), we observe an additional transition in the coordination pattern around ω ≈ 3.5[Hz]. At this frequency the anti-phase periodic solutions regain stability. Such a transition has not been observed experimentally for bimanual coordination and could be regarded as an experimentally testable model prediction.

Coupling strength and cross-talk

Next, we investigate the effects of the coupling strength ϵ and cross-talk r on the stability of the in-phase and anti-phase periodic solutions by close examination of one-parameter bifurcation diagrams in the frequency parameter ω for weak ϵ = 0.2, moderate ϵ = 1, and high coupling strengths ϵ = 5 and for two values of cross-talk r = 1 and r = 0.5. The values of the other coupling parameters, δ = 6 and τ = 0.08[s], were selected from Figure 7 such that the pattern of coexistence of bistability of the in-phase and anti-phase periodic solutions is consistent with the experimental observations.

Figure 8 demonstrates that increasing the coupling strength leads to a larger difference in the amplitudes of the in-phase and anti-phase periodic solutions. The bifurcation diagrams for r = 1 show that increasing the coupling strength ϵ has little effect on the value of ω where the anti-phase solution loses stability at a branching point bifurcation. In contrast, at a high level of cross-talk r = 0.5 the value of ω at which the anti-phase solution loses stability (via the branching point bifurcation) depends strongly on the coupling strength ϵ.

Figure 8.

Influence of coupling strength on stability of the in-phase and anti-phase oscillations. Bifurcation diagram of stability of the in-phase and anti-phase oscillations of system (2.2) in the frequency parameter ω for the coupling strength values ϵ = 0.2, 1, 5. All colors and symbols are the same as in Figure 3 and Figure 4; additionally grey × indicates pitchfork bifurcation. Grey semitransparent rectangles indicate regions enlarged in the panels (a2)–(f2). In all panels, α = 12.457, β = 0.007095, and γ = 0.641.

Figure 8 panels (a2)–(c2) and (d2)–(f2) show the details of the bifurcation diagrams for small values of ω. Specifically, we find stable nontrivial (‖x₁‖ > 0) steady states losing stability via Hopf bifurcation and disappearing in a pitchfork bifurcation. We also observe a second Hopf bifurcation. One of the Hopf bifurcations gives rise to the anti-phase periodic solutions and the other to a branch of phase-locked periodic solutions that collides with the in-phase periodic solutions at a branching point at which the in-phase periodic solutions gain stability. We further observe that both the anti-phase and period-locked periodic solutions undergo a series of bifurcations through which they lose and gain stability. For the sake of clarity, in Figure 8 we only indicate the bifurcations at which the periodic solutions gain or lose stability and bifurcations that involve connecting orbits.

2.2.3. Transient dynamics and transition between discrete and continuous movement

Finally, we investigate how the stability and solution structure presented in Figure 8 might affect transition between discrete and continuous movement as well as transient dynamics observed in experiments. Figure 9 shows details of the one-parameter bifurcation diagram in the frequency ω for the same parameters values as in Figure 8(b).

Figure 9.

Details of dynamics for Figure 8(b), including phase-locked solutions and period doubling cascade. (a) Bifurcation diagrams of (2.2) in the parameter ω. All colors and symbols are the same as in Figure 8. (b) Details of the shaded region in (a); inset shows a begging of the period doubling sequence (⧫ period doubling bifurcations; black curves period doubled solutions). (c) Maximum of the modulus of the Floquet multipliers max(|μ|) for the in-phase and anti-phase solutions from (a). (d) Phase space plot showing an attractor and unstable in-phase and anti-phase periodic orbits for ω = 0.178 [Hz]; indicated in (b). α = 12.457, β = 0.007095, and γ = 0.641.

The transient dynamics in the system (2.2) is affected by the phase-locked periodic solutions coexisting with the in- and anti-phase periodic solutions and by the rate of convergence to the stable periodic attractors. Figure 9(a) shows two branches of phased-locked solution that emerge from the branching point at which the anti-phase periodic solutions lose stability. Although both branches of the phase-locked periodic solution are unstable, one of the branches is close in terms of the max(x₁) to the stable in-phase solution and depending on initial conditions will affect the orbits converging to a stable attractor. Convergence to the stable attractor is further affected by slow attraction/repulsion rate of the in-phase and anti-phase periodic solutions for ω > 3 [Hz]. Figure 9(c) shows that for ω > 3 [Hz] the maximal nontrivial Floquet multipliers of the the in-phase and anti-phase periodic solutions have modulus close to the unit circle max(|μ|) ≈ 1.

Figure 9(b) shows a complicated structure of coexisting phase-locked periodic solutions and a sequence of period doubling bifurcations of solutions that emerge from them. The existence of the period doubling cascade indicates the presence of chaotic dynamics. To illustrate this, in Figure 9(d) we plot a complicated attractor that can be found in this region. The complex pattern of multistability presented in panel (b) highlights potentially complex dynamics underlying the transitions between discrete and continuous movement. Although such rich dynamics would be unlikely to be observed in experiments due to inherent experimental noise, it nonetheless demonstrates that the dependence of the transition between discrete and continuous motion on coupling parameters and driving frequency ω can be explored by means of bifurcation analysis of the model (2.2).

In order to demonstrate the above ideas, in Figure 10 we present results of simulations of the model (2.2) which follow the experimental protocol from [29, 30] in which pacing frequency is increased by 0.2 Hz every 10 seconds. Accordingly, we vary the parameter ω in 16 consecutive simulations (each running for 10 seconds). The initial state of each simulations is the end-state of the previous run with an additional small (5% of the amplitude) noise drawn from uniform distribution. We ran the sequence of the simulations twice, starting from the in-phase and anti-phase initial states. Figure 10 depicts time traces from the simulations in the (x₁, x₂) phase plane. Transition from anti-phase to in-phase periodic solution occurs at ω = 3 [Hz]. Further, we observe that the simulations initiated in an anti-phase state (red) deviate strongly from the both coordination patterns for 2.6 < ω < 3.4 [Hz]. In the literature, depending on the specific experiments, the transition between anti-phase and in-phase coordination regimes has been reported to occur for 1 < ω < 3 [Hz] [7, 29, 30, 44, 46]. The two bottom panels show the first five seconds of the simulation time series for ω = 2.4 [Hz], ω = 3.2 [Hz], and ω = 4 [Hz] representing the experimentally observed transition.

Figure 10.

Numerical experiment. The first four rows show 10 seconds of simulated in-phase (blue) and anti-phase (red) solutions in the (x₁, x₂) phase plane. The bottom two rows show the first 5 seconds of the in-phase and anti-phase times series for ω = 2.4 [Hz], ω = 3.2 [Hz], and ω = 4 [Hz]. In all panels, r = 1, δ = 6, τ = 0.08, ϵ = 1, α = 12.457, β = 0.007095, and γ = 0.641.

3. Discussion

We demonstrate that the hybrid oscillator (1.1) with the neurologically motivated coupling (1.3) incorporating time delay accurately captures the empirically observed features of rhythmic movement coordination. And in this respect it performs better than the HKB model with phenomenologically motivated coupling (1.2). It captures, quantitatively, two hallmark features of rhythmic movement behavior—namely, the linear amplitude-frequency relation of the oscillations and the stability transition of the coordination dynamics (from bistable in-phase and anti-phase oscillations to monostable in-phase periodic regime) as the frequency parameter ω increases. Both these characteristics were observed and consistently reproduced in many oscillatory movement experiments [3, 4, 5, 7, 8, 9, 10, 11, 24, 25, 29, 30, 34, 37, 39, 40, 41, 43, 51, 56, 59] as well as in real-life hand movements [26]. Our analysis revealed that these two properties of the periodic solutions of system (2.2) are persistent for a large, and experimentally relevant, range of the explored parameter space of the neurologically motivated coupling function (1.3) (see, e.g., Figure 3, Figure 8, Figure 9, and Figure 10).

The presented numerical bifurcation analysis shows that inclusion of the time delay in the coupling function has significant effects on altering the regions of bistability and monostability in the parameter space and is necessary to explain the experimental observations. For the explored parameter space, the stability transition in the coordination dynamics is best captured for a small value of delay τ = 0.08[s] which is consistent with electrophysically estimated delay in the neuromuscular system [60] and is closer to the lower limit for time delays estimated experimentally [33]. The observed upper limit of time delay offers a way for direct experimental validation of our findings regarding persistence of anti-phase coordination pattern for higher pacing frequencies.

We further show how, by varying the strength ϵ, nonlinearity δ, and cross-talk degree r of the coupling, one can control the driving frequency at which the anti-phase solution loses stability and the coordination patterns becomes monostable. This is essential not only for comparison to the experimental observations of rhythmic movement coordination but also in applications of this modeling approach to hybrid system such as the human-dynamic clamp [12]. Additionally, our analysis and, in particular, the interpretability of the parameters of the neurologically motivated coupling function (1.3) might help to explain changes observed in coordination patterns in people with neuropsychiatric and developmental disorders [14, 15, 16, 17, 19, 20, 21, 31, 42, 45, 49, 57, 58].

Finally, the presented theoretical and numerical analysis reveals that for small values of the parameter ω system (2.2) can be used to model transition between discrete and oscillatory movements [28], going beyond the applicability of the original HKB model [23]. The rich structure of this transition (see, e.g., Figure 9) might help in developing experimental protocols to validate these findings. Another potential future direction would be a comparison of the presented analysis with a bifurcation analysis of an alternative model of rhythmic movement with perceptual coupling [7]. Perceptual coupling provides an alternative (to neuromuscular coupling) approach to modeling socio-motor coordination with a growing experimental support [34, 52].

4. Conclusions

In this work, we investigated analytically and numerically the dynamics of two coupled hybrid oscillators that can be used to model movement coordination behavior, considering the physically relevant intrinsic parameter setting, that is consistent with experimental data. The analysis demonstrates that the periodic regimes of two hybrid oscillators coupled by neurologically motivated coupling can consistently exhibit the desired in-phase and anti-phase bistability patterns, in addition to the amplitude-frequency relation, that have been reported in many empirical studies of rhythmic movement coordination. Our analysis also highlights some parameter ranges for which the model supports the dynamics of discrete movement, which is the class of movements absent in the original HKB model.

Appendix A. Bifurcation diagram of system (2.1) in the plane of coupling coefficients a and b

Figure 11 shows bifurcation diagrams of solutions of system (2.1) in the plane of coupling strengths a and b. Panels (a) and (b), for τ_1,2 = 0, show that the region of bistability (in the enlargement) changes relatively little with increasing frequency ω. Panel (c), for τ_1,2 = 0.14[s] and ω = 1.3[Hz], demonstrates that introduction of the time delay in the coupling considerably increases the region of bistability in comparison with panel (a). The same region becomes almost in-phase monostable as the frequency parameter increases to ω = 3[Hz], as illustrated in panel (d).