Differential Focus on Probability and Losses between Young and Older Adults in Risky Decision-Making

Abstract

We examined young and older adults’ use of descriptive information about risk (i.e., probability and expected value) in financial decision-making. In Experiment 1, participants chose between lotteries in pairs of bets that offered either two risky gains or one risky gain and one sure gain. Whereas they showed a strong and indiscriminate preference for high-probability gambles in risky-risky pairs, they selected sure options at high rates and risky options at low rates in risky-sure pairs, with slightly stronger effects in older relative to young adults due to age differences in ability. Experiment 2 involved the same task but in terms of losses. Participants, especially older adults, preferred low-probability gambles not accounted for by age differences in ability. Results suggest minimal consideration of expected value and a strong focus on probabilities in decision-making. They also suggest that cognitive ability and chronic goals differentially influence age effects depending on risk context.

Old age marks a period of decline in the efficiency with which people engage fluid reasoning skills involved in analytical processing (e.g., executive control, perceptual speed, working memory; Braver & West, 2008; Luszcz, 2011). This decreased cognitive capacity due to age may increase the difficulty associated with performing mental operations, with research showing that older adults relative to young adults generally take longer, make more mistakes, and use fewer strategies in solving difficult and complex arithmetic problems (Lemaire & Arnuad, 2008). Many studies also suggest that aging-related decrements in executive control and the ability to perform mental calculations can predict poorer quality decision-making in tasks that rely on these skills (Boyle, Yu, Wilson, et al., 2012; Delazer, Kemmler, & Benke, 2013; Del Missier, Mäntylä, Hansson, Bruine de Bruin, & Parker, 2013; Henninger, Madden, & Huettel, 2010; Huang, Wood, Berger, & Hanoch, 2015; Koscielniak, Rydzewska, & Sedek, 2016). Of note, in the financial domain, older adults’ lower numeracy and cognitive ability compared to young adults often resulted in their making less adaptive choices (Chen, Wang, Kirk, Pethtel, & Kiefner, 2014), generating fewer alternatives for a medical procedure (Zwahr, Park, & Shifren, 1999), and becoming increasingly more susceptible to scams (Boyle, Yu, Wilson, et al., 2012). The degree to which processing limitations influence how people assess financial risks (i.e., calculating expected value) can therefore have important implications for health and well-being.

Stability or improvements in affective processes may also accompany advanced age (Peters, Hess, Väsfjäll, & Auman, 2007). In some cases, older adults can benefit from an enhancement in these processes, with some studies showing that they behave similarly to, if not better than, young adults when task performance depends upon the use of positive and negative information (e.g., Wood, Busemeyer, Koling, Cox, & Davis, 2005; Worthy, Otto, Doll, Byrne, & Maddox, 2015) and intuition (e.g., Huang et al., 2015). In other cases, an overreliance on affect-based processes or increased susceptibility to affective information can lead older adults to make more disadvantageous choices. Work examining age differences in the ratio bias task, for example, suggests that older adults compared to young adults choose intuitively appealing but suboptimal options more often (Mikels, Cheung, Cone, Gilovich, 2013). These findings raise questions about how age-related changes in analytical and affective processes influence choice behavior and the task-related factors that explain or moderate the use of these processes in decision making. In the current investigation, we examined how descriptive information about risk and affective factors, such as probabilities and risk context, modify the impact of age on financial decision-making.

Prospect Theory (PT; Kahneman & Tversky, 1979) proposes one way in which affective and descriptive characteristics each affect economic decisions. Concerning the latter, many tasks provide information about probabilities and outcomes that allow people to assess risk via the calculation of expected value, but many people often do not use this information effectively. One such instance relates to the fact that people weight the magnitude of the difference between two probabilities non-linearly, depending on whether such probabilities depict extreme odds, such as the impossibility or certainty of an event, or not. PT specifically describes an S-shaped trend in these subjective weights whereby the difference between two very small odds (e.g., 1% vs. 10%) or two very large odds (90% vs. 99%) is perceived as greater than the difference between odds in the middle or at non-extreme ends of the probability distribution (e.g., 40% vs. 50% vs. 60%).

Concerning affective processes, the risk context contributes to the intuitive appeal of risky choices. Tasks that present gambles between wins (gains) or those between losses elicit different behaviors, with individuals tending to avoid risk when dealing with potential gains and to seek it out when dealing with potential losses. Ample evidence further shows that people prefer sure wins to risky wins, and risky losses to sure losses. This is true even when the risky and sure options have the same expected values, a phenomenon called the certainty effect. The degree to which the certainty effect reflects a general probability weighting issue or an affective one remains undecided. We argue that the disproportionate attention paid to extreme probabilities, including sure ones, potentially underscores limitations in deliberative processing, whereas attention paid to low-risk (high-probability) gains and high-risk (low-probability) losses reflects the impact of affective forces that draw upon context-specific goals (i.e., maximizing gains and minimizing losses). Moreover, whereas aging-related decreases in cognitive ability may exacerbate the former, age-related increases in affect-based processes may further exaggerate the latter (Hess, 2015; Peters et al., 2007).

Few studies have examined aging-related effects associated with probability weighing. One study (Pachur, Mata, & Hertwig, 2017) found that older adults exhibit a similar sensitivity to differences in probabilities to that observed in young adults. However, studies that examine certainty do not consistently find the same age effects. Some find that older adults relative to younger adults take greater risks and choose sure options less often in the loss domain (Mather et al., 2012; Tymula et al., 2013), but take fewer risks and choose sure options more often in the gain domain (Boyle, Yu, Buchman, & Bennett, 2012; Mather et al., 2012; Tymula et al., 2013), even if these options have lower expected values and could subsequently result in lower payoffs (Weller, Levin, & Denburg, 2010). Others have failed to replicate either of these effects and instead report greater risk-seeking among young adults in the loss domain (Mikels & Reed, 2009) and more risk-seeking in older adults (Pachur et al., 2017) or no age differences in the gain domain (Mikels & Reed, 2009).

One possible explanation for inconsistent age effects considers variations in the demands associated with risk assessment across studies. If normal deficits in cognitive ability negatively affect effective risk assessment as people age, then we may observe particularly pronounced age differences when decisions involve difficult and complex calculations via the manipulation of descriptive information (e.g., estimation of expected values), with older adults performing worse than young adults (cf. Mata, Josef, Samanez-Larkin, & Hertwig, 2011). Those in the former group may revert to less effortful ways of processing numerical information associated with risk, such as using satisficing and non-compensatory strategies. For example, they may rely on the relative difference in probabilities associated with winning or losing the two bets in a lottery, deciding that the best bets are those that have the more advantageous odds despite their actual payoffs. Cognitive limitations may also lead to a general accentuation of affective influences by increasing the “intuitiveness” of various options (i.e., low-risk gains and high-risk losses). Challenges posed by cognitive limitations in older adults may make the perceived differences between bet probabilities in a pair more extreme, enhancing the intuitive appeal associated with a particular gamble and thereby diminishing the extent to which people carefully evaluate risk. Thus, although these behaviors can have adaptive consequences in some situations, a dependency on these cognitively frugal strategies may impair the quality of older adults’ decisions when successful performance depends on in-depth thinking and the use of fluid reasoning skills.

In the current investigation, we tested these ideas by examining age differences in the utilization of different types of information during decision-making. To do this, we developed a task in which we asked young and older adults to choose between one of two bets in multiple pairs. Pairs of bets consisted of either two risky options or one risky and one sure option. Bets also varied in the probability that they would result in a specific outcome and in their expected values. Tasks used in previous work that have examined probability weighting typically have not manipulated the level of effort required to calculate risk of each bet in a pair. Our task paired a risky option (RO) with a sure alternative (SA) in some cases and with a risky alternative (RA) in others. The probability of the RO varied across pairs (i.e., between 5% and 95%), whereas that of the two alternatives remained constant (i.e., SA = 100%, RA = 50%). (Refer to the Methods section for details.) We reasoned that varying the risk associated with the ROs and offering them with both RAs and SAs, whose riskiness did not change, would allow us to observe systematic fluctuations in cognitive effort linked to calculating expected value (EV). Studies in aging have also suggested a stronger certainty effect among older compared to young adults. We considered the possibility that certainty effects underscore a general probability weighting issue related to an aging-related reduction in cognitive capacity. Thus, in our task, indiscriminate preference for the SA would reflect low effort expenditure or limitations in processing, whereas selection of optimal bets--whether ROs, SAs, or RAs--would evidence a high level of processing and an effective use of descriptive information. Finally, we framed the gambles in terms of gains (Experiment 1) and losses (Experiment 2). This set-up enabled us to detect effects associated with affective influences (e.g., risk context).

In both experiments, we examined how often participants selected optimal bets, which they could determine by calculating expected values, across pairs. We had slightly different expectations for risky-risky pairs (i.e., the RO paired with a RA) and for risky-sure pairs (i.e., the RO paired with a SA). For risky-risky pairs, we expected that participants would show a bias towards selecting the RO if it had the higher probability of winning compared to the RA, but that they would show a bias towards selecting the RA if it had the higher probability of winning compared to the RO. This bias towards probable wins would benefit performance only when these bets had the optimal expected value but would result in poor performance in cases where these bets had a better payout but lower odds (e.g., 10% chance to win $6 versus 50% chance to win $5). For risky-sure pairs, we would either see the same pattern in the case of risky-risky pairs, again alluding to limitations in processing, or that participants would always opt for the SA irrespective of its expected value. This latter pattern would suggest an alternative explanation based in affective influences.

We also expected an amplification of these effects in older adults attributable to limitations in cognitive ability. If true, controlling for age differences in cognitive ability or numeracy should eliminate these effects. A second alternative hypothesis would suggest that age differences are context-specific, with older adults only exhibiting stronger probability and certainty effects compared to young adults in the loss domain. The reason for this specificity relates to an assumed general enhancement of affective processes in later life, whereby loss-related goals (e.g., prevention, maintenance, or minimization) take on greater importance (e.g., Depping & Freund, 2011; Freund & Ebner, 2005). For example, some research has suggested that older adults avoid losses to a greater degree than do young adults (e.g., Mather et al., 2012).

Lastly, we explored sex differences in these hypothesized effects since some studies have found lower risk-seeking behavior (for a review, see Croson & Gneezy, 2009) and less sensitivity to expected value in women compared to men (e.g., Byrne & Worthy, 2016; Cornwall, Byrne, & Worthy, 2018; Weller, Levin, & Bechara, 2010; cf. Fehr-Duda, De Gennaro, & Schubert, 2006). Concerning the former, in different reinforcement learning tasks, men preferred options with the greatest reward magnitude (i.e., expected value) and women preferred those that minimized variability in the frequency of gains and losses (i.e., probability; e.g., Cornwall, Byrne, & Worthy, 2018; Byrne & Worthy, 2016). Thus, although we might expect lower average performance as well as more biased responding in women relative to men, the extent to which these differences hold up in older age remains less clear.

Experiment 1

Participants

We conducted a power analysis a priori using G*Power 3.1 (Faul, Erdfelder, Buchner, & Lang, 2009) to determine our sample size. This analyses indicated that a total sample size of 124 would provide sufficient power at 1 – β (Type II error rate) = .80 to detect a medium effect size (Cohen’s f = .25) with a non-sphericity correction of .15, a small correlation among measures (.20), and α at 0.05., In total, 62 young adults (29 women; 18—28 years old) and 65 older adults (33 women; 65—89 years old) participated in the study. The young adults were undergraduate students who received credit towards an introductory psychology course requirement, whereas the older adults were community residents recruited through newspaper and internet ads who received a $25 honorarium. Table 1 presents the participant characteristics for the sample. The North Carolina State University IRB reviewed and approved the procedures associated with this research.

Table 1.

Means (SDs) by Age Group and Study

	Study 1: Gains		Study 2: Losses
Characteristic	Young (N=62)	Older (N=65)	Young (N=57)	Older (N=51)
Age*	19.3 (1.6)	74.0 (6.1)	19.0 (1.2)	72.1 (6.3)
Education (years)*	13.0 (0.8)	16.5 (2.3)	13.1 (1.1)	17.0 (2.5)
Vocabulary*	19.0 (4.7)	25.3 (5.5)	18.2 (6.4)	26.4 (6.6)
SF-36 physical health*	48.5 (6.4)	45.1 (5.01)	50.4 (6.1)	47.5 (5.9)
SF-36 mental health*	48.5 (10.4)	57.7 (5.8)	47.2 (9.6)	58.0 (6.8)
WAIS DSS*	84.0 (14.6)	60.0 (13.4)	87.1 (12.8)	61.3 (10.3)
WAIS LNS*	11.3 (2.7)	9.9 (2.2)	11.7 (2.5)	9.5 (3.0)
Numeracy*	9.5 (1.6)	8.0 (2.8)	8.9 (1.7)	7.8 (2.3)

Note. *Age groups within the same study significantly differ (p < .05).

Materials

Gambling Task.

We constructed a hypothetical gambling task that consisted of 64 pairs of bets. Each bet within each pair was characterized by the probability associated with winning a specific amount (e.g., 40% chance to win $30.00). As mentioned previously, each pair of bets consisted of a risky option (RO) that varied in the probability of winning, ranging from 5% to 95% in five percent intervals. We paired these variable probability ROs with sure alternatives (SA) in 32 of the problems, and with a risky alternative (RA) that had a 50% probability of paying out in the remaining 32 problems. Additionally, SAs and RAs had the higher expected values (EVs) compared to the ROs in half of the pairs, and lower EVs in the other half¹. We attempted to equate within-pair differences in EV across risky-risky and risky-sure pair types. The difference in expected value ranged from $2 to $3, except in one case where the difference was $0.50. Appendix A shows the bets used in each set.

Background Tests.

We collected basic demographic information (e.g., age, sex, education) and self-reported health (SF-36; Ware, 1993). We also assessed: (a) processing speed and working memory using the Digit-Symbol Substitution and Letter-Number Sequencing subtests from the Wechsler Adult Intelligence Scale, Third edition (WAIS-III; Wechsler, 1997); (b) verbal ability using the Vocabulary Test II (V-2) from the Kit of Factor-Referenced Cognitive Tests (Ekstrom, French, Harman, & Dermen, 1976); (c) numeracy using the Numeracy Scale (Lipkus, Samsa, & Rimer, 2001); and (d) strategy use with a modified version of the decision strategy questionnaire (Huang, Wood, Berger, & Hanoch, 2015) that assessed affective and deliberative approaches to the task².

Procedure

Participants first provided informed consent and completed a background questionnaire prior to completing the gambling task. Participants then received the following instructions about the task³:

“In this task, you will see different pairs of bets. For each pair, you will make a choice between two options, A or B. Each choice involves a chance to win a different amount of money and a chance to win nothing. You should choose the most advantageous bet. You will not see the outcome of each choice you make. Instead, you will continue to the next pair of bets, and will learn about your total earnings at the end of the session.”

Participants completed five practice problems before proceeding to the test problems. These practice problems allowed participants to become familiar with the type of problems and the presentation-response format but did not appear in the main task. We administered problems in separate blocks of 32 to reduce any potential impact of boredom and mental fatigue. Bet pairs from each set appeared without replacement in a quasi-random order such that each block of 32 problems contained 16 risky-risky and 16 risky-sure pairs. Additionally, the full range of probabilities associated with winning the RO was sampled in each block. Because we were primarily interested in decisions by description—ostensibly based in efficiency of deliberative processes—participants did not receive feedback about the outcomes of their choices nor additional compensation for hypothetical winnings. We consider the implications of these design decisions in the discussion. Participants completed the Digit-Symbol Substitution task between trial blocks and rated their strategy use during the gambling task immediately after the second block. The vocabulary test, tasks unrelated to the current study, and the numeracy and Letter-Number Sequencing assessments were then administered (Table 1), followed by debriefing and compensation.

Results

We examined the probability of selecting the bet in each pair with the higher EV. We conducted a 2 (Age group: young vs. older) x 2 (Sex: women vs. men) x 4 (Probability of winning the variable risk bet: 5–20% vs. 25–40% vs. 60–75% vs. 80–95%) x 2 (Optimal bet: alternative vs. RO) mixed ANOVA. This last factor contrasted performance in situations where the RA or SA had the higher EV with those in which the RO had the higher EV. Age group and sex were treated as between-subjects factors, whereas probability and optimal bet were treated as within-subjects factors. We ran separate analyses on risky-risky and risky-sure bets.

Risky-Risky Pairs

A main effect of sex, F(1, 123) = 8.79, p = .004, η² _partial = .07, indicated that men (M = .64, SE = .02) selected the bet with the higher EV more often than did women (M = .58, SE = .02). Additionally, a significant Probability x Optimal bet interaction, F(1.65, 202.61) = 258.185, p < .001⁴, η² _partial = .68, indicated that EV as well as the relative differences between the probabilities of the two bets influenced choices. As the probability associated with winning the RO increased, the probability of choosing the optimal RO increased, whereas that of selecting the optimal 50% RA decreased. A Sex x Probability x Optimal bet interaction, F(1.65, 202.61) = 3.47, p = .042, η² _partial = .03, suggested that these effects were somewhat stronger in women than in men (See Figure 1).

Figure 1.

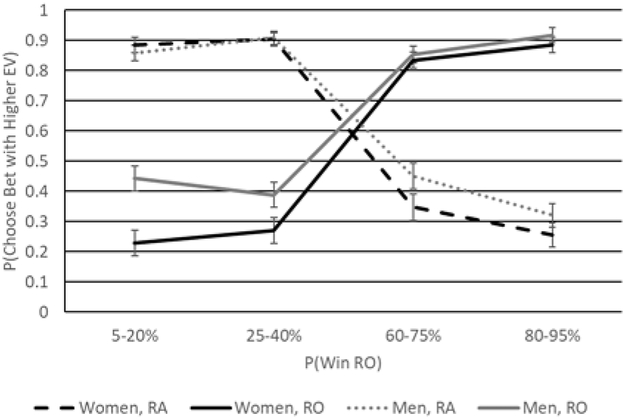
Choice probability for risky-risky pairs as a function of sex (black lines = women; gray lines = men), the probability associated with winning the RO, and the bet with the higher EV (dashed lines = SA has higher EV; solid lines = RO has higher EV). Error bars reflect standard errors.

We then explored whether these effects would remain after controlling for numeracy, processing speed, and working memory in an analysis of covariance (ANCOVA), reasoning that these abilities would have the strongest relationship to deliberation. Tests also revealed sex differences in processing speed, F(1, 121) = 17.93, p < .001, η² _partial = .13, and numeracy, F(1, 121) = 8.54, p = .004, η² _partial = .06, such that women (M = 77.10, SE = 1.69) scored better than men (M = 67.11, SD = 1.65) in the former, and that men (M = 9.32, SE = .28) scored better than women (M = 8.15, SE = .29) in the latter. Numeracy emerged as the only significant covariate, F(1, 111) = 6.64, p = .011, η² _partial = .06, reducing the three-way interaction involving sex to non-significance (p = .11).

This set of results essentially reflects the fact that participants, especially women, based their choices partly on the relative differences in probability between the two bets in each pair. They showed a greater likelihood of selecting the higher probability bet independent of EV. Variations in numeracy skills appeared to contribute to these sex differences. Importantly, we did not find any significant effects associated with age group, ps >.13.

Risky-Sure Pairs

A main effect of sex, F(1, 123) = 5.29, p = .023, η² _partial = .04, again reflected the fact that men (M = .58, SE = .02) had higher scores than women (M =.54, SE = .02). We also obtained a main effect of optimal bet, F(1, 123) = 581.41, p < .001, η² _partial = .83, a Probability x Optimal bet interaction, F(2.01, 246.79) = 10.99, p < .001, η² _partial = .08, and a Sex x Probability x Optimal bet interaction, F(2.01, 246.79) = 3.69, p = .026, η² _partial = .03. An Age x Sex x Probability x Optimal bet interaction, F(2.01, 246.79) = 3.06, p = .048, η² _partial = .02, although small, qualified these effects further. As shown in Figure 2, both young and older participants picked the high-EV SA (Ms range = .78 - .96) more often than the high-EV RO (Ms range = .13 - .33). This indicates a strong certainty bias, given that failure to select the high-EV RO means that participants opted for the SA even when inappropriate. In fact, across all Probability x Optimal bet conditions, participants selected the sure option—regardless of EV—67% to 96% of the time. Moreover, both sex and probability had a stronger influence on the choices of younger relative to older adults. Both young men and young women exhibited a strong focus on certainty, but men selected the high-EV RO at all probability levels (Ms = .43 vs. .22 vs. .21. vs. .33 from low to high probability, respectively) more than did women (Ms range = .13 vs. .12 vs. .14 vs .23 from low to high probability, respectively), suggestive of a reduced focus on certainty that resulted in better performance in men.

Figure 2.

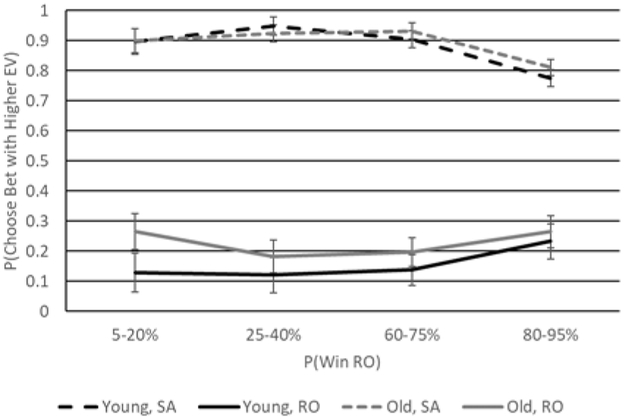
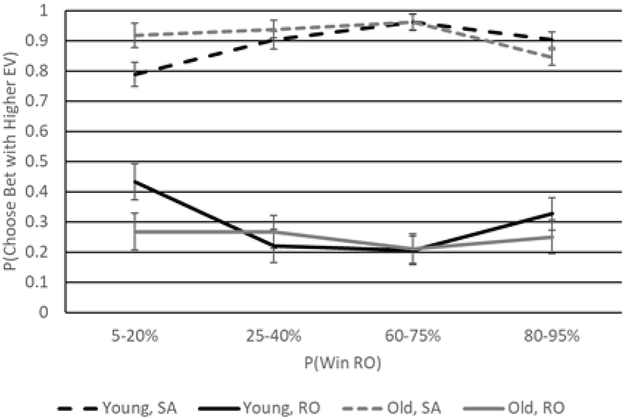
Choice probability in risky-sure pairs as a function of age (black lines = young adults; gray lines = older adults), the probability associated with winning the RO, and the bet with the higher EV (dashed lines = SA has higher EV; solid lines = RO has higher EV) in women (A) and men (B). Error bars reflect standard errors.

We conducted an ANCOVA to determine whether ability accounted for group differences in performance as in the case of the risky-risky pairs. We did not observe unique effects associated with ability or numeracy (ps > .20). The pattern of results with respect to age generally remained unchanged albeit reduced in strength to marginal significance (p = .052).

Comparison across Pairs

We compared performance across the two types of bet pairs on trials where the RO bet had the higher EV using a 2 (Age group) x 2 (Sex) x 4 (Probability of winning) x 2 (Pair type: risky-risky vs. risky-sure) mixed ANOVA to understand how the presence of a SA compared to an RA differentially influenced performance. Pair type was treated as a within-subjects factor. In this analysis, the relative differences in EV between RO and RA bets and that between RO and SA bets were approximately equal and the RAs and SAs had the lower EVs which means successful performance reflects selection of the ROs.

There were no significant effects due to age group (ps > .06). However, a Sex x Probability interaction, F(1.92, 236.09) = 4.88, p = .01, η² _partial = .04, qualified main effects of sex, F(1, 123) = 6.90, p = .01, η² _partial = .05, and probability, F(1.92, 236.09) = 94.99, p < .001, η² _partial = .44. Selection of the high-EV RO increased as the probability associated with winning increased for both women (Ms = .21 vs. .21 vs. .50 vs. .57 from low to high probability, respectively) and men (Ms = .40 vs. .32 vs. 53 vs. .60, from low to high probability, respectively), though men performed significantly better than women at the lower probability levels (ps < .038). This once again indicates that women tend to rely on relative differences in probability levels in making decisions, whereas men rely more on EV. This effect disappeared after controlling for ability. Finally, a Probability x Pair type interaction, F(2.45, 301.18) = 158.00, p < .001, η² _partial = .56, qualified a main effect of pair type, F(1, 123) = 360.88, p < .001, η² _partial = .75. As shown in Figure 3, the probability of selecting the high-EV RO significantly increased with the probability of winning it in the risky-risky bet pairs (Ms range = .34 - .90), but not in the risky-sure pairs (Ms range = .19 - .27). The presence of a sure option therefore resulted in a lower probability of selecting the high-EV alternative in general, and a reduced impact of probability on selection of the RO.

Figure 3.

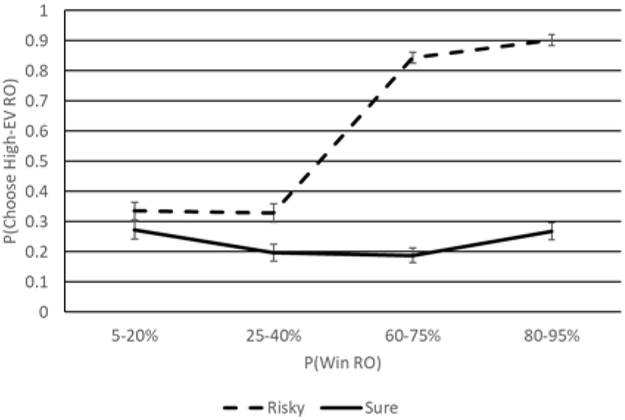
Choice probability as a function of the probability associated with winning the RO and pair type (dashed line = risky-risky pairs; solid line = risky-sure pairs) when the RO has the higher EV. Error bars reflect standard errors.

In sum, selection of the high-EV option varied greatly depending on (a) whether participants chose between two risky wins or between a risky win and a sure win, and (b) the relative difference in probability between two options in a pair in-question. Participants displayed a relatively strong focus on probability, tending to choose the bet with the highest probability of winning irrespective of its payoff. In the context of two risky bets, this tendency corresponded to performance benefits when the RO had the higher EV and performance decrements when the 50% RA did. This focus also corresponded to a pronounced certainty effect (i.e., an indiscriminate preference for a sure win) when participants could choose a SA. In other words, we can characterize the observed certainty effect as a special case of the focus on probability. Interestingly, although we observed a small age effect in risky-sure pairs that was accounted for by ability, age generally had minimal to no impact on performance.

Experiment 2

Participants

Sixty younger adults (28 women; 18—22 years old) and 51 older adults (29 women; 65—86 years old) were recruited and compensated as in Study 1. Table 1 presents the participant characteristics.

Procedure

The measures and procedure were identical to those in Experiment 1 with two exceptions. First, although we presented the same bets, we reversed the valence of the bets from positive (gain) to negative (loss), meaning that bets with the higher EV in the first study became those with the lower EVs in the current study. Additionally, participants received modified information about the task to reflect the focus on losses: “… Each choice involves a chance to lose a different amount of money.”

Results

We again examined the likelihood of selecting high-EV bets in 2 (Age group) x 2 (Sex) x 4 (Probability of losing variable-risk bet) x 2 (Optimal bet: alternative vs. variable risk) mixed ANOVAs on risky-risky and risky-sure pairs.

Risky-Risky Pairs

A main effect of age group, F(1, 107) = 7.80, p = .006, η² _partial = .07, showed that young adults (M = .63, SE = .01) had higher scores than older adults (M = .57, SE = .02). A Probability x Optimal bet interaction, F(1.65, 176.40) = 61.46, p < .001, η² _partial = .37, also showed, as in the case of gains, that this effect reflected a focus on relative differences in probability. Participants picked bets that had a lower probability of losing—RO or RA, irrespective of EVs—more often than they picked those that had a higher probability of losing. Specifically, the probability of selecting the high-EV RO decreased as the probability of losing associated with it increased (Ms = .77, 77, .47 & .43 from low to high probability, respectively). The likelihood of selecting the high-EV 50% RA, in contrast, increased across these same probability levels (Ms = .38, .44, .74, .78 from low to high probability, respectively). An Age group x Probability x Optimal bet interaction, F(1.65, 176.40) = 9.40, p < .001, η² _partial = .08, further qualified both of these effects. As shown in Figure 4, older adults showed a stronger focus on relative differences in probability than did young adults, with age differences accentuated at the lower and upper ends of the probability distribution. This pattern potentially suggests that loss aversion is particularly pronounced in older adults. Finally, we found an Age group x Sex x Probability interaction, F(3, 321) = 2.79, p = .04, η² _partial = .03, which indicated that men performed significantly better than women at the higher probability levels (ps < .03), and that older women generally scored the worst at these points. An ANCOVA revealed no significant ability-related covariates⁵ (ps > .06) and controlling for ability did not affect results.

Figure 4.

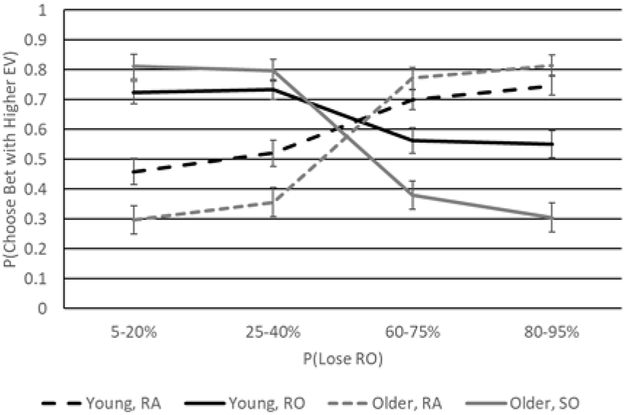
Choice probability for risky-risky pairs as a function of age (black lines = young adults; gray lines = older adults), the probability associated with losing the RO, and the bet with the higher EV (dashed lines = RA had higher EV; solid lines = RO had higher EV). Error bars reflect standard errors.

Risky-Sure Pairs

A Probability x Optimal bet interaction, F(2.10, 224.37) = 13.39, p < .001, η² _partial = .11, qualified main effects of probability, F(3, 321) = 10.89, p < .001, η² _partial = .09, and optimal bet, F(1, 107) = 97.79, p < .001, η² _partial = .48. Follow-up tests showed opposite patterns associated with probability based upon whether the RO or the SA had the higher EV in each pair. Specifically, when the RO had the higher EV, participants tended to perform better as the probability of losing increased, with scores at the lowest probability level being significantly different from the rest (Ms = .59 vs. .80, .81, & .83, ps < .001). Participants’ selection of the high-EV SA was generally low across probability levels, however, indicative of loss aversion. An Age group x Optimal bet interaction, F(1, 107) = 4.01, p = .048, η² _partial = .04, also qualified main effects of optimal bet and age group, F(1, 107) = 7.07, p = .009, η² _partial = .06. Young adults (M = .45, SE = .04) scored significantly higher than older adults (M = .31, SE = .04) when the SA had the higher EV (p = .01), but performed similarly to older adults when the RO had the higher EV (Ms = .75 vs. .77). This is suggestive of greater loss aversion in older adults; that is, older adults were more likely than younger adults to avoid a sure loss. Although a subsequent ANCOVA revealed numeracy as a significant covariate, F(1, 100) = 10.38, p = .002, η² _partial = .09, controlling for ability did not change results.

Comparison across Pairs

We once more examined how the results between pair types differed by conducting a 2 (Age group) x 2 (Sex) x 4 (Probability of losing) x 2 (Pair type: risky-risky vs. risky-sure) mixed ANOVA on the probability of selecting the high-EV RO. Analyses revealed main effects of probability, F(2.18, 233.02) = 12.63, p < .001, η² _partial = .11, and pair type, F(1,107) = 39.56, p < .001, η² _partial = .27. They also revealed significant interactions involving probability and age group, F(2.18,233.02) = 4.79, p = .003, η² _partial = .04, probability and pair type, F(2.13, 228.14) = 61.92, p < .001, η² _partial = .37, and age, probability, and pair type, F(2.13, 228.14) = 5.95, p = .002, η² _partial = .05. Finally, an Age group x Sex x Probability x Pair type interaction, F(2.13, 228.14) = 3.41, p = .032, η² _partial = .03, qualified these effects. This effect was retained in the ANCOVA controlling for ability despite significant covariates (working memory, F[1, 100] = 4.24, p = .042, η² _partial = .04; and numeracy, F[1, 100] = 8.88, p = .004, η² _partial = .08). As illustrated in Figure 5, pair type generally had a larger impact on older adults in comparison to young adults. The former group exhibited a greater tendency to avoid high probability losses, even when the RO had the favorable EV. This again underscores an age-related enhancement in loss aversion. Sex differences were largely due to young adults, with young men having scored significantly better than did young women at the higher probability levels (ps < .044).

Figure 5.

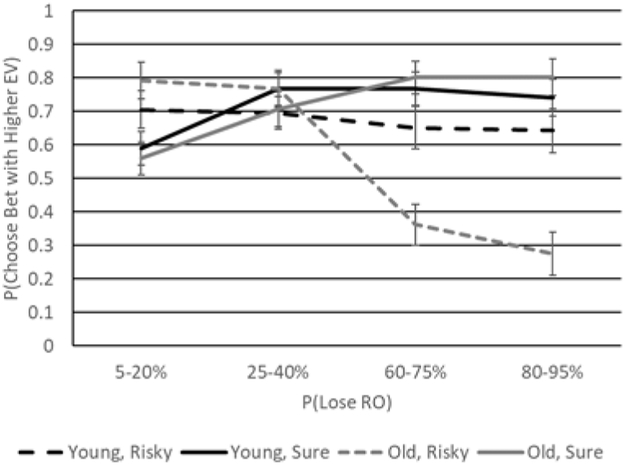
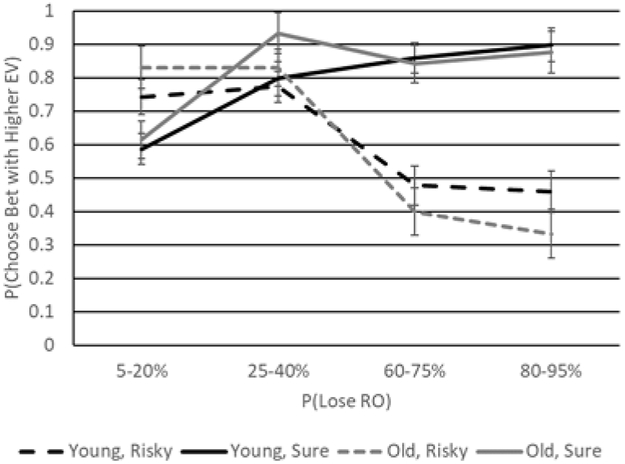
Choice probability as a function of age (black lines = young adults; gray lines = older adults), the probability associated with losing the RO when it had the higher EV, and pair type (dashed line = risky-risky pairs; solid line = risky-sure pairs) in women (A) and men (B). Error bars reflect standard errors.

This set of results demonstrates that participants considered both probability and EV when making choices between risky losses, with though the direction of effects contrasting with those found in the first study, which focused on risky gains. As expected, older relative to young adults exhibited a stronger focus on probability, showing greater avoidance of bets with relatively higher odds of losing. This focus had similar consequences for performance in these groups on both risky-risky and risky-sure problems. Comparisons of performance across the two pair types also showed slightly different sex patterns in the young and old but a general trend whereby women exhibited a somewhat stronger focus on probability than men. Controlling for ability did not alter these findings and perhaps reflects age-related differences in goals associated with avoiding losses.

Discussion

We investigated the degree to which young and older adults differentially used descriptive information about risk—expected value and probability—in two experiments that involved either decisions between possible gains or those between possible losses. We argued that we could attribute variability in performance to variations in the use of expected value, a reliance on relative differences in probabilities, and affective influences respectively reflective of complex and resource-demanding analytical processes, limitations or biases in information processing, and context-specific responding to gains versus losses. We expected that older adults in comparison to young adults would perform worse due to age-related limitations in cognitive ability as these limitations would reduce the use of expected value and heighten the focus on achieving high-probability wins and minimizing high-probability losses. We also tested the idea that, based upon developmental theory, older adults would exhibit greater risk aversion with gains and greater risk seeking with losses when compared to young adults.

Results indicated that participants altogether tended to show a weaker focus on expected value (or reward magnitude; Byrne & Worthy, 2016) and a strong focus on probability, basing their judgments on a simple comparison of probability levels. Specifically, they selected gains with low probabilities and losses with high probabilities at low rates. We observed this across pair types, but found somewhat exaggerated effects for risky-sure pairs. We argue that the effect of certainty found here and in other studies may partly reflect a focus on probability in response to cognitive challenges or task-related resource demands since its impact persisted even when bets with the preferred probabilities had lower expected values. The demands on cognitive resources in the assessment of risk accordingly became most apparent in situations wherein participants could choose whether to engage resources, such as by calculating the EV associated with a risky bet (i.e., the RO), or not to engage them, such as by selecting the option that requires little to no calculation of EV (e.g., the SA, since it always pays out).

Age differences in these strategies further depended upon the risk context. In terms of gains, we saw virtually no age effects. Closer examination of the small age effect on performance in risky-sure pairs suggested that older adults compared to young adults paid less attention to expected values. In terms of losses, we saw more pronounced age effects. Older adults in this context exhibited a stronger focus than young adults on avoiding high-probability losses, indicated by their lower likelihood of selecting (a) the optimal SAs in risky-sure problems, (b) the optimal ROs in risky-risky problems, and (c) the optimal 50% RAs in risky-risky problems and in comparisons across pair types. Controlling for ability reduced the impact of age in the case of gains but not in the case of losses. The fact that ability accounted for age effects at all supports prior findings (e.g., Pachur et al., 2017). However, that it did so in terms of gains but not losses alludes to different mechanisms. Whereas age differences in cognitive resources and their concomitant impact on information processing may partly explain performance in the former, older adults’ goals to avoid or minimize losses may further explain that in the latter. This interpretation is consistent with a goal-based account (e.g., Depping & Freund, 2011; Hess, 2015; Mata & Hertwig, 2011; Peters, Hess, & Auman, 2007) which argues that (a) age-related declines in ability can increase the demands associated with risk assessment and thereby older adults’ general susceptibility to affective influences, and (b) a shift from growth promotion in young adulthood to loss prevention in older adulthood can lead older adults to weigh or attend and react more strongly to information about losses relative to gains. Thus, decrements in resources and motivational shifts work interdependently to reduce the quality of older adults’ choices.

Regarding the impact of cognitive resources, a study conducted with mostly young and middle-aged adults (Pachur, Schulte-Mecklenbeck, Murphy, & Hertwig, 2018) provided some initial evidence for an association between resources and the processing of probability information. People in that study who exhibited greater loss aversion, sensitivity to outcomes, and sensitivity to probabilities also allocated more attention to losses relative to gains as well as to outcome and probability information, respectively. Examination of this phenomena in an aging context may help explain the degree to which the selective allocation of resources, with older adults being particularly selective, influences risky decision making. Previous research, for example, has suggested that a decreased sensitivity to expected value is partly associated with advanced age (e.g., Chen et al., 2014). Older adults may adapt to declines in their ability to process complex information by using affect-based processes (e.g., Zaval et al., 2015) in situations that place demands on cognitive resources (Hess, 2015). A disproportionate effect of affect in combination with less efficient processing abilities and greater selectivity in engaging such abilities (e.g., Hess, 2014) should therefore magnify the degree to which older adults discount important information in assessing risk. Our findings support these claims by demonstrating that processing limitations can drive inattention to expected value and reliance on probability, especially for older adults, who experience natural losses in their processing capabilities.

We also found an age-related reduction in performance related to losses and an increase in avoidance of sure losses. On one hand, these results generally support those from earlier work which shows that older adults compared to young adults exhibit lower sensitivity to expected value (Weller, Levin, & Denburg, 2010) and greater avoidance of sure gambles (Mather et al., 2012) related to losses, furthering the argument that varying effects between risk contexts underscores the activation of loss-related goals in older adulthood (e.g., Depping & Freund, 2011) over and above limitations in resource allocation. On another hand, these results contrast with findings from two studies that showed no age differences in selection of high-probability monetary gambles (Seaman et al., 2016; Seaman et al., 2018) and one study (Pachur et al., 2017) that demonstrated a positive association between sensitivity to risk-related information (i.e., outcomes and probabilities) and decision quality but, again, no age differences in such sensitivity. This latter study also revealed lower decision quality as well as lower aversion in older adults attributable to less systematic responding (i.e., higher response noise) and a positivity bias or motivational shift away from negative information (i.e., losses; Pachur et al., 2017)⁶. Although these and the current findings suggest that shifts in goals associated with aging contribute to differences in decision-making, the nature of the impact of these shifts still remains unclear since neither study included a direct assessment of the hypothesized goals. Finally, we explored sex differences in these patterns and observed a somewhat stronger bias in terms of a focus on probability in women relative to men. This provides consistent support for previous work in young adults showing that men weight expected value or reward magnitude more heavily than women and women weight reward probability or frequency more heavily than men (e.g., Cornwall, Byrne, & Worthy, 2018; Byrne & Worthy, 2016). Our findings offers some initial evidence to suggest that these differences may remain stable in older age.

The strengths of our study relate to its design. First, optimal and suboptimal bets across risky-risky and risky-sure pairs of problems had similar expected values. This may have made optimal gambles less obvious and required participants to maintain generally high levels of engagement. However, participants also had the option of choosing risky and sure bets with non-varying odds (i.e., 50% RAs and 100% SAs). The tendency to employ low-effort computational processes (e.g., comparing relative differences in probability) as opposed to demanding and complex ones (i.e., calculating EVs) could underlie the extent to which participants selected these alternatives. This set-up complements previous research based on cumulative prospect theory (e.g., Pachur et al., 2017) in some ways to the extent that it allowed us to examine the distinct contributions of a focus on probability and on certainty. Second, in keeping one of the risky gambles constant across pairs, we could ascertain whether preferences for the same RO depended on pair type and risk context.

One should also interpret the present findings in light of a few limitations. One set of these issues relates to the nature of our design and measures. First, we used a correlational, extreme age groups design, which limits our ability to draw causal conclusions about the relationship between age-related changes in ability and performance. Our young adult sample, which consisted of undergraduate students, may have had limited real-world decision-making experience, which could raise further questions about their comparability with our older adult sample. Second, we assumed that an enhancement of affective reasoning and loss-based goals in older adulthood as well as low-effort processing translated into an increased focus on or sensitivity to differences in probabilities. Future work could aim to measure goals (e.g., gain, maintain, minimize) expressly or use a different measure of strategies as well as assess subjective perceptions of effort or manipulate cognitive resources to replicate effects. Some researchers who have induced cognitive fatigue (e.g., Pocheptsova, Amir, Dhar, & Baumeister, 2009; Whitney et al., 2008), for instance, have found that individuals perform better when in an unimpaired cognitive state in other behavioral decision tasks. Finally, given some consistency of sex effects between in our study and those in tasks from different studies, new work could benefit from examining these effects in closer detail and the general mechanisms responsible for them (e.g., differences in financial expertise and ability).

Another set of issues concerns our gambling task. Specifically, we designed a fairly stylized task that allowed us to make inferences about the impacts of expected value, but limited our ability to ascertain the unique effects of reward probabilities and outcomes on decisions. In other words, due to constraints placed on expected value, reward probabilities and outcomes confound each other (i.e., bets with low probabilities also tend to have high outcomes and those with high probabilities tend to have low outcomes). This limitation may suggest an alternative account for the observed age effects. Rather than older adults having a heightened sensitivity to the frequency or probability of rewards already present in the general population, they simply react more strongly to any loss especially when steep (e.g., Worthy et al., 2015). Other studies could benefit from designing a task that dissociates these effects with different controls.

We also did not implement an incentive-compatible task in that participants based their decisions entirely on hypothetical rewards as opposed to real ones. The psychological equivalency of the task to real-world situations and behaviors, however, has implications for the observed findings as well as our interpretation of them. For example, some work has found that an age-related increase in probability discounting observed in hypothetical tasks (Seaman et al., 2016) does not hold up in incentive-compatible versions of these tasks (Seaman et al., 2018). Moreover, we used a description-only task that provided information about probabilities and outcomes, but no trial-by-trial feedback for individual choices. Although feedback could have strengthened effects by increasing the saliency of specific goals, it could also have weakened effects by (a) invoking goals at the local level that compete with those assumed to operate at the global level or (b) orienting participants to expected value and influencing deliberative processing. We consequently increased the interpretability of our findings by minimizing the impact of experience on perceptions of reward probability and magnitude during the task.

Conclusions and Implications

Lifespan accounts (e.g., Peters et al., 2007) indicate that older adults experience reductions in their ability to efficiently engage analytical processes, but maintain their affect-based abilities, which can lead to greater biases in decision-making (Hess, 2015). We have demonstrated that both young and older adults alike make poor choices when decision-making between probable gains and between probable losses involves having to consider relatively complex numerical information. A reduced ability to process information about risk, in combination with a general loss prevention focus, tended to lead to even greater biases in older adults.

The implications of these biases extend beyond simply deciding between two options. Older adults must make important decisions every day in increasingly complex contexts that vary in risk and uncertainty (e.g., assessing market effects on one’s retirement savings; Hershey et al., 2015). A diminished sensitivity to risk, although sometimes related to benefits in psychological well-being (Bruine de Bruin, Parker, & Strough, 2016), can increase the odds that older adults make real-world financial mistakes (Agarwal, Driscoll, Gabaix, & Laibson, 2009), become victims of fraud (Boyle, Yu, Wilson, et al., 2012; James et al., 2015; cf. Ross, Grossman, & Shryer, 2014), or, in the long-term, their risk of mortality (Boyle, Wilson, Yu, Buchman, & Bennett, 2013). The ability to use numerical information effectively can consequently have an important effect on decisions in the realms of finance (e.g., management of everyday and long-term finances and investments), medicine (e.g., making judgments about procedures and treatments), and personal safety (e.g., susceptibility to scams, fraud, or other forms of victimization). Interventions could perhaps effectively counteract some of the observed age-related biases associated with negative outcomes by educating older adults about expected value and providing training in various in real-world contexts. Thus, more research that specifically addresses the mechanisms associated with age-related biases in risky decision-making can inform professional practices and individual behaviors as well as policy efforts aimed at minimizing harm and protecting the health and well-being of older adults.

Appendix A

Bet Pairings in Gambling Task

	Variable risk options (ROs)
Probability (%)	5	10	15	20	25	30	35	40	60	65	70	75	80	85	90	95
Outcome	60	60	50	50	40	40	30	30	20	20	30	30	20	20	10	10
EV	3	6	7.5	10	10	12	10.5	12	12	13	21	22.5	16	17	9	9.5
	50% risky alternatives (RAs)
Low-EV options
Outcome	2	8	11	16	16	20	17	20	18	22	38	41	28	30	14	15
EV	1	4	5.5	8	8	10	8.5	10	9	11	19	20.5	14	15	7	7.5
High-EV options
Outcome	10	16	19	24	24	28	25	28	30	30	46	49	36	38	22	23
EV	5	8	9.5	12	12	14	12.5	14	15	15	23	24.5	18	19	11	11.5
	Sure alternatives (SAs)
Low-EV options	1	4	5	8	8	10	8	10	9	11	19	20	14	15	7	7
High-EV options	5	8	10	12	12	14	13	14	15	15	23	25	18	19	9	9

Note: outcomes and expected values (EVs) reflect dollar amounts ($). Low- or high-EV for the alternatives is relative to the RO option.

Appendix B

Decision Strategies Questionnaire

For the following statements, please indicate how much each statement applies to you by circling a number from (1) does not apply to me at all to (7) strongly applies to me.

1.	I solved the task instinctively or on a gut level.	1	2	3	4	5	6	7
2.	I tried to take all information into account and act systemically.	1	2	3	4	5	6	7
3.	I always looked at all the information before making my decisions.	1	2	3	4	5	6	7
4.	Success in this kind of task depends strongly on luck.	1	2	3	4	5	6	7
5.	Success in this kind of task depends strongly on skill.	1	2	3	4	5	6	7
6.	I mainly followed my feelings when making my decisions in the task.	1	2	3	4	5	6	7
7.	I made my decisions in the task through careful thinking.	1	2	3	4	5	6	7
8.	I made my decisions in the task based on intuition.	1	2	3	4	5	6	7