Distinct linear and non-linear trajectories of reward and punishment reversal learning during development: Relevance for dopamine's role in adolescent decision making

Abstract

Abnormalities in value-based decision making during adolescence have often been attributed to non-linear, inverted-U shaped development of reward-related processes. This hypothesis is strengthened by functional imaging work revealing an inverted-U shaped relationship between age and reward-related activity in the striatum. However, behavioural studies have mostly reported linear rather than non-linear increases in reward-related performance. In the present study, we investigated the mechanisms underlying the development of reward- and punishment-related processing across four age groups using a reversal learning task previously shown to depend on striatal dopamine. We demonstrate both linear and non-linear age effects on distinct components of reversal learning. Specifically, results revealed a linear shift with age in terms of valence-dependent reversal learning, with children exhibiting better punishment than reward reversal learning, adults exhibiting better reward than punishment reversal learning and adolescents exhibiting an intermediate performance pattern. In addition, we also observed a non-linear, inverted-U shaped relationship between age and valence-independent reversal learning, which was due to aberrant ability of adolescents to update behaviour in response to negative performance feedback. These findings indicate that the (linear or nonlinear) nature of the relationship between age and reward learning depends on the type of reward learning under study.

1. Introduction

Adolescence, or the transition period between childhood and adulthood, is characterized by increases in risky and reckless behaviour (Arnett, 1999, Casey and Jones, 2010). Studies using self-report and observational measures often report a peak in risk-taking and reward-seeking during adolescence (Arnett, 1999, Steinberg, 2010). Recent advances in developmental neuroscience propose that this increase in risk-taking reflects differential developmental trajectories of distinct brain regions (Casey et al., 2008, Figner et al., 2009, Somerville et al., 2010a, Somerville et al., 2010b). Specifically, evolutionary older subcortical regions, like the striatum, develop first, followed by development of prefrontal and parietal areas (Casey et al., 2008, Shaw et al., 2008). The imbalance between these early maturing subcortical regions, critical for the processing of affectively salient information, relative to less mature prefrontal areas, involved in top-down control, could account for non-linear, inverted-U shaped changes in risk-taking during development (Casey et al., 2008, Figner et al., 2009, Nelson et al., 2005, Somerville et al., 2010a, Somerville et al., 2010b). In line with this, some neuroimaging studies have shown that adolescents display exaggerated reward-related responses in the striatum compared with children and adults (Cohen et al., 2010, Galvan et al., 2006, Geier et al., 2010, Somerville et al., 2010a, Somerville et al., 2010b, Van Leijenhorst et al., 2010a, Van Leijenhorst et al., 2010b).

Ernst et al. (2005) have found that adolescents show not only stronger responses to rewards in the striatum, but also weaker responses to reward omissions in the amygdala than adults. Accordingly, they have suggested that increased risk-taking during adolescence might reflect an imbalance between the development of reward-related mechanisms, such as the striatum, and that of punishment-related mechanisms, such as the amygdala (Ernst et al., 2005, Ernst and Fudge, 2009). However, this hypothesis is not consistent with studies showing exaggerated responses in the amygdala of adolescents to both positive and negative emotional faces (Guyer et al., 2008, Hare et al., 2008, Somerville et al., 2010a). Furthermore, some studies have reported that reward-related striatal responses are attenuated, rather than exaggerated in adolescents compared with adults (Bjork et al., 2004, Bjork et al., 2010, Geier et al., 2010). Thus, there is discrepancy in the literature regarding the nature of the neural response underlying the non-linear, inverted-U shaped changes in self-reported risk- and reward-related processing during development.

In fact, there is also discrepancy regarding the degree to which self-reported non-linear changes in risk- and reward-related processing are accompanied by parallel non-linear changes in terms of performance on well-controlled laboratory tasks. On the one hand, consistent with self-report data and the suggested imbalance between reward- and punishment-related mechanisms (Ernst and Fudge, 2009), various studies have reported non-linear, inverted-U shaped changes in performance on reward-related tasks. For example, Cauffman et al. (2010) have used an Iowa gambling-like task to show an inverted-U shaped relationship between age and learning rates for advantageous decks (albeit not for disadvantageous decks). Furthermore, adolescents have been shown to exhibit reduced capacity to inhibit GO responses to happy faces in a GO-NOGO paradigm, compared with both children and adults (Somerville et al., 2010a). By contrast, other studies have revealed linear changes, for example, when choosing between high- and low-risk gambles or during feedback-based learning, so that performance was better in adults than in adolescents (Cauffman et al., 2010, Crone and van der Molen, 2004, Crone et al., 2008, Galvan et al., 2006, Koolschijn et al., 2011, van den Bos et al., 2009, van Duijvenvoorde et al., 2008, Van Leijenhorst et al., 2010a, Van Leijenhorst et al., 2010b). The lack of consistency in the functional neuroimaging data is not surprising given this discrepancy in the behavioural data. Indeed any analysis of functional neuroimaging data is only as good as the behavioural assay used to probe the neural mechanisms. The various tasks employed in these studies differed in terms of the particular demands of the task to measure behaviour. Accordingly, the differential performance patterns observed in these studies might reflect differential developmental trajectories of distinct psychological mechanisms of reward-related processing.

Here we aimed to resolve the discrepancy in the behavioural data by employing a paradigm that enabled the separate assessment of distinct components of reward-related processing. We aimed to compare age effects on reward- and punishment-learning, given recent models suggesting that risk-seeking might reflect an imbalance in the development of reward- and punishment-related mechanisms (Ernst and Fudge, 2009). To this end we employed a well-assessed paradigm measuring reversal learning based on unexpected reward and reversal learning based on unexpected punishment.

There are three distinct advantages of this paradigm. First, the neurobiological mechanisms underlying task-performance are well-characterized and known to involve striatum during reward-reversals and amygdala during punishment-reversals (Robinson et al., 2010a). In addition, task performance has been shown to implicate striatal dopamine as evidenced by studies employing neurochemical positron emission tomography (PET) (Cools et al., 2009) and dopaminergic manipulations (Cools et al., 2006, Cools et al., 2009, Robinson et al., 2010b). This enabled us to relate known neurobiological and dopaminergic changes during development (Doremus-Fitzwater et al., 2010, Kuhn et al., 2010, Shaw et al., 2008, Teicher et al., 1995, Wahlstrom et al., 2010) with age-related effects on the task. Second, reward- and punishment-learning are well-matched in terms of requirements for behavioural adjustment. Thus unlike prior studies, in which the expression of adequate punishment-learning depended more readily on behavioural shifting than did that of reward-learning, our paradigm required behavioural shifting in both conditions to the same degree. In fact our paradigm enabled the separate assessment of valence-dependent learning (in terms of the difference between the reward and punishment conditions), and of behavioural shifting (in terms of average performance across both conditions). Third, unlike most prior studies, the type of valence-dependent learning required for our task depends on Pavlovian rather than on instrumental learning mechanisms, such that adequate reversal requires the updating of stimulus-outcome rather than of response-outcome associations. This is particularly pertinent given recent suggestions that many forms of reward-related maladaptive behaviours, including enhanced risk-taking, might reflect abnormal Pavlovian control (Dayan et al., 2006, Flagel et al., 2008). Thus, we reasoned that a Pavlovian task might be more sensitive to detecting developmental changes in reward- and punishment-related learning than an instrumental task. Specifically, in accordance with current developmental theories (Ernst and Fudge, 2009), we hypothesize an inverted U-shaped relationship between age and valence-dependent learning, due to aberrant reward- relative to punishment-learning during adolescence compared with children and adults.

2. Methods

2.1. Participants

Sixty-one participants (22 male) between 10 and 25 years old were recruited from an elementary school, a high school, and Leiden University, in (the surroundings of) Leiden, the Netherlands. Participants were divided into 4 different age groups: Age group 1 with 15 participants of 10 or 11 years old (elementary school 7th grade), age group 2 with 15 participants of 13 or 14 years old (high school 2nd grade), age group 3 with 15 participants of 16 or 17 years old (high school 5th grade) and age group 4 with 16 participants between 20 and 25 years old (Leiden University). Participants had no (history of) psychiatric disorders or learning problems and did not use medication regularly. Written informed consent was given by the caretaker when the participant was under the age of 18, otherwise the participants gave informed consent themselves. Elementary school children were compensated with a bowling day, high school children and students were compensated with a small amount of money (3 and 6 euro's respectively). Non-verbal intelligence quotient (IQ) was measured with the Standard Progressive Matrices (Bauma et al., 1998, Raven et al., 1998). Also, participants were asked about the highest education level of both parents. Education level was scored as follows: 1 = primary education, 2 = secondary education/high school, 3 = middle-level applied education, 4 = higher professional education/bachelor and 5 = scientific education/master.

2.2. Task design

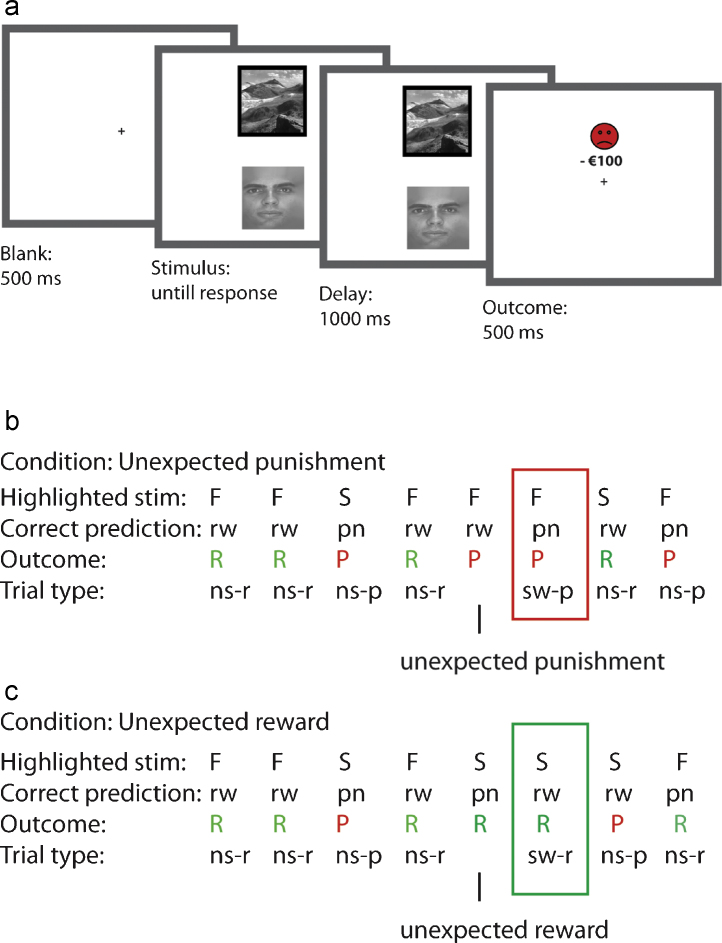
The task used in the present study enabled us to assess the ability to update reward- and punishment-predictions for pre-selected stimuli based on unexpected reward or unexpected punishment (Cools et al., 2006, Cools et al., 2008, Cools et al., 2009, Robinson et al., 2010a, Robinson et al., 2010b) (Fig. 1). Throughout the experiment, participants were presented with two vertically adjacent stimuli, a face and a scene. One of these stimuli was associated with a reward, while the other was associated with a punishment. On each trial, one of the two stimuli was highlighted with a black border. The task of the participants was to learn, based on experience, to predict whether the highlighted stimulus would be followed by a reward or a punishment. Participants indicated their prediction with a button press using the right and left hand for reward and punishment respectively (the outcome-response mappings were balanced across participants, see Table 1). A reward consisted of a green happy smiley, a “+100 euro” sign and a high-frequency jingle tone. Punishment consisted of a red sad smiley, a “−100 euro” sign and a low-frequency tone. After the prediction, the actual outcome was presented. The outcomes were directly coupled with the stimulus (100% deterministic) and did not depend on the participants’ response. Accordingly the outcome did not serve as direct performance feedback, or reinforcement. Instead, whether their response was correct or wrong had to be inferred from a comparison of the actual outcome with the predicted outcome. The outcomes administered in this task were abstract and did not correspond to actual monetary payoff. Nevertheless, the assumption that the positive and negative outcomes were perceived differentially has been confirmed by the empirically observed valence-dependent effects (see Section 3 and Cools et al., 2006, Cools et al., 2009, Robinson et al., 2010a, Robinson et al., 2010b).

Fig. 1.

Task design. (a) Example of a punishment trial. Two stimuli, a face (F) and a scene (S), were presented simultaneously. One of the two stimuli was highlighted with a black border and the task was to predict, with a button press, whether this stimulus was followed by a reward (R) or a punishment (P), after which the actual outcome was presented (100% deterministic). (b) Example of a trial sequence for the unexpected punishment condition. (c) Example of a trial sequence for the unexpected reward condition. The participant learned to predict rewards (rw) and punishments (pn) for the scene and face. The stimulus-outcome associations reversed between 4 and 6 consecutive correct predictions, signalled by either unexpected reward or unexpected punishment. Performance was measured on reversal trials immediately after the unexpected outcomes. Abbreviations: rw = reward; pn = punishment; ns-r = non-reversal reward trial; ns-p = non-reversal punishment trials; sw-r = reversal trial after an unexpected reward; sw-p = reversal trial after an unexpected punishment.

Table 1.

Subject demographics.

Age	N	Gender		Education			RAVEN IQ	Mapping		Order
		M	F	Participant	Father	Mother		R	L	rp	pr
Age 10–11	13	6	7	Primary 7th grade			113.4 (3.2)	5	8	7	6
Age 13–14	14	6	8	Secondary 2nd grade	4.3 (0.2)	4.0 (0.3)	118.4 (1.8)	6	8	8	6
Age 16–17	15	5	10	Secondary 5th grade	3.7 (0.3)	3.6 (0.2)	120.2 (2.5)	8	7	8	7
Age 20–25	16	5	11	University	4.3 (0.2)	4.0 (0.2)	122.8 (1.5)	8	8	8	8
Total	58	22	36		4.1 (0.3)	3.9 (0.2)	118.7 (2.3)	27	31	31	27

N = Number of participants, Gender: M = number of males, F = number of females, Education parents = average score of education level (standard error). RAVEN IQ = Intelligence quotient as measured with the RAVEN progressive matrices (standard error), Mapping (number of participants): R = reward prediction with right hand, L = reward prediction with the left hand. Order (number of participants): rp = reward condition − punishment condition, pr = punishment condition − reward condition.

The stimulus-outcome contingencies reversed multiple times, but only after attainment of a variable learning criterion which consisted of between 4, 5 or 6 consecutive correct predictions, to prevent anticipation of the reversal. This learning criterion was selected randomly at the beginning of each reversal stage. Reversals were signalled to the subject by either an unexpected punishment (presented after a stimulus was highlighted that was previously followed by reward) or an unexpected reward (presented after a stimulus was highlighted that was previously followed by punishment). Note that an unexpected outcome could represent two types of prediction errors: (i) a Pavlovian prediction error, which was positive when the outcome associated with the highlighted stimulus was better than expected (i.e. unexpected reward) and negative when the outcome associated with the highlighted stimulus was worse than expected (i.e. unexpected punishment), and (ii) an instrumental prediction error, which in this case was always negative, as it represented the fact that the outcome of the response was worse than expected (i.e. incorrect prediction). Performance was measured in terms of the proportion of correctly updated predictions on reversal trials after unexpected punishment (punishment reversal) and after unexpected reward (reward reversal) (see Section 2.3).

The face and scene were presented on a computer screen (top/bottom location randomized) until a (self-paced) response was made, which was followed by a 1000 ms delay and a 500 ms outcome. After the outcome, the screen was cleared for 500 ms, and the next pair of stimuli was presented. Each participant performed four experimental blocks: two reward blocks, in which reversals were signalled by unexpected rewards, and two punishment blocks, in which reversals were signalled by unexpected punishment. Participants were not made aware of this difference. The order of the conditions was approximately counterbalanced between participants (Table 1). Each block consisted of 120 trials (∼6.6 min), so that participants performed 480 trials in total (∼30 min).

Each block started with an initial acquisition stage and proceeded with a variable number of reversal stages, depending on the participant's performance. If participants made an incorrect response, the same trial was highlighted again on the next trial. The stimulus that was highlighted on the first trial of a reversal stage (i.e. the trial that was followed by an unexpected outcome signalling a reversal) was always highlighted again on the next trial, such that the participant was always required to switch responding on the reversal trials.

Two practice blocks (1 for each condition) were administered prior to the experiment and consisted of one initial acquisition stage and one reversal stage (the task proceeded to the reversal stage after 20 correct trials during acquisition). The practice block terminated after the participant reached 20 correct trials in the reversal stage or if the maximum of 80 trials was completed. All but one subject reached learning criterion in both stages of both practice blocks, indicating that they understood the task. Only one subject from age-group 3 failed to reach criterion in the acquisition stage of one of the practice blocks, but did understand the task as revealed by adequate performance on the second practice block and by the total number of completed reversal stages in the experimental blocks (20) (see Table 2 for the average number of reversals across the groups).

Table 2.

Total number of trials.

Age-group	Unexpected punishment condition			Unexpected reward condition
	Reversal	Non-reversal reward	Non-reversal punishment	Reversal	Non-reversal reward	Non-reversal punishment
Age 10–11	15 (1)	88 (4)	79 (4)	15 (1)	93 (7)	78 (5)
Age 13–14	20 (1)	92 (2)	86 (2)	19 (1)	90 (2)	84 (2)
Age 16–17	23 (1)	89 (2)	83 (1)	23 (1)	89 (3)	81 (2)
Age 20–25	22 (1)	85 (2)	86 (2)	23 (1)	89 (2)	83 (2)
Average	20 (1)	89 (3)	84 (2)	20 (1)	90 (4)	81 (3)

Average number of trials (standard error) per age-group and across participants for all six trial types.

2.3. Data analysis

Adequate reversal learning on this task depended on two separate forms of learning. First, it required participants to learn Pavlovian associations between stimuli and their rewarding or punishing outcomes. An unexpected reward constituted a positive Pavlovian prediction error, because it indicated that the stimulus was better than expected. Conversely, an unexpected punishment constituted a negative Pavlovian prediction error, because it indicated that the stimulus was worse than expected. Second, the task also required participants to learn from instrumental prediction errors. In instrumental terms, an unexpected reward constituted a negative rather than a positive prediction error, because the actual outcome of the response (unexpected reward) did not match the predicted outcome (punishment). Similarly, an unexpected punishment also constituted a negative instrumental prediction error. Accordingly, the ability to learn from instrumental prediction errors could be quantified in terms of the valence-independent reversal score, and the ability to learn from Pavlovian prediction errors could be quantified in terms of the valence-dependent, reward-signed reversal score. This enabled us to assess both valence-dependent (reward-signed) and valence-independent (unsigned) reversal learning. Valence-dependent, reward-signed reversal scores were calculated by subtracting the proportion of correct responses after unexpected punishment from the proportion of correct responses after unexpected reward. Conversely, valence-independent reversal scores were calculated by averaging the proportion of correct responses on reward- and punishment-based reversals. In addition, we also measured performance on the non-reversal trials, which were all trials that did not require stimulus-outcome updating (i.e. all trials except reversal trials).

All trials in the acquisition stage (before the first reversal) were excluded from analysis. In total, there were six different trial-types: three for the unexpected reward condition and three for the unexpected punishment condition. These three trial-types per condition were (i) reversal (i.e. trials that followed an unexpected outcome), (ii) non-reversal reward (i.e. trials that required reward-prediction, but no stimulus-outcome updating) and (iii) non-reversal punishment (i.e. trials that required punishment-prediction, but no stimulus-outcome updating). Proportions of correct responses were arcsine transformed (2 × arcsine(√x)) as is appropriate when the variance is proportional to the mean (Howell, 1997). Transformed proportions of correct responses and total numbers of reversals were analyzed using repeated measures ANOVAs (SPSS 16.0 for Windows, 2007) with the within-subject factor valence (2 levels: unexpected reward and unexpected punishment) and trial-type (3 levels: reversal, non-reversal reward and non-reversal punishment), and with the between-subject factor group (4 age groups). Significant valence-dependent and valence-independent effects (as revealed by significant valence × trial-type × group and trial-type × group interactions) were further investigated with one-way ANOVAs to assess whether these measures changed linearly with age (as revealed by a linear trend), or showed a peak over age-groups (as revealed by a quadratic trend). Significant trends revealed by these analyses were assessed further with Pearson correlational analyses between age and reversal learning scores.

IQ (as measured with the Standard Progressive Matrices, Bauma et al., 1998, Raven et al., 1998) increased linearly with age-group (F_(3,54) = 8.61, p = .005). Thus, we included IQ as a covariate in the repeated measures ANOVA as well as in the (partial) correlation analyses. To further investigate any effects of IQ, participants were divided in 4 groups based on their IQ scores using a quartile split; IQ-group 1 with 12 participants with IQ scores between 97 and 109, IQ-group 2 with 16 participants with IQ scores between 112 and 119, IQ-group 3 with 11 participants with IQ scores between 121 and 123 and IQ-group 4 with 19 participants with IQ scores between 124 and 136. The frequency distribution of the IQ scores did not allow us to form 4 bins containing exactly equal numbers of participants. For example there were 6 participants (10.3% of all participants) with the median (121) IQ score, cutting across the 50% boundary. One-way ANOVA with IQ-group as a between-subject factor was used to assess linear and quadratic effects of IQ.

Supplementary analyses were conducted to investigate whether the effects on the reversal trials, which all required response alternation, could reflect effects on the adoption of a win-stay, lose-shift strategy. In particular, this supplementary analysis was aimed at excluding the possibility that the observed age-effect on valence-dependent reversal reflected age-induced overcoming of an, in this case, maladaptive win-stay, lose-shift strategy. To this end, we calculated the proportion of correct predictions on non-reversal reward trials and non-reversal punishment trials after a correctly predicted reward outcome (win-stay and win-shift, respectively), and the proportion of correct predictions on non-reversal reward trials and non-reversal punishment trials after a correctly predicted punishment outcome (lose-shift and lose-stay respectively), averaged over the two blocks. Age-related strategy effects on trials following reward and punishment were tested separately with repeated measures ANOVA with the factors strategy (2 levels: stay, shift) and current outcome (2 levels: reward, punishment) as within-subjects factors and group as the between-subjects factor.

Greenhouse–Geisser corrections were applied when the sphericity assumption was violated. Levene's test was used to assess homogeneity of variance and Games–Howell correction was applied for post hoc testing when homogeneity of variances was violated.

3. Results

3.1. Demographics

Three participants were excluded based on poor performance: Two participants (one from age-group 1 and one from age-group 2) did not reach learning criterion in the acquisition stage in at least one of the two conditions, and one participant from age-group 2 performed 2 of the 4 experimental blocks at chance level (50%). After exclusion of these 3 participants there were 13 participants in age-group 1 (6 male), 14 participants in age-group 2 (6 male), 15 participants in age-group 3 (5 male) and 16 participants in age-group 4 (5 male). Demographics of the included participants are listed in Table 1. Education of the parents was not recorded in the youngest age-group. In the other three age-groups, education level of the parents did not differ between the groups (F₍₂₎ = 1.52). There was a significant effect of group on IQ (F_(3,54) = 3.96, p = .04). IQ measures increased linearly with age-group (F_(3,54) = 8.61, p = .005), although post hoc comparisons revealed a significant difference only between the youngest and oldest group (T₍₂₇₎ = 2.840, p = .03). In separate analyses we assessed whether there were any effects of gender, outcome-response mapping (i.e. whether reward and punishment was mapped to the left or right hand; counterbalanced across participants), or order of valence block (counterbalanced across participants). Repeated measures ANOVA with the factors valence (2 levels) and trial-type (3 levels) as within-subjects factors and mapping, order or gender as between-subjects factors did not reveal any effects of these latter factors. In addition, no effects of gender, mapping or order were found with repeated measures ANOVA on the reversal trials only with the factors valence (2 levels) as a within-subjects factor and mapping, order or gender as between-subjects factors.

3.2. Reversal learning

The average proportions of correct predictions across all trials for the four age-groups are shown in Fig. 2. The number of trials per age-group for each of the six trial-types is shown in Table 2. Accuracy per age-group for each of the six trial-types is shown in Table 3.

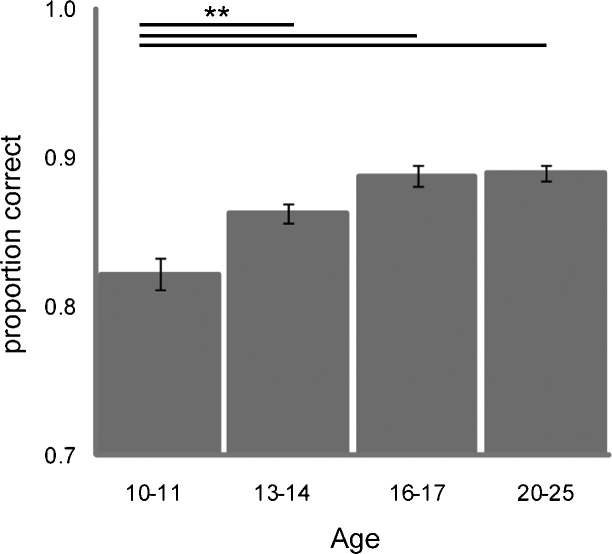
Fig. 2.

Overall accuracy (proportion of correct trials; y-axis) for the four different age-groups (x-axis). Overall accuracy was lower for the youngest (11–12 years) age-group compared with the three older age-groups. Error-bars represent the standard error of the mean. ** = significant difference at p < .005.

Table 3.

Accuracy per trial-type.

Age	Unexpected punishment condition			Unexpected reward condition
	Reversal	Non-reversal reward	Non-reversal punishment	Reversal	Non-reversal reward	Non-reversal punishment
Age 10–11	0.81 (0.03)	0.83 (0.03)	0.86 (0.02)	0.74 (0.03)	0.88 (0.01)	0.86 (0.02)
Age 13–14	0.94 (0.01)	0.91 (0.01)	0.91 (0.01)	0.92 (0.02)	0.91 (0.01)	0.91 (0.01)
Age 16–17	0.94 (0.02)	0.95 (0.01)	0.94 (0.01)	0.91 (0.03)	0.94 (0.01)	0.95 (0.01)
Age 20–25	0.85 (0.03)	0.94 (0.01)	0.95 (0.01)	0.91 (0.02)	0.95 (0.01)	0.94 (0.01)
Average	0.89 (0.02)	0.91 (0.01)	0.92 (0.01)	0.87 (0.03)	0.92 (0.01)	0.92 (0.01)

Average proportion correct trials (standard error) per age-group and across participants for all six trial types.

3.2.1. Overall performance irrespective of reversal and valence

Participants performed increasingly well with age, with overall performance reaching asymptote at adolescence. Repeated measures ANOVA with valence (2 levels) and trial-type (3 levels) as between-subjects factor, group as within-subjects factor, and IQ as a covariate revealed a main effect of group on accuracy across all trials (F₍₃₎ = 16.6, p < .001). One-way ANOVA of accuracy scores averaged across trial-types revealed a significant linear trend (F_(3,54) = 17.83, p < 001) as well as a significant quadratic trend (F_(3,54) = 6.254, p = .015). Post hoc comparisons revealed a significant increase in overall accuracy between age-groups 1 and 2 (T₍₂₅₎ = 3.234, p = .005), a marginal increase in overall accuracy between groups 2 and 3 (T₍₂₇₎ = 2.84, p = .056), while accuracy was similar in age-groups 3 and 4 (T₍₂₉₎ = −.16). Overall accuracy increased until maximum accuracy (0.89 ± 0.1) in age-group 3. Correlation analysis revealed a relationship between overall accuracy and IQ (r = .374, p_two-tailed = .004), but partial correlations between age and overall accuracy, when controlled for IQ, were still significant (r = .589, p_two-tailed < 001).

The effect of age-group on overall accuracy was paralleled by an effect of age-group on the total number of completed reversals (F_(3,54) = 7.609, p < .001). Importantly, this overall effect was not accompanied by a valence-dependent effect on the total number of completed reversals: Repeated measures ANOVA on the total number of completed reversals with the within-subjects factor valence (2 levels), the between-subjects factor group (4 levels) and IQ as a covariate did not reveal any differences between the total number or reward-reversals and punishment-reversals, or an effect of age on this difference (main effect of valence: F_(1,53) = .204, interaction effect valence × group: F_(3,53) = .63). This enabled us to assess age effects on valence-dependent accuracy scores in a manner that was not confounded by differences in the total number of trials included in the analyses.

3.2.2. Valence-dependent effects of age on reversal learning

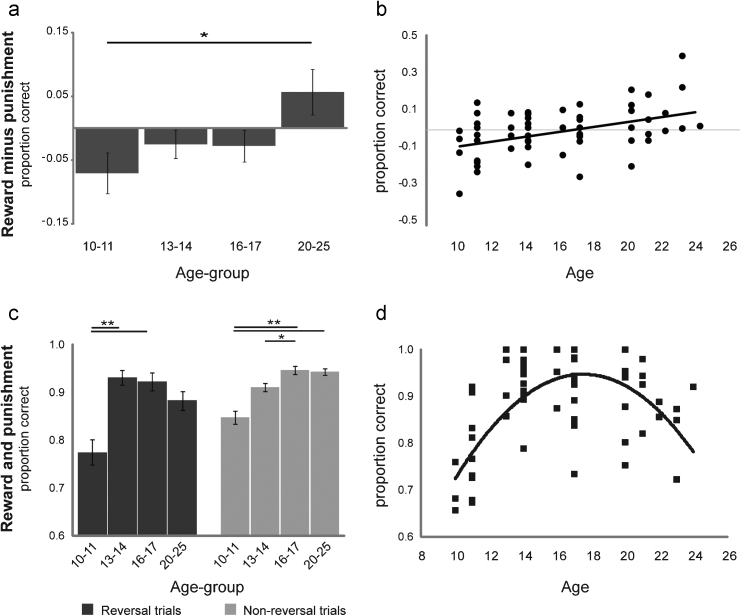
Inspection of the valence-dependent reversal scores (Fig. 3a and b) revealed a linear relationship with age, so that participants performed increasingly well with age on reward-reversals relative to punishment-reversals. This finding was confirmed by repeated measures ANOVA of the mean proportions of correct responses, with IQ as covariate, which revealed a significant 3-way interaction between valence, trial-type and group (F_(6,106) = 2.554, p = .040). Breakdown of this 3-way interaction by trial-type confirmed that the valence-dependent effect was significant for the reversal trials (valence × group: F_(3,53) = 3.176, p = .031) and not for the non-reversal trials (valence × group: F_(3,53) = .44; valence × group × trial-type (2): F_(3,53) = 2.339). Further analysis with one-way ANOVA of the valence-dependent reversal scores (proportion correct reward-reversals minus proportion correct punishment-reversals) revealed a significant linear trend (F_(3,54) = 3.71, p = .005), such that the balance between reward and punishment reversal learning shifted from better punishment reversal learning in the youngest age group to better reward reversal learning in the oldest age group. Post hoc comparisons revealed a significant difference between age group 1 and age group 4 (T₍₂₇₎ = 2.92, p = .022). There was no support for a peak in valence-dependent reversal learning as there was no significant quadratic trend (F_(3,53) = 1.42).

Fig. 3.

Age-related effects on valence-dependent and valance-independent reversal learning. (a) Valence-dependent effects of age on reversal learning. Relative reversal learning scores (y-axis) for the four different age-groups (x-axis) are calculated as the proportion correct reward-reversal trials minus the proportion correct punishment-reversal trials. (b) Significant linear trend between relative reversal scores and age (F_(3,54) = 3.71, p = .005). (c) Valence-independent effect of age on reversal and non-reversal performance. Accuracy scores on reversal and non-reversal trials (y-axis) for the four different age-groups (x-axis) are calculated as the average proportion of correct predictions on both reward- and punishment trials. (d) Significant quadratic trend between relative reversal scores and age (F_(3,54) = 19.45, p < .001). Error-bars represent the standard error of the mean. Symbols represent individual data points. **Significant difference at p < .005, *Significant difference at p < .05.

The observed linear age-related changes in valence-dependent reversal learning cannot be explained by differences in IQ between the groups. First, partial correlation analyses revealed a significant association between age and valence-dependent reversal scores after controlling for IQ (r = .359, p_two-tailed = .006). Second, repeated measures ANOVA of the reversal scores with the within-subjects factor valence and the between-subjects factor IQ-group did not reveal any significant effects of IQ-group (valence × IQ-group: F_(1,54) = 2.46), and one-way ANOVA of the valence-dependent reversal scores also did not reveal any linear or quadratic trend effects of IQ (linear: F_(3,54) = 2.25; quadratic: F_(3,54) = .16). Third, correlation analysis did not reveal any significant correlation between IQ and valence-dependent reversal scores (r = .15).

3.2.3. Differential developmental trajectories of reward and punishment reversal learning

Inspection of the reversal scores for each valence condition separately revealed that the linear shift with age towards better reward- relative to punishment-reversal was due to differential developmental trajectories of reward and punishment reversal learning (Fig. 4).

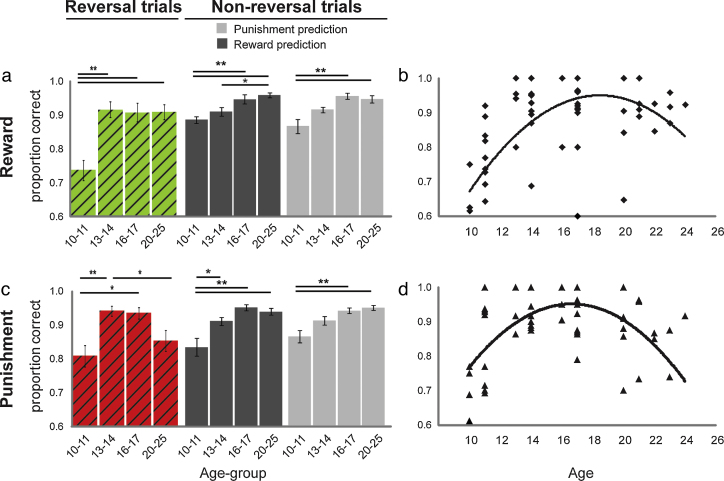
Fig. 4.

Age-related effects for the reward and punishment conditions separately. (a) Accuracy on the reversal, non-reversal reward and non-reversal punishment trials in the reward condition (y-axis) for the four different age-groups (x-axis). (b) Linear and quadratic trend between accuracy on reward-reversal trials and age (linear: F_(3,54) = 16.05, p < .001, quadratic: F_(3,54) = 9.73, p < .003). (c) Accuracy on the reversal, non-reversal reward and non-reversal punishment trials in the punishment condition (y-axis) for the four different age-groups (x-axis). (d) Quadratic trend between accuracy on punishment-reversal trials and age (F_(3,54) = 18.4, p < .001). Error-bars represent the standard error of the mean. Symbols represent individual data points. **Significant difference at p < .005, *Significant difference at p < .05.

On the one hand, follow-up repeated measures ANOVAs (with IQ as a covariate) of data from each valence condition separately revealed significant 2-way interactions between age-group and trial-type (3) for both the reward (F_(6,106) = 5.23, p = .001) and the punishment condition (F_(6,106) = 3.4, p = .013). These 2-way interactions reflected differences between age-effects on the reversal trials and age-effects on the non-reversal trials. Specifically, as discussed below (see Section 3.2.4), there was an inverted U-shaped relationship between age and reversal scores (but not non-reversal scores), for both the reward and the punishment conditions: Adolescents performed better than adults on these reversal (relative to non-reversal) trials, irrespective of valence.

However, in addition to this valence-independent effect, there was also a valence-dependent effect: The degree to which adolescents performed better than adults on reversal (relative to non-reversal) trials differed as a function of valence (as confirmed by the 3-way interaction, see Section 3.2.2). The nature of this difference was revealed by one-way ANOVAs of reward-reversal scores and punishment-reversal scores separately. The ANOVA of reward-reversal scores showed both a significant linear (F_(3,54) = 16.05, p < 001) and a significant quadratic trend (F_(3,54) = 9.73, p = 003), while ANOVA of punishment-reversal scores revealed only a significant quadratic trend (quadratic: F_(3,54) = 18.36, p < 001, linear: F_(3,54) = .61). Post hoc tests showed that reward-reversal increased near to maximum performance between age-groups 1 and 2 (T₍₂₅₎ = 4.79, p < 001), while remaining stable between age-groups 2 and 3 (groups 2–3: T₍₂₇₎ = .17; groups 1–3: T₍₂₆₎ = 4.35, p < .001) and between age-groups 3 and 4 (groups 3–4: T₍₂₉₎ = .03; groups 1–4: T₍₂₇₎ = 4.57, p < 001). Punishment-reversal, on the other hand, showed a peak in performance across age-groups. There was a significant increase in performance between age-groups 1 and 2 (T₍₂₅₎ = 3.48, p = .005), no difference between age-groups 2 and 3 (groups 2–3: T₍₂₇₎ = .31; groups 1–3: T₍₂₆₎ = 3.28, p = .011), and a performance decrease between age-groups 3 and 4 (groups 3–4: T₍₂₉₎ = −2.53, p = .086; groups 2–4: T₍₂₈₎ = −2.76, p = .045; groups 1–4: T₍₂₇₎ = .88).

3.2.4. Valence-independent effects of age on reversal learning

Inspection of the valence-independent reversal scores (Fig. 3c and d) revealed a nonlinear, inverted-U shaped relationship with age, so that participants performed best during adolescence, but poorly during childhood as well as early adulthood. This finding was confirmed by the omnibus ANOVA, which revealed a significant 2-way interaction between group and trial-type (F_(6,106) = 5.456, p = .001), irrespective of valence, as well as by significant group × trial-type interactions for each valence condition separately (see above). Breakdown of this omnibus 2-way interaction by trial-type revealed significant simple main effects of age-group both on the reversal trials (irrespective of valence) (F_(3,53) = 8.15, p < .001) and on the non-reversal trials (F_(3,53) = 11.325, p < .001).

The 2-way group × trial-type interaction was due to the finding that the relationship between age and reversal scores was inverted-U shaped, while that between age and non-reversal scores was linear (Fig. 3c). This was revealed by one-way ANOVAs on the reversal and the non-reversal scores (independent of valence), with age-group as a between-subjects factor. The ANOVA of reversal scores showed both linear, and non-linear effects of age-group (linear: F_(3,54) = 7.91, p = .007, quadratic: F_(3,54) = 19.45, p < 001), while the ANOVA of both non-reversal trial-types revealed only linear, but no non-linear effects of age (linear: F_(3,54) = 40.84, p < 001, quadratic: F_(3,54) = 3.93). Post hoc tests revealed that valence-independent reversal scores peaked during adolescence. Reversal scores were higher in age-groups 2 and 3 compared with age-group 1 (groups 1–2: T₍₂₅₎ = −4.863, p = .018, groups 1–3: T₍₂₆₎ = −4.398, p = .009), and decreased again in adults (groups 1–4: T₍₂₇₎ = −3.131). By contrast, accuracy on non-reversal trials did not show such a decrease. Non-reversal scores increased until age-group 3 (groups 1–2: T₍₂₅₎ = 2.83, p = .049, groups 2–3: T₍₂₇₎ = −3.03, p = .029) and did not differ between age-groups 3 and 4 (groups 3–4: T₍₂₉₎ = −.26, groups 1–4: T₍₂₇₎ = −5.51, p < 001).

3.3. Supplementary analyses

Both the reward- and the punishment-reversal trials required response alternation. Accordingly, it could be argued that the effects of age reflect effects on the tendency to alternate responses after punishment relative to reward, i.e., the application of a win-stay/lose-shift strategy. To asses this possibility, we analyzed the application of such a strategy on the non-reversal trials. This analysis indicated that age did not alter the degree to which participants alternated responding after punishment relative to reward. Thus there were no main effects of win-stay/lose-shift strategy or strategy × group interactions on the trials after reward (main effects of strategy: F_(3,54) = .06, strategy × group: F_(3,54) = .85) or on the trials after punishment (main effects of strategy: F_(3,54) = 2.24; strategy × group: F_(3,54) = .85).

3.4. Summary

A non-linear, inverted-U shaped relationship was observed between age and valence-independent reversal scores, so that participants performed better during adolescence than during both childhood and early adulthood. Thus, adolescents were more responsive to unexpected outcomes of their behaviour than were children or adults. However, this inverted-U shaped relationship was accompanied by linear shift with age in terms valence-dependent reversal scores, with adolescents performing at an intermediate level relative to children and adults. Specifically, the ability to reverse predictions based on unexpected reward relative to punishment improved linearly with age.

4. Discussion

The present study examined developmental differences in reward- and punishment-based reversal learning during adolescence in four different age groups between 10 and 25 years old. A reversal learning task was employed to assess effects of unexpected reward and unexpected punishment on reversal learning, while requirements for behavioural adjustments were well-matched between the conditions. This enabled assessment of the valence-dependent effects on reversal learning, by comparing effects of unexpected reward with effects of unexpected punishment on the updating of stimulus-outcome predictions. Following current theory (see Section 1), we had predicted that adolescents would display aberrant reward- relative to punishment-based reversal learning compared with children and adults.

In contrast to this hypothesis, results revealed a linear shift from better punishment- relative to reward-based reversal learning during childhood to better reward- relative to punishment-based reversal learning in young adulthood. Thus reward- relative to punishment-reversal score was not aberrant in adolescents, but rather intermediate relative to those of children and adults. This linear effect of age was remarkably robust and not mediated by non-specific factors such as IQ or other factors, such as the need for behavioural adjustment, which was matched between valence conditions. Moreover, it contrasted with the observation of a non-linear, inverted-U shaped relationship between age and valence-independent reversal learning. Thus the ability to shift responding following unexpected outcomes (irrespective of the valence of the outcome) was maximal in 13–17 year olds compared with 10–11 and 18–25 year olds. This age effect on valence-independent reversal learning could also not be accounted for by non-specific factors, such as motivation or arousal, because a similar inverted-U shaped pattern was not observed for the non-reversal trials, which improved linearly with age. Accordingly, this finding suggests that non-linear changes during adolescence might involve exaggerated tendency to shift responding based on negative performance feedback, instead of an imbalance between systems processing reward and punishment per se. Together, these data indicate the need to refine current models of overactive reward systems in adolescence.

One way to refine these models is by recognizing the existence of multiple mechanisms underlying reward learning. In particular, distinctions have been made between Pavlovian and instrumental mechanisms of learning (Balleine and O’Doherty, 2010, Maia, 2009, Maia and Frank, 2011). Such ideas have been formalized in actor-critic-like architectures, where optimal action selection involves (i) the encoding and updating of Pavlovian predictions of future outcomes associated with specific stimuli or states in the environment (the critic) and (ii) the instrumental selection of actions that, given those stimuli or states, are associated with the highest reward outcomes (the actor) (Balleine and O’Doherty, 2010, Maia, 2009, Sutton and Barto, 1998).

Adequate performance on the current paradigm depends on both learning mechanisms but their contributions are expressed in different manners. Critic-like Pavlovian learning depends on Pavlovian prediction errors, which are positive when the outcome associated with the highlighted stimulus is better than expected (unexpected reward) and negative when the outcome associated with the highlighted stimulus is worse than expected (unexpected punishments). Actor-like instrumental learning, on the other hand, depends on instrumental prediction errors, which in the present task are negative for both unexpected outcomes given that the outcome associated with the response was worse than expected (i.e. an incorrect prediction). Accordingly, any valence-dependent reversal effect on this task must reflect modulation of critic-like Pavlovian learning mechanisms. By contrast, any valence-independent effect that extends across the reward- and the punishment-reversal conditions of this task might reflect modulation of actor-like instrumental learning mechanisms. Based on this framework, we hypothesize that the observed linear relationship between age and valence-dependent reversal learning reflects a linear developmental trajectory of Pavlovian learning mechanisms. Furthermore, based on the observation that adolescents exhibited aberrant valence-independent learning, we hypothesize that this linear developmental trajectory of Pavlovian learning might be accompanied by a non-linear, inverted-U shaped development trajectory of instrumental learning.

This hypothesis concurs with current evidence for distinct neuro-developmental trajectories of the different learning mechanisms involved in our task. Thus, it has been suggested that the critic implicates the limbic striatum, including the ventral striatum and its strong connections with the amygdala, whereas the actor implicates the dorsal striatum (Montague et al., 1996). This has been supported by several human imaging studies, showing prediction error signals during instrumental learning in both dorsal and ventral striatum and prediction error signals during Pavlovian learning only in the ventral striatum (O’Doherty et al., 2004, Tricomi et al., 2009, Valentin and O’Doherty, 2009). More specifically, previous neuroimaging work with the present task has revealed neural responses in the ventral striatum for positive reward-signed prediction errors, and in the amygdala for negative reward-signed prediction errors while valence-independent responses were found in the dorsal striatum, dorsolateral prefrontal cortex and anterior cingulate cortex (Robinson et al., 2010a).

Critically, there is evidence that dopaminergic mechanisms in the dorsal and ventral striatum exhibit differential developmental trajectories. First, dopamine innervations of, and receptor density in, the dorsal striatum is maximal during adolescence, followed by back-pruning in late adolescence, while development trajectories of the ventral striatum (nucleus accumbens) develop more linearly and do not seem to show such declines after adolescence (Teicher et al., 1995, Doremus-Fitzwater et al., 2010, Kuhn et al., 2010, Wahlstrom et al., 2010). Furthermore, in the ventral striatum, D1 receptor density continues to increase until late adulthood, while D2 receptor density remains stable between adolescence and adulthood (Teicher et al., 1995, Wahlstrom et al., 2010). This increase of D1 relative to D2 receptor density in the ventral striatum is particularly pertinent here, because valence-dependent reversal learning on our task has been shown to depend critically on striatal dopamine transmission: Subjects with low dopamine function exhibit better punishment than reward reversal learning, while subjects with high dopamine function exhibit better reward than punishment reversal learning (Cools et al., 2006, Cools et al., 2009, Robinson et al., 2010b). Accumulating evidence from a combination of genetic neuroscience and computational modelling work indicates that these effects of dopamine on reward and punishment learning are mediated by action at D1 and D2 receptors respectively (Frank et al., 2007, Frank and Hutchison, 2009). Thus the shift from better punishment-based reversal learning in children to better reward-based reversal learning in adults might well reflect a combination of linear age-related increases in dopaminergic innervation of the striatum, and/or increases in the ratio of D1:D2 receptor density in the ventral striatum.

Our hypothesis might account for previous neuroimaging findings showing age-related inverted-U shaped neural changes during instrumental learning in the dorsal striatum (caudate nucleus), but not the ventral striatum (Cohen et al., 2010, Van Leijenhorst et al., 2010a) (but see Galvan et al., 2006). Interestingly, Cohen et al. (2010) reported that the location of prediction error-related neural responses shifted from the dorsal striatum in adolescents to the ventral striatum in adults, regions previously shown to reflect instrumental and Pavlovian prediction errors, respectively (O’Doherty et al., 2004). Taken together, the linear and non-linear patterns observed for valence-dependent and valence-independent reversal learning respectively fit well with the neurochemical developmental trajectories of dorsal striatum associated with instrumental learning mechanisms and of the ventral striatum associated with Pavlovian learning mechanisms.

One important implementation of this study is that decision making problems and increased risk taking during adolescence do not necessarily reflect disproportionate sensitivity to rewards and/or a lack of behavioural control (Casey et al., 2010, Ernst and Fudge, 2009, Somerville et al., 2010a, Somerville et al., 2010b), but instead might reflect aberrant responsiveness to recent negative performance feedback. Previous studies have used various paradigms that did not dissociate between possible different learning mechanisms. This study is one of the first to show enhanced feedback-based learning in adolescents, a finding that is perhaps not surprising, given the great number of high-impact transitions that adolescents undergo in this period. At the same time, it is also not difficult to imagine how aberrant responsiveness to recent negative performance feedback could lead to behaviour that is not optimal. In our noisy, stochastic environment, some feedback is misleading and should be ignored and adequate adaptation to this environment requires integration of more remote reinforcements, either in the future or in the past. Thus, behaviour is driven not only by recent, local reinforcements, but also by more remote reinforcements. In adolescents, this hypothesized aberrant focus on recent feedback at the expense of integration of more remote feedback might account for a broader range of decision making abnormalities in adolescence than an account that highlights reward oversensitivity, including paradoxical oversensitivity to immediate short-term feedback, e.g. from peers, at the expense of longer-term feedback from parents. Future work should investigate whether aberrant learning from immediately preceding negative feedback is indeed accompanied by reduced integration of more remote reinforcement either in the future or the past. These insights have considerable implications for current developmental models and might provide an interesting functional framework, within which to investigate developmental changes and impulsivity in adolescence or developmental disorders like attention deficit hyperactivity disorder (ADHD). Recent advances have already revealed interesting changes in ADHD patients compared with controls that are consistent with this framework. For example, ADHD is accompanied by reduced responses in the ventral striatum during reward-predictive cues (Scheres et al., 2007) and anatomical compression and expansion of the ventral and dorsal striatum respectively (Qiu et al., 2009, Sobel et al., 2010). Furthermore, insights relating decision making deficits during adolescence to dopamine functioning are pertinent given that various neuropsychiatric disorders that implicate dopamine, such as schizophrenia, have their onset in adolescence.

Some limitations need to be noted. First, the present study infers developmental trends based on between-subjects differences and it cannot be excluded that differences between groups might relate to unknown differences between the individuals within the groups. One such difference might result from the fact that subjects were recruited from educational institutions which could have biased the selection for different age groups. Further, IQ-scores were relatively high and differed between the youngest and oldest group. Although the present study specifically showed that IQ was not related to measurements of interest, it might have induced confounds for comparison between age-groups. Also, the relatively high IQ-scores across all subjects might have limited the generalizability of the results to lower IQ groups. Longitudinal studies are needed to avoid these confounds and confirm that our findings reflect developmental changes.

In summary, the present results demonstrate distinct developmental trajectories of different forms of reward-based learning. Accordingly they indicate that current models of the development of reward systems need to be refined. We propose that this may be achieved by considering the hypothesis that increased risk-taking in adolescence might reflect an imbalance between the critic-like Pavlovian control system and the actor-like instrumental control system such that the instrumental system, associated with the dorsal striatum is overactive relative to the Pavlovian system, associated with the ventral striatum. This hypothesis accounts for the pattern of performance observed in the present study, but is also consistent with evidence about distinct neurodevelopmental trajectories of different dopamine-dependent learning mechanisms. Clearly our proposal is speculative and requires further study, in which functional neuroimaging and dopamine psychopharmacology should be combined with the use of behavioural assays that enable the separate assessment of Pavlovian and instrumental learning.