Abstract
Mathematical performance is highly correlated with several general cognitive abilities, including working memory (WM) capacity. Here we investigated the effect of numerical training using a number-line (NLT), WM training (WMT), or the combination of the two on a composite score of mathematical ability. The aim was to investigate if the combination contributed to the outcome, and determine if baseline performance or neuroimaging predict the magnitude of improvement.
We randomly assigned 308, 6-year-old children to WMT, NLT, WMT + NLT or a control intervention. Overall, there was a significant effect of NLT but not WMT. The WMT + NLT was the only group that improved significantly more than the controls, although the interaction NLTxWM was non-significant. Higher WM and maths performance predicted larger benefits for WMT and NLT, respectively. Neuroimaging at baseline also contributed significant information about training gain. Different individuals showed as much as a three-fold difference in their responses to the same intervention.
These results show that the impact of an intervention is highly dependent on individual characteristics of the child. If differences in responses could be used to optimize the intervention for each child, future interventions could be substantially more effective.
Keywords: Cognitive training, Behavior prediction, Training personalization, Educational neuroscience
1. Introduction
Academic abilities, like mathematical attainment, are dependent on not only ability-specific training but also general cognitive skills. Mathematical performance is highly correlated with non-verbal reasoning abilities (Geary, 2011), working memory (WM) capacity (Gathercole et al., 2004, Bull et al., 2008, Dumontheil and Klingberg, 2012) and processing speed (Geary, 2011).
Given the close link between cognitive and academic abilities, one would expect that enhancing cognitive capacity through training would also improve academic performance. However, the results to date have been inconsistent with both positive and negative findings (Dahlin, 2011, Dunning et al., 2013, Bergman-Nutley and Klingberg, 2014, Cheng and Mix, 2014, Holmes and Gathercole, 2014, Schwaighofer et al., 2015). In this study, we explored the hypothesis that a combination of content-specific (i.e. mathematics) and WM training (WMT) might provide a greater benefit to improving mathematical ability when they are used in combination than when they are used individually. Key questions for such an approach are what the optimal combination is, and to what extent and for what reasons this differs between individuals. The second aim was thus to find predictors of the training gain. Both psychological testing and neuroimaging could potentially contribute to such predictions. Imaging has previously been used to predict the magnitude of response to a particular intervention (Hoeft et al., 2011, Supekar et al., 2013), but it has never been used to predict the amount of improvement among alternative interventions in children. In this study we try to make a step forward and inquire the differential predictive power of neuroimaging measures for different training types.
The current study included preschool (i.e. 6-year old) children because of the evidence that early academic skills are predictive of later achievements. For example, a meta-analysis of several longitudinal studies showed that mathematical ability at school entry was the best predictor of achievement in mathematics at age 13–15 (Duncan et al., 2007). Similarly, Jordan et al. (2009) measured number competency in kindergarten, as well as the growth of number competency from kindergarten to middle of first grade. Both measures explained the achievements in mathematics in third grade, emphasizing the importance of early number competence in order to set the children’s learning trajectories. In an evaluation of different aspects of early mathematical ability, performance on the number-line task in 6-year olds predicted the rate of development during the next five years (Geary, 2011). In the same study, cognitive performance, including visuo-spatial working memory, was also a significant predictor of future mathematical achievements. In the light of these previous results aiming at improve mathematical competencies in pre-school children seems to be the most effective ways to achieve stable and long lasting improvement.
In the current training, numbers were always represented using number-line. Addition and subtraction were performed through movements to the right and the left. Number-line training (NLT) was used because the number-line is an important construct in mathematics, and there is a strong tendency to represent numbers along a single spatial dimension (Hubbard et al., 2005, Booth and Siegler, 2008, Fischer et al., 2011). Moreover, this spatial representation is located in the intraparietal cortex (Simon et al., 2002, Cohen Kadosh and Walsh, 2009, Knops et al., 2009, Arsalidou and Taylor, 2011), possibly in areas shared by visuo-spatial representations used in WM tasks (Rotzer et al., 2009, Dumontheil and Klingberg, 2012). There has also been several studies showing that training using the number-line enhance mathematical performance (Kucian et al., 2011, Kaser et al., 2013, Link et al., 2013, Looi et al., 2016).
In order to acquire neural predictors of training-related improvement we chose to use BOLD activity during a WM task and grey matter volume (GMV). In a previous study BOLD signal during a WM task predicted math performance two years later in a developmental sample (Dumontheil and Klingberg, 2012). The use of a WM task for scanning had the additional benefit of providing less variability in behavioral performance within the scanner relative to an arithmetic task, as there is a great variability in number and basic arithmetic operation knowledge in 6 years old. The second measure used for prediction was GMV. It has been repeatedly shown that GMV in the parietal cortices is correlated to mathematical abilities, at least in dyscalculic children (Rotzer et al., 2008), premature born children (Starke et al., 2013), and children born with low weight (Isaacs et al., 2001). Moreover, a recent study found that GMV measured in the parietal cortex when children were in the first grade could predict mathematical performance in second grade (Price et al., 2016).
To investigate these questions, we randomly assigned 6-year-old children to four different combinations of NLT, WMT and reading training (RT). The RT was intended as active comparison training. Our hypothesis was that a combination of WMT and NLT would be more effective than either WM or NLT alone. Statistically, we evaluated the effect of NLT and WMT as well as the interaction between them. The outcome measure in all analyses was a combined measure of mathematical performance. Secondly, our aim was to investigate if the magnitude of the training grain could be predicted by baseline performance in mathematics or WM, or neuroimaging data. We therefore statistically evaluated the interaction between baseline data and type of training on the outcome measures.
2. Materials and methods
2.1. Subjects
The study participants, which included 239 typically developing 6-year-old children and 69 children who were included after screening with measures of WM performance, where subjects with lowest 20% performance on the WM tasks were included. No subjects had neurological or psychiatric diagnosis. To include a large number of children in this study, the project spanned two school-years; 160 of the children participated in the training in 2015 and 147 participated in 2014. Only children who trained for at least 30 days (mean = 38.1, SD = 3.4) were included in the analysis, which included 259 children (210 typically developing and 49 low WM; 132 boys; mean age = 80.3 months, SD = 3.5).
The children included in the behavioral study were invited to participate in the neuroimaging part of the study. Of the 308 children participating in the behavioral study, 62 agreed to participate in the neuroimaging study and 58 completed the neuroimaging protocol. In the analyses, we used an index of the subject’s movement in the scanner derived from fMRI acquisition, and only those subjects who completed at least one fMRI run (N = 45) were retained for further analysis. Movement parameters were also used as covariates in the analysis of BOLD signals. The imaging sample included 11 WMT/Read children (3 low WWM) 11 NLT/Read (2 low WM), 10 NLT/WMT (2 low WM) and 13 Read/Read (4 low WM).
2.2. Procedure
Two schools were contacted for the study, and they agreed to participate. A letter was sent to all families with a child attending the respective school. Written informed consent from both caregivers was obtained for all subjects.
Before and after the training period, subjects underwent a set of cognitive tests measuring abilities, including WM and mathematical abilities.
Participants were assigned to one of four training groups and underwent 30 min of training each school day for approximately 8 weeks. After performing a stratification based on a math test (verbal arithmetic WISC), school class and MR-participation, participants were assigned to one of the following groups: 50% WMT and 50% NLT, 50% WMT and 50% Reading, 50% NLT and 50% Reading, or 100% Reading.
The training took place in the classes, during regular school hours, always at the same time of the date, were compatible with regular curricular activity. For each class a teacher was responsible for ensuring the compliance of children with the training regime, and monitors the children during training.
2.3. Training programs
The training program was developed within our lab and is not available for commercial use. The program was designed for 6-year-old children and did not require previous knowledge of math, reading or tablets. The training program automatically logged out after 30 min of training and automatically switched between training programs after 15 min for the groups performing two types of training (e.g., WMT + NLT).
The WMT consisted of four different visuo-spatial working memory tasks. In each task a sequence of spatial positions had to be kept in WM and then reproduced by pointing on the screen. WM training with predominantly visuo-spatial tasks has previously been shown to be effective in increasing WM capacity (Klingberg et al., 2005). WM training using exclusively visuo-spatial tasks has also been shown to be effective in younger children (Thorell et al., 2009, Bergman-Nutley et al., 2011). Furthermore, the NLT was based on using a spatial representation of numbers, as explained in the introduction.
The NLT training consisted of tasks in which children used their index finger to drag along a number-line in order to respond. At the lowest and easiest level, Arabic numbers (e.g. “5”) was presented and the child then used a finger to drag out a line from zero to the correct position on the number-line. The line created by this movement (from 0 to 5) was built up by 5 smaller, 1-unit squares. This exercise thus connects four representations of a number: the Arabic number (5), a spatial position, a length and a number of objects. Addition was achieved by repeated dragging-lifting-dragging the finger to the right. Similarly, subtraction was achieved by dragging to the left. Addition and subtraction were thus associated with movements to the right and to the left, respectively. Negative numbers were also introduced. Children progressed through gradually higher levels, with more difficult trials. Difficulty was increased by first reducing the number of Arabic number markings on the number-line, by increasing the length of the number-line, the magnitude of the sums and also by introducing addition and subtractions with three terms (e.g. 2 + 1–2). There were no requirements of speeded responses.
About 15% of the NLT time was spend training on the ten-pals task (Butterworth et al., 2011). In this task, the children see a bar with length 0–10 appear to the left on the screen. To the right, there are always 10 different bars of length 0–10. They should choose the correct bar from the right so that the two bars add up to 10.
The reading task was based on the GraphoGame training which has been described in detail elsewhere (Lyytinen et al., 2009, Brem et al., 2010). In brief, children learn to associate letter or letter combinations with sounds. At more difficult levels, they progressed to identify short words, and at the most advanced levels performed easy cross-words.
In all three training types (WMT, NLT, RT) the difficulty level in the program automatically adapted to the subject’s performance so that the subject performed the training on a challenging level. In particular the algorithm ensured that the children reached accuracy between 60% and 70%, increasing or decreasing the level at needs. For WMT the levels simply corresponded to the length of the to-be-remembered sequence. For the NLT and the reading tasks, higher levels contained more complex and difficult items. As for the reading training, the first levels only involved matching of letter and sound, introducing grapheme and words further in the training.
2.4. Cognitive testing
2.4.1. Test of mathematics
Three math tests were administrated by a test leader in one-on-one session: addition, subtraction and verbal problem solving. The addition and subtraction tests were administered using iPads. Subjects were presented with an arithmetic problem in Arabic notation (e.g. 5 + 2=) and responded by pressing “buttons” on the screen marked 0–9. Numbers larger than 9 were entered by repeated pressing of the single buttons (e.g. 12 was entered by first pressing on the “1” button and then on the “2” button). There was thus no representation of the number-line for either presenting the problems or for responding.
The test of verbal arithmetic from the WISC-IV was manually administered. The test leader read out a problem aloud and the children responded verbally.
2.4.2. Test of working memory
Three working memory tests were used. One was administered on an iPad and contained a grid of dots (4 × 4) that were illuminated in a specific sequence, which the subject had to remember and repeat. The other two tests were the Block Repetition Forward (BRF) and Block Repetition Backwards (BRB) tests. In the BRF, the subject had to repeat a sequence of blocks shown by the test leader on a board in a specific order In BRB, the subject had to point at the blocks in the reversed order.
2.4.3. Test of reading
Reading skills were assessed using two different tasks. In the first task, the children had to recognize and pronounce letters in upper or lower case letters. In the second task, the children had to read non-words out loud.
2.5. Calculation of composite score
Composite scores were calculated for the math, working memory and reading tests. The means and standard deviations of the performance scores were calculated for the three math tests, the three WM tests and the two reading tests at baseline. Z scores were calculated for each of the tests, both at baseline and after training, using the means and standard deviations calculated using the data from baseline. The math component, WM component and reading component were then calculated as the average of the z-transformed math, working memory and reading tests, respectively (see Table 1).
Table 1.
Demographic variables, math performances and included subjects. The table reports the mean and sd of age, trained day and behavioral performance both at baseline and after training. It also reports the sex distribution within the training group and the number of children who participated in each training group with number of children who completed the training.
| WMT + NLT | NLT/Read | Read/Read | WMT/Read | |
|---|---|---|---|---|
| Age (months) (SD) | 80.9 (3.5) | 80.2 (3.9) | 80 (3.4) | 80 (3.2) |
| Sex F/M | 35/32 | 32/33 | 33/33 | 34/34 |
| Trained Days (SD) | 37.9 (3.5) | 37.8 (3.5) | 38 (3.5) | 38.6 (3) |
| Math Component pre (SD) | −0.03 (0.82) | −0.08 (0.88) | 0.04 (0.87) | 0.02 (0.8) |
| Math Component post (SD) | 0.62 (0.97) | 0.43 (0.88) | 0.52 (0.74) | 0.49 (0.89) |
| WM Component pre (SD) | −0.03 (0.78) | −0.03 (0.79) | −0.02 (0.75) | 0.08 (0.88) |
| WM Component post (SD) | 1.14 (0.88) | 0.33 (0.72) | 0.42 (0.75) | 1.19 (0.82) |
| Read Component pre (SD) | −0.11 (0.83) | −0.04 (0.88) | 0 (87) | −0.21 (0.76) |
| Read Component post (SD) | 0.76 (0.68) | 0.84 (0.58) | 0.91 (0.48) | 0.69 (0.66) |
| Included/Completed | 78/67 | 77/65 | 77/66 | 76/68 |
2.6. Statistical analysis and model selection
The effect of training on mathematical ability was tested using the following general linear models:
| Math Performance post = β0 + β1WMT + β2NLT + β3Mathbl + β4WMbl + β5WMT × NLT + β6WMT × WMbl + β7NLT × Mathbl + β8Cohort + β9Sex + β10Population + β11Age + ε |
We tested the effect of NLT, WMT and baseline performance for WM (WMbl) and math (Mathbl), together with their interactions. NLT and WMT were coded using two dummy variables that were equal to 1 if a child had performed the training or zero if they had not. The interactions to include were chosen on the basis of the Akaike Information Criterion (AIC) and the relative likelihood (RelL), an index of information loss proposed by Burnham and Anderson (2004). The linear model also included age, sex, cohort (subjects acquired in 2014 or 2015) and population (high or low WM level) as variables of no interest.
2.7. Behavior-based prediction
To assess the predictive power of the linear model selected using the AIC and the RelL we get unbiased prediction from the linear model using a leave-one-out cross validation. The accuracy of the predictions was calculated correlating the predictions with the measured math component after training. Furthermore, to show that including the type of training in the model significantly improved the prediction we used a permutation-based test: we repeated the leave-one-out procedure described in the previous paragraph 5000 times, randomly shuffling the WMT and NLT variables. In this way, we obtained an approximation of the distribution for the null hypothesis. If the correlation obtained using the real labels is higher than the 95th percentile of the distribution, one can conclude that including the training labels in the model improve the prediction with p < 0.05. The same permutation procedure was performed calculating the absolute mean error (AME) of the prediction.
2.8. Neuroimaging study
2.8.1. Neuroimaging acquisition
Magnetic resonance imaging data were acquired on a 3-T MRI medical scanner (Discovery General Electric) at the Karolinska Hospital in Solna, Sweden. The scanner was equipped with an 8-channel phased array receiving coil. The participants who volunteered for the imaging part of the study underwent two T1-weighted and fMRI acquisitions.
-
1)
T1-weighted images were acquired with a 1-mm3 isotropic voxel size (TE = 3.06 ms, TR = 7.9 ms, TI = 450 ms, FoV = 24 cm, 176 axial slices, flip angle of 12°).
-
2)
Functional MRI sequences were performed with a gradient-echo pulse sequence using a voxel size of 3 × 3 mm (TE = 30 ms, TR 2200 ms, FoV 22 cm, 46 axial slices, 3-mm thickness, flip angle of 70°). A total of 130 volumes were acquired.
2.8.2. ROI selection
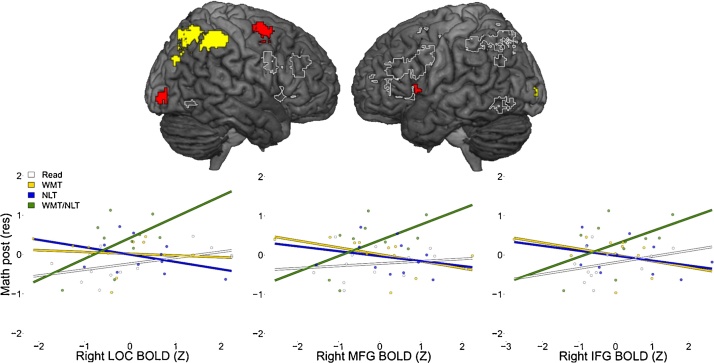
To find data-driven ROIs, we used the neurosynth software (Yarkoni et al., 2011). Briefly, neurosynth searches for a given term in a dataset of journals, finds papers containing the term and extracts the coordinates of the foci of the activation reported. The dataset of coordinates retrieved in a given search is divided into two groups according to whether the coordinates occurred in a paper that included the search term. Then, a giant meta-analysis is performed to produce statistical inference maps (Yarkoni et al., 2011). We searched for the terms “arithmetic” and “working memory” and downloaded the forward inference map. The forward inference rather than the reverse inference was chosen because we were interested in any region that could be associated to the two functions, rather than to regions that are specific for those functions. An explanation about the difference between forward and reverse inference maps is present in the original paper (Yarkoni et al., 2011). We thresholded the relative maps to p < 0.01 FDR. These maps showed the expected activations of the fronto-parieto-occipital network. The maps were then binarized, and an intersection of the two maps was determined (i.e. we performed a logical and between the two maps). This intersection map was then divided in clusters using marsbar (Brett et al., 2002). Only clusters bigger than 100 mm3 were retained The tested ROIs lying on the lateral surface of the brain are shown in Fig. 2; medial ROIs not shown in the figure were the posterior cingulate cortex, the left and right insula and the right caudate nucleus.
Fig. 2.
Imaging results predictive of training outcome. (a) The ROIs where a significant interaction between imaging parameters and training surviving multiple comparisons correction using FDR was found are shown in red, the ROIs where a significant interaction non surviving multiple comparisons correction are shown in yellow and non-significant regions are outlined in white, overlaid on a standard template. (b) Association between imaging parameters and improvement in the four training groups within the three regions of interest were an interaction surviving multiple comparisons was found. On the y axis are reported the residuals of math component after training over math at baseline, sex, population and age.
2.8.3. fMRI task
In the scanner, subjects performed a visuo-spatial WM task and a control task, similar to tasks previously used in scanning of children, and described in detail previously (Söderqvist et al., 2010, Dumontheil and Klingberg, 2012). A sequence of two (load 2) or four (load 4) symbols appeared, one at a time, within a 4 by 4 grid. A symbol representing the planet earth was used all the experimental tasks. The presentation of cues was followed by a question mark presented in one of the 16 squares. The subject had to decide if the question mark was in one of the squares were cues previously had been presented. They responded by pressing a two-key pad.
The control task was visually similar to the WM task (control 2, control 4), but the sequences presented were fixed, i.e. the mark always appeared in the upper left and upper right corners of the grid for load 2 control and in all the corners of the grid for load 4 control. Moreover, the question mark during the response period always appeared in the same position, centrally, during the control task. As a further difference, the mark using for showing the sequences was a drawing of the planet earth during the experimental task, while it was a drawing of the sun during the experimental task. The subjects were instructed to always press the NO button during the control task. Answers and reaction times were registered.
Each subject underwent two runs with 32 trials in each run (8 load 2 trials, 8 load 4 trials, 8 control 2 trials, 8 control 4 trials). Load 2 and control 2 trials lasted for 6000 ms while load 4 and control 4 trials lasted for 8000 ms. Each trial was followed by an inter trial interval of 2 s. Within each sequence, the planet which marked the spatial positions appeared, for each position, for 500 ms, followed by 500 ms delay in which the grid was empty. Before the last position cued and the appearance of the question mark there was a 1000 ms delay. The question mark remained on the screen for 3000 ms, that was the total time allowed for an answer.
2.8.4. fMRI model
The 130 functional volumes acquired with imaging were submitted to a standard preprocessing pipeline performed in SPM8 (http://www.fil.ion.ucl.ac.uk/spm/software/spm8/), which included slice timing correction, realignment, normalization to the MNI standard template and smoothing with a FWHM kernel of 6 mm. The toolbox Artifact Detection Tools (ART) was used to identify volumes corrupted by excessive motion (defined as a framewise displacement >2 mm or a root mean squared change in bold signal >9). The fMRI data were analyzed in an event-related fashion. For the first-level analysis, we used separated boxcar regressor modeled trials of the WM and the control task with durations equal to the trial durations (load 2, 6000 ms; load 4, 8000 ms). These regressors were convolved with the canonical hemodynamic response function together with regressors representing the full model for each session, which included the residual movement related artifacts, volumes marked as corrupted by the ART toolbox and the mean for the scan duration. For each subject, a first-level contrast of WM trial versus baseline was calculated, and the mean beta weight for this contrast was extracted from the ROIs described in the previous paragraph.
The functional volumes were also used to calculate the framewise displacement (FD) using fsl_motion_outliers (Jenkinson et al., 2012). The mean FD for the sample was 0.52 mm (± 0.52 mm).
2.8.5. Gray matter volume
T1-weighted images were segmented into gray and white matter using the unified segmentation procedure implemented in SPM 8 (Ashburner and Friston, 2005). The diffeomorphic anatomical registration through exponentiated lie algebra (DARTEL) algorithm (Ashburner, 2007) was then used to normalize the gray matter segmented images. The resulting modulated normalized GM images were smoothed using a 6-mm isotropic kernel at full-width at half-maximum (FWHM). These images were used to extract GMV from the previously described ROIs.
2.8.6. ROIs analyses
As a proof of principle, we tested the hypothesis that the imaging parameters measured in certain brain areas could predict the improvement that followed the training period for each training group (i.e., that an interaction exists between the imaging parameter and the training group). Because of this hypothesis, we focused the ROI analysis on the interactions between imaging parameters in the ROIs and the dummy variables coding for working memory and math training. The association between improvement in the math component and BOLD/GMV was tested in the ROIs. The model was as follows:
| Math Performance post = β0 + β1WMT + β2NLT + β3Imaging + β4NLT × WMT + β5NLT × Imaging + β6WMT × Imaging + β7NLT × WMT × Imaging + β8WMbl + β9Mathbl + β10Sessions + β11Cohort + β12Accuracy + β13Population + β14 FD + ε |
The Sessions variable controlled for the number of fMRI runs (i.e., some children only performed one out of the two fMRI runs in the protocol). The Cohort variable controlled for the possible effect of having acquired the data in two different cohorts (2014 and 2015). Accuracy referred to the child’s average accuracy in the scanner task. The variable Population represented whether the subject belonged to the low WM spectrum group. FD was the framewise displacement. Accuracy and session were only included for BOLD.
Since the present study was an exploratory study without a strict a priori anatomical hypothesis, multiple comparisons were unavoidable. Therefore, we controlled for multiple comparisons by using a correction based on the Benjamini and Hochberg procedure (Benjamini and Hochberg, 1995). The correction has been applied separately for BOLD and GMV.
The fitting of the models including the imaging parameter was assessed against a base model that included the same parameters, except for the imaging parameters using the RelL (Burnham and Anderson, 2004). The fitness was assessed separately for each ROI and only for the imaging parameter that led to a significant interaction (i.e. if BOLD signal in region A significantly interacted with training group, the model with BOLD signal from region A was compared to the base model).
The interaction terms reported in the results remained significant when BOLD signal and GMV outliers (defined as point lying outside 1.5 times the interquartile range above the upper quartile and below the lower quartile) were removed.
2.8.7. Leave-one-out cross-validation of the imaging finding
In order to obtain unbiased estimated of the predictive power of the linear models including the imaging parameters extracted from the ROIs in which we found a significant interaction between imaging parameters and training group we performed a leave-one-out cross validation. The overall performance was assessed correlating the predictions with the measured values. Furthermore, to show that including the imaging parameters in the model significantly improved the prediction, we used a permutation-based test: we repeated the leave-one-out procedure 5000 times, randomly shuffling the values of the imaging parameters. In this way, we obtained an approximation of the distribution for the null hypothesis. If the correlation obtained using the real labels is higher than the 95th percentile of the distribution, one can conclude that including the training labels in the model improve the prediction with p < 0.05. The same permutation procedure was performed calculating the absolute mean error (AME) of the prediction.
3. Results
3.1. Behavioral results
In the main analysis, we tested our hypothesis that a combination of WMT and NLT would be more effective than either one singularly, entering WMT and NLT in a factorial model using math abilities after training as dependent variable. Firstly, we examined the extent to which the training programs affected the performance in the typically developing children only (n = 210). As a second step, we repeated this analysis in the extended group (n = 259), which included children who demonstrated low measures of WM to allow for a larger range of abilities at baseline and therefore a larger power to determine whether a child’s ability at baseline affected the outcome.
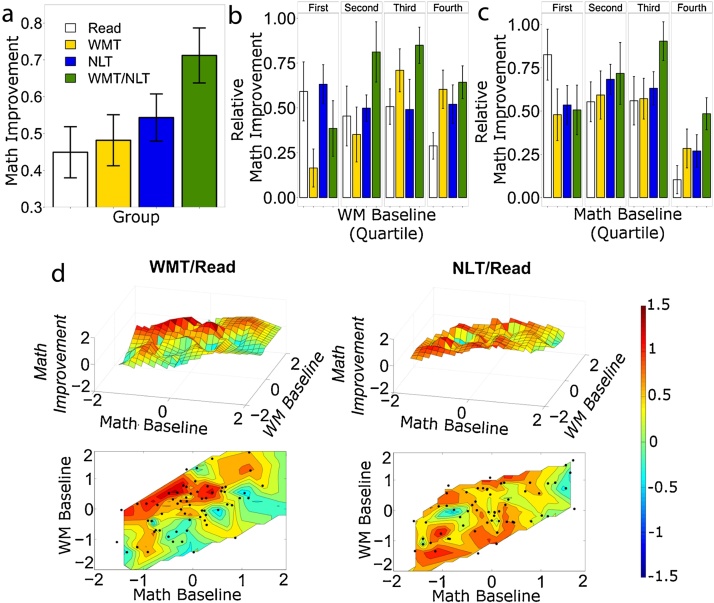
In the typically developing children (n = 210), there was a significant effect for NLT (F(1,198) = 6.65, p = 0.01, β = 0.09) but only a trend towards significance for WMT (F(1,198) = 3.04, p = 0.08, β = 0.06). There was no interaction between the two types of training (NLT × WMT) (F(1,198) = 2.27, p = 0.13, β = 0.05). There were significant interactions between WMT × WMbl (F(1,198) = 10.9, p = 0.001, β = 0.12) and trends toward interactions between NLT × Mathbl (F(1,198) = 3.24, p = 0.07 β = 0.06). The improvement in each training group is shown in Fig. 1a. The improvement in the combined group (NLT/WMT) was 0.72 standard deviations. This improvement was significantly greater than the improvement in both the Read (improvement = 0.44 standard deviations, t = 2.57, p = 0.011) and WMT groups (improvement = 0.48 standard deviations, t = 2.14, p = 0.034), with a trend towards greater improvement also compared to the NLT group (improvement = 0.54 standard deviations, t = 1.62, p = 0.097). The difference between NLT and WMT was not significant (p = 0.47). The NLT + WM group was the only group that improved significantly more than the RT group (all p > 0.42).
Fig. 1.
Improvement on the compound measure of mathematics. (a) Mean and standard error of the mean (sem) of the improvement for the 4 training groups (typically developing sample only); (b) interaction between WMbl and WMT on math improvement, the plot reports the mean and sem of the delta (i.e. the difference) between Mathpost and Mathbl; (c) interaction between Mathbl and NLT on math improvement; (d) surface and contour plots showing math improvement based on continuous interpolation of WMbl and Mathbl in the WMT/Read and NLT/Read groups. Measured points are represented by the black dots.
Next, we analyzed the full study sample (n = 259), which included both typically developing children and those with a low WM. The results of this analysis were consistent with those described above and indicated a significant effect of NLT (F(1,246) = 5.32 p = 0.02, β = 0.08), no effect of WMT (F(1,246) = 1.52, p = 0.19, β = 0.04) or interaction between the two types of training (NLT × WMT) (F(1,246) = 1.72, p = 0.19, β = 0.04). There were significant interactions between NLT and Mathbl (F(1,246) = 4.50, p = 0.034, β = 0.07) and between WMT and WMbl (F(1,246) = 3.09, p = 0.0001, β = 0.12) (Fig. 1b). Both of these interactions were positive, i.e., a high math or high WM score was associated with greater improvement in NLT or WMT, respectively. The interaction between Mathbl and WMbl was also significant (F(1,246) = 2.08, p < 0.001, β = −0.12). None of the control variables (sex, age, cohort and population) were significant (respectively p = 0.12, p = 0.23, p = 0.19, p = 0.095). This analysis thus showed a general effect of the NLT and strong interactions between baseline performance and type of training.
As a follow-up analysis, we used the statistical model used above in a sample only comprising subjects with high WM (i.e. above the median WM component at baseline). For this subsample (n = 127, NLT/Read = 29, WMT/Read = 37, WMT + NLT = 30, Read/Read = 31), the effect of WMT was significant (p = 0.044), but the effect of NLT was not (p = 0.4), highlighting the importance of baseline performance for the training outcome.
All the statistical analyses were modeled in a parametric fashion; however, to further illustrate the interactions between baseline performances and training gain, we assigned the subjects to quartiles according to their baseline performance in mathematics and WM and plotted their improvement in the math composite score (Mathpost − MathBL) (Fig. 1b, c). We also computed the mean improvement for the different quartiles and training groups. Subjects in the WMT group that were in the first quartile for the baseline WM performance improved by 0.2 standard deviations, whereas subjects in the same training group that were in the third and fourth quartiles improved by 0.70 and 0.60 standard deviations, respectively. Thus, subjects in the third and fourth quartiles showed an improvement that was approximately 3 times that of students in the first quartile. Fig. 1d illustrates math improvement as a continuous function of baseline performance.
We assessed the unbiased predictive power of the presented linear model using leave-one-out cross validation. The correlation between the predicted math component after training and the measured values was 0.84 (p = 2.2−16). The inclusion of training labels significantly improved the prediction (p = 0.0003). The cross-validated AME was 0.36, and the inclusion of training label significantly reduced it (p =0.003).
3.2. Imaging results
Next, we tested our hypothesis that information from an MRI scan at baseline could predict the training outcome differentially for the different training groups. The brain activity and GMV was assessed in 20 regions of interest (ROIs) derived from the intersection of two metanalyses identifying regions active during “working memory” and “arithmetic”.
On average, the children performed the task in the scanner above the chance level. In particular the accuracy [95% CI] was 62.5 [59.3–65.6] for load 2 and 59.5 [56.6–62.37] for load 4. The overall accuracy during the WM block (i.e. average accuracy for WM at load 2 and load 4) was significantly correlated with the WM component at baseline (r = 0.53, p < 0.001).
The interaction between BOLD signal during a WM task and training factor was significant in 5 of the ROIs (Table 2). Three of these regions (left inferior frontal gyrus, right middle frontal gyrus and right occipital gyrus) remained significant after corrections for multiple comparisons of the 20 ROIs using false discovery rate. The main effect of BOLD was not significant in any of the regions (all ps > 0.09).
Table 2.
Significant interactions between training type and imaging parameters; * p < 0.05; † p < 0.1 after correction for multiple comparisons using false discovery rate. Coordinates according to MNI for center of mass of each region. L = left; R = right.
| ROIs | ID | Modality | NLT | WMT | NLTxWMT | x, y, z (mm) |
|---|---|---|---|---|---|---|
| Occipital Pole (L) | R1 | BOLD | – | – | 0.031 | −20, −92, 0 |
| Inferior Frontal Gyrus (L) | R2 | BOLD | – | – | 0.007* | −49, 14, 6 |
| Occipital Pole (R) | R3 | BOLD | – | – | 0.013 | 17, −92, −2 |
| Middle Frontal Gyrus (R) | R4 | BOLD | – | – | 0.006* | 30, 2, 56 |
| Lateral Occipital (R) | R5 | BOLD | – | 0.047† | 0.003* | 33, −89, −3 |
| Parietal Cortex (R) | R6 | GMV | – | 0.005† | – | 33, −55, 46 |
Next, we analyzed the structural data from the 45 subjects with complete imaging data. The interaction between GMV and training factor was significant in the right parietal cortex ROI (p = 0.005), although it did not survive FDR correction (Table 2). The main effect of GMV was not significant in this region (p > 0.12). Fig. 2 shows the tested ROIs overlaid to a standard anatomical template. The scatterplots show the relationship between BOLD signal and the math improvement (defined as the residuals of math abilities after training over math at baseline, sex, population and cohort) for the four different groups. It can be noticed that for the three ROIs the relationship show a similar patter, with negative or almost flat slope in the WMT, NLT and read group and positive slope for the WMT + NLT group.
All models including the imaging parameter from the regions showing significant interaction with training group significantly reduced the Akaike Information Criterion (AIC) (model including BOLD from the Left IFG compared to base model, p = 0.021, model including BOLD from the Right MFG compared to base model, p = 0.002, Right LOC p = 0.001, model including GMV from the Right Parietal ROI compared to base model p = 0.001), except for the model including BOLD from the left occipital pole (p = 0.07). This shows that they contributed significant information, above and beyond that provided from the behavioral measures.
The models including behavioral measures and the BOLD signal from left IFG, the right MFG or the right LOC all lead to significant correlation between predictions and measured variable (0.73, 0.75 and 0.74 respectively). In order to confirm that including the imaging parameter in the model improved the prediction, we compared these correlations to the null distribution obtained by randomly permuting the imaging parameter values. The introduction of the imaging parameters significantly improved the correlation (left IFG p = 7.285−09, right MFG p = 2.997−09, right LOC p = 3.821−09). These results show that the improvement in prediction obtained introducing the imaging parameters from these regions is significant.
4. Discussion
The aims of the current study was first to investigate the impact of WMT, NLT and the interaction between the two on a compound measure of mathematics. Secondly, we aimed to identify baseline characteristics that predicted relative gain for the different types of training.
In the entire sample, we found a significant effect of NLT but not WMT, although there was a trend for the typically developing group (p = 0.08). Training using the number-line thus transferred to mathematical tests without a number-line. This study did not include a group training arithmetic without a number-line and we can thus not specify the added benefits of using a number-line. Our results, however, are consistent with other studies showing the benefit of using a number-line for mathematical training (Kucian et al., 2011, Kaser et al., 2013, Link et al., 2013, Looi et al., 2016).
There was no significant interaction between NLT and WMT. However, among the four training groups, the combination of NLT + WMT showed the largest absolute change (Fig. 1a). The NLT + WMT was also the only group which significantly differed from the reading control group. We interpret this as partial support for the hypothesis that the visuo-spatial WM skills provide a scaffold to hold spatial representations in mind that are useful for number-line processing and mathematics in general. However, all of these effects were the general trends, and as it turn out, the more interesting effects were how much children differed in their response to the intervention.
Both baseline measurements of WM and mathematics interacted with type of training, showing that individuals’ responses to the interventions differed depending on their abilities at baseline. The general trend was that children with higher WM improved more from WMT than other children, and that children with higher math at baseline improved more from the NLT. To illustrate this, a split-half analysis showed that children with higher WM at baseline improved their mathematical ability significantly by training WM, while the effect of NLT was not significant. Another way to illustrate this is to divide children into subgroups based on their baseline performance (Fig. 1 b,c). The impact of a specific training could vary by a factor of three among individuals, depending on their baseline performance. A plot of the continuous response pattern (Fig. 1d) suggests that the interactions could be more complex than the linear models capture. A more highly tuned and non-linear model of the interaction effects based on the individual profiles could be a better solution. The strong interaction of training effect with baseline performance is consistent with what has been described as the Matthews effect, noted already by Thorndike (Thorndike, 1908). The neurobiological factors causing lower plasticity, i.e. gain during training, could be the same factors that contribute to slower development and therefore lower performance at baseline(Klingberg, 2014). This dependency could also explain some inconsistencies between WM training studies, and negative findings for children selected because of their low WM (Roberts et al., 2016). The results show that WMT in principal could have a positive effect on mathematics. It is possible that children with initially low WM will need substantially more training to reach the same effects, but that can only be determined by additional studies.
The interaction between baseline characteristics and type of training is a prediction of the magnitude of training gain. However, we do not interpret this as an indication that baseline performance should be a guideline for categorical decision to administer one intervention rather than another. Instead, the conclusions that we think should be drawn is that baseline performance could indicate the relative mix, in terms of percent time spent on each type of training. In this case, we only evaluated two types of training, but future research could expand this into more areas. For example, in children with high WM at baseline, one would predict that a mixture of NLT and WMT, with more time spent on WMT, would be most beneficial.
The neuroimaging data also contributed to the prediction about how much an individual benefitted from each intervention. Both gray matter volume and brain activation during a WM task were associated to math improvement differentially in the four training groups (Table 2, Fig. 2). The association was significant beyond the contribution of the baseline behavioral variables. In particular, subjects with higher BOLD activity in the right MFG, the right LOC or the left IFG benefitted more from the combination of NLT and WMT (Fig. 2). It has previously been shown that BOLD signal during WM task performance can contribute to predict normal development of mathematical ability (Dumontheil and Klingberg, 2012), above the predictions that can be made from behavioral testing of WM. The neural mechanisms underlying this interaction are unclear. But this significant interaction is proof-of-principle that neuroimaging data can contribute to individualize interventions.
In the analysis of the structural MRI data it was found that subjects with higher grey matter volume in the right parietal cortex benefitted more from the WMT than subjects in the same training group with lower grey matter volume (p = 0.005), although this association did not survive correction for multiple comparisons. Brain activity in the right parietal region, especially the intraparietal sulcus, has been associated with WM capacity (Todd and Marois, 2004), and abnormal morphology of this area has been associated with dyscalculia (Molko et al., 2003, Cohen Kadosh and Walsh, 2007). Moreover, cortical thickness of the intraparietal sulcus has been associated with WM capacity (Darki and Klingberg, 2015). Structural measures can give more predictive information of development of WM above and beyond the predictions made from psychological measures (Ullman et al., 2014, Darki and Klingberg, 2015). It is therefore reasonable that structural measures of this region could give information about the impact of WMT on mathematical ability. Moreover, the parietal cortex is related to both mathematics and WM, but the exact localization of the two functions in relation to each other is still unclear. If some parts are more related to WM than mathematics, this could explain why the grey matter value interacts with WMT and not NLT.
The present study thus shows that imaging at baseline is associated with relative improvement or development, confirming finding from previous study (Hoeft et al., 2011, Dumontheil and Klingberg, 2012, Supekar et al., 2013, Ullman et al., 2014). Furthermore, the present findings make one step further in showing that the combination of imaging and behavior can predict an individual’s response to different types of interventions.
One limitation of the present study was the lack of a passive control group. Reading and mathematical abilities are highly correlated in children (Hecht et al., 2001), and it is possible that reading training was beneficial for some subjects (Glenberg et al., 2012). Future studies might include more subjects, more subgroups, long-term follow-up and training on other cognitive abilities that have been associated with mathematical ability, such as reasoning (Primi et al., 2010, Fischer et al., 2011) and spatial abilities (Fischer et al., 2011). A second limitation of the study is the limited number of children in each training group included in the neuroimaging arm. Although overall the neuroimaging analyses included a total of 45 subjects, each of the four groups only included between 10 and 13 subjects. For this reason, the neuroimaging results should be regarded as preliminary, and a replication using a bigger sample is needed.
In conclusion, we found that NLT was effective on the entire population, that WMT was effective in subjects with higher WM baseline, but that in most cases, the combined training was most effective. Both psychological and neural measures at baseline provide information that can be used to tailor an optimal training paradigm for the individual child. Depending on their baseline characteristics, individuals differed by a factor of three in their responses to a particular intervention. If these inter-individual differences were understood, operationalized and implemented, then future interventions could show a significantly larger improvement in their effectiveness.
Competing interest
The authors declare no competing financial interests.
Acknowledgments
We thank R. Cohen Kadosh for useful comments on a previous version of this article. This study was supported by a grant from the Marcus and Amalia Wallenberg Foundation awarded to TK. The training software is non-commercial and available upon request.
References
- Arsalidou M., Taylor M.J. Is 2 + 2=4? Meta-analyses of brain areas needed for numbers and calculations. Neuroimage. 2011;54:2382–2393. doi: 10.1016/j.neuroimage.2010.10.009. [DOI] [PubMed] [Google Scholar]
- Ashburner J., Friston K.J. Unified segmentation. Neuroimage. 2005;26:839–851. doi: 10.1016/j.neuroimage.2005.02.018. [DOI] [PubMed] [Google Scholar]
- Ashburner J. A fast diffeomorphic image registration algorithm. Neuroimage. 2007;38:95–113. doi: 10.1016/j.neuroimage.2007.07.007. [DOI] [PubMed] [Google Scholar]
- Benjamini Y., Hochberg Y. Controlling the false discovery rate—a practical and powerful approach to multiple testing. J. R. Stat. Soc. B Methods. 1995;57:289–300. [Google Scholar]
- Bergman-Nutley S., Klingberg T. Effect of working memory training on working memory, arithmetic and following instructions. Psychol. Res. Psychol. Factor. 2014;78:869–877. doi: 10.1007/s00426-014-0614-0. [DOI] [PubMed] [Google Scholar]
- Bergman-Nutley S., Sîderqvist S., Bryde S., Thorell L.B., Humphreys K., Klingberg T. Gains in fluid intelligence after training non-verbal reasoning in 4-year-old children: a controlled, randomized study. Dev. Sci. 2011;14:591–601. doi: 10.1111/j.1467-7687.2010.01022.x. [DOI] [PubMed] [Google Scholar]
- Booth J.L., Siegler R.S. Numerical magnitude representations influence arithmetic learning. Child Dev. 2008;79:1016–1031. doi: 10.1111/j.1467-8624.2008.01173.x. [DOI] [PubMed] [Google Scholar]
- Brem S., Bach S., Kucian K., Guttorm T.K., Martin E., Lyytinen H., Brandeis D., Richardson U. Brain sensitivity to print emerges when children learn letter-speech sound correspondences. Proc. Natl. Acad. Sci. U. S. A. 2010;107:7939–7944. doi: 10.1073/pnas.0904402107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brett M., Anton J.-L., Valabregue R., Poline J.-B. Region of interest analysis using an SPM toolbox. the 8th International Conference on Functional Mapping of the Human Brain. Sendai, Japan. 2002 [Google Scholar]
- Bull R., Espy K.A., Wiebe S.A. Short-term memory, working memory, and executive functioning in preschoolers: longitudinal predictors of mathematical achievement at age 7 years. Dev. Neuropsychol. 2008;33:205–228. doi: 10.1080/87565640801982312. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Burnham K.P., Anderson D.R. Multimodel inference—understanding AIC and BIC in model selection. Soc. Method Res. 2004;33:261–304. [Google Scholar]
- Butterworth B., Varma S., Laurillard D. Dyscalculia: from brain to education. Science. 2011;332:1049–1053. doi: 10.1126/science.1201536. [DOI] [PubMed] [Google Scholar]
- Cheng Y.L., Mix K.S. Spatial training improves children’s mathematics ability. J. Cogn. Dev. 2014;15:2–11. [Google Scholar]
- Cohen Kadosh R., Walsh V. Dyscalculia. Curr. Biol. 2007;17:R946–R947. doi: 10.1016/j.cub.2007.08.038. [DOI] [PubMed] [Google Scholar]
- Cohen Kadosh R., Walsh V. Numerical representation in the parietal lobes: abstract or not abstract? Behav. Brain Sci. 2009;32:313. doi: 10.1017/S0140525X09990938. [DOI] [PubMed] [Google Scholar]
- Dahlin K.I.E. Effects of working memory training on reading in children with special needs. Read. Writ. 2011;24:479–491. [Google Scholar]
- Darki F., Klingberg T. The role of fronto-parietal and fronto-striatal networks in the development of working memory: a longitudinal study. Cereb. Cortex. 2015;25:1587–1595. doi: 10.1093/cercor/bht352. [DOI] [PubMed] [Google Scholar]
- Dumontheil I., Klingberg T. Brain activity during a visuospatial working memory task predicts arithmetical performance 2 years later. Cereb. Cortex. 2012;22:1078–1085. doi: 10.1093/cercor/bhr175. [DOI] [PubMed] [Google Scholar]
- Duncan G.J., Claessens A., Huston A.C., Pagani L.S., Engel M., Sexton H., Japel C., Dowsett C.J., Magnuson K., Klebanov P., Feinstein L., Brooks-Gunn J., Duckworth K. School readiness and later achievement. Dev. Psychol. 2007;43:1428–1446. doi: 10.1037/0012-1649.43.6.1428. [DOI] [PubMed] [Google Scholar]
- Dunning D.L., Holmes J., Gathercole S.E. Does working memory training lead to generalized improvements in children with low working memory? A randomized controlled trial. Dev. Sci. 2013;16:915–925. doi: 10.1111/desc.12068. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fischer U., Moeller K., Bientzle M., Cress U., Nuerk H.C. Sensori-motor spatial training of number magnitude representation. Psychonomic Bull. Rev. 2011;18:177–183. doi: 10.3758/s13423-010-0031-3. [DOI] [PubMed] [Google Scholar]
- Gathercole S.E., Pickering S.J., Knight C., Stegmann Z. Working memory skills and educational attainment: evidence from national curriculum assessments at 7 and 14 years of age. Appl. Cogn. Psychol. 2004;18:1–16. [Google Scholar]
- Geary D.C. Cognitive predictors of achievement growth in mathematics: a 5-year longitudinal study. Dev. Psychol. 2011;47:1539–1552. doi: 10.1037/a0025510. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Glenberg A., Willford J., Gibson B., Goldberg A., Zhu X.J. Improving reading to improve math. Sci. Stud. Read. 2012;16:316–340. [Google Scholar]
- Hecht S.A., Torgesen J.K., Wagner R.K., Rashotte C.A. The relations between phonological processing abilities and emerging individual differences in mathematical computation skills: a longitudinal study from second to fifth grades. J. Exp. Child Psychol. 2001;79:192–227. doi: 10.1006/jecp.2000.2586. [DOI] [PubMed] [Google Scholar]
- Hoeft F., McCandliss B.D., Black J.M., Gantman A., Zakerani N., Hulme C., Lyytinen H., Whitfield-Gabrieli S., Glover G.H., Reiss A.L., Gabrieli J.D.E. Neural systems predicting long-term outcome in dyslexia. Proc. Natl. Acad. Sci. U. S. A. 2011;108:361–366. doi: 10.1073/pnas.1008950108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes J., Gathercole S.E. Taking working memory training from the laboratory into schools. Educ. Psychol. 2014;34:440–450. doi: 10.1080/01443410.2013.797338. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hubbard E.M., Piazza M., Pinel P., Dehaene S. Interactions between number and space in parietal cortex. Nat. Rev. Neurosci. 2005;6:435–448. doi: 10.1038/nrn1684. [DOI] [PubMed] [Google Scholar]
- Isaacs E.B., Edmonds C.J., Lucas A., Gadian D.G. Calculation difficulties in children of very low birthweight—a neural correlate. Brain. 2001;124:1701–1707. doi: 10.1093/brain/124.9.1701. [DOI] [PubMed] [Google Scholar]
- Jenkinson M., Beckmann C.F., Behrens T.E., Woolrich M.W., Smith S.M. Fsl. NeuroImage. 2012;62:782–790. doi: 10.1016/j.neuroimage.2011.09.015. [DOI] [PubMed] [Google Scholar]
- Jordan N.C., Kaplan D., Ramineni C., Locuniak M.N. Early math matters: kindergarten number competence and later mathematics outcomes. Dev. Psychol. 2009;45:850–867. doi: 10.1037/a0014939. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kaser T., Baschera G.M., Kohn J., Kucian K., Richtmann V., Grond U., Gross M., von Aster M. Design and evaluation of the computer-based training program calcularis for enhancing numerical cognition. Front. Psychol. 2013;4:489. doi: 10.3389/fpsyg.2013.00489. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klingberg T., Fernell E., Olesen P., Johnson M., Gustafsson P., Dahlstrîm K., Gillberg C.G., Forssberg H., Westerberg H. Computerized training of working memory in children with ADHD—a randomized, controlled trial. J. Am. Acad. Child Adolesc. Psychiatry. 2005;44:177–186. doi: 10.1097/00004583-200502000-00010. [DOI] [PubMed] [Google Scholar]
- Klingberg T. Childhood cognitive development as a skill. Trends Cogn. Sci. 2014;18:573–579. doi: 10.1016/j.tics.2014.06.007. [DOI] [PubMed] [Google Scholar]
- Knops A., Thirion B., Hubbard E.M., Michel V., Dehaene S. Recruitment of an area involved in eye movements during mental arithmetic. Science. 2009;324:1583–1585. doi: 10.1126/science.1171599. [DOI] [PubMed] [Google Scholar]
- Kucian K., Grond U., Rotzer S., Henzi B., Schonmann C., Plangger F., Galli M., Martin E., von Aster M. Mental number line training in children with developmental dyscalculia. Neuroimage. 2011;57:782–795. doi: 10.1016/j.neuroimage.2011.01.070. [DOI] [PubMed] [Google Scholar]
- Link T., Moeller K., Huber S., Fischer U., Nuerk H.-C. Walk the number line—an embodied training of numerical concepts. Trends Neurosci. Educ. 2013;2:74–84. [Google Scholar]
- Looi C.Y., Duta M., Brem A.K., Huber S., Nuerk H.-C. Combining brain stimulation and video game to promote long-term transfer of learning and cognitive enhancement. Sci. Rep. 2016;6:22003. doi: 10.1038/srep22003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyytinen H., Erskine J., Kujala J., Ojanen E., Richardson U. In search of a science-based application: a learning tool for reading acquisition. Scand. J. Psychol. 2009;50:668–675. doi: 10.1111/j.1467-9450.2009.00791.x. [DOI] [PubMed] [Google Scholar]
- Molko N., Cachia A., Riviere D., Mangin J.F., Bruandet M., Le Bihan D., Cohen L., Dehaene S. Functional and structural alterations of the intraparietal sulcus in a developmental dyscalculia of genetic origin. Neuron. 2003;40:847–858. doi: 10.1016/s0896-6273(03)00670-6. [DOI] [PubMed] [Google Scholar]
- Price G.R., Wilkey E.D., Yeo D.J., Cutting L.E. The relation between 1 st grade grey matter volume and 2nd grade math competence. Neuroimage. 2016;124:232–237. doi: 10.1016/j.neuroimage.2015.08.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Primi R., Ferrob M.E., Almeida L.S. Fluid intelligence as a predictor of learning: a longitudinal multilevel approach applied to math. Learn. Individ. Differ. 2010;20:446–451. [Google Scholar]
- Roberts G., Quach J., Spencer-Smith M., Anderson P.J., Gathercole S., Gold L., Sia K.L., Mensah F., Rickards F., Ainley J., Wake M. Academic outcomes 2 years after working memory training for children with low working memory: a randomized clinical trial. JAMA Pediatr. 2016;170:e154568. doi: 10.1001/jamapediatrics.2015.4568. [DOI] [PubMed] [Google Scholar]
- Rotzer S., Kucian K., Martin E., von Aster M., Klaver P., Loenneker T. Optimized voxel-based morphometry in children with developmental dyscalculia. Neuroimage. 2008;39:417–422. doi: 10.1016/j.neuroimage.2007.08.045. [DOI] [PubMed] [Google Scholar]
- Rotzer S., Loenneker T., Kucian K., Martin E., Klaver P., von Aster M. Dysfunctional neural network of spatial working memory contributes to developmental dyscalculia. Neuropsychologia. 2009;47:2859–2865. doi: 10.1016/j.neuropsychologia.2009.06.009. [DOI] [PubMed] [Google Scholar]
- Schwaighofer M., Fischer F., Buhner M. Does working memory training transfer ? A meta-analysis inclusing training conditions as moderators. Educ. Psychol. 2015;50:138–166. [Google Scholar]
- Simon O., Mangin J.F., Cohen L., Le Bihan D., Dehaene S. Topographical layout of hand, eye, calculation, and language-related areas in the human parietal lobe. Neuron. 2002;33:475–487. doi: 10.1016/s0896-6273(02)00575-5. [DOI] [PubMed] [Google Scholar]
- Söderqvist S., McNab F., Peyrard-Janvid M., Matsson H., Humphreys K., Kere J., Klingberg T. The SNAP25 gene is linked to working memory capacity and maturation of the posterior cingulate cortex during childhood. Biol. Psychiatry. 2010;68:1120–1125. doi: 10.1016/j.biopsych.2010.07.036. [DOI] [PubMed] [Google Scholar]
- Starke M., Kiechl-Kohlendorfer U., Kucian K., Peglow U.P., Kremser C., Schocke M., Kaufmann L. Brain structure, number magnitude processing, and math proficiency in 6-to 7-year-old children born prematurely: a voxel-based morphometry study. Neuroreport. 2013;24:419–424. doi: 10.1097/WNR.0b013e32836140ed. [DOI] [PubMed] [Google Scholar]
- Supekar K., Swigart A.G., Tenison C., Jolles D.D., Rosenberg-Lee M., Fuchs L., Menon V. Neural predictors of individual differences in response to math tutoring in primary-grade school children. Proc. Natl. Acad. Sci. U. S. A. 2013;110:8230–8235. doi: 10.1073/pnas.1222154110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Thorell L.B., Lindqvist S., Bergman N.S., Bohlin G., Klingberg T. Training and transfer effects of executive functions in preschool children. Dev. Sci. 2009;12:106–113. doi: 10.1111/j.1467-7687.2008.00745.x. [DOI] [PubMed] [Google Scholar]
- Thorndike E.L. The effect of practice in the case of a purely intellectual function. Am. J. Psychol. 1908;19:374–384. [Google Scholar]
- Todd J.J., Marois R. Capacity limit of visual short-term memory in human posterior parietal cortex. Nature. 2004;428:751–754. doi: 10.1038/nature02466. [DOI] [PubMed] [Google Scholar]
- Ullman H., Almeida R., Klingberg T. Structural maturation and brain activity predict future working memory capacity during childhood development. J. Neurosci. 2014;34:1592–1598. doi: 10.1523/JNEUROSCI.0842-13.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yarkoni T., Poldrack R.A., Nichols T.E., Van Essen D.C., Wager T.D. Large-scale automated synthesis of human functional neuroimaging data. Nat. Methods. 2011;8:665–670. doi: 10.1038/nmeth.1635. [DOI] [PMC free article] [PubMed] [Google Scholar]