Abstract
Background and Aims:
For updating growth references, large datasets are usually required; collection of these data are expensive and cumbersome. Using a combination of regression equations, Preece Baines model and global LMS values, synthetic growth references for the target population can be generated. The objective of this study is to compare growth references created from continuous anthropometric data using LMS method versus those created synthetically from anthropometric means at key ages.
Methods:
De-identified data on 46421 children (26037 boys) from 0-18 years of age from several multicentric studies conducted by the authors' group (2007 to 2017) were included in this study; growth references were constructed using the LMS method. For the production of synthetic references, arithmetic means of heights and weights at key ages were used and global LMS values were used from literature.
Results:
There was no difference in the medians for height, weight and BMI between the references created by the two methods. The extreme percentile values for height were similar (P < 0.05). However, the spread of values for weight and BMI was narrower in the synthetic references.
Conclusion:
Growth references produced from continuous data differ from those produced synthetically using anthropometric means mainly at the extreme centiles for weight and body mass index; synthetic references take into consideration global trends over several decades.
Keywords: Children, height, India, LMS method, synthetic growth references
INTRODUCTION
Rapid economic and social transition in India has influenced growth patterns of children especially in urban areas. Recent Indian studies suggest that there is a trend towards increase in height, especially in boys and an increase in obesity in both genders.[1,2,3] Government of India has accepted the World Health Organization (WHO) 2006 growth standards for monitoring growth of under 5 children since 2010. However, many global as well as Indian studies suggest that these standards remain aspirational and a lot of children get diagnosed as undernourished and stunted when they may be growing appropriately for the given population.[4,5]
In older children, population specific references for monitoring growth of children are often used.[6,7,8] These references in a country such as India are usually based on data collected on children and adolescents who have access to health care, nutrition and an environment conducive to growth. Hence, data for these references are usually collected crosssectionally at multiple centers on middle or upper-middle socioeconomic class children. Further, to monitor the secular trend, this exercise needs to be performed regularly.[9,10] The data collection for such studies is expensive and cumbersome. Since such data are difficult to obtain, 'synthesizing growth references' is a more feasible alternative and in recent times, many countries have opted this approach.[11,12]
For creating growth references from cross sectional continuous data, the LMS method is most popular.[13] For synthesizing anthropometry, the method by Hermanussen et al. has been extensively used.[14,15,16,17] Very few studies have compared growth references created by LMS method with synthetic reference curves. Thus, the objective of this study was to compare growth references generated using continuous data and the LMS method versus synthesized growth references on Indian children from birth to 18 years of age.
METHODS
The data included in this study are de-identified data from studies conducted by the authors' group from 2007 to 2017 on children from 0-18 years of age.[18,19,20,21,22,23,24,25,26] Most studies were multicentric and conducted for the assessment of anthropometric parameters and included children from middle and upper-middle socio-economic class from 5 zones of India namely north south, east, west and central zones.[27] For all studies, ethics approval was obtained from institutional ethics committee and parents gave consent and children assent (as appropriate). Data on decimal age, gender, height and weight were collated, body mass index (BMI) was computed with standard formula; for constructing growth references, we included height and weight data on 48166 children (21127 girls). 843 children (333 girls) were removed as obvious data entry errors (height, weight or BMI above or below 4 SD).[28] A total of 47,323 children (20794 girls) were included in the analysis. An additional 902 records (410 girls) were removed as they had weight for height z score above +2, and hence were considered to have unhealthy weights as per WHO recommendation.[29,30] Thus, a total of 46421 children (20384 girls) were included in the construction of growth references using the LMS method, whereas, for the production of synthetic references, arithmetic means of height and weight at key ages viz. birth, 2, 6, 12 and 15 years for girls and birth, 2, 6, 14 and 18 years for boys were used.
Construction of references on continuous data using the LMS Method: The cleaned data were analyzed using the LMS method which constructs growth reference percentiles adjusted for skewness. Each growth reference is summarized by 3 smooth curves plotted against age representing the median (M), the coefficient of variation (S) and the skewness (L) of the measurement distribution. The LMS chart maker software was used to generate reference curves.[13]
Synthetic Growth References: Synthetic growth references were produced using a two-step procedure. The first step was to compute means using non-linear regression equations for height, weight and BMI at all ages from birth to 18 years from the means at key ages, and in the second step, percentiles were created. The means for height and weight from birth to 18 years were produced using Hermanussen equations.[31,32] These equations take into consideration three design ages viz. birth, 6 and 15 years for girls and birth, 6 and 18 years for boys. These ages were selected in the design of the original method as these data are easy to obtain in most places in the world (Birth, school entry and adult height data is collected at many places as part of educational, health and insurance requirements). In addition, ages where maximum difference in the tempo of growth occurs were taken as auxiliary ages at 2 and 12 years for girls and 2 and 14 years for boys.[31] To assess whether it was appropriate to use the means at 12 and 14 years for girls and boys, respectively, in Indian children, we used the Preece Baines (PB) model[33] to characterize growth of Indian children based on published Indian studies by Khadilkar et al.,[22] IAP 2015,[30] Marwah et al.[34] and Agarwal et al.[35] Khadilkar et al. and IAP data showed that the peak pubertal height spurt (theta of the PB equation) was attained at the age of 11.9 years and 13.9 years in girls and boys respectively. Marwaha et al.'s data showed that the theta was at 11.5 and 14.1 years in girls and boys respectively. In Agarwal et al.'s data, the theta was at 11.7 and 13.9 years in girls and boys respectively.
We therefore concluded that Hermanussen's key ages match Indian children's growth spurt and his equations are applicable to Indian children.
The regression equations for generating height means were:[31,32]
H(t) = a(t) x H(6) + b(t) x H(2) + c(t) x H(0) for children from 0-6 y
H(t) = a(t) x H(18) + b(t) x H(6) + c(t) x H(2) for children from 7-18 y
Where H(t) was the Height at age t, H(18), H(6), H(2) and H(0) are heights at ages 18, 6, 2 and birth, respectively, and a, b, c are constants. For weight, the same formulae were used but weight replaced height. Calculated means for weight and height were further smoothed using PB model using Microsoft Excel solver 2007.[36]
The second step was to generate percentiles. Since height is a normally (Gaussian) distributed variable, it was possible to generate percentiles from relative standard deviations (SDs). SD's for height at all ages were computed from global relative SDs[30] and study children's SD at 18 years (6.8 and 5.8 cms for boys and girls respectively).
For computing percentiles for weight and BMI, a different approach was needed as these variables were skewed to the right. To generate percentiles for weight and BMI, global LMS values[32,37] were used as given by the formula:
C100 α(t) = M(t) [1 + L(t) S(t) z α ] 1/L(t); where z α is the normal equivalent deviate for tail area α, C100 α is the weight percentile corresponding to z α, t is age in years, and L(t), M(t), S(t), and C100 α(t) indicate the corresponding values of each curve at age t. Reference curves were smoothed using cubic spline.[38]
RESULTS
The means for height and weight used for constructing synthetic growth references are illustrated in Table 1. Tables 2 and 3 illustrate the comparison between growth references produced using LMS method, synthetic references vs existing IAP 2015 growth charts. A comparison of 3rd, 50th and 97th percentiles for height and weight for boys and girls are illustrated. Further, Table 4 illustrates the comparisons between charts created using continuous data with the LMS method, synthetic growth references and the IAP 2015 growth charts for 3rd, 50th, 85th and 95th percentiles for BMI for boys and girls.
Table 1.
Anthropometric means used in the production of synthetic growth references
| Age in Years | Boys | Girl | ||
|---|---|---|---|---|
| Height (cm) | Weight (Kg) | Height (cm) | Weight (kg) | |
| 0 | 50.8 | 2.9 | 50.7 | 2.9 |
| 2 | 85.3 | 10.7 | 84.6 | 10.7 |
| 6 | 114.6 | 19.3 | 113.3 | 18.5 |
| 12 | 148.7 | 39.5 | ||
| 14 | 160.6 | 48.4 | ||
| 15 | 156.0 | 48.5 | ||
| 18 | 169.9 | 61.4 | ||
Table 2.
Comparison of Height percentiles (3rd, 50th and 97th) by LMS method, Synthetic References Vs IAP 2015 (Boys 26037, Girls 20384)
| Age (years) | n | 3rd | 50th | 97th | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP205 | ||
| Boys | ||||||||||
| 0 | 319 | 46.8 | 46.5 | 50.8 | 50.8 | 56 | 55.1 | |||
| 0.5 | 191 | 58.2 | 62 | 63.2 | 67.1 | 69.6 | 72.1 | |||
| 1 | 298 | 67.3 | 69 | 73.2 | 74.6 | 80.6 | 80.2 | |||
| 2 | 351 | 78.4 | 78.4 | 85.3 | 85.3 | 94 | 92.2 | |||
| 3 | 730 | 85.2 | 86.1 | 92.9 | 94.1 | 102.3 | 102 | |||
| 4 | 965 | 92.1 | 92.5 | 100.6 | 101.4 | 110.8 | 110.2 | |||
| 5 | 1333 | 98.7 | 98.5 | 99 | 108 | 108.3 | 108.9 | 118.9 | 118 | 119.4 |
| 6 | 2085 | 104.6 | 104.3 | 104.2 | 114.6 | 114.6 | 114.8 | 126.2 | 125 | 126 |
| 7 | 1882 | 109.7 | 109.3 | 109.3 | 120.5 | 120.2 | 120.7 | 132.7 | 131 | 132.6 |
| 8 | 2216 | 114.9 | 114.2 | 114.3 | 126.5 | 125.5 | 126.4 | 139.3 | 136.8 | 139.1 |
| 9 | 1907 | 119.5 | 119.1 | 119 | 132 | 131 | 131.8 | 145.3 | 143 | 145.3 |
| 10 | 2052 | 123.6 | 123.6 | 123.6 | 137 | 136.2 | 137.2 | 150.8 | 148.9 | 151.4 |
| 11 | 2195 | 127.9 | 127.6 | 128.2 | 142.2 | 140.9 | 142.7 | 156.4 | 154.1 | 157.5 |
| 12 | 2348 | 132.6 | 131.9 | 133.2 | 147.8 | 146.3 | 148.4 | 162.4 | 160.7 | 163.7 |
| 13 | 2075 | 138.2 | 136.6 | 138.3 | 153.9 | 153.5 | 154.3 | 168.9 | 170.3 | 169.9 |
| 14 | 1791 | 143.2 | 142.3 | 143.4 | 160.6 | 160.6 | 159.9 | 175.8 | 178.9 | 175.4 |
| 15 | 1505 | 147.3 | 149.1 | 148 | 165.5 | 165.7 | 164.5 | 180.7 | 182.3 | 179.7 |
| 16 | 1122 | 150.1 | 154.3 | 151.8 | 167.9 | 168.5 | 168.1 | 182.9 | 182.8 | 182.7 |
| 17 | 485 | 153.6 | 156.9 | 155 | 169.1 | 169.7 | 171 | 183.8 | 182.5 | 184.8 |
| 18 | 187 | 155.5 | 157.1 | 158.1 | 169.9 | 169.9 | 173.6 | 184.2 | 182.7 | 186.7 |
| n | 3rd | 50th | 97th | |||||||
| Girls | ||||||||||
| 0 | 193 | 46.6 | 46.7 | 50.7 | 50.7 | 56.2 | 54.6 | |||
| 0.5 | 113 | 57.3 | 61 | 62.4 | 65.6 | 69.1 | 70.2 | |||
| 1 | 144 | 66.2 | 68.5 | 72.1 | 73.6 | 79.9 | 78.8 | |||
| 2 | 290 | 77.5 | 78.3 | 84.6 | 84.6 | 93.6 | 91 | |||
| 3 | 550 | 84.8 | 85.9 | 92.6 | 93.2 | 102.4 | 100.5 | |||
| 4 | 910 | 91 | 92.2 | 99.7 | 100.3 | 110 | 108.4 | |||
| 5 | 1020 | 97.3 | 98.1 | 97.2 | 106.8 | 107 | 107.5 | 117.7 | 116 | 119.3 |
| 6 | 1544 | 103 | 103.5 | 102.3 | 113.3 | 113.3 | 113.5 | 124.8 | 123.1 | 125.6 |
| 7 | 1480 | 108.1 | 108.5 | 107.4 | 119.2 | 119 | 119.4 | 131.1 | 129.6 | 131.9 |
| 8 | 1790 | 113.4 | 113.3 | 112.6 | 125.3 | 124.4 | 125.4 | 137.6 | 135.5 | 138.1 |
| 9 | 1538 | 118.4 | 118.1 | 117.8 | 131.1 | 129.8 | 131.4 | 143.7 | 141.6 | 144.5 |
| 10 | 1632 | 123.7 | 123.1 | 123.3 | 137.1 | 135.8 | 137.4 | 150.1 | 148.5 | 150.8 |
| 11 | 1833 | 129.3 | 128.3 | 128.8 | 143.3 | 142.5 | 143.3 | 156.5 | 156.6 | 156.8 |
| 12 | 1758 | 134.4 | 133.9 | 134 | 148.7 | 148.7 | 148.4 | 162.1 | 163.5 | 162 |
| 13 | 1621 | 138.4 | 139.3 | 138.2 | 152.6 | 153.2 | 152.2 | 165.9 | 167.1 | 165.9 |
| 14 | 1479 | 141.1 | 143.2 | 141.3 | 154.9 | 155.7 | 154.7 | 168.1 | 168.2 | 168.2 |
| 15 | 1190 | 142.8 | 143.3 | 143.3 | 156 | 156.4 | 156.1 | 169 | 169.5 | 169.5 |
| 16 | 907 | 143.9 | 143.2 | 144.7 | 156.5 | 156.3 | 156.9 | 169.3 | 169.4 | 170.1 |
| 17 | 284 | 145 | 143.4 | 145.7 | 156.9 | 156.5 | 157.4 | 169.4 | 169.6 | 170.4 |
| 18 | 108 | 145.5 | 143.8 | 146.6 | 156.8 | 156.9 | 157.8 | 169 | 170.1 | 170.6 |
Table 3.
Comparison of Weight percentiles (3rd, 50th and 97th) by LMS method, Synthetic References Vs IAP 2015 (Boys 26037, Girls 20384)
| Age (years) | 3rd | 50th | 97th | ||||||
|---|---|---|---|---|---|---|---|---|---|
| LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 | |
| Boys | |||||||||
| 0 | 2.4 | 2.3 | 2.9 | 2.9 | 3.7 | 3.5 | |||
| 0.5 | 5.8 | 5.1 | 6.9 | 6.4 | 9 | 7.8 | |||
| 1 | 7.4 | 7.1 | 8.9 | 8.8 | 11.8 | 10.7 | |||
| 2 | 8.8 | 8.8 | 10.7 | 10.7 | 14.5 | 13.2 | |||
| 3 | 10.2 | 10.3 | 12.7 | 12.6 | 17.7 | 15.6 | |||
| 4 | 11.7 | 12.3 | 14.8 | 15 | 21.4 | 18.9 | |||
| 5 | 13.1 | 14 | 13.2 | 17 | 17.2 | 17.1 | 25.4 | 22 | 24.2 |
| 6 | 14.6 | 15.5 | 14.5 | 19.3 | 19.3 | 19.3 | 29.9 | 25.3 | 28.3 |
| 7 | 16 | 17.1 | 16 | 21.7 | 21.6 | 21.9 | 34.6 | 28.9 | 33.4 |
| 8 | 17.6 | 18.9 | 17.5 | 24.6 | 24.1 | 24.8 | 40.3 | 33.3 | 39.4 |
| 9 | 19.4 | 20.9 | 19.1 | 27.8 | 27 | 27.9 | 46.2 | 38.2 | 45.5 |
| 10 | 21 | 22.9 | 20.7 | 30.9 | 30.1 | 31.1 | 51.7 | 42.8 | 51.8 |
| 11 | 22.9 | 25.2 | 22.6 | 34.3 | 33.4 | 34.7 | 57.4 | 48.2 | 58.7 |
| 12 | 25.3 | 27.9 | 24.9 | 38.6 | 37.4 | 39 | 63.8 | 54.2 | 66.1 |
| 13 | 28.1 | 31.5 | 27.5 | 43.2 | 42.7 | 43.3 | 70.4 | 60.9 | 72.6 |
| 14 | 31.4 | 35.7 | 30.7 | 48.4 | 48.4 | 48.2 | 77.3 | 67.7 | 78.3 |
| 15 | 34.7 | 40 | 34.5 | 53.1 | 53.7 | 53.1 | 83.1 | 73.5 | 83.1 |
| 16 | 37.2 | 44.2 | 37.5 | 56.5 | 57.7 | 56.8 | 86.6 | 77.9 | 85.8 |
| 17 | 39.4 | 47.3 | 39.8 | 59.1 | 60.1 | 59.5 | 88.8 | 78.9 | 87.5 |
| 18 | 41.4 | 49.6 | 41.8 | 61.4 | 61.4 | 61.6 | 90.4 | 78 | 88.4 |
| 3rd | 50th | 97th | |||||||
| Girls | |||||||||
| 0 | 2.4 | 2.3 | 2.9 | 2.9 | 3.8 | 3.5 | |||
| 0.5 | 5.6 | 5.2 | 6.8 | 6.5 | 9 | 7.9 | |||
| 1 | 7.2 | 6.8 | 8.9 | 8.4 | 11.9 | 10.3 | |||
| 2 | 8.5 | 8.7 | 10.7 | 10.7 | 14.8 | 13.1 | |||
| 3 | 9.7 | 10.2 | 12.4 | 12.6 | 17.6 | 15.6 | |||
| 4 | 11 | 11.7 | 14.4 | 14.4 | 21.1 | 18.3 | |||
| 5 | 12.4 | 13.1 | 12.3 | 16.5 | 16.4 | 16.4 | 24.8 | 21.4 | 25 |
| 6 | 13.7 | 14.6 | 13.7 | 18.5 | 18.5 | 18.7 | 28.6 | 24.8 | 29.1 |
| 7 | 15.1 | 16.2 | 15.1 | 20.9 | 20.9 | 21.2 | 32.9 | 28.7 | 33.4 |
| 8 | 16.9 | 17.9 | 16.7 | 23.9 | 23.4 | 24 | 38 | 33 | 38.1 |
| 9 | 18.7 | 19.7 | 18.5 | 26.9 | 26.2 | 27.2 | 43 | 37.5 | 43.4 |
| 10 | 21 | 22.2 | 20.7 | 30.7 | 29.9 | 31 | 48.9 | 42.9 | 49.4 |
| 11 | 23.7 | 25.4 | 23.3 | 35 | 34.6 | 35.4 | 55.4 | 49.7 | 55.9 |
| 12 | 26.6 | 28.7 | 26.2 | 39.5 | 39.5 | 39.8 | 62.1 | 55.7 | 62.1 |
| 13 | 29.2 | 31.5 | 28.9 | 43.4 | 43.7 | 43.6 | 67.6 | 60.1 | 67.1 |
| 14 | 31.4 | 34.9 | 31.3 | 46.5 | 46.7 | 46.4 | 71.5 | 65.1 | 70.4 |
| 15 | 33 | 36.9 | 33.1 | 48.5 | 48.5 | 48.4 | 73.7 | 66.6 | 72.1 |
| 16 | 34.1 | 38.4 | 34.7 | 49.6 | 49.6 | 49.7 | 74.5 | 66.5 | 72.8 |
| 17 | 35.2 | 39.9 | 36.2 | 50.6 | 50.5 | 50.9 | 75.1 | 66 | 73.3 |
| 18 | 36.2 | 41.6 | 37.6 | 51.6 | 51.5 | 52 | 75.7 | 65.5 | 73.5 |
Table 4.
Comparison of BMI percentiles (3rd, 50th, 85th and 95th): LMS vs Synthetic References Vs IAP 2015 growth charts
| Age (years) | LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 | LMS | Synthetic | IAP 2015 |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3rd | 50th | 85th | (23E) | 95th | (27E) | |||||||
| Boys | ||||||||||||
| 0 | 11.3 | 9.4 | 13.3 | 11.1 | 15.1 | 12.1 | 16.6 | 12.7 | ||||
| 0.5 | 12.1 | 12.2 | 14.3 | 14.1 | 16.2 | 15.4 | 17.8 | 16.1 | ||||
| 1 | 12.6 | 13.5 | 14.9 | 15.8 | 16.9 | 17.3 | 18.6 | 18.3 | ||||
| 2 | 12.8 | 12.7 | 15.2 | 14.7 | 17.3 | 16.1 | 19 | 17 | ||||
| 3 | 12.5 | 12.6 | 15 | 14.3 | 17.1 | 15.4 | 18.9 | 16.2 | ||||
| 4 | 12.3 | 12.8 | 14.8 | 14.4 | 17 | 15.5 | 18.8 | 16.2 | ||||
| 5 | 12.2 | 12.8 | 12.1 | 14.7 | 14.5 | 14.7 | 17 | 15.7 | 15.7 | 18.9 | 16.5 | 17.5 |
| 6 | 12.2 | 12.8 | 12.2 | 14.8 | 14.7 | 14.9 | 17.2 | 16.1 | 16 | 19.3 | 17.1 | 17.8 |
| 7 | 12.2 | 12.9 | 12.3 | 15 | 15 | 15.1 | 17.6 | 16.6 | 16.3 | 19.8 | 17.8 | 18.2 |
| 8 | 12.4 | 13.1 | 12.5 | 15.4 | 15.3 | 15.5 | 18.2 | 17.1 | 16.7 | 20.6 | 18.5 | 18.8 |
| 9 | 12.6 | 13.3 | 12.7 | 15.9 | 15.8 | 15.9 | 18.9 | 17.8 | 17.3 | 21.5 | 19.3 | 19.6 |
| 10 | 12.8 | 13.7 | 12.9 | 16.3 | 16.2 | 16.4 | 19.6 | 18.4 | 18 | 22.3 | 20.2 | 20.5 |
| 11 | 13.1 | 14 | 13.1 | 16.9 | 16.8 | 17 | 20.4 | 19.1 | 18.7 | 23.2 | 21 | 21.5 |
| 12 | 13.5 | 14.4 | 13.3 | 17.6 | 17.3 | 17.7 | 21.3 | 19.8 | 19.5 | 24.3 | 21.9 | 22.6 |
| 13 | 13.8 | 14.9 | 13.6 | 18.2 | 18 | 18.2 | 22.1 | 20.6 | 20.2 | 25.2 | 22.8 | 23.4 |
| 14 | 14.1 | 15.5 | 13.8 | 18.8 | 18.8 | 18.7 | 22.8 | 21.5 | 20.8 | 26 | 23.7 | 24.2 |
| 15 | 14.4 | 16.3 | 14.2 | 19.4 | 19.7 | 19.3 | 23.6 | 22.5 | 21.4 | 26.8 | 24.7 | 24.9 |
| 16 | 14.7 | 17 | 14.6 | 20 | 20.4 | 19.9 | 24.3 | 23.3 | 22 | 27.6 | 25.6 | 25.5 |
| 17 | 15 | 17.4 | 15.1 | 20.6 | 20.9 | 20.5 | 25 | 23.9 | 22.6 | 28.4 | 26.2 | 26 |
| 18 | 15.3 | 17.6 | 15.6 | 21.2 | 21.3 | 21.1 | 25.8 | 24.3 | 23.2 | 29.1 | 26.7 | 26.6 |
| Girls | ||||||||||||
| 0 | 11.3 | 9.8 | 13.5 | 11.3 | 15.3 | 12.2 | 16.8 | 12.8 | ||||
| 0.5 | 11.9 | 13 | 14.3 | 15.1 | 16.2 | 16.4 | 17.8 | 17.2 | ||||
| 1 | 12.4 | 13.5 | 14.8 | 15.6 | 16.8 | 17 | 18.5 | 17.9 | ||||
| 2 | 12.5 | 12.9 | 14.9 | 14.9 | 17.1 | 16.4 | 18.8 | 17.4 | ||||
| 3 | 12.2 | 12.7 | 14.7 | 14.5 | 16.8 | 15.8 | 18.6 | 16.7 | ||||
| 4 | 12 | 12.5 | 14.5 | 14.3 | 16.8 | 15.5 | 18.6 | 16.4 | ||||
| 5 | 11.9 | 12.5 | 11.9 | 14.5 | 14.2 | 14.3 | 16.8 | 15.6 | 15.5 | 18.6 | 16.5 | 18 |
| 6 | 11.8 | 12.5 | 12 | 14.5 | 14.4 | 14.5 | 16.9 | 15.9 | 15.9 | 18.9 | 17.1 | 18.6 |
| 7 | 11.9 | 12.6 | 12.1 | 14.8 | 14.7 | 14.9 | 17.4 | 16.5 | 16.4 | 19.5 | 17.8 | 19.3 |
| 8 | 12.1 | 12.7 | 12.3 | 15.2 | 15.1 | 15.3 | 18 | 17.1 | 16.9 | 20.3 | 18.6 | 20.1 |
| 9 | 12.3 | 13 | 12.4 | 15.7 | 15.6 | 15.8 | 18.7 | 17.8 | 17.6 | 21.1 | 19.5 | 21 |
| 10 | 12.7 | 13.4 | 12.7 | 16.3 | 16.2 | 16.5 | 19.5 | 18.6 | 18.4 | 22 | 20.4 | 21.9 |
| 11 | 13.1 | 13.8 | 13 | 17.1 | 16.9 | 17.2 | 20.5 | 19.5 | 19.3 | 23.1 | 21.5 | 23 |
| 12 | 13.6 | 14.4 | 13.4 | 17.9 | 17.7 | 18 | 21.5 | 20.5 | 20.2 | 24.2 | 22.7 | 24.1 |
| 13 | 14 | 15 | 13.9 | 18.7 | 18.6 | 18.8 | 22.4 | 21.5 | 21.1 | 25.2 | 23.8 | 25.2 |
| 14 | 14.5 | 15.6 | 14.3 | 19.4 | 19.3 | 19.4 | 23.2 | 22.3 | 21.8 | 26 | 24.7 | 25.9 |
| 15 | 14.8 | 16.2 | 14.7 | 19.9 | 19.8 | 19.9 | 23.8 | 22.8 | 22.3 | 26.6 | 25.2 | 26.3 |
| 16 | 15 | 16.6 | 15 | 20.3 | 20.3 | 20.3 | 24.2 | 23.2 | 22.6 | 26.9 | 25.4 | 26.5 |
| 17 | 15.2 | 17.1 | 15.4 | 20.6 | 20.6 | 20.6 | 24.5 | 23.4 | 22.9 | 27.2 | 25.4 | 26.7 |
| 18 | 15.3 | 17.5 | 15.7 | 21 | 20.9 | 21 | 24.9 | 23.5 | 23.2 | 27.6 | 25.3 | 26.8 |
Height percentiles produced using the LMS method were comparable to synthetic references as well as IAP 2015 growth charts in both boys and girls. However, in the case of weight, although the 50th percentile was similar by all three methods, there was a difference in the 3rd and 97th percentiles in both genders between the synthetic one hand and the IAP2015 and LMS method on the other. The third percentile in both genders was lower while 97th percentile was higher using LMS method and in the IAP2015 charts. For the BMI percentiles, while 50th percentile was comparable, 85th and 95th percentiles were lower and 3rd percentile was higher in the synthetic references both for boys and girls. The spread was narrower for weight and BMI in synthetic curves. The IAP2015 values for BMI for the 3rd and 50th centile were similar to those computed by the LMS method using continuous data, however, as the cut-offs for the IAP2015 for BMI are lower, the 23rd adult equivalent and the 27 adult equivalent values were lower than 85th and 95th percentile computed by LMS method and comparable to the synthetic method.
Tables 5 and 6 illustrate the synthetic growth percentiles viz, 3rd, 10th, 25th 50th, 75th, 97th for height and weight for boys and girls [Figures 1 and 3]. Table 7 depicts BMI 3rd, 25th, 50th, 85th and 95th percentiles for boys and girls [Figures 2 and 4].
Table 5.
Synthetic Growth Percentiles for Height
| Age (years) | 3 | 10 | 25 | 50 | 75 | 90 | 97 |
|---|---|---|---|---|---|---|---|
| Boys | |||||||
| 0 | 46.5 | 47.9 | 49.3 | 50.8 | 52.3 | 53.7 | 55.1 |
| 0.5 | 62.0 | 63.6 | 65.3 | 67.1 | 68.9 | 70.5 | 72.1 |
| 1 | 69.0 | 70.8 | 72.6 | 74.6 | 76.6 | 78.4 | 80.2 |
| 2 | 78.4 | 80.6 | 82.8 | 85.3 | 87.8 | 90.0 | 92.2 |
| 3 | 86.1 | 88.7 | 91.2 | 94.1 | 96.9 | 99.5 | 102.0 |
| 4 | 92.5 | 95.3 | 98.2 | 101.4 | 104.6 | 107.4 | 110.2 |
| 5 | 98.5 | 101.6 | 104.8 | 108.3 | 111.8 | 114.9 | 118.0 |
| 6 | 104.3 | 107.6 | 110.9 | 114.6 | 118.3 | 121.7 | 125.0 |
| 7 | 109.3 | 112.8 | 116.3 | 120.2 | 124.1 | 127.6 | 131.0 |
| 8 | 114.2 | 117.8 | 121.4 | 125.5 | 129.6 | 133.2 | 136.8 |
| 9 | 119.1 | 122.9 | 126.7 | 131.0 | 135.3 | 139.2 | 143.0 |
| 10 | 123.6 | 127.6 | 131.7 | 136.2 | 140.8 | 144.8 | 148.9 |
| 11 | 127.6 | 131.8 | 136.1 | 140.9 | 145.6 | 149.9 | 154.1 |
| 12 | 131.9 | 136.5 | 141.1 | 146.3 | 151.5 | 156.1 | 160.7 |
| 13 | 136.6 | 142.0 | 147.5 | 153.5 | 159.6 | 165.0 | 170.4 |
| 14 | 142.3 | 148.2 | 154.1 | 160.6 | 167.1 | 173.0 | 178.9 |
| 15 | 148.9 | 154.1 | 159.5 | 165.4 | 171.3 | 176.7 | 182.0 |
| 16 | 153.9 | 158.4 | 163.0 | 168.1 | 173.2 | 177.8 | 182.3 |
| 17 | 156.6 | 160.7 | 164.8 | 169.4 | 173.9 | 178.0 | 182.1 |
| 18 | 157.1 | 161.2 | 165.3 | 169.9 | 174.5 | 178.6 | 182.7 |
| Girls | |||||||
| 0 | 46.7 | 48.0 | 49.3 | 50.7 | 52.1 | 53.4 | 54.6 |
| 0.5 | 61.1 | 62.5 | 64.0 | 65.6 | 67.2 | 68.7 | 70.2 |
| 1 | 68.5 | 70.1 | 71.8 | 73.6 | 75.5 | 77.1 | 78.8 |
| 2 | 78.3 | 80.3 | 82.4 | 84.6 | 86.9 | 89.0 | 91.0 |
| 3 | 85.9 | 88.2 | 90.6 | 93.2 | 95.8 | 98.1 | 100.4 |
| 4 | 92.2 | 94.8 | 97.4 | 100.3 | 103.2 | 105.8 | 108.4 |
| 5 | 98.1 | 100.9 | 103.8 | 107.0 | 110.2 | 113.1 | 116.0 |
| 6 | 103.6 | 106.7 | 109.8 | 113.3 | 116.8 | 120.0 | 123.1 |
| 7 | 108.5 | 111.9 | 115.3 | 119.1 | 122.8 | 126.2 | 129.6 |
| 8 | 113.4 | 116.9 | 120.5 | 124.4 | 128.4 | 132.0 | 135.5 |
| 9 | 118.1 | 121.8 | 125.6 | 129.8 | 134.0 | 137.8 | 141.6 |
| 10 | 123.1 | 127.2 | 131.2 | 135.8 | 140.3 | 144.4 | 148.4 |
| 11 | 128.4 | 132.9 | 137.5 | 142.5 | 147.5 | 152.1 | 156.6 |
| 12 | 133.9 | 138.6 | 143.4 | 148.7 | 154.0 | 158.8 | 163.5 |
| 13 | 139.2 | 143.6 | 148.1 | 153.1 | 158.0 | 162.5 | 166.9 |
| 14 | 143.2 | 147.2 | 151.2 | 155.7 | 160.1 | 164.2 | 168.1 |
| 15 | 143.6 | 147.8 | 152.0 | 156.7 | 161.4 | 165.6 | 169.8 |
| 16 | 143.7 | 147.9 | 152.1 | 156.8 | 161.5 | 165.7 | 169.9 |
| 17 | 143.8 | 148.0 | 152.2 | 156.9 | 161.6 | 165.8 | 170.0 |
| 18 | 143.8 | 148.0 | 152.2 | 156.9 | 161.6 | 165.9 | 170.0 |
Table 6.
Synthetic growth percentiles for Weight
| Age (years) | Percentiles | ||||||
|---|---|---|---|---|---|---|---|
| 3 | 10 | 25 | 50 | 75 | 90 | 97 | |
| Boys | |||||||
| 0 | 2.3 | 2.4 | 2.6 | 2.9 | 3.1 | 3.3 | 3.5 |
| 0.5 | 5.1 | 5.5 | 5.9 | 6.4 | 6.9 | 7.3 | 7.8 |
| 1 | 7.1 | 7.6 | 8.2 | 8.8 | 9.5 | 10.1 | 10.7 |
| 2 | 8.8 | 9.3 | 10.0 | 10.7 | 11.5 | 12.3 | 13.2 |
| 3 | 10.3 | 11.0 | 11.8 | 12.6 | 13.6 | 14.6 | 15.6 |
| 4 | 12.3 | 13.1 | 13.9 | 15.0 | 16.2 | 17.5 | 18.9 |
| 5 | 14.0 | 14.9 | 15.9 | 17.2 | 18.7 | 20.3 | 22.0 |
| 6 | 15.5 | 16.6 | 17.8 | 19.3 | 21.1 | 23.0 | 25.3 |
| 7 | 17.1 | 18.3 | 19.8 | 21.6 | 23.8 | 26.1 | 28.9 |
| 8 | 18.9 | 20.3 | 22.0 | 24.1 | 26.8 | 29.7 | 33.3 |
| 9 | 20.9 | 22.6 | 24.5 | 27.0 | 30.2 | 33.7 | 38.2 |
| 10 | 22.9 | 24.8 | 27.1 | 30.1 | 33.8 | 37.9 | 42.8 |
| 11 | 25.2 | 27.3 | 29.9 | 33.4 | 37.7 | 42.4 | 48.2 |
| 12 | 27.9 | 30.4 | 33.5 | 37.4 | 42.3 | 47.6 | 54.2 |
| 13 | 31.5 | 34.5 | 38.1 | 42.7 | 48.1 | 54.0 | 60.9 |
| 14 | 35.7 | 39.2 | 43.2 | 48.4 | 54.4 | 60.6 | 67.7 |
| 15 | 40.0 | 43.8 | 48.2 | 53.7 | 60.0 | 66.4 | 73.5 |
| 16 | 44.2 | 48.0 | 52.3 | 57.7 | 64.0 | 70.5 | 77.9 |
| 17 | 47.3 | 50.9 | 54.9 | 60.1 | 66.0 | 72.1 | 78.9 |
| 18 | 49.6 | 52.9 | 56.7 | 61.4 | 66.7 | 72.1 | 78.0 |
| Girls | |||||||
| 0 | 2.3 | 2.5 | 2.7 | 2.9 | 3.1 | 3.3 | 3.5 |
| 0.5 | 5.2 | 5.6 | 6.0 | 6.5 | 7.0 | 7.4 | 7.9 |
| 1 | 6.8 | 7.3 | 7.8 | 8.4 | 9.1 | 9.7 | 10.3 |
| 2 | 8.7 | 9.3 | 9.9 | 10.7 | 11.5 | 12.3 | 13.1 |
| 3 | 10.2 | 10.9 | 11.6 | 12.6 | 13.6 | 14.5 | 15.6 |
| 4 | 11.7 | 12.4 | 13.3 | 14.4 | 15.7 | 16.9 | 18.3 |
| 5 | 13.1 | 14.0 | 15.1 | 16.4 | 17.9 | 19.5 | 21.4 |
| 6 | 14.6 | 15.7 | 16.9 | 18.5 | 20.4 | 22.5 | 24.8 |
| 7 | 16.2 | 17.5 | 18.9 | 20.9 | 23.2 | 25.7 | 28.7 |
| 8 | 17.9 | 19.4 | 21.1 | 23.4 | 26.2 | 29.3 | 33.0 |
| 9 | 19.7 | 21.5 | 23.5 | 26.2 | 29.5 | 33.1 | 37.5 |
| 10 | 22.2 | 24.2 | 26.7 | 29.9 | 33.7 | 37.9 | 42.9 |
| 11 | 25.4 | 27.9 | 30.8 | 34.6 | 39.1 | 43.9 | 49.7 |
| 12 | 28.7 | 31.7 | 35.2 | 39.5 | 44.6 | 49.8 | 55.7 |
| 13 | 31.5 | 35.0 | 38.9 | 43.7 | 49.1 | 54.4 | 60.1 |
| 14 | 34.9 | 38.1 | 41.9 | 46.7 | 52.4 | 58.3 | 65.1 |
| 15 | 36.9 | 40.1 | 43.8 | 48.5 | 54.0 | 59.9 | 66.6 |
| 16 | 38.4 | 41.5 | 45.1 | 49.6 | 54.8 | 60.2 | 66.5 |
| 17 | 39.9 | 42.9 | 46.3 | 50.5 | 55.4 | 60.4 | 66.0 |
| 18 | 41.6 | 44.4 | 47.6 | 51.5 | 56.0 | 60.5 | 65.5 |
Figure 1.
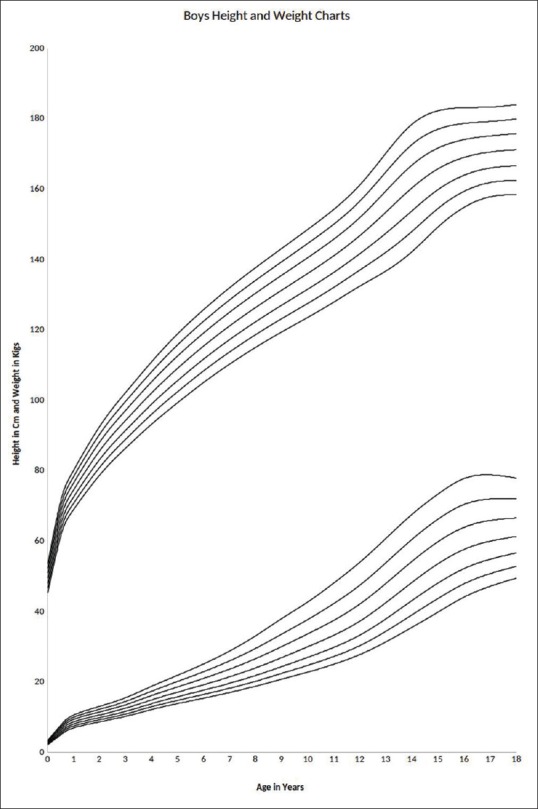
Boys Height and Weight Synthetic References
Figure 3.
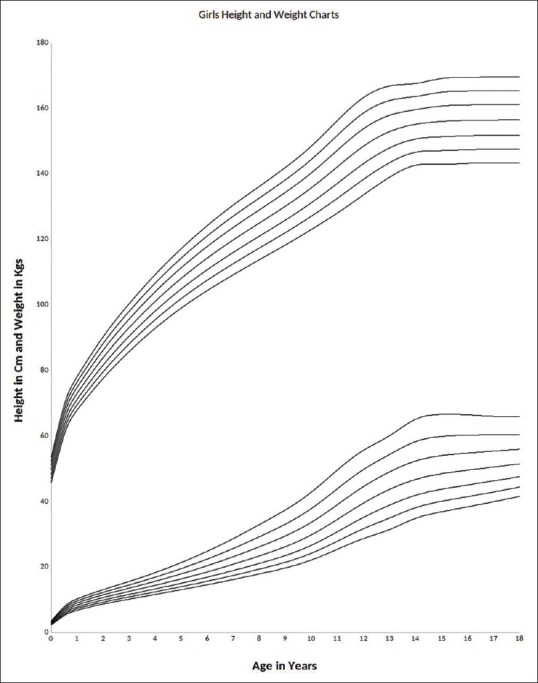
Girls Height and Weight synthetic references
Table 7.
Synthetic growth percentiles for BMI
| Age (years) | Percentiles | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 3 | 10 | 25 | 50 | 75 | 85 | 95 | |||||||
| Boys | |||||||||||||
| 0 | 9.4 | 9.9 | 10.4 | 11.1 | 11.7 | 12.1 | 12.7 | ||||||
| 0.5 | 12.2 | 12.8 | 13.4 | 14.1 | 14.9 | 15.4 | 16.1 | ||||||
| 1 | 13.5 | 14.2 | 14.9 | 15.8 | 16.8 | 17.3 | 18.3 | ||||||
| 2 | 12.7 | 13.3 | 13.9 | 14.7 | 15.6 | 16.1 | 17.0 | ||||||
| 3 | 12.6 | 13.1 | 13.6 | 14.3 | 15.0 | 15.4 | 16.2 | ||||||
| 4 | 12.8 | 13.3 | 13.8 | 14.4 | 15.1 | 15.5 | 16.2 | ||||||
| 5 | 12.8 | 13.3 | 13.9 | 14.5 | 15.3 | 15.7 | 16.5 | ||||||
| 6 | 12.8 | 13.4 | 14.0 | 14.7 | 15.6 | 16.1 | 17.1 | ||||||
| 7 | 12.9 | 13.5 | 14.1 | 15.0 | 16.0 | 16.6 | 17.8 | ||||||
| 8 | 13.1 | 13.7 | 14.4 | 15.3 | 16.4 | 17.1 | 18.5 | ||||||
| 9 | 13.3 | 14.0 | 14.7 | 15.8 | 17.0 | 17.8 | 19.3 | ||||||
| 10 | 13.7 | 14.4 | 15.2 | 16.2 | 17.6 | 18.4 | 20.2 | ||||||
| 11 | 14.0 | 14.8 | 15.6 | 16.8 | 18.2 | 19.1 | 21.0 | ||||||
| 12 | 14.4 | 15.2 | 16.1 | 17.3 | 18.8 | 19.8 | 21.9 | ||||||
| 13 | 14.9 | 15.7 | 16.7 | 18.0 | 19.6 | 20.6 | 22.8 | ||||||
| 14 | 15.5 | 16.4 | 17.4 | 18.8 | 20.4 | 21.5 | 23.7 | ||||||
| 15 | 16.3 | 17.2 | 18.3 | 19.7 | 21.4 | 22.5 | 24.7 | ||||||
| 16 | 17.0 | 17.9 | 19.0 | 20.4 | 22.2 | 23.3 | 25.6 | ||||||
| 17 | 17.4 | 18.3 | 19.5 | 20.9 | 22.8 | 23.9 | 26.2 | ||||||
| 18 | 17.6 | 18.6 | 19.7 | 21.3 | 23.1 | 24.3 | 26.7 | ||||||
| Girls | |||||||||||||
| 0 | 9.8 | 10.3 | 10.8 | 11.3 | 11.9 | 12.2 | 12.8 | ||||||
| 0.5 | 13.0 | 13.6 | 14.3 | 15.1 | 15.9 | 16.4 | 17.2 | ||||||
| 1 | 13.5 | 14.1 | 14.8 | 15.6 | 16.4 | 17.0 | 17.9 | ||||||
| 2 | 12.9 | 13.5 | 14.1 | 14.9 | 15.8 | 16.4 | 17.4 | ||||||
| 3 | 12.7 | 13.2 | 13.8 | 14.5 | 15.3 | 15.8 | 16.7 | ||||||
| 4 | 12.5 | 13.0 | 13.6 | 14.3 | 15.0 | 15.5 | 16.4 | ||||||
| 5 | 12.5 | 13.0 | 13.5 | 14.2 | 15.1 | 15.6 | 16.5 | ||||||
| 6 | 12.5 | 13.0 | 13.6 | 14.4 | 15.3 | 15.9 | 17.1 | ||||||
| 7 | 12.6 | 13.1 | 13.8 | 14.7 | 15.8 | 16.5 | 17.8 | ||||||
| 8 | 12.7 | 13.4 | 14.1 | 15.1 | 16.3 | 17.1 | 18.6 | ||||||
| 9 | 13.0 | 13.7 | 14.5 | 15.6 | 16.9 | 17.8 | 19.5 | ||||||
| 10 | 13.4 | 14.1 | 15.0 | 16.2 | 17.6 | 18.6 | 20.4 | ||||||
| 11 | 13.8 | 14.7 | 15.6 | 16.9 | 18.5 | 19.5 | 21.5 | ||||||
| 12 | 14.4 | 15.3 | 16.4 | 17.7 | 19.4 | 20.5 | 22.7 | ||||||
| 13 | 15.0 | 16.0 | 17.1 | 18.6 | 20.3 | 21.5 | 23.8 | ||||||
| 14 | 15.6 | 16.6 | 17.8 | 19.3 | 21.1 | 22.3 | 24.7 | ||||||
| 15 | 16.2 | 17.2 | 18.3 | 19.8 | 21.7 | 22.8 | 25.2 | ||||||
| 16 | 16.6 | 17.6 | 18.8 | 20.3 | 22.1 | 23.2 | 25.4 | ||||||
| 17 | 17.1 | 18.1 | 19.2 | 20.6 | 22.3 | 23.4 | 25.4 | ||||||
| 18 | 17.5 | 18.4 | 19.5 | 20.9 | 22.5 | 23.5 | 25.3 | ||||||
Figure 2.
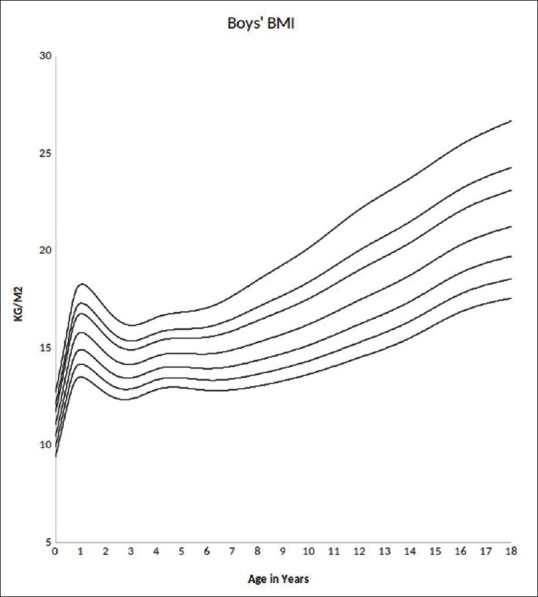
Boys BMI synthetic references
Figure 4.
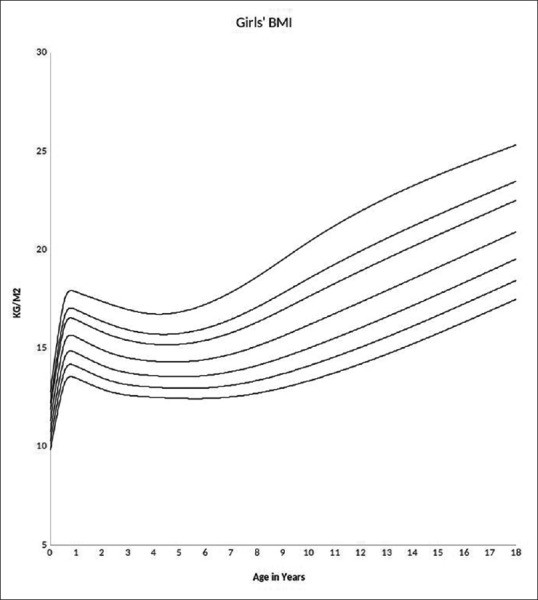
Girls BMI synthetic references
For accounting for regional variations in growth of children, we compared inter regional differences for height, weight and BMI (using ANOVA). There were no significant interregional differences at 18 years for height, weight and BMI in both genders (P > 0.1 for all) and hence separate regional charts were not computed.
DISCUSSION
We present here percentile curves for height, weight and BMI from birth to eighteen years in Indian boys and girls constructed using LMS method and compare these with synthesized references as well as IAP 2015 growth charts. While the median percentiles for height, weight and BMI were similar in both the methods, the 3rd percentile was lower and the 97th percentile for weight and 85th and 95th for BMI were higher using continuous data and the LMS method.
In countries where there is rapid nutrition transition and increasing prevalence of obesity, weight and BMI scales tend to be higher, even after using WHO recommended method of removing the +2-z score for weight for height. Thus, the references produced using continuous data are descriptive and are likely to “normalize” overweight and obesity. Also, large time consuming and expensive studies need to be conducted to collect these data. The advantage of performing such studies is that current patterns of growth, secular trends and important deviations in growth including increasing childhood obesity as well as the persistence of malnutrition are well-documented.
Synthesizing growth charts is an innovative approach of updating growth references as it reduces the need for cumbersome data collection and produces growth references which are based on global models of childhood growth where local parameters are loaded to obtain the best fit references for the target population. The technique of synthesizing growth references takes into consideration global trends over last several decades.[31] The references produced with this technique use global LMS values and hence significantly reduce the skewness of the data and limit the spread to fit the global trends for weight and BMI to the local data. This technique thus seems to prevent “normalizing” overweight and obesity. Another major advantage of this method is that updating references is less challenging as only mean values of height and weight from a representative population at key ages viz. 0, 2,612 and 15 for girls and 0, 2,614 and 18 for boys are needed which are easier to obtain than measuring a large number of children at all age groups across a large country such as India. Further, historic data from published literature may also be used to generate these references.
Various methods for synthesizing anthropometry have been described in literature, viz. regression equations, quantile regression,[13] principal component analysis and the multiplier method.[39] In this study, we have used the method by Hermanussen et al. based-on regression equations using key and auxiliary ages. This method seems most appropriate as it takes into consideration infancy, childhood and puberty (ICP) model of growth, ages at maximum variation in growth, global trends in growth patterns, global LMS values and the robust Preece-Baines growth model. The regression equations, constants and LMS values used in this method are based on a large database involving 24,000,000 measurements from more than 50 global studies, using robust statistical methods.[33]
Reports from other countries have also described the synthesis of growth references in their populations. Pulangan et al. in a study from Indonesia, which is a country with great ethnic diversity, state that it is impractical for them to use one growth chart for all, thus, they have generated synthetic references.[12] Pascanu et al. from Romania have also generated synthetic references as Romania being in nutrition transition, applicability of the WHO standards to the Romanian population was questionable.[11] As generating new references was very expensive, authors constructed synthetic growth references using anthropometric data from nine studies conducted from 1999 to 2016. For children of Turkish descent who were born and were living in Germany (and who grew differently than the Northern European children), Redlefsen et al. synthesized reference values for height, weight and BMI.[40] Thus, in situations where collecting data is expensive, the population is very diverse or numbers are too small, synthesizing growth references is an invaluable technique for creating/updating growth references.
The strength of our study is that we have proposed a method of updating growth references without the need for cumbersome and expensive data collection. To the best of our knowledge, ours is the first study comparing growth references created using continuous data to synthetic growth references. As the method uses local means and global averages, the references show less variance and hence do not 'normalize' obesity. One of our limitations is that there are no rural data included in this study. Further, although both the methods i.e. the LMS method using continuous data and creating synthetic growth references have their own advantages and disadvantages, it seems that the synthetic charts may be more useful for narrowing the spread of weight and BMI centiles. However, validation studies would be required for establishing robustness of one method over the other.
In conclusion, growth references produced from continuous data (LMS method) differ from synthetic growth references mainly at the extreme percentiles for weight and BMI. The synthetic references limit the spread of weight and BMI and may be more representative of the global growth pattern. Synthetic growth references can be created using minimal data and may be especially useful in updating growth references where collecting data on large number of children is difficult.
Financial support and sponsorship
Nil.
Conflicts of interest
There are no conflicts of interest.
Acknowledgements
The authors would like to thank Professor Michael Hermanussen, University of Kiel, for advising on the analysis and guiding the project.
REFERENCES
- 1.Khadilkar VV, Khadilkar AV, Cole TJ, Sayyad MG. Cross-sectional growth curves for height, weight and body mass index for affluent Indian children. Indian Pediatr. 2007;46:477–89. [PubMed] [Google Scholar]
- 2.Khadilkar VV, Khadilkar AV. Prevalence of obesity in affluent school boys in Pune. Indian Pediatr. 2004;41:857–8. [PubMed] [Google Scholar]
- 3.Ranjani H, Mehreen TS, Pradeepa R, Anjana RM, Garg R, Anand K, et al. Epidemiology of childhood overweight and obesity in India: A systematic review. Indian J Med Res. 2016;143:160–74. doi: 10.4103/0971-5916.180203. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Ramchandran P, Gopalan H. Assessment of Nutritional status in Indian preschool children using WHO 2006 growth standards. Indian J Med Res. 2011;134:47–53. [PMC free article] [PubMed] [Google Scholar]
- 5.Kerac M, Blencowe H, Grijalva-Eternod C, McGrath M, Shoham J, Cole TJ, et al. Prevalence of wasting among under 6-month-old infants in developing countries and implications of new case definitions using WHO growth standards: A secondary data analysis. Arch Dis Child. 2011;96:1008–13. doi: 10.1136/adc.2010.191882. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Khadilkar VV, Khadilkar AV. Revised Indian Academy of Paediatrics 2015 growth charts for height, weight and body mass index for 5-18-year-old Indian children. Indian J Endocrinol Metab. 2015;19:470–6. doi: 10.4103/2230-8210.159028. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Freeman JV, Cole TJ, Chinn S, Jones PRM, White EM, Preece MA. Cross sectional stature and weight reference curves for the UK, 1990. Arch Dis Child. 1995;73:17–24. doi: 10.1136/adc.73.1.17. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Rosario AS, Schienkiewitz A, Neuhauser H. German height references for children aged 0 to under 18 years compared to WHO and CDC growth charts. Ann Hum Biol. 2011;38:121–30. doi: 10.3109/03014460.2010.521193. Erratum in: Ann Hum Biol 2014;41:381. [DOI] [PubMed] [Google Scholar]
- 9.Vignerova J, Blaha P. The growth of the Czech child during the past40 years. In: Bodzsar BE, Susanne C, editors. Secular Growth Changes in Europe. Budapest: E€otv€os University Press. Europe; 1998. pp. 93–107. [Google Scholar]
- 10.WHO Expert Consultation. Appropriate body-mass index for Asian populations and its implications for policy and intervention strategies. Lancet. 2004;363:157–63. doi: 10.1016/S0140-6736(03)15268-3. [DOI] [PubMed] [Google Scholar]
- 11.Pascanu I, Pop R, Barbu CG, Dumitrescu CP, Gherlan I, Marginean O, et al. Development of synthetic growth charts for Rumanian population. Acta Endocrinologica. 2016;12:309–18. doi: 10.4183/aeb.2016.309. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Pulungan AB, Julia M, Batubara J, Hermanussen M. Indonesian national synthetic growth charts. Acta Scientific Paediatrics. 2018;1:20–34. [Google Scholar]
- 13.Cole TJ, Green PJ. Smoothing reference centile curves: The LMS method and penalized likelihood. Stat Med. 1992;11:1305–19. doi: 10.1002/sim.4780111005. [DOI] [PubMed] [Google Scholar]
- 14.Matthew B, Parkinson A, Matthew P, Reed B. Creating virtual user populations by analysis of anthropometric data. Int J Ind Ergon. 2010;40:106–111. [Google Scholar]
- 15.Nadadura G, Ulrich RB, Matthew B, Parkinson A. A quantile-based anthropometry synthesis technique for global user populations. Int J Ind Ergon. 2016;53:167–78. [Google Scholar]
- 16.Payande A, Tabesh H, TaghiShakeri M, Saki A, Safarian M. Growth curves of preschool children in the Northeast of Iran: A population based study using quantile regression approach. Glob J Health Sci. 2013;5:9. doi: 10.5539/gjhs.v5n3p9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Hermanussen M, Assmann C, Tutkuviene J. Statistical agreement and cost–benefit: Comparison of methods for constructing growth reference charts. Ann Hum Biol. 2010;37:57–69. doi: 10.3109/03014460903173379. [DOI] [PubMed] [Google Scholar]
- 18.Khadilkar VV, Khadilkar AV, Borade AB, Chiplonkar SA. Body mass index cut-offs for screening for childhood overweight and obesity in Indian children. Indian Pediatr. 2012;49:29–34. doi: 10.1007/s13312-012-0011-y. [DOI] [PubMed] [Google Scholar]
- 19.Khadilkar VV, Khadilkar AV, Cole TJ, Chiplonkar SA, Pandit D. Overweight and obesity prevalence and body mass index trends in Indian children. Int J Pediatr Obes. 2011;6:e216–24. doi: 10.3109/17477166.2010.541463. [DOI] [PubMed] [Google Scholar]
- 20.Khadilkar VV, Khadilkar AV, Cole TJ, Sayyad MG. Cross-sectional growth curves for height, weight and body mass index for affluent Indian children, 2007. Indian Pediatr. 2009;46:477–89. [PubMed] [Google Scholar]
- 21.Khadilkar A, Ekbote V, Chiplonkar S, Khadilkar V, Kajale N, Kulkarni S, et al. Waist circumference percentiles in 2-18-year-old Indian children. J Pediatr. 2014;164:1358–62. doi: 10.1016/j.jpeds.2014.02.018. [DOI] [PubMed] [Google Scholar]
- 22.Khadilkar V, Khadilkar A, Arya A, Ekbote V, Kajale N, Parthasarathy L, et al. Height velocity percentiles in Indian children aged 5–17 years. Indian Pediatr. 2019;56:23–8. [PubMed] [Google Scholar]
- 23.Khadilkar VV, Khadilkar AV, Chiplonkar SA. Growth performance of affluent Indian preschool children: A comparison with the new WHO growth standard. Indian Pediatr. 2010;47:869–72. doi: 10.1007/s13312-010-0147-6. [DOI] [PubMed] [Google Scholar]
- 24.Jaiswal VK, Khadilkar V, Khadilkar A, Lohiya N. Stretched penile length and testicular size from birth to 18 years in boys from Western Maharashtra. Indian J Endocrinol Metab. 2019;23:3. doi: 10.4103/ijem.IJEM_242_18. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Kajale NA, Chiplonkar SA, Khadilkar V, Khadilkar AV. Effect of breastfeeding practices and maternal nutrition on baby's weight gain during first 6 months. J Obstet Gynaecol India. 2016;66:335–9. doi: 10.1007/s13224-016-0918-7. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Khadilkar A, Ekbote V, Kajale N, Chiplonkar S, Prasad H, Agarwal S, et al. Sitting height percentiles in 3-17-year-old Indian children: A multicentre study. Ann Hum Biol. 2019;15:1–5. doi: 10.1080/03014460.2019.1637936. [DOI] [PubMed] [Google Scholar]
- 27.Shaikh Z, Pathak R. Revised Kuppuswamy and BG Prasad socio-economic scales for 2016. Int J Community Med Public Health. 2017;28:997–9. [Google Scholar]
- 28.Wright CM, Williams AF, Elliman D, Bedford H, Birks E, Butler G, et al. Using the new UK-WHO growth charts. BMJ. 2010;340:c1140. doi: 10.1136/bmj.c1140. [DOI] [PubMed] [Google Scholar]
- 29.WHO Child Growth Standards. Acta Pediatr Supplement. 2006;450:5–101. [Google Scholar]
- 30.Indian Academy of Pediatrics Growth Charts Committee. Khadilkar V, Yadav S, Agrawal KK, Tamboli S, Banerjee M, et al. Revised IAP growth charts for height, weight and body mass index for 5- to 18 yearold Indian children. Indian Pediatr. 2015;52:47–55. doi: 10.1007/s13312-015-0566-5. [DOI] [PubMed] [Google Scholar]
- 31.Hermanussen M, Burmeister J. Synthetic growth charts. Acta Paediatr Scand. 1999;88:809–14. doi: 10.1080/08035259950168702. [DOI] [PubMed] [Google Scholar]
- 32.Hermanussen M, Meigen C. Synthetic standards for body weight. Homo. 2003;54:142–56. doi: 10.1078/0018-442x-00068. [DOI] [PubMed] [Google Scholar]
- 33.Preece MA, Baines MJ. A new family of mathematical models describing the human growth curve. Ann Human Biol. 1978;5:1–24. doi: 10.1080/03014467800002601. [DOI] [PubMed] [Google Scholar]
- 34.Marwaha RK, Tandon N, Ganie MA, Kanwar R, Shiva Prasad C, Sabharwal A, et al. Nationwide reference data for height, weight and body mass index of Indian schoolchildren. Natl Med J India. 2011;24:269–77. [PubMed] [Google Scholar]
- 35.Agarwal DK, Agarwal KN, Upadhyay SK, Mittal R, Prakash R, Rai S. Physical and sexual growth pattern of affluent Indian children from 5-18 years of age. Indian Pediatr. 1992;29:1203–82. [PubMed] [Google Scholar]
- 36.Ward R, Schlenker J, Anderson GS. Simple method for developing percentile growth curves for height and weight. Am J Phys Anthropol. 2001;116:246–50. doi: 10.1002/ajpa.1120. [DOI] [PubMed] [Google Scholar]
- 37.Hermanussen M, Aßmann C, Wöhling H, Zabransky M. Harmonizing national growth references for multi-center surveys, drug monitoring and international post marketing surveillance. Acta Paediatr. 2012;101:78–84. doi: 10.1111/j.1651-2227.2011.02415.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.de Onis M. WHO Multicentre Growth Reference Study Group. WHO Child Growth Standards based on length/height, weight and age. Acta Paediatr. 2006;95:76–85. doi: 10.1111/j.1651-2227.2006.tb02378.x. [DOI] [PubMed] [Google Scholar]
- 39.Paley J, Talor J, Levin A, Bhave A, Paley D, Herzenberg JE. The multiplier method for prediction of adult height. J Pediatr Orthop. 2004;24:732–7. doi: 10.1097/00004694-200411000-00025. [DOI] [PubMed] [Google Scholar]
- 40.Redlefsen T, Commentz J, Meigen C, Hermanussen M. Reference values for height, weight and body mass index of German born Turkish children. Anthropol Anz. 2007;65:263–74. [PubMed] [Google Scholar]


