Graphical abstract
Keywords: Functional connectomics, Lifespan trajectory, Rich club, Graph theory
Highlights
-
•
We study topological organization changes of functional connectome in ages 7–85.
-
•
The functional connectome exhibits linear decreases of modularity over the lifespan.
-
•
Both rich-club and local organization have inverted-U shaped lifespan trajectories.
-
•
Heterogeneous age effects are mainly localized to hub regions.
-
•
Connectivity reorganization over lifespan is anatomically distance-dependent.
Abstract
Human brain function undergoes complex transformations across the lifespan. We employed resting-state functional MRI and graph-theory approaches to systematically chart the lifespan trajectory of the topological organization of human whole-brain functional networks in 126 healthy individuals ranging in age from 7 to 85 years. Brain networks were constructed by computing Pearson's correlations in blood-oxygenation-level-dependent temporal fluctuations among 1024 parcellation units followed by graph-based network analyses. We observed that the human brain functional connectome exhibited highly preserved non-random modular and rich club organization over the entire age range studied. Further quantitative analyses revealed linear decreases in modularity and inverted-U shaped trajectories of local efficiency and rich club architecture. Regionally heterogeneous age effects were mainly located in several hubs (e.g., default network, dorsal attention regions). Finally, we observed inverse trajectories of long- and short-distance functional connections, indicating that the reorganization of connectivity concentrates and distributes the brain's functional networks. Our results demonstrate topological changes in the whole-brain functional connectome across nearly the entire human lifespan, providing insights into the neural substrates underlying individual variations in behavior and cognition. These results have important implications for disease connectomics because they provide a baseline for evaluating network impairments in age-related neuropsychiatric disorders.
1. Introduction
The structure and function of the human brain undergo complex changes across the lifespan, which are becoming accessible through a range of neuroimaging methods. For instance, age-related structural changes have been documented in gray matter (GM) volume (Sowell et al., 2003, Ziegler et al., 2012), cortical thickness (Salat et al., 2004, Shaw et al., 2008) and white matter (WM) structural properties (Asato et al., 2010, Lebel et al., 2012, Westlye et al., 2010). Age-related functional changes have also been detected via electrical signals (Clarke et al., 2001, Polich, 1997), glucose metabolism (Alavi et al., 1993, Chugani et al., 1987, Tanna et al., 1991) and blood oxygen level-dependent (BOLD) signals (Damoiseaux et al., 2008, Grady et al., 2006, Kelly et al., 2009). These changes are thought to reflect synaptic pruning and myelination or cell shrinkage at the neuronal level (Giedd and Rapoport, 2010, Salat et al., 2005, Sowell et al., 2003) and to partly account for the maturation or decline in human cognitive function. However, these studies have focused mainly on focal brain attributes rather than integrated communication across regions.
The human brain is structurally and functionally organized into a complex network that is known as the human brain connectome (Biswal et al., 2010, Kelly et al., 2012, Sporns et al., 2005, Zuo et al., 2012) to facilitate the effective segregation and integration of information processing. Recent studies employing graph theory to describe the organization of both structural and functional brain connectomics have consistently demonstrated many non-trivial topological properties such as efficient network architecture, modular structure, central communication hubs, and rich club architecture, which is formed by the densely interconnected hubs [for reviews, see (Bassett and Bullmore, 2009, Bullmore and Sporns, 2009, Stam, 2010, van den Heuvel and Sporns, 2011, van den Heuvel and Sporns, 2013)]. In particular, by examining inter-regional correlations in spontaneous BOLD fluctuations (i.e., functional connectivity) (Biswal et al., 1995, Fox and Raichle, 2007), resting-state functional MRI (R-fMRI) can be used to non-invasively map individual functional connectomics. R-fMRI studies have explored age-related changes in functional connectivity patterns in the whole-brain network (Achard and Bullmore, 2007, Fair et al., 2009, Meunier et al., 2009a, Supekar et al., 2009, Wu et al., 2013) and in specific sub-networks involving default-mode (Fair et al., 2008, Supekar et al., 2010, Thomason et al., 2008, Wu et al., 2011), cognitive-control (Fair et al., 2007, Luna et al., 2010) and reading functions (Vogel et al., 2013). However, these studies have focused either on early (developmental) or late (aging) age-related changes. To date, two R-fMRI studies have examined age-related changes in interregional functional connectivity across the lifespan by combining data from two research sites (Wang et al., 2012, Zuo et al., 2010). Zuo et al. (2010) focused on the lifespan changes of the inter-hemispheric connectivity between two homotopic voxels. Using the same datasets as in Zuo et al. (2010), Wang et al. (2012) employed functional connectivity as the basic feature of the human brain to predict individual ages using the machine-learning algorithm. These two studies examined linear and nonlinear models of the lifespan changes in human brain connectivity. However, they did not explore the lifespan trajectories of brain network properties based on graph theory, which was the main aim of the present paper.
We used R-fMRI and graphic network analyses to chart the lifespan trajectory of the human whole-brain functional connectome based on a single-site public dataset with an age range of 7–85 years. As noted, the human brain's structure and function undergo substantial changes during normal development and aging. In this study, we sought to determine whether and how the topological organization of functional brain networks (including global network structures and pivotal regions/connections) changes with age across a wide age range encompassing most of the lifespan.
2. Materials and methods
2.1. Participants and data acquisition
The present study included a total of 126 healthy, right-handed individuals (age range, 7–85 years; mean age, 36.8 ± 21.2 years; 68 males and 58 females; Supplemental Figure 1) from the NKI/Rockland Sample (NKI-RS), which is provided by the Nathan Kline Institute (NKI, NY, USA) and publicly available at the International Neuroimaging Data-sharing Initiative (INDI) online database (http://fcon_1000.projects.nitrc.org/indi/pro/nki.html) (Nooner et al., 2012). The NKI institutional review board approved all approvals and procedures for collection and sharing of data and written informed consent was obtained from each participant. For those children who were unable to give informed consent, written informed consent was obtained from their legal guardian. Further details regarding the study image acquisition protocol are available on the INDI website. To date, there are three papers published only based upon a subset of NKI-RS sample (Uddin et al., 2011, Oler et al., 2012, Laird et al., 2013) for controls in developmental or adulthood studies. In addition, Mwangi et al. (2013) employed 188 diffusion tensor imaging datasets of this sample to study the brain structure across the lifespan. A recently accepted work used the same datasets as the current work (Yang et al., 2013) explored default network changes across the lifespan. A detailed table of the subjects’ INDI database identifiers, corresponding age and sex and a distribution histogram of the subjects are provided in the Supplementary materials (Figure S1, Table S1).
”All subjects were scanned using a Siemens TrioTM 3.0 Tesla MRI scanner. The R-fMRI scans were then collected using an echo-planar imaging (EPI) sequence (time repetition (TR) / time echo (TE) = 2500/30 ms, flip angle (FA) = 80°, field of view (FOV) = 216 × 216 mm2, voxel size = 3.0 × 3.0 × 3.0 mm3, number of slices = 38). The scanning lasted 650s (∼10 minutes), which consisted of 260 contiguous functional volumes. The subjects were instructed to keep their eyes closed, relax their minds, and remain as motionless as possible during the EPI data acquisition. The 3D T1-weighted images were acquired using a magnetization-prepared rapid gradient echo (MPRAGE) sequence (TR/TE = 2500/3.5 ms, inversion time = 1200 ms, FA = 8°, FOV = 256×256 mm2, voxel size = 1.0 × 1.0 × 1.0 mm3, number of slices = 192) and were used for spatial normalization and group-specific template generation.”
2.2. Data preprocessing
Data preprocessing was performed using the Connectome Computation System (CCS: http://lfcd.psych.ac.cn/ccs.html) (Zuo et al., 2013). The CCS provides a common platform for brain connectome analysis by integrating the functionality of AFNI, FSL and Freesurfer. The preprocessing contained both functional and structural processing steps. Briefly, functional preprocessing included the following: (i) discarding of the first four EPI volumes from each scan for signal equilibration, (ii) slice timing correction for timing offsets, (iii) 3D geometrical displacement correction for head motion, (iv) 4D global mean-based intensity normalization. Furthermore, (v) given recent concerns about the influence of micro-level head motion on functional connectivity and graphical network metrics (Power et al., 2012, Satterthwaite et al., 2012, Van Dijk et al., 2012), the Friston-24 model (Friston et al., 1996), which has been proven to well remove motion artifact (Yan et al., 2013), was employed here. Thus, we did nuisance correction by regressing out 24 motion signals, including realigned data on 6 head motion parameters, 6 head motion parameters one time point before, and the 12 corresponding squared items, individual global means, and WM and cerebrospinal fluid (CSF) mean signals derived from the WM/CSF masks output by the segmentation routine of Freesurfer. Final steps include (vi) band-pass temporal filtering (0.01–0.1 Hz) and (vii) removal of linear and quadratic trends. The structural processing steps included the following steps: (i) removal of the MR image noise using a spatially adaptive non-local means filter, (ii) brain surface reconstruction via the recon-all command in Freesurfer and (iii) spatial normalization from individual functional space to MNI152 standard brain space (FLIRT + FNIRT in FSL). A customized group T1 template in the MNI standard space was generated to reduce the error term resulting from image registration and bias in template selection. Finally, each subject's four-dimensional residual time-series in native space was registered to the standard space with a 3-mm resolution.
2.3. Network construction
In this study, we constructed macro-scale functional networks with nodes for brain regions and edges for inter-regional functional connectivity (Bullmore and Sporns, 2009, He and Evans, 2010). Specifically, to define the network nodes, a group mask in the MNI152 standard space was first generated, which includes all GM (GM tissue probability > 0.2) voxels with non-zeros standard deviations of the BOLD time series. The mean GM probability map was obtained from all individuals’ GM segmentations. We then divided the group mask into a total of 1024 contiguous and uniform regions of interests (ROIs) using a random partitioning procedure (Zalesky et al., 2010). To define network edges, we computed the intrinsic functional connectivity for each pair of 1024 ROIs by computing Pearson correlation coefficients between the regional mean time series. These correlation coefficients were converted to Z-values via using Fisher's r-to-z transform to improve the normality, resulting in a symmetric 1024 × 1024 Z-value connection matrix (i.e., functional connectivity matrix) for each subject. To remove spurious correlations, we set the matrix elements (correlations) with p-values higher than a statistical threshold (p > 0.05, Bonferroni-corrected) to zero. Due to the ambiguous biological explanation of negative correlations (Fox et al., 2009, Murphy et al., 2009), we restricted our analysis to positive correlations.
2.4. Network analyses
We systematically analyzed the global, regional and connectional properties (for illustrations, see Fig. 1) of the resultant brain functional networks as follows.
-
(i)
To examine the global network properties, we first explored the topological efficiency, modularity and vulnerability/robustness of the brain networks, which are described briefly below.
Fig. 1.
Illustrations of network measures. A weighted graph composed of 18 nodes and 32 edges is shown as an example. The line thickness represents the connectional weights. (A) depicts the characteristic path length between nodes a and b. There are many ways between nodes a and b, but the shortest one (i.e., the characteristic path length) is 3, indicated by the red lines. (B) shows that the connectivity strength of node c (red color) is calculated as the average of the weights of the edges (red lines) linking with it. Node c is a highly connected hub, with a relatively highly dense connectivity level. All hubs in this graph are shown as larger dots. (C) shows the presence of a clustered module, as indicated by seven nodes (encircled in blue) being mutually strongly interconnected, but sparsely connected to the rest of the network. (D) indicates the rich-club organization (red dots and lines), which is formed by the densely inter-connected hubs c, d and e. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Network efficiency: Specifically, for a weighted network G with N nodes, the topological length or distance of each edge is assigned by computing the reciprocal of the edge weight. The path length between any pair of nodes is defined as the sum of the edge lengths along the path and the characteristic path length is the length of the shortest ones. The inverse of the harmonic mean of the characteristic path length between each pair of nodes within the network is defined as the global network efficiency:
| (1) |
where Lij is the characteristic path length between nodes i and j in the network. The global efficiency of network G measures the global efficiency of the parallel information transfer in the network (Latora and Marchiori, 2001, Latora and Marchiori, 2003). The local network efficiency is defined as the average of the global efficiency of each node's neighborhood sub-graph:
| (2) |
where Gi denotes the sub-graph composed of the nearest neighbors of node i. The local efficiency reveals how well the network tolerates faults and illustrates the efficiency of communication among the first neighbors of the node i when it is removed.
Modularity: Modularity, which refers to the existence of multiple densely connected modules of brain regions, is a central principle in brain network organization (Meunier et al., 2009b). To explore the significance of the modular structure in the functional connectome, we calculated the modularity index Qmax using a spectral optimization algorithm (Newman, 2006). For a given partition p of a weighted network, Q(p) is defined as:
| (3) |
where Nm is the number of modules, W is the total weight of the network, is the sum of the connectional weights between all nodes in module i and Wi is the sum of the all regional functional connection strengths (i.e., rFCS, see below for details) in module i. Qmax is the largest network modularity resulting from a specific partition p. One hundred corresponding random networks with the same number of nodes, edges and degree distribution as the real networks using Maslov's wiring algorithm (Maslov and Sneppen, 2002) were generated for comparison. Each edge weight was retained during the randomization procedure to preserve the weight distribution of the network.
Notably, besides examining the absolute network properties based on the correlation thresholding method, we also examined the relative network properties based on density thresholding networks considering that different numbers of edges in networks could interfere with detecting age-related differences in topological organization (He et al., 2009, Rubinov and Sporns, 2010). We constructed the relative networks at 5 different connection densities (for definition, see below) in a range of 5–20% (the density range of the absolute networks of all subjects) and calculated the corresponding properties of each network. The graph metrics were then averaged across the density range for each subject to reduce the dependency of results on arbitrary choice of a signal connection density (Rubinov and Sporns, 2010). The absolute network metrics capture the network properties but cannot completely detect the alterations in the topological organization over the lifespan because there are a different number of edges in each network. The relative network metrics based upon same density thresholds capture the changes in network organization of each subject by imposing on each network the same number of edges for compensatory adaptations. Thus, the absolute and relative properties measures provide a way to characterize fully the organizational differences in the functional networks across individuals (He et al., 2009).
-
(ii)
To explore nodal properties, we considered the rFCS (i.e., the weighted degree centrality) due to its high test–retest reliability at both the parcel and voxel levels (Wang et al., 2009, Zuo et al., 2012). Given a brain region i, its rFCS is defined as:
| (4) |
where is the weight or strength of edge rij linking node i and j, i.e., the Pearson correlation coefficient. rFCS measures the average functional connectivity strength of this region i to all other regions in the brain network.
Regions with higher (>1 SD beyond the mean) rFCSs, referred to as hubs, are thought to play important roles in the communication of information in brain connectomics (Buckner et al., 2009, Cole et al., 2010, Zuo et al., 2012). In this study, we further explored the connectivity patterns among these functional hubs. We considered the hubs and their connections as a sub-network and calculated the correlation density using the weighted rich club coefficient measure Φ, which was computed as the ratio between the sum of weights of E connections between hub regions and the strongest E connections for the whole network, which is given by the following:
| (5) |
where is the sum of weights of connections between the hub regions, and Wranked is a vector of all connections in the examined network ranked by weight. A significantly greater rich club coefficient in a brain network than expected by chance (i.e., the results of random networks) indicates the existence of a rich club organization. In other words, the hub nodes are more densely connected among themselves than non-hub nodes and thus form a highly interconnected club. For each brain network, the rich club coefficients of 100 corresponding random networks, Φrandom, were computed. The overall Φrandom was computed as the average rich club coefficient over the 100 random networks. The normalized rich club coefficient, Φnorm, was computed as follows:
| (6) |
To evaluate the reproducibility of rich club analysis, we also used four other thresholds to define the hub regions (rFCS > 0.5, 0.75, 1.25, 1.5 SD beyond the mean).
-
(iii)
To explore the properties of functional network connectivity, we employed three measures: network connection density; network mean connectivity strength; and network mean anatomical distance. Briefly, for a network G with N nodes and K edges, the network density was calculated as follows:
| (7) |
which scales the number of edges existing in the network. The network mean connectivity strength was calculated as the average of the strength across all of the existing edges in the network:
| (8) |
where W is the total connectional weights of the network. For each connection in the functional network, we defined its anatomical distance approximately as the Euclidean distance between the two nodes. Further, we calculated the network mean anatomical distance as follows:
| (9) |
where is the anatomical distance of edge rij. Notably, we further grouped the connections of each subject's network into 17 bins with a 10-mm step according to the connections’ anatomical distances. The connection number, the occupied proportion of the whole edges and the mean connectivity strength of each bin were then calculated.
2.5. Statistical analyses
To determine the changes in the functional connectome across the lifespan, a general linear model (GLM) was used for each metric as follows. (i) To explore linear or quadratic age effects, we used two multiple linear regressions that modeled the targeted property with age or age2 as predictors along with three other covariates that included sex (female 1, male 0), one head-motion covariates, mean frame-wise displacement [meanFD, for calculation method, see Power et al. (2012)], and temporal signal-to-noise ratio [tSNR, for calculation method, see Van Dijk et al. (2012)], which was used to estimate data quality. Notably, the meanFD of all subjects was <0.50 mm (range, 0.03–0.43 mm; mean, 0.14 mm; SD, 0.08), which indicates that the subjects included in this study all had rather small head motions. The meanFD positively correlated with age (p < 0.0001, r2 = 0.25; Figure S2), while no significant sex effect was detected (p = 0.10). Specifically, the GLM models were separately formulated as follows:
| (10) |
| (11) |
Akaike's information criterion (AIC) (Akaike, 1974, Hurvich and Tsai, 1989) was used to determine the model with the best fit. One sample t-tests were performed on the regression coefficients of the predictor variables. For network properties exhibiting significant quadratic age effects, the following equation was further used to determine the peak age:
| (12) |
-
(ii)
To explore the sex-related differences and their development, we used the following GLM model, which included sex and age-by-sex interaction as predictors, to detect both positive (female > male) and negative (male > female) contrasts as well as positive and negative age-by-sex interactions:
| (13) |
2.6. Regional parcellation approaches
Several studies have demonstrated that the quantification of topological organization of brain networks is parcellation-dependent (de Reus and van den Heuvel, 2013, Wang et al., 2009). Although the high-resolution, randomly-generated template we used may positively impact the consistency of several graph characteristics (Fornito et al., 2010, van Wijk et al., 2010, Zalesky et al., 2010), we also employed two low-resolution functional atlases, L-Yeo131 (Yeo et al., 2011) and L-Dos160 (Dosenbach et al., 2010), to determine whether age-related differences were influenced by parcellation methods. Specifically, the brain is parcellated into 7 cortical networks in the L-Yeo131 atlas including 57 parcellation elements (parcels) in the cortex and 8 subcortical parcels (i.e., amygdala, caudate, hippocampus, accumbens-area, pallidum, putamen, thalamus-proper and cerebellum-cortex) for each hemisphere and brain stem. The L-Dos160 we used was identical to that used by Dosenbach et al. (2010), which was derived from a series of meta-analyses of task-related fMRI studies.
2.7. Validation analyses
Given the controversy surrounding the idea that global signal regression (GSR) can introduce negative correlations and reshape the distribution of functional connectivity across the whole brain (Fox et al., 2009, Murphy et al., 2009), we repeated the analyses without GSR to assess the influence of this preprocessing, although we focused exclusively on positive correlations in the present work.
3. Results
3.1. Age-related changes
3.1.1. Global properties
The ‘absolute’ thresholding approach (Hayasaka and Laurienti, 2010, van den Heuvel et al., 2008, van den Heuvel et al., 2009), which only preserves the significantly existing correlations, produced individual brain networks containing different edge numbers, resulting in a connection density range of 5–20%. Of the 126 networks, 83 were fully connected; the remaining had at least 99.0% of their nodes fully connected. Although age and density were unrelated (r = −0.08, p = 0.35), we employed a second ‘relative’ threshold method in which networks were constructed with the same density threshold value to have the same edge numbers. To characterize the age effects on the global network topological properties, three key graphic metrics were employed, network efficiency (global efficiency and local efficiency) and modularity, which were all calculated based on both ‘absolute’ and ‘relative’ networks. We found significant age-related differences in network local efficiency and module structure. The absolute global efficiency of brain functional networks showed no significant relationship with age, while the local efficiency showed an inverted U-shaped trajectory (absolute global efficiency: p = 0.13, r2 = 0.12; local efficiency: p = 0.03, r2 = 0.21; Fig. 2A). Although all individual brain networks exhibited significantly modular structures across the lifespan (all Z-scores > 113.3, p < 0.0001), the absolute modularity decreased linearly with age (p < 0.001, r2 = 0.15; Fig. 2A). Notably, similar age-related differences were observed for both relative global and local efficiency (relative global efficiency: p = 0.13, r2 = 0.12; local efficiency: p = 0.09, r2 = 0.14; Fig. 1B). The relative modularity also decreased linearly with age (p < 0.001, r2 = 0.22; Fig. 2B). The modularity number did not differ significantly with age for either the absolute or the relative functional networks.
Fig. 2.
The lifespan trajectories of functional network efficiency and modularity. (A) The lifespan trajectory of absolute network global efficiency, local efficiency and modularity. (B) The lifespan trajectory of relative network global efficiency, local efficiency and modularity. The dark dots represent the adjusted results of each subject after regressing out sex, head motion and image quality. The curve fits are shown by the dark lines; the red pentagrams represent the peak age. The solid lines show the significant relationships, while the dotted lines show the non-significant trends.
3.1.2. Regional properties
Using a weighted degree centrality metric, rFCS, we identified the most highly connected regions (i.e., hubs) of the networks. The brain hubs were predominantly located in the default-mode (e.g., medial frontal and parietal cortices as well as the lateral temporal and parietal cortical regions), attention-related regions (e.g., insula, dorsal anterior cingulate cortex (ACC), lateral frontal cortex and temporal-parietal junction) and the visual cortex (Fig. 3A and B). Notably, both the mean rFCS map across all subjects and the fitted rFCS maps of different age populations were highly similar to the hub probability map derived from all subjects (r = 0.54 ± 0.12, ps < 0.001; Fig. 3C). Further analyses revealed that the brain hubs were densely connected: the weighted rich club coefficients, Φ, of the sub-network composed of brain hubs were significantly larger than those of matched random networks, Φrandom (all Z-scores > 20.51 ps < 0.001). In addition, an increasing mean Φnorm over a range of hub thresholds was observed (Fig. 4A). This result suggests that the functional networks of the human brain contained a rich club architecture in which the highly connected regions were more densely linked among themselves than the weakly connected regions. Fig. 3C shows the rich club structure of the group-mean brain network. Notably, the rich club phenomenon has been recently demonstrated in the human brain structural connectome (Collin et al., 2013, van den Heuvel et al., 2012, van den Heuvel and Sporns, 2011). Intriguingly, the normalized rich club coefficient Φnorm showed inverted-U shaped lifespan trajectories (p = 0.01, r2 = 0.10; Fig. 4B), indicating that the brain's functional rich club architecture increased until approximately 40 years of age and decreased at older ages. These findings persisted over a range of hub thresholds (Figs. 4A and S3). The 3D surface visualizations of the results were implemented using the Brain Net Viewer (www.nitrc.org/projects/bnv) (Xia et al., 2013).
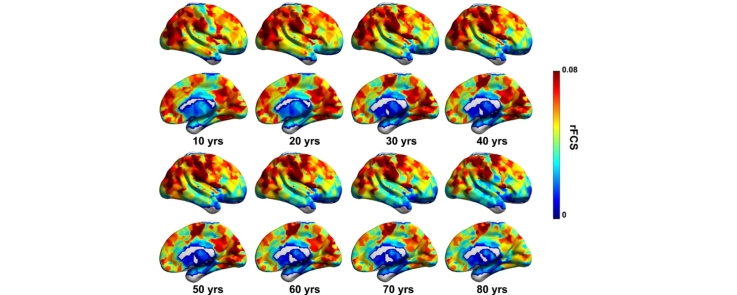
Fig. 3.
Whole-brain rFCS patterns. (A) The hub probability map across all subjects. For each individual subject, the hubs were defined as the regions with an rFCS greater than 1 SD beyond the mean. (B) The group-averaged rFCS map. (C) The adjusted rFCS maps for every decade. The adjusted rFCS values for each region for different ages were obtained after regressing out sex, motion and image quality using the fitted general linear models selected by AIC.
Fig. 4.
Rich-club organization and its lifespan trajectories. (A) The group mean rich-club coefficient curve of brain functional networks for different hub thresholds: rFCS > 0.5, 0.75, 1, 1.25, and 1.5 SD of the mean. A dark gray line indicates Φ, a light gray line for Φrandom and a red line for Φnorm. The figure shows rich-club behavior of the functional brain networks, showing an increasing normalized rich-club coefficient Φnorm for the threshold range. We show the results of the rFCS > SD of the mean threshold to represent the main results. (B) Age-related change in Φnorm. The dark dots represent the adjusted results of each subject after regressing out sex, head motion and data quality effects. The curve fits are shown by the dark lines; the red pentagram represents the peak age. (C) The rich-club origination of the group-averaged connectome. The red dots represent the hub regions, and the blue lines represent the connections between them. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
We also identified the brain regions showing significant age-related changes in the rFCS across the lifespan (Fig. 5, p < 0.05, FDR-corrected). Linear age-related decreases in rFCS were predominantly located in several default-mode regions (bilateral medial prefrontal cortex), attention regions (bilateral insula), visual cortex (bilateral middle occipital gyrus and right calcarine) and subcortical regions (bilateral putamen and left caudate; Fig. 5A). Part of the left precuneus showed a linear decreasing trend with age (p = 0.01, uncorrected; Figure S4 A). The rFCS of the left supplementary motor area, the right inferior temporal gyrus and the left temporal pole increased significantly with age (Fig. 5A). The positive quadratic (U-shaped) trajectories of rFCS with age were mainly located in the parahippocampus and thalamus (Fig. 5B). Negative quadratic age effects (inverted-U shaped) were found in the lateral frontal, parietal and temporal regions (inferior frontal gyrus, precentral gyrus, postcentral gyrus, inferior parietal gyrus, rolandic operculum, middle temporal gyrus and inferior temporal gyrus), and cuneus (Fig. 5B). Bilateral middle frontal gyrus, medial superior frontal gyrus, and left intraparietal sulcus all showed a trend of negative quadratic age effects (p < 0.01, uncorrected; Figure S4 B). Most of these age-related regions were identified as hub regions. The rFCS maps for every decade are shown in Fig. 3C.
Fig. 5.
Lifespan rFCS changes. (A) The regions showing significant linear age effects. (B) The regions showing significant quadratic age effects. p < 0.05, FDR correction was performed to correct for multiple comparisons. The bottom row shows the developmental trajectories of certain, typical regions. INS.L, left insula; MPFC.Rm right medial prefrontal cortex; HIP.L, left hippocampus; SMG.R, right supramarginal gyrus. The dark dots represent the results of each subject after adjusting for sex, head motion and data quality. The curve fits are shown by the dark lines; the red dot pentagrams represent the peak age. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.1.3. Connectional properties
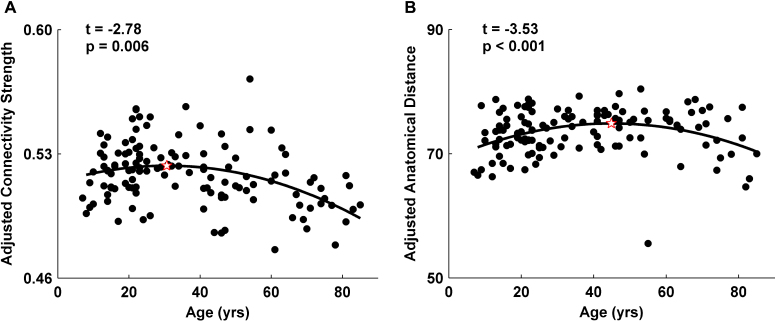
While the network density showed no significant age effects, the network mean connectivity strength (p = 0.006, r2 = 0.28) and the network mean anatomical distance (p < 0.001, r2 = 0.11) followed negative quadratic trajectories over the age range (Fig. 6A and B). The distance-associated connection analyses revealed that the proportions of short-distance connections showed U-shaped trajectories with age with peak ages at approximately 40 years (10–60 mm, ps < 0.02, r2 = 0.13 ± 0.03), while the proportions of long-distance connections showed inverted U-shaped trajectories with peaks around 45 years of age (70–140 mm, p < 0.01, r2 = 0.11± 0.038; Fig. 7A). It should be noted that for both short- and long-distance connections, when the connections were longer, the peak ages were older. In addition, the number of these connections showed no significant age effect (p > 0.07). The correlation strengths of both short- and long-distance connections exhibited negative quadratic age-related changes (20–160 mm, p < 0.02, r2 = 0.13 ± 0.03); however, the connections shorter than 20 mm decreased linearly with age (p < 0.01, r2 > 0.17; Fig. 7B).
Fig. 6.
Lifespan trajectories of the network mean connectivity strength and network mean anatomical distance. The dark dots represent the results of each subject after adjusting for sex, head motion and data quality. The curve fits are shown by the dark lines; the red dots represent the peak age. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
Fig. 7.
Distance-dependent changes in the patterns of connectivity across the lifespan. The functional connections were divided into 17 bins based on anatomical distances (in 10-mm steps). The relationships between the numbers/strengths of the connections of each bin and age were explored. (A) The lifespan trajectories of connection numbers. (B) The lifespan trajectories of connection strengths. Color represents the significance of the age effects. Bottom row: typical lifespan trajectories of different changes. The dark dots represent the adjusted results of each subject after regressing out sex, head motion and data quality. The curve fits are shown by the dark lines; the red dots represent the peak age. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.2. Sex-related differences
Significant sex differences were observed for many global properties including global efficiency (male > female, absolute: p = 0.001, relative: p < 0.001), local efficiency (male > female, absolute: p = 0.01, relative: p = 0.005; Figure S5). In addition, the network density (p = 0.008) and connectivity strength (p = 0.02) were higher in males than females (Figure S5). Other metrics such as modularity and normalized rich club coefficient showed no significant sex differences. For nodal properties, the males showed higher connectivity strength in the left supplementary motor area, insula and bilateral putamen (p < 0.05, FDR corrected). Only the cerebellum crus1 showed a significant sex and age interaction effect (p < 0.05, FDR corrected). We did not observe any significant sex by age interaction effects in any other network property (i.e., global or connectional).
3.3. Parcellation-scheme influences
Comparable results were obtained for other two low-resolution parcellation schemes. No significant age-related differences in network density were detected for either template (L-Dos: p = 0.18; L-Yeo: p = 0.52). Furthermore, all main topological findings obtained using the high-resolution template were reproduced under at least one low-resolution functional template (Fig. 8). Some parcellation-based differences emerged. Specifically, we observed linearly decreasing global and local efficiency under the L-Dos template and preserved modularity and connectivity strength under the L-Yeo template (Fig. 8). Given the incomparability of nodal location across the various parcellation schemes, we did not describe the results of the node and connection analyses.
Fig. 8.
The lifespan trajectories of network properties under two low-resolution parcellation schemes. L-Dos, low-resolution Dosenbach et al.’s functional atlas. L-Yeo, low-resolution Yeo et al.’s functional atlas. The dark dots represent the adjusted results of each subject after regressing out sex, head motion and data quality. The curve fits are shown by the dark lines; the red dots represent the peak age. The solid lines show the significant relationships, while the dotted lines show the non-significant trends. (For interpretation of the references to color in this figure legend, the reader is referred to the web version of this article.)
3.4. Robustness of findings
Regarding network analysis without GSR, we observed that several metrics, including the mean connectivity strength, mean anatomical distance, global efficiency, local efficiency, and normalized rich club coefficients showed age-related trajectories similar to the results with GSR, whereas modularity became insensitive to age effects (Figure S6). Notably, because the network density showed no significant correlation with age (p = 0.32), we only calculated the global network properties of ‘absolute’ networks here for the consideration of the calculated amount.
4. Discussion
We employed R-fMRI data and graph-theory methods to systematically characterize topological age-related effects in the global and regional organization of the human brain functional connectome across the lifespan (7–85 years). Several previous studies used the NKI-RS sample we used in this work. Oler et al. (2012) and Laird et al. (2013) employed subsets of the data to investigate the functional connectivity patterns of amygdala and visual cortex in healthy people but did not focus the lifespan age effect. In contrast, Uddin and colleagues chose the developmental and adulthood parts of the NKI-RS sample for replication analyses of the maturation of functional networks based upon their datasets and confirmed that functional hubs coupling is stronger in adults than that in children (Uddin et al., 2011). This finding supports our observation of rich-club in the functional connectomes across the human life span. Using diffusion tensor imaging (DTI) datasets of the NKI-RS sample, Mwangi and colleagues replicated previous findings that the white matter microstructure exhibits nonlinear changes across the lifespan and found the whole-brain DTI-derived scalar metrics can be useful for accurate prediction of individual ages (Mwangi et al., 2013). Most relevant to our work, using the same datasets, Yang and colleagues demonstrated different lifespan trajectories of the functional network connectivity derived by independent component analysis between the default network and the precuneus network (Yang et al., 2013). The finding that the precuneus network declines with age is consistent with our nodal strength of network connectivity.
Beyond these consistent results, this study mainly characterizes topological age-related effects in the global and regional network organization of the human brain functional connectome by using the graph theory. Our main findings included the following: (i) the brain networks showed preserved high topological global efficiency and negative quadratic (inverted-U shaped) local efficiency; (ii) the brain networks exhibited non-random modular and rich club organization, which were adjusted over the entire lifespan; (iii) heterogeneous age-related effects were mainly localized to hub regions in the frontal, parietal and occipital lobes; and (iv) brain functional connections showed age-related changes, which were distance dependent. Collectively, we observed significant topological modification of the human brain functional connectome across the lifespan, while the general structure of the connectomics was stable over time. These results may be relevant for understanding the changes in neural circuits that underlie age-related variation in cognition and behavior across the lifespan. These novel findings are discussed below in details.
In our study, we found that the global efficiencies of the brain functional networksshowed no significant age effect over the lifespan while local efficiency increased until about 30 years of age and then decreased in older individuals. High global efficiency has been interpreted as indicating an integrated network capable of rapid information exchange among the distributed elements (Bullmore and Sporns, 2012). A previous functional MRI study reported no significant changes in global efficiency over development (Wu et al., 2013), which is consistent with our results. When compared with adults, the global efficiency of the brain functional networks in the elderly has been detected as lower in the resting-state (Achard and Bullmore, 2007) but maintained during the dominated hand grip task (Park et al., 2012). In addition, we detected negative quadratic age effects on local efficiency over the lifespan. The high local efficiency, which indicates highly clustered connections between topologically nearby neighbors, has been suggested to be correlated with efficient information processing among functional specialized regions as well as high error tolerance (Bullmore and Sporns, 2009, He and Evans, 2010, Sporns et al., 2005). In this view, the inverted-U shaped change trajectory of local efficiency supports the notion that functionally related regions or segregated functional processing systems emerge during development (Fair et al., 2009), optimize during adulthood and deteriorate with aging (Meunier et al., 2009a). Previous functional brain network studies have reported increases in local efficiency during development and its reduction with aging (Achard and Bullmore, 2007, Wu et al., 2013), which are consistent with our results. The brain networks are both topologically efficient and prudently anatomically wired. Considering that we also detected distance dependent changes of connections in proportion and strength over the lifespan, the trade-offs between efficiency and energetic costs may result in the maintained global efficiency and negative quadratic local efficiency over the entire age range (Bullmore and Sporns, 2012). Collectivity, we demonstrated the changing trajectories of functional network efficiency over the entire lifespan.
Modularity is a central organizational principle for brain networks, and a modular structure enables adaptability or evolvability for information processing through the formation of relatively independent functional communities, within which regional nodes are densely interconnected (Kirschner and Gerhart, 1998, Meunier et al., 2010, Meunier et al., 2009b). Thus, modularity is a related topological property with clustering that favors specialized or segregated information processing in the brain networks. From the perspective of the entire lifespan, we demonstrated that the brain functional networks exhibit a nonrandom optimized modular structure, which suggests that the key aspects of the functional connectomics are conserved over the lifespan. We found a linear decrease in modularity over the lifespan. Previous studies have reported modularity to be consistent throughout brain development (Fair et al., 2009) and aging (Meunier et al., 2009a). This inconsistency may be related to the age range distribution, as the developmental period only accounts for approximately one quarter of the entire lifespan and these papers employed the method of groups comparison. Network construction methods and network complexity/template resolution may also contribute to the conflicting results.
Hub regions are believed to play vital roles in establishing and maintaining efficient global communication among parallel, distributed brain systems. Consistent with previous works (Cole et al., 2010, Liang et al., 2013, Tomasi and Volkow, 2011, Zuo et al., 2012), we observed that the brain's functional hub regions were predominantly located in the default-mode, attention and visual networks. Notably, the brain hub spatial locations were preserved across the human lifespan, which reflects their relatively stable roles. Hwang and colleagues also reported that functional hubs are stable over development (Hwang et al., 2013). Recently, seminal works by van den Heuvel and Sporns have demonstrated the richness of hub connections in the human brain structural network of white-matter fibers in healthy adults (Collin et al., 2013, van den Heuvel et al., 2012, van den Heuvel and Sporns, 2011, van den Heuvel and Sporns, 2013). Significantly denser connections between hub regions compared with non-hub regions form the rich club organization, which is high-cost but provides significant functional benefits by enhancing not only global information flow but also the resilience of the network to hub attacks. In this study, we observed the existence of rich club organization in the functional network over the lifespan. Interestingly, the rich club structure demonstrated significantly negative quadratic age effects. As the rich club organization makes important contributions to interregional information traffic and cognitive values in healthy populations (Bullmore and Sporns, 2012, van den Heuvel et al., 2012), changes with inverted U-shapes of this core architecture may correlate with high cognitive function changes over the lifespan (Casey et al., 2000). Besides, previous findings about the formation and degeneration of high functioning components (Fair et al., 2008, Luna et al., 2010, Supekar et al., 2010, Tomasi and Volkow, 2012), may be influenced by the rich club changes. Similar lifespan trajectories of the rich club organization and the strength and proportion of long-distance connections may indicate that communication within these rich club regions plays a central role in long-distance brain communication and in optimizing global brain communication efficiency for healthy cognitive brain functioning (van den Heuvel et al., 2012, van den Heuvel et al., 2009, van den Heuvel and Sporns, 2011).
Age-related changes in the regional nodal properties were predominately found in highly connected regions such as default-mode, attention and visual regions. The correlation strength of medial prefrontal cortex, precuneus and insula regions linearly decreased with age. The default mode and attention network regions have been reported to decrease with aging (Andrews-Hanna et al., 2007, Tomasi and Volkow, 2012). The left supplementary motor area increased linearly over the lifespan. Previous studies have found increased connectivity of this region during both development (Wu et al., 2013) and aging (Tomasi and Volkow, 2012). U-shaped lifespan trajectories were found in thalamus, which is consistent with previous findings of the rewiring and pruning of subcortical-cortical connectivity during development (Supekar et al., 2009) as well as increasing correlation strength during aging (Tomasi and Volkow, 2012). Inverted U-shape lifespan trajectories were found mainly in the dorsal attention and language regions, such as the bilateral middle frontal gyrus, precentral gyrus, left intraparietal sulcus, medial superior frontal gyrus, inferior frontal gyrus, inferior parietal gyrus, rolandic operculum, middle temporal gyrus and inferior temporal gyrus, which appear to be among the last brain regions to mature and which have been related to increasing cognitive capacity during childhood (Casey et al., 2000). In the recent remarkable work by Power and colleagues (Power et al., 2013), they reported that degree-based hubs (which we used in the current work) may heavily rely on the subsystem sizes. In this case, the fact that the aging effects mainly target the highly connected regions may indicate that these brain functional network systems altered over the lifespan. Power and colleagues also found that metrics like participant coefficient will perform better in reflecting the regions’ role or centrality in information transformation. The work of Zuo et al. also suggested that multiple centrality metrics should be considered to characterize different aspects of network hubs in applications (Zuo et al., 2012). In that study, sub-graph centrality tended more robust to community sizes. Future work should explore the age effects on regions from different perspectives of the information flow in the functional connectomics with uses of multiple centrality measures.
We observed that the adjustment of the human functional connectome over the lifespan was characterized by both functional connectivity and anatomical distance. The proportions of short- and long-distance connectivity showed inverted change trajectories: the proportion of short-distance connections decreased during development and subsequently increased with aging, while that of the long-distance connections showed the opposite change trajectories. The correlation strength of both short- and long-connections exhibited inverted U-shape change trajectories. Previous studies have demonstrated that short-distance functional connectivity is greater in children than adults (Dosenbach et al., 2010, Fair et al., 2009, Supekar et al., 2009) and predicts brain maturation (Dosenbach et al., 2010). Long-distance connections are enhanced during development (Fair et al., 2009, Kelly et al., 2009, Supekar et al., 2009) and then become vulnerable to aging effects (Tomasi and Volkow, 2012). Previous work of Supekar et al. (2009) demonstrated that connectivity rewiring at the neuronal level also operates at the systems level to help brain reconfiguration. To such a point, the synaptic pruning, which extends through childhood and adolescence (Huttenlocher et al., 1982), and the inverted U-shaped white matter volume change (Giedd and Rapoport, 2010, Good et al., 2001, Salat et al., 2005, Sowell et al., 2003), which involves maturation of fibers, myelination, decrease of myelin density and myelination of white fibers, might explain the connection changes over the lifespan. These findings indicate that the brain connectome adaption continues through the lifespan, which may correlate with underlying structural wiring changes. Importantly, our findings provide a roadmap of the specific function maturation and degeneration of brain pathways, i.e., ‘local, become distributed and then revert back to local’. In addition, short-distance connections were observed to be greater than long-distance connections through the lifespan in terms of intensity. This finding supports an economy in anatomical wiring costs in the human connectome (Bullmore and Sporns, 2012) that has been consistently demonstrated across species (Alexander-Bloch et al., 2013, Markov et al., 2011).
The construction of functional brain network is also modulated by sex. We detected significant sex effects on network efficiency, network density, correlation strength and some regions. Males showed a significantly higher network density and correlation strength than females. Thus, we inferred that males have higher cost than females, which is consistent with previous white matter structural network findings (Gong et al., 2009). Previous studies have also detected a significantly higher global efficiency of functional brain connectomics in males than females, while no differences was found with regard to local efficiency (Wu et al., 2013). Both females and males showed a similar and preserved module and rich-club structure. For nodal property, the regions related to motion showed a significantly higher correlation strength in males compared with females, which is consistent with previous findings (Zuo et al., 2012).
Several issues should be considered in interpreting the current findings. First, we regressed out the global signal to partly reduce physiological and other global noise. We also repeated analyses without global signal regression and found that most of our findings were conserved, and the modularity failed to detect age effects. This finding might be an indication of the fact that global signal removing reduces the effects of physiological and other noise across the whole brain and makes the metrics more comparable across participants. Second, to mitigate the effects of in-scanner head motion, we used the Friston-24 regression model in the preprocessing and added a motion-related parameter, meanFD, in group level, which has been proven to be a promising way to reduce the impact of motion artifacts on both individual and group-level outcomes (Yan et al., 2013). However, the effects of residual motion may remain in our results. Specifically, head movement has been found to have a distinct impact on long- and short-connections, and it significantly correlates with age (Mowinckel et al., 2012, Power et al., 2012, Satterthwaite et al., 2012, Van Dijk et al., 2012), implying a complex role of head motion in the changes of distance-dependent connectivity. This important issue should be studied carefully in future. Third, it is challenging to map the brain's parcellation-based functional connectome appropriately and precisely (Butts, 2009, Smith et al., 2011). We used a random-generated high-resolution template and showed the repeatability of most of our findings across different parcellation schemes. Notably, non-uniform findings between templates were also observed, which may originate from the differences in brain units. These findings indicate that the age effects on functional networks were template dependent. Nevertheless, the development and adoption of novel network tools and whole-brain connectivity-based parcellation approaches in the future will provide additional insight into the age effects on the functional connectome. Fourth, we attempted to explore the age-related differences of brain functional networks over a continuous age range that covered both development and aging. However, the analyzed samples were not perfectly distributed across the entire lifespan. The number of young adults was greater than the number of older people. We employed linear and quadratic (nonlinear) models to explore the age changes across the human lifespan. The incomplete distribution of ages in our sample may have affected parametric curve fitting. Exploration of larger R-fMRI datasets using non-parametrical models (e.g., smoothing splines) may reveal more robust and complex maturational processes (Fjell and Walhovd, 2010). Finally, the age-related functional connectome changes were detected based on the cross-sectional data and thus could be potentially influenced by unbalanced cohort distributions. Because different age cohorts may be different in substantive ways, investigations of the longitudinal network dynamics should be taken in the future to reveal the nature of age-related changes (Fjell and Walhovd, 2010).
5. Conclusions
We detected significant age-related changes modeled by the lifespan trajectories of the functional connectome. These findings may provide novel insights into the neural substrates underlying the behavioral and cognitive variability over the lifespan, which require verification in the future by combining the neuroimaging data and behavioral measurements. The present study reveals the dynamics of the topological organization of the intrinsic network architecture in the functional connectomics across the human lifespan and provides a baseline for evaluating the network impairments of various neuropsychiatric disorders.
Conflict of interest statement
All authors declare no competing financial interests.
Acknowledgements
We thank Dr. Andrew Zalesky for sharing codes to generate high-resolution parcellation atlas, Thomas Yeo for providing the functional parcellation of the cerebral cortex and Caitlin Hinz for the contribution of language editing. This work was supported by the Natural Science Foundation (Grant Nos. 81030028, 31221003 and 81171409), the National Science Fund for Distinguished Young Scholars (Grant No. 81225012, YH), the Major Joint Fund for International Cooperation and Exchange of the National Natural Science Foundation (Grant No. 81220108014, XNZ), the Open Research Fund of the Key Laboratory of Behavioral Science, the Startup Foundation for Distinguished Research Professor (Y0CX492S03, XNZ) from Institute of Psychology, the Hundred Talents Program and the Key Research Program (KSZD-EW-TZ-002, XNZ) of Chinese Academy of Sciences.
Footnotes
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.dcn.2013.11.004.
Contributor Information
Xi-Nian Zuo, Email: zuoxn@psych.ac.cn, zuoxinian@gmail.com.
Yong He, Email: yong.he@bnu.edu.cn.
Appendix A. Supplementary data
The following are the supplementary data to this article:
References
- Achard S., Bullmore E. Efficiency and cost of economical brain functional networks. PLoS Comput. Biol. 2007;3:e17. doi: 10.1371/journal.pcbi.0030017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Akaike H. A new look at statistical-model identification. IEEE Trans. Automat. Control. 1974;19:716–723. [Google Scholar]
- Alavi A., Newberg A.B., Souder E., Berlin J.A. Quantitative analysis of PET and MRI data in normal aging and Alzheimer's disease: atrophy weighted total brain metabolism and absolute whole brain metabolism as reliable discriminators. J. Nucl. Med. 1993;34:1681–1687. [PubMed] [Google Scholar]
- Alexander-Bloch A.F., Vertes P.E., Stidd R., Lalonde F., Clasen L., Rapoport J., Giedd J., Bullmore E.T., Gogtay N. The anatomical distance of functional connections predicts brain network topology in health and schizophrenia. Cereb. Cortex. 2013;23:127–138. doi: 10.1093/cercor/bhr388. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andrews-Hanna J.R., Snyder A.Z., Vincent J.L., Lustig C., Head D., Raichle M.E., Buckner R.L. Disruption of large-scale brain systems in advanced aging. Neuron. 2007;56:924–935. doi: 10.1016/j.neuron.2007.10.038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Asato M.R., Terwilliger R., Woo J., Luna B. White matter development in adolescence: a DTI study. Cereb. Cortex. 2010;20:2122–2131. doi: 10.1093/cercor/bhp282. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bassett D.S., Bullmore E.T. Human brain networks in health and disease. Curr. Opin. Neurol. 2009;22:340–347. doi: 10.1097/WCO.0b013e32832d93dd. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Biswal B., Yetkin F.Z., Haughton V.M., Hyde J.S. Functional connectivity in the motor cortex of resting human brain using echo-planar MRI. Magn. Reson. Med. 1995;34:537–541. doi: 10.1002/mrm.1910340409. [DOI] [PubMed] [Google Scholar]
- Biswal B.B., Mennes M., Zuo X.N., Gohel S., Kelly C., Smith S.M., Beckmann C.F., Adelstein J.S., Buckner R.L., Colcombe S., Dogonowski A.M., Ernst M., Fair D., Hampson M., Hoptman M.J., Hyde J.S., Kiviniemi V.J., Kotter R., Li S.J., Lin C.P., Lowe M.J., Mackay C., Madden D.J., Madsen K.H., Margulies D.S., Mayberg H.S., McMahon K., Monk C.S., Mostofsky S.H., Nagel B.J., Pekar J.J., Peltier S.J., Petersen S.E., Riedl V., Rombouts S.A.R.B., Rypma B., Schlaggar B.L., Schmidt S., Seidler R.D., Siegle G.J., Sorg C., Teng G.J., Veijola J., Villringer A., Walter M., Wang L., Weng X.C., Whitfield-Gabrieli S., Williamson P., Windischberger C., Zang Y.F., Zhang H.Y., Castellanos F.X., Milham M.P. Toward discovery science of human brain function. Proc. Natl. Acad. Sci. U.S.A. 2010;107:4734–4739. doi: 10.1073/pnas.0911855107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Buckner R.L., Sepulcre J., Talukdar T., Krienen F.M., Liu H., Hedden T., Andrews-Hanna J.R., Sperling R.A., Johnson K.A. Cortical hubs revealed by intrinsic functional connectivity: mapping, assessment of stability, and relation to Alzheimer's disease. J. Neurosci. 2009;29:1860–1873. doi: 10.1523/JNEUROSCI.5062-08.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bullmore E., Sporns O. Complex brain networks: graph theoretical analysis of structural and functional systems. Nat. Rev. Neurosci. 2009;10:186–198. doi: 10.1038/nrn2575. [DOI] [PubMed] [Google Scholar]
- Bullmore E., Sporns O. The economy of brain network organization. Nat. Rev. Neurosci. 2012;13:336–349. doi: 10.1038/nrn3214. [DOI] [PubMed] [Google Scholar]
- Butts C.T. Revisiting the foundations of network analysis. Science. 2009;325:414–416. doi: 10.1126/science.1171022. [DOI] [PubMed] [Google Scholar]
- Casey B.J., Giedd J.N., Thomas K.M. Structural and functional brain development and its relation to cognitive development. Biol. Psychol. 2000;54:241–257. doi: 10.1016/s0301-0511(00)00058-2. [DOI] [PubMed] [Google Scholar]
- Chugani H.T., Phelps M.E., Mazziotta J.C. Positron emission tomography study of human brain functional development. Ann. Neurol. 1987;22:487–497. doi: 10.1002/ana.410220408. [DOI] [PubMed] [Google Scholar]
- Clarke A.R., Barry R.J., McCarthy R., Selikowitz M. Age and sex effects in the EEG: development of the normal child. Clin. Neurophysiol. 2001;112:806–814. doi: 10.1016/s1388-2457(01)00488-6. [DOI] [PubMed] [Google Scholar]
- Cole M.W., Pathak S., Schneider W. Identifying the brain's most globally connected regions. Neuroimage. 2010;49:3132–3148. doi: 10.1016/j.neuroimage.2009.11.001. [DOI] [PubMed] [Google Scholar]
- Collin G., Sporns O., Mandl R.C., van den Heuvel M.P. Structural and functional aspects relating to cost and benefit of rich club organization in the human cerebral cortex. Cereb. Cortex. 2013 doi: 10.1093/cercor/bht064. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Damoiseaux J.S., Beckmann C.F., Arigita E.J., Barkhof F., Scheltens P., Stam C.J., Smith S.M., Rombouts S.A. Reduced resting-state brain activity in the “default network” in normal aging. Cereb. Cortex. 2008;18:1856–1864. doi: 10.1093/cercor/bhm207. [DOI] [PubMed] [Google Scholar]
- de Reus M.A., van den Heuvel M.P. The parcellation-based connectome: limitations and extensions. Neuroimage. 2013;80:397–404. doi: 10.1016/j.neuroimage.2013.03.053. [DOI] [PubMed] [Google Scholar]
- Dosenbach N.U., Nardos B., Cohen A.L., Fair D.A., Power J.D., Church J.A., Nelson S.M., Wig G.S., Vogel A.C., Lessov-Schlaggar C.N., Barnes K.A., Dubis J.W., Feczko E., Coalson R.S., Pruett J.R., Jr., Barch D.M., Petersen S.E., Schlaggar B.L. Prediction of individual brain maturity using fMRI. Science. 2010;329:1358–1361. doi: 10.1126/science.1194144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair D.A., Cohen A.L., Dosenbach N.U., Church J.A., Miezin F.M., Barch D.M., Raichle M.E., Petersen S.E., Schlaggar B.L. The maturing architecture of the brain's default network. Proc. Natl. Acad. Sci. U.S.A. 2008;105:4028–4032. doi: 10.1073/pnas.0800376105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair D.A., Cohen A.L., Power J.D., Dosenbach N.U., Church J.A., Miezin F.M., Schlaggar B.L., Petersen S.E. Functional brain networks develop from a “local to distributed” organization. PLoS Comput. Biol. 2009;5:e1000381. doi: 10.1371/journal.pcbi.1000381. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fair D.A., Dosenbach N.U., Church J.A., Cohen A.L., Brahmbhatt S., Miezin F.M., Barch D.M., Raichle M.E., Petersen S.E., Schlaggar B.L. Development of distinct control networks through segregation and integration. Proc. Natl. Acad. Sci. U.S.A. 2007;104:13507–13512. [Google Scholar]
- Fjell A.M., Walhovd K.B. Structural brain changes in aging: courses, causes and cognitive consequences. Rev. Neurosci. 2010;21:187–221. doi: 10.1515/revneuro.2010.21.3.187. [DOI] [PubMed] [Google Scholar]
- Fornito A., Zalesky A., Bullmore E.T. Network scaling effects in graph analytic studies of human resting-state FMRI data. Front. Syst. Neurosci. 2010;4:22. doi: 10.3389/fnsys.2010.00022. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Fox M.D., Raichle M.E. Spontaneous fluctuations in brain activity observed with functional magnetic resonance imaging. Nat. Rev. Neurosci. 2007;8:700–711. doi: 10.1038/nrn2201. [DOI] [PubMed] [Google Scholar]
- Fox M.D., Zhang D., Snyder A.Z., Raichle M.E. The global signal and observed anticorrelated resting state brain networks. J. Neurophysiol. 2009;101:3270–3283. doi: 10.1152/jn.90777.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston K.J., Williams S., Howard R., Frackowiak R.S., Turner R. Movement-related effects in fMRI time-series. Magn. Reson. Med. 1996;35:346–355. doi: 10.1002/mrm.1910350312. [DOI] [PubMed] [Google Scholar]
- Giedd J.N., Rapoport J.L. Structural MRI of pediatric brain development: what have we learned and where are we going? Neuron. 2010;67:728–734. doi: 10.1016/j.neuron.2010.08.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gong G., Rosa-Neto P., Carbonell F., Chen Z.J., He Y., Evans A.C. Age- and gender-related differences in the cortical anatomical network. J. Neurosci. 2009;29:15684–15693. doi: 10.1523/JNEUROSCI.2308-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Good C.D., Johnsrude I.S., Ashburner J., Henson R.N., Friston K.J., Frackowiak R.S. A voxel-based morphometric study of ageing in 465 normal adult human brains. Neuroimage. 2001;14:21–36. doi: 10.1006/nimg.2001.0786. [DOI] [PubMed] [Google Scholar]
- Grady C.L., Springer M.V., Hongwanishkul D., McIntosh A.R., Winocur G. Age-related changes in brain activity across the adult lifespan. J. Cogn. Neurosci. 2006;18:227–241. doi: 10.1162/089892906775783705. [DOI] [PubMed] [Google Scholar]
- Hayasaka S., Laurienti P.J. Comparison of characteristics between region-and voxel-based network analyses in resting-state fMRI data. Neuroimage. 2010;50:499–508. doi: 10.1016/j.neuroimage.2009.12.051. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y., Dagher A., Chen Z., Charil A., Zijdenbos A., Worsley K., Evans A. Impaired small-world efficiency in structural cortical networks in multiple sclerosis associated with white matter lesion load. Brain. 2009;132:3366–3379. doi: 10.1093/brain/awp089. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He Y., Evans A. Graph theoretical modeling of brain connectivity. Curr. Opin. Neurol. 2010;23:341–350. doi: 10.1097/WCO.0b013e32833aa567. [DOI] [PubMed] [Google Scholar]
- Hurvich C., Tsai C. Regression and time-series model selection in small samples. Biometrika. 1989;76:297–307. [Google Scholar]
- Huttenlocher P.R., De Courten C., Garey L.J., Van der Loos H. Synaptic development in human cerebral cortex. Int. J. Neurol. 1982;16–17:144–154. [PubMed] [Google Scholar]
- Hwang K., Hallquist M.N., Luna B. The development of hub architecture in the human functional brain network. Cereb Cortex. 2013;23:2380–2393. doi: 10.1093/cercor/bhs227. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kelly A.M., Di Martino A., Uddin L.Q., Shehzad Z., Gee D.G., Reiss P.T., Margulies D.S., Castellanos F.X., Milham M.P. Development of anterior cingulate functional connectivity from late childhood to early adulthood. Cereb. Cortex. 2009;19:640–657. doi: 10.1093/cercor/bhn117. [DOI] [PubMed] [Google Scholar]
- Kelly C., Biswal B.B., Craddock R.C., Castellanos F.X., Milham M.P. Characterizing variation in the functional connectome: promise and pitfalls. Trends Cogn. Sci. 2012;16:181–188. doi: 10.1016/j.tics.2012.02.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kirschner M., Gerhart J. Evolvability. Proc. Natl. Acad. Sci. U.S.A. 1998;95:8420–8427. doi: 10.1073/pnas.95.15.8420. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Laird A.R., Eickhoff S.B., Rottschy C., Bzdok D., Ray K.L., Fox P.T. Networks of task co-activations. Neuroimage. 2013;80:505–514. doi: 10.1016/j.neuroimage.2013.04.073. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Latora V., Marchiori M. Efficient behavior of small-world networks. Phys. Rev. Lett. 2001;87:198701. doi: 10.1103/PhysRevLett.87.198701. [DOI] [PubMed] [Google Scholar]
- Latora V., Marchiori M. Economic small-world behavior in weighted networks. Eur. Phys. J. B – Condens. Matter. 2003;32:249–263. [Google Scholar]
- Lebel C., Gee M., Camicioli R., Wieler M., Martin W., Beaulieu C. Diffusion tensor imaging of white matter tract evolution over the lifespan. Neuroimage. 2012;60:340–352. doi: 10.1016/j.neuroimage.2011.11.094. [DOI] [PubMed] [Google Scholar]
- Liang X., Zou Q., He Y., Yang Y. Coupling of functional connectivity and regional cerebral blood flow reveals a physiological basis for network hubs of the human brain. Proc. Natl. Acad. Sci. U.S.A. 2013;110:1929–1934. doi: 10.1073/pnas.1214900110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Luna B., Padmanabhan A., O’Hearn K. What has fMRI told us about the development of cognitive control through adolescence? Brain Cogn. 2010;72:101–113. doi: 10.1016/j.bandc.2009.08.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Markov N.T., Misery P., Falchier A., Lamy C., Vezoli J., Quilodran R., Gariel M.A., Giroud P., Ercsey-Ravasz M., Pilaz L.J., Huissoud C., Barone P., Dehay C., Toroczkai Z., Van Essen D.C., Kennedy H., Knoblauch K. Weight consistency specifies regularities of macaque cortical networks. Cereb. Cortex. 2011;21:1254–1272. doi: 10.1093/cercor/bhq201. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maslov S., Sneppen K. Specificity and stability in topology of protein networks. Science. 2002;296:910–913. doi: 10.1126/science.1065103. [DOI] [PubMed] [Google Scholar]
- Meunier D., Achard S., Morcom A., Bullmore E. Age-related changes in modular organization of human brain functional networks. Neuroimage. 2009;44:715–723. doi: 10.1016/j.neuroimage.2008.09.062. [DOI] [PubMed] [Google Scholar]
- Meunier D., Lambiotte R., Bullmore E.T. Modular and hierarchically modular organization of brain networks. Front. Neurosci. 2010;4:200. doi: 10.3389/fnins.2010.00200. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meunier D., Lambiotte R., Fornito A., Ersche K.D., Bullmore E.T. Hierarchical modularity in human brain functional networks. Front. Neuroinform. 2009;3:37. doi: 10.3389/neuro.11.037.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mowinckel A.M., Espeseth T., Westlye L.T. Network-specific effects of age and in-scanner subject motion: a resting-state fMRI study of 238 healthy adults. Neuroimage. 2012;63:1364–1373. doi: 10.1016/j.neuroimage.2012.08.004. [DOI] [PubMed] [Google Scholar]
- Murphy K., Birn R.M., Handwerker D.A., Jones T.B., Bandettini P.A. The impact of global signal regression on resting state correlations: are anti-correlated networks introduced? Neuroimage. 2009;44:893–905. doi: 10.1016/j.neuroimage.2008.09.036. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mwangi B., Hasan K.M., Soares J.C. Prediction of individual subject's age across the human lifespan using diffusion tensor imaging: a machine learning approach. Neuroimage. 2013;75:58–67. doi: 10.1016/j.neuroimage.2013.02.055. [DOI] [PubMed] [Google Scholar]
- Newman M.E. Modularity and community structure in networks. Proc. Natl. Acad. Sci. U.S.A. 2006;103:8577–8582. doi: 10.1073/pnas.0601602103. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nooner K.B., Colcombe S.J., Tobe R.H., Mennes M., Benedict M.M., Moreno A.L., Panek L.J., Brown S., Zavitz S.T., Li Q., Sikka S., Gutman D., Bangaru S., Schlachter R.T., Kamiel S.M., Anwar A.R., Hinz C.M., Kaplan M.S., Rachlin A.B., Adelsberg S., Cheung B., Khanuja R., Yan C., Craddock C.C., Calhoun V., Courtney W., King M., Wood D., Cox C.L., Kelly A.M., Di Martino A., Petkova E., Reiss P.T., Duan N., Thomsen D., Biswal B., Coffey B., Hoptman M.J., Javitt D.C., Pomara N., Sidtis J.J., Koplewicz H.S., Castellanos F.X., Leventhal B.L., Milham M.P. The NKI-rockland sample: a model for accelerating the pace of discovery science in psychiatry. Front. Neurosci. 2012;6:152. doi: 10.3389/fnins.2012.00152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Oler J.A., Birn R.M., Patriat R., Fox A.S., Shelton S.E., Burghy C.A., Stodola D.E., Essex M.J., Davidson R.J., Kalin N.H. Evidence for coordinated functional activity within the extended amygdala of non-human and human primates. Neuroimage. 2012;61:1059–1066. doi: 10.1016/j.neuroimage.2012.03.045. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Park C.H., Boudrias M.H., Rossiter H., Ward N.S. Age-related changes in the topological architecture of the brain during hand grip. Neurobiol. Aging. 2012;33 doi: 10.1016/j.neurobiolaging.2011.08.003. 833 e827–e837. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polich J. EEG and ERP assessment of normal aging. Electroencephalogr. Clin. Neurophysiol. 1997;104:244–256. doi: 10.1016/s0168-5597(97)96139-6. [DOI] [PubMed] [Google Scholar]
- Power J.D., Barnes K.A., Snyder A.Z., Schlaggar B.L., Petersen S.E. Spurious but systematic correlations in functional connectivity MRI networks arise from subject motion. Neuroimage. 2012;59:2142–2154. doi: 10.1016/j.neuroimage.2011.10.018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Power J.D., Schlaggar B.L., Lessov-Schlaggar C.N., Petersen S.E. Evidence for hubs in human functional brain networks. Neuron. 2013;79:798–813. doi: 10.1016/j.neuron.2013.07.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rubinov M., Sporns O. Complex network measures of brain connectivity: uses and interpretations. Neuroimage. 2010;52:1059–1069. doi: 10.1016/j.neuroimage.2009.10.003. [DOI] [PubMed] [Google Scholar]
- Salat D.H., Buckner R.L., Snyder A.Z., Greve D.N., Desikan R.S., Busa E., Morris J.C., Dale A.M., Fischl B. Thinning of the cerebral cortex in aging. Cereb. Cortex. 2004;14:721–730. doi: 10.1093/cercor/bhh032. [DOI] [PubMed] [Google Scholar]
- Salat D.H., Tuch D.S., Greve D.N., van der Kouwe A.J., Hevelone N.D., Zaleta A.K., Rosen B.R., Fischl B., Corkin S., Rosas H.D., Dale A.M. Age-related alterations in white matter microstructure measured by diffusion tensor imaging. Neurobiol. Aging. 2005;26:1215–1227. doi: 10.1016/j.neurobiolaging.2004.09.017. [DOI] [PubMed] [Google Scholar]
- Satterthwaite T.D., Wolf D.H., Loughead J., Ruparel K., Elliott M.A., Hakonarson H., Gur R.C., Gur R.E. Impact of in-scanner head motion on multiple measures of functional connectivity: relevance for studies of neurodevelopment in youth. Neuroimage. 2012;60:623–632. doi: 10.1016/j.neuroimage.2011.12.063. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Shaw P., Kabani N.J., Lerch J.P., Eckstrand K., Lenroot R., Gogtay N., Greenstein D., Clasen L., Evans A., Rapoport J.L., Giedd J.N., Wise S.P. Neurodevelopmental trajectories of the human cerebral cortex. J. Neurosci. 2008;28:3586–3594. doi: 10.1523/JNEUROSCI.5309-07.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Smith S.M., Miller K.L., Salimi-Khorshidi G., Webster M., Beckmann C.F., Nichols T.E., Ramsey J.D., Woolrich M.W. Network modelling methods for FMRI. Neuroimage. 2011;54:875–891. doi: 10.1016/j.neuroimage.2010.08.063. [DOI] [PubMed] [Google Scholar]
- Sowell E.R., Peterson B.S., Thompson P.M., Welcome S.E., Henkenius A.L., Toga A.W. Mapping cortical change across the human life span. Nat. Neurosci. 2003;6:309–315. doi: 10.1038/nn1008. [DOI] [PubMed] [Google Scholar]
- Sporns O., Tononi G., Kotter R. The human connectome: a structural description of the human brain. PLoS Comput. Biol. 2005;1:e42. doi: 10.1371/journal.pcbi.0010042. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stam C.J. Characterization of anatomical and functional connectivity in the brain: a complex networks perspective. Int. J. Psychophysiol. 2010;77:186–194. doi: 10.1016/j.ijpsycho.2010.06.024. [DOI] [PubMed] [Google Scholar]
- Supekar K., Musen M., Menon V. Development of large-scale functional brain networks in children. PLoS Biol. 2009;7:e1000157. doi: 10.1371/journal.pbio.1000157. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Supekar K., Uddin L.Q., Prater K., Amin H., Greicius M.D., Menon V. Development of functional and structural connectivity within the default mode network in young children. Neuroimage. 2010;52:290–301. doi: 10.1016/j.neuroimage.2010.04.009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tanna N.K., Kohn M.I., Horwich D.N., Jolles P.R., Zimmerman R.A., Alves W.M., Alavi A. Analysis of brain and cerebrospinal fluid volumes with MR imaging: impact on PET data correction for atrophy. Part II. Aging and Alzheimer dementia. Radiology. 1991;178:123–130. doi: 10.1148/radiology.178.1.1984290. [DOI] [PubMed] [Google Scholar]
- Thomason M.E., Chang C.E., Glover G.H., Gabrieli J.D., Greicius M.D., Gotlib I.H. Default-mode function and task-induced deactivation have overlapping brain substrates in children. Neuroimage. 2008;41:1493–1503. doi: 10.1016/j.neuroimage.2008.03.029. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D., Volkow N.D. Functional connectivity hubs in the human brain. Neuroimage. 2011;57:908–917. doi: 10.1016/j.neuroimage.2011.05.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tomasi D., Volkow N.D. Aging and functional brain networks. Mol. Psychiatry. 2012;17(471):458–549. doi: 10.1038/mp.2011.81. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Uddin L.Q., Supekar K.S., Ryali S., Menon V. Dynamic reconfiguration of structural and functional connectivity across core neurocognitive brain networks with development. J. Neurosci. 2011;31:18578–18589. doi: 10.1523/JNEUROSCI.4465-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M.P., Kahn R.S., Goni J., Sporns O. High-cost, high-capacity backbone for global brain communication. Proc. Natl. Acad. Sci. U.S.A. 2012;109:11372–11377. doi: 10.1073/pnas.1203593109. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M.P., Sporns O. Rich club organization of the human connectome. J. Neurosci. 2011;31:15775–15786. doi: 10.1523/JNEUROSCI.3539-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M.P., Sporns O. An anatomical substrate for integration among functional networks in human cortex. J. Neurosci. 2013;33:14489–14500. doi: 10.1523/JNEUROSCI.2128-13.2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van den Heuvel M.P., Stam C.J., Boersma M., Hulshoff Pol H.E. Small-world and scale-free organization of voxel-based resting-state functional connectivity in the human brain. Neuroimage. 2008;43:528–539. doi: 10.1016/j.neuroimage.2008.08.010. [DOI] [PubMed] [Google Scholar]
- van den Heuvel M.P., Stam C.J., Kahn R.S., Hulshoff Pol H.E. Efficiency of functional brain networks and intellectual performance. J. Neurosci. 2009;29:7619–7624. doi: 10.1523/JNEUROSCI.1443-09.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Dijk K.R., Sabuncu M.R., Buckner R.L. The influence of head motion on intrinsic functional connectivity MRI. Neuroimage. 2012;59:431–438. doi: 10.1016/j.neuroimage.2011.07.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van Wijk B.C., Stam C.J., Daffertshofer A. Comparing brain networks of different size and connectivity density using graph theory. PLoS ONE. 2010;5:e13701. doi: 10.1371/journal.pone.0013701. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Vogel A.C., Church J.A., Power J.D., Miezin F.M., Petersen S.E., Schlaggar B.L. Functional network architecture of reading-related regions across development. Brain Lang. 2013;125:231–243. doi: 10.1016/j.bandl.2012.12.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang J., Wang L., Zang Y., Yang H., Tang H., Gong Q., Chen Z., Zhu C., He Y. Parcellation-dependent small-world brain functional networks: a resting-state fMRI study. Hum. Brain Mapp. 2009;30:1511–1523. doi: 10.1002/hbm.20623. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wang L., Su L., Shen H., Hu D. Decoding lifespan changes of the human brain using resting-state functional connectivity MRI. PLoS ONE. 2012;7:e44530. doi: 10.1371/journal.pone.0044530. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Westlye L.T., Walhovd K.B., Dale A.M., Bjornerud A., Due-Tonnessen P., Engvig A., Grydeland H., Tamnes C.K., Ostby Y., Fjell A.M. Life-span changes of the human brain white matter: diffusion tensor imaging (DTI) and volumetry. Cereb. Cortex. 2010;20:2055–2068. doi: 10.1093/cercor/bhp280. [DOI] [PubMed] [Google Scholar]
- Wu J.T., Wu H.Z., Yan C.G., Chen W.X., Zhang H.Y., He Y., Yang H.S. Aging-related changes in the default mode network and its anti-correlated networks: a resting-state fMRI study. Neurosci. Lett. 2011;504:62–67. doi: 10.1016/j.neulet.2011.08.059. [DOI] [PubMed] [Google Scholar]
- Wu K., Taki Y., Sato K., Hashizume H., Sassa Y., Takeuchi H., Thyreau B., He Y., Evans A.C., Li X., Kawashima R., Fukuda H. Topological organization of functional brain networks in healthy children: differences in relation to age, sex, and intelligence. PLoS ONE. 2013;8:e55347. doi: 10.1371/journal.pone.0055347. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Xia M., Wang J., He Y. BrainNet Viewer: a network visualization tool for human brain connectomics. 2013 doi: 10.1371/journal.pone.0068910. PLoS One. 8, e68910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yan C.G., Cheung B., Kelly C., Colcombe S., Craddock R.C., Di Martino A., Li Q., Zuo X.N., Castellanos F.X., Milham M.P. A comprehensive assessment of regional variation in the impact of head micromovements on functional connectomics. Neuroimage. 2013;76:183–201. doi: 10.1016/j.neuroimage.2013.03.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang Z., Chang C., Xu T., Jiang L., Handwerker D.A., Castellanos F.X., Milham M.P., Bandettini P.A., Zuo X.N. Connectivity trajectory across lifespan differentiates the precuneus from the default network. Neuroimage. 2013 doi: 10.1016/j.neuroimage.2013.10.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yeo B.T., Krienen F.M., Sepulcre J., Sabuncu M.R., Lashkari D., Hollinshead M., Roffman J.L., Smoller J.W., Zollei L., Polimeni J.R., Fischl B., Liu H., Buckner R.L. The organization of the human cerebral cortex estimated by intrinsic functional connectivity. J. Neurophysiol. 2011;106:1125–1165. doi: 10.1152/jn.00338.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zalesky A., Fornito A., Harding I.H., Cocchi L., Yucel M., Pantelis C., Bullmore E.T. Whole-brain anatomical networks: does the choice of nodes matter? Neuroimage. 2010;50:970–983. doi: 10.1016/j.neuroimage.2009.12.027. [DOI] [PubMed] [Google Scholar]
- Ziegler G., Dahnke R., Jancke L., Yotter R.A., May A., Gaser C. Brain structural trajectories over the adult lifespan. Hum. Brain Mapp. 2012;33:2377–2389. doi: 10.1002/hbm.21374. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo X.N., Ehmke R., Mennes M., Imperati D., Castellanos F.X., Sporns O., Milham M.P. Network centrality in the human functional connectome. Cereb. Cortex. 2012;22:1862–1875. doi: 10.1093/cercor/bhr269. [DOI] [PubMed] [Google Scholar]
- Zuo X.N., Kelly C., Di Martino A., Mennes M., Margulies D.S., Bangaru S., Grzadzinski R., Evans A.C., Zang Y.F., Castellanos F.X., Milham M.P. Growing together and growing apart: regional and sex differences in the lifespan developmental trajectories of functional homotopy. J. Neurosci. 2010;30:15034–15043. doi: 10.1523/JNEUROSCI.2612-10.2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zuo X.N., Xu T., Jiang L., Yang Z., Cao X.Y., He Y., Zang Y.F., Castellanos F.X., Milham M.P. Toward reliable characterization of functional homogeneity in the human brain: preprocessing, scan duration, imaging resolution and computational space. Neuroimage. 2013;65:374–386. doi: 10.1016/j.neuroimage.2012.10.017. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.