Considering the Role of Adaptive Evolution in Models of the Ocean and Climate System

Abstract

Numerical models have been highly successful in simulating global carbon and nutrient cycles in today's ocean, together with observed spatial and temporal patterns of chlorophyll and plankton biomass at the surface. With this success has come some confidence in projecting the century‐scale response to continuing anthropogenic warming. There is also increasing interest in using such models to understand the role of plankton ecosystems in past oceans. However, today's marine environment is the product of billions of years of continual evolution—a process that continues today. In this paper, we address the questions of whether an assumption of species invariance is sufficient, and if not, under what circumstances current model projections might break down. To do this, we first identify the key timescales and questions asked of models. We then review how current marine ecosystem models work and what alternative approaches are available to account for evolution. We argue that for timescales of climate change overlapping with evolutionary timescales, accounting for evolution may to lead to very different projected outcomes regarding the timescales of ecosystem response and associated global biogeochemical cycling. This is particularly the case for past extinction events but may also be true in the future, depending on the eventual degree of anthropogenic disruption. The discipline of building new numerical models that incorporate evolution is also hugely beneficial in itself, as it forces us to question what we know about adaptive evolution, irrespective of its quantitative role in any specific event or environmental changes.

Key Points

• Marine microbes are key drivers of global biogeochemical cycles and have an immense capacity for evolution

• Earth system models do not currently include microbial evolution and thus may miss key feedbacks in a fully coupled system

• Understanding these feedbacks requires that ecology, evolution, and environment are dynamically represented and linked in models

“It is a recognized principle of ecology that the interactions of organisms and environment are reciprocal. The environment not only determines the conditions under which life exists, but the organisms influence the conditions prevailing in the environment.” Redfield (1958)

“At every moment natural selection is operating to change the genetic composition of populations in response to the momentary environment, but as that composition changes it forces a concomitant change in the environment itself. Thus organisms and environments are both causes and effects in a coevolutionary process.” Lewontin (2000)

1. Introduction

A particular challenge in Earth system science is to understand and successfully simulate a system in which higher‐level processes emerge from the interactions of many lower‐level processes (Levin, 1998). Climate is modulated by the global carbon cycle, which is itself driven by the metabolic activity of innumerable interacting organisms. Within the marine realm, more than 10²⁷ phototrophic organisms (Flombaum et al., 2013) contribute approximately half of total global photosynthesis (Field et al., 1998) while driving the transfer of an estimated 5–11 Pg C/year of organic carbon into the ocean interior as sinking particles and dissolved molecules (Henson et al., 2011). Interactions and feedbacks within the Earth system therefore occur across an extremely broad range of temporal and spatial scales, from subcellular processes occurring on timescales of minutes or less to global changes spanning millions of years or more (Figure 1).

Figure 1.

Schematic illustration of the temporal and spatial scales of interaction between microbes and the Earth system. Interactions and feedbacks occur across the system at all scales. Genetic mutations and recombination provide the raw materials for evolution in response to local or global changes in the environment, while evolving communities reciprocally affect global climate via their effects on ocean biogeochemistry and the carbon cycle.

Within this coupled system, environmental factors including temperature, predator abundance, and the availability of light, nutrients, and prey determine the growth of individual organisms. Conversely, the combined growth of those organisms directly impacts the physical, chemical, and biological environments, as individuals take up nutrients, absorb light, consume prey, and feed predators. As such, there exists a complex feedback loop (Figure 2) with environmental conditions and ecology changing together over a broad range of timescales.

Figure 2.

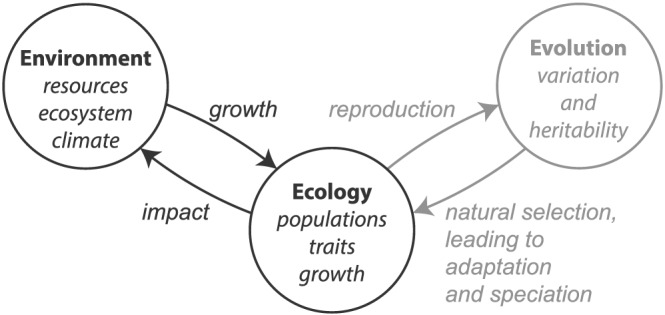
Evolution and the environmental feedback loop (modified from Claessen, 2012). Biological growth and community structure are determined as individuals interact with the physical, chemical, and biotic environment, as a function of their traits. At the same time, the growth of populations and communities impacts the environment. This environment‐ecology feedback loop forms the basis of most coupled ecosystem, biogeochemistry, and climate models. Evolution acts on this system as heritable changes in traits are selected for or against in the struggle for existence. Changes in the trait composition of the community affect the interactions of ecology and environment, completing the feedback loop.

This environmental‐ecological feedback loop is at the core of all dynamic ocean and Earth system models, which aim to understand not only how changing environmental conditions might affect marine communities but also how such changes might feedback into the broader Earth and climate system. The desire to understand potentially important feedbacks between marine ecosystems and their environment has been a key motivation in the development of more complex global ocean ecosystem models (Le Quéré et al., 2005), typically including a number of highly idealized plankton populations that are assumed to be representative of marine plankton communities at large. Increasing the degree of ecological complexity included in ocean models has allowed the exploration of how changes in ecosystem structure can affect both the community response to, and its effect on, the broader environment (Bopp et al., 2005; Dutkiewicz et al., 2013, 2015). Global models including representations of key functional groups and traits have led to new insights into the effects of ecological diversity on ecosystem function (Barton et al., 2010; Dutkiewicz et al., 2014; Monteiro et al., 2016; Prowe et al., 2012).

Despite these advances, a notable knowledge gap in current global climate and carbon cycle models is that most do not currently include an explicit representation of evolution, with microbial communities typically represented in terms of a few idealized populations with immutable traits. This is in contrast to diverse marine microbial communities that have evolved over the last 4 billion years of Earth history and that continue to evolve today on relatively short (seasonal‐to‐decadal) timescales (Irwin et al., 2015). A key driver of this rapid evolution is the amount of genetic and phenotypic variation that natural selection can potentially act upon. In addition to the generally very large standing variation already present in a community (e.g., Mock et al., 2017), large microbial populations can rapidly produce novel variation through mutation, sexual recombination (Blanc‐Mathieu et al., 2017), and horizontal gene transfer (Hall et al., 2017; Llorens‐Marès et al., 2016). While beneficial mutations themselves are rare relative to deleterious or neutral ones (Desai & Fisher, 2007), the per generation supply of beneficial mutations for marine microbes will be large, simply by virtue of their immense population sizes. For example, the mutation rate for the eukaryotic picoplankton Ostreococcus and Micromonas is estimated to be on the order of 10⁻¹⁰ mutations per genome per generation (Krasovec et al., 2017). Even though only a small proportion of these are beneficial, the surface ocean alone is inhabited by more than 10²⁷ individual microbes (Flombaum et al., 2013), with typical in situ specific net population growth rates on the order of 1 day⁻¹ (Laws, 2013). Most of this immense community will, therefore, completely turn over every few days or so. On seasonal‐to‐decadal timescales, microbial populations will go through hundreds to thousands of generations, experiencing novel environments and changing environmental fluctuations (Irwin et al., 2015). A useful supply of novel phenotypes therefore seems assured on these timescales, and laboratory experiments have demonstrated an evolutionary response on timescales as short as weeks (Bell & Collins, 2008; Collins et al., 2014). Plankton communities are correspondingly high in genetic, phenotypic, and functional diversity (Armbrust, 2009; de Vargas et al., 2015; Kashtan et al., 2014). The extrapolation of taxonomic data estimates the total number of marine eukaryote species at ~2.2 million (de Vargas et al., 2015; Mora et al., 2011). This high diversity is perhaps to be expected, given the overall complexity of the ecosystem itself, but it is worth noting that such complexity takes time to develop (see, e.g., the recovery after mass extinctions described in section 3.2).

Perhaps as a consequence of this high evolutionary capacity, dominant patterns of changing plankton diversity in the fossil record show that rates of speciation and extinction are most closely tied to long‐term environmental factors (Bown et al., 2004; Falkowski et al., 2004), especially the “greenhouse‐icehouse” oscillations that have occurred over multimillions of years (Bown et al., 2004). In contrast, at the (relatively) shorter end of the geological scale (the glacial‐interglacial cycles operating on timescales of millennia to hundreds of millennia, the submillennial oscillations associated with ice sheet dynamics, and the millennial carbon‐cycle perturbation of the greenhouse Eocene world), changes in the climate appear to have little or no effect on plankton diversity beyond normal, background levels of turnover (Gibbs et al., 2006). On these timescales, diversity and ecosystem functionality appear to be set by the broader state of the biogeochemical/climate system, particularly latitudinal gradients in temperature and nutrient supply.

Nonetheless, it still remains unclear how the changing system properties might have been different in the absence of an evolutionary response. Despite what seems like a virtually limitless ability to “evolve,” modern planktonic foraminifera and coccolithophores have surprisingly low taxonomic diversities. It appears that with only ~50 and 190 uniquely defined morphospecies (Morard et al., 2018; Young et al., 2005), evolution can become an important limiting factor in response to large and rapid environmental change, such as in the wake of mass extinctions. Following such events, timescales of recovery can be mapped out from different milestones in the fossil record. Taking the Cretaceous‐Paleogene extinction event (K/Pg) as an example, the picture that emerges in the recovering ocean is that of a succession of pioneer‐type communities, with the first arriving within the first 20,000 years (Bown, 2005; Schueth et al., 2015). These pioneer communities, dominated by new incoming taxa that are often the first representatives of new lineages, have an atypically low diversity of traits and are characterized by very small species with opportunistic ecology (Birch et al., 2016; Bown, 2005; Gallala et al., 2009). Coccolithophores and planktic foraminifera see new species emerge from a handful of survivor species over the first few hundred thousand years (i.e., ~50 million generations of coccolithophores and perhaps 3–4 million generations of foraminifera), leading to the establishment of globally distributed communities of low diversity and a slow (re)establishment of stable biogeochemical functions (Birch et al., 2016; Bown, 2005; Coxall et al., 2006; Payne et al., 2004). These communities have already displayed a basic expansion of morphologies and genetic diversity, but there is little evidence in the first 300,000 years of any vertical niche partitioning in the water column, endemism, or a full seasonal spread of productivity (Birch et al., 2016; Bown, 2005). Rather, while these opportunist taxa are found throughout the oceans, there is little specialism, with no evidence of niches associated with a fully developed environmental feedback loop, no differentiation along oligotrophic to eutrophic gradients, and no pressure from a complex trophic web. Only much later in the recovery, perhaps after 2 million years (Birch et al., 2016; Coxall et al., 2006; D'Hondt, 2005), do we see a sufficient codevelopment of the ecology and environment that niches are rapidly opening up and diversity starts to increase on the trajectory of diversity gain consistent with environmentally limited models of recovery. Similarly long (multimillion years) timescales appear required for the full reestablishment of ecosystem function and global carbon cycling in the aftermath of the end Permian extinction (Payne et al., 2004).

The grand challenge outlined in this paper is to extend current global ocean and Earth system models to include an explicit representation of adaptive evolution by natural selection. Just as “the interactions of organisms and environment are reciprocal” (Redfield, 1958), we also know that “organisms and environments are both causes and effects in a coevolutionary process” (Lewontin, 2000; Figure 2). In this paper, we discuss whether (or when) evolution should be included in such models of the ocean and climate system and what we might gain from doing so. In the following sections, we first review current approaches to modeling the ecology of marine plankton communities within Earth system models. We then introduce several techniques that might be used to extend these models to include an evolutionary perspective. From this perspective, we go on to discuss potential applications of evolutionary Earth system models, concluding with a discussion of how the development and application of these models might lead to a better understanding of the Earth system as a whole.

2. Modeling Ecology and Evolution in the Earth System

From an Earth system modeling perspective, we might start by asking, why do Earth system models even include ecology? For many scientific questions regarding distributions or fluxes of biogeochemical tracers there is little evidence that they need to, as the biological organic carbon pump (the production and transfer of organic matter from the ocean surface to depth) and the carbonate counter pump (the production and downward transfer of alkalinity associated with calcium carbonate) can, to first order, be modeled as a direct function of the prevailing physical and chemical environment at any one point in time and space (Maier‐Reimer, 1993; Orr et al., 2001; Matsumoto et al., 2004; Ridgwell et al., 2007). Nonetheless, the ecology and evolution of plankton communities are dynamically and reciprocally coupled to their environment on a broad range of timescales, from the diel to the geological (Figure 1). In the absence of any prognostic representation of plankton populations and their interactions, such models are incapable of representing key feedbacks and are thus somewhat inflexible and unavoidably coupled to the (contemporary) systems for which they were parameterized. However, as the base of the marine food web, phytoplankton are also essential to fisheries. Ecosystem models, particularly for future climate change scenarios, are starting to help in understanding the links to fisheries (Stock et al., 2017). This, together with a desire to understand the effect of climate and ocean variations on ecosystem structure and function, has motivated the development of more complex ecological models. In the following section we first give a brief overview of how and why ecological complexity has been accounted for in global ocean models. We then go on to make a similar case for how and why evolutionary processes might be similarly accounted for.

2.1. Microbial Ecology in Ocean Models

Models of ocean ecology typically condense the enormous complexity of the marine ecosystem into a limited number of state variables. At the broadest level of organization, planktonic diversity in ocean models, and especially those used in Earth system models, has frequently been condensed into a very limited number of model populations representing generic phytoplankton producers and zooplankton consumers (Aumont et al., 2015; Kriest & Oschlies, 2015; Yool et al., 2013). While such models benefit from lower computational costs and require fewer empirical parameters, those parameters are often so highly abstracted that they cannot be directly related to measurable quantities. They must instead be assigned through objective (or subjective) calibration against the state of the modern ocean (Kriest et al., 2017). This empirical tuning of coarsely resolved model structures means that these models are very closely tied to the ecosystems for which they were parameterized, and as such they will often perform poorly when transferred to novel environments (Friedrichs et al., 2007).

This issue has motivated the development of more complex models that describe a broader range of diversity, often focusing on “plankton functional types,” such as cyanobacteria, coccolithophores, diatoms, dinoflagellates, and various categories of zooplankton (Bopp et al., 2013; Le Quéré et al., 2005). Many of these broad groups have been associated with particular roles in the context of ecosystem function, biogeochemical cycling, and climate and have been incorporated into models with the goal of resolving key ecosystem feedbacks that are necessarily absent from simpler models (Hood et al., 2006; Le Quéré et al., 2005). Such models assume (consistent with the data we have for unicellular species, at least) that there is more variation between functional groups in terms of represented traits such as metabolism, size, edibility, and sinking behavior than there is within functional groups. Nonetheless, the structure and parameterization of plankton functional type models is still shaped by our observations and understanding of contemporary ocean ecosystems and thus remains closely tied to our empirical understanding of those ocean ecosystems.

More recently, models have been developed to allow a more flexible ecosystem structure, initializing the ocean with many tens or hundreds of potential populations, with ecophysiological and biogeochemical parameters either assigned randomly (Coles et al., 2017; Follows et al., 2007) or discretely sampling across a credible range of the trait space (Bruggeman & Kooijman, 2007; Ward et al., 2012). Instead of focusing on individual species or functional groups, these “trait‐based” models aim to identify and quantify how key organismal traits, varying across species and functional groups, might underpin community structure and function. Model communities are allowed to self‐organize, with particular traits becoming more or less prevalent as a function of the environmental conditions. In particular, trait‐based models have been used to better understand the ecological and biogeochemical impacts of traits related to organism size and shape, photosynthetic efficiency, and nutrient acquisition (see Follows & Dutkiewicz, 2010; Litchman & Klausmeier, 2008).

An essential component of the trait‐based approach is to identify ecophysiological constraints or “trade‐offs.” Under the reasonable assumption that fundamental physical, chemical, and biological constraints prevent the simultaneous optimization of all potentially beneficial traits, it is expected that certain beneficial characteristics will come at the expense of others. Although such trade‐offs are often hypothetical, a number have empirical support (e.g., Edwards et al., 2013; Litchman et al., 2007) and have been shown to explain observed ecological successions along environmental gradients (Tilman, 1990; Ward et al., 2013). As such, trait‐based models have achieved notable success in terms of predicting large‐scale patterns of species biogeography and, to a slightly lesser extent, ecosystem function. Nonetheless, it is worth noting that our current level of understanding is not yet at a point where we can use purely continuous trait‐based approaches to account for highly discontinuous differences between disparate lineages (e.g., diatoms vs. coccolithophores), and there remains a very important role for taxonomic approaches based on discrete classifications.

Regardless of their degree of complexity, the parameters of ocean ecosystem models are most typically constants. It is however worth noting that some models include a degree of phenotypic flexibility, with the allocation of cellular resources to different metabolic functions (e.g., nutrient uptake, light harvesting, and photosynthetic carbon fixation) optimized in order to maximize some imposed measure of fitness, which is most typically the gross population growth rate (Geider et al., 1996; Pahlow & Oschlies, 2009; Smith & Yamanaka, 2007). These optimal acclimation models go some way to capturing the dynamic behavior of the marine microbial community and its potential to change (Smith et al., 2009). This response is, however, more or less immediate, and changes will not be inherited to allow for the generation of new lineages.

While the ecological models described above may differ in their underlying construction, they all share the same mechanism of operation, in that community structure and function are determined by the outcome of competition among a predefined set of model populations. Despite the potential for the emergence of what look like new species within the community, such models should not be thought of as reflecting Darwinian evolution. All populations are defined a priori, with essentially immutable traits. (A notable exception to this limitation is the model of Coles et al., 2017, in which new species with randomly generated traits replace those that have become extinct.) There is no heritable variation of traits, and the potential for growth of different populations is limited strictly to those populations that were included in the model initially. Within this characteristic is the implicit assumption that evolution is not a rate‐limiting factor with regard to the emergence of new phenotypes. If a niche is available, it will be filled, and it is not necessary to account for the time taken for a species or function to evolve or for it to disperse globally. In other words, “Everything is everywhere, but the environment selects” (Baas‐Becking, 1934). Is this consistent with the observation that it has taken perhaps 20,000 years for the first new species to appear after the K/Pg event? A fundamental quality of evolution is that it can only act on what is already present (Jacob, 1977), and if we are interested in examining whether the state of the marine ecosystem is sensitive to its evolutionary history, it is essential that our models are able to reliably capture both standing variability and the limited generation of novel phenotypes.

2.2. Microbial Evolution in Ocean Models

At its core, Darwinian evolution requires two key features: a struggle for existence and the heritable variation of traits (Lewontin, 1970a). In isolation, the struggle for existence will lead to the regulation of population growth, and the reorganization of communities, reflected in the dominance of some species at the expense of others (Claessen, 2012). While the struggle for existence encompasses all facets of life, it is typically represented in ocean ecosystem models in terms of resource competition and, to a lesser extent, predation (e.g., Prowe et al., 2012; Vallina, Ward, et al., 2014; Ward et al., 2012).

The ecological models described in the previous section include the struggle for existence, but any variation was not heritable. In practice, the inheritance of variation can be modeled either through the generation of new individuals or populations with variant traits, or the same effects can be represented by allowing the traits of extant populations or communities to vary on intergenerational timescales. In the following, we will review a number of different evolutionary models that move from the individual to the community as the modeled unit of selection (Lewontin, 1970a).

2.2.1. IBMs

By modeling the ecology and behavior of individuals, it is, in principal, relatively straightforward to incorporate evolution by allowing the traits of offspring to deviate from those of their parents. Better adapted offspring will more likely prevail, allowing both adaptation and speciation. In practice, the evolution of marine microbial communities is determined by the interaction of more than 10²⁷ unique individuals in a highly interconnected system. It is obviously impossible to resolve anything even close to this number of agents in a model system, so microbial individual‐based models (IBMs) have typically focused on homogenized “superindividuals,” which are assumed to represent the behavior of a large number of identical individuals that exhibit the same responses to environmental conditions. The dynamics of superindividual growth may be represented in a number of ways (as reviewed by Hellweger et al., 2016), but a particular challenge for modeling their evolution in marine communities is to maintain a computationally tractable number of superindividuals in the face of rapid dispersal. As a consequence of the highly interconnected nature of marine ecosystems, local populations in a 3‐D circulation model are likely to become very rapidly diversified by a large number of immigrant populations. One way to handle this is to merge the least abundant, or alternatively the most similar, superindividuals at each location (Clark et al., 2011; Woods, 2005). This approach may, however, make it difficult to maintain anything but the most abundant species across a global model, and to date, global plankton IBMs have avoided horizontal mixing of plankton communities (Clark et al., 2013; Daines et al., 2014).

Nonetheless, a particular advantage of IBMs is that each (super)individual can be directly linked to its evolutionary antecedents, such that it should be possible to retrace the complete spatial and temporal evolutionary history of the community (given sufficient computational resources). It is also relatively straightforward to incorporate sexual reproduction, which is more problematic in population‐ or community‐based models.

2.2.2. Stochastic Generation of New Phenotypes

Plankton communities are often represented in ocean ecosystem models as a set of competing populations. Typically, these populations are fixed, but some models allow the generation of new populations with new phenotypes. For example, Coles et al. (2017) describe a model with the random generation of new phenotypes from within a predefined range of credible traits. While it should be noted that this process is not strictly analogous to Darwinian evolution by natural selection (the generation of new phenotypes is independent of the existing members of the community), it could be adapted to include the generation of new phenotypes from existing members of the community by mutation, sexual recombination, or lateral gene transfer. For example, mutant traits of a new population could be drawn from a normal distribution, centered on the appropriate trait value of the ancestral population.

In the interests of maintaining a computationally tractable model, the generation of new model populations must be balanced by the compensatory removal (i.e., extinction) of populations. In the Coles et al. (2017) model, this was achieved by replacing any populations accounting for less than 1% of the local biomass at any location in the model in a given period. While this approach successfully allowed the exploration of over 2,000 different phenotypes in just 20 years, the defined “extinction threshold” is somewhat arbitrary, and it will be important to assess the sensitivity of results to the assumed definition of extinction, and the spatial and temporal scales across which it is defined.

2.2.3. Deterministic Generation of New Phenotypes

The stochastic generation of new phenotypes allows the evolutionary exploration of the trait space, with individual traits treated as continuous variables. An alternative approach is to divide the trait space into a discrete grid, with mutations treated as a small diffusional flux between adjacent points in the grid (Leimar et al., 2008; Polechová & Barton, 2005). This approach is similar to discretized trait‐based models (Bruggeman & Kooijman, 2007), with a key difference being that a small fraction of reproduction in each population is diverted to neighboring populations in the trait space (Sauterey et al., 2017). Additionally, the assumption that no species can go extinct is removed, with new populations only emerging via mutation (or through an explicit representation of spatial dispersal).

It is, however, worth noting that the need to resolve the entire trait space as a discrete grid may be computationally intractable for high‐resolution ocean models, especially when multiple traits are considered. In addition, the diffusive nature of traits may make it difficult to provide a robust definition of species—although this may in fact be a desirable (or at least realistic) characteristic in the microbial realm (Rossberg et al., 2013).

2.2.4. Changing the Traits of a Population

As an alternative to modeling adaptation as the succession of individuals or populations with different traits, it is possible to treat a population as a fixed entity, allowing its traits to vary. This is achieved by allowing a population to undergo incremental changes to its traits, in order to maximize some defined fitness metric. This “Adaptive Dynamics” approach (Geritz et al., 1998a; Kremer & Klausmeier, 2017; Litchman et al., 2009) works by comparing an ecologically established “resident” population to a “mutant” population with slightly modified traits. This requires the definition of some metric of “invasion fitness,” which is most typically defined as the net population growth rate integrated over some temporal (and possibly spatial) scale. Under the assumption that the resident population is at (or at least close to) an equilibrium or limit cycle, its invasion fitness will be 0. A positive invasion fitness for a mutant can therefore be taken as evidence that it is better adapted to the local conditions, and the mutant is assumed to replace the resident (Geritz et al., 2002). In practice, this can be achieved by assigning the adapted traits of the mutant to the resident population. This allows for adaption and speciation, with the latter occurring if mutations in opposite directions of trait space are both associated with a positive invasion fitness (Figure 3, panel evo‐iv).

Figure 3.

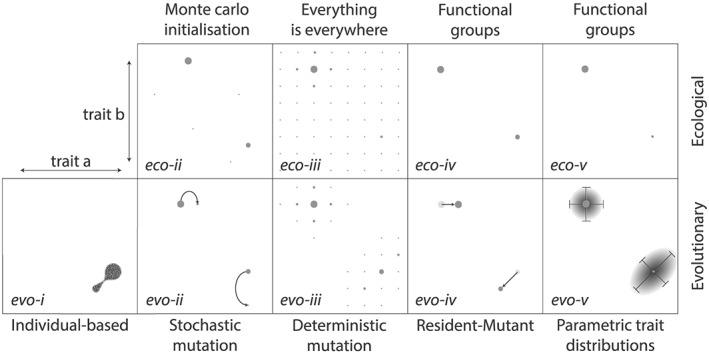
Ecological modeling approaches (upper row) and their evolutionary equivalents (lower row). In each box, the values of two continuous traits are defined by the x and y coordinates. An individual‐based model (evo‐i) represents the community in terms of (super)individuals. The trait space is explored as reproduction leads to heritable changes in trait values. (While purely ecological individual‐based models have been described, no direct equivalent is relevant here.) Instead of focusing on individuals, if the community is represented in terms of discrete populations, new populations may be generated by randomly sampling the trait space (evo‐ii; Coles et al., 2017) or by allowing a deterministic mutational flux between points adjacent in the trait space (evo‐iii; Van Der Laan & Hogeweg, 1995; Sauterey et al., 2017). Both these methods determine the success or failure of mutants by allowing them to compete directly with resident species within the model community. An alternative approach to the generation of new populations with different traits is to modify the traits of existing populations according to finite difference approximations of the fitness gradient (evo‐iv; Sauterey et al., 2015). A final evolutionary approach (eco‐v) uses an analytical approximation of the slope and curvature of the fitness landscape to define the model community in terms of its biomass, variance (i.e., diversity), and the slope of the fitness landscape (i.e., selective pressure).

In practical terms, the calculation of mutant invasion fitness is greatly simplified by the assumption that the initial abundance of mutants is sufficiently small that they have no effect on the ecosystem. The absence of any feedbacks means that the invasion fitness of mutants can be calculated as a prognostic function of the broader ecosystem, without any requirement to assess their reciprocal impact on the system.

This approach requires a number of basic assumptions that can be questioned, especially in a large‐scale spatially resolved model. First, the fact that the resident species is assumed to be at or close to equilibrium requires the artificial separation of ecological and evolutionary timescales in the model, with mutations and replacements only occurring after reequilibration of the ecological model from the previous event. Second, it is assumed that a positive mutant invasion fitness always leads to replacement of the resident (Geritz et al., 2002). This may not occur in reality if, for example, a locally maladapted species is maintained in a region by immigration. More generally, the selection of a suitable fitness metric and the temporal and spatial scales over which it is defined is an arbitrary process, and one that is likely to impact the evolutionary trajectory and endpoint in the model system.

2.2.5. Modeling the Distribution of Traits in a Community

In the models described above, microbial diversity is represented by a finite number of individuals or populations, each corresponding to a single point in the phenotypic trait space. As an alternative, we can represent the diversity within a community as a continuous distribution of biomass across the trait space, resolving state variables for the total community biomass alongside the mean and variance of the trait distribution (e.g., Bruggeman, 2009). Using this continuous approach, the fitness landscape is defined by the biomass‐specific (net or gross) growth rate, itself a continuous function of organism traits and the current environment. This function may be quite complicated, and it is typically approximated by a Taylor polynomial, under certain simplifying assumptions. In general,

1. the biomass‐specific community growth rate is approximated as the area under the fitness landscape, which is often assumed to follow a Gaussian distribution that is centered symmetrically around the mean trait value;

2. the mean trait value is assumed to move up the fitness gradient, at a rate proportional to the slope defined at the mean trait value and the variance of the biomass in trait space. This reflects the rate of adaptation increasing with both selection pressure and the standing diversity of the community; and

3. diversity (i.e., trait variance) increases if the curvature of the fitness landscape is positive. Positive curvature implies that selection pressure increases toward the optimum, with the traits of better adapted members of the community diverging from those of less well adapted members. The converse is true if the curvature of the fitness landscape is negative. As this is always the case at a fitness maximum, equilibrium diversity tends to collapse to 0, unless it is maintained by external variability or some additional mutation or immigration term (this is not necessarily unrealistic given the assumptions of the model, and certainly not an exclusive feature of this kind of model).

This “moment‐based” representation of community traits is computationally efficient and has been generalized to be applicable in a spatial context (Bruggeman, 2009; Chen et al., 2019). It is worth noting that the approach does not distinguish between ecological and evolutionary changes. Furthermore, while the approach has generally been applied to describe the ecological and evolutionary dynamics of plankton “communities,” these model communities are really more like ecological guilds, because the continuous representation of traits is best suited to the description of groups of organisms exploiting similar resources. While the approach could in principal be extended to represent the interaction of multiple guilds (or functional groups), it has so far only been used to represent generic phytoplankton (Chen et al., 2019; Merico et al., 2009). It also remains uncertain as to whether the approach can be extended to explicitly incorporate diverse predator‐prey dynamics, for which disruptive selection (i.e., speciation) is likely to play a key role (Vallina, Ward, et al., 2014). In such cases where the slope of the fitness landscape is 0 while its curvature is positive, the modeled variance would rapidly increase toward infinity.

3. What Can We Gain?

We know that adaptive evolution plays a key role in shaping the whole Earth system, but to what extent, if at all, is it advantageous to include it explicitly in models of the ocean and Earth system? While the ecological models described in section 2.1 have all been applied within global ocean ecosystem and Earth system models, this is not the case for the evolutionary models summarized in section 2.2. An outstanding challenge is, therefore, to take these idealized evolutionary models and integrate them into Earth system models, so that potential feedbacks can be explored. If we consider that the evolution of marine microbial communities takes place within a much broader and highly interconnected system, there is clearly potential for new insights, in particular, regarding how microbial evolution affects the Earth system and how the Earth system affects microbial evolution. However, the question remains: Can we reliably develop a predictive ecosystem model that is structured and parameterized according to our (limited) observations of phenotypes living in contemporary ocean communities? The marine ecosystem we see today is the current state of a coevolving system encompassing life and the planet. In this regard, it might be desirable to develop models based on the fundamental constraints that have shaped past and present ecosystems, rather than to develop models encoding the current state itself. Evolution is a central part of this process, although it remains to be seen whether modeling evolutionary processes can deliver improved predictions or novel insights that would not be available from current Earth system and ecosystem models. In the following, we will address key areas where an evolutionary perspective might help to improve our understanding of both evolution and the Earth system.

3.1. Interpreting the Past

With the plankton fossil record (planktic foraminifera, coccolithophores, and, to a lesser extent, diatoms, radiolarian, and dinoflagellates), we have unrivaled taxonomic and stratigraphic completeness compared with any other organismal groups, extinct or extant (Bown et al., 2004; Falkowski et al., 2004). We are able to track both microevolutionary and macroevolutionary patterns from millennial‐scale records of skeletal size and morphological variations (e.g., Finkel et al., 2007; O'Dea et al., 2014; Schmidt et al., 2004), up to the major landmarks of physiological innovation such as evolution of carbon concentrating mechanisms, acquisition of photosymbionts, and new biomineralization strategies (e.g., Birch et al., 2016; Bolton & Stoll, 2013; Monteiro et al., 2016). The planktonic fossil record is, therefore, a valuable source of information on both the past history of the marine ecosystem and the state of the Earth system. However, our interpretation of that record is shaped by assumptions regarding the links between the environment, ecology, and evolution—from geological records alone we can only hypothesize causation, while the quantitative (or even qualitative) outcome of the interaction of multiple feedbacks is often impossible to diagnose.

An important advance would therefore be the ability to draw self‐consistent quantitative links between precise hypotheses and paleontological/geochemical observations. One goal might therefore be the development of quantitative models describing the behavior of an evolving ecosystem in response to environmental perturbations over the appropriate timescales. For example, it is not known to what extent the pace of recovery after mass extinctions is limited by climatic, biogeochemical, or evolutionary processes, or by feedbacks among all three (D'Hondt, 2005; Hull, 2015). Taking the example of the ecological and Earth system response to the impact at the end of the Cretaceous, the marine carbon cycle transitioned into an apparently radically different “mode,” characterized by some combination of decreased export production and shallower recycling of carbon and nutrients, leading to a weaker oceanic carbon sequestration. This state persisted for over several millions of years before recovery was achieved (Coxall et al., 2006). Why? What prevented rapid recovery of the system once the initial perturbation had subsided? Does this simply reflect the timescale for the reevolution of important traits or the reestablishment of community structures? Or does it reflect the evolution of a new quasi steady state of tightly coupled ecology and carbon and nutrient cycling that was only slowly “eroded,” with full ecological function only much later reattained?

In the most general terms, does the emergence of new species occur rapidly with the emergence of new climates and habitats or is the functional response of the ecosystem limited by the evolutionary response of the plankton? Temporarily leaving aside questions of feasibility (section 2), such questions and hypotheses about the past can only be explicitly and quantitatively tested, explored, and falsified in a model system that includes adaptive evolution alongside a representation of global climate and carbon cycling. Placing an evolutionary model within a coupled Earth system model might also provide a means to generate testable predictions that can be compared to the paleoceanographic record. Alongside the evaluation of hypotheses within a constrained environmental context, such an approach might additionally help to constrain unknown parameters concerning the rate and capacity for evolution in marine microbial communities.

3.2. Understanding the Present

Evolution has shaped marine ecosystems and the Earth's biosphere over the past 4 billion years (Falkowski et al., 2004) and continues to do so in the present, on timescales of decades or even less (Collins et al., 2014; Irwin et al., 2015). Changes in the fitness of different phenotypes can be brought about by changes in any part of the overall system, across a broad range of timescales. As such, it is always likely that some kind of adaptive change is under way. In practical terms, this means that the set of phenotypes present in a community is not fixed, nor is it necessarily stable. So instead of thinking of wild populations as unchangeable archetypes upon which we should base our models, we should perhaps instead consider the current state of the system as a waypoint along a constantly developing trajectory. The key challenge in this regard is to identify the main constraints that shape the evolutionary trajectory.

The mechanisms and potential impacts of evolutionary adaptation would likely also benefit from consideration within a realistic environmental context. One possibility would be to examine the structural and functional sensitivity of microbial food webs (Loeuille & Loreau, 2005) under different assumptions of environmental dispersal, ecological productivity, and evolutionary rate. Such a model would give new insights into how ecosystems might respond to, and recover from, perturbations brought about by ocean warming and changes in circulation. It may also be revealing to examine the evolutionary stability of mechanisms related to the stoichiometry of inorganic and organic nutrient elements (Klausmeier et al., 2004; Redfield, 1958; Tyrrell, 1999). Evolutionary models may also offer new insights regarding community assembly and coexistence of marine plankton (Sauterey et al., 2015, 2017; and Figure 3), their resilience to environmental fluctuations (Kremer & Klausmeier, 2017), and their potential for catastrophic regime shifts or functional collapse (Lenton et al., 2008).

In analogy, the development of complex ecological models within ocean and Earth system models has allowed environmental scientists to explore the large‐scale impact of ecological processes that might previously have only been understood in highly idealized contexts. For example, concepts from the metabolic theory of ecology, resource competition theory, and ecological stoichiometry have recently been assessed within models accounting for complex community ecology within a heterogenous fluid environment (Ayata et al., 2014; Göthlich & Oschlies, 2012; Vallina, Follows, et al., 2014). While these concepts have a rich theoretical background, their application within more realistic environmental frameworks has allowed closer comparison to observations and better assessment of global impacts.

Adding an explicit representation of evolution to contemporary models of the ocean and Earth system will provide new constraints on the current structure and function of the marine ecosystem, in particular providing new context for a wealth of bioinformatic data. For example, while some genomic data point to the stable coexistence of many hundreds of phenotypically distinct subpopulations of Prochlorococcus (Kashtan et al., 2014), considerable uncertainty remains as to how much observed diversity is actually driven by natural selection, rather than genetic drift and neutral evolution (Hellweger et al., 2014).

3.3. Predicting the Future

Under a future “business‐as‐usual” scenario, the current generation of climate models predicts changes in global sea surface temperature of approximately 3–5 °C (Gruber, 2011; e.g., Bopp et al., 2013), manifested in a poleward shift of isotherms over the course of the 21st century (Dutkiewicz et al., 2013). On these timescales there will be increased stratification of the surface waters (Bopp et al., 2001; Gruber, 2011). Coupled to a predicted slowdown of the meridional overturning circulation (Schmittner, 2005), these changes are expected to perturb the light environment and decrease the oceanic supply of nitrate and phosphate to the euphotic zone, with an associated decrease in ocean ventilation (Shepherd et al., 2017). As pCO₂ increases, oceanic pH is predicted to fall (Doney et al., 2009; Gruber, 2011), while warming temperatures will drive a further retreat of sea ice.

Projected changes in global temperature are small in comparison to global temperature range, so it is likely that the dominant response to global warming in a well‐connected ocean (Jönsson & Watson, 2016) will continue to be range shifts (Barton et al., 2016; Dutkiewicz et al., 2013, 2015). That said, higher temperatures will affect global average growth rates, while decreased nutrient supply is generally predicted to shift communities toward smaller organisms. Such changes are expected to drive a poleward expansion in the dominance of small, warm‐adapted species (Barton et al., 2016; Bopp et al., 2005; Dutkiewicz et al., 2013). Decreasing ocean pH is also expected to affect the role of calcifying plankton with regard to carbon sequestration (Hofmann & Schellnhuber, 2009), as well as affecting phytoplankton metabolic rates (Mackey et al., 2015). Unlike temperature, open ocean pH changes are going to be larger than the current global range (Bopp et al., 2013; Dutkiewicz et al., 2013). Increasing hypoxia will diminish the metabolic capacity of animals (Deutsch et al., 2015). Alongside these largely physiological effects, we will likely see both extinctions and the opening up of new niches, especially at the extreme frontiers of environmental change, in the polar and equatorial oceans (Thomas et al., 2012).

Most current marine ecosystem models use a power law‐like function (e.g., Eppley, 1972) for increased phytoplankton growth rate with temperature. Thus, there is a playoff between reduction in growth rates with lower nutrient supplies and increased growth with higher temperatures in future world scenarios (e.g., Dutkiewicz et al., 2013; Laufkötter et al., 2015; Taucher & Oschlies, 2011). But different species of phytoplankton cannot grow over the full temperature range and in fact die out quickly beyond an optimal maximum (Thomas et al., 2012; Boyd et al., 2013; also see representation in Figure 4). Thus, current models potentially overestimate phytoplankton adaptability. Almost no models considered changes in metabolic rates with increased pH and as such also overestimate adaptability. On the other hand, though, in one study that does include pH effects on growth rates (Dutkiewicz et al., 2015), extinctions of some species occurred due to differing pH responses. However, including evolution might not allow such extinctions.

Figure 4.

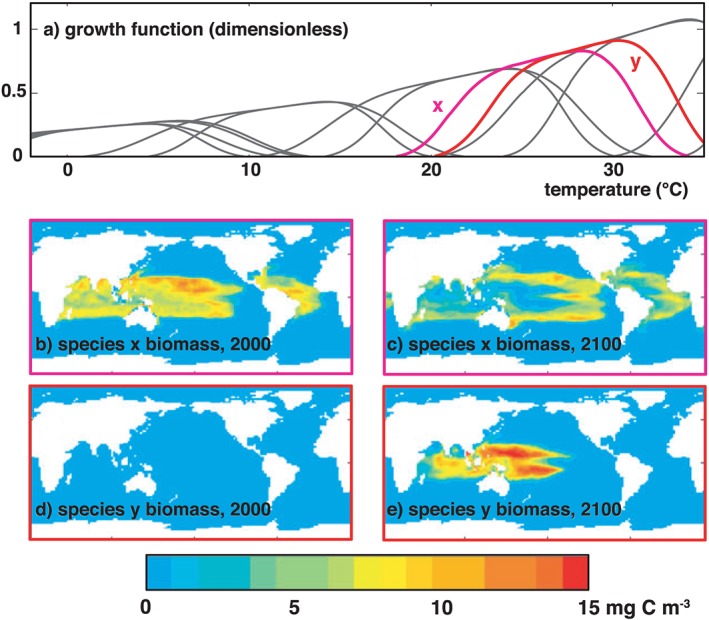
Emergence of new populations in a future ocean. In a global‐warming simulation including 100 model phytoplankton with randomly generated thermal tolerance curves (panel a). The tropical oceans in 2000 (panels b and d) are dominated by species x, which has a thermal optimum at ~27 °C. In the warmer ocean at 2100 (panels c and e), we see the establishment of a new species y (optimum ~30 °C) that was almost entirely absent in 2000. In this experiment, we see a new niche open up in the future as another contracts (see decreased biomass of species x in panel c). If model species are assigned immutable traits based on archetypes seen in the contemporary ocean, new niches associated with “no analogue environments” may remain unoccupied as others go extinct, leading to predictions of diversity collapse in a future ocean (Thomas et al., 2012). Adding an evolutionary component to such a model might change its predictions by allowing existing populations to adapt their traits in response to environmental change or by allowing exploration of new regions in the phenotypic trait space not initially included in the model.

How might adaptive capacity change the future projections made by climate models? It is important to reiterate that model predictions are based upon the characteristics of plankton communities in today's ocean. If some species were able to adapt to lower nutrient conditions, to grow even faster with increased temperatures, or to tolerate decreased pH or O₂ concentrations, some more pessimistic model predictions might be somewhat tempered. Predictions of the decline in larger phytoplankton with subsequent impact on fisheries (Stock et al., 2017) might also be altered if those phytoplankton could adapt to some of the changing conditions. The estimated vulnerability of the global plankton community might well be very different if their ability to adapt changing communities is fully and realistically accounted for. The current predictions of climate models must be remembered to be derived from a view that is restricted by the lack of evolution. Studies to explore what and how much evolution could change these results are therefore timely and important.

3.4. The Case for Adaptive Evolution in Ocean Models

While it is clear that evolution shapes marine microbial communities on all timescales from the ecological to the geological, the question remains as to whether adaptive evolution should be included in marine ecosystem and Earth system models. Arguably, the strongest signal present in the fossil record is that background species turnover and diversification following mass extinctions is paced by the coupling of ecology and the environment (Bown et al., 2004; Falkowski et al., 2004). Adaptation and the emergence of new species have occurred in lockstep with the vast majority of environmental changes over the last several hundred million years, and fossil evidence suggests that evolution will eventually fill any feasible niches that are opened up by environmental change, as long as there is enough time to do so. Among microbial species in particular, the ability to inhabit extreme environments, such as hot springs and hypersaline lakes, suggests that the evolutionary capacity to occupy diverse niches extends beyond the range of conditions we are likely to consider in ocean models. For simulations across the longest geological timescales (millions of years and beyond), as long as we are reasonably certain that it can do so within those timescales, we are perhaps less interested in how evolution fills a new niche and more in what the endpoints of the evolutionary process turn out to be. In particular, while it is generally assumed that these evolutionary endpoints are (at least functionally) singular, the presence of nonlinear eco‐evolutionary feedbacks (Figure 2) suggests we should not rule out the possibility of bifurcations and multiple stable states. However, any attempt to explicitly model the evolutionary emergence of new functional groups on such timescales is at odds with the assumed unpredictability of such large macroevolutionary changes. Instead, it might only be necessary to ensure that models include sufficient ecological flexibility to allow the restructuring of communities in response to environmental change. This sort of approach is already possible with some trait‐based models (Bown et al., 2004; Falkowski et al., 2004), but it is of course essential that constraints on the ecological community are correctly described.

As timescales constrict, the likelihood of evolution finding those endpoints decreases, and the pathways of evolution become much more important. Where we are concerned with more extreme and rapid climate change (on the order of a few tens to hundreds of thousands of years), there are hints in the fossil record that evolution acts as a general pacer for the emergence of new species (Gibbs et al., 2006), perhaps pointing to a millennial‐scale pacing of the accumulation of species‐specific trait differentiation. On the even shorter timescales of anthropogenic climate change, it appears that species are able to adapt certain traits to decadal changes in the environment (Irwin et al., 2015). This is in contrast to most empirical and mechanistic model projections for the next century, which typically assume that species traits and niches will remain fixed (Barton et al., 2016; Thomas et al., 2012). A key unknown at this stage is, therefore, how an evolutionary response might modify future projections made by climate models, in terms of the both the community response and future climate projections. For example, in a changing environment, do constraints associated with the adaptive modification of traits affect the functional sensitivity and overall resilience of the ecosystem? If they do, is there a critical rate of environmental change above which the ecosystem loses its ability to keep pace with environmental change?

More generally, an important question to answer is whether or not integrating microevolutionary processes into ocean and Earth system models is useful. From a purely practical standpoint, allowing microevolution of traits can increase efficiency by removing the need to include a very large number of potential phenotypes, the majority of which are likely to be inviable at any given time (Coles et al., 2017). More importantly perhaps, will adding a representation of microevolution change anything relative to current models? Accounting for this microevolutionary response on relatively short timescales is undoubtedly challenging, but it is probably a more realistic short‐term goal than modeling the (somewhat unpredictable) macroevolutionary emergence of new functional groups. Even though individual genetic changes may be stochastic and unpredictable, the aforementioned large population sizes coupled to strong selective pressures mean that functionally similar adaptations are likely to occur in similar environments, even if the genetic or metabolic basis for those changes may be less convergent. The more fundamental a trait is, the more likely it is to be a case of convergent trait evolution. Thus, while evolutionary trajectories are strongly history dependent, evolution in fundamental traits that are strongly correlated with fitness can evolve convergently when selection is intense enough. Nonetheless, natural selection can only act on what is present in the community, so the evolution of that community will always be somewhat constrained by its past history. This is something that the “everything is everywhere” approach cannot account for, because it imposes no limits to the emergence of new populations (beyond those dictated by prior constraints on the feasible trait space). If everything is not everywhere, then the whole‐system response to (for example) extinction events will depend on the rate and degree to which functional traits can reach new environments, either by evolution in situ or through immigration from other locations. Given that the adaptive response is inherently stochastic, it will also be important to assess the associated uncertainty in the evolutionary pathway.

Since plankton are represented in models by their functional traits, some of the key challenges to integrating microevolution into trait‐based models revolve around understanding how natural selection acts on the traits used in marine ecosystem models. Different patterns of environmental change, including the amplitude, frequency, and predictability of fluctuations, influence both the strength of natural selection and the phenotypes that it favors (Kremer & Klausmeier, 2017). Natural selection is driven by differences in fitness, but we tend instead to measure functional traits, often with only a partial understanding of how well they correlate with fitness in complex environments and over entire organismal life cycles (Rengefors et al., 2017). Because of this, representing competition between phytoplankton types in models through resource competition and temperature tolerance curves may not predict the correct succession or dominance on the timescales of interest. For example, across several types of bacteria, performance in variable thermal environments is not predicted by performance across a range of constant temperature environments (Saarinen et al., 2018), raising concerns as to the utility of these parameterizations in certain models.

Whether we are dealing with ecological or evolutionary trait‐based models, one of the key things we need to know are the fundamental limits of the feasible trait space (i.e., the full set of physically attainable and biologically viable trait combinations). While plankton traits and trade‐offs are still poorly constrained, significant advances have been made in recent years thanks to multispecies compilations of organismal traits (Edwards et al., 2012, 2013; Marañón et al., 2013). These have been worth considerably more than the sum of their experimental parts, because they have helped to identify the limits of the trait space across contemporary communities. Targeted lab experiments also provide useful constraints, particularly those that identify fundamental limits, such as temperatures of protein degradation, the minimum elemental composition of a viable cell (Finkel et al., 2016), or the fundamental size dependence of metabolism (Savage et al., 2007).

One of the limits of trait‐based approaches is that ultimately, the modeler must decide what traits to include in a model and what are the limits and trade‐offs associated with those traits. These decisions are heavily weighted toward our understanding of contemporary marine communities, for which natural selection will have likely culled the realized trait variability to a significant extent. As a result, trait distributions in extant populations may not represent the full range of trait values accessible to taxa, and in a changing ocean it is possible that previously unseen trait values or combinations will be (or have been) favored by natural selection. While it seems likely that past or future environments with “no contemporary analogue” may be of limited importance over most of the open ocean, trait‐based models parameterized using extant communities may be unable to predict how some key taxa will respond to novel environments. Here laboratory‐based evolutionary experiments may help to bridge the gap between experimental data based on extant species and the fundamental limits of plankton physiology. While such experiments are almost certainly not going to reveal what the “future” version of a particular organism will look like, they will help to identify genetic and statistical correlations between traits along the evolutionary trajectory. Additionally, they can show how far the evolutionary process can take certain traits along that trajectory before the fundamental limits of evolution are reached.

4. Concluding Remarks

Over the longest timescales spanning millions of years, we would expect that the high evolutionary capacity of marine microbes should lead to convergent evolution, at least amongst the most fundamental traits, such as organism size, maximum growth rate, or optimal temperature, even if the genetic or even physiological basis for those changes is more contingent to chance. We therefore expect that over geological timescales, ocean and climate models should give reasonably robust results regardless of whether evolution is explicitly included, as long as the model ecosystem is flexible enough to reflect all potential changes in ecosystem structure (Dutkiewicz et al., 2013).

On the other hand, including an explicit representation of evolution by natural selection is likely to become more important when model timescales overlap with the likely trajectory of evolutionary change. This would occur for questions pertaining to the recovery from mass extinctions and the contemporary ecosystem's response to anthropogenic climate change. In the former case, an evolutionary model would allow us to disentangle the interrelated effects of environmental change and the evolutionary emergence of new phenotypes and communities. In the latter case, adding evolution to climate models would allow us to assess the effects of evolution on ecosystem stability, its resistance to change, and its resilience following change, exploring how the magnitude and rate of global or local change might affect these responses.

Finally, the geological record reveals the most profound changes occurring in marine species and ecosystems, oxygenation of the atmosphere and ocean, and climate over the past 3–4 billion years of Earth history. These changes have been relatively slow (over tens to hundreds of millions of years) at times and at others, extremely rapid. Some have been directional and monotonic, others partially or even completely reversed. Many, if not all, are characterized by correlations between life and the environment. One of the most profound questions in understanding our planet is the causality of these relationships—to what degree does one drive the other, or more likely, there is a tight coupling in the colloquial “coevolution of life and the planet.” Understanding the environmental feedback loop (Figure 2) necessitates that the interaction elements (ecology, evolution, and environment) are dynamically represented and linked in models. The timescales concerned and the sparse constraints on past ecosystem and environmental conditions present immense challenges to models, both in terms of raw computational cost and developing appropriate parameterizations for only partially known elements. Hence, in our opinion, to fully address such fundamental questions about our planet's history, to better contextualize our ecological understanding of contemporary communities, and to develop more reliable projections of future marine ecosystem impacts and recovery, we need to start to incorporate the dynamics of adaptive plankton evolution into Earth system models.

Acclimation

: Physiological changes to an individual in response to environmental cues. These changes are reversible within bounds set by an individual's inherited traits.

Adaptation

Changes in the traits of a population across successive generations that lead to increases in organism fitness. These changes occur as a consequence of heritable changes to the organisms genotype, driven by processes including mutation, recombination, and horizontal gene transfer.

Genetic drift

Changes in the relative abundance of different genotypes in a population as a consequence of stochastic processes unrelated to fitness.

Neutral

Changes in genotype or phenotype that have a negligible effect on organism fitness.

Microevolution

: Small evolutionary changes within a species or functional group, driven by adaptation and genetic drift.

Macroevolution

Large evolutionary changes including the emergence of new species and functional groups.

Fitness

A measure of the relative reproductive success of genotypes, individuals, or populations within a given environment. Organisms with higher fitness are more likely to be selected in subsequent generations.

Trait

Any quantifiable and measurable characteristic of an organism.

Trait space

A hypothetical multidimensional space, with each dimension corresponding to a measurable trait.

Fitness landscape

A metaphorical extension of the trait‐space concept, with organism fitness added as an additional dimension. For a two‐dimensional trait space, the fitness landscape can be thought of as a mountain range, with fitness corresponding to elevation. Evolution by natural selection changes the values of a population's traits, such that the population ascends the slope of the mountain it sits on.

Further Reading

• Balloux, F., L. Lehmann, and T. de Meeûs. 2003. The population genetics of clonal and partially clonal diploids. Genetics 164: 1635.

• Falkowski, P. G., and M. J. Oliver. 2007. Mix and match: How climate selects phytoplankton. Nat. Rev. Microbiol. 5: 813–819.

• Geritz, S. A. H., E. Kisdi, G. Mesze´NA, and J. A. J. Metz. 1998. Evolutionarily singular strategies and the adaptive growth and branching of the evolutionary tree. Evol. Ecol. 12: 35–57. doi:10.1023/A:1006554906681

• Hendry, K. R., A. O. Marron, F. Vincent, D. J. Conley, M. Gehlen, F. M. Ibarbalz, B. Quéguiner, and C. Bowler. 2018. Competition between silicifiers and non‐silicifiers in the past and present ocean and its evolutionary impacts. Front. Mar. Sci. 5: 22–22. doi:10.3389/fmars.2018.00022

• Hull, P. M., R. D. Norris, T. J. Bralower, and J. D. Schueth. 2011. A role for chance in marine recovery from the end‐Cretaceous extinction. Nat. Geosci. 4: 856.

• Lewontin, R. C. 1970. The units of selection. Annu. Rev. Ecol. Syst. 1: 1–18. doi:10.1146/annurev.es.01.110170.000245

• Williams, H. T. P., and T. M. Lenton. 2007. Artificial selection of simulated microbial ecosystems. Proc. Natl. Acad. Sci. 104: 8918. doi:10.1073/pnas.0610038104

Ward, B. A. , Collins, S. , Dutkiewicz, S. , Gibbs, S. , Bown, P. , Ridgwell, A. , et al. (2019). Considering the role of adaptive evolution in models of the ocean and climate system. Journal of Advances in Modeling Earth Systems, 11, 3343–3361. 10.1029/2018MS001452