Intact Reinforcement Learning But Impaired Attentional Control During Multidimensional Probabilistic Learning in Older Adults

Abstract

To efficiently learn optimal behavior in complex environments, humans rely on an interplay of learning and attention. Healthy aging has been shown to independently affect both of these functions. Here, we investigate how reinforcement learning and selective attention interact during learning from trial and error across age groups. We acquired behavioral and fMRI data from older and younger adults (male and female) performing two probabilistic learning tasks with varying attention demands. Although learning in the unidimensional task did not differ across age groups, older adults performed worse than younger adults in the multidimensional task, which required high levels of selective attention. Computational modeling showed that choices of older adults are better predicted by reinforcement learning than Bayesian inference, and that older adults rely more on reinforcement learning-based predictions than younger adults. Conversely, a higher proportion of younger adults' choices was predicted by a computationally demanding Bayesian approach. In line with the behavioral findings, we observed no group differences in reinforcement-learning related fMRI activation. Specifically, prediction-error activation in the nucleus accumbens was similar across age groups, and numerically higher in older adults. However, activation in the default mode was less suppressed in older adults in for higher attentional task demands, and the level of suppression correlated with behavioral performance. Our results indicate that healthy aging does not significantly impair simple reinforcement learning. However, in complex environments, older adults rely more heavily on suboptimal reinforcement-learning strategies supported by the ventral striatum, whereas younger adults use attention processes supported by cortical networks.

SIGNIFICANCE STATEMENT Changes in the way that healthy human aging affects how we learn to optimally behave are not well understood; it has been suggested that age-related declines in dopaminergic function may impair older adult's ability to learn from reinforcement. In the present fMRI experiment, we show that learning and nucleus accumbens activation in a simple unidimensional reinforcement-learning task was not significantly affected by age. However, in a more complex multidimensional task, older adults showed worse performance and relied more on reinforcement-learning strategies than younger adults, while failing to disengage their default-mode network during learning. These results imply that older adults are only impaired in reinforcement learning if they additionally need to learn which dimensions of the environment are currently important.

Introduction

Adaptive behavior in complex multidimensional environments depends not only on the ability learn from experience, but also on the capacity to restrict attention to specifically those dimensions of the environment that are relevant to the task at hand. For instance, recall learning to operate a new smart phone: some cues, such as the location of unobtrusive 'menu' or 'back' buttons are crucially important, while other buttons, and ad pop-ups, are often distractors that are better ignored. Deficits in learning about task-relevant cues while ignoring information from distractors can severely hinder one's ability to make full use of the features of the phone. Healthy human aging has been shown to separately affect both learning from experience (Mell et al., 2005; Mata et al., 2011; Samanez-Larkin et al., 2014) and attention filtering (Braver and Barch, 2002; Hampshire et al., 2008; Schmitz et al., 2010; Campbell et al., 2012). In the present study, we aim to provide a precise computational description of the neural correlates of age-related changes in the interaction between learning and attention.

The computational framework of reinforcement learning (RL) has fundamentally reshaped our understanding of learning from experience, most notably by showing that one of the central signals in RL models, the reward prediction error, correlates with dopaminergic signaling in the ventral tegmental area and substantia nigra pars compacta (Montague et al., 1996; Schultz et al., 1997; Tobler et al., 2005), and with fMRI activation in the nucleus accumbens (Knutson and Cooper, 2005; Niv et al., 2012; Daniel and Pollmann, 2014). However, RL algorithms become notoriously inefficient in multidimensional environments, a phenomenon known as the 'curse of dimensionality' (Bellman, 1957; Sutton and Barto, 1998). Recent evidence suggests that the human brain simplifies complex learning tasks by using selective attention to narrow down the dimensionality of the task (Jones and Cañas, 2010; Wilson and Niv, 2011; Niv et al., 2015; Leong, Radulescu et al., 2017). For this strategy to work, the spotlight of attention must be focused on specifically those dimensions of the environment that are relevant for the current task.

The relevance of dimensions can be explicitly communicated, such as in an instruction manual that might have come with your new phone. More often though, one must learn the importance of each dimension through experience, suggesting a bidirectional interaction between attention and learning in multidimensional environments. This process has also been referred to as 'representation learning' (Niv et al., 2015) and an interplay between striatal areas, which support reinforcement learning, and frontoparietal attention areas, which support executive control processes, has been suggested as its neural substrate (Leong, Radulescu et al., 2017). Under this hypothesis, frontoparietal areas create and maintain task representations on which RL operates, while prediction errors relayed from the dopaminergic midbrain to the nucleus accumbens indicate how well the current task representation predicts reward, and thus whether the representation should be maintained or adapted.

Normal aging impacts on functional connectivity in the frontoparietal networks implicated in executive control and attention. These age-related declines have mainly been observed in the default mode network (DMN), but potentially also affect the dorsal attention network (Tomasi and Volkow, 2012). A reduction of dopaminergic functioning has been discussed as a contributing factor to this decline, and especially effects frontostriatal circuits (Ferreira and Busatto, 2013). In learning tasks, nucleus accumbens activation in response to prediction errors has been observed to decline with age (Mell et al., 2009; Eppinger et al., 2013; Samanez-Larkin et al., 2014), while injections of the dopamine precursor levodopa have been shown to restore these signals, as well as improve task performance in older adults (Chowdhury et al., 2013). However, other studies observed no age differences (Lighthall et al., 2018) or increased ventral striatal responses (Schott et al., 2007) during reward processing, and showed that the ventral striatum is among the brain areas with the weakest age-related decline in dopamine receptor availability (Seaman et al., 2019).

In the present experiment, we aim to clarify the roles of the DMN and nucleus accumbens across the human life span by investigating behavioral and neural changes in the interaction between reinforcement learning and attention in healthy human aging. To this end, we acquired behavioral and fMRI data from younger and older adults while they performed two variants of a task examining ongoing learning in multidimensional environments (Wilson and Niv, 2011; Niv et al., 2015), in which we have previously shown that performance decreases with age (Radulescu et al., 2016). In one variant of this three-dimensional three-armed bandit task, participants had to learn from trial and error which of the dimensions was predictive of reward, while in the other variant the reward-predicting dimension was revealed using explicit instructions. By comparing behavioral performance, latent variables from computational modeling, and fMRI activation patterns, we dissect the processes that underlie age-related behavioral and neural changes when learning in high-dimensional environments.

Materials and Methods

Participants

Forty-six participants were recruited from the Princeton University community using flyers on campus, the E-mail distribution system of the Community Auditing Program, the Paid Experiment Website of the Department of Psychology, and referral sampling. This recruiting procedure resulted in a sample with comparable educational background across groups; all 23 participants in the older adult group (OA; mean age = 70.0, range = 61–80; 12 male, 11 female) held at least a bachelor's degree, with 12 participants holding a master's and 6 a doctorate degree. All 23 participants in the younger adult group (YA; mean age = 22.7, range = 18–35; 11 male, 12 female) were either enrolled in ongoing education (n = 18) or held a bachelor's (n = 2), master's (n = 2), or doctorate (n = 1) degree. To assess general cognitive functioning, Raven's Advanced Progressive Matrices (1962 revision, even items only), a listening span test (Salthouse and Babcock, 1991; Cools et al., 2008), and the Attention Networks Test (Fan et al., 2002) were administered within 1 week of the fMRI session (12 d for one participant). All participants gave written informed consent in accordance with the protocols approved by the Institutional Review Board of Princeton University and were compensated with $12/h in the cognitive test session, and with $20/h (with a $5 bonus for satisfactory task performance) in the fMRI session.

Experimental design and statistical analysis

Behavioral task.

We used a three-dimensional three-armed bandit task that we have used previously to investigate the interaction between learning and selective attention (Gershman et al., 2010; Wilson and Niv, 2011; Niv et al., 2015; Radulescu et al., 2016). In this “dimensions task” (DT; see Fig. 1) participants chose one of three stimuli to obtain reward. Three separate features defined each stimulus: a color (red, yellow, or green), a shape (circle, square, or triangle), and a texture (dots, waves, or plaid). At any given time, only one of these dimensions was relevant for obtaining reward, and within that dimension choosing one specific feature resulted in reward with high probability (p = 75%), while choosing any of the other two features resulted in reward with low probability (p = 25%). For example, if the reward predicting dimension was color, and yellow was the highly rewarded feature, choosing the yellow stimulus would result in a point on 3/4 of the trials. In contrast, choosing the red or green stimulus would result in a point only on 1/4 of the trials. The features on the other two dimensions, in this example shape and texture, did not influence reward probabilities.

Figure 1.

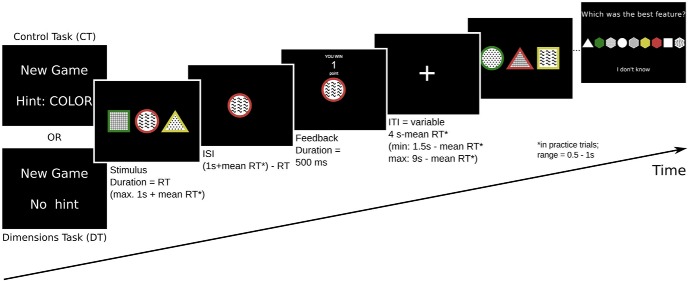
The behavioral task. At the beginning of each trial, participants were prompted to select one of three stimuli; each stimulus was defined by three different features: a color, a shape and a texture. After indicating their choice, participants received feedback about winning 1 (depicted) or 0 points. Subsequently, a new trial began with a new set of stimuli. To allow repeated measurements of learning, the task was split into several “games”. In any given game, only one of the three stimulus dimensions was predictive of reward. Choosing the most rewarding feature on that dimension resulted in a point 75% of the time, while choosing any other feature resulted in a point 25% of the time. Participants were informed when a new game began, i.e., when the identity of the reward-predicting dimension changed. In CT games, they were also explicitly informed about the identity of the reward-predicting dimension (top left). At the end of each game, a selection screen prompted participants to indicate what they thought was the most rewarding feature (or to choose “I don't know”).

Before beginning the fMRI session, participants were familiarized with these rules, and instructed that their goal is to win as many points as possible. They practiced three example games—during which they were encouraged to ask questions—to ensure that every participant fully understood the instructions. In addition to the DT, a control task (CT) was introduced. In the CT, participants were informed about the identity of the reward-predicting dimension at the start of the game, thereby reducing the DT to a regular three-armed bandit task. All participants played 10 practice games (5 CT, 5 DT) in the MRI scanner while no functional data were acquired. At the beginning of each game participants were notified that the reward predicting dimension had changed; if it was a CT game, on-screen instructions also indicated which dimension this was. At the beginning of each trial, three stimuli were presented to the participants, and they were asked to press one of three buttons to choose one of them. If no response was made within 2 s, the trial was aborted and the message “TOO SLOW” was displayed. Otherwise, the two unchosen stimuli were removed from the screen immediately after the response. Two seconds from trial onset, participants were informed whether their choice had resulted in a point. After a fixed intertrial interval (ITI) of 300 ms the next trial was initiated. Each practice game was 25 trials long, and at the end of each game a selection screen with all nine features was presented,. This screen prompted participants to pick the most rewarding feature or to answer “I don't know” (see Fig. 1).

After this practice outside the scanner, participants played 28 games (14 CT, 14 DT, randomly interleaved) while fMRI data were acquired. In the fMRI session, trial timing was adjusted to allow capturing the slow hemodynamic response and to account for individual differences in reaction times. Reaction times in the tasks can differ between individuals for many reasons, including the duration of visual search for the target feature or the speed with which a decision is mapped to a button press (Radulescu et al., 2016). We assumed these factors to vary between individuals and age groups, but were mainly interested in the cognitive component of the learning process. We therefore aimed to allow each participant a similar time to make their decision, regardless of any other factors like slowed motor responses. To this end, we calculated an individual response cutoff time based on data from each individual's practice games; this cutoff was set to 1 s plus the participant's mean reaction time (RT; min. 0.5 s, max. 1 s) from the practice trials. To account for the hemodynamic response, ITIs were drawn from an exponential distribution with a mean of 4 s (range: 1.5 s-9 s); however, to ensure equal overall trial length across participants, the mean RT from the practice trials was subtracted from the ITI duration. For a schematic representation of the task and an overview of trial timing, see Figure 1. Additionally, during fMRI data acquisition, each game lasted a minimum of 10 trials and ended after the participant chose the correct feature eight times in a row, or after a maximum of 25 trials. This performance criterion was introduced as we were interested in the learning process, which terminates once the participant has determined with certainty the highly rewarding feature. All other parameters of the tasks were the same as during the practice games.

Model-based analysis of behavioral data.

To describe the temporal dynamics of learning and compare different possible strategies across age groups, we fit a computational model to the sequence of each participant's choices. Building on previous work on modeling the Dimensions Task (Gershman et al., 2010; Wilson and Niv, 2011; Niv et al., 2015), our model combined aspects of RL (Rescorla and Wagner, 1972; Sutton and Barto, 1998) with a more statistically optimal Bayesian approach (Kruschke, 2006).

In this model, which we will refer to as hybrid RL/Bayes model, we assumed that the probability of choosing a stimulus S depends on its value V. To map the stimulus values V(S) to choice probabilities, we used a softmax action selection policy (Sutton and Barto, 1998):

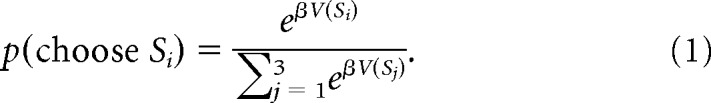This choice function assigns a higher probability to choosing a stimulus with higher value, while smaller values of the free parameter β (inverse temperature) allow for more randomness in the choices.

To estimate V(S), we used a function approximation approach (Sutton and Barto, 1998) in which separate values W for each feature f on each dimension d were learned (3 × 3 = 9 feature values W_f). The value of each stimulus was then computed as a weighted linear combination of its feature values:

where Φ_d was the weight of dimension d (see below). On each trial, a prediction error (PE) was generated:

where R indicates the reward received on that trial and V(S_chosen), the predicted value of the chosen stimulus, represents the expected reward. The value W of the each of the features f of the chosen stimulus was then updated based on the PE and a learning rate η:

In addition, the value of features f that were not chosen on a given trial were decayed to zero with a decay rate η_k:

By implementing this decay process, the model implicitly emulated selective attention to some features and not others: features that were consistently chosen and rewarded gained high value, while the values of all other features decayed toward zero (Niv et al., 2015).

In the present model, we additionally implemented an explicit attention filter Φ (see Eq. 2), which indicates the proportion of attention resources currently directed toward each dimension. Φ had two components, a reinforcement-learning based weight vector Φ^RL, and a Bayesian inference based weight vector Φ^Bayes.

In the DT, the dimension weight Φ_d^RL was δ if dimension d included the currently highest feature weight, while the remainder 1–δ was distributed equally across the other two dimensions:

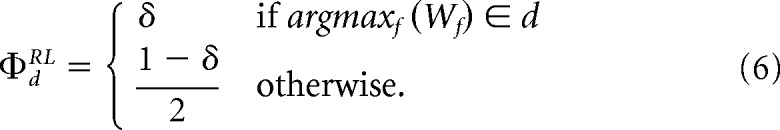In the CT, Φ_d^RL was always δ for the instructed dimension, and $\frac{1-\delta }{2}$ otherwise. This weighing based on values/instructions allows the learner to focus attention on the dimension that currently seems most predictive of reward, while the free parameter δ regulates how exclusive this focus of attention is. An alternative mapping of feature weights to an attention filter using softmax did not qualitatively change any of our results. We therefore report results from the argmax model as this formulation allows direct incorporation of explicit instructions in the CT.

The second component of Φ, Φ^Bayes, was computed using Bayesian inference. Here we assumed that participants can employ knowledge about reward probabilities to estimate the probability that each of the nine features f is the most rewarding feature f*. We initialized the probability of each f being f* to 1/9 at the beginning of the game; this probability was then recursively updated based on the choices C and rewards R using Bayes rule (Gershman et al., 2010; Wilson and Niv, 2011; Niv et al., 2015):

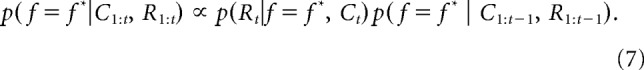If the current trial t was rewarded, p(R_t | f = f*, C_t) as 0.75 for chosen f and 0.25 for unchosen f. Conversely, on unrewarded trials p(R_t | f = f*, C_t) was 0.25 for chosen f, and 0.75 otherwise.

At the beginning of each trial, we used p(f = f* |C_1:t−1, R_1:t−1) to derive dimensional attention weights Φ^Bayes:

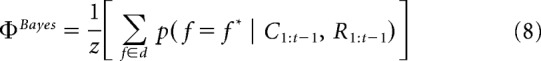where z normalized Φ^Bayes to sum up to one across the three dimensions.

Finally, we introduced an additional free parameter that gave the model flexibility to rely more on either the computationally efficient but approximate RL-based attention weighting structure, or on the statistically optimal but computationally demanding Bayesian approach. To this end, we computed Φ (Eq. 2) as a weighted sum of the RL based attention weights Φ^RL (Eq. 6) and the Bayesian inference based attention weights Φ^Bayes (Eq. 8), with α as an individual-difference free parameter determining the weight of each:

Overall, the hybrid RL/Bayes model therefore had five free parameters: β (softmax inverse temperature, Eq. 1), η (learning rate, Eq. 4), η_k (decay rate, Eq. 5), δ (RL dimension weight, Eq. 6), and α (balance between RL and Bayesian attention weights, Eq. 9). We fit the values of each of these free parameters individually for each participant by estimating the joint likelihood of all the T choices the participant completed:

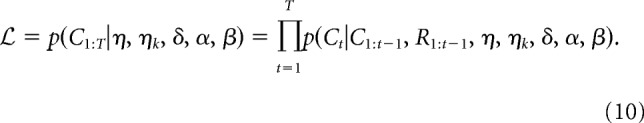In a first step, we obtained maximum likelihood estimates of all parameters by minimizing the negative log likelihood of the participant's choice data. Subsequently, we regularized the fit by adding a prior on β and determining the maximum a posteriori estimates (Daw, 2011). As a prior, we used a Gamma distribution whose parameters were set using the group estimates from the initial maximum likelihood fitting procedure. All model parameters, their range constraints, priors, and their fit to the data (mean ± SE) are reported in Table 1.

Table 1.

Best-fit parameters

Parameter	Range	Prior	Younger	Older	t(44)a
			Mean ± SE	Mean ± SE
Dimensions task: hybrid Bayes/RLb
η (learning rate)	0–1	None	0.42 ± 0.02	0.37 ± 0.02	1.75
ηk (decay rate)	0–1	None	0.48 ± 0.05	0.42 ± 0.04	1.01
δ (dimension weight)	0–1	None	0.45 ± 0.02	0.43 ± 0.02	1.15
α (balance)	0–1	None	0.20 ± 0.02	0.12 ± 0.02	2.36*
β (inv. temperature)	0–∞	Gamma (5.7,1.8)	8.9 ± 0.27	10.9 ± 0.73	−2.50*
Dimensions task: feature RL with decayc
η (learning rate)	0–1	None	0.45 ± 0.02	0.39 ± 0.08	2.12*
ηk (decay rate)	0–1	None	0.49 ± 0.04	0.45 ± 0.04	0.74
β (inv. temperature)	0–∞	Gamma (11.8,0.9)	10.0 ± 0.31	11.6 ± 0.63	−2.37*
Control task: hybrid Bayes/RLb
η (learning rate)	0–1	None	0.52 ± 0.03	0.52 ± 0.04	−0.13
ηk (decay rate)	0–1	None	0.71 ± 0.07	0.72 ± 0.07	−0.02
δ (dimension weight)	0–1	None	0.93 ± 0.03	0.88 ± 0.03	1.33
α (balance)	0–1	None	0.03 ± 0.02	0.04 ± 0.02	−1.65
β (inv. temperature)	0–∞	Gamma (5.1,2.3)	9.1 ± 0.50	11.3 ± 0.73	−2.78*
Control Task: “informed” RLc
η (learning rate)	0–1	None	0.49 ± 0.04	0.49 ± 0.04	0.01
β (inv. temperature)	0–∞	Gamma (5.8,1.6)	8.0 ± 0.45	9.4 ± 0.65	−1.8

^aIndependent-samples t test: age group comparison.

^bModel with highest predictive accuracy in this task.

^cModel with second highest predictive accuracy in this task.

*p < 0.05.

For each participant, the model's predictive accuracy was assessed using leave-one-game-out cross-validation. In this procedure, we estimated the model's free parameters for each game G using all trials from the other games and the maximum a posteriori procedure described above. These parameter estimates were then used to assign a likelihood to each of the choices in game G, to calculate the summed log likelihood of all the choices in the game. This procedure was repeated for each of the participant's games, giving us the total log likelihood of all of the participant's choices given the model (Eq. 10). To obtain a more intuitive measure of overall model fit, we calculated the geometric average predictive likelihood per trial by dividing the total log likelihood by the number of trials and exponentiating. An average predictive likelihood per trial of 1/3 indicates chance performance of the model (i.e., the model cannot, on average, predict choices above chance), whereas a value of 1 indicates perfect model performance (i.e., the model is able to predict 100% of the participants' choices correctly).

In addition to this hybrid RL/Bayes model, several other models were fit to the data. Following Niv et al. (2015), these alternative models included: (1) a naive RL model that learned the value of all 27 stimuli (three features on three dimensions, 3³), (2) a feature-RL model that learned the value of the 3 × 3 features separately, and computed the value of each stimulus as the mean of its three feature values, and (3) a feature RL model that included a decay of unchosen feature values as described in Eq. 5. In previous analyses of choice behavior in the DT, which did not include the hybrid RL/Bayes model proposed here, the feature RL model with decay (model 3) was the best of the investigated models in predicting participants' choice behavior. It is equivalent to the hybrid RL/Bayes model but does not include the attention weight Φ (Niv et al., 2015; Radulescu et al., 2016). In addition, we considered (4) a fully Bayesian model, (5) a hybrid model based on the feature RL model with Bayesian weights to compute stimulus values, and (6) a serial hypothesis model based on the assumption that participants attend to one feature at a time and test the hypothesis that this feature is the correct feature (for a detailed description models 1–6 see Niv et al. (2015)). We also fit (7) an “informed” RL model that assumed that subjects only learn about the features on the correct dimension, implying that they know which dimension to focus on; we expected this model to explain behavior well in the CT but not in the DT. This last model is the standard approach in unidimensional environments, where it is often referred to as a Rescorla-Wagner model (for a detailed description see e.g., Niv (2009)).

fMRI methods

Image acquisition.

FMRI data were acquired using a Siemens MAGNETOM Skyra whole-body 3 T MRI scanner (software platform syngo MR D11) equipped with a 20 channel head coil. Structural images were recorded using a T1-weighted magnetization-prepared rapid acquisition gradient echo (MP-RAGE) sequence (repetition time (TR) = 1900 ms, time to echo (TE) = 2.13 ms, field of view (FOV) = 240 mm, 192 sagital slices, 0.9 mm isotropic voxels). Subsequently, functional data were recorded in four separate runs using an echo planar imaging (EPI) sequence (TR = 2100 ms, TE = 30 ms, flip angle = 71°, FOV = 192 mm, 38 axial slices parallel to AC-PC, voxel size = 2.9 × 2.9 × 3 mm, distance factor = 10%, volumes acquired in an interleaved-ascending manner). These acquisition parameters resulted in a group level mask that excluded the cerebellum and left temporal pole.

Image preprocessing

All image processing was performed using the statistical parametric mapping software SPM12b (Functional Imaging Laboratory, Wellcome Trust Centre for Neuroimaging, Institute of Neurology, London, UK). To minimize T1 saturation effects, the first five images of each functional run were discarded. Subsequently, images were corrected for slice acquisition time by interpolating to the middle time of each image, and motion corrected using rigid body realignment to the mean of all images. The six estimated movement parameters were saved and later included in all statistical analyses as regressors of no interest. Next, all functional images were coregistered with the segmented and skull stripped anatomical images. To optimize intersubject registration (Ashburner, 2007) and to allow for similar normalization accuracy regardless of the age group (Samanez-Larkin and D'Esposito, 2008), a study-specific gray matter template was created by estimating the nonlinear transformations that best align the gray and white matter components of all subjects using the DARTEL toolbox (Ashburner et al., 2014). In a final step, the DARTEL toolbox was used to warp both anatomical and functional images into MNI space. This step also included spatial smoothing of the functional data with a Gaussian kernel (FWHM = 6 mm). All normalized anatomical images were averaged and used as a study-specific anatomical template to visualize the location of functional activations in Figures 3 and 4.

Figure 3.

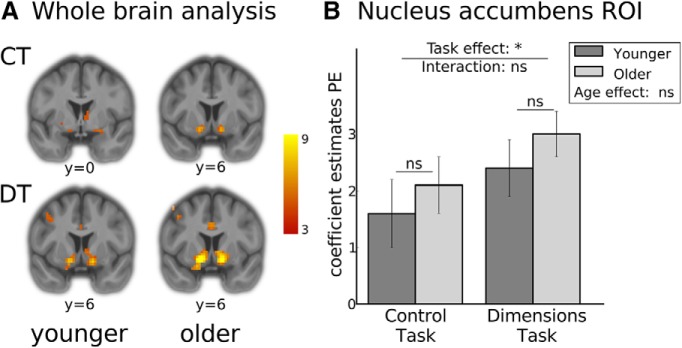
Outcome-related activation does not differ between age-groups. A, Ventral striatal activation correlated with the PE signal for all four conditions. In the CT, peak MNI coordinates were 24/0/−12 (t = 5.3) in the younger group and −15/9/−9 (t = 6.6) in the older group. In the DT, they were 15/3/−12 (t = 8.7) in the younger group, and −15/6/−9 (t = 9.6) in the older group. At the whole-brain level, no significant differences between groups or tasks were observed. Activations shown were thresholded at p_FWE <.05 and are superimposed on the averaged anatomy of all study participants. B, Averaged coefficient estimates of an anatomical ROI of the nucleus accumbens were extracted and submitted to a 2 × 2 ANOVA. In this analysis, we observed a main effect of task but no age effect or interaction with age, indicating that age did not affect outcome-related activity in the ventral striatum. *p < 0.05. ns, not significant.

Figure 4.

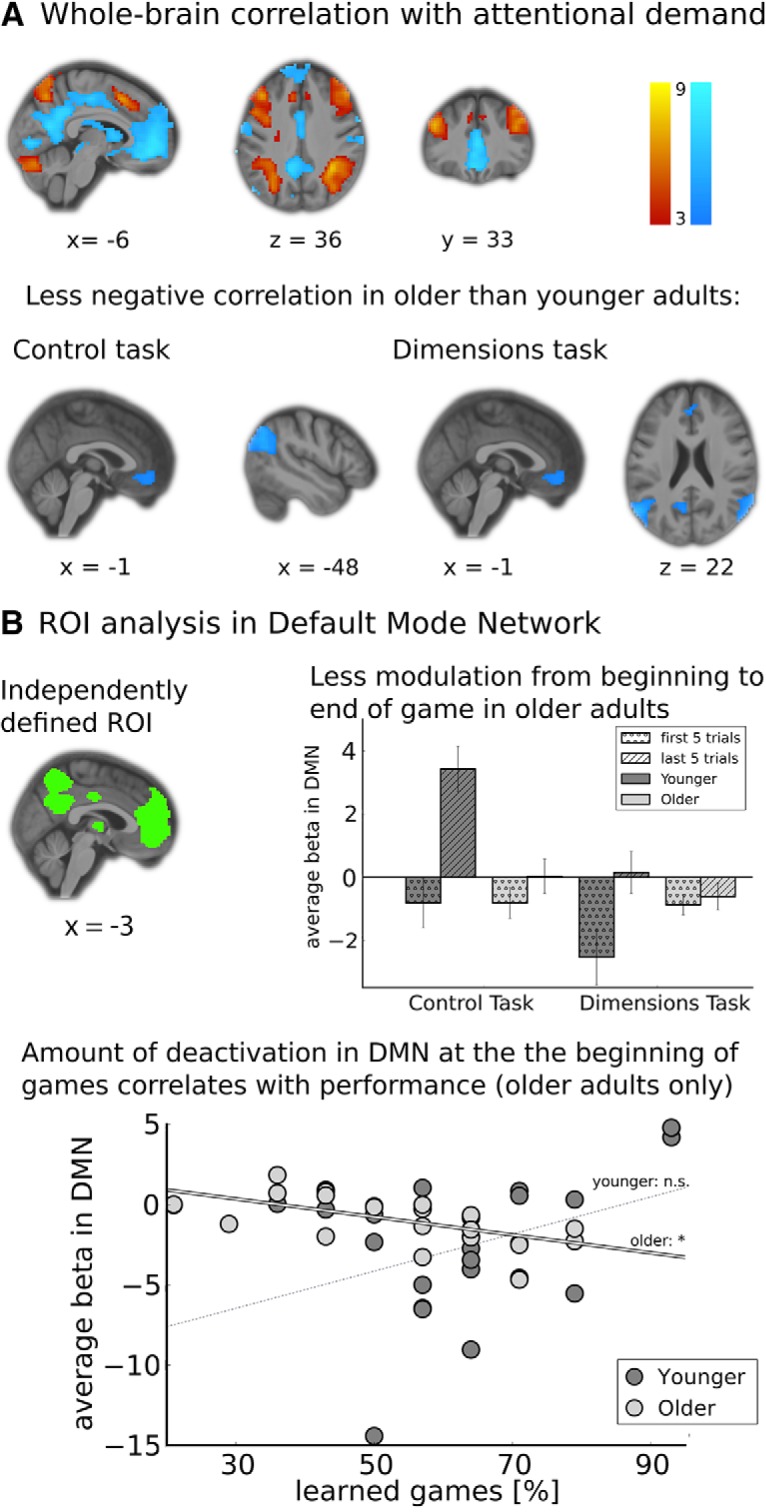
Modulation of brain activation with attention demands is less pronounced in older adults. A, Activation correlated with a model-derived regressor representing attention demands. Positive correlations (more activation for when attention demands were higher; yellow-red heat map) were observed in the attention network (IPS) and executive control network (dmPFC, dlPFC). Negative correlations (less activation when attention demands were high; blue heat map) were observed in the DMN (vmPFC, angular gyrus). Differences between age groups were only observed in the DMN. All activations shown were thresholded at p_{cluster-levelFWE} <.05 (voxel threshold p < 0.001). For a complete list see Table 3. B, ROI analysis within the DMN. In an independently defined ROI encompassing the whole DMN (top left), we observed that the difference in activation between the first and last five trials of games was smaller in older adults than in younger adults, with no significant main effect of age (top right). In addition, in older adults, deactivation within the DMN in the first five trials of games correlated with overall task performance (bottom). *p < 0.05; ns, not significant.

Model-based whole-brain analysis

To locate brain areas in which fMRI activation was correlated with attention focus and reward learning, we generated regressors representing the time course of these processes from the hybrid Bayes/RL model. Each participant's individual maximum a posteriori parameters were used to obtain a trial-by-trial estimate of (1) the variance of the feature weights of the chosen stimulus (a proxy for the amount of attention weighting), and (2) the prediction error. These estimates were then used as parametric modulators on (1) a variable epoch regressor representing stimulus presentation (duration = RT on the trial, Grinband et al. (2008)) and (2) an impulse function at outcome onset. All regressors were built separately for the DT and CT, convolved with the hemodynamic response function (HRF) and fit to the brain data of each participant using a general linear model (GLM) with a high-pass filter cutoff at 1/128 Hz, and correcting for temporal autocorrelation with an AR1 model.

Subsequently, subjects' coefficient estimates were submitted to random-effects group analyses. The factors of the 2 × 2 × 2 ANOVA were task (CT or DT), latent variable (attentional focus or prediction error), and age (YA or OA). Activation maps were thresholded at p < 0.05 with whole-brain familywise error correction (FWE) at the cluster level (voxel threshold p < 0.001).

Region of interest (ROI) analysis

To confirm and specify the results of the model-based whole-brain analysis, additional model-free analyses were run within ROIs. Regressors of interest were variable epoch regressors for the onset of the first/last five stimuli in each game (duration = RT on the trial) as indicators of brain activation at the beginning/end of the game (the minimum game duration was 10 trials), and an impulse regressor at the onset of positive/negative outcomes. An additional variable epoch regressor for the onset of all stimuli was included to control for activity that was common across all trials of a game. These regressors were built separately for the CT and DT, convolved with the HRF, and fit to each participant's data using a GLM with a high-pass filter cutoff at 1/128 Hz and AR1 correction for temporal autocorrelation. Six movement parameters as estimated in the motion correction step were also included as regressors of no interest in all analyses.

We used the MarsBar toolbox (http://marsbar.sourceforge.net) to extract data from an anatomical ROI in the bilateral nucleus accumbens from the Harvard-Oxford subcortical structural atlas as implemented in the Oxford University Centre for Functional MRI of the Brain Software Library (http://www.fmrib.ox.ac.uk), and a functional ROI in the dorsal and ventral DMN from the Functional Imaging in Neuropsychiatric Disorders Laboratory (Shirer et al., 2012). Each participant's extracted coefficient estimates were averaged within each ROI and submitted to random effects analyses on the second level. Additionally, activity for the model-based regressors for attention focus and prediction errors was extracted from both ROIs for visualization purposes.

Results

We compared a group of 23 younger adults (YA; age: M = 23, SD = 4.1) to a group of 23 older adults (OA; age: M = 70; SD = 5.5) while they performed the Dimensions Task (DT) and an associated Control Task (CT). The DT required participants to learn from trial and error which of three dimensions is predictive of reward, and what the highest-valued feature in that dimension is. In the CT, participants were informed about the identity of the reward-predictive dimension, which effectively reduced the DT to a three-armed bandit task with distractor dimensions. Each participant played 14 games of each task (randomly interleaved) while behavioral and fMRI data were acquired. Here we report results on similarities and differences between age groups in overall task performance and learning dynamics, as well as their neural correlates.

Overall task performance

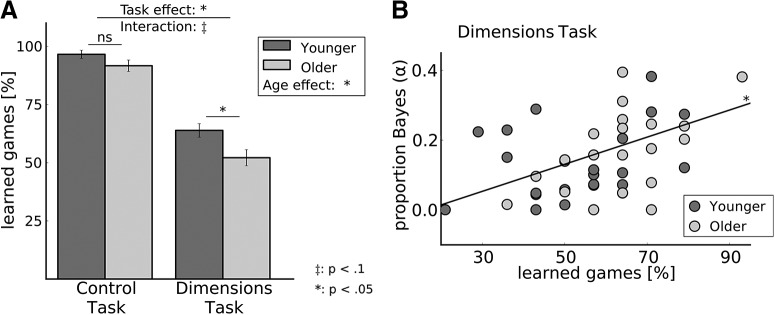
As we were interested in evaluating the learning process rather than the performance of an already learned skill, we terminated games once the participant chose the correct feature eight times in a row. As a result, to measure task performance we compared the percentage of learned games per participant rather than the raw percentage of correct choices. A game was defined as “learned” if the participant (1) chose the most rewarding feature in the last six trials of the game or (2) was able to report the most rewarding feature at the end of the game (Fig. 1). As shown in Figure 2, according to this criterion, participants learned an average of 94% (SE = 0.02) of the games in the CT (YA: M = 97%, SE = 0.02; OA: M = 94%, SE = 0.02; age difference: t₍₄₄₎ = 1.65, n.s. (p = 0.11)). In the DT, on average 58% (SE = 0.02) of the games were learned (YA: M = 64%, SE = 0.03; OA: M = 52%, SE = 0.03; age difference: t₍₄₄₎ = 2.6, p < 0.05). Thus participants in both age groups learned well over half of the games, indicating that they were engaged and able to perform the task.

Figure 2.

Behavioral results. A, Overall task performance, i.e., the percentage of learned games, was higher in the CT than in the DT, and in YA than in OA, with a trending interaction indicating that the performance difference was larger in the DT. ^‡p < 0.1; *p < 0.05; ns, not significant. B, In the DT, the percentage of learned games correlated with α, a free parameter of our best fitting behavioral model, which indicates to which degree participants used statistically optimal attention weights when computing the value of each stimulus. On average, α was higher for YA than for OA (t₍₄₄₎ = 2.36; p < 0.05; see Table 1).

Since participants did not reach criterion in 42% (SE = 0.02) of the games, a trial-to-criterion analysis is not suitable to compare overall task performance across tasks and age groups. Instead, we ran an ANOVA on percentage learned games with a within-subjects factor task type (CT or DT) and repeated measures on age (OA or YA). Results showed a main effect of both factors (task type: F_(1,44) = 327.15, p < 0.05; age: F_(1,44) = 6.44, p < 0.05), suggesting worse performance on the CT compared with the DT, and of OA compared with YA (Figure 2). In addition, we observed a trending interaction of task type×age (F_(1,44) = 2.95, p = 0.09), indicating a potentially larger performance difference between age groups in the DT than in the CT. This interaction would suggest that aging affects performance more in environments with high demands on attention resources than it does in simple reinforcement learning tasks.

Relationship between task performance and standard cognitive measures

To evaluate which cognitive measures correlated with performance on each of our tasks, we fit two separate stepwise linear regression models predicting overall performance (percentage of learned games) on the CT/DT. All acquired cognitive measures (i.e., Raven's Advanced Progressive Matrices, the Attention Networks Test (providing three separate scores for alerting, and orienting, and executive control), and the Listening Span Test; for mean scores see Table 2), as well as an indicator variable for age, and interactions between age and each cognitive measure were added to the model as predictors. In both cases, the score from Raven's Matrices was the only significant predictor (p < 0.05; DT: b = 0.19, t_(1,44) = 3.35; CT: b = 0.10, t_(1,44) = 2.7), leading to a significant overall fit of the model (DT: R² = 0.20; CT: R² = 0.14). No age effects or interactions with age were observed, indicating that for both groups general intelligence was the only acquired cognitive measure influencing performance on both of our tasks and across both age groups.

Table 2.

Cognitive test battery

	Younger	Older	t(44)a
	Mean ± SE	Mean ± SE
Raven's progressive matrices	13.0 ± 0.6	8.6 ± 0.7	4.7*
Listening span	3.9 ± 0.3	3.0 ± 0.2	3.1*
Attention networks
Alerting	43.0 ± 5.7	31.0 ± 5.8	1.5
Orienting	18.0 ± 4.5	20.0 ± 4.5	−0.3
Conflict	115.1 ± 9.5	146.3 ± 7.5	−2.6*

^a Independent-samples t test: age group comparison.

*p < 0.05.

Modeling the dynamics of learning

Although measures of overall task performance are useful to evaluate whether both groups are able to successfully perform the task, they do not provide information about the learning dynamics and strategies used by the participants. To quantify and compare these between age groups, eight different computational models were fit to both tasks. The fit models included a statistically optimal Bayesian observer, several different reinforcement learning models (see Methods: Model-based analysis of behavioral data and Niv et al. (2015)), a hybrid RL/Bayes model, as well as an “informed” RL model (which assumes, unrealistically, that participants only learn about the relevant dimension). Each model's predictive accuracy was assessed using a leave-one-game-out cross-validation procedure. Averaged per-trial predictive accuracies indicated that for both age groups and tasks the hybrid RL/Bayes model was best able to predict participants' choices. In the CT, it predicted choices with 63.0% (SE = 1.1) accuracy (YA: 62.3% (SE = 1.5), OA: 63.7% (SE = 1.6); age difference: t₍₄₄₎ = −0.6; p = 0.51); the second best model for the CT was the “informed” RL model, which predicted participants' choices with 60.5% accuracy (test for difference in predictive accuracies between models: YA: t₍₂₂₎ = −4.0, p < 0.05; OA: t₍₂₂₎ = −2.2, p < 0.05). The “informed” RL model assumes that participants only learn about the reward-predicting dimension and ignore the other two; it is equivalent to a standard Rescorla-Wagner model, which is frequently used to predict behavior in unidimensional RL tasks. It is therefore meaningful that this model's fit to behavior was significantly worse than that of the hybrid RL/Bayes model: despite the hint indicating the reward-relevant dimension, participants in both groups were not able to ignore the irrelevant dimensions entirely.

In the DT, the hybrid RL/Bayes Model predicted choices with 53.5% accuracy (YA: 51.8% (SE = 0.7), OA: 55.2% (SE = 1.3); age difference: t₍₄₄₎ = −2.3; p < 0.05); here, for both groups the feature RL model with decay (Niv et al., 2015) was the model with the second highest predictive accuracy of 52.9% (test for difference in predictive accuracies between models: YA: t₍₂₂₎ = −3.1, p < 0.05; OA: t₍₂₂₎ = −2.5, p < 0.05). All parameters of the two best fitting models in each task, along with their best fit estimates, are listed in Table 1.

The described predictive accuracies indicate that for both tasks and age groups, the hybrid RL/Bayes model described participants' learning dynamics best. This model assumes that participants use a reinforcement-learning based strategy that operates on single features, and combines their values using an attention-weighted average. Note that a predictive accuracy of 63.0% (CT)/52.9% (DT) is substantially above the chance level of 33.3%, and is high given that participants had to guess in the first few trials of a game (reflected in an initialization of all features in the model at the same values), and that games were short (10–25 trials, ending after the participant consistently chose one feature).

The parameters of a model with high predictive accuracy, such as the hybrid RL/Bayes model, allow us to uncover fine-grained differences in learning dynamics between groups of participants. Group comparisons revealed that the estimates for the softmax inverse temperature β were lower for the younger participants in both the CT and DT. This parameter governs randomness in choices, i.e., it reflects how closely the choices of the participant align with the model's prediction. Low βs can indicate that participants tend to explore suboptimal (low-value) choices; they can also indicate that the model was unable to account for certain aspects of participants' choices. This second interpretation is in line with the observed slightly lower predictive accuracy for the model for younger than older participants (see above), which indicates that the simple reinforcement-learning based strategy suggested by the model captures a higher percentage of the underlying choice processes in older as compared to younger adults.

One potential process that younger adults might employ specifically in multidimensional environments is revealed by a difference in the best-fit value of the free parameter α in the DT. This parameter reflects how much attention weighting is influenced by a more statistically optimal distribution of weights, as derived using Bayes rule. On average, in the younger group, the best-fitting α was 0.20, whereas the optimal value for α in older adults was only 0.12 (see Table 1).

To explore whether the parameter estimates of the hybrid RL/Bayes model can explain overall task performance (percentage of learned games), we ran a separate stepwise multiple linear regression for each task, with all five parameter estimates as predictors, as well as an indicator variable for age and interactions between age and all parameter estimates. In the CT, a single predictor, the learning rate η, was sufficient for a significant model (r = 0.58; F_(1,44) = 22.8, p < 0.05). In contrast, in the DT α was the single predictor that lead to a significant model (r = 0.51; F_(1,44) = 16.0, p < 0.05; Figure 2B), and no significant interactions with age were observed. To confirm that the model parameter estimates—which quantify trial-by-trial behavior specifically in (multidimensional) reinforcement learning tasks—explain variance in task performance beyond that predicted by global deficits as measured in cognitive test, we regressed each participants results from the Raven's Advanced Progressive Matrices, the Attention Networks Test (providing three separate scores for alerting, orienting, and executive control), and the Listening Span Test against overall performance in each task. We then regressed the model parameters against the residuals to test how well the model parameters explain any residual variance above and beyond that explained by general cognitive abilities. In the CT, the learning rate η accounted for 13.4% of the remaining variance (F_(1,44) = 6.8, p < 0.05), while in the DT α accounted for 20.9% of the remaining variance (F_(1,44) = 11.6, p < 0.05). The model-derived parameters thus explained significant variance that was not explained by individual differences in constructs such as working memory and general intelligence.

These results indicate that in the CT, a higher learning rate, i.e., faster updating of the feature values, was the strongest model-derived predictor of better overall task performance. This parameter was not significantly different between age groups, which is in line with the finding that overall task performance in the CT was not significantly different between age groups. However, in the multidimensional DT, more optimal attention weights were the best model-derived predictors of task performance, corresponding to a significantly lower α estimate as well as lower overall performance in OA compared with YA. A possible interpretation of these results is that in complex multidimensional environments, YA rely more on statistically optimal Bayesian learning while OA rely more on computationally efficient but suboptimal reinforcement-learning processes, leading to an overall decrease in task performance in the older group.

fMRI results: Response to rewards

Previous work has indicated that aging might affect the ability to learn from trial and error due to a decline in phasic dopaminergic signaling, and that this decline can be observed as a lower correlation of fMRI data with a prediction-error signal in the ventral striatum (Mell et al., 2005; Mata et al., 2011; Chowdhury et al., 2013; Samanez-Larkin et al., 2014). To examine this hypothesis, we correlated a parametrically modulated regressor representing trial-by-trial prediction errors at the time of outcome onset with whole brain fMRI data. Prediction errors were defined as the difference between the reward received on a given trial, and the reward that was expected (as indicated by the value of the chosen stimulus in the best-fitting tested model, the hybrid RL/Bayes model). As expected, we observed strong activations peaking bilaterally in the nucleus accumbens (left: MNI(x/y/z) = −15/6/−9, t = 12.47; right: MNI(x/y/z) = 15/3/−12, t = 12.42) across both tasks, with a whole-brain FWE cluster corrected threshold of p < 0.05 (voxel threshold: p < 0.001). This activation did not differ significantly between the CT and the DT. Contrary to our hypothesis, it also did not differ between age groups (Figure 3A).

To confirm this result with a more sensitive analysis, we extracted and averaged each participant's parameter estimates within an anatomically defined ROI of the bilateral nucleus accumbens, and subjected these values to a 2 × 2 ANOVA with repeated measures on task type, and age group as a between-subjects factor. The results of this ROI analysis (Figure 3B) revealed a significant main effect of task type (F_(1,44) = 7.4, p < 0.05), indicating that fMRI activation in the nucleus accumbens was correlated more with the prediction error regressor in the DT than in the CT. However, again no age effect (F_(1,44) = 1.3, p = 0.26) or task-by-age interaction (F_(1,44) = 0.1, p = 0.77) were observed, confirming the results of the whole brain analysis that indicated no age difference in nucleus accumbens activation related to the prediction error.

To rule out potential confounds causing the absence of an age difference in the extent to which ventral striatal activation was correlated with prediction errors, we examined the variance of the prediction-error regressor and the number of trials between tasks and age groups. No significant differences were observed analyzing the variance of the prediction error regressor (task type: F_(1,44) = 1.0, p = 0.31; age: F_(1,44) = 0.65, p = 0.43, task type × age: F_(1,44) = 0.15, p = 0.70). However, the number of trials was higher in the DT than in the CT (F_(1,44) = 294.7; p < 0.05; CT: 191.0 trials (SE = 3.3), DT: 265.0 trials (SE = 3.35)), and trended to be higher for OA than for YA (F_(1,44) = 3.2; p = 0.08; YA: 447.2 trials (SE = 6.2), OA: 464.7 trials (SE = 7.67); task type×age: F_(1,44) = 0.02, p = 0.90). A higher number of trials could potentially facilitate signal detection and thereby mask a smaller correlation between the ventral striatal fMRI signal and the prediction error regressor in OA. We therefore repeated the ROI analysis including only the first 10 trials of each game, which were played by every participant in every game. Again, we observed a main effect of task type (F_(1,44) = 9.15, p < 0.05), but no main effect of age (F_(1,44) = 1.23, p = 0.27) or task type×age interaction (F_(1,44) = 0.46, p = 0.50).

To further verify that the absence of an age effect of prediction error related brain activation in the ventral striatum was not caused by the specifics of the hybrid RL/Bayes model that was used to estimate the expected value of the chosen stimulus, we additionally ran a model-free analysis. In this analysis, we used the difference between the response to a 1 point win and the response to a 0 point win as a proxy for the prediction error. This is possible since in a wide range of models that learn predictions from outcomes, in our task a 1 point win would cause a more positive prediction error than a 0 point win. Again, the results of this model-free control analysis confirmed a main effect of task type (F_(1,44) = 4.71, p < 0.05), but no main effect of age (F_(1,44) = 0.07, p = 0.80) or task type × age interaction (F_(1,44) = 0.81, p = 0.37).

The results of our primary and control analyses therefore indicate that, in contrast to previous reports (Eppinger et al., 2012; Chowdhury et al., 2013; Samanez-Larkin et al., 2014), activation in the ventral striatum did not correlate more strongly with the prediction error in younger than in older adults. Indeed, as can be seen in Figure 3, the direction of the observed nonsignificant age difference is opposite to this hypothesis in both tasks, suggesting that the absence of the effect is not simply a false negative induced by a lack of statistical power. The fMRI results are in line with the behavioral results, indicating no significant age effects in reinforcement-learning related processes.

fMRI results: Modulation of activation with attention demands

The ability to efficiently process rewards, as supported by the frontostriatal reward network, is crucial for learning from trial and error. However, especially in multidimensional environments like our DT, performance is expected to be further enhanced using attention mechanisms. In particular, attention can help focus learning on only the reward-predicting dimensions, which in turn reduces the complexity of the task. The interplay between large cortical networks such as the attention network and the DMN (Raichle et al., 2001; Buckner et al., 2008; Petersen and Posner, 2012) has been suggested to support the ability to focus and direct attention to external stimuli.

To confirm the effect of attention demands on the engagement of the attention network/DMN in the present task, and to explore whether this relationship changes with age, we correlated a parametrically modulated regressor representing trial-by-trial attention demand with whole-brain fMRI activation. As a proxy for the attention demand AD, we took the negative variance of the feature weights of the chosen stimulus in the hybrid RL/Bayes model:

The variance of the feature weights is high when the weight of a some features is higher than the weight of the other features, for example at the end of a learned game; in this situation it can be assumed that attention is mainly focused on those few high-valued features and therefore attention demand (and AD, the negative of the variance) is low. In contrast, the negative of the variance of feature weights (and therefore AD) is high when attention is evenly distributed across all features, such as at the beginning of games (Niv et al., 2015). It is important to note that AD reflects differential attentional demands as predicted from both reinforcement-learning and Bayesian-learning components, to best capture individual trial-by-trial attentional engagement. It should therefore not be interpreted as specifically reflecting Bayesian filtering.

Using AD to parametrically modulate a whole-brain task regressor (onset = stimulus onset; duration = RT), we observed positive correlations with attention demand in areas of the attention and executive control networks (intraparietal sulcus, dorsomedial and dorsolateral prefrontal cortex), whereas areas of the DMN (ventromedial prefrontal cortex, precuneus, angular gyrus, lateral temporoparietal cortex; Buckner et al. (2008)) were negatively correlated with attention demands across both age groups (Fig. 4A). Although we did not observe a main effect of age or an age × task interaction in areas that were positively correlated with attention demands, we did observe a main effect of age in several areas that were negatively correlated with the AD regressor: the angular gyrus, precuneus and ventromedial prefrontal cortex (Fig. 4A and Table 3). These areas showed less negative correlation with attention demands in OA compared with YA, suggesting that activity in these areas of older adults' DMN were less responsive to task demands, or that our AD regressor models task demands less accurately for older adults, or both.

Table 3.

Brain areas correlating with model-derived attentional focus

Region	Hemisphere	k	Max. Z	MNI
				x	y	z
Correlation with focussed attention
Intraparietal sulcus, precuneus	b	2767	7.54	33	−63	57
Dorsolateral/medial prefrontal cortex	r	1706	7.18	30	6	60
	l	1782	6.74	−45	30	30
Cerebellum	b	1387	7.09	−33	−66	−27
Correlation coefficients more negative for CT than DT
Ventromedial prefrontal cortex		102	4.07	−9	45	18
CT: Correlation coefficients more negative for YA than OA
Dorsomedial prefrontal cortex	l	375	4.41	−12	36	51
Ventromedial prefrontal cortex	b	135	4.04	6	30	−12
DT: Correlation coefficients more negative for YA than OA
Angular gyrus	l	441	5.32	−54	−63	24
	r	176	4.16	51	−69	24
Precuneus	b	239	4.41	−9	−48	36
Ventromedial prefrontal cortex	b	350	2.23	0	45	−3
Anticorrelation with focused attention
Ventromedial prefrontal cortex, ACC, precuneus, medial temporal lobe	b	4248	7.33	3	48	12
Lateral temporoparietal cortex, pre- and postcentral gyrus	r	2028	7.11	48	−30	18
	l	503	5.31	−54	−12	12
	l	461	6.38	−30	−27	57
Angular gyrus	l	186	5.02	−54	−66	27
Middle temporal gyrus	l	102	4.96	−66	−12	−15
	r	91	4.92	51	−75	6

l, Left; r, right; b, bilateral; BA, Brodmann's area; k, cluster size in voxels (2 × 2 × 2 mm).

All activations are significant on a whole-brain cluster-level FWE-corrected level of p < 0.05 (voxel threshold: p < 0.001)

To confirm this observation and further characterize the effect, we conducted an analysis on an independently defined ROI of the DMN (both dorsal and ventral areas; Fig. 4B; Shirer et al. (2012); all reported results are based on β values indicating brain activation during task performance, averaged across the whole ROI). First, we ran a 2 × 2 ANOVA with repeated measures on task type, and age group as a between-subjects factor. We observed a significant main effect of age group (F_(1,44) = 11.3, p < 0.05), and no effect of task type (F_(1,44) = 1.9, p = 0.17). Note that in accordance to the whole brain fMRI analysis, but in contrast to the model-free ROI analysis, a task-by-age interaction on the whole ROI was not observed (F_(1,44) = 0.28, p = 0.60). The difference from the model-free result is likely due to the fact that the model-derived regressor already accounts for differences in the task demands of the two tasks for each of the age groups, and thus we do not see additional neural differences above and beyond the differences embodied by the regressor.

To verify that the observed age effect in the DMN was related to changing attention demands rather than the specific characteristics of our model-based attention regressor, we also ran a model-free analysis on extracted β values of the first and last five trials of each game. This approach is based on the assumption that trials in the beginning of each game have the highest attention demands. In contrast, trials in the end of games, when participants have already often learned which feature is most predictive of reward, will have the lowest attention demands. The cutoff of five trials at the beginning/end of each game was based on the minimum length of games (10 trials), and was also consistent with previous analyses of fMRI data from a similar task (Niv et al., 2015). We ran a 2 × 2×2 ANOVA with repeated measures on task type and time in game (first vs last five trials), and age group as a between-subjects factor, on extracted betas values from the DMN. Results showed a main effect of both task type (F_(1,44) = 8.5, p < 0.05) and time in game (F_(1,44) = 19.5, p < 0.05), indicating a stronger deactivation of DMN structures during the DT than during the CT, as well as more deactivation during the first five trials of a game compared with the last five trials (Fig. 4B). These observations are consistent with previous reports of DMN deactivation during attention-demanding tasks (Buckner et al., 2008). Additionally, we observed significant interactions between age and both task type (F_(1,44) = 4.8, p < 0.05) and time in game (F_(1,44) = 10.3, p < 0.05). This was due to weaker correlation between DMN deactivation and attentional task demands in OA compared with YA. In contrast, we did not observe a significant main effect of age (F_(1,44) = 1.3, p = 0.23), indicating that this failure to modulate activation in response to task demands was not caused by an overall difference in DMN activation levels.

Finally, to investigate whether DMN deactivation in response to attention demands was correlated with behavioral performance, we regressed β values extracted from the DMN for the first and last five trials of each game, a dichotomous indicator variable for age, as well as interactions between age and each of the measures, against overall behavioral performance. In a stepwise regression, in the CT no age effect was observed, and DMN activation in the last five trials correlated positively with task performance across both age groups (b = 0.39, t_(1,44) = 2.8, p < 0.05), indicating that DMN activation increased once the game was learned. In contrast, in the DT we observed a main effect of age (b = −0.55, t_(1,44) = −4.1, p < 0.05), as well as an interaction between age and activation in the DMN during the first trials of a game (b = −0.48 t_(1,44) = −3.5, p < 0.05; R² = 0.30). Indeed, in this task there was a positive correlation between DMN deactivation during the first five trials of games and task performance only for OA (Fig. 4B), suggesting that those older participants whose DMN decreased responding early in a game performed better than their similar-aged peers.

In summary, both a model-based whole-brain analysis and a model-free ROI analysis confirmed that aging affects the successful deactivation of the DMN during an attention-demanding reinforcement learning task. The observed interactions of DMN deactivation and age with time in game (beginning or end of the game) and task type (Control Task or Dimensions Task), both of which can serve as indicators of attention demand, suggest that, in general, older adults failed to modulate DMN activation in response to attention demands. Further investigation of this effect showed that specifically in OA, a failure to deactivate the DMN during the first five trials of a DT game correlated negatively with overall behavioral performance, indicating that adequate modulation of DMN deactivation at the beginning of a task leads to successful learning in probabilistic multidimensional environments.

Discussion

Learning from trial and error in multidimensional environments depends on the dynamic interaction of attention and reinforcement learning (Leong, Radulescu et al., 2017). Previous studies indicate that healthy aging affects both reinforcement learning (Mell et al., 2005; Mata et al., 2011; Samanez-Larkin et al., 2014) and the executive control processes that regulate the ability to focus and switch the focus of attention (Braver and Barch, 2002; Hampshire et al., 2008; Schmitz et al., 2010; Campbell et al., 2012); a reduction in dopaminergic input to brain areas that underlie reinforcement learning, such as the nucleus accumbens (Chowdhury et al., 2013), and areas that underlie attentional control processes, such as the executive control network and DMN (Volkow et al., 2000; Tomasi and Volkow, 2012; Geerligs et al., 2015; Ferreira et al., 2016), have been suggested to underlie these behavioral changes. Here we examined how healthy human aging changes the interplay between reinforcement learning and attentional control. To this end, we recorded behavioral and fMRI data from both a simple, unidimensional, reinforcement learning task, and a multidimensional reinforcement learning task that requires selective attention to focus learning on relevant dimensions. Our results indicate that behavior and neural signals during simple reinforcement learning are not significantly affected by age; however, the performance of older adults decreases with the higher attentional demands in multidimensional environments. We additionally observed that areas of the DMN, which is known to be deactivated during attentionally demanding tasks, are less deactivated in older adults, and that the degree of DMN deactivation correlated with behavioral performance.

Simple reinforcement learning not significantly affected by healthy aging

In the present experiment we compared the impact of age on behavior in a simple three-armed bandit task in which participants were instructed about the relevant dimension, and a three-dimensional bandit task in which the relevant dimension was unknown. In the latter, participants did not only have to learn which feature is associated with the highest reward, but also had to employ selective attention to learn which of three dimensions is currently predictive of reward. On average, in the one-dimensional task, younger adults successfully identified the reward-predicting feature in 97% of the games, while older adults succeeded in doing so in 94% of the games. This difference was not significant, indicating that healthy aging does not have a strong impact on simple reinforcement learning tasks. In contrast, in the multidimensional task, performance dropped from 64% learned games in younger adults to 58% in older adults, suggesting that aging does significantly affect learning in more complex environments in which distractors are present and selective attention is required to successfully optimize behavior (Radulescu et al., 2016).

Older adults rely more on RL to guide attention during multidimensional decision-making

To assess group differences in the trial-by-trial dynamics of learning, we fit eight different computational models to each participant's behavior. For both the simple and the multidimensional task, a hybrid model that incorporated elements from both RL and the statistically optimal Bayesian approach best predicted participants' choices. The model contains a balance parameter α, which regulates the interplay between RL and Bayesian learning in determining attention weights. The maximum-likelihood value of this parameter was close to zero for both age groups in the simple unidimensional RL task, suggesting that participants mainly relied on RL to guide attention and learning within the instructed dimension. This observation is in line with previous literature showing that RL models predict both human and nonhuman animal behavior in one-dimensional multiarmed bandits with high accuracy (Niv et al., 2012; Chowdhury et al., 2013; Eppinger et al., 2013).

Learning rate was the best predictor of average task performance in the control task, and average best-fit values of the learning rate parameter did not differ between age groups. In contrast, in the multidimensional learning environment, which required selective attention for optimal task performance, the best fit values for the balance parameter α were most predictive of overall task performance. Participants with higher values of α, which indicate more Bayes-optimal attention, achieved higher levels of performance. The average maximum-likelihood estimate of this parameter was also significantly lower in the group of older adults, suggesting that they relied on suboptimal RL processes to guide attention more than did the group of younger adults.

Interestingly, for both tasks, the average best-fit values for the inverse-temperature parameter of this hybrid RL/Bayes model were higher in the older than in the younger adult group. This indicates that older adults' lower performance is not simply due to more random behavior. Indeed, older adults' trial-by-trial choices were better aligned with the predictions of the model than were younger adults' choices.

Together, our computational modeling results indicate that simple RL processes, which are sufficient for learning in unidimensional environments without distractors, are largely spared in healthy human aging. However, learning in multidimensional environments, where efficient learning relies on executive control processes to focus attention on only the task relevant dimensions of the environment, is significantly affected by age. Although we cannot exclude the possibility that age-related deficits in general cognitive functions such as working memory affect performance in both our tasks (with the more modest decrease in performance in the simple reinforcement learning task not meeting significance), we note that our analyses showed that differences in model parameters explained variance in performance across participants above and beyond that explained by our measures of cognitive performance. Indeed, our model-based analysis suggests that older adults might use RL as a (less efficient) fallback strategy for directing attention, as indicated by their higher reliance on RL based predictions.

No age-related effects of prediction-error-correlated activity in nucleus accumbens

It has previously been suggested that age-related impairments in trial and error learning are related to a decline of dopaminergic functioning, and that this decline can result in a reduced correlation of nucleus accumbens activation with the prediction error signal (Schott et al., 2007; Cox et al., 2008; Chowdhury et al., 2013; Eppinger et al., 2013; Samanez-Larkin et al., 2014). In contrast, we observed a nonsignificant but numerically higher activation in the nucleus accumbens in older adults in both tasks. In conjunction with the behavioral results showing that younger adults rely more on attention-related processes during learning, this finding can be interpreted as supporting previous results on decreased involvement of the reinforcement learning system when cortical resources such as working memory support task execution (Collins et al., 2017). Alternatively, overall task performance indicates that older adults experienced the task as more challenging, and the observed activation pattern is in line with reports indicating that the ventral striatum is more sensitive to feedback in high effort tasks (Dobryakova et al., 2017).

Regardless of the interpretation of this directional result, the present experiment supports previous reports showing that aging-related effects on prediction-error related brain activity are either subtle or absent (Cox et al., 2008; Samanez-Larkin et al., 2010; Samanez-Larkin and Knutson, 2015; Lighthall et al., 2018).

DMN deactivation is lower in older adults and correlates with behavioral performance

To examine the neural correlates of attentional demands and compare them between age groups, we built a model-based regressor indicating how strongly attention is focused on each trial of the learning task. To most accurately depict trial-by-trial individual attentional demands in both groups, regardless of each individual's strategy, this regressor reflected both reinforcement-learning and Bayesian-learning derived attentional demands. For both age groups, it correlated positively with a network of brain areas that is commonly involved in tasks with high demands on executive control, including the IPS, dmPFC and dlPFC (Petersen and Posner, 2012). In parallel, we observed deactivations in the DMN. Areas of the DMN are commonly observed to be deactivated when external processing demands are high (Buckner et al., 2008), and aging has been associated with changes in functional connectivity in both attention networks and the DMN (Volkow et al., 2000; Tomasi and Volkow, 2012; Geerligs et al., 2015; Ferreira et al., 2016). Our results showed no significant age-related differences in activations within the attention network. However, deactivation within the DMN, including the angular gyrus and vmPFC, was significantly reduced in older adults.

These results were also supported by a model-free analysis that assumed that attentional demands are generally higher at the beginning of games than toward their end, when the game has been solved and learning has terminated. Younger adults showed a larger difference between DMN deactivation at the beginning compared with the end of games. This can be driven by a larger difference in the task demands between start and end of task for younger adults (e.g., due to learning more games or requiring less cognitive resources to choose the correct stimulus once the game is learned), or by a higher sensitivity of DMN deactivation to task demands in younger adults, or both. We additionally observed a negative correlation between fMRI activation in an independently defined ROI of the whole DMN with overall behavioral performance in older adults. Together, these results establish that the main age-related difference in neural activity in our task was in DMN activation, and this difference accorded with participants' behavior in the task. The more active their DMN during task performance, the worse their learning. It is important to note that we observed the correlation between DMN deactivation and behavioral performance specifically during the early trials of the game, when behavioral performance for all participants was still uniformly low. This suggests that the reported correlation is driven by a causal relationship between learning and DMN deactivation, rather than simply reflecting behavioral differences.

Conclusions

The results of the present experiment show that impaired behavioral performance of older adults in complex multidimensional learning tasks, such as are encountered in every day life, is not merely driven by an age-related deficit in reinforcement learning, but rather by the altered interplay between reinforcement learning and the attentional resources directing it. In our healthy sample of older adults, we did not observe deficits in simple unidimensional reinforcement learning, nor did we observe differences in neural signals underlying reinforcement learning. However, when learning in more challenging multidimensional environments, older adults relied more on reinforcement learning based processes than younger adults, while younger adults adopted strategies that are more in line with a statistically optimal Bayesian approach. Neurally, we observed less deactivation in the DMN in older adults, specifically during trials with high demand on attentional resources. Moreover, this deactivation within the DMN correlated with overall behavioral performance in the multidimensional task. Together, these results indicate that the observed learning impairments in older adults were not driven by a reduced efficiency within the reinforcement learning system itself, but are rather related to the executive control processes that direct reinforcement learning to operate on the currently important dimensions of the environment.