A Tutorial on Individual Participant Data Meta-Analysis using Bayesian Multilevel Modeling to Estimate Alcohol Intervention Effects across Heterogeneous Studies

Abstract

This paper provides a tutorial companion for the methodological approach implemented in Huh et al. (2015) that overcame two major challenges for individual participant data (IPD) meta-analysis. Specifically, we show how to validly combine data from heterogeneous studies with varying numbers of treatment arms, and how to analyze highly-skewed count outcomes with many zeroes (e.g., alcohol and substance use outcomes) to estimate overall effect sizes. These issues have important implications for the feasibility, applicability, and interpretation of IPD meta-analysis but have received little attention thus far in the applied research literature. We present a Bayesian multilevel modeling approach for combining multi-arm trials (i.e., those with two or more treatment groups) in a distribution-appropriate IPD analysis. Illustrative data come from Project INTEGRATE, an IPD meta-analysis study of brief motivational interventions to reduce excessive alcohol use and related harm among college students. Our approach preserves the original random allocation within studies, combines within-study estimates across all studies, overcomes between-study heterogeneity in trial design (i.e., number of treatment arms) and/or study-level missing data, and derives two related treatment outcomes in a multivariate IPD meta-analysis. This methodological approach is a favorable alternative to collapsing or excluding intervention groups within multi-arm trials, making it possible to directly compare multiple treatment arms in a one-step IPD meta-analysis. To facilitate application of the method, we provide annotated computer code in R along with the example data used in this tutorial.

1. Introduction

Individual participant data (IPD) meta-analysis is a methodological approach for generating large-scale evidence in medical research (Riley, Lambert, & Abo-Zaid, 2010; Simmonds, Stewart, & Stewart, 2015; Stewart et al., 2015) and the social and behavioral sciences (Mun, Jiao, & Xie, 2016; Mun & Ray, 2018). With IPD meta-analysis, an overall effect size estimate can be obtained in a simultaneous one-step analysis and advanced statistical models can be utilized to better accommodate study designs and outcome distributions. This tutorial provides a guide to using Bayesian multilevel modeling to combine multi-arm trials (i.e., trials where subjects are randomly allocated to two or more groups) in a distribution-appropriate IPD meta-analysis. A version of this modeling approach was implemented in Huh et al. (2015) to evaluate the efficacy of brief motivational interventions (BMIs) for college drinking and negative consequences. Here we provide an in-depth tutorial and rationale for the methods.

In this tutorial, we first introduce the motivating example data. Second, we review the challenges of combining multi-arm trials in an IPD meta-analysis and present the methods to estimate all within-study estimates of effect sizes when calculating an overall effect size (i.e., randomized group as opposed to study at the highest data level, comparing simulated posterior distributions estimated from Markov chain Monte Carlo [MCMC] methods). Third, we discuss how to address the methodological issues around zero-altered outcome measures, which are common in alcohol and substance use research. Finally, we show how to perform an IPD meta-analysis using Bayesian multilevel modeling and discuss the implications of our method for substantive research. Annotated R computer code with detailed explanations for fitting the models is available in an online repository along with example data (https://doi.org/10.17632/4dw4kn97fz.2; Huh, Mun, Walters, Zhou, & Atkins, 2019).

2. Motivating Example: The Project INTEGRATE data

Our example data are drawn from Project INTEGRATE (Mun et al., 2015), a large IPD meta-analysis project evaluating BMIs for college drinking. From the Project INTEGRATE data set, we selected 15 randomized controlled trials. Participants in each of these studies were randomized to a control group or one of three BMIs: (1) individually-delivered motivational interviewing with personalized feedback (MI+PF), (2) stand-alone personalized feedback (PF), or (3) group-based motivational interviewing (GMI). Three of the 15 studies had more than two treatment groups. The outcome measure was the average number of drinks on a typical drinking day, which was assessed using a version of the Daily Drinking Questionnaire (DDQ; Collins, Parks, & Marlatt, 1985). Non-integer numbers of drinks were rounded to the nearest whole number and if participants reported no drinking days, their alcohol consumption was coded as zero. The data set includes a total of 13,534 repeated measures from 5,952 individuals each with a baseline assessment and one to three follow-up assessments, up to 12 months post-baseline.

An IPD meta-analysis can be straightforward if studies share the same design features (i.e., participants, interventions, comparison groups, outcome measures, and settings). In practice, however, study designs typically vary between intervention trials. A key advantage of IPD meta-analysis over typical meta-analysis of aggregate data is that study-level differences can be explicitly addressed. In this tutorial, we focus on how to validly combine IPD from two-arm (e.g., intervention and control) and multi-arm trials (i.e., multiple intervention groups and a control group). A common challenge in meta-analysis is how to combine studies with imbalanced and/or varying numbers of treatments (Gleser & Olkin, 2009), a problem that also applies to IPD meta-analysis. Table 1 presents the study by treatment group combinations from our motivating example data. As illustrated in Table 1, only one study (study 9) has data from all four groups (i.e., MI+PF, PF, GMI, and control). The other studies have at least one group “missing” by study design.

Table 1.

Study by Treatment Combinations in Project INTEGRATE Subsample

Treatment Group (n)					Follow-up schedule (in months)	Reference(s)
Study	Control	MI+PF	PF	GMI
2	102	–	92	–	2	White and colleagues (2008)
7.1	22	–	–	75	1	Fromme and Corbin (2004)
7.2	110	–	–	217	1, 6	Fromme and Corbin (2004)
8a	519	–	512	–	12	Larimer and colleagues (2007)
8b	754	–	719	–	12	Larimer and colleagues (2007)
8c	147	–	127	–	12	Larimer and colleagues (2007)
9	91	87	92	86	3, 6	Lee and colleagues (2009)
10.1	157	150	–	–	12	Baer and colleagues (2001)
11	160	–	150	–	2, 3	Walters and colleagues (2007)
12	80	75	–	–	1, 3, 6	Wood and colleagues (2007)
13/14	24	54	27	–	3, 6, 12	Murphy and colleagues (2004)
						Murphy and colleagues (2001)
18	99	–	93	–	1, 6	Martens and colleagues (2010)
20	242	214	–	–	12	Larimer and colleagues (2001)
21	70	74	63	–	3, 6, 12	Walters and colleagues (2009)
22	240	228	–	–	12	Wood and colleagues (2010)

Note. MI+PF = Individually-delivered motivational interviewing with personalized feedback; PF = Stand-alone personalized feedback; GMI = Group motivational interviewing.

An initial, logical strategy for estimating treatment effects across multiple trials in a one-step IPD meta-analysis is to use a multilevel model (MLM) where study is defined at the highest level of the model (level 3), participants (level 2) are nested within study, and observations (level 1) are nested within participant. Assuming a normally distributed outcome, the 3-level MLM can be shown at each level:

$$\begin{array}{cc}\text{Level 1 (observation):}& {\text{OUTCOME}}_{tis}={\pi }_{0is}+e_{tis},\\ \text{Level 2 (participant):}& {\pi }_{0is}={\beta }_{0s}+{\beta }_{1s}{\text{MI\_PF}}_{is}+{\beta }_{2s}{\text{PF}}_{is}+{\beta }_{3s}{\text{GMI}}_{is}+r_{0is},\text{and}\\ \text{Level 3 (study):}& \begin{array}{c}{\beta }_{0s}=b_{00}+u_{0s}\\ {\beta }_{1s}=b_{10}+u_{1s}\\ {\beta }_{2s}=b_{20}+u_{2s}\\ {\beta }_{3s}=b_{30}+u_{3s}\end{array}\end{array}$$ (1a)

Equation 1a can also be expressed as a single equation, mixed model:

$$\begin{gathered} {\text{OUTCOME}}_{tis}=b_{00}+b_{10}{\text{MI\_PF}}_{is}+b_{20}{\text{PF}}_{is}+b_{30}{\text{GMI}}_{is}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{u}_{0s}+u_{1s}{\text{MI\_PF}}_{is}+u_{2s}{\text{PF}}_{is}+u_{3s}{\text{GMI}}_{is}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{r}_{0is}+e_{tis}, \end{gathered}$$ (1b)

where t indexes the assessment, i indexes individuals, and s indexes the study. At level 1, π_0is represents the average outcome level across assessments for participant i in study s, and e_tis is a within-participant residual error term. We assume that the observation-level (level 1) residual error term and participant-level (level 2) varying intercept coefficients (i.e., random effects) are each normally distributed with mean zero and a variance that is estimated from the data, while the four study-level (level 3) varying intercept (u_0s) and slope coefficients (u_1s, u_2s, and u_3s) are multivariate normally distributed with mean zero for each, and a covariance matrix that is estimated from the data, as seen in Equation 1c:

$$\begin{array}{cc}\text{Level 1 (observation):}& e_{tis}\sim \text{N}\left(0,{\sigma }_e^2\right),\\ \text{Level 2 (participant):}& r_{0is}\sim \text{N}\left(0,{\sigma }_{{\beta }_0}^2\right),\text{and}\\ \text{Level 3 (study):}& \left[\begin{array}{c}{u}_{0s}\\ u_{1s}\\ u_{2s}\\ u_{3s}\end{array}\right]\sim \text{N}\left(\left[\begin{array}{c}0\\ 0\\ 0\\ 0\end{array}\right],\left[\begin{array}{cccc}{\sigma }_0^2& {\sigma }_{10}& {\sigma }_{20}& {\sigma }_{30}\\ {\sigma }_{10}& {\sigma }_1^2& {\sigma }_{21}& {\sigma }_{31}\\ {\sigma }_{20}& {\sigma }_{21}& {\sigma }_2^2& {\sigma }_{32}\\ {\sigma }_{30}& {\sigma }_{31}& {\sigma }_{32}& {\sigma }_3^2\end{array}\right]\right)\end{array}$$ (1c)

MI_PF_is, PF_is, and GMI_is are dummy-coded variables (each coded 1) that indicate random allocation to MI+PF, PF, or GMI, respectively, compared to controls (all coded 0). The non-varying (i.e., “fixed”) intercept coefficient b₀₀ reflects the average outcome level for controls across all studies. The varying (i.e., “random”) intercept coefficient u_0s quantifies between-study variability surrounding b₀₀. The non-varying slope coefficients for the three interventions (b₁₀, b₂₀, and b₃₀) describe the average intervention effect sizes of MI+PF, PF, and GMI compared to controls, respectively, across studies. In contrast, the varying slope coefficients (u_1s, u_2s, and u_3s) quantify the study-specific deviations from their respective average intervention effects. Therefore, the study-specific intervention effect size of MI+PF can be decomposed to the average intervention effect for MI+PF across all available studies (i.e., b₁₀ = an average treatment effect for MI+PF) and the corresponding study-specific varying intercept coefficient (i.e., u_1s). This model formulation is ideal in the sense that it conceptually corresponds to a traditional random-effects meta-analysis model.

However, the MLM described above for an IPD meta-analysis would be rank deficient in the motivating example because of insufficient data to estimate the covariance matrix of the study-specific varying coefficients for each (i.e., the level 3 components in Equation 1c). Our motivating data has 15 studies at level 3 (see Table 1). The variances of the varying coefficients for treatment arm $\left({\sigma }_0^2,{\sigma }_1^2,{\sigma }_2^2,\text{and}\hspace{0.17em}{\sigma }_3^2\right)$ in Equation 1c can be estimated using available data from 15, 7, 9, and 3 studies, respectively, while there is sparse data coverage for ascertaining covariances (i.e., the off diagonals). The covariance σ₂₁ between MI+PF and PF can be estimated from three studies (studies 9, 13/14, and 21). However, it is impossible to estimate the covariance between GMI and MI+PF (σ₃₁) and GMI and PF (σ₃₂) since those treatments were evaluated together in just one study (study 9) and a minimum of two data points are needed to calculate a covariance. Consequently, the level 3 varying slope coefficients (i.e., the variance-covariance matrix in Equation 1c) cannot be estimated, nor the model as a whole. Without an alternative methodological approach, undesirable options for handling rank deficiency may include collapsing active intervention groups into a single, omnibus treatment category, removing one or more treatment groups, or constraining covariance parameters. None of these approaches are ideal.

To accommodate “missing” study by treatment combinations without compromising the original randomization, an alternative formulation of an MLM can be used in which the unique randomized groups (i.e., study by treatment arm combinations) are used as the highest level of the MLM instead of study under the assumptions that groups from the same study are orthogonal due to random allocation (i.e., there are no study by randomized group interaction effects) and that nonexistent study by treatment combinations are missing at random (see the Application section). This formulation of an MLM is conceptually equivalent to converting a 15 (study) by 4 (treatment arm) factorial design into an equivalent one-way design to allow for missing study by treatment combinations, where all the unique study by treatment combinations are defined as separate groups. This model set up can be extended further to accommodate informative covariates as fixed effects.

Through a Bayesian approach to MLM estimation, we can produce all the distributions for all estimates, including the varying coefficients. The resulting distributions can then be utilized to calculate means and confidence intervals for each intervention effect contrast. This is a key advantage of the Bayesian MLM compared with an MLM estimated with restricted maximum likelihood (REML), where the analyst has access to the point estimates and confidence intervals for estimated parameters, but not their complete distributions. We discuss the estimation of a Bayesian MLM and the calculation of intervention effect contrasts in greater detail later in the Application section. Before doing so, we discuss some of the unique features of alcohol consumption data that require consideration in an IPD meta-analysis.

3. Modeling Zero-altered Count Outcomes

In alcohol intervention research, outcome measures are often count or frequency variables, such as the number of drinks consumed per week or the number of days per week alcohol was consumed. Such outcome measures are typically highly skewed due to high frequencies of zeroes and are more appropriately modeled using count regression methods such as zero-inflated or hurdle regressions (Atkins, Baldwin, Zheng, Gallop, & Neighbors, 2013). With normally distributed outcomes, mean and variance are separate parameters. With count-distributed outcomes, there is a relationship between the mean and variance which can be complicated by additional heterogeneity (called over-dispersion) or an over-abundance of zeroes. In the Poisson generalized linear model, the most basic type of count regression, the mean is assumed to equal the variance. The negative binomial generalized linear model extends the Poisson by allowing the mean and the variance to differ from each other. In the Application section of this tutorial, we utilize the negative binomial model, which is functionally similar to the over-dispersed Poisson implemented in Huh et al. (2015), except that it handles over-dispersion implicitly.

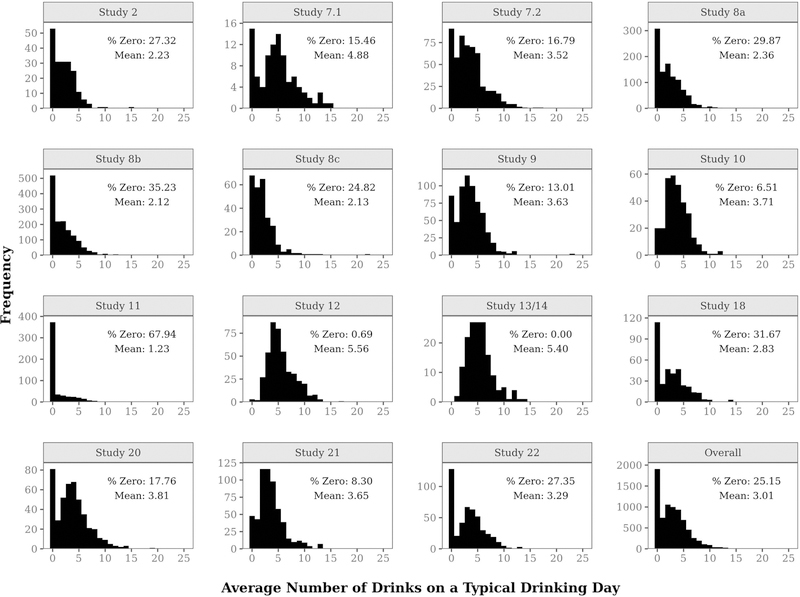
As shown in Figure 1, the outcome variable distribution in our example data – average number of drinks on a typical drinking day – is positively skewed with a high percentage of zeroes. Across studies, respondents reported drinking an average of 3.0 drinks per drinking day, with 25% reporting no drinking at all. In ten studies, the modal number of drinks per day was zero. Figure 1 also illustrates substantial between-study variability. The average number of drinks per drinking day varied from 1.2 to 5.6 across studies, and the percentage of no drinking varied from 0 to 68%. In study 13/14, the frequency of no drinking was zero since all participants had at least one drinking day with one or more drinks, during a typical week.

Figure 1.

Frequency distributions of post-baseline average number of drinks on a typical drinking day by study.

Count outcomes in which the number of zeroes is disjoint from the non-zero portion of the outcome are considered “zero-altered” relative to an ordinary count distribution. On a substantive level, however, the zeroes may represent a key feature of drinking behavior. For instance, the decision to have the first drink may be quite different than the decision to continue to drink after drinking has started. Consequently, a model that underrepresents the actual frequency of zeroes may not only violate statistical assumptions but also fail to capture an important aspect of drinking behavior. A hurdle model, a type of two-part model, assumes that a threshold must be crossed from zero into positive counts.

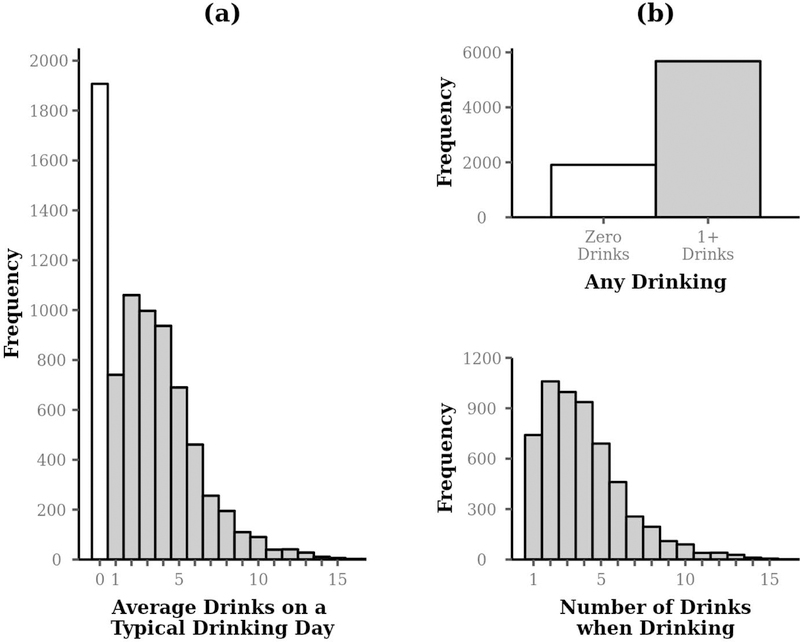
Figures 2a and 2b illustrate the zero-altered drinking outcome and how it can be divided into two respective outcomes, which are analyzed together in a multivariate model in this tutorial. One outcome is a dichotomous variable representing zero drinks vs. any drinking and includes the entire sample. The second outcome, highlighted in grey, represents the number of drinks if drinking is non-zero. Thus, the hurdle model contains two sub-models: 1) a logistic regression model for examining no drinking vs. any drinking (zero vs. non-zero; assessed as an odds ratio) and 2) a zero-truncated negative binomial model for positive counts (number of drinks when drinking; assessed as a rate ratio).

Figure 2.

Histogram of number of drinks in the motivating example data, drawn from Project INTEGRATE. The left column panel (a) illustrates the zero-altered count outcome and the right column panel (b) illustrates the division into corresponding dichotomous (examined as an odds ratio; top) and zero-truncated count (examined as a rate ratio; bottom) outcomes.

An alternative to the hurdle model is a zero-inflated model, a type of mixture model that assumes two types of zeroes: zero counts and “excess zeroes” above and beyond what would be predicted by an ordinary count distribution. Hence, the logistic regression in a zero-inflated model predicts these excess zeroes, and consequently, the count model includes zero counts and is not zero-truncated. In contrast, an advantage of hurdle models over zero-inflated models is that they are more straightforward to interpret because all zeroes and non-zero counts are handled in separate models, resulting in a clean distinction between zeroes and positive counts.

4. Application of a Bayesian Hurdle Model to the Project INTEGRATE Data

To retain all the original intervention groups, we used a Bayesian approach to MLM using MCMC sampling (for an accessible tutorial on MCMC estimation, see Hamra, MacLehose, & Richardson, 2013). MCMC is a simulation-based technique for estimating the parameters of a statistical model, including non-varying (i.e., fixed effect) coefficients, varying (i.e., random effect) coefficients, and variance parameters, by sampling from the probability distribution of the parameters, known as the “posterior distribution.” During MCMC estimation, each of the parameters in a Bayesian model is treated as part of a multidimensional space of distributions, and the goal of the MCMC algorithm is to “explore” that space by taking random samples from the distribution of each of the parameters.

The multilevel hurdle negative binomial model that incorporates a varying intercept coefficient for unique randomized groups can be seen in Equations 2a and 2b. The logistic portion of the hurdle model (Equation 2a) models whether an individual participant belonging to a specific randomized group drank at a particular assessment point. Let Pr[DRINKS_t>0,ig > 0] be the probability of individual i in randomized group g drinking one or more drinks at assessment t, and Pr[DRINKS_t>0,ig = 0] be the probability of individual i in randomized group g not drinking at assessment t. To constrain predictions to range from 0 to 1, the outcome is modeled as the natural logarithm of the odds (i.e., logit link function) of the probability of any drinking vs. no drinking, as follows:

$$\begin{gathered} \log \left(\frac{\text{Pr}\left[{\text{DRINKS}}_{t>0,ig}>0\right]}{\text{Pr}\left[{\text{DRINKS}}_{t>0,ig}=0\right]}\right)=b_{0\left(B\right)}+b_{1\left(B\right)}\left({\text{DRINKS}}_{t=0,ig}>0\right)+b_{2\left(B\right)}{\text{DRINKS}}_{t=0,ig}+b_{3\left(B\right)}{\text{MALE}}_{ig} \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}+b_{4\left(B\right)}{\text{MANDATED}}_{ig}+b_{5\left(B\right)}{\text{NONWHITE}}_{ig}+b_{6\left(B\right)}{\text{FIRSTYR}}_{ig}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{0.17em}{u}_{0g\left(B\right)}+r_{0i\left(B\right)}, \end{gathered}$$ (2a)

where (B) identifies regression coefficients from the logistic model. The zero-truncated negative binomial portion of the hurdle model (Equation 2b) models occasions where drinking did occur. Let (E[DRINKS_t>0,ig]|DRINKS_t>0,ig > 0) be the expected number of drinks when drinking was greater than zero for individual i in randomized group g at assessment t. To constrain predictions to positive counts greater than or equal to one, the outcome is modeled as the natural logarithm of the expected number of drinks (i.e., log link function), as follows:

$$\begin{gathered} \log \left(\text{E}\left[{\text{DRINKS}}_{t>0,ig}\right]|{\text{DRINKS}}_{t>0,ig}>0\right)=b_{0\left(C\right)}+b_{1\left(C\right)}\left({\text{DRINKS}}_{t=0,ig}>0\right)+b_{2\left(C\right)}{\text{DRINKS}}_{t=0,ig}+b_{3\left(C\right)}{\text{MALE}}_{ig}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}{b}_{4\left(C\right)}{\text{MANDATED}}_{ig}+b_{5\left(C\right)}{\text{NONWHITE}}_{ig}+b_{6\left(C\right)}{\text{FIRSTYR}}_{ig}+ \\ \hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{0.17em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}\hspace{1em}{u}_{0g\left(C\right)}+r_{0i\left(C\right)}, \end{gathered}$$ (2b)

where (C) identifies regression coefficients from the zero-truncated negative binomial model. The group-level varying intercept coefficients u_0g(B) and u_0g(C) in the logistic and zero-truncated negative binomial models, respectively, quantify the extent to which each randomized group differs from the covariate-adjusted average drinking outcome across groups. Similarly, the individual-level varying intercept coefficient r_0i(B) and r_0i(C) account for the variability surrounding the covariate-adjusted average drinking outcome across individuals in the drinking outcome for the two models, respectively. We assume that all varying coefficients in the logistic model (u_0(B) and r_0i(B)) and zero-truncated negative binomial model (u_0g(C) and r_0i(C)) are independently and normally distributed each with mean zero and corresponding variance that is estimated. In generalized linear models that utilize a link function, such as the logistic and zero-truncated negative binomial models, the outcome is a function of the mean of the linear predictor only, thus Equations 2a and 2b do not include a residual error term.

To accommodate varying numbers of follow-up assessments across studies, the outcome variable (DRINKS_t>0,ig) on the left-hand side of Equations 2a and 2b is limited to post-baseline assessments. Under this model specification, covariates are incorporated into both the logistic and zero-truncated negative binomial models to control for baseline drinking and demographic covariates related to alcohol consumption. The demographic covariates were gender (1 = men vs. 0 = women), race (1 = non-White vs. 0 = White), first-year student status (1 = first-year vs. 0 = non first-year), and mandated status (1 = mandated to intervention vs. 0 = volunteer). Baseline drinking (DRINKS_t=0,ig) was divided into two related covariates to account for: (1) no vs. any drinking and (2) the number of drinks for those who drank at baseline (second and third terms on the right-hand side of Equations 2a and 2b).

A key feature of Bayesian models is that a “prior” distribution must be specified for all estimated parameters. With respect to the multilevel hurdle model, the logistic and zero-truncated count portions of the model each require their own set of priors to be specified. The multilevel hurdle negative binomial model shown in Equations 2a and 2b requires prior distributions for (1) the non-varying intercept and slope coefficients for the covariates in each model, (2) the varying intercept coefficients (i.e., participants and randomized groups) in each model, and (3) an over-dispersion parameter in the zero-truncated negative binomial model. The varying intercept coefficients u_0g(B) and u_0g(C) are comprised of 34 pairs of group-specific intercepts (i.e., u_0,g=1(B), u_0,g=2(B), … , u_0,g=34(B) and u_0,g=1(C), u_0,g=2(C) … , u_0,g=34(C)), whose posterior distributions will be used to calculate intervention effect contrasts within studies. The 34 pairs of group-specific intercepts represent each of the 34 randomized groups, including active treatment (19) and control (15) groups. The 34 group-specific intercepts in each model share the same prior distribution, which is specified on the standard deviation (SD) of the varying intercept coefficient (u_0g(B) and u_0g(C)) as a whole.

In the present analyses, we use minimally-informative priors, which typically yield results comparable to those obtained from an MLM estimated with REML where the estimates are completely driven by the data. For the covariate effects on the outcomes, we used normal distributions with a mean of 0 and an SD of 1, which Gelman, Lee, and Guo (2015) suggest as a default prior for non-varying coefficients in regression models. For the SD of the varying intercepts, we used a half-Cauchy distribution with a mode of 0 and a shape parameter of 25, as suggested by Gelman (2006) for variance terms in multilevel models. For the over-dispersion parameter of the count portion of the hurdle model, we used a minimally-informative gamma distribution with shape and rate parameters of 0.01. These prior distributions are appropriate when all covariates in the model have been scaled (e.g., continuous variables that have been divided by their SD), standardized, or are on a unit scale, such as dichotomous indicator variables (i.e., 0 vs. 1). An important step in Bayesian analysis is to assess the consistency of the results under alternate prior selections. Thus, we conducted a sensitivity analysis under an alternative prior specification with larger variances using a normal distribution with a mean of 0 and an SD of 10 for the covariate effects and a half-Cauchy distribution with a mode of 0 and shape parameter of 50 for the SD of the varying intercept coefficients.

The output of a Bayesian analysis using MCMC sampling is a vector of simulated estimates for each parameter in the model, which can be plotted in a histogram to visualize the posterior distribution. To calculate the intervention effect summaries under the current MLM model specification, we use the vectors corresponding to the posterior distributions of the varying intercept coefficients for each randomized group (u_0(B), u_0g(C)) for the two outcomes, respectively.

The first step is to extract the posterior distributions of the varying intercept coefficients for all the 34 randomized groups (19 active treatment and 15 control groups) in both the logistic and zero-truncated count models. Table 2 shows how to use the posterior distributions to estimate a treatment effect size. There are a total of 2000 samples of each randomized group effect, each corresponding to a single simulated value from the posterior distribution. In the case of PF in Study 2, the intervention effect for the logistic model is calculated by taking the difference u_0,g=2(B) − u_0,g=1(B) for each row, as depicted in the third column of Table 2. This produces a vector of 2000 effect size estimates at the randomized group level (level 3), which can then be used to derive the study-specific intervention effect of PF in Study 2 and its corresponding 95% confidence interval (CI).

Table 2.

An Example Calculation of the Intervention Effect of Personalized Feedback in Study 2 based on the Posterior Distribution of the Varying Intercept Coefficient for Randomized Group

	Study 2
	Control	PF	Effect Size
Sample No.	u0,g=1(B)	u0,g=2(B)	u0,g=2(B) − u0,g=1(B)
1	0.923	0.388	−0.535
2	0.296	−0.218	−0.514
3	0.277	0.247	−0.030
⋮	⋮	⋮	⋮
2000	0.012	0.324	0.312

Note. Sample No. = Sample Number; PF = Personalized Feedback. The parameters u_0,g=1(B) and u_0,g=2(B) are the estimated varying intercept coefficients for randomized groups 1 (Study 2, Control) and 2 (Study 2, PF), respectively. There are 2000 simulated estimates for each of the varying intercept coefficients.

The intervention effects for all other active treatment groups are calculated in the same way by matching each active intervention group with its corresponding control group and calculating the difference within studies for study-specific intervention effects. This yields a total of 19 vectors of length 2000 for each portion of the hurdle model, representing the 19 treatment vs. control comparisons. Finally, an overall intervention effect (any intervention vs. control) can be derived by first averaging across all 19 vectors of treatment vs. control comparisons for each of the 2000 samples. This yields a vector of the same length (i.e., 2000) reflecting the posterior distribution of the overall intervention effect, which we subsequently summarize as a mean and its 95% CI. The mean of those 2000 simulated values would correspond to the point estimate for each model parameter (e.g., a varying intercept coefficient). The SD of those 2000 simulated values would correspond to the standard error of the parameter estimated using an REML approach.

5. Analysis of the Motivating Data and the Summary of Findings

Annotated computer code in R for fitting the model (for a general introduction to R, see Dalgaard, 2008), along with example data, can be accessed in the online repository (Huh et al., 2019). The analyses were performed in R version 3.4.4 (R Core Team, 2018) with version 2.50 of the brms (Bayesian Regression Models using ‘Stan’) package (Bürkner, 2017). The final model took 1.9 hours to estimate on a 3.4 Ghz Intel Core i7–3770-based system running Ubuntu Linux with 16 gigabytes of RAM. The Annotated Code contains technical information about the MCMC estimation and how MCMC convergence was assessed.

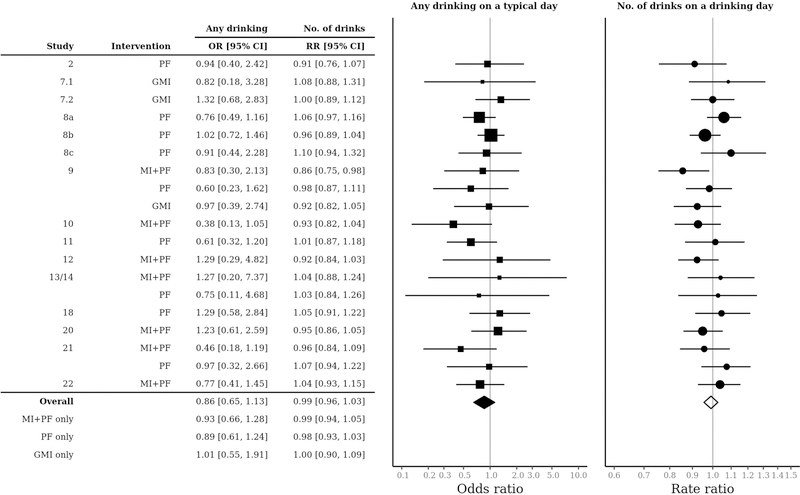
Figure 3 shows a forest plot of study-specific intervention effects on the probability of drinking (i.e., 1 = any drinking vs. 0 = no drinking) and number of drinks (i.e., mean drinks given any drinking) per drinking day. In logistic and zero-truncated negative binomial models, the non-varying (i.e., fixed effect) and varying (i.e., random effect) coefficients are on a natural log scale because of the log link function that relates the linear predictors (i.e., the right-hand side of Equations 2a and 2b) with the outcome variables. For interpretation, treatment effect estimates calculated from the logistic and zero-truncated negative binomial models are raised to the base e, to yield an odds ratio ORs and a rate ratio RRs, respectively. The distance above or below 1.0 can be interpreted as the percentage difference with respect to any drinking vs. no drinking ORs or the quantity of drinking when drinking is non-zero RRs for participants who received an intervention. ORs and RRs below 1.0 reflect lower likelihood of any drinking and lower levels of drinking (given any drinking), respectively, favoring the intervention group.

Figure 3.

Forest plot of intervention effects estimated from Equations 2a and 2b. OR = Odds ratio; RR = Rate ratio; MI+PF = Individually-delivered Motivational Interviewing with Personalized Feedback; PF = Stand-alone Personalized Feedback; GMI = Group Motivational Interviewing; No. of drinks = Number of drinks on a typical drinking day.

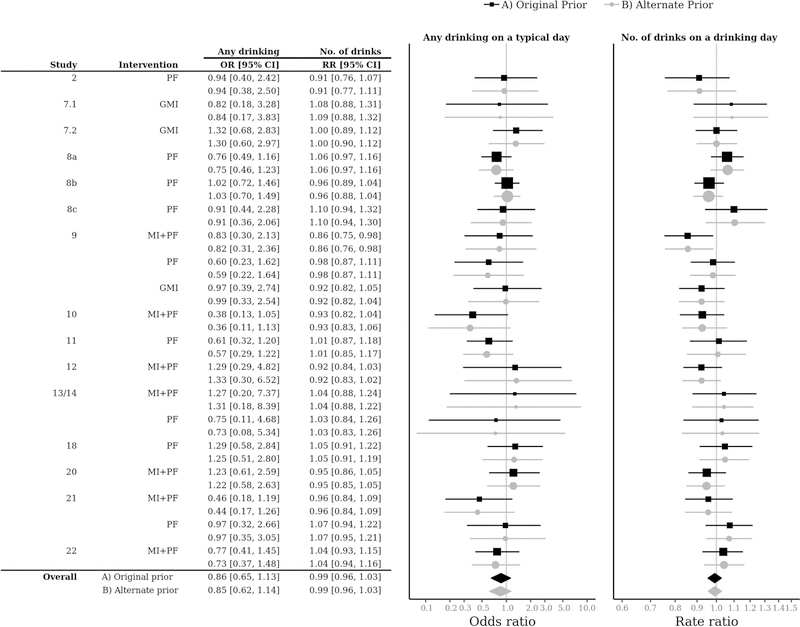
The overall OR of 0.86 for any drinking indicates that BMIs (MI+PF, PF, and GMI) were associated with a 14% difference in the odds of any drinking (OR = 0.86, 95% CI = [0.65, 1.13]), although the effect was not statistically significant as the 95% CI included an OR of 1.0. The overall RR of 0.99 for drinking quantity indicates that BMIs were associated with a 1% difference in the quantity of drinking when drinking (RR = 0.99, 95% CI = [0.96, 1.03]), an effect that was also not statistically significant. Intervention effects on the probability of any drinking varied by study from an OR of 0.38 to 1.29, with 13 of 19 intervention groups having point estimates indicating lower likelihood of any drinking relative to control. Intervention effects on the number of drinks when drinking also varied by study from an RR of 0.86 to 1.10, with 9 of 19 intervention groups with point estimates indicating lower quantity of drinking (when drinking) relative to control. However, none of these intervention effects was statistically significant, with one exception (study 9, MI+PF) in the quantity of drinking. Figure 4 shows that a sensitivity analysis using an alternative prior specification with much larger variances produced similar estimates, indicating that the results were robust to the choice of prior.

Figure 4.

Forest plot of sensitivity analysis with two different prior specifications. OR = Odds ratio; RR = Rate ratio; MI+PF = Individually-delivered Motivational Interviewing with Personalized Feedback; PF = Stand-alone Personalized Feedback; GMI = Group Motivational Interviewing; No. of drinks = Number of drinks on a typical drinking day. The “Original prior” estimates correspond with the minimally-informative priors used in the estimates reported in Figure 3; the “Alternate prior” estimates correspond with an alternative prior specification with larger variances on the covariate effects [Normal(0, 10)] and the standard deviations of all varying intercept terms [half-Cauchy(0, 50)].

6. Discussion

This tutorial describes how Bayesian MLM with MCMC estimation can be used to combine IPD from heterogeneous studies that are imbalanced and have varying numbers of treatment arms without loss of information while accounting for other important characteristics of the data, such as nested design and zero-altered count outcomes. The approach detailed can also be used without modification when studies have the same number of treatment arms. We show how to calculate effect size summaries for intervention types (e.g., MI+PF, PF, and GMI) and specific studies, as well as overall effect sizes within a single analytic model. The basic model we detail can be easily applied to zero-altered count outcomes in other applications.

A minor drawback to our approach is that it is more computationally intensive than models estimated using REML. However, advances in computing power will continually reduce the processing burden of Bayesian estimation approaches to IPD analysis. Of note, McNeish and Stapleton (2016) found that Bayesian MLMs performed well with as few as four clusters; in contrast, confidence intervals in REML-estimated MLMs were biased with as few as ten clusters, suggesting the utility of Bayesian estimation approaches for small-scale meta-analyses. Meta-analyses of five or fewer studies (clusters) are relatively common, making up nearly three-quarters of meta-analyses in the Cochrane Database of Systematic Reviews (Davey, Turner, Clarke, & Higgins, 2011).

It is important to note that our approach relies on several important assumptions. One assumption is that we conceptualized a full design that potentially includes a total of 60 treatment by study combinations (up to 15 studies, each with up to four intervention groups), of which we had observed data only from 34 groups (19 active interventions, 15 control groups). We assumed that the remaining 26 study by treatment combinations were missing by design and missing at random, and therefore did not bias estimates of the intervention effects that were observed.

Second, using randomized groups as the highest data level assumes that the groups are independent within study due to random allocation. We believe this is a reasonable assumption for this analysis since it is conceptually equivalent to converting the 15 (study) by 4 (treatment arm) factorial design to an equivalent one-way design to allow for missing study by treatment combinations. This parallels the conversion of a factorial ANOVA into an equivalent one-way ANOVA.

A final assumption, which applies to IPD meta-analysis generally, is that the outcome variable, interventions, and comparison groups should be equivalent across studies, so that the differences in the estimates across studies are not due to measurement differences or that estimates are not confounded by other study-level differences. Since the alcohol use quantity measure was similar across studies, and interventions and comparison groups were carefully selected for their equivalency across studies and subsequently coded and analyzed in Project INTEGRATE (Mun & Ray, 2018; Ray et al., 2014), we believe that this was a reasonable assumption.

The present tutorial provided an in-depth walkthrough of the challenges in an IPD meta-analysis and illustrates a feasible and flexible approach for combining IPD from heterogeneous studies that leverages all available information while accommodating common differences in study design and count outcomes with many zeroes, which are common in addictions research. The annotated R code and data further provide additional guidance, which we hope will motivate further development in IPD meta-analysis methodology and applications.