Abstract
The isotropic or anisotropic organisation of biological extracellular matrices has important consequences for tissue function. We study emergent anisotropy using fibroblasts that generate varying degrees of matrix alignment from uniform starting conditions. This reveals that the early migratory paths of fibroblasts are correlated with subsequent matrix organisation. Combined experimentation and adaptation of Vicsek modelling demonstrates that the reorientation of cells relative to each other upon collision, plays a role in generating matrix anisotropy. We term this behaviour cell collision guidance. The transcription factor TFAP2C regulates cell collision guidance, in part by controlling the expression of RND3. RND3 localises to cell-cell collision zones where it locally down-regulates actomyosin activity. Without this mechanism in place cell collision guidance fails leading to isotropic matrix generation. Cross-referencing alignment and TFAP2C gene expression signatures against existing datasets enables the identification and validation of several classes of pharmacological agents that disrupt matrix anisotropy.
Introduction
The extracellular matrix (ECM) is a scaffold of fibrillar proteins and proteoglycans that maintains the structure of tissues. The composition and organisation of the ECM is diverse and tailored to the function of the tissue, with tendons containing highly aligned ECM suitable for transmitting tensile forces and neural tissue containing looser more isotropic matrix lattices that enable neuronal connections1. In pathological contexts the ECM can undergo remodelling; a progressive transition to ECM anisotropy occurs in many cancers and ECM alignment is negative prognostic factor2–5. Aligned ECM fibres correlate with increased tissue stiffness and generate tracks for the invasion of tumour cells4,6–10.
The primary mediators of ECM deposition and maintenance are fibroblasts. In a landmark study, Abercrombie described the ability of fibroblasts to interact with and influence neighbouring cells via Contact Inhibition of Locomotion (CIL), which involves repolarisation and changing direction upon contact11,12. This behaviour depends on actomyosin contractility at the point of cell-cell contact and plays a role in tissue patterning13–18. The emergence of anisotropy has been studied in physical systems, including liquid crystals and the packing of elongated objects that lack independent motility19–21. Several models have additionally considered self-propelled particles and inelastic collisions between particles. In these models, collision properties influence alignment, but these models lack the complex biological signalling that determines cell collision behaviour 22,23,24,25. Duclos et al., and Li et al., have directly investigated the alignment of fibroblasts26,27. Both studies concur with the work of Abercrombie that fibroblasts can spontaneously align and further demonstrate fibroblast alignment with rigid boundaries. Li et al., attribute the higher order alignment to communication between fibroblasts via the ECM, while Duclos et al., observe that following mitosis daughter cells have similar orientation, thus as cells proliferate they form locally ordered regions.
Here, we combine long term imaging, computational modelling, transcriptomic analysis, siRNA, and informatics-based pharmacological screening to identify molecular regulators of fibroblast and ECM alignment. This leads to the identification of a collective behaviour of fibroblasts, which we term cell collision guidance.
Results
Characterising variation in matrix alignment
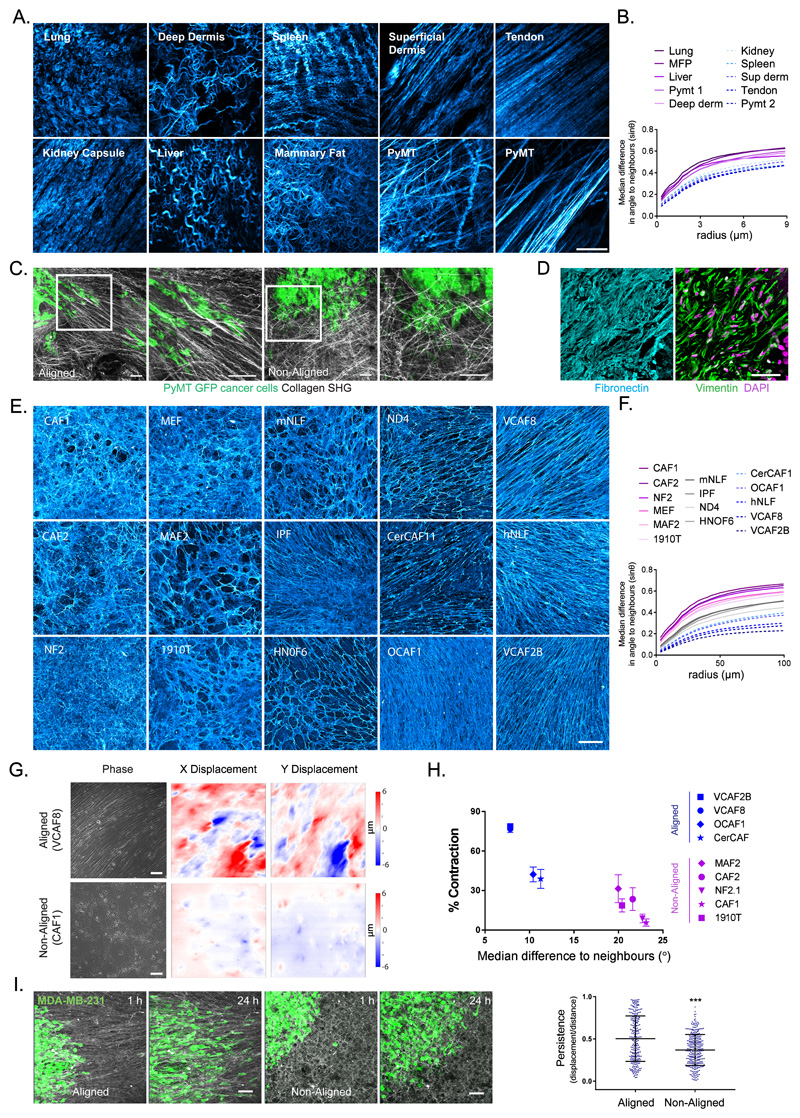
Imaging of collagen fibres confirmed the diversity of ECM organisation in vivo (Figure 1a). Measurement of the difference in angle between a fibre and its’ neighbours enabled the quantification of matrix alignment - small differences in angles indicated high matrix alignment (Figure 1b). In accordance with visual impression, tendons and superficial dermis had smaller differences in fibre angle relative to other tissues. Greater matrix alignment was seen in murine mammary tumours compared to normal tissue, however the extent of alignment varied between regions. Consistent with prior observations, the organisation of invasive breast cancer cells correlated with the dominant direction of matrix alignment (Figure 1c)4,10. Analysis of fibronectin in normal and cancerous human tissue also indicated higher ECM alignment in cancerous tissue with fibroblasts aligned in the same direction as matrix fibres (Figure 1d, Supplementary Figure 1a).
Figure 1. Extracellular matrix anisotrophy instructs cancer cell migration and enables the global co-ordination of force.
A. Collagen organisation in murine tissues imaged by second harmonic imaging (scale bar 20μm, representative image of 3 samples shown). B. Quantification of fibre alignment by median difference in angle to neighbours (sinθ) over expanding neighbourhoods (radii in μm). Higher values indicate greater disorder (images in A shown). C. Invasive patterns of PyMT-GFP tumour cells in aligned vs non-aligned collagen (visualised by second harmonic imaging - grey) (scale bar 100μm, representative images of three fields of view from two independent experiments shown). D. Human squamous cell carcinoma stained for fibronectin (cyan), vimentin (green) and DAPI (magenta) (scale bar 50μm, representative images from 6 individual samples). E. Panel of fibroblast derived matrices (FDMs) stained for fibronectin (cyan) (scale bar 100μm, representative images from three independent experiments shown). F. Quantification of ECM alignment of individual images in E. G. Traction force microscopy of aligned (VCAF8) and non-aligned (CAF1) fibroblasts at confluence, showing bright-field phase imaging of cell body organisation and substrate displacement in both x and y (scale bar 100μm, representative images of 5 fields of view from 2 independent experiments shown). H. Correlation analysis of collagen gel contraction with alignment metric (n=52 in total, from 2 independent experiments, mean and standard error of the mean (SEM) shown. Two tailed Pearson correlation test, r = -0.9187, p value= 0.0002). I. Migration of MDA-MD-23-GFP cells (green) on aligned (VCAF8 derived) or non-aligned (CAF1 derived) matrices over 24 hrs (scale bar =100μm, representative images from 3 independent experiments). Tumour cell persistence (displacement/distance) over 12 hr intervals (n=547 cells in total from 3 independent experiments, p<0.0001, two tailed unpaired t-test, bars indicate mean and standard deviation (SD)).
To understand how matrix anisotropy arises de novo we observed the emergence of order from an initial system of randomly orientated fibroblasts. We assembled a panel of fibroblasts from both normal and cancerous tissue and performed fibroblast-derived matrix assays. This panel of fibroblasts exhibited an array of matrix phenotypes; from isotropic (NF2, CAF1, MAF2) to highly anisotropic (OCAF1, VCAF2, VCAF8) (Figure 1e, quantification Figure 1f). Scanning electron microscopy and collagen staining confirmed that the pattern of fibronectin staining was indicative of the organization of other matrix components (Supplementary Figure 1b&c). Cancer-associated fibroblasts (CAFs) typically generated anisotropic ECM, although the dichotomy between normal and CAF behaviours was not absolute. We selected representative examples of fibroblasts that generate isotropic and anisotropic matrices for more detailed analysis (Supplementary Figure 1d). Traction force microscopy revealed that matrix deformation by aligning fibroblasts (VCAF8), but not non-aligning fibroblasts (CAF1), was coordinated over large areas (Figure 1g and Supplementary Figure 1e). This analysis was supported by gel contraction assays in which forces exerted by fibroblasts can generate millimetre scale contraction of polymerized collagen (Figure 1h). The difference in matrix contraction could not be attributed to intrinsic differences in actomyosin activity as there was no correlation with phosphorylated MYL9/MLC2 (P-MLC) levels nor traction forces exerted by individual cells (Supplementary Figure 1f & g). These data demonstrate that the alignment of fibroblasts enables the forces generated by individual cells to be productively coordinated leading to large matrix deformations. In agreement with previous findings, aligned ECM instructed the persistent migration of MDA-MB-231 cancer cells (Figure 1i). Thus, the alignment of ECM by fibroblasts has important consequences for macro-scale matrix remodelling and cancer cell migration6,4,7,8,9,28.
Analysis of emergent anisotropy in fibroblast cultures
To understand the emergence of alignment we combined time-lapse imaging with staining for the ECM. As fibroblasts migrate they leave behind small fibronectin fibrils that are oriented in the direction of motion, suggesting that migratory behaviour would be predictive of matrix organisation (Figure 2a and Supplementary Figure 2a). Week long imaging confirmed that the orientation of cells at high confluence is predicted by the migratory paths of cells in the preceding days. Further, cell alignment, and by extension matrix alignment, occurs prior to confluence and at cell densities that correspond to those observed in human tissues (Figure 1d, Figure 2b, Supplementary Figure 2b and Supplementary Video 1).
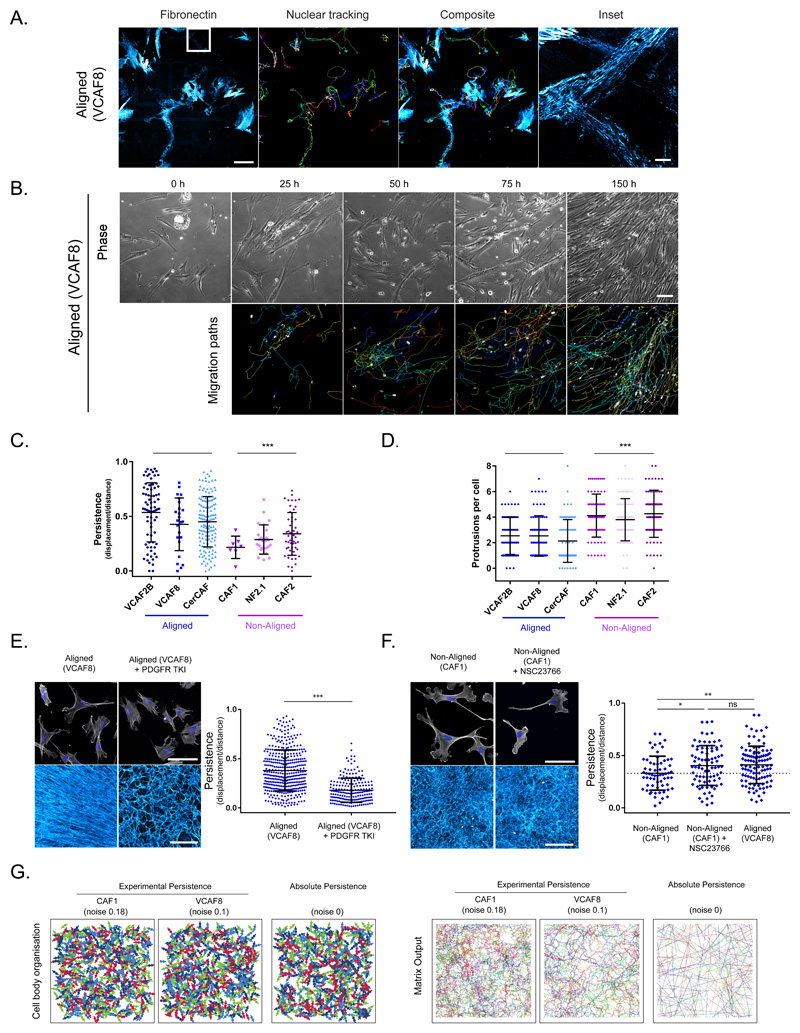
Figure 2. Aligned fibroblasts demonstrate higher intrinsic polarity and migratory persistence, but this is insufficient to drive alignment.
The migratory behaviour of fibroblasts determines their ultimate organisation. A. Correlative time-lapse microscopy of aligning (VCAF8) fibroblasts with nuclear tracking showing correlation of migration path with deposited fibronectin (cyan) over 16 hrs (representative images of 3 fields of view from 2 independent experiments shown). B. Time-lapse microscopy of aligning (VCAF8) fibroblasts over 7 days, showing bright field phase imaging and nuclear tracking. Migration paths of the previous 25 hrs are shown (representative images of 3 fields of view from 3 independent experiments shown). C. Persistence analysis (displacement/distance) over 16 hr intervals (n= 322 cells from 2 independent experiments, p<0.0001 two-tailed unpaired t-test, bars indicate mean and SD). D. Analysis of protrusions per cell (n=599 cells from 2 independent experiments, p<0.0001 two-tailed unpaired t-test, bars indicate mean and SD). E. Aligning VCAF8 stained for F-actin and DAPI, and their FDMs when treated with or without 100nM PDGFRi (representative images of 3 samples from two independent experiments). Persistence analysis of aligning VCAF8 with or without 100nM PDGFRi over 16 hr intervals (n=609 cells in total, p<0.0001 two-tailed unpaired t-test, bars indicate mean and SD). F. Non-aligning CAF1 stained for F-actin (white) and DAPI (blue) or fibroblast derived matrix (cyan) with or without 20μM NSC23766 treatment (representative images of 3 samples from two independent experiments). Persistence analysis of non-aligning CAF1 with or without NSC23766, compared to aligning VCAF8 over 16 hr intervals (n=249 cells from two independent experiments. CAF1 vs CAF1+NSC, p=0.0154, CAF1 vs VCAF8, 0.0041, CAF1+ NSC vs VCAF8, p=0.8112, two-tailed unpaired t-test, mean and SD are shown). G. Cell body and matrix organisation model outputs are shown with varying noise/persistence. Panels show persistence fitted to experimental data (noise: 0.1, aligned VCAF8, noise:0.18, non-aligned CAF1) as well as absolute persistence (noise:0) (representative images from 10 independent simulations shown).
Having established the link between migratory behaviour and ECM pattern, we investigated if cell morphology and motility parameters might correlate with ECM pattern. Fibroblasts that generate anisotropic matrices had higher migratory persistence than those that generate isotropic matrices (Figure 2c), which correlated with decreased numbers of multidirectional protrusions (Figure 2d). No correlations between anisotropic ECM generation and cell area, aspect ratio, or proliferation rate were observed (Supplementary Figure 2c-e.). We directly explored the linkage between persistence and anisotropic matrix generation using a PDGFR inhibitor. This reduced migratory persistence and ECM alignment (Figure 2e). In parallel, we increased the migratory persistence of non-aligning cells using intermediate Rac inhibition to suppress lateral protrusions29. Figure 2f and Supplementary Figure 2f shows that this increased persistence and reduced protrusions to the range of aligning VCAF8; but, crucially, it did not increase ECM anisotropy. These data indicate that migratory persistence is necessary, but not sufficient to confer higher order ECM patterning.
To explore what might be required to generate aligned ECM, we established a computational model inspired by the Vicsek model30. The model included elongated migratory cells that laid down matrix as they moved. Migratory persistence was controlled by varying the noise term that specifies the change in migration vector between time steps. We parameterised the noise term to measurements of cell migration (non-aligning CAF1: noise=0.18, aligning VCAF8: noise=0.10) and found that the elevated persistence of aligning cells was insufficient to drive alignment (Figure 2g). Even absolute persistence did not lead to anisotropic ECM. We therefore sought to identify additional mechanisms that might explain the emergence of alignment.
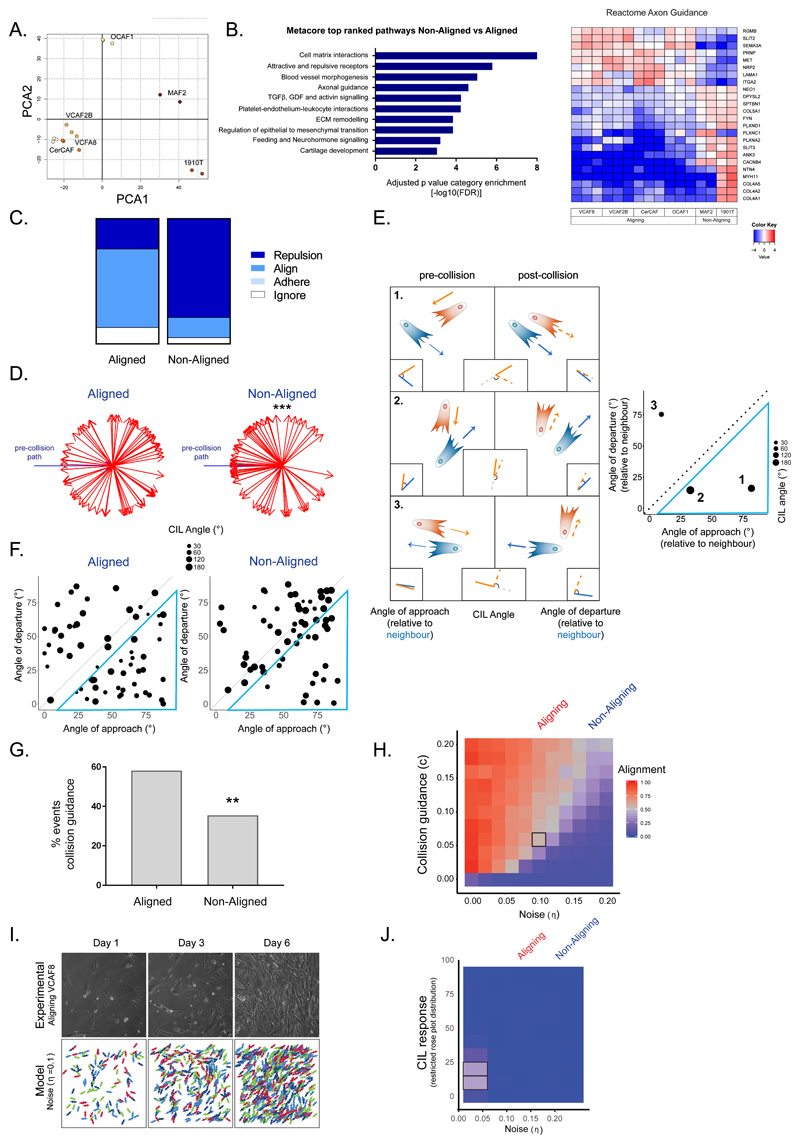
To understand better factors influencing anisotropic matrix production, we performed transcriptomic analysis. This confirmed that the fibroblasts were negative for epithelial, endothelial, and leukocyte markers and showed varying expression of fibroblast activation markers31,32,33 (Supplementary Figure 3a). Principal component analysis (PCA) revealed that the first component effectively discriminated between aligning and non-aligning fibroblasts (Figure 3a). Further analysis identified 574 genes whose expression correlated with the aligning phenotype of fibroblasts (Supplementary Figure 3b), suggesting a strong transcriptional link to the matrix anisotropy phenotype. These included ECM components (Supplementary Figure 3c) and, more intriguingly, genes involved in axonal guidance between aligning and non-aligning cells (Figure 3b and Supplementary Figure 3d). As axon growth cone migration is guided by cell–cell contact signals12,, we hypothesized that a key difference between aligning and non-aligning fibroblasts might be their re-orientation following collisions.
Figure 3. Aligned fibroblasts show supressed contact inhibition of locomotion and elevated collision guidance.
A. Principal component analysis showing segregation of fibroblast RNAseq data (n=16 from 3 independent experiments). B. Top differentially regulated Metacore pathways are shown together with heatmap of reactome axon guidance genes. Fold change is shown in log2 scale (n=16 from 3 independent experiments, Benjamini Hochberg adjusted p-values, two-sided). C. Quantification of cell collisions in aligning fibroblasts (VCAF8 and VCAF2B) and non-aligning fibroblasts (CAF1, NF2.1 and CAF2) as either repulsion, alignment (collision guidance), adhere or ignore (n=124 collisions from three independent experiments). D. Analysis of CIL response in aligned (VCAF8, VCAF2B) and non-aligned (CAF1, NF2.1, CAF2) fibroblasts. Change in cell trajectory upon collision relative to the pre-collision path (blue arrow). (n=90 collisions from three independent experiments. p=5x10-5, one-sided t-test). E. Schematic of collisions between two cells. CIL is indicated by the repolarisation of the cell, relative to its pre-collision trajectory (angle between orange and orange-dashed line. Collision guidance is assessed by comparing the angle of approach (angle between orange and blue line) and departure, relative to its neighbour (angle between orange-dashed and blue line). Plot of example collisions. Diameter of dot indicates the strength of the repolarisation/CIL response. Collisions inside blue triangle reflect collision guidance events (departure angle is more than 10 degrees smaller than approach angle). F. Analysis of collision angles in aligned (VCAF8, VCAF2B) and non-aligned (CAF1, NF2.1, CAF2) fibroblasts. Collisions inside blue triangle reflect collision guidance events (n=124 collisions from two independent experiments). G. Quantification of collision guidance events (n=124 collisions from two independent experiments. p= 0.006, one-sided z-test). H. Model exploration of alignment as noise and collision guidance are co-varied. Text above indicates noise values fitted to experimental data for aligning (VCAF8, noise =0.1) and non-aligning (CAF1, noise=0.18) fibroblasts. Each square is the average of 10 independent simulations. I. Comparison of experimental alignment against model simulation with experimental persistence of VCAF8 (noise=0.1) and collision guidance=0.06 (indicated by black square in 3H). Experimental panels show bright field time-lapse microscopy of aligning VCAF8. Model panels show simulation of cell body organisation J. Model exploration of alignment as only CIL response and noise (persistence) are co-varied. Text above indicates noise values fitted to experimental data for aligning (VCAF8: noise =0.1) and non-aligning (CAF1: noise=0.18) fibroblasts. Each square is the average of 10 independent simulations.
Cell collision behaviour influences fibroblast and matrix alignment
To explore whether collision behaviour is linked to the early emergence of anisotropic ECM, we analysed cell collision. Manual classification of cell collisions revealed clear differences between aligning and non-aligning fibroblasts (Figure 3c), and contact inhibition analysis confirmed the increased CIL in non-aligning fibroblasts (Figure 3d). The alignment of cells or matrix is a relative property between two cells or matrix fibres; however conventional analysis of contact inhibition does not capture this information, only the change in direction of one cell. Therefore, we developed a more comprehensive framework for analysing collisions. The angle of approach and departure relative to a neighbouring cell, as well as the CIL angle were recorded (Figure 3e). Figures 3f & g show a clear difference between aligning and non-aligning fibroblasts, with points in the lower right sector representing a closer alignment of cell orientation following collision (visible as small circles inside blue triangle in Figure 3f and quantified in 3g). We term this behaviour ‘cell collision guidance’, as distinct from contact guidance in response to an underlying substrate or external hard boundary 34,35. In the majority of collisions, the cell that underwent the greater change in orientation (termed ‘submissive’) displayed a higher pre-collision speed, which highlights the difference between biological systems and expected behaviour based upon the principles of mechanics. This analysis led us to focus on the hypothesis that cell collision guidance underpins anisotropic matrix generation.
The emergent pattern generated by cells with varying persistence and contact behaviour is not intuitive, therefore we turned to our computational model and added a term that controlled the change in migration vector following collision. This could be implemented in two ways: first, so that cells more closely resemble the orientation of their neighbours, reflecting collision guidance, or, secondly, a repolarisation vector upon collision, to reflect CIL. The implementation of cell collision guidance alone greatly increased the ability of cells with intermediate persistence to generate alignment (Figure 3h). Graphical output revealed the qualitative similarity between our model and experimental data (Figure 3i). In line with work from Duclos et al., interaction with a solid boundary led to fibroblast alignment along the boundary that decayed as a function of distance from the boundary 27 (Supplementary Figure 3f). Further analysis indicated that cells with a noise level = 0.1 (similar to VCAF8) can generate aligned matrices if they also exhibit cell-cell collision guidance, but that there is a threshold level of persistence below which cells cannot align, regardless of the amount of collision guidance (Figure 3h). Interestingly, non-aligning fibroblasts (noise=0.18) fall in this category. Suppression of CIL alone was inefficient at generating anisotropic matrices (Figure 3j) and combining cell collision guidance and CIL revealed that CIL could antagonise emergent alignment (Supplementary Figure 3g).
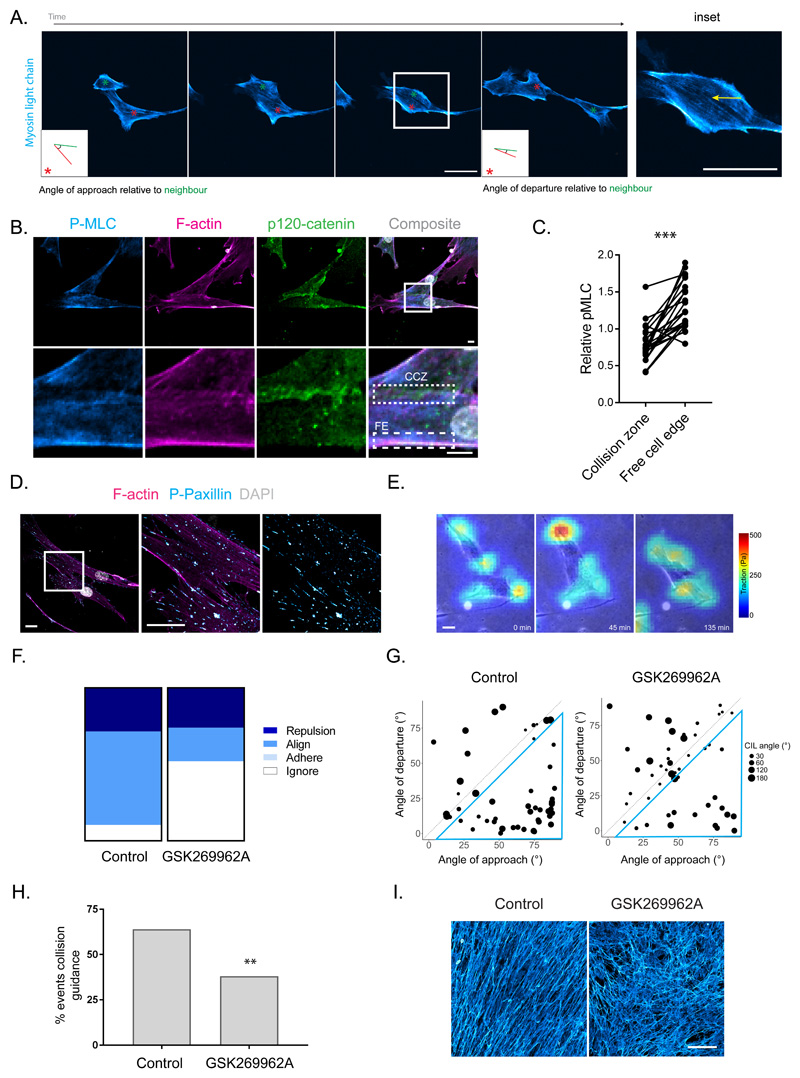
Having established that cell collision guidance can promote anisotropic fibroblast organisation, we investigated cytoskeletal changes occurring when aligning fibroblasts undergo collision guidance. This revealed that contractile actomyosin cables were suppressed near the contact zone between cells undergoing collision guidance and moving past one another in a nematic fashion (Figure 4a –yellow arrow, Supplementary Videos 2 and 4). This contrasts to collision with an inert physical boundary in which high MLC is maintained along the area of contact (Supplementary Figure 4a). In the rare cases of CIL, high F-actin and MLC were observed at the contact zone coincident with repolarisation (Supplementary Video 3 – only one cell expresses labelled MLC). Analysis of cell collision zones in fixed cells confirmed the down-regulation of pS19-MLC at cell collision zones (CCZ) compared to the free edge (FE) of fibroblasts (Figure 4b & c). Consistent with this, traction force analysis revealed low levels of force exerted on the underlying matrix at cell-cell interfaces even though paxillin containing adhesions persisted (Figure 4d & e). Depletion of focal adhesion components or perturbation with the ability to generate matrix fibres did not prevent fibroblast alignment (Supplementary Figure 4b & c), suggesting that cell matrix adhesions do not instruct the anisotropic arrangement of fibroblasts. CCZ were also characterized by the presence of p120-catenin, suggesting the transient formation of adherens junctions during cell-cell collisions (Figure 4b).
Figure 4. Collision guidance entails the suppression of actomyosin contractility at cell:cell contacts.
A. Time-lapse imaging of MLC-GFP (cyan) in aligning fibroblasts (VCAF2B) during collision guidance. Metrics for collision guidance (angle of approach and departure relative to neighbour) are shown in boxed inlay. (Representative images from three independent experiments shown). B. Immunofluorescence of pS19-MLC (cyan), p120-catenin (green) and F-actin (magenta) in aligning VCAF8 (scale bar 10μm). CCZ – Cell-cell Collision Zone, FE – Free Edge (representative images from three independent experiments shown). C. Paired measurements of pS19-MLC at cell-cell collision zones vs free edge in cells. Data are normalised to cell body pS19-MLC (n=46 in total from three independent experiments, p<0.0001 two-tailed Wilcoxon matched-pairs signed rank test). D. Immunofluorescence of p-paxillin (cyan) and F-actin (magenta) in aligning VCAF8 (scale bar 20μm, representative images from three independent experiments shown). E. Overlaid traction force (false colour – red = high traction, cyan = low traction) and phase contrast (gray) images of VCAF8 undergoing collision guidance (scale bar 10μm, representative images from two independent experiments shown). F. Fibronectin stained FDMs from aligning (VCAF8) fibroblasts with or without ROCKi treatment (GSK269962A 20nM, scale bar 100μm, representative images from three independent experiments shown). G. Quantification of cell collisions in aligning fibroblasts (VCAF8) as either repulsion, alignment (collision guidance), adhere or ignore, with or without ROCKi treatment (n=100 collisions from two independent experiments). H. Analysis of collision guidance using the angle of approach (x axis) and departure (y axis) relative to the cell it collides with. Collisions in which angle of departure < angle of approach (inside blue triangle) reflect collision guidance events. Radius of dot indicates the CIL angle (n=100 collisions from two independent experiments). I. Quantification of collision guidance events in the presence of absence of ROCKi treatment (Collision guidance classified as collisions where angle of approach – angle of departure is between 10-90°, n=100 collisions from two independent experiments, p= 0.005, one-sided z-test).
The data described above suggest that the Rho-ROCK-MLC pathway might play a role in cell collision guidance. ROCK inhibition increased migratory persistence (Supplementary Figure 4d) while simultaneously altering collision behaviour, with cell protrusions frequently moving over one another, instead of changing direction (classified as ‘ignore’ – Figure 4f), and a reduction in cell collision guidance (Figure 4g & h). The overall result was a strong reduction in ECM alignment (Figure 4i). These data argue that coordinated regulation of actomyosin contractility is critical for cell collision guidance.
TFAP2C-dependent transcription regulates cell collision behaviour and matrix anisotropy
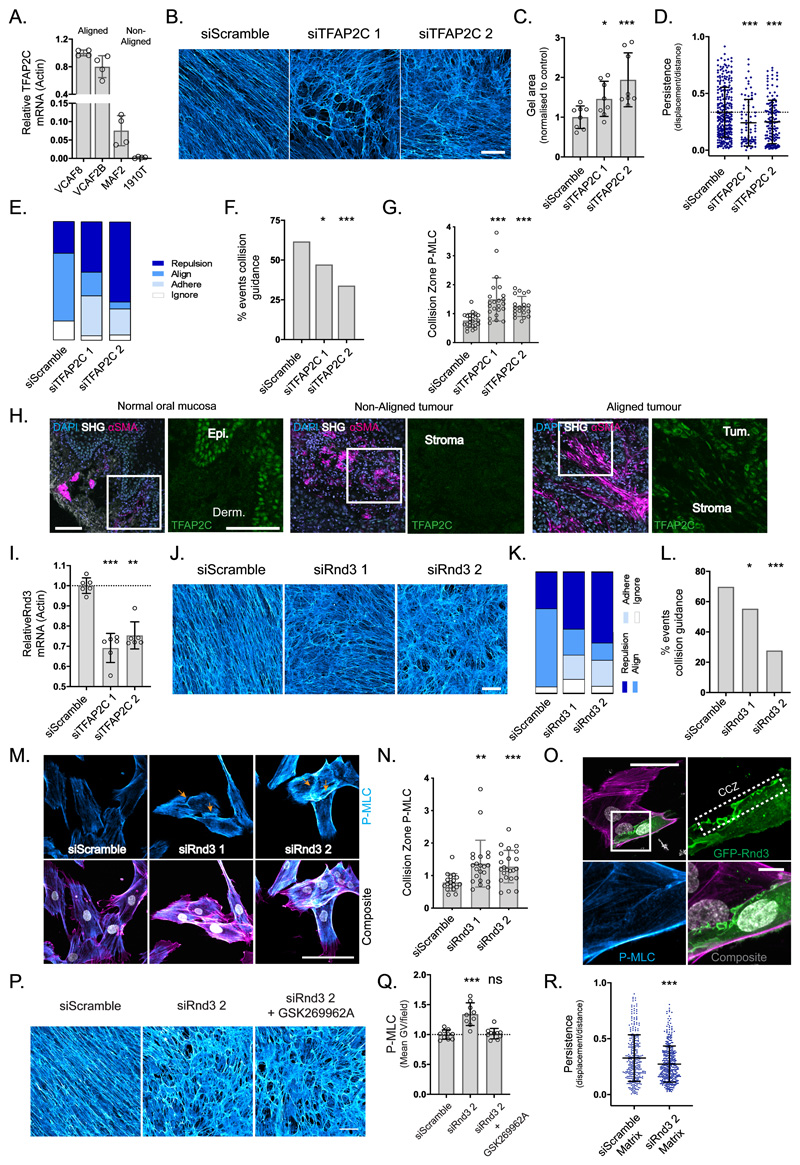
We next selected 37 genes with elevated expression in aligning fibroblasts and asked if they were required for matrix alignment; ITGB3 was used a positive control36 (Supplementary Figure 5a). This identified the transcription factor TFAP2C as required for the generation of anisotropic matrices. Figure 5a & Supplementary Table 1 confirm the increased expression of TFAP2C in aligning fibroblasts. Depleting TFAP2C with two independent siRNA disrupted matrix anisotropy and the ability of VCAF8 to contract macroscopic collagen gels (Figure 5b & c and Supplementary Figure 5b). Further, TFAP2C depletion reduced migratory persistence and changed the composition of collision behaviours, specifically decreasing collision guidance (Figure 5d-f and Supplementary 5c). This was associated with higher levels of active pS19-MLC at cell-cell collision zones (Figure 5g), without globally changing pS19- MLC levels (Supplementary Figure 5d). These data support a model in which TFAP2C regulates two pathways to enable the emergence of matrix anisotropy; one involving migratory persistence migration and the other localised tuning of actomyosin activity to enable cell collision guidance.
Figure 5. TFAP2C acts through RND3 to facilitate collision guidance and alignment.
A. qRT-PCR of TFAP2C gene expression in aligning vs non-aligning fibroblasts (n=16 from two independent experiments, mean and SD shown). B. FDMs from aligning VCAF8 transfected with two separate TFAP2C siRNA vs non-targeting control (scale bar:100μm, representative images of three fields of view from three independent experiments). C. Collagen gel contraction of aligning VCAF8 with TFAP2C knockdown vs control (n=24 from two independent experiments, p= 0.0265, p= 0.0028, unpaired two-tailed t-test, bars show mean and SD). D. Migratory persistence of aligning VCAF8 with TFAP2C knockdown vs control over 12 hr intervals (n=482 cells from two independent experiments, p=0.001, p=0.0001, unpaired two-tailed t-test, bars show mean and SD). E. Relative contribution of cell repulsion, alignment (collision guidance), adhesion or ignoring in aligning VCAF8 with TFAP2C depletion vs control (n=230 collisions in total from two independent experiments). F. Collision guidance events as a proportion of total collisions in TFAP2C knockdown vs control VCAF8 (n=230 collisions from two independent experiments. p=0.048, p= 0.00085, one-sided z-test). G. pS19-MLC at the cell-cell collision zone in TFAP2C knockdown vs control VCAF8. Values normalised to cell body pS19-MLC (n=66 cells, p<0.0001 unpaired two-tailed t-test, mean and SD are shown). H. Normal human oral mucosa and squamous cell carcinomas stained for DAPI (light blue), αSMA (magenta) and TFAP2C (green), with second harmonic imaging (grey), (scale bar: 100μm, from 6 independent samples). I. qRT-PCR analysis of relative RND3 gene expression in TFAP2C depleted cells vs control (n= 18 from three independent experiments, p<0.0001, p= 0.0014, unpaired two-tailed t-test, mean and SD are shown). J. Fibronectin stained matrices from VCAF8 with RND3 siRNA knockdown vs control (scale bar:100μm, representative images of three fields of view, from three independent experiments shown). K. Relative contribution of cell repulsion, alignment (collision guidance), adhesion or ignoring in VCAF8 with RND3 knockdown vs control (n=216 collisions in total from two independent experiments). L. Quantification of collision guidance events as a proportion of total collisions in RND3 knockdown vs control VCAF8 (n=216 collisions from two independent experiments, p=0.046, p<0.00001, one-sided z-test). M. F-actin (magenta), pS19-MLC (cyan) and DAPI (white) in RND3 depleted VCAF8 vs control (scale bar:100μm, representative images of three separate fields of view from two independent experiments shown). N. pS19-MLC values at the cell-cell collision zone in RND3 knockdown vs control VCAF8. Values normalised to cell body pS19-MLC (n=63 in total, p= 0.0027, p=0.0006, unpaired two-tailed t-test. Mean and SD are shown). O. VCAF8 transfected with eGFP-RND3 (green) and stained for pS19-MLC (cyan) and F-actin (magenta). Cell-cell collision zone (CCZ) (scale bar: 50μm, representative images from three independent experiments). P. Fibronectin stained FDMs from aligning VCAF8 with RND3 knockdown vs control, in the presence of absence of ROCK inhibitor (GSK269962A, 0.5nM) (scale bar=100μm, representative images of three fields of view, from two independent experiments shown). Q. pS19-MLC fluorescence intensity in VCAF8 from the above experiment (n=28 fields of view in total from two independent experiments, p<0.0001, p= 0.6866, bars show mean and SD). R. Migratory persistence of MDA-MB-231-GFP cells on FDMs derived from VCAF8 with Rnd3 knockdown vs control measured over 12 hr intervals (n=694 cells from 2 independent experiments, p=0.0001, two tailed unpaired t-test, bars show mean and SD).
Having established a role for TFAP2C in cultured fibroblasts, we investigated if its expression correlated with cell and ECM organisation in normal and cancerous human tissues. Figure 5h shows that TFAP2C is barely detectable in normal dermal fibroblasts, which generate isotropic ECM (note TFAP2C staining in epithelial compartment), but is readily detectable in the nuclei of highly aligned fibroblasts in the stroma of tumours. Further, stromal regions with isotropic ECM exhibited low TFAP2C levels arguing that TFAP2C up-regulation is not a generic feature of cancer-associated fibroblasts, but specific to those generating aligned ECM (further quantification in Supplementary Figure 5e & f).
To identify TFAP2C regulated genes in fibroblasts we performed RNA sequencing of control and TFAP2C depleted CAFs. ECM genes were not significantly represented within TFAP2C regulated genes, arguing that changes in matrix composition do not underlie the effect of TFAP2C depletion on matrix organization (Supplementary Figure 5g and Supplementary Table 2). Interestingly, two hits from our initial screen were reduced when TFAP2C was depleted, RND3/RHOE and MKX (Supplementary Figure 5h). Supplementary Figures 5i-k confirm the association between TFAP2C, MKX, and ECM alignment and Figures 5i & j and Supplementary 5l & m confirm the association between TFAP2C, RND3 and alignment. Expression of TFAP2C is also linked to higher RND3 levels in single cell sequencing analysis of stromal fibroblasts (Supplementary Figure 5n). RND3/RHOE antagonizes the function of ROCK kinases to modulate actomyosin contractility 37,38. We therefore tested if it controlled cell collision guidance behaviour. Depletion of RND3/RHOE increased repulsive and adhesive events, and decreased proportion of cells that aligned upon contact (Figure 5k & l and Supplementary Figure 5o). The disruption of collision guidance behaviour was associated with increased pS19-MLC at the contact zone between fibroblasts (marked with orange arrows - Figure 5m). p120-catenin localisation was also increased at cell-cell collision interfaces, potentially explaining the increase in cell-cell adhesion upon collision (Supplementary Figure 5p). RND3/RHOE was enriched at cell-cell collision zones thereby providing a mechanism for locally reducing actomyosin contractility (Figure 5n & o). To test whether RND3 regulated anisotropy by controlling the overall level of actomyosin function or local tuning of actomyosin activity, we balanced the increase in actomyosin activity following RND3 depletion with a sub-optimal dose of a ROCK inhibitor. In this context, pS19-MLC levels were equivalent to control cells, but the mechanism for spatially down-regulating actomyosin and cell-cell collision interfaces was disabled. Figure 5p & q shows that this was unable to restore ECM alignment. Further, the levels of p120 catenin at cell-cell collision zones were reduced (Supplementary Figure 5p), indicating that high contractility at the cell-cell interfaces stabilises cell-cell junctions could explain the increased adhesion after collision upon TFAP2C and RND3 depletion. Silencing of RND3/RHOE also perturbed the ability of CAFs to instruct the migration of cancer cells (Figure 5r and Supplementary Figure 5q).
Identification of diverse pharmacological tools to perturb matrix alignment
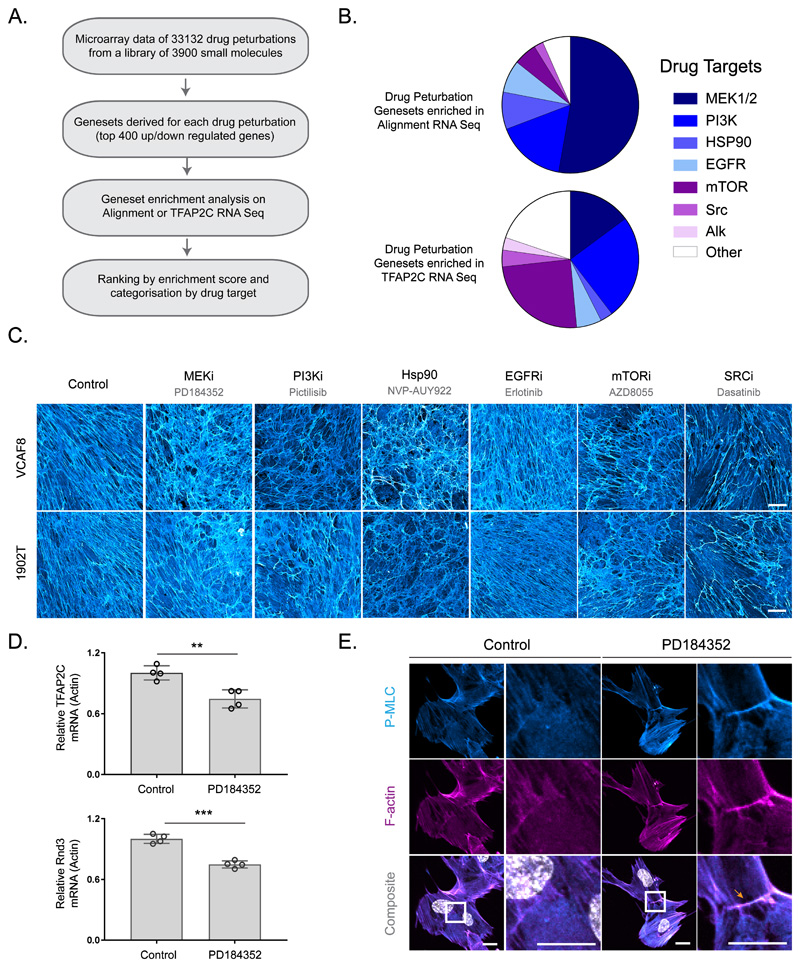
Lastly, we sought to identify pharmacological means to alter matrix alignment. We cross-referenced publically available gene expression datasets reporting the effect of pharmacological perturbations against our alignment and TFAP2C RNA sequencing data (Figure 6a). This suggested that similar coordinated changes in gene expression might be achieved by inhibition of MEK, PI3K, mTOR, EGFR, Src-family kinases and Hsp90 (Figure 6b and Supplementary Figure 6a). We tested this experimentally in both VCAF8 and 1902T fibroblasts, importantly the latter had not been used to generate the transcriptional signatures. Figure 6c shows that 5/6 of the predicted classes of compound had clear effects on ECM organisation, with MEK and Hsp90 inhibition having particularly strong effects (Supplementary Figure 6b shows additional drugs with the same molecular targets); in contrast only 4/21 of a ‘control’ set of compounds had any effect (Supplementary Figure 6c), which is a highly significant enrichment p<0.005 (Chi-square). MEK inhibition was the top prediction, and Figure 6d links this to its ability to regulate both TFAP2C and RND3/RHOE mRNA levels and pS19-MLC at cell-cell collision zones (Supplementary Figure 6d excludes the possibility that TFAP2C regulates MEK activity). Thus, our methodology opens up possibilities for utilising insights from this work to pharmacologically control matrix anisotropy.
Figure 6. Predicting pharmacological perturbation of alignment.
A. Workflow of drug perturbation analysis. B. Enrichment of drug perturbation genesets in either aligned vs non-aligned or TFAP2C knock down RNA Seq analysis. The proportion of genesets with a particular drug perturbation are represented in the pie chart. C. Fibronectin stained FDMs from aligning VCAF8 and 1902T fibroblasts treated with PD148352 (1μM), Pictilisib (0.1μM), NVP-AUY922 (0.01μM), Erlotinib (1μM), AZD8055 (0.1μM) or Dasatanib (0.5μM) (scale bar=100μm, representative images of three separate fields of view from two independent experiments shown) D. qRT-PCR analysis of TFAP2C and RND3 gene expression in aligning VCAF8 in the presence or absence of MEK inhibitor PD148352 (1μM) (n=8 in total from two independent experiments. TFAP2C: Control vs PD148352 p = 0.0042, Rnd3: Control vs PD148352 p = 0.0001, unpaired two-sided t-test). E. pS19-MLC (cyan) and F-actin (magenta) in aligning VCAF8 in the presence or absence of PD148352 (1μM). PD148352 treated cells show pS19-MLC at cell:cell contacts (scale bar=20μm, representative images of three separate fields of view from two independent experiments shown).
Discussion
The organization of ECM fibres is crucial to its functionality both in normal physiology and pathology. In tumours, aligned collagen fibres guide the migration of cancer cells and their orientation perpendicular to the tumour edge is linked to poor patient outcomes 2,3,4,5. In this study, we analyse the emergence of anisotropic extra-cellular matrix and demonstrate a key role for the reorientation of fibroblasts relative to one another following collision, which we refer to as collision guidance. This contrasts with the mechanisms of epithelial planar cell polarity that generate aligned arrays of confluent cells39. It also differs from many theoretical models described for elongated objects, either moving as the result of externally introduced energy or self-propelled23,22,24,25,40–42,43. While these models have proved informative26,27 they do not replicate the additional mechanisms for generating alignment provided by complex biochemical signalling and cytoskeletal regulation.
Although several studies have documented perturbations that disrupt the formation of aligned anisotropic matrices, the disruption of order does not necessarily explain the mechanism of its emergence 40,44,45,36. Perturbations that greatly reduce migratory persistence will prevent the emergence of anisotropic matrices, yet persistent migration on its own is not sufficient to generate alignment (Figure 2). Our combined experimental and modelling analyses, demonstrate a key role for cell collision guidance is crucial for the generation of matrix anisotropy. The failure to locally regulate actomyosin at cell-cell collision zones following TFAP2C depletion perturbs fibroblast collision guidance leading to the altered ECM organisation. We propose that RND3 localisation to cell-cell collision zones and subsequent down-regulation of P-MLC leads to supra-cellular coordination of actomyosin contractility between the colliding cells46 (Supplementary Figure 5r). Interestingly, RhoE is also temporally upregulated in aligning muscle myoblasts, where it suppresses actomyosin contractility and enables the fusion of myoblasts into multinucleated myotubes47. A contractile cytoskeleton around the outer edges of a cell doublet will tend to reduce the perimeter to area ratio, tending to generate alignment of the long axes of the two cells. This contrasts with CIL, in which the increase in actomyosin at the contact interface re-defines that region as the cell rear leading to re-polarisation of migration12,48,49.
In the earliest stages of development, embryos lack significant ECM with the production of matrix occurring concomitantly with major morphogenetic movements as development proceeds 50. We propose cell-cell collision guided mechanisms are likely to play a key role in this context. As more matrix is generated, then force-mediated ECM remodelling, especially in regions of low cellularity, and matrix feedback mechanisms will play an increasingly prominent role. Tension-dependent collagen fibre alignment can occur between points of high contractile force generation 34,51. This is particularly applicable when considering acellular matrix located between two cells generating contractile force. However, this is unlikely to be a factor in our assays utilise an underlying substrate with >109Pascal (GPa) stiffness that cannot be deformed by cells. In the future, it will be interesting to explore how different mechanisms of matrix organisation could synergise. For example, the local alignment mechanism that we show enables coordination of traction forces and thereby larger total forces that will favour strain-induced collagen fibre alignment52,53,54,55. Consistent with this, TFAP2C depletion reduces the contraction of 3D collagen gels. These data, together with the correlative analysis of TFAP2C levels and fibroblast alignment in vivo suggest that, although our analysis used predominantly 2D assays, it has relevance for 3D systems. Nonetheless, it should be noted that the reduction in collagen contraction by TFAP2C depleted fibroblasts is not absolute; if enough time is allowed, then even fibroblasts that do not align can remodel collagen gels56 57. As matrix deposition proceeds, feedback from the pre-existing matrix is also likely to generate a further level of input into fibroblast behaviour, with several studies documenting how fibroblasts respond to matrix stiffness, matrix composition, and patterning26,58,59,60,61,62.
To conclude, our study identifies molecular mechanisms underlying the ‘social behaviour’ of fibroblasts first described by Abercrombie over fifty years ago. Further, we demonstrate how this information can be leveraged to identify pharmacological tools to alter ECM organisation. In the future, this knowledge could aid efforts to rationally synthesize biological matrices of controlled anisotropy for applications in tissue engineering.
Materials and Methods
Cell lines and reagents
Human fibroblasts were isolated from a patient tissues of vulval (VCAF8, VCAF2B) cervical (CerCAF), oral (OCAF) and metastatic melanoma (MAF2) and immortalised with lentiviral HTERT as described in Gaggioli, C., et al 63. These patient samples were collected under ethical approval 10/H0304/14 and 15/EE/0151. Human breast fibroblasts (1910T, 1902T) were acquired from the Breast Cancer Now Tissue Bank under ethical approval 15/EE/0192 and immortalised as above. Cells were selected using 400 μg mL-1 hygromycin and maintained in DMEM (Invitrogen), 10% FCS (PAA Labs), 1% ITS (insulin–transferrin–selenium; #41400-045; Invitrogen) supplement.
Mouse fibroblasts (CAF1, CAF2 and NF2.1) were isolated from transgenic FVB/n mice expressing the Polyoma Middle T antigen oncogene under the Mouse Mammary Tumour Virus promoter (MMTV-PyMT) as described in Calvo, F., et al56. Cells were immortalised with HPV-E6 retrovirus, selected using 2.5 μg mL-1 puromycin and maintained in DMEM, 10% FCS and 1% ITS as above. All protocols were in accordance were kept in accordance with UK Home Office regulations under project licence PPL70/8380, which passed ethical review by the LRI Animal Welfare Ethical Review Board in 2014.
For cell tracking experiments fibroblasts were infected with the retroviral nuclear tag AcGFP-NLS (pLNCX2) and selected using 500 μg mL-1 geneticin. For imaging cytoskeletal dynamics during collisions VCAF2B were infected with LifeAct-Cherry (pLVX) and selected using 2.5 μg mL-1 puromycin or stained with 50nM siR-actin (Cytoskeleton, Inc, # CY-SC001) 6 hr prior to imaging. VCAF2B were electroporated with GFP-Rnd3 using the Neon Transfection System (ThermoFisher Scientific) as per the manufacturer’s instructions.
Tissue section sample preparation
Human head and neck squamous cell carcinoma samples were obtained from the Royal Marsden Hospital after informed consent through the project CCR2924 (Approved by the London/Chelsea NHS REC with code REC: 06/Q0403/125). All material was handled according to relevant ethical regulations by the Human Tissue Act. After excision the tumours were flash-frozen. Sections were stained as previously described 46. Briefly, fresh frozen sections were fixed in 4% paraformaldehyde, permeabilized in 0.2% Triton X-100, and stained with the following antibodies: anti-fibronectin (dilution 1/500, Sigma, F3648), anti-vimentin (dilution 1/100, Sigma,V2258), anti-TFAP2C (dilution 1:100, Abacm#218107), anti-αSMA (dilution 1/200, Cy3-conjugated clone#1a4, Sigma, C6198) and 633-phalloidin (dilution 1:500, Sigma, 68825). Sections were mounted using MOWIOL reagent and imaged using a Zeiss LSM 780 microscope.
Fibroblast derived matrix assay
The fibroblast derived matrix assay was performed as described in Franco-Barraza, J., et al 64. Briefly, 24 well glass bottom MatTek dishes (P35-1.5-14-C, MatTek Co., Ashland, MA, USA) were pre-prepared with 0.2% gelatin solution for 1 hr at 37 °C, followed by 1% glutaraldehyde for 30 min at room temperature. The plate was washed twice with PBS then incubated with 1M ethanolamine for 30 min at room temperature. The plate was washed twice with PBS before seeding 7 x 104 cells in media supplemented with 100μg/ml ascorbic acid ((+)-Sodium L-ascorbate, A4034, Sigma). The cells were maintained for 6 days and the media changed every two days. Cells were removed using the extraction buffer described and washed several times with PBS before undertaking immunofluorescence for ECM components as described below. The ECM was stained with the following antibodies: anti-fibronectin (1:1000 dilution, Sigma, F3648), anti-fibronectin-FITC (1:50 dilution: Abcam, ab72686) anti-collagen I (1:100 dilution, Abcam, ab34710) or anti-collagen I (1:100 dilution, Invitrogen, PA1-35998).
Quantification of matrix alignment
Individual fibres were extracted from resized grayscale 512 by 512 images using CT-FIRE [1]. The data from CT-FIRE was then input into MATLAB. The angle of each fibre was calculated from the first and last point of each fibre under the assumption that each fibre could be roughly approximated by a straight line. The extracted fibres were then discretized on a 512 by 512 matrix (which we shall term the Angle Matrix) and the matrix elements of each discretised fibre were given the fibre’s corresponding angles, between 0 and 180 degrees. Elements of the Angle Matrix in which no fibre was present were given NaN values. Interpolation was carried in in both the x and y dimensions of the matrix to fill in these NaN values. During the interpolation stage, care was taken to account for the periodic angular conditions (e.g. there is a difference of only 20 degrees between angles of 10 and 170 degrees, not 160 degrees). The matrix was then smoothed with a mean filter (again taking account of periodic conditions). We used this Angle Matrix to calculate the median difference in angle as a function of increasing radius. Using the strel function we generated circles of increasing radius, r, such that for each element in the Angle Matrix we could find all elements that were a distance of r gridpoints away. Using the nlfilter function we could then generate another matrix (the Angle Difference Matrix) providing the median difference in angle between each Angle Matrix element and the set of corresponding matrix elements r gridpoints away. Once again, the periodicity of the angles involved was accounted for in these calculations. Taking the sine function of the median of the resulting Angle Difference Matrix then provided our metric at the radius r. By generating the Angle Difference Matrix for increasing radii we could generate our final metric on sine of median difference in angle as a function of increasing radius. This allowed us to observe both local and global alignment.
Immunofluorescence
All immunofluorescence experiments were performed on cells seeded on 24 well glass bottom MatTek dishes or on fibroblast derived matrices as above. Cells were fixed in 4% paraformaldehyde, washed with PBS and permeabilised by incubation in 0.2 % Triton X100, PBS for 3-5 min at room temperature. Samples were subsequently blocked for 1 hr with 4%BSA, PBS before incubation with primary antibody in 4%BSA, PBS overnight at 4°C. Where indicated cells were stained with an antibody against phosphorylated-myosin light chain (pS19-MLC, dilution 1:100, NEB, 3671L). Primary antibody was washed off in 3 washes of 15 minutes with 0.05 % Tween-20, PBS. Fluorescent secondary antibody (Life Technologies) was diluted 1:500 in 4%BSA, PBS and incubated for 3 hrs, then washed off with 3 washes of 0.05 % Tween-20, PBS. Samples requiring staining for F-actin or the nucleus were also stained with 633-phalloidin (dilution 1:500, Sigma, 68825) or TRITC-phalloidin (dilution 1:500, Sigma, p1951) and DAPI (dilution 1:1000, Sigma, d5942) for 20 min. For the determination of aspect ratio and area cell masks were generated by thresholding on F-actin and using the ImageJ shape descriptors function, excluding all cell doublets or clusters.
Traction force microscopy
Traction forces were computed using Fourier-transform traction microscopy with 6 kPa polyacrylamide gels embedded with 0.2μM fluorescent beads (Invitrogen, FluoSpheres F8811) of defined thickness as previously described 65.
Gel contraction assay
Fibroblasts were mixed at a density of 1 × 105 cells in a mixture of collagen I (#354249; BD Biosciences, Oxford, UK) and Matrigel (#354234; BD Biosciences) at a final concentration of 4 mg ml-1 and 2 mg ml-1 respectively. 100μl of the fibroblast/ECM mix was seeded in a 24-well glass-bottom plate, and media added after 1 h of gel polymerization. Gel contraction was quantified by measuring the gel area on ImageJ 24h after polymerisation, relative to the gel area at the beginning of the assay.
Western blot
Cells were lysed in RIPA buffer supplemented with a cocktail of protease inhibitors (Roche) and incubated at 4 °C for 20 min. The lysate was sonicated on ice and clarified by centrifugation at 5250 g for 20 minutes at 4 °C. Protein concentration was quantified using the BCA Protein Assay Kit (Pierce, 23225) and 10ug loaded on a 4-12% gradient Bis-Tris gel (Invitrogen) and transferred to a PVDF membrane for blotting. Membrane was blocked for 1 hr in 4% BSA and incubated overnight with phosphorylated myosin light chain 2 antibody in 4% BSA (dilution 1:100, Ser19 Antibody, NEB #3671L) or for 1 hr at room temperature with β-Tubulin I antibody (dilution 1:100 000, T7816, Sigma).
Time-lapse microscopy for persistence and collision analysis
Nuclear labelled fibroblasts were seeded at approx. 7 x 103 cells per well in 24 well glass bottom MatTek dish and imaged approximately 8 hrs later. Bright-field and epifluorescence time-lapse imaging was performed at 37 °C and 5% CO2 with an inverted microscope (Nikon Ti2 inverted microscope fitted with a Okolab environmental chamber and CO2 mixer). Bright-field and epifluorescence images were taken every 10 min through a ×10 PlanFluor, NA 0.3 Ph1, Nikon objective. The imaging system includes a SpectraX LED light engine (Lumencor) fitted with standard filters and Photometrics Prime scientific CMOS camera. The microscope was managed using Micro-Manager v2.0 software.
Where indicated cell were pre-treated with PDGFR Tyrosine Kinase Inhibitor IV (Merck, 521233) at a final concentration of 500nM, NSC23766 (Tocris, 20161) at a final concentration of 20uM or GSK269962 (Tocris, 4009) at a final concentration of 20nM 2 hr prior to imaging. Images were acquired at 10 min intervals, and the cells tracked using the ImageJ Trackmate plug in. Persistence was calculated as the ratio of shortest linear distance between two points of migration (displacement) to the total distance traversed by the cell (distance) over 12 or 16 hr intervals.
Tumour cell migration assay on FDM
FDMs were prepared and stained for fibronectin as above and washed 10 times with PBS. Spheroids of MDA-MB-231-GFP cells were generated by hanging drop at 2000 cells/spheroid and seeded on the matrix 5 hr prior to time-lapse imaging. Images were acquired at 10 min intervals as above, and the cells tracked using the ImageJ Trackmate plug in. Persistence was calculated as displacement/distance travelled over 12 hr intervals.
siRNA transfection
Cells were transfected with 50nM siRNA using Dharmafect 3 (Dharmacon) as per the manufacturer’s instructions in Gibco™ Opti-MEM™ Reduced Serum Media supplemented with 10% FCS. Cells were maintained for 48 hrs for full knock-down before harvesting for further experiments. siRNA sequences are as follows: siTFAP2C 1: CACAGAACUUCUCAGCCAA, siTFAP2C 2:GCUAUUGGCGGCCCAGCAA, siRnd3 1: GACAAAGGAATCTAGTGTA, siRnd3 2:CAGATTGGAGCAGCTACTT, siMKX 1:GAAACCACUCGGGAUCUUU, siMKX 2:CAAGCAAGGAUGACACGUA, siMKX 3:CAAGCAAGGAUGACACGUA.
RNA Isolation and Sequencing
A panel of human aligning and non-aligning fibroblasts were selected according to their phenotypic stability and seeded at 7 x 104 cells/well as described in the fibroblast derived matrix assay above. Cells were grown for 5 days until cell body anisotropy or isotropy was observed. RNA was extracted from fibroblasts using RNeasy Plus Micro Kit (Cat No: 74034, Qiagen) as per manufacturer’s instructions. The quality and concentration of the total RNA was assessed using the bioanalyzer and qubit. Total RNA libraries were then prepared using KAPA HyperPrep with RiboErase in accordance with the manufacturers guidelines. Libraries were amplified with 8 cycles of PCR and QC’d using the TapeStation before sequencing on the Illumina HiSeq platform.
Bioinformatics analysis of RNA sequencing
Sequencing was performed on biological replicates for each condition generating approximately 30 million 75 or 100 base pair paired end reads per sample on an Illumina HiSeq 2500 instrument. The Trim Galore! utility (version 0.4.2) was used to remove sequencing adaptors and to quality trim individual reads with the q-parameter set to 20 The RSEM package and STAR (version 1.3.0) 66, 67 were used to align reads to the human GRCh38 release-86 transcriptome, downloaded from Ensembl [ https://www.ensembl.org/ ]. For RSEM, all parameters were run as default. TMM (treated mean of M-values) normalisation and differential expression analysis using the negative binomial model was carried out with the R-Bioconductor package Deseq2 (www.bioconductor.org R version 3. 3.2)68. Genes were considered to be differential expressed if the adjusted p value were less than 0.05. Result gene lists were filtered for low-abundance transcripts by removing all genes with an average TPM-value per sample of less than one. Differentially expressed genes were taken forward and their pathway and process enrichments were analysed using Metacore (genego.com).
Primary accessions: data files are deposited at the NCBI Gene Expression Omnibus (GEO) under GSE121536.
Drug perturbation analysis
The LINCS collection of drug perturbation datasets was used as a basis (http://lincsportal.ccs.miami.edu/SmallMolecules/). This library depicts drug-induced up- and down-regulated genes for around 3900 small molecules in various concentrations and cell lines. For each perturbation condition up to 400 up- or down-regulated genes are reported. In total the reference dataset consist of 33132 treatment conditions resulting in 33132 up- and the corresponding 33132 down-regulated gene sets.
For the above gene-sets, a gene-set enrichment analysis (GSEA) was performed. Particular attention was given to gene sets, that were enriched to opposite ends of the log-fold change values under consideration (logFC aligned vs. non-aligned). The enrichment scores (ES) was used to quantify enrichments of a gene set to the positive or negative end.
To test the predictions made by this analysis aligning VCAF8 and 1902T were treated with the drugs shown at the concentration indicated 4 h post seeding. Drug was replenished every 2 days for the course of the 7 day assay.
Collision tracking and analysis
Cell trajectories were manually tracked using ImageJ, specifically, the vector of approach and departure and the vector of the reference cell during isolated collisions. For a collision to be considered a maximum of two cells could come into contact for the duration of the tracking, and neither could undertake a cell division. Collision guidance events were defined as collisions in which the cell of interest re-orientated to be closer to the cell it collided with. Specifically, if the angle of approach – angle of departure (relative to a neighbouring cell) gave a value in the range of 10-90 degrees. This is indicated as collisions inside the blue triangle in the figures.
Statistical tests
The statistical test for collision guidance success is a z-test using a pooled estimate of variance. We want to test if two binomial distributions are significantly different from each other. This can be constructed as the following hypothesis test:
where pi is the probability of success in the binomial distribution X∼Bin(ni,pi). We calculate the test statistic as
where , and compare this statistic against the critical region value of zc = 1.645 defining a one-tailed test with significance if p<0.05. We reject H0 if z>zc.
For all other hypothesis testing, we used one or two-tailed t-tests as indicated in the figure legends. One-tailed t-tests were used when the hypotheses were:
and two-tailed t-tests were used when
Mathematical Modelling of Alignment
Cell-matrix updates
The agent-based model is adapted from the Vicsek model. CAFs are represented as two large circles with two smaller circles of half the radius at either end, approximating CAF shape. A cell i at time t + 1 can be described as having orientation
The first term describes single cell migration as a persistent random walk with η∼N(0,Var(η) ). This distribution is fitted from the data as described in the supplementary material. High Var(η) corresponds to cells with poor persistence, competing with any collective cell flocking behaviour.
The second term describes cells flocking with other cells with which they are in direct contact. This differs from the traditional idea of a circular neighbourhood used in the Vicsek model. Each cell moves at a constant speed drawn from the data and a proxy for volume exclusion is included, whereby a cell will slow down upon overlapping with another cell.
Simulation Setup
The agent-based computation model consists of cells moving in a simulation window size 1720 × 1720μm is and periodic boundary conditions are employed. Time is modelled discretely such that each time step represents one frame in the experiments, which corresponds to 15 minutes and the model simulates 7 days assays.
CAFs are represented as two large circles with two smaller circles of half the radius at either end. For most simulations, the total cell area is 1410μm, corresponding to a large circle radius of 13.5μm.
At time t = 0 , cells are seeded randomly with random orientation. A cell proliferation mechanism is implemented using a Voxel grid. If ρ(0) denotes the initial cell density at time 0, then at time t, cell density where d is the average time it takes for cell population density to double. When a new cell is to be added, a mother cell is selected at random. If there is space nearby then a daughter cell is added with the opposite orientation to its mother. If there is no space, a new candidate mother cell is chosen and so on until there is no space remaining within the entire simulation area. This method simulates the phenomenon known as contact inhibition of proliferation.
Updating cell position
Each cell i moves at a constant speed Si, which is determined from a Gaussian distribution derived from experimental data and travels at an orientation θi (t)
At every time point each cell will compute its flocking with other cells it is in contact with and its flocking with the matrix below it. All cell orientations and positions are then updated synchronously such that at time t + 1 the position xi (t + 1) of cell can be defined as
where ve is a proxy for volume exclusion defined by
The distance between cells which is considered as an overlap is set by the user but for simulations in the manuscript was set as the inner 75% of the cell’s area.
Computing cell orientation
A simplified form of the model can be written as
| (1) |
which can be expanded as follows:
The first term describes single cell migration as a persistent random walk, where η∼N(0,Var(η)). Breaking this down into its x and y components, this can be written as
| (2) |
The second term describes of equation (1) describes cell i flocking with other cells with which it is in direct contact. Breaking this down into its x and y components we can define
| (3) |
| (4) |
| (5) |
where the tilde (~) denotes the nematic flocking in the system which can be written as
| (6) |
The model in full can then be written as
| (7) |
| (8) |
| (9) |
which can then be adjusted according to which quadrant the new angle lies in to give the final new orientation as
| (10) |
Computing and fitting persistence
To avoid bias in computing cell persistence due to cell collisions, cells were tracked at low levels of confluence. The program Metamorph was used for cell tracking. A range of time intervals T was chosen over which persistence should be computed. At each point time t, the persistence was taken to be the mean directionality ratio of all cells, computed as
| (14) |
A range of values for T was used.
Cells tracked for at least one hour were recorded and a spline tracing the cell’s trajectory was produced using the loess package in R (α = 0.5). This was in order to smooth the intracellular movement, which resulted in many small fluctuations in the trajectories (Supplementary Figure 2a). For each cell, the median persistence over for each cell was computed as described above. Simulations of single cells with varying values of Var(η) were run and the persistence computed for T = one and two-hour windows. The experimental results were then matched with simulations using a least squares approach to select the most likely value of Var(η) given a cell’s persistence.
The persistence of the aligning CAFs (VCAF8) to a persistent random walk gives a noise value of Var(η) = 0.1 and the persistence of the non-aligning CAFs (CAF1) gives a noise value of Var(η) = 0.18.
Fitting level of collision guidance (w2)
Simulations were run with noise η∼N(0,0.1), describing the persistence of VCAF8 (aligning) cells for incremental values of collision guidance (w2) between 0 and 1. The short-range and long-range alignment of these simulations over time was computed and through a least squares approach, compared with the alignment of the experiments to choose the most likely value of collision guidance that would match the simulations to the experiments. This value of collision guidance is w2 = 0.04.
Quantifying Alignment
A metric was developed to quantify extent of alignment over multiple distances. For each cell i, at a specific time-point t, for a given neighborhood r between rmin and rmax, let the set J denote all cells j ≠ i which have a distance in the range [rmin,rmax] from i. If the vector ΔΘi denoting the nematic difference in angle between cell i and the cells in J has length n > 5. Then the angle un-normalised alignment of the system at time t over a given distance r = [rmin,rmax] can be defined as
| (16) |
This can be normalised to give values between 0 and 1 as
| (17) |
.
For each cell, the median angle of deviation is used as opposed to the mean in order to be less sensitive to outliers for example cells undergoing spontaneous repolarisation or proliferation. Measurements for each cell are only considered valid if the neighbourhood contains at least five neighbors (including itself) i.e. alignment in low confluence, is not meaningful.
For the manuscript, the short-range and long-range alignment neighbourhoods are defined as cells within a distance of 0 – 100μm and 100 – 400μm respectively.
Cell nuclei were tracked and used to compute short-range and long-range alignment over time for each assay. To compute the alignment of the experiments at any given time point t, cells were tracked in the interval [t − 4, t] and a line of best fit was used to give the approximate angle of orientation for the cells. The orientation of each cell at a given time was determined as the angle of the line of best fit through the cell’s migration path over the past hour. This produced a vector field, which was used to work out the median angle of deviation in cell orientations over a range of distances.
The model was challenged to reproduce the width-dependence findings by Duclos et al 27 at confluence in channels of different width. In order to replicate the Duclos experiments, the volume exclusion term in our model was set to be stricter, to prevent cells from going through the walls.
Software and Visualisation
The model is written in C++. Data analysis was carried out in R and image processing was done in Fiji (ImageJ) and Metamorph. All code is available upon request.
Supplementary Material
Acknowledgements
We are indebted to Bioinformatics and Biostatistics, Light Microscopy (in particular David Barry), Advanced Sequencing Facilities, Cell Services, and the Biological Research Facility at the Crick Institute for exceptional scientific and technical support throughout the project. We thank Charles Mein (Bart’s and the London School of Medicine and Dentistry) for support and advice with RNA sequencing. E.S, D.P, P.A.B and E.W were funded by the Francis Crick Institute, which receives its core funding from Cancer Research UK (FC001144), the UK Medical Research Council (FC001144) and the Wellcome Trust (FC001144). E.S and D.P also received funding from Breast Cancer Now (2013NovPR182).
Footnotes
Author Contributions
D.P, E.W and E.S conceived and developed the project. D.P performed the experiments and analysed the data. E.W and P.A.B developed the computational model and analysed the data. S.B performed the bioinformatic analysis of RNASeq and LINCS data. A.L performed the traction force microscopy and analysis in Figures 1F and 4E. R.P.J wrote the code for analysis of fibre alignment. S.G performed the tracking of some cell collision data. D.P and E.S wrote the manuscript with helpful assistance from E.W, A.L, R.P.J, X.T and P.A.B.
Competing Financial Interests
There are no competing financial interests to declare.
Data Availability Statement
Primary accessions: data files are deposited at the NCBI Gene Expression Omnibus (GEO) under GSE121536. The data that support the findings of this study are available from the corresponding author upon reasonable request. The code for the computational model continues to be developed and is available via the following link https://github.com/wershofe/FibroblastMatrixModel. The version pertaining to this manuscript is called cellCellModel.
References
- 1.Mouw JK, Ou G, Weaver VM. Extracellular matrix assembly: a multiscale deconstruction. Nat Rev Mol Cell Biol. 2014;15:771–785. doi: 10.1038/nrm3902. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Conklin MW et al. Aligned collagen is a prognostic signature for survival in human breast carcinoma. Am J Pathol. 2011;178:1221–1232. doi: 10.1016/j.ajpath.2010.11.076. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Conklin MW et al. Collagen Alignment as a Predictor of Recurrence after Ductal Carcinoma In Situ. Cancer Epidemiol Biomarkers Prev. 2018;27:138–145. doi: 10.1158/1055-9965.EPI-17-0720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Provenzano PP et al. Collagen reorganization at the tumor-stromal interface facilitates local invasion. BMC Med. 2006;4:38. doi: 10.1186/1741-7015-4-38. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Drifka CR et al. Highly aligned stromal collagen is a negative prognostic factor following pancreatic ductal adenocarcinoma resection. Oncotarget. 2016;7:76197–76213. doi: 10.18632/oncotarget.12772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Goetz JG et al. Biomechanical remodeling of the microenvironment by stromal caveolin-1 favors tumor invasion and metastasis. Cell. 2011;146:148–163. doi: 10.1016/j.cell.2011.05.040. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 7.Acerbi I, et al. Human breast cancer invasion and aggression correlates with ECM stiffening and immune cell infiltration. Integr Biol (Camb) 2015;7:1120–1134. doi: 10.1039/c5ib00040h. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Riching KM et al. 3D collagen alignment limits protrusions to enhance breast cancer cell persistence. Biophys J. 2014;107:2546–2558. doi: 10.1016/j.bpj.2014.10.035. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Han W, et al. Oriented collagen fibers direct tumor cell intravasation. Proc Natl Acad Sci U S A. 2016;113:11208–11213. doi: 10.1073/pnas.1610347113. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Provenzano PP et al. Collagen density promotes mammary tumor initiation and progression. BMC Med. 2008;6:11. doi: 10.1186/1741-7015-6-11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Abercrombie M, Heaysman JE. Observations on the social behaviour of cells in tissue culture. I. Speed of movement of chick heart fibroblasts in relation to their mutual contacts. Exp Cell Res. 1953;5:111–131. doi: 10.1016/0014-4827(53)90098-6. [DOI] [PubMed] [Google Scholar]
- 12.Stramer B, Mayor R. Mechanisms and in vivo functions of contact inhibition of locomotion. Nat Rev Mol Cell Biol. 2016 doi: 10.1038/nrm.2016.118. [DOI] [PubMed] [Google Scholar]
- 13.Davis JR et al. Inter-cellular forces orchestrate contact inhibition of locomotion. Cell. 2015;161:361–373. doi: 10.1016/j.cell.2015.02.015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Carmona-Fontaine C, et al. Contact inhibition of locomotion in vivo controls neural crest directional migration. Nature. 2008;456:957–961. doi: 10.1038/nature07441. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Theveneau E, et al. Chase-and-run between adjacent cell populations promotes directional collective migration. Nat Cell Biol. 2013;15:763–772. doi: 10.1038/ncb2772. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Xu Q, Mellitzer G, Robinson V, Wilkinson DG. In vivo cell sorting in complementary segmental domains mediated by Eph receptors and ephrins. Nature. 1999;399:267–271. doi: 10.1038/20452. [DOI] [PubMed] [Google Scholar]
- 17.Elsdale T, Bard J. Cellular interactions in mass cultures of human diploid fibroblasts. Nature. 1972;236:152–155. doi: 10.1038/236152a0. [DOI] [PubMed] [Google Scholar]
- 18.Elsdale TR. Parallel orientation of fibroblasts in vitro. Exp Cell Res. 1968;51:439–450. doi: 10.1016/0014-4827(68)90134-1. [DOI] [PubMed] [Google Scholar]
- 19.Bertin E, Baskaran A, Chate H, Marchetti MC. Comparison between Smoluchowski and Boltzmann approaches for self-propelled rods. Phys Rev E Stat Nonlin Soft Matter Phys. 2015;92:042141. doi: 10.1103/PhysRevE.92.042141. [DOI] [PubMed] [Google Scholar]
- 20.Wegner S, et al. Effects of grain shape on packing and dilatancy of sheared granular materials. Soft Matter. 2014;10:5157–5167. doi: 10.1039/c4sm00838c. [DOI] [PubMed] [Google Scholar]
- 21.Prost J. The physics of liquid crystals. 1995;83 [Google Scholar]
- 22.Ginelli F, Peruani F, Bar M, Chate H. Large-scale collective properties of self-propelled rods. Phys Rev Lett. 2010;104:184502. doi: 10.1103/PhysRevLett.104.184502. [DOI] [PubMed] [Google Scholar]
- 23.Peruani F, Deutsch A, Bar M. Nonequilibrium clustering of self-propelled rods. Phys Rev E Stat Nonlin Soft Matter Phys. 2006;74:030904. doi: 10.1103/PhysRevE.74.030904. [DOI] [PubMed] [Google Scholar]
- 24.Grossmann R, Peruani F, Bar M. Mesoscale pattern formation of self-propelled rods with velocity reversal. Phys Rev E. 2016;94:050602. doi: 10.1103/PhysRevE.94.050602. [DOI] [PubMed] [Google Scholar]
- 25.Grossmann R, Aranson IS, Ben Jacob E. Emergence of agent swarm migration and vortex formation through inelastic collisions. 2008;10 doi: 10.1088/1367-2630/10/2/023036. [DOI] [Google Scholar]
- 26.Li X, et al. On the mechanism of long-range orientational order of fibroblasts. Proc Natl Acad Sci U S A. 2017;114:8974–8979. doi: 10.1073/pnas.1707210114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Duclos G, Garcia S, Yevick HG, Silberzan P. Perfect nematic order in confined monolayers of spindle-shaped cells. Soft Matter. 2014;10:2346–2353. doi: 10.1039/c3sm52323c. [DOI] [PubMed] [Google Scholar]
- 28.Drifka CR et al. Human pancreatic stellate cells modulate 3D collagen alignment to promote the migration of pancreatic ductal adenocarcinoma cells. Biomed Microdevices. 2016;18:105. doi: 10.1007/s10544-016-0128-1. [DOI] [PubMed] [Google Scholar]
- 29.Pankov R, et al. A Rac switch regulates random versus directionally persistent cell migration. J Cell Biol. 2005;170:793–802. doi: 10.1083/jcb.200503152. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Vicsek T, Czirok A, Ben-Jacob E, Cohen II, Shochet O. Novel type of phase transition in a system of self-driven particles. Phys Rev Lett. 1995;75:1226–1229. doi: 10.1103/PhysRevLett.75.1226. [DOI] [PubMed] [Google Scholar]
- 31.Ohlund D, et al. Distinct populations of inflammatory fibroblasts and myofibroblasts in pancreatic cancer. J Exp Med. 2017;214:579–596. doi: 10.1084/jem.20162024. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Costa A, et al. Fibroblast Heterogeneity and Immunosuppressive Environment in Human Breast Cancer. Cancer Cell. 2018;33:463–479 e410. doi: 10.1016/j.ccell.2018.01.011. [DOI] [PubMed] [Google Scholar]
- 33.Su S, et al. CD10(+)GPR77(+) Cancer-Associated Fibroblasts Promote Cancer Formation and Chemoresistance by Sustaining Cancer Stemness. Cell. 2018;172:841–856 e816. doi: 10.1016/j.cell.2018.01.009. [DOI] [PubMed] [Google Scholar]
- 34.Provenzano PP, Inman DR, Eliceiri KW, Trier SM, Keely PJ. Contact guidance mediated three-dimensional cell migration is regulated by Rho/ROCK-dependent matrix reorganization. Biophys J. 2008;95:5374–5384. doi: 10.1529/biophysj.108.133116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Teixeira AI, Abrams GA, Bertics PJ, Murphy CJ, Nealey PF. Epithelial contact guidance on well-defined micro- and nanostructured substrates. J Cell Sci. 2003;116:1881–1892. doi: 10.1242/jcs.00383. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Attieh Y, et al. Cancer-associated fibroblasts lead tumor invasion through integrin-beta3-dependent fibronectin assembly. J Cell Biol. 2017;216:3509–3520. doi: 10.1083/jcb.201702033. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Riento K, Guasch RM, Garg R, Jin B, Ridley AJ. RhoE binds to ROCK I and inhibits downstream signaling. Mol Cell Biol. 2003;23:4219–4229. doi: 10.1128/MCB.23.12.4219-4229.2003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Hodge RG, Ridley AJ. Regulating Rho GTPases and their regulators. Nat Rev Mol Cell Biol. 2016;17:496–510. doi: 10.1038/nrm.2016.67. [DOI] [PubMed] [Google Scholar]
- 39.Butler MT, Wallingford JB. Planar cell polarity in development and disease. Nat Rev Mol Cell Biol. 2017;18:375–388. doi: 10.1038/nrm.2017.11. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Yang N, Friedl A. Syndecan-1-Induced ECM Fiber Alignment Requires Integrin alphavbeta3 and Syndecan-1 Ectodomain and Heparan Sulfate Chains. PLoS One. 2016;11:e0150132. doi: 10.1371/journal.pone.0150132. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Peruani F, et al. Collective motion and nonequilibrium cluster formation in colonies of gliding bacteria. Phys Rev Lett. 2012;108:098102. doi: 10.1103/PhysRevLett.108.098102. [DOI] [PubMed] [Google Scholar]
- 42.Borzsonyi T, et al. Orientational order and alignment of elongated particles induced by shear. Phys Rev Lett. 2012;108:228302. doi: 10.1103/PhysRevLett.108.228302. [DOI] [PubMed] [Google Scholar]
- 43.Levay S, et al. Frustrated packing in a granular system under geometrical confinement. Soft Matter. 2018;14:396–404. doi: 10.1039/c7sm01900a. [DOI] [PubMed] [Google Scholar]
- 44.Yang N, Mosher R, Seo S, Beebe D, Friedl A. Syndecan-1 in breast cancer stroma fibroblasts regulates extracellular matrix fiber organization and carcinoma cell motility. Am J Pathol. 2011;178:325–335. doi: 10.1016/j.ajpath.2010.11.039. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Gilkes DM, Bajpai S, Chaturvedi P, Wirtz D, Semenza GL. Hypoxia-inducible factor 1 (HIF-1) promotes extracellular matrix remodeling under hypoxic conditions by inducing P4HA1, P4HA2, and PLOD2 expression in fibroblasts. J Biol Chem. 2013;288:10819–10829. doi: 10.1074/jbc.M112.442939. [DOI] [PMC free article] [PubMed] [Google Scholar] [Retracted]
- 46.Hidalgo-Carcedo C, et al. Collective cell migration requires suppression of actomyosin at cell-cell contacts mediated by DDR1 and the cell polarity regulators Par3 and Par6. Nat Cell Biol. 2011;13:49–58. doi: 10.1038/ncb2133. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Fortier M, et al. RhoE controls myoblast alignment prior fusion through RhoA and ROCK. Cell Death Differ. 2008;15:1221–1231. doi: 10.1038/cdd.2008.34. [DOI] [PubMed] [Google Scholar]
- 48.Roycroft A, Mayor R. Molecular basis of contact inhibition of locomotion. Cell Mol Life Sci. 2016;73:1119–1130. doi: 10.1007/s00018-015-2090-0. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Mayor R, Carmona-Fontaine C. Keeping in touch with contact inhibition of locomotion. Trends Cell Biol. 2010;20:319–328. doi: 10.1016/j.tcb.2010.03.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 50.Wartiovaara J, Leivo I, Vaheri A. Expression of the cell surface-associated glycoprotein, fibronectin, in the early mouse embryo. Dev Biol. 1979;69:247–257. doi: 10.1016/0012-1606(79)90289-6. [DOI] [PubMed] [Google Scholar]
- 51.Shi Q, et al. Rapid disorganization of mechanically interacting systems of mammary acini. Proc Natl Acad Sci U S A. 2014;111:658–663. doi: 10.1073/pnas.1311312110. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 52.Ahmadzadeh H, et al. Modeling the two-way feedback between contractility and matrix realignment reveals a nonlinear mode of cancer cell invasion. Proc Natl Acad Sci U S A. 2017;114:E1617–E1626. doi: 10.1073/pnas.1617037114. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Checa S, Rausch MK, Petersen A, Kuhl E, Duda GN. The emergence of extracellular matrix mechanics and cell traction forces as important regulators of cellular self-organization. Biomech Model Mechanobiol. 2015;14:1–13. doi: 10.1007/s10237-014-0581-9. [DOI] [PubMed] [Google Scholar]
- 54.Sawhney RK, Howard J. Slow local movements of collagen fibers by fibroblasts drive the rapid global self-organization of collagen gels. J Cell Biol. 2002;157:1083–1091. doi: 10.1083/jcb.200203069. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Wang H, Abhilash AS, Chen CS, Wells RG, Shenoy VB. Long-range force transmission in fibrous matrices enabled by tension-driven alignment of fibers. Biophys J. 2014;107:2592–2603. doi: 10.1016/j.bpj.2014.09.044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Calvo F, et al. Mechanotransduction and YAP-dependent matrix remodelling is required for the generation and maintenance of cancer-associated fibroblasts. Nat Cell Biol. 2013;15:637–646. doi: 10.1038/ncb2756. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Hirata E, et al. Intravital imaging reveals how BRAF inhibition generates drug-tolerant microenvironments with high integrin beta1/FAK signaling. Cancer Cell. 2015;27:574–588. doi: 10.1016/j.ccell.2015.03.008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 58.Lo CM, Wang HB, Dembo M, Wang YL. Cell movement is guided by the rigidity of the substrate. Biophys J. 2000;79:144–152. doi: 10.1016/S0006-3495(00)76279-5. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 59.Lachowski D, et al. Substrate Rigidity Controls Activation and Durotaxis in Pancreatic Stellate Cells. Sci Rep. 2017;7 doi: 10.1038/s41598-017-02689-x. 2506. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Wong S, Guo WH, Wang YL. Fibroblasts probe substrate rigidity with filopodia extensions before occupying an area. Proc Natl Acad Sci U S A. 2014;111:17176–17181. doi: 10.1073/pnas.1412285111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 61.Doyle AD, Wang FW, Matsumoto K, Yamada KM. One-dimensional topography underlies three-dimensional fibrillar cell migration. J Cell Biol. 2009;184:481–490. doi: 10.1083/jcb.200810041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Wu C, et al. Arp2/3 is critical for lamellipodia and response to extracellular matrix cues but is dispensable for chemotaxis. Cell. 2012;148:973–987. doi: 10.1016/j.cell.2011.12.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 63.Gaggioli C, et al. Fibroblast-led collective invasion of carcinoma cells with differing roles for RhoGTPases in leading and following cells. Nat Cell Biol. 2007;9:1392–1400. doi: 10.1038/ncb1658. [DOI] [PubMed] [Google Scholar]
- 64.Franco-Barraza J, Beacham DA, Amatangelo MD, Cukierman E. Preparation of Extracellular Matrices Produced by Cultured and Primary Fibroblasts. Curr Protoc Cell Biol. 2016;71:10 19 11–10 19 34. doi: 10.1002/cpcb.2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 65.Tambe DT et al. Collective cell guidance by cooperative intercellular forces. Nat Mater. 2011;10:469–475. doi: 10.1038/nmat3025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 66.Li B, Dewey CN. RSEM: accurate transcript quantification from RNA-Seq data with or without a reference genome. BMC Bioinformatics. 2011;12:323. doi: 10.1186/1471-2105-12-323. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Dobin A, et al. STAR: ultrafast universal RNA-seq aligner. Bioinformatics. 2013;29:15–21. doi: 10.1093/bioinformatics/bts635. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Love MI, Huber W, Anders S. Moderated estimation of fold change and dispersion for RNA-seq data with DESeq2. Genome Biol. 2014;15:550. doi: 10.1186/s13059-014-0550-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.