Abstract
Pharmacokinetic-pharmacodynamic model is a kind of language that quantitatively describes the drug-related outcomes in the form of mathematical formula. Various outcomes can be subjected to modeling analysis if they can be expressed in numbers. Empirical models have been widely and successfully applied in drug development and research. However, a more competitive drug development environment requires more accurate and predictive models in the early stages of drug development. Accordingly, the subjects of PK-PD modeling have been extended from clinical data to preclinical and in vitro data in the discovery stage. More mechanistic and predictive models, such as physiologically based pharmacokinetic and quantitative system-based pharmacology models, are being increasingly used owing to the growing need to characterize drugs more accurately at the earliest. This tutorial briefly introduces the essential concepts of PK-PD modeling and simulation and describes the recent changing roles of PK-PD model for application in novel drug development process.
Keywords: Language, Mathematical formula, Pharmacokinetic-pharmacodynamic model, Predictive model
Introduction
Pharmacokinetic-pharmacodynamic (PK-PD) modeling and simulation are core techniques that have been successfully applied in the drug development process (Table 1).[1] As the drug development environment has become more competitive, risky, and demanding, there has been an increasing need for more accurate characterization of drug candidates and prediction of their efficacy and safety at the earliest. Novel drug development is an uncertain process with a low success rate.[2,3] Currently, the lack of significant treatment effect is considered the most common cause of attrition of new drug candidates in both phase II (51%) and phase III (66%) stages of clinical development process, followed by safety issues. The Critical Path Initiative by the United States Food and Drug Administration, which aimed to modernize the drug development process, recommended the use of modeling and simulation to streamline drug development.[4] PK-PD mixed effect modeling and Monte-Carlo simulation methods have been widely used to quantitatively characterize novel drug candidates and to predict the effects and safety outcomes for various scenarios in the drug development process.
Table 1. Application of modeling and simulation in drug development.
| Indication | Modeling approach adapted | Efficiencies gained over historical approach |
|---|---|---|
| Thromboembolism | Omit phase IIa, model-based dose–response relationship, adaptive phase IIb design | 2,750 fewer patients, 1-year shorter study duration |
| Hot flashes | Model-based dose–response relationship | 1,000 fewer patients |
| Fibromyalgia | Prior data supplementation, model-based dose–response relationship, sequential design | 760 fewer patients, 1-year shorter study duration |
| Type 2 diabetes | Prior data supplementation, model-based dose–response relationship | 120 fewer patients, 1-year shorter study duration |
| Gastroesophageal reflux | Model-based dose–response relationship | 1,025 fewer patients |
| Rheumatoid arthritis | Model-based dose–response relationship | 437 fewer patients, increased probability of success |
| Global anxiety disorder | Omit phase IIb | 260 fewer patients, 1-year shorter study duration |
| Lower urinary tract symptoms | Meta-analysis | Increased probability of success |
| Urinary incontinence | Meta-analysis | Increased probability of success |
Adopted from Clin Pharmacol Ther. 2013;93(6):502-14.
In this tutorial, I briefly introduce the essential concepts of PK-PD modeling and simulation, and the recent changing roles of PK-PD model for application in novel drug development process based on my experiences.
Pharmacokinetic-pharmacodynamic model as a useful repository for drug information
The basic property of PK-PD modeling is that it is useful language in the form of unequivocal mathematical formulae expressing drug-related biological changes. This concept implies that PK-PD modeling can be applied to almost all steps of the drug development process if the results can be expressed in numbers. In addition, there is a lot of room to be more widely used in drug researches.
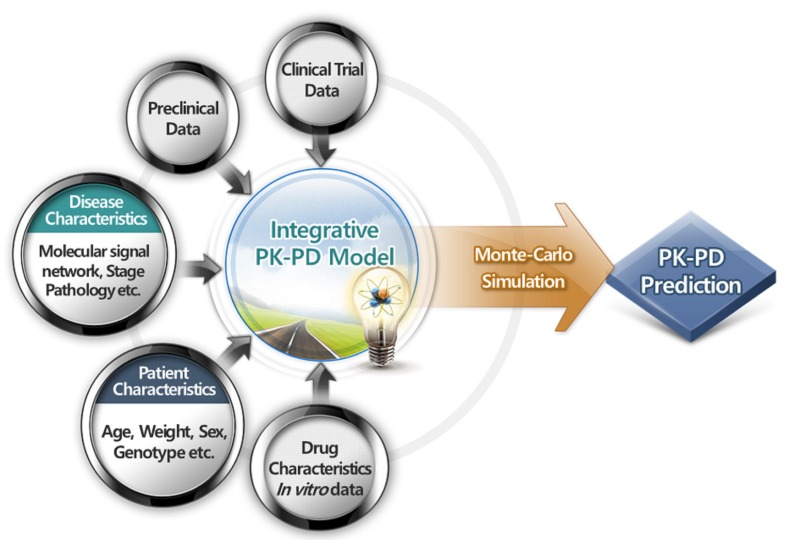
PK-PD models serve as efficient repositories of drug-related information by summarizing data. Through PK-PD models, we can understand drug characteristics, compare it with other competitive drugs, and communicate with each other. If a dose-response relationship follows a simple, linear model with a slope of 0.5, we can predict the extent of increase in response on average when the doses are doubled, which is unclear from raw data themselves. This aspect of models is important especially in drug development process, where a plethora of data is produced from various steps. Although tremendous data are generated in each step of in vitro experiments, animal studies, and clinical trials in various forms such as continuous, binary, ordered categorical, and time-to-event data, these data have been deciphered alone without being understood as an inter-connected whole. Modeling provides an excellent platform for integrating, extracting, and delivering useful drug information from these various data forms (Fig. 1). For example, in the case of time-to-event data analysis, non-parametric Kaplan-Meier analysis cannot handle the predictors of continuous variable per se. To evaluate the effect of age on the survival of cancer patients, age should be categorized. The categorization of continuous data is sometimes arbitrary and necessarily accompanied by loss of information. Analysis of time-to-event data using exponential, Weibull, log-logistic, or other models can handle continuous predictors. Thus, continuous variables, such as age, weight, drug concentration over time, or change in tumor size over time, can be implemented in the model as predictors without having to categorize them.
Figure 1. Pharmacokinetic-pharmacodynamic model as a platform on which different types of data from various sources of the drug development process can be integrated into useful information.
Physiologically based pharmacokinetic (PBPK) model is an important tool for predicting the pharmacokinetics and pharmacodynamics of a drug by integrating multiple levels of information from in vitro/in silico through clinical studies. It comprises drug-specific parameters and biological system-specific parameters. Drug-specific parameters include molecular weight, polar surface area, tissue-blood partition coefficient (Kp), negative log acid dissociation constant (pKa), lipophilicity such as log partition coefficient (logP) and log distribution coefficient (logD), permeability, plasma protein binding, transporter contribution to drug disposition, and metabolism data, which are typically obtained from in vitro experiments or sometimes in silico prediction. Biological system-specific parameters include blood flow, lymphatic flow, organ composition, and organ volume, which are often obtained from literature.[5] Such variety of data can be embraced, integrated into a PBPK model, and finally transformed into useful drug information, indicating that we can obtain most of the drug-related in vitro, literature, animal, and clinical data simultaneously using the framework of a PBPK model. Separating these parameters is extremely useful in predicting PK in various situations, including preclinical to human prediction.[6] Another advantage of PBPK model is that it can predict the target concentrations of a drug over time as well as the conventional plasma concentration. The target concentration can be linked with exposure-response model from in vitro experiments using target tissue, enabling the elucidation of PK-PD characteristics of a drug more reliably. Drug-related public literature data can also be used through model based meta- or meta-regression analysis.
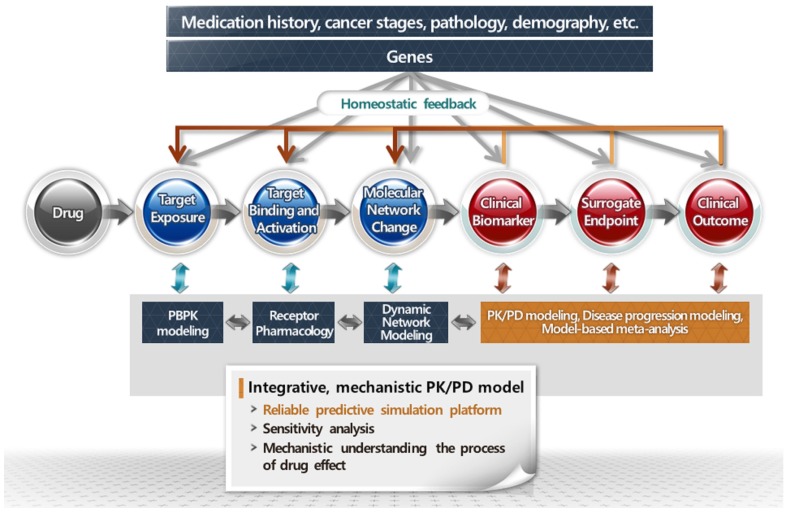
By linking models for data produced in each stage of drug development, integrative PK-PD models encompassing the whole mechanistic processes of drug action in humans could be constructed (Fig. 2). For example, biochemical signaling network model, constructed from in vitro exposure-response experiment using target cells, and receptor-ligand interaction model can be linked to PBPK model from an animal study, which provides the target concentration over time. The preclinical models can be linked to human PK and PD models from clinical data, resulting in integrative PK/PD model, which describes the whole series of drug action in human.
Figure 2. Integrative models encompassing the whole mechanistic processes of drug action.
Moving from Descriptive Towards Predictive Models in Early Stages of Drug Development
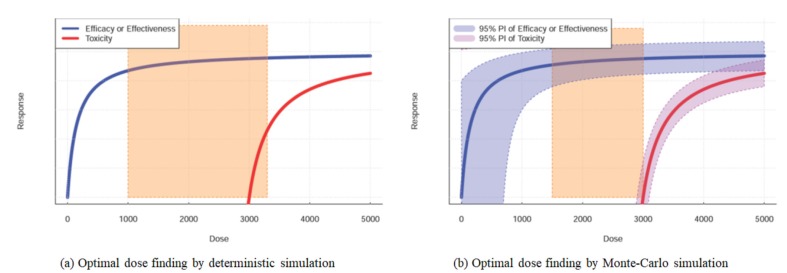
A major application of PK-PD models is in simulation. Simulation is useful for deciphering modeling analysis. The meaning of parameter estimates of a model, which are inter-linked in a non-linear and complex relationship and, therefore, cannot be easily understood per se, is often uncovered through simulation. Another important role of simulation is to predict drug effects under various, still unobserved situations. Nonlinear mixed effect models allow Monte-Carlo simulation by taking unexplained interindividual variabilities into account, and the simulation results are displayed as prediction intervals. For example, the 95% prediction interval of concentration over time indicates the range of observable or model predicted true concentrations at each time point that 95% of the general population could have. The width of a specific prediction interval from Monte-Carlo simulation is determined mainly by the size of unpredictable interindividual variations expressed as omega (Ω) in NONMEM®. Omega, a random effect parameter, indicates the size (in variance) of uncertainty of PK or PD response of an individual, which we are unaware of a priori when prescribing the drug. When a simulation-based decision is made, it is more appropriate to do it based on Monte-Carlo simulation considering interindividual variation—a real biological phenomenon, rather than the more commonly used deterministic simulation which is based only on fixed effect parameters without considering random effect. For example, if we are to determine the optimal dosages based on median (50 percentile) dose-effect and dose-toxicity curve without taking the interindividual variations into account, a lot of patients will experience treatment failure or toxicities due to interindividual variations in does-efficacy and/or dose-toxicity relationship. In this case, it is more reasonable to determine the optimal doses at which even treatment-resistant patient can be cured, while even the patients prone to toxicities do not experience toxicity, which corresponds to 2.5 percentile of prediction intervals for dose-efficacy curve, and 97.5% of those for dose-toxicity curve for example) (Fig. 3).
Figure 3. Differences in optimal doses between Monte-Carlo simulation and deterministic simulation for efficacy and toxicity versus dose curves.
Empirical models, such as compartmental PK model, have been widely used. Empirical modeling is a top-down approach in that it assumed a priori that PK or PD data follow some models with prespecified structures, such as one- or two-compartment PK models, without considering the detailed processes causing the PK or PD data. Although empirical models have been successfully implemented, there has been an increasing need for more accurate characterization of drug candidates and prediction of their efficacy and safety, because the drug development environment has become more competitive. Therefore, characterization of drugs and prediction of treatment efficacy at the earliest were emphasized with decreasing success rate while increasing cost in drug development process, which in turn asks PK and PD model for more predictive capability using early-stage data such as in vitro, preclinical, and early clinical data. Under this background, PBPK and physiologically based PD models, and quantitative systems pharmacology have been increasingly used in drug development.
Whole-body physiologically based pharmacokinetic models
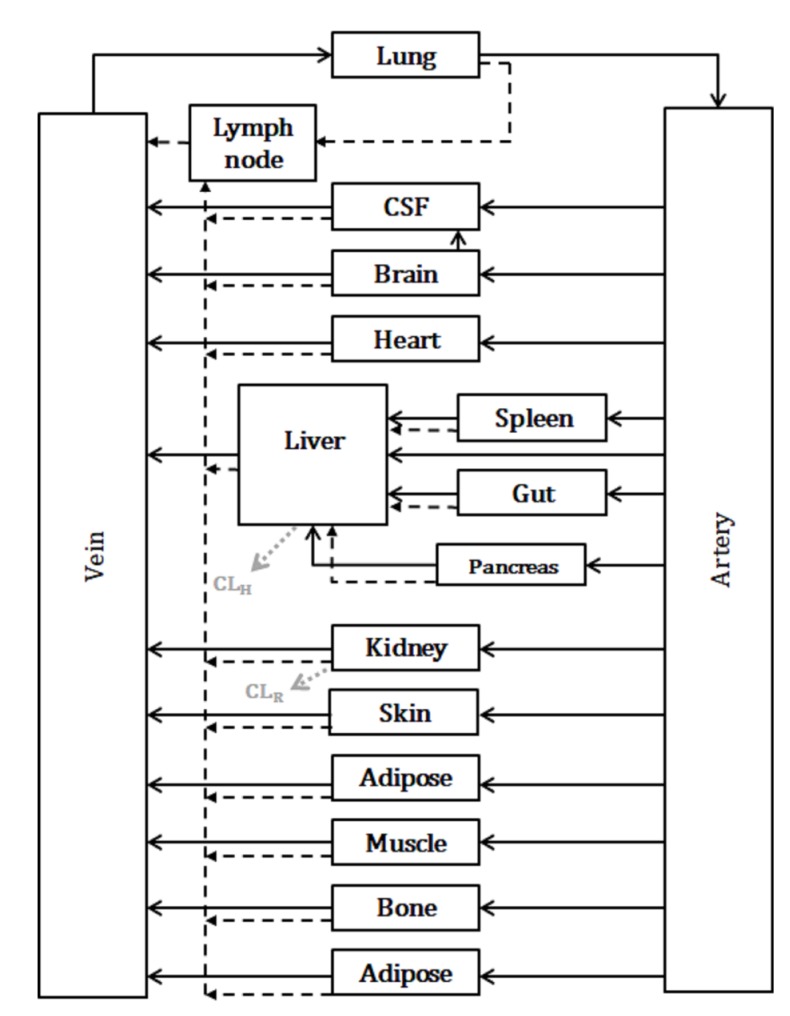
Whole-body PBPK models comprise compartments corresponding to organs inter-connected by blood and lymphatic circulation (Fig. 4). Most small molecules are drained from the interstitial space primarily via blood capillaries, while lymphatic drainage plays a major role in the drainage of larger-sized molecules such as biological agents. For example, the movement of drugs through each organ is expressed typically in differential equations as follows for small molecules.[5]
Figure 4. Diagram of whole-body physiologically based pharmacokinetic (WB-PBPK) model. †Black solid and dotted lines indicate blood flow and lymphatic flow, respectively; gray dotted line indicates clearance usually in small molecules.
For non-eliminating organs:
| VT × dCT / dt = QT × CA − QT × CVT |
where VT is tissue volume; QT is tissue blood flow; CT, CA and CVT are concentrations at tissue, arterial plasma, and tissue venous plasma, respectively.
| CVT = CT / (Kp / RB:P) |
where Kp is tissue to plasma partition coefficient; RB:P is the blood-to-plasma drug concentration ratio.
For eliminating organs:
| VT × dCT / dt = QT × CA − QT × CVT − CLint × CuT |
where CLint is intrinsic clearance; CuT is unbound drug concentration in tissue.
In many cases of PBPK modeling, the organs are sub-compartmentalized into vascular, interstitial, and intracellular spaces, which makes the prediction of drug concentration over time in each sub-compartment possible. This is useful, considering that drug targets are located in a specific sub-compartment. If the receptor of an antibody is mainly expressed extracellularly in a specific target tissue, prediction of drug concentration in the interstitial fluid over time will be more useful to identify optimal drug doses. By combining the PK prediction of interstitial fluid over time and PD data obtained from in vitro exposure-response experiments using target cells, such as changes in biochemical signaling network over time, we could obtain useful information for optimal dosing regimens.
Drug concentration in major organs, which is a useful PK biomarker, can be measured by bioimaging techniques such as positron emission tomography. However, the concentration provided by bioimaging is the average concentration of each organ, which includes vascular, interstitial, and intracellular concentrations. The organ concentrations obtained by bioimaging will be more informative when they are analyzed by PBPK modeling. Through this method, vascular, interstitial, and intracellular concentrations in each organ can be separately predicted.
Acknowledgements
This tutorial was supported by the Technology Innovation Program (grant numbers: 10067737, Establishment of risk management platform with the aim to reduce attrition of new drugs and its service) funded by the Ministry of Trade, Industry & Energy (MI, Korea).
This study was also supported by a grant from the Korea Health Technology R&D Project through the Korea Health Industry Development Institute (KHIDI) which is funded by the Ministry of Health & Welfare, Republic of Korea (grant number: HI14C1090).
We would like to thank Dr. Joon Seo Lim from the Scientific Publications Team at Asan Medical Center for his editorial assistance in preparing this manuscript.
Footnotes
Conflicts of interests: - Authors: The authors declare that they have no conflict of interests
- Reviewers: Nothing to declare
- Editors: Nothing to declare
References
- 1.Milligan PA, Brown MJ, Marchant B, Martin SW, van der Graaf PH, Benson N, et al. Model-based drug development: a rational approach to efficiently accelerate drug development. Clin Pharmacol Ther. 2013;93:502–514. doi: 10.1038/clpt.2013.54. [DOI] [PubMed] [Google Scholar]
- 2.Arrowsmith J. Trial watch: Phase II failures: 2008-2010. Nat Rev Drug Discov. 2011;10:328–329. doi: 10.1038/nrd3439. [DOI] [PubMed] [Google Scholar]
- 3.Arrowsmith J. Trial watch: phase III and submission failures: 2007-2010. Nat Rev Drug Discov. 2011;10:87. doi: 10.1038/nrd3375. [DOI] [PubMed] [Google Scholar]
- 4.Food and Drug Administration. Critical path opportunities report. [Accessed 20 February 2018]. http://www.fda.gov/ScienceResearch/SpecialTopics/CriticalPathInitiative.
- 5.Zhuang X, Lu C. PBPK modeling and simulation in drug research and development. Acta Pharm Sin B. 2016;6:430–440. doi: 10.1016/j.apsb.2016.04.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Rowland M, Peck C, Tucker G. Physiologically-based pharmacokinetics in drug development and regulatory science. Annu Rev Pharmacol Toxicol. 2011;51:45–73. doi: 10.1146/annurev-pharmtox-010510-100540. [DOI] [PubMed] [Google Scholar]