Comparison of Bioimpedance Body Composition in Young Adults in the Russian Children’s Study

Abstract

Background & Aims:

Body mass index is a simple anthropometric measure (kg/m²) used as an indirect estimate of body fat in individuals, and in assessments of population health and comparisons between populations. Bioelectrical impedance analysis (BIA) is often used to provide additional information on body fat and fat-free mass, and has been used to generate body composition reference data in national health surveys. However, BIA measurements are known to be device-specific and there are few published studies comparing results from different BIA instruments. Therefore, we compared the performance of two BIA instruments in the Russian Children’s Study (RCS) of male growth, pubertal development and maturation.

Methods:

Paired BIA measurements were obtained using the Tanita BC-418MA (Tanita Corp., Tokyo, Japan) and ABC-01 ‘Medas’ (Medas Ltd, Moscow, Russia) BIA instruments. Cross-sectional data on 236 RCS subjects aged 18–22 years were used for the BIA comparison and the development of a conversion formula between measured resistances; follow-up data (n=96) were used for validation of the conversion formula.

Results:

Whole-body resistances were highly correlated (Spearman rho=0.95), but fat mass (FM) estimates were significantly higher with the Medas than the Tanita device (median difference 3.3 kg, 95% CI: 2.9, 3.6 kg) with large limits of agreement (LoA) for the FM difference (−2.0, 8.6 kg). A conversion formula between the resistances (Res) was obtained: Medas Res = 0.882×Tanita Res+26.2 (r²=0.91, SEE=17.6 Ohm). After applying the conversion formula to Tanita data and application of the Medas assessment algorithm, the ‘converted’ Tanita FM estimates closely matched the Medas original estimates (median difference −0.1 kg, 95% CI: −0.3, 0.2 kg), with relatively small LoA for the FM difference (−2.3 to 2.1 kg), suggesting potential interchangeability of the ABC-01 ‘Medas’ and Tanita BC-418MA data at the group level.

Conclusions:

Our results support the importance of cross-calibration of BIA instruments for population comparisons and proper data interpretation in clinical and epidemiological studies.

Introduction

Body mass index (BMI; kg/m²) is frequently used as an estimate of body fat in both clinical settings and population studies. However, there are acknowledged shortcomings using BMI to evaluate body composition, e.g. fat mass [1]. Bioelectrical impedance analysis (BIA) measures the passive electrical properties of biological tissues [2], and has been used internationally to assess body fat and fat-free mass. BIA can provide a quick, safe, non-invasive, portable and relatively low-cost technique for the assessment of body composition [3]. BIA instruments have been commercially available since the mid-1980s [4], are manufactured in many countries, and used widely throughout the world [5, 6]. At present, BIA is the most common method of body composition assessment in population and clinical studies, providing a potentially useful tool for assessing body fat and lean mass in epidemiological studies [7, 8].

BIA is used to assess cross-sectional variations in body composition as well as changes in body composition over time in prospective cohort studies [9–12]. Body composition parameters, such as total body water, fat-free mass, fat mass and skeletal muscle mass, are derived from population-specific, built-in validated regression formulae which utilize the measured impedance data and some additional inputs, e.g. height, weight, age, and sex. These formulae are constructed by fitting the regression model to a criterion method [e.g., dual-energy X-ray absorptiometry (DXA) or 4-component (4C) model] using body composition data from a reference population of specific ethnicity, age, weight status and physical activity level [7, 13–15]. In general, BIA has high within-instrument reliability [16, 17]. However, measured parameters and body composition estimates using different BIA instruments may not match closely. Differences in electronic design, measurement conditions/standardization and the body composition assessment formulae which depend on the reference population and the criterion method used [18–20] may hinder between-study comparisons and impact clinical relevance and epidemiological inference.

In Russia, the BIA ABC-01 ‘Medas’ (Medas Ltd, Moscow, Russia) is extensively used in population and clinical studies, while the Tanita BC-418MA (Tanita Corp., Tokyo, Japan) is widely used outside Russia. However, there is a lack of published data comparing the ABC-01 ‘Medas’ analyzer with other BIA instruments, including the Tanita system, which limits comparability across populations. The goals of our study were to compare the performance of the ABC-01 ‘Medas’ and the Tanita BC-418MA using a well-characterized, longitudinal Russian male cohort assessed with parallel BIA measurements using these two instruments at ages 18 to 22 years, to develop a conversion formula between these two sets of BIA measurements, and to test comparability of the BIA body composition data after the conversion. We also compared BIA estimates to body composition data from skinfold measures available in a subset of participants.

Materials and Methods

Russian Children’s Study

The Russian Children’s Study (RCS) is a prospective cohort study of male growth, pubertal development and maturation, and semen quality. 516 boys aged 8 and 9 years who were residents in Chapaevsk, Samara region, Russia, were enrolled from 2003 to 2005 and followed to age 18–19 years, with a subset followed to ages 21–22 years [21–23]. Annual visits included anthropometric and pubertal staging assessments, BIA measurements, and biological sample collection. The study was approved by the local Chapaevsk Institutional Review Board, and the Institutional Review Boards of the Harvard T.H. Chan School of Public Health, and the Brigham and Women’s Hospital. Before participation, the parent/guardian provided informed consent and the boys signed assent forms; at age 18 years the young men signed informed consent forms.

Study subjects

From 2014 to 2017, the Medas instrument was used in parallel to measure BIA with the Tanita instrument on the available RCS participants in order to compare the results between the instruments. In total, 332 paired Tanita and Medas BIA measurements of 236 young men aged 18–22 years were made. Of the participants, 151 were measured once, 74 twice and 11 thrice. All measurements were obtained by the same trained physician and research nurse. Skinfold data was available at the same visit for 115 out of 236 study subjects (49%), with 126 skinfold measurements in total. To compare paired bioimpedance and skinfold data, only a single measurement per subject was utilized in our initial analyses. Among those with measurements at multiple study visits with both BIA and skinfold data, one visit was randomly selected [24]. Cross-sectional data was used for the BIA comparison and the derivation of the conversion formula between the resistances (236 paired BIA measurements). Similarly, in individuals with available skinfold data, BIA body composition data was compared cross-sectionally with skinfold-based body composition estimates (n=115). The remaining follow-up paired BIA measurements (n=96) were used for validation of the conversion formula and for comparison with Russian reference health centers’ (HCs’) data [25].

Anthropometry

Anthropometry was performed annually according to a standardized protocol [26, 27]. Standing height was measured to the nearest 0.1 cm without shoes and socks using a wall-mounted Seca stadiometer (Model 226, Hopkins Medical Products, USA). Weight (Wt) was measured to the nearest 0.1 kg in underwear using a Seca digital scale (Model 700, Vogel & Halke GmbH, Germany). Body mass index (BMI) was calculated (kg/m²). Skinfolds at biceps, triceps, subscapula, suprailium, chest, abdomen, and thigh were measured biannually using a Lange skinfold caliper (Beta Technology, USA) according to standardized protocol [26, 27] to the nearest 0.5 mm.

BIA measurements

The Tanita BC-418MA instrument has been utilized in the RCS since 2006. This 8-electrode body composition monitor utilizes low-amplitude alternating electric current with a frequency of 50 kHz. At the annual physical exam, after fasting overnight, each subject was invited to participate in morning BIA measurements. Each boy stood on the scale barefoot in contact with the 4 electrodes for the feet, dressed in underwear, hands in contact with the 4 electrodes on the handles, and the arms separated from the trunk to prevent contact, as recommended by the manufacturer.

Beginning in 2014 and continuing through 2017, BIA measurements have been obtained on both instruments at the same visit in each boy. The ABC-01 ‘Medas’ device measurements were collected after the Tanita measurement. Medas measurements were obtained in the supine position according to the conventional wrist-to-ankle 4-electrode scheme at an electric current frequency of 50 kHz [28] with the disposable surface bio-adhesive Ag-AgCl ECG electrodes (F3001ECG, FIAB SpA, Italy) placed on the right side of the body.

Body composition

According to the Tanita instruction manual [29], the fat-free mass estimate was obtained using the manufacturer’s proprietary algorithm utilizing regression formulae based on height, weight, age, sex and whole-body resistance between right hand and foot at the electric current frequency of 50 kHz.

In the Medas open assessment algorithm [25], total body water (TBW) is estimated from measured resistance value R50, height (Ht) and weight (Wt) using the following Kushner and Schoeller equation for males [30]: TBW = 0.3963×Ht²/R50 + 0.143×Wt + 8.399. Fat-free mass (FFM) was calculated from TBW assuming constant hydration of FFM according to the formula FFM=TBW/0.732. For both types of BIA instruments, fat mass (FM) was determined by the subtraction of FFM from Wt. The percentage of body weight as fat (%FM) was then calculated. The fat mass index (FMI) and fat-free mass index (FFMI) were assessed as FM and FFM, respectively, divided by height squared.

We did not have criterion data (e.g. DXA or 4C model) to assess the validity of BIA body composition estimates in our study. For the comparison, we applied respective Durnin-Womersley (D-W) [31] and Jackson-Pollock (J-P) [32] anthropometric equations for males based on skinfolds: %FM = 495/(1.1765 − 0.0744×log S₄) − 450, where S₄ is the sum of skinfold thicknesses (mm) measured at the biceps, triceps, subscapula, and suprailium [31], and %FM=495/(1.10938 − 0.0008267×S₃ + 0.0000016×(S₃)² − 0.0002574×Age) − 450, where S₃ is the sum of skinfold thicknesses (mm) measured at the chest, abdomen, and thigh, and Age is the subject’s age (years) [32].

Statistics and data process

Data analysis was performed using Minitab 18.1 and Excel 2010 software programs. For uniformity, standing height was rounded to the nearest integer, as the Tanita BC-418MA instrument utilizes only 3 digits for entering standing height (i.e., without decimals). Descriptive statistics were reported as means and standard deviations (SD), as well as medians and interquartile range (IQR) when data was not normally distributed. The agreement between the Tanita and Medas measured resistance values (Res) and body composition estimates was assessed using Spearman correlation coefficients. A conversion formula between the Medas and Tanita resistances was developed based on fitting a linear regression model. For the conversion formula, a proportion of explained variance (r²) and the standard error of estimate (SEE) were determined. The Tanita ‘converted’ resistance values (i.e., a proxy of paired Medas resistances) were then used in the open Medas body composition assessment algorithm and compared with the Medas original body composition estimates. The RCS original and ‘converted’ bioimpedance data were standardized by calculating z-scores against the Russian reference HCs’ data [25]. For comparisons between the two BIA instruments, a Wilcoxon signed rank test for paired measurements and Bland-Altman analysis [33] were utilized. Mann-Whitney tests were used to conduct comparisons between age groups. Statistical significance was set at p-value ≤ 0.05.

Results

Descriptive statistics of the study participants are shown in Table 1. According to WHO criteria for adults [34], 75% of our subjects were within the normal BMI range, 8.9% were thin, 16.1% overweight, and 4.2% obese.

Table 1.

Anthropometric (n=236) and skinfold (n=115) data for the study population.

Parameter	Mean ± SD	Median (IQR)
Age, yrs	19.7 ± 1.2	19.6 (18.6; 20.6)
Height, cm	177.4 ± 6.7	178.0 (173.0; 182.0)
Weight, kg	69.9 ± 13.5	67.9 (60.8; 75.4)
Body mass index, kg/m2	22.1 ± 3.8	21.6 (19.6; 23.2)
Waist circumference, cm	78.1 ± 8.7	76.5 (72.0; 81.5)
Hip circumference, cm	94.8 ± 8.2	93.5 (89.5; 98.4)
Waist-to-hip ratio	0.82 ± 0.04	0.82 (0.80; 0.85)
Skinfold thickness, mm
Abdominal	16.9 ± 6.6	15.0 (11.5; 21.0)
Biceps	5.7 ± 1.9	5.0 (4.0; 6.5)
Chest	12.9 ± 6.3	11.5 (7.5; 16.0)
Subscapular	10.5 ± 3.7	9.5 (8.0; 12.5)
Suprailiac	10.4 ± 6.0	8.5 (6.0; 12.5)
Thigh	14.0 ± 4.8	13.5 (10.5; 16.5)
Triceps	9.0 ± 3.1	9.0 (6.5; 11.0)

Abbreviations: n (number of measurement records); SD (standard deviation); IQR (interquartile range).

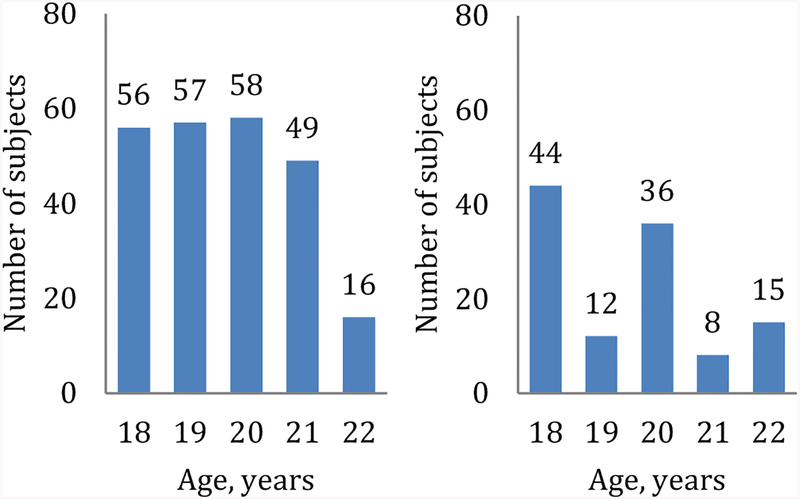
Age distribution of the selected cross-sectional paired BIA measurements (n=236) was nearly uniform, while the associated skinfold data (n=115) were mainly represented by 18 and 20 year olds (see Fig. 1). Most of the remaining paired BIA records (66/96, or 69%) used for validation of the conversion formula were obtained at 19 years of age.

Figure 1.

Age distribution of the study subjects with paired BIA measurements (left panel, n=236) and additional skinfold data (right panel, n=115).

Development of the conversion formula between measured resistances

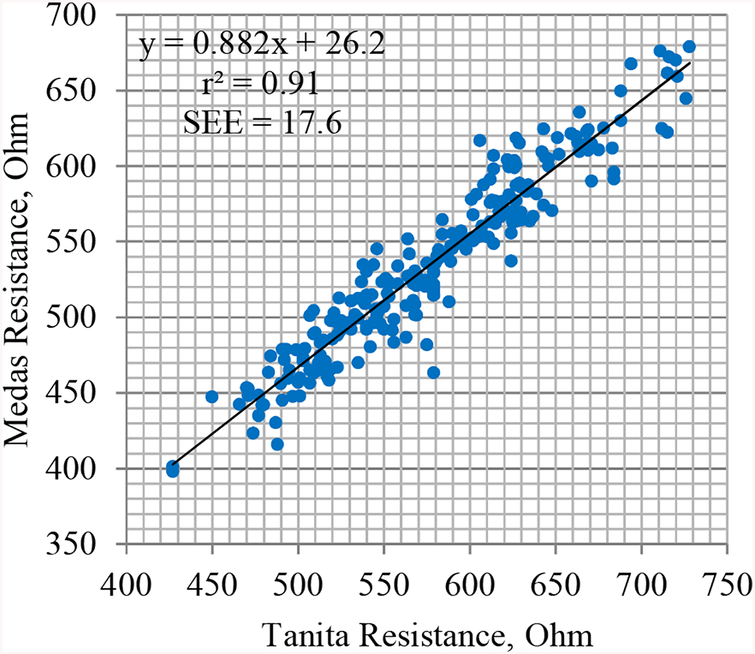
The correlation of ABC-01 ‘Medas’ and Tanita BC-418MA whole-body resistances (Res) was high (Spearman rho=0.95), but the values of Medas Res were significantly lower than the Tanita Res values (see Fig. 2 and Table 2), with the median paired difference of −42.4 Ohm.

Figure 2.

Plot of the Medas vs Tanita whole-body resistance values in our study population, n=236.

Table 2.

Bioimpedance body composition measurements in the Russian Children’s Study participants, n=236.

Parameter	ABC-01 ‘Medas’		Tanita BC-418MA
	Mean ± SD	Median (IQR)	Mean ± SD	Median (IQR)
Res, Ohm	534.9 ± 58.5	527.6a (492.0; 577.2)	577.1 ± 63.3	574.5 (526.5; 624.0)
FFM, kg	57.3 ± 6.6	56.8a (52.6; 61.1)	60.6 ± 8.4	60.1 (54.8; 65.2)
FFMI, kg/m2	18.2 ± 1.7	18.2a (16.9; 19.4)	19.2 ± 2.1	19.1 (17.8; 20.5)
FM, kg	12.4 ± 8.0	10.3a (7.2; 15.0)	9.1 ± 6.6	7.8 (4.5; 11.0)
FMI, kg/m2	3.9 ± 2.4	3.3a (2.3; 4.8)	2.9 ± 2.0	2.5 (1.5; 3.5)
%FM	16.6 ± 6.9	15.4a (11.5; 20.5)	12.2 ± 6.0	11.9 (7.2; 15.5)

Abbreviations: Res (whole-body resistance); FFM (fat-free mass); FFMI (fat-free mass index); FM (fat mass); FMI (fat mass index); %FM (percentage body mass as fat); SD (standard deviation); IQR (interquartile range).

^aStatistically significant difference according to Wilcoxon signed rank test (p<0.01) as compared to the respective TANITA BC-418MA estimate.

We obtained the following conversion formula between the whole-body resistances from the two instruments:

$$\mathit{\text{Medas }}Res=0.882\times \mathit{\text{Tanita }}Res+26.2\left({\text{r}}^2=0.91,\text{ SEE}=17.6\text{ Ohm},\text{ n}=236\right).$$

Similar proportion of explained variance (r²=0.90) and accuracy (SEE=19.3 Ohm) were observed when the Medas original and Tanita converted resistance values were compared for the rest of the paired BIA records, n=96 (data not shown).

Comparison of the original BIA body composition data

Before applying the conversion formula, the Medas body composition estimates in our study population (n=236) differed significantly from those provided by the Tanita instrument, see Table 2. The Medas FFM estimates were significantly lower, while the FM estimates significantly higher than the Tanita estimates (median paired difference=3.2 kg in both cases).

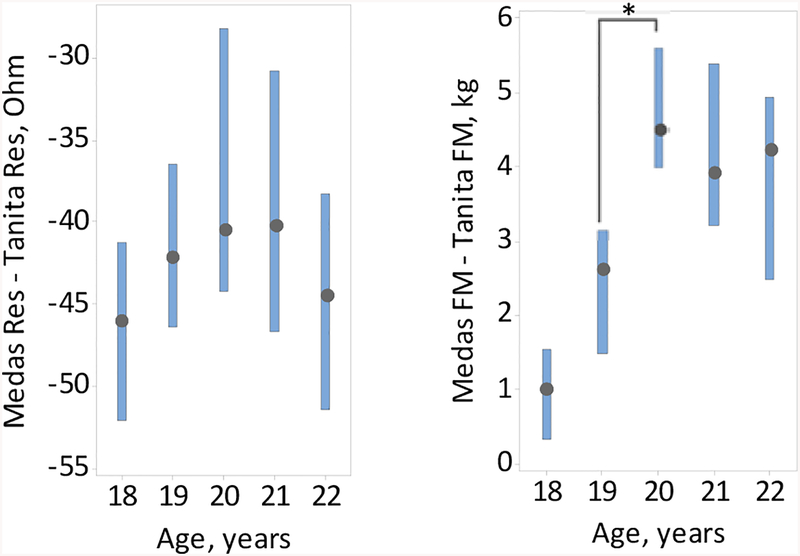
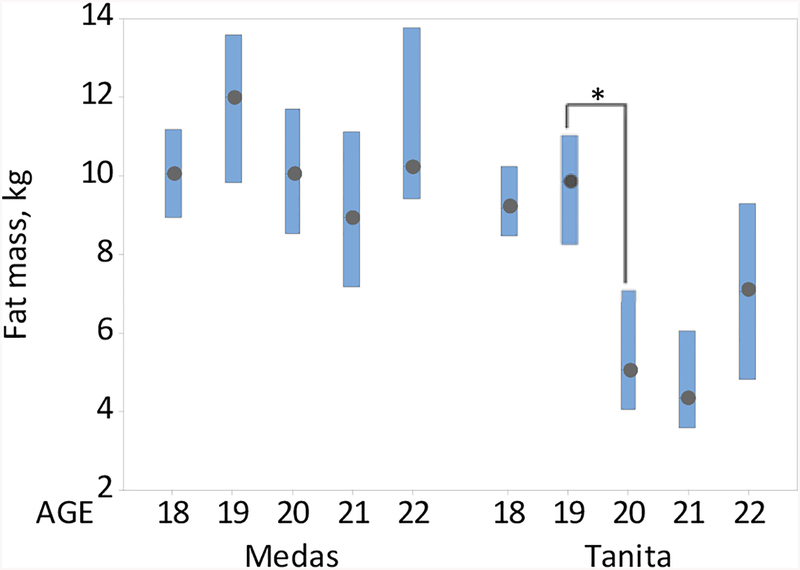
In evaluating age-related trends in BIA as measured by both the Medas and Tanita instruments, the median difference between the Medas and Tanita body composition estimates experienced a jump between age 19 and 20 (see Fig. 3). This jump was associated with the precipitous decline in the Tanita, but not Medas, FM between age 19 and 20 (see Fig. 4), suggesting that the Tanita internal formulas may change starting at age 20. At all ages, overall resistance measures from the Medas instrument were significantly lower and FM estimates were significantly higher than those of the Tanita instrument (see Fig. 4). Accordingly, the Medas FFM estimates were significantly lower than that provided by the Tanita instrument (data not shown).

Figure 3.

Boxplots of the median differences, and the respective 95% CI’s, between the Medas and Tanita resistance values (left panel) and fat mass estimates (right panel) against age, n=236. *Statistically significant difference (p<0.05).

Figure 4.

Boxplots of the Medas and Tanita fat mass against age, medians and the respective 95% CI’s, n=236. *Statistically significant difference (p<0.05).

Comparison of the original BIA and skinfold-based body composition data

In the subgroup with available skinfold data (n=115), the overall Medas FFM, FFMI, FM, FMI, and %FM medians were similar to those obtained using the Durnin-Womersley (D-W) equation, whereas the Tanita estimates were similar to those obtained using the Jackson-Pollock (J-P) equation; however, differences in body composition estimates from skinfolds and BIA were statistically significant in all cases, see Table 3.

Table 3.

BIA vs skinfold-based body composition estimates in Russian Children’s Study participants with both BIA and skinfold measures collected at the same time (n=115, Median (IQR)).

Parameter	ABC-01 ‘Medas’	D-W equation (4 skinfolds)	J-P equation (3 skinfolds)	Tanita BC-418MA
FFM, kg	56.3a (51.4; 60.2)	55.3a,b (50.5; 59.9)	57.7a,b (52.9; 62.7)	58.8b (53.1; 64.1)
FFMI, kg/m2	18.0a (16.8; 19.0)	17.5a,b (16.6; 18.7)	18.5a,b (17.3; 19.4)	18.5b (17.2; 20.1)
FM, kg	9.6a (7.1; 12.0)	9.9a,b (7.2; 13.0)	7.0a,b (4.8; 10.8)	7.2b (4.2; 9.9)
FMI, kg/m2	3.0a (2.2; 3.8)	3.2a,b (2.3; 4.3)	2.3a,b (1.5; 3.4)	2.2b (1.4; 3.1)
%FM	14.7a (11.7; 17.3)	15.2a,b (11.5; 18.9)	11.0a,b (7.9; 15.3)	11.2b (6.8; 13.6)

Abbreviations: FFM (fat-free mass); FFMI (fat-free mass index); FM (fat mass); FMI (fat mass index); %FM (percentage body mass as fat); IQR (interquartile range); D-W (Durnin-Womersley); J-P (Jackson-Pollock).

^aStatistically significant difference as compared to the Tanita BC-418MA estimate (p<0.05).

^bStatistically significant difference as compared to the ABC-01 ‘Medas’ estimate (p<0.05).

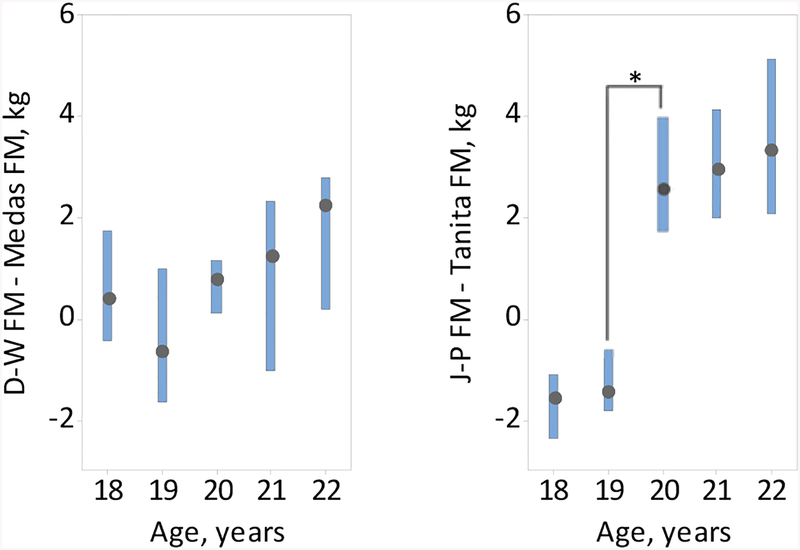
At ages 18–21 years, there was good agreement between the Medas and D-W equation-based FM estimates, but significant differences between the Tanita and J-P equation-based estimates at all ages, see Table 4 and Fig. 5. The observed jump in the Tanita, but not Medas, FM estimate between ages 19 and 20 (see Fig. 4) was not accompanied by a significant change in BMI or skinfold-based FM estimates at the same ages, see Table 4.

Table 4.

BIA vs skinfold-based FM estimates by age at measurement (n=115, Median (IQR)).

Age, years	BMI, kg/m2	Medas FM, kg	D-W FM, kg	J-P FM, kg	Tanita FM, kg
18	20.6 (18.6; 22.3)	9.2a (8.0; 10.0)	9.2a (8.0; 10.8)	6.7a,b (5.0; 7.7)	8.5b (7.8; 9.2)
19	21.4 (18.7; 23.0)	11.3a (5.7; 13.0)	10.5 (5.8; 12.1)	7.9a,b (4.6; 10.0)	9.0b,c (6.4; 10.6)
20	21.3 (19.1; 22.6)	9.6a (8.0; 10.6)	9.9a (8.5; 11.6)	6.8a,b (6.3; 8.6)	4.1b (3.7; 5.0)
21	21.9 (18.8; 24.1)	7.9a (3.5; 19.4)	9.4a (5.3; 17.7)	6.9a (4.3; 15.2)	4.0b (2.2; 12.2)
22	22.1 (20.7; 23.1)	10.4a (9.3; 14.9)	12.9a,b (9.6; 17.3)	11.0a (7.4; 14.4)	7.1b (4.6; 9.6)

Abbreviations: FM (fat mass); IQR (interquartile range); BMI (body mass index).

^aStatistically significant difference as compared to the Tanita BC-418MA estimate for this age group (p<0.05).

^bStatistically significant difference as compared to the ABC-01 ‘Medas’ estimate for this age group (p<0.05).

^cStatistically significant difference as compared to the following age group for the same instrument (p<0.05).

Figure 5.

Boxplots of the median differences, and the respective 95% CI’s, between the D-W and Medas (left panel) and J-P and Tanita fat mass estimates (right panel) against age, n=115. *Statistically significant difference (p<0.05).

Comparison of the Tanita ‘converted’ and Medas original body composition estimates

After the conversion of the Tanita resistance values to equivalent Medas resistances and application of the Medas assessment algorithm, the Tanita ‘converted’ body composition averages closely matched the Medas original averages, see Table 5. Bland-Altman analyses of the agreement between the Medas and Tanita original and ‘converted’ resistances (Res) indicated highly significant trends and large limits of agreement (LoA) in both cases, see Fig. 6 (n=96). However, after the conversion, there was no significant trend between the mean and the difference of the Medas and Tanita ‘converted’ FM (r=−0.08, p=0.44) despite the highly significant trend for the Medas and Tanita original FM data (r=0.75, p<0.001). As a result, the limits of agreement for FM significantly narrowed from −2.5 to 7.5 kg to more acceptable levels (−2.3 to 2.1 kg), see Fig. 6. Insignificant trends and relatively small limits of agreement were also observed for the Medas and Tanita ‘converted’ estimates of FMI (r=−0.08, p=0.46; LoA: −0.7 to 0.7 kg/m²) and %FM (r=−0.07, p=0.47; LoA: −3.2 to 3.1%), while the trends for FFMI (r=0.20, p=0.05; LoA: −0.7 to 0.7 kg/m²) and FFM (r=0.19, p=0.06; LoA: −2.1 to 2.3 kg) were marginally significant.

Table 5.

The Medas original vs Tanita ‘converted’ estimates: the resistances and body composition data, n=96.

Parameter	The Medas original estimates		The Tanita ‘converted’ estimates
	Mean ± SD	Median (IQR)	Mean ± SD	Median (IQR)
Res, Ohm	539.0 ± 63.3	533.3 (487.6; 576.8)	539.6 ± 58.3	533.8 (496.5; 576.8)
FFM, kg	57.7 ± 6.7	57.2 (52.4; 61.8)	57.6 ± 6.5	56.8 (52.5; 61.1)
FFMI, kg/m2	18.1 ± 1.8	18.1 (16.7; 19.4)	18.1 ± 1.7	18.0 (17.0; 19.3)
FM, kg	12.7 ± 7.4	11.1 (7.5; 16.9)	12.8 ± 7.4	10.9 (7.4; 17.1)
FMI, kg/m2	4.0 ± 2.3	3.2 (2.3; 5.5)	4.0 ± 2.3	3.4 (2.3; 5.4)
%FM	17.0 ± 7.0	15.9 (11.8;22.6)	17.1 ± 7.1	15.8 (12.0; 22.4)

Abbreviations: Res (whole-body resistance); FFM (fat-free mass); FFMI (fat-free mass index); FM (fat mass); FMI (fat mass index); %FM (percentage body mass as fat); SD (standard deviation); IQR (interquartile range).

Figure 6.

Bland-Altman analysis of the agreement between the Medas and Tanita Res (upper panels) and the Medas and Tanita FM (lower panels) before (left panel) and after (right panel) application of the conversion formula (n=96). Solid lines represent the mean difference between methods and regression line; dashed lines represent 95% limits of agreement.

Comparison with the Medas Russian reference HCs’ data

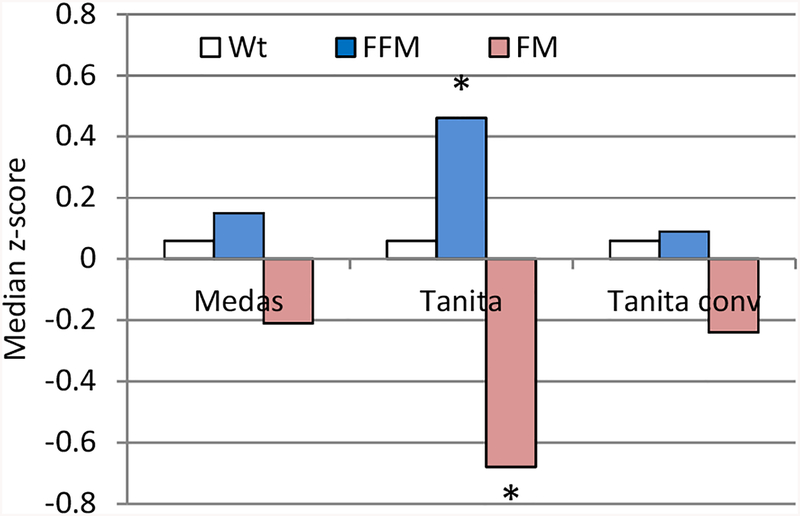
The Tanita ‘converted’ and Medas data on FFM and FM of the RCS study subjects were similar to each other and to the Medas Russian reference HCs’ data [25] while the Tanita original FFM and FM data significantly differed from them (n=96), see Fig. 7.

Figure 7.

Median z-scores of Wt, FFM and FM relative to the Medas body composition Russian HCs’ reference data [29] according to the Medas, Tanita, and Tanita ‘converted’ estimates, n=96. *Statistically significant difference as compared to the Russian reference data (p<0.05).

Discussion

BIA provides a quick, portable, and relatively inexpensive method of estimating body composition [3, 4, 5, 6]. However, potential inconsistency of body composition data because of different instruments [35, 36] is one of the main challenges of using BIA data for clinical nutrition and population studies. BIA equipment currently dominates the market for body composition instruments, with approximately 68% market share in 2017, and is expected to reach even higher rates in the coming years [37] thus making BIA the primary source of body composition data in the present [7, 8] and near future. Therefore, in order to make comparisons across populations, and for possible adjustment of BIA-based diagnostic criteria, it is important to develop methods for the assessment of the data comparability. Our study of potential inter-changeability of BIA data was based on the comparison and adjustment of the physical measurements based on bioimpedance using appropriate formulae. Given our findings, we believe that cross-calibration of BIA instruments is the most convenient way to make existing BIA data from different instruments comparable.

Both the lead-type ABC-01 ‘Medas’ and stand-on Tanita BC-418MA models have been used to generate huge datasets of body composition data for various populations [25, 38–42] thus representing a significant portion of the total BIA data pool. We compared the performance of the ABC-01 ‘Medas’ and Tanita BC-418MA instruments using data from the well-characterized Russian Children’s Study male cohort, and derived a conversion formula between the resistances (Res). The observed difference in the Medas and Tanita original whole-body resistances (mean paired difference of −42.2 Ohm) was much higher than that observed in other studies using the lead-type instruments (RJL/Akern, Xitron 4200) [35] (mean paired difference of −9.9 Ohm). This may be due to the shorter electric current path for the conventional wrist-to-ankle measurement scheme compared to the possible counter-effect of the lying vs standing bioimpedance due to hydrostatic fluid shift [43].

The differences between the resistances (SEE=17.6 Ohm) and the proportion of explained variance (r²=0.91) using our conversion formula were lower than previously reported values (r²=0.99, SEE=5.0–5.3 Ohm) in a classical study using the lead-type instruments (RJL, Valhalla) [35], and are most likely because of the difference in measurement techniques. However, despite the differences in the Medas and Tanita original resistances and body composition estimates, after application of the conversion formula, the Tanita ‘converted’ body composition estimates closely matched the Medas original estimates at the group level, thus suggesting that the ABC-01 ‘Medas’ and Tanita BC-418MA data are comparable.

The above findings demonstrate the feasibility of comparing BIA body composition data from different BIA instruments using a relative scale for comparison which is independent of a specific reference method. Importantly, this was made possible due to the open availability of the Medas assessment algorithm.

Our results also suggest that the age-related non-homogeneity of the Tanita BC-418MA body composition data may be due to differences in their proprietary formula between ages 19 and 20. Application of the same formula is, therefore, necessary to assess dynamic changes in body composition. Because different predictive equations are used for the age groups ‘under 18’ and ‘18+’ in the Medas assessment algorithm [25], a similar effect for the Medas BIA body composition data might be expected between ages 17 and 18, but we had no data to verify this assumption.

For this study, knowledge of only the Medas body composition assessment algorithm was needed. The Tanita BC-418MA algorithm can be estimated from the data, as the general structure of the regression formula for FFM is given in the Tanita manual. Similar to the Medas age-based assessment algorithms, our analysis suggests that there exist two Tanita BC-418MA formulae for FFM for the respective age intervals before and after 20 years old.

We used a cross-sectional design for the longitudinal RCS data analysis because there was sparse parallel longitudinal BIA data. Therefore, we were not able to compare individual trajectories of the BIA data from the two instruments. Because of the absence of a criterion method, the accuracy of BIA body composition estimates was not addressed here. Other conventional ‘directly measured’ analyses and indexes used in clinical nutrition, such as BIVA and phase angle, were not available in our study because the reactance is not measured with the Tanita BC-418MA instrument. Given the limited age range, small sample size, and restriction to males in our study population, additional comparisons are needed to confirm applicability of our robust conversion formula across a wider age range of individuals of both sexes.

Although, Silva et al. [36] found a lack of agreement between different BIA instruments in their study of highly physically active individuals and elite athletes and concluded they should not be used interchangeably at the individual level, our results suggest that body composition data for different BIA instruments is comparable at the group level thus providing important knowledge for nutritional epidemiology. Future studies of variation of body composition globally, in addition to reported worldwide trends in BMI [44], would contribute to planning and monitoring effectiveness of various international nutritional intervention initiatives. Contrary to the dominant paradigm about the role of obesity among populations living in cities, the rising BMI in rural populations has recently been shown to be the main driver of the global obesity epidemic in adults [45]. Comparability of global BIA body composition data may be used to establish which constituents of the BMI, namely, FMI or FFMI, are mainly responsible for the observed changes in BMI among different countries and regions, including urban and rural settings.

BMI is not recommended for diagnosis of obesity at the individual level [46, 47]. The true reference for diagnosing obesity is the percentage of body fat, a component of body composition. The BMI is the sum of FFMI and FMI, and the same BMI values may have different ‘composition’ in terms of FFMI and FMI. Lean mass and fat mass have different associations with mortality [48]. Therefore, body composition data can provide important additional information for health assessment.

Until now, there has been a lack of validated national BIA body composition formulae for the Russian population; instead, external age-, sex-, and ethnic-specific formulae have been used [25]. The development of such formulae will make it possible to clarify patterns of age-related changes, sexual dimorphism and spatial variation of body composition in the Russian population using BIA data.

Taken together, our results support the importance of methods for the adjustment of parameters generated by different BIA instruments for population comparisons and proper data interpretation in clinical and epidemiological studies. The analysis also confirms that, without preliminary cross-calibration, longitudinal changes in BIA body composition need to be assessed using the same BIA instrument while checking the consistency of the built-in assessment algorithm.

Highlights.

• Two BIA instruments were compared in the longitudinal Russian Children’s Study

• Paired ABC-01 Medas and Tanita BC-418MA data were collected in males at 18–22 years

• We observed large differences in original resistances and body composition data

• After conversion, mean body fat measures were comparable between instruments

• Converted BIA data show a potential to assess global variations in body composition

List of Abbreviations

%FM

the percentage of body weight as fat

BIA

bioelectrical impedance analysis BMI – body mass index, kg/m²

CI

confidence interval

DXA

dual-energy X-ray absorptiometry

D-W

Durnin-Womersley

FFM

fat-free mass

FM

fat mass, kg

FFMI

fat-free mass index, kg/m²

FMI

fat mass index, kg/m²

HCs

health centers

Ht

height, cm

IQR

interquartile range

J-P

Jackson-Pollock

LoA

limits of agreement

r²

a proportion of explained variance

RCS

Russian Children’s Study

Res

whole-body resistance, Ohm

SD

standard deviation

SEE

standard error of estimate

TBW

total body water, kg

WHO

World Health Organization

Wt

weight, kg