Highlights
-
•
Age-related changes in the brain regions processing number symbols were investigated.
-
•
Brain activity of a group of 6- to 14-year-old's was measured with fMR-adaptation.
-
•
Ratio-dependent activation in the left IPS correlated with age.
-
•
Age-invariant ratio-dependent activation in the right IPS was found.
-
•
The construction of symbolic number depends on left IPS engagement.
Keywords: Number development, fMRI adaptation, Symbolic numerical magnitude, Intraparietal sulcus (IPS), Number representation, Developmental changes
Abstract
The way the human brain constructs representations of numerical symbols is poorly understood. While increasing evidence from neuroimaging studies has indicated that the intraparietal sulcus (IPS) becomes increasingly specialized for symbolic numerical magnitude representation over developmental time, the extent to which these changes are associated with age-related differences in symbolic numerical magnitude representation or with developmental changes in non-numerical processes, such as response selection, remains to be uncovered. To address these outstanding questions we investigated developmental changes in the cortical representation of symbolic numerical magnitude in 6- to 14-year-old children using a passive functional magnetic resonance imaging adaptation design, thereby mitigating the influence of response selection. A single-digit Arabic numeral was repeatedly presented on a computer screen and interspersed with the presentation of novel digits deviating as a function of numerical ratio (smaller/larger number). Results demonstrated a correlation between age and numerical ratio in the left IPS, suggesting an age-related increase in the extent to which numerical symbols are represented in the left IPS. Brain activation of the right IPS was modulated by numerical ratio but did not correlate with age, indicating hemispheric differences in IPS engagement during the development of symbolic numerical representation.
1. Introduction
Numerical symbols are used in a variety of day-to-day situations. Whether you are calculating the tip for a waiter or setting the time on an alarm clock, numerals are used to guide these behaviours. Initially children view numerical symbols, such as Arabic numerals, as meaningless shapes, but as they learn their meaning (e.g., that symbol ‘3’ refers to the quantity three), rich semantic representations of number symbols and their relationships are developed. What changes in the brain as children develop increasingly fluent representations of culturally derived symbolic numbers?
Over the past years a large body of evidence has demonstrated that the intraparietal sulcus (IPS) of adults is modulated by numerical magnitudes (i.e., the number of items within a set) conveyed by numerical symbols (for reviews see: Ansari, 2008, Dehaene et al., 2003). For instance, modulation of brain activation in the IPS has been observed in tasks in which participants are asked to choose the larger or smaller of two presented numerals (e.g., Ansari et al., 2005, Holloway et al., 2010, Pinel et al., 1999, Pinel et al., 2001). Significant brain activation in the IPS has also been reported in tasks in which symbolic numerical magnitudes are manipulated in the context of calculation—such as mentally subtracting a single digit from a fixed reference number (e.g., Simon et al., 2004, Simon et al., 2002). Moreover, recent evidence has demonstrated that the IPS is engaged in tasks in which adults are asked to estimate the spatial position of a given number on a physical number line (i.e., number line estimation; Vogel et al., 2013), as well as in fMRI-adaptation in which neural signal recovery effects have been demonstrated in response to the presentation of numerical deviants (Holloway et al., 2012, Notebaert et al., 2011). Together, the current evidence from neuroimaging studies in adults suggests that the IPS represents the semantic meaning conveyed by numerical symbols. Additional evidence for the crucial role of the IPS is provided by studies that have demonstrated a relationship between individual differences of brain activation in the IPS and numerical abilities in children (e.g., Bugden et al., 2012, Emerson and Cantlon, 2014). As well, studies with patients have shown that brain damage – also artificially induced by transcranial magnetic stimulation (TMS) – to the parietal lobe impairs numerical abilities (e.g., Cipolotti et al., 1991, Cipolotti and Butterworth, 1995, Kadosh et al., 2007).
Although these studies have revealed important insights into the neural correlates of symbolic numerical magnitude representation in the adult brain, a precise understanding of how the human brain represents symbolic numerical magnitude over developmental time is largely missing. The sparse number of existing developmental imaging studies converge to suggest an ontogenetic reorganization of the functional neuroanatomy underlying symbolic number processing, whereby a shift occurs from an early engagement of prefrontal regions in children to a greater reliance on parietal regions (especially the IPS) in adults (Ansari and Dhital, 2006, Ansari et al., 2005, Holloway and Ansari, 2010, Kaufmann et al., 2006). Commonly this finding is interpreted to indicate an age-related increase in efficiency with which symbolic numerical magnitudes are processed in the brain, whereby the mapping (i.e., the associative connection) between initially arbitrary shapes of numerical symbols and their semantic meaning (i.e., numerical magnitude) is strengthened, while the decrease in prefrontal activation is explained by a reduced reliance on resources supporting the processing of initially weak representation of symbolic numerical magnitude in children.
More recent developmental neuroimaging studies, which have further investigated both symbolic and non-symbolic numerical magnitude processing, have indicated hemispheric differences in the engagement of the parietal lobe. Specifically, in response to numerical symbols developmental changes have been particularly reported in the left IPS (e.g., Emerson and Cantlon, 2014). On the other hand, neuroimaging studies investigating the processing of non-symbolic numerical magnitudes (e.g., dot-arrays) have demonstrated an early recruitment of the right IPS in preverbal infants and young children (Cantlon et al., 2006, Hyde et al., 2010, Izard et al., 2008). These findings suggest that while the right IPS is engaged during non-symbolic numerical magnitude processing from infancy onwards, the left IPS gradually increases in its response to numerical symbols. Thus, developmental changes associated with symbolic and non-symbolic numerical magnitude processing are multifaceted and involve both changes within the parietal cortex as well as a decrease in the engagement of prefrontal regions. Such changes have been argued to reflect the increasing fluency and accuracy of processing numerical magnitude. Evidence for a continued refinement in the precision of symbolic numerical representation over developmental time is provided in behavioural studies that have found age-related changes (i.e., decrease) in the size of the behavioural distance effect1 (Holloway and Ansari, 2008, Moyer and Landauer, 1967). However, the precise neurocognitive mechanisms linking changes in brain activation to behavioural performance remain opaque.
A key limitation of the studies comparing brain activation in children and adults is that developmental studies are extremely sensitive to age-related performance differences in reaction time and accuracy (Poldrack, 2000). As a consequence, it is notoriously difficult to control for general developmental changes in task performance, especially in tasks in which overt decisions – such as choosing the larger number of two presented numerals – are required (Göbel et al., 2004, Göbel and Rushworth, 2004). As such, it is currently unclear whether age-related brain activation differences observed in developmental imaging studies are a reflection of representational changes or a function of age-related non-numerical performance differences. A way to mitigate the confound between age and task performance is to use experimental paradigms such as functional magnetic resonance adaptation (fMR-A) that do not require overt behavioural responses (Grill-Spector et al., 2006, Grill-Spector and Malach, 2001).
FMR-A has been recently used in adults to investigate the neural correlates of symbolic numerical magnitude representation in order to control for non-numerical task demands. Results of these fMR-A studies have provided compelling evidence to suggest that the IPS is modulated by numerical magnitude in the absence of response selection. This research has also demonstrated that predictors that have been widely used to characterize the nature of numerical representations modulate brain activation of the left hemisphere. Specifically, numerical ratio is frequently used to measure the processing of numerical magnitudes in behavioural and neuroimaging studies. A significant increase in brain activation can be observed in number comparison experiments when the discrimination of numerals with a large ratio (e.g., 8 vs. 9: a ratio of 0.89) is contrasted with the discrimination of numerals with a small ratio (e.g., 1 vs. 2: a ratio of 0.5). Since the discrimination of numerical magnitudes is scaled by the numerical ratio between them – smaller ratios are more easily discriminated than larger ratios – it is commonly argued that numerical ratio indicates the approximate nature of noisy and imprecise representations of numerical magnitudes in the human brain (for a review see also Nieder and Dehaene, 2009). Notebaert et al. (2011) used fMR-A to investigate the numerical ratio effect of small numbers (e.g., 3, 4, 5) and large numbers (e.g., 16, 20, 26) in adults. More specifically, the participant's brain response was first adapted to either a small (i.e., the Arabic digit 6) or a large (i.e., the Arabic numeral 32) numerical value. The repeated presentation of this adaptation numeral was then interspersed with the presentation of new numerals (i.e., the numerical deviants) that systematically differed in numerical ratio from the adaptation numeral 6 or 32. A whole brain analysis, using numerical ratio as a predictor, revealed that the left IPS was the only region in the brain that showed a significant ratio dependent neural signal recovery (independent of whether large numbers 16, 20, 26 or small numbers 3, 4, 5 were presented). This result not only showed that the activation of the left IPS was significantly modulated by numerical ratio but, importantly, that the brain activation of the IPS was modulated in the absence of overt response selection.
Additional evidence for left hemispheric lateralization in adults was also reported in a cross-cultural fMR-A study by Holloway et al. (2012). This study revealed a striking hemispheric difference in IPS activation in response to the presentation of Arabic numerals and Chinese ideographs. Two groups were used: a bilingual group capable of reading Chinese and Arabic numerals, and a control group capable of reading Arabic but not Chinese numerals. The symbol 6 was presented repeatedly on a screen to induce adaptation (decrease in neuronal response) in number-sensitive regions. This stream of 6's was interspersed with the presentation of numerical deviants, which differed in numerical ratio from 6. The prediction was that deviants that differed more from the adapted numeral (have a smaller ratio) would be associated with a larger signal recovery in the adapted neuronal response compared to numerals that are close to the adaptation numeral (have a larger ratio)2 . Results demonstrated a significant ratio-dependent signal recovery in the left IPS in response to Arabic numerals across both the bilingual and control groups. However, Chinese ideographs, with which participants were less familiar, elicited a signal recovery exclusively in the right IPS of Chinese participants. In this study both groups had extensive experience with Arabic numerals and exhibited ratio-dependent signal recovery in the left IPS for this condition. The Chinese bilingual group had experience with the Chinese symbols, however, they were less familiar with these symbols than with the Arabic numerals and did not use them routinely in the context of calculation. Therefore, the result of the right lateralized ratio-dependent recovery effect in the bilingual group for Chinese symbols, combined with the left-lateralized effect in the left IPS for Arabic numerals, is suggestive of experience dependent lateralization in the way the parietal lobe of adults represents symbolic numerical formats.
Although neural activation patterns associated with the processing of numerical symbols have been studied in adults, symbolic numerical processing is the outcome of a trajectory of learning and experience. Studies with adult populations are not well suited to explain how representations of symbolic numerical magnitude – such as their fluidity and automaticity – change over the course of learning and development. Developmental neuroimaging studies have recently provided additional evidence for hemispheric lateralization in association with the representation of symbolic numerical magnitude (e.g., Bugden et al., 2012, Emerson and Cantlon, 2014). For instance, a longitudinal study with 4- to 9-year old children revealed a significant correlation between two time points separated by two years in right IPS activation (right IPS activation at time point 1 correlated with right IPS activation at time point 2). The left IPS, however, demonstrated an age related correlation between brain activation and children's numerical discrimination performance (i.e., acuity) as measured by the numerical distance effect (Emerson and Cantlon, 2014).
In view of this, the present study aimed to further investigate age-related changes in the neural correlates of numerical symbol representation in a group of children ranging from 6- to 14-years of age using fMR-A. In contrast to previous studies with children, the present fMR-A work allowed for a more stringent control over non-numerical task demands such as response selection.
In the context of adaptation it is important to note that fMR-A and number comparison experiments have reported different directional effects of numerical ratio on brain activation. More precisely, in fMR-A adaptation, larger signal change has been associated with smaller ratios (e.g., ratio of 0.5), while in number comparison experiments larger brain activation has been associated with larger ratios (e.g., 0.89). The strength of signal change in fMR-A is thought to reflect an approximate representation of numerical magnitudes, that is, numerical deviants that are close (i.e., large ratio) to the adaptation number share more representational overlap compared to numbers that are further apart. Therefore, numbers that are close (i.e., large ratio) to the adaptation number will be partially adapted themselves, leading to a smaller signal recovery than numbers that are further apart (i.e., small ratio). In other words, the further away the numerical deviant is from the adaptation number the larger the signal recovery. As such, one would predict to find a significant ratio-dependent modulation (i.e., smaller ratios elicit a larger signal recovery than larger ratios) of signal recovery in the IPS, if the IPS of children is involved in representing the semantic meaning of numerical symbols in the absence of response selection. Furthermore, it is possible that the acuity of symbolic numerical magnitude representation changes as a function of developmental time. As number representation becomes more accurate, a decrease in the overlap of number representation is to be expected. A decrease in representational overlap would result in an even larger signal recovery in response to far deviants. In other words, the more accurate the number representations (less overlap between numbers) the less adaptation occurs, leading to a larger signal recovery in response to far deviants. Consequently, if the representation of symbolic numerical magnitude has not been fully established by the age of six (the youngest age group in our sample) and does continue to exhibit age-related changes in its acuity, one would expect to see significant developmental changes in the size of the signal recovery effect in regions of the IPS that positively correlate with age. However, it is also possible that the neural representation of numbers is fully developed by the age of six and that no further changes in the representation of symbolic numerical magnitude occur. If this assumption were true, one would predict a stable, age-invariant and significant ratio-dependent modulation of the neural signal recovery in the IPS in response to the presentation of numerical deviants across all ages tested in the present study. Finally, it is possible that both age-invariant and age-dependent activation patterns are obtained, which may vary as a function of cerebral hemisphere.
2. Material and methods
2.1. Participants
We invited 33 healthy children to participate in this study. Out of these 33 participants, nineteen children (7 males and 13 females; ages range 6–14 years; mean age = 10.2 years, standard deviation = 2.55 years) achieved our cut-off criteria for excessive motion (no more than 3 mm overall deviation from the 1st volume acquired within a run and no more than 1.5 mm deviation between subsequent volumes). Moreover, to be included in the statistical analyses, participant's head motion had to be within the cut-off criteria described above in at least 2 out of the 4 functional runs within the scanner. In other words, if a child had only one run with head motion that fell within the exclusion threshold they were not included in the analysis because of a lack of statistical power. In each age cell a minimum of two children were included for each year (i.e., two 6-year-olds, two 7-year-olds, etc.). This age range was chosen so as to include participants with a wide range of formal educational experience. All participants were right-handed and had normal or corrected to normal vision. Participation was reimbursed with fifty dollars in the form of gift cards to a local toy store as well as a picture of their brain from the fMRI session. Informed consent was obtained from parents, as well as a written assent form from children. The procedures of this study were approved by the Human Subjects Research Ethics Board at the University of Western Ontario.
2.2. Stimuli
Stimuli (see Fig. 1) for the present study were created in Adobe Photoshop CS4 and consisted of black (R–G–B colour values: 0, 0, 0) coloured Hindu–Arabic numerals. Numerals were displayed on a silver gray background (R–G–B colour values: 192, 192, 192) with a font size of 40 pt. The presentation software Eprime 2.0 was used to project the stimuli onto a computer screen (resolution = 800 × 600 pixel, colour bit depth = 16) mounted within the MRI scanner. Participants viewed the presentation via a mirror system attached to the head-coil of a 3-Tesla Siemens Tim Trio whole-body MRI scanner.
Fig. 1.
Examples of stimuli used in the paradigm: (a) the adaptation numeral; (b) a numerical deviant with the ratio 2; (c) catch trial with a numeral and a smurf.
2.3. Experimental procedure
Four functional adaptation runs were administered per participant. Each run consisted of the presentation of Arabic digits interspersed with a blank screen (see Fig. 2). The numeral appeared for 200 ms on the screen, the blank screen was displayed for 1200 ms. Stimuli were presented in an event-related fashion with a jittered presentation interval of 5000-to-9000 ms (mean of 7500 ms) in order to oversample the haemodynamic response function.
Fig. 2.
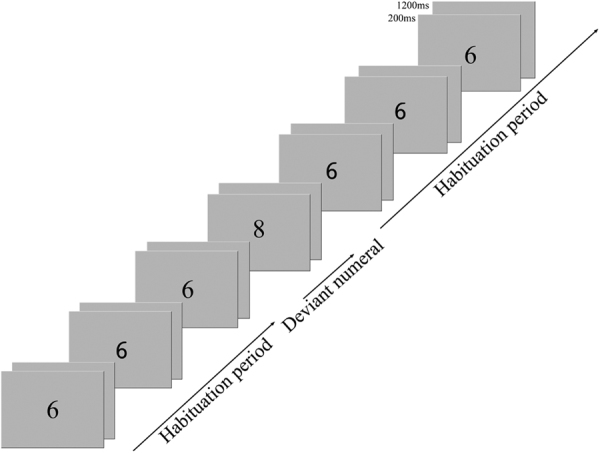
Example stimuli: the continuous presentation of the adaptation numeral “6” (habituation period) was occasionally interspersed with a numerical deviant, in this case the number 8 (ratio 0.75).
Participants’ brain response was habituated through the continuous presentation of the number “6” (i.e., the adaptation phase). The length of the adaptation phase was systematically varied by repeating the presentation of the adaptation numeral “6” between 5 and 9 times, with an overall mean of 7 repetitions across the functional runs. The repeated presentation of the adaptation numeral was randomly interrupted by 18 presentations of a numerical deviant per run (see Table 1), differing systematically in numerical ratio to the adaptation numeral “6”. The systematic manipulation of ratio was subsequently used to investigate ratio-dependent neural recovery effects in response to the presentation of numerical deviants.
Table 1.
Numerals used in the experiment. Each numeral deviates from the adaptation number with a specific numerical-ratio.
| Numerals used in the experiment | 3 | 4 | 5 | 6 | 8 | 9 | 12 |
|---|---|---|---|---|---|---|---|
| Numerical ratio to numeral 6 | 0.5 | 0.67 | 0.83 | 1 | 0.75 | 0.67 | 0.5 |
Ratio was calculated by: smaller/larger number.
Moreover, each functional run contained randomly interspersed catch trials (i.e., numerals with a “Smurf”) and null trials (i.e., the adaptation number “6”). Catch trials consisted of the presentation of a numeral (i.e., the numbers “3”, “4”,”5”,”8”,”9”, and “12”) alongside a picture of a Smurf (see also Fig. 1). The location of the smurf was systematically varied and appeared either on the left-upper, left-lower, right-upper or right-lower corner of the numeral. Participants were instructed to attend to the screen at all times and to press a predefined button with their right index finger whenever: “…a Smurf appeared on the computer screen”. The purpose of the catch trial was to assure a minimum of attentiveness towards stimuli presentation in the scanner. The null trials (i.e., the continued presentation of the number “6”) were used to estimate the baseline signal of the neural recovery effect within the general linear model (GLM). As such, null trials were entered in the parametric predictor in order to assess ratio-dependent deviations from the null trial baseline. Participants were unaware of the presence of the null trials. As with the numerical deviants and the catch trials, the null trials were randomly interspersed across the run and were always part of a train of adaptation.
In order to minimize potential low-level perceptual adaption effects, the font (Times New Roman and Courier New) as well as the spatial location of the numerals (one of six possible locations 2 degrees from the centre of the display; x/y centre-position of the six locations was 435/300, 365/300, 375/325, 425/325, 375/275 and 425/275) were varied throughout the experiment. In addition, the same spatial location did not appear in immediate succession.
2.4. General procedure
Children were familiarized with the MRI environment in a training session, which took place before the scanning day. In the beginning of the training session the experimenter used a picture book, which was specifically created for training and illustration purposes at the Numerical Cognition Laboratory to explain the nature and procedure of fMRI. The first part of this book explains, in a child-friendly way, what an MRI scanner is, what it looks like, how it is operated and what kind of safety precautions are necessary. Furthermore, the anatomical and functional scanning procedures were described, highlighting the importance of lying still in the scanner at all times during the scanning. When children felt comfortable to proceed, a short training programme within a mock 0T-scanner was performed. The mock 0T scanner at the University of Western Ontario allows for a realistic simulation of the scanning procedure without applying a magnetic field. As such, this mock scanner simulates the general environment (e.g., scanning noise, watching through a mirror onto a screen) of a scanning procedure and allows for familiarization as well as for the practice of lying still in the scanner. For this, children were first horizontally positioned into the simulation scanner and then watched a short cartoon movie in order to practice lying still. Verbal feedback was provided when children started to move too much. After this short movement training the adaptation paradigm was simulated. To avoid potential training effects, letters were used instead of numbers. Head motion was monitored at all times and immediate feedback was given when the child moved too much.
At the beginning of the actual scanning session, children were again familiarized with the procedure, using the same photo book as in the training session. In addition, children were prompted to pay attention to the computer screen at all times so that they could make sure “…to catch all the Smurfs hiding between the numbers”. Children were allowed to explore the MRI environment for a short period of time, before they were slowly positioned into the scanner.
2.5. fMRI data acquisition
Structural and functional imaging data were acquired with a 3-Tesla Siemens Tim Trio whole-body MRI scanner. A 32-channel Siemens head coil was used to measure changes in brain activity related to the task. Functional images were collected by using a blood oxygen level dependent (BOLD) sensitive T2* weighted echo planar (EPI SE) sequence. Images were acquired in an ascending—interleaved order covering the whole brain with 38 slices per volume (3 mm thickness, 64 × 64 matrix, repetition time (TR): 2000 ms, echo time (TE): 52 ms, flip angle: 78°). For each functional run 188 volumes were collected, resulting in a total length of 6 min and 16 s per run. High-resolution T1 weighted images were collected using a MPRAGE sequence (1 × 1 × 1 mm, TR: 2300 ms, TE: 4.25 ms, flip angle: 9°).
2.6. Imaging analysis
The entire imaging data set was analysed with the brain imaging software package Brain Voyager QX 2.3 (Brain Innovation, Maastricht, The Netherlands). Preprocessing steps for the functional and anatomical data sets were carried out for each participant individually. All functional images were corrected for slice-scan time acquisition (ascending-interleaved—using a cubic-spline interpolation algorithm), and high-pass (GLM-Fourier) frequency filtered with a cut off value of 2 sines/cosines cycles in order to remove low frequency signals from the data. In addition, participant's head motion parameters were corrected using a Trilinear/sinc interpolation approach. To ensure high data quality, stringent motion criteria were used. In order to be included in the analysis, participant's motion must not exceed 3 mm overall drift from the first volume acquired and must not exceed a volume-to-volume peak jump of 1.5 mm for a given functional run. Furthermore, a minimum of two good functional runs (meeting the criteria described above) were required from each subject to be included in the final analyses (see also Supplemental materials).
Anatomical 3D images were first stripped from the skull (using the implemented brain peeling tool in BV) and the resulting “peeled” brain template was used to automatically align the 3D anatomical image with the functional images of the scan as implemented in the software package Brain Voyager. The quality of the automatic alignment was manually checked for each participant and if necessary corrected manually. For group analysis, the 3D images and the functional runs were transformed into Talairach space (Talairach and Tournoux, 1988) using a Trilinear interpolation algorithm.
2.7. Statistical analysis
In order to investigate the influence that numerical deviants exerted on the brain signal, deviant stimuli were collapsed into four number ratio bins—small ratio, 0.5 (deviants 3 and 12), medium ratio, 0.67 (deviants 4 and 9), large ratio, 0.79 (deviants 5 and 8) and ratio 1 (null event: number 6; the baseline)3 . The bins were then entered as a parametric regressor into a general linear model (GLM) to reveal regions that showed a parametric increase in signal recovery scaled by numerical ratio (this approach was adopted from the study by Holloway et al. (2012) and Notebaert et al. (2011)). Moreover, to explain additional variance in the data, both the smurf catch-trials as well as the participant's individual motion parameters were entered as predictors of no-interest into the same GLM. Finally, all functional events of the GLM were convolved with a two-gamma haemodynamic response function (HRF) in order to predict the blood oxygen level dependent (BOLD) function (Friston et al., 1998) in a random effect (RFX) analysis.
The first statistical analysis aimed to identify those regions in the brain that showed a ratio-dependent neural signal recovery across the entire group independent of chronological age. In other words, this analysis was used to map out which areas of the brain showed a ratio-dependent increase in activation relative to baseline in response to the presentation of numerical deviants across the entire age range sample. To answer this question the parametric regressor of the specified GLM was contrasted against baseline (adaptation period) activation.
The second question aimed to investigate whether regions of the IPS exhibited an age related change in the strength of the ratio dependent neural signal recovery effect. For this analysis, a whole brain correlation analysis between age and the parametric regressor modelling the numerical ratio dependent modulation of the brain signal was performed.
For all analyses reported above, an initial uncorrected threshold of p < 0.005 was used to identify regions that showed a statistical effect. The resulting whole-brain maps of this initial threshold were then corrected for multiple comparisons using cluster size corrections (Forman et al., 1995, Goebel et al., 2006). In this method an initial uncorrected voxel-level threshold is estimated. The statistical whole-brain maps are then submitted to different correction criteria, based on estimates of the map's spatial pre-processing smoothness and on an iterative correction procedure (Monte Carlo simulation) that estimates cluster-level false-positive rates across the entire brain. After 1000 iterations the minimum cluster-size yielding a cluster-level false-positive rate of (α) .05 was used to cluster correct the statistical whole-brain maps. For both analyses, only those voxels whose activation reached a minimum threshold of p < 0.005, uncorrected (cluster corrected at p < 0.05 on whole-brain level) were considered to be significant.
3. Results
3.1. Behavioural results
In order to be included in the study, participants had to catch a minimum of 6 out of 8 smurf catch trials. This behavioural criterion ensured an objective measurement of minimum attentiveness of participants towards the stimuli presentation in the scanner. The children included in the study showed therefore a high accuracy in catching the smurfs (mean: 93.5%; SD = 7.4; max–min = 100–75%). It took the children an average of 643.6 ms (SD = 137.0 ms; max–min = 910.1–470.3 ms) to catch the smurfs. There was a significant positive correlation between age and accuracy (r = 0.47, p = 0.042), as well as a significant negative correlation between age and reaction time (r = −0.84, p < 0.001), indicating that older children were more accurate and faster in detecting the smurfs.
3.2. Imaging results
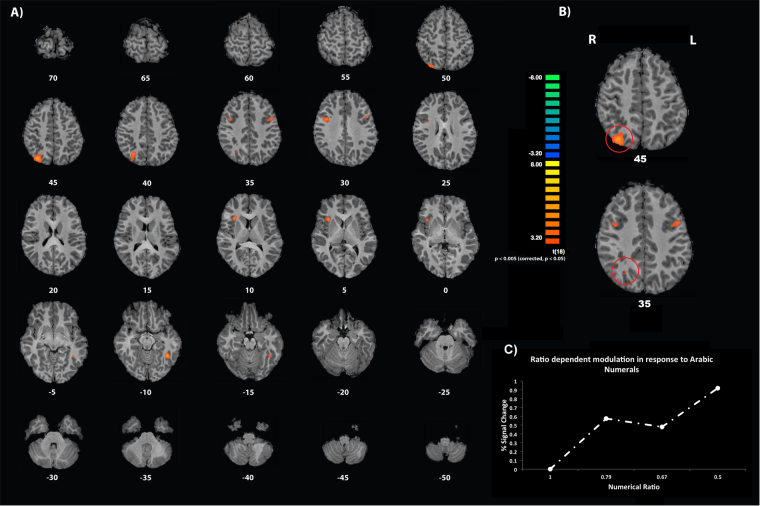
To investigate ratio-dependent neural signal recovery across the entire group, the parametric regressor of numerical ratio was contrasted against baseline activation. Analysis of this contrast revealed 5 clusters that reached the predefined statistical threshold, and, therefore, showed a significant ratio dependent increase in neural recovery in response to the presentation of numerical deviants (see Table 2). Importantly, one out of the five significant regions was situated in the superior parietal lobe (see Fig. 3). Entering the obtained Talairach coordinates into the probabilistic JuBrain-Cytoarchitectonic-Atlas-Viewer (Mohlberg et al., 2012), showed that the peak-voxel of this parietal cluster was located with a probability of 44.62% in a region of the horizontal segment of the intraparietal sulcus.
Table 2.
Talairach coordinates of activation peaks that showed a significant ratio dependent parametric modulation across participants independent of age.
| Cluster label* | Tal. coordinates |
Hemisphere | Lobe | Brodman area | Size*** | t-Value | p-Value | ||
|---|---|---|---|---|---|---|---|---|---|
| x | y | z | |||||||
| Precentral gyrus | 38 | 4 | 30 | R | Frontal | 6 | 736 | 4.751 | <0.001 |
| Superior parietal lobule** | 32 | −71 | 45 | R | Parietal | 7 | 2241 | 5.653 | <0.001 |
| Insula | 32 | 19 | 6 | R | Sub-lobar | 13 | 886 | 5.553 | <0.001 |
| Middle frontal gyrus | −46 | 7 | 33 | L | Frontal | 9 | 468 | 5.066 | <0.001 |
| Fusifrom gyrus | −40 | −47 | −9 | L | Temporal | 37 | 787 | 6.469 | <0.001 |
* Talairach daemon application was used to label anatomical locations according to Talairach coordinates (Lancaster et al., 2000).
** This structure was labelled as hIP3 in the JuBrain Cytoachitectonic Atlas (Mohlberg et al., 2012).
*** Size of the functional clusters relates to the interpolated number of voxels of the high-resolution T1 weighted images.
Fig. 3.
Statistical maps illustrating the numerical ratio dependent brain activations found across the entire group: (a) axial brain slices are arranged from superior to inferior covering the whole brain. Brain slices are labelled according to Talairach coordinates along the z-axis; (b) two brain slices highlighting the activation of the right IPS; (c) parameter estimates reported as percent signal change of the numerical ratio dependent signal recovery (numerical ratio 1 relates to the adaptation number 6).
In addition to the activation found in the parietal lobe, the analysis demonstrated significant parametric signal recovery effects in the right precentral gyrus of the frontal lobe, the right insula, the left middle frontal gyrus of the frontal lobe and in the left fusiform gyrus of the temporal lobe (see also Table 2). Note that the cluster size of the right IPS was the largest of the identified areas.
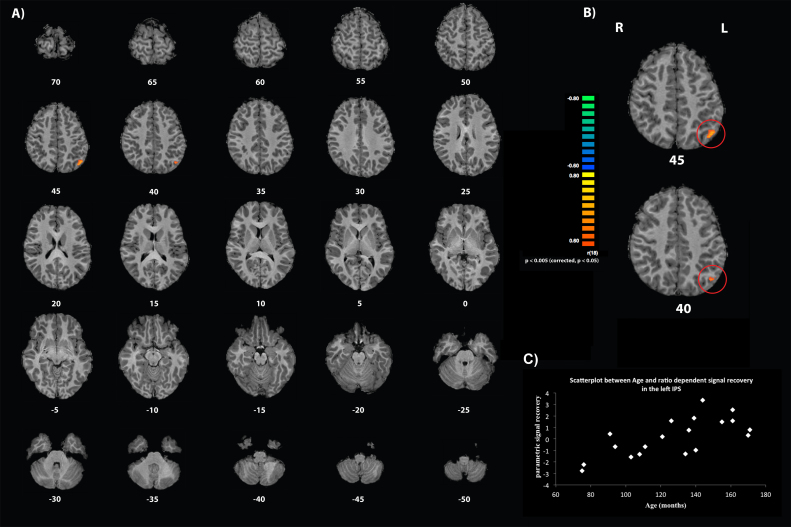
The second whole-brain analysis of the study aimed to investigate age-related changes in the neural signal recovery as a function of the parametric predictor of the numerical deviants. For this, a correlation between age and the parametric predictor was calculated. The results of this analysis revealed a single region in the left parietal lobe (peak-voxel Talairach coordinates (x,y,z): −43, −65, 42; cluster size = 529 voxel) that showed a significant positive whole-brain correlation between age and the extent of the ratio dependent neural recovery effect (see Fig. 4). In other words, this region of the inferior parietal lobe showed an age-dependent increase of signal recovery related to the presentation of numerical deviants (with greater responses to small relative to large ratios). Performing the same post-hoc cytoarchitectonic probability analysis as above revealed that the Talairach coordinates of the peak correlation were situated with a probability of 62.71% in the horizontal segment of the IPS.
Fig. 4.
Whole-brain activation map indicating the significant correlation between age and the parametric effect in the left IPS: (a) axial brain slices are arranged from superior to inferior covering the whole brain. Brain slices are labelled according to Talairach coordinates along the z-axis; (b) two brain slices highlighting the correlation between age and brain estimates of numerical ratio in the left IPS; (c) graph represents the correlation between the parametric parameter estimates of numerical ratio and age4.
Moreover, no negative correlation between age and ratio dependent parametric predictor was identified.
In contrast to the left IPS, the right IPS showed no significant association between age and numerical ratio on the level of the whole brain. Rather, a significant ratio-dependent activation across the entire group (i.e., independent of age) was found in this region of the brain. To further ascertain whether a small, but significant association between age and numerical ratio exists within the right IPS, a correlation analysis between age and numerical ratio was performed within a region of interest (ROI). Specifically, parameter estimates were extracted from the right IPS (revealed in the whole brain analysis) and correlated with participants’ chronological age. The result of this analysis revealed no significant association between numerical ratio and age (r = 0.246, p = 0.309). Further, we tested the possibility of a non-linear relationship between age and numerical ratio by calculating non-linear regressions with a quadratic and cubic term. The analyses demonstrated that neither a quadratic (F(2, 16) = 0.893, p = 0.429) nor a cubic (F(2, 16) = 0.954, p = 0.406) model showed a significant association between age and numerical ratio in the right IPS. Therefore, the results of the ROI and the whole-brain analyses converge to suggest that neither a linear nor a non-linear relationship between age and numerical-ratio exists in the right IPS, thus providing evidence for an age-invariant signal recovery in the right IPS.
While the task in the present study was passive (i.e., adaptation), we did collect behavioural performance data (i.e., reaction time RT and accuracy AC) from participants during the smurf trials. In order to ascertain whether general individual differences in response time and accuracy were associated with signal recovery response to the numerical deviants, we calculated two whole-brain correlations with the performance measurements (i.e., ACs and RTs). Results of these correlation analyses showed that neither reaction time nor accuracy were significantly associated with the ratio-dependent signal recovery in the brain. In other words, the results demonstrate that none of the parietal regions associated with individual differences in chronological age were correlated with between-subjects variability in reaction time or accuracy on the non-numerical smurf trials.
4. Discussion
A growing body of research has explored the neural correlates associated with the representation of symbolic numerical magnitude in adults (for reviews see Dehaene et al., 2003, Nieder and Dehaene, 2009). While much insight has been gained into the brain circuitry associated with symbolic number processing in adults, comparatively little is known about the way the human brain constructs rich semantic representations of numerical symbols over developmental time. The scarce number of developmental studies existing to date have demonstrated a significant shift of the functional neuroanatomy from a greater reliance on prefrontal regions in children to a larger engagement of parietal regions in older children and adults (Ansari et al., 2005, Cantlon et al., 2009, Kaufmann et al., 2006; for a review see Vogel and Ansari, 2012).
The main aim of the present functional magnetic resonance adaptation (fMR-A) study with children was to further constrain our understanding of age-related changes in the neural correlates of symbolic numerical magnitude representation. The fMR-A design (adapted from adult studies by Holloway et al. (2012) and Notebaert et al. (2011)) was used to mitigate the confounding variable of overt response selection, which may have contributed to observed differences in brain activation in previous studies. In addition, by introducing age as a continuous variable, instead of coarse group comparison between groups of children and adults, the present study allowed for a more precise investigation of how the cortical representation of symbolic numerical magnitudes changes as a function of chronological age.
The results of this study yielded two key findings. By investigating numerical ratio-dependent activation across the entire sample, an age-invariant (i.e., across all ages) signal recovery effect in regions of the right intraparietal sulcus (IPS) was found. Second, by correlating chronological age with the magnitude of the ratio-dependent signal recovery, a region on the left IPS was uncovered in which the numerical ratio-dependent signal recovery correlated positively with children's chronological age.
The observed age-related changes in the present study provide novel evidence concerning how semantic representations of symbolic numerical magnitude change as a function of age. The present work demonstrates that children's IPS, similar to adults (Holloway et al., 2012, Notebaert et al., 2011), is a critical cortical substrate underlying the representation of symbolic numerical magnitude in the absence of response selection. It also suggests age-related differences in the roles of the left and the right IPS, as well as the prefrontal cortex in symbolic number processing.
More specifically, the first analysis of this study demonstrated that the brain activation of the right IPS was significantly modulated by the presentation of numerical ratio-dependent deviants across the entire age-range. In other words, the fit of the parametric effect of numerical ratio on brain activation significantly predicted the neural activity in the IPS of the right hemisphere independent of age. The finding of a numerical ratio-dependent signal recovery in the right IPS suggests a relatively early involvement (the youngest participants were 6 years of age) of the right IPS in processing and representing the meaning of symbolic numerical magnitudes. As such it is plausible that the engagement of the right IPS indicates a crucial and maybe foundational role in mapping numerical symbols onto the magnitudes they represent. Consistent with this idea are developmental studies with infants and children that have demonstrated an early engagement of the right parietal lobe in response to non-symbolic numerical magnitudes, such as arrays of dots or squares (Cantlon et al., 2006, Hyde et al., 2010).
For instance, Hyde et al. (2010) used functional near-infrared spectroscopy and a non-symbolic (i.e., dot arrays) numerical magnitude adaptation design to investigate brain responses of 6-month-old infants. The results of that study showed that the activation of the right parietal lobe was significantly modulated by changes in the number of the presented dot arrays, indicating a possible early role of the right parietal lobe for processing non-symbolic numerical magnitude. A similar finding was also reported by an fMR-A study with 4-year-old children, which found converging evidence for a right lateralized activation of the parietal lobe in response to non-symbolic numerical magnitude (Cantlon et al., 2006). In light of these results the engagement of the right IPS in the present study might be explained by an early mapping between a functional brain system that represents non-symbolic/approximate numerical magnitude and the numerical symbols to which they refer. However, since the present study did not directly investigate this specific association (symbolic and non-symbolic processing in children), this interpretation of the present data remains speculative. To further elucidate this possibility, direct empirical testing in young children using symbolic and non-symbolic numerical magnitude stimuli would be of interest.
The second whole-brain analysis of the present study demonstrated a significant positive correlation between age and the numerical ratio dependent signal recovery in the IPS of the left hemisphere. This result indicates an increase in the size of signal recovery as a function of children's chronological age and suggests developmental changes in the acuity of the underlying cortical representation of symbolic numerical magnitudes. Numerical ratio dependent neural signal recovery effects within regions of the left IPS have been previously found in adults (Holloway et al., 2012, Notebaert et al., 2011), suggesting that the left IPS of adults is important for the semantic representation of numerical symbols. The finding of a left lateralized developmental change clearly extends this knowledge and provides further evidence to suggest that lateralization effects in adults may be an outcome of a developmental trajectory, which may be related to an increase in experience and the acuity/fluency with which symbolic numerical magnitudes are processed.
In addition to these findings in adults, there is emerging evidence from developmental fMRI studies demonstrating age-related hemispheric lateralization in the IPS. In a longitudinal fMRI study, Emerson and Cantlon (2014) recently demonstrated developmental differences in right and left IPS activation in children ranging from 4- to 9-years of age. More specifically, children were instructed to decide whether presented number pairs, consisting of dots and digits, were the same or different across these different notations. The authors were able to show that the brain activation of the right IPS was significantly correlated over a 1–2 year period in young children, whereas the brain activation of the left IPS continued to be modulated over developmental time and as a function of children's numerical discrimination acuity. Together with the reported results of the presented work, the study by Emerson and Cantlon (2014) indicates an early and possibly stable activation of the right IPS, while protracted developmental changes in the representation of symbolic numerical magnitude occur in the left. In addition, the findings by Emerson and Cantlon (2014) indicate that age-related changes in the left IPS are associated with more accurate representations of symbolic numerical magnitude and that this refinement of representations is associated with numerical skills. This finding is largely in line with the result of the present work demonstrating an age-related change in the acuity of signal recovery in the left IPS over developmental time. Therefore, the age-dependent change observed in the left IPS may be related to ongoing refinement of symbolic numerical magnitude representation. This developmental pattern of IPS involvement provides increasing evidence for the hypothesis that brain activation of the left IPS is crucial for a mature system of numerical symbol processing (Ansari, 2007, Chochon et al., 1999, Dehaene and Cohen, 1995).
The developmental changes in the left IPS demonstrated in the current study may reflect an experience-dependent process in which children gain a more refined understanding of the semantic information that is conveyed by numerical symbols. Experience dependent lateralization effects have also been observed in other culturally transmitted domains – such as reading (Dehaene and Cohen, 2011, Dehaene et al., 2010, Nuñez et al., 2011, Spironelli and Angrilli, 2009) – indicating that experience dependent specialization is common amongst culturally mediated domains. The acquisition of symbolic numerical magnitude knowledge may thereby go well beyond an initial mapping account between symbolic and non-symbolic representation (possibly mediated by the right hemisphere). Rather, it may encompass the integration of other non-magnitude related dimensions such as ordinality (i.e., the knowledge that number 5 comes before the number 6 but after the number 4) and language in order to construct fluent and efficient symbolic numerical knowledge (Lyons et al., 2012, Lyons and Beilock, 2011). There is increasing evidence that the semantics conveyed by numerical symbols (and therefore the numerical ratio effect) may contain information that go beyond a simple association between symbols and the non-symbolic numerical magnitude they refer to. For instance, there is emerging evidence that the sequential relationship between numbers (i.e., ordinal information between the symbols: 2 comes before 3 but after 1) is another critical dimension that is conveyed by numerical symbols (Lyons and Beilock, 2013, Lyons et al., 2014). As such, it can be argued that the developmental processes related to symbolic numerical representation may consist of a combination of different relevant dimensions. For instance, two recent published studies showed that mathematical achievement in grades 1 and 2 was best predicted by behavioural symbolic numerical magnitude discrimination abilities (Lyons et al., 2014, Vogel et al., 2015). In contrast, by grade 6, measurements of numerical order processing (i.e., the relationship between the numbers in the number sequence) systematically became the most important predictor of mathematical achievement in children (Lyons et al., 2014). As such, these data point towards a developmental crossover in the relative importance of numerical magnitude and numerical order processing in children and their relationship to mathematical proficiency. The differential engagement of the right and left IPS may be reflective of this development and may explain recent findings that demonstrated a significant relationship between individual differences in the children's activation of the IPS during symbolic number comparison tasks and their levels of mathematical achievement (Bugden et al., 2012). However, the precise nature of right and left IPS engagement and the mechanisms underlying developmental changes in the left IPS in the present work remain opaque; future research is required.
Moreover, while previous developmental neuroimaging studies have found a shift from prefrontal regions in children to parietal regions in adults (Ansari et al., 2005, Cantlon et al., 2009, Holloway and Ansari, 2010, Kaufmann et al., 2005, Kaufmann et al., 2006), the present study did not reveal a negative correlation between chronological age and signal recovery in the prefrontal cortex. While the absence of an effect is difficult to interpret, this null result may nevertheless indicate that previously observed frontal activations in number comparison tasks may not be related to developmental changes of symbolic numerical magnitude representation per se or the mapping between numerical magnitudes and their symbolic referents. Rather, in view of the present findings, it is plausible that regions of the prefrontal cortex are related to domain general processes such as selecting the correct stimuli for response execution. In the present study no response selection was required and no negative correlation between age and activation was found in prefrontal regions of the brain. This might suggest that age-related changes in the parietal cortex are specific to processing numerical symbols and symbolic numerical magnitude representation. Age-related changes in the prefrontal cortex however may be associated with age-related changes in response-selection and task performance that may not be number-specific.
Lastly, the results of the present study highlight the importance of using adequate designs in order to reduce and to eliminate confounding variables in developmental imaging studies (Poldrack, 2000). The striking specificity of brain activation observed in the present study, but also in the studies of Notebaert et al. (2011) and Holloway et al. (2012), demonstrates the additional value that can be gained when confounding variables such as response selection are mitigated. For instance, hemispheric differences in brain activation of the left and right IPS have been largely inconsistent in previous developmental studies (Ansari et al., 2005, Holloway and Ansari, 2010). This inconsistency might be due to the fact that most developmental imaging studies have used coarse group comparisons (i.e., comparing groups of children with wide age ranges to groups of adults) in addition to active numerical paradigms, which in combination may have washed out consistent hemispheric differences. Controlling for these variables may in fact draw a clearer picture of how the left and right IPS interact in order to generate symbolic numerical magnitude representation. The present study provides the first clear evidence that age-related changes in the neural representation of symbolic numerical magnitude are largely restricted to the left hemisphere.
However, the results of the present work trigger a set of new and unanswered questions surrounding the mechanisms that may underlie age-related changes within the left IPS. While the adaptation paradigm used in the present study eliminates common confounds – such as performance differences or response selection – alternative cognitive processes such as attention or differences in strategy use remain potential confounds and cannot entirely be ruled out. For instance, it is possible that older children repeat the presented numerals in their head more explicitly compared to younger children. As a consequence it remains somewhat unclear which precise cognitive mechanism underlies the observed age-related change in the left IPS. Moreover, it is unclear to which extent factors such as schooling (e.g., grade level), intelligence or levels of mathematical abilities contribute to the observed changes in the left IPS. These are all factors that need to be considered in future investigations to better understand the precise mechanisms that underlie the development of symbolic numerical magnitude representation in the left IPS. Answering these questions requires the inclusion of additional data (from behavioural to neuroimaging) to investigate the potential influence of these factors on age-related changes in brain activation. The present work provides an important foundation upon which to conduct further investigations into the mechanisms that drive age related changes in the brain. It is not possible from the present results to tease out the exact mechanisms driving the association between ratio-dependent brain response and chronological age. However, an analysis investigating the correlation between performance on the control (smurf) trials and brain activation did not reveal any associations between reaction time or accuracy and numerical ratio dependent brain activation in the parietal regions associated with ratio-dependent modulation. This suggests that the age-related parietal response observed in the present study cannot be attributed to general performance differences between individuals.
Taken together, the results of the present fMR-A study in children demonstrate a protracted and dynamic development of how the brain represents the meaning of numerical symbols between 6 and 14 years of age. Specifically, while the right IPS is modulated by the semantics of Arabic numerals at all ages (from 6 onwards), activation in the left IPS increases as a function of chronological age. This finding suggests an age-related developmental specialization of the left IPS for representing symbolic numerical magnitude. This age-related trajectory in brain activation may be reflective of an increase in fluency/acuity with which numerical magnitude is processed in the child's brain, pointing towards a more precise and richer representation as children age. This finding is largely consistent with behavioural findings that have demonstrated developmental changes in the fluidity with which symbolic numerical magnitudes are processed (Holloway and Ansari, 2008, Holloway and Ansari, 2009, Moyer and Landauer, 1967). In contrast to previous studies, which have investigated age-related changes underlying the processing of symbolic numerical magnitudes, the present study did not reveal a significant decrease in prefrontal brain activation as a function of numerical ratio and age. This may suggest that aforementioned findings of an association between the prefrontal cortex and age-related changes in numerical magnitude processing are unrelated to the process of constructing a semantic representation of symbolic numerical magnitude. As such, the findings of the present study open up a new set of interesting questions that could shed more light on how the human brain constructs symbolic numerical magnitude representation over developmental time.
While the findings indicate developmental changes particularly in the left IPS, there are clear limitations in interpreting developmental effects of symbolic numerical magnitude representation in a cross-sectional study. An important next step to test developmental changes in the cortical representation of symbolic numerical magnitude representation would be to measure changes in brain activity across a longitudinal sample. Moreover, the exact role and interplay between the left and the right IPS is still a mystery and additional investigations with new data analyses, such as functional connectivity, may shed new light on this issue. Although there has been evidence for a significant association between numerical magnitude processing in active number comparison tasks and mathematical achievement, it is entirely unknown whether such an association can also be found on the level of brain representation measured with fMR-A. For instance, it might be the case that acting on numbers – as in number comparison tasks – is the link between mathematical achievement and brain activation. Together, the present findings highlight the importance of developmental studies in order to further constrain our knowledge of symbolic numerical magnitude representation and to identify the exact mechanism that may guide the development of culturally transmitted representations of numerical symbols.
Conflict of interest statement
None to declare.
Acknowledgements
This research was supported by operating grants from the Natural Sciences and Engineering Research Council of Canada (NSERC) and the Canadian Institutes of Health Research (CIHR) to DA. Furthermore, additional support was provided by the Ontario Graduate Scholarship program to SV as well as the Canada Research Chairs (CRC) Program to DA.
Footnotes
No further inferential statistics were conducted on the parameter estimates plotted in Fig. 4, Panel C. The data are plotted to display the correlation, as requested by one of the reviewers of the manuscript.
Available online 10 December 2014
This is an open-access article distributed under the terms of the Creative Commons Attribution-NonCommercial-No Derivative Works License, which permits non-commercial use, distribution, and reproduction in any medium, provided the original author and source are credited.
The numerical distance effect describes an inverse relationship between the numerical distance of two numerals being compared and the time it takes to choose the larger or smaller of the presented numbers. The size of the numerical distance effect is commonly used as an indicator for the accuracy/fluency with which numbers are represented.
Please note that opposite directions of the numerical ratio effect on brain activation have been reported in tasks in which numbers are actively compared (i.e., number comparison) and in passive adaptation paradigms in which participants merely attend to the presentation of numbers. In adaptation designs greater signal changes is associated with smaller ratios, while larger brain activation has been found for larger ratios in number comparison studies.
Please note that for purposes of modelling an increasing parametric effect of numerical ratio on brain activation (i.e., larger brain activation for smaller ratios), ratio bins were mathematically redefined by dividing the larger number by the smaller number. For example, the number combination 3 and 6 was entered with a value of 2 (larger/smaller number) instead of 0.5 (smaller/larger number) as response predictor in the parametric model.
Supplementary data associated with this article can be found, in the online version, at http://dx.doi.org/10.1016/j.dcn.2014.12.001.
Appendix A. Supplementary data
The following are the supplementary data to this article:
References
- Ansari D. Does the parietal cortex distinguish between 10, ten, and ten dots? Neuron. 2007;53(2):165–167. doi: 10.1016/j.neuron.2007.01.001. [DOI] [PubMed] [Google Scholar]
- Ansari D. Effects of development and enculturation on number representation in the brain. Nat. Rev. Neurosci. 2008;9(4):278–291. doi: 10.1038/nrn2334. [DOI] [PubMed] [Google Scholar]
- Ansari D., Dhital B. Age-related changes in the activation of the intraparietal sulcus during nonsymbolic magnitude processing: an event-related functional magnetic resonance imaging study. J. Cogn. Neurosci. 2006;18(11):1820–1828. doi: 10.1162/jocn.2006.18.11.1820. [DOI] [PubMed] [Google Scholar]
- Ansari D., Garcia N., Lucas E., Hamon K., Dhital B. Neural correlates of symbolic number processing in children and adults. NeuroReport. 2005;16(16):1769–1773. doi: 10.1097/01.wnr.0000183905.23396.f1. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/16237324〉. [DOI] [PubMed] [Google Scholar]
- Bugden S., Price G.R., McLean D.A., Ansari D. The role of the left intraparietal sulcus in the relationship between symbolic number processing and children's arithmetic competence. Dev. Cogn. Neurosci. 2012;2(4):448–457. doi: 10.1016/j.dcn.2012.04.001. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon J.F., Brannon E.M., Carter E.J., Pelphrey K.a. Functional imaging of numerical processing in adults and 4-y-old children. PLoS Biol. 2006;4(5):e125. doi: 10.1371/journal.pbio.0040125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantlon J.F., Libertus M.E., Pinel P., Dehaene S., Brannon E.M., Pelphrey K.a. The neural development of an abstract concept of number. J. Cogn. Neurosci. 2009;21(11):2217–2229. doi: 10.1162/jocn.2008.21159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chochon F., Cohen L., van de Moortele P.F., Dehaene S. Differential contributions of the left and right inferior parietal lobules to number processing. J. Cogn. Neurosci. 1999;11(6):617–630. doi: 10.1162/089892999563689. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/10601743〉. [DOI] [PubMed] [Google Scholar]
- Cipolotti L., Butterworth B. Toward a multiroute model of number processing: impaired number transcoding with preserved calculation skills. J. Exp Psychol.: Gen. 1995;124(4):375–390. [Google Scholar]
- Cipolotti L., Butterworth B., Denes G. A specific deficit for numbers in a case of dense acalculia. Brain. 1991;114:2619–2637. doi: 10.1093/brain/114.6.2619. (A Journal of Neurology) Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/1782535〉. [DOI] [PubMed] [Google Scholar]
- Dehaene S., Cohen L. Towards an anatomical and functional model of number processing. Math. Cognit. 1995;1:81–120. [Google Scholar]
- Dehaene S., Cohen L. The unique role of the visual word form area in reading. Trends Cogn. Sci. 2011;15(6):254–262. doi: 10.1016/j.tics.2011.04.003. [DOI] [PubMed] [Google Scholar]
- Dehaene S., Pegado F., Braga L.W., Ventura P., Nunes Filho G., Jobert A. How learning to read changes the cortical networks for vision and language. Science. 2010;330(6009):1359–1364. doi: 10.1126/science.1194140. [DOI] [PubMed] [Google Scholar]
- Dehaene S., Piazza M., Pinel P., Cohen L. Three parietal circuits for number processing. Cogn. Neuropsychol. 2003;20(3):487–506. doi: 10.1080/02643290244000239. [DOI] [PubMed] [Google Scholar]
- Emerson R.W., Cantlon J.F. Continuity and change in children's longitudinal neural responses to numbers. Dev. Sci. 2014:1–13. doi: 10.1111/desc.12215. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Forman S.D., Cohen J.D., Fitzgerald M., Eddy W.F., Mintun M.A., Noll D.C. Improved assessment of significant activation in functional magnetic resonance imaging (fMRI): use of a cluster-size threshold. Magn. Reson. Med. 1995;33(5):636–647. doi: 10.1002/mrm.1910330508. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/7596267〉 Official Journal of the Society of Magnetic Resonance in Medicine/Society of Magnetic Resonance in Medicine. [DOI] [PubMed] [Google Scholar]
- Friston K.J., Fletcher P., Josephs O., Holmes a., Rugg M.D., Turner R. Event-related fMRI: characterizing differential responses. NeuroImage. 1998;7(1):30–40. doi: 10.1006/nimg.1997.0306. [DOI] [PubMed] [Google Scholar]
- Göbel S.M., Johansen-Berg H., Behrens T., Rushworth M.F.S. Response-selection-related parietal activation during number comparison. J. Cogn. Neurosci. 2004;16(9):1536–1551. doi: 10.1162/0898929042568442. [DOI] [PubMed] [Google Scholar]
- Göbel S.M., Rushworth M.F.S. Cognitive neuroscience: acting on numbers. Curr. Biol.: CB. 2004;14(13):R517–R519. doi: 10.1016/j.cub.2004.06.042. [DOI] [PubMed] [Google Scholar]
- Goebel R., Esposito F., Formisano E. Analysis of functional image analysis contest (FIAC) data with BrainVoyager QX: from single-subject to cortically aligned group general linear model analysis and self-organizing group independent component analysis. Hum. Brain Mapp. 2006;27:392–401. doi: 10.1002/hbm.20249. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grill-Spector K., Henson R., Martin A. Repetition and the brain: neural models of stimulus-specific effects. Trends Cogn. Sci. 2006;10(1):14–23. doi: 10.1016/j.tics.2005.11.006. [DOI] [PubMed] [Google Scholar]
- Grill-Spector K., Malach R. fMR-adaptation: a tool for studying the functional properties of human cortical neurons. Acta Psychol. 2001;107(1–3):293–321. doi: 10.1016/s0001-6918(01)00019-1. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/11388140〉. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Ansari D. Domain-specific and domain-general changes in children's development of number comparison. Dev. Sci. 2008;11(5):644–649. doi: 10.1111/j.1467-7687.2008.00712.x. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Ansari D. Mapping numerical magnitudes onto symbols: the numerical distance effect and individual differences in children's mathematics achievement. J. Exp. Child Psychol. 2009;103(1):17–29. doi: 10.1016/j.jecp.2008.04.001. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Ansari D. Developmental specialization in the right intraparietal sulcus for the abstract representation of numerical magnitude. J. Cogn. Neurosci. 2010;22(11):2627–2637. doi: 10.1162/jocn.2009.21399. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Battista C., Vogel S.E., Ansari D. Semantic and perceptual processing of number symbols: evidence from a cross-linguistic fMRI adaptation study. J. Cogn. Neurosci. 2012;25(3):388–400. doi: 10.1162/jocn_a_00323. [DOI] [PubMed] [Google Scholar]
- Holloway I.D., Price G.R., Ansari D. Common and segregated neural pathways for the processing of symbolic and nonsymbolic numerical magnitude: an fMRI study. NeuroImage. 2010;49(1):1006–1017. doi: 10.1016/j.neuroimage.2009.07.071. [DOI] [PubMed] [Google Scholar]
- Hyde D.C., Boas D.a., Blair C., Carey S. Near-infrared spectroscopy shows right parietal specialization for number in pre-verbal infants. NeuroImage. 2010;53(2):647–652. doi: 10.1016/j.neuroimage.2010.06.030. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Izard V., Dehaene-Lambertz G., Dehaene S. Distinct cerebral pathways for object identity and number in human infants. PLoS Biol. 2008;6(2):e11. doi: 10.1371/journal.pbio.0060011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kadosh R.C., Kadosh K.C., Schuhmann T., Kaas A., Goebel R., Henik A., Sack A.T. Report virtual dyscalculia induced by parietal-lobe TMS impairs automatic magnitude processing. Curr. Biol. 2007;17:1–5. doi: 10.1016/j.cub.2007.02.056. [DOI] [PubMed] [Google Scholar]
- Kaufmann L., Koppelstaetter F., Delazer M., Siedentopf C., Rhomberg P., Golaszewski S. Neural correlates of distance and congruity effects in a numerical Stroop task: an event-related fMRI study. NeuroImage. 2005;25(3):888–898. doi: 10.1016/j.neuroimage.2004.12.041. [DOI] [PubMed] [Google Scholar]
- Kaufmann L., Koppelstaetter F., Siedentopf C., Haala I., Haberlandt E., Zimmerhackl L.-B. Neural correlates of the number-size interference task in children. NeuroReport. 2006;17(6):587–591. doi: 10.1097/00001756-200604240-00007. Retrieved from 〈http://www.pubmedcentral.nih.gov/articlerender.fcgi?artid=2853705&tool=pmcentrez&rendertype=Abstract〉. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lancaster J.L., Woldorff M.G., Parsons L.M., Liotti M., Freitas C.S., Rainey L. Automated Talairach atlas labels for functional brain mapping. Hum. Brain Mapp. 2000;10(3):120–131. doi: 10.1002/1097-0193(200007)10:3<120::AID-HBM30>3.0.CO;2-8. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons I.M., Ansari D., Beilock S.L. Symbolic estrangement: evidence against a strong association between numerical symbols and the quantities they represent. J. Exp Psychol.: Gen. 2012;141(4):635–641. doi: 10.1037/a0027248. [DOI] [PubMed] [Google Scholar]
- Lyons I.M., Beilock S.L. Numerical ordering ability mediates the relation between number-sense and arithmetic competence. Cognition. 2011;121(2):256–261. doi: 10.1016/j.cognition.2011.07.009. [DOI] [PubMed] [Google Scholar]
- Lyons I.M., Beilock S.L. Ordinality and the nature of symbolic numbers. J. Neurosci. 2013;33(43):17052–17061. doi: 10.1523/JNEUROSCI.1775-13.2013. (The Official Journal of the Society for Neuroscience) [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lyons I.M., Price G.R., Vaessen A., Blomert L., Ansari D. Numerical predictors of arithmetic success in grades. Dev. Sci. 2014;(1–6):1–13. doi: 10.1111/desc.12152. [DOI] [PubMed] [Google Scholar]
- Mohlberg, H., Eickhoff, S. B., Schleicher, A., Zilles, K., & Amunts, K. (2012). A new processing pipeline and release of cytoarchitectonic probabilistic maps - JuBrain. In OHBM 2012. Peking, China.
- Moyer R.S., Landauer T.K. Time required for judgements of numerical inequality. Nature. 1967;215(2):1519–1520. doi: 10.1038/2151519a0. Retrieved from 〈http://www.nature.com/nature/journal/v215/n5109/abs/2151519a0.html〉. [DOI] [PubMed] [Google Scholar]
- Nieder A., Dehaene S. Representation of number in the brain. Ann. Rev. Neurosci. 2009;32:185–208. doi: 10.1146/annurev.neuro.051508.135550. [DOI] [PubMed] [Google Scholar]
- Notebaert K., Nelis S., Reynvoet B. The magnitude representation of small and large symbolic numbers in the left and right hemisphere: an event-related fMRI study. J. Cogn. Neurosci. 2011;23(3):622–630. doi: 10.1162/jocn.2010.21445. [DOI] [PubMed] [Google Scholar]
- Nuñez S.C., Dapretto M., Katzir T., Starr A., Bramen J., Kan E. fMRI of syntactic processing in typically developing children: structural correlates in the inferior frontal gyrus. Dev. Cogn. Neurosci. 2011;1(3):313–323. doi: 10.1016/j.dcn.2011.02.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pinel P., Dehaene S., Rivière D., LeBihan D. Modulation of parietal activation by semantic distance in a number comparison task. NeuroImage. 2001;14(5):1013–1026. doi: 10.1006/nimg.2001.0913. [DOI] [PubMed] [Google Scholar]
- Pinel P., Le Clec’ G.H., van de Moortele P.F., Naccache L., Le Bihan D., Dehaene S. Event-related fMRI analysis of the cerebral circuit for number comparison. NeuroReport. 1999;10(7):1473–1479. doi: 10.1097/00001756-199905140-00015. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/10380965〉. [DOI] [PubMed] [Google Scholar]
- Poldrack R.A. Imaging brain plasticity: conceptual and methodological issues—a theoretical review. NeuroImage. 2000;12(1):1–13. doi: 10.1006/nimg.2000.0596. [DOI] [PubMed] [Google Scholar]
- Simon O., Kherif F., Flandin G., Poline J.-B., Rivière D., Mangin J.-F. Automatized clustering and functional geometry of human parietofrontal networks for language, space, and number. NeuroImage. 2004;23(3):1192–1202. doi: 10.1016/j.neuroimage.2004.09.023. [DOI] [PubMed] [Google Scholar]
- Simon O., Mangin J.F., Cohen L., Le Bihan D., Dehaene S. Topographical layout of hand, eye, calculation, and language-related areas in the human parietal lobe. Neuron. 2002;33(3):475–487. doi: 10.1016/s0896-6273(02)00575-5. Retrieved from 〈http://www.ncbi.nlm.nih.gov/pubmed/11832233〉. [DOI] [PubMed] [Google Scholar]
- Spironelli C., Angrilli A. Developmental aspects of automatic word processing: language lateralization of early ERP components in children, young adults and middle-aged subjects. Biol. Psychol. 2009;80(1):35–45. doi: 10.1016/j.biopsycho.2008.01.012. [DOI] [PubMed] [Google Scholar]
- Talairach J., Tournoux P. Thieme; New York, NY: 1988. Co-planar Stereotaxic Atlas of the Human Brain. [Google Scholar]
- Vogel S.E., Ansari D. Neurocognitve foundations of typical and atypical number processing. Lernen und Lernstoerungen. 2012;1(2):135–149. [Google Scholar]
- Vogel S.E., Grabner R.H., Schneider M., Siegler R.S., Ansari D. Overlapping and distinct brain regions involved in estimating the spatial position of numerical and non-numerical magnitudes: an fMRI study. Neuropsychologia. 2013;51(5):979–989. doi: 10.1016/j.neuropsychologia.2013.02.001. [DOI] [PubMed] [Google Scholar]
- Vogel S.E., Remark A., Ansari D. Differential processing of symbolic numerical magnitude and order in first-grade children. J. Exp. Child Psychol. 2015;129:26–39. doi: 10.1016/j.jecp.2014.07.010. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.