A fitting machine learning prediction model for short-term mortality following percutaneous catheterization intervention: a nationwide population-based study

Abstract

Background

A suitable multivariate predictor for predicting mortality following percutaneous coronary intervention (PCI) remains undetermined. We used a nationwide database to construct mortality prediction models to find the appropriate model.

Methods

Data were analyzed from the Taiwan National Health Insurance Research Database (NHIRD) covering the period from 2004 to 2013. The study cohort was composed of 3,421 patients with acute myocardial infarction (AMI) diagnosis undergoing PCI. The dataset of enrolled patients was used to construct multivariate prediction models. Of these, 3,079 and 342 patients were included in the training and test groups, respectively. Each patient had 22 input features and 2 output features that represented mortality. This study implemented an artificial neural network model (ANN), a decision tree (DT), a linear discriminant analysis classifier (LDA), a logistic regression model (LR), a naïve Bayes classifier (NB), and a support vector machine (SVM) to predict post-PCI patient mortality.

Results

The DT model was found to be the most suitable in terms of performance and real-world applicability. The DT model achieved an area under receiving operating characteristic of 0.895 (95% confidence interval: 0.865–0.925), F1 of 0.969, precision of 0.971, and recall of 0.974.

Conclusions

The DT model constructed using data from the NHIRD exhibited effective 30-day mortality prediction for patients with AMI following PCI.

Introduction

Coronary heart disease is a major public health concern, especially in developed countries (1). Consequently, percutaneous coronary intervention (PCI) is one of the most extensively and increasingly used procedures (2), and it is indicated as the primary treatment for ST-elevation myocardial infarction (STEMI) and also for non-STEMI, atypical chest pain, stable angina, unstable angina, and positive stress tests (3). With advances in technology, periprocedural complications of PCI have declined and patients often achieve favorable outcomes (4). However, mortality risk following PCI continues to be a major concern. A risk model for predicting mortality following PCI could assist clinicians in better timed and more appropriate care delivery, as well as greater awareness of high-risk groups (5,6).

Many PCI mortality risk models have been proposed (7-15). Studies have shown that incorporating angiographic features and multiple biomarkers enhances prediction power (15,16-18). Because 50% of the mortality following PCI is due to non-cardiac reasons, creating a model that accounts for general complications post PCI appears optimal for predicting in-hospital mortality (9).

In recent years, multivariate prediction models including artificial neural network models (ANN), decision trees (DT), linear discriminant analysis classifiers (LDA), logistic regression models (LR), naïve Bayes classifiers (NB), and support vector machines (SVM) have been used in medicine (19-22). Being used a nonlinear statistical model to identify variable patterns, ANNs are the most commonly used method among these methods (23-26). However, Freeman et al. used ANN to predict in-hospital deaths following percutaneous transluminal coronary angiography (27). In their study, they did not find ANN to be superior to the LR model. With the widely used and advancing techniques of percutaneous catheterization intervention, conducting a nationally representative population study to determine an appropriate prediction model for short-time mortality following PCI is of vital importance.

The Taiwan National Health Insurance Research Database (NHIRD), with >99% coverage, includes longitudinal medical and procedure information of all insured participants (28) in a database. We aimed to find the best prediction model in predicting predict 30-day risk of mortality from the pre-PCI and post-PCI data of patients with acute myocardial infarction (AMI) who underwent PCI.

Methods

Data source

Taiwan’s National Health Insurance (NHI) program began in March 1995 and now offers comprehensive medical coverage to all residents in Taiwan (29). The study cohort was selected from the Longitudinal Health Insurance Database 2000 (LHID2000) of the NHI program. The LHID2000 comprises 1,000,000 randomly sampled people enrolled in the NHI program, and it collected all medical records of these individuals from 2004 to 2013. Disease diagnoses were identified and coded using the International Classification of Diseases, 9th Revision, Clinical Modification (ICD-9-CM).

Ethics statement

The NHIRD encrypts each patient’s personal information to protect privacy and provides researchers with anonymous identification numbers associated with relevant claims information, including sex, date of birth, medical services received, and prescriptions. Therefore, patient consent is not required to access the NHIRD. This study was approved to fulfill the condition for exemption by the Institutional Review Board (IRB) of China Medical University (CMUH104-REC2-115-CR4). The IRB also specifically waived the consent requirement.

Sampled participants

We identified patients with AMI (ICD-9-CM code 410) aged >18 years who underwent PCI intervention between January 1, 2000, and December 31, 2013. The date of the PCI intervention was assigned as the index date. A total of 3,421 patients who underwent PCI intervention including culprit lesion and multivessel PCI were enrolled in our study.

Predictive factors

Postoperative complications were defined as diagnosis or mortality occurring within 30 days after the date of PCI intervention. Complications included upper gastrointestinal bleeding, acute kidney injury that required dialysis, new onset of arrhythmia, and ICU admission. Baseline comorbidities and surgeries associated with mortality before the index date included hyperlipidemia, hypertension, diabetes mellitus, chronic obstructive pulmonary disease, heart failure, stroke, atrial fibrillation, obesity, chronic kidney disease/end-stage renal disease, peripheral arterial occlusion disease, history of PCI, coronary artery bypass graft (CABG), and intra-aortic balloon bump (IABP). Long-term medications used at baseline were also considered, including aspirin, warfarin, and clopidogrel. The aforementioned baseline comorbidities, previous interventions, previous surgeries, and 30-day postoperative complications were confirmed on the basis of ICD-9-CM codes. Each one of these predictive factors comprise the 22 features used later in the prediction models.

Statistical analysis

Chi-square test was employed to compare the differences in the distribution of PCI type, age, sex, comorbidities, and 30-day postoperative complication between patients with and without 30-day postoperative mortality. In addition, the t-test was used to compare the differences of mean ages between the two groups.

Data construction

This study comprised 3,421 patients who underwent PCI, each of whom is represented by a data point. There are 22 features per data point; the features comprised of the patients’ sex, comorbidities, medications taken, and 30-day postoperative complications. To accurately determine the performance of prediction models, the patients were split into training and test sets at a ratio of approximately 9:1. Of all 3,421 patients undergoing PCI procedure, 3,079 patients were included in train set and 342 patients were included in the test set. The use of 10% of the dataset for the test set was modeled after several research papers in the field, including research done by Avati et al. (29). Instead of splitting the data into training, validation, and test subsets and performing holdout cross-validation on the validation set, we decided to split the data into training and test sets and perform k-fold cross-validation, which is an improvement over the traditional train-validation-test split cross-validation method (30). The k-fold cross validation (k=10) weighted accuracy is stated in Table 1.

Table 1. The k-fold cross validation (k=10) weighted accuracy of all prediction models.

Model	Weighted accuracy
ANN	0.963
DT	0.949
LDA	0.944
LR	0.795
NB	0.420
SVM	0.831

ANN, artificial neural network; DT, decision tree; LDA, linear discriminant analysis classifier; LR, logistic regression; NB, naïve Bayes classifier; SVM, support vector machine.

The output data is unbalanced with a bias toward 30-day survival. To ensure that the prediction models did not skew toward the dominant class, weighting was applied to the data set prior to training. Since the ratio of 30-day death to 30-day survival was 1:26.368, each 30-day survival data point was weighted approximately 26 times greater than each 30-day death data point.

Algorithms and training

To select the hyperparameters that yield the best performance for each prediction model, we used k-fold cross-validation with a k value of 10. Owing to the limited data, k-fold cross-validation was used instead of holdout cross-validation.

ANN

We used a fully-connected multilayer perceptron (MLP) feedforward network to train the data. Our model consisted of one input layer of 22 dimensions, a hidden layer of 11 dimensions, and an output layer of 2 dimensions. During the model selection process, we also experimented with a different number of layers and more complicated ANNs such as convolutional neural networks and recurrent neural networks. However, we find that neither other types of neural networks nor ANNs with more layers exceed the performance of an MLP with three layers. Therefore, we chose the simplest model with the best performance.

The network was trained using stochastic gradient descent and optimized with Adam with default parameters outlined by Kingma et al. (30). Each layer used the scaled exponential linear unit activation function (31) except the output layer, which used the softmax activation function. A dropout of 20% was applied for the input layer and 50% for the output layer (32). Because the problem was a binary classification task, the categorical cross entropy error function was used as the loss function. The network was train for 1,600 epochs. The ANN model was implemented with the TensorFlow library (version 1.9.0) (33).

DT

The DT model used Gini impurity to measure the quality of split. The minimum samples per leaf was set to 1, while the minimum number of samples required to split a node was set to 2. The maximum depth was set to 7. While DTs with a larger maximum depth could be used, we found out that having a depth greater than 7 resulted in DTs that tended to overfit the train set. The DT model was implemented with the scikit-learn framework (version 0.19.1) (34).

LDA

The LDA used a singular value decomposition (SVD) solver to create a linear decision boundary. A SVD solver was used instead of an eigenvalue decomposition solver because calculating a covariance matrix with eigenvalue decomposition is slow with a large number of features (22). The LDA model was implemented with the scikit-learn framework (version 0.19.1) (34).

LR

The LR model used a L₂ regularization penalty with primal formulation. Primal formulation was used because there are more samples than features. Stochastic average gradient descent was used as the optimizer. The one-vs-rest scheme was used as the loss function. The regularization strength was set to 1.0, and the model was trained for 100 iterations before convergence. The LR model was implemented using the scikit-learn library (version 0.19.1) (34) and the LIBLINEAR library (version 3.21) (35).

NB

The NB classifier is a multinomial NB. A multinomial model was used instead of a Gaussian model because all of the features, except age, are discrete. The NB software was implemented using the scikit-learn library (version 0.19.1) (34).

SVM

The SVM model is a C-support vector classification (C-SVC) model that used a radial basis function (RBF) as its kernel. We also evaluated a nu-support vector classification (nu-SVC) model, but we found a C-SVC model to have a better classification performance. In order to compare the performance of the SVM model to all other models, probability estimates were enabled to plot the ROC curve. The shrinking heuristic was enabled to save training time by bounding the optimal solution. The SVM model was implemented using the LIBSVM library (version 3.21) (36).

Evaluation of prediction model performance

Because the data distribution was heavily skewed toward the positive class, the accuracy could not reliably measure prediction model performance (37). Instead, the weighted averaged F₁, precision, and recall values were used to measure prediction model performance. These three confusion matrix metrics were calculated across all data, the train set, and the test set for each model.

Additionally, the receiving operating characteristic (ROC) curve was also used as a metric to measure prediction model performance. The Area Under ROC (AUROC) of each model was compared with each other, and then the AUROC of the prediction models were compared with the AUROC of comorbidities with clinical relevance or association with PCI. This is done to demonstrate the necessity of using multivariate prediction models in this study. IBM SPSS 24.0 (SPSS, Inc., Chicago, IL, USA) was used to calculate the ROC and AUROC.

Results

Demographic features

The majority of the patients underwent culprit lesion (83.2% vs. 80.9%) and were aged ≥65 years (72.0% vs. 49.2%). The mean ages of the death group and non-death groups were 72.2 and 64.5 years, respectively, and most of the patients were men. Compared with the non-death group, the death group tended to have more comorbidities, surgeries, and 30-day postoperative complications, including stroke, history of CABG and IABP, dialysis-requiring acute kidney injury, arrhythmia, and ICU admission. By contrast, compared with the death group, the non-death group was more likely to have hyperlipidemia and history of PCI, as well as to require clopidogrel medication. The characteristics of the data set are shown in Table 2.

Table 2. Characteristics of acute myocardial infarction patients undergoing PCI intervention with 30-day postoperative mortality.

Variable	Death					P value
	No (N=3,296)			Yes (N=125)
	n	(%)		n	(%)
PCI						0.52
Culprit lesion	2,666	80.9		104	83.2
Multi-vessel PCI	630	19.1		21	16.8
Age, mean (SD) (year)*	64.5 (13.6)			72.2 (13.0)		<0.001
Gender						0.03
Women	783	23.8		40	32.0
Men	2,513	76.2		85	68.0
Comorbidity
Hyperlipidemia	2,044	62.0		64	51.2	0.01
Hypertension	2,496	75.7		100	80.0	0.27
Diabetes mellitus	1,085	32.9		42	33.6	0.87
Chronic obstructive pulmonary disease	774	23.5		30	24.0	0.89
Heart failure	707	21.5		26	20.8	0.86
Stroke	1,203	36.5		63	50.4	0.002
Atrial fibrillation	158	4.8		8	6.4	0.41
Obesity	60	1.8		1	0.8	0.24
Chronic kidney disease/ESRD	364	11.0		19	15.2	0.15
PAOD	372	11.3		19	15.2	0.18
History of PCI	2,628	79.7		88	70.4	0.01
History of CABG	95	2.9		17	13.6	<0.001
History of IABP	223	6.8		50	40.0	<0.001
Medications
Aspirin	3,278	99.5		124	99.2	0.71
Warfarin	212	6.4		9	7.2	0.73
Clopidogrel	3,243	98.4		113	90.4	<0.001
30-day postoperative complication
Upper gastrointestinal bleeding	94	2.9		1	0.8	0.17
Acute kidney injury	78	2.4		22	17.6	0.01
Arrhythmia	512	15.5		28	22.4	0.04
Admitted to ICU	124	3.8		10	8.0	0.02

Chi-square test, *, t-test comparing subjects with and without death. PCI, percutaneous coronary intervention; ESRD, end stage renal disease; PAOD, peripheral arterial occlusive disease; CABG, coronary artery bypass graft; IABP, intra-aortic balloon bump.

Evaluation of prediction models

The weighted k-fold cross validation (k=10) weighted accuracy of all prediction models are listed in Table 1. The models with the highest weighted accuracies are the ANN model (0.963), DT model (0.949), and LDA model (0.944), while the model with the lowest weighted accuracy is the NB model (0.420).

The F₁, precision, and recall values of all prediction models are listed in Table 3. The DT model has the highest overall F₁, precision, and recall values compared to all other models. For both the LR and ANN models, the precision values are significantly higher than the recall values. Since precision represents the positive predictive value and the recall represents the negative predictive value, the LR and ANN models may be overfitting the data. This hypothesis is supported by the fact that the F₁ values for the ANN and LR models are the lowest of all predictors.

Table 3. The F₁, precision, and recall values for all prediction models used in this study.

Dataset	Metric	ANN	DT	LDA	LR	NB	SVM
All (n=3,421)	F1	0.841	0.969	0.948	0.848	0.906	0.903
	Precision	0.955	0.971	0.948	0.957	0.947	0.957
	Recall	0.770	0.974	0.948	0.780	0.875	0.867
Train (n=3,079)	F1	0.843	0.960	0.948	0.852	0.906	0.906
	Precision	0.956	0.956	0.947	0.956	0.946	0.960
	Recall	0.772	0.965	0.949	0.786	0.875	0.870
Test (n=342)	F1	0.829	0.968	0.946	0.815	0.911	0.875
	Precision	0.950	0.969	0.950	0.960	0.954	0.921
	Recall	0.754	0.973	0.941	0.730	0.880	0.842

ANN, artificial neural network; DT, decision tree; LDA, linear discriminant analysis classifier; LR, logistic regression; NB, naïve Bayes classifier; SVM, support vector machine.

The ROC of all prediction models across all data is outlined in Table 4. The model with the highest AUROC is the DT model (0.895, 95% CI: 0.865–0.925), followed by the SVM model (0.882, 95% CI: 0.855–0.909) and the LR model (0.855, 95% CI: 0.827–0.883). The ROC curve is shown in Figure 1.

Table 4. The receiving operating characteristic of all prediction models used in this study across all data.

Model	AUROC	AUROC SE	AUROC 95% CI
ANN	0.828	0.019	0.790–0.866
DT	0.895	0.015	0.865–0.925
LDA	0.841	0.017	0.807–0.875
LR	0.855	0.014	0.827–0.883
NB	0.810	0.018	0.775–0.846
SVM	0.882	0.014	0.855–0.909

AUC, area under ROC curve; SE, standard error; CI, confidence interval; ANN, artificial neural network; DT, decision tree; LDA, linear discriminant analysis classifier; LR, logistic regression; NB, naïve Bayes classifier; SVM, support vector machine.

Figure 1.

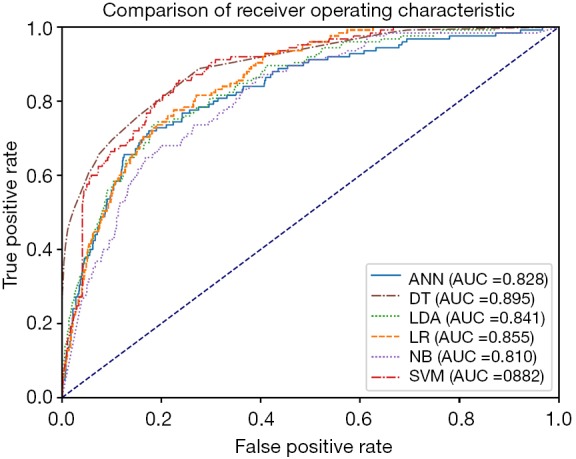
Comparison of receiver operating characteristic curve among artificial neural network, decision tree, linear discriminant analysis, logistic regression, naïve Bayes classifier, and support vector machine. ANN, artificial neural network; DT, decision tree; LDA, linear discriminant analysis classifier; LR, logistic regression; NB, naïve Bayes classifier; SVM, support vector machine.

Comparison to relevant variables

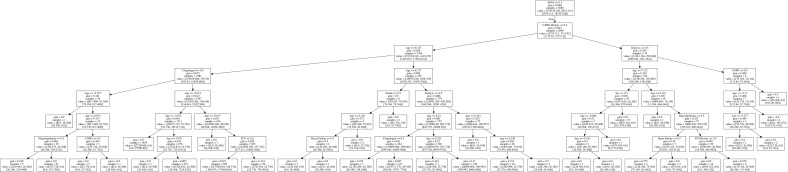
The AUROC of the prediction models were compared with the AUROC of the following variables due to their clinical relevance or association to PCI: hyperlipidemia, hypertension, diabetes mellitus, heart failure, stroke, and chronic kidney disease (CKD)/ESRD. The comorbidity with the highest AUROC is stroke (0.570, 95% CI: 0.518–0.621), while the comorbidity with the lowest AUROC is hyperlipidemia (0.446, 95% CI: 0.394–0.498) (Table 5). All of the variables are close to the null hypothesis true area of 0.5. The ROC curve is shown in Figure 2. Supplementary DT showed calculating probabilities of features for patients undergoing PCI (Figure S1).

Table 5. The receiving operating characteristic of comorbidities with significant difference between 30-day survival and death across all data.

Comorbidity	AUROC	AUROC SE	AUROC 95% CI
Hyperlipidemia	0.446	0.027	0.394–0.498
Hypertension	0.521	0.026	0.471–0.572
Diabetes mellitus	0.503	0.026	0.452–0.555
Heart failure	0.497	0.026	0.445–0.548
Stroke	0.570	0.026	0.518–0.621
CKD/ESRD	0.521	0.027	0.468–0.574

AUC, area under ROC curve; SE, standard error; CI, confidence interval; CKD, chronic kidney disease; ESRD, end stage renal disease.

Figure 2.

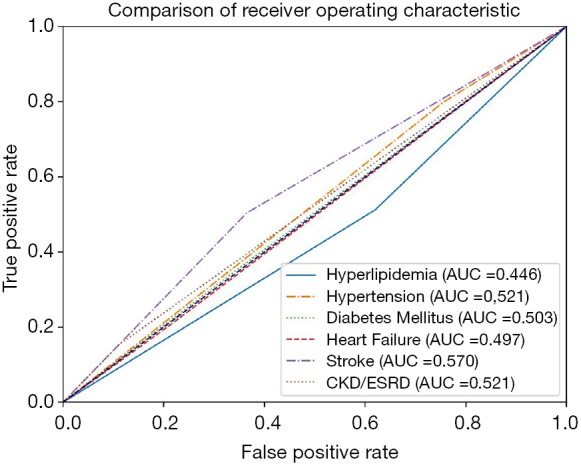
Comparison of receiver operating characteristic curve among associated features.

Discussion

Using the NHIRD, this pilot study demonstrated that a variety of multivariate prediction models can predict 30-day mortality following PCI, with the DT model having the most optimal performance and scalability. Although numerous studies have explored for prediction model of mortality and morbidity after PCI (16,27,38-43), two unique pilot points of our study could be addressed in enhancing the predictive accuracy of prediction model.

First, we added both pre-PCI and post-PCI comorbidity and complications as variables. In the study of Freeman et al. they found that the predictive accuracy of ANNs can be increased with variable selection but is not superior to traditional modeling (27). Their study suggests the importance of variable selection. Thus the pre-procedure variables chosen in this study were based on previous PCI-related studies (16,44-46). Further, we used diseases as proxies tightly linked with high cardiovascular risk after PCI (47-49). In the study of Ellis et al., the predictors they chosen included detailed angiographic findings and culprits vessels and baseline angiographic finding about ejection fraction of left ventricle and number of diseased (≥50% diameter stenosis) and treated vessels (46). Compared with the model of Ellis et al. (46), our model constructed based on the disease variables could be more easily assessed in this risk calculation. To increase the practical value, we decided to choose gastrointestinal bleeding, arrhythmia, and transfer to ICU care as post-procedure variables. It is interesting to note while we compare each feature, PCI patients had past stroke had highest risk of post-PCI mortality. This result would be clinically valuable in providing information for post-PCI care setting of these extremely high risk patients.

Second, we attempted to find the fitting model for prediction post-PCI mortality among current prediction models. We used confusion matrix and ROC metrics used to measure the prediction model performances in NHIRD database. We found that the model with the highest AUROC is the DT model (0.895, 95% CI: 0.865–0.925), followed by the SVM model (0.882, 95% CI: 0.855–0.909) and the LR model (0.855, 95% CI: 0.827–0.883). Therefore, we find DT model achieves a fitting prediction mode in our study. Evaluating the LR and ANN models, the precision values are significantly higher than the recall values, which means the LR and ANN models may be overfitting the data and might not be appropriate models in this study. In another aspect, we found that Multinomial naïve Bayes models allows for partial fitting of incomplete datasets. Our findings mean that NB models could be useful for a web-based classification system where datasets arrive one-by-one as opposed to all at the same time. Thus, in the NHIRD database, multinomial naïve Bayes models may be better than SVMs in terms of efficiency and scalability.

Ellis et al. used LR to calculate the operator-specific mortality prediction in patients following PCI (46). The area under curve of mortality is 0.85, which is comparable to our results (46). Our LR model improves upon their methodology by enabling dynamic prediction since we have incorporated the post-procedure variables. While LDA classification models are relatively uncommon in the medical field, DT models have been widely implemented in applications where a white-box classification is necessary (50). The decision path of any given data point can be determined for DTs, which makes it suitable for applications where such a decision path is necessary, such as in clinical pathology. LR models are also suitable for such applications since one can also draw statistical inferences from prediction model outputs (19).

This study had several advantages. First, because DT models are advantageous in dynamical prediction based on variable selection, we included both baseline demographics and in-hospital newly occurred complications of each patient. Thus, our model can be employed for predicting pre- and post-PCI mortality risk during hospitalization. This model could assist clinicians in their awareness of potential mortality risks when new events occur among post-PCI patients staying in hospital. Second, the NHIRD is a national database in Taiwan; therefore, the possibility of selection bias such as in a single-center database was alleviated when constructing the PCI mortality model. Third, we selected patients with AMI as our study group. Peterson et al. found that PCI in-hospital mortality was 1.27%, ranging from 0.65% in elective PCI to 4.81% in STEMI patients (16). Because mortality following PCI differed among patients with different PCI indications, patients with AMI were selected as the study cohort to effectively fulfill the critical need for interventional cardiology.

Several limitations must be mentioned. First, information regarding body mass index, HbA1C, levels of high-density and low-density lipoproteins, dietary preference, exercise, family history of heart diseases, smoking, electrocardiogram, blood pressure upon AMI, left ventricular end-diastolic pressure, ejection fraction, and culprit vessels were unavailable through the NHIRD. Furthermore, information about angiographic features and biomarkers of each patient is unobtainable in NHIRD, thus we could not corporate these data as the study features. Those missing information might have impacts on formation of prediction models. However, although we did not have such detailed information, our model achieved an AUC of 0.895 and a precision of 0.971 for the DT model on the basis of diagnostic and procedure codes. Our study demonstrated the advantages of simplicity and flexibility in assessing the mortality risk of patients with PCI. Second, although we used a validation set, it was extracted from the same database. External validation with larger data sets encompassing 20-year durations of the NHIRD are required to validate our findings. It would be useful to use the observations from 2004 to 2008 and do testing by using the observations from 2009 to 2013. However, the number of patients would be not large enough in each divided set. Third, the majority of those insured by the NHI program are Taiwanese; thus, our model which is constructed on single-country data might not be generalizable to other countries. Finally, using post-PCI complications as predictors might limit the usability of the algorithm to post-PCI settings, which should also be mentioned here.

Conclusions

This study reported that DT models can be applied to the NHIRD in order to predict 30-day mortality following PCI in patients with AMI. We hope work could provide insights for further studies about applying prediction model on ICD-coded database. This model may enable more dynamic and timely predictions of mortality during hospitalization. Additional studies are necessary for external validation and to test the applicability of this model in patients undergoing PCI without AMI.

Figure S1.

Decision tree in this study.

Ethical Statement: The authors are accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved. The investigation conforms to the principles outlined in the Declaration of Helsinki. This study was approved to fulfill the condition for exemption by the Institutional Review Board (IRB) of China Medical University (CMUH104-REC2-115-CR4). The IRB also specifically waived the consent requirement.