Microstructurally Motivated Constitutive Modeling of Heart Failure Mechanics

Abstract

Heart failure (HF) is one of the leading causes of death worldwide. HF is associated with substantial microstructural remodeling, which is linked to changes in left ventricular geometry and impaired cardiac function. The role of myocardial remodeling in altering the mechanics of failing hearts remains unclear. Structurally based constitutive modeling provides an approach to improve understanding of the relationship between biomechanical function and tissue organization in cardiac muscle during HF. In this study, we used cardiac magnetic resonance imaging and extended-volume confocal microscopy to quantify the remodeling of left ventricular geometry and myocardial microstructure of healthy and spontaneously hypertensive rat hearts at the ages of 12 and 24 months. Passive cardiac mechanical function was characterized using left ventricular pressure-volume compliance measurements. We have developed a, to our knowledge, new structurally based biomechanical constitutive equation built on parameters quantified directly from collagen distributions observed in confocal images of the myocardium. Three-dimensional left ventricular finite element models were constructed from subject-specific in vivo magnetic resonance imaging data. The structurally based constitutive equation was integrated into geometrically subject-specific finite element models of the hearts and used to investigate the underlying mechanisms of ventricular dysfunction during HF. Using a single pair of material parameters for all hearts, we were able to produce compliance curves that reproduced all of the experimental compliance measurements. The value of this study is not limited to reproducing the mechanical behavior of healthy and diseased hearts, but it also provides important insights into the structure-function relationship of diseased myocardium that will help pave the way toward more effective treatments for HF.

Significance

Most constitutive models of passive myocardium are formulated based on phenomenological approaches. Although such constitutive models can reproduce aspects of the biomechanical behavior of myocardium, they generally do not reflect the microstructural and material changes that occur as myocardium progressively remodels during growth or disease. This study proposes a, to our knowledge, novel structurally motivated constitutive model of passive myocardium that directly links quantitative characteristics of myocardial collagen organization to the mechanical function of the heart. As such, it provides insight into the biophysical relationship between structure and function of the myocardium that can be used to inform the development of more effective treatments for heart failure.

Introduction

The progression of heart failure (HF) is associated with substantial changes in geometry of the left ventricle (LV) and organization of the myocardial microstructure that lead to an alteration in the mechanical behavior and hence the impairment of cardiac function. Despite a long history of research in this area, the morbidity and mortality from HF remain high (1). Contributing to this lack of progress in managing HF is its complexity and multifactorial nature. HF can be broadly divided into either impaired systolic function or impaired diastolic function, although there is still much debate about whether these are distinct diseases or overlapping phenotypes within the HF spectrum (2, 3). Because both HF types appear to have similar symptomatic effects but different pathophysiological mechanisms, it is clear that treatment strategies aimed at HF symptoms alone are not adequate, and there is a pressing need for more specific treatments targeting the underlying mechanisms of HF progression (4).

Because of rapid advances in cardiac imaging and animal models, it is now possible to investigate the pathophysiological mechanics underpinning HF (5, 6, 7). The spontaneously hypertensive rat (SHR) is a well-established animal model of genetic hypertension that develops HF with aging and exhibits many features of human HF. Diastolic abnormality can be observed in SHRs at approximately the age of 12 months. Continued pathophysiological progression eventually leads to impaired systolic function and death in aged SHRs (8). In a previous study by our group (9) using high-resolution extended-volume confocal microscopy, we showed that 12-month-old SHRs exhibited significant differences in myocardial architecture when compared to age-matched control Wistar Kyoto (WKY) rats (10). The microstructural differences included a greater amount of collagen between myocardial laminae, effectively scarring them together, and also an increase in the collagen surrounding individual myocytes. We proposed that these gross alterations in myocardial microstructure lead to detrimental changes in myocardial mechanical behavior and result in impaired cardiac function.

To date, most biomechanical constitutive equations (11, 12, 13, 14, 15, 16, 17) that have been developed to describe the mechanical behavior of myocardial tissue have been based on phenomenological approaches, whereby strain-energy density functions are derived from fits to conventional mechanical tests (i.e., uniaxial, biaxial, and/or simple shear tests). Although those phenomenological approaches are theoretically simple and often easy to compute, they lack the ability to reflect the material and mechanical changes that occur as myocardium progressively remodels during growth or heart disease (18). Moreover, the material parameters of phenomenological models are not based on anatomical or physiological phenomena and can be highly correlated because of the functional form of the equations and the coupling effects of the parameters on myocardial tissue deformation (19, 20). Driven by those drawbacks and the need to understand the underlying mechanisms of heart disease, an alternative approach has been to develop constitutive equations that are framed in terms of tissue constituents and are referred to as “structural” constitutive equations. In contrast to phenomenological constitutive models, structural constitutive models aim to directly link the physical properties of the tissue constituents to the mechanical function of the heart (21).

Although much work has been carried out on heart modeling over the past three decades, few research efforts (22, 23, 24) have been focused on the development of structurally based models that could potentially bridge the gap between myocardial microstructure remodeling and the underlying mechanics during HF. Our objective in this work was to develop a new, structurally based constitutive model of the myocardium that can directly link the physical properties of myocardial collagen organization, acquired using high-resolution imaging, to the mechanical function of the heart obtained from ex vivo pressure-volume compliance measurements. To the best of our knowledge, this study is the first to quantify and directly incorporate the three-dimensional (3D) shape and orientation of collagen morphology into a structurally based constitutive model for myocardial tissues. Such a model provides more insight into the relationship between the structure and function of the myocardium, which will help to pave the way toward the development of more effective treatments that target the underlying mechanisms of HF progression.

Methods

The experimental study was approved by the Animal Ethics Committee of the University of Auckland and conforms to the National Institutes of Health Guide for the Care and Use of Laboratory Animals (National Institutes of Health Publication No. 85-23). The animals were taken from two previous studies by our research group (9, 25). Four extended-volume confocal images, used in this study to investigate the myocardial microstructural remodeling, were taken from two hypertensive SHRs and two control WKY rats, with one of each at the ages of 12 and 24 months, as previously reported in (9). In addition, four in vivo cardiac magnetic resonance imaging (MRI) and passive left ventricular inflation experiments were taken from two hypertensive SHRs and two control WKY rats, with one of each at the approximate ages of 12 and 24 months, as previously reported in (25). In this work, we have combined the experimental data taken from those previous studies to build biomechanical models of two diseased SHRs and two control WKY rats, with one of each at the ages of 12 and 24 months, to investigate the biomechanical link between myocardial microstructural remodeling and mechanical dysfunction during the progression of hypertensive HF.

Myocardial microstructural architecture

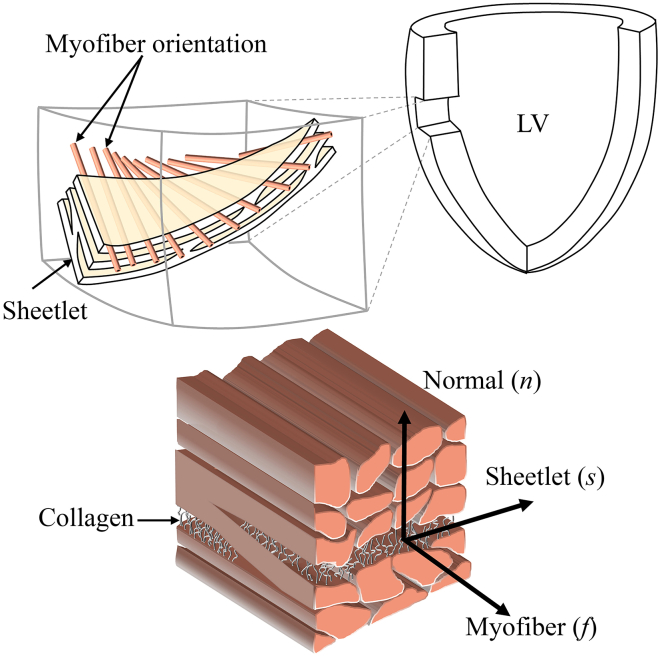
The 3D laminar microstructure of the ventricular myocardium sees myocytes organized into groups of sheetlets separated by cleavage planes and interconnected by a dense collagen network (26) (see Fig. 1). The 3D microstructure can be characterized at any point by a set of three orthogonal directions that have distinct material properties (27): 1) aligned with the myocyte direction (f), 2) perpendicular to the myocyte axis within the sheetlet layer (s), and 3) normal to the sheetlet layer (n).

Figure 1.

Myocardial microstructure. This figure is adapted from (26). To see this figure in color, go online.

The passive mechanical properties of the myocardium are mainly dependent on the 3D organization of the collagen because it is the major stress-bearing component of the myocardium (28, 29). This emphasizes the fact that any change in the collagen architecture is often associated with pathological disorders like those observed in aged SHRs (9).

Imaging microstructural remodeling: Extended-volume confocal microscopy

To obtain information on remodeling of microstructure during HF, an extended-volume confocal microscopic technique was used. A detailed description of the experiments can be found in (9). Briefly, tissue blocks excised from the LV midwall were labeled using picrosirius red staining to visualize the collagen. The stained tissues were embedded in resin and mounted on a high-precision three-axis stage and imaged using a confocal laser scanning microscope. Images were acquired at high (1 μm) resolution in a series of two-dimensional overlapping images. The top of the mounted sample was then milled at a depth of 20 μm, and the process was repeated to create extended high-resolution 3D image volumes. Further details about the imaging protocol and technique are given in (30, 31).

Quantifying myocardial microstructure

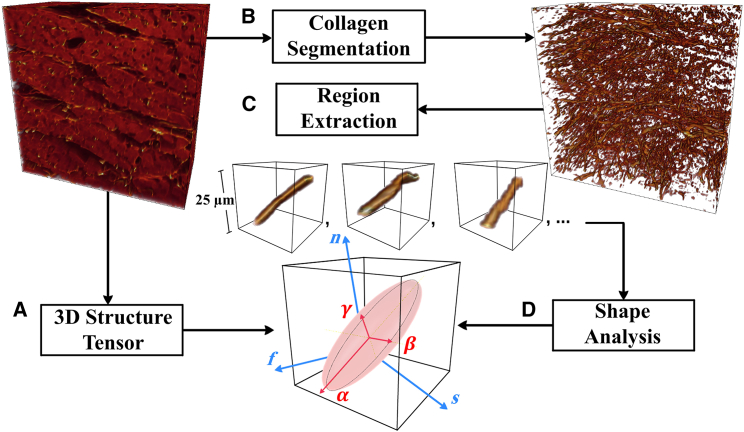
Here, we propose a, to our knowledge, novel method to quantify the myocardial microstructure from the confocal images. The proposed method was implemented using a customized MATLAB (The MathWorks, Natick, MA) code and is summarized in Fig. 2.

Figure 2.

A framework for quantification of myocardial microstructure. (A) A local myocardial coordinate system is defined using a 3D structure tensor. (B) The collagen network is segmented in the confocal images using a pipeline of image processing. (C) A number of ROIs are extracted with a single, connected collagen structure at the center. (D) The overall representative collagen shape and organization can be fully described in terms of eigenvalues and eigenvectors of the lumped inertia matrix (see text for details). To see this figure in color, go online.

3D structure tensor

The 3D structure tensor is a well-known mathematical operator that has been used extensively in image analysis for estimating the local structure and local orientation. We have applied the 3D structure tensor to the confocal images to define the local myocardial coordinate system (f, s, n) using the same method as in our previous study (32).

Collagen segmentation

The confocal images usually suffer from blurring effects and a high level of intensity variations, which makes collagen segmentation challenging. So, to reduce intensity heterogeneity, we have used an image processing pipeline to segment the collagen network from the confocal images. Further details about the pipeline are given in (33).

Region extraction

To study the collagen microstructure at a local level, we randomly selected sampling locations throughout the 3D segmented volume image. The sample locations here were randomly selected (using randi in MATLAB) from all voxels labeled as collagen in the 3D image and constrained to be unique and at least 7 μm apart. At each sampling location, we defined a region of interest (ROI) with a single and complete collagen structure at the center. The volume of the ROI in this study was set to 25 × 25 × 25 μm to represent the collagen microstructural organization at a local level.

Shape analysis

The shape and orientation of each segmented collagen object (C) was characterized using eigenanalysis of the inertia matrix of C (34, 35). The first-order moments define the center mass of C as

$$M_{1x}=\sum _C{x}_i,M_{1y}=\sum _C{y}_i,M_{1z}=\sum _C{z}_i,$$ (1)

where (xi, yi, zi) are the coordinates of a voxel in the object C. From the first-order moments, we can directly calculate the second-order moments as

$$M_{2xx}=\sum _C{\left(x_i-M_{1x}\right)}^2,M_{2xy}=\sum _C\left(x_i-M_{1x}\right)\left(y_i-M_{1y}\right),M_{2yy}=\sum _C{\left(y_i-M_{1y}\right)}^2,M_{2yz}=\sum _C\left(y_i-M_{1y}\right)\left(z_i-M_{1z}\right),M_{2zz}=\sum _C{\left(z_i-M_{1z}\right)}^2,M_{2xz}=\sum _C\left(x_i-M_{1x}\right)\left(z_i-M_{1z}\right)$$ (2)

and then compute the symmetric inertia matrix (m) as

$$m=\left[\begin{array}{ccc}{M}_{2xx}& M_{2xy}& M_{2xz}\\ M_{2xy}& M_{2yy}& M_{2yz}\\ M_{2xz}& M_{2yz}& M_{2zz}\end{array}\right].$$ (3)

Eigenanalysis of the inertia matrix (m) provides a quantitative description of the collagen shape because the eigenvalues indicate the shape of the collagen structure, for which (λ_α, λ_β, λ_γ) denote the largest, middle, and smallest eigenvalues, respectively, such that λ_α ≥ λ_β ≥ λ_γ > 0. From the eigenvalues, three morphological parameters—elongation $\left(\mathbb{E}\right)$, flatness $\left(\mathbb{F}\right)$, and anisotropy $\left(\mathbb{A}\right)$—were derived to quantify the local collagen shape distributions:

$$\mathbb{E}=\frac{{\lambda }_{\beta }}{{\lambda }_{\alpha }},\mathbb{F}=\frac{{\lambda }_{\gamma }}{{\lambda }_{\beta }},\mathbb{A}=\frac{{\lambda }_{\gamma }}{{\lambda }_{\alpha }}.$$ (4)

By definition, the morphological parameters in Eq. 4 lie in the range (0, 1) and are independent of the collagen volumes. It should be noted that any two morphological parameters are needed to quantify the local collagen shape in three dimensions because they are correlated such that $\mathbb{A}$ = $\mathbb{E}$ $\mathbb{F}$. The distribution of collagen shapes can be investigated by computing the inertia matrix (m) for each ROI.

The overall representative collagen structure was computed using the average of the inertia matrices of all ROIs as

$$\overline{m}=\frac{1}{r}\sum _{r}m,$$ (5)

where r is the number of ROIs. The method of using lumped inertia matrices has been extensively used in structural dynamics (36, 37), feature extraction applications (38), and data analysis (39), in which the lumping formulation is based on the architecture information of given inertia matrices. Such a formulation lumps the collagen network based on collagen volume, shape, and orientation information at each ROI. Similarly, the eigenanalysis was applied on $\overline{m}$, where ($\overline{{\lambda }_{\alpha }}$, $\overline{{\lambda }_{\beta }}$, $\overline{{\lambda }_{\gamma }}$) represent the largest, middle, and smallest eigenvalues, respectively, and indicate the overall collagen shape. Meanwhile, the eigenvectors carry the collagen orientation information. Consequently, three representative structural parameters

$$\overline{\mathbb{E}}=\frac{\overline{{\lambda }_{\beta }}}{\overline{{\lambda }_{\alpha }}},\overline{\mathbb{F}}=\frac{\overline{{\lambda }_{\gamma }}}{\overline{{\lambda }_{\beta }}},\overline{\mathbb{A}}=\frac{\overline{{\lambda }_{\gamma }}}{\overline{{\lambda }_{\alpha }}}$$ (6)

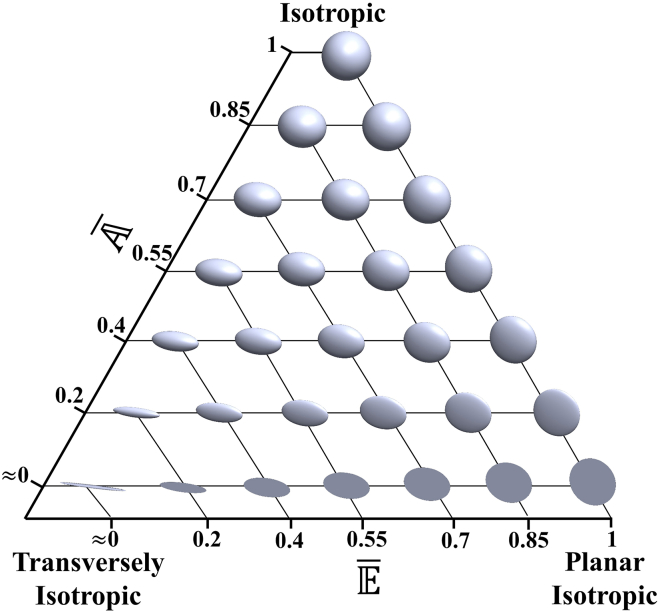
can be used to quantify the overall representative collagen shape. It should be noted that structural parameters $\mathbb{E}$, $\mathbb{F}$, and $\mathbb{A}$ (see Eq. 4) are only associated with the description of collagen shape without accounting for differences in collagen orientation, whereas representative structural parameters $\overline{\mathbb{E}}$, $\overline{\mathbb{F}}$, and $\overline{\mathbb{A}}$ (see Eq. 6) are used to quantify a representative collagen structure based on a superposition of all ROI inertia matrices, taking into account collagen volume, shape, and orientation (an illustrative example is given in the Appendix). Given that only two structural parameters are needed to fully quantify the collagen shape in three dimensions without loss of generality, we have chosen to use structural parameters $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ to represent a continuous variation between isotropic, transversely isotropic, and planar isotropic configurations (see Fig. 3). It should be noted that the representative structural parameters ($\overline{\mathbb{E}}$, $\overline{\mathbb{A}}$) are normalized and hence independent of collagen volume. Collagen volume fraction (V_f) is taken into consideration to reflect collagen architecture. V_f was measured directly from the 3D confocal images as the segmented collagen volume as a proportion of the total volume of the confocal image.

Figure 3.

3D visualization of object shape variation based on structural parameters $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$. To see this figure in color, go online.

Structurally based constitutive model formulation

We have developed a constitutive model to describe the mechanical response of myocardial tissue using a strain-energy density function W, which is defined as a function of the Green-Lagrange strain components E_ij referred to the local collagen coordinate system (α, β, γ) (Eq. 7). The anisotropic nature of the myocardium was addressed using two shape parameters ($\overline{\mathbb{E}}$, $\overline{\mathbb{A}}$) and V_f as collagen volume.

$$W=\frac{a{V}_f}{2b}\left[e^{bQ}-1\right],Q=E_{\alpha \alpha }^2+\overline{\mathbb{E}}{E}_{\beta \beta }^2+\overline{\mathbb{A}}{E}_{\gamma \gamma }^2+2\left[\overline{\mathbb{E}}{E}_{\alpha \beta }^2+\overline{\mathbb{A}}{E}_{\alpha \gamma }^2+\sqrt{\overline{\mathbb{E}}\overline{\mathbb{A}}}{E}_{\beta \gamma }^2\right]$$ (7)

This strain-energy density function consists of five parameters in total: $\overline{\mathbb{E}}$, $\overline{\mathbb{A}}$, and V_f are positive structural parameters that can be quantified directly from the confocal images, and only the two parameters a (stiffness-like parameter) and b (dimensionless parameter) are used to represent the overall stiffness of the myocardium and nonlinear nature of the passive mechanical response. In comparison to existing constitutive models, the two shape parameters $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ are used to relate the local collagen structure analysis directly to the mechanical function, as illustrated in Fig. 3. This constitutive model allows us to describe the mechanical response for different degrees of anisotropy and orientations spanning between the extreme cases of transversely isotropic, planar isotropic, and isotropic mechanical response (see Appendix for more details).

For computational cardiac mechanics, typically the stress-strain relationship is expressed with respect to the myocardial coordinate system (f, s, n). Therefore, a tensor transformation is required to express the local collagen strain tensors in terms of myocardial material axes:

$${\mathbf{E}}_{\mathbf{C}}={\mathbf{R}}^T{\mathbf{E}}_{\mathbf{M}}\mathbf{R}\mathbf{,}{\mathbf{E}}_{\mathbf{C}}=\left[\begin{array}{ccc}{E}_{\alpha \alpha }& E_{\alpha \beta }& E_{\alpha \gamma }\\ E_{\alpha \beta }& E_{\beta \beta }& E_{\beta \gamma }\\ E_{\alpha \gamma }& E_{\beta \gamma }& E_{\gamma \gamma }\end{array}\right],{\mathbf{E}}_{\mathbf{M}}=\left[\begin{array}{ccc}{E}_{ff}& E_{fs}& E_{fn}\\ E_{fs}& E_{ss}& E_{ns}\\ E_{fn}& E_{ns}& E_{nn}\end{array}\right],\mathbf{R}=\left[\begin{array}{ccc}{R}_{f\alpha }& R_{f\beta }& R_{f\gamma }\\ R_{s\alpha }& R_{s\beta }& R_{s\gamma }\\ R_{n\alpha }& R_{n\beta }& R_{n\gamma }\end{array}\right],$$ (8)

where E_C denotes the strain tensor specified with respect to the orthogonal axes within the collagen, E_M denotes the myocardial strains, and R is a matrix of direction cosines that relate the collagen axes (from eigenanalysis of the collagen) to the myocardial axes (from structure-tensor analysis). The nine direction cosines R_ij (Eq. 8) are defined as the cosine of the angle between the i and j axes, where i ∈ {f, s, n} and j ∈ {α, β, γ}. By substituting Eq. 8 into Eq. 7, we can rewrite the strain-energy function with respect to the myocardial coordinate system.

Simulating passive myocardial mechanics

To assess the suitability of the constitutive equation (Eq. 7), we integrated it into subject-specific finite element (FE) models of the LV to simulate the mechanical function of the heart as quantified by the ex vivo compliance measurements.

FE model of LV

In vivo cine MRI was performed on isoflurane-anesthetized rats using a Varian 4.7T MRI scanner. To provide a good representation of the LV geometry, six short-axis MRI slices were obtained at equally spaced locations (spacing = 0.6–1.0 mm) spanning from the base to the apex, and three long-axis slices were obtained with an angular separation of 60° around the long-axis of the LV. The slices were captured at 18 time points throughout the cardiac cycle. For more details about the experimental protocol, see (25).

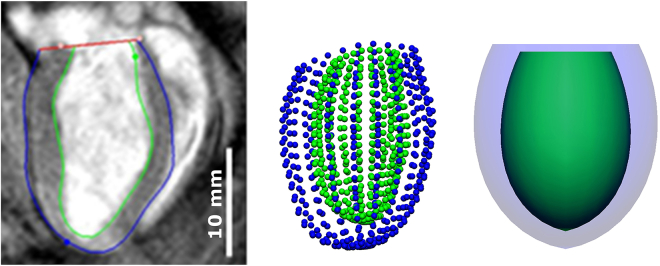
Subject-specific LV FE models of SHRs and WKY rats were created by analyzing the MRI data using the Cardiac Image Modeler (CIM) software package (40), which generates a 16-element FE model by tracking the boundaries of endocardial (inner layer of LV cavity) and epicardial (outer layer of LV cavity) tissue throughout the cardiac cycle interactively. Surface points were generated from the CIM model at diastasis and then fitted to a single-element, thick-walled, truncated axisymmetric prolate-spheroidal model. This model was chosen to minimize the simulation cost while preserving the 3D information of the LV geometry (see Fig. 4).

Figure 4.

Long-axis view of MRI data processed in CIM (left), endocardial and epicardial surface points (center), and fitted single-element LV model (right). To see this figure in color, go online.

Passive LV pressure-volume measurements

Measurements of the ex vivo pressure-volume relationship were used to characterize passive ventricular function. Pressure-volume measurements were made by attaching the excised heart to a Langendorff apparatus with a saline-filled balloon catheter inserted into the LV via the mitral valve. The volume of the balloon was controlled by inflating and deflating the balloon using a pump syringe while the pressure was measured using a differential pressure transducer connected to a side port in the balloon catheter (9, 25). LV compliance, which is the inverse of LV stiffness, was then calculated as the change in volume (ΔV) over the change in pressure (ΔP). Derivatives were calculated using a central difference method to provide smooth compliance estimates. Finally, LV passive compliance as a function of filling pressure was used to determine trends of LV chamber stiffness between all groups independent of changes in LV size.

Constitutive parameter estimation

The structurally based constitutive equation (Eq. 7) was integrated into the single-element FE model using an in-house FE analysis software package, CMISS (www.cmiss.org). To describe the underlying microstructure, the myofiber orientations in both SHR and WKY rat single-element models were set to vary transmurally from −60° at the epicardium to +70° at the endocardium, whereas the sheet angle was fixed at +30° based on previous studies (26, 41). Passive inflation of the LV was simulated by kinematically constraining the LV base and applying pressure on the endocardial surfaces of the models. The pressure was applied homogeneously and increased in small increments from 0 to 15 mmHg, matching the range of filling pressures from a physiological perspective. Model-predicted compliance was derived from the simulated pressure-volume curves using a technique similar to the one that was applied to the experimental data (see the previous section).

The material parameters, denoted θ ∈ {a, b}, were identified using a nonlinear optimization procedure by minimizing the least-squares objective function Ω

$$\mathit{\Omega }=\sum _r\sum _d{\Vert {\mathbb{C}}^{model}\left(\theta \right)-{\mathbb{C}}^{experiment}\Vert }^2,$$ (9)

where ${\mathbb{C}}^{model}$ represents the model-predicted LV compliance and ${\mathbb{C}}^{experiment}$ denotes the experimentally measured compliance. The sums over d and r stand for the sum over data points and rats, respectively. Each case in this study had 11 compliance data points for comparison. Note that we only fitted a single pair of parameters (a, b) for all four cases to match the experimental results.

The optimization process was implemented using the lsqnonlin function of the MATLAB optimization toolbox with initial estimates of the constitutive parameters set to a = 5 kPa and b = 5. The errors between ${\mathbb{C}}^{model}$ and ${\mathbb{C}}^{experiment}$ were minimized by tuning the constitutive parameters a and b until the value of the objective function satisfied the convergence criterion (≤10⁻⁵ mL² ⋅ mmHg⁻²) or a maximal iteration count of 1000 was reached. A typical optimization process took approximately 4 h on a 3.7 GHz processor.

To assess the identifiability of the model parameters (a, b), the shape of the objective function was investigated using two standard measures, cond(H) and det$\left(\tilde{\mathbf{H}}\right)$, which are derived from the Hessian matrix as proposed in (42, 43). The surface of the objective function was also explored by varying each of the material parameters (a, b) in a range of ±5% around their optimal values. Finally, at the optimal solution, the constitutive model was examined under equibiaxial loading in the fs-plane of the myocardium (see Fig. 1) to examine the influence of the structural parameters on mechanical behavior. Further detail on the analytical expressions of the constitutive model under equibiaxial deformations are given in the Appendix.

Results

Quantifying collagen microstructure remodeling

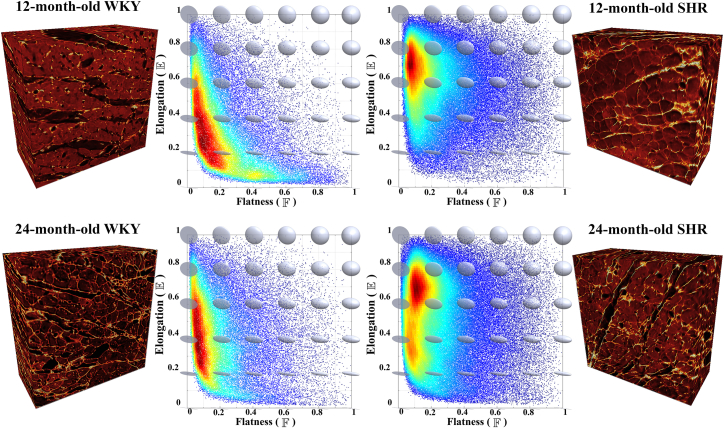
In Fig. 5, distributions of collagen were investigated using two morphological parameters, elongation $\left(\mathbb{E}\right)$ and flatness $\left(\mathbb{F}\right)$, in four tissue blocks comprising SHRs and WKY rats at each of 12 and 24 months of age. The collagen organization in hypertensive SHR and control WKY rat hearts exhibited fundamentally different distributions in terms of elongation. In WKY rat hearts, the elongation distributions were approximately centered around 0.2–0.6, whereas in SHR hearts, they were mostly concentrated around 0.7. These distinct differences in elongation indicate that the collagen distributions in the control WKY rat hearts mostly form elongated structures, whereas in the diseased SHR hearts, the collagen is arranged predominantly in a sheet-like form. Kolmogorov-Smirnov tests of two samples (44) were used to compare elongation $\left(\mathbb{E}\right)$ distributions of collagen morphology among the four hearts (see Fig. 5). In this study, all four hearts had statistically different elongation distributions of collagen shape (all p-values < 0.01).

Figure 5.

Distributions of collagen morphology described using elongation $\left(\mathbb{E}\right)$ and flatness $\left(\mathbb{F}\right)$ parameters in the LV midwall of 12-month-old (top) and 24-month-old (bottom) SHR (right) and WKY (left) rat hearts. Confocal image volumes (400 × 400 × 200 μm): myocytes have variable intensity, whereas collagen appears brighter. Dark gaps in the confocal images indicate the cleavage planes. Heat maps: data points represent collagen shape for each ROI, with the red and blue colorscale indicating high and low normalized density of collagen shapes. To see this figure in color, go online.

The representative structural parameters for all four cases are listed in Table 1. Overall, the values of V_f for the diseased SHR hearts were higher than those for the control WKY rat hearts. The value of $\overline{\mathbb{E}}$ was increased with age in the WKY group compared to a decrease in the SHR group. On the other hand, the value of $\overline{\mathbb{A}}$ was increased with age in all animals.

Table 1.

Microstructural Parameters V_f,$\overline{\mathbb{E}}$, and $\overline{\mathbb{A}}$, Quantified Directly from the Confocal Images, for Diseased SHRs and WKY Rat Hearts as Controls

Animal	Vf	$\overline{\mathbb{E}}$	$\overline{\mathbb{A}}$
12-month-old WKY	0.06	0.66	0.24
24-month-old WKY	0.05	0.73	0.31
12-month-old SHR	0.11	0.82	0.40
24-month-old SHR	0.07	0.62	0.46

It should be noted that $\mathbb{E}$ and $\mathbb{F}$ were used in Fig. 5 only to illustrate the distributions of collagen shape across the ROIs without accounting for differences in collagen orientation. On the other hand, $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ (Table 1) were used to quantify a representative collagen structure based on a superposition approach that sums up all ROI inertia matrices, taking into account both collagen shape and orientation.

Quantifying LV geometric remodeling

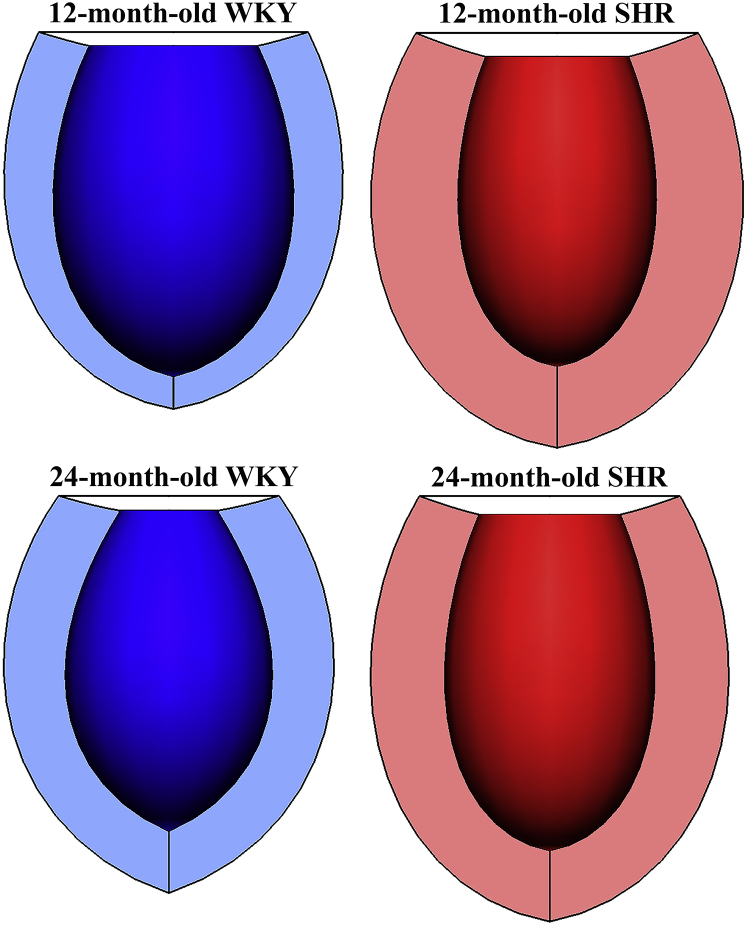
Subject-specific 3D LV geometric FE models constructed using in vivo MRI data are shown in Fig. 6. A comparison of the LV mass, end-diastolic volume (EDV), wall thickness (WT), and ejection fraction (EF) for all four cases is given in Table 2. The LV masses of the two SHR hearts were significantly greater than the control WKY rat hearts, implying the development of concentric hypertrophy in the diseased hearts. In the WKY rats, LV mass and WT for the 24-month-old animal were larger than those for 12-month-old animal, which is likely due to normal growth, and this was accompanied by a lower EDV in the older animal. The values of EF were similar for all animals; thus, the diseased SHR hearts were classified as exhibiting features of HF with preserved EF. The EDV of the 24-month-old SHR was greater, with a lower WT, compared to the 12-month-old SHR, showing a tendency toward eccentric hypertrophy.

Figure 6.

3D LV FE models constructed from subject-specific in vivo MRI data at diastasis. To see this figure in color, go online.

Table 2.

LV Mass, EDV, WT, and EF for Different Animal Strains and Age Groups

Animal	LV mass (mg)	EDV (μL)	WT (mm)	EF (%)
12-month-old WKY	794	639	2.1	63
24-month-old WKY	961	420	2.7	60
12-month-old SHR	1475	414	3.4	61
24-month-old SHR	1301	500	2.9	64

Quantifying LV functional remodeling

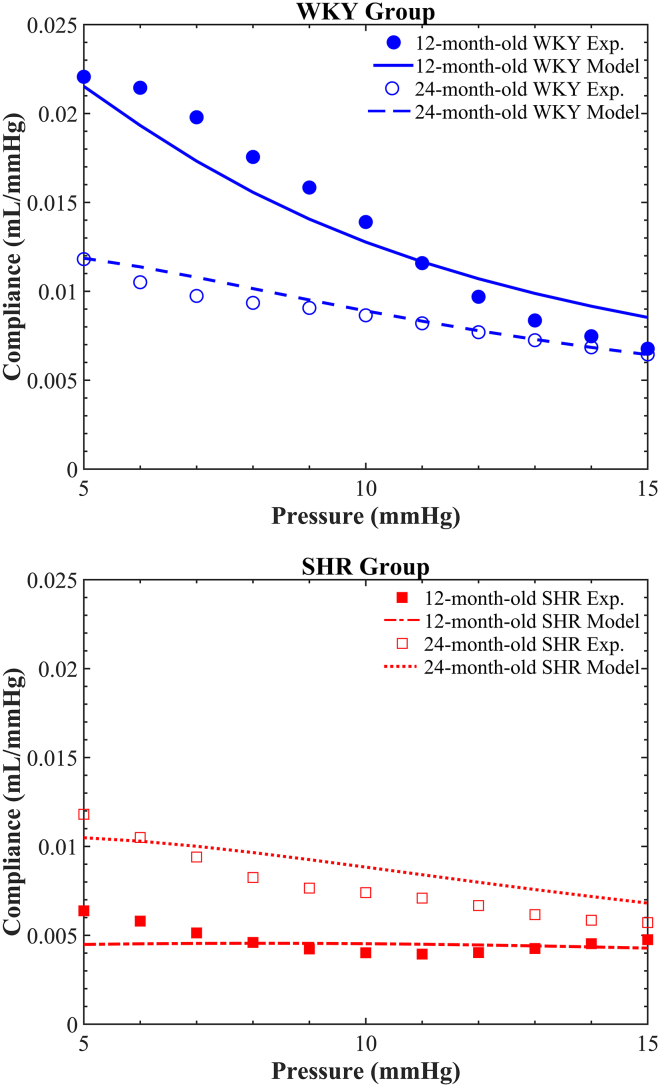
The degree of passive LV functional remodeling was quantified by deriving a relationship between LV compliance and filling pressure from the ex vivo passive pressure-volume inflation experiments (Fig. 7). For filling pressures less than 15 mmHg, the passive LV compliance curve for the 12-month-old SHR heart was relatively shallow (indicating a stiffer LV), whereas that for 12-month-old WKY rat heart was markedly higher compared to the 24-month-old animals. Moreover, the LV compliance curves for both the diseased SHR and control WKY rat hearts at the age of 24 months were rather similar. On the other hand, for filling pressures greater than 15 mmHg, LV compliance was similar for all animals.

Figure 7.

Derived LV compliance pressure for diseased SHR (red) and control WKY (blue) rat hearts, at each of 12 months (filled circles) and 24 months (empty circles) of age. To see this figure in color, go online.

Parameter estimation and identifiability

To link the observed differences in cardiac microstructure and ventricular mechanical function described above, we built LV FE models (Fig. 6) from the in vivo cardiac MRI data. Microstructural details from the confocal images (Table 1) were integrated into the LV mechanics models using Eq. 7. A single set of material parameters (a, b) were fitted by minimizing the objective function (Eq. 9) simultaneously across all four predicted LV compliance curves and their associated experimental data. The optimal parameters were found to be a = 117.6 kPa and b = 37.9. The model-predicted passive LV compliance curves for all four cases matched their corresponding experimental data (see Fig. 8) with a sum of squared errors of 5.5 × 10⁻⁵ mL² ⋅ mmHg⁻². The goodness-of-fit measures were 2.9 × 10⁻⁵, 2.8 × 10⁻⁶, 6.7 × 10⁻⁶, and 1.7 × 10⁻⁵ (all in units of mL² ⋅ mmHg⁻²) for 12-month-old WKY rat, 24-month-old WKY rat, 12-month-old SHR, and 24-month-old SHR, respectively.

Figure 8.

Model predictions of LV compliance curves (lines) versus experimental data (symbols) for SHR (bottom) and control WKY rat (top) hearts at each of 12 and 24 months of age. Heart-specific microstructural parameters (derived from confocal images) were used for each case, whereas a single set of fitted material parameters (a = 117.6 kPa, b = 37.9) was used for all four cases. To see this figure in color, go online.

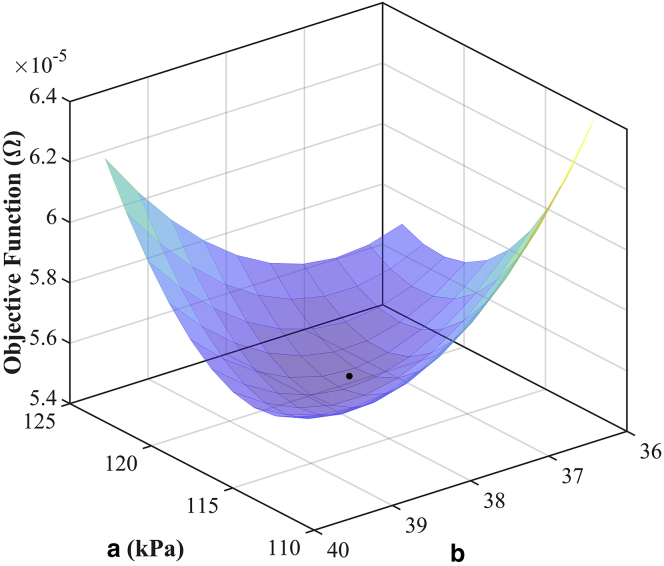
The objective function variation of the two material parameters (a, b) was obtained by varying the parameters in a range of ±5% around their optimal values and plotted as a surface function (Fig. 9), which illustrates the convexity of the objective function. The identifiability of the material parameters was measured using the metrics cond(H) and det$\left(\tilde{\mathbf{H}}\right)$. A value of cond(H) close to zero indicates poor identifiability of the parameters. det$\left(\tilde{\mathbf{H}}\right)$, also called M-optimality, is a normalized index of the interaction between parameters in which a value of one indicates no interaction between the parameters. In our study, the condition number, cond(H), was 0.06, and the det$\left(\tilde{\mathbf{H}}\right)$ was measured as 0.64. These values indicated that the material parameters (a, b) were only very weakly correlated with respect to the observed compliance data.

Figure 9.

Surface plot of objective function (Eq. 9) obtained by varying each of the material parameters (a, b) in a range of ±5% around their optimal values (black point). To see this figure in color, go online.

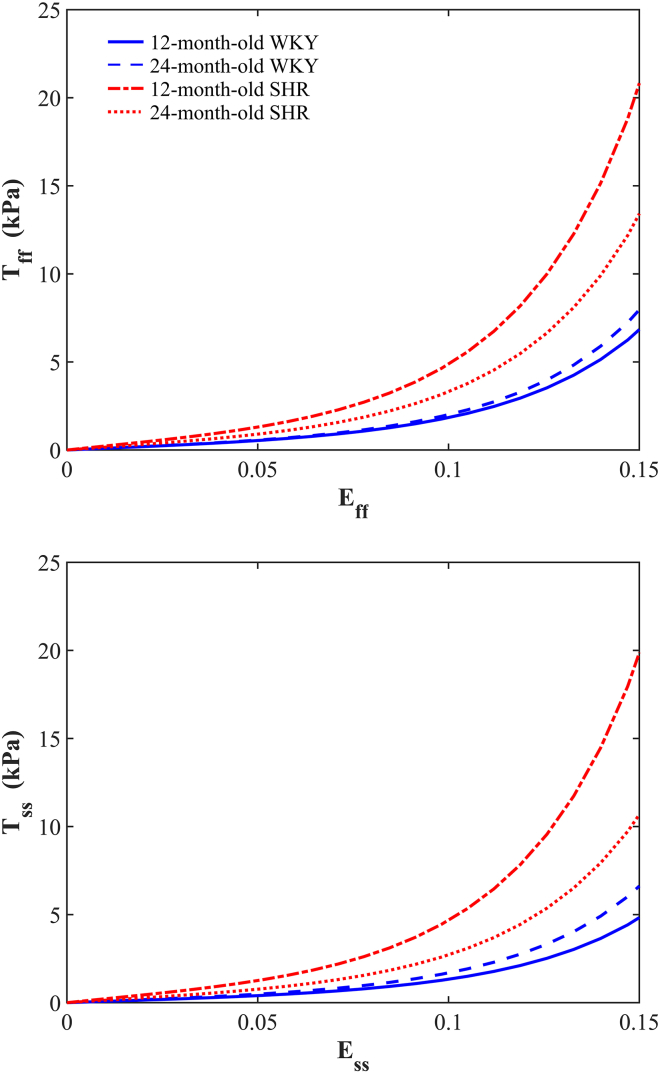
At the optimal values of the material parameters (a, b), we investigated the influence of the structural parameters (see Table 1) on the mechanical response under equibiaxial loading in the fs-plane (see Fig. 10). The SHR group appeared to be stiffer than the WKY group in both the myofiber and sheetlet directions. In particular, the 12-month-old SHR exhibited the highest stiffness of all animals, which may be attributed to the largest collagen volume fraction observed (see Table 1). On the other hand, although collagen volume fraction in the 12-month-old WKY rat was greater than the 24-month-old WKY rat, the younger WKY rat showed the lowest stiffness of all animals, which corresponded to the smallest values of $\overline{\mathbb{A}}$. The corresponding stress ratios T_ff/T_ss at strain of 0.2 were 1.44, 1.21, 1.05, and 1.29 for the 12-month-old WKY rat, 24-month-old WKY rat, 12-month-old SHR, and 24-month-old SHR, respectively. Overall, the stiffness in the myofiber direction was greater than the stiffness in the sheetlet direction (i.e., T_ff/T_ss > 1). However, the stress ratio T_ff/T_ss was very close to one in the 12-month-old SHR, suggesting approximately isotropic behavior in the fs-plane. It should be noted that the mechanical behavior shown in Fig. 10 only considers the stiffness of myocardial tissue without taking into consideration the change in LV geometry. See the Appendix for detailed information on the influence of each of the structural parameters on the mechanical response.

Figure 10.

Stress-strain curves for equibiaxial loading in the myofiber (top) and sheetlet (bottom) directions for SHRs and control WKY rats at 12 and 24 months of age. To see this figure in color, go online.

Discussion

In this study, we advanced our understanding of the underlying mechanisms of HF by developing a, to our knowledge, new structurally based constitutive model of passive myocardium. The structural remodeling between the healthy and diseased hearts as they age was captured using two types of medical images: extended-volume confocal microscopy and MRI. Subject-specific 3D FE models were built using in vivo MRI data. A, to our knowledge, novel method was proposed to quantify structural parameters directly from confocal images and then integrate these parameters into a, to our knowledge, novel constitutive equation (Eq. 7), reflecting the observed differences in cardiac microstructure between healthy and diseased hearts. The constitutive model captured the remodeling of the myocardial collagen network and is based on an exponential strain-energy density function expressed in terms of components of collagen strain referred to the local myocardial coordinate system.

Development of the, to our knowledge, new constitutive equation was inspired by the orthotropic exponential constitutive model of Costa et al. (15), which has seven material parameters. Issues with this model are that the material parameters are highly coupled. Many cardiac constitutive equations are phenomenological models. Such phenomenological models are certainly very useful in capturing the overall biomechanical behavior of the myocardium. However, they lack the ability to reflect the material and mechanical changes that occur as myocardium progressively remodels during processes such as growth or disease. To address this issue, structurally guided constitutive models are being explored (45). Reducing the number of fitted parameters and including parameters derived directly from microstructural imaging are important steps in this direction.

Most of the existing structurally based constitutive models for collagenous soft tissue account for the collagen fiber dispersion using either an angular integration approach based on Lanir’s work (46) or a generalized structure tensor approach as proposed by Gasser et al. (47). Both approaches represent anisotropic tissue behavior based on the distributions of collagen fiber orientation and/or crimp. In our study, the anisotropic characteristic of the myocardium is reproduced using a superposition approach, which sums up all ROI inertia matrices, encapsulating the volume, shape, and orientation of the local collagen architecture in 3D. This approach reduces the computation time considerably in comparison to the angular integration approach and is relatively straightforward to implement.

A key novelty of this study was the explicit use of image-derived microstructural parameters in the constitutive equation to link observed differences in cardiac tissue architecture to ventricular mechanical function during HF. In contrast to previous structurally based constitutive models (e.g., (24, 48, 49, 50)), here, a single set of only two material parameters (a, b) were estimated to reproduce the observed functional data. In previous models, strain-energy function fitting procedures have involved estimation of multiple material parameters defined separately for each specimen considered. The identifiability of the parameters for many of these earlier models has not yet been established, but detailed structural models have been shown to suffer from lack of specificity with respect to data from two-dimensional multiaxial tension experiments (51), which can confound comparisons of the parameters across specimens. In our study, we have limited the fitting to consider only two material parameters (a, b), which resulted in reduced parameter correlation and improved parameter identifiability. It is worth noting that the parameters of Fung-type exponential constitutive equations have been shown to be correlated with respect to load-displacement data for individual cases (16). However, that is not important to this study because our goal was to test the hypothesis that observed structural and geometric remodeling could account for observed differences in LV compliance between the different animals. Although a strictly convex strain-energy function may ensure the physical meaning of the mechanical behavior and avoid any mathematical instability for the computational implementation, the strain-energy function can have negative components. In our formulation, all coefficients of our constitutive equation (Eq. 7) are positive to ensure convexity of the strain-energy function (see Appendix for more details).

There are a number of limitations to this study. A major limitation is that the experimental data were taken from two separate studies (9, 27). However, the combined experimental data were taken from the same strain of animals of approximately the same ages, taking advantage of the consistency observed in the microstructural and mechanical function within each group, as has been reported previously (9, 27). Extended-volume confocal microscopy provides precise information about the 3D organization of the myocardial microstructure. However, confocal images of the whole LV are difficult. In this study, we had access to images from the LV midwall and assumed that the microstructural parameters quantified from these images were representative of the entire LV myocardium, but we acknowledge that some variation is present. Because of the absence of imaging data, the myofiber and sheetlet orientations in all four cases were assumed to be identical based on our observations from previous studies (26, 41). This assumption could be addressed in a future study by using diffusion tensor MRI, which can provide estimates of microstructural orientations based on the orientational dependence of the diffusivity of water molecules (52), although this has only been established in normal myocardium. Additionally, a single-element FE model constructed from subject-specific in vivo MRI data may have neglected some of the geometrical complexity of each heart. Increasing the number of elements to represent the LV geometry more precisely would come at the expense of computation time. It is unlikely that adding such complexity into the biomechanical model would affect the parameter estimation, but this remains to be confirmed. Finally, this study hypothesized that collagen structural remodeling and LV geometrical remodeling can directly account for the observed differences in passive LV function. Thus far, we have tested this hypothesis using just two normal and two diseased hearts at two different time points, which incorporates different microstructural remodeling and changes in LV geometry. Nonetheless, more data is needed to confirm these results.

Conclusions

This work presents a quantitative description of the 3D collagen morphology of diseased SHRs and control WKY rats at 12 and 24 months of age. A new, to our knowledge, structurally based constitutive equation was developed, in which the structural parameters were quantified directly from confocal images of the LV myocardium. The geometric remodeling between the healthy and diseased hearts as they aged was captured using in vivo MRI, from which we built 3D LV FE models. The constitutive equation was developed such that many of the constitutive parameters could be directly related to the observed differences in cardiac microstructure. To the best of our knowledge, this is the first study to link the 3D collagen shape and orientation directly to the mechanical behavior of the myocardium.

The results of this study demonstrate that the model was able to reproduce the experimental compliance data. Importantly, only a single set of just two material parameters (a, b) was required to match the ex vivo LV compliance measurements for all four cases, providing that we accounted for the geometric and microstructural remodeling. Such a model is important for deepening our understanding of the mechanisms of myocardial tissue mechanical behavior in health and disease.

Editor: Zhilin Qu.

Appendix: Structural Parameters and Representative Collagen Structure

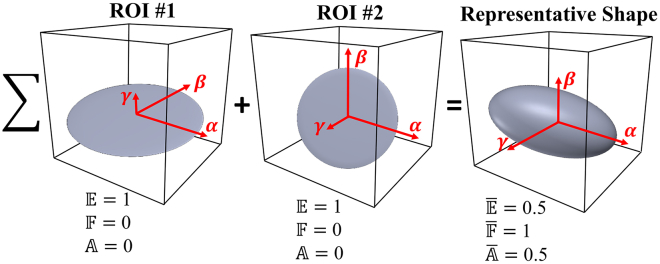
This section describes the difference between localized structural parameters ($\mathbb{E}$, $\mathbb{F}$, $\mathbb{A}$) and representative structural parameters ($\overline{\mathbb{E}}$, $\overline{\mathbb{F}}$, $\overline{\mathbb{A}}$). Assume that two ROIs have the same collagen volume and shape but are oriented at different angles with respect to the image coordinates. Accordingly, the structural parameters $\mathbb{E}$, $\mathbb{F}$, and $\mathbb{A}$ are the same for both ROIs because these parameters only reflect the distributions of collagen shape in each ROI without accounting for the differences in orientation (see Fig. 11). On the other hand, representative structural parameters $\overline{\mathbb{E}}$, $\overline{\mathbb{F}}$, and $\overline{\mathbb{A}}$ are used to quantify the representative collagen structure based on a superposition, which sums up all ROI inertia matrices that combine information on the volume, shape, and orientation of the local collagen architecture in three dimensions. From Fig. 11, although collagen shapes in ROI #1 and ROI #2 are oriented at different angles, the localized structural parameters ($\mathbb{E}$, $\mathbb{F}$, $\mathbb{A}$) are the same because the shape within each ROI is the same. Representative structural parameters ($\overline{\mathbb{E}}$, $\overline{\mathbb{F}}$, $\overline{\mathbb{A}}$) are used to characterize the overall collagen structure, taking into consideration the distributions of summed collagen shapes, orientations, and volumes. This case study illustrates how the values of $\overline{\mathbb{E}}$, $\overline{\mathbb{F}}$, and $\overline{\mathbb{A}}$ cannot be considered as mean values of $\mathbb{E}$, $\mathbb{F}$, and $\mathbb{A}$, respectively.

Figure 11.

Representative collagen structure resulting from two ROIs having the same collagen shape and volume. The collagen structure at ROI #2 is rotated by −90° about the α-direction compared to the collagen shape in ROI #1. The resultant ellipse generated by the superposition of the two ROIs, represents a different shape compared to the individual ROIs. To see this figure in color, go online.

Convexity of the new strain-energy function

To ensure that the new strain-energy density function W(E_ij) grows with increasing stretch, a strictly convex function is required. For W(E_ij) to be convex (see Eq. 7), it requires that a, b, V_f > 0 and that e^Q be strictly convex. Given that e^Q will always be convex if Q is convex, it is sufficient to only force Q to be convex. For Q to be convex, the second derivative of Q with respect to E_ij must be a positive definite. The matrix form of the second derivative can be written as

$${\left[\frac{{\partial }^{2}Q}{\partial E_i\partial E_j}\right]}_{i,j\in \left\{\alpha ,\beta ,\gamma \right\}}=\left[\begin{array}{ccc}2& 0& 0\\ 0& 2\overline{\mathbb{E}}& 0\\ 0& 0& 2\overline{\mathbb{A}}\end{array}\right].$$ (10)

For a positive definite matrix, the principal minors of the second derivative matrix must be positive, which adds the constraint $8\overline{\mathbb{E}}\overline{\mathbb{A}}>0$. Given that all coefficients of the constitutive model are nonzero positive values, we can ensure convexity of the strain-energy function that complies with all constraints a, b, V_f, $\overline{\mathbb{E}},\overline{\mathbb{A}}$ > 0. It should be noted that, from a physical perspective, $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ will be always greater than zero because the segmented 3D objects have positive dimensions and thus positive eigenvalues (see Eq. 6; Fig. 3).

Special cases of constitutive models

In this section, we demonstrate the capability of our constitutive model (Eq. 7) to mimic a wide range of mechanical behaviors based on the shape parameters $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$. Several limiting cases with differing collagen organization are discussed in detail below as special cases.

The second Piola-Kirchhoff stress tensor (T) is one of the most commonly used measures of stress in continuum mechanics. T can be computed as the derivative of the strain-energy function with respect to the Green-Lagrange strain tensor E.

$$T=\frac{\mathit{\partial }W\left(E\right)}{\mathit{\partial }E}$$ (11)

Because T describes material behavior at a point in the reference configuration, and represents stresses with respect to material coordinates, we will use it to compare different mechanical models.

Perfect alignment

In case of aligned fibers, both shape parameters $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ are zero. Hence, the constitutive model simplifies to

$$W=\frac{a{V}_f}{2b}\left[e^{b{E}_{\alpha \alpha }^2}-1\right].$$ (12)

The second Piola-Kirchhoff stress tensor components can then be calculated as

$$T_{\alpha \alpha }=a{V}_f{E}_{\alpha \alpha }{e}^{b{E}_{\alpha \alpha }^2},T_{\beta \beta }=T_{\gamma \gamma }=T_{\alpha \beta }=T_{\alpha \gamma }=T_{\beta \gamma }=0.$$ (13)

Transversely isotropic

In this case, the shape parameters correspond to $\overline{\mathbb{E}}=\overline{\mathbb{A}}=\kappa$ < 1, and the constitutive model has the form

$$W=\frac{a{V}_f}{2b}\left[e^Q-1\right],Q=b\left[E_{\alpha \alpha }^2+\kappa \left(E_{\beta \beta }^2+E_{\gamma \gamma }^2\right)+2\kappa \left(E_{\alpha \beta }^2+E_{\alpha \gamma }^2+E_{\beta \gamma }^2\right)\right],$$ (14)

whereas the second Piola-Kirchhoff stress tensor components can be written as

$$\begin{array}{c}{T}_{\alpha \alpha }=a{V}_f{E}_{\alpha \alpha }{e}^Q,\\ T_{\beta \beta }=a{V}_f\kappa E_{\beta \beta }{e}^Q,\\ T_{\gamma \gamma }=a{V}_f\kappa E_{\gamma \gamma }{e}^Q,\\ T_{\alpha \beta }=a{V}_f\kappa E_{\alpha \beta }{e}^Q,\\ T_{\alpha \gamma }=a{V}_f\kappa E_{\alpha \gamma }{e}^Q,\\ T_{\beta \gamma }=a{V}_f\kappa E_{\beta \gamma }{e}^Q.\end{array}$$ (15)

In this case, the mechanical behavior is the same in any direction perpendicular to the primary collagen direction (α-direction), which is stiffer in comparison to the other directions.

Planar isotropic

For this case, the shape parameters correspond to $\overline{\mathbb{E}}$ = 1 and $\overline{\mathbb{A}}$ = 0. The constitutive model can be written as

$$W=\frac{a{V}_f}{2b}\left[e^Q-1\right],Q=b\left(E_{\alpha \alpha }^2+E_{\beta \beta }^2+2E_{\alpha \beta }^2\right).$$ (16)

The resulting second Piola-Kirchhoff stress tensor components can be written as

$$\begin{array}{c}{T}_{\alpha \alpha }=a{V}_f{E}_{\alpha \alpha }{e}^Q,\\ T_{\beta \beta }=a{V}_f{E}_{\beta \beta }{e}^Q,\\ T_{\alpha \beta }=a{V}_f{E}_{\alpha \beta }{e}^Q,\\ T_{\gamma \gamma }=T_{\alpha \gamma }=T_{\beta \gamma }=0.\end{array}$$ (17)

In this case, the constitutive behavior is isotropic in the αβ-plane.

Isotropic

With shape parameters $\overline{\mathbb{E}}$ = $\overline{\mathbb{A}}$ = 1, the mechanical behavior is uniform in all directions. Thus, there is no preferred direction, and the constitutive model has the form

$$W=\frac{a{V}_f}{2b}\left[e^Q-1\right],Q=b\left[E_{\alpha \alpha }^2+E_{\beta \beta }^2+E_{\gamma \gamma }^2+2\left(E_{\alpha \beta }^2+E_{\alpha \gamma }^2+E_{\beta \gamma }^2\right)\right].$$ (18)

Associated with the Green-Lagrange strain tensor E is the right Cauchy-Green tensor C, defined by C = 2E + I, where I is the identity tensor. The principal invariants of C are defined as

$$I_1=\text{tr}\mathbf{C},I_2=\frac{1}{2}\left[I_1^2-\text{tr}\left({\mathbf{C}}^2\right)\right].$$ (19)

We can rewrite the constitutive model in Eq. 18 in terms of principal invariants I₁ and I₂ as

$$W=\frac{a{V}_f}{2b}\left[e^{b\left[\frac{{\left(I_1-3\right)}^2}{4}+\left(I_1-3\right)-\frac{\left(I_2-3\right)}{2}\right]}-1\right].$$ (20)

This demonstrates that Eq. 18 represents a fully isotropic constitutive model. The second Piola-Kirchhoff stress tensor components are then given by

$$\begin{array}{c}{T}_{\alpha \alpha }=a{V}_f{E}_{\alpha \alpha }{e}^Q,\\ T_{\beta \beta }=a{V}_f{E}_{\beta \beta }{e}^Q,\\ T_{\gamma \gamma }=a{V}_f{E}_{\gamma \gamma }{e}^Q,\\ T_{\alpha \beta }=a{V}_f{E}_{\alpha \beta }{e}^Q,\\ T_{\alpha \gamma }=a{V}_f{E}_{\alpha \gamma }{e}^Q,\\ T_{\beta \gamma }=a{V}_f{E}_{\beta \gamma }{e}^Q.\end{array}$$ (21)

Application to equibiaxial deformation and influence of structural parameters

In this section, we illustrate how structural parameters influence the mechanical behavior based on equibiaxial simulations in the fs-plane. Bearing in mind that there are two coordinate systems—the local collagen coordinate system (α, β, γ) and the myocardial coordinate system (f, s, n)—and to simplify the analytical expressions, we assume here, without loss of generality, that both coordinate systems are aligned, and the component vectors of the myocardial orthogonal axes are given as

$$f={\left[\begin{array}{ccc}1& 0& 0\end{array}\right]}^T,s={\left[\begin{array}{ccc}0& 1& 0\end{array}\right]}^T,n={\left[\begin{array}{ccc}0& 0& 1\end{array}\right]}^T.$$ (22)

Consequently, we can rewrite the, to our knowledge, new constitutive model (Eq. 7) in the myocardial coordinate system as

$$W=\frac{a{V}_f}{2b}\left[e^{bQ}-1\right],Q=\left[E_{ff}^2+\overline{\mathbb{E}}{E}_{ss}^2+\overline{\mathbb{A}}{E}_{nn}^2+2\left(\overline{\mathbb{E}}{E}_{fs}^2+\overline{\mathbb{A}}{E}_{fn}^2+\sqrt{\overline{\mathbb{E}}\overline{\mathbb{A}}}{E}_{ns}^2\right)\right].$$ (23)

For an equibiaxial stretch in the myofiber (f) and sheelet (s) directions, the deformation gradient tensor F and Green-Lagrange strain tensor E can be written as

$$\mathbf{F}=\left[\begin{array}{ccc}\delta & 0& 0\\ 0& \delta & 0\\ 0& 0& \frac{1}{{\delta }^2}\end{array}\right],\mathbf{E}=\left[\begin{array}{ccc}\frac{{\delta }^2-1}{2}& 0& 0\\ 0& \frac{{\delta }^2-1}{2}& 0\\ 0& 0& \frac{1}{2}\left(\frac{1}{{\delta }^4}-1\right)\end{array}\right],$$ (24)

where δ is the extension ratio (stretch) along each of the biaxial coordinate axes. The resulting second Piola-Kirchhoff stress tensor components can be written as

$$\begin{array}{c}{T}_{ff}=a{V}_f{E}_{ff}{e}^{b\left[\left(1+\overline{\mathbb{E}}\right)E_{ff}^2+\frac{\overline{\mathbb{A}}}{2}\left(\frac{1}{{\left(2E_{ff}+1\right)}^2}-1\right)\right]}-\frac{p}{2E_{ff}+1},\\ T_{ss}=a{V}_f\overline{\mathbb{E}}{E}_{ss}{e}^{b\left[\left(1+\overline{\mathbb{E}}\right)E_{ss}^2+\frac{\overline{\mathbb{A}}}{2}\left(\frac{1}{{\left(2E_{ss}+1\right)}^2}-1\right)\right]}-\frac{p}{2E_{ss}+1},\\ T_{nn}=a{V}_f\overline{\mathbb{A}}{E}_{nn}{e}^{b\left[\left(1+\overline{\mathbb{E}}\right)\frac{\sqrt{\frac{1}{2E_{nn}+1}}-1}{2}+\overline{\mathbb{E}}{E}_{nn}^2\right]}-\frac{p}{2E_{nn}+1}=0,\\ T_{fs}=T_{fn}=T_{ns}=0,\end{array}$$ (25)

where p is the unknown hydrostatic pressure to enforce incompressibility. p is calculated from T_nn, noting that T_nn = 0 for equibiaxial stretch, and then is inserted in T_ff and T_ss.

The influence of the structural parameters (see Table 1) on mechanical behavior was investigated using the 12-month-old WKY rat case, in which the collagen and myocardial coordinate systems were almost aligned with angle differences of less than 5° (θ_{f − α} = 3°, θ_{s − β} = 5°, θ_{n − γ} = 1°). The analysis was carried out by changing each of the structural parameters listed in Table 1 by ±15%, taking one structural parameter at a time and keeping the remaining structural and material parameters unchanged. The optimal material parameters (a = 117.6 kPa, b = 37.9) were used in this analysis (see Fig. S1). From Eq. 25, it is clear that V_f only linearly scales the stress-strain curves, whereas $\overline{\mathbb{A}}$ contributes to the nonlinear part of the constitutive model (i.e., is inside the exponential). On the other hand, the structural parameter $\overline{\mathbb{E}}$ contributes to both the linear scaling and the nonlinear parts of the constitutive model in the case of T_ss. However, for T_ff, $\overline{\mathbb{E}}$ only influences the nonlinear part of the constitutive model. In the myofiber direction, the influence of $\overline{\mathbb{E}}$ and $\overline{\mathbb{A}}$ on the mechanical response was the same and less than that of V_f (see Fig. S1). On the other hand, in the sheetlet direction, the constitutive model was most sensitive to changes in the $\overline{\mathbb{E}}$.

Author Contributions

M.P.N., I.J.L., and A.A.Y. designed the research. M.P.N., V.Y.W., and G.B.S. assisted with all preliminary data analysis and helped in developing the computational model. A.J.W. performed the MRI and passive inflation experiments. A.I.H. performed all computations and wrote most of the manuscript. All authors edited the manuscript.