A Spatiotemporal Ventricular Myocyte Model Incorporating Mitochondrial Calcium Cycling

Abstract

Intracellular calcium (Ca²⁺) cycling dynamics in cardiac myocytes are spatiotemporally generated by stochastic events arising from a spatially distributed network of coupled Ca²⁺ release units that interact with an intertwined mitochondrial network. In this study, we developed a spatiotemporal ventricular myocyte model that integrates mitochondria-related Ca²⁺ cycling components into our previously developed ventricular myocyte model consisting of a three-dimensional Ca²⁺ release unit network. Mathematical formulations of mitochondrial membrane potential, mitochondrial Ca²⁺ cycling, mitochondrial permeability transition pore stochastic opening and closing, intracellular reactive oxygen species signaling, and oxidized Ca²⁺/calmodulin-dependent protein kinase II signaling were incorporated into the model. We then used the model to simulate the effects of mitochondrial depolarization on mitochondrial Ca²⁺ cycling, Ca²⁺ spark frequency, and Ca²⁺ amplitude, which agree well with experimental data. We also simulated the effects of the strength of mitochondrial Ca²⁺ uniporters and their spatial localization on intracellular Ca²⁺ cycling properties, which substantially affected diastolic and systolic Ca²⁺ levels in the mitochondria but exhibited only a small effect on sarcoplasmic reticulum and cytosolic Ca²⁺ levels under normal conditions. We show that mitochondrial depolarization can cause Ca²⁺ waves and Ca²⁺ alternans, which agrees with previous experimental observations. We propose that this new, to our knowledge, spatiotemporal ventricular myocyte model, incorporating properties of mitochondrial Ca²⁺ cycling and reactive-oxygen-species-dependent signaling, will be useful for investigating the effects of mitochondria on intracellular Ca²⁺ cycling and action potential dynamics in ventricular myocytes.

Significance

Intracellular calcium (Ca²⁺) cycling dynamics in cardiac myocytes are spatiotemporally generated by stochastic events arising from a spatially distributed network of coupled Ca²⁺ release units that interact with an intertwined mitochondrial network. In this study, we developed a spatiotemporal ventricular myocyte model that integrates mitochondria-related Ca²⁺ cycling components into our previously developed ventricular myocyte model consisting of a three-dimensional Ca²⁺ release unit network. We propose that this new, to our knowledge, spatiotemporal ventricular myocyte model, incorporating properties of mitochondrial Ca²⁺ cycling and reactive-oxygen-species-dependent signaling, will be useful for investigating the effects of mitochondria on intracellular Ca²⁺ cycling and action potential dynamics in ventricular myocytes.

Introduction

Spatiotemporal intracellular calcium (Ca²⁺) cycling dynamics in cardiac myocytes are generated by stochastic phenomena arising from a three-dimensional (3D) Ca²⁺ release unit (CRU) network composed of ryanodine receptor (RyR) clusters in the sarcoplasmic reticulum (SR) membrane. The SR is the major Ca²⁺ store in cardiac myocytes, and the CRUs are coupled via Ca²⁺ diffusion in both the cytosolic and SR space. The intracellular Ca²⁺ dynamics that arise from this network include Ca²⁺ sparks, spark clusters, partial and persistent Ca²⁺ waves, and whole-cell Ca²⁺ oscillations, which play important roles in excitation-contraction, signal transduction, and arrhythmogenesis. In addition to the SR, mitochondria also store Ca²⁺ by taking up Ca²⁺ via mitochondrial Ca²⁺ uniporter (MCU) and extruding Ca²⁺ via mitochondrial Na⁺-Ca²⁺ exchange (NCX_m) or mitochondrial permeability transition pores (MPTPs). It has also been shown that mitochondrial depolarization and other metabolic stress affect the Ca²⁺ cycling dynamics, including Ca²⁺ spark (1, 2), Ca²⁺ alternans (3, 4, 5, 6, 7, 8), and spontaneous Ca²⁺ release and waves (9, 10). Mitochondrial depolarization and Ca²⁺ cycling can also affect the action potential dynamics, such as promoting early afterdepolarizations (11, 12), and lower membrane excitability by opening of K_ATP channels (13, 14, 15) to promote arrhythmias or modulating the pacemaking activity of cardiomyocytes (16, 17).

Mitochondria are coupled to intracellular Ca²⁺ cycling and the cardiac action potential in several ways. First, mitochondria directly influence intracellular Ca²⁺ cycling via mitochondrial Ca²⁺ cycling in which cytosolic Ca²⁺ is sequestered in mitochondria via MCU and then is released back to the cytosol via NCX_m or opening of MPTPs. Second, mitochondria-related reactive oxygen species (ROS) signaling and redox regulation affect RyR open probability and SERCA pump activity (18, 19, 20, 21, 22, 23) as well as ion channel open probability. Third, the SERCA pump and other sarcolemmal ion pumps require ATP. Low ATP may impair these pumps and trigger the opening of the ATP-dependent K⁺ channels. Mitochondrial ROS production and SR Ca²⁺ release form a positive feedback loop because leaky RyRs may result in more mitochondrial Ca²⁺ uptake, which can cause mitochondrial depolarization and ROS production (24, 25). Moreover, a ventricular myocyte contains thousands of mitochondria, forming a mitochondrial network exhibiting spatiotemporal dynamics (26, 27, 28, 29, 30, 31, 32, 33). This network, coupled with the CRU network, also influences spatiotemporal Ca²⁺ cycling dynamics. In addition, the elementary Ca²⁺ release events (e.g., Ca²⁺ sparks) occur randomly because of random L-type Ca²⁺ channel (LCC) and RyR openings (34, 35). Similarly, the mitochondrial membrane potential flickering (36, 37) and ROS flashes (38, 39) also occur randomly in the single mitochondrion level. Therefore, to understand the interactions between mitochondria and intracellular Ca²⁺ cycling and action potential, both the spatial distribution of subcellular components and random behaviors arising from ion channel stochasticity need to be considered.

In this study, we developed a ventricular myocyte model that includes a detailed spatial network of CRUs and mitochondria, which couples to membrane voltage, intracellular cytosolic, SR, and mitochondrial Ca²⁺ cycling. The model also incorporates intracellular ROS signaling, oxidized Ca²⁺/calmodulin-dependent protein kinase II (CaMKII) signaling, stochastic MPTP opening, and mitochondrial Ca²⁺ buffering. Rather than incorporating detailed models of glycolytic and metabolic pathways, we used simplified models for mitochondrial membrane potential, ATP, and ROS described by phenomenological functions. The model was validated against experimental data from literature and predicts Ca²⁺ cycling dynamics such as mitochondrial-depolarization-induced Ca²⁺ alternans and Ca²⁺ waves. This model provides a new, to our knowledge, platform to investigate the effects of mitochondria on intracellular Ca²⁺ cycling and action potential dynamics of ventricular myocytes.

Methods

The mathematical equations and parameters of the model were described in detail in Supporting Materials and Methods. Here, we outline the basics and the major changes we made from previous models.

The overall ventricular myocyte model structure

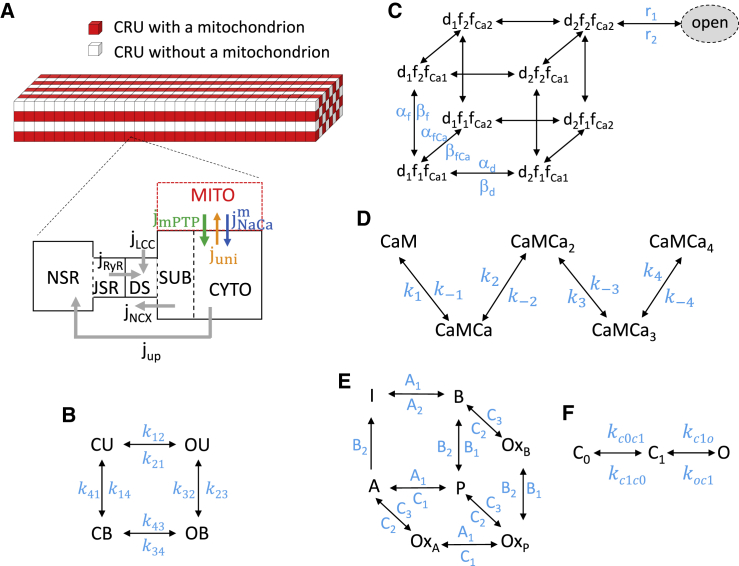
The spatiotemporal myocyte model (Fig. 1 A) consists of a 3D coupled network of CRUs and mitochondria, modified from the model in our recent study (12), which contains 21,504 (64 × 28 × 12) CRUs and 5376 (64 × 14 × 6) mitochondria. These numbers can be changed for modeling different cell sizes. The CRU distance is ∼2 μm in the longitudinal direction and ∼1 μm in the transverse directions. According to Vendelin et al. (40), the average distance between mitochondria is ∼2 μm in longitudinal direction and ∼1.5 μm in the transverse direction in cardiac myocytes. Therefore, we attached a mitochondrion to every CRU along the longitudinal direction and every other CRU along the transverse direction, resulting in a 4:1 CRU/mitochondrion ratio. RyRs and LCCs were modeled by random Markovian transitions (Fig. 1, B and C). The major improvements in the model from our previous study (12) are an incorporation of 1) a new, to our knowledge, stochastic MPTP gating model (Fig. 1 F), a new, to our knowledge, model for mitochondrial Ca²⁺ buffering, and simplified models for cytosolic ROS and ATP; 2) the MCU formulation by Williams et al. (41) and the oxidized CaMKII signaling formulation by Foteinou et al. (42) (Fig. 1, D and E); and 3) ATP, ROS, and CaMKII signaling effects on RyRs, SERCA pump, and the relevant ionic currents based on previous models and experimental information.

Figure 1.

Schematic diagram of the ventricular myocyte model. (A) A schematic diagram of the CRU-mitochondria network consisting of 64 × 28 × 12 CRUs and 64 × 14 × 6 mitochondria is shown. Mitochondria are attached to each CRU in the longitudinal direction and every other CRU in the transverse direction. The compartments contained in a CRU are cytosolic space (CYTO), submembrane space (SUB), dyadic space (DS), junctional SR (JSR), network SR (NSR). Gray arrows indicate the Ca²⁺ fluxes via LCC, NCX, RyRs, and SERCA. When a mitochondrion is attached to a CRU, Ca²⁺ fluxes via MCU, NCX_m, and MPTP are indicated by the colored arrows. (B) The four-state RyR model is shown. (C) The nine-state LCC model is shown. (D) The five-state CaM model is shown. (E) The seven-state CaMKII model is shown. (F) The three-state MPTP model is shown. To see this figure in color, go online.

Membrane potential of the cell

The membrane potential (V) of the cell is described in the following differential equation:

$$C_m\frac{dV}{dt}=I_{Na}+I_{Na,L}+I_{Ca,L}+I_{NCX}+I_{K1}+I_{Kr}+I_{Ks}+I_{to,f}+I_{to,s}+I_{NaK}+I_{K,ATP}+I_{Ca,b}-I_{sti},$$ (1)

where C_m = 1 μF/cm² is the cell membrane capacitance, and I_sti = −50 μA/cm² is the stimulus current density. The ionic current formulations were taken from the rabbit ventricular myocyte model by Mahajan et al. (43) with modifications, which are summarized below.

Na⁺ current

I_Na is the Na⁺ current density and I_Na,L is the late Na⁺ current density, both of which are CaMKII dependent using the formulations by Hund et al. (44).

L-type Ca²⁺ current

I_Ca,L is the L-type Ca²⁺ current density. Because the stochastic opening of LCCs plays important roles in the stochastic firing of Ca²⁺ sparks, the gating of LCCs was modeled using a nine-state Markovian model (12) to describe the different states of the LCCs (Fig. 1 C). We added the CaMKII-dependent regulation by slowing the inactivation of the LCCs (45), using the formulation by Hund and Rudy (46).

Na⁺/K ⁺ pump current

The Na⁺-K⁺ pump current density (I_NaK) model was modified from the formulation by Cortassa et al. (47) to incorporate dependencies on ATP and ADP.

ATP-sensitive K⁺ current

An ATP-sensitive K⁺ current (I_KATP) was added to the model using the formulation by Matsuoka et al. (48).

Cytosolic and SR Ca²⁺ cycling

We incorporated CaMKII, ATP, and ROS regulation of RyRs and SERCA pumps into the model as described below.

RyR open probability

The effects of mitochondrial depolarization on the RyR open probability are mediated by both oxidized CaMKII signaling (49) or redox regulation (20), which increase the RyR open probability. To simulate these effects, we modified the close-to-open rate of RyRs in the following equation:

$$k_{12}=k_{base}\times K_u\times \left(1+\mathit{\Delta }{k}_{CaMKII}+\mathit{\Delta }{k}_{ROS}\right)\times {\left[C{a}^{2+}\right]}_p^2,$$ (2)

where $\mathit{\Delta }{k}_{CaMKII}$ is the CaMKII-dependent component, and $\mathit{\Delta }{k}_{ROS}$ is the ROS-dependent component. k_base and K_u are two rate constants, and ${\left[C{a}^{2+}\right]}_p$ is the local Ca²⁺ concentration in the corresponding dyadic space.

SERCA pump

The formulation by Cortassa et al. (47) was used for the dependence of SERCA pump on ATP. The effects of ROS on SERCA activity are via direct redox regulation (20), which slows the SERCA pump, or via CaMKII phosphorylation of phospholamban, which reduces the half-maximal value $\left(k_i\right)$ to increase SERCA activity. The effects of CaMKII signaling on phospholamban (and thus SERCA activity) were simulated using the formulation by Hund and Rudy (46). Thus, the formulation of SERCA pump is described in the following equation:

$$J_{up}=v_{up}\times f_{up,ATP}\times f_{up,ROS}\times \frac{{\left[C{a}^{2+}\right]}_i^2}{{\left[C{a}^{2+}\right]}_i^2+{\left(k_i-PLB\left({\left[CaMKII\right]}_{act}\right)\right)}^2},$$ (3)

where f_up,ATP is an ATP-dependent function taken from Cortassa et al. (47), and f_up,ROS is an ROS-dependent function.

Background SR leak

We added a CaMKII-dependent background SR Ca²⁺ leak flux following the formulation by Hund et al. (44).

Mitochondrial membrane potential

Because metabolism is not the focus of this study, we ignored the details for mitochondrial membrane potential $\left(\mathit{\Delta \psi }\right)$ generation and usage (50) and used a simple equation to describe $\mathit{\Delta \psi }$ from our previous publication (32), that is, for each mitochondrion in the cell, $\mathit{\Delta \psi }$ is described by the following differential equation:

$$\frac{d\mathit{\Delta \psi }}{dt}=V_{\psi S}-k_{\psi U}\times \mathit{\Delta }\psi -I_{uni}-I_{NC{X}_m},$$ (4)

where $V_{\psi S}=3.5mV/ms$ is the $\mathit{\Delta \psi }$ production rate, $k_{\psi U}=0.192m{s}^{-1}$ is the usage rate constant, $I_{uni}$ is the current density via the MCU of the mitochondrion, and $I_{NC{X}_m}$ is the current density via its NCX_m. Note that Eq. 4 only holds when the MPTP is closed. MPTP opening is known to effectively dissipate the mitochondrial membrane (51); therefore, we assume that $\mathit{\Delta \psi }$ is immediately depolarized to zero once the MPTP opens.

A three-state model of MPTP gating kinetics (Fig. 1 F) from our previous study (51) was used. The transition rate from the state C₀ to the state C₁ was assumed to be Ca²⁺-dependent as in the following equation:

$$k_{c0c1}={\alpha }_0\left(1+199\times \frac{{\left[C{a}^{2+}\right]}_m^{h_{MPTP}}}{{\left[C{a}^{2+}\right]}_m^{h_{MPTP}}+{\left[C{a}^{2+}\right]}_0^{h_{MPTP}}}\right),$$ (5)

where h_MPTP = 5 is the Hill coefficient, [Ca²⁺]_m is the free Ca²⁺ concentration in the corresponding mitochondrion, and [Ca²⁺]₀ is the K_d for the half-maximal value. Other transition rates are assumed to be constant.

Mitochondrial Ca²⁺ cycling

Mitochondrial Ca²⁺ uptake

We incorporated the MCU formulation by Williams et al. (41) into the model, which was fitted to experimental MCU fluxes over a wide range of cytosolic Ca²⁺ concentration.

Mitochondrial Na⁺-Ca²⁺ exchange

We incorporated the mitochondrial Na⁺-Ca²⁺ exchange formulation by Cortassa et al. (47).

Mitochondrial Ca²⁺ buffering

The mitochondrial Ca²⁺ buffering capacity under physiological conditions has been estimated from 33:1 to 30,000:1 (bound/free) (52). Previous studies showed that most matrix Ca²⁺ is buffered by Π in a pH-sensitive manner, and when MPTP opens, the buffering capacitance is reduced because of the decrease in matrix pH (53, 54). In a recent study (55), the time course of mitochondrial free Ca²⁺ was recorded during MPTP opening induced by NCX_m inhibition. After MPTP closure, the mitochondrial free Ca²⁺ reaccumulated with a steep slope and then exponentially relaxed to a constant slope with a timescale of ∼20 s. A possible interpretation could be that the buffering capacitance immediately after MPTP closure is still relatively low, and it takes time for the mitochondrial Ca²⁺ buffers to recover to their high capacitance. Therefore, to reproduce this behavior in our model, we assumed that there is a relaxation time constant for mitochondrial Ca²⁺ buffers to adjust their capacitance in response to MPTP closure. Thus, when MPTP opens, the buffering capacitance is set to ${\beta }_{m,on}$, and when MPTP closes, the buffering capacitance relaxes to ${\beta }_{m,off}$ with a time constant τ_m, as in the following equation:

$${\beta }_m=\{\begin{array}{c}{\beta }_{m,on}\text{after}\text{MPTP}\text{opens}\\ {\beta }_{m,off}-\left({\beta }_{m,off}-{\beta }_m\right)e^{-\frac{t}{{\tau }_m}}\text{after}\text{MPTP}\text{closes}\end{array}.$$ (6)

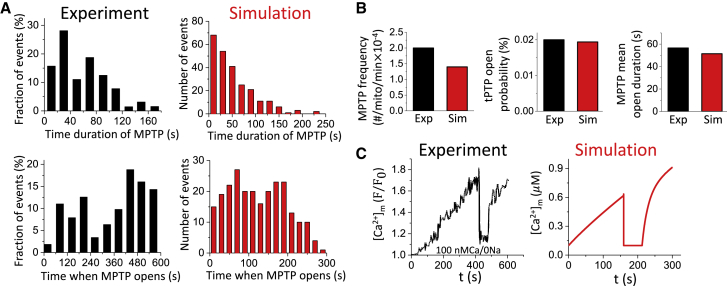
The parameters were chosen to be within the physiological range (52) and were adjusted to reproduce the experimental results by Lu et al. (55) (see Fig. 4).

Figure 4.

MPTP activity and Ca²⁺ cycling behavior in a single mitochondrion. The membrane potential is clamped at −80 mV. The free cytosolic Ca²⁺ maintains at ∼0.1 μM by adjusting the background Ca²⁺ current. The total simulated time is 300 s for each simulation. (A) Distributions of MPTP open duration and time when MPTP opens from experiments by Lu et al. (55) and our simulations are shown. (B) MPTP open frequency, open probability, and mean open duration from experiment by Lu et al. (55) and our simulations are shown. (C) Time course of mitochondrial free Ca²⁺ with MPTP opening and closing from experiment by Lu et al. (55) and our simulation in a single mitochondrion are shown. To see this figure in color, go online.

Cytosolic ROS

Mitochondrial depolarization causes an ROS burst as shown in many experiments (56, 57). In our model, we assume the cytosolic ROS production rate is high when MPTP opens and remains low when MPTP closes. Accurate measurement of cytosolic ROS in cells remains difficult (58), but it is estimated to be less than 0.25 $\mu M$ under normal conditions and could be 100-fold greater under diseased conditions (59). We applied the following governing equation for the cytosolic ROS dynamics in each CRU:

$$\frac{d\left[ROS\right]}{dt}=V_{SODC}-V_{DC}+J_{ROS,Diff},$$ (7)

where V_SODC is the mitochondrial ROS production rate, which is a function of mitochondrial membrane potential. If the CRU does not have a mitochondrion attached to it, this term becomes zero. V_DC = K_DC[ROS] is the cytosolic ROS degradation rate. Based on the fact that the lifetime of H₂O₂ is reported to be ∼10 ms (60), K_DC was set to be 0.1 $m{s}^{-1}$. J_ROS,Diff is the cytosolic ROS diffusion flux between neighboring CRUs with the diffusion constant from Yang et al. (32). V_SODC is formulated such that when a mitochondrion depolarizes, the cytosolic ROS level reaches ∼200 μM, and when mitochondrion remains repolarization, the cytosolic ROS level is ∼0.1 μM, which are reasonably within the pathophysiological range (42, 59).

Cytosolic ATP

ATP cycling in our previous study (50) was formulated using a detailed glycolysis model. Here, because glycolysis dynamics is not the focus of this study, we used a simplified ATP model as in the following equation:

$$\frac{d\left[ATP\right]}{dt}=-V_{ATP,consum}+V_{ATPase}+J_{ATP,Diff},$$ (8)

where V_ATPase is the mitochondrial ATP production rate, and V_ATP,consum is the ATP consumption rate. J_ATP,Diff is the ATP diffusion flux between neighboring CRUs with the diffusion constant from Hubley et al. (61). Under the control condition, the cytosolic ATP level is ∼4.9 mM.

CaMKII signaling

The CaMKII signaling model (Fig. 1 E) developed by Foteinou et al. (42), which includes the oxidation activation pathway, was incorporated into our model.

Computer simulation

Stochastic transitions of LCCs, RyRs, and MPTP were simulated using a modified Gilespie method (62), and the differential equations were solved using the Euler method with a time step of 0.01 ms. A time adaptive method (with a time step varying from 0.001 to 0.01 ms) was used for computing the action potential upstroke of the ventricular cell and the Ca²⁺ dynamics in the dyadic space. All computer programs were coded in CUDA C with double precision. Simulations were carried out on a high-throughput computation cluster consisting of Nvidia Tesla K20c and K80 GPU cards (Santa Clara, CA). To simulate an action potential of a PCL 1 s, it takes ∼140 s of computer time.

Results

Effects of MCU localization on whole-cell intracellular Ca²⁺ cycling properties under normal conditions

Mitochondria are tethered in close proximity to SR Ca²⁺ release sites (63), where changes in cytosolic Ca²⁺ concentration are the most dynamic in cardiac cells. For instance, MCUs located close to the dyadic space sense much higher free Ca²⁺ concentration (∼100 $\mu$M) than those in the bulk cytosol (∼1 μM). To investigate how the MCU localization affects the intracellular and mitochondrial Ca²⁺ cycling dynamics, we simulated our cell model under normal conditions with MCU facing the bulk cytosol, the submembrane space, or the dyadic space only.

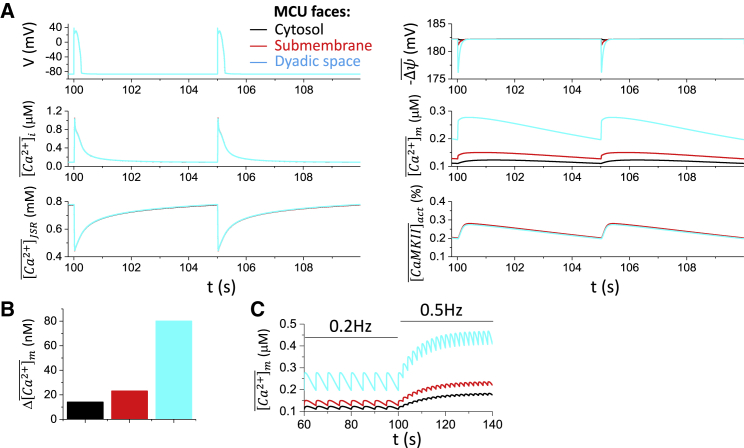
Fig. 2 A shows the time courses of cell membrane potential (V), whole-cell averaged cytosolic free Ca²⁺ concentration $\left({\overline{\left[C{a}^{2+}\right]}}_i\right)$, whole-cell averaged free Ca²⁺ concentration in the junctional SR (JSR) $\left({\overline{\left[C{a}^{2+}\right]}}_{JSR}\right)$, whole-cell averaged mitochondrial membrane potential $\left(-\overline{\mathit{\Delta \psi }}\right)$, whole-cell averaged free mitochondrial Ca²⁺ concentration $\left({\overline{\left[C{a}^{2+}\right]}}_m\right)$, and whole-cell averaged active CaMKII activity $\left({\overline{\left[CaMKII\right]}}_{act}\right)$ for PCL = 5 s and MCU facing different compartments. For all three cases, the action potential, the whole-cell Ca²⁺ transient ${\overline{\left[C{a}^{2+}\right]}}_i$, and SR Ca²⁺ ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$, as well as the CaMKII activity exhibit almost no change for MCU sensing Ca²⁺ in different compartments. The mitochondrial membrane potential $\left(\overline{\mathit{\Delta \psi }}\right)$ exhibits a small change in which a larger depolarization occurs when MCU senses the dyadic Ca²⁺. Altering MCU localization mainly altered the mitochondrial Ca²⁺ load, with MCU facing the dyad resulting in the highest ${\overline{\left[C{a}^{2+}\right]}}_m$ and MCU facing the bulk cytosol the lowest ${\overline{\left[C{a}^{2+}\right]}}_m$. The ${\overline{\left[C{a}^{2+}\right]}}_m$ diastolic-to-systolic variations are ∼15%, ∼20%, and ∼40%, respectively, depending on the MCU localization (Fig. 2 B). This variation is in line with the experiments by Lu et al. (64) who showed that during the steady-state pacing (PCL = 5 s), mitochondrial Ca²⁺ concentration $\left({\overline{\left[C{a}^{2+}\right]}}_m\right)$ rises to the peak rapidly and declines much more slowly with a 10–20% diastolic-to-systolic variation.

Figure 2.

MCU localization on action potential and Ca²⁺ cycling properties under normal conditions. (A) Time courses of V, ${\overline{\left[C{a}^{2+}\right]}}_i$, ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$, $\overline{\mathit{\Delta }\psi }$, ${\overline{\left[C{a}^{2+}\right]}}_m$, and ${\overline{\left[CaMKII\right]}}_{act}$ for MCU facing cytosol (black), submembrane space (red), and dyadic space (cyan), respectively, are shown. In the model, MCU only senses local Ca²⁺. For example, when the MCU faces cytosol, it only senses the local Ca²⁺ concentration in the corresponding cytosolic space, that is, [Ca²⁺]_i. Because MCU localization exhibits small effects on action potential and intracellular Ca²⁺ cycling properties, the colors are overlapped except in the panels for $\overline{\mathit{\Delta }\psi }$ and ${\overline{\left[C{a}^{2+}\right]}}_m$. (B) Mitochondrial free Ca²⁺ amplitude $\mathit{\Delta }{\overline{\left[C{a}^{2+}\right]}}_m$ for the three MCU localizations is shown. (C) Mitochondrial free Ca²⁺ in response to fast pacing is shown. Colored traces correspond to different MCU localizations. To see this figure in color, go online.

Fast pacing causes the ${\overline{\left[C{a}^{2+}\right]}}_m$ diastolic level to rise with a reduced systolic amplitude (Fig. 2 C), replicating the pacing-dependent behavior of mitochondrial free Ca²⁺ reported in experiments by Lu et al. (64). Our simulations predict that MCU localization affects the mitochondrial Ca²⁺ level, which may rise significantly during fast pacing. For instance, if MCU faces the dyadic space, at a PCL of 2 s, the ${\overline{\left[C{a}^{2+}\right]}}_m$ can reach ∼0.4–0.5 μM.

Effects of MCU activity on the whole-cell Ca²⁺ transient

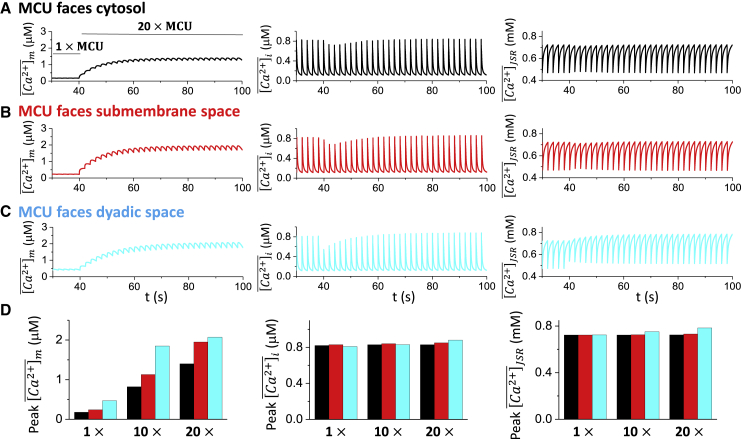
As shown in Fig. 2, changing MCU localization can affect the mitochondrial Ca²⁺ but has almost no effect on Ca²⁺ transient and action potential. However, MCU has been reported to be upregulated under disease conditions, such as heart failure (12). Therefore, we performed simulations to further investigate how the maximal MCU activity affected the intracellular Ca²⁺ cycling dynamics. In our simulations, the maximal MCU activity was commanded to increase from control to a higher value after 20 beats (PCL = 2 s). Different MCU localizations as in Fig. 2 were simulated. Fig. 3, A–C shows the time courses of ${\overline{\left[C{a}^{2+}\right]}}_m$, ${\overline{\left[C{a}^{2+}\right]}}_i$, and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$ for the three different MCU localizations. The maximal MCU activity was increased 20-fold at time t = 40 s, causing mitochondrial Ca²⁺ to gradually increase as expected. However, ${\overline{\left[C{a}^{2+}\right]}}_i$ showed a sudden decrease and then gradually increased and eventually reached a value higher than the control for all the three cases. ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$ exhibits a similar behavior as the cytosolic Ca²⁺. For comparison, the steady-state peak values (after 50 beats) of Ca²⁺ concentration in mitochondria, bulk cytosol and SR were measured for 1-fold, 10-fold, and 20-fold increases of the maximal MCU activity (Fig. 3 D). The results show that increasing the MCU activity up to 20-fold resulted in slight increases in the steady-state peak values of ${\overline{\left[C{a}^{2+}\right]}}_i$ and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$, with MCU facing the dyadic space having the most pronounced effect (Fig. 3 D, cyan). However, as shown in our previous study (12), under heart failure conditions, increasing MCU activity can promote early afterdepolarizations because of the positive feedback loop between Ca²⁺ cycling and action potential.

Figure 3.

MCU strength on intracellular Ca²⁺ cycling. The maximal MCU activity was increased to a higher level after the cell was paced into the steady state (20 beats). The total number of simulated beats for each case is 50, and the PCL is 2 s. From left to right, time courses of ${\overline{\left[C{a}^{2+}\right]}}_m$, ${\overline{\left[C{a}^{2+}\right]}}_i$, and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$are shown. (A) MCU faces the cytosolic space. (B) MCU faces the submembrane space. (C) MCU faces the dyadic space. (D) Bar plots summarize the peak values of ${\overline{\left[C{a}^{2+}\right]}}_m$ (left), ${\overline{\left[C{a}^{2+}\right]}}_i$ (middle), and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$ (right) at the 50th beat for different MCU localizations and different maximal MCU activity. To see this figure in color, go online.

MPTP and Ca²⁺ cycling behaviors in single mitochondria

We next compared the effects of MPTP opening on Ca²⁺ cycling properties in single mitochondria from our cell model to those reported experimentally by Lu et al. (55). In the simulations, we set V = −80 mV, maintained the diastolic ${\overline{\left[C{a}^{2+}\right]}}_i$ in close to 0.1 μM by tuning the background Ca²⁺ current across the cell membrane, and inhibited NCX_m to mimic the experimental condition in Lu et al. (55). We recorded the time when MPTP opens and the opening duration of each event. The histograms of those quantities are shown in Fig. 4 A along with the experimental results by Lu et al. (55). The transition rates of the Markovian MPTP model are chosen such that the average MPTP open frequency, MPTP open probability, and the open time in the model were $1.4\times {10}^{-4}mit{o}^{-1}{\text{min}}^{-1}$, $0.012\text{\%}$, and 51.49 s, respectively, which agree approximately with the experimental data (Fig. 4 B). The time course of [Ca²⁺]_m is shown in the right panel of Fig. 4 C, which agrees with the experimental observations by Lu et al. shown in the left panel of Fig. 4 C.

Effects of MPTP opening on Ca²⁺ sparks and the whole-cell Ca transient

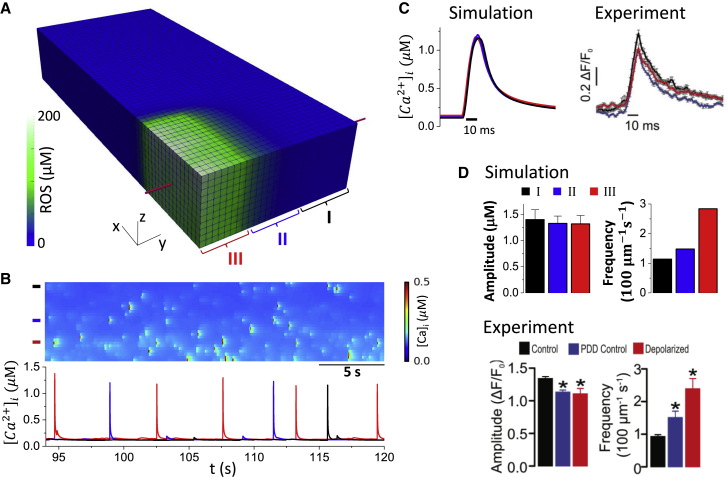
Experiments have shown that mitochondrial depolarization through MPTP opening exhibits a small effect on Ca²⁺ spark amplitude (∼15%) but dramatically increases spark frequency (∼3-fold) (1, 2, 52). Here, we followed the protocol by Boyman et al. (52) in which photon stress was used in a region of the cell to generate ROS in the mitochondria, leading to mitochondrial depolarization. In our model, mitochondria were depolarized in a region (Fig. 5 A) by increasing the close-to-open rate of MPTPs to ensure ∼100% open probability of MPTP within this region. ROS in the depolarized region reached ∼200 μM and quickly declined outside the region because of a short lifetime of ROS (Fig. 5 A). Fig. 5 B shows a line-scan (Fig. 5 A, marked by the red line) image of the cytosolic Ca²⁺ and Ca²⁺ profiles from the three zones (I, far away from the depolarized region; II, intermediate region; and III, depolarized region as marked in Fig. 5 A). The spark frequency was much higher in the depolarized zone, but the spark amplitude remained similar in all three regions. We compare our results with the experimental results from Boyman et al. (52) in Fig. 5, C and D. Fig. 5 C plots the sample profiles of Ca²⁺ sparks from the three different zones, which are almost identical, in agreement with the experimental recordings by Boyman et al. (52). We then collected Ca²⁺ spark events for 100 s and plotted the Ca²⁺ spark amplitude and frequency from the three different zones (Fig. 5 D), which shows the amplitude was reduced by ∼15%, and the frequency was increased by ∼3-fold for sparks from the depolarized zone (III) compared to those from the far away region (I), also agreeing with the experimental results by Boyman et al. (52).

Figure 5.

MPTP opening on the properties of Ca²⁺ sparks. The cell remains at rest (V = $-$80 mV). The MPTPs in the region where n_x$\le$16 and n_y$\le$6 are depolarized by increasing the MPTP close-to-open rate 2000-fold are shown. The total time simulated is 100 s. We define three zones similar to those in Boyman et al. (52): I: region that is far from the depolarized region (20$<$n_y$\le$28); II: intermediate region (7$<$n_y$\le$20); and III: depolarized region (n_x$\le$16, n_y$\le$6). (A) ROS distribution in the cell during mitochondrial depolarization in assigned region is shown. (B) The top panel shows a line-scan image of Ca²⁺ sparks along the red line marked in (A). The bottom panel shows sample Ca²⁺ traces from the three zones as marked by the color bars in the top panel. (C) The left panel shows overlap plot of the Ca²⁺ spark profiles from the three zones. The right panel shows experimental measurement of Ca²⁺ spark profiles in different zones by Boyman et al. (52). (D) The top panel shows Ca²⁺ spark amplitude and frequency measured from our simulations. The bottom panel shows the same quantities from experiments by Boyman et al. (52). To see this figure in color, go online.

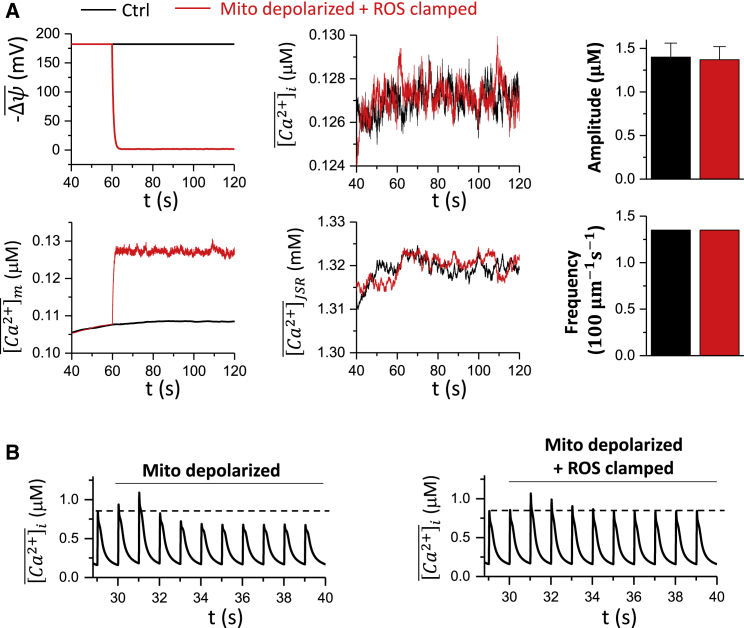
The experiments by Boyman et al. (52) showed that Ca²⁺ spark frequency and amplitude remained the same when mitochondria depolarized without ROS elevation, indicating that ROS may play a key role in changing the properties of Ca²⁺ sparks. To test effects of ROS generated by mitochondrial depolarization on Ca²⁺ sparks, we clamped ROS at the control level, that is, 0.1$\mu$M. The cell was at rest with no pacing. After mitochondrial depolarization, the mitochondrial Ca²⁺ level increased slightly (from 0.11 to 0.13 μM), tracking the cytosolic Ca²⁺. However, the whole-cell averaged Ca²⁺ concentration ${\overline{\left[C{a}^{2+}\right]}}_i$ and SR load ${\overline{\left[C{a}^{2+}\right]}}_{SR}$ exhibited almost no change after the depolarization (Fig. 6 A). Both the Ca²⁺ spark amplitude and frequency remained almost the same as the control. These results agree with the experimental observation by Boyman et al. (52) that ROS are required to change spark properties. We also carried out simulations with pacing at a PCL of 1 s (Fig. 6 B). After mitochondrial depolarization, the whole-cell Ca²⁺ transient ${\overline{\left[C{a}^{2+}\right]}}_i$ exhibited a transient increase and returned to a new steady state at which the peak Ca²⁺ was lower than the control. For comparison, we performed the same simulation but with ROS being clamped to the control level (0.1 μM). Under this condition, the cytosolic Ca²⁺ exhibited similar transient increase after mitochondria were depolarized, but at steady state, the peak Ca²⁺ was the same as the control. These results suggest that the buffered Ca²⁺ inside the mitochondria may transiently affect intracellular Ca²⁺, but it is the ROS that play a key role in altering intracellular Ca²⁺ dynamics during mitochondrial depolarization.

Figure 6.

Effects of ROS on Ca²⁺ spark and Ca²⁺ transient behaviors. (A) Time courses of $\overline{\mathit{\Delta }\psi }$, ${\overline{\left[C{a}^{2+}\right]}}_i$, ${\overline{\left[C{a}^{2+}\right]}}_m$, and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$ without (black) and with (red) clamped ROS (0.1 $\mathit{\mu }\text{M}$) are shown. The right panels show the corresponding Ca²⁺ spark amplitude and frequency. In the simulations, the cell remained at rest (V = −80 mV). The total time simulated is 120 s. (B) The whole-cell Ca²⁺ transient during mitochondrial depolarization with MCU sensing the dyadic Ca²⁺ for free running ROS (left) and clamped ROS (right) is shown. The cell is paced at PCL 1 s. The total time simulated is 40 s. To see this figure in color, go online.

Mitochondrial depolarization promotes Ca²⁺ alternans and spontaneous Ca²⁺ waves

Many experimental studies (3, 4, 5, 6, 9) have shown that metabolic stress or mitochondrial depolarization can cause Ca²⁺ alternans and spontaneous Ca²⁺ waves. Here, we used our model to simulate the effects of mitochondrial depolarization on Ca²⁺ alternans and waves.

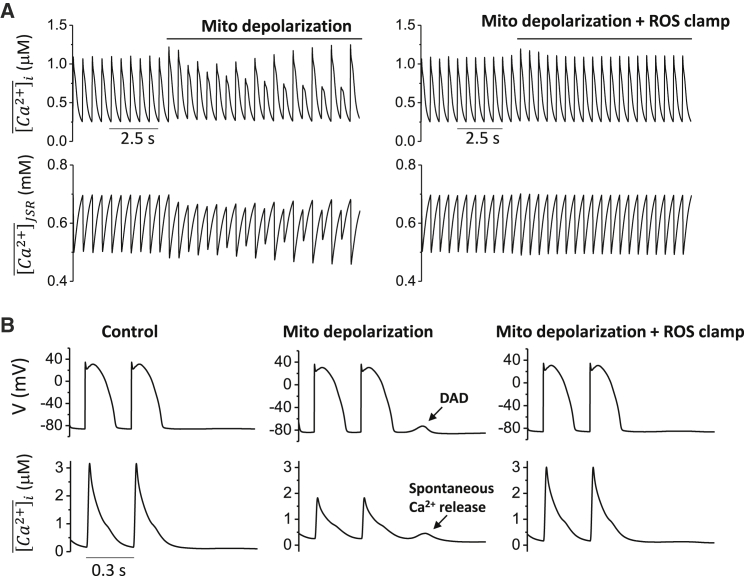
To investigate the effect of mitochondrial depolarization on Ca²⁺ alternans, a PCL of 0.5 s was chosen such that under control conditions, the cell did not exhibit Ca²⁺ alternans. With the cell model paced into the steady state, mitochondria in the cell were depolarized through the commanded opening of MPTP. Immediately after the mitochondrial depolarization, Ca²⁺ alternans developed (Fig. 7 A, left). However, when the ROS level was clamped to 0.1 $\mathit{\mu }\text{M}$ during the mitochondrial depolarization, Ca²⁺ alternans was not observed (Fig. 7 A, right).

Figure 7.

Mitochondrial depolarization promotes Ca²⁺ alternans and spontaneous Ca²⁺ waves. (A) Time courses of ${\overline{\left[C{a}^{2+}\right]}}_i$, and ${\overline{\left[C{a}^{2+}\right]}}_{JSR}$ at PCL = 0.5 s for free running ROS and clamped ROS (0.1 μM) are shown. Mitochondria are depolarized after the cell is paced into the steady state. (B) Time courses of cell membrane potential (V) and Ca²⁺ transient $\left({\overline{\left[C{a}^{2+}\right]}}_i\right)$ at PCL = 0.3 s for control, mitochondrial depolarization with free running ROS, and mitochondrial depolarization with clamped ROS (0.1 μM) are shown.

To study the effect of mitochondrial depolarization on spontaneous Ca²⁺ waves and DADs, SERCA pump activity was increased ($v_{up}=0.8\mathit{\mu }\text{M}\times {\text{ms}}^{-1}$ and $k_i=0.3\mu M$), and the ROS effect on RyR leakiness was enhanced $\left(\mathit{\Delta }{\text{k}}_{\text{ROS},\text{max}}=2\right)$. The cell model was paced into the steady state at a PCL of 0.3 s and then abruptly stopped. When no MPTP opened after pacing, no spontaneous Ca²⁺ release or DADs were observed (Fig. 7 B, left). However, when MPTP opening occurred such that mitochondria depolarized, spontaneous Ca²⁺ release and DADs did occur after the pacing stopped (Fig. 7 B, middle), unless ROS levels were clamped to 0.1 $\mathit{\mu }\text{M}$ (Fig. 7 B, right).

These results show that our model successfully reproduced experimental observations that mitochondrial depolarization promotes Ca²⁺ alternans and spontaneous Ca²⁺ waves. Furthermore, these simulations suggest that intracellular ROS generation in response to mitochondrial depolarization plays a key role in these phenomena.

Discussion

In this study, we developed a new, to our knowledge, spatiotemporal ventricular myocyte model that integrates membrane voltage, cytosolic, SR, and mitochondrial Ca²⁺ cycling, as well as ROS and oxidative CaMKII signaling. The model correctly simulates the effects of mitochondrial Ca²⁺ cycling and depolarization on intracellular Ca²⁺ cycling and action potential dynamics observed in experiments. Specifically, we show that under normal conditions, MCU localization can exhibit a large effect on mitochondrial load but has very small effects on intracellular Ca²⁺ cycling and action potential. Altering MCU activity exhibits similar effects. Mitochondrial depolarization via MPTP opening slightly lowers Ca²⁺ spark amplitude but causes a more than twofold increase of spark frequency. Mitochondrial depolarization promotes spontaneous Ca²⁺ release causing DADs and can induce intracellular Ca²⁺ alternans. These effects are mediated mainly via ROS signaling because they disappear if ROS levels are clamped.

Computer models of mitochondrial metabolism and its coupling with excitation and contraction have been developed previously (47, 65, 66, 67, 68, 69, 70, 71, 72). Some of the models have been used to study the action potential dynamics in single cells (11) and tissue (15). However, most of these models are not spatially extended models and thus cannot simulate the spatiotemporal aspects of intracellular Ca²⁺ cycling dynamics (9, 10) and mitochondrial depolarization dynamics (26, 27, 28, 29, 30, 31, 32, 33). Our model is a spatiotemporal model that can be used to simulate these spatiotemporal dynamics and unravel the dynamical mechanisms arising from coupling of mitochondrial membrane potential and mitochondrial Ca²⁺ cycling, intracellular Ca²⁺ cycling, and action potential of ventricular myocytes. As shown in this study, our model accurately captures the experimentally observed properties of single Ca²⁺ sparks, Ca²⁺ cycling properties of single mitochondria, and whole Ca²⁺ transient dynamics caused by mitochondria.

There are a couple of advantages of the current model over the existing ones. Because the model consists of single mitochondrion and random MPTP opening, it can be used for simulating the mitochondrial membrane potential flickering (36, 37) and ROS flashes (38, 39) and their spatiotemporal dynamics. Because the model is a coupled network of mitochondria and SR, it can be used for investigating the spatiotemporal dynamics of both mitochondrial depolarization wave and Ca²⁺ waves. A distinct advantage of our current model is that the mitochondrial network is a 3D structure, which can be extended to take into account the mitochondrial-mitochondrial or mitochondrial-SR tethering and their heterogeneous distributions (58, 73, 74, 75). Moreover, the model can be easily extended to include mitochondrial coupling via ROS-induced ROS release, as shown in models of previous studies (29, 32, 33). This feature of the model is important for investigating the effects of mitochondrial network structure and coupling remodeling in diseased conditions, such as heart failure (76).

Although in this study we only used the model to investigate the effects of mitochondrial depolarization on Ca²⁺ cycling, we can also use it to investigate the effects of mitochondrial repolarization on Ca²⁺ cycling dynamics during reperfusion injury of ischemic myocardium (77, 78). During this phase, openings of MPTPs occur because of high ROS and mitochondrial Ca²⁺ accumulation (77, 79). Ca²⁺-dependent openings of MPTPs have been incorporated in our MPTP model. However, the mitochondrial reenergization or repolarization and the Ca cycling dynamics may be much more complex than what our current model can properly simulate and need to be considered in future studies.

Other limitations also still exist in this model. We ignored detailed glycolytic and metabolic pathways that have been described in detail in other models (47, 65, 66, 67, 68, 69, 70, 71, 72), which were replaced with simplified models to describe $\mathit{\Delta \psi }$, ROS, and ATP. One rationale for this simplification is that the timescale of metabolism is much slower than electrophysiology, so it is not unreasonable to treat them as parameters instead of variables. Detailed models of glycolysis and mitochondrial metabolism have been developed in previous models (32, 50, 51), which can be easily incorporated into this model if desired. In addition, Ca²⁺ in the mitochondria may directly participate in mitochondrial metabolism to affect mitochondrial membrane potential and ROS production (80), which is not incorporated in our current model. We used a very simple mitochondrial Ca²⁺ buffering to match the experimental data by Lu et al. (55), but the Ca²⁺ buffering is very complex (52, 81), which needs to be considered properly in future studies. Nevertheless, our current model integrates mitochondrial Ca²⁺ cycling and ROS signaling with the SR Ca²⁺ cycling and action potential in a spatiotemporal model of ventricular myocyte, which can be used to simulate the spatiotemporal dynamics of mitochondrial depolarization waves and intracellular Ca²⁺ wave and their effects on action potential dynamics of ventricular myocytes.

Author Contributions

Z.S. and Z.Q. designed the overall research; Z.S. performed the simulations; L.-H.X. and J.N.W. contributed to the overall research design; Z.S., L.-H.X., J.N.W., and Z.Q. analyzed data and wrote the article.

Editor: Daniel Beard.

Supporting Citations

References (82, 83, 84, 85, 86) appear in the Supporting Material.