Confined Quasiparticle Dynamics in Long-Range Interacting Quantum Spin Chains

Abstract

We study the quasiparticle excitation and quench dynamics of the one-dimensional transverse-field Ising model with power-law (1/r^α) interactions. We find that long-range interactions give rise to a confining potential, which couples pairs of domain walls (kinks) into bound quasiparticles, analogous to mesonic states in high-energy physics. We show that these quasiparticles have signatures in the dynamics of order parameters following a global quench, and the Fourier spectrum of these order parameters can be exploited as a direct probe of the masses of the confined quasiparticles. We introduce a two-kink model to qualitatively explain the phenomenon of long-range-interaction-induced confinement and to quantitatively predict the masses of the bound quasiparticles. Furthermore, we illustrate that these quasiparticle states can lead to slow thermalization of one-point observables for certain initial states. Our work is readily applicable to current trapped-ion experiments.

Long-range interacting quantum systems occur naturally in numerous quantum simulators [1–10]. A paradigmatic model considers interactions decaying with distance r as a power law 1/-r^α. This describes the interaction term in trapped-ion spin systems [3,11–15], polar molecules [16–19], magnetic atoms [5,20,21], and Rydberg atoms [1,2,22,23]. One remarkable consequence of long-range interactions is the breakdown of locality, where quantum information bounded by linear “light cones” in short-range interacting systems [24] can propagate superballistically or even instantaneously [25–31]. The nonlocal propagation of quantum correlations in 1D systems has been observed in trapped-ion experiments [12,13]. Moreover, 1D long-range interacting quantum systems can host novel physics that is absent in their short-range counterparts, such as continuous symmetry breaking [32,33].

Recently, it has been shown that confinement—which has origins in high-energy physics—has dramatic signatures in the quantum quench dynamics of short-range interacting spin chains [34]. Owing to confinement, quarks cannot be directly observed in nature as they form mesons and baryons due to strong interactions [35,36]. An archetypal model with analogous confinement effects in quantum many-body systems is the 1D short-range interacting Ising model with both transverse and longitudinal fields [37–42]. For a vanishing longitudinal field, domain-wall quasiparticles propagate freely and map out light-cone spreading of quantum information [41–44]. As first proposed by McCoy and Wu [45,46] (see also Ref. [47]), a nonzero longitudinal field induces an attractive linear potential between two domain walls and confines them into mesonic quasiparticles. Recently, Kormos et al. investigated global quenches in this system and showed that the nonequilibrium dynamics can be used to probe the confined quasiparticle excitations [34].

In this work, we study the nonequilibrium dynamics of the long-range interacting transverse-field Ising model without a longitudinal field after a global quantum quench. We find that long-range interactions introduce an effective attractive force between a pair of domain walls, thus, confining them into a bound state analogous to the meson in high-energy physics. We calculate time-dependent order parameters and connected correlation functions, both of which feature clear signatures of confined quasiparticle excitations [41,42]. The masses of these bound quasiparticles—the energy gaps relative to the ground state—can be directly extracted from the Fourier spectrum of time-dependent order parameters [34,41,42]. We introduce a two-kink model to explicitly show that the confining potential comes from long-range interactions. This effective model also gives good predictions for the quasiparticles’ masses and their dispersion relations. Furthermore, we study the effect of confined quasiparticles on the thermalization of different initial states. We find that for certain initial states, one-point observables exhibit slow thermalization [41,42,48,49], which might help protect ordered phases in the prethermal region [50–52].

We note that our study is in agreement with the general mechanism of global quantum quenches, first formulated in Refs. [41,42,44] for short-range interacting systems, and demonstrates that the general theory developed in Refs. [41,42,44] holds for systems with long-range interactions. Our work is well within the reach of current trapped-ion experiments [15] and other atomic, molecular, and optical (AMO) experimental platforms [1,9,53].

The model.—

Let us consider a quantum spin chain with long-range interactions described by the following Hamiltonian,

$$H=-\sum _{i<j}^L\frac{J}{r_{ij}^{\alpha }}{\sigma }_i^z{\sigma }_j^z-B\sum _{i=1}^L{\sigma }_i^x,$$ (1)

where ${\sigma }_i^{\mu }$ are the Pauli matrices on site i, L is the system size, r_ij is the distance between sites i and j (nearest-neighbor spacing is set to 1), J sets the overall energy scale (set to 1), B is a global transverse field, and α describes the power-law decay of long-range interactions. In this work, we consider periodic boundary conditions unless otherwise specified [r_ij = min (|i − j|, L − |i – j|)].

In the nearest-neighbor interacting limit (α → ∞), H is exactly solvable via a Jordan-Wigner mapping to spinless fermions. It exhibits a phase transition at B = 1, which separates the ferromagnetic and paramagnetic regions [54]. The phase transition persists for long-range interactions, while the critical value of B increases [55–58]. In trapped-ion experiments, the range of the exponent can be tuned within 0 ≤ α ≤ 3 by changing the detuning of the applied optical fields from phonon sidebands. We restrict the numerics to α > 1 in order to ensure a well-behaved thermodynamic limit (the case of α ∈ [0, 1] will be discussed later). Several experiments have investigated the real-time dynamics of the above model (or closely related models), including dynamical phase transitions [15,59], the nonlocal propagation of correlations [12,13], time crystals [50], and many-body localization [14].

Quench dynamics.—

We first study the quench dynamics of the above model. We focus on an initial state with all spins polarized in the z direction |Ψ₀〉 = |…↑↑↑…〉, which is easily preparable in trapped-ion experiments [15]. The system is allowed to evolve under the Hamiltonian (1). This is equivalent to a global quantum quench from zero to finite B [15,41,42]. In order to explore the physics of domain walls, we focus on quantum quenches within the ferromagnetic phase [43,60]. We mention that similar features persist when the initial state is chosen as the ground state of Eq. (1) with finite B in the ferromagnetic region.

We use the Krylov-space method to simulate the quench dynamics of our system [61,62]. Figures 1(a)–1(c) show the equal-time connected correlation functions ${\langle {\sigma }_j^z(t){\sigma }_k^z(t)\rangle }_c=\langle {\sigma }_j^z(t){\sigma }_k^z(t)\rangle -\langle {\sigma }_j^z(t)\rangle \langle {\sigma }_k^z(t)\rangle$ after the sudden quench (k indicates the central lattice site). In the short-range interacting limit [Fig. 1(a)], we recover the exactly solvable case, where correlations spread with a velocity (4B) equal to twice the maximal speed of free domain walls [34,43,44]. Increasing the Ising interaction range (decreasing α) strongly suppresses the magnitude of ${\langle {\sigma }_j^z(t){\sigma }_k^z(t)\rangle }_c$, as shown in Figs. 1(b) and 1(c). One can also see the oscillatory behavior of correlations [Figs. 1(b) and 1(c)], similar to that of Ref. [34]. However, we emphasize that the light-cone spreading of correlations is always present [34,44], though it may have a different velocity depending on the quasiparticles in the system [44]. The actual extent of the light cone becomes clearer by displaying the correlation functions presented in Figs. 1(b) and 1(c) on a different intensity scale (see Supplemental Material [63]). This result is in agreement with the general mechanism of global quantum quenches first derived in Ref. [44].

FIG. 1.

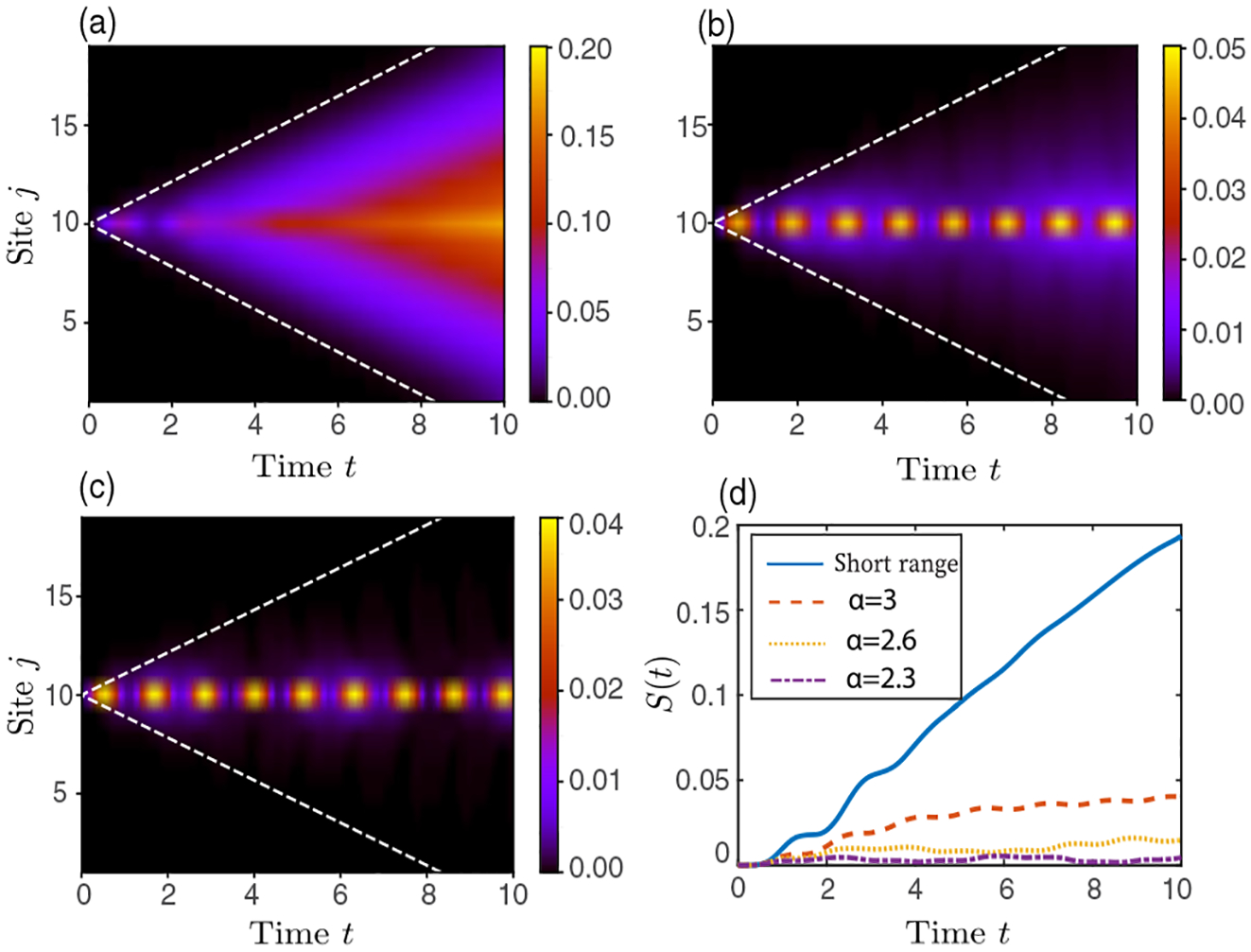
(a)–(c) ${\langle {\sigma }_j^z{\sigma }_k^z\rangle }_c$ and (d) S_A(t) versus t after a quantum quench with initial state |Ψ₀〉. L = 19, k = 10, and B = 0.27. (a) Short-range interacting case (α → ∞), (b) α = 2.6, (c) α = 2.3. The dashed white lines illustrate the maximal velocity 4B of freely propagating domain walls in the short-range interacting case [34]. (d) S_A(t) for various α.

The propagating quasiparticles produced by the quench map out the light-cone spreading of correlations [44,63] and lead to the growth of entanglement entropy [34]. Figure 1(d) shows the growth of entanglement entropy, S_A(t) = −Tr{ρ_A(t) ln[ρ_A(t)]}, where ρ_A(t) is the reduced density matrix of one-half of the chain for various α. As one can see, the entanglement entropy growth for smaller α is much slower than the short-range case (linear growth) [28]. This is because the propagating quasiparticles have smaller velocities for longer-range interactions [63].

We plot time-dependent order parameters $\langle {\sigma }^z(t)\rangle =(1/L){\sum }_i\langle {\sigma }_i^z(t)\rangle$ in Figs. 2(a) and 2(b) [64]. Different from the rapid exponential decay of the magnetization for the short-range case, 〈σ^z(t)〉 exhibits periodic oscillations with almost no decay [41,42,65–67] in the time window shown here. We emphasize that the qualitative change in dynamics is caused by the long-range interactions, not by an additional longitudinal field as in the short-range interacting case [34]. The Fourier spectrum of 〈σ^z(t)〉 illustrates that the oscillations are associated with multiple frequencies [Figs. 2(c) and 2(d)]. As we will see, these frequencies coincide with the masses (and their differences) of quasiparticles [41,42].

FIG. 2.

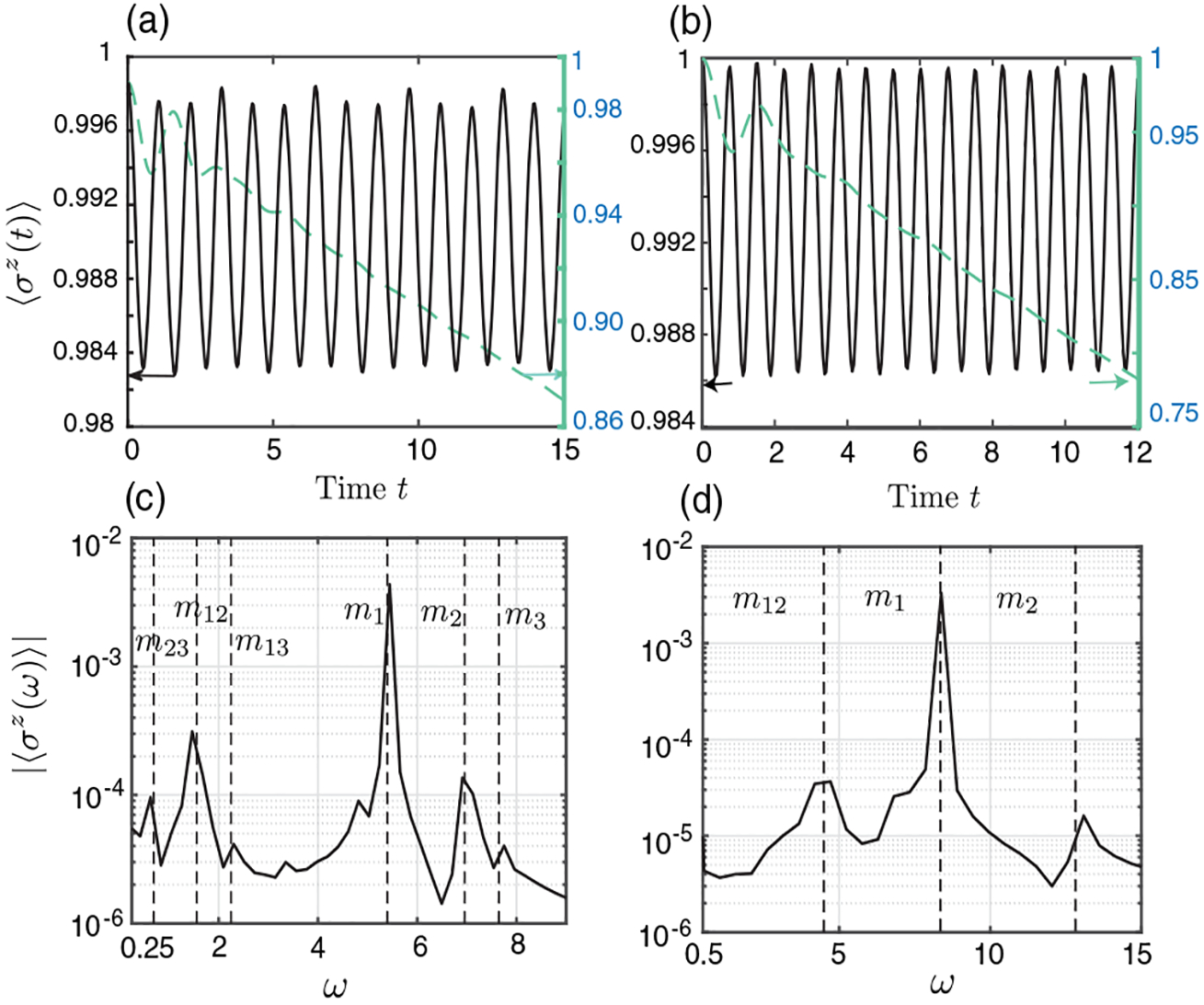
(a),(b) 〈σ^z(t)〉 (black line) versus time after quenching to (a) α = 2.3, B = 0.27, (b) α = 1.4, B = 0.35 for L = 20. The dashed green lines show 〈σ^z(t)〉 for the short-range model (same B). (c),(d) Fourier spectrum of 〈σ^z(t)〉 for the long-range case in (a) and (b), respectively. The largest time for the Fourier transform is t = 30 and 12 for (c) and (d), respectively. The parameters in (b),(d) are accessible in current trapped-ion experiments [15]. The dashed lines show the mesonic masses (m_i) and their differences (m_ij ≡ m_j – m_i) calculated using the two-kink model.

Two-kink model and bound states.—

To understand the quasiparticles in our system, we use a two-kink model to perturbatively study the low-energy excitations of Eq. (1). The two-kink model has been used to phenomenologically study excitations in short-range interacting quasi-1D compounds [37,68]. The idea is to restrict the Hilbert space to two-domain-wall states [see inset of Fig. 3(a)], where regions of different magnetization are separated by the two domain walls. The projected model is expected to work well when B is much smaller than J [34].

FIG. 3.

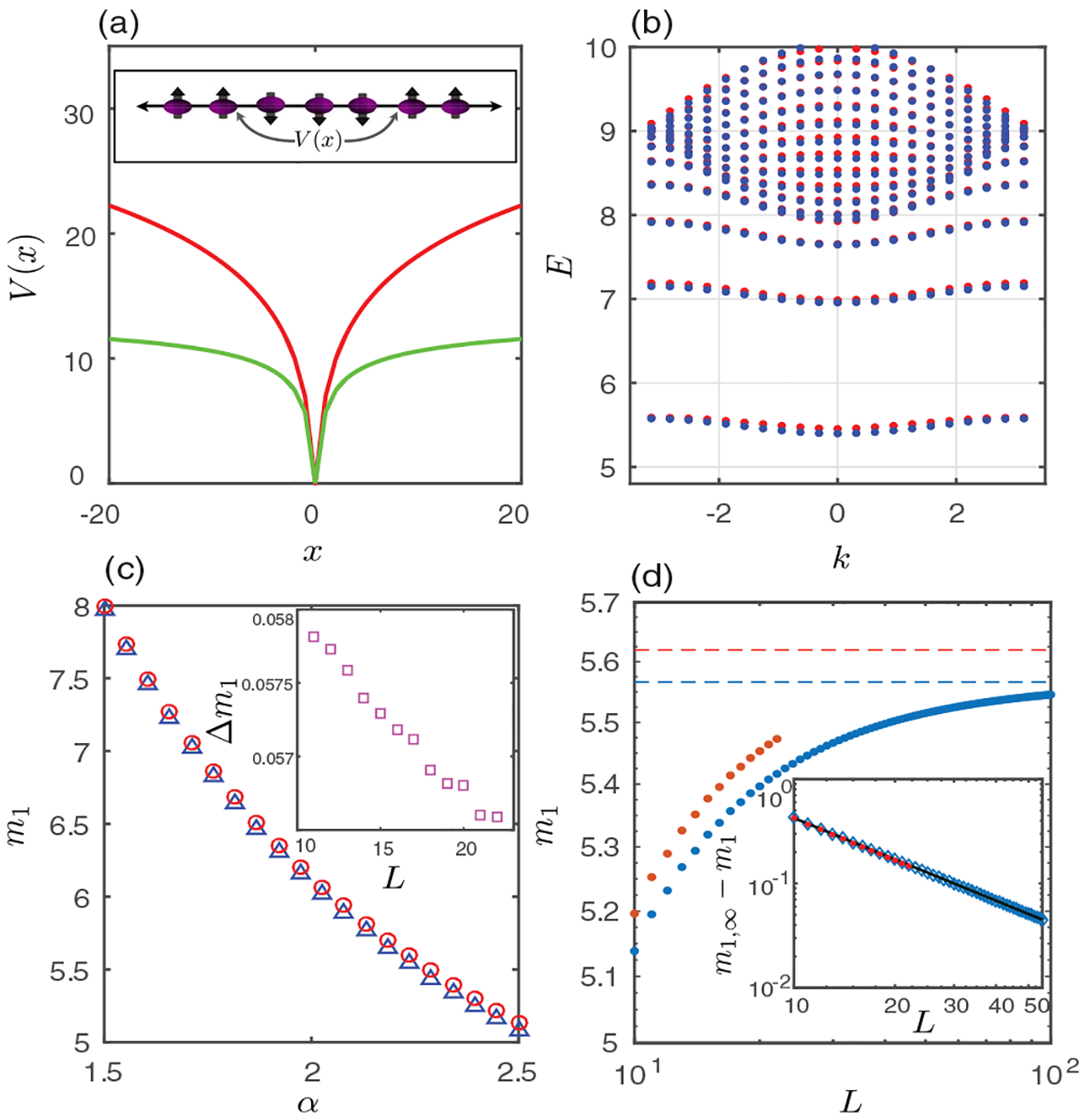
(a) Potential energy as a function of distance x between the two domain walls (n = |x|). Red line, α = 1.9; green line, α = 2.3. Inset: Typical spin configuration of two-domain-wall states. (b)–(d) Comparison of two-kink model (blue) and ED results (red). (b) Energy spectrum. Parameters: α = 2.3, B = 0.27, L = 20. (c) m₁ versus α with parameters B = 0.27 and L = 22. Inset: Difference of m₁ between the two methods Δm₁ versus L. (d) m₁ versus L [same parameters as (b)]. The dashed lines are m_1,∞. The inset shows m_1,∞ − m₁ versus system size. The black line shows the fitting of the two-kink model’s data to (1/L)^β, with β = 1.315. ED data have similar scaling with β = 1.34. m_1,∞ is chosen as 5.56 (5.62) for the two-kink model (ED).

The Hilbert space of the projected model is spanned by states of n down spins (clustered together) represented as |j, n〉 = |…↑↑↓_j↓…↓↓_(j+n−1)↑↑…〉, where j is the starting position of the cluster. The projected Hamiltonian $\mathcal{P}H\mathcal{P}$ ($\mathcal{P}$ denotes the projection operator to the two-domain-wall subspace) acts on |j, n〉 as follows:

$$\mathcal{H}|j,n\rangle =V\left(n\right)|j,n\rangle -B[|j,n+1\rangle +|j,n-1\rangle +|j+1,n+1\rangle +|j-1,n+1\rangle ].$$ (2)

Here, we have defined the potential energy as $V\text{(}n\text{)=}\langle j,n\left|\mathcal{H}\right|j,n\rangle -\langle {\mathrm{\Psi }}_0\left|\mathcal{H}\right|{\mathrm{\Psi }}_0\rangle$. Utilizing translational invariance, we transform the two-domain-wall state into momentum basis $|k,n\rangle =(1/\sqrt{L}){\sum }_{j=1}^L\text{exp}(-ikj-ikn/2)|j,n\rangle$, which gives

$$\mathcal{H}=\sum _{k,n}V\left(n\right)|k,n\rangle \langle k,n|-2B\text{cos}\frac{k}{2}|k,n\rangle \langle k,n+1|-2B\text{cos}\frac{k}{2}|k,n\rangle \langle k,n-1|.$$ (3)

For L → ∞, the potential energy of a two-domain-wall spin configuration is

$$V(n)=4n\zeta (\alpha )J-4J\sum _{1\le l<n}\sum _{1\le r\le l}\frac{1}{r^{\alpha }},$$ (4)

where $\zeta (\alpha )={\sum }_{z=1}^{\infty }\left(1/z^{\alpha }\right)$ denotes the Riemann zeta function. As plotted in Fig. 3(a), V(n) increases with the distance between domain walls. For the short-range model studied in Ref. [34], the confining potential is due to an additional on-site longitudinal magnetic field. In our case, the confining potential is intrinsically generated by the long-range interactions.

The picture now becomes clear: The long-range Ising interaction gives rise to an effective potential, which increases with separation between the two domain walls, while the transverse magnetic field acts as kinetic energy for domain walls (changing the size of the cluster). Therefore, a pair of domain walls, each of which is a free quasiparticle in the short-range limit, becomes bounded together when α decreases. Note that V(n) has an upper bound when α > 2, as illustrated in Fig. 3(a) (see Supplemental Material [63]). This indicates that the lower part of the energy spectrum is composed of domain-wall bound states, while above some energy threshold, we have a continuum of states [Fig. 3(b)]. For α ≤ 2, however, all excitations within the two-kink model are bound quasiparticles, as the confining potential V(n) becomes unbounded when n → ∞ [63]. This is in contrast with finite-range interacting models, where the potential becomes flat for n greater than the interaction range. In other words, for finite-range interacting systems, two domain walls will behave like freely propagating particles if the domain size of the initial state exceeds the interaction range.

Figure 3(b) shows the energy spectrum calculated by the two-kink model (blue dots) and exact diagonalization (ED) of the full Hamiltonian (red dots). The energy spectrum agrees well for the two methods, demonstrating that low-energy excitations are dominated by two-domain-wall states. The bound states’ masses [69] and dispersion relations can be simply read out from the energy spectrum. Moreover, the Fourier frequencies of 〈σ^z(t)〉 [Figs. 2(c) and 2(d)] coincide, to high accuracy, with the masses of the bound states (and their differences) calculated using the two-kink model [41,42]. This demonstrates that the quench dynamics of the long-range interacting model is indeed dominated by confined quasiparticles.

We compare the smallest quasiparticle mass m₁ as a function of α calculated using the two-kink model and ED [Fig. 3(c)]. For a large range of α, we see excellent agreement between the two methods, and the numerical difference does not increase for larger L [inset of Fig. 3(c)]. The masses increase with L as longer chains have more interaction terms [63]. However, V(n) is finite (for finite n) in the thermodynamic limit, since the Riemann zeta function converges for α > 1 [70]. This leads to finite masses, even for an infinite system for α > 1 (see Supplemental Material [63]). As shown in Fig. 3(d), the mass calculated from the two-kink model indeed exhibits convergence in the thermodynamic limit. For the two-kink model, the difference between m₁ and its thermodynamic value m_1,∞ scales as (1/L)^β, with β ≈ α − 1 [63], as shown in the inset. While we cannot verify convergence using ED, we do observe similar scaling of m₁ [inset of Fig. 3(d)]. For 0 ≤ α ≤ 1, V(n) becomes infinite, even for finite n, and thus, the quasiparticles have infinite energy (as the Riemann zeta function diverges for 0 ≤ α ≤ 1 [70]), consistent with the results of Ref. [71].

Strong and weak thermalization.—

For the quenches we have considered, both the order parameter decay and entanglement growth are slow (Fig. 1). This motivates us to study thermalization in our long-range model. Previous studies of the short-range Ising model have observed rapid (strong) or slow (weak) thermalization of one-point functions for different initial states [41,42,48,49,72–75]. As first shown in Ref. [41], undamped oscillations (weak thermalization) of a one-point observable occur within an intermediate time window when the matrix elements between the initial state and the quasiparticle state of the quench operator and of the observable are both nonzero [41,42]. Rapid decay occurs when this condition is not satisfied. Numerical results consistent with this finding have been observed [34,42,48,49,74]. Here, we illustrate that these two distinct behaviors also occur in the long-range Ising model and that slow thermalization can arise when the quasiparticles are the result of confinement [34,42,74].

In order to see this, we consider the time evolution of two different initial states (with the same quenched Hamiltonian): |Z₊〉 = ∏_j|↑_j〉 (the same state considered before) and $|Y_{+}\rangle ={\prod }_j(1/\sqrt{2})\left(|{\uparrow }_j\rangle +i|{\downarrow }_j\rangle \right)$ [48]. For |Z₊〉, the quenched operator has the same parity as the two-kink bound state, and thus, the matrix elements mentioned above have nonzero values [41,42]. We therefore expect slow dynamics with oscillations due to the bound quasiparticles [41,42]. On the other hand, |Y₊〉 does not satisfy this condition, which suggests rapid thermalization.

We calculate the difference between the time-dependent expectation value of single-body observables 〈σ^μ(t)〉 and their thermal expectation value ${\langle {\sigma }^{\mu }\rangle }_{\text{th}}=\text{tr}\left(e^{-{\beta }_{\mathrm{\Psi }}H}{\sigma }^{\mu }\right)/\text{tr}\left(e^{-{\beta }_{\mathrm{\Psi }}H}\right)$, where the temperature 1/β_Ψ is determined by [76]

$$\frac{\langle \mathrm{\Psi }\left|H\right|\mathrm{\Psi }\rangle }{\langle \mathrm{\Psi }|\mathrm{\Psi }\rangle }=\frac{\text{tr}\left(H{e}^{-{\beta }_{\mathrm{\Psi }}H}\right)}{\text{tr}\left(e^{-{\beta }_{\mathrm{\Psi }}H}\right)}.$$ (5)

Here, |Ψ〉 denotes the initial state. As illustrated in Fig. 4(a), for |Y₊〉, all single-body observables converge to 〈σ^μ〉_th rapidly, indicating strong thermalization, as expected. For |Z₊〉, we instead observe strong oscillatory behavior [41,42], with Fourier frequencies consistent with the masses of the bound quasiparticles, around 〈σ^μ〉_th [Fig. 4(b)]. Within the time window shown, we observe almost no decay of these observables, indicating much slower thermalization compared to |Y₊) [48,49].

FIG. 4.

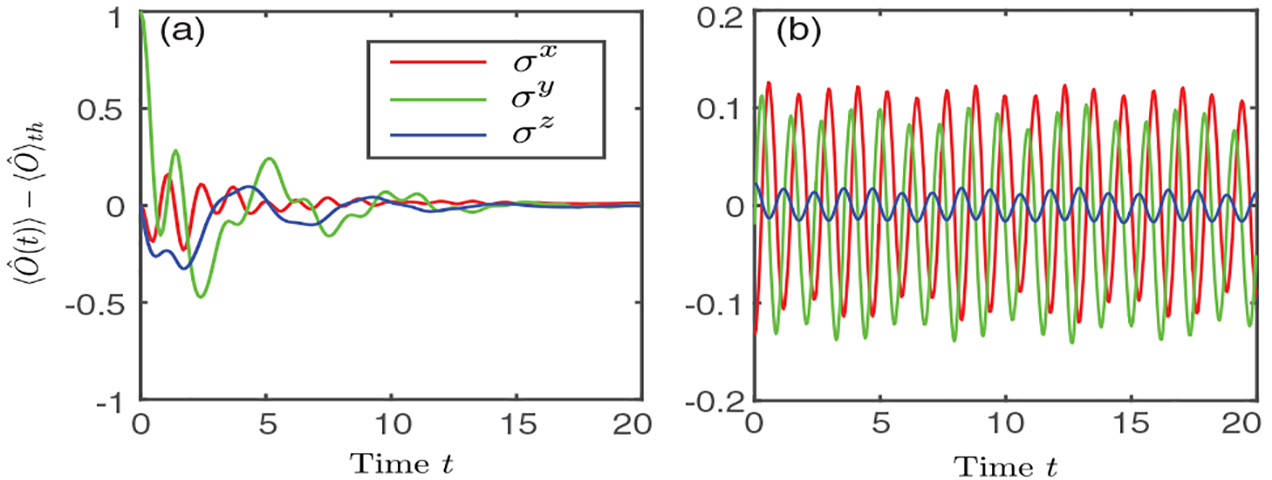
Strong (a) and weak (b) thermalization for different initial states. (a) 〈σ^μ(t)〉 − 〈σ^μ〉_th for initial state |Y₊〉. (b) Same as (a) but for initial state |Z₊〉. Parameters: α = 2.3, B = 0.37, L = 20.

Conclusions and outlook.—

We have found that the low-energy excitations of the long-range transverse-field Ising model are confined domain walls. These bound quasiparticles, which arise due to long-range interactions, have clear signatures in the quench dynamics of the system [34,41,42]. Furthermore, our work has shown that general quantum mechanisms of quench dynamics developed for short-range interacting systems [41,42,44] hold for long-range interacting systems. These results can be readily investigated in trapped-ion experiments [15] and other AMO systems with long-range interactions [1,9,53]. The slow thermalization of one-point functions induced by long-range interactions has potential applications for stabilizing nonequilibrium phases of matter, such as time crystals [50–52] and Floquet symmetry-protected topological phases of matter [77–81]. Finally, it would be interesting to study the effects of long-range interactions on quench dynamics of q-state Potts models, which admit mesonic as well as baryonic excitations [82–85].