Skip to main content
PMC home page
ACS Omega logoLink to ACS Omega
. 2020 Jan 10;5(3):1708–1716. doi: 10.1021/acsomega.9b04004

Solubility Measurement and Various Solubility Parameters of Glipizide in Different Neat Solvents

Mohd Abul Kalam †, Aws Alshamsan †, Musaed Alkholief †, Ibrahim A Alsarra ‡, Raisuddin Ali ‡, Nazrul Haq ‡, Md Khalid Anwer §, Faiyaz Shakeel ‡,*
PMCID: PMC6990636  PMID: 32010845

Abstract

graphic file with name ao9b04004_0003.jpg

Glipizide (GLZ) is an oral hypoglycemic agent, which is a weakly aqueous soluble drug. The solubility values of GLZ in various neat solvents are scarce in the literature. Hence, the solubility of GLZ in 12 different neat solvents, namely, “water, methanol, ethanol, isopropanol (IPA), 1-butanol, 2-butanol, ethylene glycol (EG), propylene glycol (PG), poly(ethylene glycol)-400 (PEG-400), ethyl acetate (EA), dimethyl sulfoxide (DMSO), and Transcutol-HP (THP)”, at “T = 298.2–318.2 K” and “p = 0.1 MPa” was measured. The recorded solubilities of GLZ were correlated by “van’t Hoff and Apelblat models” using root-mean-square deviation (RMSD). The overall RMSD was obtained as 1.21 and 1.40% for “Apelblat and van’t Hoff models”, respectively. Different solubility parameters of all studied materials including drug and solvent were calculated to find the best solvent for GLZ. The solubilities of GLZ (expressed in mole fraction) have been found highest in DMSO (2.81 × 10–2), followed by THP, EA, 2-butanol, 1-butanol, IPA, PEG-400, ethanol, PG, methanol, EG, and water (1.98 × 10–4) at “T = 318.2 K”. All investigated solubility parameters of GLZ were recorded very close to the DMSO. “Apparent thermodynamic analysis” showed an “endothermic and entropy-driven dissolution” of GLZ in the 12 different neat solvents. The highest molecular interactions were recorded in GLZ–DMSO compared to other combinations. Overall, DMSO has been considered as the best solvent for the solubilization of GLZ.

Introduction

Glipizide (GLZ) [chemical structure: Figure 1; chemical name: N-[2-(4-{[(cyclohexyl carbamoyl)amino]sulfonyl}phenyl)ethyl]-5-methylpyrazine-2-carboxamide; molecular formula: C21H27N5O4S; molar mass: 445.53 g mol–1; and CASRN: 29094-61-9] was found as a white solid powder, and it has been reported as stable at T = 298.2 K.1,2

Figure 1.

Figure 1

Open in a new tab

Molecular structure of GLZ.

It is a second-generation sulfonylurea used as an oral hypoglycemic agent for the treatment of type-II diabetes (non-insulin-dependent diabetes mellitus).3 It has been reported as a class II drug, which has a low solubility and high permeability. Class II drugs have oral bioavailability problems due to poor aqueous solubility.4 The originator of GLZ is Pfizer. The melting point of GLZ has been reported as 481.2–482.2 K. Being a weak acid (pKa = 5.9), GLZ is practically insoluble in water, sparingly soluble in acetone, and soluble in dichloromethane.3 The log P value of GLZ was obtained as 1.91 in the n-octanol–water system. The terminal elimination half-life of GLZ is 2–7 h, and the initial oral dosage of GLZ is 5–20 mg once daily. Compared to tolbutamide, it is 100 times more potent. It acts to decrease the blood glucose level by motivating the pancreatic β-cells liberation, which causes an increased insulin secretion.4 GLZ has also been reported as a significant anticancer agent that acts by suppressing the tumor angiogenesis (obstruct the formation and development of blood vessels), tumor growth, and metastasis.5 The anticancer efficacy of GLZ is neither because of its antiproliferative effects nor due to its antidiabetic properties. Rather, GLZ inhibits the migration and formation of endothelial cells and tubular structures, respectively. Thus, it “inhibits angiogenesis by upregulating the expression of natriuretic peptide receptor-A”.5,6 Because of the poor aqueous solubility and minimal dissolution, the oral bioavailability of GLZ has been reported to be very low after oral administration. Poor aqueous solubility causes reduced absorption of the drug. The bioavailability of a BCS class II drug (e.g., GLZ) depends on its solubility; therefore, in such cases, dissolution is the rate-limiting step. Being an antidiabetic drug, GLZ should be absorbed quickly; therefore, increasing the solubility is an essential criterion for its enhanced bioavailability.

The solubility, dissolution, and eventually the bioavailability of GLZ can be improved by different techniques such as development of liquisolid tablets by using poly(ethylene glycol)-400 (PEG-400) as a liquid vehicle,4 polymeric microparticles,7,8 polymeric nanoparticles,9 co-solvent solubilization approach,2 complexation of GLZ with α and β-cyclodextrins,10−12 solid self-nanoemulsification,3 microemulsion technology,13,14 preparation of osmotically controlled oral drug-delivery system,15 solid dispersion,16−20 nanosuspension,21 microwave-generated bionanocomposites,22 transdermal drug-delivery system,23 floating bioadhesive drug-delivery system,24 and microcrystallization.25 The solubility data of GLZ in various neat solvents (NS) are scarce in research database. The solubility data of drugs and pharmaceuticals in various neat solvents had a greater impact in many industrial processes including “drug discovery process and formulation development”.26−28 Hence, the solubility of GLZ in 12 different neat solvents, such as “water, methanol, ethanol, isopropanol (IPA), 1-butanol, 2-butanol, ethylene glycol (EG), propylene glycol (PG), PEG-400, ethyl acetate (EA), Transcutol-HP (THP), and dimethyl sulfoxide (DMSO)”, within the temperature range “T = 298.2–318.2 K” and pressure “p = 0.1 MPa” was estimated by applying various experimental and computational approaches. The investigated temperature range at the interval of 5 K was chosen randomly based on the melting point of GLZ and boiling temperatures of each investigated solvent. Therefore, the temperature range, i.e., T = 298.2–318.2 K, was chosen in such a way that the maximum studied temperature, i.e., “T = 318.2 K”, should not exceed the melting point of GLZ and boiling temperatures of each investigated solvent. The melting point of GLZ was obtained as 484.21 K by thermal analysis. The maximum studied temperature (T = 318.2 K) was much lower than the melting point of GLZ and boiling temperature of each studied solvent. Therefore, the studied temperature range was selected in this work. Different solubility parameters were also determined for the evaluation of the best solvent for GLZ. “Apparent thermodynamic analysis” was performed to evaluate the thermodynamic behavior of GLZ. The molecular interactions between GLZ and 12 different neat solvents were also investigated. The solubility values, solubility parameters, and thermodynamic parameters of GLZ recorded in the proposed work could be helpful in “purification, recrystallization, drug discovery, preformulation studies, and formulation development” of GLZ.

2. Results and Discussion

2.1. Characterization of GLZ in Solid States

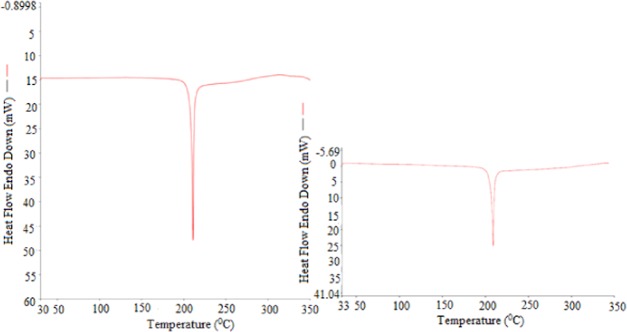
The characterization of GLZ in the solid states of pure and equilibrated GLZ was performed by “differential scanning calorimetry (DSC)” analysis. The recorded DSC thermogram of GLZ in pure form is summarized in Figure 2A, which shows a sharp crystalline peak of GLZ at 484.21 K, suggesting the fusion temperature (Tfus) of GLZ. The molar fusion enthalpy (ΔHfus) for pure GLZ was recorded as 63.33 kJ mol–1. The recorded DSC thermogram of equilibrated GLZ (which was recovered from EA) is summarized in Figure 2B, which also presents a sharp crystalline peak of equilibrated GLZ at 482.24 K, suggesting the Tfus value of equilibrated GLZ. The ΔHfus value for equilibrated GLZ was recorded as 66.42 kJ mol–1.

Figure 2.

Figure 2

Open in a new tab

DSC spectra of (A) pure GLZ and (B) equilibrated GLZ (recovered from EA after slow evaporation).

The DSC thermograms and thermal parameters (Tfus and ΔHfus) of pure and equilibrated GLZ were not changed significantly (P > 0.05), suggesting that the crystalline form of GLZ was not changed into the formation of solvent complexes, solvates, hydrates, polymorphs etc. after solubility experiments/equilibrium. The Tfus value of GLZ was determined as 484.60 K by Dash et al.3 Choudhary et al. determined the Tfus value of GLZ as 478.20 K.18 Shende and Fiske found the Tfus value of GLZ as 489.28 K.19 The determined Tfus value of GLZ at 484.21 K in the proposed study was very close to that reported by Dash et al.3 However, it was little deviated from those reported by Choudhary et al. and Shende and Fiske.18,19

2.2. Experimental Solubility Data of GLZ

The experimental solubility (xe) values of GLZ in 12 different neat solvents at T = 298.2–318.2 K and p = 0.1 MPa are summarized in Table 1. The solubility of GLZ in water has been reported by many researchers. However, the quantitative solubility values of GLZ in other studied neat solvents have not been reported.

Table 1. Experimental Solubilities (xe) of GLZ in Mole Fraction in 12 Different Neat Solvents (NS) at T = 298.2–318.2 K and p = 0.1 MPaa.

  xe
NS T = 298.2 K T = 303.2 K T = 308.2 K T = 313.2 K T = 318.2 K
water 4.85 × 10–7 7.60 × 10–7 1.05 × 10–6 1.50 × 10–6 1.98 × 10–6
EG 4.81 × 10–5 6.37 × 10–5 8.08 × 10–5 1.02 × 10–4 1.37 × 10–4
methanol 1.09 × 10–4 1.42 × 10–4 1.94 × 10–4 2.59 × 10–4 3.38 × 10–4
PG 1.37 × 10–4 1.66 × 10–4 2.05 × 10–4 2.56 × 10–4 3.26 × 10–4
ethanol 1.60 × 10–4 2.09 × 10–4 2.86 × 10–4 3.82 × 10–4 4.98 × 10–4
IPA 2.16 × 10–4 2.83 × 10–4 3.86 × 10–4 5.15 × 10–4 6.61 × 10–4
PEG-400 2.42 × 10–4 2.95 × 10–4 3.58 × 10–4 4.56 × 10–4 5.64 × 10–4
1-butanol 2.71 × 10–4 3.56 × 10–4 4.82 × 10–4 6.45 × 10–4 8.23 × 10–4
2-butanol 2.99 × 10–4 3.96 × 10–4 5.32 × 10–4 6.98 × 10–4 8.98 × 10–4
EA 4.78 × 10–4 6.72 × 10–4 9.29 × 10–4 1.22 × 10–3 1.52 × 10–3
THP 9.39 × 10–4 1.24 × 10–3 1.59 × 10–3 1.98 × 10–3 2.40 × 10–3
DMSO 1.74 × 10–2 1.96 × 10–2 2.22 × 10–2 2.47 × 10–2 2.81 × 10–2
xidl 4.88 × 10–4 6.33 × 10–4 8.19 × 10–4 1.05 × 10–3 1.35 × 10–3
Open in a new tab
a

The standard uncertainties u are u(T) = 0.24 K, u(p) = 0.003 MPa, and ur(xe) = 1.56%.

The solubility of GLZ was determined as 10.20 μg mL–1 (converted to 4.14 × 10–7 in mole fraction) at “T = 298.2 K” by Seedher and Kanojia.2 However, Manjila et al. found the solubility of GLZ as 51.80 μg mL–1 (converted to 2.09 × 10–6 in mole fraction) at T = 298.2 K.25 On the other hand, the solubility of GLZ was reported as 33.00 μg mL–1 (converted to 1.33 × 10–6 in mole fraction), 7.79 μg mL–1 (converted to 3.15 × 10–7 in mole fraction) and 4.46 μg mL–1 (converted to 1.80 × 10–7 in mole fraction) at “T = 310.2 K” by Dash et al. (2015), Yang et al. (2009), and Jadhav and Bharat (2012), respectively.3,20,29 The solubility of GLZ was recorded as 4.85 × 10–7 in mole fraction at T = 298.2 K, which was very close to that reported by Seedher and Kanojia2 but deviated from that reported by Manjila et al.25 The solubility of GLZ at T = 310.2 K was not determined directly in the proposed study, but it was estimated from the interpolation of graph constructed between ln xe and 1/T. The solubility of GLZ in mole fraction at T = 310.2 K by interpolation of graph was obtained as 1.24 × 10–6 in the present study. This value was found to be close to that reported by Dash et al.3 but deviated from those reported by Yang et al.29 and Jadhav and Bharat.20

Overall, the xe values of GLZ increased significantly with increase in temperature in all neat solvents evaluated (P < 0.05). The xe values of GLZ were obtained highest in DMSO (2.81 × 10–2), followed by THP (2.40 × 10–3), EA (1.52 × 10–3), 2-butanol (8.98 × 10–4), 1-butanol (8.23 × 10–4), IPA (6.61 × 10–4), PEG-400 (5.64 × 10–4), ethanol (4.98 × 10–4), PG (3.26 × 10–4), methanol (3.38 × 10–4), EG (1.37 × 10–4), and water (1.98 × 10–4) at T = 318.2 K. The xe values of GLZ were significantly higher in DMSO in comparison to other neat solvents evaluated (P < 0.05). The solubility values of GLZ in various alcohols such as methanol, ethanol, IPA, EG, PG, 1-butanol, and 2-butanol were not significantly different, which could be possible due to their similar polarities and Hansen solubility parameters (HSPs).

The highest solubilities of GLZ in DMSO were possible due to the fact that different solubility parameters of DMSO were more close to that of GLZ in comparison to other neat solvents evaluated. Based on the present results, GLZ has been considered as freely soluble in DMSO; slightly soluble in THP, EA, PEG-400, 2-butanol, 1-butanol, IPA, ethanol, methanol EG, and PG; and practically insoluble in water.30

2.3. Computational Approach for Calculation of Various Solubility Parameters

Different solubility parameters including HSPs of GLZ and 12 different neat solvents are tabulated in Table 2. The HSPs of GLZ and neat solvents were calculated using “HSPiP software”. Total HSP for GLZ was found as 31.10 MPa1/2, suggesting that GLZ had medium polarity. Although some solvents such as EG (total HSP = 31.60 MPa1/2), methanol (total HSP = 30.30 MPa1/2), and PG (total HSP = 29.20 MPa1/2) have total HSP very close to that of the GLZ, the experimental solubility of GLZ was much lower in these solvents. This observation might be due to the fact that dispersion, polar, and hydrogen-bonded HSPs of GLZ were much different from EG, methanol, and PG. Moreover, three-dimensional solubility parameter space (Ra) was recorded >15.0 MPa1/2 in all neat solvents except DMSO, suggesting a weak solubility of GLZ in these solvents. The literature suggests that the solvents/excipients with Ra < 5.6 MPa1/2 are the most compatible for solubility of drugs.31,32 Although none of the studied neat solvents had Ra value in the above-said range, DMSO (Ra = 8.08 MPa1/2) was found to be the closest to the above-said range. Hence, the maximum solubility of GLZ was considered in DMSO. The “Van Krevelen and Hoftyzer” solubility parameter (Δδ̅) was also obtained >15.0 MPa1/2 in many neat solvents, including water, EG, methanol, PG, IPA, 1-butanol, 2-butanol and EA, suggesting the poor solubility of GLZ in these neat solvents. The literature suggests that the materials with Δδ̅ < 5.0 MPa1/2 could be the most compatible for solubility of drugs and pharmaceuticals.33,34 Only DMSO (Δδ̅ = 7.21 MPa1/2) was found to be closest to the above-said range. Other solubility parameters, namely, Greenhalgh’s solubility parameter (Δδ), were estimated to be higher in water, PEG-400, EA, and THP, suggesting the weak solubility of GLZ in these neat solvents. The literature suggests that the materials with Δδ < 7.0 MPa1/2 could be the most compatible for solubility of drugs and pharmaceuticas.35 Many solvents such as methanol, ethanol, EG, PG, and DMSO have Δδ < 7.0 MPa1/2. According to Greenhalgh’s theory, the neat solvents methanol, ethanol, EG, PG, and DMSO were suitable for solubility with GLZ. Overall, DMSO was selected the best solvent for solubility of GLZ.

Table 2. Different Solubility Parameters of GLZ and 12 Neat Solvents at T = 298.2 K.

  Hansen solubility parameters
      
components δd/MPa1/2 δp/MPa1/2 δh/MPa1/2 δ/MPa1/2 Ra/MPa1/2 Δδ̅/MPa1/2 Δδa/MPa1/2
GLZ 19.30 21.10 9.30 30.10      
water 15.50 16.00 42.30 47.80 34.24 33.60 17.70
EG 18.00 11.10 23.40 31.60 17.48 17.33 1.50
methanol 17.40 10.60 22.40 30.30 17.21 16.89 0.20
PG 17.40 9.10 21.70 29.20 17.66 17.36 0.90
ethanol 16.20 8.40 17.60 25.40 16.38 15.48 4.70
IPA 15.80 6.60 14.30 22.30 17.29 16.19 7.80
PEG-400 14.60 7.50 9.40 18.90 16.53 14.38 11.20
1-butanol 15.90 6.30 15.20 22.90 17.32 16.29 7.20
2-butanol 15.80 5.40 12.40 20.80 17.46 16.38 7.30
EA 15.70 5.60 7.00 18.10 17.24 16.07 12.00
THP 16.30 7.20 11.90 21.40 15.36 14.45 8.70
DMSO 17.40 14.20 7.30 23.60 8.08 7.21 1.90
Open in a new tab
a

These values were calculated between GLZ and respective neat solvent.

2.4. Ideal Solubilities and Activity Coefficients

The objective of determining the activity coefficient was to study the interactions between the GLZ and various neat solvents at molecular level to obtain the best solvent for solubility of GLZ. Activity coefficient is related to the ideal solubility of the drug, and hence the ideal solubility of GLZ was also determined. Hence, the ideal solubility and activity coefficients of GLZ were determined to obtain the best solvent for GLZ. The ideal solubility (xidl) values for crystalline GLZ are tabulated in Table 1. The xidl values were recorded in the range of 4.88 × 10–4–1.35 × 10–3 at T = 298.2–318.2 K. The xidl values of GLZ were slightly lower than its experimental solubilities in THP but slightly higher than methanol, PG, ethanol, IPA, PEG-400, 1-butanol, 2-butanol, and EA. However, the xidl values of GLZ were significantly higher than its experimental solubilities in water and EG (P < 0.05). On the other hand, the xidl values of GLZ were found to be significantly lower than its experimental solubilities in DMSO (P < 0.05). Therefore, DMSO was found as the best solvent for solubility of GLZ.

The activity coefficient (γi) values for GLZ in 12 different neat solvents at T = 298.2–318.2 K are listed in Table 3.

Table 3. Activity Coefficients (γi) of GLZ in 12 Different Neat Solvents (NS) at T = 298.2–318.2 K.

  γi
NS T = 298.2 K T = 303.2 K T = 308.2 K T = 313.2 K T = 318.2 K
water 1005.730 832.700 779.029 705.170 683.386
EG 10.153 9.942 10.136 10.374 9.918
methanol 4.494 4.446 4.218 4.076 4.007
PG 3.572 3.821 3.997 4.119 4.152
ethanol 3.045 3.031 2.860 2.759 2.718
IPA 2.261 2.235 2.123 2.048 2.049
PEG-400 2.019 2.143 2.288 2.312 2.402
1-butanol 1.800 1.778 1.698 1.635 1.645
2-butanol 1.630 1.599 1.539 1.510 1.508
EA 1.020 0.942 0.881 0.861 0.890
THP 0.519 0.508 0.513 0.531 0.563
DMSO 0.028 0.032 0.036 0.042 0.048
Open in a new tab

The γi values for GLZ were calculated as <1.0 in DMSO and THP at all five temperature points studied. However, the γi value for GLZ was found to be significantly larger in water, EG, methanol, PG, ethanol, IPA, and PEG-400. On the other hand, the γi value for GLZ was found to be >1.0 but <2.0 in 1-butanol, 2-butanol, and EA. The γi values of GLZ in all investigated neat solvents were not increased/decreased significantly with respect to temperature (P > 0.05). Based on the estimated values of γi, the maximum solute–solvent molecular interactions were found in GLZ–DMSO in comparison to other combinations of GLZ and neat solvent.

2.5. Computational Approaches for Solubility Correlation

Experimental solubilities of GLZ were validated and correlated with two computational models, namely, “Apelblat and van’t Hoff models”.36−38 The graphical correlation between ln xe and ln Apelblat solubility (xApl) values of GLZ in 12 different neat solvents against 1/T is summarized in Figure 3, which suggests a good correlation between the ln xe and ln xApl values of GLZ in all 12 different neat solvents. The results of “Apelblat correlation” are listed in Table 4. The root-mean-square deviation (RMSD) values for GLZ in 12 different neat solvents were calculated as (0.43–2.24)% with an overall RMSD of 1.06%. The regressed values of coefficient of determination (R2) for GLZ in 12 different neat solvents were estimated as 0.9982–0.9999. The higher values of R2 and lower values of RMSD showed a good correlation of the xe values of GLZ with the “Apelblat model”.

Figure 3.

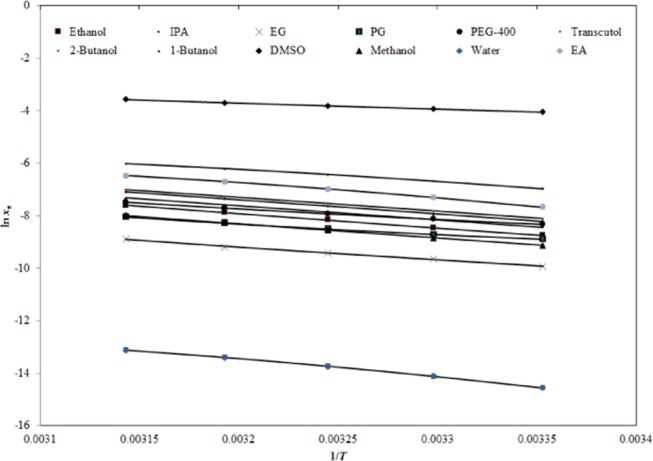
Figure 3

Open in a new tab

Correlation of ln xe values of GLZ with Apelblat model in 12 different neat solvents as a function of 1/T; the symbols represent the experimental solubilities of GLZ, and the solid lines represent the solubilities of GLZ calculated by the Apelblat model.

Table 4. Results of the Apelblat Model in Terms of Apelblat Parameters (A, B, and C), R2, and % RMSD for GLZ in 12 Different Neat Organic Solvents (NS).

NS A B C R2 RMSD (%) overall RMSD (%)
water 1068.37 –55 332.10 –157.49 0.9995 2.24  
EG –318.76 10 056.29 48.28 0.9982 1.57  
methanol –132.28 1030.12 21.00 0.9994 1.01  
PG –649.04 25 876.74 97.12 0.9999 0.98  
ethanol –153.36 2007.39 24.20 0.9991 1.27  
IPA 25.30 –6119.12 –2.32 0.9992 1.15 1.21
PEG-400 –437.19 16 254.26 65.70 0.9988 1.08  
1-butanol 56.12 –7490.50 –6.88 0.9992 1.21  
2-butanol 87.99 –8865.62 –11.65 0.9997 0.75  
EA 981.29 –50 088.20 –144.09 0.9995 1.56  
THP 677.53 –35 200.40 –99.42 0.9998 1.13  
DMSO –94.15 2209.97 14.51 0.9994 0.43  
Open in a new tab

The graphical correlation between xe and van’t Hoff solubility (xvan’t) values of GLZ in 12 different neat solvents against 1/T is summarized in the Supporting Information (Figure S1), which also shows a good correlation between xe and xvan’t values of GLZ. The results of “van’t Hoff correlation” are listed in Table 5. The values of RMSD for GLZ in 12 different neat solvents were obtained as (0.46–3.16)% with an overall RMSD of 1.40%. The regressed R2 values for GLZ in 12 different neat solvents were estimated as 0.9954–0.9997. The higher values of R2 and lower values of RMSD again showed a good correlation of xe values of GLZ with “van’t Hoff model”.

Table 5. Results of van’t Hoff Model in Terms of Model Parameters (a and b), R2, and % RMSD for GLZ in 12 Different Neat Solvents (NS).

NS a b R2 RMSD (%) overall RMSD (%)
water 7.74 –6632.80 0.9960 3.16  
EG 6.31 –4849.40 0.9976 1.95  
methanol 9.11 –5442.80 0.9994 1.04  
PG 4.91 –4125.20 0.9962 1.89  
ethanol 9.53 –5452.70 0.9991 1.27  
IPA 9.59 –5382.20 0.9992 1.46 1.40
PEG-400 5.19 –4037.40 0.9970 1.70  
1-butanol 9.69 –5343.60 0.9992 1.45  
2-butanol 9.47 –5246.20 0.9997 0.93  
EA 10.94 –5536.00 0.9954 2.85  
THP 7.99 –4457.40 0.9969 2.06  
DMSO 3.55 –2267.50 0.9992 0.46  
Open in a new tab

2.6. Thermodynamic Analysis

The estimated values of three different thermodynamic parameters and R2 for GLZ dissolution are summarized in Table 6. The “apparent standard enthalpy (ΔsolH0) values” for GLZ dissolution in 12 different neat solvents were found as (18.87–55.21) kJ mol–1. The maximum “ΔsolH0 value” of GLZ was recorded in water (55.21 kJ mol–1) with the minimum one in DMSO (18.87 kJ mol–1). The minimum ΔsolH0 value of GLZ in DMSO was possibly due to the highest solubility of GLZ in DMSO. The ΔsolH0 values of GLZ were generally higher in neat solvents with poor solubilities. The “apparent standard Gibbs free energy (ΔsolG0) values” for GLZ dissolution were found as (9.75–35.30) kJ mol–1. The “ΔsolG0 value” of GLZ was also found to be minimum in DMSO (9.75 kJ mol–1) and maximum in water (35.30 kJ mol–1), due to the highest and lowest solubilities of GLZ in DMSO and water, respectively. The positive values of “ΔsolH0 and ΔsolG0” for GLZ dissolution in all neat solvents indicated an “endothermic dissolution” of GLZ.36,39 The “apparent standard entropy (ΔsolS0) values” for GLZ dissolution were found as (29.60–91.22) J mol–1 K–1, indicating an “entropy-driven dissolution” of GLZ in all 12 different neat solvents.40 The average relative uncertainties in ΔsolH0, ΔsolG0, and ΔsolS0 for GLZ were obtained as 0.22, 0.33, and 0.26, respectively. Overall, the dissolution behavior of GLZ was found as an “endothermic and entropy-driven”.39,40

Table 6. Apparent Thermodynamic Parameters (ΔsolH0, ΔsolG0, and ΔsolS0) along with the R2 Values for GLZ in 12 Different Neat Solvents (NS)a.

NS ΔsolH0/kJ mol–1 ΔsolG0/kJ mol–1 ΔsolS0/J mol–1 K–1 R2
water 55.21 35.30 64.63 0.9958
EG 40.37 24.13 52.72 0.9976
methanol 45.31 21.91 75.97 0.9994
PG 34.34 21.71 41.01 0.9964
ethanol 45.39 20.91 74.46 0.9991
IPA 44.80 20.15 80.02 0.9993
PEG-400 33.08 9.98 74.99 0.9947
1-butanol 44.89 19.58 80.85 0.9992
2-butanol 43.67 19.34 78.99 0.9998
EA 46.08 17.98 91.22 0.9953
THP 37.10 16.56 66.67 0.9967
DMSO 18.87 9.75 29.60 0.9993
Open in a new tab
a

The relative uncertainties are u(ΔsolH0) = 0.22, u(ΔsolG0) = 0.33, and u(ΔsolS0) = 0.26.

3. Conclusions

Both experimental and computational approaches were used for the solubility determination of a poorly soluble antidiabetic drug GLZ in 12 different neat solvents in the proposed study. Different solubility parameters including HSPs were calculated to find the best solvent for GLZ. Experimental solubilities of GLZ were determined at T = 298.2–318.2 K and p = 0.1 MPa. The experimental solubilities of GLZ were validated/correlated well with “van’t Hoff and Apelblat” models. The solubility of GLZ was enhanced significantly with the rise in temperature (P < 0.05). The data of activity coefficients showed maximum solute–solvent interactions in GLZ–DMSO in comparison to other combinations of solute and solvent. The solubility of GLZ was recorded in the order of DMSO > THP > EA > 2-butanol > 1-butanol > IPA > PEG-400 > ethanol > PG > methanol > EG > water at T = 318.2 K. Apparent thermodynamic analysis showed an “endothermic and entropy-driven dissolution” of GLZ in all 12 different neat solvents. Based on various factors such as maximum solubility, lower solubility parameters, lower activity coefficients, and lowest values of apparent standard enthalpies and Gibbs energies, DMSO has been considered as the best solvent for solubility of GLZ.

4. Materials and Methods

4.1. Materials

THP was obtained from “Gattefosse (Lyon, France)”. GLZ, ethanol, IPA, 1-butanol, 2-butanol, EG, PG, PEG-400, EA, and DMSO were procured from “E-Merck (Darmstadt, Germany)”. Methanol was obtained from “BDH PROLABO (Leuven, Belgium)”. The purified water was obtained by “Milli-Q water purifier (Millipore, Lyon, France)”. The detailed information of different materials is summarized in Table S1.

4.2. Quantification of GLZ

“Waters Acquity H-class Ultra-Performance Liquid Chromatography (UPLC)” equipment equipped with a “Waters diode array-ultraviolet (DAD-UV) detector (Acquity UPLC, Waters, MA)” was used to quantify GLZ in this study. The proposed UPLC system contains “quaternary solvent manager, sample manager (Acquity, UPLC Waters, MA) and a column heater”. The injection volume capacity was 10 μL. The separation of GLZ was executed using “Acquity UPLC BEH C18 column (2.1 × 50 mm2, 1.7 μm, Waters)” maintained at T = 303.2 ± 1 K. The proposed UPLC-UV technique was used to quantify GLZ with some modifications in the reported HPLC-UV methods.41−44 In the proposed analytical methodology, the mobile phase (composed of 80:20, v/v methanol and 10 mM KH2PO4 buffer of pH 4.2 adjusted with orthophosphoric acid) was flowed with an isocratic mode. The flow rate and injection volume were set at 0.08 mL min–1 and 5 μL, respectively. The total time for analysis was 3 min. The quantification of GLZ was performed in the UV mode at λmax = 230 nm. The retention time of GLZ was recorded as 1.684 min. “EMPOWER software” was utilized for data analysis and interpretation.

The standard stock solution (SSS) of GLZ (200 μg g–1) was prepared in methanol by using DMSO as a co-solvent. From SSS, the serial dilutions were made to obtain the concentration in the range of 0.5–100 μg g–1. The calibration curve was obtained between the concentrations of GLZ (μg g–1) and the peak areas of GLZ obtained through UPLC-UV analysis. The calibration curve of GLZ was found to be linear in the above concentration range with R2 of 0.9999. The straight-line (regressed) equation for the calibration data was found to be Y = 184 862x – 26 911, where Y is the peak UPLC area for GLZ and x is the concentration of GLZ.

4.3. Characterization of GLZ in Solid States

The characterization of GLZ in solid states was done by DSC. “DSC-8000 Instrument (PerkinElmer)” equipped with chiller (T = 253.2 K) and autosampler was used for this experiment. For DSC analysis, approximately 4.50 mg of pure GLZ and 3.90 mg of equilibrated GLZ samples were put into aluminum pans and the pans were sealed hermetically. DSC thermograms of the pure and equilibrated GLZ samples were obtained under a nitrogen purge of 20 mL min–1 at the heating rate of 10 K min–1, and the temperature range was kept from 298.2 to 623.2 K for pure GLZ and from 301.2 to 633.2 K for equilibrated GLZ. DSC analysis was done to investigate various thermal parameters and possible transformations (if any) of GLZ. DSC was done on initial material (pure GLZ) as well as on the equilibrated GLZ sample obtained from equilibrium sample (EA) by evaporating the solvent at T = 298.2 K.40,45

4.4. Experimental Approach for Solubility Determination

The solubility of GLZ in all studied solvents was determined using an experimental approach such as the “isothermal saturation shake flask method” at T = 298.2–318.2 K and p = 0.1 MPa.46 The operational conditions and experimental procedures were same as mentioned in our previous work.40,45 Therefore, the experimental details are not included in the present study. Experiments were carried out in triplicate manner (n = 3). The content of GLZ in the solubility samples of 12 different neat solvents was analyzed by the UPLC-UV technique described above at λmax = 230 nm. The content of GLZ (μg g–1) was estimated using a calibration curve of GLZ. The xe values of GLZ were calculated by applying eq 1(26,27)

4.4. 1

where m1 = mass of GLZ; m2 = mass of neat solvent; M1 = molar mass of GLZ; and M2 = molar mass of neat solvent.

4.5. Computational Approaches for Determination of Solubility Parameters

If the solubility parameter of drug is close to that of neat solvent, then it will show the maximum solubility in that solvent.47 To obtain the best solvent for the solubility of GLZ, different solubility parameters for GLZ and 12 different neat solvents were estimated using various computational approaches. The HSP (δ) value was obtained by applying eq 2(47−49)

4.5. 2

where δ = total HSP; δd = dispersion HSP; δp = polar HSP, and δh = hydrogen-bonded HSP. The data of δ HSP, δd HSP, δp HSP, and δh HSP for GLZ and 12 different neat solvents were calculated using “HSPiP software (version 4.1.07, Louisville, KY)” by taking smiles of GLZ and each solvent into the software.

The Δδ̅ value was calculated using eq 3(33,49)

4.5. 3

It has been reported that the possibility of solubility between the drug and solvent is maximum if the value of Δδ̅ < 5.0 MPa1/2.33,34

The Bagley solubility parameter (δv) was estimated by applying eq 4(50)

4.5. 4

By applying the Bagley concept, Ra was estimated by applying eq 5(31)

4.5. 5

where Ra indicates the solubility between the drug and neat solvent. For the maximum solubility, the value of Ra should be <5.6 MPa1/2.31,32

The Δδ value was estimated by applying eq 6(35)

4.5. 6

According to this concept, the solubility between the drug and solvents is maximum at Δδ < 7.0 MPa1/2, while the value of Δδ > 10.0 MPa1/2 has been considered for immiscibility between the drug and solvents.35

4.6. Ideal Solubilities and Activity Coefficients

The xidl value of GLZ was calculated by applying eq 7(51)

4.6. 7

where R = universal gas constant; Tfus = fusion temperature of GLZ; ΔHfus = fusion enthalpy of GLZ; and ΔCp = the difference in molar heat capacity of the solid state with that of liquid state.51,52 It has been assumed that ΔCp can be set approximately as the entropy of fusion (ΔSfus), and hence, ΔCp = ΔSfus.51,53 The ΔCp value for GLZ was estimated by applying eq 8(51)

4.6. 8

The Tfus and ΔHfus values for GLZ were determined as 484.21 K and 63.33 kJ mol–1, respectively, from thermal evaluation. Using eq 8, the ΔCp value of GLZ was calculated as 130.79 J mol–1 K–1. The xidl values for GLZ were estimated now by using eq 7.

The γi values for GLZ in 12 different neat solvents were estimated by applying eq 9(51,53)

4.6. 9

4.7. Computational Approaches for Solubility Correlation

Various computational approaches were used for the validation of experimental solubility data. Hence, the experimental solubilities of GLZ in 12 different neat solvents were correlated by applying two computational approaches, namely, Apelblat and van’t Hoff models.36−38 “Apelblat model solubility (xApl)” of GLZ was calculated using the modified Apelblat model by applying eq 10(37,38)

4.7. 10

where “A, B, and C” are the parameters of the Apelblat model, which were estimated by applying “nonlinear multivariate regression analysis” of the xe values of GLZ tabulated in Table 1.36 The xe and xApl values of GLZ were correlated using the RMSD and R2 values. The RMSD for GLZ was estimated by applying eq 11

4.7. 11

where N = number of experimental data points.

The xvan’t value of GLZ was calculated using the “van’t Hoff” model by applying eq 12(36)

4.7. 12

where a and b are the parameters of the van’t Hoff model. These parameters were estimated by plotting the ln xe values of GLZ against 1/T.

4.8. Thermodynamic Analysis

To calculate different thermodynamics parameters of GLZ in 12 different neat solvents, an apparent thermodynamic analysis was carried out. Three different thermodynamic parameters, such as ΔsolH0, ΔsolG0, and ΔsolS0, for the GLZ dissolution were estimated by applying the “van’t Hoff and Krug et al. analysis”.51,54,55 The ΔsolH0 values for the GLZ dissolution in 12 different neat solvents were estimated at “mean harmonic temperature (Thm)” of 308 K by “van’t Hoff analysis” by applying eq 13(51,54)

4.8. 13

The ΔsolH0 values were obtained by the van’t Hoff plots made between the ln xe values of GLZ and 1/T – 1/Thm.

The ΔsolG0 values for the GLZ dissolution in 12 different neat solvents were also estimated at Thm of 308 K using the “Krug et al. analysis” by applying eq 14(55)

4.8. 14

where the intercept values for GLZ in 12 different neat solvents were estimated from the “van’t Hoff plot” shown in Figure S2.

Finally, the “ΔsolS0 values” for the GLZ dissolution were estimated by applying eq 15(51,54,55)

4.8. 15

4.9. Statistical Analysis

Experimental solubility data of GLZ were compared by applying the “Kruskal–Wallis analysis” followed by “Denn’s test” using “GraphPad In Stat software (San Diego, CA)”. The estimated values of P < 0.05 were considered as statistically significant.

Acknowledgments

The authors extend their sincere appreciation to the Deanship of Scientific Research at King Saud University for funding this research via research group number RG-1435-005”.

Supporting Information Available

The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b04004.

  • List of materials and their properties (Table S1); correlation of experimental solubilities of GLZ in various neat solvents with the van’t Hoff model (Figure S1); and van’t Hoff plots for the determination of thermodynamic parameters (Figure S2) (PDF)

The authors declare no competing financial interest.

Supplementary Material

ao9b04004_si_001.pdf (173KB, pdf)

References

  1. Lakhsmi Narasimham Y. S.; Barhate V. D. Kinetic and intrinsic solubility determination of some β-blockers and antidiabetics by potentiometry. J. Pharm. Res. 2011, 4, 532–536. [Google Scholar]
  2. Seedher N.; Kanojia M. Co-solvent solubilization of some poorly-soluble antidiabetic drugs. Pharm. Dev. Technol. 2009, 14, 185–192. 10.1080/10837450802498894. [DOI] [PubMed] [Google Scholar]
  3. Dash R. N.; Mohammed H.; Humaira T.; Ramesh D. Design, optimization and evaluation of glipizide solid self-nanoemulsifying drug delivery for enhanced solubility and dissolution. Saudi Pharm. J. 2015, 23, 528–540. 10.1016/j.jsps.2015.01.024. [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Mahajan H. S.; Dhamne M. R.; Gattani S. G.; Rasal A. D.; Shaikh H. T. Enhanced dissolution rate of glipizide by a liquisolid technique. Int. J. Pharm. Sci. Nanotechnol. 2011, 3, 205–121. [Google Scholar]
  5. Qi C.; Zhou Q.; Li B.; Yang Y.; Cao L.; Ye Y.; Li J.; Ding Y.; Wang H.; Wang J.; He X.; Zhang Q.; Lan T.; Lee K. K.; Li W.; Song X.; Zhou J.; Yang X.; Wang L. Glipizide, an antidiabetic drug, suppresses tumor growth and metastasis by inhibiting angiogenesis. Oncotarget 2014, 5, 9966–9979. 10.18632/oncotarget.2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
  6. Gu Q.; Wang C.; Wang G.; Han Z.; Li Y.; Wang X.; Li J.; Qi C.; Xu T.; Yang X.; Wang L. Glipizide suppresses embryonic vasculogenesis and angiogenesis through targeting natriuretic peptide receptor A. Exp. Cell Res. 2015, 333, 261–272. 10.1016/j.yexcr.2015.03.012. [DOI] [PubMed] [Google Scholar]
  7. Madhusudhan S.; Panda A. K.; Parimalakrishnan S.; Manavalan R.; Manna P. K. Design, in vitro and in vivo evaluation of glipizide Eudragit microparticles. J. Microencapsulation 2010, 27, 281–291. 10.3109/02652040903131319. [DOI] [PubMed] [Google Scholar]
  8. Behera B. C.; Sahoo S. K.; Dhal S.; Barik B. B.; Gupta B. K. Characterization of glipizide-loaded polymethacrylate microspheres by an emulsion solvent evaporation method. Trop. J. Pharm. Res. 2008, 7, 879–885. 10.4314/tjpr.v7i1.14672. [DOI] [Google Scholar]
  9. Emami J.; Boushehri M. S.; Varshosaz J. Preparation, characterization and optimization of glipizide controlled release nanoparticles. Res. Pharm. Sci. 2014, 9, 301–314. [PMC free article] [PubMed] [Google Scholar]
  10. Aly A. M.; Mazen K. Q.; Mahrous O. A. Enhancement of the dissolution rate and bioavailability of glipizide through cyclodextrin inclusion complex. Pharm. Technol. 2003, 27, 54–62. [Google Scholar]
  11. Huang H.; Wu Z.; Qi X.; Zhang H.; Chen Q.; Xing J.; Chen H.; Rui Y. Compression-coated tablets of glipizide using hydroxypropylcellulose for zero-order release: in vitro and in vivo evaluation. Int. J. Pharm. 2013, 446, 211–218. 10.1016/j.ijpharm.2013.01.039. [DOI] [PubMed] [Google Scholar]
  12. Patel V. P.; Patel N. M. Evaluation of some methods for preparing glipizide-β-cyclodextrin inclusion complexes. Iran. J. Pharm. Sci. 2009, 5, 191–198. [Google Scholar]
  13. Lavanya N.; Aparna C.; Umamahesh B. Formulation and evaluation of glipizide microemulsion. Int. J. Pharm. Pharm. Sci. 2016, 8, 171–176. [Google Scholar]
  14. Sarkar B. K.; Hardenia S. S. Microemulsion drug delivery system: for oral bioavailability enhancement of glipizide. J. Adv. Pharm. Educ. Res. 2011, 1, 195–200. [Google Scholar]
  15. Mehramizi A.; Alijani B.; Pourfarzib M.; Dorkoosh F. A.; Rafiee-Tehrani M. Solid carriers for improved solubility of glipizide in osmotically controlled oral drug delivery system. Drug Dev. Ind. Pharm. 2007, 33, 812–823. 10.1080/03639040601128753. [DOI] [PubMed] [Google Scholar]
  16. Isaac J.; Kaity S.; Ganguly S.; Ghosh A. Microwave-induced solid dispersion technology to improve bioavailability of glipizide. J. Pharm. Pharmacol. 2012, 65, 219–229. 10.1111/j.2042-7158.2012.01595.x. [DOI] [PubMed] [Google Scholar]
  17. Dehghan M. H. G.; Saifee M.; Hanwate R. M. Comparative dissolution study of glipizide by solid dispersion technique. J. Pharm. Sci. Technol. 2010, 2, 293–297. [Google Scholar]
  18. Choudhary D.; Kumar S.; Gupta G. D. Enhancement of solubility and dissolution of glipizide by solid dispersion (kneading) technique. Asian J. Pharm. 2009, 3, 245–251. 10.4103/0973-8398.56306. [DOI] [Google Scholar]
  19. Shende M. A.; Fiske P. V. Fabrication and optimization of novel glipizide sustained release matrices for solubility and dissolution enhancement by solid dispersion through hydrophilic carriers. J. Drug Delivery Ther. 2017, 7, 38–48. 10.22270/jddt.v7i6.1538. [DOI] [Google Scholar]
  20. Jadhav Y. L.; Bharat P. Formulation and evaluation of mouth dissolving tablet of glipizide by solid dispersion. Int. J. Pharm. Sci. Res. 2012, 3, 4929–4937. [Google Scholar]
  21. Mahesh K. V.; Singh S. K.; Gulati M. A comparative study of top-down and bottom-up approaches for the preparation of nanosuspensions of glipizide. Powder Technol. 2014, 256, 436–449. 10.1016/j.powtec.2014.02.011. [DOI] [Google Scholar]
  22. Kushare S. S.; Gattani S. G. Microwave-generated bionanocomposites for solubility and dissolution enhancement of poorly water-soluble drug glipizide: in-vitro and in-vivo studies. J. Pharm. Pharmacol. 2013, 65, 79–93. 10.1111/j.2042-7158.2012.01584.x. [DOI] [PubMed] [Google Scholar]
  23. Akula P.; Lakshmi P. K. Effect of pH on weakly acidic and basic model drugs and determination of their ex vivo transdermal permeation routes. Braz. J. Pharm. Sci. 2018, 54, E00070 10.1590/s2175-97902018000200070. [DOI] [Google Scholar]
  24. Patel J. K.; Chavda J. R. Formulation and evaluation of glipizide floating-bioadhesive tablets. Braz. Arch. Biol. Technol. 2010, 53, 1073–1085. 10.1590/S1516-89132010000500010. [DOI] [Google Scholar]
  25. Manjila S. B.; Baby J. N.; Bijin E. N.; Constantine I.; Pramod K.; Valsalakumari J. Microcrystallization of glipizide: effect of type of stabilizer on particle size, solubility and dissolution. Res. J. Pharm., Biol. Chem. Sci. 2013, 4, 405–409. [Google Scholar]
  26. Kalam M. A.; Khan A. A.; Alshamsan A.; Haque A.; Shakeel F. Solubility of a poorly soluble immunosuppressant in different pure solvents: measurement, correlation, thermodynamics and molecular interactions. J. Mol. Liq. 2018, 249, 53–60. 10.1016/j.molliq.2017.11.028. [DOI] [Google Scholar]
  27. Shakeel F.; Haq N.; Alshehri S.; Ibrahim M. A.; Elzayat E. M.; Altamimi M. A.; Mohsin K.; Alanazi F. K.; Alsarra I. A. Solubility, thermodynamic properties and solute-solvent molecular interactions of luteolin in various pure solvents. J. Mol. Liq. 2018, 255, 43–50. 10.1016/j.molliq.2018.01.155. [DOI] [Google Scholar]
  28. Dadmand S.; Kamari F.; Acree W. E. Jr.; Jouyban A. A new computational model for drug solubility prediction in methanol + water mixtures. J. Mol. Liq. 2019, 292, 111369 10.1016/j.molliq.2019.111369. [DOI] [Google Scholar]
  29. Yang X.-l.; Jin S.; Zhong-Gui H. Determination of equilibrium solubility and partition coefficient of glipizide. Chin. J. Pharm. 2009, 7, E3. [Google Scholar]
  30. United States Pharmacopeia . National Formulary USP 23-NF 18; The United States Pharmacopeial Convention, Inc.: Rockville, MD, 1994. [Google Scholar]
  31. Mohammad M. A.; Alhalaweh A.; Velaga S. P. Hansen solubility parameter as a tool to predict cocrystal formation. Int. J. Pharm. 2011, 407, 63–71. 10.1016/j.ijpharm.2011.01.030. [DOI] [PubMed] [Google Scholar]
  32. Albers J.Hot-Melt Extrusion with Poorly Soluble Drugs; Cuvillier Verlag: Goettingen, Germany, 2008; p 145. [Google Scholar]
  33. Van Krevelen D. W.; te Nijenhuis K.. Properties of Polymers: Their Correlation with Chemical Structure; Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier: Amsterdam, The Netherland; Tokyo, Japan, 2009; p 189. [Google Scholar]
  34. Güner A. The algorithmic calculations of solubility parameter for the determination of interactions in dextran/certain polar solvent systems. Eur. Polym. J. 2004, 40, 1587–1594. 10.1016/j.eurpolymj.2003.10.030. [DOI] [Google Scholar]
  35. Greenhalgh D. J.; Williams A. C.; Timmins P.; York P. Solubility parameters as predictors of miscibility in solid dispersions. J. Pharm. Sci. 1999, 88, 1182–1190. 10.1021/js9900856. [DOI] [PubMed] [Google Scholar]
  36. Anwer M. K.; Muqtader M.; Iqbal M.; Ali R.; Almutairy B. K.; Alshetaili A.; Alshahrani S. M.; Aldawsari M. F.; Alalaiwe A.; Shakeel F. Estimating the solubility, solution thermodynamics and molecular interactions of aliskiren hemifumarate in alkylimidazolium based ionic liquids. Molecules 2019, 24, E2807 10.3390/molecules24152807. [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Apelblat A.; Manzurola E. Solubilities of o-acetylsalicylic, 4-aminosalicylic, 3,5-dinitrosalicylic and p-toluic acid and magnesium-DL-aspartate in water from T = (278–348) K. J. Chem. Thermodyn. 1999, 31, 85–91. 10.1006/jcht.1998.0424. [DOI] [Google Scholar]
  38. Manzurola E.; Apelblat A. Solubilities of L-glutamic acid, 3-nitrobenzoic acid, acetylsalicylic, p-toluic acid, calcium-L-lactate, calcium gluconate, magnesium-DL-aspartate, and magnesium-L-lactate in water. J. Chem. Thermodyn. 2002, 34, 1127–1136. 10.1006/jcht.2002.0975. [DOI] [Google Scholar]
  39. El-Badry M.; Haq N.; Fetih G.; Shakeel F. Measurement and correlation of tadalafil solubility in five pure solvents at (298.15 to 333.15) K. J. Chem. Eng. Data 2014, 59, 839–843. 10.1021/je400982r. [DOI] [Google Scholar]
  40. Kalam M. A.; Alshehri S.; Alshamsan A.; Alkholief M.; Ali R.; Shakeel F. Solubility measurement, Hansen solubility parameters and solution thermodynamics of gemfibrozil in different pharmaceutically used solvents. Drug Dev. Ind. Pharm. 2019, 45, 1258–1264. 10.1080/03639045.2019.1594884. [DOI] [PubMed] [Google Scholar]
  41. Bae J. W.; Kim N. T.; Choi C. I.; Kim M. J.; Jang C. G.; Lee S. Y. HPLC Analysis of plasma glipizide and its application to pharmacokinetic study. J. Liq. Chromatogr. Relat. Technol. 2009, 32, 1969–1977. 10.1080/10826070903091712. [DOI] [Google Scholar]
  42. Atif M.; Khalid S. H.; Onn Kit G. L.; Sulaiman S. A.; Asif M.; Chandersekaran A. Development and validation of RP-HPLC-UV method for the determination of glipizide in human plasma. J. Young Pharm. 2013, 5, 26–29. 10.1016/j.jyp.2013.01.005. [DOI] [PMC free article] [PubMed] [Google Scholar]
  43. Pani N. R.; Acharya S.; Patra S. Development and validation of RP-HPLC method for quantification of glipizide in biological macromolecules. Int. J. Biol. Macromol. 2014, 65, 65–71. 10.1016/j.ijbiomac.2014.01.007. [DOI] [PubMed] [Google Scholar]
  44. Dhawan S.; Singla A. K. High performance liquid chromatographic analysis of glipizide: application to in vitro and in vivo studies. J. Chromatogr. Sci. 2003, 41, 295–300. 10.1093/chromsci/41.6.295. [DOI] [PubMed] [Google Scholar]
  45. Shakeel F.; Imran M.; Haq N.; Alshehri S.; Anwer M. K. Synthesis, characterization and solubility determination of 6-phenyl-pyridazin-3-(2H)-one in different pharmaceutical solvents. Molecules 2019, 24, E3404 10.3390/molecules24183404. [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Higuchi T.; Connors K. A. Phase-solubility techniques. Adv. Anal. Chem. Instrum. 1965, 4, 117–122. [Google Scholar]
  47. Kitak T.; Dumicic A.; Planinsek O.; Sibanc R.; Srcic S. Determination of solubility parameters of ibuprofen and ibuprofen lysinate. Molecules 2015, 20, 21549–21568. 10.3390/molecules201219777. [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Hansen C. M.Hansen Solubility Parameters: Asser’s Handbook, 2nd ed.; CRC Press, Taylor and Francis Group: Boca Raton, FL, 2007; p 544. [Google Scholar]
  49. Zhu Q. N.; Wang Q.; Hu Y. B.; Abliz X. Practical determination of the solubility parameters of 1-alkyl-3-methylimidazolium bromide ([CnC1im]Br, n = 5, 6, 7, 8) ionic liquids by inverse gas chromatography and the Hansen solubility parameter. Molecules 2019, 24, 1346 10.3390/molecules24071346. [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. Bagley E. B.; Nelson T. P.; Scigliano J. M. Three-dimensional solubility parameters and their relationship to internal pressure measurements in polar and hydrogen bonding solvents. J. Paint Technol. 1971, 43, 35–42. [Google Scholar]
  51. Ruidiaz M. A.; Delgado D. R.; Martínez F.; Marcus Y. Solubility and preferential solvation of indomethacin in 1,4-dioxane + water solvent mixtures. Fluid Phase Equilib. 2010, 299, 259–265. 10.1016/j.fluid.2010.09.027. [DOI] [Google Scholar]
  52. Hildebrand J. H.; Prausnitz J. M.; Scott R. L.. Regular and Related Solutions; Van Nostrand Reinhold: New York, 1970. [Google Scholar]
  53. Manrique Y. J.; Pacheco D. P.; Martínez F. Thermodynamics of mixing and solvation of ibuprofen and naproxen in propylene glycol + water cosolvent mixtures. J. Solution Chem. 2008, 37, 165–181. 10.1007/s10953-007-9228-0. [DOI] [Google Scholar]
  54. Holguín A. R.; Rodríguez G. A.; Cristancho D. M.; Delgado D. R.; Martínez F. Solution thermodynamics of indomethacin in propylene glycol + water mixtures. Fluid Phase Equilib. 2012, 314, 134–139. 10.1016/j.fluid.2011.11.001. [DOI] [Google Scholar]
  55. Krug R. R.; Hunter W. G.; Grieger R. S. Enthalpy-entropy compensation. 2. Separation of the chemical from the statistic effect. J. Phys. Chem. A. 1976, 80, 2341–2351. 10.1021/j100562a007. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

ao9b04004_si_001.pdf (173KB, pdf)

Articles from ACS Omega are provided here courtesy of American Chemical Society

RESOURCES