Abstract
In a recent study, a new procedure for Z-selective olefin synthesis by reductive coupling of alkyl iodides with terminal alkynes in the presence of iron salts is described. This transformation is representative of many newly developed synthetic routes through the involvement of multiple species and phases, which makes mechanistic insight hard to obtain. Here, we report computational work aimed at exploring the possible reaction pathways. DFT calculations lead to two suggested routes, one involving C–I reduction by metallic zinc and radical addition to the alkyne and the other involving addition of two reduced iron species to the alkyne bond followed by reductive elimination. Comparison to experimental results as well as kinetic modeling is used to discuss the likelihood of these and related mechanisms.
Introduction
In recent years, many new synthetic procedures have been developed for carrying out reactions such as cross-coupling using non-noble metal containing species as catalysts. Non-noble-metal catalysts can in principle have many environmental and cost advantages, but from the mechanistic point of view, many of the newly developed reactions are much less straightforward to understand than more conventional catalyst systems based on second- and third-row transition metals.1 This problem is compounded in the popular class of reactions involving a solid metal as the coreagent and reducing agent.2,3
Within the burgeoning field of non-noble-metal catalysis, iron compounds play an important part, with the extensive work on the topic having already led to a number of reviews.4−8 The synthetic scope of the developed transformations is already impressive, though obtaining a full mechanistic understanding remains highly challenging. Many mechanistic suggestions have been made based on extrapolation from the single-metal-center mechanisms that are common in palladium-catalyzed reactions, but these suggestions fail in many cases to account for all experimental observations.9,10
Computational chemistry has become one of the most commonly used tools to examine reaction mechanisms1,11 and has been used, in particular, in many studies of iron catalysis to provide additional insight12 and here, too. In some cases, computation has been used to predict structures and energies for key intermediates and transition states in possible reaction steps.13 There have also been studies of putative complete catalytic reaction cycles.14−16 In other cases, though, given the immense complexity of predicting mechanisms against a background of incomplete experimental mechanistic input, computation has been assigned only the ancillary role of characterizing the structure and spectroscopic properties of intermediates.17 These difficulties in non-noble-metal catalysis are only magnified when considering complex multiphase processes involving solid metal coreagents.
One of the most widely studied and developed iron-catalyzed reactions is the Kumada18 type that involves a Grignard reagent as a transmetalating nucleophile reacting with an organic halide molecule.19 Cross-coupling reactions of the Negishi20 and Sonogashira21−23 types have also been studied. Extensive work is being carried out nowadays to develop new ligands for iron-catalyzed cross-coupling reactions.24−26 In this computational investigation, we study an unusual type of cross-coupling reaction involving an iron catalyst with no added ligand, and alkyne and alkyl iodide substrates, which are reductively coupled in the presence of metallic zinc to produce Z-alkenes with high selectivity.27 This reaction is challenging to study computationally for a number of reasons, such as the absence of added ligands for the metal center, implying instead of solvent ligation, the use of Zn(0) as the reducing agent, and the lack of direct identification of intermediates. The cross-coupling reaction we modeled has phenylacetylene and cyclohexyl iodide as reactants, dissolved in the N,N-dimethylacetamide (DMA) solvent, and in the presence of a reducing agent. The experimental study was previously reported.27
Results
The starting point for this investigation was a suggested mechanism put forward in the original communication of the synthetic results.27 This mechanism involved, in brief, (i) reduction of the starting Fe(II) catalyst to an Fe(I) species by metallic Zn, (ii) electron transfer from Fe(I) to the alkyl iodide followed by dissociation into iodide and alkyl radical, (iii) alkyl radical addition to the β-position of the (terminal) alkyne to form a vinyl radical, (iv) recombination of the vinyl radical with a second equivalent of Fe(I) species to form an Fe(II)-vinyl product, with steric factors favoring Fe addition E to the alkyl group, and (v) transmetalation from Fe to Zn to form a vinyl-zinc species, the hydrolysis of which during workup would lead to the product. This mechanism was suggested based on observed reactivity and selectivity, including careful testing of the scope of the reaction, varying the metal catalyst, alkyne and halide substrates, the solvent, and so on. These results provide valuable information concerning possible mechanistic variants, but no detailed mechanistic study was performed. We set out to investigate the proposed steps and possible variants using computation, but before doing so, some methodological choices needed to be made.
First of all, the starting iron bromide catalyst as well as all the related iron complexes must presumably react after dissolving in the polar solvent used, DMA. Related amide solvents NMP and DMF were also observed experimentally to lead to reasonable reactivity, while a reaction in THF was found to be much less favorable.28 Clearly, the metal must form complexes with the solvent, whose structure is presumably important for determining reactivity. Accordingly, we started by exploring the structure and relative Gibbs energy of the key metal species FeBr2, FeBr, and ZnBr2 in complex with variable numbers of explicit DMA solvent molecules together with an implicit, continuum, to model the effect of the bulk solvent. For Fe(I)Br, a trigonal disolvated complex is predicted to be most stable, well below the tri- and monosolvated forms in free energy. For Fe(II)Br2, a tetrahedral disolvated state is most stable. Finally, the zinc(II) complex is also predicted to favor a disolvated tetrahedral structure. In this case, there is experimental29 and computational30 evidence supporting the disolvated structure (Figure 1).
Figure 1.
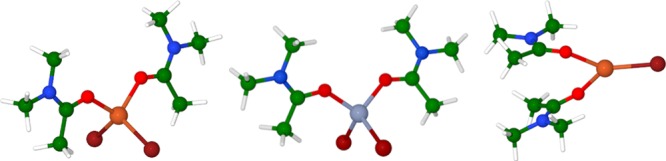
Fe(II) and Zn(II) complexes on the left and center, with quintet and singlet ground state, respectively; Fe(I) complex on the right with quartet ground state. Color code: orange: Fe, gray: Zn, bordeaux: Br, blue: N, red: O, green: C, white: H.
For the iron species, it is also important to carefully consider different possible spin states. The assignment of the spin state for iron complexes is not trivial, as shown in many works from the literature,31−37 with computational results known to be quite sensitive to the DFT functional. The B3LYP38 hybrid functional used here appears to be reasonably accurate for iron complexes, and this is supported by our benchmarking results (see the Supporting Information) for compounds similar to those studied here. Detailed results on calculated relative energies for different spin states are in the Supporting Information. In brief, our calculations show that the iron complexes prefer high-spin states, with solvated FeBr2 adopting a quintet state and FeBr a quartet state. For other monoiron complexes described below, we find the same preference, with Fe(I), Fe(II), and Fe(III) species adopting quartet, quintet, and quartet ground states, respectively. For bimetallic species, the individual metal centers are also high-spin, and indeed, these centers also prefer to couple in a high-spin manner (the antiferromagnetic couple returns slightly higher energies) (Figure 1).
Treatment of Metallic Zn(0)
The reaction considered here involves metallic zinc as one of the key reagents, which requires that relative free energies of solid zinc, dissolved zinc-containing species, and transition states for Zn-oxidation steps be obtained. This is not trivial within the framework of molecular quantum chemical methods. While solid zinc (and species at its surface) can of course be treated using periodic density functional theory methods, this makes it challenging to obtain relative energies compared to solution-phase species, assuming that these are treated using standard molecular quantum chemical techniques. Instead, we have used a combined technique based on quantum chemical calculations on isolated species only, together with experimental data for solid and gaseous zinc to compute thermodynamics for steps involving solid zinc. In this procedure, we calculated the free energy of a single zinc atom in the gas phase at the same level of theory as for the other species, from which we subtracted the experimental39 sublimation free energy for a mole of solid zinc (22.7 kcal/mol), paying attention to consistent use of standard states in both the computational and experimental values. In this way, we obtain an estimate of the Gibbs energy of formation of solid zinc that can be combined with regular computed Gibbs energies for other zinc-containing species such as ZnBr2. For the kinetics of reactions with solid zinc, we use an approach again based on the experiment, as outlined below.
Reduction Steps
The active species of the reaction appears unclear due to the significant challenge of detecting experimentally the oxidation state of the iron salts during the reaction process. This is a common problem in cross-coupling catalysis by iron compounds, with suggested oxidation states covering the range from Fe(−II) to Fe(III) having been suggested.40−44 In recent publications, the Fe(I) species has been proposed as the active species for the ligand-free reaction45 and indeed was also suggested for the present reaction.27 However, our calculations suggest that reduction of FeBr2 to FeBr by metallic zinc in DMA is prohibitively endergonic, with a Gibbs energy difference of 27 kcal/mol. Taking into account that there will additionally be a kinetic barrier to reduction, this strongly suggests that formation of discrete FeBr (with only DMA as the additional ligand) in the target reaction can be ruled out.
Neither bromide or DMA is able to display ligand non-innocence, so they cannot stabilize the unfavorable Fe(I) oxidation state by imparting partial Fe(0) or Fe(II) character, as commonly occurred for other reported Fe(I) species.46,47 In the presence of ligands, however, the stability of Fe(I) can be enhanced, and this changes the calculated free energy of reduction. In the present case, initial coordination of alkyne 6 to 1 to form complex 9 affords a more easily reducible species. The binding step is calculated to be moderately uphill in Gibbs energy, by 6.4 kcal/mol, such that the alkyne complex will be present in small amounts. Reduction of 9 by solid zinc to form Fe(I)-phenylacetylene complex 10 is only slightly endergonic, by 1.3 kcal/mol. This reflects the ability of the alkyne π* to accept d-electrons by back-bonding. Indeed, in a previous study, Fe(I) has been shown to bind strongly to alkynes.48 Here, the back-bonding is also evident from some topological characteristics of our calculated complexes. One notable feature is the significant bending of both the Ph–C–C and H–C–C angles in 10, with values of 156.50° and 147.86°, respectively, compared to the Fe(II) species 9 where the angles are more linear, with values of 177.20° and 163.68°, respectively. The C≡C bond distance also shows the effect, increasing from 1.21 Å in the free alkyne 6 to 1.23 Å in 9 and 1.27 Å in 10. Finally, the Fe–C bonds also show evidence for the enhanced interaction in 9, decreasing in length from 2.40 (Fe–C(H)) and 2.22 Å (Fe–C(Ph)) in 9 to 1.96 and 2.00 Å, respectively, in 10.
Another route for the initial reduction involves direct cleavage of the C–I bond in cyclohexyliodide 5 to generate the cyclohexyl (Cy) radical 8. This step is predicted by the method we use to be favorable in Gibbs energy terms, by 3.4 kcal/mol. As for all steps involving the reaction with solid zinc, estimating the barrier height is not trivially feasible within a molecular quantum chemical protocol, and a discussion of the approach that we have used to estimate reactivity for such steps is deferred until a later section. The radical can add almost without a barrier to 1 to form Fe(III) adduct 11 in an exergonic way (−3.6 kcal/mol). Complex 11 can be further reduced by zinc, in an exergonic process, to form Fe(II) complex 12. This species can also be formed by displacement of alkyne from 10.
In most of the experiments,27 an iodinated substrate was used together with an iron-bromide catalyst. Good results were also obtained with iron iodide as the catalyst. Due to the presence of two different halides, many of the intermediates and TSs to be discussed below could in principle exist as different isomers with varying numbers of Br and I groups. For simplicity, we have chosen to model the C–X bond breaking steps (Figure 2) with X = I; all other halides have been modeled as Br. Atom abstraction requires the use of iodide given the weaker C–I bond. However, for other steps, the halide plays a less important role, so this simplification seems reasonable. However, to test its impact, we modeled some iron reduction steps with iodide instead of bromide leading to formation of ZnI2 (see the Supporting Information). These steps were found to be slightly more favorable in free energy terms than the corresponding bromine transfer steps. For the C–C bond formation and transmetalation steps discussed below, we expect that the use of Br in place of I does not have a major effect on calculated energies, and overall, the approach used here should be acceptable.
Figure 2.
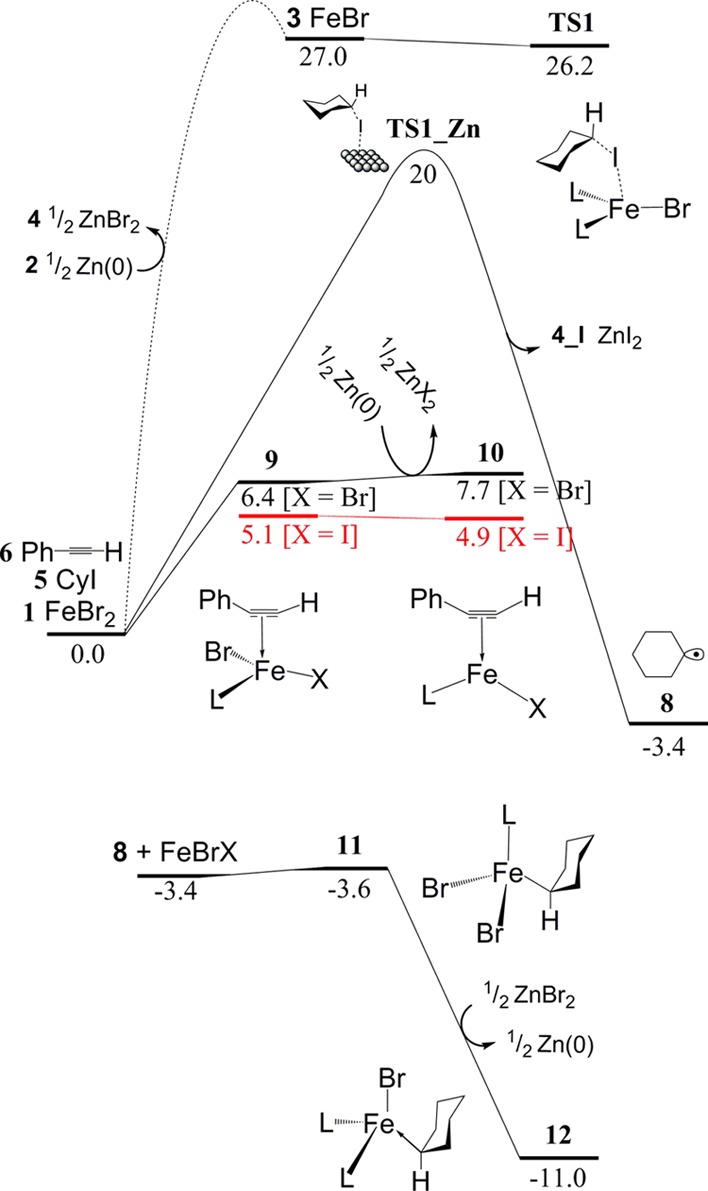
Fe(II) reduction with and without coordination of phenylacetylene or the cyclohexyl radical, and atom abstraction reaction by solid Zn(0) calculated using experimental data. The possibility of a bromide or iodide group has been shown to compare the small change in free energy. All the free energy values are calculated at the B3LYP-D3BJ-DKH/BS2 level of theory and shown in kcal/mol relative to the isolated reactants at the beginning of the reaction. The correct amount of solvent molecules is included. L = DMA solvent molecule.
We note that adding TMEDA to the reaction medium does not affect reactivity,27 even though it has been shown to inhibit formation of iron clusters in Kumada-type reactions.49−54 This suggests that iron nanoparticles are not responsible for catalysis, and we have not attempted to model them here.
C–C Bond Formation Steps
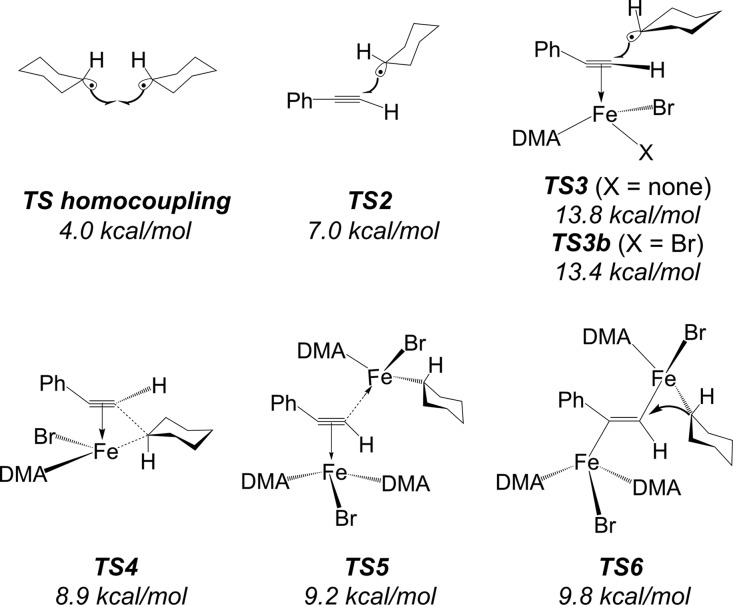
The above reduction steps lead to a variety of reduced species that are in principle able to undergo cross-coupling steps with formation of a C–C bond. We have modeled several of these possible steps (Figure 3). The first option is addition of the bare cyclohexyl radical to the alkyne, as suggested in the original experimental study.27 The corresponding TS2 is quite low in potential energy terms, but there is a significant barrier in free energy terms (10.4 kcal/mol). The resulting metal-free vinyl radical can add either to the zinc surface or to an Fe(II) or Fe(I) species to form a metal-vinyl species. Another possibility is that the radical can add to the coordinated alkyne, in complex either with an Fe(I) (10) or an Fe(II) (9) center, leading over TS3, TS3b, or TS4 to the iron-vinyl species P1z (Z) or P1e (E) (Figure 4 and Supporting Information). TS3 has an overall triplet ground state formed by a quartet iron center and a doublet radical with antiferromagnetic coupling of the spins. This TS has a negative (spin-down) spin density of −0.89 on the radical carbon atom. TS3b has an overall quartet spin state with electron density similar to TS3 but with the iron center as the quintet state. The structure of TS4 can be best described in terms of the FeBrCy(alkyne) complex 14 that is formed upon addition of the cyclohexyl radical to 10. This species can undergo migratory insertion of the alkyne into the Fe–C bond. Accordingly, TS4 has a quintet ground state with the four unpaired electrons located on the iron center.
Figure 3.
Located transition-state structures potentially involved in the reaction mechanism with the respective free energy value referred to the separated reactants as a zero. All the free energy values are calculated at the B3LYP-D3BJ-DKH/BS2 level of theory.
Figure 4.
Transmetalation process shown using aFischer projection, looking at the C=C bond from the terminal side. All the free energy values are calculated at the B3LYP-D3BJ-DKS/BS2 level of theory. The values are shown in kcal/mol and relative to the isolated reactants at the beginning of the reaction including the correct amount of solvent molecules. L = DMA solvent molecule.
A more complicated mechanism involves addition of the Fe(II) 12 to the alkyne complex 10 through TS5, yielding the diiron complex 13, which can then undergo reductive elimination through TS6 with formation of the C–C bond. Both TS5 and TS6 are calculated to have octet ground states, corresponding to a total of seven unpaired electrons, corresponding to three unpaired electrons in the iron of 10 and four in 12. This last mechanism necessarily leads to a Z-vinyl species due to the anti-arrangement of the two iron centers in TS5, and so, this step could in principle account for the Z-selectivity of the reaction. The other TSs (TS2 to TS4) can yield either E- or Z-vinyl-metal species.
Transmetalation
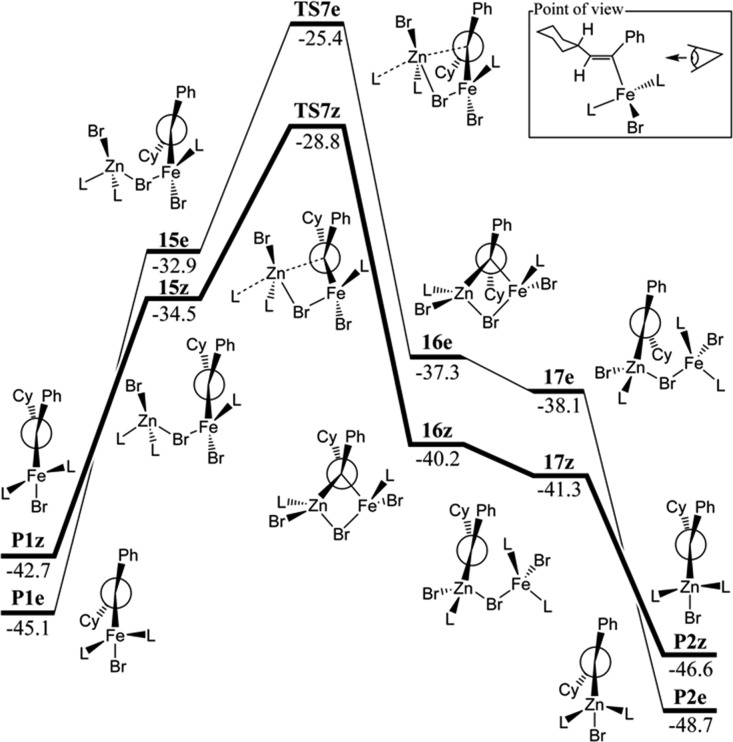
Formation of vinyl-iron species is not the end of the reaction since only catalytic amounts of iron are used. A transmetalation process involving a Zn(II) complex interacting with the adducts P1e and P1z leads to formation of the vinyl-zinc species P2z (Z) and P2e (E) and releases 1 (Figure 4). We have explored the mechanism followed in this process in some detail and suggest that the reaction proceeds by initial interaction of zinc dibromide 4 with the products P1e/z creating a bromide bridged complex 15e/z connecting the two metal centers; this step is accompanied by loss of a coordinating solvent molecule. Afterward, the zinc atom can interact with the vinylic carbon atom by crossing a transition state TS7e/z with activation barriers of 8 and 6 kcal/mol, respectively, for the E and Z diastereoisomers, leading to a diamond-like structure 16 where both the iron and zinc atoms are coordinating the central vinylic carbon atom as well as a bridging bromide. The product is subsequently formed by breaking the interaction between the Fe(II) center and the vinylic carbon. This step also involves coordination of an incoming solvent molecule to iron. Despite multiple attempts, no saddle point could be found for this step, either with or without inclusion of the additional solvent molecule. It appears that, in each case, there is no potential energy barrier (see the Supporting Information for relevant scans). Releasing iron dibromide 1 from 17 then yields the final vinyl-zinc species P2—this step is exergonic due to coordination of a solvent molecule.
As mentioned above, some mechanisms naturally lead to E- or Z-vinyl-iron species, and it is interesting to examine whether the transmetalation process can be accompanied by Z- to E-isomerization. For each step along the transmetalation route, isomerization transition-state structures were located, but they were all found to lie quite high in free energy, so they appear not to play an important role. The lowest energy isomerization TS, TS_iso, lies at relative free energies of −20.7 and 22 kcal/mol above P1z, thereby higher by almost 5 kcal/mol than TS7e, suggesting that isomerization should not compete with transmetalation.
Summing up
The above landscape of possible reactive steps provides some first insights into the mechanism of the cross-coupling, but firm mechanistic conclusions require an assessment of the relative probability of each route. Some indication is given by the relative free energies. As already mentioned, the high standard free energy predicted for the unligated Fe(I) bromide suggests that a route involving initial reduction of the metal salt is not possible. Next, similar free energies for TS2 and TS4 to TS6 suggest that each of the corresponding steps could be competitive under catalytic conditions. However, given the complex interplay between reduction steps involving metallic zinc and these steps, it is difficult to predict which of them should dominate. It should also be noted that the cyclohexyl radical (and perhaps the vinyl radical formed from addition through TS2) can undergo radical homocoupling and/or dismutation. These steps would most likely involve no potential energy barrier and so should in principle be rather fast, though they require a reaction between two a priori low-concentration highly reactive species, whereas the other steps mentioned above do not.
Overall, while the structures and energies calculated for the various species provide valuable insight into the reaction mechanism, they do not on their own provide quantitative insight into how exactly cross-coupling occurs. For this purpose, we turn to kinetic modeling of the reactions.
Kinetics
In order to deduce the behavior of the reactants and understand which are the main reaction steps that lead to the most abundant product (P2z), a kinetic analysis seems mandatory.55 To do so, we need access to the rate constants for all modeled steps, which together with initial concentrations allow us to integrate the rate equations to provide a time course of the reaction. There are three types of steps that need to be modeled. First, where we could locate a saddle point on the potential energy surface, we can use the Eyring equation of transition-state theory, combined with the corresponding relative free energies, to obtain forward and reverse rate constants. Next, some steps are found to be barrierless in either the forward or the reverse direction. In line with our previous work,56 we assume that these steps are diffusion-controlled in the direction where they are exergonic. A simple theory for such reactions57 approximates their rate constants to be kd = 8RT/3η, where η is the viscosity of the solvent. Here, using η = 0.92 cP for the viscosity of DMA,58 we obtain kd = 7.23 × 109 dm3 mol–1 s–1, which corresponds to a free energy barrier of about 4 kcal/mol in terms of the Eyring equation. The rate constant for the reverse of such diffusion-controlled reactions can then be obtained from the detailed balance.
Finally, we need to model
reactions with the zinc surface. Here, we rely on a combination of
experimental data and a form of Marcus theory to obtain a rough estimate
of the corresponding rate constants. The experimental data59 concerned the kinetics of bromide or chloride
abstraction from alkyl halides by solid zinc in the DMF solvent, which
has been shown60 to have as the first and
presumably rate-limiting step a halogen atom transfer to the surface
with formation of a radical, which then undergoes slower conversion
to an alkyl-zinc species. We assume that the measured rate constants59 can provide an estimate of the rate constants
for related steps corresponding to halogen atom transfer to solid
zinc. Our analysis, described in detail in the Supporting Information, also makes certain assumptions about
the surface area of the zinc metal used in the reaction. Analysis
of the experimental data suggests that the free energy barriers ΔG‡ for halogen atom transfer steps to
solid zinc could be approximately described in terms of the Marcus
theory equation: 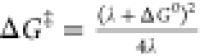 . The required inputs here are the calculated
free energy of reaction ΔG0 and
an intrinsic barrier height λ, which we determine
from analysis of reference experimental rates59 to be 86.7 kcal/mol.
. The required inputs here are the calculated
free energy of reaction ΔG0 and
an intrinsic barrier height λ, which we determine
from analysis of reference experimental rates59 to be 86.7 kcal/mol.
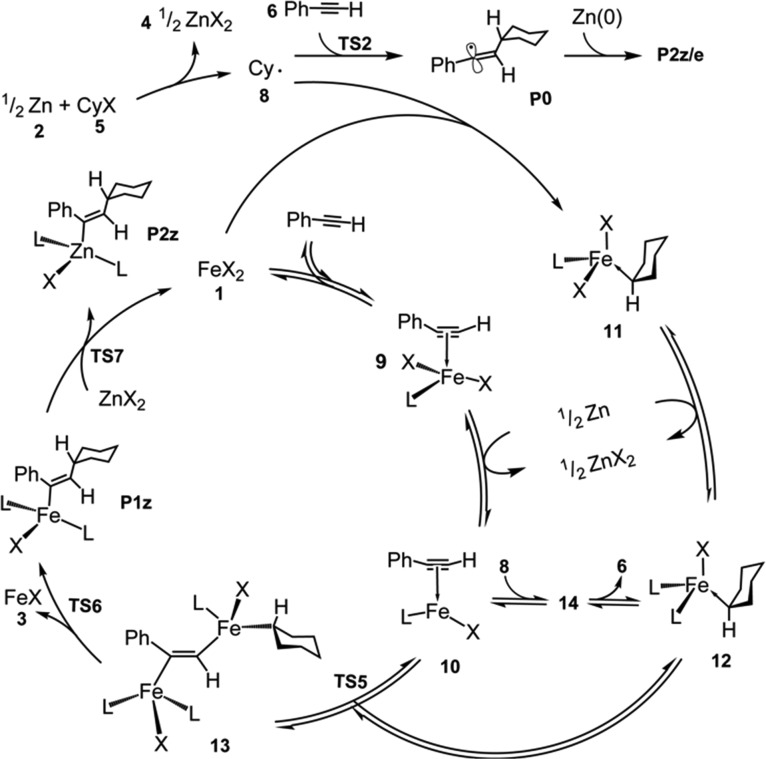
After this set up, we run a kinetic analysis using the software Tenua61 and initial conditions corresponding to [1] = 0.1 M, [2] = 2 M, [5] = 1.2 M, and [6] = 1.0 M. A summary of all the key steps modeled is shown in the catalytic cycle of Figure 5.
Figure 5.
Catalytic cycle for the main reaction path calculating after kinetic analysis by using the free energy values described on the thermodynamic section at the B3LYP-D3BJ-DKH/BS2 level of theory. L = DMA solvent molecule.
The kinetic model obtained in a manner just described gives as an outcome that the reaction is predicted to occur somewhat too quickly (a timescale of a few minutes, compared to experiments,27 which occur on a timescale of hours). A mismatch in timescales is not too surprising given that our Marcus analysis for reactions at the Zn surface is approximate and may lead to an overestimate of the reactivity. Adjusting the intrinsic barrier λ tunes the speed of the overall conversion without affecting in a major way the selectivity between the different pathways.
Next, in terms of the mechanism followed, this kinetic model predicts that C–C bond formation proceeds entirely through TS2, that is, by addition of the cyclohexyl radical to the free alkyne, to form a vinyl radical P0 in essentially quantitative yield (99%) with respect to the initial amount of alkyne in the reaction. This radical is assumed to then couple to the zinc surface ultimately forming a vinyl-zinc species that yields product upon aqueous workup. This is the step that was suggested in the experimental study. The preferential C–Zn bond forming at the less hindered side of the vinyl radical could account for the 14:1 Z:E alkene selectivity observed. The kinetic model also predicts the formation of some (at full conversion of alkyne, roughly 4% with respect to the amount of cyclohexyl iodide) radical–radical homocoupling product. This reaction (forming dicyclohexyl) is expected to be accompanied by some radical disproportionation (yielding cyclohexene plus cyclohexane), with an experiment reporting a branching ratio of roughly 1:1 for these channels,62 but we have treated this as a single step. In the experiments, traces of the homocoupling and disproportionation products are observed, but the amounts appear to be less than what is modeled here. The increased yields of these products here could again be due to the approximate methods used to compute the rate constant for radical production—slower formation of the radical will lead to lower standard-state concentrations and less self-reaction.
On the other hand, the model yields only tiny amounts of products via the iron-containing routes. The formation rate of the species such as 9 and 10 turns out to be uncompetitive with the formation and reaction of the radical with the phenyl acetylene. The concentration of these iron-containing intermediates is modeled to be of the order of only 10–6 M. In the model, they do then react to form product P1e through TS4, but the associated yield is very low, roughly 0.0001%. The yield of products through the bimetallic mechanism involving species 10 and 12 and TS5 and TS6 is also roughly 0.0001%, reflecting similar free energies of TSs TS4, TS5, and TS6. This is because the rate of the bimetallic mechanism depends on the concentrations of two iron-containing species (e.g., 10 and 12), whereas the rate of the monometallic mechanism only depends on one species.
Our kinetic model is dependent on multiple calculated rate constants that could be inaccurate. Therefore, we also explored modified kinetic models to assess how large the errors in individual calculated rate constants would need to be in order for the bimetallic mechanism to become dominant in product formation. The minimally modified free energy surface needed for this is shown in Figure S7. We found that the most natural way to drive the model toward the bimetallic mechanism was to change the free energy of formation of alkyne complex 9 (by 6 kcal/mol). All the iron-contained species formed from 9 are also shifted by this amount, and the TS for reduction of 9 to 10 is lowered by an additional 1 kcal/mol. This modified model shows a dominance for the bimetallic mechanism with the yield of the related product P2z of 82%, with roughly 5% of E-conformer P2e, which originates from the migratory insertion reaction through TS4. Roughly 13% of the vinyl radical is still formed through TS2. The outcome of this revised model agrees better with observed Fe-dependent reaction outcomes (see below). The large change in the calculated relative free energy seems to be slightly beyond the uncertainties associated with the quantum chemical procedure, but we do note that changes in relative energies of 3–4 kcal/mol do occur when changing the functional (see the Supporting Information).
Neither the original kinetic model nor the modified one can explain all of the experimental observations. First, addition of iron salt leads to a much increased yield of the cross-coupling product (in its absence, that is, with only alkyne, cyclohexyl iodide, and zinc powder, only 34% of the product is formed, whereas with 10% FeBr2, this increases to 91%).27 The reaction through TS2 should be able to proceed even without iron, so this large effect on the yield is not well explained by the original kinetic model. On the other hand, the product is formed (and with a similar E:Z ratio), albeit with low yield, in the absence of the iron additive, so an iron-free mechanism must be taken into account when discussing possible mechanisms. Also, good yields of cross-coupling products, with roughly the same 13:1 Z:E ratio, are obtained with CuBr2 or CrCl2 additives in place of FeBr2.
Discussion
Modeling reactions of this type using quantum chemical methods is extremely challenging. The fundamental reason for this is the extreme complexity of the reaction mixture, involving different oxidation, spin and solvation states of the iron catalyst, and a solid zinc coreagent. This means that mechanism prediction needs to consider many different sorts of species and treat them in an accurate and balanced way. This is arguably too challenging at the present time, although the present work contains suggestions for dealing with two issues. First, we suggest the use of experimental thermodynamic data for solid and gaseous zinc metal as a way to bridge the gap between the quantum chemical models of the molecular-zinc-containing species and the experimental presence of solid zinc. Second, we suggest that the Marcus equation can be used as a way to combine experimental data for a model reaction and computationally derived reaction energies to estimate rate constants for reactions taking place at the solid zinc surface.
Based on the quantum chemical free energies and the kinetic model, the preferred mechanism appears to be as shown in the top part of Figure 5, with zinc affecting reduction of the carbon–halide bond in the reagent, with the resulting radical then adding to the alkyne to form a vinyl radical product P0, which is then trapped as a vinyl-zinc species. An alternative route involving C–C bond formation through formation of the diiron intermediate 13 and then the reductive elimination is predicted to be significantly less favorable. This second possibility can only be made to be favored upon carrying out rather large adjustments to the quantum chemical free energies.
As mentioned at the end of the previous section, though, the kinetic model does not reproduce one key experimental observation, whereby addition of an iron salt enhances the yield of the reaction quite considerably, from 34 to 91%. One possible explanation is that the bimetallic mechanism occurs instead or as well, which would require similar mechanisms to also be competitive in the case of copper or chromium catalysts.
Another possibility is that the mechanism is more complex than either model suggested here. We have modeled some of the diversity of species that could be formed under the reaction conditions, but in fact the possible speciation range is much broader than what we have modelled. Charged species (the solvent used is quite polar) or some types of clusters could for example play a role. Another possibility is heterogeneous chemistry: so far, we have considered as possible redox partners the alkyl iodide, the iron salt, and various intermediate iron complexes. In each case, we have assumed that reduction leads to a solution-phase molecular species together with a zinc salt. However, more complex processes can occur on the zinc surface, with formation of adsorbed partly reduced species such as low-valent iron. Such species may play important roles and thereby modify the chemistry occurring in the presence of solid zinc only. For example, the presence of iron atoms at the zinc surface could accelerate the reduction of the C–X bond, leading to faster formation of cyclohexyl radicals. More complex effects, whereby iron at the surface could change the competition between formation of cyclohexyl radicals, which then add to alkyne over TS2, and formation of zinc-bound cyclohexyl, which does not react under the experimental conditions, are also possible. Such effects go well beyond what can be modeled in the present work.
Computational Details
The mechanistic study of the iron-catalyzed cross-coupling reaction between phenylacetylene and cyclohexyl iodide in the N,N-dimethylacetamide (DMA) solvent has been computationally explored using density functional theory with Gaussian09 rev. E01.63 Geometry optimization was performed employing the hybrid functional B3LYP38 including the empirical dispersion correction with Becke and Johnson damping D3BJ.64 The Pople basis set 6-31g(d)65 for O, N, C, and H and the Stuttgart basis set SDD66 with the associated effective core potential (ECP) for Zn, Fe, I, and Br (BS1) were used. Improved electronic energies at the optimized structures were obtained by recalculating the energy using the same B3LYP-D3BJ functional while also including scalar relativistic effects by using the Douglas–Kroll–Hess Hamiltonian (DKH)67,68 and using an expanded basis set consisting of aug-cc-pwCVQZ-DK for the metal center and aug-cc-pVTZ-DK for every other atom except for H where cc-pVDZ-DK was used (BS2).69−71 This method has been validated in two ways, described in detail in the Supporting Information. First, we computed the reaction energy for the key Fe(II) to Fe(I) reduction step for a model system: FeCl2(DMF)2 + 1/2 Zn(0) + DMF → FeCl(DMF)2 + 1/2 ZnCl2(DMF)2 using the same B3LYP-D3BJ protocol as described above and with CCSD(T)72−74 with an extended basis set. The agreement is better than 2 kcal/mol. Next, for most of the key species, single-point energies with the other DFT functionals MN1575 and M06L76 have been computed, and the resulting relative energies were compared. These other functionals, especially M06L, perform somewhat less well for the CCSD(T) benchmark and hence have not been used in our main analysis. They do provide some independent validation, though, because especially MN15 yields relative predicted energies close to those obtained with B3LYP-D3BJ, typically within 6 kcal/mol on average. Vibrational frequency calculations were performed at the same level of theory as used for geometry optimization and were used to define the nature of the stationary points (minima and TSs) involved in the reaction mechanism and to obtain zero-point and thermal energy corrections at 298.16 K. The free energy correction applied to the electronic energy was calculated using the quasi-harmonic approach as suggested by the Truhlar group77 with a cutoff for a small vibrational frequency of 100 cm–1. Also, we used the solution-phase standard state of 1 mol/L instead of the gas-phase 1 atm used by default in Gaussian. For the DMA solvent, the standard state used was the pure liquid, with a concentration of 10.76 mol/L. Kinetic simulations were done by using the software Tenua.61 The presence of a solvent (DMA) has been also considered by treating explicitly the solvent molecules but also implicitly with the continuum solvent SMD.78
Conclusions
The iron-catalyzed reductive cross-coupling reaction between phenyl acetylene and cyclohexyl iodine in the presence of solid zinc has been extensively explored with computational methods. A mechanistic scheme suggested in the original experimental study has been examined, as well as a number of variants. Two broadly plausible mechanisms have been put forward based on quantum chemical investigations, as well as new models for treating the free energy change of reactions involving solid zinc. The first mechanism is a modified form of the mechanism suggested in the experimental study, whereby the cyclohexyl iodide species undergoes reduction not by reduced Fe(I) species but by metallic zinc. The second is a mechanism involving formation of a diiron-alkene species through addition of two iron moieties to the alkyne followed by reductive elimination. Both of these pathways involve relatively modest free energy barriers and can be used to account for the Z-selectivity of the reaction.
However, discriminating between the two mechanisms based on quantum chemical data alone is not possible, and this motivated the second large part of the study, based on integration of the kinetic equations to obtain models of the reaction course. This modeling shows that, based on the raw quantum chemical free energy values, the first mechanism is significantly favored, and quite large adjustments to the free energies would be needed in order to make the second mechanism dominant. Such adjustments could in principle be required to take into account errors in the quantum chemical methodology.
In our discussion, we suggest that several experimental features of the reaction make the interpretation of the results even more challenging. Most importantly, the reaction leads to the same products (albeit with much lower yields) even in the absence of iron salts, and good yields of the same products can be obtained when replacing the iron catalyst by chromium or copper salts. We suggest that this pattern of reactivity is possibly explained by assuming that the reaction follows a pathway that is similar to the first mechanism proposed here based on quantum chemistry, with initial formation of a cyclohexyl radical upon reductive cleavage of the C–I bond. However, the detailed mechanism and outcome of this reductive step are suggested to be sensitive to the presence of metal salts at the zinc surface. This type of effect has been discussed elsewhere, for example, in the context of heterogeneous single-atom catalysis79 or in the context of “cocktail-type” systems at the borderline between homogeneous and heterogeneous chemistry.80
Overall, our study starts out from the methods of quantum chemistry as typically applied to homogeneous catalytic reactions to try to describe a modern catalytic synthetic transformation that also includes many important heterogeneous steps. The study not only includes a number of techniques for handling the complexity introduced by heterogeneous steps but also points toward the need for enhanced theories at the borderlines of theoretical homogeneous and heterogeneous catalytic chemistry.
Acknowledgments
The authors thank Mr. Marten Ploeger (EPFL) for the extensive discussions on the experimental aspects and Dr. Quan Phung for valuable advice on some aspects of the calculations.
Supporting Information Available
The Supporting Information is available free of charge at https://pubs.acs.org/doi/10.1021/acsomega.9b03578.
Extra calculations regarding the solvation study, the spin state analysis, and the halide abstraction step involving metallic complexes are presented, as well as benchmark results using different DFT functionals and high-level ab initio methods (PDF)
This work has been conducted thanks to funding from the European Union’s Horizon 2020 Research and Innovation Program under the Marie Curie Skłodowska–Curie grant agreement (Project ID: 675020. Project name: Non-Noble Metal Catalysis – NoNoMeCat). The computational resources and services used in this work were provided by the VSC (Flemish Supercomputer Center), funded by the Research Foundation Flanders (FWO) and the Flemish Government – department EWI.
The authors declare no competing financial interest.
Supplementary Material
References
- Vogiatzis K. D.; Polynski M. V.; Kirkland J. K.; Townsend J.; Hashemi A.; Liu C.; Pidko E. A. Computational Approach to Molecular Catalysis by 3d Transition Metals: Challenges and Opportunities. Chem. Rev. 2019, 119, 2453–2523. 10.1021/acs.chemrev.8b00361. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friedfeld M. R.; Zhong H.; Ruck R. T.; Shevlin M.; Chirik P. J. Cobalt-Catalyzed Asymmetric Hydrogenation of Enamides Enabled by Single-Electron Reduction. Science 2018, 360, 888–893. 10.1126/science.aar6117. [DOI] [PubMed] [Google Scholar]
- Pye D. R.; Mankad N. P. Bimetallic Catalysis for C-C and C-X Coupling Reactions. Chem. Sci. 2017, 8, 1705–1718. 10.1039/C6SC05556G. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bolm C.; Legros J.; Le Paih J.; Zani L. Iron-Catalyzed Reactions in Organic Synthesis. Chem. Rev. 2004, 104, 6217–6254. 10.1021/cr040664h. [DOI] [PubMed] [Google Scholar]
- Plietker B.Iron Catalysis Fundamentals and Applications; Springer Science & Business Media, 2011; Vol. 33. [Google Scholar]
- Bauer E. B.Iron Catalysis Historic Overview and Current Trends . In Topics in Organometallic Chemistry; Springer, 2015; Vol. 50, pp 1–18. [Google Scholar]
- Bullock R. M.Catalysis without Precious Metals; John Wiley & Sons, 2010. [Google Scholar]
- Marek I.; Rappoport Z.. The Chemistry of Organoiron Compounds; John Wiley & Sons, Incorporated, 2014. [Google Scholar]
- Mako T. L.; Byers J. A. Recent Advances in Iron-Catalysed Cross Coupling Reactions and Their Mechanistic Underpinning. Inorg. Chem. Front. 2016, 3, 766–790. 10.1039/C5QI00295H. [DOI] [Google Scholar]
- Hazari N.; Melvin P. R.; Beromi M. M. Well-Defined Nickel and Palladium Precatalysts for Cross-Coupling. Nat. Rev. Chem. 2017, 1, 0025 10.1038/s41570-017-0025. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Harvey J. N.; Himo F.; Maseras F.; Perrin L. Scope and Challenge of Computational Methods for Studying Mechanism and Reactivity in Homogeneous Catalysis. ACS Catal. 2019, 9, 6803–6813. 10.1021/acscatal.9b01537. [DOI] [Google Scholar]
- Bittner M. M.; Kraus D.; Lindeman S. V.; Popescu C. V.; Fiedler A. T. Synthetic, Spectroscopic, and DFT Studies of Iron Complexes with Iminobenzo(Semi)Quinone Ligands: Implications for o-Aminophenol Dioxygenases. Chem. - Eur. J. 2013, 19, 9686–9698. 10.1002/chem.201300520. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Casitas A.; Krause H.; Goddard R.; Fürstner A. Elementary Steps of Iron Catalysis: Exploring the Links between Iron Alkyl and Iron Olefin Complexes for Their Relevance in C-H Activation and C-C Bond Formation. Angew. Chem., Int. Ed. 2015, 54, 1521–1526. 10.1002/anie.201410069. [DOI] [PubMed] [Google Scholar]
- Bauer G.; Wodrich M. D.; Scopelliti R.; Hu X. Iron Pincer Complexes as Catalysts and Intermediates in Alkyl-Aryl Kumada Coupling Reactions. Organometallics 2015, 34, 289–298. 10.1021/om501122p. [DOI] [Google Scholar]
- Heggen B.; Thiel W. Theoretical Investigation on the Mechanism of Iron Catalyzed Cross Coupling Reactions via Ferrate Intermediates. J. Organomet. Chem. 2016, 804, 42–47. 10.1016/j.jorganchem.2015.12.026. [DOI] [Google Scholar]
- Ren Q.; Guan S.; Shen X.; Fang J. Density Functional Theory Study of the Mechanisms of Iron-Catalyzed Aminohydroxylation Reactions. Organometallics 2014, 33, 1423–1430. 10.1021/om401141r. [DOI] [Google Scholar]
- Kneebone J. L.; Fleischauer V. E.; Daifuku S. L.; Shaps A. A.; Bailey J. M.; Iannuzzi T. E.; Neidig M. L. Electronic Structure and Bonding in Iron(II) and Iron(I) Complexes Bearing Bisphosphine Ligands of Relevance to Iron-Catalyzed C-C Cross-Coupling. Inorg. Chem. 2016, 55, 272–282. 10.1021/acs.inorgchem.5b02263. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tamao K.; Sumitani K.; Kumada M. Selective Carbon-Carbon Bond Formation by Cross-Coupling of Grignard Reagents with Organic Halides. Catalysis by Nickel-Phosphine Complexes. J. Am. Chem. Soc. 1972, 94, 4374–4376. 10.1021/ja00767a075. [DOI] [Google Scholar]
- King A. O.; Okukado N.; Negishi E.-i. Highly general stereo-, regio-, and chemo-selective synthesis of terminal and internal conjungated enynes by the Pd-catalysed reaction of alkynylzinc reagents with alkenyl halides. Chem. Commun. 1977, 683–684. 10.1039/c39770000683. [DOI] [Google Scholar]
- Hatakeyama T.; Nakagawa N.; Nakamura M. Iron-Catalyzed Negishi Coupling toward an Effective Olefin Synthesis. Org. Lett. 2009, 11, 4496–4499. 10.1021/ol901555r. [DOI] [PubMed] [Google Scholar]
- Sonogashira K. Development of Pd-Cu Catalyzed Cross-Coupling of Terminal Acetylenes with Sp2-Carbon Halides. J. Organomet. Chem. 2002, 653, 46–49. 10.1016/S0022-328X(02)01158-0. [DOI] [Google Scholar]
- Johansson Seechurn C. C. C.; Kitching M. O.; Colacot T. J.; Snieckus V. Palladium-Catalyzed Cross-Coupling: A Historical Contextual Perspective to the 2010 Nobel Prize. Angew. Chem., Int. Ed. 2012, 51, 5062–5085. 10.1002/anie.201107017. [DOI] [PubMed] [Google Scholar]
- Carril M.; Correa A.; Bolm C. Iron-catalyzed Sonogashira reactions. Angew Chem Int Ed Engl. 2008, 47 (26), 4862–4865. 10.1002/anie.200801539. [DOI] [PubMed] [Google Scholar]
- Matouzenko G. S.; Borshch S. A.; Schünemann V.; Wolny J. A. Ligand Strain and Conformations in a Family of Fe(II) Spin Crossover Hexadentate Complexes Involving the 2-Pyridylmethyl-Amino Moiety: DFT Modelling. Phys. Chem. Chem. Phys. 2013, 15, 7411–7419. 10.1039/c3cp44570d. [DOI] [PubMed] [Google Scholar]
- Messinis A. M.; Luckham S. L. J.; Wells P. P.; Gianolio D.; Gibson E. K.; O’Brien H. M.; Sparkes H. A.; Davis S. A.; Callison J.; Elorriaga D.; et al. The Highly Surprising Behaviour of Diphosphine Ligands in Iron-Catalysed Negishi Cross-Coupling. Nat. Catal. 2019, 2, 123–133. 10.1038/s41929-018-0197-z. [DOI] [Google Scholar]
- Blanchard S.; Derat E.; Desage-El Murr M.; Fensterbank L.; Malacria M.; Mouriès-Mansuy V. Non-Innocent Ligands: New Opportunities in Iron Catalysis. Eur. J. Inorg. Chem. 2012, 2012, 376–389. 10.1002/ejic.201100985. [DOI] [Google Scholar]
- Cheung C. W.; Zhurkin F. E.; Hu X. Z -Selective Olefin Synthesis via Iron-Catalyzed Reductive Coupling of Alkyl Halides with Terminal Arylalkynes. J. Am. Chem. Soc. 2015, 137, 4932–4935. 10.1021/jacs.5b01784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheung C. W.; Hu X. Stereoselective Synthesis of Trisubstituted Alkenes through Sequential Iron-Catalyzed Reductive Anti-Carbozincation of Terminal Alkynes and Base-Metal-Catalyzed Negishi Cross-Coupling. Chem. - Eur. J. 2015, 21, 18439–18444. 10.1002/chem.201504049. [DOI] [PubMed] [Google Scholar]
- Gossage R. Zinc (II) Bromide: An Overview of Its Solution Chemistry and Recent Applications in Synthesis. Curr. Org. Chem. 2006, 10, 923–936. 10.2174/138527206777435544. [DOI] [Google Scholar]
- Del Pozo J.; Pérez-Iglesias M.; Álvarez R.; Lledós A.; Casares J. A.; Espinet P. Speciation of ZnMe2, ZnMeCl, and ZnCl2 in Tetrahydrofuran (THF), and Its Influence on Mechanism Calculations of Catalytic Processes. ACS Catal. 2017, 7, 3575–3583. 10.1021/acscatal.6b03636. [DOI] [Google Scholar]
- Besora M.; Carreón-Macedo J.-L.; Cowan A. J.; George M. W.; Harvey J. N.; Portius P.; Ronayne K. L.; Sun X.-Z.; Towrie M. A Combined Theoretical and Experimental Study on the Role of Spin States in the Chemistry of Fe(Co)5 Photoproducts. J. Am. Chem. Soc. 2009, 131, 3583–3592. 10.1021/ja807149t. [DOI] [PubMed] [Google Scholar]
- Besora M.; Carreón-Macedo J. L.; Cimas Á.; Harvey J. N. Spin-State Changes and Reactivity in Transition Metal Chemistry: Reactivity of Iron Tetracarbonyl. Adv. Inorg. Chem. 2009, 61, 573–623. 10.1016/S0898-8838(09)00210-4. [DOI] [Google Scholar]
- Manner V. W.; Lindsay A. D.; Mader E. A.; Harvey J. N.; Mayer J. M. Spin-Forbidden Hydrogen Atom Transfer Reactions in a Cobalt Biimidazoline System. Chem. Sci. 2012, 3, 230–243. 10.1039/C1SC00387A. [DOI] [Google Scholar]
- Harvey J. N. Computational Chemistry: A Multitude of Spins. Nat. Chem. 2013, 5, 643–644. 10.1038/nchem.1719. [DOI] [PubMed] [Google Scholar]
- Ye S.; Neese F. Accurate Modeling of Spin-State Energetics in Spin-Crossover Systems with Modern Density Functional Theory. Inorg. Chem. 2010, 49, 772–774. 10.1021/ic902365a. [DOI] [PubMed] [Google Scholar]
- Swart M. Accurate Spin-State Energies for Iron Complexes. J. Chem. Theory Comput. 2008, 4, 2057–2066. 10.1021/ct800277a. [DOI] [PubMed] [Google Scholar]
- Kepp K. P. Theoretical Study of Spin Crossover in 30 Iron Complexes. Inorg. Chem. 2016, 55, 2717–2727. 10.1021/acs.inorgchem.5b02371. [DOI] [PubMed] [Google Scholar]
- Lee C.; Yang W.; Parr R. G. Development of the Colle-Salvetti correlation-energy formula into a functional of the electron density. Phys. Rev. B 1988, 37, 785. 10.1103/PhysRevB.37.785. [DOI] [PubMed] [Google Scholar]
- NIST WebBook; https://Webbook.Nist.Gov/Cgi/Inchi?ID=C7440666, Accessed on September 2016.
- Bedford R. B. How Low Does Iron Go? Chasing the Active Species in Fe-Catalyzed Cross-Coupling Reactions. Acc. Chem. Res. 2015, 48, 1485–1493. 10.1021/acs.accounts.5b00042. [DOI] [PubMed] [Google Scholar]
- Cassani C.; Bergonzini G.; Wallentin C. J. Active Species and Mechanistic Pathways in Iron-Catalyzed C-C Bond-Forming Cross-Coupling Reactions. ACS Catal. 2016, 6, 1640–1648. 10.1021/acscatal.5b02441. [DOI] [Google Scholar]
- Lefèvre G.; Jutand A. Activation of Aryl and Heteroaryl Halides by an Iron(I) Complex Generated in the Reduction of [Fe(Acac)3] by PhMgBr: Electron Transfer versus Oxidative Addition. Chem. - Eur. J. 2014, 20, 4796–4805. 10.1002/chem.201304716. [DOI] [PubMed] [Google Scholar]
- Bekhradnia A.; Norrby P.-O. New Insights into the Mechanism of Iron-Catalyzed Cross-Coupling Reactions. Dalton Trans. 2015, 44, 3959–3962. 10.1039/C4DT03491K. [DOI] [PubMed] [Google Scholar]
- Hedström A.; Lindstedt E.; Norrby P. O. On the Oxidation State of Iron in Iron-Mediated C-C Couplings. J. Organomet. Chem. 2013, 748, 51–55. 10.1016/j.jorganchem.2013.04.024. [DOI] [Google Scholar]
- Adams C. J.; Bedford R. B.; Carter E.; Gower N. J.; Haddow M. F.; Harvey J. N.; Huwe M.; Cartes M. Á.; Mansell S. M.; Mendoza C.; et al. Iron(I) in Negishi Cross-Coupling Reactions. J. Am. Chem. Soc. 2012, 134, 10333–10336. 10.1021/ja303250t. [DOI] [PubMed] [Google Scholar]
- Hedström A.; Izakian Z.; Vreto I.; Wallentin C. J.; Norrby P. O. On the Radical Nature of Iron-Catalyzed Cross-Coupling Reactions. Chem. - Eur. J. 2015, 21, 5946–5953. 10.1002/chem.201406096. [DOI] [PubMed] [Google Scholar]
- Guisán-Ceinos M.; Tato F.; Buñuel E.; Calle P.; Cárdenas D. J. Fe-Catalysed Kumada-Type Alkyl-Alkyl Cross-Coupling. Evidence for the Intermediacy of Fe(I) Complexes. Chem. Sci. 2013, 4, 1098–1104. 10.1039/c2sc21754f. [DOI] [Google Scholar]
- Yu Y.; Smith J. M.; Flaschenriem C. J.; Holland P. L. Binding Affinity of Alkynes and Alkenes to Low-Coordinate Iron. Inorg. Chem. 2006, 45, 5742–5751. 10.1021/ic052136+. [DOI] [PubMed] [Google Scholar]
- Parchomyk T.; Koszinowski K. Solution and Gas-Phase Reactivity of Me12Fe8– and Related Cluster Ions. Chem. - Eur. J. 2017, 23, 3213–3219. 10.1002/chem.201605602. [DOI] [PubMed] [Google Scholar]
- Sears J. D.; Muñoz S. B. III; Daifuku S. L.; Shaps A. A.; Carpenter S. H.; Brennessel W. W.; Neidig M. L. The Effect of β-Hydrogen Atoms on Iron Speciation in Cross-Couplings with Simple Iron Salts and Alkyl Grignard Reagents. Angew. Chem., Int. Ed. 2019, 58, 2769–2773. 10.1002/anie.201813578. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neidig M. L.; Carpenter S. H.; Curran D. J.; Demuth J. C.; Fleischauer V. E.; Iannuzzi T. E.; Neate P. G. N.; Sears J. D.; Wolford N. J. Development and Evolution of Mechanistic Understanding in Iron-Catalyzed Cross-Coupling. Acc. Chem. Res. 2018, 52, 140–150. 10.1021/acs.accounts.8b00519. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sears J. D.; Muñoz S. B. III; Cuenca M. C. A.; Brennessel W. W.; Neidig M. L. Synthesis and Characterization of a Sterically Encumbered Homoleptic Tetraalkyliron(III) Ferrate Complex. Polyhedron 2019, 158, 91–96. 10.1016/j.poly.2018.10.041. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Carpenter S. H.; Baker T. M.; Muñoz S. B. III; Brennessel W. W.; Neidig M. L. Multinuclear Iron-Phenyl Species in Reactions of Simple Iron Salts with PhMgBr: Identification of Fe4(μ-Ph)6(THF)4 as a Key Reactive Species for Cross-Coupling Catalysis. Chem. Sci. 2018, 9, 7931–7939. 10.1039/C8SC02915F. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Muñoz S. B. III; Daifuku S. L.; Brennessel W. W.; Neidig M. L. Isolation, Characterization, and Reactivity of Fe8Me12-: Kochi’s S = 1/2 Species in Iron-Catalyzed Cross-Couplings with MeMgBr and Ferric Salts. J. Am. Chem. Soc. 2016, 138, 7492–7495. 10.1021/jacs.6b03760. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besora M.; Maseras F. Microkinetic Modeling in Homogeneous Catalysis. Wiley Interdiscip. Rev.: Comput. Mol. Sci. 2018, 8, e1372 10.1002/wcms.1372. [DOI] [Google Scholar]
- Rush L. E.; Pringle P. G.; Harvey J. N. Computational Kinetics of Cobalt-Catalyzed Alkene Hydroformylation. Angew. Chem., Int. Ed. 2014, 53, 8672–8676. 10.1002/anie.201402115. [DOI] [PubMed] [Google Scholar]
- Atkins P. W.; De Paula J.; Keeler J.. Atkins’ Physical Chemistry; Oxford university press, 2018. [Google Scholar]
- Iloukhani H.; Khanlarzadeh K. Densities, Viscosities, and Refractive Indices for Binary and Ternary Mixtures of N,N-Dimethylacetamide (1) + 2-Methylbutan-2-Ol (2) + Ethyl Acetate (3) at 298.15 K for the Liquid Region and at Ambient Pressure. J. Chem. Eng. Data 2006, 51, 1226–1231. 10.1021/je050538q. [DOI] [Google Scholar]
- Egorov A. M. Kinetics and Mechanism of the Reaction of Benzyl Halides with Zinc in Dimethylformamide. J. Phys. Org. Chem. 2006, 19, 664–675. 10.1002/poc.1114. [DOI] [Google Scholar]
- Guijarro A.; Rosenberg D. M.; Rieke R. D. The Reaction of Active Zinc with Organic Bromides. J. Am. Chem. Soc. 1999, 121, 4155–4167. 10.1021/ja9844478. [DOI] [Google Scholar]
- Wachsstock D.Tenua, a Chemical Kinetics Simulation Program. Available Free online http://bililite.com/tenua, 2011.
- Knyazev V. D.; Popov K. V. Kinetics of the Self Reaction of Cyclopentadienyl Radicals. J. Phys. Chem. A 2015, 119, 7418–7429. [DOI] [PubMed] [Google Scholar]
- Frisch M. J.; Trucks G. W.; Schlegel H. B.; Scuseria G. E.; Robb M. A.; Cheeseman J. R.; Scalmani G.; Barone V.; Petersson G. A.; Nakatsuji H.; Li X.; Caricato M.; Marenich A. V.; Bloino J.; Janesko B. G.; Gomperts R.; Mennucci B.; Hratch D. J.. 09, Revision E. 01. Gaussian Inc.,Wallingford: 2009.
- Grimme S.; Ehrlich S.; Goerigk L. Effect of the Damping Function in Dispersion Corrected Density Functional Theory. J. Comput. Chem. 2011, 32, 1456–1465. 10.1002/jcc.21759. [DOI] [PubMed] [Google Scholar]
- Hariharan P. C.; Pople J. A. The Influence of Polarization Functions on Molecular Orbital Hydrogenation Energies. Theor. Chim. Acta 1973, 28, 213–222. 10.1007/BF00533485. [DOI] [Google Scholar]
- Bergner A.; Dolg M.; Küchle W.; Stoll H.; Preuß H. Ab InitioEnergy-Adjusted Pseudopotentials for Elements of Groups 13-17. Mol. Phys. 1993, 80, 1431–1441. 10.1080/00268979300103121. [DOI] [Google Scholar]
- Douglas M.; Kroll N. M. Quantum Electrodynamical Corrections to the Fine Structure of Helium. Ann. Phys. 1974, 82, 89–155. 10.1016/0003-4916(74)90333-9. [DOI] [Google Scholar]
- Hess B. A. Relativistic Electronic-Structure Calculations Employing a Two-Component No-Pair Formalism with External-Field Projection Operators. Phys. Rev. A 1986, 33, 3742–3748. 10.1103/PhysRevA.33.3742. [DOI] [PubMed] [Google Scholar]
- Balabanov N. B.; Peterson K. A. Systematically Convergent Basis Sets for Transition Metals. I. All-Electron Correlation Consistent Basis Sets for the 3d Elements Sc-Zn. J. Chem. Phys. 2005, 123, 064107 10.1063/1.1998907. [DOI] [PubMed] [Google Scholar]
- Dunning T. H. Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. I. The Atoms Boron through Neon and Hydrogen. J. Chem. Phys. 1989, 90, 1007–1023. 10.1063/1.456153. [DOI] [Google Scholar]
- Wilson A. K.; Woon D. E.; Peterson K. A.; Dunning T. H. Jr. Gaussian Basis Sets for Use in Correlated Molecular Calculations. IX. The Atoms Gallium through Krypton. J. Chem. Phys. 1999, 110, 7667–7676. 10.1063/1.478678. [DOI] [Google Scholar]
- Bartlett R. J. Perspective on “on the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods”. Theor. Chem. Acc. 2000, 103, 273–275. 10.1007/s002140050033. [DOI] [Google Scholar]
- Watts J. D.; Gauss J.; Bartlett R. J. Coupled-Cluster Methods with Noniterative Triple Excitations for Restricted Open-Shell Hartree-Fock and Other General Single Determinant Reference Functions. Energies and Analytical Gradients. J. Chem. Phys. 1993, 98, 8718–8733. 10.1063/1.464480. [DOI] [Google Scholar]
- Čéžek J. On the Correlation Problem in Atomic and Molecular Systems. Calculation of Wavefunction Components in Ursell-Type Expansion Using Quantum-Field Theoretical Methods. J. Chem. Phys. 1966, 45, 4256–4266. 10.1063/1.1727484. [DOI] [Google Scholar]
- Yu H. S.; He X.; Li S. L.; Truhlar D. G. MN15: A Kohn-Sham Global-Hybrid Exchange-Correlation Density Functional with Broad Accuracy for Multi-Reference and Single-Reference Systems and Noncovalent Interactions. Chem. Sci. 2016, 7, 5032–5051. 10.1039/C6SC00705H. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhao Y.; Truhlar D. G. A New Local Density Functional for Main-Group Thermochemistry, Transition Metal Bonding, Thermochemical Kinetics, and Noncovalent Interactions. J. Chem. Phys. 2006, 125, 194101. 10.1063/1.2370993. [DOI] [PubMed] [Google Scholar]
- Ribeiro R. F.; Marenich A. V.; Cramer C. J.; Truhlar D. G. Use of Solution-Phase Vibrational Frequencies in Continuum Models for the Free Energy of Solvation. J. Phys. Chem. B 2011, 115, 14556–14562. 10.1021/jp205508z. [DOI] [PubMed] [Google Scholar]
- Marenich A. V.; Cramer C. J.; Truhlar D. G. Universal Solvation Model Based on Solute Electron Density and on a Continuum Model of the Solvent Defined by the Bulk Dielectric Constant and Atomic Surface Tensions. J. Phys. Chem. B 2009, 113, 6378–6396. 10.1021/jp810292n. [DOI] [PubMed] [Google Scholar]
- Wang A.; Li J.; Zhang T. Heterogeneous Single-Atom Catalysis. Nat. Rev. Chem. 2018, 2, 65–81. 10.1038/s41570-018-0010-1. [DOI] [Google Scholar]
- Eremin D. B.; Ananikov V. P. Understanding Active Species in Catalytic Transformations: From Molecular Catalysis to Nanoparticles, Leaching, “Cocktails” of Catalysts and Dynamic Systems. Coord. Chem. Rev 2017, 346, 2–19. 10.1016/j.ccr.2016.12.021. [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.