Efficient Small Blob Detection based on Local Convexity, Intensity and Shape Information

Abstract

The identification of small structures (blobs) from medical images to quantify clinically relevant features, such as size and shape, is important in many medical applications. One particular application explored here is the auto mated detection of kidney glomeruli after targeted contrast enhancement and magnetic resonance imaging. We propose a computationally efficient algorithm, termed the Hessian-based difference of Gaussians (H0oG), to segment small blobs (e.g. glomeruli from kidney) from 30 medical images based on local convexity, intensity and shape information. The image is first smoothed and pre-segmented into small blob candidate regions based on local convexity. Two novel 30 regional features (regional blobness and regional flatness) are then extracted from the candidate regions. Together with regional intensity, the three features are used in an unsupervised learning algorithm for auto post-pruning. H0oG is first validated in a 20 form and compared with other three blob detectors from literature, which are generally for 20 images only. To test the detectability of blobs from 30 images, 240 sets of simulated images are rendered for scenarios mimicking the renal nephron distribution observed in contrast-enhanced, 30 MRI. The results show a satisfactory performance of H0oG in detecting large numbers of small blobs. Two sets of real kidney 30 MR images (6 rats, 3 human) are then used to validate the applicability of H0oG for glomeruli detection. By comparing MRI to stereological measurements, we verify that H0oG is a robust and efficient unsupervised technique for 30 blobs segmentation.

INTRODUCTION

Segmenting many small structures is often important in medical imaging analysis as it labels regions of interest from which quantitative measures (e.g., size, shape) can be drawn for disease diagnosis, prognosis and staging. Examples of small structures may include cells or cell nuclei in histopathology/fluoroscopic images or MR images , exudative lesions in retinal images , breast lesions in ultrasound images , and glomeruli in contrast-enhanced MR images of the kidney . One common observation is that small structures preserve local homogenous imaging properties such as convexity of the intensity function and shape. In the field of computer vision, the problem of detecting such structures is known as blob detection.

Detecting blobs from medical images is challenging due to issues including but not limited to 1) large image intensity variation around the blobs, 2) clustering of the blobs and ambiguous boundaries, and 3) imaging artifacts (e.g. signal noise). Extensive work has been done to overcome these issues. One classic approach is the Laplacian of Gaussian (LoG) . The LoG is based on scale-space theory. In scale- space theory, a 2D image or a slice of a 3D image is treated as part of a stack of images controlled by a scale parameter t. A multi-scale Gaussian scale-space representation of the image is derived as the convolution of the raw image over the Gaussian kernel with respect to t, preserving the key spatial properties of the imaged structures . When t increases, the number of local minima in a dark blob does not increase and the number of local maxima in a bright blob does not decrease, so a diffusion process can be employed to identify the blobs. For similarly sized blobs, one “optimal” scale exists. If the image has blobs with a large range of sizes, multiple values of t may apply. Detectors based on LoG kernels have had some success in detecting symmetric blobs but are known to have limitations in identifying rotationally asymmetric blobs. The generalized Laplacian of the Gaussian (gLoG) was developed to detect rotationally asymmetric structures by employing multiple asymmetric Gaussian kernels. Both detectors pinpoint the centroid of the blob, and a regular ellipse with an estimated radius over the centroid is superimposed on the images to obtain the required measurements. Since the convolution kernels (e.g. LoG, gLoG) are set globally for the whole image, it is very likely that the local noise is not fully attenuated by a global filter, which would create unnecessary local extrema. For images with considerable noise, (e.g., MRI), and relatively small (or even tiny) blobs, the performance of these types of detectors may deteriorate due to local extrema in the convolution response map, which was empirically shown in. Therefore, post-pruning is usually required for improved performance of this type of detector. Most recently, the Hessian-based Laplacian of Gaussian (HLoG) was proposed to increase the detectability of small blobs from noisy medical images, since it used regional features that are tolerant to local noise for post-pruning. However, all the detectors reviewed above are restricted to 2D images due to the computational burden of the multi-scale LoG transformation.

Here we focus on the specific problem of detecting contrast-labeled kidney glomeruli from 3D MR images. The kidney is a life-sustaining organ with an enormous ability to adapt structurally and functionally to meet the needs of each individual across a multitude of environments. The nephron is the individual filtering unit of the kidney and is comprised of a glomerulus, a tuft of fenestrated capillaries responsible for filtering the blood that enters from the afferent arteriole, and an attached tubule, which reabsorb certain constituents of the blood prior to urinary excretion. A decline in renal function, a late surrogate of reduced nephron mass, is strongly associated with significant cardiovascular morbidity and mortality, even in the earliest stages of chronic kidney disease. Although clinicians can measure glomerular filtration rate and this will decline with progressive chronic kidney disease, this assessment is a measure of the total surface area of all glomeruli and cannot account for glomerular hypertrophy that occurs as an adaptive mechanism to low nephron number. To date, the standard methods for nephron enumeration are post mortem, destructive techniques that only estimate glomerulus number. It is highly desirable to have a clinically translatable method to count a living individuals nephron mass to evaluate kidney morphology and function. Recent advances in MRI and contrast agents makes the detection of glomeruli in vivo feasible, which could transform kidney disease diagnosis using cationic-ferritin enhanced (CFE) MRI. In CFE-MRI, a cationic, magnetic ferritin-based nanoparticle is intravenously injected. The agent binds temporarily to the basement membrane of the renal glomerulus, allowing in vivo and ex vivo detection and counting of individual glomeruli and nephrons. This approach requires 3D detection and measurement of each glomerulus in the MR image, in some ways similar to computational problem in pattern recognition in other systems. However, there is especially challenging for glomeruli because they are very small and have a high spatial frequency close to that of the image noise. Furthermore, glomerulus detection requires considerable computational effort due to the MRI resolution; only highly efficient detectors are suitable for high-throughput in vivo studies leading to the potential for clinical applications.

In this research we propose the Hessian-based Difference of Gaussians (HDoG) that incorporates local convexity, intensity and shape information to efficiently detect blobs in 3D images. In HDoG, we first apply the Difference of Gaussians (DoG) transformation to the raw image to quickly smooth out local noise and enhance blob structures. Hessian- based convexity analysis is then conducted to pre-segment and delineate the blob candidate regions with the same local convexity. Since the Hessian analysis may also identify false blobs (e.g. artifacts), post-pruning is necessary to remove the false identification. To achieve this, two novel 3D regional local shape features with fast computation are introduced: regional blobness (RT) and regional flatness (ST). The average image intensity, is also introduced. These three features are derived from each blob candidate region and fed into a tuning- free, unsupervised clustering algorithm - the variational Bayesian Gaussian mixture model (VBGMM) as a post- pruning process. Since most blob detectors from existing literature are for 2D images, we modified HDoG to identify the 2D version of the regional features and compared HDoG- 2D with LoG, gLoG and HLoG to detect cells in 15 pathological images and 200 fluorescence microscopy images. We observe that, while comparable to HLoG-2D and gLoG (most cases, see Section IV.A), HDoG-2D outperformed LoG and had the least computing time, as expected. Next, we comprehensively evaluated the use of HDoG to detect 3D blobs. Due to a lack of 3D datasets in the literature for comparison, we generated simulated images with known ground truth as a first validation. 240 sets of simulated images (each set has 10 images, total 2400 images) were created with 12 different blob sizes and 20 different blob counts mimicking the kidney glomerulus distributions. After observing satisfactory performance, we studied two sets of real kidney MR and compared the results from HDoG against the stereological estimates. The two sets of kidney MR images were: six rat kidney MR images of matrix size 256×256×256 (each glomerulus is sized 1.5 ~ 2.5 voxels in radius) and three human kidney MR images of matrix size 512×512×896 (each glomerulus is sized 1.5 ~ 2.5 voxels in radius). Stereological estimates of glomerulus number, (considered the gold standard histological approach), were available for both datasets for comparison. Based on the results from both 2D (HDoG-2D) and 3D (HDoG) experiments, we conclude that the HDoG detector is able to automatically and accurately segment small blobs.

In summary, the contributions of this research were three- fold: (1) We develop a validated efficient 3D blob detector (HDoG) using local convexity, intensity and shape information; (2) In HDoG, we employ the DoG to approximate LoG convolution to successfully address the computational challenges of blob detection from 3D images; and (3) We develop the two novel 3D shape features of regional blobness and regional flatness to assist 3D blob detection. Fast calculation of the features is provided. The remainder of the paper is organized as follows: Section II discusses the acquisition of the image data. Section III describes our proposed HDoG in detail, and Section IV demonstrates comparison experiments on 2D medical images and validation experiments on 3D synthetic data. Two 3D real kidney MR image datasets of different image sizes are evaluated in Section V, followed by the discussion of the computational performance and novel regional features of HDoG. The conclusions are drawn in Section VI.

IMAGE DATA ACQUISITION

Five image datasets, including two sets of 2D images, one set of 3D synthetic images, and two sets of 3D MR kidney images, were used in this paper to test the performance of the proposed algorithm

A. 2D Pathological and Fluorescent Microscopic Images

15 pathological images with image size 600×800 were obtained from and 200 synthetic fluorescent microscopic images with image size 256×256 were obtained from.

B. 3D Synthetic Image Data

Based on the kidney glomerulus distribution from MRI, we rendered 240 simulated scenarios with 12 different sizes and 20 different quantities of Gaussian blobs. For each scenario, ten 3D images were randomly generated, yielding a total of 2400 3D images. Specifically, a 3D Gaussian function was used to generate blobs with size controlled by Gaussian parameterσ. The radius of the blob was estimated by 2 × σ +0.5 voxels by observation. Then N identical blobs at size were randomly spread and stacked in a 3D image with matrix size 256×256 × 256. The 240 scenarios were simulated based on the blob size σ ranging from 0.5 to 6 with step size 0.5, and the number of blobs N ranging from 1,000 to 96,000 with step size 5,000. As shown in Fig. 1, when the size and the number of blobs were small, the blobs were sparse and well separated from each other (e.g., Fig. 1(A)). When the size and the number of blobs was large, the blobs were dense and were highly likely to be clumped together (e.g., Fig. 1(D)).

Fig. 1.

Slice 100 (of 256) from Simulated 3D Blob Images with Different Parameter Settings ranging from least dense to the densest scenario: (A) 3D Blob Image with o=1 and N=1,000. (B) 3D Blob Image with o=6 and N=1,000. (C) 3D Blob Image with o=1 and N=96,000. (D) 3D Blob Image with o=6 and N=96,000.

C. 3D Rat and Human Image Data

1). Rat kidney data

All animal experiments were approved by the Institutional Animal Care and Use Committee. Six rat kidney glomeruli were magnetically labeled using the cationic ferritin (CF) nanoparticle, derived from horse spleen ferritin (Sigma Aldrich, St. Louis, MO). CF is a natural nanoparticle proposed as a nontoxic contrast agent for renal imaging. CF was synthesized by the method in with some modification described in . Male Sprague Dawley Rats (215–245 g) were anesthetized using inhaled isoflurane and given three intravenous bolus injections of CF, (5.75 mg/100 g total in phosphate buffered saline), spaced 1.5 h apart. The rats were then euthanized under anesthesia by transcardial perfusion of saline followed by 10% formalin. Kidneys were removed and stored and imaged in glutaraldehyde. MRI was performed using a Varian (Agilent, Palo Alto, CA) 800 MHz NMR with an 89 mm bore using a DOTY three-axis imaging gradient set. A 3D gradient-echo image was acquired with TE/TR=7/40 ms and a resolution of 62 × 62 × 78 μm. 3D images were reconstructed with image size 256×256×256.

2). Human kidney data

Three human donor kidneys, not suitable for transplant, were obtained from the International Institute for the Advancement of Medicine (IIAM, Edison, NJ, USA). All kidneys were procured by the organization with informed consent and with the approval of the Internal Review Board. Kidneys were perfused at cross-clamp with saline and University of Wisconsin preservative solution, removed, and stored in the solution on ice for transfer. They were received on site within 24 hours. Kidneys were first perfused with 120 ml phosphate buffered saline (PBS) and glomeruli were labeled by intravenous injection of 300 mg of CF. The kidneys were again flushed with PBS via the renal artery to clear intravascular CF, fixed with 10% neutral buffered formalin, and stored in formalin for at least 24 hours. The kidneys were removed and washed three times in 500 ml PBS over 24 hours prior to MRI. They were imaged in a sealed plastic container in PBS using a Bruker 7T/35 MRI scanner with a 72 mm quadrature transmit/receive radiofrequency coil (Bruker, Billerica, MA). Kidneys were imaged with a 3D gradient- recalled echo (GRE) pulse sequence with TE/TR=29/30 ms and a 117 μm3 isotropic resolution . The 3 human kidney 3D MR images were reconstructed with image size 512×512×896.

HESSIAN-BASED DIFFERENCE OF GAUSSIAN DETECTOR

The proposed HDoG detector has four-phase: (1) DoG transformation, (2) Hessian pre-segmentation, (3) local feature extraction, and (4) post-pruning for final identification. Each phase is discussed below.

D.Phase I: DoG approximation of LoG transformation

A blob is a region in an image that is darker (or brighter) than its surroundings. The convexity of the intensity function within a blob is consistent. However, image noise may lead to discontinuities in the convexity of the intensity function. The noise must be smoothed out so the asymptotic convex (or concave) shape of the blobs is highlighted. The DoG is chosen for this purpose because (1) it smooths the image noise by enhancing objects at the selected scale , (2) it is a fast approximation of the LoG filter highlighting blob structure , and (3) compared to LoG, DoG is computationally efficient and preserves detection accuracy .

Let a 3D image be$f:R^2\to R$. The scale-space representation L(x,y,z;t) at point (x,y,z) , with scale parameter t, is the convolution of image f(x,y,z) with the Gaussian kernel G(x,y,z;t) :

$$L\left(x,y,z;t\right)=G\left(x,y,z;t\right)\ast f\left(x,y,z\right)$$

Here * is the convolution operator Gaussian kernel:

${1/\left(2\pi t^2\right)}^{3/2}{e}^{-\left(x^2+y^2+z^2\right)/\left(2t^2\right)}$. The Laplacian of L(x,y,z;t) is:

$${\nabla }^{2}L\left(x,y,z;t\right)=L_{xx}+L_{yy}+L_{zz}$$

Since${\nabla }^{2}L\left(x,y,z;t\right)={\partial }_{t}L\left(x,y,z;t\right)/t$, we have:

$${\nabla }^{2}L\left(x,y,z;t\right)=\underset{\text{δ}t\to 0}{lim}\frac{L\left(x,y,z;t+\delta t\right)-L\left(x,y,z,;t\right)}{t\delta t}$$

$$\approx f(x,y,z)*\frac{G(x,y,z;t+\delta t)-G(x,y,z;t)}{t\delta t}$$

To locate an optimal scale for the blobs, similar to , we add γ-normalization to the LoG detector as the normalized LoG detector$t^{\gamma }{\nabla }^{2}L\left(x,y,z;t\right)$. Thus, the approximation of normalized LoG is:

$$Do{G}_{nor}\left(x,y,z;t\right)=t^{\gamma -1}f\left(x,y,z\right)\ast \frac{\left(G\left(x,y,z;t+\delta t\right)-G\left(x,y,z;t\right)\right)}{\delta t}$$

Here γ is introduced to automatically determine the optimum scale for the blobs. It is usually set to two. For details on tuning γ, refer to.

The major disadvantage of the LoG kernel in computational efficiency is that the kernel is not separable (cannot be decomposed to multiple one dimensional kernels). For a 3D image with matrix N1 × N2 × N3 , the kernel size is r1 × r2 × r3 (e.g., 9 × 9 × 9), the convolution of the LoG kernel has complexity O (N₁ N₂ N₃ r₁r₂r₃)Gaussian kernel is separable, that is, the 3D image can be convolved by three 1D Gaussian kernels, the complexity of DoG is O (N₁ N₂ N₃ ×(r₁ +r₂ +r₃ )). DoG reduces the complexity of LoG degree of the by the power kernel size.

During the normalized DoG transformation, a dark blob is converted to a bright blob and vice versa. To avoid confusion, we subsequently refer to the normalized DoG blob as the “transformed blob”. The following discussion focuses on identifying the dark blobs that are transformed into bright blobs, (called “transformed bright blobs”),| but the same process applies to identifying bright blobs (transformed into dark blobs) for other applications. This is demonstrated by experimental validation in Section IV.A.2). This normalized DoG transformation underlies the Hessian analysis for the pre-segmentation.

E. Phase II: Hessian pre-segmentation

If the image is smoothed by the normalized DoG, for a voxel (x,y,z) in the normalized DoG image DoG_nor (x, y, z;t) at scale , the Hessian matrix is:

$$H\left(Do{G}_{nor}\left(x,y,z;t\right)\right)=\left[\begin{array}{ccc}\frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial x^2}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial x\partial y}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial x\partial z}\\ \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial x\partial y}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial y^2}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial y\partial z}\\ \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial x\partial z}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial y\partial z}& \frac{{\partial }^{2}Do{G}_{nor}\left(x,y,z;t\right)}{\partial z^2}\end{array}\right]$$

Since the transformed bright blob is shaped as a concave ellipse, where brightness fades isotropically, every voxel within the blob is a concave ellipse. Therefore, we identify the transformed bright blobs using the following proposition.

Proposition 1. In a normalized DoG-transformed 3D image, every voxel of a transformed bright blob has a negative definite Hessian matrix.

Proof. provides a detailed discussion of the relationship between the eigenvalues and geometric shape. Specifically, if voxel (x,y,z) is concave elliptical, all the eigenvalues of H (DoG_nor (x, y, z;t)) are negative, that is, λ1,λ 2, λ₃ < 0 Since each voxel in the transformed bright blob is concave elliptical, its eigenvalues are all negative and the Hessian matrix of the voxel is negative definite.

Proposition 1 provides a necessary but not sufficient property that a voxel in a transformed bright blob must satisfy. That is, if a voxel resides in a transformed bright blob, the Hessian matrix of the voxel is negative definite. However, not every voxel containing a negative definite Hessian matrix must be within a transformed bright blob. This proposition ensures the construction of the blob candidate set, (see Definition 1), which is a superset of the true blobs and some falsely identified blobs.

Definition 1. A blob candidate T in normalized DoG space is a 6-connected component of set $U=\left\{\left(x,y,z\right)|\left(x,y,z\right)\in Do{G}_{nor}\left(x,y,z;t\right),I\left(x,y,z;t\right)=1\right\},$whereI (x, y, z;t) is the binary indicator such that if the voxel (x, y, z) has a negative definite Hessian matrix, then I (x, y, z; t ) = 1 ; otherwise, I (x, y, z;t ) = 0.

Fast Hessian analysis: As a more computationally efficient alternative to computing the eigenvalues λ₁, λ₂, λ₃ of H (DoG_nor (x, y, z;t)), the definiteness of the Hessian matrix can be assessed by the three leading principal minors D₁, D₂ and D3 . The Hessian matrix is negative definite if and only if D₁ < 0, D₂ > 0 and D₃ >0 . As a result, from Proposition 1 and the Definition 1, we can highlight the voxels belonging to transformed bright blobs using the three leading principal minors.

Theoretically, the candidate set will contain all the true blobs and some false ones. Next, we derive regional features (Phase III) from the superset and conduct post pruning (Phase IV) to remove the false blobs.

F. Phase III: Extracting 3D regional features

The Hessian describes the second order ellipsoid of the blob structure and the absolute eigenvalues λ_1, λ_2, λ₃ of the Hessian denote the semi-axis lengths of the ellipsoid. Reference introduced two classic geometric features in blob detection: the R_B the likelihood of blobness, and S_B, flatness (the second- Order structureness). Based on the assumption that |λ₁|≤|λ₂|≤|λ₃|, these are defined as:

$$R_B=\frac{\left|{\lambda }_1{\lambda }_2{\lambda }_3\right|}{\max {\left(\left|{\lambda }_1{\lambda }_2\right|,\left|{\lambda }_2{\lambda }_3\right|,\left|{\lambda }_1{\lambda }_3\right|\right)}^{\frac{3}{2}}}$$

$$S_B=\sqrt{{\lambda }_1^2+{\lambda }_2^2+{\lambda }_3^2}$$

Where 0 <R_B≤ 1 for an idealized blob, that is |λ₁|=|λ₂|=|λ₃|, R_B = 1.0 < S_B ≤ ∞. The higher S_B is the more salient the blob is against the local background.

Fast Regional Blobness Extraction:

To calculate RB , the eigenvalues λ1 , λ2 , λ3 of the Hessian matrix H (DoGnor(x,y,z;t))are computed for each voxel, requiring intensive computations. To address this concern, we propose regional blobness feature motivated by the Hessian-affine detector in .

For the Hessian matrix of each voxel, defined in Eq.(5), the regional Hessian matrix of the DoG-transformed (smoothed) image is defined as:

$$H_T\left(Do{G}_{nor}(x,y,z;t)\right)={\displaystyle \sum _{(x,y,z)\in T}\left[\begin{array}{ccc}\frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial x^2}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial x\partial y}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial x\partial z}\\ \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial x\partial y}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial y^2}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial y\partial z}\\ \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial x\partial z}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial y\partial z}& \frac{{\partial }^{2}Do{G}_{nor}(x,y,z;t)}{\partial z^2}\end{array}\right]}$$

Eq. (8) is the summed Hessian matrices of voxels within the candidate region T. This regional Hessian matrix describes the candidate blob. We let λ ₁´, λ ₂´, λ ₃´ be the eigenvalues of the or regional Hessian matrix, and Eq.(6) can be rewritten as:

$$R_{B_T}=\frac{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}{\max {\left(\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|,\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|,\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|\right)}^{\frac{3}{2}}}$$

By substituting the denominator (maximum) with $\frac{\left(\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|+\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|+\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|\right)}{3}$ (average),

$$R_{B_T\prime }=\frac{3^{\frac{3}{2}}\times \left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}{{\left(\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|+\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|+\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|\right)}^{\frac{3}{2}}}$$

The value of R_T is calculated by

$$R_T={\left(R_{B_{T\prime }}\right)}^{\frac{2}{3}}=\frac{3\times {\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|+\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|+\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}$$

Proposition 2. RT retains the property of RB_T that 0<R_T≤ 1.

Proof. Since:

$$R_T=\frac{3\times {\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|+\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|+\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}=\frac{3}{\frac{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}+\frac{\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}+\frac{\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}}$$

Based on Arithmetic-Geometric Mean Inequality, we have:

$$\frac{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}+\frac{\left|{\lambda }_1^{\prime }{\lambda }_3^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}+\frac{\left|{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^{\frac{2}{3}}}\ge 3\sqrt[3]{\frac{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^2}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^2}}$$

Therefore, $R_T\le 3/(3\sqrt[3]{\frac{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^2}{{\left|{\lambda }_1^{\prime }{\lambda }_2^{\prime }{\lambda }_3^{\prime }\right|}^2}})=1$, we conclude that RT retains the property 0<R_T≤ 1.

The use of RT improves the efficiency of computation because we can compute the principal minors rather than the eigenvalues. Since the Hessian matrix is negative definite in every voxel within a candidate blob, the regional Hessian matrix is negative definite and λ_1, λ_2, λ₃ <0. Thus,

$$R_T=\frac{3\times {\left|det(H_T)\right|}^{\frac{2}{3}}}{pm(H_T)}$$

where pm(H_T)=λ₁^´λ₂^´+ λ₂^´λ₃^´+ λ₁^´λ₂^´, using pm(H_T) can be computed by three 2×2 principal minors of H_T

$${\lambda }_1^{\prime }{\lambda }_2^{\prime }+{\lambda }_2^{\prime }{\lambda }_3^{\prime }+{\lambda }_1^{\prime }{\lambda }_3^{\prime }=\det \left(\begin{array}{cc}{H}_T^{1,1}& H_T^{1,2}\\ H_T^{2,1}& H_T^{2,2}\end{array}÷\right)+\det \left(\begin{array}{cc}{H}_T^{2,2}& H_T^{2,3}\\ H_T^{3,2}& H_T^{3,3}\end{array}÷\right)+\det \left(\begin{array}{cc}{H}_T^{1,1}& H_T^{1,3}\\ H_T^{3,1}& H_T^{3,3}\end{array}÷\right)$$

Fast Regional Flatness Extraction:

We second-order distribution of derivatives in the region of the define regional flatness as:

$$S_T=\sqrt{\lambda {\prime }_1^2+\lambda {\prime }_2^2+\lambda {\prime }_3^2}$$

or

$$S_T=\sqrt{{({\lambda }_1^{\prime }+{\lambda }_2^{\prime }+{\lambda }_3^{\prime })}^2-2({\lambda }_1^{\prime }{\lambda }_2^{\prime }+{\lambda }_2^{\prime }{\lambda }_3^{\prime }+{\lambda }_1^{\prime }{\lambda }_3^{\prime })}=\sqrt{tr{(H_T)}^2-2\times pm(H_T)}$$

R_T and S_T reduce the computational cost in Eqs. (6) and (7) significantly. This is because and only calculate trace tr(H_T), determinant det (H_T) and 2×2 principal minors pm (H_T) . Additional computation solve the characteristic polynomial: ${(\lambda \text{'})}^3-tr(H_t){(\lambda \text{'})}^2+pm(H_T)\lambda -\det (H_T)=0$(expanded from det$(HT-\lambda \text{'}I)=0$) to retain the eigenvalues of the Hessian HT . Secondly, R_T and S_T are calculated from the regional Hessian matrix for each blob candidate region every voxel. In this research, blob candidates v.s. voxels is 90K v.s.16777K in rat MR images and 1M v.s. 235M in human MR images.

G. Phase IV: Auto post-pruning

Other thanR_T and S_T the third feature R_T and S_T the average intensity of region T, (commonly used in the literature as post pruning thresholding feature) , is computed. We then input these three features into an unsupervised variational Bayesian Gaussian Mixture Model (VBGMM) to remove false positive identifications from the blob candidate set. The VBGMM is more robust than maximum likelihood Gaussian Mixture Models because it treats parameters like mean vector and variance-covariance matrix in Gaussian Mixtures Models as distributions instead of deterministic values and uses hyper parameters to control them. This helps avoid the singularity issues faced by the maximum likelihood Gaussian mixture models. In addition, unlike other pruning algorithms which are thresholding based, the VBGMM requires no parameter tuning. The blob candidate regions form a multivariate Gaussian mixture and therefore are clustered into blob regions and non-blob regions using Bayesian inference.

VALIDATION EXPERIMENTS

In the literature, ground truth data are usually provided in the form of the coordinates of the blob centers. Following , a blob candidate i is true positive if and only if its center is in a detection pair (i,j) for which the corresponding (nearest) ground truth center has not been paired, and their Euclidean distance D_ij is within the scope of certain diameter d. Therefore the number of true positives (TP) is calculated by Eq. (16). Precision, recall, and F-score are calculated by Eqs. (17), (18), and (19), respectively:

$$\begin{gathered} TP=\min \left\{\#\{(i,j):{\min }_{j=1}^m{D}_{ij}\le d\},\#\{(i,j):{\min }_{i=1}^n{D}_{ij}\le d\}\right\} \\ precision=TP/n \\ recall=TP/m \\ F-score=2\times \frac{precision\times recall}{\left(precision+recall\right)} \end{gathered}$$

where m is the number of ground truth points and n is the number of blob candidates. As in , is a diameter threshold and can be set to a positive value(0,+∞) If d is small, fewer blob candidates will be counted because the distance between the blob candidate centroid and the ground truth point must be small. If d is large, more blob candidates will be counted because the threshold distance is relaxed. Ideally, the upper bound of d should be set to no more than the diameter of a blob, since if d is too large a neighborhood blob will be miscounted. Since the blob structures may have irregular shapes, the upper bound of d can be set marginally higher than the estimated diameter to take this into account.

H.Validation tests on 2D images

To assess the performance of HDoG, we performed initial tests on 2D images using three evaluation metrics: precision, recall, and F-score. Three state-of-art detectors, LoG, gLoG and HLoG, were studied for comparison.

For 2D images, the 2D versions of the regional Hessian matrix H_T, the regional blobness R_T, and the regional flatness S_T are used in :

$$\begin{gathered} H_{T,2D}={\displaystyle \sum _{(x,y)\in T}\left[\begin{array}{cc}\frac{{\partial }^{2}Do{G}_{nor}(x,y;t)}{\partial x^2}& \frac{{\partial }^{2}Do{G}_{nor}(x,y;t)}{\partial x\partial y}\\ \frac{{\partial }^{2}Do{G}_{nor}(x,y;t)}{\partial x\partial y}& \frac{{\partial }^{2}Do{G}_{nor}(x,y;t)}{\partial y^2}\end{array}\right]}, \\ {R}_{T,2D}=\frac{2}{\frac{{\lambda }_{1,2D}^{\prime }}{{\lambda }_{2,2D}^{\prime }}+\frac{{\lambda }_{2,2D}^{\prime }}{{\lambda }_{1,2D}^{\prime }}}=\frac{2{\lambda }_{1,2D}^{\prime }{\lambda }_{2,2D}^{\prime }}{{\left({\lambda }_{1,2D}^{\prime }+{\lambda }_{2,2D}^{\prime }\right)}^2-2{\lambda }_{1,2D}^{\prime }{\lambda }_{2,2D}^{\prime }}, \\ {S}_{T,2D}=\sqrt{{\left({\lambda }_{1,2D}^{\prime }+{\lambda }_{2,2D}^{\prime }\right)}^2-2{\lambda }_{1,2D}^{\prime }{\lambda }_{2,2D}^{\prime }} \end{gathered}$$

Where λ’_1,2D are eigenvalues of λ’_2,2D.are eigenvalues of H_T,_2D

1). Dataset 1: 2D pathological images

15 pathological images were used to compare HDoG with the LoG, gLoG and HLoG methods. Since the average blob candidate diameter is 13.46 pixels, diameter threshold d was varied from 0 to 16 to reflect the distance of two adjacent blobs. F-scores are reported in Table I.

TABLE I.

VALIDATION RESULTS (F-SCORE) ON 15 2D PATHOLOGIC IMAGES

d	HDoG F-score	LoG F-score	HDoG vs. LoG p-value	gLoG F-score	HDoG vs. gLoG p-value	HLoG F-score	HDoG vs. HLoG p-value
0	0.049	0.041	0.051=	0.046	0.496=	0.042	0.071=
1	0.197	0.172	0.008+	0.193	0.696=	0.184	0.131=
2	0.405	0.348	0.000+	0.402	0.858=	0.385	0.154=
3	0.623	0.531	0.000+	0.616	0.708=	0.609	0.391=
4	0.738	0.634	0.000+	0.737	0.953=	0.731	0.648=
5	0.81	0.703	0.000+	0.816	0.687=	0.811	0.923=
6	0.847	0.738	0.000+	0.849	0.871=	0.849	0.842=
7	0.868	0.76	0.000+	0.867	0.877=	0.87	0.789=
8	0.885	0.777	0.000+	0.88	0.579=	0.886	0.860=
9	0.894	0.79	0.000+	0.891	0.702=	0.895	0.772=
10	0.901	0.801	0.000+	0.897	0.642=	0.904	0.544=
11	0.906	0.807	0.000+	0.903	0.643=	0.909	0.561=
12	0.911	0.813	0.000+	0.907	0.596=	0.915	0.512=
13	0.918	0.82	0.000+	0.912	0.419=	0.922	0.497=
14	0.923	0.827	0.000+	0.917	0.423=	0.928	0.370=
15	0.927	0.838	0.000+	0.921	0.456=	0.934	0.300=
16	0.931	0.849	0.000+	0.927	0.541=	0.938	0.322=

The normalizing factor γ =2 based on prior experiments. Detailed of the parameter setting please refer to ). Paired T-tests were performed at a significance level of 0.05. Symbols in cell means: + statistically outperformed; = Statistically Comparable; - Statistically Underperformed

As shown in Table I, the average F-score for HDoG was higher than for LoG and gLoG, but marginally lower than for HLoG. The statistical difference between HDoG and LoG was significant (d>0, p<0.05, two-sample t-test). We thus conclude that HDoG statistically outperforms LoG. The F-score difference between HDoG and gLoG was not significant. Although the F-score of HDoG was lower than HLoG, the difference was not significant. We conclude that HDoG is statistically comparable HLoG. We also note that, even for the 2D images, gLoG needed 30 seconds per image and HDoG was 5 times faster than that of gLoG (6 seconds per image) on the same computational environment (Windows PC with Intel Xeon 2.0 GHz CPU and 32 GB of memory). The computation time of HLoG was 10 seconds per image.

2). Dataset 2: 2D fluoroscopic images

The second 2D validation experiment used 200 2D fluorescent microscopy images. Additional noise was added to the images to test the robustness of the detectors . Unlike Dataset 1, these images contained bright blobs rather than dark blobs. Therefore, the data were converted into images containing small dark structures using . (We Assume varied from 0 to 1, or we would have to standardize to the range). The parameter settings for LoG and gLoG were as suggested in . Similarly to Dataset 1, we varied the parameter d from 0 to 12 (the estimated blob candidate diameter is ~ 9.1 pixels). The F-score results are summarized in Table II. (Precision and recall are in Supplementary).

TABLE II.

VALIDATION RESULTS (F-SCORE) ON 200 2D FLUORESCENT IMAGES

d	HDoG F-score	LoG F-score	HDoG vs. LoG p-value	gLoG F-score	HDoG vs. gLoG p-value	HLoG F-score	HDoG vs. HLoG p-value
0	0.07	0.075	0.014-	0.077	0.009-	0.105	0.233=
1	0.3	0.28	0.000+	0.317	0.009-	0.395	0.350=
2	0.586	0.471	0.000+	0.593	0.431=	0.696	0.283=
3	0.829	0.579	0.000+	0.796	0.002+	0.867	0.685=
4	0.89	0.61	0.000+	0.834	0.000+	0.887	0.741=
5	0.897	0.624	0.000+	0.837	0.000+	0.89	0.742=
6	0.898	0.628	0.000+	0.838	0.000+	0.89	0.995=
7	0.898	0.633	0.000+	0.838	0.000+	0.89	0.700=
8	0.898	0.642	0.000+	0.838	0.000+	0.89	0.475=
9	0.899	0.654	0.000+	0.838	0.000+	0.89	0.526=
10	0.899	0.669	0.000+	0.838	0.000+	0.89	0.323=
11	0.899	0.689	0.000+	0.838	0.000+	0.89	0.321=
12	0.9	0.713	0.000+	0.838	0.000+	0.891	0.250=

The normalizing factor γ =1 based on prior experiments. Details of the parameter settings are described in ). Paired T-tests were performed at a significance level of 0.05. + Statistically Outperformed; = Statistically Comparable; - Statistically Underperformed

For smaller blobs in this dataset, HDoG statistically outperformed LoG and gLoG on the F-score measure (d>2), and was statistically comparable to HLoG. We note that HDoG does not perform as well as LoG and gLoG when d is extremely tight (d≤2). The reason is that HDoG naturally generates blob regions but not the centroid of the blobs. It is expected the extrema (from HDoG) is not perfectly spot on the true centroid. When d is small, this difference is more apparent. As for the computing time, the average processing time for HDoG was 0.9 second/per image, 1.2 second/ per image for HLoG, 10 second/per image for gLoG, using a Windows PC with Intel Xeon 2.0 GHz CPU and 32 GB of memory.

In summary, initial tests with both 2D datasets showed that HDoG-2D has the potential for accurate blob detection in 3D images. It had statistically similar or better performance compared to the 2D detectors from the literature, but was more computationally efficient. This advantage will be more obvious with the larger sized 3D images.

I. Validation tests on 3D synthetic imaging data

We further explored how well the HDoG segments blobs in 3D images. 240 scenarios were tested to evaluate the performance of HDoG. For each scenario, the average F-score of the 10 images was calculated. In this set of experiment, since the blobs were generated by regular Gaussian kernels, to calculate the F-score, the evaluation parameter d is set to be the diameter of the blobs i.e. d=σ+1. Results are shown in the contour plot of Fig. 2. As the blob sizes (σ) increased, the F-score decreased. As the number of blobs (N) increased, the F-score also decreased. This may reflect that the likelihood of blobs touching (overlapping) increases, leading to a deteriorated performance in segmentation. One special case was observed when σ=0.5, with a blob of diameter 3, since radius is 2σ+1, and N=1000 or 6000. This may be explained by the blob intensity relative to imaging noise. Detailed numbers for each scenario are listed in Supplementary.

Fig. 2.

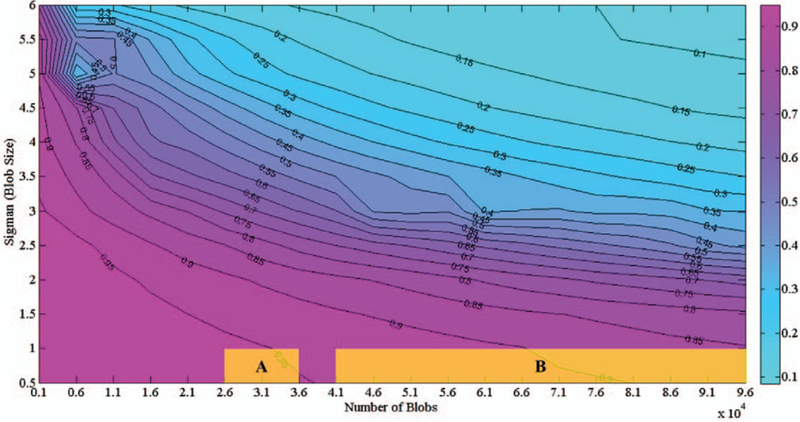
Contour Plot of F-Scores on Simulated 3D Images with Different Parameter Settings. In terms of blob size and quantity, the yellow shadow area A shows the scenarios of glomerulus detection on rat kidney images, and yellow shadow area B shows scenarios for glomerulus detection in human kidney images in our cases (based on the estimation of image size 256 × 256 × 256)

As seen in Fig. 2, when the blob size varies from 0.5 to 3, (with diameter ranges from 3 to 13), and the number of blobs ranges from 1000 to about 40,000, the F-score can be 0.95 or higher. When the blobs are small and sparse, imaging properties such as size, convexity, and intensity distribution may be well preserved, leading to more accurate detection. When the blob size was above 5.5 (diameter 23 and higher) and the number of blobs was 81,000 and higher, the F-score was lower than 0.1. This is because a large number of blobs were stacked, as shown in Fig. 1(D). We conclude that HDoG performs well in detecting small, and even tiny blobs. When the blob size was small, even with a large number (>95000) of blobs, an F-score of 0.85 can still be achieved. In the present application of segmenting glomeruli from 3D kidney MR image, where the size of glomeruli is small and the count is high, HDoG should be useful to identify the glomeruli for clinical applications. In the next section, we explore the application of HDoG on one rat kidney dataset and one human kidney dataset. The scenarios of the rat kidney data can be mapped to area “A” highlighted in Fig. 2, and the scenarios of the human kidney data can be mapped to area “B” highlighted in Fig.2.

GLOMERULUS SEGMENTATION USING HDoG

In this section, the applicability of HDoG to segmenting kidney glomeruli from MRI is studied. We conducted experiments on rat and human kidney 3D MR images separately. Clinically, there are three major differences between the healthy rat and human kidney that affect glomerular morphology: 1) Human kidneys contain many more glomeruli than rat kidney (200,000–2,000,000 compared to 20,000 – 40,000, in our simulation, we simulated the cases of 700,000 – 1,500,000 glomeruli for human comparing to 26,000 – 36,000 for rat). 2) Glomeruli in humans are typically larger than those of the rat, and 3) The human kidney comprises many lobes, each of which contains a distinct set of glomeruli, nephrons, and medullary region, while the rat kidney contains only one. Despite these structural differences and the difference in size, rat models have been essential to understanding human disease. Two notable models are the spontaneously hypertensive rat (SHR) model of human hypertension and the puromycin-induced model of focal and segmental glomerulosclerosis . Rat models provide a critical window into the direct correlation between the microstructural bases of the pathophysiology of disease, which is typically impossible to observe in humans. Thus, both rat and human studies are critical to translation of these MRI techniques to the clinic

Two sets of real data were studied: six CF-labeled 3D MR images of rat kidneys and three CF-labeled 3D MR images of human kidneys. Since there are no labeled blobs (glomeruli) for those empirical MR images, the blob count obtained by HDoG is compared with that obtained using a manual acid maceration method and the disector-fractionator stereological method . Both methods are established histological techniques for estimating glomerular number.

J. Dataset 1: six 3D rat kidney MR images

Table III shows the glomerular counts obtained with each method (HDoG, acid maceration, and disector-fractionator stereology) for the six rat kidneys.

TABLE III.

GLOMERULUS COUNTS FOR SIX RAT KIDNEYS USING THE HDOG, ACID MACERATION, AND STEREOLOGY METHODS

Rat	Acid Maceration	Stereology	HDoG	Time (seconds)
CF1	27,504	34,504	29,484	268
CF2	31,190	35,421	34,460	294
CF3	28,944	24,156	27,051	242
CF4	31,075	-	35,296	243
CF5	33,321	-	31,196	237
CF6	31,478	-	35,248	242
Avg	30,585	31,360	32,122.5	255
Std	2,053	6,256	3131.6	20

γ =2, Intel Xeon 2.0 GHz CPU and 32 GB of memory. Only 3 CF rats were counted by stereology

For this experiment we have three stereological counts missing. Although stereology is most accurate, it is extremely expensive and time-consuming to perform. For this reason, we performed stereology in three rats as published in . Acid maceration is more commonly used, but is less accurate. Therefore we use them both for comparison. From Table III, we observed that HDoG consistently identified glomeruli in all six kidneys with reasonable computation times (<5 min). Although there were some differences between the glomerular counts, the three methods generally agreed well. Fig. 3 shows the segmentation results on representative axial view slices of the six rats, where slice 100 (of 256) is shown for rats CF1, CF2, and CF3, and slice 150 (of 256) is shown for rats CF4, CF5, and CF6. From the figure, we see the glomerular size is very small (radius is less than 2 voxel) and the most glomeruli were identified and contoured in green. Ideally, with all the blobs being Gaussian blobs, the detection capability of HDoG can reach up to about 0.95 in F-score as the region A in Fig. 2 (blob number ranging 26,000 to 36,000, and size σ<1). Fig.3 (M) and (N) are a sample of visually checking on the segmentation results. After comparing count numbers, visually checking the accuracy and referring to the scenarios in Fig. 2 A, we concluded that HDoG can automatically identify glomeruli in rat MR images.

Fig. 3.

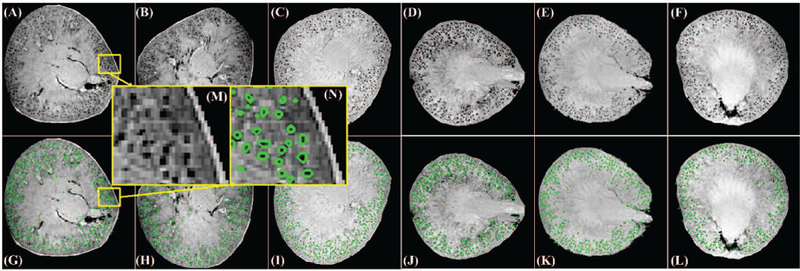
Glomerular segmentation results from 3D MR images of rat kidneys (selected slices presented). (A-C) Slice 100 for rats CF1, CF2, and CF3. (D- F) Slice 150 for rats CF4, CF5, and CF6. (G-I) segmentation results for (A- C), respectively. Identified glomeruli are contoured in green. (J-L) segmentation results for (D-F), respectively, where identified glomeruli are contoured in green. (M) is the zoomed-in region from (A) while (N) is the segmentation result of (M).

K. Dataset 2: three 3D human kidney MR images

We validated the MRI-based glomerular counts using the physical dissector/fractionator stereological method described by Cullen-McEwen et al. .We applied the HDoG algorithm to each human 3D MR image using the same platform as for the rats. The results are shown in Table IV.

TABLE IV.

GLOMERULUS COUNTS FOR THREE HUMAN KIDNEYS USING THE HDOG AND STEREOLOGY TECHNIQUES

			Time (seconds)
Human	Stereology	HDoG	DoG & Feature Extraction	VBGMM		Total
CF1	1,130,000	1,242,008	942	12,375		13,317
CF2	740,000	711,397	935	2,366		3,301
CF3	1,460,000	1,370,095	1,072	2,088		3,160
Avg	1,110,000	1,107,833	983	5610		6593
Std	360,416	349,246	77	5861		5824

γ=2, Intel Xeon 2.0 GHz CPU and 32 GB of memory.

From Table IV, HDoG consistently counted glomeruli in all three kidneys with reasonable computing times (<1 h for CF2 and CF3, <4h for CF1). We again observed discrepancies between the glomerular counts, but our histology experts confirmed that the two methods generally agreed well. Fig. 4 shows the segmentation results on selected axial-view slices of the human kidneys. As seen on the figure, the glomeruli are very small (radius is less than 2 voxels), and almost all glomeruli were identified by HDoG, (contoured in green), and the image intensity distribution was inhomogeneous across slices. To illustrate the ability of HDoG to segment glomeruli in different regions, a top slice (slice 100/896) and a middle slice (slice 500/896) are shown. To map the scenarios in Fig.3, we converted the images from the matrix size 512×512×896 to 256×256×256, as a result, the relative glomerular quantities are reduced to the range of 41,000 ~ 96,000 to keep the blob density, of which the performance of HDoG could be around 0.85. Fig. 4 (M) and (N) show a sample of visually checking on the segmentation results from human kidney data. After comparing count numbers, visually checking the accuracy and referring to scenarios in Fig. 2 B, we concluded that the HDoG algorithm can automatically identify glomeruli in human MR images.

Fig. 4.

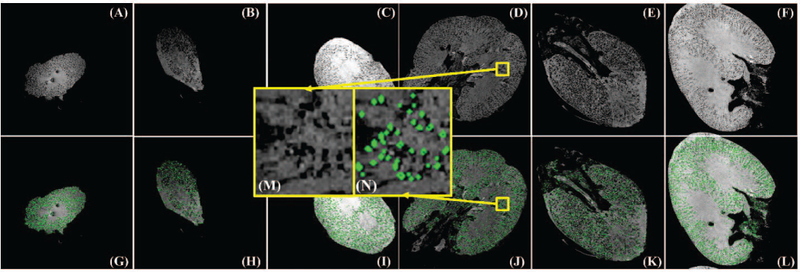
Glomerular segmentation results for 3D MR images of human kidneys (selected slices): (A-C) Original slice 100 for human CF1, CF2, and CF3 kidneys. (D-F) Slice 500 for human CF1, CF2, CF3 kidneys. (G-I) Identification results for (A-C), respectively, where identified glomeruli are contoured in green. (J-L) Identification results for (D-F), respectively, where identified glomeruli are contoured in green. (M) is the zoomed-in region from (D) while (N) is the segmentation result of (M).

L. Discussion of computation time

Since the computing time on the rat MRI is satisfactory (less than 5 minutes/image), we focus the discussion on the human MRI in this section. We observed that the glomerular segmentation of Human CF1 kidney took a much longer time than the other two. The time is mainly determined by the VBGMM clustering process. We contend the low contrast of CF1 vs. CF2 and CF3 may be the main factor leading to the longer time. To explore the variations of contrast among the three human kidneys, the intensity distribution of both glomeruli vs. the whole image is generated and shown in Fig. 5. The x-axis of the figure shows the bins of absolute value of the features, while the y-axis shows the frequency of the value bins. As seen, the difference of the distribution mode between the true glomeruli and the image (an indicator of contrast), highlighted in the figure, shows that CF1 had the lowest contrast while CF3 had the highest contrast. As a result, CF1 required a longer time for VBGMM for converged solution (12,375 seconds). While CF2 has medium contrast, it has comparable computing time (2366 seconds) to that of CF3 (2088 seconds). This can be explained by the fact that CF2 is from the hypertensive patient, having fewer perfused glomeruli and regions of vascular and glomerular sclerosis, coupled with glomerular hypertrophy in the perfused portions of the kidney . We suspect that variation in image contrast, either through normal physiological variation or image acquisition, will impact computation time.

Fig. 5.

Intensity frequency histograms of glomeruli against whole kidney image from: (A) Human CF1 (B) Human CF2 kidney (C) Human CF3. Frequency range was [0, 0.6] and the intensity range was [0, 1] in the figure. Vertical lines indicate the modes of the intensity distribution.

M. Discussion on novel regional features

A significant contributor to HDoG performance is the regional features used in the post-pruning process. Unlike the simulated data, the distributions of the three features in real data are shown in Fig. 6. Fig. 6 (A), (B) and (C) are the distributions for the true glomeruli, while the (D), (E) and (F) are the distributions for the non-glomeruli from CF1, CF2 and CF3 respectively. It is evident that the true glomerular cluster had distinct pattern on the distributions of average intensity (in blue), regional blobness (in red) and regional flatness (in green). We note the regional flatness and regional blobness of true glomeruli are higher in average value than those of non- glomeruli since the values fall more frequently at high value bins as shown in figure 6. The true-glomerular cluster also has a lower average intensity compared to the non-glomerular cluster (e.g., background) as expected. This can be explained that in the nanoparticle-enhanced MR imaging, a glomeruli is shown as a dark ellipse, which has higher blobness, higher flatness and lower intensity measures.

Fig. 6.

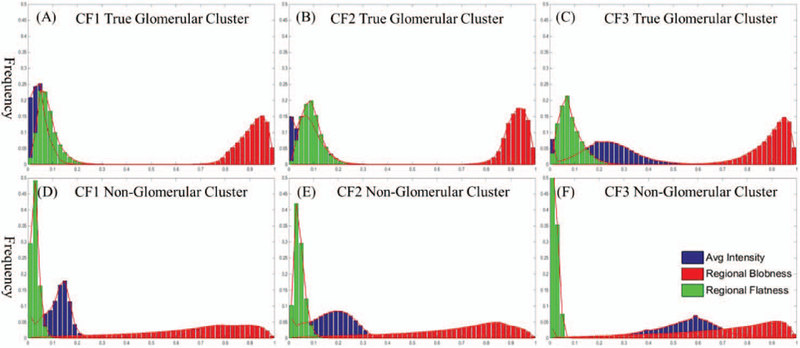
Frequency histograms of average intensity, regional blobness and regional flatness for human CF1, CF2 and CF3 kidney 3D MR images. (A)-(C) True glomerular cluster frequency histograms for human CF1, CF2 and CF3 respectively. (D)- (F) Non-glomerular cluster frequency histograms for human CF1, CF2 and CF3 respectively. Frequency range was [0, 0.5] and the x-axis range was [0, 1] in the Figure.

N. The limitations of HDoG

While promising, we do observe some limitations of HDoG. One of these is missed detection and a false positive detection problem (Fig. 7). For example, some glomeruli in the images may have shown discontinuity due to the imaging acquisition artifact. As in our Definition 1, a blob is a connected region; this discontinuity will lead to the missed detection even after applying the DoG transformation (smoothing process). A second possible reason for missed detection may arise from the post-pruning process, where some true glomeruli may be clustered into the non-glomerular group (False negatives, also known as a Type II error). A similar issue from the post-pruning unsupervised algorithm is the false positive (also known as Type I error).

Fig. 7.

Glomerular segmentation results for 3D MR images of Rat CF1 kidney and Human CF1 Kidney (part of the slice on Fig.5): (A) Part of Slice for Rat CF1. (B) Identification results for (A), where identified glomeruli centers are marked in red-cross. (C) Part of Slice for human CF1. (D) Identification results for (C), where identified glomeruli centers are marked in red-cross. Circles show the error of missed detection while the rectangles show the error of false positive detection

To minimize those error, some studies have attempted to segment blobs from 3D images using supervised learning algorithms, for example to detect breast lesions in ultrasound images , to identify coronary calcifications in CT scans , etc. However, the supervised learning algorithms require prior knowledge of labeled training blobs. Without prior knowledge being available, as the case in the glomerular segmentation, supervised classifiers do not apply. Though it is possible to have some glomeruli manually labeled as prior to support the use of supervised classifier, unfortunately, given the large number of blobs (~30k in the rat and 200,000–2,000,000 in the human kidney), and the small sized blobs (some even overlapped), manual labeling is labor intensive, and may not be accurate. Therefore, in this work we focused on unsupervised blob detectors. Future work may incorporate a semi-supervised algorithm requiring partial labeling as training. Additional prior knowledge inputs, (for example, glomeruli mostly lie on the area of kidney cortex), may help improve detection accuracy.

CONCLUSION

In this study, we propose a computationally efficient blob detector, called the Hessian-based difference of Gaussians (HDoG) detector, to detect 3D glomeruli, an instance of 3D blob from 3D kidney MR images. HDoG has two main improvements on computational efficiency. First, DoG is employed in the imaging smoothing process to address the computing challenge. Second, two novel 3D blob shape features with fast extractions are proposed. We have thoroughly validated the HDoG with blob detectors from literature in 2D image datasets. In addition, we test the performance of HDoG on 3D blob detection using 240 synthetic simulated 3D images. Last, two sets of kidney 3D MR images are studied. Experimental results indicate that HDoG can automatically and accurately count and label glomeruli in a reasonable time frame (<5 minutes per rat MRI; <4 hours per human MRI). To our knowledge, this is the first report of a robust, unsupervised technique to detect a magnetically labeled structure in both 2D and 3D images. We conclude HDoG may be a powerful preclinical or clinical tool to noninvasively detect molecular structures in medical images. It is noted that MR is of particular interest here as this research is motivated by the disease mechanism (kidney glomeruli). We want to highlight that our proposed HDoG is generalized algorithm that uses regional geometric information to detect small blobs. From this aspect, it has the potential to be applied to a wide range of imaging modalities such as CT, Ultrasound, Ophthalmic Photography, for small blob detection.