The Correspondence between Causal and Traditional Mediation Analysis: The Link is the Mediator by Treatment Interaction

Abstract

Mediation analysis is a methodology used to understand how and why behavioral phenomena occur. New mediation methods based on the potential outcomes framework are a seminal advancement for mediation analysis because they focus on the causal basis of mediation. Despite the importance of the potential outcomes framework in other fields, the methods are not well known in prevention and other disciplines. The interaction of a treatment (X) and a mediator (M) on an outcome variable (Y) is central to the potential outcomes framework for causal mediation analysis and provides a way to link traditional and modern causal mediation methods. As described in the paper, for a continuous mediator and outcome, if the XM interaction is zero, then potential outcomes estimators of the mediated effect are equal to the traditional model estimators. If the XM interaction is nonzero, the potential outcomes estimators correspond to simple direct and simple mediated contrasts for the treatment and the control groups in traditional mediation analysis. Links between traditional and causal mediation estimators clarify the meaning of potential outcomes framework mediation quantities. A simulation study demonstrates that testing for a XM interaction that is zero in the population can reduce power to detect mediated effects, and ignoring a nonzero XM interaction in the population can also reduce power to detect mediated effects in some situations. We recommend that prevention scientists incorporate evaluation of the XM interaction in their research.

Mediating variables are central to theory and applied research in prevention, psychology, epidemiology, and other disciplines because they elucidate how and why constructs are related (MacKinnon, Krull, & Lockwood, 2000). In this way, mediation analysis allows researchers to move beyond whether an effect occurs to ask detailed questions about the underlying mechanisms responsible for effects. In prevention research, mediating variables guide program development and are critical to evaluating how programs achieve or fail to achieve effects. A seminal recent development in mediation analysis is causal mediation methods based on the potential outcomes framework (Imai, Keele, & Tingley, 2010; Pearl 2001; VanderWeele, 2015). In epidemiology and biostatistics, the potential outcomes framework has been called revolutionary and a great step forward, because the framework provides methods to estimate causal quantities that are the focus of science (Chiolero, 2018; Glymour & Hamad, 2018; Hernán, 2018; Pearl, 2012, Pearl& MacKenzie, 2018). In general, prevention has been slow to adopt new causal methods with some exceptions (Imai, Keele, & Tingley 2010; Jo, 2008; Liu, Kuramoto, & Stuart, 2013; Pearl, 2014, Stuart, Bradshaw, & Leaf, 2015; Valeri & VanderWeele, 2013), at least in part because the links between the potential outcomes framework and traditional analysis have not been made explicit.

Strengths of the potential outcomes framework over the traditional model include the estimation of causal quantities rather than regression associations and clarification of the assumptions required for causal conclusions. For mediation, the potential outcomes framework clarifies the influence of confounding variables, the assumptions of mediation analysis, and the estimators required to assess mediated effects for persons receiving a treatment compared to persons not receiving a treatment. Often, these distinctions are not clear in traditional mediation analysis.

Much of the literature on modern causal mediation analysis implies that traditional and causal mediation methods represent very different approaches to investigating mediating mechanisms. The lack of clear links between traditional and causal mediation approaches hinders the adoption of modern mediation methods and causal analysis in general. In this article, we demonstrate the equivalence of traditional and potential outcomes framework models, specifically for the case of a randomized treatment and the single mediator model. In this case, the interaction of the treatment and the mediator, referred to as the XM interaction, provides the link between potential outcomes and traditional mediation models. The purpose of this paper is fourfold. First, we describe the traditional mediation model, the potential outcomes framework for mediation, and the correspondence between traditional and potential outcomes frameworks. Second, we describe differences in bias, empirical power, Type 1 error rates, and confidence interval coverage between the traditional and potential outcomes framework estimators of direct and mediated effects. Third, throughout the article we illustrate concepts by applying them to a real prevention study. Finally, we provide guidance on how to test for mediation when an XM interaction is hypothesized. The overall goal of the manuscript is to describe and demystify potential outcomes framework mediation methods by showing that for linear models, the causal estimators correspond to contrasts in traditional mediation analysis.

To help illustrate the methods, we use a prevention example from a randomized study of an anabolic steroid prevention program for high school football players, which we have simplified by using complete, individual-level, data and a single mediator model (see Goldberg et al., 2000 and MacKinnon et al., 2001 for more details about the study). The example describes analysis of a social norms mediator that was hypothesized to improve strength training self-efficacy. X is a binary intervention variable representing program and control, M is a continuous measure of the change in norms about resisting offers of anabolic steroid use, and Y is the change in self-efficacy for strength training. Norms were selected for intervention because of prior empirical and theoretical evidence for the importance of norm change as a cause of behavior change. The purpose of mediation analysis is to evaluate the causal effect of the intervention on change in strength training self-efficacy through its effect on change in norms.

Traditional Statistical Mediation Analysis

Statistical mediation analysis is traditionally conducted by using two of the following three equations (MacKinnon, 2008),

$$Y=i_{0Y,1}+cX+e_{Y,1}$$ (1)

$$Y=i_{0Y,2}+c^{\prime }X+bM+e_{Y,2}$$ (2)

$$M=i_{0M}+aX+e_M$$ (3)

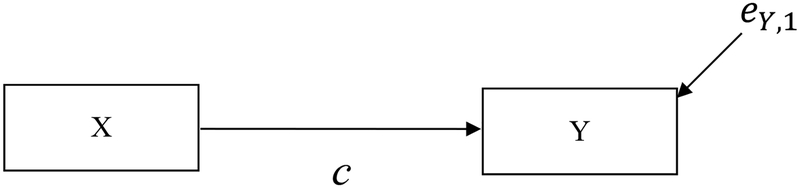
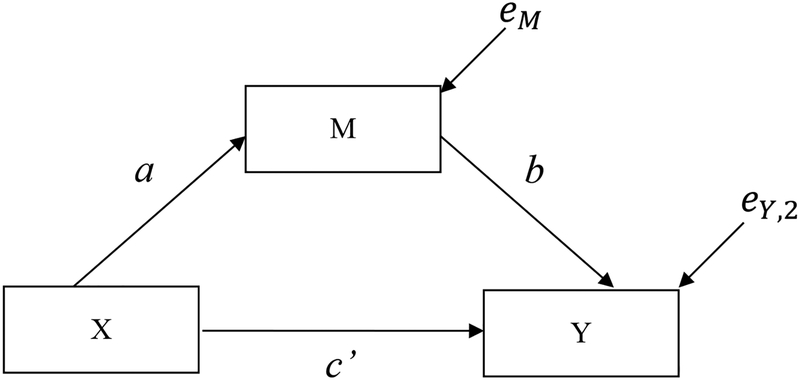
where Y is the dependent variable, M is the mediator, and X is the binary randomized independent variable. Note that Y and M are continuous variables and linearly related. The c coefficient represents the relation between X and Y (see Figure 1); the c’ coefficient represents the relation between X and Y, adjusted for M; the b coefficient represents the relation between M and Y adjusted for X; and the a coefficient represents the relation between X and M (see Figure 2). The regression residuals are e_Y,1, e_Y,2, and e_M, and the intercepts are i_0Y,1, i_0Y,2, and i_0M. In a sample, $\widehat{a}$, $\widehat{b}$, $\widehat{c}$ and ${\widehat{c}}^{\prime }$ are estimators of a, b, c, and c’, respectively. The interaction of X and M (coefficient h) is sometimes specified when a treatment modifies the strength of the relation between M and Y (coefficient b) across levels of X as shown in Equation 4,

$$Y=i_{0Y,3}+c^{\prime }X+bM+hXM+e_{Y,3}$$ (4)

In practice, measured confounders are included in the equations above. We do not include them in the equations to simplify explanation. If $\widehat{h}$ is zero, the product of $\widehat{a}$ and $\widehat{b}$, $\widehat{ab}$, is the estimator of the mediated effect. If $\widehat{h}$ is nonzero, then $\widehat{b}$ and $\widehat{ab}$ differ across levels of X, and ${\widehat{c}}^{\prime }$ differs across levels of M. There are several assumptions in traditional mediation analysis to attribute $\widehat{ab}$ a causal interpretation: a self-contained model with no omitted influences, correct functional form for the relations in the mediating process, psychometrically-sound measures, uncorrelated errors across equations, correct temporal precedence, and correct timing of measurement to capture the mediation process (MacKinnon, 2008). In addition, four no-unmeasured-confounding assumptions identify direct and indirect effects as described in the causal mediation literature (Pearl, 2001; VanderWeele & Vansteelandt, 2009; Valeri & VanderWeele, 2013):

1. No unmeasured confounders of the effect of the independent variable X on the dependent variable Y conditional on covariates.

2. No unmeasured confounders of the effect of the mediator M on the dependent variable Y conditional on the independent variable X and covariates.

3. No unmeasured confounders of the effect of the independent variable X on the mediator M conditional on covariates.

4. No measured or unmeasured confounders of the effect of the mediator M on the dependent variable Y that are affected by the independent variable X

Assumptions 1 and 3 are typically satisfied if X represents assignment to levels of a randomized treatment, so $\widehat{a}$ and $\widehat{c}$ represent causal effects. Assumptions 2 and 4 are not satisfied even if X represents assignment to levels of a randomized treatment because individuals self-select their values on the mediator given their observed level of the treatment and covariates (Holland, 1988; Imai, Keele, & Tingley; MacKinnon, 2008; MacKinnon & Pirlott, 2015). In other words, $\widehat{h}$, $\widehat{b}$, and ${\widehat{c}}^{\prime }$ do not have a causal interpretation without further assumptions even in a randomized study (Holland, 1988; MacKinnon, 2008; Robins & Greenland, 1992; VanderWeele & Vansteelandt, 2009).

Figure 1.

X to Y Model.

Figure 2.

X to M to Y Mediation Model.

For the prevention example, we assume valid and reliable measures for norms and strength training self-efficacy, a linear form for the relations between variables, and correct timing of measurement to capture the mediated effect. Given randomization to conditions, the program effect on norms (a) and the program effect on strength training self-efficacy (c) can be interpreted as causal effects because participants were randomized to levels of X. The relations from Eq. 4 (b, norms to strength training self-efficacy; c’, program to strength training self-efficacy; and h, the interaction due to a different relation of norms to self-efficacy across groups) do not have a causal interpretation unless the no confounding assumptions are met.

Examples of the Interaction between Treatment and the Mediator

The importance of the XM interaction has been discussed in the mediation analysis literature primarily as an assumption and sometimes as a substantive hypothesis to be tested with data (Judd & Kenny, 1981; Kraemer et al., 2008; MacKinnon, 2008; Merrill, 1994; Morgan-Lopez & MacKinnon, 2006). Often the XM interaction is assumed to be zero because the causal relation between M and Y is thought to be consistent across treatment conditions. For intervention studies, the mediator M is selected for treatment because previous theoretical and empirical research has established evidence for a consistent causal relation between M and Y. There are overlapping theoretical and methodological cases when the relation between M and Y would differ across groups, resulting in an XM interaction, as shown in Table 1. A theoretical example is an intervention designed to remove the relation between M and Y, such as an intervention to reduce the effects of offers of anabolic steroid use—the relation between offers and use would approach zero in the treatment group but be nonzero in the control group. A methodological example is an XM interaction that occurs when M and Y have a nonlinear relation, and the intervention changes M to a level where the relation between M and Y differs between treatment and control groups. As for most studies, in our prevention example it is expected that the relation between social norms and strength training efficacy would be the same for the control and treatment groups. In the next section, we discuss how the XM interaction is more clearly understood in the context of contrasts comparing the M to Y relation across levels of X. Although the traditional mediation model would often not include the XM interaction, we demonstrate in the next sections how including the XM interaction in the traditional mediation model and testing simple mediated and simple direct effects corresponds to the potential outcomes framework effects.

Table 1.

Hypothetical Examples of XM interactions

Reasons	Hypothetical Examples
Theoretical Examples
Intervention changes mediator interest	Example: Program (X) affects tobacco use (Y) through changing interest in tobacco after offer (M)
	Control: M to Y relation is high
	Treatment: M to Y relation is reduced by program teaching participants to refuse tobacco offers
Intervention changes mediator meaning	Example: Program (X) improves participant’s diet (Y) through increasing health food knowledge (M)
	Control: M to Y relation is low
	Treatment: M to Y relation is increased by gaining knowledge about healthy diets
Intervention changes social context	Example: Program (X) changes the social context (M) to reduce fighting (Y)
	Control: M to Y relation is high
	Treatment: M to Y relation decreases after social competence passes a threshold
Methodological Examples
Longitudinal	Example: In a pre- and post-treatment study, there is change in M for the treatment, but M for the control group is stable
	Control: M to Y relation is low
	Treatment: M to Y relation is higher because of the increased variability in M
Nonlinear relations	Example: There is a nonlinear relation between M and Y, so the relation of M on Y depends on the value of M.
	Control: The M to Y relation is linear
	Treatment: Intervention changes the value of M, thus changing the linear relation between M and Y compared to the control group
Restriction of range	Example: The variability of M is non-constant across the observed values
	Control: The M to Y relation is the same as pre-intervention
	Treatment: Intervention changes M to a range of values where there is reduced (increased) variability, so the M to Y relation may artificially decrease (increase)
Measurement	Example: The intervention changes how participants in the study answer questionnaire items.
	Control: The M to Y relation represents typical response behavior
	Treatment: Intervention changes the way participants answer a questionnaire, endorsing items at a higher (lower) rate, so the M to Y relation may increase or decrease.

Note: The examples are for a binary X (treatment = 1 versus control = 0) not continuous X case, and are for different M to Y relations, not different X to Y relations.

Contrasts for the XM interaction in the Single Mediator Model

Main effects of X on Y and M on Y do not provide a complete picture of the relations in the mediation model in the presence of a significant XM interaction (assuming it is not a Type 1 error). The implication of a statistically significant XM interaction is that the mediated effect is moderated by X, and the direct effect is moderated by M. Investigating simple mediated effects and simple direct effects clarify the meaning of the interaction effect (MacKinnon, 2008). The term simple refers to the relation between two variables (e.g., M and Y) at one level of the independent variable X (borrowing the term from analogous simple effects and simple slope tests in regression and analysis of variance; Aiken & West, 1991). There are four simple effects of interest in the presence of a significant XM interaction: two simple mediated effects and two simple direct effects.

Simple Mediated Effects.

Simple mediated effects refer to the mediated effect at certain values of the X variable. If X is binary with X = 0 for control and X = 1 for treatment, then there is a simple mediated effect for the control group and a simple mediated effect for the treatment group. Simple mediated effects are estimated by multiplying the same $\widehat{a}$ path for both groups (from Eq. 3) and group-specific $\widehat{b}$ paths (from Eq. 4). With X = 0 for the control group, the $\widehat{b}$ path, standard error, and significance tests are only for the control group. To obtain the simple mediated effect for the treatment group, X is recoded so that X = 0 is for the treatment and X = 1 is for the control group. For the prevention example, there will be a simple mediated effect in the control group using the $\widehat{b}$ path from the control group and a simple mediated effect in the treatment group using the $\widehat{b}$ path from the treatment group. Both simple mediated effects use the same $\widehat{a}$ path.

Simple Direct Effects.

Simple direct effects refer to the X to Y relation at certain values of M (c’ path from Eq. 4). When M is continuous, typically researchers probe simple direct effects at the mean of M (and +/− 1 standard deviations), or at clinically relevant values of M (Aiken & West, 1991). It is possible, however, to probe a simple direct effect at the control group mean of M and a simple direct effect at the treatment group mean of M. Although the strategy of group-mean centering a continuous moderator variable is not common in prevention, it is a key component relating simple direct effects in traditional mediation analysis to the causal direct effects in the potential outcomes framework. In the next sections, we describe the potential outcomes framework for mediation and how contrasts in traditional mediation analysis are equivalent to indirect and direct effects in the potential outcomes framework. For the prevention example, there will be a simple direct effect on strength training self-efficacy in the control group and a simple direct effect on strength training self-efficacy in the treatment group, both obtained in a similar manner as the simple mediated effects by recoding the X variable and estimating Equation 4.

Potential Outcomes Mediation Analysis

The potential outcomes framework for estimating causal effects (Holland, 1986, 1988; Rubin, 1974) distinguishes an individual’s observed and counterfactual outcomes. Consider the case where X represents assignment to levels of a randomized treatment with level x (x = 1 for the treatment, x = 0 for the control), and Y represents a continuous outcome variable. The potential outcomes framework starts by assuming there is an outcome value Y for each level of the treatment variable. That is, before an individual is randomized to a level of X, there are two potential outcomes that exist for this individual: an outcome for the participant in the treatment group Y (1) and an outcome for the same individual in the control group Y (0). If an individual is assigned to the treatment group, the potential outcome Y (1) is the observed outcome Y. The counterfactual outcome for that individual is the value of the outcome had that individual been assigned to the control group, Y (0). Ideally, researchers would estimate the individual causal effect by comparing the potential outcomes for each individual Y (1) -Y (0), but this not possible because individuals cannot simultaneously serve in two treatment conditions. Therefore, there will be missing data on one of the potential outcomes for each individual regardless of the treatment condition in which they participate. It is possible, however, to compute a causal effect averaged across individuals in each group. The average treatment effect, defined as E[Y (1) -Y (0)], can be identified by the difference in average Y between treatment and control groups, i.e., E[Y|X=1] – E[Y|X=0], assuming individuals have been successfully randomized to levels of the treatment.

The potential outcomes framework for mediation introduces a mediating variable M, with observed values of the mediator denoted by m, that mediates the relation between X and Y. For indirect effects, the potential outcomes for Y are a function of X and M. That is, E[Y(x, M(x))] indicates that the average-level potential outcomes for Y are a function of a direct effect of X on Y (i.e., the first x in E[Y(x, M(x))]) and an indirect effect of X on Y through M (i.e., M(x) in E[Y(x, M(x))]). The mediator M may be affected by X (i.e., M(x) indicating potential values of the mediator under the treatment and control groups) or the mediator M may be held at some constant value for all participants, m, resulting in potential outcomes in the form E[Y(x, m)]. Valeri and VanderWeele (2013) used the potential outcomes framework to define the following effects which we use in this article; the controlled direct effect (CDE), a direct effect under the control condition called the pure natural direct effect (PNDE), a direct effect under the treatment condition called the total natural direct effect (TNDE), an indirect effect under the control condition called the pure natural indirect effect (PNIE), and an indirect effect under the treatment condition called the total natural indirect effect (TNIE; Pearl, 2001; Robins & Greenland, 1992). The same effects with different names are described in other literature on the potential outcomes framework (Imai et al., 2010).

The controlled direct effect, CDE, of X on Y is the direct effect of treatment on the outcome at a fixed level of the mediator at m in the population: CDE = E[Y (1, m) – Y (0, m)]. The natural direct effect of X on Y is different from the CDE in that M is set to the level M(x), the level that would have naturally occurred under one of the conditions of X. Therefore, there are two natural direct effects corresponding to treatment and control groups. In the case of M(0), the pure natural direct effect, PNDE, is the effect of X on Y if X did not influence the mediator M (or the participants had the mediator level under the control condition), PNDE = E[Y (1, M(0)) – Y (0, M (0))]. Note that the (bolded) potential outcome, Y(1, M(0)), is impossible to observe because it is the value of Y for a participant in the treatment group, but a mediator value that would have been obtained had they been in the control group. Using our prevention example, this would be the training self-efficacy value for a person under the treatment group at the norms value that the person would have under the control condition. The total natural direct effect, TNDE, is the effect of the treatment X on outcome Y when the mediator value is held to what it would have been under the treatment group (or when the participants were assigned the mediator level under the treatment condition), TNDE = E[Y(1, M(1)) – Y(0, M(1))]. The pure natural indirect effect, PNIE, is the effect of X on Y due to a change in M in the control condition. In other words, the PNIE is the effect of X on Y when the level of M is changed due to X and assuming participants were in the control group when they were evaluated on the outcome, PNIE = E[Y(0, M(1)) – Y(0,M(0))]. The total natural indirect effect (TNIE) is the effect of X on Y due to a change in M in the treatment condition. In other words, the TNIE is the effect of treatment on the outcome when the level of M is changed due to X, assuming participants were in the treatment group when they were evaluated on the outcome, TNIE = [Y(1, M(1)) – Y(1, M(0))]. For the prevention example, the PNIE is the indirect effect that would be obtained if all persons were in the control group but their mediator value changed from their norms mediator value in the control group to their norms value in the treatment group.

The total effect, TE, is equal to the PNDE plus TNIE, which is also equal to the sum of the PNIE and TNDE. For the case of continuous M and Y, if the XM interaction is zero, then the two direct effects are equal and the two indirect effects are equal, and these results are equivalent to the estimators of the direct and indirect effects in the traditional mediation model, respectively. Pearl (2001) demonstrated that the decomposition of the total effect into the natural direct and indirect effects holds even in models with interactions and nonlinear models such as logistic or Poisson regression. More on these models, including software, can be found in Muthén and Asparouhov (2015) and Pearl (2012).

Correspondence between Traditional Mediation and Potential Outcomes Methods

There is a direct correspondence between the traditional mediation contrasts with the XM interaction and the causal estimators from the potential outcomes framework for continuous M and Y, shown in Table 2 and based on results from the causal mediation formula (Pearl, 2012). The total effect (TE) for both models is equal to c. The simple mediated effect in the treatment group is called the Total Natural Indirect Effect (TNIE = ab+ah), and the simple mediated effect in the control group is called the Pure Natural Indirect Effect (PNIE = ab). The Total Natural Direct Effect (TNDE) is the direct effect in the treatment group (c’+hi_0m+ah), and the Pure Natural Direct effect (PNDE) is the direct effect in the control group (c’+hi_0m).

Table 2.

Equivalence between traditional mediation estimators and potential outcomes framework estimators

Traditional Mediation terminology	Potential Outcomes Framework terminology	Estimator
Simple indirect effect in the control group	Pure Natural Indirect Effect (PNIE)	ab
Simple indirect effect in the treatment group	Total Natural Indirect Effect (TNIE)	ab + ah
Simple direct effect at the control group mean of the mediator	Pure Natural Direct Effect (PNDE)	c’ + h i0m
Simple direct effect at the treatment group mean of the mediator	Total Natural Direct Effect (TNDE)	c’ + h i0m + ah
Total effect	Total Effect (TE)	c
Interaction term	N/A	h
N/A	Mediated Interaction	ha
N/A	Reference Interaction	h(i0m−μm)

There is an important additional quantity in the potential outcomes framework that is not included in traditional mediation analysis. The test of the mediated interaction in the potential outcomes framework (Ikram & VanderWeele, 2015; VanderWeele, 2014) corresponds to the difference between PNIE and TNIE (also the difference between the PNDE and TNDE). In the potential outcomes mediation analysis, the mediated interaction tests if there is a difference between the simple mediated effect of the treatment and the control group. That is, it is a test of the product of the a-path (from Equation 3) and the h-path from Equation 4 (ha). The mediated interaction is not tested in traditional mediation analysis because the mediated interaction tests the equality of the mediated effect at the value of the mediator under the control condition to the mediated effect at the mediator value under the treatment condition. In traditional analysis, the analogous test for the difference in the mediated effects would be tested at the same value of the mediator in each group. Using the prevention example, the mediated interaction tests the equality of the simple mediated effect through norms on self-efficacy in the control group to the simple mediated effect through norms to self-efficacy in the treatment group. The reference interaction is closely related to the mediated interaction and reflects the effect of X on Y that is due to the interaction only. We do not discuss the reference interaction further because it is so similar to the mediated interaction and is not directly relevant to this paper.

Although the estimates from the traditional and potential outcomes models may be identical, the meaning and interpretation of the effects are different. While the traditional model estimates simple direct and indirect effects, the goal of the potential outcomes model is to obtain estimates of the potential outcomes (e.g., Y[0,M(1)] and Y[0, M(0)]) that are then compared to test effects (e.g., PNIE = Y[0,M(1)] - Y[0, M(0)]). In the potential outcomes model, the different indirect and direct effects are interpreted in terms of different groups in which a participant could serve. For example, the PNIE is the indirect effect if all participants were in the control group, and the TNIE is the indirect effect if all participants were in the treatment group. It is important to note that if a different method other than regression was used to estimate the potential outcomes, such as a machine learning algorithm (e.g., random forest), then the estimates of the potential outcomes model could be somewhat different than the estimates from the traditional model but would still correspond to the traditional contrasts. However, the correspondence between the equations for traditional mediation contrasts and the potential outcomes model does not always apply for nonlinear models such as logistic, Poisson, or negative binomial regression (Coffman, MacKinnon, Zhu, & Ghosh, 2016).

In summary, the potential outcomes framework mediation estimators correspond to contrasts in the traditional mediation model. As a result, the causal estimators are tested as contrasts in traditional mediation analysis when the XM interaction is included in the model. However, it is commonly assumed that the interaction of X and M is zero in traditional mediation analysis, mainly because theory and previous research predicts that the M to Y relation should not differ across groups. Estimating models with irrelevant parameters reduces statistical power to detect other parameters (Cohen, Cohen, West, & Aiken, 2003). Therefore, all else being equal, it is hypothesized that power to detect effects in the potential outcomes model (using Eq. 3 and 4) would be lower than the power to detect mediated effects using the traditional model (using Eq.2 and 3) when the XM interaction effect is zero. In contrast, there are situations where failing to include the interaction may suggest no mediation when in fact there is mediation in one or both groups.

We conducted a simulation to investigate the power to detect mediated effects using the traditional and potential outcomes models. We evaluated bias, empirical power, Type 1 error rates, and confidence interval coverage for the tests of the interaction, simple mediated effects, and the mediated interaction when the XM interaction is zero or nonzero in the population. To conserve journal space, we only include the most important results for the goals of this article but present additional results in the supplemental materials for this paper. To simplify presentation, we define the traditional model as not including the XM interaction (even though contrasts in this model correspond to potential outcome estimators) and the potential outcomes model as including the XM interaction. The rationale of the simulation study is to demonstrate the similarities and differences between the potential outcomes and traditional mediation models and to provide guidance for researchers regarding the estimation of the XM interaction.

Methods

Simulation Design

A statistical simulation study was conducted in the SAS (9.4) programming language with variables generated from the normal distribution using the RANNOR function using Equations 3 and 4. The mediating variable and dependent variable were simulated to be continuous, and the independent variable was binary with an equal number of cases in each group. We varied the factors of effect size of path a, effect size of path b, effect size of path c’, effect size of XM interaction h, and sample size (50, 100, 200, 500, 1,000), for a total of 1,280 different conditions. There were a total of 500 replications in each condition.

Parameter values a, b, c’, and h were chosen to correspond approximately to effect sizes of zero, small (2% of the variance in the dependent variable), medium (13% of the variance in the dependent variable), and large (26% of the variance in the dependent variable) (Cohen, 1988). These parameters were 0, 0.14, 0.39, and 0.59, corresponding approximately to partial correlations of 0, 0.14, 0.36, and 0.51, respectively. These effect sizes are approximate because the effect size depends on other variables in the regression equation (see Supplemental Materials for the specific R-square effect sizes). We ran additional simulations (i.e., an additional 36 conditions) with a negative value of h (i.e., h = −.39) to investigate cases where power to detect the potential outcomes indirect effects is greater than power to detect the traditional mediated effect.

The simulated datasets were analyzed using the traditional mediation model and the potential outcomes model. The traditional mediation model ignored the XM interaction (path h), and estimated the mediated effect ab using Equations 2 and 3. For the potential outcomes model, the XM interaction was estimated using Equation 4, and the potential outcomes estimators (TNIE, TNDE, PNIE, and PNDE) were estimated using the regression coefficients from Equations 3 and 4 as outlined in Table 2. As previously mentioned, when the XM interaction is included in the traditional mediation model, the traditional mediation contrasts yield the same estimates as the potential outcomes model.

Evaluation Criteria

Bias of Parameter Estimates.

Bias and relative bias were computed for the estimation of mediated effects (ab, TNIE, and PNIE), the direct effects (PNDE, TNDE, and c’), and the interaction effects (h, ha). Bias for estimators of the mediated, direct, and interaction effects was considered acceptable if relative bias was less than .10 (e.g., Flora & Curran, 2004).

Confidence Intervals and Significance Testing.

Significance testing was conducted using the percentile bootstrap within each replication. For each replication, the mediated, direct, and interaction effects were estimated in each of 500 bootstrap samples. Parameter estimates were deemed significant if zero was not contained between the 2.5^th and 97.5^th percentiles of the bootstrap empirical distribution of the parameter estimate in each replication. Type 1 error rates for each parameter were the proportion of times across the 500 replications per condition that parameter estimates were statistically significant when true values of the respective parameters were equal to zero. Consistent with Bradley’s (1978) liberal criterion, Type 1 error rates were deemed acceptable if they fell within the range of [.025, .075]. Power to detect each parameter was the proportion of times across the 500 replications per condition that the parameter estimates were statistically significant when true values of the parameters were nonzero. Information about confidence interval coverage is included in the supplemental material for this paper. A computer program that can be used to obtain Monte Carlo power estimates of the mediated, direct, and interaction effects for any value of a, b, c’, and h for both traditional and potential outcomes methods is included in the supplemental material.

Results

Estimation of Traditional and Causal Estimates of the Mediated Effect

Bias, relative bias, and coverage were minimal for the mediated, direct, and interaction effects and Type 1 error rates never exceeded the upper bound of the robustness interval.

Power to Detect Mediated Effects.

Table 3 displays empirical power values for the test of ab, PNIE, and TNIE as a function of parameter values for selected sample sizes and parameter values. Looking at the section of Table 3 for cases where h = 0 provides an examination of testing for mediation when there is a zero XM interaction in the population, which is often the situation in prevention research because the mediator was selected for intervention because it is consistently related to the outcome variable. Table 3 suggests that there is more power to detect ab than detecting PNIE and TNIE when h = 0 in several situations. For example, when N = 100 and a = .59 and b = .39, the power to detect ab is .786 while the power to detect PNIE and TNIE was .602 and .601, respectively. Differences in power among PNIE, TNIE, and ab decreased as sample size and effect sizes increased mainly because power increased overall.

Table 3.

Power for ab, PNIE, and TNIE as a function of parameter values, and sample size

							h
				−0.39			0			0.39
			ab	PNIE	TNIE	ab	PNIE	TNIE	ab	PNIE	TNIE
N	a	b
100	0.14	0	0.028	0.002	0.054	0.005	0.006	0.005	0.044	0.005	0.078
		0.14	0.002	0.024	0.040	0.020	0.013	0.014	0.092	0.013	0.104
		0.39	0.044	0.072	0.004	0.095	0.069	0.066	0.103	0.069	0.102
		0.59	0.096	0.094	0.014	0.109	0.101	0.098	0.118	0.108	0.118
	0.59	0	0.362	0.058	0.626	0.048	0.051	0.041	0.380	0.051	0.609
		0.14	0.092	0.152	0.348	0.216	0.119	0.144	0.712	0.140	0.761
		0.39	0.344	0.612	0.054	0.786	0.603	0.601	0.823	0.598	0.821
		0.59	0.788	0.788	0.246	0.830	0.800	0.797	0.843	0.800	0.843
200	0.14	0	0.106	0.004	0.148	0.004	0.008	0.009	0.103	0.009	0.152
		0.14	0.018	0.044	0.112	0.084	0.048	0.047	0.161	0.038	0.163
		0.39	0.134	0.188	0.012	0.167	0.160	0.152	0.161	0.148	0.161
		0.59	0.150	0.152	0.070	0.180	0.179	0.180	0.184	0.183	0.184
	0.59	0	0.742	0.060	0.970	0.048	0.048	0.049	0.709	0.053	0.947
		0.14	0.094	0.302	0.670	0.501	0.277	0.280	0.977	0.272	0.983
		0.39	0.696	0.950	0.044	0.985	0.947	0.948	0.983	0.934	0.983
		0.59	0.994	0.994	0.456	0.982	0.982	0.981	0.986	0.986	0.986
500	0.14	0	0.312	0.016	0.328	0.008	0.009	0.012	0.335	0.007	0.348
		0.14	0.082	0.170	0.346	0.295	0.187	0.182	0.362	0.183	0.362
		0.39	0.306	0.318	0.008	0.349	0.349	0.349	0.344	0.344	0.344
		0.59	0.372	0.372	0.324	0.334	0.334	0.334	0.348	0.348	0.348
	0.59	0	0.982	0.046	1.000	0.052	0.059	0.057	0.984	0.056	1.000
		0.14	0.234	0.592	0.984	0.871	0.597	0.594	1.000	0.590	1.000
		0.39	0.980	1.000	0.026	1.000	1.000	1.000	1.000	1.000	1.000
		0.59	1.000	1.000	0.860	1.000	1.000	1.000	1.000	1.000	1.000

Table 3 also displays power values when h was nonzero. In these models for all positive coefficients, the power to detect the TNIE was similar to the power to detect ab (i.e., the product of a and b from Equations 2 and 3) because the estimator of the TNIE includes the quantity ha. Differences in power to detect TNIE and ab decreased as sample size and the effect size of the XM interaction increased. By N = 200, the difference in power between TNIE and ab was almost negligible. For example, for N = 200 and a = .14, b = .14, and h = .39 the power to detect TNIE was .163 and the power to detect ab was .161. In contrast, the power to detect PNIE was always lower than the power to detect either TNIE or ab for sample size of N = 100. When the sample size was greater than or equal to N = 200 and b = .59, the power to detect PNIE was similar to the power to detect either TNIE or ab.

For the situation with h = −.39, there were cases when the power to detect PNIE and TNIE was greater than the power to detect ab without the interaction. For example, when N=500 and a =.59, b = .14 and h = −.39, the power to detect ab was .234 and the power to detect PNIE was .592 and TNIE was .984 demonstrating that the power to detect mediated effects within each group can be substantially greater than when ignoring the interaction. Note also when b =0, whether h is zero or nonzero, table entries reflect Type I error for the test of ab, not power.

Power to detect the XM interaction.

The power to detect the XM interaction was investigated in two ways, (1) the power to detect h and (2) the power to detect ha (the mediated interaction). The numerical results are easily summarized so they are only presented in the supplemental material along with the results for the reference interaction. In general, there was higher statistical power to detect a significant interaction (h) than power to detect a significant mediated interaction (ha). As sample size and the effect size of a increased, differences in power to detect h and ha decreased.

Summary of Results.

Overall, results suggest that when the XM interaction is zero in the population, there is lower power to detect the mediated effect using PNIE and TNIE from the potential outcomes framework than using ab from the traditional mediation model. This discrepancy in power is particularly relevant in conditions with a small sample size or with a small effect size of either a or b. Also, results suggest that when the XM interaction is nonzero in the population, power can be greter to detect the mediated effect using PNIE or TNIE from the potential outcomes model than ab from the traditional mediation model. The results also demonstrated that failure to include the h coefficient when it is nonzero in the population can reduce power to detect mediated effects because there can be nonzero simple mediated effects. However, differences in power decreased as sample size and the effect size of the b-path increased. Finally, results suggest that there is more power to detect h than ha.

Analysis of the Prevention Example

The test of the XM interaction was not statistically significant (h = −0.020, p > .5) as expected because it was hypothesized that the relation of norms to strength training self-efficacy would not differ between treatment and control groups. The PNIE = 0.041 (Lower Confidence Limit (LCL) =.008, Upper Confidence Limit (UCL) = .082) and TNIE= 0.046 (LCL = .012, UCL = .090) were statistically significant but did not differ as shown in the nonsignificant mediated interaction (ha = −0.005, LCL= −.052, UCL = .027). Both direct effects PNDE = 0.541 (LCL=.411, UCL=.672), and TNDE = 0.546 (LCL=.409, UCL=.682) were statistically significant indicating that there may be other potential mediators of the program effects. The direct and indirect effects were statistically significant when the XM interaction was not included in the statistical modeling. There is evidence that the treatment caused change in norms that then improved strength training self-efficacy. In every mediation analysis including our example, even when X is randomized, the M to Y relation is not, so it is important to explore the sensitivity of results to confounders of the norms to self-efficacy relation (MacKinnon & Pirlott, 2015). Although there was no evidence of a statistically significant interaction for this example, it is still possible that the interaction may be present for other dependent variables. It is also possible that the interaction may be expected in other contexts for the reasons described in Table 1.

Discussion

There is a direct correspondence between the traditional mediation estimators and the potential outcomes estimators for the case of a continuous M and Y. When the XM interaction is zero, the mediated and direct effects are the same in both models. When the XM interaction is nonzero, the mediated effects in the potential outcomes model, PNIE and TNIE, correspond to contrasts in the traditional model, the simple mediated effect in the control group and the simple mediated effect in the treatment group, respectively. Direct effects in the potential outcomes framework also correspond to direct effect contrasts in the traditional model. The use of the XM interaction in the traditional model provides the link to the potential outcomes framework. Despite the equivalence of estimates of direct and mediated effects, the meaning of effects in the traditional and potential outcomes framework differs. Traditional model estimators are interpreted in terms of adjusted and unadjusted linear associations between variables and represent descriptive rather than causal relations. Potential outcomes framework estimators correspond to causal effects in which all persons were in treatment or control conditions and are interpreted as causal differences between conditions in which participants could serve. The potential outcomes framework defines effects in terms of predicted potential outcomes, which makes it straightforward to extend to nonlinear and other types of models. It is important to note that the estimators from both frameworks are identical given all assumptions are satisfied but will not be identical if there are violations of assumptions. Because the potential outcomes methods were developed to obtain causal estimates, it is a better framework to investigate violations of model assumptions that compromise estimators of causal effects.

This study replicated earlier simulation studies of traditional mediation models where the power to detect mediated effects is low unless effect size is large or sample size is large (MacKinnon et al., 2002). Several new results were obtained from evaluating models with the XM interaction. When there was no XM interaction in the population, the power to detect the causal mediated effects, PNIE and TNIE, can be less than the power to detect the traditional estimator of the mediated effect, ab. In prevention research, it is often costly to obtain a large number of participants so studies are typically designed to obtain a sample size with a reasonable power to detect an effect (typically .8). Because including the h coefficient reduces power to detect mediated effects, testing mediation first and then testing the interaction as an assumption is likely the best strategy. When the XM interaction was non-zero in the population however, and all other population parameters were positive, the power to detect ab and the TNIE were similar because both estimators take into account the XM interaction. The TNIE includes this information directly by including the quantity, ha. The traditional estimator, ab, takes into account the XM interaction because the b coefficient is inflated when there is a positive XM interaction in the population, but the XM interaction is not included in the outcome regression model (i.e., Equation 2 is estimated). When h is negative, ab and PNIE would have similar performance rather than ab and TNIE. Simulations with a negative value of h demonstrated situations where failure to estimate the interaction can lead to reduced power to find mediated effects. Finally, the power to detect the XM interaction, h, was higher than the power to detect the mediated interaction (i.e., ha) because the mediated interaction is a product of two regression coefficients which has a more complicated distribution than the distribution of h.

Recommendations

The XM interaction is included in the potential outcomes framework, but the interaction is rarely tested and described in traditional mediation analysis. Although there are situations in which an XM interaction may be expected, for the most part researchers do not estimate this interaction in traditional mediation analysis because the relation between M and Y is expected to be the same across treatment conditions based on prior theory and empirical research. However, there are compelling reasons for testing the XM interaction. First, unlike other assumptions of mediation analysis, or more generally, path analysis (McDonald, 1997), this assumption can be tested with data. Second, there are methodological and substantive reasons for an XM interaction to be present in some situations as shown in Table 1. Third, if the XM interaction is not tested, important information about differential effects of treatments may be missed. Therefore, we recommend that the XM interaction be routinely tested in prevention research as part of a causal mediation analysis if the interaction is hypothesized or after mediation analysis as a check on the assumption that the relation does not change across experimental groups. Investigation of the XM interaction is also important for exploratory studies.

In this paper, we showed that for the case of continuous M and Y, there is a direct correspondence between estimators from traditional and potential outcomes mediation models, so researchers using traditional mediation analysis with the XM interaction have been calculating causal mediation effects all along as contrasts. With violations of assumptions and for more complicated models such as logistic regression for categorical M and Y, the indirect effect estimators for the traditional and potential outcomes models do not always correspond. Overall, we recommend that causal mediation analysis be more widely applied in prevention research because it focuses on the estimation of causal quantities.