Computational Fluid Dynamics of Vascular Disease in Animal Models

Abstract

Recent applications of computational fluid dynamics (CFD) applied to the cardiovascular system have demonstrated its power in investigating the impact of hemodynamics on disease initiation, progression, and treatment outcomes. Flow metrics such as pressure distributions, wall shear stresses (WSS), and blood velocity profiles can be quantified to provide insight into observed pathologies, assist with surgical planning, or even predict disease progression. While numerous studies have performed simulations on clinical human patient data, it often lacks prediagnosis information and can be subject to large intersubject variability, limiting the generalizability of findings. Thus, animal models are often used to identify and manipulate specific factors contributing to vascular disease because they provide a more controlled environment. In this review, we explore the use of CFD in animal models in recent studies to investigate the initiating mechanisms, progression, and intervention effects of various vascular diseases. The first section provides a brief overview of the CFD theory and tools that are commonly used to study blood flow. The following sections are separated by anatomical region, with the abdominal, thoracic, and cerebral areas specifically highlighted. We discuss the associated benefits and obstacles to performing CFD modeling in each location. Finally, we highlight animal CFD studies focusing on common surgical treatments, including arteriovenous fistulas (AVF) and pulmonary artery grafts. The studies included in this review demonstrate the value of combining CFD with animal imaging and should encourage further research to optimize and expand upon these techniques for the study of vascular disease.

1. Introduction

Patient-specific computational modeling of vascular hemodynamics from image data has emerged as a powerful technique with the potential to improve clinical care [1]. In contrast to traditional vascular assessments, computational fluid dynamics (CFD) simulations of blood flow can be used to assess complex hemodynamics. As such, determining which metrics can assist in predicting disease development and progression has become of paramount interest. While most CFD research has focused on human patient data, recent improvements in imaging techniques have allowed for similar CFD studies in animal models of vascular disease.

Animal models are commonly used in the study of vascular diseases and provide several advantages as compared to clinical models. Animal studies allow for the systematic collection of hemodynamic and geometric imaging information prior to disease initiation, or baseline, and throughout progression—data uncommon in humans as patients are rarely imaged before pathology develops. Animal vascular disease models can also be representative of many aspects of the human condition as the models can be controlled to have similar genetic, cellular, and biochemical mechanisms as humans [2]. While human vascular tissue is difficult to acquire at different stages of disease progression, animal studies can be designed to collect tissue at multiple time points for ex vivo analyses including mechanical testing, mRNA expression levels, and histology [3]. By combining ex vivo analysis with in vivo imaging and subsequently CFD in animal studies, the interaction of tissue mechanics and hemodynamics can be studied throughout disease progression.

There are several CFD considerations that should be taken into account when running simulations from animal imaging data. First, the resolution of different imaging modalities provides inherent challenges when studying small animals. Many initial studies in mice and rats (hereafter considered small animals) utilized ex vivo corrosion casting due to resolution difficulty with in vivo imaging modalities. Improvements to temporal and spatial resolutions have largely eliminated these issues; however, in smaller vessels, resolution is still of concern and may necessitate the use of larger animal species (e.g., pigs, minipigs, dogs, and sheep). Further considerations in animal research are cost, model availability, and biological similarities to humans. Due to their size, small animals are inexpensive with easier husbandry compared to larger animals. Large animals are often more expensive, labor intensive, and require advanced veterinary care. Rabbits provide an intermediate solution in terms of size and ease of housing, but because of the fast breeding cycle and ability to transgenically modify rodents, the majority of biomedical mammalian research is still performed in small animals [4]. Because mice have been genetically modified for decades, many different transgenic disease models have been created. Yet, pigs maintain the most similar anatomy, physiology, and genome and lipid profile to humans, suggesting that their pathophysiology is often easier to translate to humans. In general, the wide variety of animal models enables researchers to select the species based on their specific needs.

The purpose of this review is to highlight the benefits of CFD to assess hemodynamics in animal models. These animal-based studies allow for more control over factors contributing to disease initiation and progression, yielding a more precisely controlled description of the associated vascular hemodynamics. Different small and large animal models exist for a variety of vascular diseases, allowing flexibility in body size, genetic modifications, and pathophysiology. Clinical data are often from a highly variable patient population that typically only begins to monitor after diagnosis and is analyzed on a case-by-case basis, whereas animal studies can be used to monitor disease progression and identify trends in a relatively homogenous population. The relevant fundamental and region-specific animal-model CFD details are discussed below.

2. Computational Fluid Dynamics Background

2.1. Overview.

Computational fluid dynamics modeling has emerged as a tool for predicting vascular hemodynamics noninvasively [5]. Since early work in the mid-1990 s [6], the number of papers in vascular CFD modeling continues to grow each year, with studies ranging from disease progression [7] to impact in surgical planning [8]. Today, a variety of commercial and open-source software packages specific for vascular CFD are available [9], bringing a range of tools to the forefront of this emergent field [10].

In general, CFD uses numerical methods to solve the Navier–Stokes (N–S) equations. The N–S equations represent the conservation of mass and momentum in flows, mathematically given in their incompressible form by (1) and (2), respectively

$$\nabla \cdot \mathbf{u}=0$$ (1)

$$\frac{\partial \mathbf{u}}{\partial t}+\left(\mathbf{u}\cdot \nabla \right)\mathbf{u}=-\frac{\nabla P}{\rho }+\upsilon {\nabla }^2\mathbf{u}$$ (2)

Here, u is the velocity vector, P is the pressure, ρ is the density, and ν is the viscosity of the working fluid. While the focus of this review is on recent advancements and applications of CFD to blood vessels, a more detailed description of CFD for a variety of biomedical applications can be found in the following paper [11].

Most vascular CFD modeling studies share a similar process in order to quantify hemodynamics from imaging data. This framework includes: (1) identifying critical vasculature from volumetric imaging data (Fig. 1(a)), (2) forming a model from the identified vasculature, (3) selecting and generating a volume mesh of the model (Fig. 1(b)), and (4) running a CFD solver with appropriate physiological boundary conditions based on observations and assumptions (Fig. 1(c)). Noninvasive vascular imaging techniques used in modeling include magnetic resonance imaging (MRI), fluoroscopy or computed tomography (CT), and more recently, ultrasound (U.S.) [12]. Several commercial or open-source software, including amira, geomagic, mimics, polydata [13], scanip, avizo [14], or parasolid, can be used to render models through either surface or volume triangulation methods.

Fig. 1.

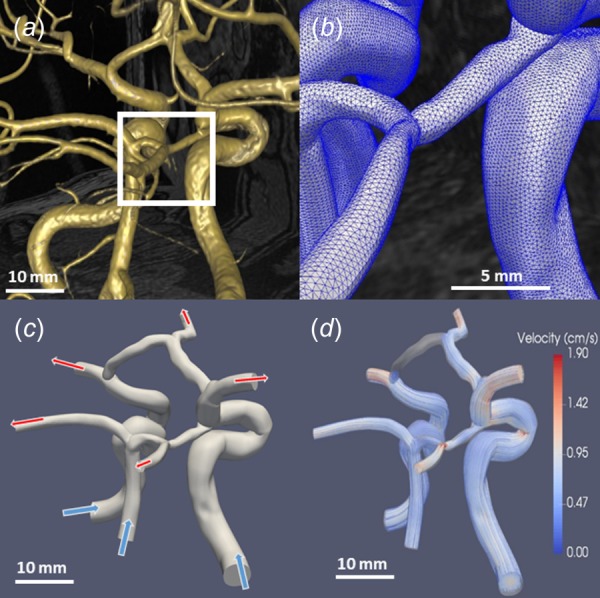
Basic progression highlighting the steps from MRI visualization to CFD simulation results. (a) Vessel rendering by simvascular allows for simple and fast visualization [10]. (b) Acloser view of the mesh reveals the individual elements. (c) Arrows (top) represent the outflow of blood while arrows (bottom) show inflow. The inflow of blood was prescribed by volume flow rate waveforms, while outflows are often determined by scaled cross section mass flow, resistor–capacitor–resistor models, or simplified resistor-only boundary conditions. (d) Velocity streamlines used to visualize the results of CFD simulations (unpublished data).

Volume meshes are usually generated using structured or unstructured grids and are composed of either tetrahedral or hexahedral elements. Structured grid schemes have the same number of adjacent elements surrounding each interior nodal point; unstructured grids allow the number of adjacent elements to vary [10]. Unstructured, tetrahedral element grid schemes are primarily used in vascular CFD models, since vessels must be fully resolved for flows at different length scales. Tetrahedral elements are computationally inexpensive and easily allow for mesh refinement; however, they introduce stiffness into the solver, adding artificial noise [15]. Alternative mesh strategies such as the multiblock unstructured hexahedral scheme [16] have the potential to overcome the inherent limitations in single mesh style strategies. Additional analysis of strengths and limitations for mesh element types can be found in Table 1. A full review of mesh geometry can be found in the following paper [15].

Table 1.

Model Generation

Method	Strengths	Limitations	Software
Surface render	Lower computational cost	Internal features not rendered	avizo, geomagic, mimics, parasolid, polydata, scanip
Fast refinement
Volume render	Internal features rendered	High computational cost	amira, avizo, polydata
Intuitive implementation
Meshing element shape
Method	Strengths	Limitations	Software
Hexahedral	Easy and intuitive to implement	Not useful for complex models	ANSYS
	Offers higher equation accuracy	No near-wall grid refinement
	Structured and unstructured methods	High computational cost
Fewer equations solved
Tetrahedral	Fully resolves complex geometries	Difficult to implement	ANSYS, gridex, meshsim, tetgen
	Allows for easier grid refinement	Problem specific
		Introduces equation stiffness
		Unstructured methods only
More equations solved

Selecting a numerical solver for vascular flow largely depends on the vessel of interest. In the majority of studies, three-dimensional (3D) flow with rigid vessel wall assumption are used [17], allowing for simple N–S equations solvers to be employed. In the cerebral vasculature, use of a rigid assumption is often considered valid as the muscular arteries surrounding and within the brain, although not truly rigid, do not undergo significant pulsations in vivo [18]. Other regions of the vasculature, however, undergo substantial expansion and contraction throughout the cardiac cycle, making the rigid wall assumption problematic. This is especially true in large elastic arteries such as the aorta, iliacs, and carotids. More recent studies in large arterial flows have begun to use fluid–structure interaction (FSI) models that account for flow-altering tissue deformation both spatially and temporally [19]. While powerful and often more accurate, FSI techniques require assumptions about vessel properties and have an increased computational demand compared to traditional CFD approaches.

Appropriate boundary condition selection is critical and especially important in vascular flow modeling where hemodynamics are highly dependent on subject physiology. Conditions must be assigned for inlets, vessel walls, and outlets. A no-slip boundary condition is commonly used along the vessel walls. FSI simulations with deformable walls, however, must also take into account vessel pulsatility when predicting flow along the endothelium [17]. Additionally, a variety of inlet and outlet boundary flow conditions have been described in detail in the literature [20]. Examples include prescribed volumetric flow, pressure, and 0D lumped models that are designed to mimic large vascular networks and ideal when site-specific hemodynamic information is unknown. Considerations for selecting proper animal model boundary conditions are discussed in further detail in Sec. 2.2, Table 2 provides an overview of strengths and limitations for select boundary conditions.

Table 2.

Boundary condition

Location	Condition type (implicit/explicit)	Strengths	Limitations
Wall	Rigid(explicit)	Easy implementation	Cannot resolve pressure wave
Low computational cost	Propagates error in pressure and wall stress
	Moving(explicit)	Useful in large wall motion problems	Requires accurate spatiotemporal information of motion
	Fluid–structure interaction (FSI, implicit)	Resolves pressure wave	High computational cost High implementation complexity
Good for coupled problems
Inlet	Prescribed model(explicit)	Easy implementation	Oversimplifies flow complexity
	Subject-specific(Explicit)	Accurate representation	Requires accurate spatiotemporal flow information
	Pressure(explicit)	Flow can develop to best fit model	Need pressure measurements
	0D Lumped models(Implicit)	Good for unknown conditions	Need to model the flow through the rest of the body accurately
Outlet	Prescribed flow rate(explicit)	Simple implementation	Flow may not be accurate
Allows unique solution
	Pressure(explicit)	Flow can develop to best fit model	Need pressure measurements
	0D Lumped models(implicit)	Good for unknown conditions	Need to model the flow through the rest of the body accurately

After a simulation has been run, postsimulation quantification can be used to calculate velocity and pressure maps. These fields can provide initial insight into altered flow in cases such as stenosis and aneurysms. Pressure and velocity, however, are only the start of the hemodynamic metrics that can be quantified. For example, velocity measurements can be used to calculate stream-traces and wall shear stress (WSS) along the lumen boundary (Table 3). Complex flow with regions of recirculation can be much more easily visualized with stream-traces [12], while conventional WSS measurements give a description of stresses felt by endothelial cells. Other shear stress metrics include time-averaged WSS (TAWSS) and oscillatory shear index (OSI), both of which have shown potential to better predict cell signaling changes. Furthermore, relative residence time (RRT), a measurement of blood stagnation along the walls [13], is often used in studies of platelet accumulation and thrombus formation [21]. However, in order to obtain reliable WSS and RRT values, the near-wall boundary layer must be sufficiently resolved [17]. Without sufficient resolution, these measurements may be biased low. Other researchers have shown that while OSI and RRT may not correlate with murine aneurysm rupture risk [17], they are useful for observing stress alterations near locations of disturbed flow. In addition, combined and advanced novel metrics such as transverse WSS (transWSS) [22] and WSS exposure time [21] may eventually be able to improve clinicians' ability to predict disease progression. Specifically, transWSS allows researchers to observe the stresses generated when flow is redirected at either bifurcations or in regions of recirculation.

Table 3.

Common postprocessing measurements

Parameter	Description	Physical relevance
Stream-trace	Trace of particle(s) within a flow field at a single time	Allows user to observe regions where flow moves toward or away from the walls, where flow stagnates, and where regions of recirculation occur
Wall shear stress (WSS)	Instantaneous measurement of fluid stress near walls, as a result of no slip conditions	Used to observe regions stress along vascular wall is altered, indicating possible regions where endothelium may thicken or thin
Time-averaged WSS (TAWSS)	Average value of WSS along the wall for a cardiac cycle	Indicates direction tangential to the overall flow, used to identify regions where flow reversal persists
Oscillatory shear index (OSI)	Dimensionless quantity indicating direction of WSS in relation to TAWSS	Used to quantify the presence and duration of flow reversal
Relative residence time (RRT)	Dimensionless ratio of OSI and normalized WSS	Provides a characteristic value for locations of flow stagnation and long recirculation periods
Transverse WSS (transWSS)	Quantifies wall shear stress in the direction opposite of flow	Can quantify regions where flow may redirect, or regions where flow needs time to re-orient in the flow direction

2.2. Computational Fluid Dynamics Considerations : in Animal Models

2.2.1. Image Acquisition and Geometry Selection.

Obtaining 3D geometry in animal models, especially small animal models, can be challenging due to the need for increased resolution. One method of ex vivo geometry acquisition is corrosion casting [22,23]; however, animal sacrifice and vascular harvesting make longitudinal studies impossible with this approach [24]. In addition, the casting process can slightly alter vascular geometry. Multiple studies have reported corrosion casting of the aorta resulted in altered diameters and bifurcation angles compared to MRI [25] and μCT [23], both noninvasive approaches. While previous work has shown that these differences may be insignificant, for instance when calculating RRT values from both corrosion casting and MRI in the proximal portion of the abdominal aorta [13], the potential for error in casting measurements and the lack of longitudinal assessment has meant that more recent studies employ contrast-enhanced μCT [17,24], MRI [25,26], and volumetric U.S. [27,28]. Given the translational potential of these noninvasive approaches, the trend favoring in vivo imaging for modeling vasculature is likely to continue.

Geometric assumptions and simplifications are often incorporated into models for practical reasons. As model complexity increases, the computational cost also increases, making a perfect representation of an entire vascular network impossible [20,29,30]. Nonessential branches are often excluded, but the effects of doing so are highly dependent on the region of interest. For example, when performing flow simulations along the abdominal aorta, inclusion of the ascending and descending thoracic aorta, both far away from the infrarenal aorta, has little downstream effect on the flow profile [31]. Figure 2, however, illustrates different variations of a murine abdominal aortic aneurysm (AAA) simulation with major branches either included or excluded, revealing that the expected physiological pressures are seen within the aneurysm only when abdominal branching vessels are incorporated (unpublished data). Similarly, a cerebral vasculature study indicated the need to include downstream vessels as geometric simplifications reduced the simulation reliability [32]. Thus, exclusion of upstream or downstream branches must be made deliberately, knowing that this decision may indeed influence the simulation results.

Fig. 2.

Pressure distributions down a mouse aorta with a saccular dissecting AAA. The inclusion of (a) no branching vessels, (b) only abdominal branching vessels, (c) only thoracic branching vessels, and (d) both thoracic and abdominal branching vessels had substantial effects. Expected physiological pressures are seen around the AAA only when abdominal branching vessels are included; otherwise, overestimations of pressure were observed (unpublished data).

2.2.2. Boundary Conditions.

Small animal vascular CFD inlet conditions (Table 2) are often based on in vivo imaging measurements from pulsed wave Doppler U.S. (PW-US) [33] or phase-contrast MRI (PC-MRI) [18,34]. When using PW-US, one-dimensional Doppler velocity measurements are extrapolated to volumetric flow profiles utilizing different waveforms including uniform [35], blunt [36], parabolic [31], or fully developed Womersley flow [22,37]. Under these assumptions, maximum inflow velocity is located along the vessel centerline; however, profile skewing toward walls, even in relatively straight vessels, such as the carotid, is observed in multiple in vivo imaging approaches [38]. In addition, image acquisition errors (e.g., inaccurate sample volume location and angle corrections) can contribute to further waveform inaccuracy [39]. PC-MRI, on the other hand, can provide two-dimensional and 3D flow profiles, providing more inflow information. Still, PC-MRI has decreased temporal resolution and increased acquisition time compared to PW-US. A comparison of PW-US, PC-MRI, and numerical simulations showed that while subtle differences exist (i.e., PW-US extrapolation overestimates total flow), there was a good overall agreement between all approaches [22]. Pressure and lumped parameter conditions, though available, are used less frequently at the inlet. This is because accurate, localized pressure measurements ideally require invasive measurements via a catheter that are difficult to acquire and may not be possible in small vessels. Furthermore, realistic lumped parameter models are complex and require a detailed knowledge of cardiac function.

Outlet boundary conditions can also be prescribed based on PW-US [33] and PC-MRI [18] measurements. However, acquisition of all outflow boundary waveforms can be challenging and time intensive in complex vascular models. Thus, rather than using subject-specific boundary conditions, many studies utilize generalized boundary conditions based on either previous literature [12,22], Murray's law [40], or pressure and lumped parameter models [22,31,35]. For example, Trachet et al. explored the influence of outlet boundary conditions in apolipoprotein E-deficient (apoE^−/−) mouse aortic models when using: (1) mouse-specific, (2) literature-based, or (3) flow splitting based on Murray's law boundary conditions [41]. Results indicated that literature values were similar to subject-specific boundary conditions, but Murray's law was found to be unreliable. Accuracy of Murray's law calculation was improved when an exponential of 2, instead of 3, was incorporated. This study suggests that care should be used when employing nonsubject-specific boundary conditions, especially in situations of altered or disturbed flow.

Both rigid and deformable wall FSI simulations are often used in vascular CFD, but the differences between these can be dramatic, especially in elastic arteries. Trachet et al. first showed that there is a natural phase lag in peak flow along the aorta from ascending thoracic to abdominal due to wall elasticity [41]. In rigid models, this phase lag has to be accounted for in order to make up for differences in mass flow [42]. If unaccounted, this can lead to increased and nonphysical outflow velocities as shown in a subsequent publication [35]. However, in certain cases, such as aortic aneurysms [28], vessel stiffness has increased so significantly that a rigid wall assumption may be valid [32]. In the future, it is likely vascular flow simulations will tend toward FSI as computing power and algorithm designs improve. Multiple groups are now showing how FSI predictions better capture physiological flows. In a recent paper by Ferraro et al., the authors demonstrate that assuming uniform wall thickness and making geometry simplifications greatly alter vessel strain, both of which can adversely affect FSI simulations [43]. These types of studies are important since open-source computational software platforms such as simvascular [10] have also begun to incorporate FSI, allowing even novice researcher the ability to quickly perform deformable simulations.

2.3. Summary.

Computational fluid dynamics techniques can be applied to human, large animal, and small animal studies to better understand vascular hemodynamics. Beyond investigating experimental disease models, animal studies are also commonly used to help validate new CFD techniques in cases where human data are not available or difficult to acquire. Sections 3–5 highlight vascular hemodynamic simulations in various animal models, discussing select region-specific applications and identifying both limitations and potential future directions.

3. Abdominal

3.1. Overview.

An AAA is a localized dilation of the aorta in the abdominal region. The primary risk is aneurysm rupture, which can be fatal [29]. Current clinical guidelines recommend that human AAAs of 5–5.5 cm and larger undergo surgical intervention [44]; however, aneurysm geometry alone is inadequate for predicting rupture risks [45]. Quantification of hemodynamics within AAAs has clinical relevance as correlations can be made between fluid flow patterns and aneurysm initiation and growth. This, in turn, may be able to provide clinicians with more robust formation-risk and growth-rate assessments beyond that of diameter alone, leading to better selection of appropriate treatment.

3.1.1. Abdominal Aortic Aneurysms in Animal Models.

A common AAA small animal model for CFD studies is the Angiotensin II-infused (AngII) apoE^−/− mouse model. The AngII apoE^−/− model induces suprarenal dissecting AAAs. Although human AAA are most commonly infrarenal and fusiform, the AngII apoE^−/− model mimics the human condition as male mice are more prone to developing aneurysms and both hyperlipidemia and hypertension are contributing factors. Additionally, both mice and humans have complex abdominal aortic waveforms with biphasic (mice) and triphasic (humans) patterns [46]. That, in conjunction with robust aneurysm formation, good reproducibility, and ease of creation has made the apoE^−/− mouse an attractive AAA model. Other animal models to investigate AAA are discussed in Refs. [47] and [48], but CFD studies using these models are lacking.

In addition to the differences in the pathophysiology in this animal model, the mechanics of the aorta also differ due to the smaller size of mice. For instance, WSS is higher in small animals than in humans [22], thus preventing a direct comparison of results between mice and larger mammals. While hemodynamic differences have been reported between mice and humans [46], allometric scaling can be used to help translate hemodynamic results between species [49].

3.2. Current Research Using Computational Fluid Dynamics in Abdominal Aortic Aneurysm.

As noted earlier, WSS, TAWSS, OSI, and RRT are four hemodynamic metrics that are used to quantify simulation results. While these parameters are individually useful, their connate implementation allows for clearer description of vascular hemodynamics. For example, OSI is known to affect endothelial cells, leading to higher endothelial cell turnover rates, higher low density lipoprotein accumulation, and morphological changes within the vessel wall [24]. Consequently, increases in OSI have been linked to atherosclerosis, an important risk factor for both vessel stenosis and AAA formation [24]. Additionally, Trachet et al. used baseline mouse data to map the hemodynamics prior to AAA formation and found that aneurysms tended to form in locations proximal to low OSI [50]. While the relationship between TAWSS and RRT with AAA location in mice is currently unclear [17], these hemodynamic metrics are still being investigated as potential predictors of aneurysm formation [45].

In addition, recent research in CFD modeling of AAAs has focused on longitudinally assessing AAA development and growth at several time points for one animal. By combining multiple imaging techniques and using higher resolution imaging, these longitudinal studies may provide insight into the development of AAA. Trachet et al. studied the effect of disturbed flow on the location of the developed aneurysm in apoE^−/− mice [17]. Geometry and flow profiles were obtained from micro-CT and high-frequency U.S., respectively. Disturbed flow was primarily observed on the same side as the formed aneurysm, with aneurysm formation proximal to altered flow region. There was no consistent relationship between hemodynamics and AAA formation; however, this study showed promise for longitudinal studies of the AngII apoE^−/− mouse model with CFD simulations.

Vortex formation in AAA has also been explored. Ford et al. used high temporal resolution U.S. (electrocardiogram-based kilohertz visualization or EKV) [12] to study hemodynamics in AAA. Twenty-one animal-specific images were taken, and three image datasets were used to run a CFD model to study the hemodynamics within the lesion. In these models, the largest correlation existed between the remodeled area and OSI. In addition, vortices were associated with areas of low velocity, which in turn caused increased remodeling in these areas of low shear stress. However, this study did not consider baseline measurements for individual mice or flow within the aorta proximal or distal to the AAA; analysis of which could be included as a control in future studies.

In order to track hemodynamic changes throughout the formation of an AAA, Phillips et al. combined in vivo high-frequency U.S. with in vitro optical coherence tomography to build complex 3D models, run simulations, and characterize AAA hemodynamics (Fig. 3) [28]. U.S. provides noninvasive monitoring of the animals to determine when the aneurysm formation began and how it progressed throughout the study, while optical coherence tomography was able to distinguish the false and true lumen of the dissecting aneurysm that compared well with the histology. By tracking the animals throughout the study, mild progressing to severe disease states were observed. The aneurysm expanded slowly after the initial focal dissection, but subsequent timing of AAA formation varied. The authors further noted that the false lumen cavities caused recirculating flow. Open versus thrombotic false lumens were also differentiated between animals, unlike in Ford et al. that did not make this distinction [12]. The use of multiple imaging modalities strengthened the amount of accurate information available to construct a CFD model, suggesting the value of combining one imaging modality that accurately defines the geometry and one that accurately provides blood flow and boundary condition information.

Fig. 3.

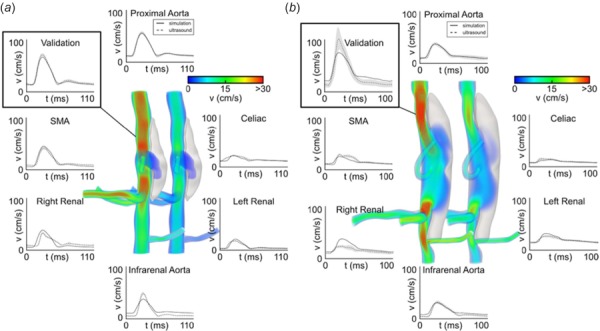
Volumetric rendering and mean velocity waveforms from two mice with moderate (a) and severe (b) dissecting aortic aneurysms. Simulations show the magnitude of the velocity at systole (left) and diastole (right). Solid lines represent simulated velocity waveforms compared to ultrasound measurements, shown in dashed lines, at all major inlets and outlets and at an intermediate proximal location used to validate the models [28].

3.3. Future Directions of Abdominal Computational Fluid Dynamics Modeling.

As illustrated in this section, CFD modeling using AngII-infused apoE^−/− mice has provided insight into hemodynamic influences on AAA formation. However, to the authors' knowledge, no other AAA model in mice has been combined with CFD simulations, such as the periarterial calcium chloride or elastase models. AAAs in these models are surgically induced by focal application of either calcium chloride or elastase, and are not driven by hemodynamic changes. As a result, hemodynamic predictors of aneurysm formation are less interesting. However, assessment of how CFD simulations differ during disease progression with these other animal models could provide insight into how specific alterations to the aorta affect hemodynamics. In addition, longitudinal studies of AAA formation in mice can continue to characterize the hemodynamics involved in AAA formation, as the use of multiple and higher quality imaging modalities make flow measurements and the characterization of complex geometries possible. Although CFD models of the abdominal aorta often use a rigid wall approximation due to computational necessity or lack of experimental data, such an assumption fails to incorporate the dynamic motion of the proximal and distal vessel. Current efforts are directed toward better incorporation of this deformation (including through FSI models [35]); however, these studies are still limited in number. Finally, recent research has begun to assess how aortic growth and remodeling affects continued aneurysm expansion [17].

4. Thoracic

4.1. Overview.

The thoracic cavity has been divided into two main vascular regions for this review: (1) the thoracic aorta, including the aortic arch and proximal portions of branching vessels, and (2) the coronary arteries. The thoracic aorta is the initial and largest artery in the body, responsible for distributing blood to systemic circulation, and can be subject to a variety of diseases such as aortic coarctation, thoracic aortic aneurysm, dissection, and atherosclerosis. Unfortunately, animal models for each of these pathologies with associated CFD research remains limited (e.g., thoracic aortic aneurysm and dissection). Thus, the following discussion will focus on diseases that have been studied in greater detail. For example, the coronary arteries ensure healthy cardiac function by providing oxygen and nutrients to myocardial tissue. Compromises to coronary blood flow (e.g., coronary artery disease) can thus have rapid systemic effects and often require immediate clinical intervention. Understanding the hemodynamics of both the aorta and coronary arteries is critical to ensuring the proper type and timing of potential interventions.

4.2. Aortic Coarctation.

Coarctation of the aorta is a localized narrowing of the aortic arch that accounts for roughly 5% of all congenital heart defects [51,52]. Even after repair, patients with coarctation have reduced lifespans due to compounding cardiovascular problems such as hypertension, aneurysms, and early onset coronary artery disease [53]. It has been hypothesized that altered hemodynamics and vascular mechanics from coarctation are the primary factors associated with these complications [54], prompting further investigation using CFD models. Menon et al. studied the hemodynamics in rabbit aortic arches before and after coarctation repair [53,55]. Rabbits had either permanent silk or degradable Vicryl sutures placed around their aortas to mimic untreated and treated coarctation patients, respectively. Magnetic resonance angiography and PC-MRI captured vascular geometry and blood velocity information as inputs for the simulations. Blood pressure, WSS, TAWSS, and OSI were calculated and compared between groups. The authors found that even with a successful coarctation repair and restored blood pressure gradient, WSS values distal to the coarctation remained compromised compared to healthy control rabbits, suggesting further improvements to current coarctation treatments are needed [53].

Comparable studies have also been performed in smaller animal models, incorporating inflammatory protein expression information. Willett et al. studied a murine model of coarctation to test how low magnitude OSI versus unidirectional high-magnitude WSS affects the inflammatory protein profile of endothelial cells [56]. While aortic coarctation more commonly forms in the thoracic aorta in humans [57], this mouse model was produced by placing a heat-reactive expandable nitinol clip underneath the aorta directly above the celiac artery. MRI data of the healthy and compromised aorta were acquired to build a CFD model and simulate the underlying hemodynamics, subsequently quantifying WSS and cross-sectional velocity vectors. Co-localized protein expression showed that the area of low OSI distal to the coarctation had increased vascular cell adhesion molecule-1 (VCAM-1) levels, a representative inflammatory protein. These results suggest that the coarctation disturbed the unidirectional flow distal to coarctation and induced an athero-susceptible environment within the aorta [56]. Interestingly, while this study focused on the hemodynamics distal to the coarctation, the relationship found between OSI and inflammatory protein expression has also been shown to hold up in additional studies focused on plaque formation, as discussed below.

4.3. Aortic Atherosclerosis.

Atherosclerotic plaque development within the aortic arch increases the risk of cerebrovascular disease and stroke [58]. Recent CFD studies of plaque-forming animal models have provided insight into the role of aortic geometry and blood hemodynamics on atherosclerosis formation. Peiffer et al. studied the effects of aortic taper on wall shear stress in atherosclerotic lesion formation [59]. Micro-CT images of corrosion casts from rabbit aortas were used to reconstruct tapered and un-tapered geometries with varied degree of taper and blood flow velocities. WSS patterns were altered with the degree of taper within atherosclerotic lesions, with plaque forming more frequently in areas of low shear stress [59].

In a similar study, researchers examined the effects of wall shear stresses on atherosclerotic plaque formation in mice [36]. Micro-CT images were acquired from C57BL/6 wild-type mice to obtain aortic geometries, and Doppler U.S. was used to measure blood velocity in the ascending aorta. Protein expression of intercellular adhesion molecule-1 (ICAM-1) and VCAM-1 was mapped and compared with WSS estimates at several locations within the aortic arch and its branching arteries. Areas with low WSS were predominantly found in the inner curvature of the arch and demonstrated lower expressions of ICAM-1 and VCAM-1. Furthermore, cell nuclei in those areas aligned parallel with WSS vectors, suggesting that the directionality of WSS vectors might be more crucial to lesion development than magnitude alone [36]; however, further research is necessary to fully support this claim.

Comparable studies have shown similar trends of low WSS in the aortic arch correlating with the spatial distribution of atherosclerotic plaques [14,42,60–63]. Figure 4 illustrates these common findings, showing the spatial relationship between low TAWSS, higher OSI, and the distal portion of a large plaque, suggesting a mechanism for continued plaque growth. These studies have also suggested the potential for high WSS to play a role in plaque rupture, causing downstream cerebrovascular complications such as myocardial infarction and stroke. Nevertheless, scaling considerations between small animals and humans must be made due to the differences in hemodynamics properties. For example, some studies have noted the role of relatively high Reynolds numbers in humans and subsequent higher variation in WSS along the aortic arch [62,63]. This indicates a need for a more complete understanding of the hemodynamic environment to translate findings from small animal to larger species.

Fig. 4.

Surface and cross-sectional reconstruction of a mouse aortic arch: (a) showing the ascending aorta (AA), descending aorta (DA), brachiocephalic artery (BCA), left common carotid artery (LCC), and left subclavian artery (LS) afflicted by atherosclerotic plaques. Cross-sectional image from a μCT scan (b) from which geometries are derived. CFD results were used to quantify time-averaged wall shear stress (TAWSS; (c)), oscillatory shear index (OSI; (d)), and relative residence time (RRT; (e)) [42].

4.4. Coronary Atherosclerosis.

The coronary arteries branch off the aorta at the sinus root and provide oxygenated blood to the cardiac musculature. Assessing the health of coronary arteries presents a unique problem due to their relatively small cross-sectional area and rapid translation with the myocardium. Due to these obstacles, most animal coronary research utilizes either pigs or dogs [64–67]. The use of smaller animals (e.g., rats and mice) limits the accessibility of standard methods for assessing coronary pathologies, including cardiac catheterization and angiograms, which are invasive and designed for human-sized subjects [68]. While the majority of the coronary-oriented CFD research field has focused on human data, potentially due to the routine acquisition of such information in the clinic, animal models have proved to be an important test-bed for novel clinical interventions. LaDisa et al. used a canine model to investigate both hyperplasia and restenosis, and in both notable side effects observed clinically, after placement of different types of coronary stents [69]. By placing a slotted-tube stent in the left anterior descending (LAD) artery, they found that wall shear stress was reduced by 77% in their CFD model. These results implicate stent geometry as a possible cause of coronary restenosis.

Although both dogs and pigs are commonly used in coronary research, pigs demonstrate closer morphology to humans [70]. Su et al. recently used the CT datasets of swine hearts as a basis for an anatomically accurate CFD simulation with pulsatile flow to better understand both upstream and downstream flow changes due to atherosclerotic lesions [71]. Stenosis severity varied within the CFD simulation to mimic disease progression over time. They confirmed that CFD can determine the significance of a stenotic lesion based on cross-sectional area reduction. As shown in Fig. 5, the left anterior descending artery lesion was nonsignificant up to 75% area reduction, defined as having a minimal pressure drop and unchanged flow distribution of downstream branches. Zhang et al. recently published comparable findings regarding the use of CFD in the left anterior descending coronary arteries of swine hearts [50]. They compared CT-derived fractional flow reserve (FFR_CT) via CFD to invasive angiography, the gold standard for determining coronary artery intervention. They found evidence of branch stealing (nonstenotic branches “stealing” blood from stenotic branch) and confirmed the >75% area reduction requirement for significant stenosis. In addition, by using the same modeling strategy, they could obtain nearly identical FFR_CT values to that of invasive FFR in two human patients. Although the use of CFD within the clinical setting is not yet commonplace, these findings corroborate the usefulness of this technique as a noninvasive method to guide clinicians in the future treatment of coronary artery disease, a focus of HeartFlow, Inc. (Redwood City, CA) [72].

Fig. 5.

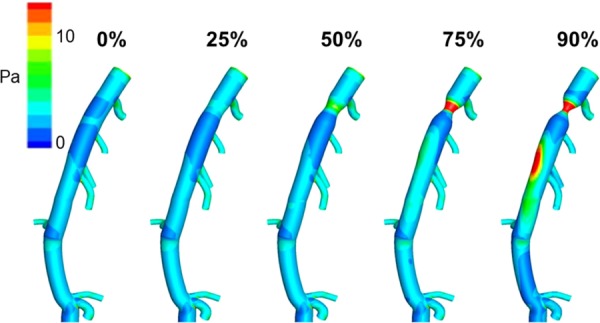
Time-averaged wall shear stress distributions at varying levels of proximal stenosis on a porcine LAD model. Points of maximal WSS (black arrows) shift from the ostium of branching vessels to the point of stricture when the stenosis reaches 75%. At 90% stenosis, regions of maximal WSS are also observed distal to the stricture along the outer curvature of the LAD [71]. (Reprinted with permission from Elsevier copyright 2014).

4.5. Future Directions in Thoracic Computational Fluid Dynamics Modeling.

While only a few vascular diseases are highlighted previously, a wide variety of pathologies afflict the thoracic aorta and the use of CFD in combination with animal studies has been underutilized. For example, the presented coarctation studies in rabbits used 10-week-old animals which are representative of an adult human; however, coarctation in humans often manifests as a congenital disease; thus, a more developmentally appropriate animal model may be beneficial. Furthermore, improvements to in vivo imaging technologies would likely enhance the accuracy of the corresponding CFD simulations. The study by Willett et al. did note imaging artifacts at the location of the nitinol clip in both MRI and U.S.; thus, slight errors in their geometrical models may exist [56]. Improved imaging protocols may eventually mitigate such issues and ensure reliability in the corresponding CFD simulations. Regarding the coronary vasculature, translation of CFD modeling into clinical care has already begun, as demonstrated with the HeartFlow FFR_CT technology [72]. Thus, the use of animal models may be particularly useful to help evaluate the next generation of coronary artery disease treatments. Overall, animal models of thoracic disease provide increased flexibility for experimenting with novel treatments, meaning that data collected from baseline, acute, and chronic stages can be systematically combined with CFD simulations both before and after intervention to quantify changes in hemodynamics.

5. Cerebral

5.1. Overview.

The cerebral vascular system includes blood vessels that carry blood to, from, and around the brain, including the carotid arteries, vertebral arteries, circle of Willis, and jugular veins. Common forms of cerebrovascular disease include carotid artery atherosclerosis, and intracranial aneurysms (ICA). Similar to other regions of the body, onset and prognosis of cerebrovascular diseases is dependent on local flow properties, vascular biomechanics, and tissue remodeling [20,73–76], creating a need for animal models and CFD analysis. CFD enables quantification of local flow properties including WSS and OSI, while small animal models allow observations on vascular remodeling [77]. This section highlights the relationship between hemodynamics, vascular remodeling, and the pathogenesis of both carotid artery atherosclerosis and ICAs.

5.1.1. Carotid Artery Atherosclerosis and Intracranial Aneurysms in Animal Models.

Common animal models for carotid artery atherosclerosis and ICA studies include mice, rabbits, and minipigs [78]. Carotid artery atherosclerosis is characterized by the buildup of plaque within the arterial wall, causing stenosis. Carotid artery atherosclerosis and ICAs can be induced by systemic or local methods [78], or some combination of the two [75,79]. Systemic methods most often incorporate genetic knockout or modification, hyperlipidemia, hyperglycemia, or hypertension. However, because mice, rabbits, and swine are generally resistant to atherosclerosis and carotid artery stenosis [78], systemic methods are often not practical. Thus, local and surgical methods are needed to induce carotid artery stenosis or ICA in animals. The most common methods to surgically induce carotid atherosclerosis in animal models include balloon injury, partial or complete ligation of the carotid artery, or implantation of a carotid artery collar or “cuff.” ICAs form as one or more weakened arterial walls swell outward, most often into a saccular or berry shape. Some aneurysms may tear and cause a subarachnoid hemorrhage or stroke. Age, hypertension, sex, familial history of aneurysms, and defective capillaries caused by cholesterol deposits increase the risk of both aneurysm occurrence and rupture [80].

5.2. Carotid Artery Atherosclerosis.

Carotid artery stenosis frequently causes downstream vortices and circulating flow. This circulating flow creates a low-pressure region, where blood may oscillate with increased residence times near the arterial wall. Ultimately, this disturbed flow disrupts the local WSS distribution commonly leading to endothelial dysfunction. Similar to other areas of the body, low and oscillatory WSS is a main contributor to the build-up of unstable plaque [33,74,81] and can also lead to arterial remodeling, a natural response aimed at restoring the WSS to normal levels. Arterial remodeling is marked by neointimal thickening, the reduction of smooth muscle cells, and disruption of the endothelium [82]. The modeling approaches discussed in this section can be categorized into either fluid-only (standard CFD) or FSI approaches.

To investigate how different CFD approaches influence simulation results in terms of WSS distribution for the study of atherosclerosis, De Wilde et al. tested three computational techniques: steady-state CFD (SS-CFD), pulsatile CFD, and FSI [83]. The study concluded that the normalized WSS patterns were the same for all the modeling approaches despite the different blood flow and boundary conditions. In the FSI simulations, external tissue support was considered and modeled using linear springs, taking into account the elastic capacity of the wall [84]. The simulations showed consistent spatial distribution maps of TAWSS and RRT, both of which are indicators of atherosclerosis-prone regions when low [84]. These data suggest that different CFD approaches can lead to similar results while still providing a robust description of cerebral hemodynamics.

By coupling in vivo and ex vivo data with CFD, animal studies have improved our understanding of both the pathology and the hemodynamics of carotid artery atherosclerosis in a way that would be challenging with human subjects. Studies have found that changes in flow and WSS lead to ECM degradation through matrix metalloproteinase activity and collagen deposition [81]. Furthermore, changes in flow have also been found to lead to an inflammatory response through changes in endothelial cell function [85]. Analysis of isolated RNA from tissue ex vivo allowed the quantification of proatherogenic gene expression in hyperlipidemic mice after partial carotid ligation [33]. The data from this study showed that regions of low and oscillatory WSS were correlated with increased accumulation of cholesterol clefts and intraplaque neovascularization [33]. The study of both mechanical stress and inflammation suggest that lowered TAWSS and OSI both contribute to atherosclerosis formation and may influence which lesions become vulnerable plaques [81]. These results provide evidence directly linking disturbed flow to atherogenesis through the comparison of CFD simulations with mechanosensitive gene expression.

5.3. Intracranial Aneurysm.

Mechanical stresses and molecular changes influence geometry, flow, and wall remodeling where hemodynamics plays an important role [82]. Thus, the study of ICA has begun to focus on other factors besides WSS distributions and changes over time [33,81,82,86]. For instance, Wang et al. correlated molecular expressions with the local hemodynamics determined by CFD of a de novo bifurcation canine aneurysm model. Comparison between immunohistochemistry and the detailed in vivo 3D flow field led to the identification of a specific hemodynamic environment in which pathological molecular changes were confined to areas of high WSS and high positive WSS gradient [86]. In a similar fashion, Meng et al. investigated destructive remodeling in the vessel wall with ex vivo analysis using a canine model [3]. Three different hemodynamic microenvironments with varying flow characteristics were identified along the wall of the carotid bifurcation. The region undergoing destructive remodeling resembled the early stages of ICA development in terms of endothelium loss and vessel wall thinning [3].

Other work using an elastase-induced, saccular aneurysm model in rabbits created at the origin of the right common carotid artery to investigate how hemodynamics affects ICAs [87]. The use of extensive ex vivo analysis including immunohistochemistry, gel zymography, Western blots, and scanning electron microscopy revealed a spatially localized correlation between decreased WSS and the biological response [87]. These data have helped to improve our understanding of the molecular influences on disease progression that stem from hemodynamics changes.

5.3.1. Computational Fluid Dynamics Model Improvements.

As discussed previously, a major goal of CFD is to accurately simulate specific disease states or vasculature and to use this information to predict or influence a clinical outcome. Wong et al. reviewed the potential CFD has to become a tool for clinical decision-making [30]. After consulting neurosurgeons and reviewing CFD ICA literature from 1970 to 2010, the authors suggested that in the future there is a role for CFD models in the clinic as more work is done to incorporate multivariate analysis [30]. This review showed that a focus on repeatability was critical, something that more studies have taken the time to incorporate [88].

Recent work has focused on combinational studies to glean novel information from multiple techniques. For example, co-mapping histology and simulation results have been used to generate hemodynamic profiles and quantify the corresponding vascular response from the same region within the basilar terminus in a rabbit model [89,90]. The results revealed that regions of high WSS with a positive WSS gradient were associated with destructive remodeling and possible aneurysm initiation [90]. In summary, these animal studies support the idea that CFD combined with other types of imaging or ex vivo analysis can provide novel insight into vascular disease initiation and progression.

5.3.2. Computational Fluid Dynamics Models That Employ Devices.

As CFD simulations have become more comprehensive, research questions associated with devices have begun to be studied. Treatment outcomes associated with endovascular devices, such as a flow diverter used to treat cerebral aneurysms, can be predicted using CFD. Previous work characterized stent deployment with an adaptive grid embedding technique [91] or workflow-based finite element analysis [92]. Other studies used two-dimensional and 3D modeling to identify the optimal stent strut shape for minimizing the velocity of the blood flow through the diverter [93], estimate the effects of undersizing or oversizing flow diverter stents [94], and quantify the reduction in flow rate when flow diverter stents unintentionally block off or “jail” collateral arteries [95]. Finally, Huang et al. used CT scans of rabbit aneurysms treated with flow diverters as inputs for CFD simulations (Fig. 6). This study confirmed that the flow diverters improved the hemodynamics by inducing thrombus formation within the aneurysm sac [96], a finding confirmed by others [97]. These studies highlight the power of CFD to study the hemodynamic effects of implantable endovascular devices.

Fig. 6.

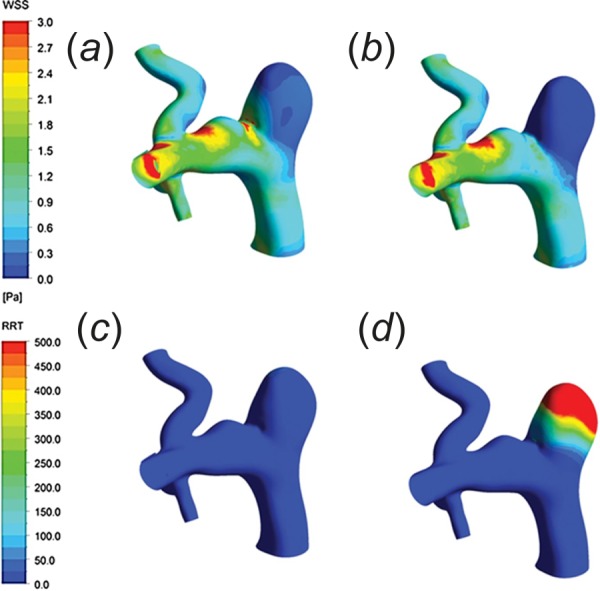
Wall shear stress distribution before (a) and after (b) implantation of a flow diverter. Relative residence time distribution before (c) and after (d) implantation illustrates higher values within the aneurysm after the device was deployed [96]. (Reprinted with permission from Wolters Kluwer Health, Inc., copyright 2013).

5.4. Future Directions in Cerebral Computational Fluid Dynamics Modeling.

Moon et al. suggests that future cerebral CFD work may focus on characterizing the non-Newtonian properties of blood, capturing the elasticity of complex vasculature, and better recreating precise pulsatile blood flow waveforms [20]. The challenge with subject-specific cerebral image data stems, in part, from the limited ability of MR or CT to visualize the small cerebral vessels [29] and uncertainty when prescribing appropriate boundary conditions [20]. For example, zero pressure outlet and traction free boundary conditions are regularly applied for boundary outlets due to their modeling simplicity [20]. However, these approaches have difficulty accounting for backward pressure from wave reflections. This influx of blood is the result of complex interactions between downstream arteries, pulsatile flow, and the elasticity of blood vessels [20]. To capture this, more advanced approaches, such as an impedance boundary condition, can be used which better reflect the true hemodynamic environment by mimicking the timing and the magnitude of the wave reflections associated with pulsatile flow [20]. As the ability to utilize more advanced imaging techniques and incorporate more sophisticated CFD approaches continues to expand, CFD simulations have the potential to become a powerful and accurate tool capable of impacting the care of patients with cerebrovascular disease [20,29].

6. Further Applications

This section highlights animal CFD studies of arteriovenous fistulas (AVF) and pulmonary artery grafts, both common surgical treatments that are not described in the previous sections.

6.1. Arteriovenous Fistulas.

Computational fluid dynamics assessment has been used to understand the hemodynamics within surgically created AVF for hemodialysis patients with end stage renal disease [98–101]. The preferred access method for long-term hemodialysis is an autologous AVF that is created through an anastomosis of an artery and vein. Most AVFs are created in the upper limb by connecting the radial/brachial artery with the cephalic vein or the brachial artery with the basilic vein. An important clinical consideration is the vessels' configuration, which can be side-to-side, end-to-side, or end-to-end. Since limited anatomical locations exist for placement of autologous AVFs in humans, the high incidence of AVF failure due to nonmaturation or early failure due to restenosis is a serious clinical issue. The common failure mechanism is venous stenosis that is caused by altered velocity and WSS due to the increased flow rate. To study the mechanisms of AVF failure, canine [98] and swine [99–102] animal models have been used to compare different AVF surgical procedures, namely parallel or perpendicular arterial connection to the venous system. Based on the CFD results, the arteriovenous junction orientation had a significant effect on WSS [100–102], leading to reduced vessel diameter and intimal thickening when not optimized [98,99], and highlights the usefulness of CFD and animal research for the improvement of AVF creation for hemodialysis access.

6.2. Pulmonary Artery Grafts.

Improving surgical repair strategies for congenital abnormalities that affect the heart and pulmonary circulation is an area of clinical interest [103]. Specifically, in the right ventricle and pulmonary arteries, hemodynamics has been shown to influence the degeneration of implanted valves, locations of thrombus deposition, atherosclerosis, and conduit dysfunction [104,105]. In a series of studies, Berdajs et al. used intravascular flow probes and postmortem sizing of porcine pulmonary arteries to run CFD simulations that consistently identified local low-shear stresses, relatively high pressures, and complex flows in the right ventricular outflow tract when it is oversized [64,104]. These findings could help explain the observed intimal hyperplasia and arteriosclerosis that prompt the need for re-intervention [104–106]. Although these initial studies used a steady flow assumption, they still demonstrate a useful application of CFD to a clear clinical implication. Further work focused on using CFD to study the hemodynamics associated with Glenn, Fontan, and Norwood procedures; however, the primary body of research for these procedures uses human data [107–109]. As animal models for significant congenital heart defects improves, CFD modeling stands ready as a tool to help obtain prognostic information with potential clinical insight.

7. Discussion

Computational modeling of cardiovascular hemodynamics is becoming an increasingly popular tool in biomedical research. Adoption has been aided by advancing computational technology, a growing community of CFD researchers, and a developing array of software options. Today, select commercial cfd software packages can provide physicians with important clinical metrics from patient-specific data [110]. These bridges to clinical integration suggest that CFD techniques may soon take on a greater role in cardiovascular disease diagnosis and treatment planning. While this has rightfully prompted a large body of CFD research to focus on human data, the use of these techniques in animal studies should not be overshadowed.

Animal models afford researchers the opportunity to easily perform longitudinal studies and optimize computational schemes in a controlled study. Recent works by several groups have investigated the use of CFD for surgical treatment planning and prognosis of patients with rare disorders such as Kawasaki's disease [111], aortic coarctation, and the Fontan procedure [112–116]. These early publications illustrate the use of CFD in rare disease studies and lay a roadmap for work going forward. However, given their rarity, it is difficult to find an appropriate number of patients with sufficient image data and outcomes. Animal models, while not ideal for all rare disorders, could be developed and used as an alternative to patient studies, becoming a key component when studying these less common disorders. Furthermore, animal studies combined with CFD can be used to predict outcomes that would result from a variety of surgical options. It would be valuable to quantify flow changes caused by different flow altering surgeries aimed at treating fusiform ICAs [117]. Animal studies could be used to image and simulate the flow conditions before and after vessel occlusion, or be used to prescribe boundary conditions for CFD simulations of postoperative flow fields in patients. While the focus should remain on improving our understanding of human disease progression and treatment planning, animal studies remain an invaluable tool when human data are not available or difficult to obtain. Additionally, the opportunity for longitudinal studies increases CFD's utility to many more common diseases.

Vascular imaging to obtain vessel geometry has become commonplace in animals regardless of size, but direct quantification of hemodynamics remains a challenge in small animals [118–120]. PC-MRI can provide blood velocity; however, spatial resolution is limited which often prevents the study of flow in small arteries, arterioles, and capillaries. Spatial resolution limitations are not as prevalent with high-frequency U.S., but U.S. requires proper positioning of the transducer and is highly sensitive to gas and large bones [119]. Small animals exhibit fast cardiac and respiratory rates, making high frame rate hemodynamic imaging extremely difficult without gating. Even though current CFD techniques allow for complex simulations to be performed in small animals, improvements in direct hemodynamic imaging are still needed to allow for direct comparisons between simulation and experimental results. Indeed, future small animal efforts can be advantageous in terms of cost, cohort size, and the ability to transgenically modify the animals compared to large animal studies.

While CFD modeling in animal studies has been underutilized for the most part, the scope of applications up to this point has been impressively broad. In the studies highlighted in this review, models range from large elastic arteries branching directly from the heart to small muscular arteries leading to the brain and peripheral limbs. For the most part, early computational flow models in humans and animals utilized highly idealistic vascular geometries [6,121]. With technology advancements and application- and subject-specific CFD algorithms, animal models have benefited from increasingly accurate imaging information, mitigating the need for idealized geometries. Further, unlike humans who experience flow in larger arteries that can approach turbulence, small animal models are well below this range [22,122], a feature that is beneficial to simulations assuming laminar flow.

In summary, improving computational modeling approaches in animal studies may someday afford greater understanding of the relationship between disease models and the human conditions they mimic. With continued effort, disease progression can be captured through noninvasive imaging and CFD simulations, both of which can aid in understanding how changes in vascular geometry alter flow, and vice versa. Although species differences should always be considered, allometric scaling studies can be performed to elucidate how differences between species size may play a role in disease progression. For now, CFD in animal studies remains underutilized, but modeling of physiological flow in preclinical studies has great promise for both further development of computational methods and the study of vascular disease.