Optimizing Machine Learning Methods to Improve Predictive Models of Alzheimer’s Disease

Abstract

Background:

Predicting clinical course of cognitive decline can boost clinical trials’ power and improve our clinical decision-making. Machine learning (ML) algorithms are specifically designed for the purpose of prediction; however. identifying optimal features or algorithms is still a challenge.

Objective:

To investigate the accuracy of different ML methods and different features to classify cognitively normal (CN) individuals from Alzheimer’s disease (AD) and to predict longitudinal outcome in participants with mild cognitive impairment (MCI).

Methods:

A total of 1,329 participants from the Alzheimer’s Disease Neuroimaging Initiative (ADNI) were included: 424 CN, 656 MCI, and 249 AD individuals. Four feature-sets at baseline (hippocampal volume and volume of 47 cortical and subcortical regions with and without demographics and APOE4) and six machine learning methods (decision trees, support vector machines, K-nearest neighbor, ensemble linear discriminant, boosted trees, and random forests) were used to classify participants with normal cognition from participants with AD. Subsequently the model with best classification performance was used for predicting clinical outcome of MCI participants.

Results:

Ensemble linear discriminant models using demographics and all volumetric magnetic resonance imaging measures as feature-set showed the best performance in classification of CN versus AD participants (accuracy = 92.8%, sensitivity = 95.8%, and specificity = 88.3%). Prediction accuracy of future conversion from MCI to AD for this ensemble linear discriminant at 6, 12, 24, 36, and 48 months was 63.8% (sensitivity = 74.4, specificity = 63.1), 68.9% (sensitivity = 75.9, specificity = 67.8), 74.9% (sensitivity = 71.5, specificity = 76.3), 75.3%, (sensitivity = 65.2, specificity = 79.7), and 77.0% (sensitivity = 59.6, specificity = 86.1), respectively.

Conclusions:

Machine learning models trained for classification of CN versus AD can improve our prediction ability of MCI conversion to AD.

INTRODUCTION

The burden of Alzheimer’s disease (AD) is estimated to more than double current levels by 2060, when 13.9 million Americans are projected to have the disease [1]. Despite the high burden of this disease, preventive and therapeutic interventions for AD have largely failed. Failure of these trials are thought to be partially due to biological heterogeneity of AD and due to the frequent occurrence of mixed dementia pathologies [2, 3]. Many investigators have attempted to characterize this heterogeneity using different predictive methods with varying degrees of success [4]. In recent years neuroimaging techniques such as positron emission tomography (PET) and magnetic resonance imaging (MRI) have been proposed as a proxy for brain pathology and are recommended as effective diagnostic and prognostic tools [5]. However, a significant proportion of population are cognitively normal and biomarker positive or vice versa, making the utility of using these biomarkers as in univariate models for predicting clinical outcomes questionable [6].

A growing number of studies have been using machine learning (ML) and multivariate analysis methods to classify individuals at risk of progression to AD. A combination of demographics and imaging markers are typically entered into these models [7]. These studies largely suggest the advantage of using multivariate analysis over univariate techniques as they account for the relationship between variables and are less prone to classification errors. Some of the prior studies that have used ML methods for predictive analysis are limited by reporting performance of the models at short and single follow-up times (e.g., 1 or 2 years) and using a relatively small sample [8, 9]. Performance of ML methods in larger samples with longer duration of follow-up is not well studied. When sample size is smaller, the ratio of measures (features) to participant will be higher and predictive models are more prone to overfitting. Therefore, to develop generalizable prediction models we need to evaluate validity of models in larger samples.

In this study, we used demographics and structural MRI measures for classification of cognitively normal (CN) versus AD participants (training set) from the Alzheimer Disease Neuroimaging Initiative (ADNI) and applied the trained model to participants with mild cognitive impairment (MCI) from ADNI (independent test set) to predict AD conversion. Our specific aims were 1) to compare the performance of different linear and non-linear classifiers for the classification of CN versus AD; 2) to compare the effective gain in classification accuracy by using multiple brain structures as opposed to a single brain region (hippocampus); 3) evaluate the additive effect of age, sex, education, and APOE4 genotype on performance of classifiers; and 4) evaluate the performance of the best classifier in prediction of conversion to AD in the test sample at different follow-up times up to 4 years.

METHODS

Study design and participants

The data used for this analysis were downloaded from the ADNI database (http://www.adni.loni.usc.edu) in September 2018. The ADNI is an ongoing cohort, which was launched in 2003 as a public–private partnership. The individuals included in the current study were initially recruited as part of ADNI-1, ADNI-GO, and ADNI-2 between September 2005 and December 2013. This study was approved by the Institutional Review Boards of all participating institutions. Informed written consent was obtained from all participants at each site.

A total of 1,329 participants from ADNI-1, ADNI-GO, and ADNI-2 were eligible for this study. Eligible individuals completed baseline MRI and had at least one wave of follow up. Participants whose scans failed to meet quality control or had unsuccessful automated image analysis were excluded from this study. At the time of enrollment, each individual was assigned to one of the three diagnostic groups of cognitively normal (CN), MCI, or mild AD. The CN, MCI, and mild AD groups included in current study comprised of 424, 656, and 249 individuals, respectively.

All ADNI participants with the diagnosis of MCI, were diagnosed as having amnestic MCI; this diagnostic classification required Mini-Mental State Examination (MMSE) scores between 24 and 30 (inclusive), a memory complaint, objective memory loss measured by education-adjusted scores on the Wechsler Memory Scale Logical Memory II, a Clinical Dementia Rating (CDR) of 0.5, absence of significant impairment in other cognitive domains, essentially preserved activities of daily living, and absence of dementia. The participants with AD had to satisfy the National Institute of Neurological and Communicative Disorders and Stroke–Alzheimer’s Disease and Related Disorders Association (NINCDS-ADRDA) criteria for probable AD, and have MMSE scores between 20 and 26, and CDR of 0.5 or 1.

Each participant received a baseline clinical evaluation and was revaluated during follow-up at 6 months, 1 year, 2 years, 3 years, and 4 years. At each clinical visit, participants were assigned to a diagnostic group (CN, MCI, or AD). Based on diagnosis at each follow up, participants with an initial diagnosis of MCI were assigned to one of the three subgroups:

1. Progressive MCI subgroup (MCI-p): Individuals who progressed to AD during the follow-up.

2. Stable MCI subgroup (MCI-s): Individuals who did not have a change of diagnosis and remained stable during the follow up time.

3. MCI reversion subgroup (MCI-r): Individuals who had a reversion to CN during the follow up time.

To facilitate interpretation of the performance of the classifier, MCI-r and MCI-s groups were merged into one group of non-progressive MCI (MCI-np). To train classifiers with measurements that belong to CN participants, they were assigned to two groups: 1) stable CN (CN-s; remained CN after 2 years of follow-up; and 2) progressive CN (CN-p who progressed to MCI or AD after 2 years of follow up). None of the individuals with AD diagnosis at baseline had reversion to MCI or normal during follow up (Fig. 1).

Fig. 1.

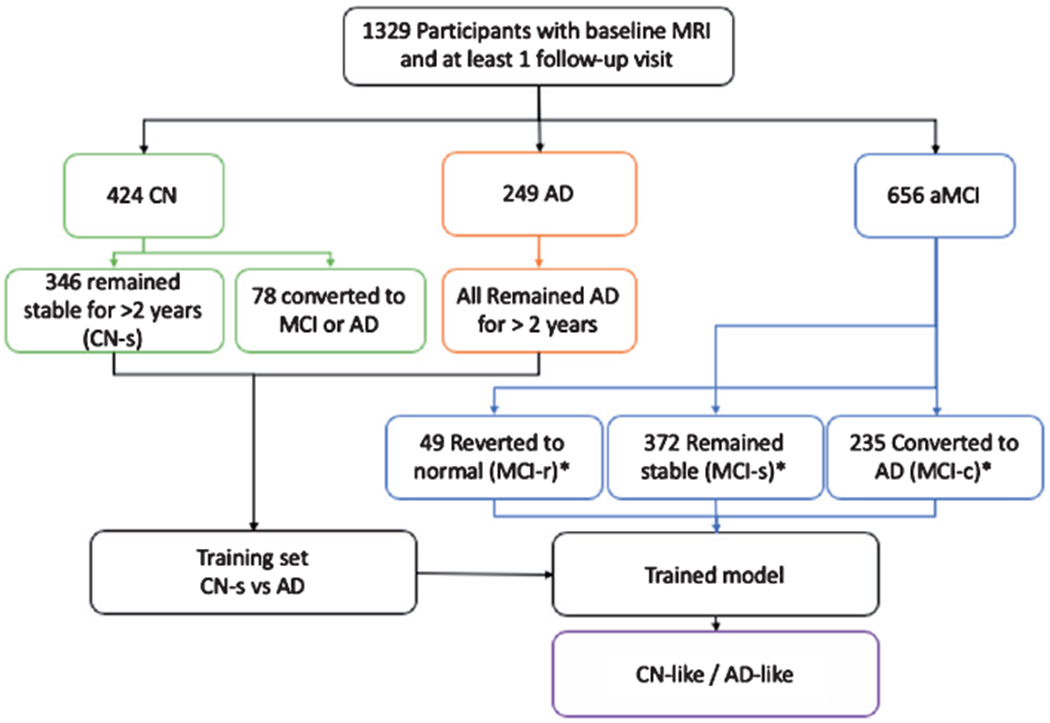
Study design diagram. *based on diagnosis at last follow-up visit.

MRI acquisition and preprocessing

MRIs were obtained across different sites of ADNI study with a unified protocol (For more information, please see http://www.adni.loni.usc.edu). MRI data were automatically processed using the FreeSurfer software package (available at http://surfer.nmr.mgh.harvard.edu/) by the Schuff and Tosun laboratory at the University of California-San Francisco as part of the ADNI shared data-set. FreeSurfer methods for identifying and calculation of regional brain volume are previously described in detail [10].

Data analysis

Feature selection

Demographics including age, sex, and education, APOE4 status, and volumetric MRI measures were used as features in the predictive models. MRI measures of interest were volumetric measures regions of interests (ROIv) derived from FreeSurfer software. A total of 47 cortical and subcortical ROIs, parcellated by FreeSurfer, were included. ROIv were normalized for total intracranial volume (TICV) and the ratio of ROIv to TICV [i.e., (ROIv/TICV) x mean whole population ROIv] was used in the analyses and reported throughout manuscript unless otherwise specified.

We chose four different feature-sets and compared the accuracy of models using each set: 1) Hippocampal volume; 2) Hippocampal volume plus age, sex, education, APOE4; 3) All MRI volumetrics; 4) All MRI volumetrics plus age, sex, education, APOE4. Hippocampal volume has been reported as the single most useful structural measure in previous prediction models in preclinical stages [8]. Therefore, we specifically chose hippocampal volume as the only ROI in two of the feature-sets.

Classification and pattern recognition models

In the present study, we used six different linear and nonlinear supervised machine learning methods for classification and pattern recognition:

1. Decision trees (DT). DTs are powerful classifiers that sequentially dichotomize the feature space into regions associated with different classes. As such, they are capable of learning arbitrarily complex Boolean functions that map the features/predictors to class labels [11]. While they are widely used due to their ease of training based on labeled data, and robustness to missing features, they are known to be unstable due to their hierarchical structure: an incorrect decision at a high node in the tree would propagate down the nodes and results in misclassification (for details, see [12]). We used a fine DT (f-DT) model in the current study.

2. Support Vector Machines (SVMs). SVMs aim at inferring regularities from a set of labeled training examples by modeling the mapping from features to labels as a linear combination of kernels. When the kernel is a linear function of the features, the classifier is referred to as a linear SVM (L-SVM). While there are countless choices of decision boundaries that can separate two classes, SVM finds a decision function with the maximal the margin between the training examples and the resulting decision surface, namely the optimal margin hyperplace (OMH). The support vectors refer to examples in the data set that line on the margin, and are thus critical to the separation of the two classes. In brief, given a training set of size K: (x_k, y_k)_k = _1…K, where x_k in R^d are observations, and y_k in (−1, 1) are corresponding labels, linear SVMs find a hyperplane separating the two classes with the optimal margin (for details, see [13, 14]). We used an L-SVM in this study.

3. K-nearest neighbor classification (KNN). KNNs are among the simplest, yet effective machine learning methods that use the idea of polling among the labels of the training examples closest to a new sample, and assigning the majority vote as its predicted label. To this end, for a positive integer K, the Euclidean distance between the new sample and the elements of the training set are computer and K training examples with the smallest distance are chosen to poll from (for details, see [15]). In brief, the Euclidean distance is specified by the following formula, where p is the new sample to be labeled and q is any of the examples in the training set, each having n features. The term p_i refers to the value of the i^th feature of example p, while q_i refers to the value of the i^th feature of example q, for i = 1,2, … , n:

   $$dist\left(p,q\right)=\sqrt{{\left(p_1-q_1\right)}^2+{\left(p_2-q_2\right)}^2+\cdots +{\left(p_n-q_n\right)}^2}$$

4. Ensemble Linear Discriminant (ELD). This technique is among the family of classification methods known as ensemble learning, in which the output of an ensemble of simple and low-accuracy classifiers trained on subsets of features are combined (e.g., by weighted average of the individual decisions), so that the resulting ensemble decision rule has a higher accuracy than that obtained by each of the individual classifiers [16, 17]. In this work, we combined linear discriminant functions (i.e., hyperplanes that dichotomize the samples based on subsets of features) to construct the ensemble classifier.

5. Boosted Decision Trees (BDT). Similar to other ensemble methods, boosting is a method of combining many weak learners (in this case DTs) to a strong learner. At each step of the sequence of combining weak learners, participants that were incorrectly classified by the previous classifier are weighted more heavily than participants that were correctly classified. The predictions from this sequence of weak classifiers are then combined through a weighted majority vote to produce the final prediction. Details of the theoretical foundation of boosting and its relationship with established statistical methods is described previously [18, 19].

6. Random Forests (RF). RFs are a combination of DT predictors such that each tree depends on the values of a random vector sampled independently and with the same distribution for all trees in the forest. In other words, a RF is a classifier consisting of a collection of tree-structured classifiers {h(x, θ_k), k = 1,…} where the {θ_k} are independent identically distributed random vectors and each tree casts a unit vote for the most popular class at input x. Details and foundation of RFs techniques used in this paper are described elsewhere [20].

Analysis and computation of machine learning methods were conducted using MATLAB ©(version 2017b) using standard libraries of the classification learner toolbox.

Training models

Data from the two groups of CN-s and AD participants (training-set) were used for training of the models. Models were trained to recognize CN-s versus AD using each of the four feature-sets mentioned above. Considering that we used four classification methods, a total of 16 models were created. A 10-fold cross-validation procedure was used in all models for testing validity of the models. Cross-validation is an established statistical method for validating a predictive model, which involves training several parallel models, each based on a subset of the training data. Then, the model performance is evaluated based on the average accuracy in predicting the labels of the omitted portion of the training data [21]. Cross-validation can detect if models are overfitted by determining how well the model generalizes to other subsets of datasets by partitioning the data.

The performance of each model was calculated based on the percentage of correct classification (accuracy), sensitivity, specificity, positive predictive value (PPV), negative predictive value (NPV), and area under the ROC curve (AUC).

Comparison of classification performance

We used the McNemar test to select the most accurate model [22]. Based on the results of this test the best model was selected for the next step (prediction models).

Prediction of future outcome in MCI participants

Following training of the models, we used the model with best classification performance to predict the clinical outcome of all MCI participants (independent test set). Using baseline data, models assigned MCI participants to CN-like or AD-like groups. The accuracy of the predicted outcome (CN-like or AD-like) was evaluated using the available clinical outcomes from follow-up data. Considering change in proportion of MCI subgroups over time (due to drop outs, death, etc.), the accuracy is reported separately for each wave of follow-up at 6, 12, 24, 36, and 48 months. Furthermore, we computed sensitivity, specificity, PPV, and NPV of the model for predicting conversion to AD at each follow-up time-point.

Assessment of time-to-conversion from MCI to AD

Cox-proportional hazards regression models were used to determine the hazard ratio of incident AD in MCI participants predicted as AD-like versus those predicted to be CN-like. The time variable was amount of time, in years, from baseline to the visit in which AD was diagnosed, or to the most recent visit for censored cases (6-month intervals). Kaplan Meier survival curve for Dementia is presented based on this prediction. Statistical analyses were carried out using SPSS version 25.0.

RESULTS

Demographics and baseline characteristics

Table 1 summarizes participants’ demographics and clinical characteristics. Among MCI participants with 1-year of follow up data available, 87 persons (13.8%) progressed to dementia at 1-year follow up. The number who progressed increased to 109 persons (34.3% of n =318) for participants with available follow-up data at 4 years.

Table 1.

Demographics and clinical characteristics of study participants according to group

Variables	Diagnostic group
	CN (n = 424)	MCI-r b (n = 49)	MCI-s b (n = 372)	MCI-p b (n = 235)	AD (n = 249)
Age	74.3 ± 5.5	68.9 ± 7.6	72.8 ± 7.4	73.0 ± 7.1	74.7 ± 7.7
Sex, male %	50.4	53.1	59.1	57.9	55.3
Education, y	16.3 ± 2.7	17.0 ± 2.3	15.8 ± 3.0	15.7 ± 2.8	15.2 ± 2.8
APOE4 carrier, % a	27	40.8	43.5	69.4	71
Cognitive scores
CDR-sum of boxes	0.03 ± 0.1	1.2 ± 0.8	1.5 ± 0.8	2.0 ± 0.9	4.3 ± 1.6
MMSE	29.1 ± 1.1	28.7 ± 1.4	27.9 ± 1.7	26.9 ± 1.8	23.2 ± 1.9
ADAS-cog	5.9 ± 2.9	6.4 ± 2.7	9.1 ± 3.8	13.11 ± 4.4	19.4 ± 6.7
RAVLT delayed recall	5.9 ± 2.3	3.8 ± 2.4	4.5 ± 2.5	5.0 ± 2.2	1.7 ± 1.7

Plus–minus values are means ± SD.

^aProportion of individuals carrying at least one E4 allele.

^bBased on diagnosis at last available follow-up visit. CDR, Clinical Dementia Rating scale; MMSE, Mini-Mental State Exam; ADAS, Alzheimer’s Disease Assessment Scale; RAVLT, Rey Auditory Verbal Learning Test.

Effect of feature-set on performance of classifiers

As shown in Table 2, feature sets that included demographics and APOE4 status (set 2 and set 4) generally performed better than feature sets without these measures. The choice of feature-set also had distinct effect on performance of different ML method: while decision trees and ensemble linear discriminant models had higher accuracy when multiple MRI volumetrics were included in the feature set, SVM and KNN models performed worse when all volumetric measures were included in the models.

Table 2.

Performance of classifiers in differentiating cognitively normal from Alzheimer’s disease participants

Model/feature set	Accuracy (%)	Sensitivity (%)	Specificity (%)	PPV (%)	NPV (%)	AUC
Fine Decision Trees
HipV	78.3	80.7	74.7	82.1	72.9	0.82
HipV, Demographics, APOE4	81.7	85.1	76.9	83.5	79.1	0.82
MRIv	82.5	86.0	77.5	84.6	79.4	0.81
MRIv, Demographics, APOE4	83.0	85.5	79.4	85.7	79.1	0.82
Linear SVM
HipV	83.4	88.5	75.9	84.0	82.1	0.90
HipV, Demographics, APOE4	85.2	88.5	80.3	86.6	83.0	0.92
MRIv	76.3	95.8	48.1	72.3	88.9	0.94
MRIv, Demographics, APOE4	76.8	96.5	49.0	73.0	89.7	0.95
Fine KNN
HipV	77.8	78.7	76.3	82.7	71.4	0.78
HipV, Demographics, APOE4	79.9	83.5	74.7	82.6	75.9	0.79
MRIv	71.8	94.4	39.3	69.1	83.0	0.80
MRIv, Demographics, APOE4	73.3	95.8	40.9	70.0	87.2	0.83
Ensemble linear discriminant
HipV	83.2	87.1	77.5	84.7	80.7	0.90
HipV, Demographics, APOE4	85.6	90.9	77.7	85.2	85.1	0.90
MRIv	90.8	94.4	85.5	90.3	91.4	0.95
MRIv, Demographics, APOE4	92.8	95.8	88.3	92.2	93.6	0.96
Boosted Trees
HipV	79.4	86.8	68.9	79.9	78.4	0.88
HipV, Demographics, APOE4	83.9	86.9	79.5	85.9	80.8	0.92
MRIv	88.3	91.1	84.3	89.3	86.8	0.93
MRIv, Demographics, APOE4	88.5	91.6	83.9	89.1	87.5	0.93
Ensemble Random Forest
HipV	75.5	81.3	67.1	78.0	71.4	0.88
HipV, Demographics, APOE4	82.9	86.3	77.9	84.9	79.8	0.92
MRIv	88.0	90.5	84.3	59.2	86.1	0.93
MRIv, Demographics, APOE4	88.5	90.8	85.1	89.8	86.5	0.94

HV, hippocampal volume; SVM, support vector machine; KNN, k-nearest neighbors; PPV, positive predictive value; NPV, negative predictive value; AUC, area under curve; HipV, hippocampal volume; MRIv, all MRI volumetrics.

Performance of different ML methods in classification of CN versus AD

Performance of each ML method using four different sets of features is summarized in Table 2. Ensemble linear discriminant models trained with all volumetric measures and demographics showed the highest overall accuracy, specificity, PPV, and NPV and very high sensitivity in comparison with other classifiers. McNemar test also confirmed that ensemble linear discriminant models have the best overall performance (p < 0.001 in all model comparisons). Based on this result, ensemble linear discriminant model trained with feature-set 4 (All volumetrics plus demographics and APOE4 status) were selected and used for predicting the outcome of the test dataset (MCI group).

Prediction accuracy for clinical outcome in MCI subgroup

In the next step, the ensemble linear discriminant model with the full baseline feature set (all volumetric measures, demographics, and APOE4 status), which had the best performance in the training dataset was used to assign MCI participants to either CN-like or AD-like subgroups. Prediction accuracy of future conversion from MCI to AD for this model at 6, 12, 24, 36, and 48 months was 63.8%, 68.9%, 74.9%, 75.3%, and 77.0%, respectively. Table 3 summarizes the accuracy of this assignment for in prediction of clinical outcome at different follow-up times (6, 12, 24, 36, and 48 months) for each MCI subgroup.

Table 3.

Accuracy of ensemble linear discriminant models in predicting the outcome of MCI subgroups at different follow-up time-points based on baseline indicators

Model (SD)	N (% of total)	AD-like, N (% of AD like)	CN-like, N (% of CN-like)
At 6 months
Total	656	256	400
MCI-p	39 (6.0)	29(11.3)	10 (2.5)
MCI-np	615 (94.0)	227 (88.7)	388 (97.5)
At 12 months
Total	631	241	390
MCI-p	87 (13.8)	66 (27.4)	21 (5.4)
MCI-np	544 (86.2)	175 (72.6)	369 (94.6)
At 24 months
Total	543	201	342
MCI-p	151 (27.8)	108 (53.7)	43 (12.6)
MCI-np	392 (72.2)	93 (46.3)	299 (87.4)
At 36 months
Total	461	157	304
MCI-p	141 (30.6)	92 (58.6)	49 (16.1)
MCI-np	320 (69.4)	65 (41.4)	255 (83.9)
At 48 months	320 (69.4)	65 (41.4)	255 (83.9)
Total	318	94	224
MCI-p	109 (34.3)	65 (69.1)	44 (19.6)
MCI-np	209 (65.7)	29 (30.9)	180 (80.5)

MCI-p, individuals who progressed to AD, MCI-np, individuals who did not progress to AD.

Among MCI participants assigned to AD-like group, 11.3% at 6 months, 27.4% at 12 months, 53.7% at 24 months, 58.6% at 36 months, and 69.1% at 48 months converted to AD. Among MCI participants assigned to CN-like group, 97.5% at 6 months, 94.6% at 12 months, 87.4% at 24 months, 83.9% at 36 months, and 80.4% at 48 months converted to AD. In other words, PPV of the model rose from 11.3% at 6 months to 69.1% at 48 months, and NPV of the model decreased from 97.5% at 6 months to 80.3% at 48 months. The sensitivity and specificity of model for prediction of conversion to AD at each follow-up time point is summarized in Table 4.

Table 4.

Model sensitivity and specificity for prediction of conversion to AD among MCI participants who progressed to AD at different follow-up time-points based on baseline indicators

Follow-up time	Sensitivity	Specificity
At 6m	74.4	63.1
At 12m	75.9	67.8
At 24m	71.5	76.3
At 36m	65.2	79.7
At 48m	59.6	86.1

Assessment of time-to-conversion from MCI to AD

A Cox-proportional hazards model indicated that participants who were determined to be AD-like by the ensemble linear discriminant model based on the full feature set at baseline had a significantly higher proportion of conversion to AD during longitudinal follow up (HR = 5.36, 95%CI 4.13–6.98, p < 0.001; Fig. 2).

Fig. 2.

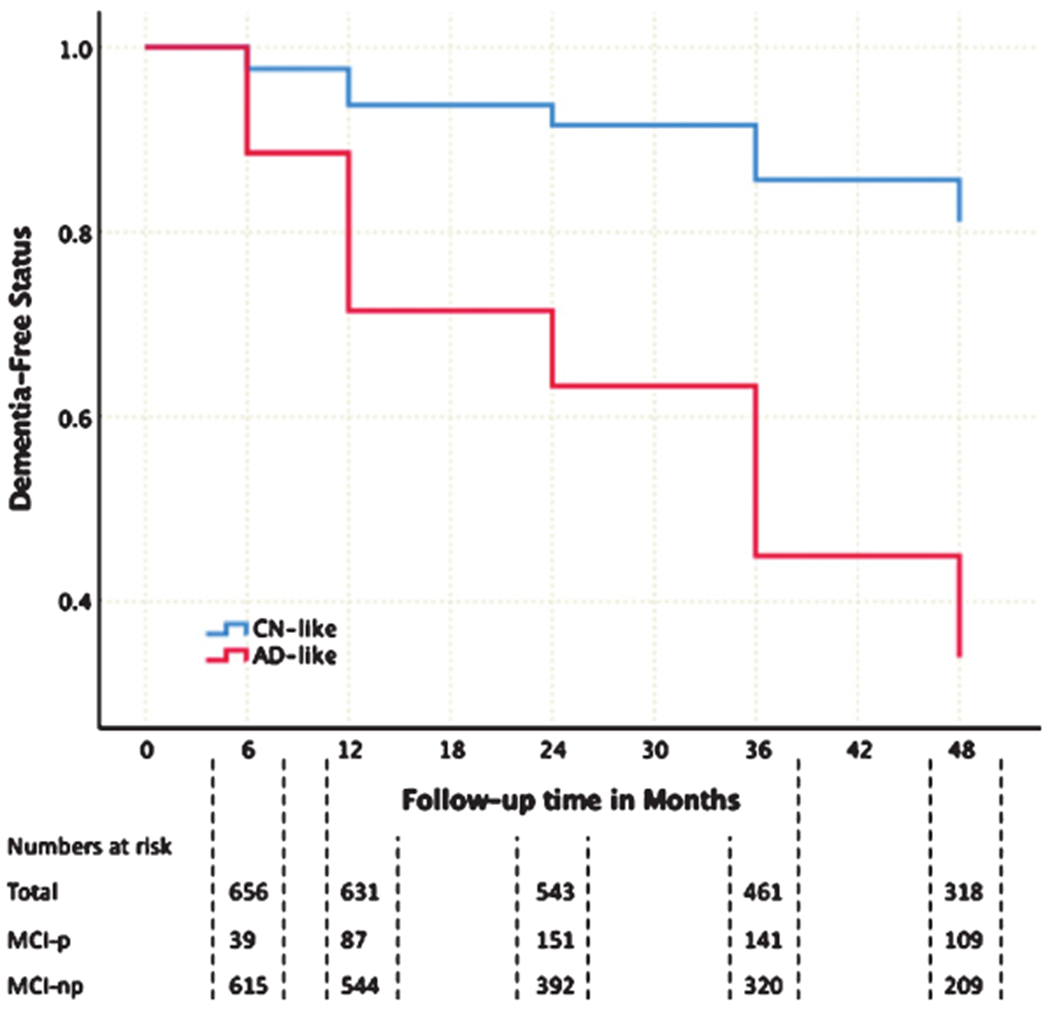
(Color Legend) Kaplan-Meir Survival Curves for MCI participants assigned to AD-like (red) or CN-like (blue) groups using ensemble linear discriminant models based on baseline measurements. MCI-p, individuals who progressed to AD; MCI-np, individuals who did not progress to AD.

DISCUSSION

Our results indicate that although performance of machine learning classifiers is generally high in terms of accuracy, sensitivity, or specificity, some methods (specially ensemble methods) can perform better than the others. This performance is partially dependent on the selected feature-set and characteristics of data-set. Inclusion of demographics and APOE4 status in training feature-sets improves the performance of all models. Furthermore, our results indicated that performance of the models in for prediction of outcome in MCI group (as an independent test set) is time-dependent: PPV of models rose from 11.3% at 6 months to 69.1% at 48 months, while NPV evolved from 97.5% to 80.3%. Moreover, after 48 months of follow-up individuals who were classified as abnormal (AD-like) were 5.36 times more likely to convert to AD than individuals who were classified as normal (CN-like).

The performance of classifiers used in the current study are in general agreement with previous studies, which have used MRI features for classification in different cohorts including ADNI [8, 23–25] and reported accuracies ranging from 80% to 92%. The differences between accuracy of these models is likely multi-factorial and due to differences in size of sample, training feature set, and the model itself. Our results indicate that the feature set selected for training affects performance of models significantly. We showed including multiple volumetric measures in the feature-set does not always lead to an increase in the performance of the classifier and such increase in performance is dependent on the type of classifier. Similar to previous studies [8], our results indicated that inclusion of demographics and APOE4 status as part of the training feature-set improves classification performance regardless of classification method.

We found that the classifier based on the ensemble linear discriminant method with the full feature set at baseline was able to predict progression from amnestic MCI to AD or lack thereof over up to 48 months of follow-up with an accuracy of 77%. Results from other studies show substantial differences in the ability of structural imaging to predict conversion from amnestic MCI to AD. Korf et al. [26] showed that atrophy in the medial temporal lobe could predict conversion to AD with a global accuracy of 69%. Devanand et al. [27] found that a combination of cognitive scores and hippocampal and entorhinal cortex volumes could predict conversion to AD with an accuracy of 87.7%; however, age alone correctly classified 71.9% of the participants. Querbes et al. [28] reported an accuracy of 76% in prediction of conversion to AD using a normalized thickness index comprised of cortical thickness of 22 different regions. Of note, the duration of follow-up was different for each these studies ranging from 2 years to 5 years, which makes a direct comparison between studies difficult.

Different applications for predictive models such as the ones presented in this study have been proposed. One major clinical application of these predictive models is for boosting power for clinical trials by reducing sample size estimates required to observe the effect of intervention. In a clinical trial with the aim of slowing the rate of cognitive decline, the trials could be enriched by inclusion of subpopulation of participants who are more likely to decline. Models that show higher PPV in comparison with observed prevalence in the population are particularly useful. For example, our models showed PPV of 53.7% at 24 months of follow-up (25.9% more than the base prevalence 27.8% progression at 24 months), and PPV of 69.1% at 48 months (34.8% higher than the base prevalence of 34.3% progression at 48 months). Another application of these classifiers is to choose the next step in management in care of patients. Considering that some diagnostic tests (e.g., CSF studies) are invasive or expensive (PET imaging), selecting the appropriate subpopulation of patients who have higher chance of benefitting from such tests, can decrease undesired side-effects and costs in the whole population.

A limitation of this study is that ADNI is not a population-based study and there are strict inclusion and exclusion criteria for selection of participants, which can affect generalizability of our findings. Therefore, validating our findings in other population-based studies and in data from clinical trials is an essential next step. To increase the number of eligible participants for this study, we focused only on structural MRIs and demographics as features for the models. However, using multimodal measures (e.g., biomarkers from PET imaging and CSF) as predictive features can increase performance of classifiers [29, 30]. Despite the potential increase in predictive accuracy of models with additional measures, the cost-effectiveness of processing data to collect such measures and ‘real-world’ clinical applicability are the other aspects which are not well studied. Finally, we selected the features for ML models based on prior hypotheses and did not use feature-selection methods.

To conclude, our results indicate factors such as choice of features, choice of ML algorithm, and time-frame of prediction each have significant effect on performance of models predicting cognitive outcomes. Therefore, each of these factors should be comprehensively evaluated before claiming we have developed valid, reliable, and high-performance predictive models. Multivariate and machine learning techniques have huge potential for use as tools of clinical decision making; however, they need to be carefully tested and validated against conventional diagnosis in different clinical settings and on population-based cohorts.