The Information Theoretic Perspective on Medical Diagnostic Inference

Abstract

The goal of this work is to present information theory, specifically Claude Shannon’s mathematical theory of communication, in a clinical context and elucidate its potential contributions to understanding the process of diagnostic inference. We use probability theory, information theory, and clinical examples to develop information theory as a means to examine uncertainty in diagnostic testing situations. We begin our discussion with a brief review of probability theory as it relates to diagnostic testing. An outline of Shannon’s theory of communication theory and how it directly translates to the medical diagnostic process serves as the essential justification for this article. Finally, we introduce the mathematical tools of information theory that allow for an understanding of diagnostic uncertainty and test effectiveness in a variety of contexts. We show that information theory provides a quantitative framework for understanding uncertainty that readily extends to medical diagnostic contexts.

Introduction: Probability Theory

Ideally, diagnostic testing would provide reliable measurements that translate into unequivocal diagnoses. However, as every experienced clinician knows, diagnosis is inherently “fuzzy” rather than deterministic; from start to finish, the practice is inextricably mired in uncertainty. From the perspective of testing, uncertainty may emerge from constraints of time, cost, and safety that may preclude the use of “gold standard” tests. Moreover, patients may provide misleading, ambiguous, or incomplete medical histories, forcing testing to operate under uncertain or inaccurate initial assumptions, or causing a clinician to choose an inappropriate test. Sometimes the only test capable of providing a diagnosis with certainty is an autopsy.

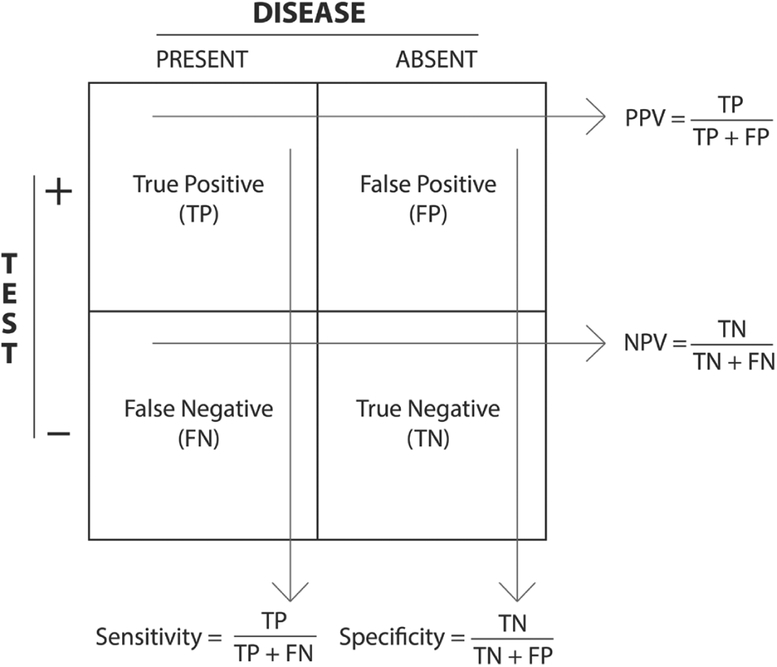
Assigning probabilities to different possible patient states (eg, healthy vs ill) represents the natural means to express our uncertainty in various stages of the diagnostic process. Suppose we believe a patient might have streptococcal pharyngitis because he exhibits a fever, sore throat, and tonsillar exudate in the absence of a cough. We know that approximately 40% of patients with this array of symptoms have strep throat and thus warrant antibiotic treatment.¹ A rapid strep antigen detection test returns a positive result. Realizing that even good tests can occasionally yield false positives (type I errors) and false negatives (type II errors), it is incumbent upon the physician to ask: What is the probability that the patient has strep throat given the positive test result and his pretest probability of 40%? To answer this question, we need to know the test’s sensitivity, or true positive rate, and its specificity, or true negative rate. Intuitively, both of these test performance metrics can be calculated in terms of the false-positive and false-negative rates as shown in the familiar 2 × 2 box in Figure 1, which also outlines some of the notational conventions used throughout this article. Given a population divided into the 4 categories with respect to a certain diagnostic test, one can calculate sensitivity, specificity, positive predictive value (PPV), and negative predictive value (NPV). Note that PPV and NPV are defined with respect to the population on which the box is based, whereas sensitivity and specificity are intrinsic properties of the diagnostic test. The PPV and NPV identify the proportion of those patients with a particular test result who are correctly diagnosed. Thus, the PPV and NPV represent the probability that a patient with a positive or negative diagnosis, respectively, actually has the disease (posttest probability).

Figure 1.

A 2 × 2 box and notational conventions.

Abbreviations: NPV, negative predictive value; PPV, positive predictive value.

Bayes’ theorem shows how to calculate posttest disease probability from pretest probability, sensitivity, and specificity. It is usually expressed as $Pr(A|B)=\frac{Pr(B|A)Pr(A)}{Pr(B)}$ where A is the disease in question, and B is the diagnostic test result obtained, and Pr(A) represents the probability that A is true. (Later, when speaking of the probability that a numerical outcome X has a particular value x, Pr[X = x], we will adopt the standard “lowercase p” convention of substituting for Pr[X = x] with the simpler expression p[x].) This equation can be rewritten as $Pr(A|B)=\frac{Pr(B|A)Pr(A)}{Pr(B\left|A)Pr(A)+Pr(B\right|\overline{A})Pr(\overline{A})}$ using the law of total probability to express the denominator in terms of more readily available values. (The law of total probability answers the following question: Given an outcome B, with known conditional probabilities given any of the mutually exclusive events A₁, A₂, …, A_n, each with a known probability itself, what is the total probability that B will happen? The answer is given by the formula: Pr[B] = Pr[A₁] Pr[B|A₁] + Pr[A₂] Pr[B|A₂] + … Pr[A_n] Pr[B|A_n]. In words, the probability that B occurs is the weighted average of the probabilities that it will occur in each possible alternative scenario A₁, A₂, …, A_n.) In the clinical context, we can think of Pr(A|B) as the posttest probability of disease presence (the value of interest), Pr(A) as the pretest probability (where $Pr[\overline{A}]=1-Pr[A]$, or the pretest probability of disease absence), Pr(B|A) as the probability of a positive test result given disease presence (or true positive rate), and $Pr(B|\overline{A})$ the probability of a positive test result given disease absence (or false-positive rate). (Explicitly, the translation of Bayes’ rule into terms of pretest probability [preTP], posttest probability [postTP], sensitivity [Sens], and specificity [Spec] is: postTP = preTP · Sens/[preTP · Sens + (1 − preTP) × (1 − Spec)].) The true-positive rate, of course, is the sensitivity of the test in question, and the false-positive rate is the complement of the true negative rate, or 1 – specificity. Although these quantities consider a patient who tested positive, for a negative result Pr(B|A) becomes the probability of a negative test result given disease presence (false negative rate, or 1 – sensitivity), and $Pr(B|\overline{A})$ becomes the true negative rate, or specificity. Returning to our example of a patient with a 40% pretest probability for strep throat, the rapid strep test has a reported sensitivity of 70% and specificity of approximately 95%.² Using Bayes’ theorem, a positive test result in this example yields a posttest probability of 90%.

Is 90% enough to confirm our suspicion that the patient has strep throat? How uncertain are we about the diagnosis at a probability of 90%, and how uncertain were we at 40%? How much information did we gain in adjusting our estimate from 40% to 90% based on the positive test result? If the patient had tested negative instead, would the result be more informative or less so? Relatively unknown in medicine, Claude Shannon’s mathematical theory of communication—information theory—provides a general framework for the quantitative understanding of issues involving probabilistic inferences, and is therefore conveniently applicable to diagnostic test interpretation.^3,4 Some of these concepts have been discussed previously in the context of the diagnostic process.^5–8 Others have been extended to related clinical issues such as information loss as a result of data dichotomization and aggregation⁹ and the insufficient information content of diagnostic test results in the literature.^10,11

In light of the above discussion, we felt a need to write a new tutorial on introducing information theory to physicians for several reasons. First, despite the efforts of previous authors, the concepts of information theory are still little known by the medical community. Second, our presentation takes the novel approach of organizing the discussion of diagnostic testing around Shannon’s fundamental schematic of a general communication system, which we believe provides a powerful and vivid perspective for understanding the concepts presented. Finally, we explain entropy, mutual information, and relative entropy, the key concepts in information theory, in a single unified presentation, allowing the reader to compare and contrast these concepts in detail as they relate to medical reasoning.

At the outset, we should emphasize 4 critical conceptual points regarding the limitations and scope of this article: (1) In any discussion of probability theory and its extensions, including information theory, it is important to keep in mind the distinction between application and theory. Information theory provides a very general framework of concepts and the language necessary to discuss, in a mathematically precise manner, the amount of uncertainty inherent in any inference problem, including medical diagnostic inference. However, understanding information theory does not automatically lead to more effective ways of solving medical problems, just as understanding the basic concepts of probability theory does not automatically allow one to produce sophisticated applications such as “normative expert diagnostic systems.”^12,13 In other words, a grasp of “traditional” probabilistic concepts, such as sensitivity, specificity, positive and negative predictive value, receiver operating characteristic curves, decision trees, and so on, may suffice for practical day-to-day diagnostic reasoning. Nevertheless, understanding the basic concepts of information theory is worthwhile for physicians, which brings us to the second and third points. (2) Information theory is widely considered to be one of the most important intellectual achievements of the past century, and physicians are in a unique position to relate in a deep way to the core concepts of information theory, namely uncertainty and information, given the fundamental daily role in medicine of diagnostic reasoning in the face of imperfect information. (3) As we elaborate later in this paper, information theory is the only cogent way to quantify the fundamental currency of diagnostic inference, namely, information. Having some understanding of the theory governing uncertainty as it applies to reaching medical diagnoses provides a perspective that may be more intuitive, analogous to using Bayes’ theorem as a more intuitive approach to the 2 × 2 box, which fundamentally contains the same information. An analogous argument has often been made by authors who believe that physicians should be able to critically appraise arguments involving probability and statistics, rather than leaving the theory entirely to formally trained mathematicians. (4) A basic understanding is a prerequisite for developing and utilizing future applications and automated diagnostic systems based on information theory.

Throughout this article we rely on relatively simple examples to illustrate the main concepts, rather than developing a decision support application per se. For example, we sometimes refer to diseases as “present” or “absent,” and to test results as “positive” or “negative.” In practice, of course, patients may have multiple diseases; diseases and test results need not be binary (ie, entirely present or entirely absent); the next best test may depend on the results of previous tests rather than being determined a priori; and results from different tests performed on the same patient frequently do not provide independent information. Real-world applications of probabilistic diagnostic reasoning to medical problems certainly should incorporate these complexities.^12–17 Still, the key concepts of probability theory and information theory are accessible through relatively simple examples, and thus we use these as illustrations, providing references to more sophisticated applications for interested readers.

We hasten to add that, although this article is primarily limited to issues of medical diagnosis, the practice of medicine typically goes well beyond inference, into matters of decision making. That is, medicine is not simply about how likely a patient is to have a disease, but also about whether or not, and how, to work up and treat a patient’s medical problems. In the formal analysis of medical decisions, which is the domain of decision theory, diagnostic decision making depends not only on probability assignments but also on complete decision trees or influence diagrams, which include utility functions for all outcomes (consequences or costs of treatments), and in practice such utilities should generally involve the patient’s own values to the extent possible, as stressed in the recent literature on “shared decision making.” Thus, although in this article we restrict our attention to one essential aspect of medical decision making—namely, diagnostic inference—the reader should keep in mind that inference is an integral component of a more complex overall decision-making process.

The reader should also understand that information theory does not provide alternatives to familiar concepts in probability theory, statistics, and decision theory, such as sensitivity, specificity, PPV, NPV, and decision trees. Rather, information theory is an extension or outgrowth of probability theory that provides insights into the rules governing information and uncertainty. Likewise, it is not possible for information theory to substitute for or contradict results from decision theory, because, as mentioned above, decision theory is also an outgrowth of (and thus fully consistent with) probability theory, supplemented with additional considerations of the role of values in decision making (utility theory). In the same manner that Bayes’ theorem provides a different way to gain intuition into concepts typically represented by the 2 × 2 box, information theory provides a conceptual framework for what are fundamentally the same basic probability principles involved in traditional diagnostic inference.

The above caveats and qualifications notwithstanding, optimal diagnostic inference in the presence of uncertainty requires thinking clearly about probability. Hence, information theory and its foundation, probability theory, deserve a place in the intellectual foundation of the practice of medicine.

Communication Channels and the Diagnostic Process

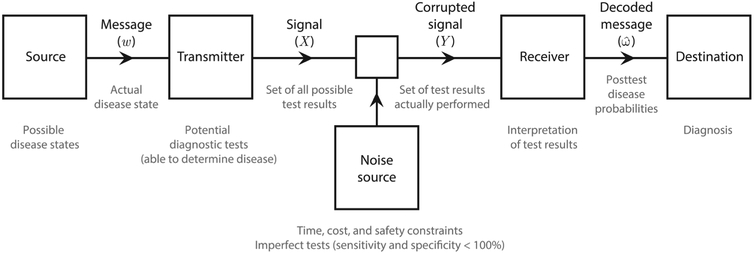
One of the core concepts of information theory is the communication channel. In essence, a channel is a pathway for the transfer of information between 2 entities that can be described as a number of distinct stages: a signal source outputs a message that is encoded and sent by a transmitter, received and decoded by a receiver, and finally conveyed to its intended destination. In its passage from the transmitter to the receiver, sources of “noise” can corrupt the signal, in which case this communication process is referred to as a “noisy channel.” Figure 2 shows the channel model that Shannon described in his 1948 paper that forms the basis of information theory; the large text and diagram are taken directly from a similar figure in Shannon’s 1949 paper, whereas the small text provides a clinical interpretation of each step in the communication channel. Beyond its historical importance, Shannon’s communication channel provides a powerful framework for understanding the process of diagnostic inference. The process of reaching a correct medical diagnosis in the presence of incomplete and imperfect data is analogous to communication over a channel corrupted by noise, as both diagnostic tests and the clinical assessments contributing to pretest probability estimates contain uncertainty. In the following discussion we provide a clinical interpretation to accompany each step in the process.

Figure 2.

Shannon’s noisy communication channel.

In this basic model, the source is a set of possible disease states, each with an appropriate probability determined by patient characteristics (eg, age, demographic information, past medical history, etc) from a list of all possible disease states (including “normal”). The source is an all-encompassing abstraction in that each “disease state” can in practice be one of infinitely many complex, multifaceted physiological states defined by the data contained in all physical signs and symptoms, both measurable and unmeasurable, observable and unobservable. The message (the true disease state, w) is one of the possible states defined by the source.

The transmitter encodes w into a set of diagnostic test results and observable symptoms, denoted X. These “ideal data” would consist of a fully accurate list of all possible signs and symptoms plus the results of all possible diagnostic tests, and all of the test results would accurately reflect the true disease state (ie, there would be no false positives or negatives and no uncertainty in the test results). We will further assume that in the hypothetical situation of unlimited tests and perfectly accurate test results, one could in principle uniquely deduce w from X. The expression of the underlying true disease state in terms of this hypothetical ideal data set X is analogous to the process of converting a message into a transmittable signal in an engineered communication system, such as the conversion of a spoken word into a digital stream of bits for cell-phone to cell-phone transmission.

In real-world practice, however, cost, time, and safety constraints prohibit subjecting patients to the entire universe of tests, and few tests are perfectly accurate. This failure to administer certain tests and the inaccuracy of others constitutes the main source of noise. Thus, the set of test results available to a clinician, Y, is only a small and usually inaccurate subset of X—which would be needed to decode the disease state unambiguously. The receiver, or clinician, will then interpret the test results to produce a decoded message, $\stackrel{⌢}{w}$, that it is hoped would result in a unique diagnosis equal to w, but more typically yielding a distribution across multiple disease states (ie, a differential diagnosis). This distribution reflects the truism that the posttest probability of each possible disease state is not cleanly 0% or 100%, due to the inherent uncertainty of the clinician’s non-ideal set of observations and non-ideal test results. Based on the differential diagnosis of posttest probabilities ($\stackrel{⌢}{w}$), the clinician will consider whether or not to order additional tests.

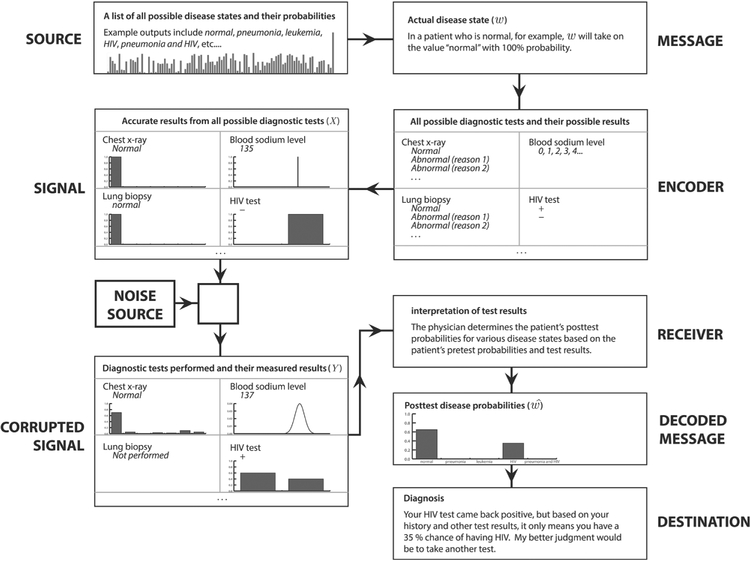
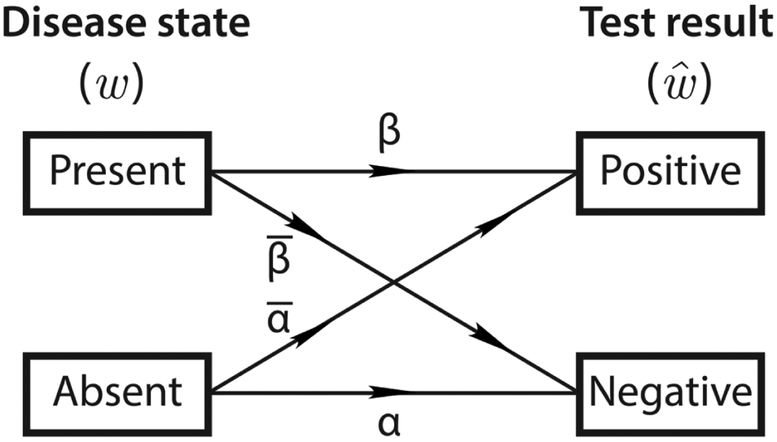
Figure 3 illustrates this diagnostic channel model in action, for a scenario in which a healthy patient receives a falsely positive HIV test. The message, or true disease state, in this case “normal,” is defined by the source, a theoretical library consisting of every possible state (which can be any combination of conditions) and its prior probability. As the message passes through the encoder, it is translated to the language of diagnostic test results and symptoms, whether observable or not; this is the signal which comprises every possible symptom and diagnostic test and its fully accurate, unambiguous results. From the signal, it is possible to determine the message unequivocally. The “noise” that corrupts the signal can be anything from the decision not to perform some tests, to fallacious or imprecise results, to the unobservability of certain symptoms. Almost certainly, it will be a combination of a multitude of factors. The corrupted signal is the first part of the communication channel that is actually observable to the clinician, or receiver, who must “decode” the corrupted signal and make his or her diagnosis, the ultimate “destination.” The final decision in this example is to order another test that it is hoped will determine with greater accuracy whether or not the patient has HIV. In this binary case (considering just one yes-or-no test result), we see how imperfect sensitivities and specificities cause errors in a simplified binary channel diagram. In Figure 4, w will either be “disease present” or “disease absent” with 100% probability. However, $\stackrel{⌢}{w}$, will always contain some nonzero probability for the wrong result if the sensitivity or specificity is < 100% (for negative or positive test results, respectively). Using a simplified version of the communication channel in Figure 4 to represent a binary diagnostic test allows us to interpret imperfect sensitivities and specificities as noise sources. Here, sensitivity = Pr(r + |D) = β = 0.7 and $\text{specificity}=\text{Pr}(r-|\overline{D})=\alpha =0.95$. It should be evident that this binary diagram appears similar to, and contains much of the same information as, the familiar 2 × 2 box presented in Figure 1. This further highlights the analogy between diagnostic testing and communication over noisy channels.

Figure 3.

The diagnostic reasoning process as a noisy communication channel, as illustrated for a patient receiving a false-positive HIV test.

Abbreviation: HIV, human immunodeficiency virus.

Figure 4.

A binary communication channel.

In light of the fact that physicians are rarely able to predict the true disease state perfectly, our goal is to understand how accurate our diagnoses are, taking into account the noise sources that render diagnostic test results imperfect. This was essentially Shannon’s motivation for developing information theory: to determine how much information a noisy channel can theoretically transmit. In what follows, we discuss how 3 concepts developed in information theory, namely entropy, mutual information, and relative entropy, quantify the degree of uncertainty inherent in diagnostic situations, and how to assess the amount by which uncertainty is changed in response to new data (eg, diagnostic test results). We focus mainly on examples involving single binary tests. However, the reader should keep in mind that the ideas are in fact quite general, and can be readily extended to situations involving batteries of tests with nonbinary results, as suggested by the preceding discussion and Figures 2 and 3.

Uncertainty and Entropy

Entropy, a measure of the uncertainty associated with a random event, is possibly the most central concept of information theory. The same term is used in thermodynamics, where it can be thought of as a measure of the disorder or randomness of a physical system, and in fact the formulas for information theoretic and physical entropy are closely related. The mathematical formula for information theoretic, or Shannon entropy is H(X) = E_p[−log Pr(X = x)] = −Σ_x∈X Pr(X = x) log Pr(X = x) where H is the entropy function, X is the set of all possible events (a list of possible disease states), x’s are individual elements or events within X (specific disease states), and Pr(X = x) is the probability of each event (disease state). To simplify notation, from here on instead of Pr(X = x) we will write simply p(x) to indicate the probability that X takes on a particular value x.

To gain insight into this formula, we consider 4 related viewpoints regarding the interpretation of entropy, from a medical perspective: entropy as uncertainty, average surprise, average information gained, and average code-word length. If X is a patient’s true (but initially unknown) disease state, it turns out that entropy can be thought of as a measure of the following properties of X: (1) The amount of “information” gained in reaching the final (true) diagnosis; (2) The amount of “surprise” one will have on learning the final diagnosis; (3) The amount of uncertainty about X; (4) The number of binary tests results needed reach the final diagnosis.

In this section we provide informal examples illustrating these ideas. However, it is worth emphasizing that H(X) measures the above concepts in a precise mathematical sense as well. Moreover, although there are other functions sharing some of the properties above, information theory shows that entropy is unique in being the only measure that possesses the properties needed to provide a mathematically coherent account of uncertainty. Afterward, we will comment further on the uniqueness of the entropy function as a measure of uncertainty.

Entropy as Uncertainty, Average Surprise, and Average Information Gained

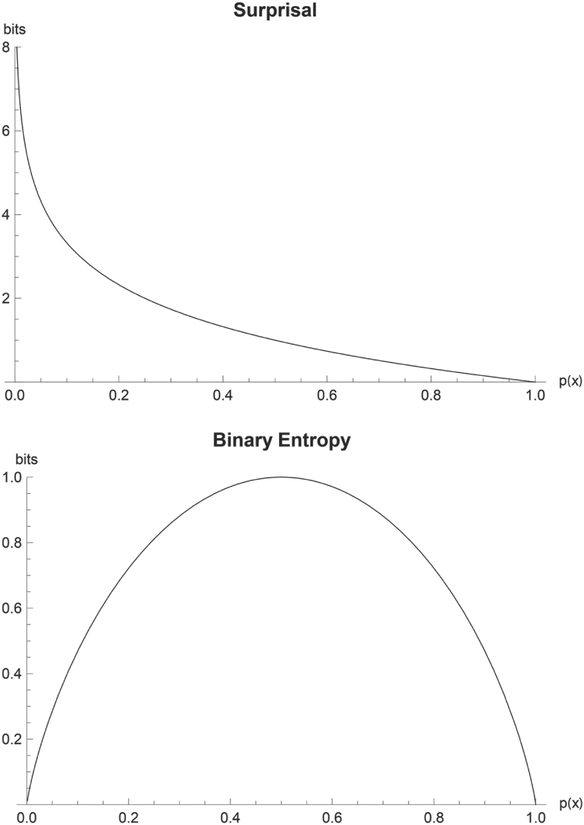
Let us define the function S(x) = −log Pr(X = x) = −log p(x), where Pr(X = x) = p(x) represents the probability that the true value of the unknown disease state X is in fact the particular disease state x. The logarithm is taken to base 2 by convention, in which case a unit of information is called a “bit,” meaning the amount of information required to distinguish between 2 (equally likely) alternatives. Clearly, H(X) is the average (or “expected”) value of S(x). The function S(x) can be interpreted as the information provided by finding out the result that X = x. According to this interpretation, the less probable a disease state is, the more information we receive when a patient is found to have it. Alternatively, we can say that S(x) measures the amount of surprise one feels on learning a diagnosis, thus a definitive test resulting in the diagnosis of a rare disease is more surprising than a routine diagnosis. Thus, S(x) is sometimes called the “intrinsic information” function,^18,19 and sometimes the “surprisal.”⁸ Figure 5a, a plot of the surprisal function across all probabilities, illustrates that one is infinitely surprised by observing an impossible event (p = 0) and not at all surprised by observing an inevitable event (p = 1). Intuitively, the surprise associated with an impossible event (p[x] = 0) is infinite, whereas surprise is 0 for a certain event ((p[x] = 1)).

Figure 5.

(A) Plot of the surprisal function versus probability. (B) Plot of the binary entropy function versus probability.

Suppose a certain clinician routinely performs chest computed tomography scans on patients who present with a cough lasting > 1 month, which for the sake of discussion we will assume are definitively diagnostic, and further suppose that in this patient population the prevalence of lung cancer is 1%. The amount of information the physician receives from any individual test is captured by the concept of surprisal, S(x), whereas the average amount of information learned is captured by the entropy, H(x). Before learning the results, the physician may feel somewhat anxious about the true disease status, reflecting the fact that uncertainty exists about what the result will be. The degree of this uncertainty may also be said to be measured by H(x). From the patient perspective, assuming the patient also knows the pretest probability, anxiety and uncertainty will exist, with H(x) being a reasonable degree of anxiety to have, because it lies between the amount of surprise a positive or negative result will bring, the more likely possibility carrying the most weight. The individual patient’s surprise on learning the test result is measured by S(x), whereas the average amount of surprise a population of tested patients experience is measured by H(x).

In the binary case, when a clinician performs a single test to determine the presence or absence of a single disease, the entropy function simplifies to $H(X)=h(p)=-p\text{log}p-\overline{p}\text{log}\overline{p}$, where h(p) is called the binary entropy function, p is the probability of disease, and $\overline{p}$ is the probability of no disease $(\overline{p}=1-p)$. For example, in our initial example with a patient who we suspect might have strep throat, entropy before testing is h(0.4) = −0.4 × log 0.4−0.6 × log 0.6 = 0.971 bits, based on a pretest probability of 40%. Figure 5b, a plot of h(p), shows that expected surprise is 0 when an event is either certain to occur or certain not to occur, that is, when p = 0 or when p = 1. At p(x) = 0 and 1, the outcome of the event is known so there is no uncertainty. At p(x) = 0.5, the outcomes are equally likely, so uncertainty is maximized. Intuitively, we would not need any diagnostic tests to establish whether a patient had a disease if we were sure one way or the other. Consequently, the following statements are all true and equivalent when the diagnosis is already known (ie, when p = 0 or p = 1): there is no information to be gained by further testing; the results of any testing would produce no surprise; the amount by which the uncertainty regarding the diagnosis can be reduced by further testing is 0; the diagnostic entropy h(p) is equal to 0. The interpretations of entropy as residual uncertainty, potential for surprise, and the necessary amount of information to reach certainty also immediately suggest that entropy should have a “floor,” which by mathematical convention [as reflected in the plot for h(p)] is equal to 0. We are most uncertain about disease presence when the probability of disease is 50%, that is, when we have no leaning in either direction. (Although the maximal uncertainty about whether to initiate a treatment or intervention might incur a significantly lower value, particularly when the treatment is relatively benign and the consequences of a false-negative diagnosis are high.) In this case, a test with high specificity is required to confirm disease presence, and one with high sensitivity is required to rule it out. Note that we use the word uncertain here in the information theory sense, rather than the decision theory sense: any disease probability could in principle exceed a threshold to test or treat, even the maximally “uncertain” value of 50%.

Twenty Questions: Entropy as Average Code-Word Length, or Number of Tests Needed

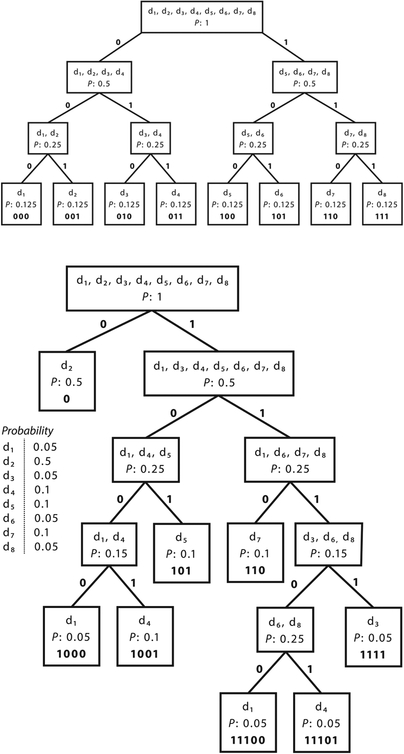
Suppose that you suspect a patient has 1 of 8 diseases. How many perfect diagnostic tests would you have to perform to determine the patient’s disease, and in what order would you administer them so as to have the best chance of minimizing the number of tests required? Many readers will be familiar with the game 20 Questions, in which one player thinks of an object, and the other player attempts to guess the object by answering the smallest possible number (traditionally, no more than 20) of yes/no questions. Any reader who has played the game knows that it will be inefficient first to ask, “Is it disease 1?” and then “Is it disease 2?” and so on. Using this method, you would have to ask 4 questions on average in our example with a patient with 1 of 8 disease states, and sometimes up to 7 questions. A better strategy is to ask questions that can eliminate multiple possibilities simultaneously. Similarly, it is best to choose diagnostic tests that can rule out the possibility of several diseases at once. Let us first assume that the patient is no more likely to have 1 of the 8 diseases than any other (that is, the probability distribution p over the disease states is uniform). Figure 6 shows that the optimal sequence of binary diagnostic tests to distinguish among 8 disease states is illustrated for 2 cases in which each disease state is equally probable (Figure 6a) and the states are not equally probable (Figure 6b). Because Figure 6a shows the uniform distribution across 8 states, entropy is maximized at 3 bits. Indeed, we see that 3 binary tests are necessary to determine disease state and we can express each state as a 3-digit binary code-word. The nonuniform case (Figure 6b) has entropy 2.361 bits, reflecting that < 3 binary tests will be necessary on average and that each state on average has a shorter binary code word. Figure 6a shows that the best way to determine the disease state is to break the 8 possibilities into groups of equal size (and, more generally, equal probability) again and again. For 8 disease states of equal probability, 3 tests are required. The first one should narrow the differential diagnosis to a group of 4 possibilities, the second to a group of 2, and the third should choose between the remaining 2. Using this scheme, the sequence of test results that would lead to each specific diagnosis can be thought of as “code words” for the disease states. Figure 6a shows the optimal binary code-word for each disease state. Three binary digits (or bits) are required to define each disease state in our population of 8. Indeed, H(p) = 3 bits for this example. In general the average optimal code-word length and, in turn, the average number of yes–no questions required to determine the value of a random variable such as the disease state example turns out to be always very close to H(p). (More precisely, the number of binary questions required is never < H(p), and never > H(p) + 1. The reason that the “+1” is needed is that technically one cannot ask a fractional number of questions.)

Figure 6.

Entropy as the expected code-word length. (A) Each disease state is equally probable. (B) The states are not equally probable.

Figure 6b presents the same situation with nonuniform probabilities for each disease state. The disease states are arranged into groups as close as possible in probability. In this case, the entropy of the disease state distribution is 2.361 bits. The average code-word length (and number of tests you would perform on average) is 2.4 bits (or tests), again close to H(p).

The higher entropy value in Figure 6a than in Figure 6b also reveals something fundamental: for a given set of events, the uniform distribution across those events always maximizes the entropy. Clinically, it is intuitive that one would be most uncertain about a patient’s disease state when one suspects a certain set of states with equal probability, because any information regarding the patient or knowledge of prior probabilities in the general population would cause the clinician to weight some disease states as more probable than others and thus be less uncertain.

It is important to realize that although the entropy function quantifies one’s uncertainty throughout the diagnostic process and may help determine the order in which to perform the available tests, in practice it may be impossible to find a sequence of tests that achieves the minimum specified by entropy because it may be impossible or impractical to find a set of tests conveniently able to group disease states into subsets of equal probability. Thus, a larger number of tests may be required. However, the converse is not true: it is not possible to determine the diagnosis (on average) with an average number of (binary) tests smaller than the entropy.

The reader should keep in mind that this “20 questions” explanation of entropy is artificial, designed for illustrative purposes. In practice, test results need not all be binary, and need not be obtained in a strict order or 1 at a time. Mathematically the concept of entropy can be readily extended to these more realistic cases; however, we have kept the discussion deliberately simple to clearly convey the essence of the more general ideas.

Are There Alternative Ways to Characterize Uncertainty?

We have tried to provide some intuition for why entropy, H(X), is a reasonable measure of uncertainty. Are there other possible measures that are just as reasonable? The answer is no. It turns out that, once we agree on a few simple “obvious” properties that a measure of uncertainty should have, then entropy follows inevitably as the only option. Although the proof of this fact, owing to the work of Shannon,³ is beyond the scope of this paper, it is important to understand the basic premises that led to the result. Shannon suggested that 3 simple requirements should be true for any reasonable measure of uncertainty:

Requirement 1: For equally probable events, more possible outcomes mean greater uncertainty. For any given patient symptom, the larger the number of equally likely disease states consistent with it, the more difficult it is to predict the final diagnosis and hence the greater the uncertainty. Conversely, if the physician is “lucky” enough to detect a physical sign pathognomonic for a single disease, there exists no uncertainty regarding the diagnosis.

Requirement 2: The uncertainty depends on the probability of each possible outcome. For example, consider 2 different diagnostic situations, A and B, both with a differential diagnosis containing 10 possibilities. In A, the disease pretest probabilities are 91% for 1 and 1% for each of the remaining 9, whereas in B the pretest probability is spread evenly at 10% for each possibility. Clearly, the amount of uncertainty is greater in situation B.

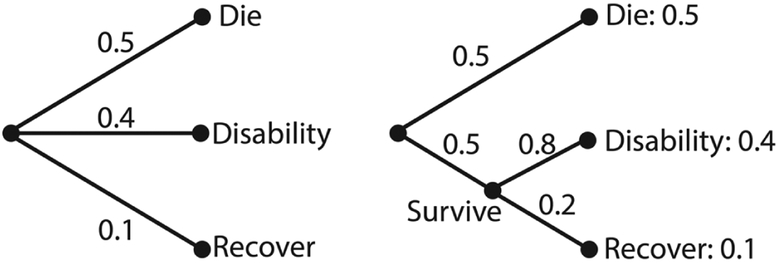
Requirement 3: If an outcome can be broken down into 2 successive events, then the overall uncertainty should be the weighted sum of the uncertainties for the individual events. The meaning of this requirement is illustrated in Figure 7. A requirement as we define the entropy function is that when we break an outcome into multiple events, the weighted total entropies of the new set of events will be equal to the original entropy of the old one. Suppose that there are 3 possible outcomes for patients in the intensive care unit with a particular disease state, with the following probabilities: die, 50%; recover but with permanent disability, 40%; fully recover, 10%; this is illustrated on the left of Figure 7. On the right, we break this down first into expiration versus survival (50% vs 50%), and then second, among survivors, into disability versus full recovery (80% vs 20%). The final results have the same probabilities as before. In this case, our requirement is that H(X) = H(0.5, 0.4, 0.1) = H(0.5, 0.5) + 0.5 H(0.8, 0.2). The weighting factor 0.5 in the second term is because the second possibility (survival) only occurs half of the time. We confirm that the above relation holds and both sides of the equation are equal to 1.36 bits. This means that for a question with multiple independent sources of uncertainty, the total uncertainty should be the sum of the entropies associated with the component sources of uncertainty. Only the entropy function satisfies this requirement for additivity of uncertainty—clearly, probabilities alone do not.

Figure 7.

The probability of successive events.

Weaver and Shannon proved that these simple requirements lead to an essentially unique mathematical measure for uncertainty, given by the entropy formula. The only feature not fully determined by the 3 requirements above is the base used for the logarithm, which simply determines the units in which information theoretic quantities are expressed. By convention, base 2 is used, so that the traditional units are “bits,” which satisfyingly correspond to yes–no questions—or the number of binary tests required to determine a disease state.

Some readers may wonder whether the statement that entropy is the only reasonable measure of uncertainty is too strong. After all, is not disease probability itself already a summary of diagnostic uncertainty? Of course, entropy is a function of event probabilities; however, following Weaver and Shannon’s argument, it is an indirect measure, because the overall probabilities of compound events are multiplicative, hence when expressed in probabilities the overall uncertainty is not the sum of the uncertainties of the individual events (requirement 3). Thus, although probabilities are vital to the diagnostic process, and are the sole ingredient in entropy calculations, probabilities do not provide a direct measure of uncertainty in the strict sense because they do not adhere to Shannon’s axioms. Entropy is the only measure that satisfies all 3 of Shannon’s general requirements for a measure of uncertainty.

Information Theoretic Quantities in Diagnostic Testing

Entropy

In a binary testing situation, we can calculate our uncertainty before administration of the test as H(D) = h(p), where H(D) is uncertainty about disease state, h is the binary entropy function, and p is the pretest probability. After testing, our uncertainty given the result, or posttest entropy (notation: H[D|r+] for a positive result and H[D|r−] for a negative result), is also quantified by h(p), with posttest probability obtained through Bayes’ theorem as the input probability. The average value of the posttest entropy, averaging over each of the 2 possible results with each weighted by its probability, tells us the average level of uncertainty we will have after learning a test result: H(D|R) = Σ_r∈R p(r)H(D|R = r). Note that this average quantity only makes sense when calculated across identical tests given individuals with identical pretest probabilities. On a case-by-case basis, uncertainty is expressed with H(D|r+) and H(D|r−).

As an example of these quantities, consider our hypothetical patient with a pretest probability of 40% for strep throat. Before testing, our uncertainty is H(D) = h(0.4) = 0.971 bits. After a rapid strep test comes back positive, the posttest probability that the patient has strep throat is 90.3% (as calculated using Bayes’ theorem) rather than 100%, due to the imperfect sensitivity and specificity of the test (70% and 95%, respectively), effectively adding noise to our binary channel (see Figure 4, $\text{letting sensitivity}=\text{Pr}[r+|D]=\overline{\beta }=0.7$ and $\text{specificity}=\text{Pr}[(r-|\overline{D})]=\overline{\alpha }=0.95$. Our posttest uncertainty for a positive test result is therefore H(D|r+) = h(0.903) = 0.459 bits. Had the patient tested negative instead, the posttest probability would have been 17.4%, with posttest entropy: H(D|r−) = h(0.174) = 0.667 bits. The average posttest entropy, H(D|R), for a group of patients with prior probabilities equal to that of our hypothetical patient is 0.602 bits.

A well-known theorem in information theory is that “conditioning reduces entropy.” That is, posttest entropy is always ≤ pretest entropy, or H(D|R) ≤ H(D) (note that this was true in the previous example). It is important to remember that this inequality applies only to average uncertainty. A single result may either increase (in the case of an unexpected result²⁰) or decrease one’s uncertainty (in the case of an expected result), but in the long run, averaged over many cases, a test will decrease one’s uncertainty, because expected results by definition occur more frequently than unexpected ones. If disease state and test result are independent (ie, the test is useless), then H(D|R) = H(D). In a mathematical sense, although the worst tests do not help to diagnose, they do not necessarily do harm by virtue of being uninformative, as long as they are recognized as such. This is intuitive, and perhaps (in a limited, superficial sense) clinically comforting—whereas in reality it is generally a bad idea to administer uninformative tests for reasons such as cost and safety. Furthermore, in a general sense it is essential to balance the risks of performing a test (eg, false-positive results might lead to unnecessary, harmful interventions) against the possible benefit of obtaining additional information. This amounts to a restatement of the distinction between diagnostic inference and decision making, emphasized in the introduction of this article.

Mutual Information

If diagnostic tests are supposed to reduce entropy, one might evaluate the efficacy of a test based on the average reduction in entropy that it provides. This quantity, H(D)–H(D|R), is called the mutual information of the test given the result (notation: I[D; R]). Because pretest and posttest entropy are dependent on the population being tested (ie, on pretest probability), it follows that mutual information is dependent as well. As a sanity check, we expect that a test provides no information about populations with either 100% or 0% pretest probabilities because the disease state is already known. Indeed, I(D; R) = 0 bits for these populations, because H(D) = 0 bits for pretest probabilities of 0% or 100%, and H(D|R) ≤ H(D) as we showed earlier, and entropy cannot be negative, I(D; R) must be equal to 0. Conversely, a test provides the most information when sensitivity and specificity are both 100%, because, with no risk of false positives or false negatives, we are not at all uncertain about disease state given the result from such a test (so H[D|R] = 0). For such a test, the maximum amount of information that it can provide is I(D; R) = 1 bit because for a binary test H(D) has a maximum value of 1 bit—specifically, when pretest probability is 50% (note that the amount of information provided by the test depends on the amount of uncertainty we have before doing the test, H[D]). Mutual information is superior to sensitivity and specificity alone as a measure of test performance because it considers not only those values but also the prior probabilities of the population tested as well.

Plots of mutual information across pretest probability values are shown for a few combinations of sensitivity and specificity in Figure 8. Tests with sensitivity (specificity) greater than specificity (sensitivity) have mutual information skewed in the direction of higher (lower) prior probability values because such tests yield the greatest information when unexpected negatives (positives) occur. Note that mutual information conveniently combines sensitivity, specificity, and prior probability into a single value between 0 and 1. Maximum values are also indicated in the plots. These maxima are called channel capacity, which is defined as the maximum mutual information over all possible distributions. In the case of a binary diagnostic test such as in the figure, to achieve the channel capacity, we would simply choose the prior probability that yields the largest information. Note that in communications engineering one is in fact often free to design the transmitted signals in such a way that they maximize the mutual information (channel capacity). Nothing analogous is typically possible in medicine; that is, there is not typically any sense in which one is able to “engineer” the disease probabilities within a patient population.

Figure 8.

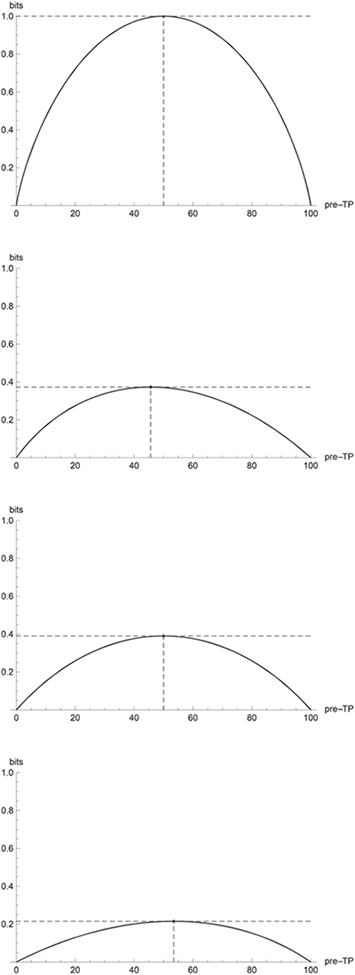
Plots of mutual information versus pretest probability for binary diagnostic tests with sensitivity and specificity (A) 100 and 100, (B) 70 and 95, (C) 85 and 85, (D) 90 and 60.

Returning to the strep throat example, given a pretest entropy of 0.971 bits and average posttest entropy of 0.602 bits, mutual information tells us that our average reduction in uncertainty will be 0.369 bits.

Relative Entropy

Although mutual information is the natural measure of test informativeness across a population, it does not describe how much a clinician’s diagnostic perspective should be changed in light of a single test result. For this, we naturally require a metric that is not an average value across both positive and negative test results, but rather captures the circumstance of obtaining a particular test result.

One might assume that a good possibility would be simply to subtract posttest entropy from pretest entropy—that is, H(D)–H(D|r+) for a positive result and H(D)–H(D|r−) for a negative one. This correctly reflects our reduction in uncertainty mathematically, but is often a clinically counterintuitive quantity. For instance, if a positive test result transformed a pretest probability of 10% into a posttest probability of 90%, the test would seem to have provided a great deal of information. But H(D) = 0.469 bits = H(D|r+), so H(D)–H(D|r+) = 0 bits, indicating that the test provided no reduction in uncertainty. In the mathematical sense, this is indeed the case; although the pretest and posttest probabilities are flipped (and they provide clinically useful information), they are numerically identical and therefore introduce equal uncertainty.

Relative entropy, also known as Kullback-Leibler divergence, provides a way to quantify the amount of information gained from a specific test result. Relative entropy is notated as D(a||b), where a and b are both probability distributions over the same variable. As we will see, a and b could correspond to pretest probability and posttest probability. The formula is

$$\begin{gathered} D\left(p\Vert p^{\prime }\right)={\sum }_{d\in D}{p}^{\prime }(d)\text{log}\frac{p^{\prime }(d)}{p(d)} \\ =-{\sum }_{d\in D}{p}^{\prime }(d)\text{log}{p}^{\prime }(d)+{\sum }_{d\in D}{p}^{\prime }(d)\text{log}p(d) \end{gathered}$$

where p is the pretest probability distribution and p′ is the posttest probability distribution. The relative entropy function works by comparing the clinician’s expected surprise—or uncertainty—after learning the test result to his expected surprise before testing. It works on the premise that before the test is conducted, one’s surprise at learning that the patient has a disease (or does not) is based only on the pretest probability, but the probability that one will be surprised is based on the posttest probability.

Satisfyingly, relative entropy is closely related to sensitivity and specificity. Tests with high sensitivities generally provide more information with negative results than with positive ones; those with high specificities are more informative for positive results.²¹

In our initial strep throat example, relative entropy for a positive result was 0.807 bits and 0.172 bits for a negative result. This is in accordance with the aforementioned trend (because sensitivity was 70% and specificity was 95%) and reflects our intuition that a greater absolute change in disease probability occurs with a positive result and that in this case we gain more information, especially when a positive result is unexpected.

One would expect relative entropy, which provides information about a single test result, to be closely related to mutual information. It can be shown that mutual information is in fact the average of the relative entropies for positive and negative results, weighted by their probabilities. Plots illustrating the mathematical relationship between relative entropy and pretest probability are included in the supplemental material.

A Role for Information Theory in Diagnosis

Although it is clear that information theory gives us insight into the uncertainty present at various stages in the diagnostic process and allows us to quantify the amount of information we gain by administering diagnostic tests, some readers might naturally wonder what one should do with this knowledge. Shannon’s theory per se usually cannot tell us how to proceed; the diagnostic process cannot rely on information theoretic considerations alone. As we saw in the 20 questions example, entropy can help determine the optimal order of test administration, but this presumes that we have a set of tests available from which to choose, and that we are able to determine the relevant probabilities at each stage. We have shown that relative entropy is a measure of information gained as the result of a test outcome, but this alone is insufficient to determine what is the best course of action, that is, whether or not and in which way to provide medical intervention. Others have attempted to tackle these challenges, with some encouraging success, by using advanced applications of probability theory to create probabilistic decision support systems.^{12,13,22–24} Information theoretic concepts could be usefully incorporated into any manifestation of such a system, from knowledge-based incarnations such as INTERNIST-I,¹⁴ to stochastic diagnostic models,¹⁵ to deterministic systems that try to mimic a clinician’s “thought process.”¹⁶

With this in mind, one could conceivably develop a system whereby a chain of diagnostic tests—whose order is determined by entropy at each stage—are chosen based on their potential to inform, as measured by relative entropy. Of course, the algorithm would still need to decide which tests to administer and if the posttest probabilities at each stage were significant, but this could be accomplished by integration with a diagnostic decision-support system. In this connection we emphasize that although information theoretic concepts can be fruitfully integrated into discussions of these systems (eg, in discussing how the outputs of such systems alter degree of uncertainty, or equivalently, how much information such systems are able to provide), information theory does not provide an “alternative” to probabilistic inference, on which these systems are based. Rather, information theory provides a precise mathematical language for expressing the informativeness of probabilistic statements. In this sense, the information theoretic “approach” is not different from or competitive to strictly probabilistic approaches to medical diagnosis, but it is rather a complementary enhancement.

Conclusion

We have shown that information theory, the mathematical theory of communication, provides natural quantitative concepts to describe the impact of uncertainty on the results of diagnostic tests in clinical settings. We justified the application of these tools to diagnostic testing by noting that the concept of a noisy communication channel, central in information theory, extends naturally to the medical diagnostic reasoning process through a clinical interpretation presented herein. It is our hope that the concepts presented herein will provide additional clarity and insight to physicians’ thinking about data interpretation in reaching medical diagnoses.