Na⁺-binding modes involved in thrombin’s allosteric response as revealed by molecular dynamics simulations, correlation networks and Markov modeling

Abstract

The monovalent sodium ion (Na⁺) is a critical modulator of thrombin. However, the mechanism of thrombin’s activation by Na⁺ has been widely debated for more than twenty years. Details of the linkage between thrombin and Na⁺ remain vague due to limited temporal and spatial resolution in experiments. In this work, we combine microsecond scale atomic-detailed molecular dynamics simulations with correlation network analyses and hidden Markov modeling to probe the detailed thermodynamic and kinetic picture of Na⁺-binding events and their resulting allosteric responses in thrombin. We reveal that ASP189 and ALA190 comprise a stable Na⁺-binding site (referred as “inner” Na⁺-binding site) along with the previously known one (referred as “outer” Na⁺-binding site). The corresponding newly identified Na⁺-binding mode introduces significant allosteric responses in thrombin’s regulatory regions by stabilizing selected torsion angles of residues responsive to Na⁺-binding. Our Markov model indicates that the bound Na⁺ prefers to transfer between the two Na⁺-binding sites when an unbinding event takes place. These results suggest a testable hypothesis of a substrate-driven Na⁺ migration (ΔG ~ 1.7 kcal mol⁻¹) from the “inner” Na⁺-binding site to the “outer” one during thrombin’s catalytic activities. The binding of a Na⁺ ion at the “inner” Na⁺-binding site should be inferred as a prerequisite for thrombin’s efficient recognition to the substrate, which opens a new angle for our understanding of Na⁺-binding’s allosteric activation on thrombin and sheds light on detailed processes in thrombin’s activation.

1. Introduction

Thrombin is a serine protease that plays a critical role in cancer development^1–4 and blood coagulation.^5,6 Many experimental^7–11 and computational works^12–14 have revealed that the molecular properties and enzymatic activities of thrombin are mediated by monovalent sodium (Na⁺) ions. In particular, experiments show that thrombin presents higher catalytic efficiency in coagulant reactions it is involved in when sodium ions are available in the aqueous solution.^7–9,11 However, it has been an over 20 year debate about the mechanism of thrombin’s activation by Na⁺ ions.^{10,12,14–19}

X-ray crystallographic studies indicate that a sodium ion can be bound between thrombin’s 220s and 180s loops and coordinated by 220s loop residues ARG221^‡ and LYS224 and 180s loop residue TYR184A.^20,21 The 220s loop that contributes two binding residues is thereby often referred to as a “sodium binding loop” or “sodium loop” in literature (e.g. see Lechtenberg et al.¹⁵ and Davie and Kulman²²), although different articles have used different ranges of residues to denote this Na⁺-binding loop (e.g. see Davie and Kulman,²² Fuglestad et al.,²³ and Huntington²⁴). Moreover, mutagenesis experiments also show that mutations of other residues, including ASP189, GLU217, ASP222, TYR225, TYR215, ASP221, GLY223 etc., result in a dramatic deficiency of Na⁺-binding and/or perturbation of thrombin’s function.^24–26 Because of these apparent associations between sodium-binding and sodium’s regulations on thrombin’s activities, the binding of a Na⁺ ion to the sodium binding loop has been widely interpreted as a critical allosteric effector that facilitates the functional switch between the anticoagulant “slow” and coagulant “fast” forms of thrombin.^{10,11,15–18} The activation reaction scheme of thrombin has been described as described as E* ↔ Na–E ↔ E-substrate, where E* and E denote the “slow” and “fast” thrombin respectively.²⁷

As a result, in the literature, the Na⁺-bound and Na⁺-unbound thrombin were respectively referred to as the high activity “fast” and low activity “slow” forms. Based on measurements of Na⁺-binding’s affinity, Dang et al. estimated that thrombin respectively adopts a “fast” and “slow” form conformation for 60% and 40% of time in vivo in 1995.¹⁸ In several later studies, the blockage of the substrate-binding pocket S1, S2, and/or the active site cleft were treated as the structural characters that distinguish the “slow” form against the “fast” one.^19,28,29 However, different solved structures of the putative “slow” thrombin don’t reach an agreement on what conformational features of the “slow” thrombin should have.^16,24,28,29 In fact, while substrate-like binding ligands (such as PPACK inhibitor and its analogs) were commonly used in most crystallographic studies on thrombin, all solved crystal structures of wild-type thrombin share an overlapped backbone structure regardless of the presence of a bound Na⁺ ion.²⁴ The structural differences seen in these crystal structures of the putative “slow” and “fast” forms are ascribed to small conformational changes in the inherently flexible regions,^16,24 suggesting that it is improper to interpret the mechanistic differences between the “fast” and “slow” thrombin merely based on their putative static crystal structures.

Nuclear magnetic resonance (NMR) spectroscopies reveal that thrombin’s surface loops establish more dynamic motions in the absence of Na⁺ ions and the binding of Na⁺ can alter the conformational distribution of the active state.¹⁶ These observations raise another explanation of thrombin’s activation by Na⁺. Huntington thereby prosed a dynamic model that thrombin should be considered as a “plastic” enzyme instead of the allosteric one in 2012.¹⁶

Leveraging the development of hardware and software parallelizations, molecular dynamics (MD) simulations on thrombin have presented experimentally consistent but more detailed pictures of thrombin’s conformational ensembles and dynamics.^12,30,31 Particularly, our previous simulations on thrombin illustrate a Na⁺-mediated generalized allostery,³² i.e. Na⁺-binding subtlely perturbs the conformational distribution of the catalytic pocket instead of induced new conformations.¹² Our observations are not only consistent with Huntington’s dynamic model¹⁶ but also explain why all putative “fast” and “slow” thrombin should present similar structures.¹² Interestingly, through MD simulations, Kurisaki and Nagaoka found that the bound Na⁺ ion can release from the sodium binding site and enter the S1 pocket.¹⁹ Their analyses on Na⁺-binding’s impact on thrombin’s S1 pocket suggest that Na⁺-binding is irrelevant to the S1 pocket formation.¹⁹ As an open S1 pocket was treated as a distinct structural feature in the active thrombin by some studies,^28,29 Kurisaki and Nagaoka pointed out a possibility that Na⁺-binding is irrelevant to thrombin’s functional switch.¹⁹ Moreover, Kurisaki et al. further proposed that Na⁺-binding is a negative effector in thrombin–substrate stereospecific complex formation based on their calculations on the interactions between substrate’s primary binding residue (ArgP1) and thrombin’s functional sites.³³

Despite decades of efforts for understanding how thrombin is activated by Na⁺, there appears to be still divergence in Na⁺’s role in thrombin’s functional activities. A detailed study on Na⁺’s binding/unbinding processes and its influence on thrombin is necessary to clarify how sodium binding site and the thereby residues are linked to thrombin’s functions. Here, we employ MD simulations to characterize detailed interactions – in both spatial and temporal space – between Na⁺ ions and residues of apo-thrombin (i.e., unliganded thrombin). Our present study not only bridges knowledge from previous structural and mutagenesis experiments but also reveals the existence of an new stable Na⁺-binding site. Our correlation calculations between the torsion angles and Na⁺ occupancy to each residue display the new Na⁺-binding mode introduces dramatical allosteric responses in thrombin’s regulatory regions. Finally, the hidden Markov modeling quantifies the Na⁺-binding/unbinding processes and leads to a testable hypothesis on a substrate-driven migration of the bound Na⁺ during thrombin’s recognition to the substrate.

2. Materials and methods

2.1. Simulation configuration

Apo-thrombin in the 125 mM sodium chloride buffer was simulated in five runs of all-atom molecular dynamics simulations. All simulations were run using CHARMM22/CMAP force field^34,35 under the isothermal–isobaric (NPT) ensemble. In particular, simulations were run using Berendsen pressure control³⁶ with a 400 fs relaxation time to maintain 1 atm pressure (P). Langevin thermostat³⁷ with a damping coefficient of 0.1 was applied to set the temperature (T) as 300 K.

The initial coordinates of thrombin was determined based on the protein structure in the PDB 4DIH³⁸ and the missing residue fill-in protocol in the comparative modeling tool Modeller.³⁹ To balance the reliability and conformational sampling, and through visual assessments of possible hydrogen bonds on the X-ray structure, missing hydrogen atoms were added to set all ioniz-able residues to their default protonation state at physiological pH. Particularly, all histidine residues were assigned delta protonation. More details about initial protein structure setup and corresponding validity discussion can be seen in the Materials and Method section in our previous work.¹²

Thrombin was solvated in an explicit TIP3P⁴⁰ water box with nm-padding in each of x, y, and z direction. Leveraging the GPU parallelization enabled by ACEMD simulation package⁴¹ and Metrocubo workstations produced by Acellera, the simulations we performed in this study can reach the microsecond time scale. Such long time scales ensure different Na⁺-binding and unbinding events can naturally take place up to thousands of times in the MD simulations (Table S1, ESI†). Therefore, without loss of generality, all ions, including 22 Na⁺ cations, were randomly placed in the 1 nm-padding (each of x, y, and z direction) solvent box initially. As seen in our previous work,¹² the same set of simulations presented an experimentally consistent sodium occupancy in the thrombin’s sodium cavity, suggesting the system has reached thermodynamic equilibrium with regard to Na⁺-binding to thrombin.

2.2. Characterizations of Na⁺-binding activities

2.2.1. Na⁺-occupancy and residence time.

To quantify how frequent and how long Na⁺ ions interact with each thrombin residue, the occupancy and residence time of all possible residue-Na⁺ contacts were computed. A contact $C_{i,j}^t$ between the ith residue and the jth Na⁺ was defined if the jth Na⁺ is within 0.38 nm away from the ith thrombin residue at time frame t. Such distance was used as previous work has shown that it is a proper threshold separating the unbound and bound Na⁺ ion from both thermodynamic and kinetic aspects.¹² Therefore, the instantaneous number of bound Na⁺ ions on the ith thrombin residue $n_i^t$ is

$$n_i^t=\sum _j{C}_{i,j}^t,$$ (1)

where $C_{i,j}^t$ is 1 if the minimum distance between heavy atoms in thrombin’s ith residue and the jth Na⁺ is within 0.38 nm at frame t and 0 otherwise. The time-average Na⁺-occupancy to the ith thrombin residue in MD trajectories with total frames of T is

$$\langle n_i\rangle =\frac{1}{T}\sum _t{n}_i^t.$$ (2)

Meanwhile, given the binary time series of all residue-Na⁺ contacts (i.e. a set of time series of $C_{i,j}^t$), we can estimate the residence time of any Na⁺ ion to a specific residue i based on the mean first passage time from the Na⁺-on state (i.e. $C_{i,j}^t=1$) to Na⁺-off one (i.e. $C_{i,j}^t=0$). In particular, the mean first passage time for a residue was directly calculated by counting how many frames the Na⁺-on state remains on average over all Na⁺ ions in all simulation frames and it was assumed that any Na⁺ ion would not be in contact with thrombin residues after a simulation (i.e. $C_{i,j}^{T+1}=0$ for any i and j, given T is the length of a simulation). The error due to this mandatory assumption should be small given we have ample enough sampling in the microsecond scale simulations.

2.2.2. Cooperativity in Na⁺ binding.

As multiple residues can accommodate the bound Na⁺ and non-Na⁺-binding site residues appeared also linked to the binding of Na⁺,^20,21,25,26 it is important to quantitatively assess the binding cooperativity of Na⁺ with respect to different residues. To differentiate positive and negative couplings, we calculated Pearson correlation coefficients between the numbers of bound Na⁺ ions of pairs of thrombin residues using

$${\rho }_{n_i,n_j}=\frac{1}{{\sigma }_{n_i}{\sigma }_{n_j}}\sum _t\left(n_i^t-\langle n_i^t\rangle \right)\left(n_j^t-\langle n_j^t\rangle \right),$$ (3)

where the ${\sigma }_{n_i}and{\sigma }_{n_j}$ are standard deviations of the time series of the numbers of bound Na⁺ ions on the ith and jth residues of thrombin (i.e. $n_i^{t}and{n}_j^t$ from eqn (1)) respectively. Two residues will present high positive – up to 1 – correlation if they both interact with the bound Na⁺. On the other hand, a negative correlation of −1 will be seen if the Na⁺-binding events never take place simultaneously on these residues. In other words, when a Na⁺-binding event occurs on one of these two residues, there will be a Na⁺-unbinding event happening at the same time on the other residue. The transportation of a Na⁺ between a pair of residues is a primary kinetic process that results in a negative correlation coefficient we see here. Random short-lived surface binding/unbinding activities among different residues should act as noise that can either lead to a near zero Pearson correlation coefficient for the linearly uncoupled residue pairs or reduce the magnitude of the Pearson correlation coefficient for the pairs responsible for coorperative binding.

Furthermore, we constructed a network graph to visualize the resultant correlation matrix whose elements were calculated according to eqn (3). In the network graph, the nodes represent thrombin’s residues and the thicknesses of edges are proportional to the magnitude of the correlation coefficients between two residues whose corresponding nodes were connected. Such representation illustrates the detailed kinetic linkages among residues with respect to the Na⁺-binding activities. To highlight the most significant linkages, 0.3 and −0.15 were used as the thresholds in the constructions of networks for positive and negative coorperative binding respectively. For the network representing positive coorperative binding, a pair of residues were connected by a line if ${\rho }_{n_i{n}_j}>0.3;$ for the network representing the negative coorperative binding, only pairs with ${\rho }_{n_i,n_j}<-0.15$ were connected as the negative couplings were all very weak. In general, positive couplings are stronger and more often than the negative ones since residues within the same secondary structure tend to present the similar dynamic behaviors.

2.2.3. Changes in backbone torsion angles upon Na⁺-binding.

To identify what residues are responsive to Na⁺-binding/unbinding, we measured the correlation (denoted as $r_{n_i,{\alpha }_j}$) between the number of bound Na⁺ ions on the ith residue (denoted as n_i) and the jth residue’s backbone torsion angles $\left({\alpha }_j\right).$ Since the torsion angles – Φ and ψ – are circular variables, which do not have meaningful arithmetic means, we quantified such correlation using linear-circular correlation coefficients $r_{n_i},{\alpha }_j$ as follows,⁴²

$$r_{n_i,{\alpha }_j}=\sqrt{\frac{{{\rho }_{n_i,\cos ({\alpha }_j)}}^2+{\rho }_{n_i,\sin ({\alpha }_j)}{}^2-2\cdot {\rho }_{n_i,\cos ({\alpha }_j)}\cdot {\rho }_{n_i,\sin ({\alpha }_j)}\cdot {\rho }_{\cos ({\alpha }_j),\sin ({\alpha }_j)}}{1-{{\rho }_{\cos ({\alpha }_j),\sin ({\alpha }_j)}}^2}},$$ (4)

where ρ denotes the Pearson correlation function as already shown by eqn (3) except for changing related variables according to the corresponding subscripts of ρ. The value of $r_{n_i},{\alpha }_j$ ranges from 0 to 1, where the value of 1 indicates linearly dependence and the value of 0 indicates the opposite.

Weighted directed graphs were also constructed to visualize the networks of the backbone torsion angles’ responses upon changes in the number of bound Na⁺ for each residue. Thrombin residues were denoted by the nodes. The thicknesses of edges are proportional to the corresponding correlation and a cutoff threshold of 0.3 was set here to only show couplings which have at least an intermediate strength.^43,44 As the correlation matrix here is asymmetric $(i.e.r_{n_i,{\alpha }_j}\ne r_{n_i,{\alpha }_i}\text{if}i\ne j),$ arrows were added for the edges and the directions of arrows were from the residue being counted the number of bound Na⁺ to the one being measured the backbone torsion angles. In other words, the direction of the edge, which was weighted by $r_{n_i},{\alpha }_j,$ is from residue i to residue j. The backbone torsion angles were obtained via the coordinate featurizer module in Python package PyEmma.⁴⁵

2.2.4. Hidden Markov modeling.

Markov modeling has proven useful for understanding conformational states of biomolecules and their transitions.⁴⁶ Given the large-scale atomic molecular simulations, we seek a Markov model to obtain an insightful kinetic model that quantitatively describes the association and dissociation of Na⁺ relative to the major Na⁺ sodium binding residues.

As we are interested in the slow binding/unbinding processes rather than the fast thermal fluctuations, a time-lag independent component analysis. (Also called time-structure independent component analysis in literature. In the following context, we used TICA to stand for this decomposition method)^47,48 was performed before conducting clustering to obtain discretized trajectories. Choosing a time lag of 100 ps and using the distance matrix between the major Na⁺ sodium binding residues (i.e., ASP189, ALA190, ARG221 and LYS224) and their nearest Na⁺ ion as the input feature, we obtained dominant TICA components that retain 95% kinetic variance.⁴⁹ Afterwards, the original feature space was efficiently discretized into 100 microstates by running k-means clustering on the TICA projections along these dominant TICA components.

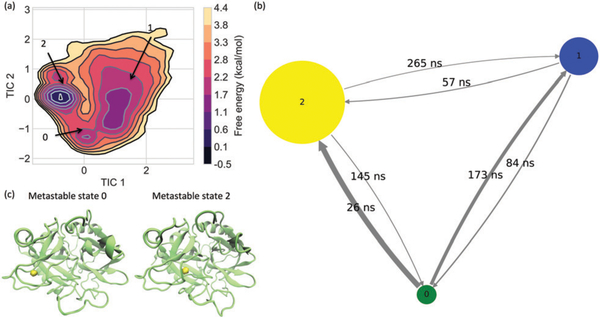
As demonstrated by other studies,^50–52 when being described by its cluster discretization of the state space, the system doesn’t necessarily hold Markovian dynamics anymore. Therefore, we constructed a hidden Markov model (HMM) instead of a direct observed Markov model from clustering algorithms. The HMM is also a type of Markov model but its construction doesn’t rely on a potentially improper assumption of Markovianity of the discrete dynamics.⁵⁰ Moreover, because of the Bayesian statistics employed during the hidden Markov modeling, the resulting HMMs are more robust even for a bad discretization when comparing to the direct observed Markov models.⁴⁹ By optimally grouping fast mixing microstates into metastable macrostates using the reversible Bayesian HMM estimator,⁵⁰ the HMMs provide coarse-grained kinetic models describing the complete Na⁺ dissociation and association processes to thrombin. The number of macrostates was set to 3 based on the following three factors: (1) structural investigations of frames in the three major wells in the free energy surfaces constructed along TICA projections clearly demonstrate outer Na⁺-binding, inner Na⁺-binding, and Na⁺-unbound modes (Fig. 4(a)); (2) there are three separable timescales of processes (Fig. S2, ESI†); and (3) trial and error using different values of macrostates suggests that setting 3 macrostates during Markov modeling results in the highest quality of Markov models (Fig. S3 and S4, ESI†). An HMM with a 1 ns Markov lag time was picked for further analyses as the relaxation timescales appeared independent of the lag time at this point (Fig. S2, ESI†) and this model successfully passed the Chapman–Kolmogorov test.⁵³ The generation and validation of the HMMs as well as the quantities representing the model (such as transition matrix and mean first passage time between states) were carried out and computed via the Python package PyEmma.⁴⁵

Fig. 4.

Metastable states from Hidden Markov modeling. (a) Three metastable states are identified from the free energy surface constructed along the first TICA components. The transition among these three metastable states are illustrated in panel (b), where the size of nodes and the thickness of the transition arrows are respectively proportional to the stationary probability of the corresponding states and transition matrix. The quantities above the arrows indicate the mean first passage times from one state to another. Structural representations for the Na⁺-bound metastable states are shown in panel (c), where the bound Na⁺ are indicated by the yellow isosurfaces with a number density of 0.5.

3. Results

3.1. Multiple Na⁺ binding sites exist

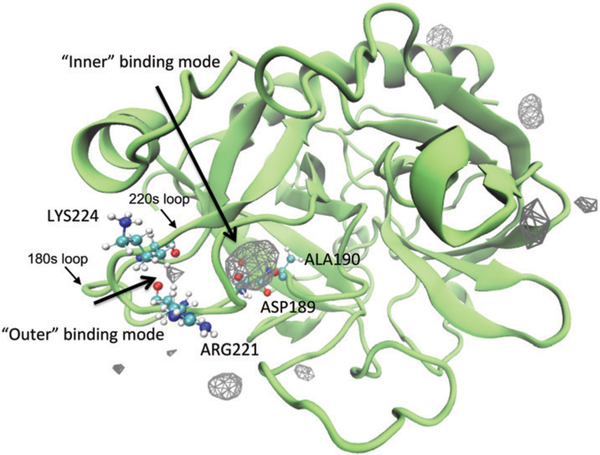
Although all simulations here were not started from a thrombin–Na⁺ complex with a bound Na⁺ at the known sodium binding site, the Na⁺ cations can recognize the “sodium binding loop” and bind to it in the microsecond MD simulations. As seen in Fig. 1, we illustrated the density map of Na⁺ ions. Consistent with several studies in literature,^12,14 here we also see that Na⁺ ions establish both surface and interior bindings to the molecule of thrombin. The surface bindings of Na⁺ appear associated with the side chains of residues in the 60s, 220s and γ loops and chain termini, while the interior bindings are located between the 220s and 180s loops. Setting different number density values as the isovalue for the isosurface construction, the isosurfaces corresponding to the surface bindings largely vanish. These results indicate that the interior binding modes are highly populated and relatively stable, as our previous work showed that the system has reached thermodynamic equilibrium with respect to stable Na⁺-binding to the sodium binding loop in the same set of simulations.¹²

Fig. 1.

A density map of Na⁺ around thrombin. To show the density map as isosurfaces, a fractional occupancy of 0.05 was used as the isovalue. The protein is shown as the structure closest to the average structure in the simulations. Two different interior binding modes are identified between 220s and 180s loops. They are referred to as “outer” and “inner” binding modes in the following context. The residues accommodate these two binding modes are indicated by the labels beside their CPK representations.

Calculations of each residue’s Na⁺ ion occupancy reveal that ASP189, ALA190, GLU247, ARG17, ASP15, and GLY219 stand out as the top six residues with the most frequent contacts with Na⁺ (Table S1, ESI†). While the highly flexible chain terminus residues GLU247, ARG17, and ASP15 are more likely to encounter the Na⁺ ions in the solution by chance rather than stably interact with them, only ASP189, ALA190, and GLY219 are in contact with a Na⁺ ion for more than 20% of time (56.3%, 54.9%, and 26.3% respectively). ASP189, ALA190, and GLY219 are involved in thrombin’s substrate pocket S1, although these three residues are also spatially adjacent (within ~0.4 nm) to the known Na⁺ binding site (i.e., ARG221, LYS224, and TYR184A). The ARG221 and LYS224 in the 220s loop are bound to a Na⁺ ion for ~4% of time, while the nearby ASP221A has a higher Na⁺ occupancy of ~9%. Moreover, the 180s loop residue TYR184A doesn’t present frequent interactions with Na⁺ ions (less than 1% of time). This result is consistent with the observation that TYR184A does not directly coordinate the bound Na⁺ via its backbone oxygen atom like LYS224 and ARG221 do.^21,25

Despite the fact that the previously known Na⁺ binding site residues (i.e., ARG221, LYS224, and TYR184A) are not very thermodynamically favorable for Na⁺-binding comparing with several other residues, ARG221 and LYS224 stand out due to their kinetic aspect regarding Na⁺-binding. These two residues establish the third and fourth longest Na⁺-binding residence time among all thrombin residues. As seen in Table S1 (ESI†), ASP189, ALA190 have 31.2 ± 0.3 ns and 20.5 ± 0.2 ns Na⁺ residence time respectively, which is about 1–3.7 fold longer than ARG221 and LYS224 do. Full statistics of Na⁺-binding to other thrombin residues indicate ASP189, ALA190, ARG221 and LYS224 are most kinetically favorable residues for Na⁺’s attachment.

Therefore, along with the known Na⁺ binding site (ARG221 and LYS224), there should exist another one – composed of ASP189 and ALA190 – in the deeper interior region near thrombin’s primary substrate binding pocket S1. This newly identified binding site is both thermodynamically and kinetically stable for the binding of a Na⁺ ion. In the following and based on the relative positions of the residues ASP189, ALA190, ARG221 and LYS224, we refer to the deeper Na⁺-binding site as “inner” Na⁺-binding site and the known Na⁺-binding site as “outer” Na⁺-binding site. While it is well-known that the bound Na⁺ ion at the “outer” Na⁺-binding site interacts with four water molecules and the backbone oxygen atoms of ARG221 and LYS224,²¹ the Na⁺ at the “inner” Na⁺-binding site appears to be coordinated to the side chain oxygen atoms of ASP189 and the backbone oxygen atom of ALA190 and to be hydrated with three water molecules (Fig. S1, ESI†). In addition, other nearby fluctuating residues such as GLY219 and water molecules can also occasionally provide energetic stabilization of the “inner”- Na⁺-binding mode.

3.2. “Inner” and “outer” Na⁺-binding modes are competitive

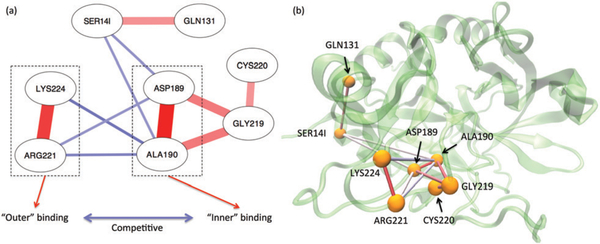
Given multiple binding modes of a Na⁺ ion, the correlation network of each residue’s Na⁺-occupancy status sheds insights into linkages between each pair of thrombin residues with respective to Na⁺-binding/unbinding. Our calculation reveals that the giant component – as shown in Fig. 2(a) – is composed of eight residues (~2.7% of total thrombin residues), suggesting the binding/unbinding events on most residues are transient and non-cooperative. Negative coupling with a magnitude greater than 0.15 only occurs in the kinetically slow binding/unbinding processes involved residues ASP189, ALA190, ARG221 and LYS224.

Fig. 2.

Cooperativity in Na⁺ bindings. Panel (a) illustrates the giant component of the thrombin residues’ coupling network with respect to number of bound Na⁺. Panel (b) shows these coupling on the structure plot. The red and blue lines on both panels represent the positive and negative correlations respectively. A darker and thicker line indicates a stronger coupling.

As seen in Fig. 2, the contacts of Na⁺-LYS224 and Na⁺-ARG221 are positively coupled with a high strength, indicating the bound Na⁺ is coordinated by both LYS224 and ARG221 in the “outer” Na⁺-binding mode. Similarly, ASP189 and ALA190 coordinate a Na⁺ in the “inner” Na⁺-binding mode. As the Na⁺ occupancy of GLY219 presents some positive correlation with ones of ASP189 and ALA190, residues GLY219 also directly contributes to the inner Na⁺-binding. On the other hand, the Na⁺ occupancies of ASP189 and ALA190 exhibit negative coupling with the one of LYS224 and ARG221, suggesting the attachment of a Na⁺ ion at one of these interior Na⁺-binding sites prevents the binding of Na⁺ at the another one.

Furthermore, it is interesting to observe that the distant light chain residue SER14I is negatively coupled with ASP189 and ALA190 (Fig. 2). Meanwhile, SER14I is also positively coupled with the heavy chain residue GLN131 (Fig. 2). These phenomena suggest a linkage between thrombin’s light and heavy chains, which can be seen given various aspects in the literature.^54–62

3.3. Na⁺ binding induces allosteric changes via stabilizing selected backbone torsion angles

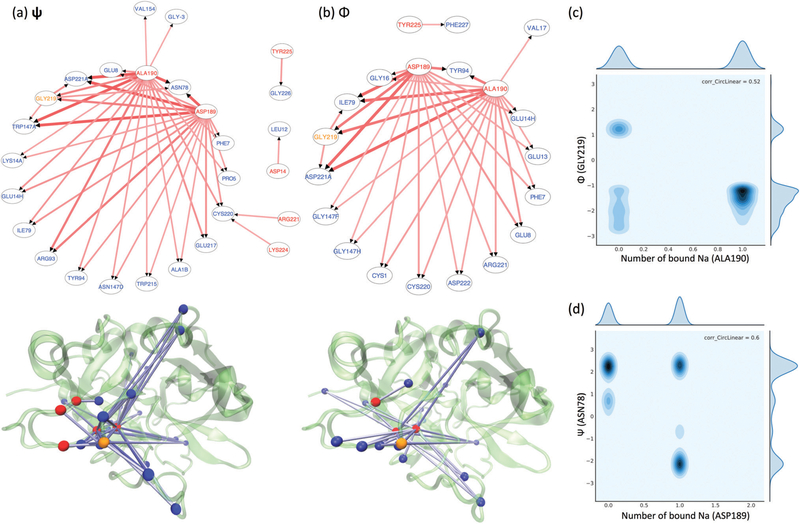
To understand thrombin residues’ allosteric linkages regarding the bound Na⁺, we examined the coupling between the Na⁺- bindings and residue torsion angles. For most residues, the numbers of locally bound Na⁺ do not correlate with the fluctuations of other residues’ backbone torsion angles (i.e. ψ and Φ). However, there are a group of residues presenting considerable coupling – correlation coefficient greater than 0.3 – between their ψ and Φ angles and other residues’ Na⁺-occupancy. As listed in Fig. 3(a and b), when a Na⁺ is bound to ASP189, ALA190, ARG221, LYS224, GLY219, TYR225 or ASP14 (indicated by red node labels in the network graphs and red beads in the structure plots except for GLY219 as it is also responsive to the Na⁺-binding to other residues), specific backbone torsions of other residues (indicated by the blue node labels and blue beads in the structure plots) are affected. Consistent with residence time analysis, ASP189, ALA190, ARG221 and LYS224 keep distinguishing themselves as major Na⁺-binding residues by presenting considerable correlations with other residues’ ψ and Φ angles. In particular, as indicated by the arrows from ASP189/ALA190 and ARG221/LYS224 in Fig. 3(a and b), the “inner” Na⁺-binding mode induces significantly distinct allosteric responses in other residues’ ψ and Φ angles than the “outer” Na⁺-binding mode does. The regions responsive to the Na⁺-binding at the “inner” binding site covers the most known regulatory regions of thrombin, which includes the 180s, 220s and γ loops and exosite I/II.

Fig. 3.

Allosteric responses to the Na⁺-binding/unbinding. Correlation networks between residues’ Na⁺-occupancy and ψ/Φ angles are displayed in panels (a and b). The arrows point from the Na⁺-bound residues to the highly responsive residues. In both the network graphs and structural mapping plots in panels (a and b), the Na⁺-bound residues are indicated by red labels or red beads, while the responsive residues are indicated by blue ones. GLY219 is the only residue in orange, representing its Na⁺-binding can affect other residues’ torsion angles and its torsion angles are also responding other residues’ Na⁺-binding. Panels (c and d) illustrate the heat maps of the joint distributions of one residues’ Na⁺-occupancy and another residue’s ψ/Φ angles. (c) Shows the most common heat map representing generalized allosteric responses, while (d) is the only case exhibiting “induced-fit”-like responses.

The most common effect introduced by Na⁺-binding is to stabilize the torsion angle fluctuations of residues in thrombin’s functional regions. For example, as suggested by the heat-map in Fig. 3(c), the binding of a Na⁺ ion on residue ALA190 stabilizes a particular Φ angle (~ –π/2) of residue GLY219. Such effect is known as the generalized allosteric effect^32,63–65 because the selected Φ angle can naturally occur before the Na⁺-binding event. Another type of effect is “induced-fit”^63,65-like. The bound Na⁺ results in a unique new conformation such that another residue only presents that torsion angle after Na⁺-binding. We could observe the “induced-fit”-like response just once in our analysis. As seen in Fig. 3(d), the conformations with a negative ψ angle of residue ASN78 does not occur until a Na⁺ is in contact with residue ASP189.

Along with the construction of the Markov model described in the Method section as well as the next subsection, clustering analysis on the residues that allosterically respond to Na⁺-binding (see nodes in Fig. 3) further demonstrates that the inner Na⁺- binding selectively stabilizes a conformational cluster of backbone torsion angles of these residues (Fig. S5, ESI†). The most obvious influence of Na⁺-binding we saw here is the perturbation of the conformational distribution, although the conformational changes appear to be subtle. This observation is also consistent with our previous work,¹² which explains why it is too difficult to solve the distinct enough X-ray structures of the “slow” and “fast” thrombin and suggests the mechanism of this functional switch should be a Na⁺-mediated generalized allostery instead of induced-fit.

3.4. “Inner” and “outer” Na⁺-binding modes are preferentially transferable into each other

As two distinct Na⁺-binding modes in thrombin were identified, we proceeded to characterize the Na⁺ association and dissociation processes via the construction of a three-state Markov model. Through the time-lag independent component analysis (TICA) using lag time of 100 ps, 95% kinetics of the nearest Na⁺ to the major Na⁺-binding residues ASP189, ALA190, ARG221, and LYS224 were captured by the three slowest TICA components. As shown in Fig. 4(a), the free energy surface estimated along the slowest two kinetic processes also illustrates three major wells, rationalizing the choice of three metastable states in the construction of a coarse-grained kinetic model.

Hidden Markov modeling has proved more tolerant of trajectory discretization errors than the directed observed Markov modeling.⁵⁰ After clustering the dominant TICA projections, using a Markov lag time of 1 ns (Fig. S2, ESI†), we optimally grouped fast mixing microstate into metastable macrostates (Fig. S3, ESI†). As a result, we built a hidden Markov model (HMM) that approximates the complete Na⁺ dissociation and association processes to thrombin. Such coarse-grained model is statistically robust as it passed a Chapman–Kolmogorov test⁵³ in 95% confidence interval (Fig. S4, ESI†). Moreover, as illustrated in Fig. 4c, structurally, the metastable sets in the resulting HMM as well as different wells in the free energy surface were respectively identified as the Na⁺-unbound, “inner” Na⁺-bound, and “outer” Na⁺-bound states, suggesting the rationality of the model physically.

Consistent with Na⁺-occupancy results, the metastable state with a Na⁺ ion near the “inner” binding site appears energetically more favorable (ΔG ~ –1.7 kcal mol⁻¹) than the one with a Na⁺ ion near the “outer” binding site. As illustrated by size of nodes in the transition network of the HMM (in Fig. 4(b)), the “outer” Na⁺-bound state is the least populated one. Meanwhile, “inner” Na⁺-bound, “outer” Na⁺-bound and Na⁺-unbound states are completely connected and transferable, indicating that there are two Na⁺-binding/unbinding pathways for each Na⁺-binding site.

The labels above the arrows in Fig. 4(b) demonstrate the mean first passage time from one metastable state to another. While it takes 26–57 ns for a Na⁺ ion to bind to the “inner” Na⁺-binding site, it takes 145–265 ns for that Na⁺ ion to release to the “outer” Na⁺-binding site or the external Na⁺ reservoir. On the other hand, the “outer” Na⁺-binding site presents the opposite kinetic behavior such that it is faster for a Na⁺ to dissociate from the “outer” Na⁺-binding site than to attach to this site. These values demonstrate that, kinetically, it is easier for a Na⁺ ion to bind to the “inner” Na⁺-binding site than the “outer” one. Moreover, Fig. 4(b) also illustrates it takes shorter time for a bound Na⁺ at either Na⁺-binding sites to migrate to another one (26 ns and 145 ns for 0 ↔ 2) than to unbind and diffuse back to the Na⁺ reservoir (265 ns for 2 → 1 and 173 ns for 0 → 1). Therefore, it is kinetically more favorable for a bound Na⁺ ion migrate between two Na⁺-binding sites than to release to the Na⁺ reservoir directly.

4. Discussion

Experimental techniques such as crystallography and NMR spectroscopy offer essential information to understand structures of biomolecules and corresponding mechanisms of their role in biological processes. At the same time, computational modeling has proved useful to shed insights into atomic-detailed dynamic perspectives of the system and fill the gaps between our understanding and observations. One example of this is when MD simulations have been employed to refine the metal ion binding site found by solution NMR experiments⁶⁶ as well as to reveal new ion binding sites in proteins in a de novo way.^67,68 Although the crystal structure of thrombin with a Na⁺ at the “inner” Na⁺-binding site has not been seen yet, several previous MD simulations using different MD force fields – including CHARMM,^34,35 Amber⁶⁹ as well as parameter adjustments^70,71 for corresponding water models^40,72 – have also shown the large density of a Na⁺ in vicinity of ASP189¹⁴ and suggested a second binding site in thrombin for Na⁺.⁶² Moreover, recent NMR experiments⁶¹ have confirmed the allosteric pathways revealed by our previous MD studies.^12,31,62 Such an excellent agreement between experiments and computations indirectly validates the simulation protocol in the present study, given our previous work employed the same MD protocol as we did here.

Consistent with mutagenesis experiments,^24–26 our calculations also identified a list of residues presenting strong linkages with the binding of Na⁺ (Fig. 2). The correlation network of residues’ Na⁺-occupancy helps understand these mutagenesis experiments by providing insights into the mechanism of the direct linkage among residues regarding two major Na⁺-binding events – “outer” and “inner” Na⁺-bindings. The sodium binding loop is a blurred name representing what region accommodates the bound Na⁺ ion. More precisely, we observed that LYS224, ARG221, ASP189, ALA190, GLY219, CYC220, SER14I and GLN131 are directly linked regarding Na⁺-binding. Particularly, as it has been revealed by mutagenesis experiments,^24–26 mutating residue ASP189 will extremely impair Na⁺-binding. Such weakening Na⁺-binding seems a direct consequence of disrupting the “inner” Na⁺-binding site and the whole correlation network related to Na⁺-binding. Meanwhile, there are other residues affecting Na⁺-binding (see the review article by Huntington in 2008²⁴) not showing in the giant component of the Na⁺-occupancy correlation network. Such a result doesn’t indicate these residues are irrelevant to Na⁺-binding. Instead, our analysis clarifies that these residues should indirectly contribute to Na-binding. Most of these residues are spatially closed to the residues in the correlation networks shown in Fig. 2 and 3, implying that the mutations of these residues may affect Na⁺-binding by perturbing the structural ensembles or cause hostile local environment changes for Na⁺-binding kinetics.

While mutagenesis studies have already revealed the importance of ASP189 and other sodium binding loop residues in modulating Na⁺-binding and thrombin’s activation,^24–26 it was also suggested by Kurisaki et al. that Na⁺-binding in the vicinity of residue ASP189 may present a negative effect on thrombin’s recognition to substrate.³³ Note that ASP189 is involved in the primary substrate binding pocket S1 and it is responsible for the specific interactions with the positively charged P1 residue (usually ARG/LYS) in the substrate. We agree that the stable binding of Na⁺ on ASP189 we demonstrate here may potentially impede substrate’s recognition of the S1 subpocket due to the repulsive force between the bound Na⁺ and the positively charged P1 residue. On the other hand, the repulsive force between the substrate P1 residue and the bound Na⁺ may lead to a ion transition like the ion knock-on process in K⁺ channel examined by Sumikama and Oiki in 2016.⁷³ As indicated by our HMM (Fig. 4(b)), a bound Na⁺ prefers transferring between the “inner” and “outer” Na⁺-binding site rather than going back to the external Na⁺ reservoir directly. As a result, during the binding of thrombin’s substrate, the substrate’s P1 residue may induce a migration of the bound Na⁺ from the “inner” Na⁺-binding site to the “outer” one. The free energy difference between the these two Na⁺-binding states (~1.7 kcal mol⁻¹) as well as the free energy barrier (~2.8 kcal mol⁻¹) suggests the ion migration from the “inner” Na⁺-binding site to the “outer” one is not likely to occur under thermal fluctuations (~0.6 kcal mol⁻¹). This substrate or ligand induced ion migration is likely one of the reasons crystal structures of thrombin display the “outer” Na⁺-binding mode, especially considering there is some substrate-like binding ligands (such as PPACK inhibitor and its analogs) at the active site in most crystal structures of thrombin. One can commonly observe these ligands interacting with ASP189 through the polar interaction, which likely have forced the Na⁺ ion away from the “inner” Na⁺-binding site. For the small selection of the thrombin structures, which are available without a ligand interacting (see PDB 2UUF⁷⁴ and 3U69⁷⁵), they may not be germane due to other ligands bound at either the allosteric regulation site (for PDB 2UUF) or the S3 and S4 subpockets adjacent to S1 (for PDB 3U69). Unlike the conformations in “inner” Na⁺-binding state, the subtle rearrangement of the side chains of residues around ASP189 and ALA190 partially occludes the “inner” Na⁺-binding site. Instead, the water-binding in the S1 subpocket, as seen in these crystal structures, suggests the possibility that Na⁺-binding at the “inner” binding site binding site competes with the water-binding. Detwetting of the same region has been previously discussed by Kurisaki et al. as a rate-limiting process in the interaction of the S1 pocket.⁷⁶ In summary, based on the evidence from our calculation and experimental works, it is highly likely there is a substrate-driven ion migration during thrombin–substrate interaction. High-resolution crystallographic studies on inhibitor- and ligand-free thrombin are needed to obtain more samples of the thrombin–Na complex, which may provide more direct evidence of the predicted inner-Na⁺-binding site prior to thrombin’s recognition to the substrate. On the other hand, as experimental approaches may be limited to the unphysiologically relevant conditions during the structural determination, computational methods such as MD simulations may provide further insights. Long timescale (hundred of microseconds to milliseconds) MD simulations that simulate the thrombin–substrate recognition process in the presence of Na⁺ ions are needed to test if the inner Na⁺-binding is indeed a prerequisite for thrombin’s recognition to the substrate. If the proposed hypothesis is true, in the simulations, the substrate should appear to recognize the active site of thrombin more efficiently (i.e. k_on is larger) after a Na ion binds to the “inner” Na⁺-binding site and allosterically stabilizes the enzyme. It is also expected to see that, during the association process of the substrate, the bound Na⁺ ion should release from the “inner” Na⁺-binding site and move to the “outer” Na⁺-binding site.

Na⁺-binding has been revealed as an allosteric effector of thrombin by many experimental and computational works.^{7–9,11–14} In particular, our previous study indicates the binding of Na⁺ doesn’t perturb the backbones of the catalytic pocket residues but their side chains’ orientation.¹² Here the side chains’ allosteric responses upon Na⁺-binding to each residue are quantified by the correlation coefficients between ψ/Φ angles and Na⁺’s occupancies. Fig. 3 displays the Na⁺-bindings at the “inner” and “outer” Na⁺-binding sites introduce extremely different allosteric responses. The “outer” Na⁺-binding mode only appears to stabilize the Ψ angle of the nearby residue CYS220. In contrast, the “inner” Na⁺-binding mode results in a much more significant influence on adjacent and distant residues. These affected residues are located in the 180s, 220s and γ loop, exosite I/II, catalytic pocket and light chain, which are all functionally related to Na⁺-binding and catalytic efficiency.^22,77,78 Except for residue ASN78, whose Ψ angle can adopt a completely new value after a Na⁺ binds to residue ASP189 (Fig. 3), the effect induced by the Na⁺-binding at the “inner” Na⁺-binding site is to select and stabilize a priorly occurring Ψ/Φ torsion angle of the other responsive residues. In other words, the “inner” Na⁺-binding mode stabilizes a selected conformation (Fig. S5, ESI†). Therefore, these findings demonstrate the “inner” Na⁺-binding induced generalized allostery^32,63–65 is the main mechanism of Na⁺’s mediation on thrombin, which also agrees with previous discussions on thrombin’s conformational ensembles.^12,79

With respect to the debate about whether Na⁺-binding is critical for thrombin’s activation, while our previous work also demonstrated the importance of the unbound Na⁺ ions,¹² this work emphasizes that Na⁺-binding is a necessary biological event for thrombin’s activation. Our quantitative and detailed results appear to align with various experimental studies.^{7–11,25,26,61} On the other hand, Kurisaki et al.’s delicate calculations also pointed out that the existence of a bound Na⁺ ion at the “outer” Na⁺-binding site should result in about 4 kcal mol⁻¹ energy disadvantage in the interaction between the substrate residue ArgP1 and thrombin’s S1, 220s loop residues, implying the bound Na⁺ may play a negative role for thrombin–substrate stereospecific complex formation.³³ However, these calculations were based on MD simulations starting from the thrombin-substrate complex in the presence or absence of the bound Na⁺ ion. Such an initial setup was only able to capture the late formation stage of the thrombin-substrate complex, particularly given that the simulation length of 500 ns may not be long enough to well study the complete association/dissociation process of a substrate to thrombin. Along with our previous work,¹² our simulations illustrate that the binding of a sodium ion perturbs thrombin’s conformational distribution. As the equilibrium constant for conformational transition can significantly affect molecular recognition,⁸⁰ the Na⁺-binding-induced conformational distribution shift should be profound for thrombin–substrate interactions. The Na⁺ binding event at the “inner” sodium binding site stabilizes specific residues’ torsion angles (Fig. S5, ESI†). The resultant conformation is likely favorable for interact with the substrate, given the apparent experimentally demonstrated association between Na⁺-binding and thrombin’s functional activities. The relatively small free energy barriers among each Na⁺ binding/unbinding states may actually reflect how Na-binding subtly regulates the thrombin’s activation. If these free energy differences are too large, the bound Na ion may provide too large resistance for positively charged P1 residue of the substrate to recognize the active pocket, which is against the experimental observations that Na ions are favorable for efficient interactions between thrombin and its substrate. Therefore, despite the repulsive force between the bound Na⁺ and substrate P1 residues, Na⁺ may not necessarily be a negative effector for the entire thrombin–substrate formation process. The bound Na⁺ ion seems to play a positive role in the early stage of thrombin–substrate formation in terms of stabilizing the specific conformation of thrombin. In this sense, the inner Na⁺-binding may be more like a promoter, which promotes thrombin’s catalytic activities by shifting thrombin’s conformational ensembles from “slow” form (denoted as E*) the towards the “fast” form (denoted as E) in the traditional activation reaction scheme of enzyme.²⁷ To further validate this hypothesis, Hundreds of microsecond to millisecond scale MD simulations are be needed in future work to examine the role of Na⁺ ions in the entire thrombin-substrate recognition processes.

5. Conclusions

Combining extensive all-atom MD simulations and various analyses, we have characterized all possible residue-Na⁺ contacts and demonstrated the existence of a new Na⁺-binding site in apo-thrombin. This Na⁺-binding site is located beside the previously known Na⁺-binding site (referred to as “outer” Na⁺-binding site in the context) and largely accommodated by ASP189 and ALA190 of the S1 subpocket. Compared with the “outer” Na⁺-binding site, this “inner” Na⁺-binding site is thermodynamically and kinetically more favorable for the binding of a Na⁺ ion.

Instead of the binding activity at the “couter” Na⁺-binding site, it is actually the “inner” binding mode that induces significant allosteric responses in thrombin’s 180s, 220s and γ loop, exosite I/II, catalytic pocket and light chain. Such a Na⁺ binding stabilizes selected torsion angles of the residues in these regulatory regions. Our findings do not only provide another evidence of the generalized allostery as the mechanism of Na⁺’s regulation on thrombin, but also depict a more detailed picture of the allosteric pathways. The allosterically linked residues’ dihedral angles are stabilized by the Na⁺-binding at the “inner” Na⁺-binding site. The stabilized conformation with selected dihedral angles is likely favorable for the “fast” thrombin.

Hidden Markov modeling offers a coarse-grained kinetic model that quantifies the complete association and dissociation processes of Na⁺ relative to the “outer” and “inner” Na⁺-binding sites. We observed that a bound Na⁺ at either of these two sites prefers transferring to another Na⁺-binding site than going to the solution directly. This property explains why we saw a competitive binding between the two Na⁺-binding modes in our correlation analysis. Moreover, our kinetic model proposes a testable hypothesis on the underlying process of thrombin–substrate recognition. The bound Na⁺ at the “inner” Na⁺-binding site first stabilizes a particular conformation that is favorable for thrombin’s catalytic efficiency. Secondly, the substrate recognizes the well-formed stable catalytic pocket of thrombin and starts binding. During this substrate-binding process, the bound Na⁺ ion at the “inner” Na⁺-binding site is being repelled by the positively charged P1 residue of the substrate and then transfers to the “outer” Na⁺-binding site (ΔG ~ 1.7 kcal mol⁻¹). This hypothesis provides a likely explanation why crystal structures of thrombin do not display the “inner” Na⁺-binding mode yet, given the fact that the ASP189 is mostly occupied by a bound chemical compound (e.g. PPACK inhibitor) in these crystal structures. Further studies, such as inhibitor-free structural determination or large scaled inhibitor-bound molecular dynamics of thrombin–substrate complex in NaCl buffer, could test this hypothesis.