pH-Dependent Protonation of the Phl p 6 Pollen Allergen Studied by NMR and cpH-aMD

Abstract

We use state-of-the-art NMR experiments to measure apparent pK_a values in the native protein environment and employ a cutting-edge combination of enhanced sampling and constant pH molecular dynamics (MD) simulations to rationalize strong pK_a shifts. The major timothy grass pollen allergen Phl p 6 serves as an ideal model system for both methods due to its high number of titratable residues despite its comparably small size. We present a proton transition analysis as intuitive tool to depict the captured protonation state ensemble in atomistic detail. Combining microscopic structural details from MD simulations and macroscopic ensemble averages from NMR shifts leads to a comprehensive view on pH dependencies of protonation states and tautomers. Overall, we find striking agreement between simulation-based pK_a predictions and experiment. However, our analyses suggest subtle differences in the underlying molecular origin of the observed pK_a shifts. From accelerated constant pH MD simulations, we identify immediate proximity of opposite charges, followed by vicinity of equal charges as major driving forces for pK_a shifts. NMR experiments on the other hand, suggest only a weak relation of pK_a shifts and close contacts to charged residues, while the strongest influence derives from the dipolar character of α helices. The presented study hence pinpoints opportunities for improvements concerning the theoretical description of protonation state and tautomer probabilities. However, the coherence in the resulting apparent pK_a values from simulations and experiment affirms cpH-aMD as a reliable tool to study allergen dynamics at varying pH levels.

Introduction

The pH level is well known to be a critical environmental determinant of protein function and stability.¹⁻³ Small changes in solution pH can be sufficient to completely destabilize a protein or change its activity profile.^4,5 Proteins react to pH changes via protonation or deprotonation of titratable residues, thereby changing their charge distribution. The nature and strength of this effect depends on the number of affected titratable residues, on their structural environment, and on possible compensation of introduced charges. The acidity of a titratable group is represented by its pK_a value and directly dependent on its electrostatic surroundings.^6,7 Thus, while for isolated amino acids in solution these pK_a values are easily measurable, they can be drastically perturbed and challenging to measure within the context of a protein.⁸ Yet, an accurate representation of protonation states and tautomers is paramount for reliable experimental and especially computational studies of protein structures.⁹

An additional challenge arises from the dynamic nature of proteins.¹⁰ The free-energy surface of proteins in solution is vast and rugged, where each minimum represents a different conformational state.^11,12 From the multitude of constantly interchanging conformational states of a protein, each exhibits individual solvent accessibility, charge distribution, etc., resulting in variations of the according microscopic pK_a values.^13,14 The ensemble average of these microscopic pK_a values is then represented as the macroscopic or apparent pK_a value. NMR spectroscopy offers the unique possibility of directly measuring such apparent pK_a values experimentally. Numerous homonuclear and heteronuclear approaches can be employed for monitoring protonation probabilities of titratable groups in pH titrations and extracting their pK_a values in a native, dynamic protein environment.^8,15

Similar to NMR experiments, molecular dynamic (MD) simulations also capture an ensemble of protein conformations.^16,17 While the accuracy of simulations is restricted by the accuracy of the applied force field and the captured sampling time, they provide a time-resolved representation of the configurational ensemble of proteins in atomistic detail. However, classic MD simulations do not allow the breaking of bonds and are thus not able to simulate changes in protonation states. Hence, the protonation states of each amino acid must be chosen during the structure preparation steps and cannot change during the simulation. Choosing an appropriate protonation state can be very challenging and requires either available experimental pK_a values of the studied system or reliable means to predict the unknown pK_a values.⁹

Over the last decades, a plethora of pK_a prediction tools have been developed.¹⁸ Most commonly, static methods like PROPKA¹⁹ or H++²⁰ are applied, which estimate pK_a values from a single input structure and employ an implicit solvent model, making the calculation relatively fast and the input preparation straightforward. However, as discussed above, proteins do not occur as one single static structure. Hence, dynamic methods were developed, like the family of constant pH molecular dynamics (cpH-MD) methods, which rely on an ensemble of structures to estimate pK_a values. In contrast to static methods, these approaches are capable of capturing the interplay of changes in pK_a and changes in structure, yet at a higher computational cost.⁹

In the following, we will only briefly discuss the key points of cpH-MD; for more in-depth discussions, the reader is pointed to the respective works.²¹⁻³⁴ There are mainly two different approaches to cpH-MD: using continuous²⁸ or discrete protonation states.^22,27 In the first, originally implemented in the software package CHARMM,³⁵ the protonation states are sampled along a continuous titration coordinate employing the λ-dynamics approach. In contrast to that, discrete protonation states are sampled via Metropolis Monte Carlo (MC³⁶) moves, which happen at defined intervals over the course of the simulation. While originally implicit solvent models³⁷ were used, both methods have seen further adaptations to also make use of explicit solvent models.^30,32,33,38 In this study, we employed the discrete protonation state approach, as implemented in the AMBER³⁹ simulation package.^27,32 To achieve faster pK_a convergence as well as higher pK_a prediction accuracy, combinations of cpH-MD and enhanced sampling techniques like replica exchange (REMD⁴⁰) and accelerated MD (aMD⁴¹) have been reported.^31,32,42,43 Especially, the coupling with aMD showed that an extensive conformational sampling significantly increased the accuracy of the predicted pK_a values.⁴³ In this study, we perform a detailed investigation on how the conformational states from cpH-aMD simulations and their respective microscopic pK_a values relate to macroscopic pK_a values from NMR experiments.

We employ the major timothy grass pollen allergen Phl p 6 as a model system for this study. Phl p 6 is one of the most important grass allergens with over 75% of grass pollen allergic patients having IgE antibodies recognizing Phl p 6.^44,45 As it is the case for many allergen proteins, the biological function of Phl p 6, as well as the source of its allergenicity, is unknown.

Phl p 6 excels as a model system for our study on the one hand, because with 111 residues it is a rather small protein, which facilitates efficient sampling of its conformational space. On the other hand, based on major antigen processing pathways, pH stability is considered a decisive factor for a protein’s allergenicity.^46,47 In general, after uptake, e.g., by inhalation in the case of pollen allergens, the allergen enters an antigen-presenting cell via endocytosis. In the endosome, the proteins are proteolytically processed into peptides, which are then loaded onto class II major histocompatibility complex (MHC) molecules. The MHC peptide complexes are transported to the cell surface and presented to naïve T-cells. Recognition of the linear T-cell epitope then triggers the immune response.^48,49 The digestion of the proteins is tightly coupled to a strong acidification of the endosome during its maturation, i.e., a drop in pH from around 7 to around 4. The higher the stability of the protein, the harsher the condition in terms of pH that is needed to digest the protein.^46,47,50 As discussed by Scheiblhofer et al., the fold stability of a protein during this process determines the associated immune response. As already discussed above, a protein’s reaction to pH changes is determined by its titratable, i.e., charged residues. With 28 residues, including histidines, out of the 104 residues present in the X-ray structure (PDB code 1NLX(51)), Phl p 6 shows a rather large number of charged residues for its small size. In Figure 1, all glutamic, aspartic, and histidine residues, which we consider titratable in the acidic pH range up to a pH of 8.0, are shown as sticks. Thus, predicting the redistribution of protonation states upon acidification is far from trivial.

Figure 1.

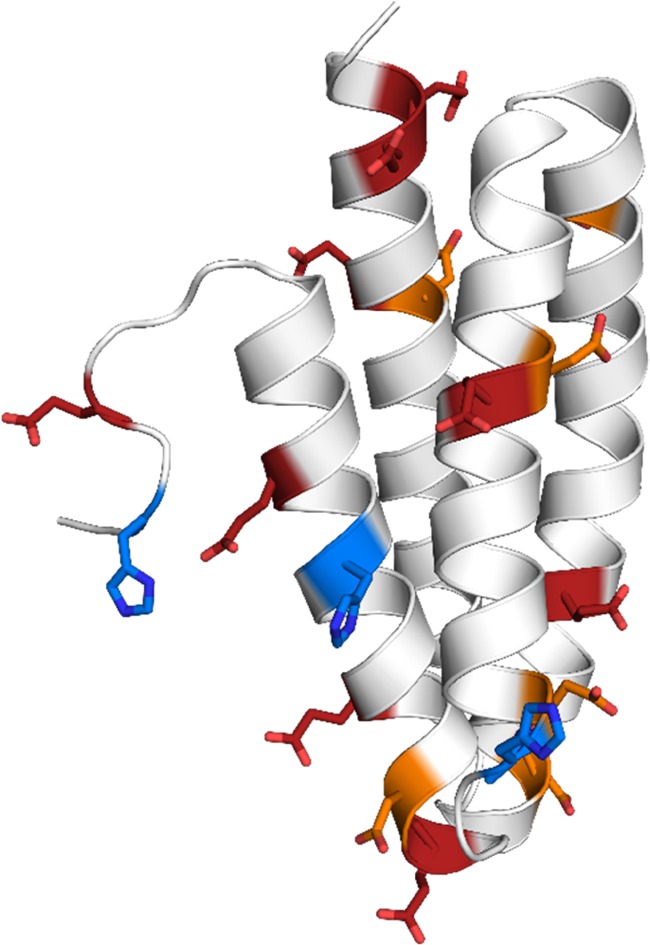
Crystal structure of the Phl p 6 allergen (PDB code 1NLX).⁵¹ Aspartic, glutamic, and histidine residues are shown as orange, red, and blue sticks, respectively. With 28 charged residues out of 111 residues in total (104 residues resolved in crystal structure), the protein has a very high ratio of charges relative to its small size. Of the 28 charged residues, the 18 residues shown in the picture were allowed to titrate in the simulation.

Combining cpH-aMD simulations and NMR experiments, we present a strategy for detailed studies on the titration behavior of proteins. We envisage our approach as a reliable foundation to investigate the structural stability of antigens during endolysosomal degradation.

Methods

Simulation Setup

The starting structure for the simulation was prepared from the wildtype X-ray structure of Phl p 6 (PDB code 1NLX, chain A⁵¹) with the program MOE (molecular operating environment⁵²). Of the 111 residues, only 104 residues were resolved in the crystal structure. Specifically, four residues on the C-terminus and three residues at the N-terminus of the protein are missing, including the starting methionine. However, the missing residues did not include any aspartates, glutamates, or histidines. In the NMR experiments, all 111 amino acids were present.

The protein shows exclusively α-helical structure elements, connected by short loops (see Figure 1). Notably, the C-terminal residues 96–104 are not part of a helix but in fact adopt a looplike conformation.

The LEaP module of AmberTools 17³⁹ was used to add missing hydrogens, as well as create topology and starting coordinate files. The AMBER ff99SB force field⁵³ was used, along with the necessary force field modifications for constant pH simulations.^27,32 The GB radii of the aspartate and glutamate oxygens were reduced to 1.3 Å, as suggested by Swails et al.³² The protein was soaked in a truncated octahedral TIP3P water box with a minimum wall distance of 10 Å.⁵⁴

Before production simulations were carried out, the systems were minimized and relaxed with an elaborate protocol previously developed in our group.⁵⁵

All simulations were performed with the graphics processing unit implementation of the pmemd module of AMBER 17.⁵⁶ The Berendsen barostat⁵⁷ with a relaxation time of 2 ps was used to maintain atmospheric pressure, as well as the Langevin thermostat with a collision frequency of 5 ps^–1 to keep the system at 300 K.⁵⁸ The SHAKE⁵⁹ algorithm was used to restrain all bonds involving hydrogens, allowing the use of a 2 fs timestep. Long-range electrostatics were treated with the particle-mesh Ewald method,⁶⁰ and a nonbonded cutoff of 8 Å was used. Simulations were performed from pH 2.5 to 8.0 with a 0.5 spacing. Protonation state changes were performed every 200 steps, followed by 200 steps of solvent relaxation after a successful exchange. For the GB calculations a salt concentration of 0.1 was used. Acceleration was achieved with the dihedral boost algorithm of AMBER 17, appropriate boosting parameters were calculated according to the work of Pierce et al. from short classical MD simulations and can be found in the Supporting Information.(61) Frames were collected every 1000 steps. All simulations were run for 1 μs, resulting in a total simulation time of 12 μs.

Analysis

All analyses were performed using the programs cpptraj and pytraj from the AmberTools 17 package,⁶² as well as inhouse python scripts. All structural visualizations were produced with PyMol.⁶³

For all analyses, the trajectories were reweighted using a McLaurin series to the 10th order.^61,64

Titration data from constant pH simulations were collected with the program cphstats from AmberTools.³⁹ The modified Hill equation was used to estimate pK_a values. Histidine tautomer distributions were calculated directly from the simulation output. The δ-tautomer will be denoted as HID in the following sections, ε-tautomer as HIE and the doubly protonated, i.e., positively charged form as HIP. Shifts in pK_a were calculated using the pK_a values for free tripeptides of the form acetyl-GXG-amide (N- and C-terminally blocked tripeptides), as measured by Platzer and McIntosh as references.⁸ Convergence of the calculated pK_a values was monitored by computing the cumulative averages with cphstats.

Distance histograms were calculated between titrated residues and nontitrated basic residues. We used the heavy atom centers of mass of the titratable head groups of glutamate, aspartate, and histidine, as well as for the guanidinium group of arginine as reference points. For lysine only, the position of the side-chain nitrogen was used. Furthermore, distances to helix termini were measured for all titrated residues. Reference points for helix termini were defined as the center of mass of the Cα carbon atoms of the first three residues of the respective helix. Angles between the titrated residues and the helix were calculated by calculating the angle between the helix axis, defined as the vector from the C- to the N-terminal end of the helix, and the distance vector from the center of the helix to the titrated residue.

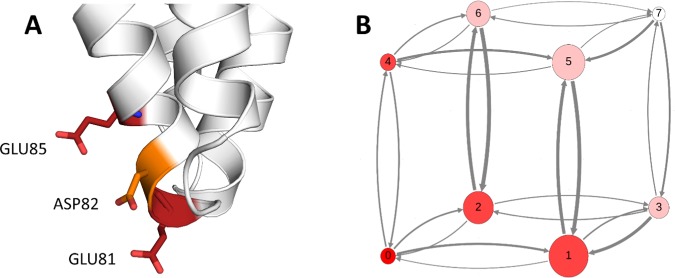
To analyze the transition probabilities between strongly coupled protonation states, we calculated transition matrices for all pH values. For this, we focused on the close interaction of residues GLU81, ASP82, and GLU85. We defined 8 states based on the titration state of these residues, as shown in Table 2. For this purpose, we considered all 4 protonated states of glutamate and aspartate as one state. The transition matrices were visualized as network plots, in which the circle size relates to state populations and arrow sizes to transition probabilities. State positions were chosen so that transitions on the edges correspond to single protonation state changes, diagonal transitions encode a double transition, and finally a transition over the main diagonal relates to a change in all three protonation states at the same time.

Table 2. State Definition of the Model System for the Protonation State Transition Analysis.

state	GLU81	ASP82	GLU85
0	0	0	0
1	0	0	1
2	0	1	0
3	0	1	1
4	1	0	0
5	1	0	1
6	1	1	0
7	1	1	1

^aProtonation states of the residues are denoted as 0 (deprotonated, negatively charged) or 1 (protonated, neutral). State number represents binary encoding of the protonation of the three residues.

NMR Spectroscopy

Phl p 6 (residues 1–111) was recombinantly expressed in Escherichia coli BL21(DE3) Star cells using M9 minimal media supplemented with ¹³C₆-d-glucose and ¹⁵NH₄Cl as carbon and nitrogen sources, respectively. The protein was purified by hydrophobic interaction and size exclusion chromatography employing HiTrap Phenyl FF and HiLoad 16/600 Superdex 75 columns (GE Healthcare). NMR samples contained 1 mM protein, 10 mM citrate-phosphate buffer, and 10% D₂O. All NMR experiments were performed at 25 °C on 500 MHz Agilent DirectDrive 2 and 700 MHz Bruker Avance Neo spectrometers. Backbone amide resonance assignment was obtained by use of two-dimensional ¹H–¹⁵N-HSQC and three-dimensional HNCACB, CBCA(CO)NH experiments at pH 7.0.

Side-chain pK_a values of Asp and Glu were determined using two-dimensional spectra that correlate side-chain C′ and backbone amide ¹H^N chemical shifts as reported.⁶⁵ For His side chains, ¹⁵N chemical shifts were recorded in two-dimensional ¹H¹⁵N HSQC spectra where the INEPT transfer delay was adjusted to ²J_HN couplings. Histidine H^δ2 assignments were obtained from a HBCBCGCDHD experiment,⁶⁶ and the corresponding H^ε1 were identified in the two-dimensional ¹H¹⁵N HSQC spectra. In titration experiments, pH values were adjusted between pH 2.2 and 8.5 by adding small aliquots of HCl or NaOH. All pH values were measured using ¹⁵N imidazole and formic acid ¹³C chemical shifts as internal pH references in two-dimensional ¹H¹⁵N and ¹H¹³C correlation spectra as described.⁶⁷ Side-chain ¹³C′ (Asp, Glu) and ¹⁵N (His) chemical shift data were fit by standard equations for a single ionizable group¹⁵ to obtain pK_a and limiting chemical shift values (fitting equations are shown in the Supporting Information). Tautomeric distributions of His side chains were determined from the so-obtained ¹⁵N^δ1 and ¹⁵N^ε2 limiting chemical shifts and pK_a values as described.⁶⁸

Results

pK_a Values

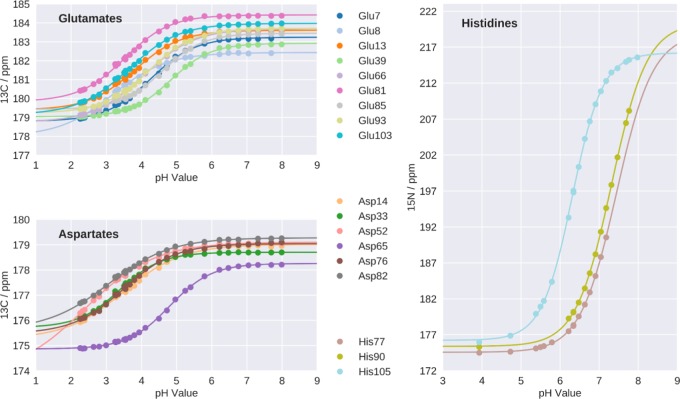
Side-chain pK_a values of all six aspartates, all nine glutamates, and the three histidines in Phl p 6 were determined experimentally using heteronuclear two-dimensional NMR spectroscopy (Figure 2). The data reveal pK_a values for aspartates and glutamates between 2.4 and 4.8, while for histidines, experimental pK_a values are in the range between 6.5 and 7.4. In cpH-aMD simulations, pK_a values for all 18 titratable residues were calculated. The respective titration curves can be found in the Supporting Information (Figure S1). To estimate the accuracy of the simulation-derived protonation state ensemble, we benchmarked these pK_a values against the experimental (NMR) pK_a values (see Table 1). The correlation between both methods is visualized in Figure 3 with a root mean square error of 0.89 and a Pearson correlation coefficient of 0.81. Out of 18 titrated residues, 11 predictions lie within an error of 1 pK_a unit, visualized as gray lines in Figure 3.

Figure 2.

Experimental titration curves with chemical shifts of side chain ¹³C′ for ASP and GLU, ¹⁵Nδ1 for HIS77 and HIS90 and ¹⁵Nε2 for HIS105.

Table 1. Comparison of the pK_a Values Measured by NMR and Predicted by Simulation with Absolute Differences.

ResID	NMR	simulation	difference
GLU7	4.25	4.20	0.05
GLU8	3.19	3.70	0.51
GLU13	3.80	4.83	1.03
ASP14	3.50	3.06	0.44
ASP33	3.38	4.37	0.99
GLU39	4.84	6.04	1.20
ASP52	2.4	2.30	0.10
ASP65	4.80	3.92	0.88
GLU66	4.06	5.25	1.19
ASP76	3.50	3.48	0.02
HIS77	7.4	6.96	0.44
GLU81	3.52	4.76	1.24
ASP82	3.06	4.81	1.75
GLU85	4.59	5.30	0.71
HIS90	7.3	6.00	1.30
GLU93	4.21	4.27	0.06
GLU103	3.65	4.66	1.01
HIS105	6.5	6.52	0.02

Figure 3.

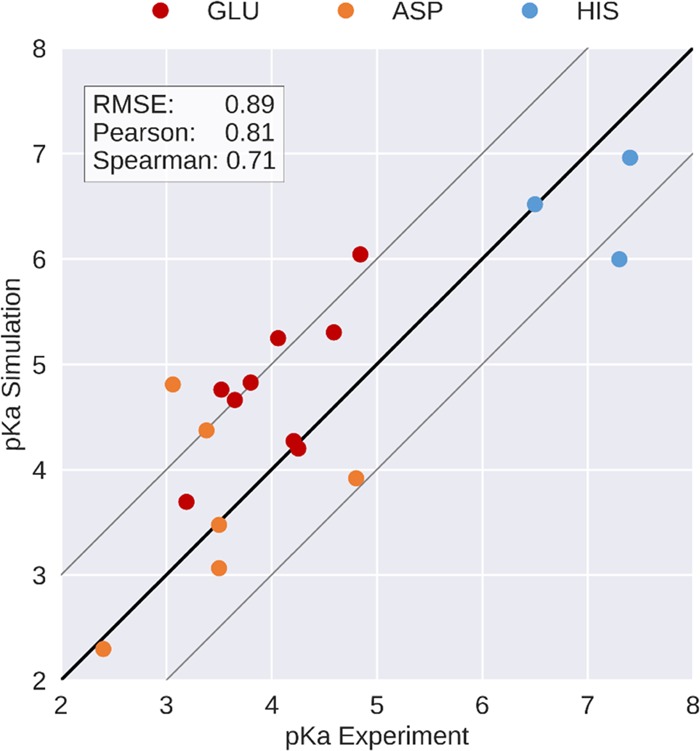
Correlation plot between the pK_a values measured by NMR and predicted by simulation. Pearson and Spearman correlation coefficients and RMSE are shown. The black line denotes the ideal correlation and gray lines denote the prediction error margin of ±1 pK_a unit, as typically reported in the literature.

In both experiment and simulation, we identified residues with pK_a values strongly deviating from reported pK_a values of the corresponding tripeptides.⁸Figure 4 shows the absolute deviations of the measured and predicted pK_a values from the reference values for free tripeptides. Notably, ASP52 shows the largest negative pK_a shift of all titratable residues, i.e., a strong acidification, consistently in both experiment and simulation. Other notable acidic (GLU8 and ASP14) and basic shifts (GLU39, HIS77 and GLU85) were identified with acceptable agreement between simulation and NMR. However, some shifts seen in the experiment were significantly mispredicted in the simulation (GLU13, GLU81, ASP82, HIS90) in the opposite direction. The strongest disagreement is shown by ASP82 with an unsigned error of 1.75 pK_a units. Also, its neighboring residue GLU81 shows a significant prediction error of 1.24 pK_a units. Of the three titrated histidines, HIS90 shows a notable prediction error of 1.30, while HIS77 only shows a moderate error of 0.44 pK_a units and HIS105 is in almost perfect agreement with experiment.

Figure 4.

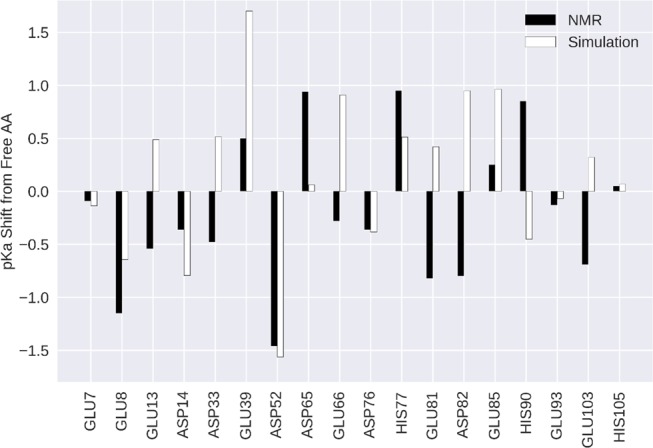
Deviations of measured and predicted pK_a values from the respective tripeptide pK_a values. Reference values are 3.86 for ASP and 4.34 for GLU and 6.45 for HIS as published by Platzer et al.⁸ Black and white bars represent experiment and simulation respectively.

Transition Analysis

A generally poor pK_a prediction can be seen for residues GLU81, ASP82 (both mispredicted), and GLU85 (shift strongly overestimated). For both ASP82 and its flanking residue GLU85 the fit to the Hill equation is not optimal (see Supporting Information). The structural interplay of these residues is visualized in Figure 5A, which shows that all three residues are oriented in the same direction, pointing into the solvent. To ensure that our sampling of the protonation state space is sufficient and to investigate the correlation of protonation states of spatially close residues, we performed a protonation state transition analysis. For this, we focused on the close arrangement of GLU81, ASP82, and GLU85. We defined eight states based on the titration state of these residues, as shown in Table 2. To this end, we considered all four protonated states of glutamate and aspartate as one state. The transition matrices were visualized as network plots, in which circle sizes relate to state populations and arrow sizes, to transition probabilities. State positions were chosen so that transitions on the edges correspond to single protonation state changes, diagonal transitions encode a double transition, and finally a transition over the main diagonal relates to a change in all three protonation states at the same time.

Figure 5.

(A) Interaction and spatial vicinity of the residues GLU81, ASP82, and GLU85 in Phl p 6 the crystal structure, which was used as input for the simulations. (B) Analysis of protonation state population and transitions of the 3-residue model system. Analysis at pH 5 is shown as representative. States denoted as 0–7 (see Table 2), circle size denotes state population, and arrow thickness indicates transition probability from one state to the other (cutoff at 0.01). At pH 5, states 0 and 7, i.e., fully deprotonated and fully protonated, are predicted to be least populated, with high transition probabilities to different states. No transitions over a diagonal, i.e., 2 protonation state change, can be observed at this pH within the cutoff.

We found a distinct, pH-dependent pattern in their protonation states as well as in the transitions between the states we defined in Table 2. The transition count matrices show high numbers of transition between the different states across all pH values. At extreme pH values, i.e., 2.5 and 8.0, the completely protonated and completely unprotonated states, respectively, are populated almost exclusively. However, a few transitions to sparsely populated states are still visible. As the pH value starts to increase from 2.5, state populations start to shift, with states 1 (GLU85 protonated) and 5 (GLU81 and GLU85 protonated) being the prominent ones at moderate pH values (between 4.0 and 5.5). As the pH further increases, the populations shift first to the monoprotonated states 1 and 2 and finally almost completely to the unprotonated state 0 at pH 8. An exemplary visualization of the data of pH 5.0 is shown in Figure 5B. Visualizations for all pH values can be found in the Supporting Information (Figure S2).

Tautomer Estimation

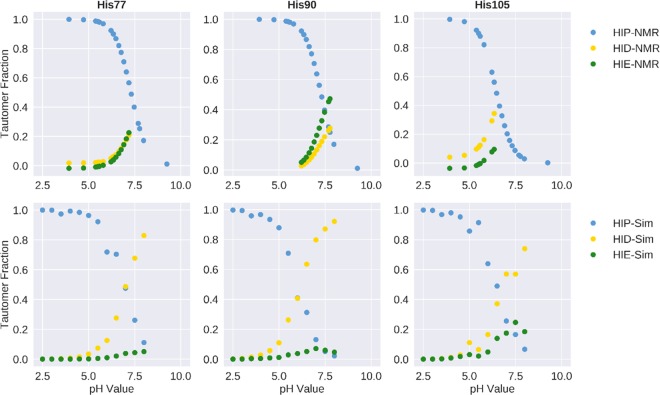
From both the experimental as well as the simulation data, we calculated the tautomer distribution of the histidines at each measured and simulated pH value (Figure 6). Clearly, the prediction is poor for HIS77 and HIS90. In both cases, the fraction of the δ-tautomer is significantly overestimated in the simulations, whereas in the experiment, a nearly 1:1 ratio of δ- and ε-tautomer is observed. As shown above, also the pK_a prediction for these two residues is not optimal (see Table 1), especially for HIS90. However, for HIS105, we find perfect agreement between simulation and experiment for both the pK_a value (see Table 1) and the tautomer ratio.

Figure 6.

Tautomer distributions for all three histidines in the system were calculated for experiment (top) and simulation (bottom). Clear overestimation in the prediction of the δ-tautomer for HIS77 and HIS90 can be observed, whereas a good agreement can be seen for HIS105.

Distance Analysis

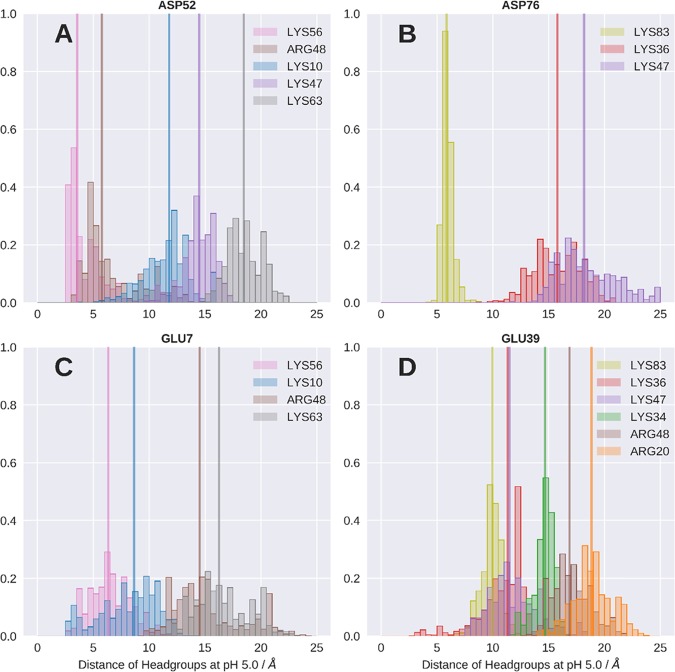
To elucidate the origin of pK_a perturbances, we analyze the microscopic chemical environment of each titratable acidic residue. We calculated distance histograms of nearby positively charged residues. We find that a few of the acidic residues show strong and close interactions with nearby positively charged residues with the medians of the distributions below 5 Å across all pH values. The histogram of ASP52 at pH 5.0 is shown in Figure 7A as an example. A close interaction with LYS56 with the median (vertical lines) of the distance distribution at 3.5 Å is visible. Another, more distant contact is formed with ARG48 with a distance median of 5.8 Å. On the other hand, we also find residues that only form less pronounced and more distant interactions; exemplary histograms are shown in Figure 7B–D.

Figure 7.

Normalized histograms of the distances between the carboxyl group of selected acidic residues and the head groups (amino and guanidinium group for LYS and ARG, respectively) of near positively charged residues. Analysis at pH 5.0 is shown representatively. Vertical lines denote the median of the respective distance distribution.

Discussion

In the presented work, we use NMR experiments and MD simulations to profile protonation probabilities within the folded protein environment of the major timothy grass allergen Phl p 6. The interplay of both methods not only unveils the molecular origin of several strongly shifted residue pK_a values but also outlines the current limitations of protonation state predictions.

As can be seen from Figure 3, we find a remarkable overall correlation between experiment and simulation in terms of pK_a values indicating that both approaches capture similar protonation state ensembles. For 11 out of the 18 titrated residues, the difference between experiment and simulation is less than 1 pK_a unit, an error margin typically reported in the literature. Also, the predicted pK_a values of the remaining residues do not exceed this margin substantially, with the exception of ASP82.

Furthermore, the convergence analysis of the predicted pK_a values (see Figure S3) suggests that while a few residues reach a converged pK_a value within 50 ns of simulation time, other residues need significantly longer to reach a converged pK_a value, with the most prominent example being ASP52, which reaches a converged pK_a value after about 800 ns. The majority of the residues show converged pK_a values after about 100–200 ns of simulation time. Moreover, we generally see an improvement in the pK_a prediction with longer simulation times.

As highlighted in Figure 4, both methods identify strong pK_a shifts, i.e., large deviations of pK_a values within the protein from the pK_a values of the respective tripeptides. This analysis further illustrates the overall remarkable consistency between the predicted pK_a shifts and the NMR experiments. Notably, the strong acidic shift of ASP52 was found with both approaches with near perfect agreement. Also, the basic shift of GLU39 was found with both techniques but was overestimated in the simulation—an effect that has been reported previously.³² Despite the overall agreement between NMR and cpH-aMD in terms of pK_a values, we can note a few residues with significant prediction errors. In the following text, we will discuss in detail analyses and hypotheses rationalizing potential driving forces for the observed inaccuracies.

The strongest discrepancy is found for ASP82 with an unsigned error of 1.75 pK_a units. With a measured pK_a value of 3.06, the residue is found to be distinctly more acidic than the free tripeptide (pK_a of 3.86⁸). However, in the simulation the opposite is the case, in that a more basic pK_a value of 4.81 is predicted. In the crystal structure (visualized in Figure 5A), ASP82 is flanked by two other acidic residues GLU81 and GLU85, packed closely together with the side chains oriented in the same direction. Unintuitively, the pK_a of ASP82 is experimentally determined to be the most acidic one of these three residues. The pK_a of the flanking residue GLU81 is also measured to be considerably more acidic than that of the free tripeptide (3.52 vs 4.34⁸), while the pK_a of GLU85 (4.59) shows no strong perturbation. As can clearly be seen from Table 1, the simulation fails to predict the pK_a values for all three residues.

To evaluate the ability to capture the correct titration behavior of strongly coupled residues, we performed a protonation state-based transition analysis for the GLU81, ASP82, and GLU85 residue pack. This method allowed a very detailed yet intuitive representation of the protonation state probabilities and exchange rates between them at each simulated pH level. From the high numbers of transitions between the states across all pH levels, we conclude that at no pH level the simulation gets trapped in a protonation state configuration. Also, the shifts in the state probabilities and correlation of protonation states in dependence of the change in pH value appear to be conclusive. On the basis of these observations, we can exclude insufficient sampling of protonation states as a cause of the large prediction error.

As mentioned above, the transition analysis additionally provided us with insights into the underlying kinetics of the protonation state changes. From the transition probabilities (Figure 5B), we can clearly see that within our cutoff of 0.01 no transitions occur at any pH value over the principal diagonal, i.e., all protonation states change at the same constant pH step. Also, other diagonal transitions, i.e., 2-proton transitions are very rare. The fact that transitions occur almost exclusively by changing one protonation state at a time, despite the fact that multititrations would be possible, suggests that a short local structural equilibration of the new protonation state is necessary to adapt to the new electrostatic potential and to make the next change possible.

While we surmise that the reason for the prediction error of the three discussed residues is not an inefficient protonation state sampling, we do see a few other possible reasons for the disagreement of experiment and simulation.

First, the correct description of tightly packed acidic residues is a known issue of implicit solvent models.^69,70 Paired with the lack of counter ions in the simulations, this might lead to mispredicted pK_a values. Furthermore, the acidification of GLU81 and ASP82 coupled with their exposed position in a loop between two helices in contrast to GLU85 indicates that they are stabilized by a cation during the experiments and GLU85 is not. This effect would be completely missed in the simulations since they are not considered in the implicit solvent steps.

Secondly, although the protonation state space is well covered, the sampled conformational ensemble might still be insufficient. Limited conformational sampling in turn also limits the protonation state ensemble and hence affects the accuracy of apparent pK_a values estimated from this limited ensemble.

This assessment is supported by the pK_a and tautomer predictions of the histidines. As can be seen in the crystal structure in Figure 1, HIS77 and HIS90, for which both the pK_a and the tautomer estimation are quite poor (Table 1 and Figure 6), are located within stable α-helices. In contrast, HIS105, for which both estimations are in perfect agreement with experiment, is located in the highly flexible C-terminal loop. We surmise that the conformational sampling of HIS77 and HIS90 will be hindered compared to that of HIS105, which, in turn, limits the sampled protonation state ensemble. This is supported by a H-bond analysis (see Supporting Information, Table S2), which shows, that both HIS77 and HIS90 form a frequent H bonds with the backbone amide oxygen of neighboring residues, thereby locking the residue in this position and in consequence also in the tautomeric form. Clearly, despite boosting the dihedral angle energy in our aMD approach, the histidine side chains could not escape from this conformation. A change to the other tautomer during a constant pH step would break the hydrogen bond and thereby render it highly unfavorable in the Metropolis evaluation. As with the mispredictions of residues GLU81, ASP82, and GLU85 discussed above, this limitation in conformational sampling will lead to a limited protonation state ensemble and thereby to inaccuracies in the estimated apparent pK_a values.

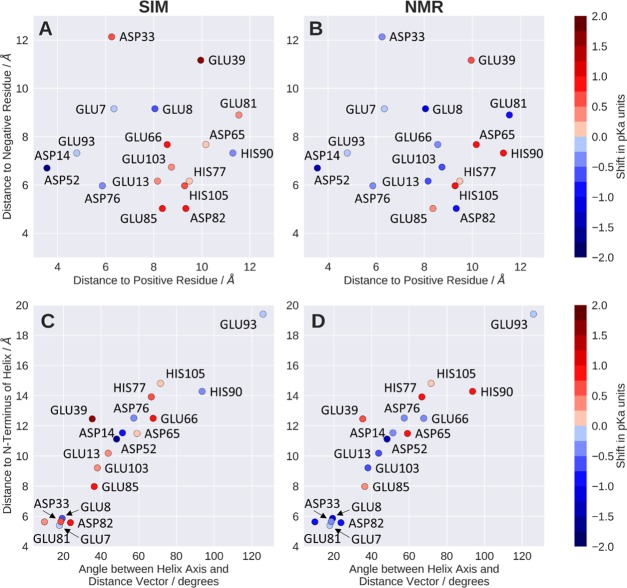
Besides a general evaluation of the computational methodology for studying allergen dynamics at low pH, our scope was to illuminate the molecular determinants causing the observed pK_a shifts. As an initial approximation for the electrostatic environment, we measured distances from the titratable residues to the closest charged residues. The strongest acidic shift and also the strongest overall shift of all titrated residues is found for ASP52. From the conducted simulations, we indeed find that the strong perturbation of the pK_a value of ASP52 can be explained by the formation of an ion pair with LYS56 (Figure 7A). The stability of this ion pair is underlined by the sharp peak of the distance distribution of the positively charged side-chain amine group of LYS56.

Following this concept, we can consistently also explain less pronounced and also negligible pK_a perturbations shown in Figure 4. For example, ASP76 shows a moderate acidic shift of about 0.5 pK_a units in both experiment and simulation. The respective distance histogram (Figure 7B) shows that there is indeed no ion pair formation; the closest stable contact is found with LYS83 at a distance of 5 Å. Also, the rather small perturbations of GLU7 or GLU93 are reflected by broad and less pronounced distance distributions during the simulations (GLU7 shown in Figure 7C). GLU39 shows a basic shift, which is in agreement with the respective histograms (Figure 7D) showing no pronounced ion pair or even close contact with a positively charged residue (closest median 10.0 Å). Moreover, we neither find close interactions of GLU39 with negatively charged residues throughout the entire simulation. GLU39 is indeed surrounded by hydrophobic residues, rendering the uncharged form of GLU39 more favorable in this position and thereby raising the pK_a value. Figure 8A summarizes the observed correlation of charge proximity and shifts in the predicted pK_a values. However, while this connection seems to be a major determinant in the simulations, the correlation is less pronounced with the NMR-derived pK_a values (Figure 8B). As we assume that the underlying cause for the perturbed pK_a values has to be rooted in their electrostatic environment, we explored less obvious effects which could explain the experimentally observed shifts. It has been reported previously that titratable residues located at α-helix termini show perturbed pK_a values due to the dipole moment of the helix, whereby the N-terminus was shown to lead to an acidification and the C-terminal end to more basic pK_a values.^7,71 In our system, five residues are located at N-termini of α-helices. As shown in Figure 4, both GLU7 and GLU8 show an acidic shift in their pK_a, where the perturbation is much stronger for GLU8. However, since both residues are located near the protein’s N-terminus, their pK_a value will most likely also be influenced by the proximity to its positive charge. However, ASP33, which is also located at the N-terminus of a helix, was found to be acidified in the NMR experiments, yet the simulation fails to predict this shift. Similar coherence is found for the experimentally determined acidification of GLU81 and ASP82, both close to the N-terminal helix dipole. Also, here, the simulation fails to predict the acidification of both residues, as can clearly be seen from Figures 4 and 8. Since the treatment of polarization is a known weakness of classical force fields, we expect to be prone to entirely miss its effects with the applied simulation setup.^69,72 We further illustrate the impact of the helix dipole by defining distinct observables representing the dipolar character of the helices, i.e., the smallest distances of the titrated group to the closest N-terminal helix end and the angle between the titrated group and the helix axis. Figure 8D depicts the striking concurrence of acidification in all residues that show small distances as well as small angles, yet only for the NMR pK_a values. As anticipated, however, this trend is not reproduced for pK_a values predicted from the cpH-aMD simulations. We surmise that the incorporation of polarizable force fields might allow for proper treatment of this effect.

Figure 8.

(A, B) Smallest medians of the distance histograms to positive and negative residues, respectively. Colors indicate pK_a shift from simulation (A) and NMR (B). (C, D) Smallest medians of distances to the nearest N-terminal helix end against respective angle between titrated group and helix axis. Colors indicate the pK_a shift of the residue, as predicted by simulation (A, C) and measured by NMR (B, D).

However, there are numerous other and maybe more severe shortcomings we face with our simulation approach. First and foremost, the utilization of implicit solvent models at the constant pH step, coupled with the necessary removal of water molecules and ions, excludes the incorporation of ionic stabilizations and thereby distorts the predicted pK_a values, as already discussed above. This limitation might be overcome with the use of continuous cpH techniques, as they allow a fully explicit solvent approach, including ions.

Furthermore, as already stated above, the pK_a values measured in experiments correspond to a much higher timescale compared to our simulations, which, in turn, could mean that the conformational ensemble behind the measured pK_a values could be much broader and diverse than the simulated one.

Nevertheless, despite the discussed shortcomings, the overall agreement in predicted and experimentally measured protonation state probabilities is strongly convincing for the Phl p 6 pollen allergen.

Conclusions

The combination of structural as well as dynamical information from the cpH-aMD simulations and NMR experiments allowed us to unveil the sources of the observed perturbations in the protonation state ensembles. In particular, we identify formation of ion pairs to cause the strongest acidifications. Persistent hydrogen bonds between charged residues as well as the N-terminal dipole moment of α-helices lead to weaker but still notable perturbations. However, the effect of the helix dipole on the pK_a values was only captured in our NMR experiment and not in our simulations. We surmise that this is due to the use of classical force fields and might be resolved with the use of polarizable force fields. Our results concerning the tautomer distribution of the three histidines in the system underlines the importance of conformational sampling to obtain a reasonable protonation state distribution.

The reliable modeling of protonation state probabilities at varying pH levels is specifically crucial for allergen proteins and will be essential for further studies on their dynamics and endolysosomal degradation mechanism. However, the presented processing and interpretation of NMR and cpH-aMD data is designed to find a broad applicability.

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.jctc.9b00540.

• Boosting parameters; fitting equations for obtaining titration curves; residue-wise pK_a values; pK_a convergence analysis; H-bond analysis for histidines; transition analysis for pH values (PDF)

The authors declare no competing financial interest.