Skip to main content
PMC home page
Reports of Practical Oncology and Radiotherapy logoLink to Reports of Practical Oncology and Radiotherapy
. 2020 Jan 10;25(2):187–192. doi: 10.1016/j.rpor.2019.12.029

Monte Carlo study on the secondary cancer risk estimations for patients undergoing prostate radiotherapy: A humanoid phantom study

Amir Ghasemi-Jangjoo a,b, Hosein Ghiasi a,⁎
PMCID: PMC6994283  PMID: 32021575

Abstract

Aim

The aim of this study was to estimate the secondary malignancy risk from the radiation in FFB prostate linac-based radiotherapy for different organs of the patient.

Background

Radiation therapy is one of the main procedures of cancer treatment. However, the application the radiation may impose dose to organs of the patient which can be the cause of some malignancies.

Materials and methods

Monte Carlo (MC) simulation was used to calculate radiation doses to patient organs in 18 MV linear accelerator (linac) based radiotherapy. A humanoid MC phantom was used to calculate the equivalent dose s for different organs and probability of secondary cancer, fatal and nonfatal risk, and other risks and parameters related to megavoltage radiation therapy. In out-of-field radiation calculation, it could be seen that neutrons imparted a higher dose to distant organs, and the dose to surrounding organs was mainly due to absorbed scattered photons and electron contamination.

Results

Our results showed that the bladder and skin with 54.89 × 10−3 mSv/Gy and 46.09 × 10−3 mSv/Gy, respectively, absorbed the highest equivalent dose s from photoneutrons, while a lower dose was absorbed by the lung at 3.42 × 10−3 mSv/Gy. The large intestine and bladder absorbed 55.00 × 10−3 mSv/Gy and 49.08 × 10−3, respectively, which were the highest equivalent dose s due to photons. The brain absorbed the lowest out-of-field dose, at 1.87 × 10−3 mSv/Gy.

Conclusions

We concluded that secondary neutron portion was higher than other radiation. Then, we recommended more attention to neutrons in the radiation protection in linac based high energy radiotherapy.

Keywords: Secondary malignancy, Monte Carlo simulation, Prostate radiotherapy, Radiation contamination, Equivalent dose

1. Background

Megavoltage electron linear accelerators (linacs) are widely used to treat deep-seated tumors, and they offer advantages in cancer radiation therapy over low-energy machines.1, 2, 3 Researchers have conducted extensive studies on the dosimetric properties of linacs, their primary photon beams, secondary radiation contamination characteristics, and other aspects of megavoltage linacs, both with experimental methods and Monte Carlo (MC) simulation.4, 5, 6, 7, 8 There is agreement among various researchers regarding MC simulation and experimentally derived results. Additionally, the radiation dose following linac that is absorbed by patient’s tumor or absorbed by normal organs out of field, as well as scattered and secondary radiation have been subjects of several studies. Based on the absorbed doses delivered to different organs in cancer radiotherapy, induction of secondary malignancies in organs has been estimated using international reports and data from the International Commission on Radiological Protection (ICRP).9, 10, 11, 12, 13, 14, 15, 16 Primary photon doses scattering to out-of-field organs and the dose from radiation contamination, such as electrons and photoneutrons produced in linac components, have been reported as sources of probable secondary malignancies. Photoneutrons originate from heavy components in the linac head and propagate peripherally in a nearly isotropic pattern.5 Photons scatter from the linac collimator, as well as the patient body and walls of the room.5,17 Electron contamination5,18 in X-ray radiotherapy is produced mainly in components such as the flattening filter in the pathway of the primary photons. The aim of the current study was to use MC estimation of the out-of-field organ doses in 18 MV prostate external radiotherapy and calculate the secondary cancer risk, fatal and non-fatal risks due to received radiation equivalent dose for the normal organs. Linac photon beam in field and out of field were also characterized using MC simulation.

2. Aim

The aim of this study was to estimate the secondary malignancy risk from the radiation in FFB prostate linac-based radiotherapy for different organs of the patient.

3. Materials and methods

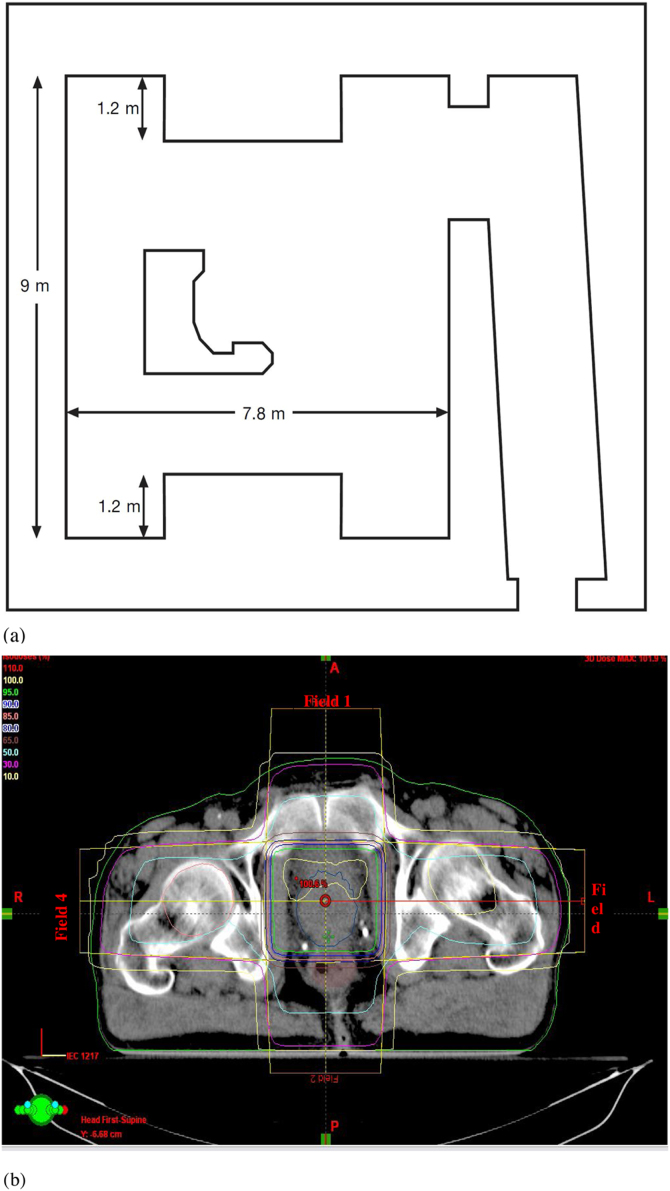
Monte Carlo general purpose N-Particle transport code MCNPX (2.7. E) developed by Los Alamos National Library (LANL) was used for simulation and dose calculation in this study. An 18 MV Varian 2100C linac in a treatment room made of ordinary concrete (density of 2.35 g/cm3) was simulated to evaluate scattering radiation. Fig. 1(a) shows the simulated room dimensions and layout. Percent depth dose and photon beam profile for the simulated linac was derived by MCNPX code in a 50 cm × 50 cm × 50 cm water phantom modeled to simulate full scatter as in a real phantom at a source-to-surface distance (SSD) of 100 cm and compared with the measured data. Using the comparison of the percentage depth dose (PDD) and photon beam profile (PBP) datasets comparison, our linac model was verified for the photon dose calculations. Furthermore, the number of neutrons produced per 1 Gy of a X-ray dose at the isocenter was scored and the result was compared with results. A humanoid phantom was then modeled at the hospital bed so that the prostate of the phantom was modeled at the isocenter as the target organ. The modeled linac was rotated, and the prostate was irradiated by four fields. Irradiating the prostate using the four-field box (FFB), out-of-field doses from secondary neutrons, scattered photons, electron contamination, and captured gamma rays were calculated for different organs. The irradiation description can be summarized as follows according to the CorePlan treatment planning system (TPS) derived from the plan for prostate tumor irradiation.

  • •

    Field sizes of 8 × 8 cm2, SSD of 92.1 cm, monitor unit of 58;

  • •

    Field sizes of 8 × 8 cm2, SSD of 92.5 cm, monitor unit of 58;

  • •

    Field sizes of 7 × 8 cm2, SSD of 84.0 cm, monitor unit of 64; and

  • •

    Field sizes of 7 × 8 cm2, SSD of 84.9 cm, monitor unit of 62.

Fig. 1.

Fig. 1

Open in a new tab

(a) The room layout and dimensions simulated in this study. The 3.65 m high room with the 55 cm thick concrete ceiling was simulated. Additionally, 110 cm concrete bulk simulated on top of the linac head in linac rotation direction for shielding the upper space from the primary radiation while the linac irradiates below the patient. The bulk performs as primary barrier with thickness of 1.65 m. (b) Axial view of the prostate and the treatment plan by which a patient is treated and our MC simulation was carried out. Isodoses curves can be seen in the plan provided by CorePlan TPS and used field sizes (two fields of 8 × 8 cm2 and two fields of 7 × 8 cm2) applied for simulations. Isocenter relative dose was shown in red color as 100.6%.

Fig. 1(b) presents the isodose and the treatment pan of the prostate using the FFB treatment technique. Because electron contamination decreases over a specific distance in a field size, the difference between in-field and out-of-field doses is very high in comparison with other radiation types. Electron contamination is not negligible, but the majority of contamination is in field. The derived absorbed equivalent doses for patient organs and ICRP recommendations were used to calculate organ doses, organ accumulated doses, probability of secondary cancer (cases per 10,000 persons).18 Data obtained is reported in the result section and comparisons made with literature reports. ICRP 103 provides updated data for various parameters for absorbed dose in organs as a result of cancer therapy.16 In the recommendation, absorbed dose by a mass (tissue or organ) is defined as follows:

D=d∈¯dm (1)

where D is absorbed dose, the numerator is average energy of the radiation absorbed by a mass, and dm is the mass. This definition can be applied to small masses, and the energy is defined as the average value of energy delivered to the mass. Because some parts of the mass absorb more or low energy in comparison with other parts, ICRP has recommended that an average value of delivered energy be applied in dose calculation.16 In nano-scale dose calculations, energy is applied as the value of absorbed energy in the small mass, and the definition does not consider energy as an average value. In macroscopic scales, dose is considered uniformly, but it is a fluctuating value in very small masses, such as in nano-scale dosimetry. The same dose absorbed in different types of tissues has different biologic effect. For the relation of a different tissue dose to the biologic effects in the tissues, equivalent dose concept (HT) was introduced and it was defined as16

HT=∑RwRDT,R (2)

wR is the radiation weighting factor, DT,R is absorbed dose from radiation R by tissue T. Absorbed dose (D) was derived by MC simulation in the 18 MV external photon beam prostate radiotherapy for different organs and wR was applied for the conversion to HT. wR is reported as 1 for all energies of photon and electrons and is not energy dependent for the mentioned types of radiation. Photoneutron spectra at the maze entrance do not contain the contribution of the high-energy neutrons. For the neutron radiation weighting factor was reported as an energy dependent factor, so, according to the neutrons energy, the neutron weighting factor can be used and without knowledge about the neutron radiation energy, one cannot apply the factor correctly. Because it differs up to 20 according to the neutrons energy and its maximum is in the energy range from 100 keV to 200 keV. In the neutron equivalent dose we used a radiation weighting factor to convert an absorbed dose to an equivalent dose. In the current study, we used MC simulation to derive the studied radiation spectra around the linac in an entrance maze as well as on a patient couch. Calculated portion and also total spectra were reported in the next. section. More detailed information can be found in the ICRP recommendation 103.16 Gamma-rays from (n,γ) reactions induced in interactions between low energy (specially thermal) neutrons and low atomic number (Z) materials. The gamma-ray production is dominant at maze entrance because of lower energy neutron presence. HT for different out-of-field organs used for secondary cancer risk estimation and other health-related parameters of the patients undergoing megavoltage external beam therapy were obtained. ICRP provided data for secondary cancer risk estimation for different organs in cases per 10,000 persons per Sv. The obtained organ equivalent doses were also used for fatal and non-fatal risk estimation as well as nominal risk adjusted for lethality and quality of life using the coefficients reported for different organs doses.16 All of the calculated parameters for the studied organs are tabulated and reported in the next section and compared with the literature. Any difference or agreement with other works are discussed and the source of difference or conditions, methods and causes of the agreement are discussed and reported.

4. Results

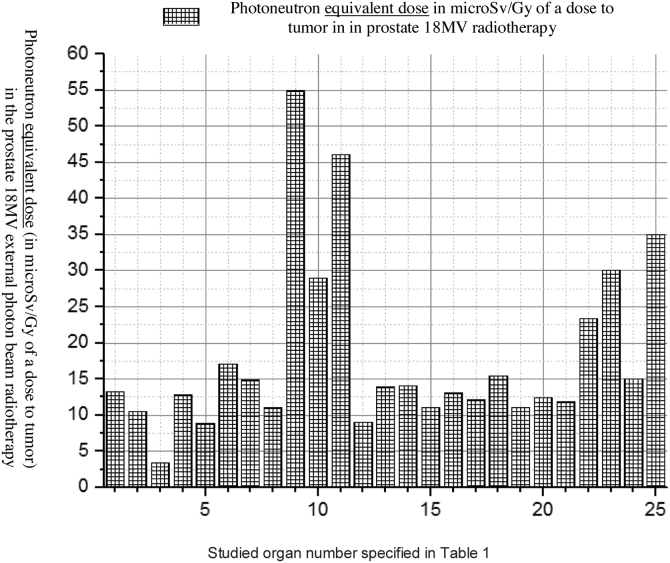
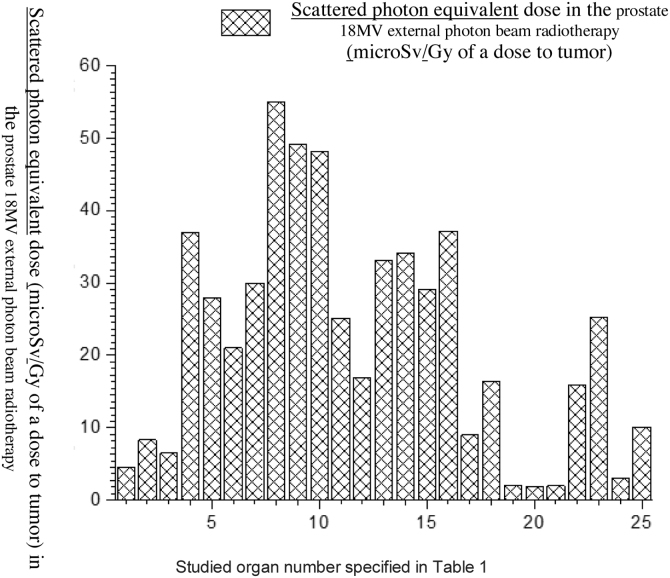
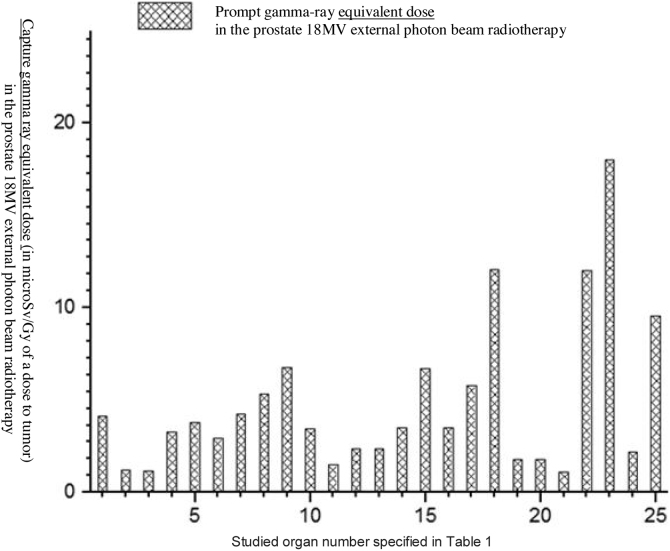
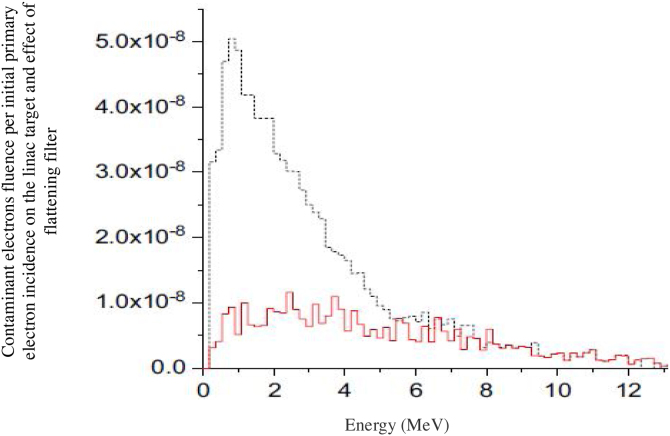
An 18 MV Varian linac was simulated and PDD and PBP data were derived in the simulated water phantom. MC calculated dataset was compared with the measured one and the minimum difference of 0.8% was found in the PBP dataset at the central region of the field, while the maximum difference of 1.08% for the standard 10 × 10 cm2 field size was obtained in field edges. At the penumbra site the deference between the measured and calculated dataset increased to 0.0288 with increasing distance from the center of the field at out-of-field. At the isocenter the difference was 0.0005 while above and below the isocenter the differences were increasing. The maximum difference was observed at the phantom surface. On the other hand, the number of photons per electron incident on the linac target is 1.2 × 10−14 at the isocenter. Thus, our calculation showed that for delivering the 1 Gy photon dose to isocentre for the 6.28 × 104 gr mass of water 8.33 × 1014 initial electrons were required to incidence on the tungsten target. Furthermore, in the fully closed field, 1.56 × 10−8 n0/cm2 was obtained at a spherical surface around the linac with the center in the linac target. The calculated number of neutrons per 1 Gy of X-rays at the isocentre was 1.3 × 1012 n/Gy which corresponds to the definition of the neutron source strength (QN) which is an essential factor for neutron dose calculation. For speeding out the photon calculation by MC, in the input file data card the parameter of BNUM, which controls bremsstrahlung production and tracking, was set to 5. As a consequence, 5 photons were generated per initial electron, whereas only 1 photon is initiated for the default set. For 10 × 10 cm2, 20 × 20 cm2 and 40 × 40 cm2 regular field sizes QN was calculated to be 1.28 × 1012, 1.23 × 1012 and 1.09 × 1012 neutrons per 1 Gy of the X-ray dose at the isocenter and the number of produced neutrons per 1 Gy of the X-ray dose was revealed to decrease at the isocenter with the increasing field size. For simulation of the TPS derived plan we rotated the modeled linac so that the simulated irradiations were conducted for 0, 90, 180 and 270°. Doses to the prostate as the target organ and to in-field as well as to out-of-field organs, from linac scattered photons, photoneutrons, gamma-rays produced in the patient body and from electron contamination were scored in the prostate for the mentioned irradiation conditions. Low Z and hydrogenous materials present in tissue capture low energy neutrons in the (n,γ) reaction. Table 1 shows accumulated equivalent doses estimated by the MC calculations for each organ. Additionally, probability of secondary cancer per 1 Sv, fatal and non-fatal risk due to absorbed equivalent dose, nominal risk adjusted for lethality and quality of life were estimated for all considered organs (see Table 2). Figs. 2, Fig. 33 and Fig. 44 show the estimated organ equivalent doses from neutrons, photons and gamma-rays. According to the results, the bladder and skin with 54.89 × 10−3 mSv/Gy of the dose to tumor and 46.09 × 10−3 mSv/Gy of the dose to tumor were the organs which absorbed the highest equivalent dose from the photoneutrons while the lower dose was absorbed by the lung with 3.42 × 10−3 mSv/Gy of tumor. Large intestine and bladder with 55.00 × 10−3 mSv/Gy of tumor and 49.08 × 10−3 absorbed the highest equivalent dose from the photons while the brain of the patient with 1.87 × 10−3 mSv/Gy of tumor was the organ of the lowest out-of-field dose. In accumulated dose data, we found the ratio of minimum to maximum accumulated equivalent dose to be 9.902 × 10−3 mSv/Gy. Maximum and minimum probability of secondary cancer in cases per 10,000 individuals was obtained for skin and brain tissues, respectively. Fatal and non-fatal risk estimation, according to Table 2, showed that the brain was characterized by the minimum fatal and non-fatal risk. The highest nominal risk adjusted for lethality and quality of life was observed for the skin. The results of the performed electron contamination study are included in Table 3. Fig. 5 shows the effect of the flattening filter on the electron contamination production. Our study performed for the 10 × 10 cm2 and 40 × 40 cm2 field sizes showed that for the unflattened photon beam the obtained electron fluence was 6.18 times higher than for the flattened beam. Removing the flattening filter affected the neutron production in the photon mode for the standard 10 × 10 cm2 field size: a 34% reduction in photoneutron production was observed at the isocentre.

Table 1.

Scattered photon, neutron and capture gamma-ray equivalent dose for prostate cancer irradiation with the 18 MV beam averaged for the prostate four field box irradiation. (Photon and neutron doses for the rectum are excluded from the calculations).

Organ Neutron equivalent dose in mSv per Gy Photon equivalent dose in mSv per Gy Prompt gamma-ray equivalent dose dose in mSv per Gy Accumulated equivalent dose from photons and neutrons in mSv per Gy
1. Thyroid 13.28 × 10−3 4.60 × 10−3 4.15 × 10−3 4.15 × 10−3
2. Esophagus 10.50 × 10−3 8.35 × 10−3 1.18 × 10−3 1.18 × 10−3
3. Lungs 3.42 × 10−3 6.49 × 10−3 1.16 × 10−3 1.16 × 10−3
4. Liver 12.77 × 10−3 36.99 × 10−3 3.24 × 10−3 3.24 × 10−3
5. Stomach 8.83 × 10−3 27.93 × 10−3 3.78 × 10−3 3.78 × 10−3
6. Bone marrow 17.10 × 10−3 21.00 × 10−3 2.90 × 10−3 2.90 × 10−3
7. Small intestine 14.85 × 10−3 30.01 × 10−3 4.23 × 10−3 4.23 × 10−3
8. Large intestine 11.01 × 10−3 55.00 × 10−3 5.33 × 10−3 5.33 × 10−3
9. Bladder 54.89 × 10−3 49.0810−3 6.76 × 10−3 11.07 × 10−2
10. Testes 29.02 × 10−3 48.11 × 10−3 3.42 × 10−3 3.42 × 10−3
11. Skin 46.09 × 10−3 25.09 × 10−3 1.47 × 10−3 1.47 × 10−3
12. Adrenals 9.03 × 10−3 16.98 × 10−3 2.34 × 10−3 2.34 × 10−3
13. Kidney 13.88 × 10−3 33.17 × 10−3 2.37 × 10−3 2.37 × 10−3
14. Pancreas 14.10 × 10−3 34.18 × 10−3 3.48 × 10−3 3.48 × 10−3
15. Spleen 11.07 × 10−3 29.09 × 10−3 6.67 × 10−3 6.67 × 10−3
16. Liver 13.05 × 10−3 37.13 × 10−3 3.50 × 10−3 3.50 × 10−3
17. leg bone 12.09 × 10−3 8.99 × 10−3 5.76 × 10−3 5.76 × 10−3
18. Spine bones 15.43 × 10−3 16.39 × 10−3 12.07 × 10−3 12.07 × 10−3
19. Scull bone 11.04 × 10−3 2.07 × 10−3 1.80 × 10−3 1.80 × 10−3
20. Brain 12.38 × 10−3 1.87 × 10−3 1.77 × 10−3 1.77 × 10−3
21. Thymus 11.85 × 10−3 2.00 × 10−3 1.09 × 10−3 1.09 × 10−3
22. Uterus 23.38 × 10−3 15.98 × 10−3 12.00 × 10−3 12.00 × 10−3
23. Ovaries 30.08 × 10−3 25.29 × 10−3 18.00 × 10−3 18.00 × 10−3
24. Scapulae 15.00 × 10−3 3.09 × 10−3 2.19 × 10−3 2.19 × 10−3
25. Arm bones 34.98 × 10−3 10.10 × 10−3 9.55 × 10−3 9.55 × 10−3
Open in a new tab

Table 2.

Secondary risk estimation due to the equivalent dose estimated for the organs in the out-of-field radiations. Data used from ICRP recommendations.16

Studied organ Probability of secondary cancer risk (cases per 10,000 persons) Fatal risk due to absorbed equivalent dose (cases per 10,000 persons) Non-Fatal risk due to absorbed equivalent dose (cases per 10,000 persons) Nominal risk adjusted for lethality and quality of life
1. Thyroid 0.56 0.07 0.08 0.12
2. Esophagus 0.24 0.05 0.07 0.10
3. Lungs 0.93 0.08 0.09 0.16
4. Liver 1.44 0.09 0.09 0.14
5. Stomach 0.89 0.09 0.10 0.17
6. Bone marrow 1.22 0.08 0.08 0.11
7. Small intestine 0.63 0.04 0.05 0.10
8. Large intestine 0.55 0.04 0.04 0.10
9. Bladder 1.93 0.07 0.08 0.99
10. Testes 1.10 0.09 0.09 0.10
11. Skin 51.67 0.13 0.15 0.19
12. Adrenals 0.65 0.07 0.08 0.99
13. Kidney 0.43 0.06 0.07 0.10
14. Pancreas 0.43 0.06 0.07 0.08
15. Spleen 0.38 0.08 0.08 0.98
16. Liver 1.68 0.07 0.07 0.08
17. Leg bone 0.31 0.03 0.05 0.07
18. Spine bones 0.29 0.03 0.05 0.07
19. Scull bone 0.25 0.02 0.04 0.08
20. Brain 0.28 0.01 0.03 0.08
21. Thymus 0.69 0.04 0.05 0.07
22. Uterus 1.66 0.08 0.12 0.18
23. Ovaries 2.29 0.10 0.17 0.23
24. Scapulae 0.51 0.03 0.05 0.08
25. Arm bones 0.99 0.02 0.03 0.06
Open in a new tab

Fig. 2.

Fig. 2

Open in a new tab

Neutron equivalent dose equivalent to different organs in the prostate radiotherapy from out-of-field radiation scored by MC simulation.

Fig. 3.

Fig. 3

Open in a new tab

Scattered photon equivalent dose in the prostate radiotherapy from out-of-field radiation scored by MC simulation.

Fig. 4.

Fig. 4

Open in a new tab

Capture gamma ray equivalent dose to different organs in the prostate radiotherapy from out-of-field radiation scored by MC simulation.

Table 3.

Estimated equivalent dose from the electron contamination in 18 MV X-ray prostate radiotherapy and probability of secondary cancer in cases per 10,000 persons.

Organ Equivalent dose (mSv/Gy of tumor dose) Probability of secondary cancer
Thyroid 1.05 0.04428
Lungs 0.58 0.24861
Esophagus 0.04 0.02049
Stomach 0.01 0.0051
Liver 0.38 0.16677
Bladder 0.82 0.35508
Skin 0.80 0.34485
Bone marrow 0.06 0.0258
Open in a new tab

Fig. 5.

Fig. 5

Open in a new tab

Electron contamination spectra derived by MC simulation for 40 × 40 cm2 field size and two linac configurations; solid red line is under condition with flattening filter and dot black line shows the contamination spectra without flattening filter. The flattening filter is a main part of a linac that contaminant electron production is attributed to. The figure shows the considerable effect of flattening filter on the electron contamination fluence.

5. Discussion

In the current study the 18 MV linac was modeled and the prostate was considered as a target organ. The prostate was a part of a modeled humanoid phantom in our simulations. We considered that prostate absorbed the X-ray dose of 72 Gy which was the basis of other calculations. Verification and benchmark method of MC simulated linac was explained in the Section 3 as well as in our previous work.19, 20, 21, 22, 23, 24, 25, 26 Out-of-field dose to the patient normal organs from the photoneutron, scattered photon, gamma-rays, and contaminant electron was estimated and converted to equivalent dose using the ICRP 103 recommended factor.16 Probability of secondary cancer risk, fatal and non-fatal risk due to equivalent absorbed dose, nominal risk adjusted for lethality and quality of life for the prostate as the target organ were estimated. Good agreements were observed between our calculation and other reported results. A comprehensive study was conducted for normal organs risk estimation in the course of prostate cancer treatment. Different researchers have studied the mentioned parameters in megavoltage prostate radiation therapy.27,29,31, 32, 33, 35, 36 Distant organ high doses may be attributed to the photoneutrons and gamma-rays due to the almost isotropic neutron propagation. Isotropic pattern of the neutrons emission and low attenuation because of zero electric charge made the distant organ dose difference lower than that for the same organ difference in the absorbed photon dose.37, 38, 39, 40, 41, 42 These organs are close to the target organ or have characteristics which make them likely to develop secondary malignancies. Electron contamination had been studied in the literature and a sharp drop in electron contamination was the cause why we report the results of organ doses due to electron contamination separately. But, in the case of electron contamination, we obtained results in agreement with the results reported in the literature.43, 44, 45 Based on the results, one can say that organs absorbed a dose mainly from the photoneutrons and their secondary malignancy risk is also, to a large degree, due to the neutron contamination in contrast of closer organs which mainly absorb a dose from photons and electrons. As a whole, we concluded that neutrons because of a high radiation weighting factor and a low gradient dose in distances around 0.5−1 m have more contribution in the secondary malignancy induction and organ doses in contrast to photon and electron contamination. It should be stated that gamma-rays are due to the photoneutron dose to patent’s body. Room dimensions and concrete thickness were taken into account in the simulation because of the effect of wall thickness and room dimensions on the neutron and gamma-ray production.40,46 Our simulation did not consider gamma-ray production for atoms and isotopes in the linac head, room walls, patient body and air atoms. Such data can be found in the literature.47, 48, 49 The obtained doses were the sum of equivalent doses of gamma-rays originating from the simple capture reaction (n,γ). The presented results and considerations are in good agreement with those published in the literature.20, 21, 22, 23, 24, 25,36,37,43, 44, 45, 46, 47, 48, 49

6. Conclusions

In the current study, we estimated organs doses in prostate megavoltage linac-based radiation therapy for different organs. The organ received doses from radiation contamination were also calculated and secondary malignancy induction calculation and cancer risk estimation were conducted on the basis of the organ equivalent doses. It was revealed that using megavoltage machines to irradiate patients’ tumoral organs was associated with non-negligible radiation contamination dose received from the patients. Secondary neutron doses were observed to dominate in radiation contamination. The authors recommend more studies on the issue to reduce the secondary risks of linac-based radiotherapy.

Finacial disclosure

None declared.

Conflict of interest

None declared.

Acknowledgement

The authors would like to thank for Tabriz University of Medical Sciences researches affair office for the supports.

References

  • 1.Piedbois P., Bataini J.P., Colin P. Conventional megavoltage radiotherapy in the management of malignant epithelial tumours of the parotid gland. Radiother Oncol. 1989;16:203–209. doi: 10.1016/0167-8140(89)90020-0. [DOI] [PubMed] [Google Scholar]
  • 2.Lonski P., Ramachandran P., Franich R., Kron T. Surface dose measurements in and out of field: implications for breast radiotherapy with megavoltage photon beams. Z Med Phys. 2017;27(4):318–323. doi: 10.1016/j.zemedi.2017.05.002. [DOI] [PubMed] [Google Scholar]
  • 3.Mellanby R.J., Herrtage M.E., Dobson J.M. Long-term outcome of eight cats with non-lymphoproliferative nasal tumours treated by megavoltage radiotherapy. J Feline Med Surg. 2002;4:77–81. doi: 10.1053/jfms.2001.0159. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 4.Ghal–Eh N., Goudarzi H., Rahmani F. FLUKA simulation studies on in–phantom dosimetric parameters of a LINAC–based BNCT. Radiat Phys Chem. 2017;141:36–40. [Google Scholar]
  • 5.Cerón Ramírez P.V., Díaz Góngora J.A., Paredes Gutiérrez L.C., Rivera M.T., Vega Carrillo H.R. Neutron H*(10) estimation and measurements around 18MV linac. Appl Radiat Isot. 2016;117:2–7. doi: 10.1016/j.apradiso.2016.05.006. [DOI] [PubMed] [Google Scholar]
  • 6.Gracanin V., Guatelli S., Cutajar D. A convenient verification method of the entrance photo-neutron dose for an 18MV medical linac using silicon p-i-n diodes. Radiat Meas. 2017;106:391–398. [Google Scholar]
  • 7.Cortés J.R., Romero R.A., Nieto J.A., Montalvo T.R. Electron absorbed dose measurements in LINACs by thermoluminescent dosimeters. Appl Radiat Isot. 2014;83:210–213. doi: 10.1016/j.apradiso.2013.06.013. [DOI] [PubMed] [Google Scholar]
  • 8.Sangeetha S., Sureka C.S. Comparison of flattening filter (FF) and flattening-filter-free (FFF) 6MV photon beam characteristics for small field dosimetry using EGSnrc Monte Carlo code. Radiat Phys Chem. 2017;135:63–75. [Google Scholar]
  • 9.Dasu A., Toma-Dasu I. Models for the risk of secondary cancers from radiation therapy. Phys Med. 2017;42:232–238. doi: 10.1016/j.ejmp.2017.02.015. [DOI] [PubMed] [Google Scholar]
  • 10.Guckenberger M., Klement R.J., Allgäuer M. Local tumor control probability modeling of primary and secondary lung tumors in stereotactic body radiotherapy. Radiother Oncol. 2016;118:485–491. doi: 10.1016/j.radonc.2015.09.008. [DOI] [PubMed] [Google Scholar]
  • 11.Liu Z., Gray B.D., Barber C. Characterization of TCP-1 probes for molecular imaging of colon cancer. J Control Release. 2016;239:223–230. doi: 10.1016/j.jconrel.2016.08.033. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Ruggieri R., Stavreva N., Naccarato S., Stavrev P. Applying a hypoxia-incorporating TCP model to experimental data on rat sarcoma. Int J Radiat Oncol Biol Phys. 2012;83:1603–1608. doi: 10.1016/j.ijrobp.2011.10.015. [DOI] [PubMed] [Google Scholar]
  • 13.Vojtíšek R., Mužík J., Slampa P. The impact of PET/CT scanning on the size of target volumes, radiation exposure of organs at risk, TCP and NTCP, in the radiotherapy planning of non-small cell lung cancer. Rep Pract Oncol Radiother. 2014;19:182–190. doi: 10.1016/j.rpor.2013.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Shen Z.W., Luo M.Y., Hu H.H. Screening and verifying potential NTCP inhibitors from herbal medicinal ingredients using the LLC-PK1 cell model stably expressing human NTCP. Chin J Nat Med. 2016;14:549–560. doi: 10.1016/S1875-5364(16)30065-6. [DOI] [PubMed] [Google Scholar]
  • 15.Stam B., Peulen H., Rossi M.M.G., Belderbos J.ÑS.A., Sonke J.J. Validation of automatic segmentation of ribs for NTCP modeling. Radiother Oncol. 2016;118:528–534. doi: 10.1016/j.radonc.2015.12.014. [DOI] [PubMed] [Google Scholar]
  • 16.International Commission on Radiological Protection . 2007. ICRP report 103. Annals of the ICRP (ICRP 2007 report No. 103) [DOI] [PubMed] [Google Scholar]
  • 17.González W., García-Ferreira I.-B., Anguiano M., Lallena A.M. A general photon source model for clinical linac heads in photon mode. Radiat Phys Chem. 2015;117:140–152. [Google Scholar]
  • 18.Jagtap A.S., Palani Selvam T., Patil B.J. Monte Carlo based investigations of electron contamination from telecobalt unit head in build up region and its impact on surface dose. Appl Radiat Isot. 2016;118:175–181. doi: 10.1016/j.apradiso.2016.09.012. [DOI] [PubMed] [Google Scholar]
  • 19.Mesbahi A., Ghiasi H., Mahdavi S.R. Photoneutron and capture gamma dose calculations for a radiotherapy room made of high density concrete. Nucl Technol Radiat Prot. 2011;26(2):147–152. [Google Scholar]
  • 20.Beigi M., Afarande F., Ghiasi H. Safe bunker designing for the 18MV Varian 2100 Clinac: a comparison between Monte Carlo simulation based upon data and new protocol recommendations. Rep Pract Oncol Radiother. 2016;21:42–49. doi: 10.1016/j.rpor.2015.10.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 21.Ghiasi H., Mesbahi A. A new analytical formula for neutron capture gamma dose calculations in double-bend mazes in radiation therapy. Rep Pract Oncol Radiother. 2012;17:220–225. doi: 10.1016/j.rpor.2012.03.011. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Ghiasi H. Monte Carlo characterizations mapping of the (γ,n) and (n,γ) photonuclear reactions in the high energy X-ray radiation therapy. Rep Pract Oncol Radiother. 2014;19:30–36. doi: 10.1016/j.rpor.2013.07.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Ghiasi H., Mesbahi A. Monte Carlo characterization of photoneutrons in the radiation therapy with high energy photons: a comparison between simplified and full Monte Carlo models. Int J Radiat Res. 2010;8:187–193. [Google Scholar]
  • 24.Ghiasi H., Mesbahi A. Gantry orientation effect on the neutron and capture gamma ray equivalent dose at the maze entrance door in radiationtherapy. Nucl Technol Radiat Prot. 2012;17:220–225. [Google Scholar]
  • 25.Mesbahi A., Azarpeyvand A.A., Shirazi A. Photoneutron production and backscattering in high density concretes used for radiation therapy shielding. Ann Nucl Energy. 2011;38:2752–2756. [Google Scholar]
  • 26.Mesbahi A., Ghiasi H., Mahdavi S.R. Photoneutron and capture gamma equivalent dose for different room and maze layouts in radiation therapy. Radiat Protect Dosim. 2010;140:242–249. doi: 10.1093/rpd/ncp303. [DOI] [PubMed] [Google Scholar]
  • 27.Atwell W., Hardy A.C., Peterson L.E. Organ radiation doses and lifetime risk of excess cancer for several space shuttle missions. Adv Space Res. 1996;18:139–148. [Google Scholar]
  • 29.Wanderås E.H., Fosså S.D., Tretli S. Risk of subsequent non-germ cell cancer after treatment of germ cell cancer in 2006 Norwegian male patients. Eur J Cancer. 1997;33:253–262. doi: 10.1016/s0959-8049(96)00458-3. [DOI] [PubMed] [Google Scholar]
  • 31.Stewart F.A., Akleyev A.V., Hauer-Jensen M. ICRP publication 118: ICRP statement on tissue reactions and early and late effects of radiation in normal tissues and organs-threshold doses for tissue reactions in a radiation protection context. Ann ICRP. 2012;41:1–322. doi: 10.1016/j.icrp.2012.02.001. [DOI] [PubMed] [Google Scholar]
  • 32.Skrobala A., Adamczyk S., Kruszyna-Mochalska M. Low dose out-of-field radiotherapy, part 2: calculating the mean photon energy values for the out-of-field photon energy spectrum from scattered radiation using Monte Carlo methods. Cancer Radiother. 2017;21(5):352–357. doi: 10.1016/j.canrad.2017.04.010. [DOI] [PubMed] [Google Scholar]
  • 33.Paix A., Antoni D., Adeduntan R., Noël G. Stereotactic radiation therapy of brain metastases from colorectal cancer: a single institution cohort. Cancer Radiother. 2017;21:199–204. doi: 10.1016/j.canrad.2017.01.010. [DOI] [PubMed] [Google Scholar]
  • 35.Pickett B., Roach M. The impact of isocenter placement errors associated with dose distributions used in irradiating prostate cancer. Med Dosim. 1996;21:61–68. doi: 10.1016/0958-3947(96)00028-3. [DOI] [PubMed] [Google Scholar]
  • 36.Rosewall T., Kong V., Heaton R., Currie G., Milosevic M., Wheat J. The effect of dose grid resolution on dose volume histograms for slender organs at risk during pelvic intensity-modulated radiotherapy. J Med Imaging Radiat Sci. 2014;45:204–209. doi: 10.1016/j.jmir.2014.01.006. [DOI] [PubMed] [Google Scholar]
  • 37.Sumini M., Isolan L., Cucchi G., Sghedoni R., Iori M. A Monte Carlo model for photoneutron generation by a medical LINAC. Radiat Phys Chem. 2017;140:345–348. [Google Scholar]
  • 38.Di Fulvio A., Domingo C., De San Pedro M. Superheated emulsions and track etch detectors for photoneutron measurements. Radiat Meas. 2013;57:19–28. [Google Scholar]
  • 39.Vagena E., Stoulos S., Manolopoulou M. Geant4 simulations on medical Linac operation at 18MV: Experimental validation based on activation foils. Radiat Phys Chem. 2016;120:89–97. [Google Scholar]
  • 40.Łaciak M., Konefał A. Dependence between the size of the treatment room and the fluence of neutrons undesirable in radiotherapy for the high-energy therapeutic X-rays generated by the linear medical accelerator. Acta Phys Pol B. 2014;45(2):559–564. [Google Scholar]
  • 41.Naseri A., Mesbahi A. A review on photoneutrons characteristics in radiation therapy with high-energy photon beams. Rep Pract Oncol Radiother. 2010;15:138–144. doi: 10.1016/j.rpor.2010.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 42.Facure A., Falcão R.C., Silva A.X., Crispim V.R., Vitorelli J.C. A study of neutron spectra from medical linear accelerators. Appl Radiat Isot. 2005;62:69–72. doi: 10.1016/j.apradiso.2004.05.072. [DOI] [PubMed] [Google Scholar]
  • 43.Kumar M., Sahani G., Chourasiya G. Magnetic removal of electron contamination for 60Co panoramic gamma ray exposure-Investigations with CaSO4:Dy and LiF based dosimeters. Appl Radiat Isot. 2010;68:1173–1176. doi: 10.1016/j.apradiso.2009.12.034. [DOI] [PubMed] [Google Scholar]
  • 44.Nilsson B., Brahme A. Electron contamination from photon beam collimators. Radiother Oncol. 1986;5:235–244. doi: 10.1016/s0167-8140(86)80053-6. [DOI] [PubMed] [Google Scholar]
  • 45.Smit C., du Plessis F.C.P. Deriving electron contamination characteristics using Monte Carlo beam data. Phys Med. 2015;31:S11. [Google Scholar]
  • 46.Bieniasiewicz M. Measurements of thermal and resonance neutron fluence and induced radioactivity inside bunkers of medical linear accelerators in the center of oncology in Opole, Poland. Acta Phys Pol B. 2016;47(3):771–776. [Google Scholar]
  • 47.Janiszewska M., Polaczek-Grelik K., Raczkowski M. Secondary radiation dose during high-energy total body irradiation. Strahlenther Onkol. 2014;190:459–466. doi: 10.1007/s00066-014-0635-z. [DOI] [PubMed] [Google Scholar]
  • 48.Konefał A., Polaczek-Grelik K., Zipper W. Undesirable nuclear reactions and induced radioactivity as a result of the use of the high-energy therapeutic beams generated by medical linacs. Radiat Prot Dosimetry. 2008;128:133–145. doi: 10.1093/rpd/ncm318. [DOI] [PubMed] [Google Scholar]
  • 49.Konefał A., Orlef A., Bieniasiewicz M. Measurements of neutron radiation and induced radioactivity for the new medical linear accelerator, the Varian TrueBeam. Radiat Meas. 2016;86:8–15. [Google Scholar]

Articles from Reports of Practical Oncology and Radiotherapy are provided here courtesy of Via Medica sp. z o.o. sp. k.

RESOURCES