A computational model for understanding the oligomerization mechanisms of TNF receptor superfamily

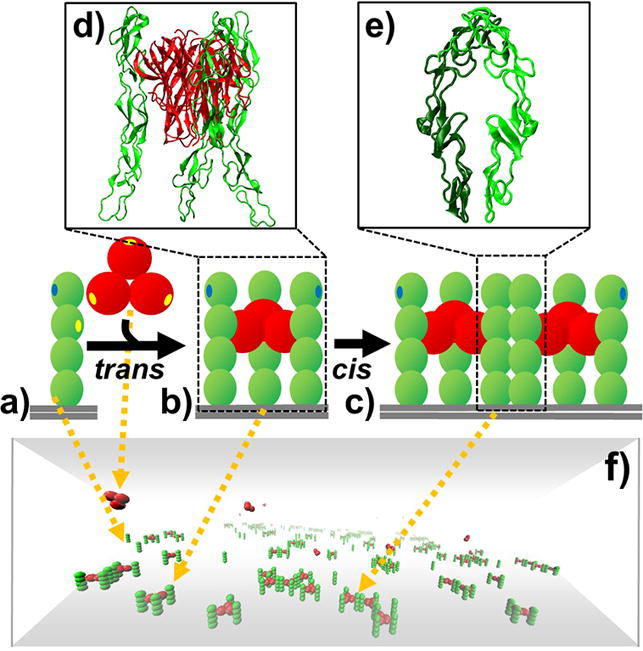
Graphical abstract

Abstract

By recognizing members in the tumor necrosis factor (TNF) receptor superfamily, TNF ligand proteins function as extracellular cytokines to activate various signaling pathways involved in inflammation, proliferation, and apoptosis. Most ligands in TNF superfamily are trimeric and can simultaneously bind to three receptors on cell surfaces. It has been experimentally observed that the formation of these molecular complexes further triggers the oligomerization of TNF receptors, which in turn regulate the intracellular signaling processes by providing transient compartmentalization in the membrane proximal regions of cytoplasm. In order to decode the molecular mechanisms of oligomerization in TNF receptor superfamily, we developed a new computational method that can physically simulate the spatial-temporal process of binding between TNF ligands and their receptors. The simulations show that the TNF receptors can be organized into hexagonal oligomers. The formation of this spatial pattern is highly dependent not only on the molecular properties such as the affinities of trans and cis binding, but also on the cellular factors such as the concentration of TNF ligands in the extracellular area or the density of TNF receptors on cell surfaces. Moreover, our model suggests that if TNF receptors are pre-organized into dimers before ligand binding, these lateral interactions between receptor monomers can play a positive role in stabilizing the ligand-receptor interactions, as well as in regulating the kinetics of receptor oligomerization. Altogether, this method throws lights on the mechanisms of TNF ligand-receptor interactions in cellular environments.

1. Introduction

The tumor necrosis factor (TNF) receptor superfamily (TNFRSF) is a major group of cell surface proteins recognizing the co-stimulatory molecules which belong to the TNF superfamily [1], [2], [3]. The specificity of binding between ligands and receptors in these two superfamilies constitute a complex network of protein-protein interactions that regulate different pathways of human inflammation response [4], [5], [6], [7]. Therapeutic targeting of TNFRSF signaling therefore is a promising treatment for a wide variety of autoimmune diseases such as rheumatoid arthritis and multiple sclerosis [8], [9]. The ligands in TNF superfamily generally adopt a β-sandwich “jelly-roll” fold and further organize into a homo-trimeric quaternary structure [10]. On the other hand, the ectodomains of their receptors contain tandem repeats of cysteine-rich domains (CRDs) [11]. For almost all trimeric ligands in TNF superfamily, the receptor binding interfaces are located at the interprotomer grooves between every two adjacent subunits, leading into the assembly of a basic unit of ligand-receptor complex with a 3:3 stoichiometry (Fig. 1d) [12]. It has been further found that the formation of these complexes can trigger the receptor oligomerization for different members in TNFRSF [13]. For instance, highly organized oligomers on cell surfaces were observed for death receptor 5 (DR5) after it binds to the TNF-related apoptosis-inducing ligand (TRAIL) [14]. In another example, experiments showed that interactions between the extracellular domains of receptor Fas and its ligand FasL are sufficient to induce the formation of supramolecular clusters [15], [16]. Moreover, a specific extracellular region, called pre-ligand assembly domain (PLAD), was identified to modulate the assembly between receptors [17], [18]. This region does not overlap with the ligand-receptor binding interfaces [19] and is functionally conserved across the TNFR superfamily [20]. These evidences indicate that highly ordered spatial organization is a general behavior for receptors in TNFRSF to carry out their functions of signal transduction, and there is a universal mechanism underlying the clustering of receptors in different systems. However, a mechanistic understanding of this ligand-induced receptor oligomerization for TNFRSF is so far still missing.

Fig. 1.

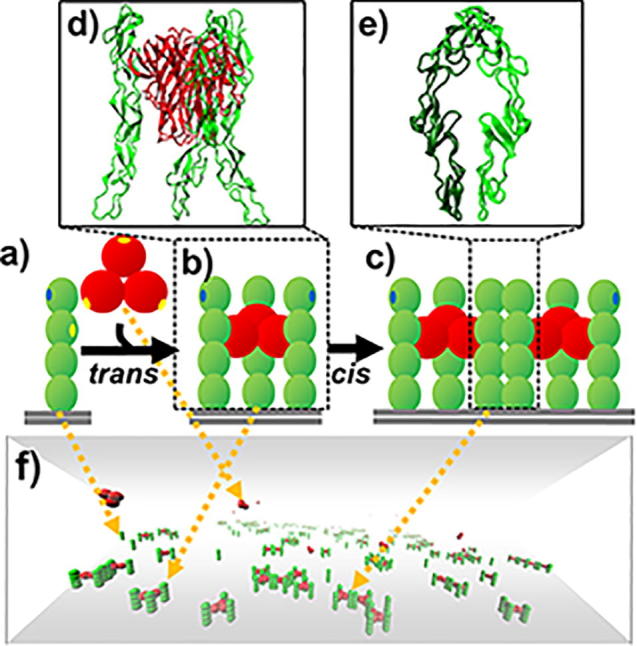
A coarse-grained model was constructed to simulate the spatial-temporal process of binding between TNF ligands and their receptors. (a) The trimeric TNF ligand is represented by three rigid bodies that are spatially arranged into a three-fold symmetry, while CRD domains in a TNF receptor are spatially aligned into a rod-like shape. (b) Through the trans-binding sites (yellow dots) on the surface of each ligand subunit and the second N-terminal domain of receptor, a ligand can simultaneously bind to three receptors and form a basic unit of signaling complex. (c) Furthermore, cis-binding site (blue dots) is assigned on the surface of the N-terminal domains in TNF receptors so they can be laterally connected together. (d) The x-ray crystal structures of ligands and receptors that form trans-interactions. (e) The x-ray crystal structures of two receptors that form cis-interactions. (f) Finally, a kinetic Monte-Carlo algorithm is applied to simulate the system, in which TNF receptors are distributed on the plasma membrane represented by the bottom surface of a three-dimensional simulation box. The space above the plasma membrane represents the extracellular region, where TNF ligands are located. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Detecting the dynamic process of receptor oligomerization through super-resolution imaging [21] or electron tomography (ET) [22] is currently limited by the spatial-temporal resolution of these experimental techniques. In contrast, computational modeling possesses of unique advantages that permit one to reach the conditions that are infeasible in the laboratory. Molecule-based simulation approaches have been used to study the dynamic properties of specific membrane receptors [23], [24], [25], [26], [27], [28], [29], [30]. For instance, molecular dynamic (MD) or Brownian dynamic (BD) simulations were developed to study the interactions between proteins [31], [32], [33]. Unfortunately, these methods are so far difficult to reach the time scale in which a membrane receptor associates and dissociates with its ligand, or deal with a system containing large amounts of receptors that form complexes or clusters. On the other hand, there are a variety of computational modeling approaches incorporating spatial information on the subcellular level [34], [35], [36], [37], [38], [39], [40], [41], [42], [43], such as partial differentiation equations (PDE) and lattice-based simulations. These models aimed to describe how collective behaviors of membrane receptors lead to spatial patterning on cell surfaces or at cellular interfaces. Due to the coarse-grained features of these models, molecular details of ligands and receptors, as well as the energetics of their interactions, are rarely included. Only qualitative picture can be derived from these models. Therefore, it is highly demanding to develop new simulation methods that can compensate the limitations between molecule-based and lower-resolution models, and further applied them to the specific biological systems.

Top tackle the problem, we present a new computational method in this article to unravel the molecular mechanisms of oligomerization for receptors in TNFRSF. A domain-based representation is constructed to delineate the basic structural information of TNF ligands and receptors. The trans-binding interface between ligand and receptor, as well as the cis-binding interface between two receptors, are also defined based on the structural evidences. Multiple copies of these receptors and ligands are included in the simulation system, in which their diffusion and binding are guided by a kinetic Monte-Carlo algorithm. We first found that the initial spatial organization of TNF ligands as homotrimers can promote their ability to bind more receptors, revealing the function of binding avidity in multivalent TNF ligands. Moreover, our simulations show that the spatial patterns formed by TNF ligand-receptor complexes are highly dependent not only on the molecular properties such as trans and cis binding affinities, but also on the cellular factors such as the concentration of TNF ligands in the extracellular area or the density of TNF receptors on cell surfaces. An interesting discovery is that strong cis-interactions between complexes or high surface density of TNF receptors prevent the systems from forming large-size oligomers through kinetic trapping and local crowding effect. Finally, the results suggest that the lateral interactions between TNFR monomers without ligands can kinetically affect the oligomerization of ligand-receptor complexes. In summary, our computational model is a useful addition to a suite of existing experimental techniques to compare oligomerization of different receptors in TNFRSF and further understand their functions in regulating the downstream signaling events. At the same time, the modeling strategy and simulation algorithm can be potentially generalized to study the spatial organization of other membrane receptor systems.

2. Model and methods

2.1. Construction of a domain-based coarse-grained model

The extracellular regions of membrane receptors usually consist of multiple domains [44], while their ligands are normally organized into multimeric complexes [45]. TNF and TNFR superfamilies are typical examples, as we mentioned in the introduction. In order to take account of these details into our simulations, we constructed a new domain-based coarse-grained model to describe the structural arrangement of TNF ligands and receptors. In specific, each subunit in a TNF ligand trimer is represented by a rigid body with a radius of 3 nm. The rigid bodies in a ligand are spatially aligned together with a three-fold symmetry (Fig. 1a). Considering a receptor in TNFRSF normally contains tandem repeats of one to six CRD domains, a standard model with four domains is adopted, which is also the most frequently observed in TNFRSF. Correspondingly, each CRD domain in a receptor is coarse-grained into a rigid body with a radius of 2 nm. The rigid bodies in a receptor are spatially aligned into a rod-like shape (Fig. 1a).

The extracellular domains of TNF receptors are further distributed on the plasma membrane, which is represented by the bottom surface of a three-dimensional simulation box. The space above the plasma membrane represents the extracellular region, where TNF ligands are placed (Fig. 1f). On the surface of each ligand subunit, we further assigned a trans-binding site (yellow dots), so that it can bind to a receptor. The trans-binding site for a receptor is located at the surface of the second N-terminal domain (yellow dots). Through the trans-interactions, the ligand trimer can simultaneously bind to three receptors and form a basic unit of signaling complex (Fig. 1b). Moreover, in a recently solved X-ray structure [19], receptors were found to be in a parallel dimer that is connected by a cis-binding interface (Fig. 1e). The ligand-binding interface is on the opposite side of the receptor in this dimer, which provides the possibility for ligand-receptor signaling complexes to further form higher-order oligomers [46]. We also integrated this structural evidence of cis-interaction between receptors into our model. As a result, a cis-binding interface (blue dots in Fig. 1) is assigned on the surface of the N-terminal domains for each receptor, so that upon ligand binding, two signaling complexes can be laterally connected together (Fig. 1c).

2.2. Implementation of the kinetic monte-carlo simulation algorithm

Given the concentration and surface density of TNF ligands and receptors, an initial configuration is constructed by randomly distributing receptors on the plasma membrane and ligands in the extracellular region. Starting from this initial configuration, the simulation of the dynamic system is then guided by a kinetic Monte-Carlo algorithm. The algorithm follows a standard diffusion-reaction protocol, as we developed earlier [47], [48]. Specifically, within each simulation time step, stochastic diffusions are first selected for randomly selected molecules. Translational and rotational movements of TNF receptors are confined on the surface at the bottom of the simulation box, while TNF ligands are free to make translational and rotational diffusions within the volume above the surface. The amplitude of these movements within each simulation step is determined by the diffusion coefficients of each ligand and receptor. We applied the 2D periodic boundary condition to membrane-bound receptors. For free ligands, periodic boundary conditions are imposed along X and Y directions of the extracellular region. Along the Z direction, any ligand moving beyond the top or below the bottom of the simulation box will be bounced back.

After the diffusion scenario, the reaction of association for a trans-interaction will be triggered by a given probability if the binding criteria are satisfied between a receptor and an unbound subunit from a ligand trimer. Similarly, the reaction of association for a cis-interaction will be triggered by a given probability if the binding criteria are satisfied between two receptors. Two types of cis-interactions are specifically considered in this study: one is between two monomeric receptors; while the other is between two ligand-bound receptor complexes. The probability of association is directly calculated by multiplying the on rate of the reaction with the length of the simulation time step. At the same time, dissociations are triggered for any randomly selected trans-interaction or cis-interaction with the probability that is calculated by multiplying the off rate of the corresponding reaction with the length of the simulation time step. If a ligand binds to a receptor, or a receptor joins an incomplete ligand-receptor complex with vacant receptor binding sites, they will move together on the surface of the plasma membrane. If two complexes are connected together with a lateral interaction, the entire assembly will then stop diffusing and provides a seed for further oligomerization. Finally, above procedure is iterated until the system evolves into equilibrium patterns in both configurational and compositional spaces.

2.3. Parameter determination in the coarse-grained simulations

The basic simulation parameters, including time step and binding criterion, were adopted from our previous study [49]. Specifically, the binding criterion (i.e. the distance cutoff to trigger association between two proteins) is 2 nm, while the length of each simulation tine step is 10 ns. The values of these parameters were determined based on the benchmark tests in order to optimize the balance between simulation accuracy and computational efficiency. The length of each side in the square plasma membrane surface is 1000 nm, along both X and Y directions, which gives a total area of 1 µm². Along the Z direction, the height of the simulation box is 100 nm. In the simulation, we changed the number of receptors on the membrane surface from 150 to 750, leading to the surface density in the range of ~10²mol/µm². This surface density of membrane receptors is within the typical range that was experimentally observed in T cells [50]. Given the molecular weight of the TNF ligand trimer, its diffusion constant was obtained by fitting data calculated using a precise boundary element method [51]. Consequently, the translational diffusion constant of a soluble ligand trimer is taken as 72.6 μm²/s and the rotational coefficient as 0.34° per ns. Relatively, the two-dimensional diffusions of a monomeric receptor or a ligand-bound receptor are much slower due to the restriction from the surface of plasma membrane, with a translational constant of 10 μm²/s and rotational coefficient of 1° per ns. The values of these parameters were derived from our previous simulation results for the diffusions of a membrane receptor on the lipid bilayer [52]. Moreover, the surface diffusions of a complex consisting of a TNF ligand and more than one receptor are considered as even slower, with a translational constant of 5 μm²/s and rotational coefficient of 0.28° per ns. When more than two ligand-receptor complexes form an initial seed for oligomerization, as mentioned above, the entire assembly will stop diffusing for computational simplicity.

The reaction parameters were chosen within the range that is typical for the interactions between protein ligands and membrane receptors. For instance, the on rates for trans and cis interactions were calibrated to a reasonable value to make the simulation computationally accessible. They are on the scale from 10⁵M⁻¹s⁻¹ to 10⁷M⁻¹s⁻¹, a typical range for the diffusion-limited rate constants, in which association is guided by complementary electrostatic surfaces at binding interfaces [53]. On the other side, a wide range of off rate, between 10⁻²s⁻¹ and 10⁴s⁻¹, was used to test simulations for dissociation of both trans and cis interactions. Therefore, our tests cover the dissociation constants from millimolar (mM) to nanomolar (nM), which is within the typical range for binding of signaling receptors on the surfaces of immune cells [54].

3. Results

3.1. Characterize the general dynamics of TNF receptor oligomerization

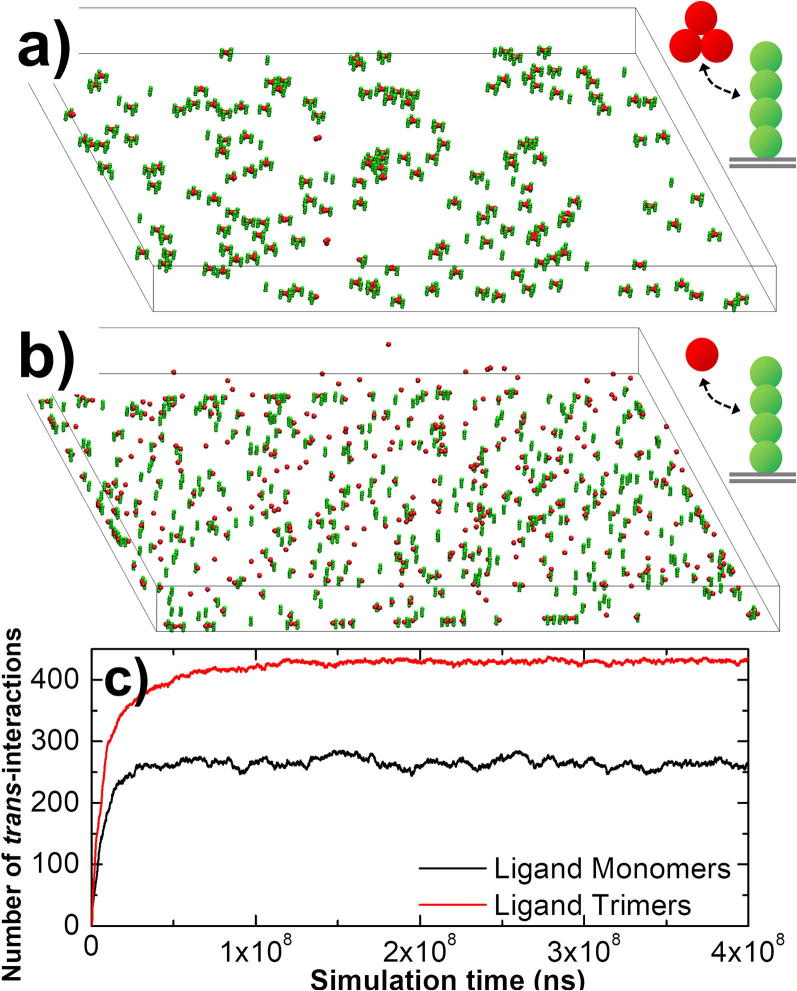
Using the modeling scheme and simulation algorithm described above, we first investigated how the spatial organization of a trimeric ligand affects its binding with TNF receptors. Specifically, 150 TNF trimeric ligands were randomly placed in the extracellular region, while 450 TNF receptors were distributed on the surface below. In order to focus on the binding effect of trimeric ligand complexes, the lateral interactions between receptors were turned off. The final configuration from the simulation was plotted in Fig. 2a. In comparison, a control simulation was carried out, in which each TNF ligand is represented by a monomer with single binding site. As a result, ligand-receptor complex can only be formed with a 3:3 stoichiometry. We placed 450 ligand monomers in the control simulation to maintain the same level of possible interactions as in the first simulation scenario. All other parameters such as diffusion constant, rates of association and dissociation between ligands and receptors remain unchanged. The final configuration from the control simulation was plotted in Fig. 2b. The total number of ligand-receptor interactions formed during simulations in the first system is plotted in Fig. 2c as red curve, while the black curve shows the total number of interactions formed in the control simulation.

Fig. 2.

We investigated impacts of trimeric ligands on their binding with TNF receptors using two comparative simulations. (a) In one scenario, 450 receptors were distributed on the surface below the extracellular region. They interacted with 150 trimeric ligands. (b) In the other scenario, there were 450 ligand monomers in the extracellular region to target receptors. All other parameters remain unchanged. (c) The total number of ligand-receptor interactions formed during simulations in the first scenario is plotted as red curve, while the black curve shows the total number of interactions formed in the second scenario. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

Interestingly, Fig. 2c shows that although both systems contain the same number of ligand binding sites (450), 250 binding sites were occupied by receptors after equilibrium if ligands are monomers. However, there were more than 400 ligand binding sites were occupied by receptors in the trimeric ligand scenario. Therefore, much more interaction can be formed if ligands are organized into higher-order complexes. We suggest that this is due to the following fact. Binding of any binding sites in a trimeric ligand simultaneously brings other unbound binding sites in the ligand close to cell surface. This increase of local concentration makes ligands easier to find their target receptors. In another word, avidity enhances binding by causing the coupling effects between different binding sites in a ligand complex. Moreover, we also found that the interactions between receptors and trimeric ligands show relatively smaller fluctuations than monomeric ligands, indicating that the system of trimeric ligands is more resistant to external noises. This suggests that the formation of trimers is important to increase the sensitivity of TNF-mediated signaling.

To further characterize the dynamic properties of receptor oligomerization after ligand binding, we turned on the cis-interactions between ligand-bound receptors. The cis-interactions between unbound receptors were not considered at this stage to avoid complexity in data analysis. This is based on the assumption that the cis-interactions between unbound receptors could be weaker than the cis-interactions between ligand-bound receptors with several orders of magnitude, which have been demonstrated in the clustering of classic cadherin [55]. To illustrate the effect of cis-interactions, two systems were specifically simulated and compared with each other. In the first system, two ligand-bound TNF receptors can form a lateral interaction with the on rate of 10⁵M⁻¹s⁻¹ and the off rate of 10²s⁻¹. In the second system, no lateral interactions can be formed between receptors. All other parameters such as ligand receptor concentrations, diffusion constant, binding rates of trans-interactions between ligands and receptors remain unchanged. As a result, the kinetics profiles in both systems are plotted in Fig. 3a.

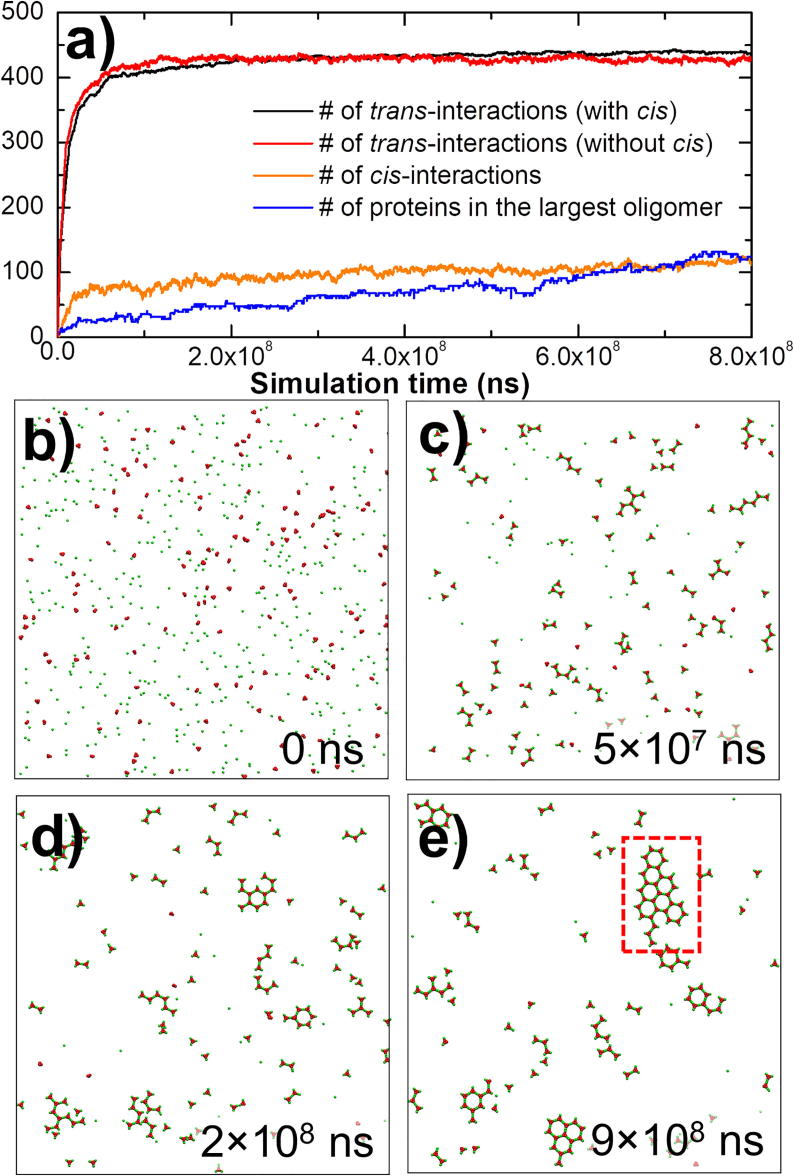
Fig. 3.

We turned on the cis-interactions between ligand-bound receptors to characterize the dynamic properties of receptor oligomerization after ligand binding. (a) The kinetic profiles of the simulation, including the number of trans-interactions (black curve), the number of cis-interactions (orange curve), and the size of the largest oligomer (blue curve) are plotted. The number of trans-interactions is further compared with a control system (red curve) in which the cis-interactions between ligand-bound receptors were turned off. (b) We show the initial configuration of the simulation. (c-d) Some representative snapshots along the simulation trajectory are also plotted. (e) The oligomer with the maximal size formed at the end of the simulation is highlighted. In the oligomer, ligand-receptor complexes are clustered as hexagonal lattice. (For interpretation of the references to colour in this figure legend, the reader is referred to the web version of this article.)

The total number of trans-interactions formed between ligands and receptors formed along the simulation of the first system is plotted by the black curve in the figure, while the total number of trans-interactions formed in the second system is plotted by the red curve. Although the binding constants of trans-interactions in both systems are the same, the simulation results show that the number of trans-interactions in the system with cis-interactions grows more slowly but reaches a higher level with lower fluctuations than the system without cis-interactions. This interesting finding suggests that the cis-interactions between receptors can affect the binding kinetics of trans-interactions. Moreover, the ligand-receptor interactions can be stabilized by forming lateral oligomers. In order to further assess the statistical significance of obtained differences of trans-interactions between these two systems, a two-sample student's t-test was performed to the data points among the last 10⁸ns of two trajectories. The comparison of these two data points along with the simulation time is plotted in Fig. S1a, while their distributions are plotted as histograms in Fig. S1b. As a result, the average number of trans-interactions in the simulation without cis-interactions is 427.49 and the standard deviation of the distribution is 2.67. On the other hand, the average number of trans-interactions in the simulation with cis-interactions is 439.55 and the standard deviation of the distribution is 1.41. The null hypothesis that no difference exists between two sets was tested at a 95% confidence interval. Consequently, the calculated t-score equals 196.0 and the corresponding P-value is lower than 0.001. Therefore, the small P-value for the t-test suggests that we can reject the null hypothesis and accept the alternative hypothesis, i.e., the differences in numbers of trans-interactions between the simulations with and without cis-interactions are significant.

On the other hand, the total number of cis-interactions form in the first system and the largest oligomer found along the simulation are plotted by orange and blue curves in Fig. 3a, respectively. Comparing with the trans-interactions, the number of cis-interactions increases much slower and shows a linear growth in oligomerization instead of the exponential growth in trans-dimerization. This is partially due to the reason that cis-interactions can only be formed after trans-interactions, while the oligomerization is triggered only after the concentration of ligand-receptor complexes in the system is high enough. Finally, some representative snapshots of receptor clustering are plotted along the simulation trajectory from Fig. 3b–e. The figures show that after the formation of individual ligand-receptor complexes (Fig. 3c), the small oligomers start to grow (Fig. 3d) and the spatial organization of complexes as hexagonal lattice are finally clustered, as described in previous studies [54]. The largest oligomer that contains more than 100 proteins, including ligands and receptors, is highlighted in the final configuration (Fig. 3e).

3.2. Explore the impacts of concentration and stoichiometry on oligomerization

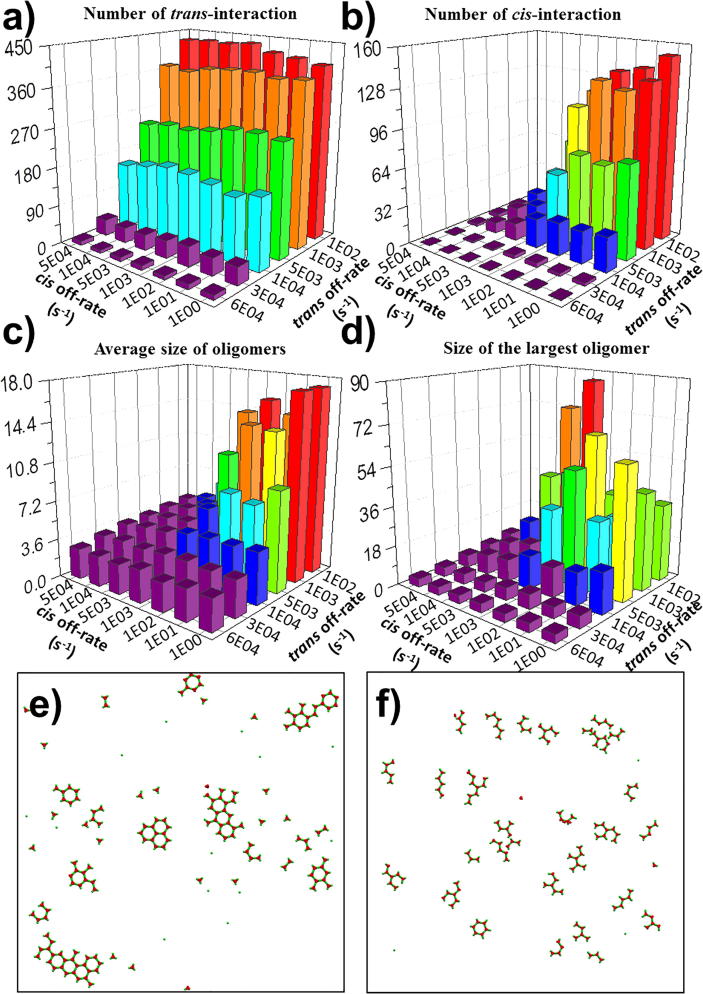
To illustrate the effect of concentration and stoichiometry between ligands and receptors on oligomerization, we changed the number of trimeric ligands in the extracellular region, as well as the number of receptors on the surface below. In order to further exclude other factors, we fixed the on rate and off rate for both trans-interaction and cis-interaction at 10⁷M⁻¹s⁻¹ and 10²s⁻¹ in all systems, respectively. All simulations were terminated at the same time (1 × 10⁸ns). At the end of each simulation trajectory, we calculated the number of ligand-receptor trans-interactions, the number of receptor-receptor cis-interactions, the average size of formed oligomers, and the largest oligomer found in the system. The distributions of our calculated results are plotted as histograms in Fig. 4. Each bar in the figure was actually based on the average values calculated from the data that were collected within the last 10⁷ns of the corresponding simulation trajectories. The simulations were updated every 5 × 10⁴ns. As a result, the height in the histograms of Fig. 4 corresponds to the statistical average of the last 200 data points along the simulations. All the raw data of the figures can be found from Tables S1-1 to S1-4 in the supporting information.

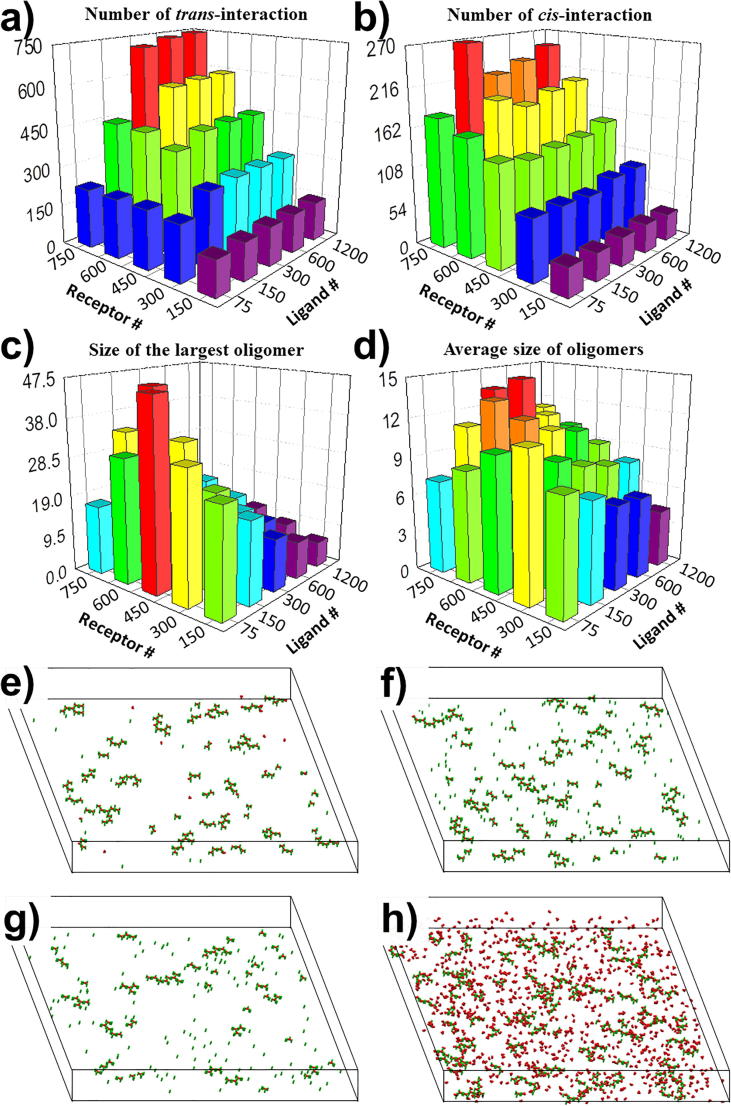
Fig. 4.

We changed the number of ligands in the extracellular region and the number of receptors on the surface below to illustrate the effect of concentration and stoichiometry on receptor oligomerization. TNF ligands are in their trimeric state. Simulations were carried out for all combinations of ligand concentrations and surface densities of receptors. At the end of each simulation trajectory, we calculated and plot the histograms for the distributions of (a) the number of ligand-receptor trans-interactions, (b) the number of receptor-receptor cis-interactions, (c) the largest oligomer found in the system, and (d) the average size of formed oligomers, respectively. Given the same number of trimeric ligands (150), we found that the number of cis-interactions keeps increasing with the increasing density of receptors. In (e), we plot the configuration with low surface densities of receptors (450). In (f), we plot the configuration with high surface densities of receptors (750). (g) Moreover, we plot the configuration with a relative low ligand concentration (450 receptors, 75 ligands). (h) In comparison, we also plot the configuration with a relative high ligand concentration (750 receptors, 1200 ligands).

The figure shows that overall the number of interactions are positively correlated with the ligand concentration and surface density of receptors. However, there is a threshold of ligand concentration above which the ligand-receptor interactions cannot grow further (Fig. 4a). The value of this threshold depends on the surface density of receptors. For instance, when there are 450 receptors in the system, the number of trans-interactions is saturated after the number of trimeric ligands reaches 150. When there are 750 receptors in the system, the number of trans-interactions does not increase after the number of trimeric ligands reaches 300. This threshold is resulted from the ligand-receptor stoichiometry and similar phenomena also exist for receptors. On the other hand, the distribution of cis-interactions is slightly different and no threshold effects were observed (Fig. 4b). For an example, when there are 150 trimeric ligands in the system, the number of trans-interactions is saturated at the value around 450 after the number of receptors reaches 450. In another word, almost all ligands bind to receptors with the stoichiometry of 3:3, and no further trans-interactions can be formed even if the number of receptors further increase.

In contrast, given the same number of trimeric ligands (1 5 0), the number of cis-interactions keeps increasing with the number of receptors, as shown in Fig. 4b. There are 131 cis-interactions attained in the system with 450 receptors, while the number of cis-interactions became 270 in the system with 750 receptors, although the same numbers of trans-interactions exist in both systems. The comparison of their configurations explains the difference. In the first system with 450 receptors, almost all receptors are involved in the trans-interactions, leading into the formation of all complete ligand-receptor complexes with a stoichiometry of 3:3 (Fig. 4e). In the other system, much more receptors are involved in the trans-interactions, leading into the formation of many more incomplete ligand-receptor complexes extensively distributed on the cell surface (Fig. 4f). As a result, more cis-interactions are formed between the receptors in these incomplete complexes. Additionally, since the formation of cis-interactions between two receptors requires that at least one of them are ligand-bound, while there are a large number of monomeric receptors and incomplete ligand-receptor complexes under the conditions of low ligand concentration and high receptor density, the numbers of cis-interactions thus become sensitive to the number of trans-interactions in these systems. For instance, as shown in Fig. 4b, there are 178 cis-interactions attained in the system with 75 ligands and 750 receptors, while the number of cis-interactions reached 269 in the system with 150 ligands and the same number of receptors. Under the conditions of lower receptor densities or higher ligand concentrations, on the other hand, the formation of complete ligand-receptor complexes is saturated. In these systems, the numbers of cis-interactions are not sensitive to the number of trans-interactions, as well as the ligand concentration.

In order to further quantify the spatial patterns of oligomerization, the distributions of average and maximal size of clusters form in different systems are plotted in Fig. 4c and d, respectively. Comparing with the positively correlation between concentrations and numbers of interactions, the figures show very different patterns in distributions of oligomer sizes. Specifically, Fig. 4c suggests that large oligomers can form even in a very low ligand concentration. For instance, a large oligomer containing around 50 proteins was found in the system with 450 receptors and only 75 trimeric ligands, the final configuration of which is shown in Fig. 4g. Surprisingly, based on the measurement of largest and average size of formed oligomers, our simulation results indicate that ligand-receptor complexes cannot effectively organized into spatial pattern under high concentrations, although the numbers of cis-interactions between receptors are large in these systems. Based on the final configuration system with 1200 trimeric ligands and 750 receptors (Fig. 4h), we speculate that after forming lateral interactions, these ligand-receptor complexes are trapped in a crowded environment. The high ligand and receptor concentrations lead to slower diffusions and lower probability for association and dissociation, which makes the oligomerization kinetically inaccessible.

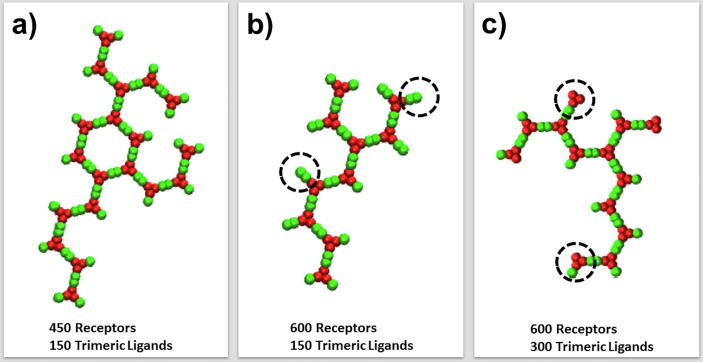
To further explore the mechanism in the dynamic process of oligomerization, we analyzed the detailed structures of all ligand-receptor complexes at the end of each simulation. The specific configurations of some representative oligomers are plotted in Fig. 5 under different ligand concentrations and receptor densities. Given 450 receptors and 150 trimeric ligands in the systems, our results indicate that most oligomers are formed by complexes with an overall ligand-receptor stoichiometry of 3:3. One typical example is shown in Fig. 5a. This is due to the specific ratio between the concentration of ligands and the density of receptors. When the density of receptors further increased, we found that ligand-unbound receptors presented at the edges of most oligomers through the cis-interactions with ligand-bound receptors. One typical example is shown in Fig. 5b, with some ligand-unbound receptors highlighted by dashed circles. We further found that these oligomers were able to keep growing when more ligands formed trans-interactions with the receptors at the edges. When the concentration of ligands reached to a high level, on the other hand, we found that some oligomers are formed by incomplete complexes in the system. One typical example is shown in Fig. 5c, in which the incomplete ligand-receptor complexes are highlighted by dashed circles. Some of these incomplete complexes have ligand-receptor stoichiometry of 3:2, while others have ligand-receptor stoichiometry of 3:1. These oligomers were also able to keep growing when more monomeric receptors joined through the trans-interactions. It is worth mentioning that incomplete complexes were experimentally observed in some systems of TNF superfamily, such as the complex formed between TNF receptor CD40 and its ligand CD154 [56]. Therefore, our simulation results provide evidences that either ligand-unbound TNF receptors or incomplete ligand-receptor complexes can be incorporated into the process of oligomerization through different kinetic pathways.

Fig. 5.

In order to explore the mechanism in the dynamic process of oligomerization, we plotted the specific configurations for some representative oligomers under different ligand concentrations and receptor densities. a) Given 450 receptors and 150 trimeric ligands in the systems, most oligomers are formed by complexes with an overall ligand-receptor stoichiometry of 3:3. b) When the number of receptors in the system increased to 600, we found that ligand-unbound receptors presented at the edges of most oligomers through the cis-interactions with ligand-bound receptors. Finally, c) when the number of ligands increased to 300, on the other hand, we found that some oligomers are formed by incomplete complexes in the system.

Taken together, these results suggest that oligomerization of TNF receptors is a highly sensitive process which can be triggered by introducing a low concentration of ligands. On the other hand, the overexpression of TNF ligands or receptors plays a negative role in regulating oligomerization.

3.3. Understand how binding energies at different interfaces regulate oligomerization

In attempt to further understand how binding stability affect the dynamics of ligand receptor interactions and patterns of oligomerization, we fixed the ligand receptor concentrations and turned the binding affinity into different values. In specific, the binding constants were changed by keeping the on rates as constant at 10⁷M⁻¹s⁻¹ for both trans-interaction and cis-interactions. The values of off rate for trans-interaction were adjusted within the range from 10²s⁻¹ to 6 × 10⁴s⁻¹, while the values of off rate for cis-interaction were adjusted within the range from 10⁰s⁻¹ to 5 × 10⁴s⁻¹. Simulations were carried out for all different combinations of off rates. In all these systems, the number of trimeric ligands was fixed at 150 and the number of receptors was fixed at 450 to avoid further complexity. After the termination of these simulation trajectories at the same time (3.6 × 10⁸ns), we calculated the number of ligand-receptor trans-interactions, the number of receptor-receptor cis-interactions, the average and maximal size of formed oligomers. The distributions of our calculated results are plotted as histograms from Fig. 6a–d. Each bar in the figure was actually based on the average values calculated from the data that were collected within the last 10⁷ns of the corresponding simulation trajectories. The simulations were updated every 5 × 10⁴ns. As a result, the height in the histograms of Fig. 6 corresponds to the statistical average of the last 200 data points along the simulations. All the raw data of the figures can be found from Tables S2-1 to S2-4 in the supporting information.

Fig. 6.

In order to understand how stability of binding affects the dynamics of ligand receptor interactions and patterns of oligomerization, we turned the binding affinity into different values by keeping the on rates of trans and cis interactions as constant and changing their values of off rate. TNF ligands are in their trimeric state. Simulations were carried out for all different combinations. At the end of each simulation trajectory, we calculated and plot the histograms for the distributions of (a) the number of ligand-receptor trans-interactions, (b) the number of receptor-receptor cis-interactions, (c) the average size of formed oligomers, and (d) the largest oligomer found in the system, respectively. We found that large oligomers cannot be derived from the strongest cis-interactions. For instance, we compared the simulations between the weak and strong cis-interactions, but with the same trans-interactions. (e) We plot the configuration with weak cis-interactions (off rate equals 1 × 10³s⁻¹). (f) Under the same trans-interactions (off rate equals 1 × 10²s⁻¹), we plot the configuration with strong cis-interactions (off rate equals 1 × 10⁰s⁻¹).

The distribution for the number of trans-interactions is shown in Fig. 6a. The figure indicates that the number of trans-interactions is largely determined by the strength of ligand-receptor interactions. Stronger trans-interactions lead to more binding between ligands and receptors. However, a closer look at the data reveals the effect of cis-interactions on trans-interactions. In detail, when trans-interactions are not very strong, stronger cis-interactions result in slightly more interactions between ligands and receptors. For instance, when the off rate of trans-interaction equals 5 × 10³s⁻¹, there are on average 239 trans-interactions under a weak cis-interaction (a corresponding high off rate at 5 × 10⁴s⁻¹). Given the same off rate of trans-interaction (5 × 10³s⁻¹), the average number of trans-interactions increases to 265 when the cis-interaction becomes stronger (a corresponding low off rate at 1 × 10⁰s⁻¹). Similarly, when the off rate of trans-interaction equals 1 × 10³s⁻¹, there are on average 373 trans-interactions under a weak cis-interaction (a corresponding high off rate at 5 × 10⁴s⁻¹). Given the same off rate of trans-interaction (5 × 10³s⁻¹), the average number of trans-interactions increases to 382 when the cis-interaction becomes stronger (a corresponding low off rate at 1 × 10⁰s⁻¹). On the other hand, stronger cis-interactions lead to slightly less interactions between ligands and receptors when trans-interactions are strong. For instance, under the lowest off rate of trans-interaction (1 × 10²s⁻¹), there are on average 429 trans-interactions under a weak cis-interaction (a corresponding high off rate at 5 × 10⁴s⁻¹). Given the same off rate of trans-interaction, the average number of trans-interactions first increase to 436 when the cis-interaction becomes stronger (a low off rate at 1 × 10³s⁻¹), but then reduces to 404 when the cis-interaction becomes further stronger (a lower off rate at 1 × 10⁰s⁻¹). This phenomenon is resulted from the oligomerization of ligand-receptor complexes, as we will discuss later.

The distributions for the number of cis-interactions and average size of oligomers formed along simulations are shown in Fig. 6b and c, respectively. These two figures show the similar patterns. Only the systems with both high affinities of cis-interactions and high affinities of trans-interactions obtained a large number of cis-interactions (Fig. 5b). Similarly, the average sizes of oligomers in these systems are also much larger than the systems in which either cis- or trans-interactions are not strong (Fig. 5c). Moreover, as shown in these two figures, almost no cis-interaction and oligomer were observed under weak interactions (high values of cis and trans off rates). However, a small drop in both cis and trans off rates leads to the raise of cis-interactions and the appearance of oligomers, indicating that oligomerization is a phase transition and there are thresholds in both trans and cis interactions to trigger the oligomerization. Interestingly, the distribution of the largest oligomer formed along simulation shows a very different pattern (Fig. 6d), comparing with the average size of oligomers. The figure suggests that large oligomers cannot be derived from the strongest cis-interactions. For instance, when the off rate of trans-interaction equals 1 × 10²s⁻¹, we found a large oligomer containing around 90 proteins given the off rate of cis-interaction equals 1 × 10³s⁻¹. However, given the same off rate of trans-interaction (1 × 10²s⁻¹), the largest oligomer can be found in the system only contain around 35 proteins when the cis-interaction becomes stronger (a corresponding low off rate at 1 × 10⁰s⁻¹). The comparison of final configurations between these two systems is shown in Fig. 6e and f. Our results therefore suggest that the oligomerization is kinetically trapped by the strong trans and cis interactions. Additionally, when the ligands are stuck in these small oligomers due to the strong cis-interactions, they are less likely to encounter with other unbound receptors when the trans-interactions are also strong, which was observed earlier.

The binding affinities of trans-interactions between ligands and receptors of many members in TNFRSF are on the level of nanomolar (nM) [20]. In order to test the receptor oligomerization in this biologically relevant scale, we further decreased the off rate of trans-interactions down to 10⁻²s⁻¹. Keeping the on rates as constant at 10⁷M⁻¹s⁻¹, this gave us a binding affinity of 1 nM. On the other hand, the affinities of cis-interactions were thought to be much weaker than the trans-interactions [19]. Therefore, simulations were carried out for all different cis off rates from 10⁰s⁻¹ to 5 × 10⁴s⁻¹ in the system with 150 trimeric ligands and 450 receptors. As a result, the numbers of cis-interactions and the average sizes of oligomers under different off rates are shown in Fig. S2 and compared between two scenarios: the affinity of trans-interactions equals 1 nM (trans off rate = 10⁻²s⁻¹) and 10 μM (trans off rate = 10²s⁻¹). As shown in Fig. S2a, under strong cis-affinities, the system can obtain more cis-interactions when the trans-interactions are strong (1 nM), relative to the system with weak trans-interactions (10 μM). This result suggests that strong trans-interactions can stimulate the formation of cis-interactions. On the other hand, our simulation results suggest that the average oligomer sizes in the system with strong trans-interactions are smaller than the system with weak trans-interactions (Fig. S2b), indicating that oligomers are kinetically trapped by the strong trans and cis interactions. As a result, the tests on nM level of trans binding affinity are consistent with our observations above. This demonstrates that our simulations are predictive within the biologically relevant range of ligand-receptor binding affinities.

In summary, the simulations illustrated that the spatial organization of complexes between TNF ligands and receptors is fine-tuned by the cooperativity between their trans and cis binding stabilities. This correlation between binding energetics and spatial patterns of oligomerization can be validated by measuring the TNF ligand-receptor binding affinity using experimental techniques such as surface plasma resonance (SPR) [57] and detecting the size of TNFR oligomers using supra-resolution microscopy.

3.4. Investigate how cis-interactions of TNFR monomers regulate oligomerization

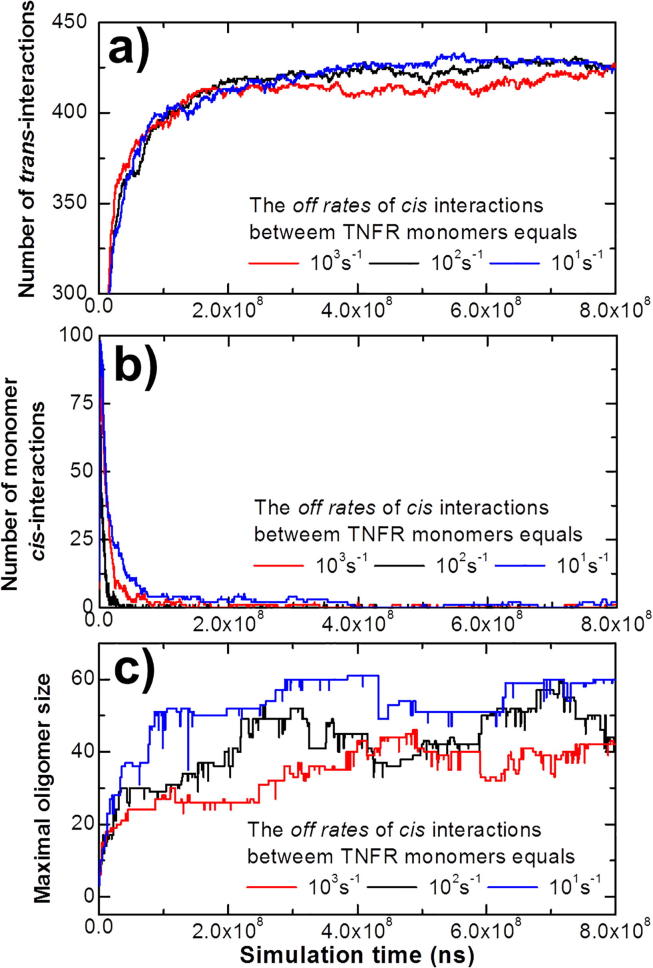
In previous sections we focused on the oligomerization of ligand-receptor complexes by turning off the cis-interactions between ligand-unbound TNFR monomers. However, it has been found that some members of TNFR superfamily, such as TNFR1 and TNFR2, can form dimers on cell surfaces through an additional interface called pre-ligand assembly domain (PLAD) [58]. This preassembly is independent of ligand binding, indicating that the lateral interactions between TNFR monomers exist at least for some members in TNFRSF [18]. However, the mechanism of the preassembly and it function related to the ligand-receptor oligomerization is not clear. Therefore, here we are tackling this problem by turning on the cis-interactions between ligand-unbound TNFR monomers in addition to the cis-interactions between ligand-bound receptor complexes. In detail, three different binding affinities of monomer cis-interactions were tested. The on rates of these interactions were fixed at 10⁷M⁻¹s⁻¹, while the values of off rates were increased from 10¹s⁻¹ to 10³s⁻¹. The number of trimeric ligands was fixed at 150 and the number of receptors was fixed at 450 among all three systems. All other binding parameters, such as on and off rates of trans-interactions (10⁶M⁻¹s⁻¹ and 10²s⁻¹), as well as the cis-interactions between ligand-receptor complexes (10⁶M⁻¹s⁻¹ and 10²s⁻¹), were also set as the same values to avoid further complication. As a result, the kinetics profiles of these three simulation scenarios are plotted in Fig. 7.

Fig. 7.

It has been found that some members of TNFR superfamily can pre-assemble into dimers on cell surfaces prior to their ligand binding. In order to understand the mechanism and functions of this pre-assembly, we turned on the cis-interactions between ligand-unbound TNFR monomers in addition to the cis-interactions between ligand-bound receptor complexes. As a result, three different binding affinities of monomer cis-interactions were tested and all other parameters were fixed in these three systems. In (a), we plot the number of trans-interactions formed in these three simulation scenarios. In (b), we plot the number of cis-interactions between monomeric receptors formed in these three simulation scenarios. In (c), we plot the largest size of oligomer formed in these three simulation scenarios.

Overall, the figure shows that the numbers of trans-interactions in all three conditions increase and reach equilibrium after 3 × 10⁸ns (Fig. 7a). The numbers of cis-interaction between unbound receptor monomers, on the other hand, increase at the very beginning of the simulations due to their higher on rate, but then drop very fast before 1 × 10⁸ns (Fig. 7b). At the meantime, the oligomers grow with a much slower kinetics (Fig. 7c). By comparing the detailed kinetics among three systems, we further found some more interesting behaviors. For instance, the numbers of trans-interactions with the strongest monomer cis-interactions (blue curve in Fig. 7a) grows more slowly at first, comparing with the system with the weakest monomer cis-interactions (red curve in Fig. 7a). However, the system with the strong monomer cis-interactions can form larger number of trans-interactions after equilibrium than the system with relatively weaker monomer cis-interactions. Correspondingly, if the cis-interactions between TNFR monomers are stronger, their number will drop more slowly than the systems with weaker monomer cis-interactions, as shown in Fig. 7b.

These results indicate the competition between trans-interactions and monomer cis-interactions along the simulations. Similar as the previous experimental observation, TNF receptors are preassembled into dimers before they bind to their extracellular ligands. These cis-dimers between TNFR monomers are later competed over by the ligand binding and the ligand-receptor complexes start to form oligomers. Receptors with strong monomer cis-interactions are more competitive against the trans-interactions. Surprisingly, the simulation results suggest that the stronger competition with the ligands can lead to a higher number of trans-interactions. We speculate that this phenomenon is caused by the fact that dimeric TNFR are kinetically less accessible to trimeric ligands than the more mobilized monomeric TNFR, but thermodynamically more stable after ligand binding. More interestingly, Fig. 7c shows that the stronger monomer cis-interactions can not only result in larger oligomer size, but also can accelerate the kinetics of oligomerization. We assume the underlying mechanism is that lateral interactions between monomeric receptors can serve as the initial seeding for oligomerization.

Based on these simulation results, we thus propose that TNF receptors can be pre-organized into dimers before ligand binding. These lateral interactions between receptor monomers play a positive role in stabilizing the ligand-receptor interactions, as well as in regulating the kinetics of receptor oligomerization. Our computational hypothesis can be experimentally justified by carrying out mutagenesis studies on PLAD region in TNFR receptors and testing the effect of these mutations on ligand binding and oligomerization.

4. Concluding discussions

Members of proteins that belong to the TNF superfamily are expressed predominantly by immune cells and function as a cytokine [59]. They trigger the signaling pathways in diverse cell functions, including inflammation, proliferation, and apoptosis, by recognizing the specific members of cell surface proteins in TNFR superfamily [3]. Almost all TNF superfamily ligands exist as homo-trimer and thus can simultaneously bind to three receptors on cell surfaces [12]. By forming these ligand-receptor complexes, it was found that they can further form oligomers using different experimental techniques. Here we developed a new computational model to simulate the dynamic process of TNF receptor oligomerization and try to understand its underlying mechanisms. The model is specifically designed for the biological system in which each subunit in the TNF ligand trimer and each CRD domain in the TNF receptor are spatially distinguishable to implant the basic structural information in the simulations. Binding interfaces are further assigned on the surfaces of each subunit in ligands or domain in receptors to guide the trans-interactions between ligands and receptors or cis-interactions between two receptors. Starting from the initial configuration with a large number of ligands and receptors randomly distributed in a subcellular environment, the dynamics of the system can be evolved through a diffusion-reaction simulation strategy. We explored a large variety of simulation conditions such as concentration or binding energetics, and showed that the ligand-receptor complexes under different conditions can be spatial-temporally organized into distinctive patterns, such as the average and maximal sizes of oligomers. These spatial patterns play important functional roles in regulating the intracellular signal transduction. For instance, after the clustering of the signaling complexes, they provide transient compartmentalization to the cytoplasmic domains of TNF receptors, which greatly enhances the efficiency of intracellular signaling processes due to the spatial proximity [60], [61]. As a result, the distribution of oligomers in size and space quantitatively modulate the kinetics and strength of signals transferred to the downstream pathways. Therefore, our computational results give insights to the cellular functions of protein-protein interactions in TNF and TNFR superfamily.

Our study also sheds lights on the likely mechanism of interplay between trans and cis-interactions in shaping the dynamics of TNF receptor oligomerization. Under the same binding constants, we compare the number of trans-interactions in the system with cis-interactions between ligand-bound receptors with the systems without cis-interactions. The statistical analysis of our simulation results indicates that the number of trans-interactions in the first system grows more slowly but reaches a higher level with lower fluctuations than the second system. This dynamic behavior suggests that the binding kinetics of trans-interactions is modulated by the cis-interactions between ligand-bound receptors. More specifically, we propose that through the formation of lateral oligomers, the ligand-receptor interactions can be stabilized. Furthermore, after we turned on the cis-interactions between monomeric receptors, we found that these receptors monomers are preassembled into dimers before they bind to their extracellular ligands. Consequently, the stronger competition between trans-interactions and monomer cis-interactions can not only result in larger oligomer size, but also can accelerate the kinetics of oligomerization. The mechanisms underlying these observations have been proposed in the results.

On the other hand, the cis-interactions can also be affected by the status of trans-interactions. As shown in the results, we started our simulations of ligand-receptor oligomerization by only considering the cis-interaction between ligand-bound receptors. This simplification is based on the assumption that the trans-interactions between receptors and ligands can improve the association rate of the cis-interactions between receptors by eliminating the potential conformational fluctuations in the monomeric receptors and thus decreasing the entropy loss upon the formation of cis-interactions. The similar mechanism in which the cis-interactions are enhanced by trans-interactions was also previously proposed in the cadherin-mediated junction formation [55]. However, more quantitative estimations about the amplitude of conformational fluctuations in the monomeric receptor and how much flexibility will be eliminated after trans-interaction are beyond the scope of this work. They will be carried out in the future by implementing the higher resolution structure-based simulation methods, such as atomic level molecular dynamic simulations [62]. Additionally, the binding parameters of trans and cis interactions were taken from a wide range of rate constants with biological relevance. To evaluate the kinetics of oligomerization for a specific system in the future, these binding rates can be calculated by simulation methods with higher resolution. For instance, physical-based scoring functions were used to simulate the association between two proteins with residue-based representation in our recently developed method [63]. The estimated binding rates calculated from these methods can then be fed back into the current model to guide the simulations of oligomerization [64].

In the current model, TNFs are presented as soluble ligands in the extracellular area, while TNFRs are confined on cell surfaces. This scenario is based on the fact that most TNF ligands are type II transmembrane proteins and become functional by releasing from the cell membrane after extracellular proteolytic cleavage. Under certain circumstances, however, TNF receptors can be only recognized by, or react differently to membrane-bound ligand trimers. For instance, it was found that membrane-bound TNFα can exert opposing effects on tumor growth from its soluble isoform [65]. Similarly, it has been shown that some ligands in TNF superfamily, such as CD40L, don’t fully activate cells as soluble trimers at any concentration [66]. These differences could be caused by the fact that the differences in diffusions of TNF ligands on cell surfaces from the diffusions of soluble ligands might lead to different dynamics of receptor oligomerization. On the other hand, the genes of some members in TNFRSF do not encode transmembrane and cytoplasmic segments, and thus produce as soluble forms. For an example, the decoy receptor 3 (DcR3) is secreted as a soluble molecule and functions as a decoy to compete with other TNFRs for ligand binding [67], [68]. This decoy receptor is highly elevated in patients with various tumors [69]. Different from normal membrane-bound receptors with binding specificity, it can bind to a wide spectrum of TNF ligands and prevent them from binding to their own receptors, thus provide the opportunity that tumor cells evade host immune surveillance. The simulations of these special cases for membrane-bound TNF ligands or soluble TNF receptors can be easily implemented in the future to understand their biological implications.

The computational model developed for TNF and TNFR superfamily can be generalized to study the spatial organization in many other membrane receptor systems. A common feature of these receptors is that their extracellular regions can be divided into multiple copies of different domains. The ligands of these receptors, on the other hand, are usually organized into multivalent complexes. As a result, ligand binding causes the assembly of receptors into high-ordered molecular architecture on cell surfaces, as observed in various examples. One typical case is epidermal growth factor receptor (EGDR). Its extracellular region comprises 4 domains, while its ligand epidermal growth factor (EGF) is naturally dimerized [70]. Ligand binding further induces EGFR oligomerization, which in turn organizes kinase domains of the receptor into competent signaling platforms [71]. Another example is the interactions between the multivalent binding sites in extracellular matrix (ECM) and integrin, which results in its clustering as a trigger for focal adhesion [72]. The domain-based model developed in this study can be applied to these systems as a natural extension. However, it was discovered that the ligand binding can induce a large conformational change in the complex of EGFR, comparing with its monomer [73]. The effect of conformational dynamics between different domains in a receptor is not considered in current model. Therefore, in the future, more specific information about structural fluctuations in ligands and receptors can be achieved by higher-resolution simulation methods such as molecular dynamics simulations or Langevin dynamic simulation [74]. These data can be fed into the current rigid-body based model by the further development of a multi-scale framework.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Appendix A. Supplementary data

The following are the Supplementary data to this article: