Abstract
This paper investigates the need to use stems in conjunction with cementless metaphyseal sleeves in total knee replacement (TKR) to treat cavity type-3 defects. Finite element models of TKR with type-3 defects of two sizes were modelled with and without stems. The use of sleeves result in stress concentrations at the bone/sleeve interface. The use of stems shows a reduction in these stresses but also an increased risk of bone resorption in the proximal tibia. Based on this investigation the authors recommend that stems are not required in TKR with cementless metaphyseal sleeves.
Keywords: Metaphyseal sleeves, Finite element analysis, Total knee replacement
1. Introduction
Current revision rates for total knee replacement have been estimated to be 8.1%.1 The presence of large cavity tibial defects in primary and revision knee arthroplasty can pose a threat to tibial prosthesis stability. Type-3 defects refer to large damage to proximal metaphyseal bone usually below the level of the tibial tubercule, with damage being either unicondylar or bicondylar, classified as type-3A and type-3B defects respectively. These defect types are usually treated with metaphyseal sleeves (see Fig. 1), cones, bone graft, cement, cement and screws or a hinge prosthesis.2,3 To ensure correct tibial component fixation and alignment it is important to take corrective measures to ensure a stable platform for the implanted prosthesis and prevent loosening of the prosthesis by choosing an appropriate method to fill the defect. Types of cones manufactured by Zimmer® include step cones where the tibia has a larger defect on one side and full cones where there is symmetric loss of bone in the tibia.4 Metaphyseal Sleeves (manufactured by DePuy Synthes, Warsaw IN, USA) vary by size but are composed of a stepped, conical profile. Historically they have been used in modular hinge implants but more recently they have been used in less constrained prostheses such as the modular-bearing rotating platform revision knee system (Sigma Revision System, DePuy Synthes, Warsaw IN, USA).5
Fig. 1.

Large metaphyseal sleeve (DePuy Synthes, Warsaw, IN).
Alexander et al., 2013 examined the use of the DePuy Synthes metaphyseal sleeve (Sigma TC3 prosthesis – implanted as cementless) in a clinical study of 30 patients with type 2B and type 3 defects.6 Minimum follow up was 2 years with radiographs at follow up showing good sleeve fixation with bone in-growth. Chalmers et al., 2017 examined the use of the metaphyseal sleeve (both cemented and cementless sleeves) in a 5-year follow up study and found a survivorship rate (i.e. free from aseptic loosening) of 96% and 99.5% in femoral and tibial sleeves respectively.7 Similarly, Watters et al., 2017 in a mean-follow up of 5.3 years found a 98.5% survivorship with no cases of revision for aseptic loosening, excellent osteointegration and fixation.8
Quílez et al. 20159 conducted an FE study of a single size sleeve with and without a stem and analysed the bone density changes after a period of 300 days simulation. Their findings included that the use of a metaphyseal sleeve generates less bone resorption when used without a stem.
This study outlines a 3D FE study of mobile tray TKR models with cementless metaphyseal metal sleeves to treat contained AORI type-3 defects. Clinical applications using metaphyseal sleeves have generally been carried out in conjunction with stems (both cemented and press-fit) and have been used in both primary and revision studies. The difficulty with the use of sleeves can be in their placement and hence the use of a stem can aid the surgeon in desired placement.10 The use of stems in primary surgery can pose problems should revision surgery become necessary due to stem removal difficulties. Therefore, the use of metaphyseal sleeves without stems is an option that should be considered. A standard tibial TKR model (i.e. non-defect) was also included in this study as a reference against which stresses produced in the metaphyseal sleeve models could be compared. Two metaphyseal sleeves of different sizes were examined in this study and these were modelled with and without a press-fit stem to assess the necessity of using stems with metaphyseal sleeves and their effect on cancellous bone stresses. Stresses in the metaphyseal sleeves were also examined.
2. Materials and methods
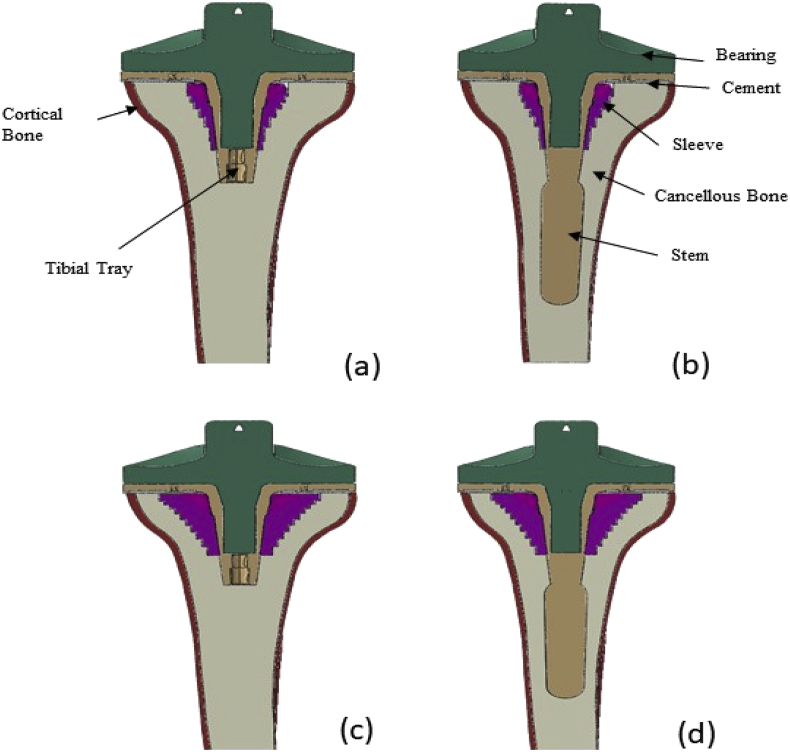
Three dimensional, static, FE models of the proximal tibia implanted with a mobile bearing revision tray using ABAQUS 6.7 (Simulia, Warrington, UK) were created. Four models were produced which represent the TKR with contained type-3 cavity defects of two sizes, both with and without a press-fit stem. A fifth model of a tibial TKR containing no defects was also produced – hereby referred to as the standard non-sleeve model. A 1.5 mm thick cement layer was used to fix the tibial tray underside to the resected surface. The metaphyseal sleeve was used to create a matching cavity in the resected tibia. The tray, stem (where applicable), sleeve and the cement were assembled into the tibia. The models are hereby referred to as the small metaphyseal standard (SMS), small metaphyseal press-fit stem (SMP), large metaphyseal standard (LMS) and large metaphyseal press-fit stem (LMP) models (see Fig. 2). The geometry of the native tibial bone was acquired from a previous study of the authors.11 The cortical bone was modelled as a 2 mm thick layer surrounding the cancellous bone (see Fig. 2). The value of the proximal cortical bone thickness is consistent with an image of a tibia proximally sectioned for a TKA.12 In practice, the thickness increases distally but it was felt important to reflect the thickness in the proximal region of the tibia as this is the key region of interest. The material properties used for each part are shown in Table 1. It was assumed that all parts were isotropic, homogenous and linearly elastic although the analysis was non-linear due to the contact modelling. The modulus of the cortical bone has been used by Nyman et al.13 and is within the range of moduli cited and used by other authors. Au et al.14 cite a range of modulus values for cancellous bone (389–1132 MPa) and cortical bone (12000–19600 MPa) and the uniform values used in the current study are well within this range.
Fig. 2.
Section cut in the frontal of the (a) SMS, (b) SMP, (c) LMS and (d) LMP TKR models.
Table 1.
Material properties used in TKR model.22
| Material | E (GPa) | υ |
|---|---|---|
| Cancellous | 0.7 | 0.3 |
| Cortical | 17 | 0.3 |
| PMMA (Cement) | 2.27 | 0.46 |
| Ti4Al6V (Stems and metaphyseal sleeve) | 110 | 0.3 |
| UHMWPE (Bearing) | 2.3 | 0.25 |
All elements used were quadratic solid 10 node tetrahedral elements. A mesh convergence study was undertaken to ensure a sufficient number of elements (e.g.171,586 elements were used in the SMS model) were used in the models. Comparable mesh sizes were used in all models (see Fig. 3). Although a comparison was not made between predicted and measured bone strains in this study such a comparison has been undertaken by Completo et al.15 The mesh used in this study, employing quadratic elements, is considered more accurate than that used by Completo et al. who used linear elements. This provides further confidence of the mesh used in this study.
Fig. 3.
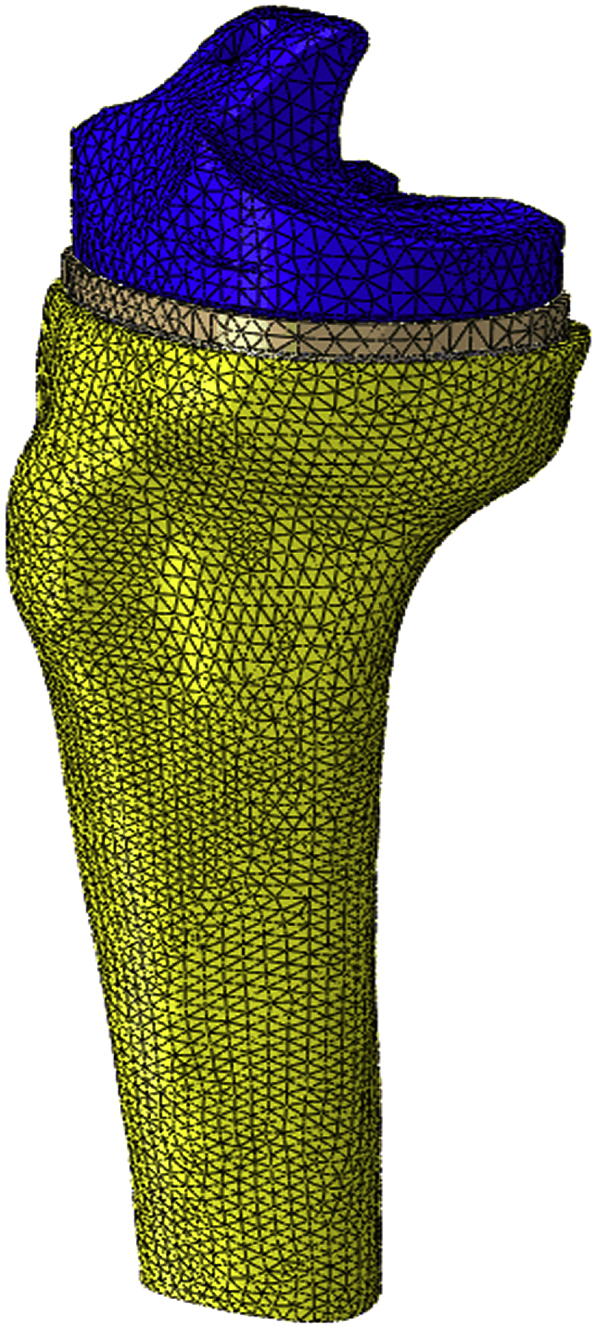
TKR model meshed assembly.
The contact between the mobile bearing and tibial tray was modelled using a surface-to-surface contact algorithm and a constant coefficient of friction of 0.1 in all models, as used by Villa et al.16 on exactly the same mobile bearing tray implant system. In their study they undertook detailed experimental in-vitro measurements of the contact area and pressure distribution which showed excellent correlation with the associated FE modelling with a coefficient of friction of 0.1. Relative movement was allowed between the press-fit stem contacting surfaces (i.e. stem and bone). Contact between the cancellous bone and the stem was also modelled using a surface-to-surface contact algorithm and a constant coefficient of friction of 0.25 as used by Completo et al.17 To support this value Completo et al. cite experimental measurements of this value and further show an excellent regression fit between in-vitro measured and FE calculated tibial strain distribution. No other relative motion was allowed between adjoining parts as tied contact was applied to these. In practice the metaphyseal sleeve contains a porous coated surface which promotes bony ingrowth which holds the sleeve in place. The models detailed in this paper assume that this bony ingrowth provides full fixation of the sleeve to the bone and thus is modelled using tied contact. On the other hand, the stem does not have such a bone ingrowth promoting surface finish and this is the reason that friction conditions were used to model the surface contact between the stem and the bone.
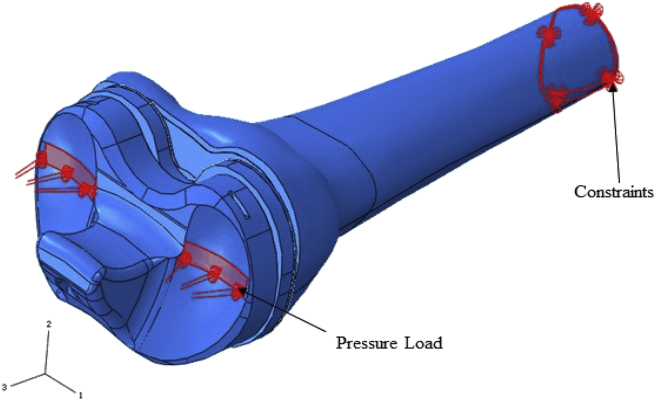
Loading was applied as a uniform pressure load to selected surfaces of the bearing where the medial and lateral femur condyles would make contact. The load application region (see Fig. 4) and values used were based on the conditions that occur in late stance phase of gait where maximum joint reaction occurs.18 This is the phase of the gait that will produce highest stresses in the proximal bone and the sleeve. The gastrocnemius muscle is the only active muscle at this late stance phase of gait. As the gastrocnemius muscle does not attach to any region of the proximal tibia, it was not necessary to include any ligaments or muscles in the models. The effect of the gastrocnemius however is represented in the applied joint reaction force. Traditionally the loads applied to the knee to represent level gait in FE modelling have been between 2.5 and 3 times body weight. These data have been based on developments of the knee biomechanics developed by Morrison.18 More recently, somewhat lower levels of loading (2.2 times body weight) have been actually measured in-vivo19 and thus the authors considered it more appropriate to use these loads. Thus, a total load of 1618 N (representing a 75 kg person) was used in this study. In all models the distal end of the tibia was assumed to be constrained in all directions (see Fig. 4) and the total load was applied in a 50:50 ratio between the medial and lateral condyles. The pressure load application areas were determined from the work of Villa et al.16 who evaluated contact locations using Fuji Prescale pressure-sensitive films and in-vitro TKR models. These pressure distributions were fairly consistent with the distributions computed from the in-vivo data by Zhao et al.19 at the same phase of the gait cycle.
Fig. 4.
TKR model assembly showing pressure load applied and constraints.
In order to verify the load transfer between the different components, the axial loads carried by each component were plotted at 4 mm increments from the proximal bone cut. These values were plotted for each component in all models. The equivalent stresses of the cancellous bone in all models were examined to determine if the size of sleeve used and the absence of a stem (as stems typically reduce proximal bone stresses) was likely to result in the increased likelihood of bone failure due to increased stresses. A conservatively low value for damage stress (2.8 MPa, equivalent to 4000 με for the cancellous modulus used in this study) was adopted.20 Cancellous bone stresses were also examined to assess whether reduced stresses might lead to bone resorption. A resorption threshold of 0.1 MPa (equivalent to about 150 με) was adopted.20 Also, the stresses in the sleeve parts were examined to determine how these stresses compare with their respective material fatigue endurance limits, as shown in Table 2.
Table 2.
Fatigue strength values of materials used.22
| Material | Fatigue Endurance Limit (@107 cycles) |
|---|---|
| Ti6Al4V | 510 MPa |
| Bone Cement | 8.1 MPa |
3. Results
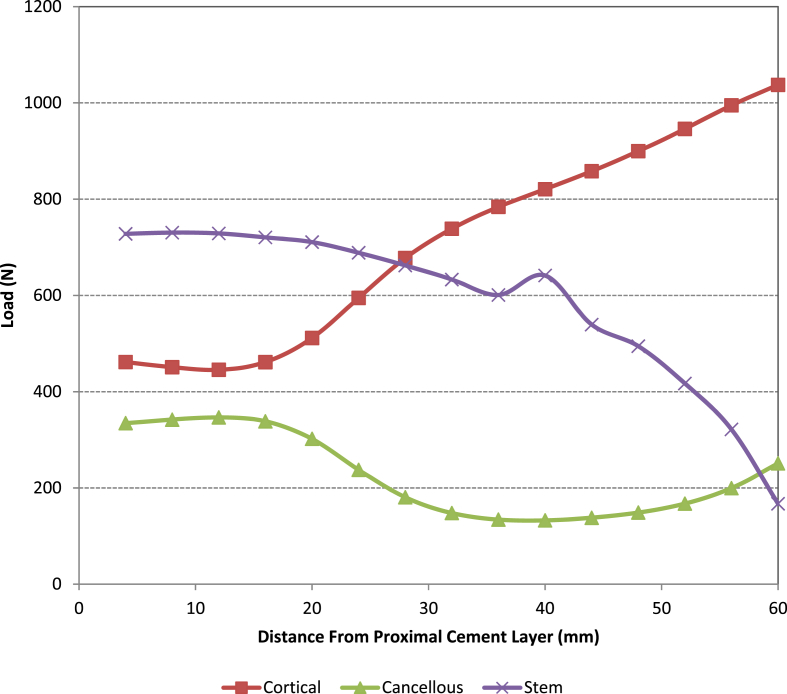
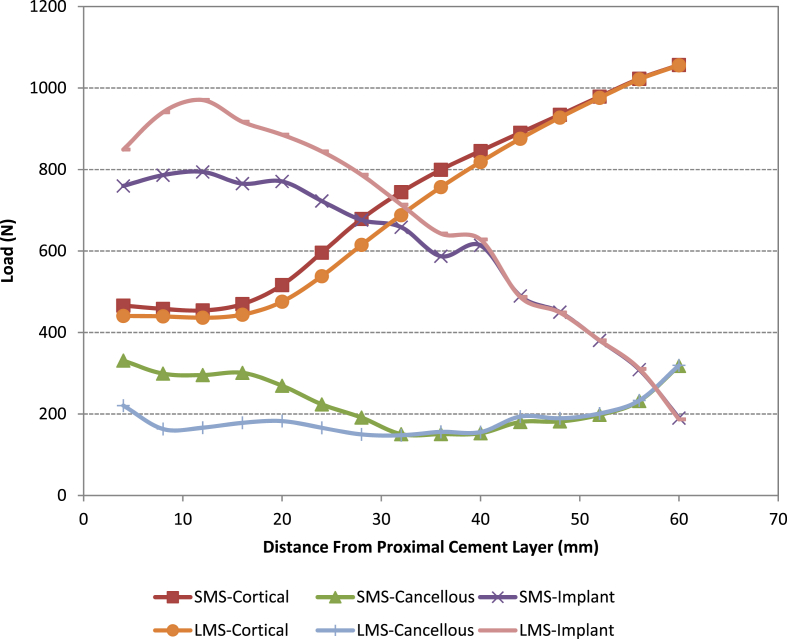
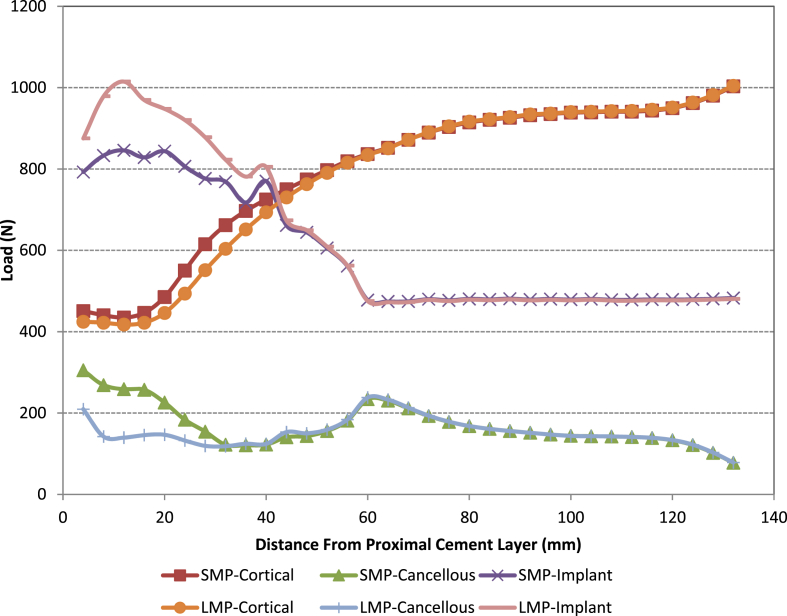
When analysing the load sharing (see Fig. 5, Fig. 6, Fig. 7) by each of the parts in all the models it was found that the loading taken by the cancellous bone is significantly reduced when using the large metaphyseal sleeve compared with the small metaphyseal sleeve or when no sleeve is present (standard non-sleeve model). This is primarily because the sleeve “replaces” the cancellous bone. In all four models the amount of load taken by the cement was negligible and thus is omitted from the figures. The use of a stem reduces the load taken by the cancellous bone proximally (the load being taken up by the stem/sleeve) in both the small and large metaphyseal models (particularly in the region close to the base of the original tibial stem i.e. 60 mm from resection cut). This is more noticeable in the large metaphyseal model. As might be expected, significantly more load is taken by the stem/sleeve in the LMS model compared with the SMS model.
Fig. 5.
Load distribution along the z-axis in the standard non-sleeve model.
Fig. 6.
Load distribution along the z-axis in the SMS and LMS models.
Fig. 7.
Load distribution along the z-axis in the SMP and LMP models.
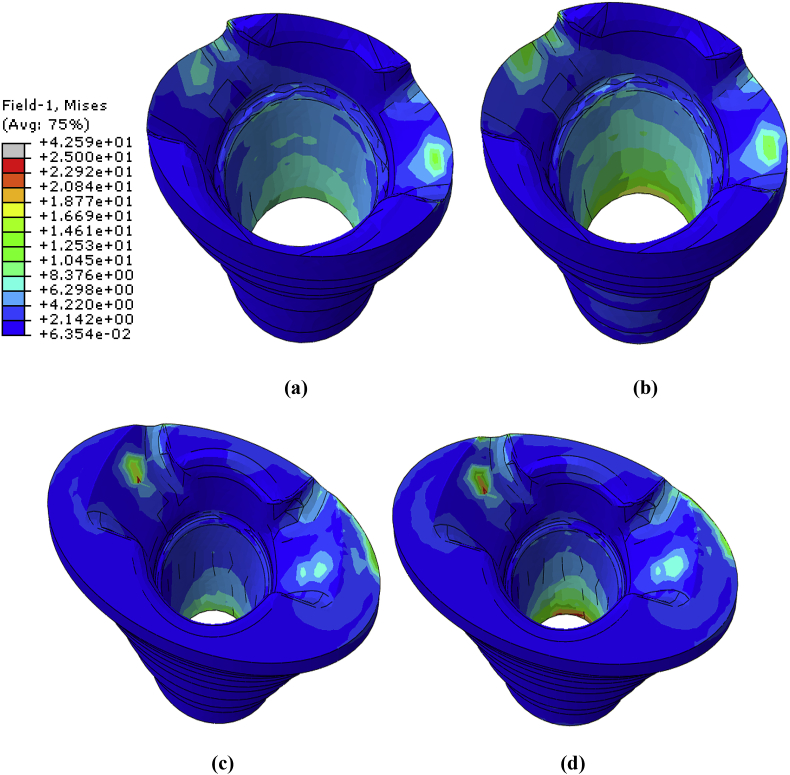
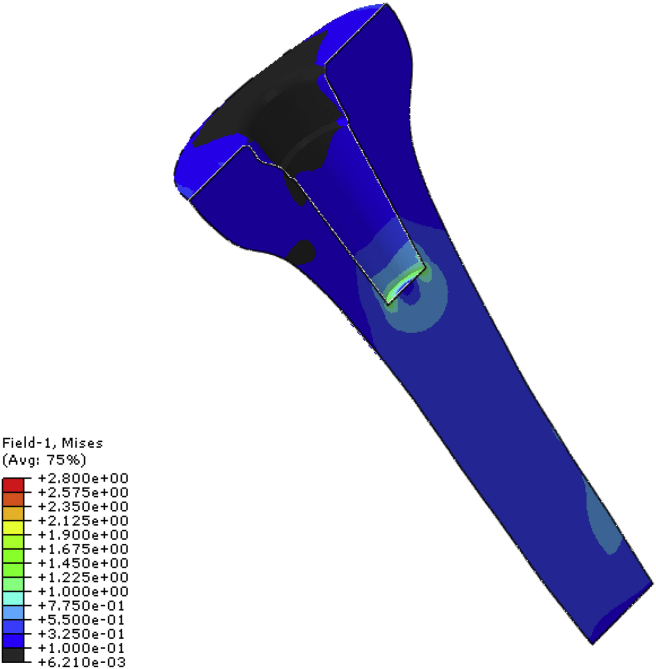
Fig. 8 shows the von Mises stress distribution in the small and large metaphyseal sleeves. The stresses (~13–20 MPa) do not exceed those of the endurance limit of the titanium alloy used (i.e. 510 MPa for 10 million cycles). Stress concentrations were found at the base of the sleeve component in all the models. These stresses were higher in the SMP and LMP models compared with the SMS and LMS models respectively. This is probably due either to the additional bending moment that occurs with the stem (and hence higher sleeve stresses) or that the stem and cone carry more load (see Fig. 8, Fig. 9).
Fig. 8.
Von Mises stress distribution of the metaphyseal sleeve used for (a) SMS (b) SMP (c) LMS and (d) LMP models.
Fig. 9.
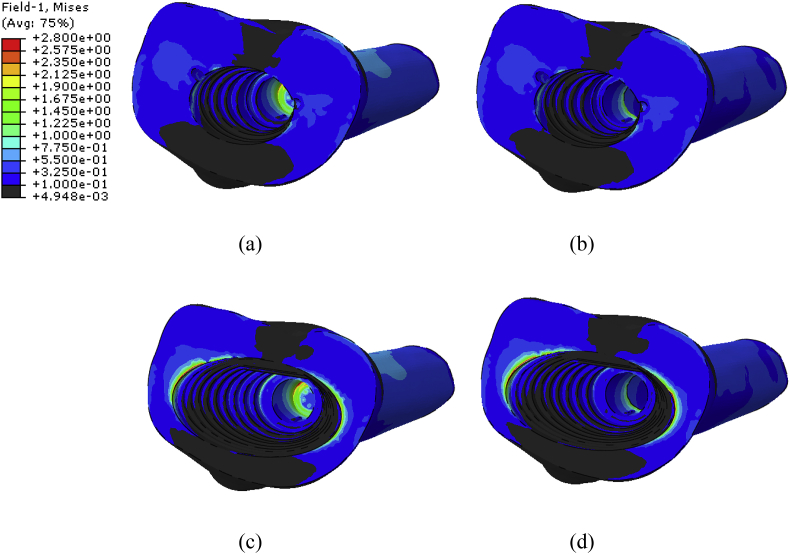
Von Mises (proximal view) stress distribution of the cancellous bone for (a) SMS (b) SMP (c) LMS (d) and LMP models.
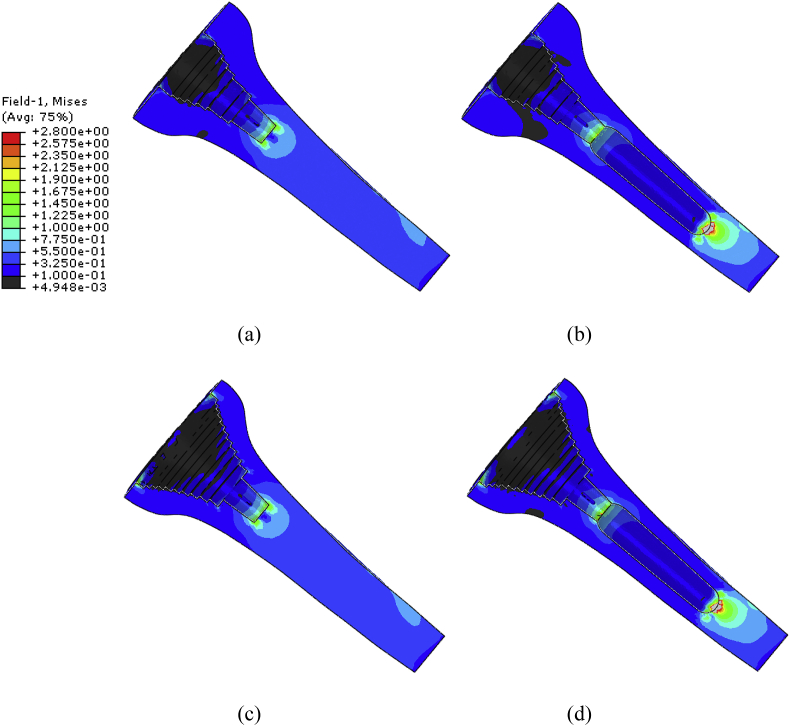
Fig. 10, Fig. 11 give two views of the stresses in the cancellous bone. Bone in the lowest contour band has stresses below the threshold for bone resorption (0.1 MPa, 150 με) and can be considered as a region of potential bone loss. Bone in the highest contour band has stress in excess of the conservative threshold used for bone damage by overloading (2.8 MPa, 4000 με) and can be considered as regions of potential overloading failure. However, when considering these results, it should be noted that an extremely conservative threshold has been used for bone overloading, as values of up to 20,000 με can be found in the literature.
Fig. 10.
Von Mises (section view) stress distribution of the cancellous bone for (a) SMS (b) SMP (c) LMS and (d) LMP.
Fig. 11.
Von Mises stress distribution of the cancellous bone for the standard non-sleeve model.
Considering first the effect of the sleeve size, Fig. 10, Fig. 11 show that the larger sleeve causes larger regions of potential bone resorption. It can also be seen that very proximally the addition of the stem does not significantly increase this. However, moving towards the cancellous bone adjacent to the distal end of the metaphyseal sleeve it can be seen that the stem increases the stress shielding (i.e. lowers the cancellous stresses).
Regions of high cancellous bone stresses in the models without stems are localised in small regions at the base of the stem and, for the larger sleeve, on the resected surface adjacent to the medial and lateral sides of the sleeve. In these regions the stresses only just exceed the conservative damage by overload threshold. There are small concentrations of stress at each of the steps of the sleeve, but the level of stress is lower than the other locations cited. Thus, failure in this mode is unlikely, but the larger sleeve is the more critical. Adding a stem does not reduce the very proximal high stress region but slightly reduces the high stresses at the tip of the stem. However, this is achieved at the cost of even larger regions of bone prone to damage by overload occurring at the tip of the stem.
4. Discussion
It is suggested that as the use of a stem is i) likely to lead to modest increases in potential bone resorption and ii) does little to reduce the high stresses in the tray region and iii) increases the clinical complexity; then the metaphyseal sleeves should be used without a stem unless there are other mitigating factors to take into account. In a recent in-vitro study Nadorf et al.21 found reduced micro-motions when using a metaphyseal sleeve with a stem compared to that of no stem and hypothesized that this may contribute to proximal stress shielding. However, it should be noted that this is a preliminary finding based on a number of limitations and simplifications for a comparative study. These include the assumption of a uniform thickness of cortical bone, the homogeneity of the cancellous bone, the simulation of only one loading scenario and only one bone specimen geometry. Also the material properties chosen for bone in this study represent those of healthy human bone which is unlikely to be the case with a sleeved TKR. Thus the findings of this research will need to be validated using bone models which take into account the limitation factors listed above. These factors are the subject of current research where the FE model has been reconstructed from CT images and the effect of these limitations will be assessed when this ongoing research is completed.
It is informative to compare the cancellous bone stresses from the sleeve models with those from a non-sleeve, TKR of the same geometry, which can be seen in Fig. 11. It can be seen that the stresses are quite similar. In the non-sleeve model there is a slightly smaller region of bone that might be prone to resorption and the stresses at the stem tip are slightly smaller. The metaphyseal sleeve appears to shift the load distribution distally and this effect is greatest with the largest sleeve. As it is widely accepted that standard TKRs have good short and long-term stability in clinical practice these stresses are representative of stresses which are unlikely to cause instability or loosening of prosthesis. The match between the stresses in the sleeve and non-sleeve models is further indication of the stability of the metaphyseal sleeve, without the need for a stem.
5. Conclusion
Due to the nature of the geometry of metaphyseal sleeves, their usage in TKR has been shown to produce stress concentrations at various bone/sleeve interfaces and at the stem tip in the FE study outlined above. These stress concentrations are however not considered to pose a threat to prosthesis stability. There is evidence that the inclusion of a press-fit stem has the capability to reduce some of these stress concentrations (but not the ones on the resected surface). However there is a tendency for the stem to promote more resorption in the cancellous bone adjacent to the sleeve. Thus this study does not present any reason to justify the use of stems in treating type-3 defects with metaphyseal sleeves. In some clinical cases proximal defects may be uncontained with large amounts of damage to the cortical bone. In these cases the use of a stem may be considered necessary to support the metaphyseal sleeve. The findings in this study are preliminary and it is recommended that a more refined programme of modelling with a more realistic distribution of cancellous bone properties be undertaken to provide further clarification.
Smaller metaphyseal sleeves are also recommended where possible (however they may not be feasible depending on defect size) as these produce lower stress concentrations immediately distal of the sleeve in the proximal cancellous bone and on the resected surface. Overall large metaphyseal sleeves also produce a more significant stress shielding effect in the very proximal cancellous bone and thus should also be avoided where possible.
Funding
This study was supported by the Engineering and Physical Sciences Research Council (EPSRC) and DePuy International Ltd.
References
- 1.Agarwal S., Neogi D.S., Morgan-Jones R. Metaphyseal sleeves in revision total knee arthroplasty: minimum seven-year follow-up study. The Knee. 2018;25(6):1299–1307. doi: 10.1016/j.knee.2018.09.010. [DOI] [PubMed] [Google Scholar]
- 2.Dalury D.F., Barrett W.P. The use of metaphyseal sleeves in revision total knee arthroplasty. The Knee. 2016;23(3):545–548. doi: 10.1016/j.knee.2016.02.005. [DOI] [PubMed] [Google Scholar]
- 3.Radnay C.S., Scuderi G.R. Management of bone loss: augments, cones, offset stems. Clin Orthop Relat Res. 2006;446:83–92. doi: 10.1097/01.blo.0000214437.57151.41. [DOI] [PubMed] [Google Scholar]
- 4.Lachiewicz P.F., Bolognesi M.P., Henderson R.A., Soileau E.S., Vail T.P. Can tantalum cones provide fixation in complex revision knee arthroplasty? Clin Orthop Relat Res. 2012;470(1):199–204. doi: 10.1007/s11999-011-1888-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Bugler K.E., Maheshwari R., Ahmed I., Brenkel I.J., Walmsley P.J. Metaphyseal sleeves for revision total knee arthroplasty: good short-term outcomes. J Arthroplast. 2015;30(11):1990–1994. doi: 10.1016/j.arth.2015.05.015. [DOI] [PubMed] [Google Scholar]
- 6.Alexander G.E., Bernasek T.L., Crank R.L., Haidukewych G.J. Cementless metaphyseal sleeves used for large tibial defects in revision total knee arthroplasty. J Arthroplast. 2013;28(4):604–607. doi: 10.1016/j.arth.2012.08.006. [DOI] [PubMed] [Google Scholar]
- 7.Chalmers B.P., Desy N.M., Pagnano M.W., Trousdale R.T., Taunton M.J. Survivorship of metaphyseal sleeves in revision total knee arthroplasty. J Arthroplast. 2017;32(5):1565–1570. doi: 10.1016/j.arth.2016.12.004. [DOI] [PubMed] [Google Scholar]
- 8.Watters T.S., Martin J.R., Levy D.L., Yang C.C., Kim R.H., Dennis D.A. Porous-coated metaphyseal sleeves for severe femoral and tibial bone loss in revision TKA. J Arthroplast. 2017;32(11):3468–3473. doi: 10.1016/j.arth.2017.06.025. [DOI] [PubMed] [Google Scholar]
- 9.Quílez M.P., Pérez M.A., Seral-García B. Biomechanical study of the tibia in knee replacement revision. Rev Española Cirugía Ortopédica Traumatol. 2015;59(5):365–371. doi: 10.1016/j.recot.2014.12.003. [DOI] [PubMed] [Google Scholar]
- 10.Graichen H., Scior W., Strauch M. Direct, cementless, metaphyseal fixation in knee revision arthroplasty with sleeves – short term results. J Arthroplast. 2015;30(12):2256–2259. doi: 10.1016/j.arth.2015.06.030. [DOI] [PubMed] [Google Scholar]
- 11.Frehill B., Crocombe A.D., Agarwal Y., Bradley W.N. Finite element assessment of block augmented total knee arthroplasty. Comput Methods Biomech Biomed Eng. 2015;18(15):1726–1736. doi: 10.1080/10255842.2014.948429. [DOI] [PubMed] [Google Scholar]
- 12.Brigstocke G., Agarwal Y., Bradley N., Frehill B., Crocombe A. Finite element analysis of cement shear stresses in augmented total knee replacement. J Bone Jt. Surg. 2012;94-B(Supp 29):59. [Google Scholar]
- 13.Nyman J.S., Hazelwood S.J., Rodrigo J.J., Martin R.B., Yeh O.C. Long stemmed total knee arthroplasty with interlocking screws: a computational bone adaptation study. J Orthop Res. 2004;22(1):51–57. doi: 10.1016/S0736-0266(03)00159-1. [DOI] [PubMed] [Google Scholar]
- 14.Au A.G., Liggins A.B., Raso V.J., Amirfazli A. A parametric analysis of fixation post shape in tibial knee prosthesis. Med Eng Phys. 2005;27(2):123–134. doi: 10.1016/j.medengphy.2004.09.010. [DOI] [PubMed] [Google Scholar]
- 15.Completo A., Fonseca F., Simões J. Finite element and experimental cortex strains of the intact and implanted tibia. J Biomech Eng. 2007;129(5):791–797. doi: 10.1115/1.2768382. [DOI] [PubMed] [Google Scholar]
- 16.Villa T., Migliavacca F., Gastaldi D., Colombo M., Pietrabissa R. Contact stresses and fatigue life in a knee prosthesis: comparison between in vitro measurements and computational simulations. J Biomech. 2004;37(1):45–53. doi: 10.1016/s0021-9290(03)00255-0. [DOI] [PubMed] [Google Scholar]
- 17.Completo A., Rego A., Fonseca F., Ramos A., Relvas C., Simoes J.A. The influence of different tibial stem designs in load sharing and stability at the cement-bone interface in revision TKA. The Knee. 2008;15(3):227–232. doi: 10.1016/j.knee.2008.01.008. [DOI] [PubMed] [Google Scholar]
- 18.Morrison J.B. The mechanics of the knee joint in relation to normal walking. J Biomech. 1970;3(1):51–61. doi: 10.1016/0021-9290(70)90050-3. [DOI] [PubMed] [Google Scholar]
- 19.Zhao D., Banks S.A., D'Lima D.A., Colwell C.W., Fregly B.J. In vivo medial and lateral tibial loads during dynamic and high flexion activities. J Orthop Res. 2007;25(5):593–602. doi: 10.1002/jor.20362. [DOI] [PubMed] [Google Scholar]
- 20.Huiskes R., Weinans H., Dalstra M. Adaptive bone remodelling and biomechanical design considerations. Orthopedics. 1989;12(9):1255–1267. doi: 10.3928/0147-7447-19890901-15. [DOI] [PubMed] [Google Scholar]
- 21.Nadorf J., Kinkel S., Gantz S., Jakubowitz E., Kretzer J.P. Tibial revision knee arthroplasty with metaphyseal sleeves: the effect of stems on implant fixation and bone flexibility. PLoS One. 2017;12(5) doi: 10.1371/journal.pone.0177285. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Frehill B., Crocombe A., Cirovic S., Agarwal Y., Bradley N. Initial stability of type-2 tibial defect treatments. Proc Inst Mech Eng H J Eng Med. 2010;224(1):77–85. doi: 10.1243/09544119JEIM673. [DOI] [PubMed] [Google Scholar]