Abstract.
Spatial frequency domain imaging (SFDI) has witnessed very rapid growth over the last decade, owing to its unique capabilities for imaging optical properties and chromophores over a large field-of-view and in a rapid manner. We provide a comprehensive review of the principles of this imaging method as of 2019, review the modeling of light propagation in this domain, describe acquisition methods, provide an understanding of the various implementations and their practical limitations, and finally review applications that have been published in the literature. Importantly, we also introduce a group effort by several key actors in the field for the dissemination of SFDI, including publications, advice in hardware and implementations, and processing code, all freely available online.
Keywords: spatial frequency domain imaging, diffuse optical imaging, quantitative imaging
1. Introduction
Optical imaging has become increasingly impactful in the fields of medicine and biology over the last decade. Important contributions range from benchtop studies to gain new knowledge of fundamental biological processes, to bedside validation of improved medical outcomes in clinical studies. These success stories are a result of the unique capability of photons to noninvasively probe the functional and structural contrast of living tissues at multiple imaging scales. Due to the diverse sources of optical contrast, a number of optical instruments have been developed to quantify these contrast mechanisms on spatial scales ranging from the microscopic () to macroscopic (). In turn, investigators have utilized these instruments to address unmet clinical needs, leading to exciting new discoveries (Fig. 1).
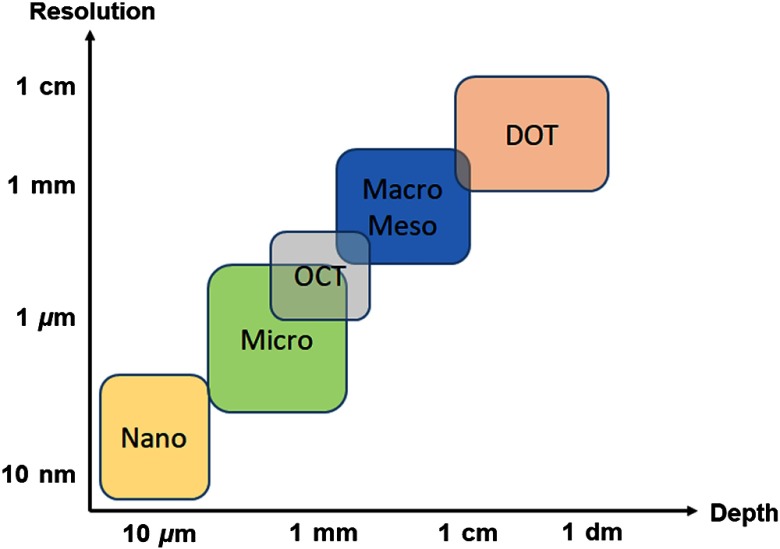
Fig. 1.
Resolution versus depth in biomedical optics: the inherent trade-off between depth of imaging and resolution is illustrated. SFDI is naturally fitting in the diffuse macroscopic imaging region, with resolution limited by the diffusion of light in tissues and depth of penetration typically up to the centimeter scale. Nano, nanoscopy; micro, microscopy; OCT, optical coherence tomography; meso, mesoscopy; macro, macroscopy; and DOT, diffuse optical tomography.
One of the practical challenges for implementation of optical techniques for many clinical situations is the desire by clinicians to survey a large area () with modest resolution () in rapid fashion (seconds to minutes); all while utilizing endogenous contrast that is predictive of functional status. This review is focused on the current status (year 2019) of a mesoscopic and macroscopic imaging technique called spatial frequency domain imaging (SFDI) that fits these broad requirements and contextualizes recent developments in terms of technical advancements, implementation, and clinical applications. The review will cover SFDI measurement of tissue optical properties in visible (VIS; 400 to 650 nm), near-infrared (NIR; 650 to 1000 nm), and short-wave infrared (SWIR; 1000 to 2500 nm) regimes. Over this range of wavelengths, photons probe tissue constituents relatively deeply (typically up to 5 mm in the NIR), and reflectance is attenuated by functional tissue constituents like oxyhemoglobin, deoxyhemoglobin, lipids, water, and melanin due to absorption. The measurement challenge for any in vivo measurement in this regime is decoupling the change in reflectance from absorption, with that due to tissue scattering arising from structural components of tissue like nuclei, mitochondria, and collagen. SFDI provides a unique advantage over most large field-of-view (FoV) imaging methods, using light propagation models to quantify the optical properties of tissues, namely absorption () and reduced scattering () to better quantify physiological contrast from tissue constituents. Among the quantitative imaging approaches generally referred to as diffuse optical imaging (DOI) methods, SFDI has particular strengths in spatial multiplexing, calibration, and relative simplicity of instrumentation.
1.1. Introduction to Spatial Frequency Domain Imaging
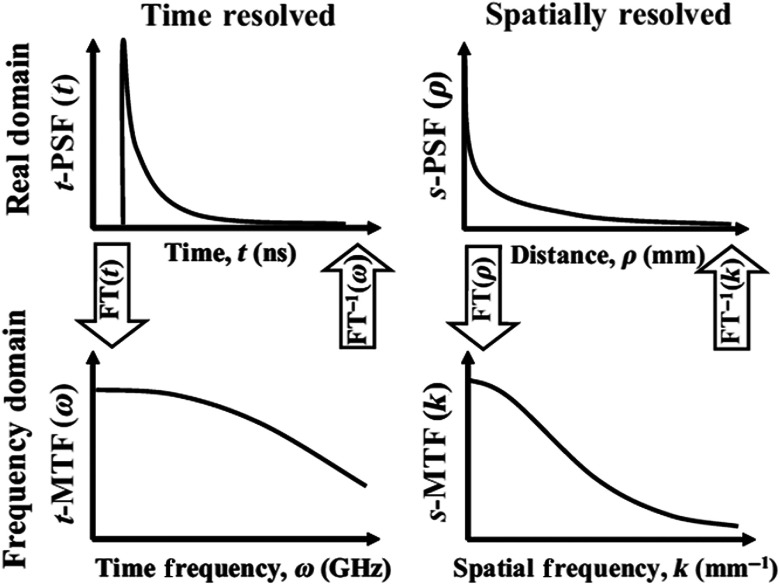
Typically, the measurement of tissue optical properties (absorption and scattering) within a turbid (diffusive) medium relies on a technique to resolve either the temporal or spatial behavior of photon propagation. As depicted in Fig. 2, the measurement of these properties is, therefore, characterized by the tissue’s response to the input light, either in the real domain as the response to a pulse in time or a point in space [point-spread function (PSF)], or demodulation and/or phase retardation of periodic illumination in the time-frequency or spatial-frequency domains [modulation transfer function (MTF)].1
Fig. 2.
Measurement domains (adapted from Ref. 1): optical properties can be measured in either space or time, and in either the real or the frequency domains. In all methods, the propagation and “spreading” of the light, either spatially or temporally, can be related to the optical properties of the medium. While the real space, the real time, and the frequency-time domains were known and exploited for some time, imaging methods in the spatial frequency domain were more recently introduced in 1998 (Ref. 2) and developed as a diffusive imaging method since 2002.
Measurements in either domain have their respective advantages and disadvantages; the trade-offs must be considered in the context of the specific application’s requirements (e.g., signal-to-noise ratio, ambient light conditions, imaging speed, computation time/accuracy, spatial/temporal resolution, compatibility/size/cost of instrumentation, and calibration requirements). Temporal light propagation is the most information-rich, as it fully expresses the characteristics of the time-dependent transport equation, which can best decouple optical properties, especially in heterogeneous systems. In comparison with other methods, however, extraction of this information via temporal measurements relies on more complex computational models and is often associated with slower acquisition rates and/or expensive instrumentation that is not easily duplicated or easily deployed into clinical environments. On the other hand, the measurement of the spatial light propagation can be relatively straightforward and inexpensive and relies on a simpler mathematical model. In traditional “point-source and point-detector” geometries, these approaches can suffer from the spatial averaging of the measured properties (i.e., the impact of inhomogeneities and/or “partial volume” effects). In a similar manner, measurements performed in the real domain provide high signal-to-noise ratio data, but typically require point scanning for imaging large FoVs, making them impractical for real-time implementations. Due to the nature of the instrumentation used, measurements in the frequency domain can be easily multiplexed across several pixels simultaneously, allowing wide FoVs () to be imaged at once. It is to be noted that wide-field, temporally modulated imaging in the real domain has been successfully performed, but still suffers from high cost and complexity.
Offering wide FoV imaging capabilities with relatively short measurement times and low instrumentation costs, spatial frequency domain (SFD) measurements have gained interest by many research groups, which have explored its potential in various applications for providing useful functional and structural information. As an introduction, we will shortly describe here the different acquisition and processing steps used in SFDI.
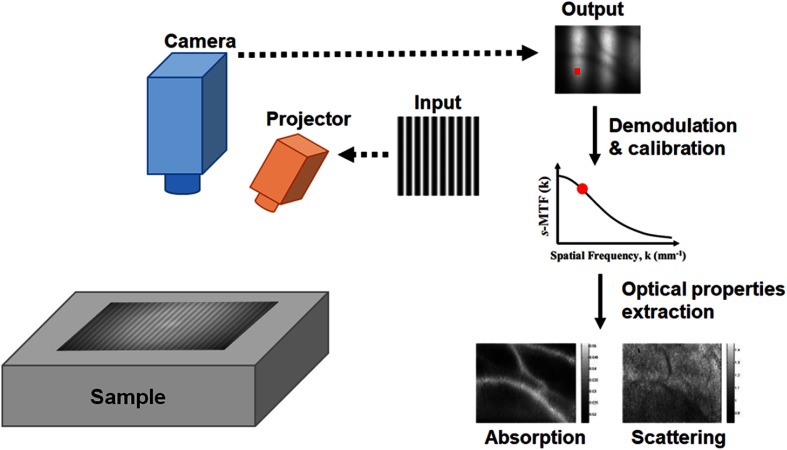
Essentially, imaging in the spatial frequency domain consists of projecting a two-dimensional (2-D) pattern of light and analyzing the effect of multiple scattering and absorption onto the reflected or transmitted pattern’s amplitude as a function of the pattern spatial frequency. As shown in Fig. 3, sinusoidal patterns are typically used to facilitate the analysis of a single-spatial frequency per projected pattern. Multiple scattering and absorption in the medium will cause a decrease in the amplitude of the projected sinewave. The reflectance image of this diffused and absorbed sinusoidal pattern is then captured by a digital camera and further processed. Amplitude modulation for every pixel of the image is calculated by a process called demodulation. Various calibration approaches can subsequently measure the optical system’s frequency response or system modulation transfer function () to arrive at the tissue spatial modulation transfer function (), also known as the diffuse reflectance. The entire process is repeated at several spatial frequencies (at least 2). Finally, using a light propagation model, optical properties are extracted for all pixels in the image. Spectral instrumentation can further extend this process to multiple wavelengths, either via serial or parallel (multiplexed) multiwavelength acquisition schemes.
Fig. 3.
SFDI: a pattern is projected onto the sample and the reflectance imaged with a digital camera. Due to the diffusion and absorption process, the amplitude modulation of this pattern will decrease. The amplitude modulation is extracted through the demodulation step and corrected for other factors (e.g., system MTF). This process is repeated at several spatial frequencies and optical properties extracted used a light propagation model.
Due to its unique capabilities in providing fast and wide-field quantitative images of biological samples, SFDI has been rapidly evolving over the last few years with an increased interest in the field of biomedical optics. In this paper, we describe the fundamental principles underlying (SFDI), review the modeling of light propagation in this domain, describe acquisition methods, provide an understanding of the various implementations and their practical limitations, and finally review applications that have been published in the literature.
2. Spatial Frequency Domain Imaging: Principles
2.1. Theory and Forward Models
There is a strong history of spatial frequency domain approaches to solving the radiative transport equation for light propagation.2–6 Although early efforts typically had the ultimate goal to provide real-domain solutions (by inverse-transforming at the final step), Dognitz and Wagnieres2 were among the first to apply SFD models to the analysis of Fourier-domain light transport signals, and Cuccia et al.1 took this one step further toward native SFD measurement.
2.1.1. Diffusion
Although not precise at all spatial scales and for all optical properties, the diffusion approximation to the radiative transport equation remains an efficient tool to model the propagation of light into turbid media by providing analytical solutions that are easily implemented and intuitive. Spatially modulated light propagation has been thoroughly described in Refs. 1 and 2 and we will only highlight here the most important steps.
The time-independent diffusion equation can be written as
| (1) |
where is the fluence, is the transport coefficient, is the absorption coefficient, is the reduced scattering coefficient, is the anisotropy factor, is the effective attenuation coefficient, and is the source term.
We assume here that the source is sinusoidally modulated in one direction only with the spatial frequency and the spatial phase .
Provided this description, the diffuse reflectance () becomes
| (2) |
where
As we will explain later, the diffuse reflectance obtained through the resolution of the diffusion equation can be related to the measured amplitude modulation by taking into account the optical system response, and therefore, used to solve the inverse problem to extract the optical properties and . From this description, it is interesting to note the influence of the spatial frequency onto the photon density wave attenuation that depends on both the optical properties of the medium and on the spatial frequency. As the spatial frequency increases, the attenuation increases, which is consistent with the observation that high spatial frequencies do not propagate well into turbid media, acting as a low-pass filter.
It is also important to remind the reader that the use of the diffusion theory is limited to spatial frequencies much lower than the transport coefficient:
| (3) |
where being the transport mean free path.
2.1.2. Transport
To overcome the limitations of the diffusion equation, other light propagation models can be used with fewer limitations of spatial scales. Multiple methods have been developed to more-closely represent the full solution to the radiative transport equation, including Monte Carlo simulations,7,8 discrete-ordinate methods,9 or analytic solutions.6 The most popular method remains Monte Carlo, either by Fourier transforming the spatial point spread function integrated over the medium (the same can be done with higher-order anisotropic diffusion models, such as with “-P1” solutions), or tallied directly in the frequency domain.1,8,10 Further, these methods allow to measure not only the absorption and reduced scattering coefficients at small spatial scales, but also the scattering coefficient itself and multiple moments of the phase function, allowing measurements of structural parameters at a sub-mm range,11,12 and assessment of sampling depths on mesoscopic scales.13
2.2. Measurement
Alongside forward modeling used to predict the photon fluence as a function of optical properties in the spatial frequency domain, measurements are performed and used together with the models to extract the optical properties of the sample under interrogation. In this section, we describe the different aspects of spatial frequency domain acquisition from both the instrumentation point of view and from the acquisition protocol.
2.2.1. Instrumentation
Instrumentation in SFDI is rather simple with, as illustrated in Fig. 4(a), the use of a light source, either broadband or monochromatic, a projector to form patterns and a camera system to collect images. Despite this simplicity various embodiments can be found in the literature depending on the needs of the authors. The main differences are typically in: (1) type of source used [light emitting diodes (LEDs), light amplification by stimulated emission of radiation (LASER), or lamps]; (2) the wavelength choices (i.e., number and range); (3) spectral filtering (i.e., discrete light sources, liquid crystal tunable filter, and bandpass filters); and (4) the camera architecture (i.e., bit depth, imaging speed, and multiplexing). The company Modulim (previously Modulated Imaging, Inc.) has commercialized a research platform system (Reflect RS™) which includes flexible acquisition, processing, and visualization software [Fig. 4(b)]. The Reflect RS system is composed of a digital micromirror device projector, a single-monochrome camera, and triggered LEDs with discrete wavelengths centered at 470, 525, 590, 625, 658, 690, 730, 850, and 970 nm. The system architecture allows rapid sequential acquisition of SFDI data at these wavelengths along with co-registered color images and is used by researchers in academia and industry to measure turbid systems. More recently, Modulim has released the Clarifi Imaging system [Fig. 4(b)], which is U.S. food and drug administration (FDA)-cleared for measurement of tissue oxygenation in patients with potential circulatory compromise. Other systems that have been developed include a custom surgical guidance system that has been translated to first-in-human pilots studies [Fig. 4(c)]. This system developed at the Beth Israel Deaconess Medical Center uses a LASER diode source capable of projecting light at 670, 690, 730, 760 860, and 980 nm.14 In this system, two monochrome cameras allow for the simultaneous imaging of two wavelengths at once, enabling rapid oxygenation imaging, along with co-registered color video. Other systems have been developed to couple SFDI with other modalities. Figure 4(d) presents a system developed at the University of California Irvine to couple with photodynamic therapy (PDT) treatment. This system was designed to measure optical properties at 460, 525, 630, 730, and 850 nm and was coupled with PDT treatment wavelengths between 630 and 640 nm to assist in preparation and monitoring of PDT treatment.15 Figure 4(e) (left, assembled and right, open) presents an endoscope configuration exploiting specifically real-time acquisition and processing advancements using single snapshot of optical properties (SSOP) developed at the University of Strasbourg, France.16 These hardware advancements enable advanced intraoperative clinical acquisition in endoscopic applications where an open-field is not accessible. Finally, various other custom systems have been described by research groups around the world. Each of these systems was designed to address specific needs by modifying a component of the system. Some examples include: using cooled high-dynamic range frame-transfer cameras for rapid and low-signal imaging, using both tunable light sources and hyperspectral cameras for spectral multiplexing, using multiple polarizer orientations to combine with polarization imaging, using commercial projectors to reduce costs, integrating SFDI within existing medical instruments such as surgical microscopes or endoscopes, and using coherent sources to get flow data from speckle. These systems are a combination of benchtop imaging systems with some being transportable to preclinical or clinical sites,12,17–25 as well as improved methods for robust measurement during clinical conditions [motion correction and three-dimensional (3-D) correction].26,27
Fig. 4.
Example of SFDI instruments: (a) the working principle of the SFDI instrumentation is illustrated, including a light source, a projector, and a digital camera adapted from Ref. 1. Note that the simplicity of the imaging setup; (b) left and right: the reflect RS and Clarifi imaging systems, commercialized by Modulim; (c) the system developed at the Beth Israel Deaconess Medical Center that performed a first-in-human study during reconstructive surgery adapted from Ref. 14; (d) the system developed at the University of California Irvine that combines SFDI measurement with PDT treatment adapted from Ref. 15; and (e) endoscopic system developed at the University of Strasbourg, France, left: assembled, right: open.16
2.2.2. Demodulation
The acquisition process should in essence allow the measurement of the diffuse reflectance () at multiple projected spatial frequencies () and at every position in the image (), which in the case of SFDI can be obtained from the measurement of the amplitude modulation (). These two parameters are related through a calibration step that isolates the contribution of the sample’s diffuse reflectance from that of the optical system used to perform the acquisition, the latter being called the optical . The calibration step is detailed in Sec. 2.2.3. The diffuse reflectance is related to the optical through the following relationship:
| (4) |
with the illumination expressed as
| (5) |
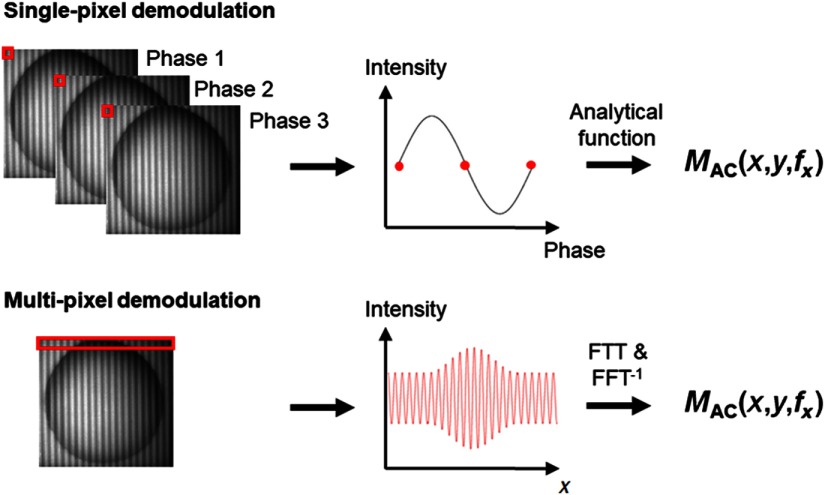
The measurement of the amplitude modulation () of the medium, which consists in the envelope of the AC modulation re-emitted by the medium following propagation, is the critical step for data acquisition. Two approaches can be chosen to measure this parameter: the first uses sequential projection of different phases of the same spatially modulated sinewave and/or several spatial frequencies with demodulation performed using the phase of each pixel encoded in time (single-pixel demodulation methods), and the other projecting a single pattern at a single phase with demodulation performed using several pixels (multipixel demodulation methods).
Single-pixel demodulation methods. This approach uses several frames of data acquired sequentially to extract the .1 With these methods, every single pixel in the image is independently characterized by an amplitude modulation. As shown in Fig. 5, the intensity of each pixel is analyzed for multiple phase images to deduce its amplitude modulation. Several implementations of this method exist. The first method, historically inherited from previous work in telecommunication and later in microscopy, relies on projecting three equally spaced phases of a spatially modulated sinewave to extract the at a single-spatial frequency according to the following equation:
| (6) |
Fig. 5.
Demodulation methods: two main demodulation schemes can be used: either at a single-pixel level by acquiring several frames with phase shifts allowing to use a simple analytical formula to obtain the amplitude modulation, or at a multipixel level by taking a Fourier transform of a line or of the entire image and extract the useful information for obtaining the amplitude modulation.
The process is then repeated for every desired spatial frequency. Typically, this is done at two spatial frequencies, one low frequency (e.g., ) and one high frequency (e.g., ), if the goal is to extract subsurface optical properties.
One approach to get the data at low frequency (called ) is based on the fact that planar illumination (i.e., spatial frequency) is always present when projecting patterns of light. However, care must be taken in taking into account the DC noise of the detection system (automatically suppressed in the previous case)
| (7) |
This method produces images at the native resolution of the camera in the system with relatively simple math to extract the amplitude modulation which is advantageous. However, sequential image acquisition requires samples to be static between images and the light source to be stable between images. Second, the math in the equation above require close to perfect sine waves with well-characterized phase shifts in the illumination scheme to get artifact-free images.
Multipixel demodulation methods. In this approach, the intensity of several pixels in the image is analyzed as a function of space in order to extract the envelope of the signal, as shown in Fig. 5.28,29 There is, therefore, a natural dependency between neighboring pixels in space, in a similar way to any existing processing technique in the temporal domain (such as audible signals). The first implementation of this method called SSOP has been introduced by Vervandier et al., recently refined by Van de Giessen et al., and makes use of a single pattern at a single-spatial frequency, i.e., a single image, to extract both the at (i.e., the ) and the at a higher spatial frequency, as well as phase for measuring the sample’s surface profile. The projected illumination is acquired and processed in the Fourier domain, either in a line-by-line manner, or in 2-D to extract the amplitude modulation at and at a higher spatial frequency.
The second implementation of this method, described by Nadeau et al., relies on acquiring one DC planar illumination, along with a single-phase spatially modulated sinewave.30 The DC planar illumination is then used to extract the at and subtracted from the spatially modulated image, which is then processed in the Fourier domain to extract the at a higher spatial frequency. Because the acquisition of two sequential frames in time is necessary, along with a spatial demodulation method, this approach is hybrid in time and space. An extension of this approach, termed multifrequency synthesis, has also been proposed by the same group using square waves and a Fourier transform to separate contributions to multiple spatial frequencies contained in a particular periodic, nonsinusoidal illumination.31
Although this approach has the merit to allow true real-time acquisition of images quantitatively, one of the main drawbacks of reducing the amount of acquired images is the degradation of image quality and resolution.28,29 However, recent work on improving processing and filtration in the spatial frequency domain has demonstrated significant image quality improvement making such a method viable for clinical use.32
2.2.3. Calibration
Once the signal has been demodulated to extract the amplitude modulation at several spatial frequencies, the instrument response function must be taken into account to extract the corresponding diffuse reflectance [see Eq. (4)]. In essence, while the diffuse reflectance corresponds to the MTF of the tissue of interest, the MTF of the optical system itself as well as the illumination intensity (heterogenous) should be measured and corrected to isolate the diffuse reflectance of the sample. This is analogous to PSF deconvolution in the real domain, but becomes a simple division operation in the SFD transform space. For this purpose, the amplitude modulation of a reference tissue-mimicking phantom with known optical properties is measured (). The expected diffuse reflectance is predicted using a photon propagation model and the reference optical properties (). Finally, the is deduced with knowledge of the illumination intensity ():
| (8) |
This calibration factor is then used on all acquisitions (typically applied to the demodulated signal) to correct for the contributions from the instrumentation. Typically, reference tissue-mimicking phantoms used are made of silicone or optically stable acrylic, with titanium dioxide as a scattering agent and nigrosin, or India ink, as an absorbing agent.33–35
2.2.4. Topography correction
The spatial multiplexing of SFDI allows for characterization of optical properties over large tissue surfaces in a noncontact geometry, but careful attention must be taken to correctly account for height variations between the imaging system and the sample, as well as from the sample’s surface angle with respect to both source and detector. Indeed, SFDI being a calibrated technique, every image is referenced to a calibration phantom that is flat and at a fixed distance from the imaging system. Errors in optical properties have been shown at a level of 10% per cm difference in vertical distance between the sample and the imaging system.26 Similarly, the diffuse reflectance photons exiting the medium exhibit an angular dependency resembling the one of Lambertian surfaces, close to a cosine of the angle between the photon exiting direction and the normal of the medium. Errors in optical properties have been shown to reach 86% at a 40-deg surface angle.26
To account for these effects, SFDI has been coupled with surface profilometry, which is particularly convenient since both are based onto the projection of patterns of light. Profilometry was used along with multiple calibration heights and used to correct optical properties for the effect of height and angle.26 Recently, van de Giessen et al.29 introduced a real-time approach allowing the measurement of 3-D surface corrected optical properties from a single image. Recent developments by Zhao et al.36 proposed an empirical approach to increase the 3-D correction up to 75-deg surface angle. An alternate approach was developed in the context of SFDI by Nguyen et al.37 by measuring the profile of the sample, fabricating a 3-D calibration phantom, and measuring this calibration phantom to correct for the effects of distance and surface angle.
2.2.5. Key considerations
As with any measurement technology, SFDI can suffer from various sources of errors. Recent publications reviewed some of the potential sources of errors in SFDI, and we will attempt here to broaden this previous work by reviewing important considerations required for a proper measurement.38,39
The first category of errors can be attributed to assumptions made when using models of light propagation. As reviewed in 2.1, a broad set of models have been developed and adapted specifically for SFDI and different applications. These models range from the most accurate and small scale approach with the radiative transport equation, to the most simple (here analytic) form at large scales with the diffusion approximation and finally with what is considered the gold standard of accuracy at large scales, Monte-Carlo methods. All of these models have been successfully used in their target applications, from tomography to wide-field functional mapping of chromophores. One of the challenges in model selection is the inherent trade-off between the model accuracy and the speed at which a measurement and processing can be achieved. Acquiring multiple spatial frequencies and multiple phases can improve SFDI model fits but at the practical expense of acquisition and processing speed. For that reason, a reasonable compromise is commonly used with Monte-Carlo generated inverse look-up tables (LUTs) at two spatial frequencies (e.g., 0 and ), allowing at the same time rapid and accurate measurements and processing of wide FoV. Finally, one should keep in mind that the errors linked to wrong assumptions in modeling, including spatial accuracy, phase function description, refractive index modeling, and sample boundaries are not inherent to the use of SFDI, but impact any measurement method in diffuse optics. Extra care in particular must be taken in the case of coherent light imaging, where laser speckle can cause mesoscopic spatial and temporal variations which should be appropriately modeled, isolated, or averaged.
Other sources of errors not inherent to the use of SFDI should be mentioned. As with any spatial method, there is a compromise between resolving depth-dependent optical properties and the numerical stability of optical property determination. Careful attention to the potential that multivalued solutions exist is crucial, as is an awareness that resolution degrades quickly with depth. This effect is inherent to any spatial method and in one case a confounding factor for subsurface imaging applications, and the basis for depth sectioning and tomographic applications. In addition, still specifically for subsurface imaging, current models assume that each measured pixel is independent laterally from the other, which in reality is not the case. It should be noted that it would be possible to develop models that take into account the pixels’ interdependency (i.e., correlation of lateral information) to obtain a more accurate measurement of the sample’s properties.
Another set of errors is linked to the practical implementation of the technology. Particularly, there are several factors that can influence the accuracy and precision of the measurement. By essence, SFDI is a calibrated imaging method, therefore, the calibration plays an important role in the accuracy of the measurements. First, it should be noted that the use of a calibration standard allows to lessen the effect of many instrumental sources of errors, such as illumination inhomogeneity or the optical . Second, if not accounted for, the surface profile (height and angle from the imaging system) has been shown to introduce errors. Methods that measure the sample’s profile can be implemented to correct for these effects (see Sec. 2.2.4). Third, the optical properties of the calibration standard could be misevaluated, as they are typically dependent on another measurement method, such as a temporal-domain measurement. However, from our experience, only a few absolute references exist, all methods and systems measure physically different volumes, as well as use different models, and as a consequence, absolute referencing is a challenge. Referencing of homogenous systems is most achievable with diligent phantom recipes (i.e., intralipid, microspheres, and blood) and titration experiments. However, in most clinical applications, the tissue is complex and matching phantom optical properties to the tissue of interest remains a challenge.
Fourth, the divergence of the projection beam could cause issues in measuring optical properties through a broadening of the spatial frequencies with distance. Depending on the imaging configuration, care must be taken to evaluate the local spatial frequency and adapt the processing to take it into account. Multispatial frequency processing codes were developed to take into account this effect in cases where divergence is significant, such as within an endoscope.16,40 Finally, many other sources of errors such as camera linearity, projection linearity, and source stability, as in any optical design should be taken into account, either by calibration or monitoring and/or appropriate analytic or empirical corrections.41,42 One aspect that should not be neglected is the quality of the projection and acquisition, and the resulting demodulation as this will have a direct influence onto the precision and accuracy of the measurement. In particular, these instrumental factors can limit the frequency range used, as the signal-to-noise ratio greatly decreases with spatial frequency.1,39 Although the specific requirements of tolerances will depend on the objectives of a specific project, in general data should be as clean and noise-free as possible to ensure proper computation, and several technological factors should be considered, such as the resolution, dynamic range and noise of the camera or the resolution, dynamic range, and the refresh rate of the projector.
2.3. Inverse Models and Data Processing
Multiple approaches have been developed for analyzing SFD signals to determine homogeneous or spatially resolved optical properties, including least-squares methods,2,43 LUTs,1,44 machine learning and deep learning,40,45 and data matching to empirical phantom grids.46 The choice of computation model is important and application specific. Criteria including imaging depth, computational time, and tissue geometry are important in making this decision. A summary of a few key approaches are discussed below.
2.3.1. Inverse modeling and processing for subsurface imaging
The first and most wide-spread current use for SFDI is in the determination of optical property maps over a wide FoV.1,17,47–51 The capability to quantify tissue properties over a relatively large FoV () for every pixel in an image and in a rapid manner has been a breakthrough in biomedical optics, opening a broad spectrum of applications from agriculture to healthcare. In this embodiment, SFDI has the unique capability of sampling the tissue response to structured illumination using a few images only and obtain subsurface information used to characterize biological processes within the sample. Subsurface refers to photons that diffused into the sample, as opposed to reflectance that originates only from the surface typically consists of specularly reflected photons. It should be noted that the term “subsurface” remains ambiguous in nature since depth penetration and information content inherently depend on the optical properties of the sample. In the case of SFDI, low spatial frequencies are sampling both short- and long-photon trajectories (pathlengths), providing deep and shallow information content, and are influenced by both scattering and absorption; high spatial frequencies are sampling short photon paths and are primarily influenced by scattering.
Typically, absorption and reduced scattering have been the parameters imaged with SFDI in a subsurface large FoV geometry. The models used to extract these properties have been mostly based on diffusion theory and Monte-Carlo simulations, the latter offering a broad range of applications in biological media that is not limited by the albedo of the sample. Recently, a very high spatial frequency approach has been developed, allowing the recovery of absorption and scattering, as well as the gamma parameter, i.e., moments of the phase function.11,12,52 Such a development offers many perspectives in using scattering as a subcellular structural parameter that has been shown critical for the diagnosis of various diseases such as cancer. Altogether, optical parameters in a subsurface geometry have enabled the investigation of many applications, owing to its simplicity, ease of use and fast imaging capabilities.
2.3.2. Inverse modeling and processing for optical sectioning and tomography
As for any modulation method (in space or time), SFDI measurements can be used to perform depth-sensitive or even tomographic optical properties measurements. Indeed, imaging several spatial frequencies is analogous to measuring several source–detector separations that can be used to interrogate the turbid medium at several depths.
The first implementation of this principle described consists of obtaining depth-sensitive measurements, also called optical sectioning. 2-D maps of depth sensitive diffuse reflectance are measured as a function of spatial frequency, with higher spatial frequencies being in nature more superficial.43 Images with depth-sensitive contrast can then be generated using the recovered diffuse reflectance and knowing the spatial frequency used.
A second category of optical sectioning in SFDI leverages known properties of tissue structure to create layered models. The most common example and perhaps pervasive application is in skin research where researchers have modeled tissue in multiple layers to represent the epidermis and the layers of the dermis. The result is fit for layer specific optical properties that provide insight into physiology.43,53–55
Finally, more advanced implementations allow to recover tomographic information, i.e., a more precise representation of optical properties as a function of depth. In this case, advanced light propagation models are used along with state-of-the-art reconstruction methods. Various approaches have been described in the literature, from improved formulations of the diffusion equation, perturbation methods, and approximation to finite elements methods.56–65
3. Spatial Frequency Domain Imaging: Implementations
3.1. SFDI and Chromophore Imaging
One of the main motivations in separating absorption from scattering quantitatively is to be able to use Beer–Lambert law to obtain chromophores concentration, such as oxygenated hemoglobin, deoxygenated hemoglobin, lipids, water, and melanin. This is typically achieved by applying a linear combination of multiple wavelengths measurements to obtain concentrations based on the tissue constituents (called chromophores) molar extinction coefficients:
| (9) |
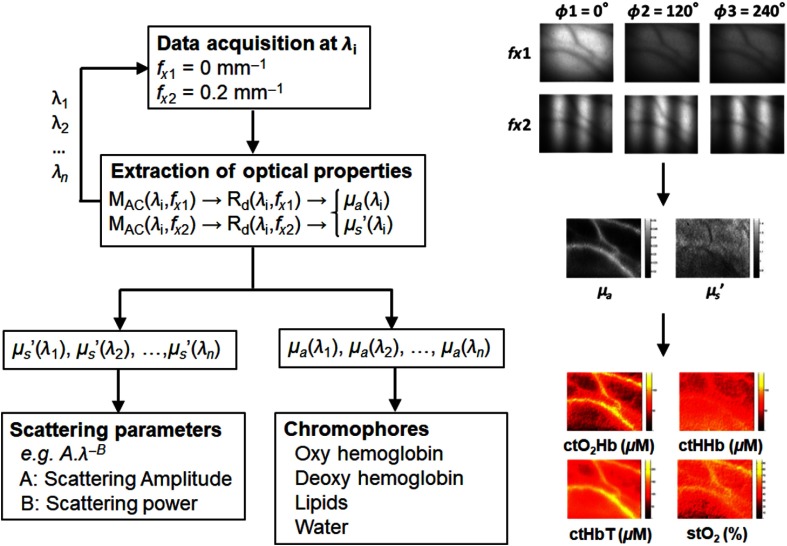
Figure 6 illustrates the full acquisition workflow for obtaining tissue blood parameters. The wavelengths should be carefully chosen to minimize the cross talk between each constituents’ extinction properties. For instance, it has been demonstrated that choosing 650 and 860 nm was optimal to determine oxyhemoglobin and deoxyhemoglobin concentrations.14,66 It should be noted that this method typically measures what is referred to as “tissue molar concentration,” noted with the prefix “ct” (e.g., stands for oxyhemoglobin tissular concentration), a quantitative measure of the content of oxyhemoglobin within the tissue volume visited by light and that differs from a typical chemistry definition of a concentration within a diluted medium.
Fig. 6.
Full acquisition workflow: the typical acquisition workflow for reduced scattering and absorption properties is shown. (a) A diagram depicts the different steps from data acquisition, to processing and to the extraction of scattering parameters and chromophores. (b) Example images for each step are provided.
3.2. SFDI and Structure Orientation
Orientation of structures within biological samples (or lack of thereof), in particular collagen or muscle fibers, can be an indication of alterations useful for diagnosis. SFDI has shown promise in imaging structure orientation through two main approaches. The first one relies on the measurement of scattering properties at various pattern angles.67 Attenuation of the AC waves as a function of angle has been shown to indicate preferential orientation in highly organized structures such as fibrous structures or chicken breast. The second one analyzes the polarization at several angles from an SFDI measurement.21,22 The polarization dependence of scattering will indicate the dominant fibers orientation as demonstrated onto collagen-rich samples such as tendons.
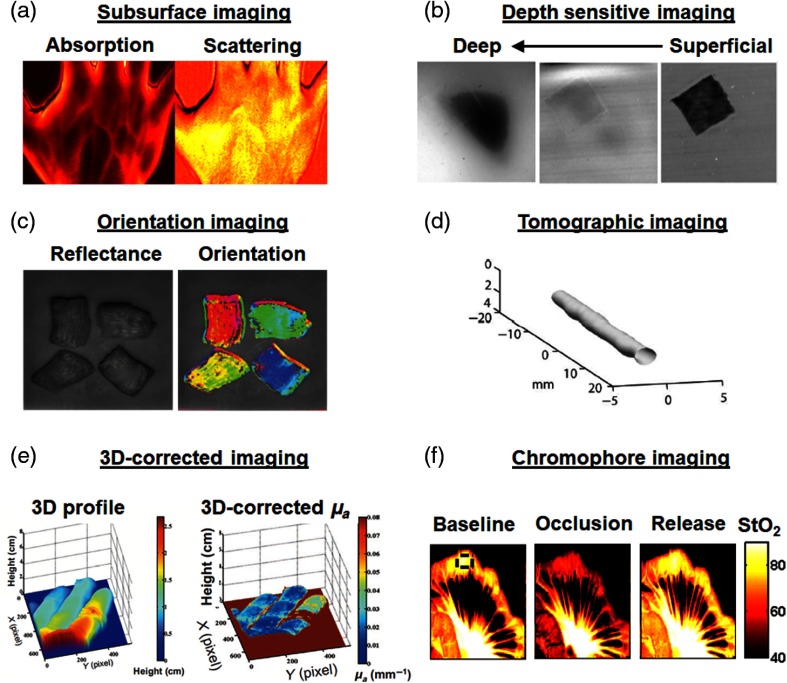
Figure 7 provides examples taken from the literature: subsurface imaging of optical properties [Fig. 7(a)], depth-sensitive imaging in a phantom [Fig. 7(b)], ex vivo orientation imaging [Fig. 7(c)], endogenous tomographic imaging in a phantom [Fig. 7(d)], 3-D corrected imaging of a human hand [Fig. 7(e)], and oxygen saturation imaging of a pig bowel during blood supply occlusion and release [Fig. 7(f)].
Fig. 7.
Examples of applications with SFDI: various applications using SFDI principles are provided. (a) Imaging of absorption and scattering of a human hand adapted from Ref. 28, (b) depth sensitive imaging by optical sectioning on a tissue mimicking phantom (depth of the deep inclusion is 2 mm) adapted from Ref. 43, (c) orientation imaging of biological samples adapted from Ref. 67, (d) tomographic imaging of a tissue simulating phantom (depth of the tube is 2.5 mm) adapted from Ref. 56, (e) combination of SFDI with 3-D imaging of a human hand adapted from Ref. 26, and (f) chromophore imaging of a pig bowel during blood supply occlusion adapted from Ref. 14.
3.3. SFDI and Fluorescence
In vivo fluorescence imaging using contrast agents has been adopted by clinicians for surgical guidance, mainly by providing a relative metric of tissue perfusion and tumor margin identification. However, fluorescence signals are generally reported qualitatively, and sometimes can be blurry/low resolution due to scattering in tissue. The attenuation of both excitation and fluorescence emission light impedes the proper localization and calculation of the local amount of fluorescence, a metric that may aid surgeons when using fluorescence for quantitative diagnosis. SFDI can be applied in a fluorescence system to quantify scattering and help quantify and localize fluorescence signals.
Early work demonstrated the benefit of optical sectioning in fluorescence using SFDI in turbid systems68,69 and was recently extended to in vivo imaging.70 The simple method allows users to preferentially select either long or short pathlengths by varying the spatial frequency of the projection. By changing the spatial frequency of illumination, significant improvements were demonstrated in both lateral and axial resolution when detecting fluorescent inclusions in diffusive media with background contrast. The main caveat of the method is its incapacity to directly select deep fluorescence only. Indeed, increasing spatial frequency results in more superficial detection, but when decreasing spatial frequency, both superficial and deep fluorescence is detected. To overcome this limitation, a method in the real domain was developed that allows to select either deep or shallow fluorescence independently.71,72
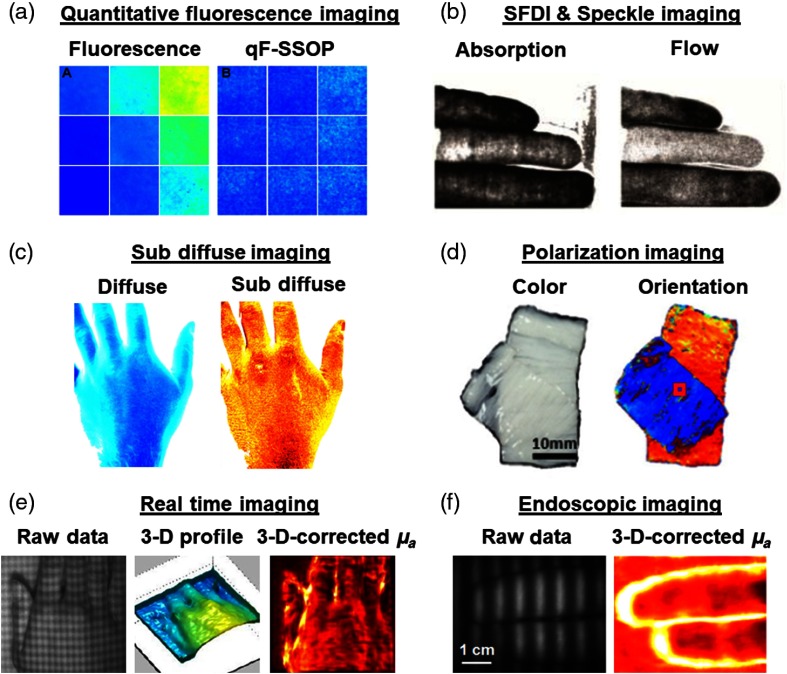
The concept of using optical properties map from SFDI to quantify fluorescence signals in a co-registered image was introduced early and recently gained interest in the field of fluorescence-guided surgery.23,73,74 This concept in principle allows quantitative fluorescence, at a subsurface level, to be performed rapidly. Quantitative fluorescence means absolute numbers can be attributed to signal for diagnostic purposes. Valdes et al.75 recently applied the principles of real-time optical properties imaging (SSOP) to the quantitative measurement of fluorescence (termed qF-SSOP), allowing to predict fluorescence concentration within 5% in various turbid media optical properties, and in real time, making it amenable to be used during surgery [Fig. 8(a)].
Fig. 8.
Recent developments in SFDI: recent developments using SFDI include: (a) correction of absorption and scattering properties of tissues to improve fluorescence imaging in real time on tissue phantoms adapted from Ref. 75, (b) the combination of speckle flow imaging with SFDI imaging on a human hand allowing in the future to extract metabolic information adapted from Ref. 76, (c) subdiffuse SFDI allowing to observe fine structural changes on a human hand through the measurement of scattering itself and the moments of the phase function adapted from Ref. 11, (d) the combination of polarization and SFDI to image structure orientation of biological samples adapted from Ref. 22, (e) 3-D corrected real-time imaging of a human hand using SSOP adapted from Ref. 29, and (f) endoscopic imaging of a human hand using SSOP adapted from Ref. 16.
In addition to correct absorption and scattering of tissue for a more accurate quantification of fluorescence, the use of SFDI with fluorescence allows to measure additional parameters such as the fluorophore quantum yield.77 Further than just measuring SFDI with fluorescence, the combination of temporal and spatial modulation was used to not only provide a framework for wide-field diffuse optical tomographic imaging of thick tissues, but also to perform tomographic fluorescence lifetime measurements.78,79
3.4. SFDI and Speckle
The measurement of oxygen saturation has been a strong motivation for the development of functional diagnostic and monitoring methods for healthcare. Recently, this metric has been complemented by the measurement of blood flow, with the hypothesis that variations of oxygenation could originate from either perfusion defects or metabolism. Therefore, measuring both perfusion (blood flow) and oxygenation in the same sample can provide indication on the metabolism of tissues.
For this purpose, speckle imaging has been coupled with oxygenation imaging using SFDI. It should be noted that SFDI and speckle imaging can be naturally combined together since, typically, the spatial frequencies related to speckle are much higher than those used for SFDI. The instrumentation involves using a spatially coherent source to illuminate the sample along with a spatial light modulator. Patterns of light are processing using standard SFDI processing and speckle is separately analyzed either through its variation in space or in time. This general concept was introduced and validated (called coherent-SFDI, or c-SFDI) during finger occlusion experiments [Fig. 8(b)].76,80–82 The concept has been extended to real-time measurements using SSOP combined with speckle flow measurement into coherent-SSOP (c-SSOP), which has been validated onto arm-cuff occlusions in human subject and is now tested clinically.83,84
3.5. SFDI and Point Spectroscopy
Although widely used for imaging purposes, spatial frequency domain measurements can also be performed using a point sensor. In this case, it is possible to use white light and a spectrophotometer to obtain directly the spectral measurement of this point in absorption and scattering. To make this measurement, a sinusoidally modulated white light illumination is projected onto a sample and the reflectance from a single-point illumination is measured by a spectrophotometer. A temporal acquisition and demodulation method is used to separate absorption and scattering for all the wavelengths measured through the spectrophotometer.85
Figure 8 provides examples taken from the literature: real-time quantitative fluorescence imaging [Fig. 8(a)], simultaneous flow and absorption imaging [Fig. 8(b)], subdiffuse imaging [Fig. 8(c)], polarization imaging [Fig. 8(d)], real-time 3-D corrected imaging of a human hand [Fig. 8(e)], and quantitative imaging through an endoscope [Fig. 8(f)].
3.6. SFDI in the Short-wave Infrared Regime
Imaging in the SWIR (1000 to 2500 nm) regime has recently gained strong interest owing to high penetration depth, high optical resolution, and the capacity to better measure endogenous constituents such as water and lipids.86 In this particular implementation, indium gallium arsenide (InGaAs) detectors are used for their sensitivity in this wavelength range, sometimes in combination of a standard silicon detector to cover the VIS and NIR region of the spectrum. Standard SFDI processing can be used to extract optical properties and deduce endogenous constituents’ concentrations.
3.7. Toward Real-time Imaging
Real-time imaging in this context means near video rate ( frames per second) data acquisition and processing. Real-time acquisition methods necessitate reducing the number of images acquired to solve the inverse problem for optical properties extraction. As mentioned in Sec. 2.2.2 demodulation, multipixel demodulation methods have a definite advantage (1) by requiring down to a single-image acquisition and (2) by exploiting Fourier transforms to rapidly demodulate images. Recent work demonstrated single-image acquisitions leading to optical maps of absorption and reduced scattering that are corrected for topography.16,29
Processing methods rely on solving the inverse problem by either iteratively updating a model to match a measurement or by precomputing a grid of solutions generated through the forward model.1 In the first case, a typical implementation consists of measuring several the diffuse reflectance at several spatial frequencies that can be fit to Eq. (2) using a least-square minimization. This method, while accurate and precise, can be time consuming, both through the acquisition of multiple spatial frequencies and the least-square minimization process.
An alternative approach when performing subsurface imaging exploits the sensitivity characteristics of the diffuse reflectance to absorption and scattering changes at low and high spatial frequencies. As demonstrated by Cuccia et al., low spatial frequencies are sensitive to both absorption and scattering changes. However, high spatial frequencies are primarily sensitive to scattering changes only. As a consequence, measuring using two spatial frequencies only, one low (i.e., ) and one high (e.g., ), allows the extraction of both the absorption and reduced scattering coefficients. These spatial frequencies are typically used since they represent a good compromise in terms of signal-to-noise ratio for the detection of the amplitude modulation, hence a rapid measurement, and because they allow good a separation of optical properties without enhancing sensitivity to model inaccuracy when depth-dependent contrast exists. For this purpose, a grid of solutions for the diffuse reflectance can be precomputed for given range of absorption and reduced scattering values. Once the diffuse reflectance is measured at these two spatial frequencies, the corresponding values of absorption and reduced scattering can be located in the grid. This method is called the LUT method.1,46
LUT processing methods have recently been improved in computation time by replacing time-consuming interpolation approaches with direct coordinates approaches. Briefly, the latter solution relies on resampling the LUT to be linear in diffuse reflectance, and rounding measurements such that one can call directly coordinates in the LUT instead of searching and interpolating within the table.44 For instance, for a dataset, processing time could be improved from 2.5 s down to 18 ms.44
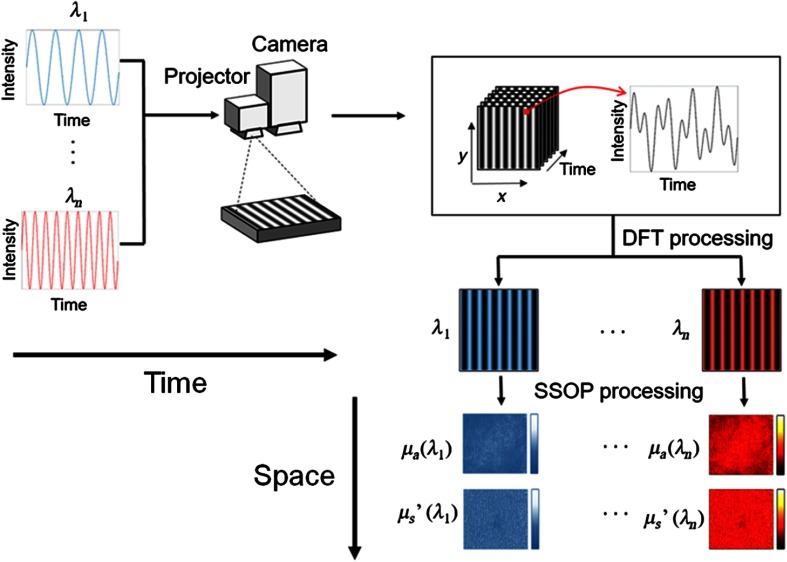
As processing time has been reduced through the optimization of both data acquisition and processing at a single wavelength, more recent developments have focused on multiplexing the acquisition of multiple wavelengths by modulating the illumination both in time and space.87,88 In this method depicted in Fig. 9, time is used to encode wavelengths and space to extract optical properties, both in the frequency domain. Light sources of different wavelengths are modulated in time at specifically chosen temporal frequencies and combined together in the same optical fiber. The fiber is coupled to a spatial light modulator that projects patterns of light onto the sample. The resulting images are first demodulated in time using a discrete Fourier transform to separate the different wavelength contributions, and then processed in space to extract the optical properties.88,89 Other approaches have focused on multiplexed data collection on the detector side by introducing advanced camera hardware to simultaneously capture spectral content.90
Fig. 9.
Spatiotemporal modulation of light: multiple light sources are modulated in time and combined into a single-fiber output. The resulting light is projected through a spatial light modulator and images collected using a fast camera (e.g., 200 frames per s). The resulting images are first processed in the temporal domain to separate wavelengths contributions and then in space to extract optical properties at these wavelengths.88
4. Spatial Frequency Domain Imaging: Applications
Research in SFDI is highly application-driven due to translational nature of the method. Below, we summarize some of the main areas of focus. Examples of applications are illustrated in Fig. 10.
Fig. 10.
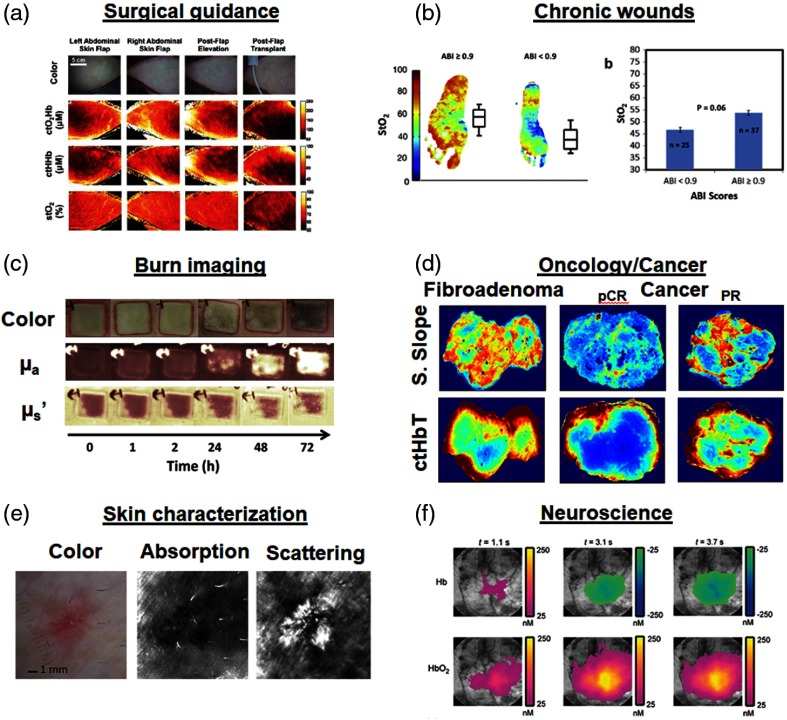
Example of in vivo applications of SFDI: (a) surgical guidance with the imaging of flap transplants oxygenation and chromophore concentration adapted from Ref. 14; (b) chronic wounds with the imaging of feet oxygenation to assess a compromise in circulation that can potentially lead to ulceration adapted from Ref. 91; (c) assessment of burns with the imaging of scattering () and absorption () adapted from Ref. 95; (d) imaging of excise breast cancer specimen for surgical margin assessment adapted from Ref. 109. pCR, pathological complete response; PR, partial response; (e) skin condition characterization with the diagnosis of nonmelanoma skin cancer adapted from Ref. 15; and (f) imaging of brain activity in rat cortex adapted from Ref. 117.
4.1. Chronic Wounds
Chronic ulcers due to poor circulation are a highly challenging medical problem for people with diabetes as well as the elderly. In diabetes, these issues often manifest themselves in the lower extremity and eventually lead to foot ulceration and amputations. These complications are very preventable if there was a quantitative tool to identify those patients most at risk due to the circulation compromise. Recent work in SFDI has demonstrated the ability to differentiate vascular disease in patients with diabetes by identifying unique circulation signatures of tissue oxygenation and superficial/deep hemoglobin. Of note, this study measured an elevated oxygen saturation in diabetes population, likely due to poor oxygen extraction caused by arteriovenous shunting in the skin.91 This effect was combined with compartment changes in hemoglobin distribution suggesting that it is important to track both hemoglobin oxygenation and distribution for comprehensive assessment in tissue. SFDI has been demonstrated preclinically to track wound healing in a diabetes model.92 Clinically, another feasibility study has used SFDI for staging decubitus ulcers.93 The majority of these applications require consistent imaging in order to prevent complications. With larger studies, the efficacy to identify those at risk can be confirmed and the potential in this area remains high due to fit of the technology with community care environments where a solution is needed.
4.2. Burn Imaging
Early assessment of burn severity is a clinical challenge that is done subjectively by surgeons but still resulting in high variability in quality of care. A quantitative assessment of burn severity in early stages () can inform surgeons whether to pursue a path of aggressive grafting or less-aggressive wound care; all with the goal of better outcomes and lower complications. Multiple groups have used established preclinical models to show that SFDI can be used to assess burn depth.18,94–98 The most unique finding thus far is the correlation of SFDI scattering changes to gold standard measurements of burn depth with histology (H&E, Masson’s trichrome, and Vimentin immunostain). Another key finding was that SFDI assessment of burn depth was accurate within 72 h of the initial injury—a major issue for clinicians who often have to wait up to a week for the hard to diagnose burns. Other SFDI-derived biomarkers such as hemoglobin, water concentration, and tissue oxygen saturation have also been tracked longitudinally to monitor burn progression. In other aspects of burn care, Nguyen et al.18 demonstrated the potential of SFDI to monitor infection status of burn injuries—one of the most common causes of complications. Most recently, Ponticorvo et al.99,100 did a comparison between multiple noninvasive modalities to diagnose burn severity and showed that SFDI was one of the most sensitive and specific techniques for burn diagnosis. There has been some pilot clinical work reported in the literature but the potential for SFDI as an adjunct method to measure burn depth and guide patient management is promising due to rapid wide-field assessment and SFDI specific signatures in an area where the error margin is still quite large.41
4.3. Surgical Guidance
One of the earliest use cases for SFDI was to quantify early ischemic onset to guide surgical decision-making. Surgeons often transplant large amounts of tissue from one site to another by terminating and reattaching blood supply routes to these sites. One of the main concerns for the surgeon is monitoring tissue viability after leaving the operating room. Monitoring is often done by experience, feel, and clinical guidelines but a quantitative metric could identify compromise earlier on and help reduce expensive complications. As discussed above, maps of oxyhemoglobin, deoxyhemoglobin and tissue oxygen saturation can be derived from SFDI-derived absorption maps. Multiple groups have demonstrated the feasibility of SFDI to measure ischemic onset in a number of organs: including skin flaps,14,101–104 kidney,105 bowel,14 liver,14 and facial transplants.106 These studies have served as benchmarks to establish validity, sensitivity, and clinical relevance of SFDI oxygenation and hemoglobin measurements. It was first demonstrated in 2011 that oxygenation measurements trends using SFDI during an occlusion matched trends measured by FDA-cleared oximeter devices.14 Following this work, further studies demonstrated that SFDI could detect partial changes in flap circulation (50% blockage) prior to measurable changes in visual color.104 Confirming the diagnostic potential of SFDI, additional work demonstrated that severe ischemic conditions measured by SFDI in a cutaneous pedicle flaps was predictive of necrosis.101 Beyond the diagnostic potential of oxygenation imaging, it was also demonstrated that the source of the occlusion (arterial versus venous) could be identified as early as 2 min after blockage in a hemifacial composite flap transplants.106 Published clinical data using SFDI have been limited. A first-in-human pilot study involving three patients established the capability of SFDI to work under the constraint of flap transplantation surgeries.107 Although clinical work has been exploratory, the most important outcome of the work has been core algorithm development to enable rapid assessment of wide-field circulation across complicated curved surfaces. Detection of early-onset ischemia remains a high-end use case for surgical guidance and SFDI measures of circulation could help surgeons in planning, intraoperative, and postoperative stages of care.
4.4. Oncology/Cancer
SFDI applications in oncology have primarily focused on two main areas: margin detection and tumor response monitoring. In the area of margin detection, SFDI has been proposed as a tool to improve two sources of optical contrast. First, SFDI has been used to improve measurement of fluorescence signals by correcting for the confounding effects of absorption and scattering. One of the main applications for this is PpIX fluorescence guided resection in both glioma models and nonmelanoma cancers.23,25,73,108 Recent work by Valdes et al. has prototyped a real-time fluorescence measurement embodiment to facilitate translation to operating room and real-time scenarios.75 SFDI-derived subdiffusive endogenous reflectance and scattering contrast has also become a useful tool for classifying excised tissue types. The main goal for this is work is to enable intraoperative assessment of lumpectomy margins by differentiating between normal, fibroadenoma, ductal carcinoma in situ (DCIS), and invasive cancer.109,110 Recently, the development of subdiffuse SFDI has shown an even stronger potential for highlighting structural changes related to scattering and the phase function moments on freshly excised human specimen.52,111,112 Nandy et al. have extended this concept of in vitro tissue analysis for in vivo ovarian cancer applications113 as well as colon pathologies.114 The other arm of activity is focusing on treatment/monitoring side. These efforts including follow-up of drug delivery in the brain tumors in rats,115 and the monitoring of chemotherapy treatment in mice.116 The work to date in the area has advanced correction algorithms for small animal imaging but more importantly highlighted the potential of using SFDI to longitudinally track the efficacy of drug therapies that affect circulation or other treatments that eradicate tumors.36,116 The potential for SFDI to link preclinical discovery and clinical translation makes oncology applications a good fit in both preclinical environment and intraoperative assessment.
4.5. Skin Characterization
Characterization of skin properties is a key input for diagnosis and treatment in dermatological practices. SFDI can quantify skin optical properties and provide a basis for laser power, pulse duration, and treatment endpoints. For example, SFDI was used to image port-wine stains prior to and after treatment to quantify optical property changes and purpura.118,119 This study demonstrated feasibility of measurement over a complex surface (the human face) but further work is needed in larger cohorts to determine efficacy. Similar to treatment of birthmark defects, lasers are used for tattoo removal. SFDI has been proposed to characterize highly variable ink properties to provide objective measures for ablative laser-based tattoo removal.120 Another example is the imaging of absorption and scattering properties of skin for the diagnosis of nonmelanoma cancer.15,19 Skin characterization using SFDI has also been used to quantify different layers of skin to gain insight into the structure. The need to better quantify skin properties lead to the development of spatial frequency domain spectroscopy (SFDS) to get high-resolution spectra.121 Saager et al. correlated spatial frequency domain signals with multiphoton signals to gain a better understand of skin structure,121 and the same teams used SFDI signals interpret metabolic signals in skin.122 The idea of tracking skin optical properties is pervasive in aesthetic applications as well and the concept of pre- and post-SFDI characterization can be applied to any number of laser treatment paradigms.
4.6. Neuroscience
SFDI has primarily been used in preclinical models to investigate functional status in neurological activity. The first work showed spatio-temporal absorption and scattering changes in an induced cortical spreading depression wave. Unique SFDI scattering signatures preceded functional hemoglobin changes suggested the capability to measure depolarization.123 SFDI of the brain is primarily used to provide insight into the neuroplasticity of the brain for diagnosis and treatment of functional brain episodes that include ischemic strokes,48 epilepsy, traumatic brain injury,124 cardiac arrest,90 and migraines. SFDI also has the unique ability to provide the additional depth section capability for tomographic localization of hemodynamic signals during functional activation imaging.117,125 Lin et al.126–128 have also done work to characterize SFDI optical signatures in degenerative diseases like Alzheimer’s and characterized baseline properties while measuring vascular impairment due to neuronal death and amyloid-beta plaques. Due to continuous noninvasive imaging capability, treatments and disease can be tracked much more efficiently in preclinical research. However, since the SFDI cannot image through the intact skull, SFDI brain research has focused mostly on the preclinical side with some clinical intraoperative applications for tumor resection (see Sec. 4.4).
4.7. Turbid Sample Characterization
Characterization of turbid systems extends beyond biological applications that are the primary focus of this review. One group, however, has used SFDI to look at the surface layering properties of intralipid phantoms. In particular, SFDI enabled a wide-field depth sensitive characterization of an emulsion of intralipid in water, a material often used to make reference measurements in diffuse optics.129 Their findings, confirmed by independent spatially-resolved reflectance measurements, show that a two-layer model should be used when using intralipid as a reference measurement. Multiple groups have depended on SFDI as a tool to characterize calibration phantoms and validate new fabrication methods.130,131 Konecky et al. have also demonstrated the use of multiple orientation SFDI to characterize scattering orientation in both biological and nonbiological samples.67 Yang et. al22 introduced polarized SFDI to further characterize soft tissue fiber orientation in multiple tissue types—most notably heart tissue. Sample characterization is also critical for other modalities. Simply combining SFDI-derived optical properties with other modalities such fluorescence, laser speckle imaging, multiphoton imaging, multispectral imaging, and Cerenkov can enhance the quantitative nature of each modality.75,84,88,132 Finally, SFDI applications extend to wherever turbidity is an issue—including nonmedical applications. As an example, multiple groups are using SFDI to characterize produce and identify subsurface bruising in apples and pears as a quality control tool.133,134 This makes SFDI a versatile tool that can be customized by a number of research groups.
5. SFDI resources
As part of a recent effort to disseminate SFDI technology in the field of biomedical optics, several leading groups decided into join efforts in providing an open web-based support resources to any researcher interested in developing theory and application based on the SFD method. The main collaborative website is www.openSFDI.org, implemented and maintained by Matt Applegate. Additional resources can be also found at www.healthphotonics.org. Overall the following resources are available:
-
•
Training code with a stepwise tutorial using MATLAB functions, allowing to develop a practical understanding of the different steps in the processing of data in the SFD.
-
•
Raw data acquired by a validated imaging system (optical phantoms and a hand), as well as a reference executable processing code allowing to test new processing methods as well as validating new imaging devices.
-
•
Hardware guidance in making a simple and inexpensive SFDI system, along with validation data for precision and accuracy, also providing references to develop new imaging systems.
-
•
A regularly updated list of publications, along with a link to submit publications to be listed in the website.
-
•
Resources to make optical phantoms that are necessary for implementing correctly the SFDI method.
This initiative is open and community driven, and any contributions or suggestions are welcome.
6. Conclusion
In this review, we summarized the principles of SFDI, described the underlying theory, analyzed limitations, and finally depicted a contemporary view of its applications. Through this description, it becomes evident that SFDI has built quickly on its main advantage for imaging wide FoV quantitatively and rapidly. In less than a decade, many researchers have joined the effort to develop theory, instrumentation and applications for this unique technology, resulting in over 130 peer-reviewed publications (all referenced on the openSFDI website). Over the next years, developments are expected to rapidly mature. First, the capacity for DOI to obtain data that is highly specific and sensitive to both tissue status and disease condition will be further realized. This development is a direct continuation from the work performed using single-point spectroscopic measurement (absorption or scattering or both), which has already confirmed the potential of these metrics in the context of biology and health. Second, we anticipate the combination of SFDI with additional modalities, combining the advantages of multiple measurements using a single system. The use of laser speckle imaging and SFDI has already paved the way in this regard, as did the combination of endogenous and exogenous (fluorescence) contrast imaging. Finally, we look forward to the design and translation of novel SFDI instrumentation into various preclinical and clinical outcome studies. This area remains mainly unexplored, and we can expect many discoveries from increasing collaborations with healthcare professionals and biologists. Overall, SFDI has generated great interest in our community, and we can expect it to grow as a major player in the applications of DOI.
Acknowledgments
The authors would like to thank all researchers in the Diffuse Optical and SFDI community for their contributions toward this review article and their help with the 2019 SFDI special section in the Journal of Biomedical Optics. Some of the work presented in this paper is supported by the European Research Council (ERC) under the European Union’s Horizon 2020 Research And Innovation Program under Grant Agreement No. 715737 (QuantSURG; S.G.), France Life Imaging WP3 (S.G.), the French program “Investissement d’Avenir” run by the “Agence Nationale de la Recherche” under Grant Agreement No. ANR-11-INBS-006 (S.G.), and the University of Strasbourg IdEx (S.G.).
Biography
Biographies of the authors are not available.
Disclosures
D. C. is the Chief Executive Officer and Chief Technology Officer, and A. M. is the Vice-President of Research and Development at Modulim, and together disclose patents related to SFDI technology. S. G. declares that there are no conflicts of interest related to this paper.
References
- 1.Cuccia D. J., et al. , “Quantitation and mapping of tissue optical properties using modulated imaging,” J. Biomed. Opt. 14(2), 024012 (2009). 10.1117/1.3088140 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Dognitz N., Wagnieres G., “Determination of tissue optical properties by steady-state spatial frequency-domain reflectometry,” Lasers Med. Sci. 13(1), 55–65 (1998). 10.1007/BF00592960 [DOI] [Google Scholar]
- 3.Ishimaru A., Wave Propagation and Scattering in Random Media, Elsevier, New York: (1978). [Google Scholar]
- 4.Li X. D., et al. , “Diffraction tomography for biochemical imaging with diffuse-photon density waves,” Opt. Lett. 22(8), 573–575 (1997). 10.1364/OL.22.000573 [DOI] [PubMed] [Google Scholar]
- 5.Kienle A., et al. , “Noninvasive determination of the optical properties of two-layered turbid media,” Appl. Opt. 37(4), 779–791 (1998). 10.1364/AO.37.000779 [DOI] [PubMed] [Google Scholar]
- 6.Markel V. A., Schotland J. C., “Inverse problem in optical diffusion tomography. I. Fourier-Laplace inversion formulas,” J. Opt. Soc. Am. A 18(6), 1336–1347 (2001). 10.1364/JOSAA.18.001336 [DOI] [PubMed] [Google Scholar]
- 7.Wang L. H., Jacques S. L., Zheng L. Q., “MCML—Monte Carlo modeling of photon transport in multi-layered tissues,” Comput. Methods Prog. Biomed. 47, 131–146 (1995). 10.1016/0169-2607(95)01640-F [DOI] [PubMed] [Google Scholar]
- 8.Gardner A. R., Venugopalan V., “Accurate and efficient Monte Carlo solutions to the radiative transport equation in the spatial frequency domain,” Opt. Lett. 36(12), 2269–2271 (2011). 10.1364/OL.36.002269 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Kim A. D., “Transport theory for light propagation in biological tissue,” J. Opt. Soc. Am. A 21(5), 820–827 (2004). 10.1364/JOSAA.21.000820 [DOI] [PubMed] [Google Scholar]
- 10.Yao R., Intes X., Fang Q., “Generalized mesh-based Monte Carlo for wide-field illumination and detection via mesh retessellation,” Biomed. Opt. Express 7(1), 171–184 (2016). 10.1364/BOE.7.000171 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Kanick S. C., et al. , “Sub-diffusive scattering parameter maps recovered using wide-field high-frequency structured light imaging,” Biomed. Opt. Express 5(10), 3376–3390 (2014). 10.1364/BOE.5.003376 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Bodenschatz N., et al. , “Detecting structural information of scatterers using spatial frequency domain imaging,” J. Biomed. Opt. 20(11), 116006 (2015). 10.1117/1.JBO.20.11.116006 [DOI] [PubMed] [Google Scholar]
- 13.Hayakawa C. K., et al. , “Optical sampling depth in the spatial frequency domain,” J. Biomed. Opt. 24(7), 071603 (2018). 10.1117/1.JBO.24.7.071603 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Gioux S., et al. , “First-in-human pilot study of a spatial frequency domain oxygenation imaging system,” J. Biomed. Opt. 16(8), 086015 (2011). 10.1117/1.3614566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Saager R. B., et al. , “A light emitting diode (LED) based spatial frequency domain imaging system for optimization of photodynamic therapy of nonmelanoma skin cancer: quantitative reflectance imaging,” Lasers Surg. Med. 45(4), 207–215 (2013). 10.1002/lsm.v45.4 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Angelo J. P., van de Giessen M., Gioux S., “Real-time endoscopic optical properties imaging,” Biomed. Opt. Express 8(11), 5113–5126 (2017). 10.1364/BOE.8.005113 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Weber J. R., et al. , “Multispectral imaging of tissue absorption and scattering using spatial frequency domain imaging and a computed-tomography imaging spectrometer,” J. Biomed. Opt. 16(1), 011015 (2011). 10.1117/1.3528628 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Nguyen T. T. A., et al. , “Novel application of a spatial frequency domain imaging system to determine signature spectral differences between infected and noninfected burn wounds,” J. Burn Care Res. 34(1), 44–50 (2013). 10.1097/BCR.0b013e318269be30 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Rohrbach D. J., et al. , “Preoperative mapping of nonmelanoma skin cancer using spatial frequency domain and ultrasound imaging,” Acad. Radiol. 21(2), 263–270 (2014). 10.1016/j.acra.2013.11.013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Lin A. J., et al. , “Visible spatial frequency domain imaging with a digital light microprojector,” J. Biomed. Opt. 18(9), 096007 (2013). 10.1117/1.JBO.18.9.096007 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Ghassemi P., et al. , “A polarized multispectral imaging system for quantitative assessment of hypertrophic scars,” Biomed. Opt. Express 5(10), 3337–3354 (2014). 10.1364/BOE.5.003337 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Yang B., et al. , “Polarized light spatial frequency domain imaging for non-destructive quantification of soft tissue fibrous structures,” Biomed. Opt. Express 6(4), 1520–1533 (2015). 10.1364/BOE.6.001520 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Sibai M., et al. , “Quantitative spatial frequency fluorescence imaging in the sub-diffusive domain for image-guided glioma resection,” Biomed. Opt. Express 6(12), 4923–4933 (2015). 10.1364/BOE.6.004923 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Nandy S., et al. , “Characterizing optical properties and spatial heterogeneity of human ovarian tissue using spatial frequency domain imaging,” J. Biomed. Opt. 21(10), 101402 (2016). 10.1117/1.JBO.21.10.101402 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Wirth D., et al. , “Feasibility of using spatial frequency-domain imaging intraoperatively during tumor resection,” J. Biomed. Opt. 24(7), 071608 (2018). 10.1117/1.JBO.24.7.071608 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Gioux S., et al. , “Three-dimensional surface profile intensity correction for spatially modulated imaging,” J. Biomed. Opt. 14(3), 034045 (2009). 10.1117/1.3156840 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Nguyen J. Q., et al. , “Effects of motion on optical properties in the spatial frequency domain,” J. Biomed. Opt. 16(12), 126009 (2011). 10.1117/1.3662454 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 28.Vervandier J., Gioux S., “Single snapshot imaging of optical properties,” Biomed. Opt. Express 4(12), 2938–2944 (2013). 10.1364/BOE.4.002938 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.van de Giessen M., Angelo J. P., Gioux S., “Real-time, profile-corrected single snapshot imaging of optical properties,” Biomed. Opt. Express 6(10), 4051–4062 (2015). 10.1364/BOE.6.004051 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Nadeau K. P., Durkin A. J., Tromberg B. J., “Advanced demodulation technique for the extraction of tissue optical properties and structural orientation contrast in the spatial frequency domain,” J. Biomed. Opt. 19(5), 056013 (2014). 10.1117/1.JBO.19.5.056013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 31.Nadeau K. P., et al. , “Multifrequency synthesis and extraction using square wave projection patterns for quantitative tissue imaging,” J. Biomed. Opt. 20(11), 116005 (2015). 10.1117/1.JBO.20.11.116005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Aguenounon E., et al. , “Single snapshot of optical properties image quality improvement using anisotropic 2D windows filtering,” J. Biomed. Opt. 24(7), 071611 (2019). 10.1117/1.JBO.24.7.071611 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Ayers F., et al. , “Fabrication and characterization of silicone-based tissue phantoms with tunable optical properties in the visible and near infrared domain,” Proc. SPIE 6870, 687007 (2008). 10.1117/12.764969 [DOI] [Google Scholar]
- 34.Pogue B. W., Patterson M. S., “Review of tissue simulating phantoms for optical spectroscopy, imaging and dosimetry,” J. Biomed. Opt. 11(4), 041102 (2006). 10.1117/1.2335429 [DOI] [PubMed] [Google Scholar]
- 35.Saager R. B., et al. , “Low-cost tissue simulating phantoms with adjustable wavelength-dependent scattering properties in the visible and infrared ranges,” J. Biomed. Opt. 21(6), 067001 (2016). 10.1117/1.JBO.21.6.067001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Zhao Y., et al. , “Angle correction for small animal tumor imaging with spatial frequency domain imaging (SFDI),” Biomed. Opt. Express 7(6), 2373–2384 (2016). 10.1364/BOE.7.002373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Nguyen J. T., et al. , “Bone flap perfusion assessment using near-infrared fluorescence imaging,” J. Surg. Res. 178(2), e43–e50 (2012). 10.1016/j.jss.2012.05.014 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 38.Bodenschatz N., et al. , “Sources of errors in spatial frequency domain imaging of scattering media,” J. Biomed. Opt. 19(7), 071405 (2014). 10.1117/1.JBO.19.7.071405 [DOI] [PubMed] [Google Scholar]
- 39.Pera V., et al. , “Optical property uncertainty estimates for spatial frequency domain imaging,” Biomed. Opt. Express 9(2), 661–678 (2018). 10.1364/BOE.9.000661 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Zhao Y., et al. , “Deep learning model for ultrafast multifrequency optical property extractions for spatial frequency domain imaging,” Opt. Lett. 43(22), 5669–5672 (2018). 10.1364/OL.43.005669 [DOI] [PubMed] [Google Scholar]
- 41.Mazhar A., et al. , “Implementation of an LED-based clinical spatial frequency domain imaging system,” Proc. SPIE 8254, 82540A (2012) 10.1117/12.909813 [DOI] [Google Scholar]
- 42.Nadeau K. P., et al. , “Component and system evaluation for the development of a handheld point-of-care spatial frequency domain imaging (SFDI) device,” Proc. SPIE 8573, 857304 (2013). 10.1117/12.2004909 [DOI] [Google Scholar]
- 43.Cuccia D. J., et al. , “Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain,” Opt. Lett. 30(11), 1354–1356 (2005). 10.1364/OL.30.001354 [DOI] [PubMed] [Google Scholar]
- 44.Angelo J., et al. , “Ultrafast optical property map generation using lookup tables,” J. Biomed. Opt. 21(11), 110501 (2016). 10.1117/1.JBO.21.11.110501 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Panigrahi S., Gioux S., “Machine learning approach for rapid and accurate estimation of optical properties using spatial frequency domain imaging,” J. Biomed. Opt. 24(7), 071606 (2018). 10.1117/1.JBO.24.7.071606 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Erickson T. A., et al. , “Lookup-table method for imaging optical properties with structured illumination beyond the diffusion theory regime,” J. Biomed. Opt. 15(3), 036013 (2010). 10.1117/1.3431728 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Bassi A., et al. , “Spatial shift of spatially modulated light projected on turbid media,” J. Opt. Soc. Am. A 25(11), 2833–2839 (2008). 10.1364/JOSAA.25.002833 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 48.Abookasis D., et al. , “Imaging cortical absorption, scattering, and hemodynamic response during ischemic stroke using spatially modulated near-infrared illumination,” J. Biomed. Opt. 14(2), 024033 (2009). 10.1117/1.3116709 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.Bassi A., et al. , “Detection of inhomogeneities in diffusive media using spatially modulated light,” Opt. Lett. 34(14), 2156–2158 (2009). 10.1364/OL.34.002156 [DOI] [PubMed] [Google Scholar]
- 50.Weber J., Cuccia D. J. D., Tromberg B. J., “Noncontact imaging of absorption and scattering in layered tissue using spatially modulated structured light,” J. Appl. Phys. 105, 102028 (2009). 10.1063/1.3116135 [DOI] [Google Scholar]
- 51.Liemert A., Kienle A., “Spatially modulated light source obliquely incident on a semi-infinite scattering medium,” Opt. Lett. 37(19), 4158–4160 (2012). 10.1364/OL.37.004158 [DOI] [PubMed] [Google Scholar]
- 52.McClatchy D. M., 3rd, et al. , “Wide-field quantitative imaging of tissue microstructure using sub-diffuse spatial frequency domain imaging,” Optica 3(6), 613–621 (2016). 10.1364/OPTICA.3.000613 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 53.Weber J. R., Cuccia D. J., Tromberg B. J., “Modulated imaging in layered media,” in Conf. Proc. IEEE Eng. Med. Biol. Soc., pp. 6674–6676 (2006). 10.1109/IEMBS.2006.260918 [DOI] [PubMed] [Google Scholar]
- 54.Yudovsky D., Nguyen J. Q., Durkin A. J., “In vivo spatial frequency domain spectroscopy of two layer media,” J. Biomed. Opt. 17(10), 107006 (2012). 10.1117/1.JBO.17.10.107006 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 55.Saager R. B., et al. , “In vivo measurements of cutaneous melanin across spatial scales: using multiphoton microscopy and spatial frequency domain spectroscopy,” J. Biomed. Opt. 20(6), 066005 (2015). 10.1117/1.JBO.20.6.066005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 56.Konecky S. D., et al. , “Quantitative optical tomography of sub-surface heterogeneities using spatially modulated structured light,” Opt. Express 17(17), 14780–14790 (2009). 10.1364/OE.17.014780 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 57.Lukic V., Markel V. A., Schotland J. C., “Optical tomography with structured illumination,” Opt. Lett. 34(7), 983–985 (2009). 10.1364/OL.34.000983 [DOI] [PubMed] [Google Scholar]
- 58.Belanger S., et al. , “Real-time diffuse optical tomography based on structured illumination,” J. Biomed. Opt. 15(1), 016006 (2010). 10.1117/1.3290818 [DOI] [PubMed] [Google Scholar]
- 59.D’Andrea C., et al. , “Fast 3D optical reconstruction in turbid media using spatially modulated light,” Biomed. Opt. Express 1(2), 471–481 (2010). 10.1364/BOE.1.000471 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 60.Ducros N., et al. , “Full-wavelet approach for fluorescence diffuse optical tomography with structured illumination,” Opt. Lett. 35(21), 3676–3678 (2010). 10.1364/OL.35.003676 [DOI] [PubMed] [Google Scholar]
- 61.Saager R. B., et al. , “Method for depth-resolved quantitation of optical properties in layered media using spatially modulated quantitative spectroscopy,” J. Biomed. Opt. 16(7), 077002 (2011). 10.1117/1.3597621 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 62.Ducros N., et al. , “A virtual source pattern method for fluorescence tomography with structured light,” Phys. Med. Biol. 57(12), 3811–3832 (2012). 10.1088/0031-9155/57/12/3811 [DOI] [PubMed] [Google Scholar]
- 63.Konecky S. D., et al. , “Spatial frequency domain tomography of protoporphyrin IX fluorescence in preclinical glioma models,” J. Biomed. Opt. 17(5), 056008 (2012). 10.1117/1.JBO.17.5.056008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 64.Kristensson E., Berrocal E., Alden M., “Quantitative 3D imaging of scattering media using structured illumination and computed tomography,” Opt. Express 20(13), 14437–14450 (2012). 10.1364/OE.20.014437 [DOI] [PubMed] [Google Scholar]
- 65.Ducros N., et al. , “Fluorescence molecular tomography of an animal model using structured light rotating view acquisition,” J. Biomed. Opt. 18(2), 020503 (2013). 10.1117/1.JBO.18.2.020503 [DOI] [PubMed] [Google Scholar]
- 66.Mazhar A., et al. , “Wavelength optimization for rapid chromophore mapping using spatial frequency domain imaging,” J. Biomed. Opt. 15(6), 061716 (2010). 10.1117/1.3523373 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 67.Konecky S. D., et al. , “Imaging scattering orientation with spatial frequency domain imaging,” J. Biomed. Opt. 16(12), 126001 (2011). 10.1117/1.3657823 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 68.Mazhar A., et al. , “Structured illumination enhances resolution and contrast in thick tissue fluorescence imaging,” J. Biomed. Opt. 15(1), 010506 (2010). 10.1117/1.3299321 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 69.Yang B., Sharma M., Tunnell J. W., “Attenuation-corrected fluorescence extraction for image-guided surgery in spatial frequency domain,” J. Biomed. Opt. 18(8), 080503 (2013). 10.1117/1.JBO.18.8.080503 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 70.Sun J., et al. , “Enhancing in vivo tumor boundary delineation with structured illumination fluorescence molecular imaging and spatial gradient mapping,” J. Biomed. Opt. 21(8), 080502 (2016). 10.1117/1.JBO.21.8.080502 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 71.Angelo J., et al. , “Masked detection of structured illumination (MDSI): depth sensitive fluorescence measurement,” Proc. SPIE 8578, 85780Q (2013). 10.1117/12.2004645 [DOI] [Google Scholar]
- 72.Fantoni F., et al. , “Laser line scanning illumination scheme for the enhancement of contrast and resolution for fluorescence reflectance imaging,” Proc. SPIE 8572, 85720L (2013). 10.1117/12.2004320 [DOI] [Google Scholar]
- 73.Saager R. B., et al. , “Quantitative fluorescence imaging of protoporphyrin IX through determination of tissue optical properties in the spatial frequency domain,” J. Biomed. Opt. 16(12), 126013 (2011). 10.1117/1.3665440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 74.Sibai M., et al. , “Quantitative subsurface spatial frequency-domain fluorescence imaging for enhanced glioma resection,” J. Biophotonics 12(5), e201800271 (2019). 10.1002/jbio.2019.12.issue-5 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 75.Valdes P. A., et al. , “qF-SSOP: real-time optical property corrected fluorescence imaging,” Biomed. Opt. Express 8(8), 3597–3605 (2017). 10.1364/BOE.8.003597 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 76.Mazhar A., et al. , “Laser speckle imaging in the spatial frequency domain,” Biomed. Opt. Express 2(6), 1553–1563 (2011). 10.1364/BOE.2.001553 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 77.Zhao Y., Roblyer D., “Spatial mapping of fluorophore quantum yield in diffusive media,” J. Biomed. Opt. 20(8), 086013 (2015). 10.1117/1.JBO.20.8.086013 [DOI] [PubMed] [Google Scholar]
- 78.Chen J., et al. , “Time-resolved diffuse optical tomography with patterned-light illumination and detection,” Opt. Lett. 35(13), 2121–2123 (2010). 10.1364/OL.35.002121 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 79.Kumar A. T., “Fluorescence lifetime detection in turbid media using spatial frequency domain filtering of time domain measurements,” Opt. Lett. 38(9), 1440–1442 (2013). 10.1364/OL.38.001440 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 80.Rice T. B., et al. , “Quantitative determination of dynamical properties using coherent spatial frequency domain imaging,” J. Opt. Soc. Am. A 28(10), 2108–2114 (2011). 10.1364/JOSAA.28.002108 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 81.Rice T. B., et al. , “Determination of the effect of source intensity profile on speckle contrast using coherent spatial frequency domain imaging,” Biomed. Opt. Express 3(6), 1340–1349 (2012). 10.1364/BOE.3.001340 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 82.Rice T. B., et al. , “Quantitative, depth-resolved determination of particle motion using multi-exposure, spatial frequency domain laser speckle imaging,” Biomed. Opt. Express 4(12), 2880–2892 (2013). 10.1364/BOE.4.002880 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 83.Ghijsen M., et al. , “Real-time simultaneous single snapshot of optical properties and blood flow using coherent spatial frequency domain imaging (cSFDI),” Biomed. Opt. Express 7(3), 870–882 (2016). 10.1364/BOE.7.000870 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 84.Ghijsen M., et al. , “Quantitative real-time optical imaging of the tissue metabolic rate of oxygen consumption,” J. Biomed. Opt. 23(3), 036013 (2018). 10.1117/1.JBO.23.3.036013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 85.Saager R. B., Cuccia D. J., Durkin A. J., “Determination of optical properties of turbid media spanning visible and near-infrared regimes via spatially modulated quantitative spectroscopy,” J. Biomed. Opt. 15(1), 017012 (2010). 10.1117/1.3299322 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 86.Wilson R. H., et al. , “Quantitative short-wave infrared multispectral imaging of in vivo tissue optical properties,” J. Biomed. Opt. 19(8), 086011 (2014). 10.1117/1.JBO.19.8.086011 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 87.Applegate M. B., Roblyer D., “High-speed spatial frequency domain imaging with temporally modulated light,” J. Biomed. Opt. 22(7), 076019 (2017). 10.1117/1.JBO.22.7.076019 [DOI] [PubMed] [Google Scholar]
- 88.Schmidt M., et al. , “Real-time, wide-field, and quantitative oxygenation imaging using spatiotemporal modulation of light,” J. Biomed. Opt. 24(7), 071610 (2019). 10.1117/1.JBO.24.7.071610 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 89.Aguenounon E., et al. , “Real time hyperspectral imaging using high frame rate video camera and GPGPU processing,” in SIGNAL, Nice, France: (2018). [Google Scholar]
- 90.Wilson R. H., et al. , “High-speed spatial frequency domain imaging of rat cortex detects dynamic optical and physiological properties following cardiac arrest and resuscitation,” Neurophotonics 4(4), 045008 (2017). 10.1117/1.NPh.4.4.045008 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 91.Weinkauf C., et al. , “Near-instant noninvasive optical imaging of tissue perfusion for vascular assessment,” J. Vasc. Surg. 69(2), 555–562 (2018). 10.1016/j.jvs.2018.06.202 [DOI] [PubMed] [Google Scholar]
- 92.Saidian M., et al. , “Characterisation of impaired wound healing in a preclinical model of induced diabetes using wide-field imaging and conventional immunohistochemistry assays,” Int. Wound J. 16(1), 144–152 (2018). 10.1111/iwj.2019.16.issue-1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 93.Yafi A., et al. , “Quantitative skin assessment using spatial frequency domain imaging (SFDI) in patients with or at high risk for pressure ulcers,” Lasers Surg. Med. 49(9), 827–834 (2017). 10.1002/lsm.v49.9 [DOI] [PubMed] [Google Scholar]
- 94.Nguyen J. Q., et al. , “Spatial frequency domain imaging of burn wounds in a preclinical model of graded burn severity,” J. Biomed. Opt. 18(6), 066010 (2013). 10.1117/1.JBO.18.6.066010 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 95.Mazhar A., et al. , “Noncontact imaging of burn depth and extent in a porcine model using spatial frequency domain imaging,” J. Biomed. Opt. 19(8), 086019 (2014). 10.1117/1.JBO.19.8.086019 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 96.Ponticorvo A., et al. , “Quantitative assessment of graded burn wounds in a porcine model using spatial frequency domain imaging (SFDI) and laser speckle imaging (LSI),” Biomed. Opt. Express 5(10), 3467–3481 (2014). 10.1364/BOE.5.003467 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 97.Burmeister D. M., et al. , “Utility of spatial frequency domain imaging (SFDI) and laser speckle imaging (LSI) to non-invasively diagnose burn depth in a porcine model,” Burns 41(6), 1242–1252 (2015). 10.1016/j.burns.2015.03.001 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 98.Travis T. E., et al. , “A multimodal assessment of melanin and melanocyte activity in abnormally pigmented hypertrophic scar,” J. Burn Care Res. 36(1), 77–86 (2015). 10.1097/BCR.0000000000000154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 99.Ponticorvo A., et al. , “Evaluating clinical observation versus Spatial Frequency Domain Imaging (SFDI), Laser Speckle Imaging (LSI) and thermal imaging for the assessment of burn depth,” Burns 45(2), 450–460 (2018). 10.1016/j.burns.2018.09.026 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 100.Ponticorvo A., et al. , “529 Evaluating clinical observation, spatial frequency domain imaging (SFDI) and laser speckle imaging (LSI) for the assessment of burns,” J. Burn Care Res. 39(suppl_1), S238–S239 (2018). 10.1093/jbcr/iry006.452 [DOI] [Google Scholar]
- 101.Pharaon M. R., et al. , “Early detection of complete vascular occlusion in a pedicle flap model using quantitation spectral imaging,” Plast. Reconstr. Surg. 126(6), 1924–1935 (2010). 10.1097/PRS.0b013e3181f447ac [DOI] [PMC free article] [PubMed] [Google Scholar]
- 102.Yafi A., et al. , “Postoperative quantitative assessment of reconstructive tissue status in a cutaneous flap model using spatial frequency domain imaging,” Plast. Reconstr. Surg. 127(1), 117–130 (2011). 10.1097/PRS.0b013e3181f959cc [DOI] [PMC free article] [PubMed] [Google Scholar]
- 103.Ponticorvo A., et al. , “Quantitative assessment of partial vascular occlusions in a swine pedicle flap model using spatial frequency domain imaging,” Biomed. Opt. Express 4(2), 298–306 (2013). 10.1364/BOE.4.000298 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 104.Ponticorvo A., et al. , “Evaluating visual perception for assessing reconstructed flap health,” J. Surg. Res. 197(1), 210–217 (2015). 10.1016/j.jss.2015.03.099 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 105.Nadeau K. P., et al. , “Quantitative assessment of renal arterial occlusion in a porcine model using spatial frequency domain imaging,” Opt. Lett. 38(18), 3566–3569 (2013). 10.1364/OL.38.003566 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 106.Vargas C. R., et al. , “Intraoperative hemifacial composite flap perfusion assessment using spatial frequency domain imaging: a pilot study in preparation for facial transplantation,” Ann. Plast. Surg. 76(2), 249–255 (2016). 10.1097/SAP.0000000000000631 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 107.Nguyen J. T., et al. , “A novel pilot study using spatial frequency domain imaging to assess oxygenation of perforator flaps during reconstructive breast surgery,” Ann. Plast. Surg. 71(3), 308–315 (2013). 10.1097/SAP.0b013e31828b02fb [DOI] [PMC free article] [PubMed] [Google Scholar]
- 108.Sunar U., et al. , “Quantification of PpIX concentration in basal cell carcinoma and squamous cell carcinoma models using spatial frequency domain imaging,” Biomed. Opt. Express 4(4), 531–537 (2013). 10.1364/BOE.4.000531 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 109.Laughney A. M., et al. , “System analysis of spatial frequency domain imaging for quantitative mapping of surgically resected breast tissues,” J. Biomed. Opt. 18(3), 036012 (2013). 10.1117/1.JBO.18.3.036012 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 110.Laughney A. M., et al. , “Spectral discrimination of breast pathologies in situ using spatial frequency domain imaging,” Breast Cancer Res. 15(4), R61 (2013). 10.1186/bcr3455 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 111.McClatchy D. M., et al. , “Light scattering measured with spatial frequency domain imaging can predict stromal versus epithelial proportions in surgically resected breast tissue,” J. Biomed. Opt. 24(7), 071605 (2018). 10.1117/1.JBO.24.7.071605 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 112.Lin W., et al. , “Quantitative diagnosis of tissue microstructure with wide-field high spatial frequency domain imaging,” Biomed. Opt. Express 9(7), 2905–2916 (2018). 10.1364/BOE.9.002905 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 113.Nandy S., et al. , “Quantitative multispectral ex vivo optical evaluation of human ovarian tissue using spatial frequency domain imaging,” Biomed. Opt. Express 9(5), 2451–2456 (2018). 10.1364/BOE.9.002451 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 114.Nandy S., et al. , “Quantitative optical discrimination of benign and malignant human colon pathologies using spatial frequency domain modulated imaging,” in Biophotonics Congr. Biomed. Opt. Congr. (Microscopy/Translational/Brain/OTS), Optical Society of America, Hollywood, Florida: (2018). 10.1364/TRANSLATIONAL.2018.JW3A.46 [DOI] [Google Scholar]
- 115.Singh-Moon R. P., et al. , “Spatial mapping of drug delivery to brain tissue using hyperspectral spatial frequency-domain imaging,” J. Biomed. Opt. 19(9), 096003 (2014). 10.1117/1.JBO.19.9.096003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 116.Tabassum S., et al. , “Feasibility of spatial frequency domain imaging (SFDI) for optically characterizing a preclinical oncology model,” Biomed. Opt. Express 7(10), 4154–4170 (2016). 10.1364/BOE.7.004154 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 117.Konecky S. D., et al. , “Hyperspectral optical tomography of intrinsic signals in the rat cortex,” Neurophotonics 2(4), 045003 (2015). 10.1117/1.NPh.2.4.045003 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 118.Mazhar A., et al. , “Spatial frequency domain imaging of port wine stain biochemical composition in response to laser therapy: a pilot study,” Lasers Surg. Med. 44(8), 611–621 (2012). 10.1002/lsm.22067 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 119.Sharif S. A., et al. , “Noninvasive clinical assessment of port-wine stain birthmarks using current and future optical imaging technology: a review,” Br. J. Dermatol. 167(6), 1215–1223 (2012). 10.1111/j.1365-2133.2012.11139.x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 120.Ayers F. R., et al. , “Wide-field spatial mapping of in vivo tattoo skin optical properties using modulated imaging,” Lasers Surg. Med. 41(6), 442–453 (2009). 10.1002/lsm.v41:6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 121.Saager R. B., et al. , “Portable (handheld) clinical device for quantitative spectroscopy of skin, utilizing spatial frequency domain reflectance techniques,” Rev. Sci. Instrum. 88(9), 094302 (2017). 10.1063/1.5001075 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 122.Balu M., et al. , “In vivo multiphoton NADH fluorescence reveals depth-dependent keratinocyte metabolism in human skin,” Biophys. J. 104(1), 258–267 (2013). 10.1016/j.bpj.2012.11.3809 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 123.Cuccia D. J., et al. , “Quantitative in vivo imaging of tissue absorption, scattering, and hemoglobin concentration in rat cortex using spatially modulated structured light,” in In Vivo Optical Imaging of Brain Function, Frostig R. D., ed., CRC Press, Boca Raton, Florida: (2009). [PubMed] [Google Scholar]
- 124.Shaul O., et al. , “Application of spatially modulated near-infrared structured light to study changes in optical properties of mouse brain tissue during heatstress,” Appl. Opt. 56(32), 8880–8886 (2017). 10.1364/AO.56.008880 [DOI] [PubMed] [Google Scholar]
- 125.Reisman M. D., et al. , “Structured illumination diffuse optical tomography for noninvasive functional neuroimaging in mice,” Neurophotonics 4(2), 021102 (2017). 10.1117/1.NPh.4.2.021102 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 126.Lin A. J., et al. , “Spatial frequency domain imaging of intrinsic optical property contrast in a mouse model of Alzheimer’s disease,” Ann. Biomed. Eng. 39(4), 1349–1357 (2011). 10.1007/s10439-011-0269-6 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 127.Lin A. J., et al. , “In vivo optical signatures of neuronal death in a mouse model of Alzheimer’s disease,” Lasers Surg. Med. 46(1), 27–33 (2014). 10.1002/lsm.v46.1 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 128.Lin A. J., et al. , “Optical imaging in an Alzheimer’s mouse model reveals amyloid-beta-dependent vascular impairment,” Neurophotonics 1(1), 011005 (2014). 10.1117/1.NPh.1.1.011005 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 129.Bodenschatz N., et al. , “Surface layering properties of Intralipid phantoms,” Phys. Med. Biol. 60(3), 1171–1183 (2015). 10.1088/0031-9155/60/3/1171 [DOI] [PubMed] [Google Scholar]
- 130.Kennedy G. T., et al. , “Solid tissue simulating phantoms having absorption at 970 nm for diffuse optics,” J. Biomed. Opt. 22(7), 076013 (2017). 10.1117/1.JBO.22.7.076013 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 131.Greening G. J., et al. , “Characterization of thin poly(dimethylsiloxane)-based tissue-simulating phantoms with tunable reduced scattering and absorption coefficients at visible and near-infrared wavelengths,” J. Biomed. Opt. 19(11), 115002 (2014). 10.1117/1.JBO.19.11.115002 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 132.Hachadorian R., et al. , “Correcting Cherenkov light attenuation in tissue using spatial frequency domain imaging for quantitative surface dosimetry during whole breast radiation therapy,” J. Biomed. Opt. 24(7), 071609 (2018). 10.1117/1.JBO.24.7.071609 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 133.Anderson E., Cuccia D. J., Durkin A. J., “Detection of bruises on golden delicious apples using spatial-frequency-domain imaging,” Proc. SPIE 6430, 643010 (2007). 10.1117/12.717608 [DOI] [Google Scholar]
- 134.Hu D., et al. , “Noncontact and wide-field characterization of the absorption and scattering properties of apple fruit using spatial-frequency domain imaging,” Sci. Rep. 6, 37920 (2016). 10.1038/srep37920 [DOI] [PMC free article] [PubMed] [Google Scholar]