Abstract.
Single-shot, two-frame, -shifted spatially multiplexed interference microscopy (-SMIM) is presented as an improvement to previous SMIM implementations, introducing a versatile, robust, fast, and accurate method for cumbersome, noisy, and low-contrast phase object analysis. The proposed -SMIM equips a commercially available nonholographic microscope with a high-speed (video frame rate) enhanced quantitative phase imaging (QPI) capability by properly placing a beam-splitter in the microscope embodiment to simultaneously (in a single shot) record two holograms mutually phase shifted by radians at the expense of reducing the field of view. Upon subsequent subtractive superimposition of holograms, a -hologram is generated with reduced background and improved modulation of interference fringes. These features determine superior phase retrieval quality, obtained by employing the Hilbert spiral transform on the π-hologram, as compared with a single low-quality (low signal-to-noise ratio) hologram analysis. In addition, -SMIM enables accurate in-vivo analysis of high dynamic range phase objects, otherwise measurable only in static regime using time-consuming phase-shifting. The technique has been validated utilizing a NA objective in a regular Olympus BX-60 upright microscope for QPI of different lines of prostate cancer cells and flowing microbeads.
Keywords: digital holographic microscopy, interference microscopy, quantitative phase imaging, phase retrieval, fringe analysis
1. Introduction
Among a suite of modern microscopy techniques, quantitative phase imaging (QPI)1–3 stands out as a vividly blossoming and extremely capable label-free approach. It provides a unique means for imaging cells and tissues, merging beneficial features established at the core of microscopy,1 interferometry and holography,4 and numerical computations. Using the refractive index as an intrinsic contrast agent,5 QPI numerically converts the holographically encoded complex optical field of micro-objects into a nanoscale-precise subcellular-specific 2-D/3-D/4-D map of the examined transparent specimen.6,7 Impressive details can be imaged, e.g., via superresolution approaches,8 even in live organisms, without severe photo-damage. Application-oriented QPI research provided recently outstanding solutions in numerous exciting biomedical fields, i.e., in neuroscience, methods such as digital holographic microscopy (DHM),9 spatial light interference microscopy (SLIM),10 and optical diffraction tomography (ODT);11 in cell/tissue biology, ODT,11 SLIM,10 transport of intensity,12 Fourier ptychography,13 and quadriwave interferometry;14 and in cancer diagnosis, DHM15 and diffraction phase microscopy,16,17 to name only some approaches. It is also worth showcasing the importance of in-flow quantitative phase measurements.18,19
The QPI setup stability and simplicity can be enhanced using common-path strategies,20 while partial coherence may be employed to decrease speckle noise.21 Among those methods, spatially multiplexed interferometric microscopy (SMIM) proposes a straightforward and low-cost way to convert a commercially available regular microscope into a holographic one with only minimal modifications.22,23 SMIM is based on a common-path interferometric layout; the modifications consist of saving a clear region at the input plane for a reference beam, providing a coherent light source, and properly inserting diffraction grating. In this paper, we significantly advance this technique and propose an extremely robust and capable QPI method using a laser diode source, beam-splitter, and phase retrieval algorithm to upgrade a wide-field microscope into a versatile holographic one.
All QPI solutions are full-field optical techniques relying on the virtue of storing object information in an optical complex amplitude, which is subsequently encoded in a digital image. The characteristic quasi-periodic intensity pattern—the hologram (I)—is generated upon interference of object and reference beams, which are clearly distinguishable in coherent (holographic) coding. The hologram comprises a sum of three fundamental intensity components: background (incoherent sum of intensities of interfering beams and ), noise (uncorrelated and/or structured, ), and coherent interference fringes constituted by a cosine function modulated in phase () and amplitude :
| (1) |
Phase distribution () is of interest and is represented as a local shape of the period and orientation variations of fringes. Therefore, an extremely important step of each full-field QPI method comprises the fringe pattern (hologram) phase demodulation understood as phase map decoding from the registered intensity distribution.
There are two fundamental QPI architectures with respect to the phase demodulation strategy employed: on-axis with temporal phase shifting-based phase demodulation24 and off-axis with Fourier transform (FT)-based phase retrieval.25 The on/off axis term refers to the inclination angle between object and reference beams, which is significantly increased in the off-axis case to produce high spatial frequency carrier. Thus, it provides separation of the otherwise overlapped object terms and autocorrelation peak in the center of Fourier domain to facilitate spectral filtering. Both approaches are somewhat promoted and penalized: on-axis recording, despite being very accurate and well optimized in terms of the detector space-bandwidth product, has limited time resolution due to the need of phase-shifting sequence recording. The off-axis approach aided by the FT can quickly analyze dynamic events in a single-shot manner (phase is retrieved from a single hologram). However, it requires a sufficiently high hologram spatial carrier frequency limiting the space-bandwidth product and imposing constraints on phase details of imaged biostructures, as generally an object should be low pass banded with respect to the carrier frequency. Objects introducing strong phase shifts (high phase dynamic range) are therefore especially ponderous. It is worth emphasizing that third configuration emerged recently, namely the slightly off-axis regime. It attempts space-bandwidth product optimization by means of full spectral separation of conjugated object lobes, while leaving the autocorrelation term partially overlapped with information carrying terms.26–28
The recently proposed Hilbert–Huang single-shot SMIM (H2S2MIM) method29 combines the advantages of the common-path SMIM layout with single frame hologram analysis using the Hilbert–Huang phase microscopy (H2PM) algorithm.30 Together with superresolution technique,26 they embody two main advancements of the classical SMIM method: single-shot operational principle even outside off-axis holographic recording regime29 and the capability of overcome the field of view (FOV) restriction.31 The H2PM works in two steps: (1) it filters out hologram background using the two-dimensional (2-D) empirical mode decomposition (EMD) and (2) performs phase demodulation of background-filtered hologram using Hilbert spiral transform (HST). The H2PM accepts a very wide range of holograms recorded in various architectures—from on-axis to off-axis with special emphasis on slightly off-axis regimes26–28—regardless of the local shape of interference fringes. It provides unique flexibility in terms of optical setup design and expands the suite of measurable objects into high phase dynamic range ones. Phase details can be successfully imaged under low carrier spatial frequency, and generally it enables accurate phase estimation of holograms with overlapped spectrum.30 The Hilbert–Huang transform exhibits phase demodulation errors; however, in very challenging cases when high noise levels originated in a highly scattering sample it merged with low contrast of interference fringes caused by low coherence or mismatch in intensities or polarizations of interfering beams. These phenomena contribute to a significant decrease of the hologram signal-to-noise ratio (SNR) and preclude accurate, single-shot phase estimation of problematic yet interesting biosamples. Therefore, there is a need to fill this gap and enable accurate analysis of low signal-to-noise holograms recorded using the SMIM paradigm.
We propose a single-shot two-frame -shifted spatially multiplexed interference microscopy (-SMIM) to overcome the limitations imposed by highly scattering samples resulting in low SNR of recorded holograms. The -SMIM adds high-speed (video framerate) accurate and robust QPI capability to a commercial nonholographic microscope with enhanced phase reconstruction by properly placing a beam-splitter to record in a single-shot two holograms mutually phase shifted by radians. Although we have previously reported on a single-shot approach for QPI using a beam-splitter interferometric architecture,32 the method here presented is conceptually different from the previous one in the following sense. The previous approach32 was targeted to provide an external add-on module to be adapted into the exit port of a regular microscope in order to update it with coherence sensing capabilities. This external module is based on a beam-splitter cube interferometer working in slightly off-axis configuration, but the approach32 does not imply internal modifications of the microscope as one needs in SMIM. As a consequence, the beam-splitter interferometer introduces a nonnegligible amount of astigmatism that must be compensated using a Stoke lens device, which is included in the add-on module itself. Here, the beam-splitter is inserted in the microscope embodiment [as the one-dimensional (1-D) diffraction grating in SMIM technique is inserted], that is, in the collimated beam light path meaning that no astigmatism is introduced, and no need for complex compensating devices is required. So, the technique reported in this paper is related with an SMIM improvement and cannot be packaged as an add-on module to be easily coupled in a conventional white-light microscope for upgrading it into holographic microscope for QPI. Moreover, the significant enhancement of phase demodulation efficiency is achieved using the two complementary hologram recording and subtraction schemes.
2. System Description
2.1. Experimental Layout
Figure 1 shows the optical implementation of the proposed -SMIM method highlighting its working principle, with the main modifications depicted for clarity. Essentially, a fiber-coupled red diode laser (OSI Laser Diode, TCW RGBS-400R, 635 nm) replaces the white light illumination provided by the mercury lamp. Light passes through a linear polarizer (P) to adjust the intensities of both replicas provided by the BS. This is a critical point in the reconstruction process, since the more similar the fringe contrast of the two single-shot -shifted holograms, the better the reconstructed phase image. The trinocular head of the microscope has been removed to avoid unwanted spurious reflections, so a tube lens (TL) has been added to maintain the infinity corrected imaging mode. The TL () is just placed at the circular dovetail mount of the microscope trinocular port.
Fig. 1.
Upright microscope updated with -SMIM capability. TL, tube lens; BS, beam splitter; P, linear polarizer; LD, laser diode.
The BS (polarizing cube, 25.4 mm side) is inserted within the microscope embodiment into the collimated light path between the objective and TL. It is placed in a nonconventional way, that is, rotated 45 deg regarding the position for splitting an incoming beam into two orthogonally separated ones. In this position, it defines a common-path interferometric configuration providing two simultaneous slightly off-axis holograms with a radians phase step between them.32–34 This capability enables single-shot low-quality hologram phase demodulation at the expense of the FOV reduction. The BS is mounted onto a tilting platform including different screws for fine adjustment and alignment. Finally, a CMOS imaging device (Ximea MQ042MG-CM USB3.0) is placed at the microscope output’s port for recording the -SMIM holograms.
A number of dual-channel interference-based phase imaging techniques/setups were introduced in the literature.35–40 They mainly differ in the optical configuration employed and strategy for phase retrieval. In Ref. 35, the off-axis configuration with low-coherence source and optical path difference minimization strategy was proposed. In Ref. 36, different off-axis configuration with beam-splitter for QPI was introduced. The authors of Ref. 37 report the use of Wollaston prism in an external module based on lateral phase shifting interferometer. The work in Ref. 38 extends concept of Ref. 37 by introducing a white-light, phase-shifting, polarization-driven standalone QPI module. The authors of Ref. 39 proposed to employ Wollaston prism and additional 4F imaging system and 1-D Hilbert transform for phase retrieval with rather obvious limitations (mainly scanning and loosing correlation between scans). The authors of Ref. 40 introduced off-axis configuration for QPI based on the retro reflectors. Although several dual-channel approaches were reported in the literature (i.e., Refs. 35–40), our proposed configuration is unique and novel in terms of inserting the BS into a regular biological microscope in its collimated beam path and enabling efficient phase demodulation in slightly off-axis26–28 and quasi on-axis regimes. Experimental results introduced in Sec. 2.2 will corroborate this statement successfully.
2.2. Algorithm Implementation
Two recorded holograms constitute the two halves of the camera FOV and can be modeled as
| (2) |
| (3) |
where denotes the left half and denotes the right half of the hologram (see inset in Fig. 1). Upon subsequent subtractive superimposition of the left and right holograms (left and right half of the registered image), a -hologram is generated with boosted SNR due to eliminated background and improved amplitude modulation of interference fringes. It can be modeled as
| (4) |
where denotes -hologram residual background term (in theoretically ideal case as a consequence of identical background present in left and right holograms) and denotes -hologram noise. A similar approach of data enhancement through two interferograms subtraction was reported to improve the amplitude demodulation process in interferometric full-field vibration studies41 and for volumetric imaging using structured illumination microscopy and optical sectioning.42 In this paper, we introduce two-frame scheme for phase map calculation improvement.
The phase demodulation is performed using the HST.43 The analytic -hologram () is calculated having its real part defined as -hologram () and imaginary part as the HST of -hologram designated as
| (5) |
| (6) |
where is the local fringe orientation map,43–45 SPF denotes spiral phase function, and denote forward and inverse FT, respectively. The analytic -hologram grants easy access to the phase map of interest
| (7) |
where the angle is a Matlab (MathWorks, Natick, Massachusetts) function computing the argument map of complex valued image. Phase unwrapping using the transport of intensity method46 completes the phase demodulation path.
Prior to the subtraction of left and right holograms, it is highly recommended to numerically refine optically predefined alignment of both left and right holograms (find correct scale and rotation angle) using the feature matching function from the Matlab environment. To facilitate, the viewpoint on our strategy exemplifying left and right holograms are presented in Figs. 2(a) and 2(b), respectively. Holograms were recorded investigating prostate cancer cells from line LNCaP using the proposed -SMIM method. The -hologram is shown in Fig. 2(c). Some residual background (a) can be observed in Fig. 2(d) as a consequence of uneven background illumination in the FOV. We propose to decompose the -hologram using the enhanced fast empirical mode decomposition (EFEMD)47 like it is conducted in the first part of the H2PM for single hologram phase analysis.29,30 Sum of first two modes is designated as the adaptively filtered -hologram, whereas other decomposition components form the -hologram background, Fig. 2(d), to be eliminated in filtering. Merging optically generated two holograms subtraction with numerically employed additional filtering a very robust -SMIM phase retrieval scheme is composed.
Fig. 2.
Demonstration of the -SMIM working principle: (a) left hologram, (b) right hologram, (c) -hologram, (d) its background term. (e)–(h) Phase maps calculated using single hologram, -hologram, filtered -hologram, and phase-shifting sequence, respectively. Scale bars in (e)–(h) represent optical phase shift values in radians.
From the computational load point of view, the demonstrated -SMIM technique is the same as H2PM enabling complete phase demodulation under 1 s on a regular PC (CPU 2.6 GHz RAM 16 GB).
3. Experimental Results
3.1. Validation of the π-SMIM Working Principle
Experimental validation of the proposed approach has been divided into three sections. The aim of the first one is to provide a detailed implementation of the working principle and comparative analysis with other previously established techniques (recently established H2S2MIM and temporal phase-shifting approach).
Figure 2 shows the results considering prostate cancer cells. The cells were cultured in RPMI 1640 (GIBCO, Invitrogen, Life Technologies, California) medium with 10% fetal bovine serum, Penicillin, and Streptomycin at standard cell culture conditions (37°C in 5% in a humidified incubator). After the cells reach a confluent stage, they are released from the culture support and centrifuged. The supernatant fluid is discarded and cells are resuspended in a cytopreservative solution and mounted in a slide using the ThinPrep® 2000 system (Hologic, Marlborough, Massachusetts). The cells (LNCaP line) included in Fig. 2 are isolated from a needle aspiration biopsy of the left supraclavicular lymph node of a Caucasian male with confirmed diagnosis of metastatic carcinoma.
The -hologram (partial) background rejection and (full) amplitude modulation amplification obtained upon subtractive superimposition of the two simultaneously recorded holograms [readily noticeable in Fig. 2(c) in comparison with Figs. 2(a) and 2(b)] are the main features determining superior quality of the phase retrieval using the -hologram in comparison with single hologram analysis (right or left). This fact is corroborated by comparing four phase maps, Figs. 2(e)–2(h), obtained using different techniques.
The phase map obtained from just the left hologram is presented in Fig. 2(e) with general low quality and noisy appearance. The phase map calculated using the -hologram is shown in Fig. 2(f). It compares favorably with single hologram phase map as it exhibits richer cellular details; however, the periodic artifact significantly deteriorating its quality can be observed. The origin of this artifact can be traced back to the uneven background of the -hologram. After the EFEMD-based background correction [subtracting Fig. 2(d) from Fig. 2(c)] the retrieved phase map, Fig. 2(g), is now free of the periodic error. On the optical table, we assembled the Mach–Zehnder digital holographic microscope, performed reference measurement of the optical path delay introduced by studied sample and presented the “ground-truth” outcome in Fig. 2(h). Six phase-shifted holograms were captured and the advanced iterative algorithm was employed for the reference phase map retrieval.48 With established reference phase map, the root mean square errors for single hologram, -hologram, and filtered -hologram cases can be computed and rounded to 0.86, 0.56, and 0.52 rad, respectively. Assessing the retrieved phase quality, the RMS analysis quantitatively indicates the superiority of the proposed -SMIM technique over single hologram H2S2MIM and highlights the importance of the residual background removal using the EFEMD-based additional filtering.
3.2. Validation of the π-SMIM: Samples with Variable Size and Density
In this section, phase objects with different size and density are investigated. For the experimental validation, two biosamples are considered: prostate cancer cells coming from a different cell line (PC-3 initiated from a bone metastasis of a grade IV prostatic adenocarcinoma from a Caucasian male) and dry red blood cells. The former introduces a different sample sizing while the latter is a dense sample with clustered degenerated cells. They often result in difficult shape of interference fringes [Figs. 3(a) and 3(d)] precluding their efficient single-frame phase demodulation using classical FT approach. The -SMIM enables accurate in vivo analysis of those problematic specimens alleviating the problem of significant local fringe shape variation (overlapped spectrum) and very low SNR. High visual quality phase maps calculated using the -SMIM and presented in Figs. 3(c) and 3(f) advocate its robustness and versatility analyzing complicated size-variable [PC-3, Fig. 3(c)] and clustered [dry red blood cells, Fig. 3(f)] biosamples. Subcellular resolution is to be highlighted, Fig. 3(c).
Fig. 3.
(a)–(c) PC-3 cells and (d)–(f) red blood cells phase analysis for validation of the -SMIM versatility and robustness: (a) and (d) holograms, (b) and (e) -holograms, (c) and (f) phase maps. Scale bars in (c) and (f) represent optical phase values in radians.
3.3. Validation of the π-SMIM: Dynamic Samples
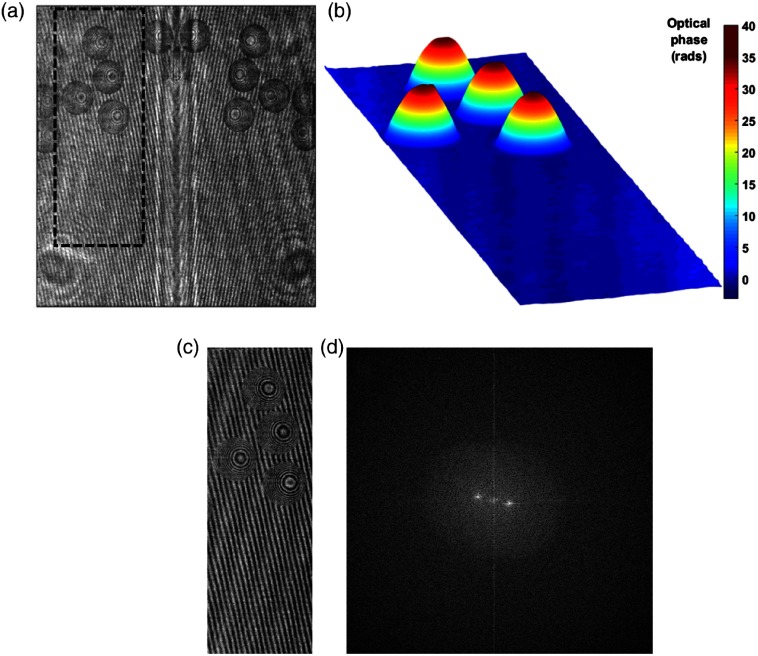
Last but not least, Fig. 4 shows the -SMIM capability to study transient events. Probably this is the most attractive capability of the proposed technique since it enables real-time analysis of very challenging dynamic samples. Several microbeads flowing in the water-filled microchamber were investigated. Figure 4(a) shows the exemplifying two-channel hologram and Fig. 4(b) shows the final retrieved 3-D phase map (Video 1) and corresponding with the rectangular black dashed ROI included in Fig. 4(a). As expected, the phase profile of the flowing microbeads is successfully retrieved using the proposed -SMIM concept regardless the low SNR of left and right holograms. It was ensured by virtue of the -hologram generation, Fig. 4(c), and its further analysis for phase demodulation. The problem of complicated closed fringes in bead-areas coming from overlapped spectrum produced in quasi on-axis configuration, Fig. 4(d), is also successfully surpassed using the proposed -SMIM method. We would like to showcase at this point that proposed technique can work not only in slightly off-axis regime, where separation of conjugated object lobes in Fourier domain is fulfilled, but also in quasi on-axis configuration with overlapped spectrum of two conjugated terms. Results presented in Fig. 4 prove this statement.
Fig. 4.
Dynamic case: flowing beads phase analysis using the -SMIM corroborating its high-speed imaging capabilities. (a) Example FOV, (b) successful phase reconstruction of the area within the black dashed rectangle (see Video 1 for full dynamic sequence), (c) -hologram of selected region of interest, and (d) logarithmic modulus of the FT of the utilized -hologram (overlapping conjugated complex amplitudes are clearly observable implying quasi on-axis regime). Three-dimensionally unwrapped phase profile of dynamic beads flowing into a water-filled counting chamber (Video 1, MOV, 1.15 MB [URL: https://doi.org/10.1117/1.JBO.24.9.096004.1]).
4. Discussion
Two main novelties reported in this contribution are to be highlighted. Beam splitter cube is directly introduced here in a straightforward manner to the commercially available bright field microscope upgrading it to an interferometric one (having provided the coherent light source first)—this is the first time to the best of the authors knowledge that the beam splitter and regular microscope are merged within the embodiment of the latter to enhance the capabilities of the microscope. Previous works in this line have reported on the use of diffraction gratings in SMIM technique (Refs. 22, 23, 29, and 31). The beam-splitter is working with the plane wave illumination, hence no additional spurious astigmatism is generated, as it was in the previous case in Ref. 32.
It is well-known that a tilted plane-parallel plate with collimated illumination (parallel rays) only causes a lateral displacement of rays without additional aberrations. But a tilted plane-parallel plate under nonparallel rays can cause a large amount of aberrations.49,50 This was the case in Ref. 32 where convergent illumination passes the tilted BS cube; when examining the experimental images, it is evident it produced astigmatism.32 Using the Stokes lens, an astigmatism of 0.25 diopters was measured which, according to theoretical calculations in the layout, corresponds with a Sturm interval of 3.5 mm, approximately. This is the separation between both focal lines due to the tilt of the BS. According to Eq. 4 in Ref. 51, the amount of astigmatism () introduced by a tilted plane-parallel plate when using convergent rays is given as
| (8) |
where denotes the thickness of the plane-parallel plate (25.4 mm), is the rotation angle, and is the glass index value at the illumination wavelength (1.52 assuming BK7 at 532 nm). Since , the rotation angle of the BS cube can be computed from Eq. (8) yielding in . This value is perfectly plausible since we started from an initial position where the BS was rotated 45 deg and then applied a small rotation to implement a slightly off-axis configuration. So, this quantitative analysis seems reasonable.
Nevertheless, and in order to qualitatively validate that the proposed approach does not generate additional spurious astigmatism due to the BS positioning, Fig. 5 includes a comparison between the intensity images produced by the former layout32 and the actual one. Figure 5(a) presents the image produced without holographic recording and when no Stokes lens is considered in the layout of Ref. 32. Since the BS was placed in the convergent light path between the TL and the digital sensor, a non-negligible amount of astigmatism causes horizontal defocus in the recorded image. However, the BS is inserted in the collimated light path in the actual layout, leaving the system free of astigmatism. Figure 5(b) shows an intensity image free of astigmatism.
Fig. 5.
Comparison between former32 and actual layouts highlighting astigmatism avoidance: (a) image obtained with previous layout32 and (b) image provided by the proposed layout.
Second novelty is connected with the enhanced numerical phase retrieval scheme. The HST is applied for the phase demodulation of the -hologram. Novelty resides in expanding the range of phase-objects to be examined by the HST. Employing the -hologram generation strategy allows for analyzing phase maps otherwise encoded in cumbersome holograms of very low SNRs. Low SNR is understood here as combination of high noise, strong out of focus background and low contrast possibly caused by polarization, intensity or coherence mismatch. It is worth emphasizing that proposed -SMIM technique exhibits the attractive ability to study in real-time dynamic phase objects with strong local phase variations (i.e., closed fringes in microbead area). Moreover, it provides an efficient means to demodulate holograms with low carrier frequency recorded in configurations ranging from quasi off-axis through slightly off-axis up to quasi on-axis architectures.
It is worth emphasizing that interferograms/holograms presented in Figs. 2–4 cannot be successfully analyzed using the FT due to rich spectrum versus too low carrier frequency, see Fig. 4(d) as an exemplifying quasi on-axis spectrum. In Ref. 32, the add-on module was proposed offering more room for appropriate data recording—the FT-based phase demodulation could be therefore possibly applied tilting the beam-splitter to create relatively high carrier frequency. The upper limit on carrier frequency is related also to the temporal coherence of the light source and utilizing broader spectra, i.e., SLDs, one may not be able to generate interference fringes in a large tilt regime. Additionally, in some cases of high dynamic range phase-objects (of rich spectrum), the FT method exhibits too limited bandwidth to provide efficient phase demodulation even with high carrier frequency employed. This manifests in partial overlapping of two information lobes (complex apertures) and autocorrelation term in Fourier domain in so-called slightly off-axis regime. In Ref. 32, it was proposed to subtract two BS-generated holograms removing autocorrelation term therefore eliminating described cumbersome overlap. This way FT phase demodulation could be introduced in Ref. 32 to a slightly off-axis regime once the central spectral term is removed. But the FT cannot be applied to the quasi on-axis case when the two complex apertures overlap due to a low carrier frequency; see, for example, the case studied in Fig. 4. This can happen while approaching the on-axis interferometric configuration or increasing the dynamic range of object introduced phase change. Dynamic range of phase increases when one is analyzing optically denser and richer structures or physically thicker ones (or both), e.g., microbeads in Fig. 4.
By employing beam-splitter, proposed biomedical QPI -SMIM microscope generates two holograms shifted by radians in a single shot. The holograms are in turn subtracted creating background-reduced and amplitude-enhanced differential hologram, so-called -hologram. It is worth to highlight that this two-channel subtractive concept can be naturally used to enhance phase demodulation in full-field interferometric studies of technical objects, i.e., testing of MEMS/MOEMS (microlenses, micromembranes, etc.) and optical elements. Showcased versatility makes our approach scalable.
5. Conclusions
In this paper, we have proposed a new single-shot two-frame -SMIM technique for upgrading a regular microscope into a versatile interference-based real-time phase imager with the ability to accurately study cumbersome micro-objects encoded in very low quality holograms (low carrier frequency, strong background and noise, low contrast, locally variable fringe shape, etc.). The -SMIM hologram enhancement is conducted upon subtraction of two simultaneously recorded interference patterns generated by the beam-splitter at the expanse of FOV reduction. Robust phase retrieval is performed combining 2-D EMD numerical filtering and HST hologram demodulation. Unique features of the presented method were corroborated by successfully analyzing static (prostate cancer and red blood cells) and dynamic (flowing microbeads) highly scattering microsamples—quantitative evaluation was presented employing phase-shifting DHM as a reference method. As main outcome, -SMIM enables accurate in-vivo analysis of noisy low-contrast high dynamic range phase objects, otherwise measurable only in static regimes using time-consuming phase-shifting.
Supplementary Material
Acknowledgments
This work has been partially funded by the National Science Center Poland (2017/25/B/ST7/02049), Faculty of Mechatronics Warsaw University of Technology statutory funds, Polish National Agency for Academic Exchange (PPN/BEK/2018/1/00511), and by the Spanish Ministerio de Economía, Industria y Competitividad Fondo Europeo de Desarrollo Regional (FIS2017-89748-P).
Biography
Biographies of the authors are not available.
Disclosures
The authors declare that there are no conflicts of interest related to this article.
References
- 1.Park Y., Depeursinge C., Popescu G., “Quantitative phase imaging in biomedicine,” Nat. Photonics 12, 578–589 (2018). 10.1038/s41566-018-0253-x [DOI] [Google Scholar]
- 2.Popescu G., Quantitative Phase Imaging of Cells and Tissues, McGraw-Hill, New York: (2011). [Google Scholar]
- 3.Shaked N. T., Zalevsky Z., Satterwhite L. L., Biomedical Optical Phase Microscopy and Nanoscopy, Academic Press, Oxford: (2012). [Google Scholar]
- 4.Gabor D., “A new microscopic principle,” Nature 161, 777–778 (1948). 10.1038/161777a0 [DOI] [PubMed] [Google Scholar]
- 5.Zernike F., “How I discovered phase contrast,” Science 121, 345–349 (1955). 10.1126/science.121.3141.345 [DOI] [PubMed] [Google Scholar]
- 6.Cuche E., Bevilacqua F., Depeursinge C., “Digital holography for quantitative phase-contrast imaging,” Opt. Lett. 24, 291–293 (1999). 10.1364/OL.24.000291 [DOI] [PubMed] [Google Scholar]
- 7.Kemper B., von Bally G., “Digital holographic microscopy for live cell applications and technical inspection,” Appl. Opt. 47, A52–A61 (2008). 10.1364/AO.47.000A52 [DOI] [PubMed] [Google Scholar]
- 8.Cotte Y., et al. , “Marker-free phase nanoscopy,” Nat. Photonics 7, 113–117 (2013). 10.1038/nphoton.2012.329 [DOI] [Google Scholar]
- 9.Marquet P., et al. , “Digital holographic microscopy: a noninvasive contrast imaging technique allowing quantitative visualization of living cells with subwavelength axial accuracy,” Opt. Lett. 30, 468–470 (2005). 10.1364/OL.30.000468 [DOI] [PubMed] [Google Scholar]
- 10.Wang Z., et al. , “Spatial light interference microscopy (SLIM),” Opt. Express 19, 1016–1026 (2011). 10.1364/OE.19.001016 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Choi W., et al. , “Tomographic phase microscopy,” Nat. Methods 4, 717–719 (2007). 10.1038/nmeth1078 [DOI] [PubMed] [Google Scholar]
- 12.Paganin D., Nugent K. A., “Noninterferometric phase imaging with partially coherent light,” Phys. Rev. Lett. 80, 2586–2589 (1998). 10.1103/PhysRevLett.80.2586 [DOI] [Google Scholar]
- 13.Sun J., et al. , “Single-shot quantitative phase microscopy based on color-multiplexed Fourier ptychography,” Opt. Lett. 43, 3365–3368 (2018). 10.1364/OL.43.003365 [DOI] [PubMed] [Google Scholar]
- 14.Bon P., et al. , “Quadriwave lateral shearing interferometry for quantitative phase microscopy of living cells,” Opt. Express 17, 13080–13094 (2009). 10.1364/OE.17.013080 [DOI] [PubMed] [Google Scholar]
- 15.Kemper B., et al. , “Investigation of living pancreas tumor cells by digital holographic microscopy,” J. Biomed. Opt. 11, 034005 (2006). 10.1117/1.2204609 [DOI] [PubMed] [Google Scholar]
- 16.Bhaduri B., et al. , “Diffraction phase microscopy: principles and applications in materials and life sciences,” Adv. Opt. Photonics 6, 57–119 (2014). 10.1364/AOP.6.000057 [DOI] [Google Scholar]
- 17.Uttam S., et al. , “Early prediction of cancer progression by depth-resolved nanoscale mapping of nuclear architecture from unstained tissue specimens,” Cancer Res. 75, 4718–4727 (2015). 10.1158/0008-5472.CAN-15-1274 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Merola F., et al. , “Tomographic flow cytometry by digital holography,” Light Sci. Appl. 6, e16241 (2017). 10.1038/lsa.2016.241 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19.Bianco V., et al. , “Optofluidic holographic microscopy with custom field of view (FoV) using a linear array detector,” Lab Chip 15, 2117–2124 (2015). 10.1039/C5LC00143A [DOI] [PubMed] [Google Scholar]
- 20.Mico V., Zalevsky Z., García J., “Common-path phase-shifting digital holographic microscopy: a way to quantitative phase imaging and superresolution,” Opt. Commun. 281, 4273–4281 (2008). 10.1016/j.optcom.2008.04.079 [DOI] [Google Scholar]
- 21.Soto J. M., Rodrigo J. A., Alieva T., “Label-free quantitative 3D tomographic imaging for partially coherent light microscopy,” Opt. Express 25, 15699–15712 (2017). 10.1364/OE.25.015699 [DOI] [PubMed] [Google Scholar]
- 22.Mico V., et al. , “Spatially-multiplexed interferometric microscopy (SMIM): converting a standard microscope into a holographic one,” Opt. Express 22, 14929–14943 (2014). 10.1364/OE.22.014929 [DOI] [PubMed] [Google Scholar]
- 23.Picazo-Bueno J. A., et al. , “Spatially multiplexed interferometric microscopy with partially coherent illumination,” J. Biomed. Opt. 21, 106007 (2016). 10.1117/1.JBO.21.10.106007 [DOI] [PubMed] [Google Scholar]
- 24.Creath K., “Phase-measurement interferometry techniques,” Prog. Opt. 26, 349–393 (1988). 10.1016/S0079-6638(08)70178-1 [DOI] [Google Scholar]
- 25.Takeda M., Ina H., Kobayashi S., “Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry,” J. Opt. Soc. Am. 72, 156–160 (1982). 10.1364/JOSA.72.000156 [DOI] [Google Scholar]
- 26.Ikeda T., et al. , “Hilbert phase microscopy for investigating fast dynamics in transparent systems,” Opt. Lett. 30, 1165–1167 (2005). 10.1364/OL.30.001165 [DOI] [PubMed] [Google Scholar]
- 27.Shaked N. T., et al. , “Two-step-only phase-shifting interferometry with optimized detector bandwidth for microscopy of live cells,” Opt. Express 17, 15585–15591 (2009). 10.1364/OE.17.015585 [DOI] [PubMed] [Google Scholar]
- 28.Xue L., et al. , “Single-shot slightly-off-axis interferometry based Hilbert phase microscopy of red blood cells,” Biomed. Opt. Express 2, 987–995 (2011). 10.1364/BOE.2.000987 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Picazo-Bueno J. A., et al. , “Hilbert-Huang single-shot spatially multiplexed interferometric microscopy,” Opt. Lett. 43, 1007–1010 (2018). 10.1364/OL.43.001007 [DOI] [PubMed] [Google Scholar]
- 30.Trusiak M., et al. , “Quantitative phase imaging by single-shot Hilbert-Huang phase microscopy,” Opt. Lett. 41, 4344–4347 (2016). 10.1364/OL.41.004344 [DOI] [PubMed] [Google Scholar]
- 31.Picazo-Bueno J. A., et al. , “Superresolved spatially multiplexed interferometric microscopy,” Opt. Lett. 42, 927–930 (2017). 10.1364/OL.42.000927 [DOI] [PubMed] [Google Scholar]
- 32.Picazo-Bueno J. A., Trusiak M., Micó V., “Single-shot slightly off-axis digital holographic microscopy with add-on module based on beamsplitter cube,” Opt. Express 27, 5655–5669 (2019). 10.1364/OE.27.005655 [DOI] [PubMed] [Google Scholar]
- 33.Ferrari J. A., Frins E. M., “Single-element interferometer,” Opt. Commun. 279, 235–239 (2007). 10.1016/j.optcom.2007.07.038 [DOI] [Google Scholar]
- 34.Gao P., et al. , “Parallel two-step phase-shifting microscopic interferometry based on a cube beamsplitter,” Opt. Commun. 284, 4136–4140 (2011). 10.1016/j.optcom.2011.04.049 [DOI] [Google Scholar]
- 35.Gabai H., Shaked N. T., “Dual-channel low-coherence interferometry and its application to quantitative phase imaging of fingerprints,” Opt. Express 20, 26906–26912 (2012). 10.1364/OE.20.026906 [DOI] [PubMed] [Google Scholar]
- 36.Gabai H., et al. , “Continuous wide-field characterization of drug release from skin substitute using off-axis interferometry,” Opt. Lett. 38, 3017–3020 (2013). 10.1364/OL.38.003017 [DOI] [PubMed] [Google Scholar]
- 37.Lee K., Park Y., “Quantitative phase imaging unit,” Opt. Lett. 39, 3630–3633 (2014). 10.1364/OL.39.003630 [DOI] [PubMed] [Google Scholar]
- 38.Baek Y., et al. , “White-light quantitative phase imaging unit,” Opt. Express 24, 9308–9315 (2016). 10.1364/OE.24.009308 [DOI] [PubMed] [Google Scholar]
- 39.Shaked N. T., Rinehart M. T., Wax A., “Dual-interference-channel quantitative-phase microscopy of live cell dynamics,” Opt. Lett. 34, 767–769 (2009). 10.1364/OL.34.000767 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Girshovitz P., Shaked N. T., “Compact and portable low-coherence interferometer with off-axis geometry for quantitative phase microscopy and nanoscopy,” Opt. Express 21, 5701–5714 (2013). 10.1364/OE.21.005701 [DOI] [PubMed] [Google Scholar]
- 41.Patorski K., Trusiak M., “Highly contrasted Bessel fringe minima visualization for time-averaged vibration profilometry using Hilbert transform two-frame processing,” Opt. Express 21, 16863–16881 (2013). 10.1364/OE.21.016863 [DOI] [PubMed] [Google Scholar]
- 42.Patorski K., Trusiak M., Tkaczyk T., “Optically-sectioned two-shot structured illumination microscopy with Hilbert–Huang processing,” Opt. Express 22, 9517–9527 (2014). 10.1364/OE.22.009517 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 43.Larkin K. G., Bone D. J., Oldfield M. A., “Natural demodulation of two-dimensional fringe patterns. I. General background of the spiral phase quadrature transform,” J. Opt. Soc. Am. A 18, 1862–1870 (2001). 10.1364/JOSAA.18.001862 [DOI] [PubMed] [Google Scholar]
- 44.Yang X., Yu Q., Fu S., “A combined method for obtaining fringe orientations of ESPI,” Opt. Commun. 273, 60–66 (2007). 10.1016/j.optcom.2006.12.026 [DOI] [Google Scholar]
- 45.Trusiak M., Służewski Ł., Patorski K., “Single shot fringe pattern phase demodulation using Hilbert–Huang transform aided by the principal component analysis,” Opt. Express 24, 4221–4238 (2016). 10.1364/OE.24.004221 [DOI] [PubMed] [Google Scholar]
- 46.Martinez-Carranza J., Falaggis K., Kozacki T., “Fast and accurate phase-unwrapping algorithm based on the transport of intensity equation,” Appl. Opt. 56, 7079–7088 (2017). 10.1364/AO.56.007079 [DOI] [PubMed] [Google Scholar]
- 47.Trusiak M., Wielgus M., Patorski K., “Advanced processing of optical fringe patterns by automated selective reconstruction and enhanced fast empirical mode decomposition,” Opt. Lasers Eng. 52, 230–240 (2014). 10.1016/j.optlaseng.2013.06.003 [DOI] [Google Scholar]
- 48.Wang Z., Han B., “Advanced iterative algorithm for phase extraction of randomly phase-shifted interferograms,” Opt. Lett. 29, 1671–1673 (2004). 10.1364/OL.29.001671 [DOI] [PubMed] [Google Scholar]
- 49.Habegger M. A., “Astigmatism in light-deflector elements,” J. Opt. Soc. Am. 60, 326–331 (1970). 10.1364/JOSA.60.000326 [DOI] [Google Scholar]
- 50.Simon M. C., “Image formation through monoaxial plane-parallel plates,” Appl. Opt. 27, 4176–4182 (1988). 10.1364/AO.27.004176 [DOI] [PubMed] [Google Scholar]
- 51.Zhong X., et al. , “Aberrations correction of tilted plane-parallel plate in convergent rays,” Appl. Opt. 54, 1758–1764 (2015). 10.1364/AO.54.001758 [DOI] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.