GRANAR, a Computational Tool to Better Understand the Functional Importance of Monocotyledon Root Anatomy^,

Generator of Root Anatomy in R (GRANAR) is a new open-source computational tool that can be used to rapidly generate digital versions of monocotyledon root anatomical networks.

Abstract

Root hydraulic conductivity is a limiting factor along the water pathways between the soil and the leaf, and root radial conductivity is itself defined by cell-scale hydraulic properties and anatomical features. However, quantifying the influence of anatomical features on the radial conductivity remains challenging due to complex time-consuming experimental procedures. We present an open-source computational tool, the Generator of Root Anatomy in R (GRANAR; http://granar.github.io), that can be used to rapidly generate digital versions of contrasted monocotyledon root anatomical networks. GRANAR uses a limited set of root anatomical parameters, easily acquired with existing image analysis tools. The generated anatomical network can then be used in combination with hydraulic models to estimate the corresponding hydraulic properties. We used GRANAR to reanalyze large maize (Zea mays) anatomical datasets from the literature. Our model was successful at creating virtual anatomies for each experimental observation. We also used GRANAR to generate anatomies not observed experimentally over wider ranges of anatomical parameters. The generated anatomies were then used to estimate the corresponding radial conductivities with the hydraulic model MECHA (model of explicit cross-section hydraulic architecture). Our simulations highlight the large importance of the width of the stele and the cortex. GRANAR is a computational tool that generates root anatomical networks from experimental data. It enables the quantification of the effect of individual anatomical features on the root radial conductivity.

Root water uptake is influenced by a multiscale combination of structural and hydraulic properties (Lobet et al., 2014; Passot et al., 2018). At the root system scale, the overall root architecture defines the potential uptake sites within the soil domain. Hydraulic properties of individual roots (radial and axial conductivities) further constrain these uptake sites, thus establishing a global hydraulic architecture of the plant (Meunier et al., 2017). Changes in these local hydraulic properties, which have a global influence, are thought to be an important target in breeding programs for drought resistant crops (Tardieu et al., 2018).

At a finer scale, on the organ level, radial and axial conductivities can also be defined by hydraulic and structural properties. On the hydraulic side, the radial conductivity (k_r) of a root segment is influenced by the expression and location of water channels (Hachez et al., 2006), the formation of hydrophobic barriers (Enstone et al., 2003), and the conductivity of plasmodesmata (Couvreur et al., 2018). On the structural side, k_r is influenced by anatomical features, such as the number of cell layers in the cortex (Chimungu et al., 2014a), the size of cortex cells (Lynch et al., 2014), or the presence of aerenchyma (Fan et al., 2007). Generally speaking, a plant controls its hydraulics in the short and medium-term (Hachez et al., 2012), and its structural features over longer developmental timelines (Vetterlein and Doussan, 2016). As such, root anatomy defines the baseline for the root radial hydraulic properties.

Root anatomical traits are diverse within species, such as maize (Zea mays; Burton et al., 2013a, 2013b; Tai et al., 2016), rice (Oryza sativa; Vejchasarn et al., 2016) or cassava (Manihot esculenta; Bomfim et al., 2011), between species (Wahl and Ryser 2000; McDonald et al., 2002), and in different biomes (Ma et al., 2018). However, to our knowledge, an assessment of the functional implication of anatomical features in water uptake properties has never been done in a systematic way. Indeed, the in vivo quantification of radial and axial conductivities is usually performed with a root pressure probe (Hose et al., 2000; Schreiber et al., 2005; Schneider et al., 2017), which is experimentally restrictive, because it is hard to perform on soil-grown roots and is generally seen as a low-throughput procedure. This experimental restriction has hindered the investigation of the relation between root hydraulic properties and anatomical features.

Recently the development of a modeling tool of transverse water flow in roots from the subcellular scale, MECHA (model of explicit cross-section hydraulic architecture), opened the way to the systematic analysis of the influence of anatomical and cell hydraulic properties on k_r (Couvreur et al., 2018). A remaining limitation of the approach is that it requires explicit anatomical networks as input. Such networks can be obtained by digitizing cross section images with semiautomated tools, such as CellSeT (Pound et al., 2012). However, that procedure is very time consuming for large datasets. Therefore, there is a need for a high throughput method of acquisition of root anatomical networks (Passot et al., 2018).

Here, we present a new computational tool, the Generator of Root Anatomy in R (GRANAR), that can generate digital versions of monocotyledon root anatomical networks. GRANAR uses easily accessible anatomical features as input. These tissue-scale parameters can be acquired from open-access image analysis software and root cross section images. In combination with the model MECHA, GRANAR opens up new possibilities to systematically analyze the impact of root anatomy on hydraulic conductivity in a high-throughput fashion. GRANAR has been validated using published datasets of maize anatomical data and hydraulic measurements. GRANAR is an open-source project available at https://granar.github.io/.

RESULTS

Overview of GRANAR

The GRANAR model generates cell networks of root cross sections from a small set of root anatomical features (Table 1). The root anatomical features can typically be gathered by using software image analysis, such as ImageJ (Schneider et al., 2012), or with more automated software, such as RootScan (Burton et al., 2012), PHIV-RootCell (Lartaud et al., 2015) or RootAnalyzer (Chopin et al., 2015). Briefly, the anatomy generation process is based on the placing of cell layers around the center of the root. The position and size of each cell and cell layer is a function of the cell type radius and user-defined randomness. As a result of this randomness, each simulation produces a slightly different anatomy, even with the same input parameter set. The thickness of a specific tissue is therefore a function of its cells’ size and its number of layers. Specific vascular tissue patterns are created depending on whether the user chooses to simulate a monocot or a dicot anatomy (Fig. 1). The vascular pattern of dicotyledon is illustrative with the current version of the GRANAR model. Independent of the species, in Figure 1, GRANAR was able to reproduce cross section anatomies with high similitude (relative error: 3.4%, R²: 0.9997) over the total area of the cross section between the experimentally obtained cross section and the one obtained with GRANAR.

Table 1. List of parameters used by the model to generate root cross sections.

Tissues	Parameter
Stelar parenchyma	Cell diameter	Diameter of the stele tissue not including the pericycle
Pericycle	Cell diameter	Number of layers	–
Endodermis	Cell diameter	Number of layers	–
Cortex	Cell diameter	Number of layers	–
Exodermis	Cell diameter	Number of layers	–
Epidermis	Cell diameter	Number of layers	–
Xylem	Max cell diameter	Number of xylem poles	Ratio (# protoxylem vs # metaxylem)
Aerenchyma	Proportion	Number of radial cavities	–

Figure 1.

Visual comparison between root cross section images of different plants and their simulation with GRANAR. A, Rice adventitious root grown hydroponically and collected 10 cm above the root tip. B, Wheat (Triticum aestivum) ‘Savannah’ mature adventitious root grown in soil and collected 5 cm from stem. C, Arabidopsis primary root grown on an agar plate collected 5 cm from the root tip. Initial image cross section comes from figure 4 in Atkinson and Wells (2017). D, Maize (B73 line) crown root grown aeroponically and collected 5 cm from the root tip. Initial image cross section comes from Hachez et al. (2006). E, Mature Ranunculus root (Reynolds, 2014). The model parameters used for the simulations were gathered with ImageJ and are available at https://github.com/granar/granar_examples. The area information below each image corresponds to the total area of the cross sections.

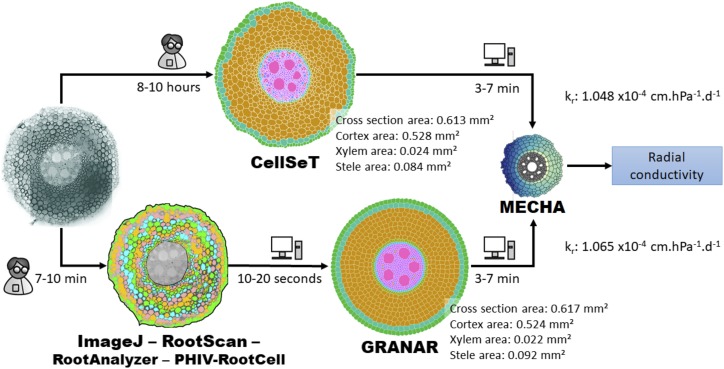
Once the root anatomy is created, the cell network can be saved in a file in eXtended Markup Language (XML). The file in XML can serve as the geometry input for the MECHA model. As such, both tools can be linked, and the GRANAR-MECHA model can be used to estimate hydraulic properties (e.g. k_r) of any type of root anatomy. The format of the XML created by GRANAR is identical to the ones created by CellSeT which also generates a fully digitized root anatomical network. Using the same format for both tools makes them modular and facilitates the intercomparison of their outputs (Fig. 2).

Figure 2.

Comparison of GRANAR- and CellSeT-based methods used to estimate single-root scale hydraulic properties. The input parameters of GRANAR in the figure were gathered with ImageJ. The radial hydraulic conductivity (k_r) values were calculated using the MECHA model assuming an endodermal Casparian strip as the only apoplastic barrier and uniform cell-scale hydraulic properties. The time (indicated as either person or computational using associated graphics) required for each procedure is detailed next to each arrow.

The time (both computational and labor time) required to access the level of network detail with CellSeT in Figure 2 is around 10 h in cross sections with thousands of cells, such as maize (image blending and correction [30 min] + automated segmentation [3 s] + iterative corrections of the segmentation and labeling [∼10 h]). In comparison, generating a complete network anatomy only takes 10 min (root anatomical features [7-min RootScan/image or 10-min ImageJ/image] + GRANAR/cross section [15 s]). However, when we compare the k_r obtained by MECHA using either CellSeT or GRANAR anatomy as input, the difference is less than 2% (Fig. 2).

GRANAR Generates Accurately Stereotypic Maize Root Anatomies from Large Anatomical Datasets

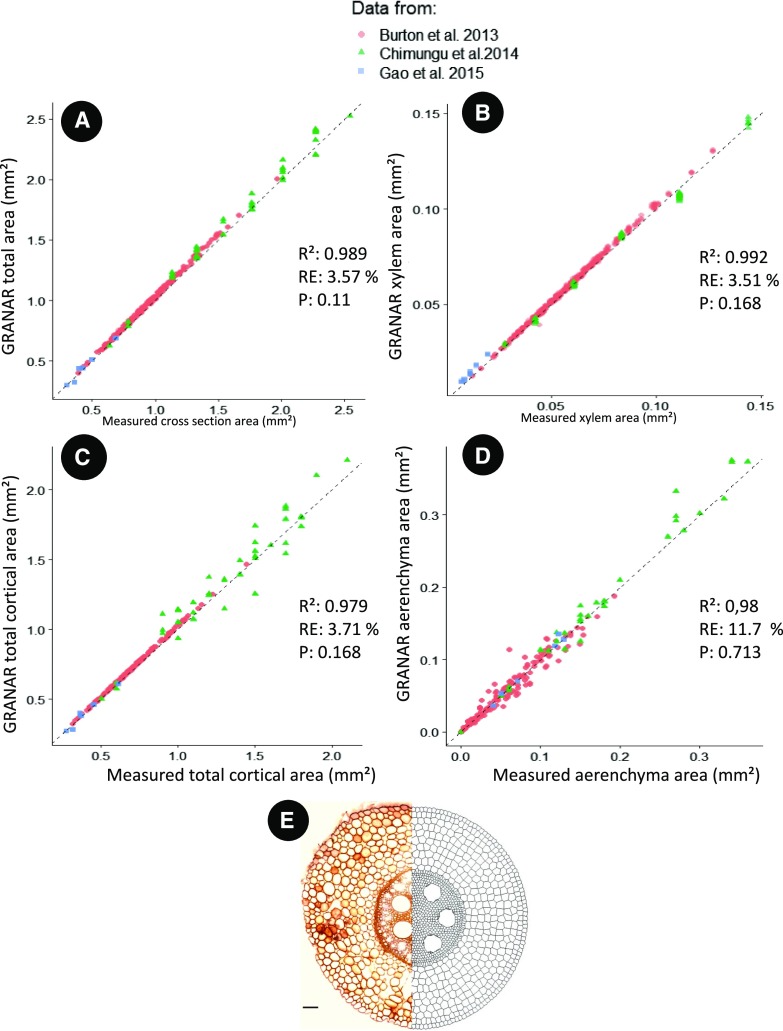
We validated the output of GRANAR for maize, whose root anatomy is well documented in the literature. We used the experimental data from three independent datasets showing large phenotypic diversity of maize anatomical features. The three root anatomical datasets were from Burton et al. (2013a; 195 landraces from a diversity panel), from Chimungu et al. (2014b; 38 maize genotypes with large variance of cortex features), and from Gao et al. (2015; 1 cultivar with 3 different root types and a large proportion of aerenchyma in all the 3 root types). These different datasets contain tissue-scale anatomical data that could be used as input for GRANAR, such as the size of the stele or the number of cortex layers (details about how these data were compiled to create the GRANAR input files are presented in the “Materials and Methods”). Using the 239 data points, we generated 717 maize root cross sections. Each data point was used to generate three replicates of each root, taking advantage of the randomness in the positions of the individual cells. Another root anatomical dataset from Wahl and Ryser (2000) containing 19 different perennial grass species was also converted into input parameter files for GRANAR. Their anatomies were generated as well. Similar results were found as compared with the three maize datasets (Supplemental Dataset 1).

Once all the anatomies were created, we compared organ-scale area-based metrics (that were not directly used as input to create the anatomies) between the experimental and simulated data (Fig. 3). Area-based comparison is relevant to assess anatomical similarities between the generated anatomies and the ones used as input as demonstrated in the sensitivity analysis. GRANAR was able to accurately represent the total areas and sizes of the different tissues of the root (e.g. Fig. 3A, total cross section area; Fig. 3B, total cortex area, Fig. 3C, xylem area; Fig. 3D, aerenchyma area). For each variable analyzed, the r-squared value between the simulated and experimental data was greater than 0.95. The relative error of GRANAR was less than 5% for the total cross section area, the total cortical area, and the xylem area and less than 15% for the aerenchyma area. For each variable analyzed, no significant differences were found between experimental and simulated data (P > 0.05).

Figure 3.

Comparison between simulated and experimental anatomies for four anatomical features. A, Total cross section area. B, Cortical area. C, Xylem area. D, Aerenchyma area. The different colors and shapes represent the different datasets. RE, relative error; R², R-squared; P, P-value for the F test. E, Illustration depicting one initial image (Chimungu et al. 2014b) and the generated anatomy side by side. Bar = 100 µm.

GRANAR-MECHA Enables the Estimation of Radial Conductivity from Simulated Anatomical Data

By design, the anatomical output of GRANAR can be used as an input for the MECHA model (Couvreur et al., 2018). We were therefore able to estimate the k_r for each of the experimental data points, assuming constant cell-scale hydraulic properties (see “Materials and Methods” for details). The simulated k_r(across the different root cross sections) varied between 21.1 and 8.1 ×10⁻⁸ m.MPa⁻¹.s⁻¹ assuming a hydrophobic endodermal Casparian strip as the only apoplastic barrier.

Using the results of these simulations, we were able to attribute the main changes of k_r to three parameters using a linear regression model (Table 2). The simulated k_r for those data points can then be estimated using the following equation:

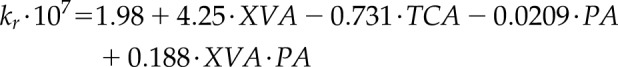(1)

Table 2. Summary of the ANOVA for the effect of the xylem and the total cortical area combined with the aerenchyma proportion on the k_r when the only apoplastic barrier is an endodermal casparian strip.

Variable	Sum of Squares	F Values	P-Value
Xylem area	1.069E-14	157	<0.0001
Total cortical area	2.452E-13	3599.9	<0.0001
Aerenchyma proportion	4.09E-14	600.5	<0.0001
Xylem area*aerenchyma proportion	6.54E-15	96.1	<0.0001
Residuals	7.00E-17	–	–

where k_r is the simulated radial conductivity (m MPa^-1 s^-1), XVA is the xylem vessel area (mm²), TCA is the total cortical area (mm²), and PA is the aerenchyma proportion (defined as the ratio between the aerenchyma area and nonstelar tissues area). Quantile-Quantile (QQ) plot of the model is shown in Supplemental Figure 1.

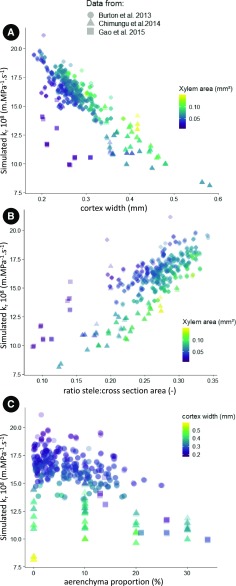
The most substantial correlation factor to the simulated k_r was for the cortex width (corr: −0.84; P < 0.05, Table 3). As a general rule, as the cortex width increases, the k_r decreases (Fig. 4A). In addition, for a given cortex width, as the xylem area increases, the k_r increases (Fig. 4A). The ratio between the stele area and the total area of the cross section is also highly correlated to the k_r(corr: 0.79, P < 0.05, Table 3). In this regard, as the ratio between the stele and the cross section area increases, the k_rincreases (Fig. 4B). Additionally, for a given ratio between the stele and the cross section area, as the xylem area decreases, the k_r increases (Fig. 4B). Moreover, in the analyzed dataset, an increase in aerenchyma proportion seems to only slightly decrease the simulated k_r (Fig. 4C). The simulated k_r of our study and the ones measured in the literature for maize were in the same range (Fig. 5).

Table 3. Summary of the ANOVA for the effect of one-by-one anatomical feature on the simulated k_r assuming an endodermal casparian strip as the only apoplastic barrier.

Each line shows results from a single one-way ANOVA.

Variable	Radial Conductivity
	Correlation Coefficient of Pearson	R Squared Value (R2)	F Values	P Value
Total cross section area	−0.624	0.389	448.4	<0.0001
Stele area	−0.222	0.049	36.64	<0.0001
Total cortex area	−0.715	0.511	736.5	<0.0001
Living cortex area	−0.638	0.407	483.1	<0.0001
Number of xylem poles	−0.252	0.063	47.54	<0.0001
Xylem area	−0.175	0.03	26.61	<0.0001
Cortex cell number	0.037	0.001	0.962	0.327
Aerenchyma area	−0.632	0.4	468.4	<0.0001
Proportion of aerenchyma	−0.505	0.255	241.3	<0.0001
Cortex width	−0.841	0.708	1704	<0.0001
Ratio stele:cross section	0.792	0.627	1181	<0.0001

Figure 4.

Relationship between simulated k_r and anatomical features for each dataset. Scenario with endodermal Casparian strip. Symbol shape corresponds to dataset. A, Effect of the cortex width on the simulated k_r. Colors represent the xylem area. B, Effect of the ratio between the stele area and the total cross section area. Colors represent the xylem area. C, Effect of aerenchyma presence on the simulated k_r. Colors represent the cortex width.

Figure 5.

Comparison between simulated and measured k_r values in maize.

GRANAR-MECHA Enables Sensitivity Analysis of Anatomical Features on Root Radial Conductivity

In the previous section, we used the GRANAR-MECHA model to study the theoretical effect of experimental root anatomical features on the root k_r. The advantage of a modeling approach is that each anatomical feature can be changed independently from the others, which is often impossible experimentally. The capability to change anatomical features independently allows for a more complete exploration of the theoretical phenotypic spectrum.

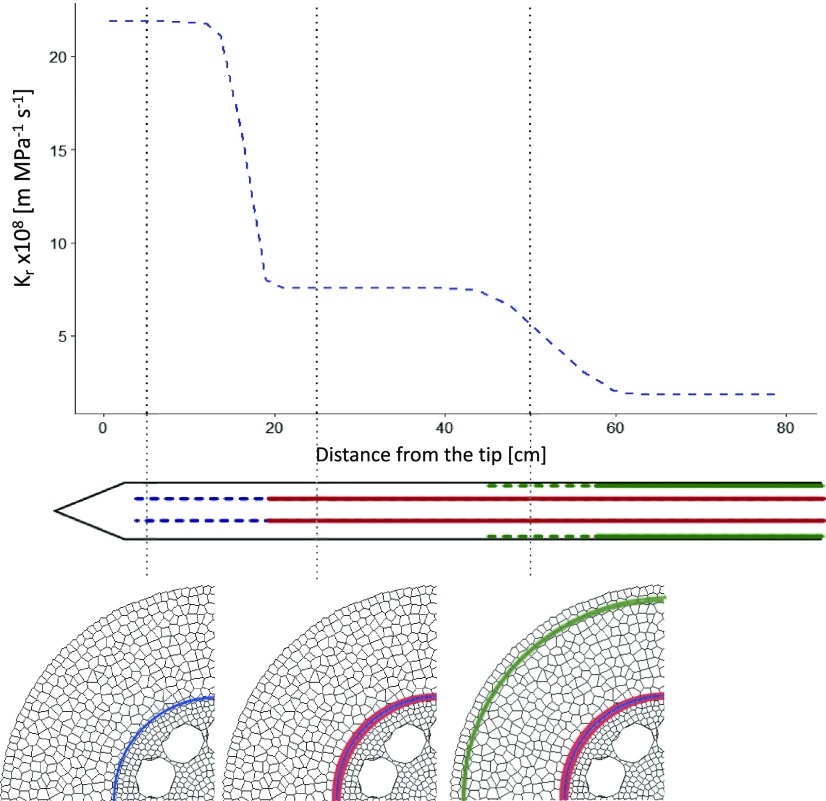
Here, we chose to vary the proportion of aerenchyma, the size of the cortex, and the size of the stele as well as the number and area of xylem poles. For each trait combination, we computed the k_r for three different maturity levels (Fig. 6). The maturity levels account for three approximate distances from the root tip corresponding to different levels of apoplastic barrier development. Based on Doussan et al. (1998) and Enstone and Peterson (2005) we assumed the following apoplastic barrier types for the different distances: 1 = presence of endodermal Casparian strip (5 cm); 2 = presence of suberized endodermis (25 cm); and 3 = presence of suberized endodermis and exodermal Casparian strip (30 cm).

Figure 6.

Estimated evolution of the k_r in main axes of the maize root system derived from Doussan et al. (1998). Top, k_r as a function of distance from the maize root tip. Bottom, the illustrations depict our assumption of the evolution of main apoplastic barriers based on Enstone and Peterson (2005). The different lines represent different level of apoplastic barriers. 1: Endodermal Casparian strip (dashed blue); 2: Endodermal suberization (red); 3: Endodermis full suberization and exodermal Casparian strip (dashed green).

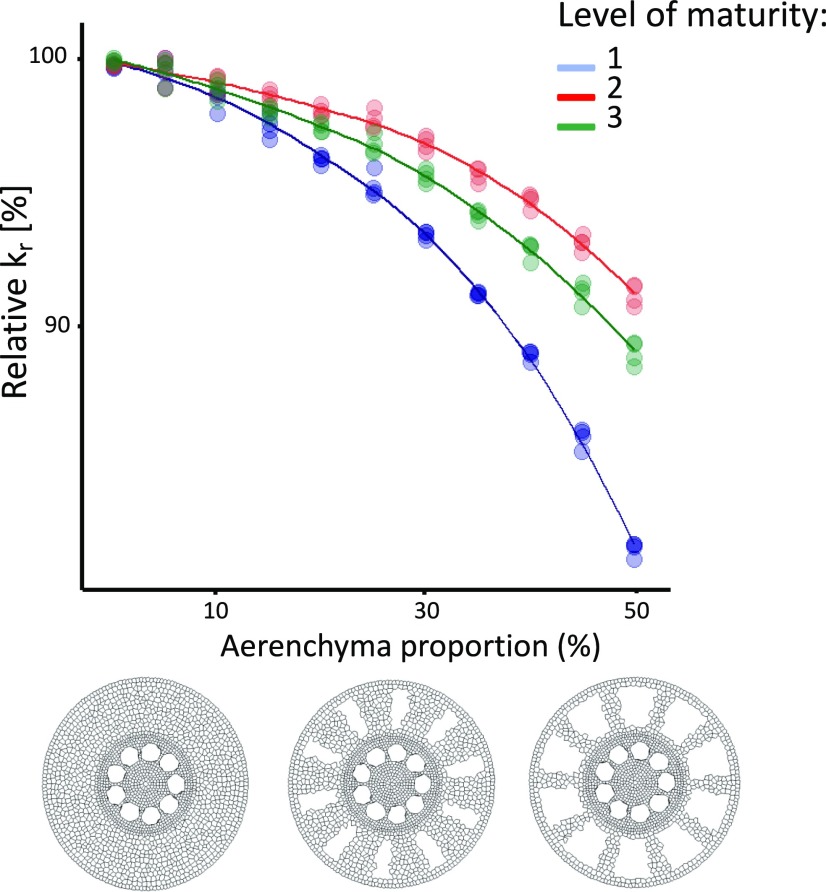
The first anatomical feature we chose to vary was the proportion of aerenchyma, which ranged from 0% to 50% of the cortex area (Fig. 7). The range observed in the experimental datasets spanned 0 to 35% (see previous section). An increase in aerenchyma induced a decrease in the simulated k_r. The effect was less important as the endodermis started to suberize. However, under the maturity level 3, with a fully suberized endodermis and an exodermal Casparian strip, the relative k_r decrease was stronger than the one observed at maturity level 2 with a suberized endodermis (Fig. 7). The stronger relative decrease can be explained by the reduced number of cells after the exodermis layer, which allow the water to pass from a cell-to-cell to an apoplastic pathway, whereas there is no shifting of preferential pathway of water next to the exodermis at maturity level 2.

Figure 7.

Influence of the proportion of aerenchyma on the relative k_r for simulated monocot anatomies. The colors represent different levels of hydrophobic barrier development. 1: Endodermal Casparian strip (blue); 2: Endodermal suberization (red); 3: Endodermis full suberization and exodermal Casparian strip (green). The cross sections at the bottom of the figure, from left to right, show examples of roots with 0%, 25%, and 50% of aerenchyma.

To observe the influence of the cortex features on the k_r, a range of cross sections were simulated with increasing cortex cell diameter and number of cortex layers (Fig. 8). We observed an increase of all components induces a decrease in the simulated k_r (Fig. 8, A, C, D). Moreover, the cortex width (isolines in Fig. 8A) accounts for the coupled effect of the cell diameter and the number of layers on the simulated k_r. This feature neatly captures the decreasing trend of k_r with increasing cortex width for the global simulated dataset included in Figure 8B (unlike Fig. 8, C and D, displaying a single transect across the parametric space each).

Figure 8.

Influence of cortex anatomy (number of cortex layers and cell size) on k_r for simulated monocot anatomies. A, Overview of k_r values across the parametric space where endodermal Casparian strip is the only apoplastic barrier. The colored dashed lines represent the cortex width isoline (mm), and the dotted lines are a visual representation of the fixed parameters for the two subplots (C and D). B, Evolution of the relative k_r as the cortex width increases. C, Evolution of the relative k_r as the cortex cell diameter increases for the number of cortex layers fixed to six. D, Evolution of the relative k_r as the number of cortex layers increases for a cortex cell diameter set to 0.03 mm. B to d, The colors represent different levels of hydrophobic barrier development. 1: Endodermal Casparian strip (blue); 2: Endodermal suberization (red); 3: Endodermis full suberization and exodermal Casparian strip (green).

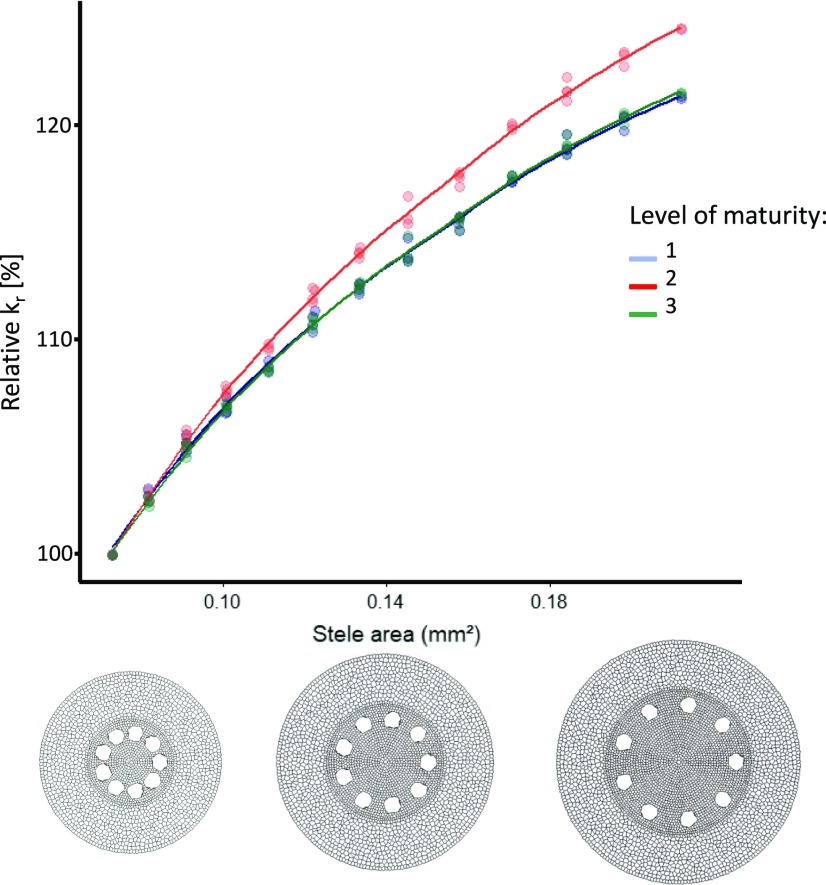
The relative influence of each cortex feature was greater at maturity level 1 than for the other maturity level tested. Each additional apoplastic barrier reduced the relative influence of the cortex features over the water flow. Moreover, under maturity level 3, the cortex features had the lowest relative influence on the conductivity in comparison with the other ones. Increasing the stele area while keeping the cortex width constant led to an increase of the simulated k_r (Fig. 9). The influence of the stele area was highest in the scenario with maturity level 2.

Figure 9.

Influence of stele area on the relative k_r for simulated monocot anatomies. The colors represent different levels of hydrophobic barrier development. 1: Endodermal Casparian strip (blue); 2: Endodermal suberization (red); 3: Endodermis suberization and exodermal Casparian strip (green). The cross sections at the bottom of the figure, from left to right, show examples of roots with 0.3, 0.4, and 0.5 mm stele diameter.

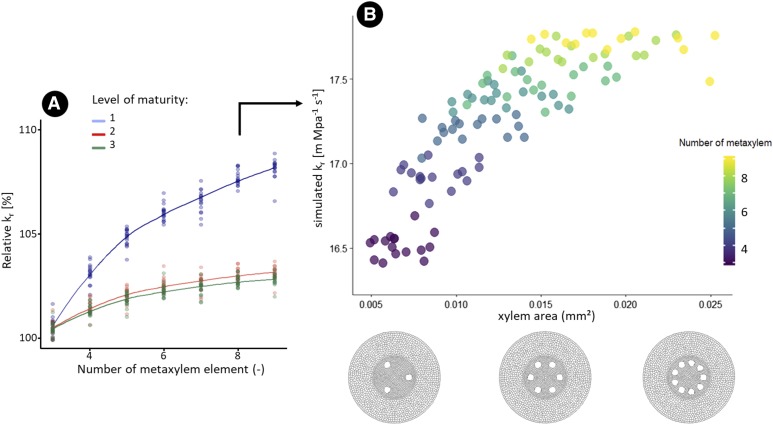
Figure 10 shows the influence of increased xylem area on k_r. To increase the xylem area, the number of the xylem poles was increased as well as the size of each pole. As a general rule, having more xylem poles increases the simulated k_r. However, k_r reached a plateau when the xylem nearly covered the whole stele perimeter (Fig. 10A). The relative influence of the increase of xylem number was the greatest at maturity level 1 compared with other maturity levels.

Figure 10.

Influence of xylem features on the k_r for simulated monocot anatomies. A, Influence of the number of xylem poles on the simulated relative k_r. The colors represent different levels of hydrophobic barrier development. 1: Endodermal Casparian strip (blue); 2: Endodermal suberization (red); 3: Endodermis full suberization and exodermal Casparian strip (green). B, Influence of the xylem area on the simulated k_r. The simulated k_r was calculated using an endodermal Casparian strip as the only apoplastic barrier.

DISCUSSION

Previously, when analyzing root anatomical data, scientists had to make compromises. On the one hand, a complete digitalization of the root anatomical network, which might be needed for further computational analysis, was possible using semiautomated tools, such as CellSeT (Pound et al., 2012). However, this procedure is time consuming, especially for large roots. On the other hand, tissue-scale metrics could be automatically obtained from large datasets using other tools, such as RootScan (Burton et al., 2012), PHIV-RootCell (Lartaud et al., 2015), or RootAnalyzer (Chopin et al., 2015). Such a high throughput pipeline yields quantitative descriptive properties, but does not reach the level of detail required for analysis of the functional role of root anatomy in functional structural plant models (Passot et al., 2018).

With GRANAR, we aimed to bridge the gap between these two pipelines so that researchers do not have to make tradeoffs between time consumption and quality of the analysis. Our new method uses tools that gather anatomical features to create GRANAR input parameters (examples are given in the “Materials and Methods”). GRANAR then generates a complete root anatomical network, which can be used for downstream root functional analysis (Fig. 2).

GRANAR coupling with other tools enables the estimation of functional properties from root anatomical networks. For instance, combining GRANAR with MECHA (Couvreur et al., 2018) enables the estimation of the k_r of a root cross section (Fig. 2). Other computational tools, such as OpenAlea (Pradal et al., 2008), could use the complete cell network anatomy generated by GRANAR to analyze other functional properties, such as root radial growth. As such, cell wall geometrical information can be integrated with mathematics to simulate how cell tissue behaves with different growth rates, local strain, and elastic deformation of cells under turgor pressure (Chopard et al., 2007). For Arabidopsis (Arabidopsis thaliana), a single stereotypical root cross section was modeled by Dyson et al. (2014) to understand how cell properties and shapes contribute to tissue‐level extensibility and yield. Their study could be extended to more diverse and larger roots with GRANAR.

Overall, our simulations showed the cortex width is one of the major predictors of k_r. When the size of the cortex increases, the conductivity decreases, and it is mostly due to an increase in the length of the apoplastic pathway, as shown in our simulation cases. The larger the cortex is, the longer the path between the soil surface and the xylem vessels. Even when apoplastic barriers are fully developed, the cortex thickness still influences the conductivity greatly (Fig. 8). The influence of the cortex width on k_r was already found experimentally for a wide range of species (Rieger and Litvin, 1999). Cortex features have also been found as a factor of drought tolerance (Chimungu et al., 2014a, 2014b; Lynch et al., 2014). Chimungu et al. (2014b) showed increasing the cortex cell diameter would reduce metabolic cost of soil exploration and consequently improve drought tolerance. In that regard, our results showed for the same amount of cell layer, increasing cortex cell size would also reduce k_r and limit water uptake. Reduced k_r would constitute a water saving strategy for the plant (Lynch et al., 2014). Additionally, Chimungu et al. (2014a) showed a reduction of the number of cortical layers would also reduce metabolic cost and therefore improve drought tolerance by enabling deeper rooting depth and increased water uptake. Here, our results showed a reduction of the number of cortical layers would increase k_r and effectively ease water uptake. Thus, as Lynch (2015) suggested, roots with a small number of cortex layers and large cortex cells should have a small metabolic cost. However, our results showed this would have a compensatory effect on k_r because few cortical layers and large cortical cells have an opposite effect (Fig. 8, C and D). We suggest instead a combination of few but large cortical cell layers should show deep rooting ability thanks to the low metabolic cost and a small value of k_r.

Our simulations show an increase in the aerenchyma proportion leads to a decrease in root k_r. This has also been shown experimentally in maize (Fan et al., 2007). The reduction of the number of parallel pathways due to the formation of aerenchyma is likely the cause of the observed reduction of k_r (Fig. 7). Lynch and Brown (2008) showed increasing the aerenchyma reduces the root metabolic cost, which in turn enables deeper rooting depth and improves drought tolerance. It has to be noted the aerenchyma proportion is an anatomical feature independent from the many other anatomical traits (Burton et al., 2013a). We acknowledge we do not know if cell hydraulic properties change with the aerenchyma formation in nature. This discrepancy may explain why in Fan et al. (2007) the observed k_r reduction is stronger than what we estimated with our simulation.

Recent studies show a large number of metaxylem vessels with small diameters improves drought tolerance (Souza et al., 2013; York et al., 2015). A hypothesis to explain the drought tolerance mechanism of small xylem diameter is the reduction of cavitation likelihood (Li et al., 2009). Another hypothesis is the reduction of axial water fluxes (Lewis and Boose, 1995), which correspond to the water saving strategy (Lynch et al., 2014). In addition, our results showed an increase of the k_r as the number of xylem poles increases. Moreover, Huang and Nobel (1993) have found a positive correlation between the number of xylem vessels and the k_r in Ferocactus acanthodes and in Opuntia ficus-indica. Nevertheless, our simulation also showed the decreasing size of xylem vessels alone would also decrease the k_r (Fig. 10), which would lead to a water-saving strategy. Another study showed a drought tolerant plant (sorghum, Sorghum bicolor) expresses few xylem vessels and large cortex (Salih et al., 1999). In this case, the two factors would limit k_r.

The stele area, to our knowledge, has not been explored as a drought tolerant factor in the field. However, Moreno-Ortega (2016) experiment on maize lateral roots showed a strong correlation between stele diameter and the number of xylem poles, which was discussed above. In our study, we simulated the change of stele diameter without changing the number of xylem poles, and the stele alone had a strong impact on k_r (Fig. 9). The increased simulated k_r as the stele area increased was mostly due to the increase of the pathway area.

The influence of anatomical features changes with the development of apoplastic barriers. As detailed in the sensitivity analysis for each of the anatomical features, the relative influence of each feature generally decreases as the number and strength of apoplastic barriers increase. The reason for this decrease is that the relative influence on water flow of the apoplastic barriers in comparison with anatomical variation is increasingly strong. This behavior typically occurred with the simulation for the cortex features and with the simulation for the xylem. Rieger and Litvin (1999) justifiably show apoplastic barriers alone do not explain all changes in k_r. However, our simulation shows relative influence of anatomical variation changes as the apoplastic barriers increase (Figs. 7–10). This, to our knowledge, has not been pointed out in the literature. Further investigation could shed light on experimental data, where such trends are observed.

As shown in this manuscript, GRANAR is able to reproduce the general anatomical features of varied experimental data. However, the anatomies produced by GRANAR remain a stereotypical representation of root cross sections. Specific features, such as uneven cell divisions (for instance, due to the formation of a lateral root) in specific locations, will not be represented using GRANAR. As a result, scientists might want to use manual image analysis tools to capture such specific anatomical features. At this stage, it is also worth noticing GRANAR does not represent structures formed during secondary growth (secondary xylem and phloem).

Another current limitation of GRANAR is its static aspect. The model does not explicitly simulate the growth and development of the different cell layers. The root anatomy is the result of a generative algorithm and is fixed in time. One possible improvement to GRANAR would be to include a developmental module within the model, similar to the current root architectural models (Postma et al., 2017; Barczi et al., 2018; Schnepf et al., 2018). This would allow the model to create root anatomies for different root ages in one simulation, enabling the estimation of the evolution of the root conductivity with the root maturation. The downside would be that such a model would be more difficult to parametrize, making it more difficult to link to experimental datasets.

A third limitation of our current pipeline is the lack of information regarding some of the cell layers. Although tools such as RootScan (Burton et al., 2012) or PHIV-RootCell (Lartaud et al., 2015) can automatically extract some of the needed variables, they do not extract all of them. For instance, some assumptions were made in our research regarding the cell size in the epidermis, endodermis, pericycle, stele, and exodermis (see “Materials and Methods” for details). It would therefore be useful to have a concerted development for both the model and the image analysis tools to create a fully integrated pipeline.

Finally, most of the data presented here were obtained on maize. This choice was a practical one, as maize was the only plant for which we could find sufficiently large and detailed datasets. In the future, additional validation of GRANAR should be performed for other species. The data on the 19 different perennial grass species from Wahl and Ryser (2000) show the way toward the global validation of GRANAR for monocotyledons. This would be facilitated if experimental data (in this case the images) were more widely shared within the community (e.g. on figshare or Zenodo).

CONCLUSIONS

GRANAR is a new open-source computational tool that is able to generate a range of root anatomies for both monocots and dicots (http://granar.github.io). The input of the models can be rapidly acquired using existing image analysis tools. As output, GRANAR produces an explicit representation of the root anatomy as a network of connected cells. These networks can serve as input for other models, such as MECHA, and be used to estimate functional properties (here radial hydraulic conductivities) of specific anatomies.

In this manuscript, we validated GRANAR by reanalyzing large published datasets of maize root anatomies. GRANAR was able to represent the large range of experimental root anatomies. In addition, by coupling GRANAR with MECHA, we were able to estimate the hydraulic properties of the different anatomies in the dataset. This analysis highlighted the importance of cortex width and stele area as major factors influencing the root radial conductivity.

We also used GRANAR-MECHA to further explore the theoretical link between anatomy and radial conductivity. By creating 1000s of theoretical anatomies, we were able to assess the functional importance of individual anatomical properties such as the number of xylem vessels, the proportion of aerenchyma or the size of the stele. The analysis highlighted most anatomical variables have an influence on the hydraulic properties of the root. Their relative importance varied and functioned at the level of apoplastic barrier development. As a general rule, the influence of anatomical feature was smaller when apoplastic barriers (in the endodermis and exodermis) were present.

In conclusion, we presented GRANAR, a new computational pipeline for the functional characterization of root anatomy.

MATERIALS AND METHODS

Description of the GRANAR Model

GRANAR was developed in R and is available as an R package (http://doi.org/10.5281/zenodo.3068505).

To create a network anatomy of a root cross section, the GRANAR model is based on the placement of the cell layers around the center of the root. The model first places the innermost cell layer (the stele), then progressively builds the root toward the outermost layer (the epidermis). Coordinates of the cell center for each tissue type are established as a function of the diameter of the cells that compose the tissue. The cell type diameter is defined by the cell_diameter parameter for each cell type. The parameter n_layers defines the number of cell layers for each tissue type independently (Table 1). The only exception is for the stele, where the number of cell layers is calculated by dividing the diameter of the stele (layer_diameter) by the stele cell diameter. To create a unique network for every run of GRANAR, a random factor (randomness) adds a slight variation to the coordinate of stele and cortex cell centers.

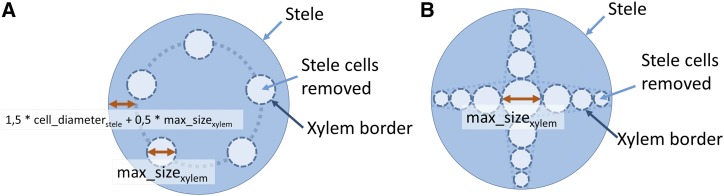
Specific vascular tissue patterns are created depending on whether the user chooses to simulate monocot or dicot anatomy. For monocot, the xylem poles of a defined radius (max_size) are placed at the periphery of the stele. For dicots, the vascular blades are placed on defined radius from the center to the last layer of the stele. The size of the largest xylem element in the centrum is determined by the max_size parameter. The other xylem elements along the vascular blade have a decreasing size, which is proportional to the distance from the center until it reaches the minimum size of a stele cell diameter (Fig. 11).

Figure 11.

Overview of the methodology to create the vascular elements. A, Monocotyledon stele cross section. B, Dicotyledon stele cross section. In both (A) and (B), the stele cells inside the xylem border (dark blue) are removed to create xylem cells, indicated by light blue arrows. The different parameters used to build the root cross section simulation are described in light blue shaded boxes and indicated by double-headed red arrows.

Once all cell centers are placed, the model creates the cell boundaries (cell walls). A voronoi tessellation of the cell centrums (using the deldir package [Turner, 2019]) creates the cell walls at middistance between every cell center previously set. The epidermis cells do not have any neighbor cells on the outer part; however, an outside layer similar to the epidermis is created for the sake of the voronoi tessellation, then removed once it is done. Once the tessellation is done, the area of the different cells is then computed by the polygon function of the “sp” package.

Description of the GRANAR Package

The GRANAR model is available as an R package. The package contains the following functions:

• - read_param_xml (path = “name_of_the_parameter_file.xml”)

  Loads the parameter files that are under XML format and produces a data frame object with the information needed to generate a root cross section with the function create_anatomy.

• - create_anatomy (parameter = parameter_for_granar, path = “name_of_the_parameter_file.xml”)

  Generates a root cross section with a data frame containing the needed parameter or calls the read_param_xml function to load a parameter file under XML format directly. The object returned by the function is a list containing four data frames:

  • - A nodes data frame with the coordinates of all points of all the cells, their identity, and the information needed to create the cell polygons.

  • - A walls data frame with the condensed information of all cell walls.

  • - A cells data frame with the detailed information about the cells: area, distance from the center, and their angle in the cross section.

  • - An output data frame with details information for each tissue.

• - get_root_section (path = “name_of_the_root_cross_section.xml”)

  Imports the geometry information (the nodes data frame) about root cross section from the file generated with GRANAR or CellSeT.

• - plot_anatomy (sim = Simulation, col = “type”)

  Makes a figure which represents the given geometrical data.

  Accepted arguments for the col (color) parameter are 'type', 'area', 'dist', 'id_cell' and 'angle'. Default = 'type'

• - write_anatomy_xml (sim = Simulation, path = “name_of_the_simulation.xml”)

  Saves the geometry information generated with GRANAR in an XML file (the same output format as CellSeT).

It can be installed very easily on R thanks to the “devtools” package (Wickham and Chang, 2019) with the function: install_github(“granar/granar”). The “granar” package relies on few dependencies. These dependencies are: the “deldir” package (Turner, 2019), the “alphahull” package (Rodríguez-Casal and Pateiro-López, 2010), and the “retistruct” package (Sterratt et al., 2013). They should be installed (e.g. install.packages[deldir]) before loading the “granar” package.

Description of the MECHA - GRANAR connection

MECHA reads XML-formatted CellSeT data to load the geometry information it needs to compute the radial conductivity. GRANAR was built to generate outputs in the same format as CellSeT. Therefore, the coupling of those tools is easily made and examples can be found at this address: https://github.com/granar/granar_examples [10.5281/zenodo.3068671]. The coupling is done by file exchange.

Description of the Experimental Data used for the Validation of Maize (Zea mays) Root Anatomies

The Burton et al. (2013a) and Chimungu et al. (2014b) datasets were produced using RootScan software. RootScan produces a range of root anatomical features, most of which are identical as the input parameter for GRANAR. Nonetheless, a few transformations were needed to pass from RootScan output to GRANAR input. They are summarized below in Table 4. In addition, some anatomical features were not calculated by RootScan. For instance, stele and pericycle cells were assumed to have a diameter of 0.011 mm. The stele cell diameter assumption was made by pooling known data (Steudle et al., 1993; Gao et al., 2015; Couvreur et al., 2018). The endodermis and the exodermis were also assumed to have the same diameter as cortex cells, and epidermis cells were assumed to have a third of the cortex cell diameter because RootScan does not distinguish differences between those cell types. Additionally, epidermis cells were not accounted for in the number of cortex layer in RootScan. In that regard only two cell layers were removed to the cortex layer count of RootScan data in the transformation procedure (Table 4). One last assumption was made concerning the number of xylem poles. Thanks to Moreno-Ortega (2016) data, which show a linear regression between the stele diameter and the number of xylem poles, the number of xylem poles was estimated based on the stele diameter.

Table 4. Overview of the methodology to transform RootScan data into GRANAR parameters.

GRANAR Input	Transformation	RootScan Output
Stele cell diameter (mm) Pericle cell diameter (mm)		–
Stele diameter (mm)	=	Stele area (mm2)
Number of metaxylem element (−)	=	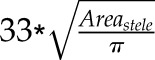Stele area (mm2)
Xylem diameter (mm)		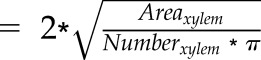Xylem area (mm2)
Number of cortex layer (−)		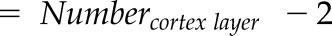Number of cortex layer
Cortex cell diameter (mm) Endodermis cell diameter Exodermis cell diameter		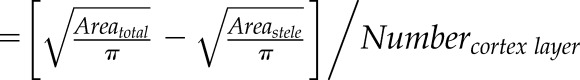Cross section area (mm2)
Epidermis cell diameter (mm)		–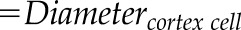
Aerenchyma proportion (%)	–	Aerenchyma proportion (%)

The Burton et al. (2013a) dataset used in this study included the anatomical features of 195 landraces emphasizing accessions from stressful soil environments. The data are available in their Supplemental Tables S1 and S2. The Chimungu et al. (2014b) dataset used in this study was imported from their Supplemental Tables S3 and S4, which were lists of genotype anatomical features selected from the IBM (Intermated B73 x Mo17) population and from the Malawi maize breeding program.

The extraction of the anatomical features from the Gao et al. (2015) dataset was conducted with ImageJ software. The anatomical features gathered were exactly the same as the input parameters of GRANAR except for units. The anatomical features data used in our study can be found in their Table 1. The aerenchyma features of Gao et al. (2015) were found in their Figure 8. The Gao et al. (2015) dataset includes the anatomical features of three root types of maize cv Zhengdan958 exposed to a low nitrogen treatment.

To create the three replicates of each data point, three runs of GRANAR were made and saved separately for each data point (Supplemental Dataset S1).

Description of MECHA Hydraulic Parameters

The simulation framework MECHA (Couvreur et al., 2018) estimates k_r from the root transverse anatomy generated with GRANAR or CellSeT (Pound et al., 2012) and from the subcellular scale hydraulic properties of walls, membranes, and plasmodesmata. Cell wall hydraulic conductivity was set to 2.8 10⁻⁹ m²s^-1MPa⁻¹, as measured by Zhu and Steudle (1991) in maize. Lignified and suberized wall segments in the endodermis and exodermis (Fig. 6) were considered hydrophobic and attributed null hydraulic conductivities. The protoplast permeability (L_pc, 7.7 10⁻⁷ m s^-1MPa⁻¹) measured by Ehlert et al. (2009) was partitioned into its three components: the plasma membrane intrinsic hydraulic conductivity (k_m), the contribution of aquaporins to the plasma membrane hydraulic conductivity (k_AQP), and the conductance of plasmodesmata per unit membrane surface (k_PD). The latter parameter was estimated as 2.4 10⁻⁷ m s^-1MPa⁻¹ (Couvreur et al., 2018), based on plasmodesmata frequency data from Ma and Peterson (2001), and the plasmodesmata conductance estimated by Bret-Harte and Silk (1994). By blocking aquaporins with an acid-load treatment, Ehlert et al. (2009) measured a k_AQP of 5.0 10⁻⁷ m s^-1MPa⁻¹. The remaining value of k_mafter subtraction of k_AQP and k_PD from L_pc was 0.3 10⁻⁷ m s^-1MPa⁻¹. Each value of k_m, k_AQP, k_PD, and L_pc was set uniform across tissue types. For details on the computation of k_r, see Couvreur et al. (2018).

Data Analysis

All statistical analyses were made using R. No distinction between the three datasets was made to compute R squared, correlation, and p values in the validation experiment. All ANOVAs were performed using the aov function from ‘stat’ package. Correlation analysis was performed using the ‘ggpairs’ function from ‘GGally’ package.

Model and Data Availability

GRANAR was developed as an open-source project under a GNU General Public License v3.0. Different sets of code and data were produced for this research:

• - Web application: https://plantmodelling.shinyapps.io/granar/

• - R package: https://github.com/granar/granar [10.5281/zenodo.3068505]

• - R Markdown example: https://github.com/granar/granar_examples [10.5281/zenodo.3068671]

• - Script and data: https://github.com/granar/PlantPhys2019 [10.5281/zenodo.3471485]

Supplemental Data

The following supplemental materials are available.

• Supplemental Figure S1. Quantile-Quantile (QQ) plot based on the residuals of the model summarized in Equation 1.

• Supplemental Dataset S1. Spreadsheet containing the anatomical features and radial conductivity of all simulations.