Skip to main content
PMC home page
Journal of Applied Crystallography logoLink to Journal of Applied Crystallography
. 2020 Feb 1;53(Pt 1):148–158. doi: 10.1107/S1600576719016832

Structure analysis of supported disordered molybdenum oxides using pair distribution function analysis and automated cluster modelling

Troels Lindahl Christiansen a, Emil T S Kjær a, Anton Kovyakh b,c, Morten L Röderen c, Martin Høj d, Tom Vosch a, Kirsten M Ø Jensen a,*
PMCID: PMC6998784  PMID: 32047409

Using pair distribution function analysis, the structure of amorphous supported molybdenum oxides is characterized using a new automated data modelling approach.

Keywords: molybdenum oxides, nanostructure, pair distribution function analysis, supported catalysts, automated modelling

Abstract

Molybdenum oxides and sulfides on various low-cost high-surface-area supports are excellent catalysts for several industrially relevant reactions. The surface layer structure of these materials is, however, difficult to characterize due to small and disordered MoOx domains. Here, it is shown how X-ray total scattering can be applied to gain insights into the structure through differential pair distribution function (d-PDF) analysis, where the scattering signal from the support material is subtracted to obtain structural information on the supported structure. MoOx catalysts supported on alumina nanoparticles and on zeolites are investigated, and it is shown that the structure of the hydrated molybdenum oxide layer is closely related to that of disordered and polydisperse polyoxometalates. By analysing the PDFs with a large number of automatically generated cluster structures, which are constructed in an iterative manner from known polyoxometalate clusters, information is derived on the structural motifs in supported MoOx.

1. Introduction  

Nanostructured metal oxides of, for example, molybdenum, chromium or vanadium supported on cheap high-surface-area supports, e.g. titania, alumina or zeolites, are attractive candidates in many areas of heterogeneous catalysis (Zaera, 2013 ▸; Shiju & Guliants, 2009 ▸; Munnik et al., 2015 ▸; Banares, 1999 ▸; Zhang et al., 2013 ▸). To develop the field further and realize the full potential of these nanostructured oxides, a comprehensive understanding of the structure/property relationship is essential (Macht & Iglesia, 2008 ▸; Bell, 2003 ▸). Currently, structural information for these nanomaterials is obtained through spectroscopic methods, e.g. Raman spectroscopy, X-ray photoelectron spectroscopy, UV–visible or X-ray absorption, as the small domain sizes and amorphous nature of the materials challenge traditional microscopy and diffraction techniques (Macht & Iglesia, 2008 ▸). X-ray total scattering, where diffuse scattering arising from disordered atomic arrangements is included in the data treatment, has over the past decade evolved into a powerful technique for structural characterization of nanomaterials with limited structural order. As opposed to traditional powder diffraction, total scattering allows for observation of the atomic arrangement in nanostructures without long-range order and with ångström resolution (Billinge & Kanatzidis, 2004 ▸).

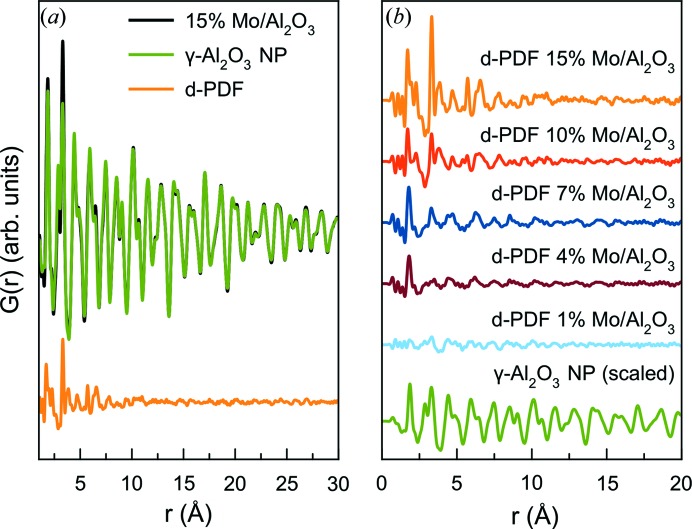
Total scattering data are usually analysed through the pair distribution function (PDF), which is the Fourier transform of the scattering signal; it expresses the probability of finding a pair of atoms at a distance r, which provides an intuitive way of analysing structures. PDF analysis has previously been shown to be a very powerful technique to elucidate atomic structures of supported materials, e.g. arsenate or large cations adsorbed on γ-Al2O3, ferrihydrite or δ-MnO2 (Harrington et al., 2010 ▸; Li et al., 2011 ▸; van Genuchten & Pena, 2016 ▸; Chupas et al., 2011 ▸). By acquiring X-ray total scattering data and obtaining PDFs for both the clean support and the sample on the support, and subtracting the former from the latter, it is possible to obtain a PDF describing the supported structure only, as demonstrated in Fig. 1 ▸. The resulting PDF is often referred to as the differential PDF (d-PDF) (Chapman & Beauchamp, 2006 ▸).

Figure 1.

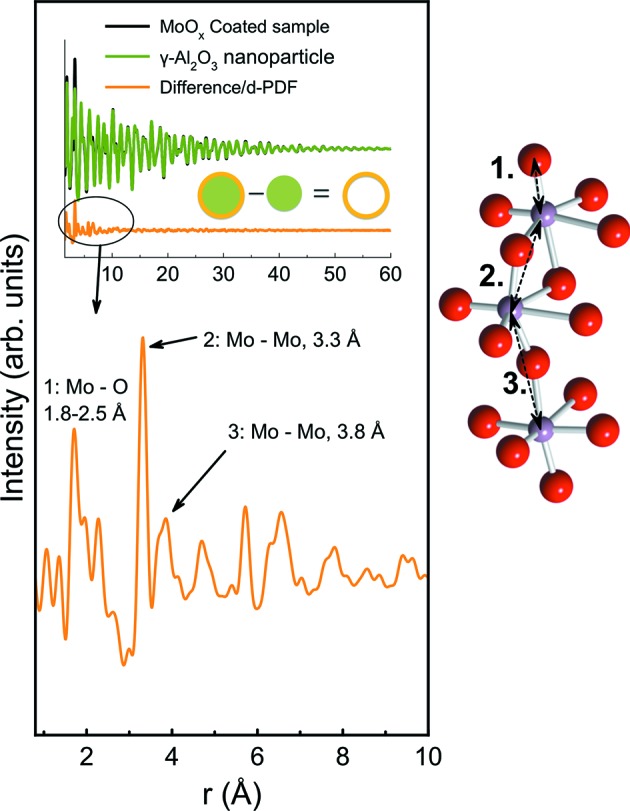
Figure 1

Open in a new tab

Illustration of the generation of the d-PDF. A PDF is acquired from the supported sample as well as from the clean support, and the d-PDF is obtained by subtraction of the former from the latter. This results in a PDF expressing the structure of the supported material only. This is illustrated here for molybdenum oxide supported on alumina nanoparticles. The most significant peaks of the d-PDF can be assigned, namely the Mo–O peak (1.8–2.5 Å), the edge-sharing Mo–Mo peak (3.3 Å) and the corner-sharing Mo–Mo peak (3.8 Å).

Here, we present d-PDF studies of supported nano­structured MoOx samples on different supports. We use a new method for analysing the obtained d-PDFs of disordered nanoclusters, where the data are fitted with a large number (thousands) of cluster models, which are automatically built on the basis of known metal oxido cluster structures. A similar approach to ‘automated modelling’ has recently been successfully applied to structural analysis of metal clusters (Banerjee et al., 2019 ▸). By studying metal oxido clusters and fitting this large number of structures to the d-PDF, we can extract information on the structural motifs present in the disordered molybdenum oxide systems. We first demonstrate this method for nanostructured MoOx on γ-Al2O3. This system has received much attention due to its use in oxidative dehydrogenation of small alkanes and other industrially relevant catalytic reactions (Cavani et al., 2007 ▸; Høj et al., 2014 ▸; Setnička et al., 2015 ▸). Subsequently, we apply the same method to MoOx supported on zeolites. MoOx supported on zeolites are promising candidates for catalysing the conversion of waste methane into liquid aromatic hydrocarbons (Gao et al., 2015 ▸), but there is limited structural knowledge of the MoOx layer (Li et al., 2006 ▸). We show that the MoOx layer on both alumina and zeolites under ambient conditions consists of [MoO6] octahedra forming small clusters with a structural domain length of approximately 1 nm. The structures, which are hydrated from atmospheric air, contain similar motifs to known polyoxometalate structures found in solution, although they are not monodisperse and include a much larger degree of structural disorder.

2. Results and discussion  

2.1. Molybdenum oxide supported on γ-Al2O3  

Several hypotheses regarding the structure of molybdenum oxide on alumina have been presented in recent decades. For high MoOx loadings, corresponding to more than monolayer MoOx coverage on the support, crystalline MoO3 is formed on the particles, while a nanostructured and catalytically active structure forms at lower loadings (Mestl & Srinivasan, 1998 ▸). It has previously been speculated that the supported nano­structured molybdenum oxide has a local structure similar to that of MoO3. However, further structural work, using primarily Raman spectroscopy, has indicated that at low loadings (below monolayer coverage) isolated, tetrahedrally coordinated [MoO4] units occupy the alumina surface and bind directly to the alumina structure (Chen et al., 2001 ▸; Drake & Stair, 2017 ▸; Tsilomelekis & Boghosian, 2013 ▸; Wachs, 1996 ▸). When the MoOx coverage is large enough for monolayer coverage, the dominant structural unit is believed to be octahedral [MoO6], and it has been suggested to be in conformations similar to polymolybdate units found in solutions such as [Mo7O24]6− or [Mo8O26]4− in oligomeric chains (Mestl & Srinivasan, 1998 ▸). The structural arrangements are highly dependent on several factors, including the support and the degree of hydration of the samples from atmospheric air (Deo & Wachs, 1991 ▸). No unambiguous surface structure model exists with regards to molybdate species and the extent of ordering (Tsilomelekis & Boghosian, 2013 ▸). Using d-PDF, we can test existing hypotheses and develop a structural model for the supported molybdenum oxide.

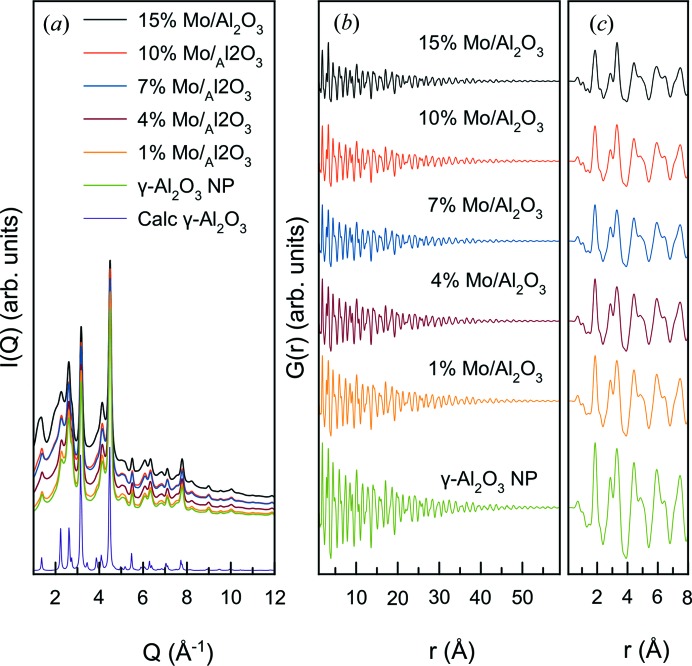
Fig. 2 ▸(a) shows X-ray total scattering data for a range of MoOx/γ-Al2O3 samples with molybdenum content from 0 to 15 wt% Mo. The samples all show very broad Bragg reflections, which can be assigned to the γ-Al2O3 support (Paglia et al., 2003 ▸). No additional Bragg peaks are seen in any of the samples; however, the presence of increasing amounts of MoOx is seen in the scattering pattern as a rise in diffuse scattering intensity over the entire Q range. Diffuse scattering originates from nanostructured, amorphous and highly disordered phases, and the increase in diffuse scattering is thus indicative of a disordered MoOx layer on the substrate, agreeing with previous observations. Note that the disordered nature of the alumina support also contributes to the diffuse scattering signal.

Figure 2.

Figure 2

Open in a new tab

(a) X-ray total scattering data obtained from supported MoOx/γ-Al2O3 samples, as well as data showing the calculated signal from ordered γ-Al2O3 nanoparticles. (b) PDFs derived from the measured X-ray total scattering data. (c) Local region of the PDFs.

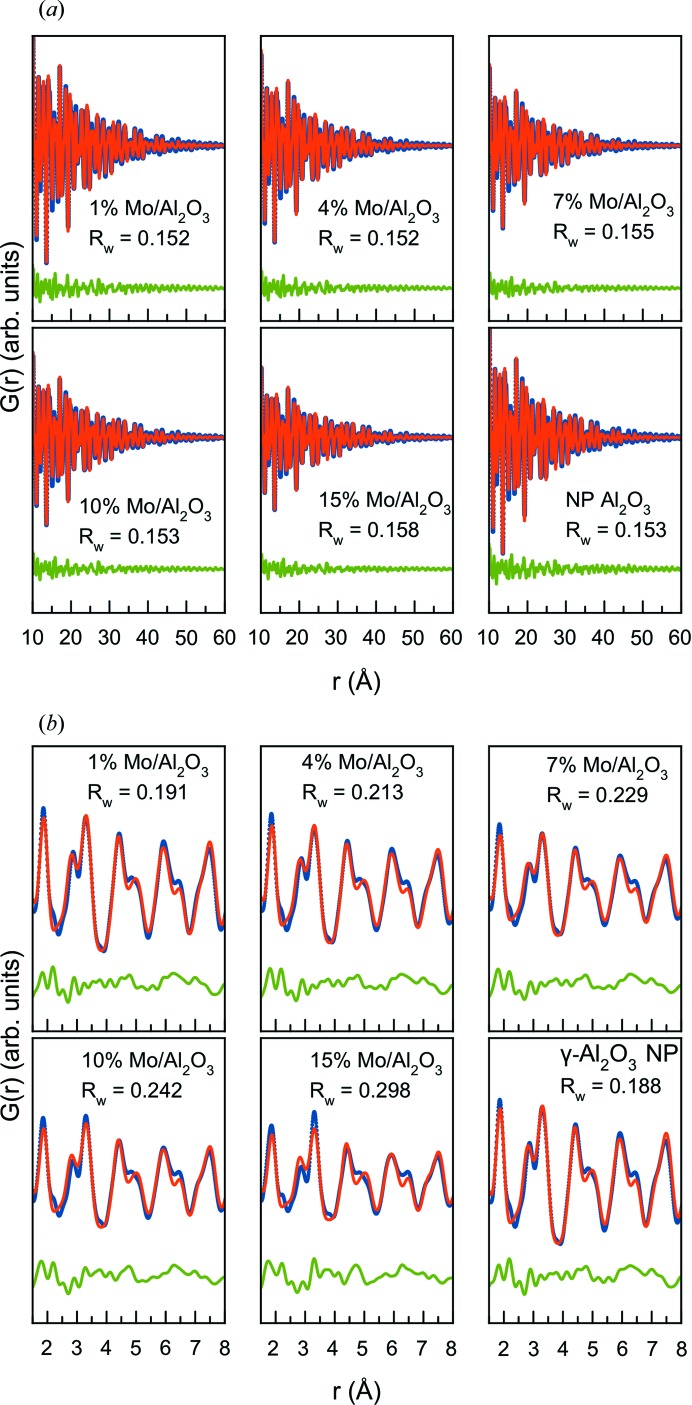
Before calculating the d-PDFs from the X-ray total scattering data for further structural analysis, the PDFs from all samples are analysed to establish the existence of a nano­structured MoOx layer and to facilitate calculation of the d-PDFs. The PDFs calculated from the data sets in Fig. 2 ▸(a) are shown in Fig. 2 ▸(b). All PDFs show similar features, except in the local range [ca 1–8 Å, Fig. 2 ▸(c)]. The PDFs show damping at high r, and when analysed in the range 10–60 Å the data can be fitted by the tetragonal γ-Al2O3 model (space group I41/amd) (Paglia et al., 2003 ▸) using a damping factor for spherical particles (sp-diameter) after taking into account instrumental damping. The refinements can be seen in Fig. 3 ▸(a) (10–60 Å range) and yield unit-cell parameters of a, b ≃ 5.62 Å and c ≃ 7.83 Å and an sp-diameter of ca 8 nm when assuming monodisperse spherical particles. The agreement of the fitted parameters and R w values between the six samples demonstrates that the structure of the γ-Al2O3 support is largely unaffected by the MoOx coating. All refinement results are given in Table S1 in the supporting information.

Figure 3.

Figure 3

Open in a new tab

(a) Real-space fits of the measured PDFs in long range (10–60 Å) using the bulk tetragonal γ-Al2O3 structure and (b) fits to the local range (1–8 Å) using the fine-scale alumina model of Paglia et al. (2006 ▸). In all fits, the experimental PDF is displayed as blue dots, the calculated fit as a red line and the difference curve as a green line.

The bulk γ-Al2O3 model does not fit the local structure of the data, no matter what the MoOx loading. This is well known for γ-Al2O3 and has previously been studied in detail by Paglia et al. (2006 ▸), who derived a local structure model for the compound. A fit using this local structure model is shown in Fig. 3 ▸(b) (1–8 Å range). The model shows a good fit to the data from pure γ-Al2O3 nanoparticles (NPs) and the 1% Mo/γ-Al2O3 sample, which is comparable in fit quality to those reported previously (Paglia et al., 2006 ▸). As expected, an increasing discrepancy in the fit and R w factor can be observed for increasing MoOx loading. Importantly, this increase is only observed in the local-range fit, meaning that the MoOx only shows short-range structural correlations. This facilitates the generation of the d-PDFs, as the intensity of the peaks originating from the support seen in the long-range region can be scaled to match in intensity with the MoOx/γ-Al2O3 sample before subtraction. The scaling and generation of the d-PDF are demonstrated for the sample with 15% Mo in Fig. 4 ▸(a), where the substrate PDF has been scaled to match the intensity in the sample PDF for a γ-Al2O3 peak at 17.3 Å. In Fig. S1 we demonstrate that it is possible to obtain equivalent PDFs by subtracting the scattering signal from the substrate in Q space before the Fourier transform; however, subtraction in r space was preferred due to the convenient and reliable method of scaling the substrate intensity before subtraction.

Figure 4.

Figure 4

Open in a new tab

Generation of d-PDFs. (a) Scaling and subtraction of the NP γ-Al2O3 PDF from the 15% Mo/γ-Al2O3 PDF. (b) Comparison of generated d-PDFs.

All d-PDFs are shown in Fig. 4 ▸(b) where they are compared with the clean γ-Al2O3 NP sample. The PDF from the sample containing 1% Mo shows no PDF peaks that can confidently be assigned to MoOx structural motifs. This is surprising as the d-PDF technique has previously been shown to be sensitive to low loading percentages using elements with lower scattering power than Mo (Chapman et al., 2006 ▸; Harrington et al., 2010 ▸). However, this observation may be explained by the nature of the highly defective Al2O3 structure (Paglia et al., 2003 ▸), where Mo may be incorporated into the γ-Al2O3 structure by occupying cation vacancies in the surface. If this is the case, the [MoOx] signal is then mostly subtracted along with the γ-Al2O3 support.

Distinct structural peaks are seen in d-PDFs for samples with MoOx loading higher than 4% Mo. The first PDF peak from the MoOx structure is at 1.8 Å, which falls within the typical Mo—O bond distances (Hardcastle & Wachs, 1990 ▸; Pope, 1991 ▸), confirming the presence of [MoOx] units on the surface. On the basis of known crystal structures, the Mo–Mo distances are expected to be 3.3 Å (edge-sharing [MoO6] octahedra) or 3.8 Å (corner-sharing [MoO6] octahedra or tetrahedra), as illustrated in Fig. 1 ▸. In the sample with 4% Mo loading, no clear peaks are seen in this range, indicating that the [MoOx] units are isolated on the substrate surfaces; this is in agreement with observations in other studies of low-loading MoOx/γ-Al2O3 samples, suggesting the presence of tetrahedral monomolybdate ions, [MoO4]−, in hydrated samples (Mestl & Srinivasan, 1998 ▸; Drake & Stair, 2017 ▸). In the sample with 7% Mo, increased intensity is seen in the PDF at ca 3.3 Å and at higher r values, which shows the beginning of the formation of larger MoOx cluster structures. These peaks are clearly present in the samples with 10–15% Mo loading, where PDF peaks to ca 12 Å are apparent, which is also the wt% where monolayer coverage is expected to form (Høj et al., 2014 ▸). These two samples show distinct peaks at both 3.3 and 3.8 Å, indicating that both edge- and corner-sharing [MoOx] motifs are present in the clusters. A peak is found at ca 6.6 Å, i.e. double the edge-sharing distance of 3.3 Å, which indicates that edge-sharing [MoOx] units are a dominant structural motif. The d-PDFs thus clearly show that, in these samples, the [MoOx] units are not isolated but form a nanostructure with correlation between several units which must be sharing predominantly edges, but also to some degree corners. This is similar to polymolybdate ions primarily built from [MoO6] octahedra in solution (Pope & Müller, 1991 ▸). Such structures are expected for supported oxides under ambient conditions, as moisture from the air adsorbs on the material surface leading to solvation of the oxide species (Bañares & Wachs, 2002 ▸).

Note that, in our analysis, we have not considered peaks originating from Al–Mo correlations, i.e. between the substrate and MoOx. An Mo–Mo correlation will yield approximately four times the intensity of an Mo–Al correlation in the PDF due to the larger scattering power of Mo. The Al–Mo correlation should be most clear for the [MoO4] tetrahedra in the 4% sample, where an extended network of Mo–Mo correlation has yet to form. However, as mentioned, very little signal is seen in the 4% d-PDF other than the Mo–O peak. The lack of Mo–Al correlation can possibly be explained by the low scattering power of Al and large variations in angle/bond lengths of the Al—O—Mo unit on the disordered surface of the particles.

For further analysis of the larger cluster structure, we focus on the sample containing 15% Mo. We first attempted to fit the d-PDFs with existing crystalline models which have previously been suggested for supported molybdenum oxides. The lack of long-range order was taken into account with a spherical damping function (Gilbert, 2008 ▸), reducing the intensity of PDF peaks in the high-r region after accounting for instrumental PDF damping. This analysis was done using PDFgui (Farrow et al., 2007 ▸). Four fits are displayed in Fig. 5 ▸ using models of structures most commonly discussed in relation to supported molybdenum oxide, i.e. MoO3, [Mo7O24]6− (hepta­molybdate), and [Mo8O26]4− (octamolybdate) in both the α and β isomers (Bridgeman, 2002 ▸). In the MoO3 model, the structure in space group Pbnm was used, while [Mo7O24]6− was derived from (NH4)6Mo7O24(H2O)4 (Evans et al., 1975 ▸), and the α and β [Mo8O26]4− models from (C18H20N4)2[Mo8O26] (Wang et al., 2007 ▸) and (NH4)6(Mo8O27)(H2O)4 (Böschen et al., 1974 ▸), respectively. The models were prepared by removing all atoms except Mo atoms and O atoms bonded to Mo from the unit cell. The unit-cell parameters, isotropic atomic displacement parameters, a parameter relating to the correlated atomic motion (delta2) (Jeong et al., 1999 ▸) and a parameter for the spherical damping were refined along with a scale factor. Fit results are listed in Table S2.

Figure 5.

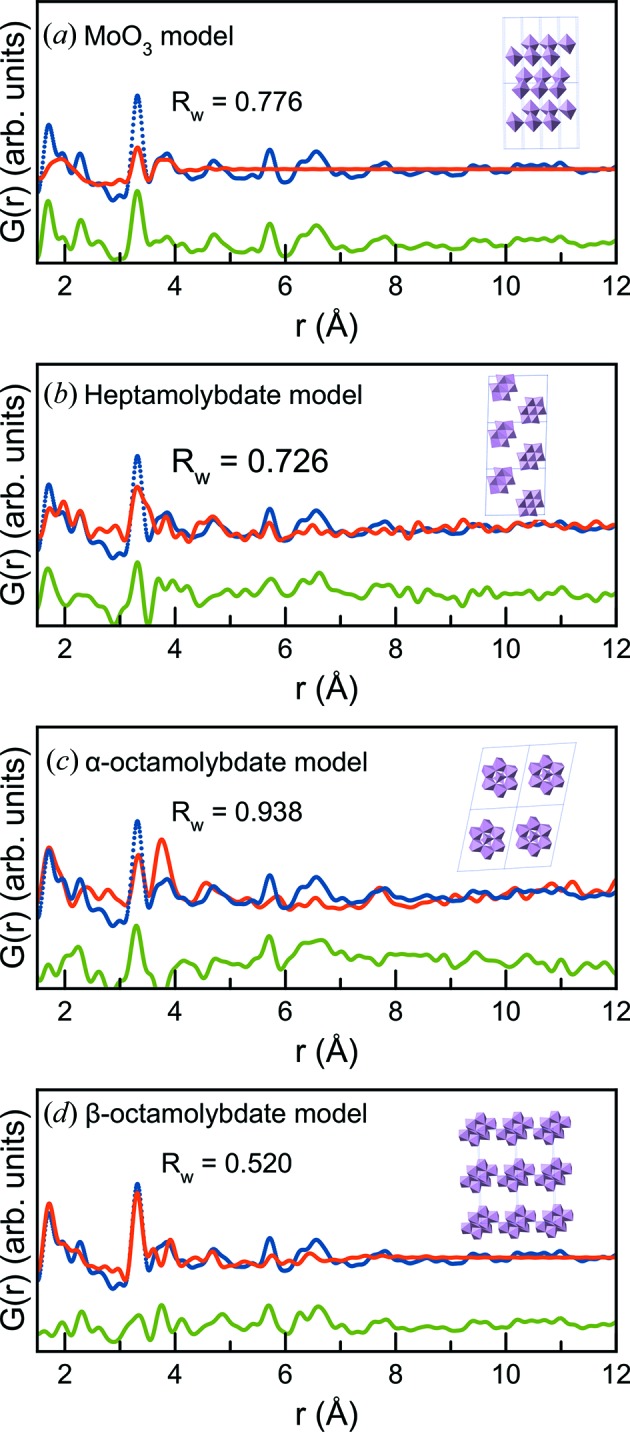
Figure 5

Open in a new tab

PDF fits to the data obtained from 15% Mo/γ-Al2O3 data with well-known crystal structures: (a) MoO3, (b) heptamolybdate (NH4)6Mo7O24(H2O)4, (c) α-octamolybdate (C18H20N4)2[Mo8O26] and (d) β-octamolybdate (NH4)6(Mo8O26)(H2O)4. In all fits, the experimental PDF is displayed as blue dots, the calculated model as a red line and the difference curve as a green line.

The fit to the MoO3 model, shown in Fig. 5 ▸(a), fails to fit anything but the closest edge- and corner-shared peaks. The [Mo7O24] model [Fig. 5 ▸(b)] performs slightly better and provides the correct peak position for some higher-order peaks, thus giving a better description of the connection between the [MoOx] units. However, the model contains too much disorder in the edge-sharing octahedra, making the peak at 3.3 Å too broad, and the intensity in the peaks above 5 Å is poorly described. The α-[Mo8O26] model in Fig. 5 ▸(c) overestimates the 3.8 Å peak compared with the 3.3 Å peak and also fails to provide a good description for peaks over 5 Å. The β-[Mo8O26] structure provides the best fit of the three models as seen in Fig. 5 ▸(d), although the peak intensities above 5 Å are still poorly described.

When fitting crystal structures to the PDF, as is done here, interactions between the individual clusters are also part of the calculated PDF. While heptamolybdate and the two octamolybdate isomers have similar local structure motifs in the clusters, the relations between the individual cluster units in the crystal structures vary significantly. In (NH4)6Mo7O24(H2O)4 and (C18H20N4)2[Mo8O26] the [Mo7O24] and α-[Mo8O26] units are isolated with a distance of 5–7 Å between the units, while in (NH4)6(Mo8O26)(H2O)4 the β-[Mo8O26] units form polymeric chains by corner sharing between the units, as seen in the inset of Fig. 5 ▸(d). While the clusters present on the substrate surface may be arranged in a semi-ordered manner, there is no reason to believe that this is similar to the arrangement of the clusters in the crystal structures. To simplify the models, we therefore attempt to treat the clusters as finite structural models, without assuming periodicity or symmetry. This is done by using the Debye scattering equations to calculate the PDFs (Gelisio & Scardi, 2016 ▸) from atomic coordinates applying the Diffpy-CMI program package (Juhás et al., 2015 ▸). The xyz coordinates of the cluster models used can be found online (Lindahl Christiansen et al., 2019 ▸).

Debye fits using the α-[Mo8O26] cluster and two units of the β-[Mo8O26] extracted from the crystal structures used for the pseudo-crystalline models are shown in Figs. 6 ▸(a) and 6 ▸(c), respectively. The fits were performed in a highly constrained manner to avoid unphysical bond distances and geometries, allowing only expansion or contraction of the full cluster structure and otherwise only fitting isotropic atomic dis­place­ment parameters of the Mo and O atoms (Jensen et al., 2016 ▸). The fit quality is comparable to the pseudo-crystalline fits seen in Figs. 5 ▸(c) and 5 ▸(d), although the fit above 5 Å is improved for β-[Mo8O26] as the envelope function now does not quench the intensity at higher r values. As seen in Table S3, the anisotropic expansion/contraction parameters are close to 1 (0.98–1.00), illustrating that the geometry and structure of the cluster are kept in the fitting process. The fits with the cluster models and the damped crystalline models can both be greatly improved by refining the Mo atomic positions in the structures; however, this introduces far too many parameters in the model compared with the information available in the PDF and results in unphysical atomic distances in the model.

Figure 6.

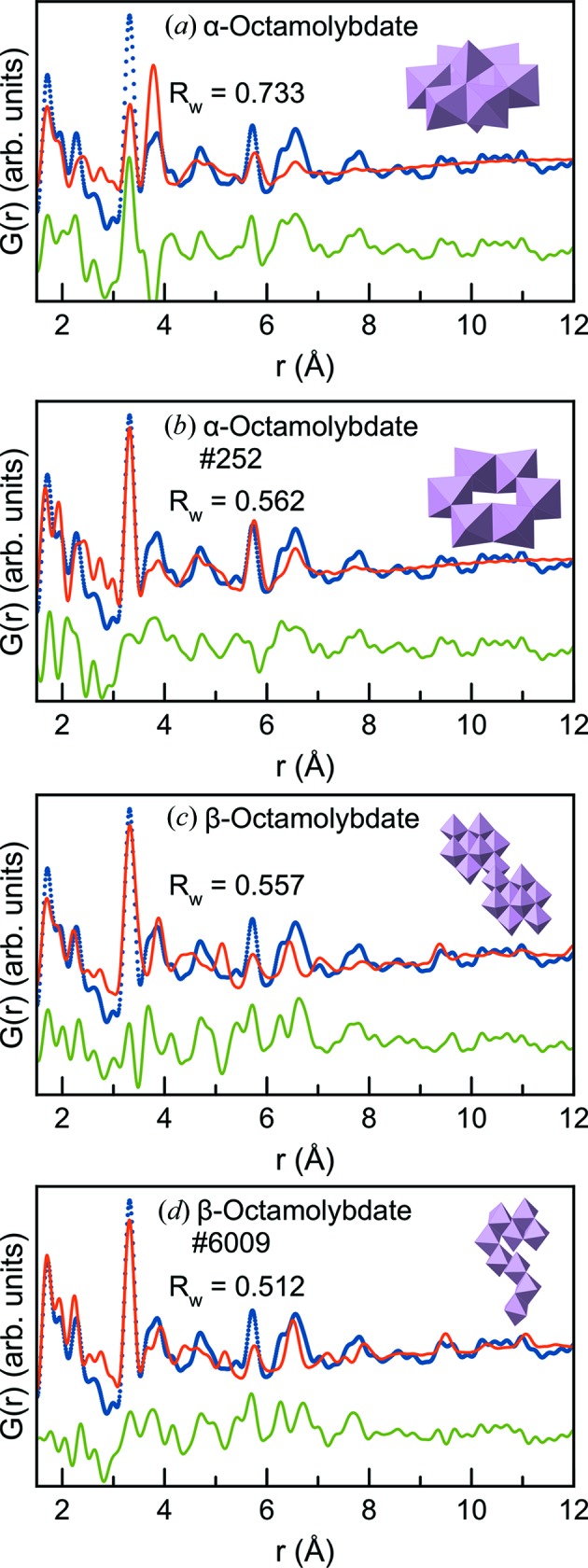
Figure 6

Open in a new tab

(a) Fit of the α-[Mo8O26] cluster structure to the d-PDF obtained from the sample with 15% Mo. (b) Fit of the best-fitting α-[Mo8O26]-derived cluster structure. (c) Fit of the β-[Mo8O26] cluster structure to the d-PDF. (d) Fit of the best-fitting β-[Mo8O26]-derived cluster structure. In all fits, the experimental PDF is displayed as blue dots, the calculated model as a red line and the difference curve as a green line.

While the fits above demonstrate that the octamolybdate clusters give a reasonable fit to the data, it is clear that the molybdenum oxide species present in the sample are not monodisperse units of either heptamolybdate or octamolybdate clusters as has previously been suggested (Mestl & Srinivasan, 1998 ▸). This is highlighted when considering other samples, where the clusters are in fact monodisperse, i.e. as is the case for molybdate ions and other polyoxometalates in aqueous solution (Juelsholt et al., 2019 ▸). Examples of such structures and fits to data from polyoxometalate clusters are shown in Fig. S2. These fits show a much smaller discrepancy between fit and data, and the Mo–Mo peaks are better defined. If comparing this with the fits shown in Figs. 6 ▸(a) and 6 ▸(c), it is clear that the MoOx surface layer is disordered and polydisperse, consisting of a range of different cluster sizes with a different number of [MoO6] octahedra. To demonstrate this, we generated a large number of new models by iteratively modifying known polyoxometalate cluster structures. New structures were created by iteratively removing [MoO6] octahedra from a starting cluster so that all possible sizes of a given Mo–oxido cluster are created. Using e.g. the octamolybdate cluster structures shown in Figs. 6 ▸(a) and 6 ▸(c) (insets) as starting models, one or more of the Mo atoms were removed, thus generating new clusters. Whenever an Mo atom was removed, all O atoms not bonded to another Mo were also removed from the structure. In this way, 28 = 256 and 216 = 65 536 new models were created from α- and β-[Mo8O26], respectively. The new structures will thus contain the same octahedra/tetrahedra as the octamolybdate clusters, but in different arrangements. We fitted all the new clusters to the d-PDF in the r range of 3–12 Å. This range was chosen so as to not let the broad Mo–O peak centred at 1.8 Å dominate the fit result, but rather focus on the Mo–Mo correlations. Note that, due to the symmetry of the clusters, some of the newly generated clusters will be duplicates. Duplicate structures are identified by checking if any other models yield the same R w value and have the same number of Mo and O atoms in the model. For α-[Mo8O26] the number of new, unique models is 160, and for β-[Mo8O26] it is 14 054.

Several cluster models were fitted initially to determine good candidates for starting structures. A good candidate provides a reasonable fit, but most importantly features peaks in the correct positions, as the method fundamentally just changes relative intensity between peaks. The tested structures are listed in Table S4.

Figs. 6 ▸(b) and 6 ▸(d) show the two best fits obtained using the method starting from α-[Mo8O26] and β-[Mo8O26], respectively. From comparison with the original fits, it is evident that both the visual fit and R w value are improved, specifically the 3.3 and 3.8 Å peaks are better fitted by the new model, as well as the peaks past r = 6 Å for the β-[Mo8O26]-derived models. However, the models still have significant discrepancies, which can be ascribed to the disordered and polydisperse nature of the nanostructure. While the structure presented here should not be seen as a single representation of the clusters present on the alumina surface, we can use our results to identify important structural motifs by considering the trends in the newly generated models that improve the fit. The results, discussed below, are summarized in Table S5.

Considering first the 160 models of α-[Mo8O26], 57 (36%) gave a better fit to the experimental PDF than the starting α-[Mo8O26] model, and 45 (28%) lower the R w value by 5% or more. An overview of the fit quality (R w values) for all cluster structures can be found in Fig. S3. The minimum R w value is reached for models that contain around five to six Mo atoms; however, as the models do not describe the peaks above 7 Å, this is probably too few Mo atoms to provide a full description of the nanostructure. Comparing the structures of the initial model with the best-fitting model in the insets of Fig. 6 ▸(a) and Fig. 6 ▸(b), respectively, it can be seen that the improved model is identical to the initial model, except that the tetrahedral [MoO4] units present in the structure have been removed. Of the 160 newly generated models, 120 (75%) contain tetrahedral units; however, this number falls to 30 of 57 (53%) for the models improving the original fit, and 18 of 45 (40%) for the models improving the fit by 5% or more. Thus, it appears that the best models do not contain any tetrahedral units, and it is likely that they are not a dominant structural unit. This is supported by an identical fall in the prevalence of tetrahedral units when applying the same method using decamolybdate as a starting point (Table S6), another polyoxometalate which also contains tetrahedral [MoO4] units.

Evaluation of the 14 054 new structures for β-[Mo8O26] by the fit agreement (R w value) shows that 2530 (18%) of the new clusters improve on the original fit, and 538 (4%) structures lowered the R w value by 5% or more. The overview in Fig. S3 shows that, generally, clusters with ten or fewer Mo atoms give a significantly better fit to the data than larger clusters, and the average number of octahedra in all of the 538 best-fitting structures is 8.97. This number is more reasonable than the average from the α-[Mo8O26] fitting (4.5 Mo) due to the better fit to the PDF at high r shown in Fig. 6 ▸(d). The best-fitting cluster, containing nine Mo atoms, is shown in the inset in Fig. 6 ▸(d), along with its fit to the data. Notably, a dominating structural motif of the clusters originating from the β-[Mo8O26] cluster is three edge-sharing octahedra, often referred to as a triad, which form the main building block of many polyoxometalate clusters. In fact, 7333 of the 14 054 (52%) new β-[Mo8O26]-based structures contain a triad. However, if we look at structures improving the fits by 5% or more, 2062 of 2530 (82%) and 438 of 538 (81%) contain triad units. This significant increase in triad frequency reveals the triad to be an important structural motif in the supported molybdenum oxides, and this is confirmed by the same trend when the method is applied to a paratungstate cluster (Averbuch-Pouchot et al., 1979 ▸) as the starting point (Table S5).

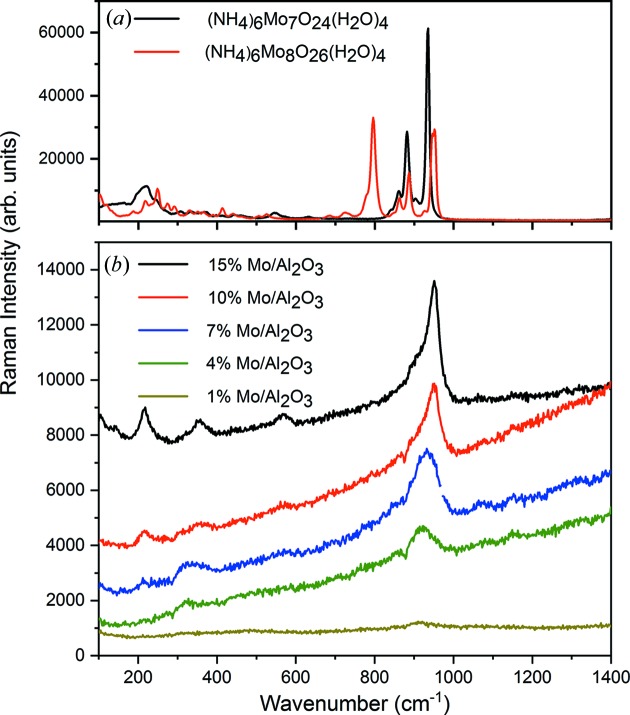
To gain further insight, the d-PDF analysis was complemented with Raman spectroscopy. The bands in the Raman spectra from the five samples [Fig. 7 ▸(b)] are all very broad when compared with the reference compounds, (NH4)6Mo7O24(H2O)4 and (NH4)6(Mo8O26)(H2O)4, whose spectra are seen in Fig. 7 ▸(a). This could be an indication of disorder as also observed in the d-PDFs. At low Mo loadings (1–7%), bands are visible at 920–950 cm−1 and ca 360 cm−1, which have previously been associated with Mo–O vibrational modes (Tian et al., 2010 ▸; Mestl & Srinivasan, 1998 ▸). As the loading increases, bands at ca 220 and 560 cm−1 become more prevalent. These are known to be characteristic of Mo–O–Mo bridging (Tian et al., 2010 ▸). The 220 cm−1 band and the 560 cm−1 band have been ascribed to an Mo–O–Mo bending mode and symmetric stretch, respectively, while the 360 cm−1 peak arises from an Mo–O bending mode (Tian et al., 2010 ▸). Thus, the Raman analysis confirms the increasing polymerization of [MoO6] octahedra as the loading increases. The higher sensitivity of Raman spectroscopy also confirms the presence of molybdenum oxide for the sample with 1% Mo loading, which was difficult to resolve from the PDF analysis. A significant shift can be observed for the most prominent Mo–O band from ca 920 cm−1 in the 4% sample to 952 cm−1 in the 15% sample. Such a shift has previously been attributed to an increased degree of polymerization, which agrees well with the d-PDF observations (Cheng, 1979 ▸; Ng et al., 1985 ▸). Note that other factors such as Mo—O bonding may also affect the Raman peak positions (Tian et al., 2010 ▸), and from these highly disordered samples it is therefore difficult to extract quantitative structural information from the Raman data. The 920–950 cm−1 band narrows with increasing Mo content, indicating a higher structural order with higher Mo content.

Figure 7.

Figure 7

Open in a new tab

(a) Raman spectra of (NH4)6Mo7O24(H2O)4 and (NH4)6(Mo8O26)(H2O)4 in the solid state. (b) Micro-Raman spectra of MoOx supported on γ-Al2O3 nanoparticles with loadings from 1 to 15 wt%.

The results from the PDF and Raman analyses show that there is not a single structural motif that can describe the experimental data of the nanostructured molybdenum oxide. However, it is clear from the refinements that the structures formed at high MoOx loadings have motifs related to several known structures, but are not identical to the commonly known, monodisperse polyoxometalate clusters.

2.2. Molybdenum oxides supported on zeolites  

Having established the d-PDF method and automated cluster modelling for molybdenum oxides supported on γ-Al2O3 nanoparticles, we can now apply the same methodology to the zeolite-supported samples.

As discussed above, there is no prevailing structural model for MoOx supported on zeolites (Li et al., 2006 ▸). The optimum loading for catalysis is known to be ca 2–3 wt% molybdenum, and the molybdenum species supported on zeolites can form both in the channels of zeolites and on the surface. Depending on where the molybdenum oxide is situated, the structure is expected to differ (Ma et al., 2000 ▸). On the external surface, it is suggested that the structure is similar to MoO3 and contains octahedral [MoO6] units (Ma et al., 2000 ▸; Li et al., 2006 ▸), while both isolated [MoOx] and more extended [Mo5O12] clusters have been suggested for the intra-zeolite structures (Gao et al., 2015 ▸; Li et al., 2006 ▸); however, the structures also depend on the zeolite nature (Okamoto et al., 2002 ▸). Here, three zeolite-supported samples were analysed on similar zeolite (ZSM) supports and Mo loadings (3–4%): sample Z1 2.8% Mo on ZSM5-SAR50; sample Z2 3.0% Mo on ZSM5-SAR50; and sample Z3 4.2% Mo on ZSM5-SAR23. The PDFs of the MoOx-coated zeolites [Fig. 8 ▸(a)] are dominated by the zeolite signal and thus all appear similar. The corresponding Q-space data can be found in Fig. S5. The d-PDFs obtained by subtracting the PDF from the pure zeolite support from the data are shown in Fig. 8 ▸(b). From the first peak positions (1.8–2.5, 3.3 and 3.85 Å) it is clear that the MoOx nanostructures supported on the zeolite samples are also built from edge- and corner-sharing motifs that are common to molybdenum oxides, and similar to the nanostructured MoOx layer supported on γ-Al2O3 described above.

Figure 8.

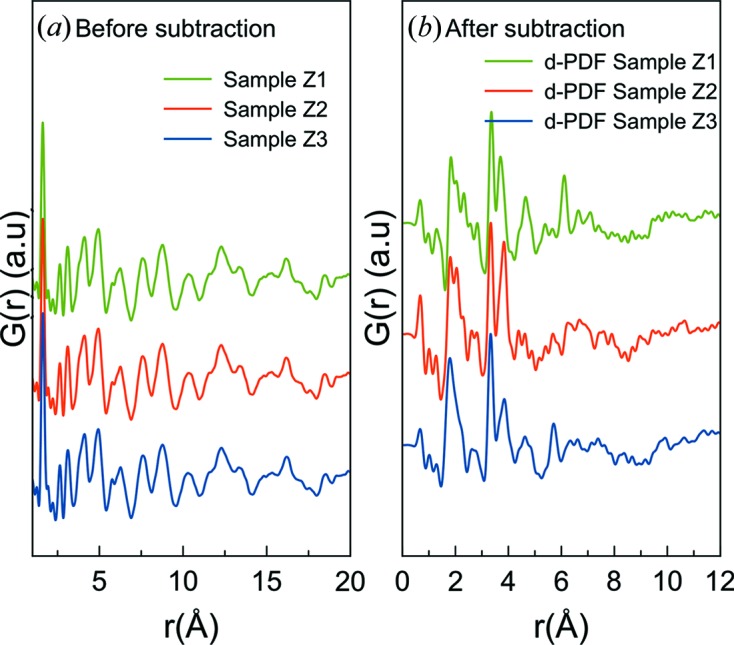
Figure 8

Open in a new tab

PDFs (a) and d-PDFs (b) obtained after subtraction of the pure zeolite signal for samples Z1, Z2 and Z3.

The d-PDFs show significant differences between the structures of the three samples. Firstly, the ratio of edge- and corner-sharing [MoOx] units differs in the three samples, as can be inferred by the change in relative intensity of the peaks at 3.3 and 3.8 Å. Furthermore, sample Z2 shows no clear structural peaks other than the first edge- and corner-sharing peaks, whereas both sample Z1 and sample Z3 show peaks beyond the first Mo–Mo coordination peaks, with clear peaks at 4.65 and 6.1 Å and at 4.65 and 5.71 Å, respectively.

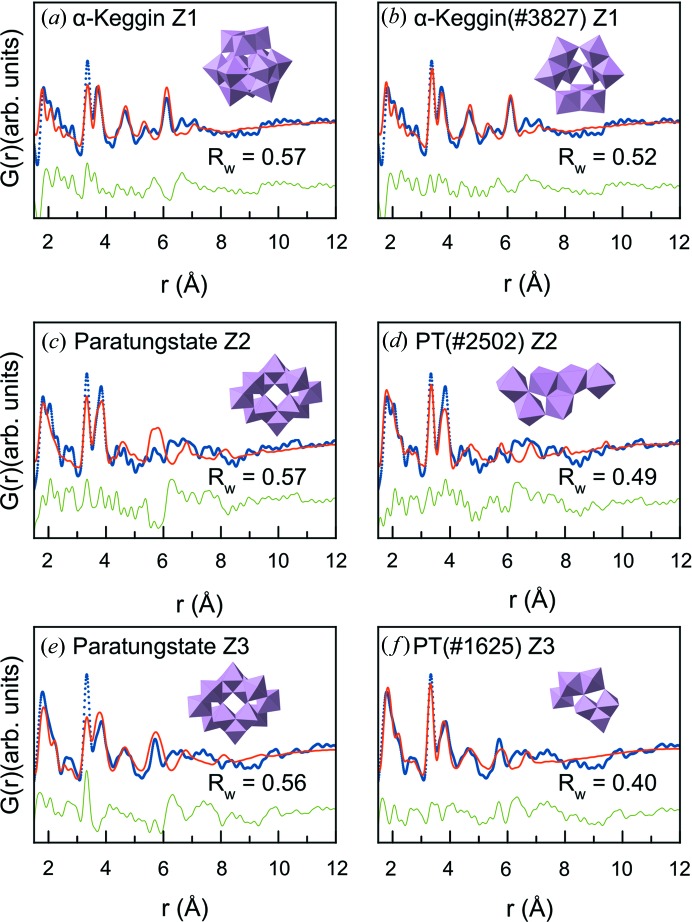
The experimental d-PDFs were tested against the polyoxometalate cluster structures listed in Table S4, as also done for the γ-Al2O3-supported samples. Interestingly, an [Mo12O40] α-Keggin cluster (Boeyens et al., 1976 ▸; Keggin, 1934 ▸) gave an excellent fit to the PDF of sample Z1 [Fig. 9 ▸(a)], while the paratungstate cluster described the main peaks in the PDF for sample Z2 and sample Z3, as seen in Figs. 9 ▸(c) and 9 ▸(e), respectively. The same algorithm as described above was used to determine the cluster fragments and thus structural motifs giving the best fit, with the results shown in Figs. 9 ▸(b), 9 ▸(d) and 9 ▸(f). Again, information about the sample structures is extracted by analysing the groups of clusters that give the best fit by using the R w value as a metric. For sample Z1, 76 of the 2317 new, unique cluster structures tested yielded an improvement in R w value by 5% or more. The cluster fragment giving the best fit [Fig. 9 ▸(b)] is very close to a full α-Keggin structure, just with one triad of octahedra missing, which improves the fit of the intensity ratio of the edge-sharing/corner-sharing peaks at 3.3 and 3.8 Å, and yields the best fit found using this method for any sample.

Figure 9.

Figure 9

Open in a new tab

(a) Fit of the α-Keggin cluster structure to the d-PDF obtained from sample Z1. (b) Fit of the best-fitting α-Keggin-derived cluster structure to the d-PDF obtained from sample Z1. (c) Fit of the paratungstate cluster structure to the d-PDF obtained from sample Z2. (d) Fit of the best-fitting paratungstate-derived cluster structure to sample Z2. (e) Fit of the paratungstate cluster structure to the d-PDF obtained from sample Z3. (f) Fit of the best-fitting paratungstate-derived cluster structure to sample Z3. In all fits, the experimental PDF is displayed as blue dots, the calculated model as a red line and the difference curve as a green line.

The PDFs for both samples Z2 and Z3 indicate that the samples contain smaller molybdenum oxide clusters than sample Z1. Firstly, for sample Z2, 91 of the 1944 (5%) new structures derived from the paratungstate cluster structure improved the fit by 5% or more. Common for these structures is that they result in weak PDF peaks above 4 Å, where the experimental data show very little structure. From this, we can infer that the main structural motifs present in the samples are small clusters of both edge- and corner-sharing molybdenum oxide units. The fit to sample Z3 improved significantly during the iterative search, as seen in Fig. 9 ▸(f). Of 1935 new structures 293 (15%) resulted in fit improvement by 5% or more, compared with the paratungstate starting model. Note that tests of the presence of [MoO4] tetrahedra in the structures were also performed on the zeolite-supported samples; however, the results were inconclusive. Because the Mo–Mo distances in e.g. edge-sharing octahedra and edge-sharing tetrahedra are indistinguishable, the structural motifs can only be identified from their extended Mo–Mo connection at higher r values. The MoOx domains present in zeolites (especially sample Z2) appear too small to fully identify the molybdenum coordination. However, the best fits to the data were obtained using models containing octahedra, as presented in Fig. 9 ▸.

A common structural motif seen in the best-fitting cluster models in the zeolite samples is again the triad, consisting of three [MoO6] units that share edges, as depicted in the inset of Fig. S8. We quantify this again by looking at the occurrences of triads in the structures giving the best fit to the data. Considering the structures improving the fit R w by 5% or more, 76 of 76 (100%) of the structures identified for sample Z1, 35 of 91 (38%, up from 15%) of the structures identified for sample Z2 and 127 of 180 (71%) of the structures identified for sample Z3 contain triads, again confirming the importance of the triad unit. In the PDF of all three samples, and especially samples Z2 and Z3, the corner-sharing peak at ca 3.8 Å is much broader that that originating from edge-sharing octahedra at 3.3 Å. For example, for sample Z3 the full width at half-maximum of the corner-sharing peak is approximately 70% larger than that of the edge-sharing peak, as seen from a single peak fitting in Fig. S7. From a structural point of view, this indicates a much broader distribution of corner-sharing distances. This points to the existence of a well-defined core consisting primarily of triads of edge-sharing [MoO6] octahedra, with these motifs more loosely connected by corner sharing. The broad distribution of distances reflects the larger degree of freedom in the connection, and the formation of a very disordered network, which is similar to what was observed for Mo/γ-Al2O3.

The size of a triad cluster is approximately 6.3 Å, when considering the distance between the two furthest oxygen atoms. Molecules of similar size have been shown to be able to reside in the ZSM5 zeolite network (Olson et al., 1981 ▸), making it possible that the MoOx structures observed here are situated both inside and on the surface of the zeolite. Further speculation can be made with respect to the coordination of the core cluster structures within the structure. As shown in Fig. S8 broad features appear in the d-PDF with a periodicity of approximately 12 Å in sample Z3. A possible explanation for the periodicity in the structure is a packing of the core clusters in the large pores of the zeolite, which are spaced ca 12 Å apart, as indicated in Fig. S8. However, other structural effects, e.g. the presence of oligomeric chains with cores spaced 12 Å apart, could result in similar features in the PDF, and the effect somewhat resembles that seen in C60 bucky balls (Juhás et al., 2006 ▸) and small organic compounds (Prill et al., 2015 ▸) with well-defined intramolecular peaks and broad intermolecular peaks.

Raman spectra were also collected for the zeolite-supported MoOx samples and can be found in Fig. S9. The samples show higher heterogeneity of the MoOx presence on the support and less signal from the MoOx layer, due to a poorer distribution on the larger zeolite particles compared with the MoOx/γ-Al2O3 samples. The limited conclusion that can be drawn from these data is that the Mo–O bands between 920 and 950 cm−1 can be observed, similar to the MoOx/γ-Al2O3 samples, but the Mo–O–Mo bridging bands are harder to observe.

3. Conclusions  

Using differential pair distribution function analysis and automated cluster fitting, we have shown that the atomic structure of nanoscale MoOx supported on γ-Al2O3 nanoparticles can be described by a distribution of polymeric [MoOx] cluster fragments closely related to known polyoxometalate structures. The structures present on the surface are not monodisperse, well-defined polyoxometalates, but the structural motifs are very reminiscent of those known from polyoxometalate clusters. Notably, triads built from [MoO6] have been identified as an important structural motif. When supported on ZSM5 zeolites, the MoOx structures share many similarities with those observed on γ-Al2O3, however with much smaller structural coherence lengths. Both Keggin-like and paratungstate-like clusters have been identified in the zeolite-supported samples, which are small enough to fit in the cavities in the zeolite structure. All cluster structures have been identified by a new approach to structural characterization and identification, taking advantage of known, stable cluster structures and polyoxometalate chemistry. By using known, chemically sensible structures as a starting point, we automatically generate a large number of new, related structures that both provide better fits and allow us to extract information on average structural motifs present in the sample. The method has the potential to become a valuable tool in handling the challenges of characterizing nano­structures that are often both highly polydisperse and disordered.

4. Experimental  

4.1. Material preparation  

The Mo/γ-Al2O3 samples were prepared by flame spray pyrolysis, as described in detail elsewhere (Høj et al., 2013 ▸, 2014 ▸). In brief, solutions of molybdenum 2-ethyl hexanoate and aluminium acetylacetonate in toluene were sprayed with oxygen as dispersion gas into a premixed methane/oxygen flame. The flammable mixtures combusted completely with entrainment of air from the surroundings and solid oxides condensed from the gas phase. Due to the difference in boiling point the alumina condenses first. The solid products were collected on glass fibre filters.

The Mo/zeolite samples were synthesized via a continuous hydrothermal flow method in a purpose-built reactor (Ma et al., 2000 ▸; Kallesøe et al., 2014 ▸). The zeolite is mixed into an MoVI precursor solution made from molybdenum acetylacetonate (99.9%, Sigma Aldrich), polyvinylpyrrolidine (99.99%, Sigma Aldrich), absolute ethanol (99.9%) and ethylene glycol (99.9%, Alfa Aesar). As the suspension is pumped through the reactor, the precursor (Mo + zeolite) meets the solvent (H2O) which is heated to 723 K and at a pressure of 210 bar (1 bar = 100 kPa). At the high temperature and pressure, the MoVI precursor is reduced and hydrolysed in a fast reaction forming molybdenum oxide in the zeolite network. The product of the hydrothermal synthesis was then washed in ethanol to remove excess solvent and organic residue, dried for 24 h and calcined in air at 773 K for 6 h.

4.2. PDF  

X-ray total scattering data were obtained at the Advanced Photon Source at Argonne National Laboratory at beamline 11-ID-B. The powders were packed in Kapton capillaries. The X-ray wavelength was 0.2112 Å with a detector distance of 150 mm in the RA-PDF setup (Chupas et al., 2003 ▸). The obtained data were integrated using Dioptas (Prescher & Prakapenka, 2015 ▸) and Fourier transformed to obtain the PDF using xPDFsuite (Yang et al., 2015 ▸) with the following parameters: Q min = 0.5 Å−1, Q max = 24 Å−1, Q maxins = 24 Å−1 and R poly = 0.9. d-PDFs were obtained by subtracting the normalized PDFs of the support from those of the samples, as described further in the main text. The PDFs were modelled using PDFgui (Farrow et al., 2007 ▸) and Diffpy-CMI (Juhás et al., 2015 ▸). For all refinements, the instrumental PDF damping was included through the Qdamp parameter, which was determined through refinement of the PDF obtained from a bulk CeO2 standard, measured in the same instrumental configuration.

4.3. Micro-Raman spectroscopy  

Raman measurements were performed using a micro-Raman setup in backscattering geometry. The 514.5 nm line of an argon-ion laser (CVI Melles-Griot 35MAP431-200) was used (430 µW for the γ-Al2O3 samples and 125 µW for the zeolite samples, above the objective). The beam was focused in an inverted confocal microscope (Olympus IX71) by an Olympus 100X, 1.4-NA oil immersion objective into a diffraction-limited spot. Raman spectra were collected using a Princeton Instruments SPEC 10:100 B/LN-eXcelon CCD detector and an SP 2356 spectrometer with a 600 grooves per millimetre grating. An LL01-514 filter (Semrock) was used to clean the laser light, a 30:70 beam splitter (XF122 Omega Optical) was used instead of a dichroic mirror and two LP02-514RE filters (Semrock) were used to block the remaining laser light in the detection path. X-axis calibration was performed with a neon spectral lamp (6032 Newport). No Y-axis corrections or background removal procedures were performed. Only a constant value was added or subtracted for display purposes. The spectra were not averaged. Because a limited amount of material is probed in the confocal micro-Raman experiments, heterogeneities in the Raman spectra might be present. The signal comes from a diffraction-limited area, and the signal-to-noise ratio depends on the amount of sample present, which can vary from spot to spot. Three or four spectra were recorded for each sample and all the spectra can be found in Figs. S9 and S10.

5. Related literature  

The following reference is cited in the supporting information: Kihlborg (1963 ▸).

Supplementary Material

Details on models and modelling results; Raman data. DOI: 10.1107/S1600576719016832/kc5101sup1.pdf

j-53-00148-sup1.pdf (2.9MB, pdf)

Funding Statement

This work was funded by Villum Foundation grant . Horizon 2020 grants 804066 and 680777. Danish Agency for Science and Higher Education grant . U.S. Department of Energy, Office of Science grant DE-AC02-06CH11357.

References

  1. Averbuch-Pouchot, M. T., Tordjman, I., Durif, A. & Guitel, J. C. (1979). Acta Cryst. B35, 1675–1677.
  2. Banares, M. A. (1999). Catal. Today, 51, 319–348.
  3. Bañares, M. A. & Wachs, I. E. (2002). J. Raman Spectrosc. 33, 359–380.
  4. Banerjee, S., Liu, C.-H., Jensen, K. M. O., Juhas, P., Lee, J. D., Tofanelli, M., Ackerson, C. J., Murray, C. B. & Billinge, S. J. L. (2019). arXiv:1901.08754v1.
  5. Bell, A. T. (2003). Science, 299, 1688–1691. [DOI] [PubMed]
  6. Billinge, S. J. L. & Kanatzidis, M. G. (2004). Chem. Commun. pp. 749–760. [DOI] [PubMed]
  7. Boeyens, J. C. A., McDougal, G. J., Van, R. & Smit, J. (1976). J. Solid State Chem. 18, 191–199.
  8. Böschen, I., Buss, B. & Krebs, B. (1974). Acta Cryst. B30, 48–56.
  9. Bridgeman, A. J. (2002). J. Phys. Chem. A, 106, 12151–12160.
  10. Cavani, F., Ballarini, N. & Cericola, A. (2007). Catal. Today, 127, 113–131.
  11. Chapman, C. E. & Beauchamp, E. (2006). J. Neurophysiol. 96, 1664–1675. [DOI] [PubMed]
  12. Chapman, K. W., Chupas, P. J., Maxey, E. R. & Richardson, J. W. (2006). Chem. Commun. pp. 4013–4015. [DOI] [PubMed]
  13. Chen, K., Xie, S., Bell, A. T. & Iglesia, E. (2001). J. Catal. 198, 232–242.
  14. Cheng, C. P. (1979). J. Catal. 60, 276–294.
  15. Chupas, P. J., Chapman, K. W. & Halder, G. J. (2011). J. Am. Chem. Soc. 133, 8522–8524. [DOI] [PubMed]
  16. Chupas, P. J., Qiu, X., Hanson, J. C., Lee, P. L., Grey, C. P. & Billinge, S. J. L. (2003). J. Appl. Cryst. 36, 1342–1347.
  17. Deo, G. & Wachs, I. E. (1991). J. Phys. Chem. 95, 5889–5895.
  18. Drake, T. L. & Stair, P. C. (2017). Top. Catal. 60, 1618–1630.
  19. Evans, H. T., Gatehouse, B. M. & Leverett, P. (1975). J. Chem. Soc. Dalton Trans. pp. 505–514.
  20. Farrow, C. L., Juhas, P., Liu, J. W., Bryndin, D., Božin, E. S., Bloch, J., Proffen, Th. & Billinge, S. J. L. (2007). J. Phys. Condens. Matter, 19, 335219. [DOI] [PubMed]
  21. Gao, J., Zheng, Y., Jehng, J.-M., Tang, Y., Wachs, I. E. & Podkolzin, S. G. (2015). Science, 348, 686–690. [DOI] [PubMed]
  22. Gelisio, L. & Scardi, P. (2016). Acta Cryst. A72, 608–620. [DOI] [PubMed]
  23. Genuchten, C. M. van & Pena, J. (2016). Environ. Sci.-Proc. Imp. 18, 1030–1041. [DOI] [PubMed]
  24. Gilbert, B. (2008). J. Appl. Cryst. 41, 554–562.
  25. Hardcastle, F. D. & Wachs, I. E. (1990). J. Raman Spectrosc. 21, 683–691.
  26. Harrington, R., Hausner, D. B., Bhandari, N., Strongin, D. R., Chapman, K. W., Chupas, P. J., Middlemiss, D. S., Grey, C. P. & Parise, J. B. (2010). Inorg. Chem. 49, 325–330. [DOI] [PubMed]
  27. Høj, M., Jensen, A. D. & Grunwaldt, J.-D. (2013). Appl. Catal. Gen. 451, 207–215.
  28. Høj, M., Kessler, T., Beato, P., Jensen, A. D. & Grunwaldt, J.-D. (2014). Appl. Catal. Gen. 472, 29–38.
  29. Jensen, K. M. Ø., Juhas, P., Tofanelli, M. A., Heinecke, C. L., Vaughan, G., Ackerson, C. J. & Billinge, S. J. L. (2016). Nat. Commun. 7, 11859. [DOI] [PMC free article] [PubMed]
  30. Jeong, I.-K., Proffen, T., Mohiuddin-Jacobs, F. & Billinge, S. J. L. (1999). J. Phys. Chem. A, 103, 921–924.
  31. Juelsholt, M., Christiansen, T. L. & Jensen, K. M. Ø. (2019). J. Phys. Chem. C, 123, 9.
  32. Juhás, P., Cherba, D. M., Duxbury, P. M., Punch, W. F. & Billinge, S. J. L. (2006). Nature, 440, 655–658. [DOI] [PubMed]
  33. Juhás, P., Farrow, C., Yang, X., Knox, K. & Billinge, S. (2015). Acta Cryst. A71, 562–568. [DOI] [PubMed]
  34. Kallesøe, C., Clausen, H. F., Christenen, L. H., Lund-Olesen, T., Mamakhel, M. A. H, Iversen, B. B., Becker-Christensen, J., Aarup, D. F., & Hales, J. (2014). US Patent 2015/0202598 A1.
  35. Keggin, J. F. (1934). Proc. R. Soc. London Ser. A, 144, 75–100.
  36. Kihlborg, L. (1963). Ark. Kemi. 21, 357–364.
  37. Li, B., Li, S., Li, N., Chen, H., Zhang, W., Bao, X. & Lin, B. (2006). Microporous Mesoporous Mater. 88, 244–253.
  38. Li, W., Harrington, R., Tang, Y., Kubicki, J. D., Aryanpour, M., Reeder, R. J., Parise, J. B. & Phillips, B. L. (2011). Environ. Sci. Technol. 45, 9687–9692. [DOI] [PubMed]
  39. Lindahl Christiansen, T., Kjaer, E. T. S., Kovyakh, A., Vosch, T. & Jensen, K. M. Ø. (2019). Structural Files of Algorithmically Generated Molybdenum Oxide Clusters, https://doi.org/10.5281/zenodo.3260233.
  40. Ma, D., Shu, Y., Bao, X. & Xu, Y. (2000). J. Catal. 189, 314–325.
  41. Macht, J. & Iglesia, E. (2008). Phys. Chem. Chem. Phys. 10, 5331–5343. [DOI] [PubMed]
  42. Mestl, G. & Srinivasan, T. K. K. (1998). Catal. Rev. 40, 451–570.
  43. Munnik, P., de Jongh, P. E. & de Jong, K. P. (2015). Chem. Rev. 115, 6687–6718. [DOI] [PubMed]
  44. Ng, K. Y. S., Zhou, X. & Gulari, E. (1985). J. Phys. Chem. 89, 2477–2481.
  45. Okamoto, Y., Oshima, N., Kobayashi, Y., Terasaki, O., Kodaira, T. & Kubota, T. (2002). Phys. Chem. Chem. Phys. 4, 2852–2862.
  46. Olson, D. H., Kokotailo, G. T., Lawton, S. L. & Meier, W. M. (1981). J. Phys. Chem. 85, 2238–2243.
  47. Paglia, G., Božin, E. S. & Billinge, S. J. L. (2006). Chem. Mater. 18, 3242–3248.
  48. Paglia, G., Buckley, C. E., Rohl, A. L., Hunter, B. A., Hart, R. D., Hanna, J. V. & Byrne, L. T. (2003). Phys. Rev. B, 68, 144110.
  49. Pope, M. T. (1991). Prog. Inorg. Chem. 30, 181–257.
  50. Pope, M. T. & Müller, A. (1991). Angew. Chem. Int. Ed. Engl. 30, 34–48.
  51. Prescher, C. & Prakapenka, V. B. (2015). High. Press. Res. 35, 223–230.
  52. Prill, D., Juhás, P., Schmidt, M. U. & Billinge, S. J. L. (2015). J. Appl. Cryst. 48, 171–178.
  53. Setnička, M., Tišler, Z., Kubička, D. & Bulánek, R. (2015). Top. Catal. 58, 866–876.
  54. Shiju, N. R. & Guliants, V. V. (2009). Appl. Catal. Gen. 356, 1–17.
  55. Tian, H., Roberts, C. A. & Wachs, I. E. (2010). J. Phys. Chem. C, 114, 14110–14120.
  56. Tsilomelekis, G. & Boghosian, S. (2013). Catal. Sci. Technol. 3, 1869–1888.
  57. Wachs, I. E. (1996). Catal. Today, 27, 437–455.
  58. Wang, L.-J., Jiang, H., Wang, Y., Shao, K.-Z. & Su, Z.-M. (2007). Acta Cryst. E63, m584–m586.
  59. Yang, X., Juhas, P., Farrow, C. L. & Billinge, S. J. L. (2015). arXiv:1402.3163.
  60. Zaera, F. (2013). Chem. Soc. Rev. 42, 2746–2762. [DOI] [PubMed]
  61. Zhang, Q., Lee, I., Joo, J. B., Zaera, F. & Yin, Y. (2013). Acc. Chem. Res. 46, 1816–1824. [DOI] [PubMed]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Details on models and modelling results; Raman data. DOI: 10.1107/S1600576719016832/kc5101sup1.pdf

j-53-00148-sup1.pdf (2.9MB, pdf)

Articles from Journal of Applied Crystallography are provided here courtesy of International Union of Crystallography

RESOURCES