Abstract
Statistical Design of Experiments (DoE) is a widely adopted methodology in upstream bioprocess development (and generally across industries) to obtain experimental data from which the impact of independent variables (factors) on the process response can be inferred. In this work, a method is proposed that reduces the total number of experiments suggested by a traditional DoE. The method allows the evaluation of several DoE combinations to be compressed into a reduced number of experiments, which is referred to as intensified Design of Experiments (iDoE). In this paper, the iDoE is used to develop a dynamic hybrid model (consisting of differential equations and a feedforward artificial neural network) for data generated from a simulated Escherichia coli fermentation. For the case study presented, the results suggest that the total number of experiments could be reduced by about 40% when compared to traditional DoE. An additional benefit is the simultaneous development of an appropriate dynamic model which can be used in both, process optimization and control studies.
Keywords: Design of Experiments, Dynamic modeling, Intensified Design of Experiments, Upstream bioprocess development, Upstream bioprocess optimization
Abbreviations
- C1‐C8
Constraint 1 to 8, respectively
- CHO
Chinese hamster ovary cell
- DoE
Design of Experiments
- E. coli
Escherichia coli
- HMiDoE
Hybrid model developed on the data obtained from the iDoE
- HMDoE
Hybrid model developed on the data obtained from the DoE
- iDoE
intensified Design of Experiments
- ODEs
Ordinary Differential Equations
1. Introduction
The understanding of how factors (design/control parameters) impact on the response of a (bio)process is of critical importance for the effective manipulation of the system 1, 2. Generally one differentiates between controllable and uncontrollable factors 1. Design of Experiments (DoE) is a methodology that varies the controllable factors in a systematic way such that the impact of the factors (as well as the impact of their interactions) on the response variable can be distinguished (to some degree) with the help of multivariate data analysis methods 1, 2, 3. The affect of the uncontrollable factors is typically accounted for by replication, randomization and/or blocking. The degree to which the contribution of each controllable factor and/or interaction of factors can be distinguished, i.e. the resolution, depends on the number of levels incorporated for each factor and combinations accounted for. However, for an increasing number of controllable factors and levels, there can be a significant increase in the respective number of experiments, up to an exponential increase depending on the chosen design and specified resolution.
In upstream bioprocess development there exist a number of process parameters (factors) that require investigation depending on the product and production host, i.e. E.coli, CHO, etc 4, 5. In light of the Process Analytical Technology initiative and the promoted Quality by Design paradigm it is of critical importance to show that the impact of all the process parameters (factors) on the process are understood 4, 6. High‐throughput platforms and single‐use equipment have found increasing application in recent years allowing parallel studies of entire DoEs 5, 7, 8, 9, which has the potential to reduce process development / optimization timelines significantly. The data that results from DoE are typically investigated using multivariate data analysis methods, in particular Response Surface Models are popular 2, 3, 5. These approaches work well in the vicinity of the process optimum since the solution surface can be approximated by quadratic functions, but the time‐course of every experiment is typically reduced to a static representation. Recently, it was shown that the combination of process knowledge with a data‐driven approach to dynamic hybrid model development could make efficient use of time‐course data obtained from DoE experiments, allowing decisions to be made about the end or induction time without performing additional experiments 10 . This approach also allowed the assessment of the impact of temporal deviations in the factors on process performance. Optimal design of experiment approaches exploit the process dynamics and time‐course of the experiments. This can be used to discriminate between competing model structures 11, to improve the parameter estimates 11, 12 or to explore the process operation space in a better way 13. Cruz Bournazou and coworkers 14 proposed a methodology that makes use of the time course and parallel experiments to infer the parameters of a mechanistic model while the fermentations are running, re‐optimizing the excitation in the factors using an adaptive optimal experimental design approach. However, this approach, and more generally optimal design of experiment approaches 11, 12, require a model structure, which a priori typically is unknown. Georgakis 15 proposed a design of dynamic experiments method, in which factors that are changing (or have to change) during the experiment are added to the typically static factors that remain constant throughout the experiment. The approach does not require a model, however the addition of factors will result in an increase in the number of experiments. Von Stosch and coworkers 16 proposed varying the factors according to a classical DoE for a fixed number of stages during each experiment, referring to this as intensified experiments. In their approach, the planning of the experiments does not require a model, however the analysis of the data requires the adoption of advanced modeling techniques. Therefore, a dynamic model was developed on the basis of the intensified experiments. This model could accurately describe experiments carried out at static conditions within the explored region. The general findings are in agreement with those that have performed excitation in the feeding rate to elucidate the impact on the process 17, 18, 19. However, to date no methodology for the systematic planning of the iDoE has been proposed, this is because an iDoE strategy is difficult to establish for an increasing numbers of factors and levels. In what follows a methodology for the optimal planning of iDoEs is proposed in parallel with the estimation of a dynamic model, which is used to evaluate the impact of the varying factors on the response. Thus, instead of performing experiments with constant process conditions, the conditions are changed during an experiment and therefore altogether less experiments can be performed. The methodology is applied to a simulated E. coli fermentation.
2. Methods
2.1. Bioreactor system
The common backbone of bioreactor models is the material balances which, assuming ideally mixed conditions, are the set of coupled ordinary differential equations.
| (1) |
c a vector of concentrations (g/l), V the reactor volume (l), r a vector of reaction rates(g/l/h), is a vector which comprises a set of factors that directly (linearly) impact on the material balances (e.g. substrate feeding)1 (g/h) and a set of factors that might have an indirect impact on the material balances (e.g. temperature or pH). The initial conditions, i.e. the initial concentrations , can have an impact on the time evolution of the concentrations and can constitute an additional set of factors .
DoE studies of this system typically focus on the impact of the set of factors on the response of the system for one concentration at some specified moment in time 2, 20, 21. The values of can obviously only be chosen once per experiment, but also the values of the factors and are typically kept constant throughout each experiment. The idea behind the iDoE methodology is to vary the level of the and values according to a classic DoE at a number of specified time intervals during each experiment, referred to as stages. How many variations/stages can be tested per experiment depends on the response time of the cultures, i.e. the time required for the entire response to the varied conditions to be observed. In E. coli this time was observed to be in the magnitude of hours 16 for mammalian cells it is expected to be days. Typical process operation results in three to four stages per experiment. In the following, the experiments with intra‐experiment variations in the levels of the and are referred to as intensified experiments as opposed to DoE experiments, in which the levels of the and are constant/static throughout the experiments. The methodology, which is introduced in the following section of the paper, provides an optimal sequence in which DoE combinations should be performed for any of the intensified experiments.
2.2. Planning of intensified design of experiments
The objectives of the iDoE approach are: 1) to reduce the number of experiments that are required to characterize the input/output behavior of a system for a desired resolution; and 2) to gain insights into the dynamic behavior of the process, which can alongside process optimization be used for process control. The planning of the iDoE can be formulated as a binary optimization problem, the basis of which constitutes a classical DoE with the desired resolution. The DoE contains a number of combinations of factors. Each intensified experiment contains a number of sequential stages (process phases). Therefore, the dimension of the optimization problem is defined by the number of combinations covered by the classical DoE (), the number of DoE combinations that are gathered into every intensified experiment () and the number of experimental runs in the planned iDoEs (). The problem can be represented by a () cube of elements, see Fig. 1, where each element can either take the value 1 – if the experiment should be executed ‐ or the value 0 otherwise.
Figure 1.
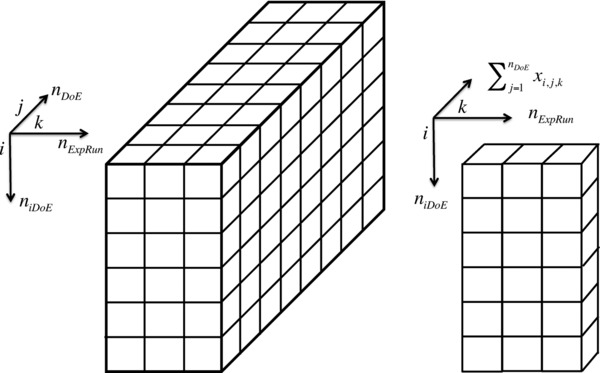
Representation of the entire search space (left) and the affect of summing in one dimension (right).
2.3. Objective function
The minimum number of experiments that can be obtained with the iDoE is given by the number of combinations of the classical DoE divided by the number of stages that are considered in every experimental run. However, the minimum number of experiments might increase with the introduction of constraints.2 Hence, the minimal number of experiments might a priori be unknown and the initial guess of set slightly higher than the theoretical lower limit. Therefore, the aim is a minimization of the number of intensified experiments such that all constraints are satisfied, i.e. we want to minimize the dimension of the cube along the axis. Instead of minimizing which would change the dimension of the problem, binary variables are used for every element of the cube, which take the value 1 if the experiment at position is executed and 0 otherwise. Thus, for the experiments that are not required as part of the iDoE the respective plane in the cube is comprised of binary variables that are all zeros. The number of intensified experiments is such given by the number of planes in direction that contain elements different from zero. This can be implemented by minimizing the following cost function:
| (2) |
consisting of the binary variables and an increasing cost factor (weighting) for an increase in the number of iDoE, i
| (3) |
The fraction in the bracket will typically result in a number that is lower than one (iff , which would normally be expected, however if a greater number of experiments is required in order to fulfill the constraints then this might not necessarily be the case, though the objective function still works), but this increases for an increase in the number of intensified experiments required to fulfill the constraints, i.e. there will be an increasing cost when plane of the cube contains at least one element with a one. The increase in the cost is further amplified using an exponent of three. The costing could have been established in several other ways (e.g. using an exponent of two or four), but the employed function proved computationally efficient.
2.4. Constraints
The need for several constraints becomes apparent when looking at the cube and elements shown in Fig. 1. For instance, at the first stage of the first intensified experiment physically only one DoE combination can be evaluated. Other additional constraints may also be introduced; the nature of these constraints (and their need) is discussed in this section of the paper.
Constraint 1 (C1) is an operational constraint, that allows for only one experimental condition to be tested at every stage of any of the intensified experiments, i.e.:
| (4) |
Referring to Fig. 1 the sum in this constraint effectively compresses the dimension along the axis of into the plane spanned by and .
Constraint 2 (C2) limits the repetition of any DoE combination for the different stages of the intensified experiments. This constraint has a direct impact on the use of the DoE combinations in the intensified experiments and the overall number of intensified experiments. In order to optimize the intensified experiments, each DoE combination should only appear once at every position across all intensified experiments:
| (5) |
Constraint 3 (C3) restricts the number of repetitions of any DoE combination through any of the intensified experiments. Though, the DoE combinations might be repeated during another stage in any of the intensified experiments (to fulfill constraint C6 to C8), the number of repetitions of the same DoE combination in the same intensified experiment should be repressed. This constraint ensures that the stages are explored throughout the entire iDoE and providing grounds for a better consideration of impacts from uncontrolled factors. A maximum of two repetitions per experiment were chosen in this study:
| (6) |
Constraint 4 (C4) controls the overall number of every DoE combination that can be repeated within the iDoE. This limit might be varied depending on the number of stages involved in each intensified experiment as well as with the choice of configuration in C6 to C8. For two to five stages a twofold repetition of the DoE combinations in the iDoE plan seems to be an appropriate upper limit:
| (7) |
Constraint 5 (C5) ensures that every DoE combination is included within the iDoE, i.e.:
| (8) |
Constraint 6 (C6) provides the user with the opportunity to manage at which stages the DoE combination should be repeated across all intensified experiments. The repetition of the DoE combination at another process stage can be important to account for changes in uncontrolled factors, which might impact on the system's response. Consider for instance the term within Eq. (1). The response of this term will depend on both and. Thus by repeating the combination at another stage it is likely that changes in c can be accounted for. For each of the stages a summation factor is introduced, , and a minimum total score is defined for each of the DoE combinations, . The constraint can then be defined as:
| (9) |
Both, and , can be chosen by the user. For instance, consider the example shown in Figure 2 with (four stages). We want every experiment to be repeated twice but at different phases of the process. We choose a summation factor for every stage of the process, and by choosing we impose that every combination must be repeated at least twice. By the choice of the summation factors we also can direct at which stages the combination should be repeated, e.g. stage 1 with stage 3 or 4. For three stages and provided a good option. If the center‐point experiment is repeated a couple of times in the original DoE then a low value for for these DoE combinations provides some flexibility for the optimization. This constraint introduces some complexity into the planning that could have been thus far easily achieved manually.
Figure 2.
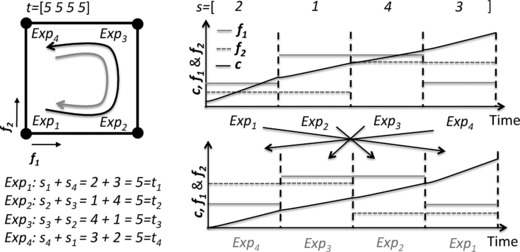
An example of C6 on a two factor to level design for an experiment with four stages.
Constraint 7 (C7) delimits the variation in a specified factor between DoE combinations of two sequential stages. This constraint is important to account, for instance for limitations in the process equipment, to avoid metabolic shifts that are triggered by drastic changes to the cellular environmental, etc. An upper limit is defined, , for the difference in the values of factor l at experiment i,j between the two sequential stages k and ( is the value in the j combination of the classical DoE of factor). The constraint is therefore,
| (10) |
Since the constraint in the present form cannot be used in standard binary optimization methods it is reformulated into two complementary constraints (which represent the logical “AND” function):
| (11) |
| (12) |
Constraint 8 (C8) originates from considerations regarding the best manner to explore the space spanned by the factors of the DoEs. By enforcing some variation in a set of factors in every intensified experiment, the iDoE plan spans and crosses the experimental space more efficiently. In essence C8 is very similar to C7, only that a lower limit for the overall differences in the values of factor l for an entire intensified experiment i is defined, . The constraint is,
| (13) |
The reformulation of this constraint for use in standard optimization methods follows the formulation of logical “OR” constraints (known as big M method 22). For the set of constraints are,
| (14) |
| (15) |
and :
| (16) |
| (17) |
The coefficients M and L are large but not identical values. The variables and are additional binary decision variables that need to be added to the objective function, but at zero cost.
2.5. Implementation
The optimization problem was implemented in MATLAB and solved with the bintprog function. It should be note that the solution is not generally unique, and there may exist a number of variants. These variants could be computed by excluding prior solutions from the search space, see e.g. 23. The constraints C6 to C8 were introduced to reduce the number of variants to those of interest.
3. Results and discussion
3.1. E. coli simulation case study
The production of viral capsid protein production by E. coli was simulated adopting the model proposed by 24 in order to provide a platform to investigate the iDoE concept (see appendix for equations). The process comprises two phases, a growth and production phase. The factors ‐ process parameters of the production phase, which can be varied, are temperature and the substrate feeding rate. The substrate feeding rate is typically ramped up during the fermentation to meet the increased demand for biomass growth and maintenance. This is accounted for by using an exponential profile in which a set‐point for the specific biomass growth is introduced, , (see appendix for details), which is then used as a factor in the DoE instead of the substrate feeding rate. The response variables are the product and biomass concentrations. Critical to capturing the dynamic response characteristics of these variables is the sufficient (frequent) measurement of the concentrations (which are typically measured off‐line) throughout each experiment.
3.2. Intensified design of experiments plan
The basis for this study is a two‐factor Doehlert‐design, containing three levels for temperature and five levels for specific biomass growth set‐point, , as well as three repetitions for the center‐point (a total of nine experiments). In Fig. 3 the impact of the constraints on the iDoE plan can be observed. When only constraints C1 to C5 are used, none of the experiments are repeated. This was expected because it is the least expensive to use every DoE combination only once. The additional use of constraint C6 with , and resulted, also as expected, in the repetition of the DoE combinations during the different stages of the intensified experiments (apart from the central points because of ). However, it can be seen that the variation between the experimental conditions in an intensified experiment can be large, e.g. for intensified experiment 4, sequence 8→ 8→ 9, passes directly from the lowest temperature (8: 29°C) to the highest temperature (9: 33°C). By introducing maximum stage‐to‐stage variations for the factors, i.e. constraint C7 with , significant variation in the values of the factors between sequential stages can be avoided. The introduction of a minimum variation in each factor for each intensified experiment, C8, can also help to avoid combinations like 6 – 2 – 4 with no variation in temperature. The idea behind enforcing variation in all factors within every intensified experiment is that interactions of the factors are captured more efficiently. Also the changes between combinations are more appropriately bridged and the search space is explored in a more homogenous way. While for the presented Doehlert design this constraint does not have too much impact on the solution space –in fact only combinations of 2 – 4 – 6 would violate the constraint (which for Doehlert designs of greater factors is also true due to their shell nature 25) in the case of other designs this constraint might have a greater impact. The iDoE plan with constraints C1 to C8 was used for the generation of simulation data using the model developed in the Appendix.
Figure 3.
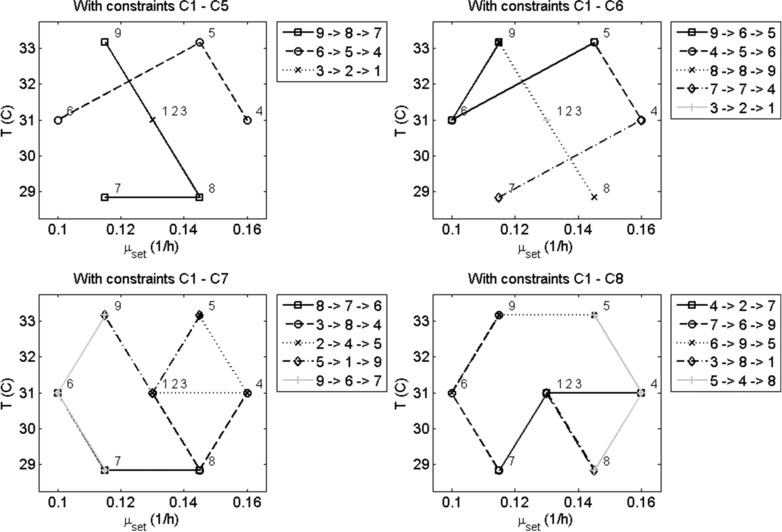
Four intensified designs obtained for the 2‐factor Doehlert design using different subsets of constraints as indicated by the title. The legend on the right side of each figure shows the sequence of experimental conditions (obtained from the Doehlert design and enumerated 1 to 9 referring to the positions shown in the figure) that are contained within each intensified experiment (which each comprise three stages).
3.3. Analysis of dynamic model performance
Two data based hybrid dynamic models, HMiDoE and HMDoE were developed using data obtained from the iDoE and DoE experiments (for details of the hybrid modelling approach see the Appendix). The HMiDoE model was developed using data obtained from the five intensified experiments, whereas the HMDoE model was developed using nine experiments carried out according to the 2 factor‐Doehlert design with constant set‐points for each experiment. Having developed the models their prediction capabilities were tested on the data that were used to develop the other model, the idea being to investigate whether the model can predict well over the entire range of process conditions covered in the DoE, including the dynamic behavior for the iDoE. In Fig. 4 the HMiDoE and HMDoE estimation and prediction performance are compared using the iDoE experimental data. It can be seen that the HMiDoE describes the iDoE experimental data excellently across the training, validation and test partitions. The prediction performance of the HMDoE model also is very good, only over‐predicting during the last stage of the second experiment in the HMiDoE‘s training data set. In this experiment, the feeding rate increased from the second to the third stage. With this increase in the feeding rate, while the specific biomass growth rate increases (due to the increase in the substrate concentration) there is an adverse effect on the product formation, which appears not to be captured by the HMDoE model. In addition, the prediction of biomass concentration by the HMDoE model appears to be less sensitive to variations in the factors than the HMiDoE model, as the changes from stage to stage observed for the time profiles obtained with the HMDoE are less distinct. However, generally the HMDoE model, which was developed using the “static” experimental data can effectively describe the process dynamics. This result corroborates the findings in von Stosch et al. 16 where real wet‐lab E. coli fermentations had been modeled.
Figure 4.
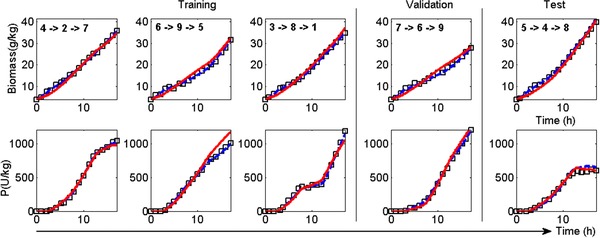
Biomass and product concentration profiles over time for the iDoE plan (the sequence for each experiment is shown in the plot). The training, validation and test set were used to develop the HMiDoE model. (black squares – simulated experimental data (5% white noise), blue dashed line ‐ HMiDoE model estimations/predictions, red continuous line predictions of the HMDoE model).
The estimations and predictions of the HMiDoE and HMDoE models obtained from the static experiments can be seen in Fig. 5. It can be seen that the HMDoE model describes the DoE experimental data very well across the training, validation and test partitions. Only in the second experiment of the validation partition the product concentration is slightly over‐predicted. This experiment was executed at the lowest feeding rate of all experiments and the model inputs are therefore different to those on which the model was developed. Again the HMDoE model seems to be less sensitive to the changes in the factors, which can in particular be seen for the switch from growth to production phase at 2.6(h). The HMiDoE model predicts both concentration profiles very well across the investigated conditions, only in case of the product concentration for the 4th DoE experiment a slight under‐prediction is observed towards the end of the experiment. The biomass concentration is greater than those concentrations experienced during the training of the HMiDoE model and the conditions are somewhat similar to those captured in the iDoE data that were used in the test set, where the product formation stopped. Overall the model developed using the intensified experiments can predict the static DoE data accurately. This observation is in line with the findings in von Stosch et al 16, where a dynamic hybrid model developed on a set of intensified wet‐lab experiments could accurately describe several fermentations executed at distinct conditions, but in the standard static way.
Figure 5.
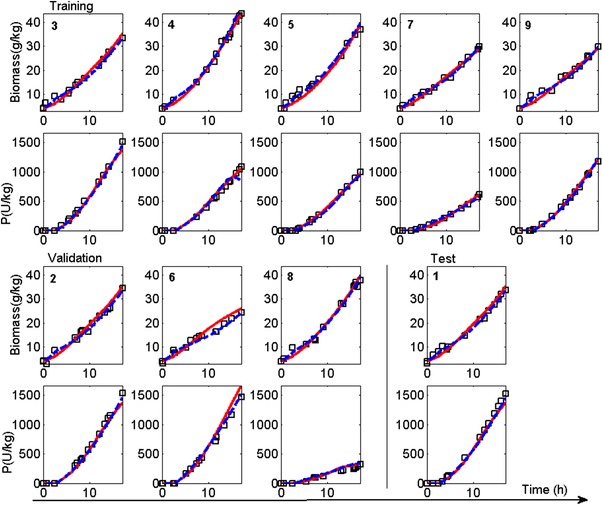
Biomass and product concentration profiles over time for the 2‐factor Doehlert‐design (number in the plots correspond to the DoE). The training, validation and test set were used to develop the HMDoE model. (black squares – simulated experimental data (5% white noise), blue dashed line ‐ HMiDoE model predictions, red continuous line predictions of the HMDoE model).
3.4. Analysis of the covered process operation space
The analysis of the process region covered by each of the model requires studying 1) the model inputs in the domain covered by the DoE; and 2) the surface of the response variable of interest at a specified process time (since DoEs are typically used for optimization studies), e.g. product concentration at the end of the process (final product titer).
The process region investigated in the DoE defines the boundaries in which the model can be expected to accurately predict. In the present case, this region translates into and shapes the input domain of the neural networks (which are an inherent part of the hybrid models). The input domain comprises the predicted biomass concentration, the measured feeding rate and the measured temperature and is shown for each of the models in Fig. 6. The different process conditions (the changes in temperature and feeding rate, which are caused by the changes in ) at which the experiments were executed can clearly be observed and also the intensified and regular experiments can be distinguished well. The intensified experiments span the process region in a similar manner to the regular experiments, apart from a region of high feeding rate (though not high ), high biomass concentration and high temperatures. This region is not explored due to the varying nature of the intensified experiments, which limits the achievable biomass concentrations and such inherently higher feeding rate values. The reduced coverage of this region in the present case is not critical since the HMiDoE model can predict the experiments that were carried out at these conditions very well, as observed before. Generally, and bearing the particular focus of DoE studies in mind, the region would most likely be explored by subsequent experiments. A model (that captures the behavior of the experiments up to a certain value of biomass/feeding rate) when interrogated via optimization methods would direct further studies towards this region, if the optimum was to be found in there.
Figure 6.
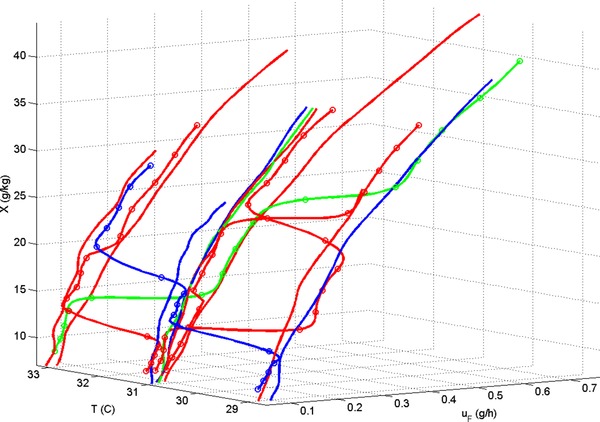
Input Domain of the HMiDoE (continuous‐lines with circles) and HMDoE (continuous lines) model. The training data are shown in red, the validation data in blue and the test data are shown in green.
It can be seen in Fig. 7 that the surface of final product concentration values predicted by the HMiDoE model is similar to the true response surface (note that any process time could be chosen, since the model is dynamic and can therefore produce a response surface at any desired time). In particular, the nonlinear impact of the feeding rate seems to be described more accurately than with the HMDoE model, which is in agreement with the results from above. This may be because the systems inherent nonlinearity has not been sufficiently captured by the HMDoE model (which could be a result of the underlying neural network being too simple – despite the fact that the chosen neural network structure yielded the best performance). The intra‐experiment variation can be expected to yield a more varied measured response (dynamically more rich), which can only be modeled if the impact of the factors is accounted for. The application of C6 and the resulting repetition of every DoE combination at a different stage, in addition seems to have enhanced the learning process of the neural network in that the repeated DoE combinations provide different values of biomass concentrations and feeding rates, which enabled the network to learn the nonlinear system better. Thus the iDoE data appear to differentiate between the impact of the factors on the process dynamics and overall process response. Given that advanced process control is expected to reduce process variation ultimately allowing for closed‐loop product quality control 26 and that advanced process control relies on dynamic predictive models 27, the iDoE also provides an opportunity to integrate process development and process control activities.
Figure 7.
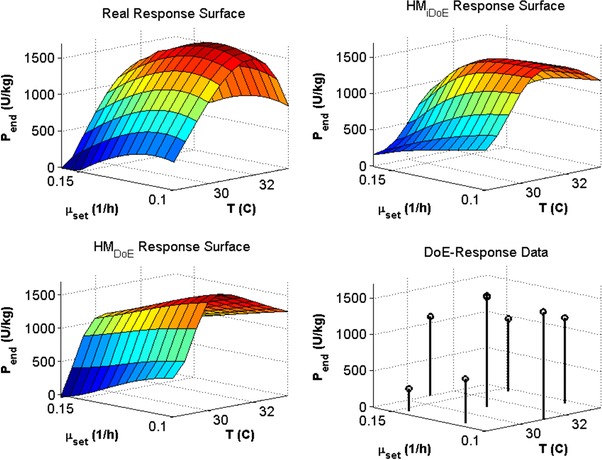
End‐time product concentrations over and T (referred to in the figure as response surface) for the true simulation system, the HMiDoE model, the HMDoE model and the simulated experimental data.
3.5. General validity of the iDoE strategy
The results obtained in this study suggest that the number of experiments required in a traditional DoE can be reduced significantly with the proposed iDoE procedure. The presented case study, a simulated E. coli fed‐batch fermentation, is similar to the experimental case previously studied 16 and the results obtained in this work agree very well, with the previously published results. This suggests that the iDoE methodology will generally work for E. coli fermentations (at least) as well as the classical DoE. However, in previous work it was hypothesized that the iDoE could be more likely to cause metabolic shifts, because many of the influences of the factors such as the temperature and the feeding rate are interconnected 28 and simultaneous excitations might trigger a shift. While this has not been observed in the experimental study, it should be kept in mind for the analysis of future data. Also the possibility of obtaining different responses to the same cellular environment due to the dependence of response on the intracellular state (which depends on the exposure of the cell to the prior environment) should be borne in mind. Further experimental studies could reveal to which degree these cellular behaviors are more prone to occur in case of iDoE than normal DoE conditions. However, since the range of the values is typically relatively small (such that quadratic functions can be fitted to the data for the optimization) we expect that the occurrence of these phenomena in optimization studies will be relatively rare.
Another point to consider is that the history of the microorganism might be important (i.e. time‐sensitive behavior). While the dynamic model explicitly captures the history dependence of the modelled compounds, other un‐modelled inherent compounds might have an impact on the trajectory. Due to constraint 6, with which the user can enforce the repetition of process conditions in other stages and experiments, the sensitivity of the process with respect to changes in the magnitude and direction of set‐point changes can be assessed, see also 16. This additional information in principle allows to detect and repair model inconsistencies during the model development life‐cycle. Lag‐phases, such as those observed during substrate replacements, may impact on the response time and therefore they need to be considered (e.g. by increasing the length of each stage) if their occurrence can be expected.
The application of the iDoE framework for the optimization/development of cultivations of other cell types such as insect, yeast or mammalian cells should yield similar results, but needs investigation since the behavior of these cells is more complex. Though the iDoE approach was studied for fed‐batch operation, its application in batch or continuous operation would be straight‐forward.
4. Concluding remarks
A method is proposed to compress a DoE into a smaller set of intensified experiments, referred to as iDoE. The intensification is obtained by evaluating a given number of DoE combinations in every experiment. Due to the transient nature of the experiment a dynamic model is adopted for the analysis of the time course of the response variables.
The method was applied to plan an iDoE, which was employed to generate data using simulated E. coli fermentations. The resulting data was analyzed using a dynamic hybrid model and the results were contrasted with a hybrid model developed on data obtained using traditional DoE. It was observed that the model developed on the intensified experiments was capable of predicting across the entire region explored by the DoE and could describe the transient behavior of the processes, which agrees with previous findings 16. In the presented case study the number of experiments could be reduced from 9 to 5 using the iDoE plan in combination with a dynamic hybrid model, a reduction of >40% in the number of experiments. We expect that similar reduction in the number of experiments can generally be achieved for the development of E. coli processes, potentially also for the development of processes of other cell types and in general for systems that can be described by a set of ODEs which form is similar to that of Eq. (1). Whether, the approach also works for other types of systems that e.g. require the investigation of spacial co‐ordinates (partial differential equations) is at this stage not clear (but would be an interesting area of future research). While the theoretical minimum number of intensified experiments is known, the actual number is determined by the constrained optimization and as such cannot be predicted ahead of the application. Generally, the total number of experiments will not be greater than that predicted by the traditional DoE, however if the applied constraints are used to e.g. repair model deficiencies then additional experiments might become necessary.
It is suggested that the iDoE method could help to integrate process development and process control activities, as process dynamics seem to be captured more faithfully. This would be interesting for the optimization and control of continuous processes, as it would facilitate the understanding of the transient behavior between steady state operations.
The authors have declared no conflict of interest.
Acknowledgments
The authors thank Jan‐Martijn Hamelink for the fruitful discussions on the iDoE method.
Appendix 1.
1.1. Simulation case study
The production of viral capsid protein production by E. coli was simulated adopting the model proposed by 24 to act as the ‘process’ by which the approaches discussed in this paper are applied. The model comprises the material balances for biomass, substrate, and product concentration as well as the overall mass balance, i.e.:
With μ, and the specific rates of biomass growth (1/h), substrate uptake (1/h) and product formation (U/g/h), X, S and the biomass (g/kg), substrate (g/kg) and product concentrations (U/kg), (1/h) the dilution rate and the feeding rate (kg/h). The initial values are (g/kg), 0(g/kg), 0 (U/kg) and 5(kg).
The specific biomass growth rate was modeled using the expression:
where = 0.737 (1/h), = 0.00333 (g/kg), (g/kg), (1/C), (C) and T the temperature of the culture broth.
The specific substrate uptake rate is modeled via:
with (g/g) and (g/g/h).
The specific product formation rate is modeled by:
with
where (J/mol), (J/mol), (J/mol/K), (h),(U/g),(1/h), (U/g), (1/h) and the induction parameter before induction and afterwards.
For the feeding rate and exponential profile was adopted to match a desired constant specific biomass growth, , i.e.:
where (g/kg) is the initial biomass concentration and (kg) is the initial weight of the culture broth.
The process was divided into two phases, a growth and a production phase. During the growth phase (1/h) and (C). The duration of the growth phase is 2.6(h). For the production phase the levels of and T, were investigated using the classic 2‐factor Doehlert‐design or the proposed iDoE. Data for online variables were logged every 6 minutes. The biomass and product concentrations (offline variables) were measured 20 times during each fermentation. During the growth four samples were taken. In the production phase the samples were evenly distributed. It was ensured that a sample was always taken before step‐changes were applied. The data were corrupted with 5% Gaussian (white) noise.
1.2. Dynamic hybrid models
Two dynamic hybrid models were developed, either using the data from the iDoE design or from the classical Doehlert design. The parametric structure of both models is identical, i.e. the material balance equations for biomass and product (with and designating biomass and product concentrations, respectively) assuming specific rates:
with the dilution , the specific biomass growth rate and vP, ANN the specific product formation rate.
The two specific rates ( and ) are modeled using an artificial neural network. Each network has three layers (input, hidden and output layer), which typically is sufficient for the modeling of arbitrary continuous nonlinear functions. The transfer functions of the nodes of the layers are linear, hyperbolic tangent and linear, respectively. Three inputs were identified to be sufficient to describe the rate functions, namely biomass concentration, the feeding rate and temperature. The performance of different numbers of nodes in the hidden layer of the neural network was studied. For the training, validation and testing of the model performance the data were separated into three corresponding partitions, i.e. a training, validation and test partition (for details about the partitions see Figs. 4 and 5). The parameters were adapted to minimize a weighted least square function of the concentrations using the training data. The weighting was established by the standard deviations of every concentration, therefore accounting for the differences of the magnitude of the concentration values. The validation data were used to stop the training once the fit of the model estimates to the experimental data for the validation data did not improve further. The training was re‐initiated 60 times using random parameter values as initial weights and the best performing parameter set was chosen in order to avoid local minima. The test partition was used to evaluate the model performance on new, unseen data. The neural network structure that performed best on the validation data in terms of the Bayesian Information Criteria (BIC)3 wvvas chosen for comparison. Four nodes in the hidden layer were found to perform best in case of the HMiDoE, three in case of the HMDoE. For a more detailed description of this hybrid model development procedure, see 29.
Practical application
The proposed method can be applied to intensify classical Design of Experiment plans in cases where i) the control degrees of freedom comprise process parameters that can be changed; and ii) the intra‐experiment changes in the process parameters result in a change in the process response (which has to be quantifiable). In this paper, the method is applied to upstream bioprocess development and/or optimization (where the impact of temperature and feeding rate on the simulated process performance is investigated), but it could also be adapted to the development/optimization of chemical synthesis processes. Experimental applicability of this concept has been shown for an E.coli fed‐batch processes elsewhere. Future research on using the iDoE method for the development of processes with other organisms (e.g. mammalian cells) is expected to show that the number of experiments required for model development can be reduced significantly.
Footnotes
Whether and to which extend is a degree of freedom depends on the operation regime, i.e. batch, fed‐batch or continuous.
The addition of constraints can reduce the solution space of the optimization problem. However, the reduction of the solution space might exclude solutions that until the addition of the constraint have been optimal in the sense of the optimization objective. Therefore the minimum number of experiments might increase with the introduction of constraints.
The BIC balances the fit of the model estimates and experimental data against the number of model parameters, i.e. model complexity. For instance, in case of equal performance in terms of fit the model with the lower number of parameters is chosen.
5 References
- 1. Montgomery, D. C. , Design and Analysis of Experiments, John Wiley & Sons, 2008. [Google Scholar]
- 2. Mandenius, C.‐F. , Brundin, A. , Bioprocess optimization using design‐of‐experiments methodology. Biotechnol. Prog. 2008, 24, 1191–1203. [DOI] [PubMed] [Google Scholar]
- 3. Kumar, V. , Bhalla, A. , Rathore, A. S. , Design of experiments applications in bioprocessing: Concepts and approach. Biotechnol. Prog. 2014, 30, 86–99. [DOI] [PubMed] [Google Scholar]
- 4. Rathore, A. S. , Winkle, H. , Quality by design for biopharmaceuticals. Nat. Biotech. 2009, 27, 26–34. [DOI] [PubMed] [Google Scholar]
- 5. Sadowski, M. I. , Grant, C. , Fell, T. S. , Harnessing QbD, programming languages, and automation for reproducible biology. Trends in Biotec., 34, 214–227. [DOI] [PubMed] [Google Scholar]
- 6. Chew, W. , Sharratt, P. , Trends in process analytical technology. Ana. Met. 2010, 2, 1412–1438. [Google Scholar]
- 7. Tai, M. , Ly, A. , Leung, I. , Nayar, G. , Efficient high‐throughput biological process characterization: Definitive screening design with the Ambr250 bioreactor system. Biotech. Prog. 2015, 31, 1388–1395. [DOI] [PubMed] [Google Scholar]
- 8. Betts, J. I. , Baganz, F. , Miniature bioreactors: Current practices and future opportunities. Microb. Cell Fact. 2006, 5, 21. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9. Bareither, R. , Pollard, D. , A review of advanced small‐scale parallel bioreactor technology for accelerated process development: Current state and future need. Biotech. Prog. 2011, 27, 2–14. [DOI] [PubMed] [Google Scholar]
- 10. von Stosch, M. , Hamelink, J.‐M. , Oliveira, R. , Hybrid modeling as a QbD/PAT tool in process development: An industrial E. coli case study. Bioproc. Biosyst. Eng. 2016, 39, 773–784. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11. Kreutz, C. , Timmer, J. , Systems biology: Experimental design. FEBS J. 2009, 276, 923–942. [DOI] [PubMed] [Google Scholar]
- 12. Banga, J. R. , Balsa‐Canto, E. , Parameter estimation and optimal experimental design. Essays Biochem. 2008, 45, 195–210. [DOI] [PubMed] [Google Scholar]
- 13. Brendel, M. , Marquardt, W. , Experimental design for the identification of hybrid reaction models from transient data. Chem. Eng. J. 2008, 141, 264–277. [Google Scholar]
- 14. Cruz Bournazou, M. N. , Barz, T. , Nickel, D. , Neubauer, P. , Sliding‐window optimal experimental re‐design in parallel microbioreactors. Chem. Ing. Tech. 2014, 86, 1379–1380. [Google Scholar]
- 15. Georgakis, C. , Design of dynamic experiments: A data‐driven methodology for the optimization of time‐varying processes. Ind. Eng. Chem. Res. 2013, 52, 12369–12382. [Google Scholar]
- 16. von Stosch, M. , Hamelink, J.‐M. , Oliveira, R. , Towards intensifying Design of Experiments (iDoE): An industrial E.coli case study. Biotechnol. Prog. 2016. DOI: 10.1002/btpr.2295. [DOI] [PubMed] [Google Scholar]
- 17. Åkesson, M. , Hagander, P. , Axelsson, J. P. , Avoiding acetate accumulation in Escherichia coli cultures using feedback control of glucose feeding. Biotechnol. Bioeng. 2001, 73, 223–230. [DOI] [PubMed] [Google Scholar]
- 18. Dietzsch, C. , Spadiut, O. , Herwig, C. , A dynamic method based on the specific substrate uptake rate to set up a feeding strategy for Pichia pastoris. Microb. Cell Fact. 2011, 10, 14. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 19. Schaepe, S. , Kuprijanov, A. , Simutis, R. , Lübbert, A. , Avoiding overfeeding in high cell density fed‐batch cultures of E. coli during the production of heterologous proteins. J. Biotechnol. 2014, 192, 146–153. [DOI] [PubMed] [Google Scholar]
- 20. Ye, J. , Ly, J. , Watts, K. , Hsu, A. et al., Optimization of a glycoengineered Pichia pastoris cultivation process for commercial antibody production. Biotechnol. Progr. 2011, 27, 1744–1750. [DOI] [PubMed] [Google Scholar]
- 21. Ferreira, A. R. , Dias, J. M. L. , Stosch, M. , Clemente, J. et al., Fast development of Pichia pastoris GS115 Mut+ cultures employing batch‐to‐batch control and hybrid semi‐parametric modeling. Bioproc. Biosyst. Eng. 2013, 37, 629–639. [DOI] [PubMed] [Google Scholar]
- 22. Griva, I. , Nash, S. G. , Sofer, A. , Linear and Nonlinear Optimization, Society for Industrial and Applied Mathematics, Philadelphia, 2009. [Google Scholar]
- 23. de Figueiredo, L. F. , Podhorski, A. , Rubio, A. , Kaleta, C. et al., Computing the shortest elementary flux modes in genome‐scale metabolic networks. Bioinformatics 2009, 25, 3158–3165. [DOI] [PubMed] [Google Scholar]
- 24. Levisauskas, D. , Galvanauskas, V. , Henrich, S. , Wilhelm, K. et al., Model‐based optimization of viral capsid protein production in fed‐batch culture of recombinant Escherichia coli. Bioproc. Biosyst. Eng., 2003, 25, 255–262. [DOI] [PubMed] [Google Scholar]
- 25. Doehlert, D. H. , Uniform Shell Designs. J. Roy. Stat. Soc. C‐App 1970, 19, 231–239. [Google Scholar]
- 26. Gomes, J. , Chopda, V. R. , Rathore, A. S. , Integrating systems analysis and control for implementing process analytical technology in bioprocess development. J. Chem. Technol. Biotechnol. 2015, 90, 583–589. [Google Scholar]
- 27. Seborg, D. E. , Mellichamp, D. A. , Edgar, T. F., III , F. J. D., Process Dynamics and Control, John Wiley & Sons, New York, 2010. [Google Scholar]
- 28. Shimizu, K. , Metabolic regulation of a bacterial cell system with emphasis on escherichia coli metabolism. ISRN Biochem. 2013, 2013, 645983. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29. Oliveira, R. , Combining first principles modelling and artificial neural networks: A general framework. Comput. Chem. Eng. 2004, 28, 755–766. [Google Scholar]


