Abstract
At over 40 years, the Landsat satellites provide the longest temporal record of space-based land surface observations, and the successful 2013 launch of the Landsat-8 is continuing this legacy. Ideally, the Landsat data record should be consistent over the Landsat sensor series. The Landsat-8 Operational Land Imager (OLI) has improved calibration, signal to noise characteristics, higher 12-bit radiometric resolution, and spectrally narrower wavebands than the previous Landsat-7 Enhanced Thematic Mapper (ETM+). Reflective wavelength differences between the two Landsat sensors depend also on the surface reflectance and atmospheric state which are difficult to model comprehensively. The orbit and sensing geometries of the Landsat-8 OLI and Landsat-7 ETM+ provide swath edge overlapping paths sensed only one day apart. The overlap regions are sensed in alternating backscatter and forward scattering orientations so Landsat bi-directional reflectance effects are evident but approximately balanced between the two sensors when large amounts of time series data are considered. Taking advantage of this configuration a total of 59 million 30m corresponding sensor observations extracted from 6,317 Landsat-7 ETM+ and Landsat-8 OLI images acquired over three winter and three summer months for all the conterminous United States (CONUS) are compared. Results considering different stages of cloud and saturation filtering, and filtering to reduce one day surface state differences, demonstrate the importance of appropriate per-pixel data screening. Top of atmosphere (TOA) and atmospherically corrected surface reflectance for the spectrally corresponding visible, near infrared and shortwave infrared bands, and derived normalized difference vegetation index (NDVI), are compared and their differences quantified. On average the OLI TOA reflectance is greater than the ETM+ TOA reflectance for all bands, with greatest differences in the near-infrared (NIR) and the shortwave infrared bands due to the quite different spectral response functions between the sensors. The atmospheric correction reduces the mean difference in the NIR and shortwave infrared but increases the mean difference in the visible bands. Regardless of whether TOA or surface reflectance are used to generate NDVI, on average, for vegetated soil and vegetation surfaces (0 ≤ NDVI ≤ 1), the OLI NDVI is greater than the ETM+ NDVI. Statistical functions to transform between the comparable sensor bands and sensor NDVI values are presented so that the user community may apply them in their own research to improve temporal continuity between the Landsat-7 ETM+ and Landsat-8 OLI sensor data. The transformation functions were developed using ordinary least squares (OLS) regression and were fit quite reliably (r2 values >0.7 for the reflectance data and >0.9 for the NDVI data, p-values <0.0001).
Keywords: Landsat, continuity, reflectance, NDVI, OLI, ETM+
1. Introduction
At over 40 years, the Landsat satellites provide the longest temporal record of space-based land surface observations, and the successful 2013 launch of Landsat-8 carrying the Operational Land Imager (OLI) and the Thermal Infrared Sensor (TIRS) is continuing this legacy (Irons et al. 2012; Roy et al. 2014a). Multi-temporal optical wavelength satellite data acquired under different acquisition conditions and by different sensors may have reflectance inconsistencies introduced by factors including atmospheric and cloud contamination (Kaufman 1987, Masek, et al. 2006), variable sun-surface-sensor geometry (Roy et al. 2008, Nagol et al. 2015, Ju et al. 2010), sensor degradation and calibration changes (Markham and Helder, 2012), between sensor spectral band pass and spatial resolution differences (Steven et al. 2003; Tucker et al. 2005), and data processing issues (Roy et al. 2002). The need for multi-year consistent data records for both research and applications is well established. For example, the global coverage Moderate Resolution Imaging Spectroradiometer (MODIS) products have been generated from 2000 to present (Justice et al. 1998) and have been reprocessed several times using improved calibration and geometric knowledge and refined product generation algorithms (Masuoka et al. 2011). Similarly, substantial research effort has been developed to generate global long term data records derived from coarse resolution Advanced Very High Resolution Radiometer (AVHRR) observations available since 1981, although those that are publically available are subject to scientific debate (Myneni et al. 1998; Pedelty et al. 2007; Beck et al. 2011; Fensholt and Proud 2012; Pinzon and Tucker 2014). Unlike past AVHRR sensors, which carried no onboard reflective wavelength calibration capability, the Landsat Thematic Mapper, ETM+ and OLI sensors are well calibrated (Markham and Helder 2012) and with the free Landsat data availability the systematic generation of consistent global long-term Landsat products has been advocated (Roy et al. 2014a).
The primary Landsat-8 mission objective is to extend the Landsat record into the future and maintain continuity of observations so that Landsat-8 data are consistent and comparable with those from the previous Landsat systems (Roy et al. 2014a). Because of the importance of continuity, the Landsat legacy is one in which there has been relatively consistent mission objectives, but with capabilities modified by incremental improvements in satellite, sensor, transmission, reception and data processing and storage technologies (Irons and Masek 2006; Irons et al. 2012). There is a need to define quantitative spectral reflectance transformations between all the Landsat sensors to provide consistent long term Landsat reflectance data. This paper is limited to the Landsat-7 and Landsat-8 sensors and compares their spectrally overlapping reflective wavelength bands and develops statistical functions to transform between them. In addition, between sensor transformations for the normalized difference vegetation index (NDVI) are developed as the NDVI is one of the most commonly used remote sensing indices. The transformations are developed by statistical comparison of contemporaneous sensor satellite observations which is quite a common approach (Brown et al. 2006, Gallo et al. 2005, Miura et al. 2006). However, this is challenging for several reasons. First, spectral response differences between the sensors mean that the observed sensor radiances differ in a way that is dependent on the observed surface components (Steven et al. 2003) except when the surface reflectance changes linearly over the band passes which is not usually the case for Landsat (Miura et al. 2006; Zhang and Roy 2015). Second, top of atmosphere (TOA) reflective wavelength differences between the sensors depend on the atmospheric state and at reflective wavelengths atmospheric effects are coupled to the surface reflectance (Tanre et al. 1981). Third, Landsat atmospheric correction algorithms are imperfect, particularly at shorter visible wavelengths (Ju et al. 2012; Vermote et al. this edition). Fourth, despite the relatively narrow 15° Landsat sensor field of view, Landsat bi-directional reflectance effects occur (Roy et al. 2008; Li et al., 2010, Nagol et al. 2015; Gao et al., 2014) and so comparison of Landsat data with different solar and view zenith geometry may introduce differences when surfaces are non-Lambertian. Fifth, unless the sensor data are observed closely together in time, the surface state and condition may change due to anthropogenic factors (e.g., land cover change, agricultural harvesting) and natural factors (e.g., phenology, moisture changes due to precipitation, fire and wind disturbances) which can be difficult to detect reliably using Landsat data (Huang et al. 2010; Kennedy et al. 2010; Hansen et al. 2014; Zhu and Woodcock 2014). For these reasons, reliable and representative determination of statistical functions to transform between sensor bands requires a comparison of data sensed over a wide range of surface conditions. Previous researchers have reported comparisons between Landsat-7 ETM+ and Landsat-8 OLI data but considered only a relatively small (compared to this study) amount of data in Australia (Flood 2014) and in China and Korea (Ke et al. 2015) and did not take into account the per-pixel spectral saturation status that we show is important.
In this study, a total of 59 million 30m corresponding sensor observations extracted from 6,316 Landsat-7 ETM+ and Landsat-8 OLI images acquired over three winter and three summer months for all the conterminous United States (CONUS) are examined. Statistical calibrations are derived to document between sensor differences for TOA and also surface reflectance and derived NDVI. The transformations are provided so that the user community may apply them in their own research to improve temporal continuity of reflectance and NDVI between the Landsat OLI and ETM+ sensors. First, the Landsat data and pre-processing required to allow their meaningful comparison are described, then the analysis methodology and results are described, followed by concluding remarks with implications and recommendations.
2. Data
The Landsat-8 OLI has narrower spectral bands, improved calibration and signal to noise characteristics, higher 12-bit radiometric resolution, and more precise geometry, compared to the Landsat-7 ETM+ (Irons et al. 2012). The OLI dynamic range is improved, reducing band saturation over highly reflective surfaces, and the greater 12-bit quantization permits improved measurement of subtle variability in surface conditions (Roy et al. 2014a). The Landsat-7 ETM+ has a 5% absolute radiometric calibration uncertainty (Markham and Helder 2012) and the Landsat-8 OLI has a 3% absolute radiometric calibration uncertainty (Markham et al. 2014). The OLI has two new reflective wavelength bands, a shorter wavelength blue band (0.43–0.45μm) and a shortwave infrared cirrus band (1.36–1.39μm), but these are not considered in this study as they have no direct ETM+ equivalent. Comparison of thermal wavelength sensor data is complex because the processes controlling thermal emittance are highly variable in space and time (Moran et al. 1994; Norman et al. 1995) and because of this, and the stray light contamination in one of the two TIRS bands (Montanaro et al. 2014), the Landsat thermal bands are also not considered in this study.
The OLI bands are defined at 30m like the ETM+ but are spectrally narrower and cover different spectral ranges (Figure 1). The OLI and ETM+ spectral band passes are tabulated in Roy et al. (2014a). The blue, green and red OLI band spectral response functions intersect with 82.76%, 71.08% and 60.63% of the corresponding ETM+ band spectral response functions. Conversely, the blue, green and red ETM+ band spectral response functions intersect with 98.83%, 98.30% and 98.90% of the corresponding OLI band spectral response functions. Notably, the OLI near-infrared (NIR) band (~0.85μm) avoids a water absorption feature that occurs in the ETM+ NIR band (Irons et al. 2012). The OLI NIR and the shortwave infrared band (~1.16 μm and ~2.11 μm) spectral response functions fall entirely within the ETM+ spectral response functions and occupy only 23.14%, 42.22% and 66.69% of the ETM+ spectral response functions respectively.
Figure 1.
Landsat-7 ETM+ and Landsat-8 OLI spectral response functions for the approximately corresponding reflectance bands used in this research (source WWW1 and WWW2).
The Landsat-8 is in the (now decommissioned) Landsat 5 orbit and so Landsat-8 and 7 have the same approximately 710 km sun-synchronous circular 98.2° inclined orbit and overpass every Earth location every 16 days but are offset from each other by 8 days (Teillet et al., 2001, Loveland and Dwyer 2012). Both Landsat sensors have 15° fields of view and their data are available in approximately 185 km × 180 km scenes defined in a Worldwide Reference System (WRS) of path (groundtrack parallel) and row (latitude parallel) coordinates (Arvidson et al. 2006; Loveland and Dwyer 2012). Every daytime sunlit Landsat-7 and 8 overpass of the CONUS is ingested into the U.S. Landsat archive, located at the United States Geological Survey (USGS) Earth Resources Observation and Science (EROS), with an annual maximum of 22 or 23 acquisitions per path/row. In May 2003 the Landsat-7 ETM+ scan line corrector failed, reducing the usable data in each Landsat ETM+ scene by 22% (Markham et al. 2004). The Landsat-8 OLI has no such missing data issue. The Landsat-7 and 8 acquisitions are precision terrain corrected (termed Level 1T) with processing that includes radiometric correction, systematic geometric correction, precision correction using ground control, and the use of a digital elevation model to correct parallax error due to local topographic relief (Lee et al. 2004; Storey et al. 2014). Certain acquisitions may not have sufficient ground control, typically due to cloud cover, and instead, the best level of correction is applied to generate systematically terrain corrected (termed L1Gt) processed acquisitions (Storey et al. 2014). Unlike previous Landsat data, the Landsat-8 Level 1 data product includes a spatially explicit 30m quality assessment band with cloud, cirrus cloud, and snow masks (USGS 2012, 2015). The snow mask is derived using the normalized difference snow index, defined as the green minus shortwave infrared reflectance divided by their sum (Hall et al. 1995), using OLI specific thresholds (USGS 2015). The cirrus cloud mask is also new to the Landsat satellite series and provides a pixel assessment of the presence of low or high confidence cirrus found by thresholding the Landsat-8 OLI 1375 μm reflectance band (Kovalskyy & Roy 2015).
In this study, to ensure that a representative range of reflectance spectra were obtained (i.e., capturing land cover, land use, vegetation phenology and soil moisture variations), all the Landsat-7 ETM+ and Landsat-8 OLI acquisitions for three CONUS winter months (26th November 2013 to 4th March 2014) and three summer months (28th May 2013 to 2nd September 2013) were obtained from the U.S. Landsat archive. The most recent Version LPGS_2.3.0 OLI data (that were reprocessed in February 2014 to fix a significant change in the OLI TIRS band calibration and cloud mask product) and Version LPGS_12.4.0 ETM+ data were used. Only acquisitions processed to L1T and with metadata GEOMETRIC_RMSE_MODEL values ≤ 30m were used to ensure high geolocation accuracy needed for pixel-level Landsat-7 and 8 data comparison. In addition, only daylight acquisitions, defined as those with metadata SUN_ELEVATION values >5°, were used. This filtering resulted in a total of 6317 acquisitions with 4272 Landsat-8 OLI (2752 summer and 1520 winter) and 2045 Landsat-7 ETM+ (1767 summer and 278 winter) acquisitions. There were fewer ETM+ than OLI acquisitions because a greater proportion of ETM+ scenes failed the geometric filtering criteria, most likely due to the presence of ETM+ scan line corrector failure missing pixels combined with clouds (Roy et al. 2010) and because the OLI has higher geolocation accuracy than the ETM+ (Storey et al. 2014). There were fewer acquisitions for either sensor in Winter due to the greater seasonal CONUS likelihood of clouds at the time of Landsat overpass (Ju and Roy, 2008; Kovalskyy and Roy, 2015).
Figure 2 illustrates the geographic locations of a summer week of Landsat OLI (blue) and ETM+ (red) data. There is an evident across-track overlap of each Landsat acquisition that increases further north due to the poleward convergence of the Landsat orbits. Because the OLI and ETM+ are in the same orbit offset by 8 days the western and eastern sides of a sensor acquisition are overlapped by the eastern and western sides respectively of the other sensor, and are acquired with only a one day separation. The one day separation between OLI and ETM+ is advantageous as surface changes are less likely to occur within such a short period, although atmospheric conditions may change. The solar zenith changes in one day by a negligible amount at the time of OLI and ETM+ overpass (typically less than 0.2° for the data considered in this study) and the between sensor overlap region is always acquired in the forward scattering direction from one sensor and the backward scattering direction from the other sensor. Consequently, backscatter and forward scattering effects due to the reflectance anisotropy of the land surface are present, although pronounced bi-directional reflectance “hot-spot” effects observed by MODIS from a similar orbit as Landsat (Vermote and Roy 2002) will not occur because of the much narrower field of view of Landsat (Zhang et al. 2015). Across the CONUS there are typically more than 20 orbits of OLI and ETM+ per week and bi-directional reflectance effects are captured by both sensors in an approximately balanced way when many months of data are considered, as in this study, due to the systematic overlapping area backward and forward scatter sensor acquisition geometry.
Figure 2.
Geographic locations of Landsat-8 OLI (blue) and Landsat-7 ETM+ (red) acquisitions derived from their metadata latitude and longitude scene corner coordinates for a seven day period, 28th July 2013 to 3rd August 2013, shown in the Web Enabled Landsat Data (WELD) Albers projection. See text for explanation of coverage differences.
3.0. Data pre-processing
3.1. Top of atmosphere reflectance computation
The data sensed by each Landsat-7 ETM+ detector are stored in the L1T product as an 8-bit digital number (Markham et al. 2006) and was converted to spectral radiance using sensor calibration gain and bias coefficients derived from the L1T file metadata (Chander et al. 2009). The radiance for the reflective bands was then converted to top of atmosphere (TOA) reflectance using standard formulae (Roy et al. 2010) as:
| [1] |
where is the top of atmosphere (TOA) reflectance (unitless), sometimes termed the bidirectional reflectance factor, for ETM+ band λ, Lλ is the TOA spectral radiance (W m−2 sr−1 μm−1), d is the Earth-Sun distance (astronomical units), ESUNλ is the mean TOA solar spectral irradiance (W m−2 μm−1), and θs is solar zenith angle at the center of the Landsat acquisition (radians). The quantities ESUNλ and d are tabulated by Chander et al (2009) and θs is calculated from the solar elevation angle stored in the L1T file metadata. The data sensed by each Landsat-8 OLI detector are stored in the L1T product as a 16-bit digital number (the OLI detectors have 12-bit radiometric resolution) and were converted to TOA reflectance using the scaling factors and dividing by the cosine of the solar zenith angle that are stored in the OLI L1T metadata. The 30m for each ETM+ and OLI reflective band were stored as signed 16-bit integers after being scaled by 10,000 and the TOA NDVI was computed (as the NIR minus red TOA reflectance divided by their sum) and stored as signed 16-bit integers after being scaled by 10,000.
3.2. Spectral saturation and cloud computation
Highly reflective surfaces, including snow and clouds, and sun-glint over water bodies, may saturate the reflective wavelength bands, with saturation varying spectrally and with the illumination geometry (Dowdeswell and Mcintyre, 1986, Oreopoulos et al. 2000, Bindschadler et al. 2008, Roy et al. 2010). As the reflectance of saturated pixels is unreliable the spectral band saturation status was stored for each 30m pixel. Saturated pixels are designated by specific ETM+ L1T digital numbers (Roy et al. 2010) and for the OLI L1T are straightforward to derive by comparison of the stored OLI digital numbers with OLI L1T metadata saturation values. The OLI data were expected to be saturated much less frequently than the ETM+ because of the greater OLI dynamic range.
Optically thick clouds preclude remote sensing of the surface at reflective wavelengths and so cloud mask results were stored for each 30m pixel. It is well established that cloud masking is complex. For example, the boundary between defining a pixel as cloudy or clear is sometimes ambiguous, and a pixel may be partly cloudy, or a pixel may appear as cloudy at one wavelength and appear cloud-free at a different wavelength (Kaufman, 1987; Ackermann et al. 2008; Tackett and Di Girolamo 2009; Kovalskyy and Roy, 2015). In this study, the automatic cloud cover assessment algorithm (ACCA) that takes advantage of known spectral properties of clouds, snow, bright soil, vegetation, and water, and consists of twenty-six rules applied to five of the ETM+ bands (Irish 2000, Irish et al. 2006), and a decision tree (DT) cloud detection algorithm based on training using approximately 13 million and 5.4 million unsaturated and saturated ETM+ training pixels (Roy et al. 2010), were applied to the ETM+ data. The ACCA and DT cloud mask algorithms provide binary cloud detection status information. The OLI already has per-pixel cloud information available in the L1T product that indicates if the 30m pixel is either (a) high confidence cloud, (b) medium confidence cloud, (c) low confidence cloud, and if it is either (d) high confidence cirrus cloud, or (e) low confidence cirrus cloud (USGS 2012; Kovalskyy and Roy, 2015). In addition, the OLI L1T product includes a 30m low, medium and high confidence snow flag that was also considered (USGS 2012, 2015).
3.3. Surface reflectance computation
Surface reflectance, i.e., TOA reflectance corrected for atmospheric effects, is needed because atmospheric gases and aerosols are variable in space and time and may have significant impacts on Landsat data (Ouaidrari and Vermote 1999; Masek et al. 2006; Roy et al. 2014b). In this study the Landsat Ecosystem Disturbance Adaptive Processing System (LEDAPS) atmospheric correction algorithm (Masek et al. 2006) was used as it is developed for both ETM+ and OLI application, and explicitly models their spectral response functions (Vermote et al. this edition). The 30m surface reflectance for each ETM+ and OLI reflective band, and the surface NDVI derived from the surface reflectance NIR and red bands, were stored as signed 16-bit integers after being scaled by 10,000.
The LEDAPS uses the 6SV radiative transfer code (Vermote et al. 1997; Kotchenova et al. 2006) with aerosol characterizations derived independently from each Landsat acquisition, and assumes a fixed continental aerosol type and uses ancillary water vapor. Recently, Landsat-7 ETM+ LEDAPS atmospherically corrected data were validated by comparison with independent 6SV atmospherically corrected ETM+ data using AERONET (Aerosol Robotic Network) atmospheric characterizations at 95 10 km × 10 km 30 m subsets located across the CONUS (Ju et al. 2012). The reported mean reflectance normalized residual for the LEDAPS atmospherically corrected ETM+ data was 11.8% (blue band), 5.7% (green band), 5.9% (red band), 4.8% (NIR band), and 1.0% to 2.0% for the two short wave infrared bands. Other LEDAPS assessment studies have been undertaken (Maiersperger et al. 2013; Feng et al. 2013). Validation of Landsat-8 LEDAPS atmospheric correction is underway and is more accurate than for ETM+ because of the improved OLI sensor characteristics (Vermote et al. this edition). A minority of atmospherically corrected pixels may have values outside their theoretical limits, i.e., or , due primarily to “over correction” by the atmospheric correction algorithm (Roy et al. 2014b). Therefore as these out of range surface reflectance values are unreliable they were removed from the analysis.
3.4. Reprojection and gridding
The Landsat TOA and surface reflectance data and cloud and saturation data were reprojected and gridded for the ETM+ and OLI independently. Figure 2 illustrates that at CONUS latitudes over a 7-day period only the edges of the OLI and ETM+ acquisitions overlap. Therefore the ETM+ and OLI data acquired in the same consecutive weekly (7-day) period were reprojected independently. The data were reprojected into the Albers equal area projection with nearest neighbor resampling into fixed 5000 × 5000 30m pixel tiles using the Web Enabled Landsat Data (WELD) processing software (Roy et al. 2010). In this way a tile of ETM+ data and a tile of OLI data was generated for each week at each WELD tile location.
3.5. Data sampling
To generate data for the analysis, pixels were sampled systematically in the row and column directions across each weekly OLI and ETM+ CONUS WELD tile. Pixel locations where there were corresponding ETM+ and OLI data were extracted and by definition occurred in the sensor acquisition overlap and were sensed one day apart. A sampling density of every 20th pixel (i.e., every 600m) across the CONUS was used to ensure a very large systematically collected sample of corresponding OLI and ETM+ pixel values.
4.0. Data analysis
Spectral scatter plots of the OLI versus ETM+ TOA reflectance, and also for the surface reflectance, were generated considering all six months of weekly sample data for each of the comparable OLI and ETM+ reflective wavelength bands. Similarly, scatterplots for the TOA and surface NDVI data were generated.
The correspondence between the comparable sensor bands and sensor NDVI values was first examined using reduced major axis (RMA) regression. The RMA regression results are symmetric so that a single line defines the bivariate relationship, regardless of which variable is the dependent (i.e., OLI or ETM+ data) and which is the independent variable (Smith 2009). The RMA regression allows for both the dependent and independent variables to have error (Cohen et al. 2003, Smith 2009) which is useful because of the sensor calibration uncertainty and because the TOA and surface sensor reflectance data have non-negligible atmospheric effects and residual atmospheric correction errors respectively. Statistical functions to transform between the comparable sensor bands and sensor NDVI values were then developed using ordinary least squares (OLS) regression. The OLS regression results are asymmetric, so that the slope and resulting interpretation of the data are changed when the variables assigned to the dependent and independent variables are reversed. The OLS regressions were derived for OLI versus ETM+ data, and conversely for ETM+ versus OLI data, to provide transformation functions from OLI to ETM+ and from ETM+ to OLI. The goodness of fit of the OLS regressions were defined by the coefficient of determination (r2) and the significance of the OLS regressions was defined by examination of the regression overall F-statistic p-value.
To provide simple overall measures of similarity, the mean difference, the root mean square deviation, and the mean relative difference, between the OLI and ETM+ data were derived as:
| [2] |
| [3] |
| [4] |
where , RMSD, and are the mean difference, the root mean square deviation, and the mean relative difference respectively between corresponding Landsat-8 OLI and Landsat-7 ETM+ values (TOA or surface spectral reflectance or NDVI) for n pixel values. The mean relative difference values are easier to compare between spectral bands as they are normalized for spectral reflectance differences, whereby, for example, healthy vegetation has low red reflectance but high near-infrared reflectance.
Scatterplots considering different levels of filtering, including removal of the saturated and the cloudy pixel values, were generated to provide insights into the impacts of the per-pixel data screening. The ETM+ and OLI spectral band saturation information was used to discard pixel values if either sensor values were saturated for the spectral band considered. Saturated red or NIR band pixel values were used to discard saturated NDVI values. The ETM+ and OLI cloud masks were used to discard pixel values if either sensor value was flagged as cloudy. Landsat-7 ETM+ pixels were considered cloudy if they were labeled as cloudy in either the ACCA or the decision tree cloud masks. This ensured a generous cloud definition (Roy et al. 2010) but meant that cloud-free pixels were sometimes flagged as cloudy and discarded. Similarly, a generous Landsat-8 OLI cloud pixel definition was used and OLI pixels were considered cloudy if they were labeled as high or medium confidence cloud, or as high confidence cirrus cloud. The OLI cirrus cloud status was included because a recent study reported for a year of CONUS Landsat-8 data that about 7% of pixels were detected as high confidence cirrus but low confidence cloud (Kovalskyy and Roy, 2015). The Landsat-8 OLI snow pixel state was also used to remove corresponding OLI and ETM+ pixel values that were labelled by the OLI as high or medium confidence snow.
To remove land cover and surface condition changes that may have occurred in the one day difference between OLI and ETM+ pixel observation, a filter was applied to the TOA reflectance data:
| [5] |
where and are the TOA blue reflectance for the ETM+ (band 1: 0.45–0.52μm) and the OLI (band 2: 0.45 – 0.51μm) respectively. Thus, only corresponding ETM+ and OLI values sensed one day part that had a blue TOA reflectance difference greater than 100% of their average were discarded. The blue band is the shortest wavelength ETM+ band and is the most sensitive of the ETM+ bands to atmospheric effects. In a recent study considering approximately 53 million 30m pixel locations sampled systematically across the CONUS for 12 months, the mean absolute difference between the surface and TOA blue band ETM+ reflectance expressed as a percentage of the surface reflectance was 45% (Roy et al. 2014b). Consequently, the filter [5] only rejects pixel values where the relative change between the ETM+ and OLI blue reflectance in one day was more than twice the average effect of the atmosphere, i.e., only pixel values with significant surface change will be removed. In addition, as cloud and snow have much higher blue reflectance than soil and vegetated surfaces (Dozier 1984; Ustin et al., 1998; Painter et al., 2009), the filter may remove pixel values where either (but not both) of the OLI or the ETM+ observations was cloud or snow contaminated.
5.0. Results
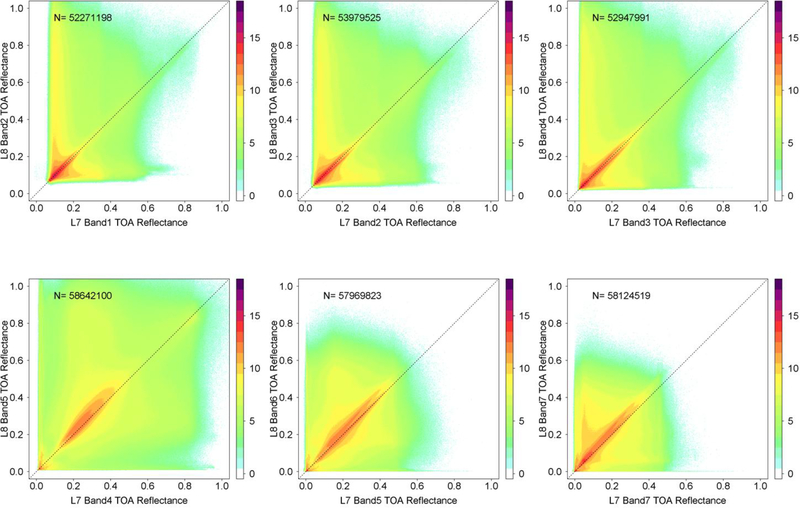
A total of 59,490,068 30m pixel values for each spectral band was extracted from the six months of CONUS overlapping sensor data. Figure 3 shows scatter plots for the six comparable OLI and ETM+ reflective bands. No filtering was applied to the data, but regardless, the higher dynamic range of the OLI (y-axis) compared to the ETM+ (x-axis) is evident in the greater dispersion of the OLI TOA reflectance compared to the ETM+ TOA reflectance. The anomalously high frequency of ETM+ visible band reflectance values at around 0.35 and 0.55 is due to sensor saturation. Figure 4 shows the same data as Figure 3 but discarding pixel values that were saturated (see Section 3.2) and these features are gone. Of the 59,490,068 values only a very small minority of the OLI values (1,289) were saturated in any of the six reflective bands compared to the ETM+ (8,210,656). The small incidence of saturated OLI data has been documented previously (Morfitt et al. 2015). The ETM+ shorter wavelength visible bands were more frequently saturated (12.1% of the blue band and 11.0% of the red band values were saturated) compared to the longer wavelength bands and the NIR band was the least saturated (1.4% of the NIR values were saturated). Comparison of Figures 3 and 4 indicate that the saturated ETM+ pixels have a wide range of TOA reflectance values and not just high values. Initially this seemed counter-intuitive. However, from [1] it is clear that large (i.e., saturated) radiance values may have reduced when observed with lower solar zenith angles (i.e., when the sun is higher in the sky), and this effect is has been documented previously (Dozier 1984; Karnieli et al. 2004). Inspection of all the ETM+ L1T acquisition metadata used in this study revealed that (i) there were only two sets of digital number to radiance calibration coefficients, and (ii) the solar zenith angles for the study data ranged from 20.85° to 74.76°. These two sets of calibration coefficients combined with the solar zenith angle variations resulted in the apparent “folding” of the saturated ETM+ reflectance values. For example, in the ETM+ blue band, which was the most sensitive to saturation, the first and second saturation peaks appear close to 0.35 and 0.55 reflectance (Figure 3) and correspond to calibration gain and offset coefficients of 0.779 and −6.97874 and of 1.181 and −7.38071 respectively. These results highlight the need to take into account the reflective wavelength saturation status when analyzing Landsat data. In particular, comparison of Landsat-8 OLI and Landsat-7 ETM+ reflectance will be quite imbalanced if the saturation status is not taken into consideration due to the improved radiometric resolution of the OLI sensor.
Figure 3.
Spectral scatterplots of Landsat-8 OLI top of atmosphere (TOA) spectral reflectance plotted against comparable Landsat-7 ETM+ TOA spectral reflectance bands. Data extracted from three winter and three summer months of overlapping OLI and ETM+ 30m pixel locations sampled systematically every 600m across the CONUS. Only reflectance values in the range 0.0 to 1.0 are illustrated. The six comparable reflective wavelength bands are illustrated, OLI bands 2 (blue: 0.45 – 0.51μm), 3 (green: 0.53 – 0.59μm), 4 (red: 0.64 – 0.67μm), 5 (near infrared: 0.85 – 0.88μm), 6 (shortwave infrared 1.57 – 1.65μm), and 7 (shortwave infrared: 2.11 – 2.29μm) plotted against ETM+ TOA bands 1 (0.45 – 0.52μm), 2 (0.52 – 0.60μm), 3 (0.63 – 0.69μm), 4 (0.77 – 0.90μm), 5 (1.55 – 1.75μm) and 7 (2.09 – 2.35μm) respectively. The dotted lines are 1:1 lines superimposed for reference. The frequency of occurrence of pixels with the same reflectance is illustrated by colors shaded with a log2 scale from 0 (white), 60 (green, log2(6) = 26 = 64), 4000 (orange, 212 = 4096), >250000 (purple, 218 = 262,144).
Figure 4.
TOA spectral reflectance as Figure 3 but after discarding saturated OLI and ETM+ pixel values.
Figure 5 illustrates the impact of removing cloudy and snow covered pixel values. Clouds and snow typically have relatively high visible and NIR reflectance compared to vegetation and soil and more similar reflectance in the Landsat shortwave bands (Dozier 1984; Ustin et al., 1998; Painter et al., 2009). Evidently, from comparison of Figure 5 and 4, the filtering resulted in the removal of some non-cloudy and non-snow contaminated data. However, given the large amount of Landsat data considered and the study goals this is preferable to retaining cloud and snow contaminated pixel values. A minority (less than 0.5%) of the pixels values illustrated in Figure 5 have OLI visible and NIR reflectance values greater than approximately 0.6. A previous OLI cloud study, that evaluated a year of CONUS OLI data, found a minority of systematic cloud detection commission errors over highly reflective exposed soils/sands in New Mexico and Utah but did not examine cloud omission errors (Kovalskyy and Roy, 2015). Detailed examination of the OLI L1T images used in this study where the OLI visible and NIR reflectance values were greater than 0.6 revealed rare but unambiguous OLI cloud detection omission errors, typified by the example shown in Figure 6.
Figure 5.
TOA unsaturated spectral reflectance as Figure 4 but after discarding cloudy ETM+ pixel values and discarding cloudy and snow OLI pixels.
Figure 6.
Illustration of Landsat-8 OLI cloud mask omission for a 500 × 800 pixel subset of an OLI image: (Left) TOA true color reflectance; (right) the same TOA true color reflectance image with the high confidence cloud (blue) and medium confidence cloud (light blue) detections overlain. A minority of unambiguous interior cloud pixels are undetected by the OLI cloud mask. OLI image sensed 31st July 2013 over Southern Georgia (WRS-2 path 18 and row 39).
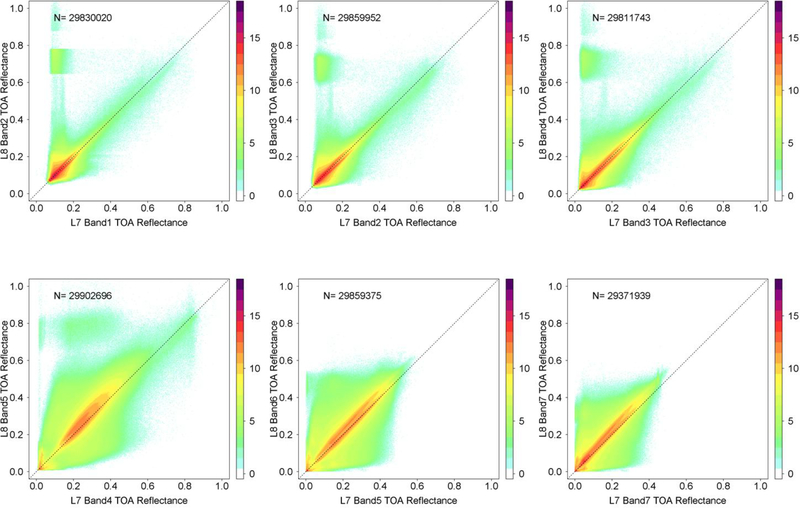
Figure 7 shows the unsaturated cloud- and snow-free TOA reflectance scatterplots with the filtering (Equation [5]) to remove pixel values where the relative one day change between the ETM+ and OLI blue reflectance was more than twice the average effect of the atmosphere. The filtering removed the OLI omission errors evident in Figure 5. Approximately 29.7 million pairs of Landsat 8 OLI and Landsat 7 ETM+ reflectance values are plotted (Table 1). The range of the OLI and ETM+ values corresponds spectrally to a great variation in surface types and conditions. Of the plotted data 11% were from the winter months and the remainder was from the summer months. This is because, as noted in Section 2.0, there were fewer winter acquisitions used for either sensor due to the greater seasonal incidence of clouds at the time of Landsat overpass. In addition, in the winter the CONUS is more snow covered (Sheng et al. 2015) and this has been observed in CONUS coverage Landsat 5 and 7 data sets (Roy et al. in review).
Figure 7.
TOA spectral reflectance as Figure 3 but after discarding saturated OLI and ETM+ pixel values, cloudy ETM+, cloudy and snow OLI pixels (Figure 5) and filtering as Equation [5]. The solid black lines show reduced major axis (RMA) regression fits of these data, the blue lines show ordinary least squares (OLS) regression of the OLI against the ETM+ data, and the green line shows OLS regression of the ETM+ data against the OLI data. The dotted lines are 1:1 lines superimposed for reference.
Table 1:
Top of atmosphere reflectance sensor transformation functions (ETM+ to OLI and OLI to ETM+) derived by ordinary least squares (OLS) regression of the data illustrated in Figure 7, reduced major axis (RMA) regression coefficients, the number of 30m pixel values considered (n), the OLS regression coefficient of determination (r2 ), the OLS regression F-test p-value, the mean difference [2], the mean relative difference [4], and the root mean square deviation [3], between the OLI and ETM+ TOA reflectance data.
| Regression type | Between sensor OLS transformation functions and RMA regression coefficients | n | OLS r2 (p-value) | mean difference OLI – ETM+ (reflectance) | mean relative difference OLI – ETM+ (%) | root mean square deviation (reflectance) | |
|---|---|---|---|---|---|---|---|
| Blue λ (∼0.48μm) | RMA | OLI = −0.0029 + 1.0333 ETM+ | 29,697,049 | 0.710 (<0.0001) | 0.0013 | 0.69 | 0.0259 |
| OLS | OLI = 0.0173 + 0.8707 ETM+ | ||||||
| OLS | ETM+ = 0.0219 + 0.8155 OLI | ||||||
| Green λ (∼0.56μm) | RMA | OLI = 0.0014 + 0.9885 ETM+ | 29,726,550 | 0.776 (<0.0001) | 0.0001 | 0.11 | 0.0272 |
| OLS | OLI = 0.0153 + 0.8707 ETM+ | ||||||
| OLS | ETM+ = 0.0128 + 0.8911 OLI | ||||||
| Red λ (∼0.66μm) | RMA | OLI = 0.0009 + 1.0026 ETM+ | 29,678,433 | 0.838 (<0.0001) | 0.0012 | 1.13 | 0.0302 |
| OLS | OLI = 0.0107 + 0.9175 ETM+ | ||||||
| OLS | ETM+ = 0.0128 + 0.9129 OLI | ||||||
| Near infrared λ (∼0.85μm) | RMA | OLI = −0.0058 + 1.1007 ETM+ | 29,767,214 | 0.711 (<0.0001) | 0.0194 | 6.45 | 0.0637 |
| OLS | OLI = 0.0374 + 0.9281 ETM+ | ||||||
| OLS | ETM+ = 0.0438 + 0.7660 OLI | ||||||
| Shortwave infrared λ (∼1.61μm) | RMA | OLI = −0.0001 + 1.0659 ETM+ | 29,725,068 | 0.780 (<0.0001) | 0.0137 | 6.41 | 0.0543 |
| OLS | OLI = 0.0260 + 0.9414 ETM+ | ||||||
| OLS | ETM+ = 0.0246 + 0.8286 OLI | ||||||
| Shortwave infrared λ (∼2.21μm) | RMA | OLI = 0.0048 + 1.0983 ETM+ | 29,237,762 | 0.837 (<0.0001) | 0.0180 | 13.59 | 0.0441 |
| OLS | OLI = 0.0490 + 0.9352 ETM+ | ||||||
| OLS | ETM+ = 0.0075 + 0.8329 OLI |
The solid lines in Figure 7 show RMA (black) and OLS (colored) regression fits that are summarized in Table 1. If the OLI and ETM+ sensors were identical and sensed at the same time then all the data in each Figure 7 scatterplot would reside on the 1:1 line and the regression fits would have zero intercepts and slopes of unity. Departures from the 1:1 line are due to the factors described in the introduction, namely (a) spectral response differences between the sensors, (b) surface and atmospheric changes over the one day OLI and ETM+ acquisition difference, and (c) bi-directional reflectance effects. Surface changes due to the one day sensor acquisition difference are assumed to be removed by the application of [5]. In addition, bidirectional reflectance effects can be largely discounted. This is because, as explained in Section 2.0, the sensor overlap region (Figure 2) is always acquired in the forward scattering direction from one sensor and the backward scattering direction from the other sensor. Bi-directional effects are typified by higher reflectance in the backscatter direction than in forward scatter direction due to shadow hiding (except for specular reflectance in the forward scattering direction) (Roujean et al. 1992; Roberts 2001; Kokhanovsky and Breon, 2012). These effects are apparent in the scatterplots, with lobes of frequently occurring values (red tones) that occur symmetrically around the RMA regression lines because the forward and backscatter viewing geometry is approximately balanced between the sensors. However, because of the bi-directional effects the OLS r2 are likely decreased and the mean difference values inflated (Table 1).
Among the six TOA reflectance bands there is a clear pattern (Figure 7) which is most easily summarized by consideration of the RMA regression fits. The RMA regression intercepts are close to zero for all the bands. However, the RMA slopes are close to unity for the visible wavelength bands and further from unity for the NIR and the two shortwave infrared bands (Table 1, Figure 7). This is likely due to the spectral response differences between the OLI and ETM+ sensors. In particular, the NIR and then the two shortwave infrared bands have RMA slopes furthest from unity because their spectral response functions are the most different (Figure 1). On average the OLI TOA reflectance is greater than the ETM+ TOA reflectance for all bands, with positive but small mean differences from 0.0001 to 0.0013 for the visible bands, the greatest positive difference for the NIR band (0.0194), and intermediate mean differences of 0.0137 and 0.0180 for the shortwave infrared (SWIR) bands. The RMSD differences show similar pattern with smaller values for the visible than the NIR and SWIR bands. The mean relative difference values are easier to compare between Landsat bands as they are normalized for spectral reflectance differences [4]. The mean relative difference values increase almost monotonically with wavelength from 0.69% (blue band) to 13.59% (~2.21 μm band).
The OLS regression results provide between sensor spectral transformations of the form (blue lines, Figure 7) and (green lines, Figure 7). The OLS regression lines fall symmetrically around the RMA regression lines and they intersect at the mean of the plotted variable values, which is expected from statistical theory (Smith 2009). The OLS r2 values are all greater than 0.7 and the regressions are all highly significant with p-values <0.0001, indicating that the between sensor spectral transformations (Table 1) can be applied to transform ETM+ TOA reflectance from OLI TOA reflectance or vice versa.
Figure 8 and Table 2 show the surface reflectance results. The impact of the atmospheric correction is clearly evident, acting to increase the range of the surface reflectance (Figure 8) relative to the TOA reflectance (Figure 7). This occurs primarily because Rayleigh and aerosol backscatter into the sensor adds to the TOA signal at low surface reflectance and aerosol absorption attenuates the TOA signal at higher surface reflectance (Tanre et al. 1981; Ouaidrari and Vermote 1999). Most evidently, the frequently occurring surface reflectance values (red tones, top row) are shifted to lower reflectance values compared to the TOA reflectance values. This pattern was also observed in a previous study that considered CONUS Landsat ETM+ data (Roy et al. 2014b). There were about 1% fewer surface reflectance than TOA reflectance pixel values for each band (see n values in Tables 1 and 2). This is because out of range surface reflectance values, i.e. or , that occurred due to “over correction” by the atmospheric correction algorithm were removed as they are unreliable. The bi-directional reflectance pattern, i.e., lobes of frequently occurring reflectance values (red tones) that occur symmetrically around the RMA regression lines, remains apparent in the atmospherically corrected data. The OLS r2 values for the surface reflectance bands are all greater than 0.7, and similar to the TOA reflectance r2 values, and the regressions are all highly significant with p-values <0.0001 indicating that the between sensor spectral transformations (Table 2) can be applied to transform ETM+ surface reflectance from OLI surface reflectance or vice versa.
Figure 8.
Atmospherically corrected surface spectral reflectance equivalent of results shown in Figure 7. Only surface reflectance values in the range 0.0 to 1.0 are illustrated. The solid black lines show reduced major axis (RMA) regression fits of these data, the blue lines show ordinary least squares (OLS) regression of the OLI against the ETM+ data, and the green line shows OLS regression of the ETM+ data against the OLI data. The dotted lines are 1:1 lines superimposed for reference.
Table 2:
Surface reflectance sensor transformation functions (ETM+ to OLI and OLI to ETM+) derived by ordinary least squares (OLS) regression of the data illustrated in Figure 8, reduced major axis (RMA) regression coefficients, the number of 30m pixel values considered (n), the OLS regression coefficient of determination (r2), the OLS regression F-test p-value, the mean difference [2], the mean relative difference [4], and the root mean square deviation [3], between the OLI and ETM+ surface reflectance data.
| Regression type | Between sensor OLS transformation functions and RMA regression coefficients | n | OLS r2 (p-value) | mean difference OLI – ETM+ (reflectance) | mean relative difference OLI – ETM+ (%) | root mean square deviation (reflectance) | |
|---|---|---|---|---|---|---|---|
| Blue λ (∼0.48μm) | RMA | OLI = −0.0095 + 0.9785 ETM | 29,607,256 | 0.750 (<0.0001) | −0.0110 | −22.32 | 0.0313 |
| OLS | OLI = 0.0003 + 0.8474 ETM+ | ||||||
| OLS | ETM+ = 0.0183 + 0.8850 OLI | ||||||
| Green λ (∼0.56μm) | RMA | OLI = −0.0016 + 0.9542 ETM | 29,670,363 | 0.790 (<0.0001) | −0.0060 | −7.34 | 0.0317 |
| OLS | OLI = 0.0088 + 0.8483 ETM+ | ||||||
| OLS | ETM+ = 0.0123 + 0.9317 OLI | ||||||
| Red λ (∼0.66μm) | RMA | OLI = −0.0022 + 0.9825 ETM | 29,505,658 | 0.848 (<0.0001) | −0.0041 | −5.12 | 0.0333 |
| OLS | OLI = 0.0061 + 0.9047 ETM+ | ||||||
| OLS | ETM+ = 0.0123 + 0.9372 OLI | ||||||
| Near infrared λ (∼0.85μm) | RMA | OLI = −0.0021 + 1.0073 ETM | 29,618,412 | 0.706 (<0.0001) | −0.0002 | −0.19 | 0.0644 |
| OLS | OLI = 0.0412 + 0.8462 ETM+ | ||||||
| OLS | ETM+ = 0.0448 + 0.8339 OLI | ||||||
| Shortwave infrared λ (∼1.61μm) | RMA | OLI = −0.0030 + 1.0171 ETM | 29,520,670 | 0.772 (<0.0001) | 0.0009 | 0.03 | 0.0562 |
| OLS | OLI = 0.0254 + 0.8937 ETM+ | ||||||
| OLS | ETM+ = 0.0306 + 0.8639 OLI | ||||||
| Shortwave infrared λ (∼2.21μm) | RMA | OLI = 0.0029 + 0.9949 ETM | 29,028,669 | 0.831 (<0.0001) | 0.0021 | 1.52 | 0.0453 |
| OLS | OLI = 0.0172 + 0.9071 ETM+ | ||||||
| OLS | ETM+ = 0.0116 + 0.9165 OLI |
The RMSD difference between the OLI and ETM surface reflectance is comparable for the visible bands, is greater in the SWIR bands and the greatest for the NIR band (Table 2). On average the OLI surface reflectance is smaller than the ETM+ surface reflectance in the visible and NIR bands, with negative but small mean differences from −0.0110 (blue) to −0.0002 (NIR). Conversely, the OLI surface reflectance is greater than the ETM+ surface reflectance for the two shortwave infrared bands with small positive mean surface reflectance differences of 0.0009 and 0.0021. The mean relative surface reflectance difference values increase monotonically with wavelength, like the TOA reflectance relative differences (Table 1), but from −22.32% (blue band) to 1.52% (~2.21μm band).
The magnitude of the surface reflectance mean difference values (Table 2) is greater than the TOA equivalents (Table 1) for the visible bands and smaller for the NIR and shortwave infrared bands. The visible band surface RMSD values are also greater than the TOA RMSD values, but the NIR and SWIR RMSD values are comparable. This spectral pattern is apparent in the RMA regression fits. The NIR and the two shortwave infrared bands have RMA slopes closer to unity (Figure 8, Table 2) than the TOA reflectance slopes (Figure 7, Table 1). Evidently, the impact of atmospheric effects over the quite different NIR and shortwave infrared band spectral response functions is reduced by the atmospheric correction. The red band TOA and surface reflectance RMA fits are similar. However, the green and blue band surface reflectance RMA fits are further from unity than the TOA equivalents. This is likely because the ETM+ atmospheric correction is less accurate than the OLI atmospheric correction for these bands (Vermote et al. this edition). As has been noted previously the accuracy of the blue and green surface reflectance is lower than in the longer wavelengths, and these bands should be used with caution (Vermote and Kotchenova 2008, Ju et al. 2012, Roy et al. 2014a).
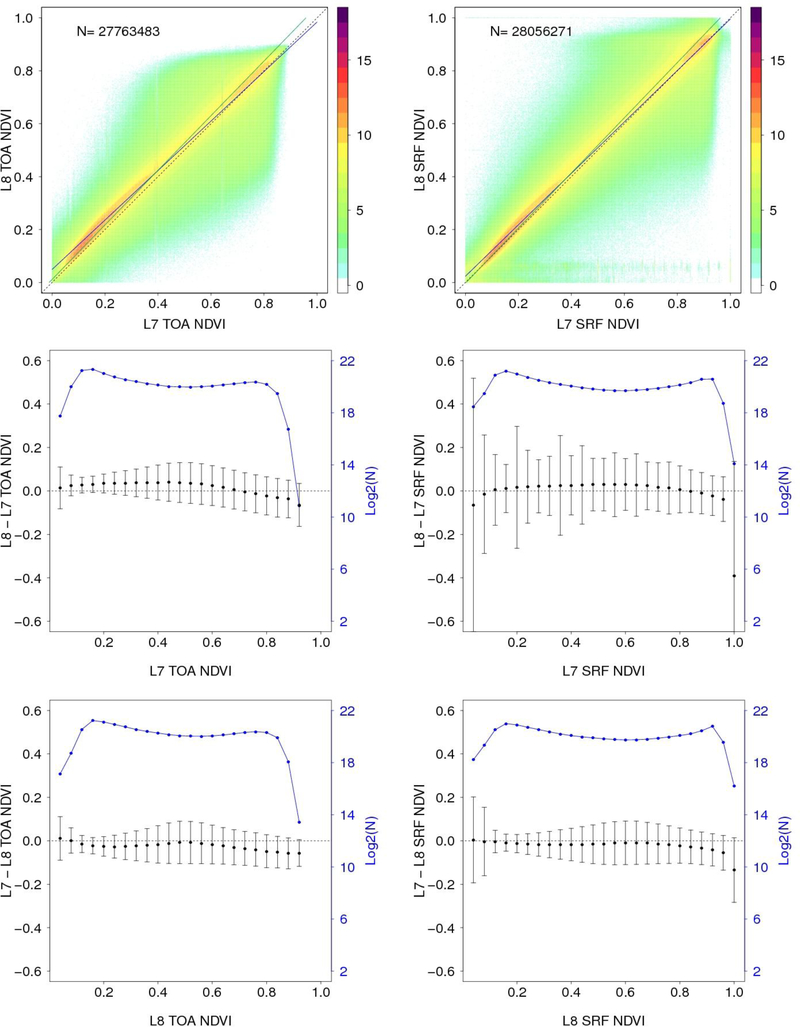
Figure 9 and Table 3 summarize the results for TOA and surface NDVI. There were different numbers of TOA and surface NDVI values because they were derived independently from the TOA and the surface red and NIR reflectance and any NDVI values less than zero were discarded. By restricting the NDVI from 0 to 1 the results reflect typical vegetated soil and vegetation surfaces. The impact of the atmospheric correction is to increase the range of the surface NDVI relative to the TOA NDVI (Figure 9). In particular, the surface NDVI has generally higher values than the TOA NDVI. This pattern was also observed in a previous study that considered CONUS Landsat-7 ETM+ data (Roy et al. 2014b) and it is well established that the atmosphere acts to depress NDVI values over land (Holben 1986; Liu and Huete 1995; McDonald et al., 1998; Roy 1997).
Figure 9.
TOA (left) and surface (right) NDVI comparisons derived from the filtered results shown in Figures 7 and 8 respectively. Top row: Sensor NDVI scatterplots considering NDVI values in the range 0 to 1; the blue lines show ordinary least squares (OLS) regression of the OLI against the ETM+ data, the green lines shows OLS regression of the ETM+ data against the OLI data, and the dotted lines are 1:1 lines superimposed for reference. Middle and Bottom rows: mean (black solid circles) ±one standard deviation (black vertical lines) sensor NDVI differences for contiguous 0.04 NDVI ranges. The number of NDVI values considered (log2 scale) is shown in blue (right Y-axis).
Table 3:
Top of atmosphere and surface NDVI sensor transformation functions (ETM+ to OLI and OLI to ETM+) derived by ordinary least squares (OLS) regression of the data illustrated in Figure 9, reduced major axis (RMA) regression coefficients, the number of 30m pixel values considered (n), the OLS regression coefficient of determination (r2), the OLS regression F-test p- value, and the mean difference [2], mean relative difference [4], and the root mean square deviation [3], between the OLI and ETM+ NDVI data.
| Regression type | Between sensor OLS transformation functions and RMA regression coefficients | n | OLS r2 (p-value) | mean difference OLI – ETM+ (reflectance) | mean relative difference OLI – ETM+ (%) | root mean square deviation (reflectance) | |
|---|---|---|---|---|---|---|---|
| TOA NDVI | RMA | OLI = 0.0306 + 0.9824 ETM | 27,763,483 | 0.906 (<0.0001) | 0.0238 | 9.88 | 0.0765 |
| OLS | OLI = 0.0490 + 0.9352 ETM+ | ||||||
| OLS | ETM+ = −0.0110 + 0.9690 OLI | ||||||
| Surface NDVI | RMA | OLI = 0.0149 + 1.0035 ETM | 28,056,271 | 0.926 (<0.0001) | 0.0165 | 4.86 | 0.0779 |
| OLS | OLI = 0.0235 + 0.9723 ETM+ | ||||||
| OLS | ETM+ = 0.0029 + 0.9589 OLI |
On average the OLI NDVI is greater than the ETM+ NDVI by 0.0238 (TOA NDVI) and by 0.0165 (surface NDVI) with comparable RMSD values (Table 3). The mean relative sensor NDVI differences are 9.88% (TOA NDVI) and 4.86% (surface NDVI) respectfully. Although not insignificant, these between sensor NDVI differences are considerably smaller than the CONUS average 0.1 and 28% relative impact of the atmosphere on Landsat ETM+ NDVI over vegetated surfaces reported by Roy et al. (2014b). The RMA intercepts and slopes are closer to zero and unity respectively for the surface NDVI than the TOA NDVI (Table 3). This is expected given that the atmospheric correction also similarly improved the RMA regression fit for the NIR reflectance and made relatively little difference to the red reflectance (Tables 1 and 2).
The middle and bottom rows of Figure 9 illustrate the mean and standard deviation of the difference between sensor NDVI defined over 25 contiguous NDVI ranging from 0 to 1. The number of pixels in each 0.04 NDVI range is also illustrated (blue) and in each range there are typically one to four million values, although for low and high NDVI ranges fewer values are available. The bottom row of Figure 9 illustrates that for a given OLI NDVI value the ETM+ NDVI is lower usually than the OLI NDVI except for near zero OLI NDVI values. The middle row of Figure 9 illustrates that for a given ETM+ NDVI the OLI NDVI is usually greater for ETM+ NDVI values from 0 to about 0.7 (TOA) and from 0 to about 0.8 (surface). The reasons for these differences are complex being dependent on the sensor differences in the red and NIR reflectance used to derive the NDVI, and influenced by NDVI saturation whereby NDVI values become similar over increasingly vegetated (higher biomass, leaf area index, ground cover) surfaces (Huete et al. 2002). The standard deviations of the surface NDVI differences vary with respect to NDVI (Figure 9 right column) in a more complex manner than the TOA results (Figure 9 left column) reflecting the different sensor impacts of the LEDAPS atmospheric correction on the red and NIR bands. We note that despite the apparent curvilinear pattern in the mean NDVI sensor differences with respect to NDVI (black dots, middle and bottom rows of Figure 9) OLS regression of these data, similar to Trishchenko et al. (2002), provided insignificant first and second order regressions (r2 values less than 0.07). Considering all the NDVI data in the 0 to 1 range (Figure 9, top row) provided highly significant OLS regressions (r2 values > 0.9, p-values <0.0001) for TOA and surface NDVI (Table 3). The NDVI ratio formulation to first order reduces bi-directional reflectance effects (Gao et al. 2002). This is perhaps one reason why the NDVI OLS r2 values are greater than the r2 values for the red and NIR reflectance bands. The OLS results indicate that the NDVI between sensor spectral transformations (Table 3) can be reliably applied to transform ETM+ NDVI from OLI NDVI or vice versa.
6.0. Conclusion
Continuity between Landsat sensors is required so that long time series multi-sensor analyses can be undertaken in an unbiased way. The multi-decadal continuity of the Landsat program, with consecutive, temporally overlapping Landsat observatories and cross-sensor calibration, is a key reason the Landsat program has value for climate and global change studies (Trenberth et al., 2013; Roy et al. 2014a). The Landsat-8 OLI and Landsat-7 ETM+ sensors are well characterized but reflectance differences imposed by their different specifications will also depend on the surface reflectance and atmospheric state that are difficult to model comprehensively. Consequently, in this study a statistical analysis of a very large sample of corresponding OLI and ETM+ 30m observations extracted systematically across the conterminous United States (CONUS) from six months of weekly independently gridded sensor observations was conducted.
A key requirement for this sensor comparison study was to capture sensor differences and not differences due to surface and atmospheric changes. The importance of appropriate data screening for analysis of Landsat data was very evident when the spectral scatter plots of the OLI versus ETM+ reflectance with different levels of per-pixel screening were compared. Notably, although the OLI was very infrequently saturated the ETM+ bands were frequently saturated, particularly in the shorter wavelength visible bands. Similarly, the impact of cloud masks on both sensor data was evident and necessitated the generous removal of cloudy pixels and all saturated pixels before meaningful statistical comparison of the OLI and ETM+ sensor data could be undertaken. To remove any land cover and surface condition changes that may have occurred in the one day difference between OLI and ETM+ pixel observation, and to remove residual clouds particularly due to an infrequent OLI cloud commission error (affecting less than 0.5% of the OLI data), a filter was applied to the TOA reflectance data. The filter rejected pixel values when the relative change between the ETM+ and OLI blue reflectance was more than twice the average effect of the atmosphere quantified in a previous CONUS study (Roy et al. 2014b).
On average, considering all six months of CONUS data, the OLI TOA reflectance was greater than the ETM+ TOA reflectance, with positive but small mean differences for the visible bands, the greatest positive difference for the near-infrared (NIR) band, and intermediate mean differences for the shortwave infrared bands. Reduced major axis (RMA) of the sensor data captured this spectral pattern. The NIR, and then the two shortwave infrared bands, had RMA slopes furthest from unity and the visible bands had slopes close to unity. This is due to spectral response functions differences between the sensors which are most different in the NIR and then the shortwave infrared bands. The impact of the LEDAPS OLI and ETM+ atmospheric correction was clearly evident, acting to increase the range of the surface reflectance and NDVI. The atmospheric correction increased the magnitude of the mean between sensor reflectance differences in the visible bands and decreased the differences in the NIR and shortwave infrared bands. This spectral pattern was apparent in the RMA regression fits, the NIR and the two shortwave infrared bands had RMA slopes closer to unity than the TOA reflectance slopes, the red band RMA slopes were similar, and the green and blue band surface reflectance RMA fits were further from unity than the TOA equivalents. This is likely because at shorter visible wavelengths the atmospheric correction is less reliable, and because the ETM+ atmospheric correction is less accurate than the OLI atmospheric correction for the shorter wavelength green and blue bands (Vermote et al. this edition). The NDVI data were compared over the range 0 to 1 to reflect typical vegetated soil and vegetation surfaces. Regardless of whether TOA or surface red and NIR reflectance were used to generate the NDVI, on average the OLI NDVI was greater than the ETM+ NDVI, and the RMA intercepts and slopes were closer to zero and unity respectively for the surface NDVI than the TOA NDVI.
Ordinary least squares regressions (OLS) were used to quantify linear differences between the two Landsat sensors and the regression coefficients provided so that the user community may apply them in their own research. The TOA and surface reflectance OLS regressions had good fits for all bands (r2 values >0.7, p-values <0.0001) indicating that the between sensor spectral transformations can be applied to broadly normalize the reflectance of one sensor to the other. The OLS NDVI regressions had better fits (r2 >0.9, p-values <0.0001), indicating that the NDVI between sensor spectral transformations can be reliably applied to transform ETM+ NDVI from OLI NDVI or vice versa. Although sensor differences are quite small they may have significant impact depending on the Landsat data application.
Acknowledgements
This research was funded by the U.S. Department of Interior, U.S. Geological Survey (USGS), under grants G12PC00069 and also by the NASA Making Earth System Data Records for Use in Research Environments (MEaSUREs) program under Cooperative Agreement NNX13AJ24A. The U.S. Landsat project management and staff at USGS Earth Resources Observation and Science (EROS) Center, Sioux Falls, South Dakota, are thanked for provision of the Landsat data used in this study. The anonymous reviewers are thanked for their comments which helped to improve this paper.
References
- Ackerman S, Holz R, Frey R, Eloranta E, Maddux B, & McGill M (2008). Cloud detection with MODIS. Part II: validation. Journal of Atmospheric and Oceanic Technology, 25, 1073–1086. [Google Scholar]
- Arvidson T, Goward S, Gasch J, & Williams D (2006). Landsat-7 Long-Term Acquisition Plan. Photogrammetric Engineering & Remote Sensing, 72, 1137–1146. [Google Scholar]
- Beck HE, McVicar TR, van Dijk AI, Schellekens J, de Jeu RA, & Bruijnzeel LA (2011). Global evaluation of four AVHRR–NDVI data sets: Intercomparison and assessment against Landsat imagery. Remote Sensing of Environment, 115, 2547–2563. [Google Scholar]
- Bindschadler R, Vornberger P, Fleming A, Fox A, Mullins J, Binnie D, Paulsen SJ, Granneman B, & Gorodetzky D (2008). The Landsat image mosaic of Antarctica. Remote Sensing of Environment, 112, 4214–4226. [Google Scholar]
- Brown ME, Pinzón JE, Didan K, Morisette JT, & Tucker CJ (2006). Evaluation of the consistency of long-term NDVI time series derived from AVHRR, SPOT-vegetation, SeaWiFS, MODIS, and Landsat ETM+ sensors. IEEE Transactions on Geoscience and Remote Sensing, 44, 1787–1793. [Google Scholar]
- Chander G, Markham BL, & Helder DL (2009). Summary of current radiometric calibration coefficients for Landsat MSS, TM, ETM+, and EO-1 ALI sensors. Remote Sensing of Environment, 113, 893–903. [Google Scholar]
- Cohen WB, Maiersperger TK, Gower ST and Turner DP (2003). An improved strategy for regression of biophysical variables and Landsat ETM+ data. Remote Sensing of Environment 84:561–571. [Google Scholar]
- Dowdeswell JA, & McIntyre NF (1986). The saturation of Landsat MSS detectors over large ice masses. International Journal of Remote Sensing, 7, 151–164. [Google Scholar]
- Dozier J (1984). Snow reflectance from Landsat-4 thematic mapper. IEEE Transactions on Geoscience and Remote Sensing, 323–328. [Google Scholar]
- Feng M, Sexton JO, Huang C, Masek JG, Vermote EF, Gao F, Narasimhan R, Channan S, Wolfe RE, & Townshend JR (2013). Global surface reflectance products from Landsat: Assessment using coincident MODIS observations. Remote Sensing of Environment, 134, 276–293. [Google Scholar]
- Fensholt R, & Proud SR (2012). Evaluation of earth observation based global long term vegetation trends—Comparing GIMMS and MODIS global NDVI time series. Remote Sensing of Environment, 119, 131–147. [Google Scholar]
- Flood N (2014). Continuity of Reflectance Data between Landsat-7 ETM+ and Landsat-8 OLI, for Both Top-of-Atmosphere and Surface Reflectance: A Study in the Australian Landscape. Remote Sensing, 6, 7952–7970. [Google Scholar]
- Gallo K, Ji L, Reed B, Eidenshink J, & Dwyer J (2005). Multi-platform comparisons of MODIS and AVHRR normalized difference vegetation index data. Remote Sensing of Environment, 99, 221–231. [Google Scholar]
- Gao F, Jin Y, Xiaowen L, Schaaf CB, Strahler AH, (2002). Bidirectional NDVI and atmospherically resistant BRDF inversion for vegetation canopy, IEEE Transactions on Geoscience and Remote Sensing, 40:1269–1278. [Google Scholar]
- Gao F, He T, Masek JG, Shuai Y, Schaaf CB, & Wang Z (2014). Angular Effects and Correction for Medium Resolution Sensors to Support Crop Monitoring. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 7, 4480–4489. [Google Scholar]
- Hall DK, Riggs GA, & Salomonson VV (1995). Development of methods for mapping global snow cover using moderate resolution imaging spectroradiometer data. Remote Sensing of Environment, 54(2), 127–140. [Google Scholar]
- Hansen M, Egorov A, Potapov P, Stehman S, Tyukavina A, Turubanova S, Roy D, Goetz S, Loveland T, & Ju J (2014). Monitoring conterminous United States (CONUS) land cover change with web-enabled landsat data (WELD). Remote Sensing of Environment, 140, 466–484. [Google Scholar]
- Holben BN (1986). Characteristics of maximum-value composite images from temporal AVHRR data. International Journal of Remote Sensing, 7, 1417–1434. [Google Scholar]
- Huang C, Goward SN, Masek JG, Thomas N, Zhu Z, & Vogelmann JE (2010). An automated approach for reconstructing recent forest disturbance history using dense Landsat time series stacks. Remote Sensing of Environment, 114, 183–198. [Google Scholar]
- Huete A, Didan K, Miura T, Rodriguez EP, Gao X, & Ferreira LG (2002). Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sensing of Environment, 83(1), 195–213. [Google Scholar]
- Irish RR (2000). Landsat 7 automatic cloud cover assessment. In Shen SS, & Descour MR (Eds.), Proc. SPIE 4049, Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI (pp. 348–355). Orlando, FL. [Google Scholar]
- Irish RR, Barker JL, Goward SN, & Arvidson T (2006). Characterization of the Landsat-7 ETM+ automated cloud-cover assessment (ACCA) algorithm. Photogrammetric Engineering & Remote Sensing, 72, 1179–1188. [Google Scholar]
- Irons JR, Dwyer JL, & Barsi JA (2012). The next Landsat satellite: The Landsat data continuity mission. Remote Sensing of Environment, 122, 11–21. [Google Scholar]
- Irons JR, & Masek JG (2006). Requirements for a Landsat data continuity mission. Photogrammetric Engineering and Remote Sensing, 72, 1102–1108. [Google Scholar]
- Ju J, & Roy DP (2008). The availability of cloud-free Landsat ETM+ data over the conterminous United States and globally. Remote Sensing of Environment, 112, 1196–1211. [Google Scholar]
- Ju J, Roy DP, Vermote E, Masek J, & Kovalskyy V (2012). Continental-scale validation of MODIS-based and LEDAPS Landsat ETM+ atmospheric correction methods. Remote Sensing of Environment, 122, 175–184. [Google Scholar]
- Justice CO, Vermote E, Townshend JR, Defries R, Roy DP, Hall DK, Salomonson VV, Privette JL, Riggs G, & Strahler A (1998). The Moderate Resolution Imaging Spectroradiometer (MODIS): Land remote sensing for global change research. IEEE Transactions on Geoscience and Remote Sensing, 36, 1228–1249. [Google Scholar]
- Karnieli A, Ben-Dor E, Bayarjargal Y, & Lugasi R (2004). Radiometric saturation of Landsat-7 ETM+ data over the Negev Desert (Israel): problems and solutions. International Journal of Applied Earth Observation and Geoinformation, 5(3), 219–237. [Google Scholar]
- Kaufman YJ (1987). The effect of subpixel clouds on remote sensing. International Journal of Remote Sensing, 8, 839–857. [Google Scholar]
- Ke Y, Im J, Lee J, Gong H, & Ryu Y (2015). Characteristics of Landsat 8 OLI-derived NDVI by comparison with multiple satellite sensors and in-situ observations. Remote Sensing of Environment. 164, 298–313. [Google Scholar]
- Kennedy RE, Yang Z, & Cohen WB (2010). Detecting trends in forest disturbance and recovery using yearly Landsat time series: 1. LandTrendr—Temporal segmentation algorithms. Remote Sensing of Environment, 114, 2897–2910. [Google Scholar]
- Kokhanovsky AA, & Breon FM (2012). Validation of an analytical snow BRDF model using PARASOL multi-angular and multispectral observations. IEEE Geoscience and Remote Sensing Letters, 9, 928–932. [Google Scholar]
- Kotchenova SY, Vermote EF, Matarrese R, & Klemm FJ Jr (2006). Validation of a vector version of the 6S radiative transfer code for atmospheric correction of satellite data. Part I: Path radiance. Applied Optics, 45, 6762–6774. [DOI] [PubMed] [Google Scholar]
- Kovalskyy V, & Roy DP (2015). A One Year Landsat 8 Conterminous United States Study of Cirrus and Non-Cirrus Clouds. Remote Sensing, 7, 564–578. [Google Scholar]
- Lee DS, Storey JC, Choate MJ, & Hayes RW (2004). Four years of Landsat-7 on-orbit geometric calibration and performance. IEEE Transactions on Geoscience and Remote Sensing, 42, 2786–2795. [Google Scholar]
- Li F, Jupp DL, Reddy S, Lymburner L, Mueller N, Tan P, & Islam A (2010). An evaluation of the use of atmospheric and BRDF correction to standardize Landsat data. IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, 3, 257–270. [Google Scholar]
- Liu Q & Huete A (1995). A feedback based modification of the NDVI to minimize canopy background and atmospheric noise. IEEE Transactions on Geoscience and Remote Sensing, 33(2), 457–465. [Google Scholar]
- Loveland TR, & Dwyer JL (2012). Landsat: Building a strong future. Remote Sensing of Environment, 122, 22–29. [Google Scholar]
- Markham BL, Storey JC, Williams DL, & Irons JR (2004). Landsat sensor performance: history and current status. IEEE Transactions on Geoscience and Remote Sensing, 42, 2691–2694. [Google Scholar]
- Markham B, Goward S, Arvidson T, Barsi J, & Scaramuzza P (2006). Landsat-7 long-term acquisition plan radiometry-evolution over time. Photogrammetric Engineering & Remote Sensing, 72, 1129–1135. [Google Scholar]
- Markham BL, & Helder DL (2012). Forty-year calibrated record of earth-reflected radiance from Landsat: A review. Remote Sensing of Environment, 122, 30–40. [Google Scholar]
- Markham B, Barsi J, Kvaran G, Ong L, Kaita E, Biggar S, Czapla-Myers J, Mishra N, & Helder D (2014). Landsat-8 Operational Land Imager radiometric calibration and stability. Remote Sensing, 6, 12275–12308. [Google Scholar]
- Masek JG, Vermote EF, Saleous NE, Wolfe R, Hall FG, Huemmrich KF, Gao F, Kutler J, & Lim T-K (2006). A Landsat surface reflectance dataset for North America, 1990–2000. IEEE Geoscience and Remote Sensing Letters, 3, 68–72. [Google Scholar]
- Masuoka E, Roy D, Wolfe R, Morisette J, Sinno S, Teague M, Saleous N, Devadiga S, Justice C, & Nickeson J (2011). MODIS Land Data Products: Generation, Quality Assurance and Validation In Ramachandran B, Justice CO, & Abrams MJ (Eds.), Land Remote Sensing and Global Environmental Change (pp. 509–531). New York: Springer. [Google Scholar]
- McDonald AJ, Gemmell FM, Lewis PE (1998). Investigation of the utility of spectral vegetation indices for determining information on coniferous forest, Remote Sensing of Environment, 66, 250–272. [Google Scholar]
- Maiersperger TK, Scaramuzza PL, Leigh L, Shrestha S, Gallo KP, Jenkerson CB, & Dwyer JL (2013). Characterizing LEDAPS surface reflectance products by comparisons with AERONET, field spectrometer, and MODIS data. Remote Sensing of Environment, 136, 1–13. [Google Scholar]
- Miura T, Huete A, & Yoshioka H (2006). An empirical investigation of cross-sensor relationships of NDVI and red/near-infrared reflectance using EO-1 Hyperion data. Remote Sensing of Environment, 100, 223–236. [Google Scholar]
- Montanaro M, Gerace A, Lunsford A, & Reuter D (2014). Stray light artifacts in imagery from the Landsat 8 Thermal Infrared Sensor. Remote Sensing, 6, 10435–10456. [Google Scholar]
- Moran M, Clarke T, Inoue Y, & Vidal A (1994). Estimating crop water deficit using the relation between surface-air temperature and spectral vegetation index. Remote Sensing of Environment, 49, 246–263. [Google Scholar]
- Morfitt R, Barsi J, Levy R, Markham B, Micijevic E, Ong L, Scaramuzza P, Vanderwerff K (2015). Landsat-8 Operational Land Imager (OLI) radiometric performance on-orbit. Remote Sensing, 7(2), 2208–2237. [Google Scholar]
- Myneni R, Tucker C, Asrar G, & Keeling C (1998). Interannual variations in satellite-sensed vegetation index data from 1981 to 1991. Journal of Geophysical Research: Atmospheres (1984–2012), 103, 6145–6160. [Google Scholar]
- Nagol JR, Sexton JO, Kim D-H, Anand A, Morton D, Vermote E, & Townshend JR (2015). Bidirectional effects in Landsat reflectance estimates: Is there a problem to solve? ISPRS Journal of Photogrammetry and Remote Sensing, 103, 129–135. [Google Scholar]
- Norman JM, Divakarla M, & Goel NS (1995). Algorithms for extracting information from remote thermal-IR observations of the earth’s surface. Remote Sensing of Environment, 51, 157–168. [Google Scholar]
- Oreopoulos L, Cahalan RF, Marshak A, & Wen G (2000). A new normalized difference cloud retrieval technique applied to Landsat radiances over the Oklahoma ARM site. Journal of Applied Meteorology, 39, 2305–2321. [Google Scholar]
- Ouaidrari H, & Vermote EF (1999). Operational atmospheric correction of Landsat TM data. Remote Sensing of Environment, 70, 4–15. [Google Scholar]
- Painter TH, Rittger K, McKenzie C, Slaughter P, Davis RE, & Dozier J (2009). Retrieval of subpixel snow covered area, grain size, and albedo from MODIS. Remote Sensing of Environment, 113, 868–879. [Google Scholar]
- Pedelty J, Devadiga S, Masuoka E, Brown M, Pinzon J, Tucker C, Roy D, Ju J, Vermote E, et al. Generating a long-term land data record from the AVHRR and MODIS Instruments. Geoscience and Remote Sensing Symposium, 2007. IGARSS 2007, Barcelona (2007), pp. 1021–1025 [Google Scholar]
- Pinzon JE, & Tucker CJ (2014). A non-stationary 1981–2012 AVHRR NDVI3g time series. Remote Sensing, 6, 6929–6960. [Google Scholar]
- Roberts G (2001). A review of the application of BRDF models to infer land cover parameters at regional and global scales. Progress in Physical Geography, 25, 483–511. [Google Scholar]
- Roujean J-L, Leroy M, & Deschamps P-Y (1992). A bidirectional reflectance model of the Earth’s surface for the correction of remote sensing data. Journal of Geophysical Research: Atmospheres, 97, 20455–20468. [Google Scholar]
- Roy DP (1997). Investigation of the maximum normalized difference vegetation index (NDVI) and the maximum surface temperature (Ts) AVHRR compositing procedures for the extraction of NDVI and Ts over forest. International Journal of Remote Sensing, 18, 2383–2401. [Google Scholar]
- Roy DP, Borak J, Devadiga S, Wolfe R, Zheng M, Descloitres J, (2002). The MODIS land product quality assessment approach, Remote Sensing of Environment, 83:62–76. [Google Scholar]
- Roy DP, Ju J, Lewis P, Schaaf C, Gao F, Hansen M, & Lindquist E (2008). Multi-temporal MODIS–Landsat data fusion for relative radiometric normalization, gap filling, and prediction of Landsat data. Remote Sensing of Environment, 112, 3112–3130. [Google Scholar]
- Roy DP, Ju J, Kline K, Scaramuzza PL, Kovalskyy V, Hansen M, Loveland TR, Vermote E, & Zhang C (2010). Web-enabled Landsat Data (WELD): Landsat ETM+ composited mosaics of the conterminous United States. Remote Sensing of Environment, 114, 35–49. [Google Scholar]
- Roy DP, Wulder M, Loveland T, Woodcock C, Allen R, Anderson M, Helder D, Irons J, Johnson D, Kennedy R, Scambos TA, Schaaf CB, Schott JR, Sheng Y, Vermote EF, Belward AS, Bindschadler R, Cohen WB, Gao F, Hipple JD, Hostert P, Huntington J, Justice CO, Kilic A, Kovalskyy V, Lee ZP, Lymburner L, Masek JG, McCorkel J, Shuai Y, Trezza R, Vogelmann J, Wynne RH, & Zhu Z (2014a). Landsat-8: Science and product vision for terrestrial global change research. Remote Sensing of Environment, 145, 154–172. [Google Scholar]
- Roy DP, Qin Y, Kovalskyy V, Vermote E, Ju J, Egorov A, Hansen M, Kommareddy I, & Yan L (2014b). Conterminous United States demonstration and characterization of MODIS-based Landsat ETM+ atmospheric correction. Remote Sensing of Environment, 140, 433–449. [Google Scholar]
- Roy DP, Zhang HK, Ju J, Gomez-Dans JL, Lewis PE, Schaaf CB, Sun Q, Li J, Huang H, Kovalskyy V, A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance, Remote Sensing of Environment. In review. [Google Scholar]
- Sheng C, Jian Z, Mullens E, Yang H, Behrangi A, Yudong T, Xiao-Ming H, Junjun H, Zengxin Z, & Xinhua Z (2015). Mapping the precipitation type distribution over the contiguous United States using NOAA/NSSL national multi-sensor mosaic QPE. IEEE Transactions on Geoscience and Remote Sensing, 53, 4434–4443. [Google Scholar]
- Smith RJ (2009). Use and misuse of the reduced major axis for line-fitting. American Journal of Physical Anthropology, 140, 476–486. [DOI] [PubMed] [Google Scholar]
- Steven MD, Malthus TJ, Baret F, Xu H, & Chopping MJ (2003). Intercalibration of vegetation indices from different sensor systems. Remote Sensing of Environment, 88, 412–422. [Google Scholar]
- Storey J, Choate M, & Lee K (2014). Landsat 8 Operational Land Imager On-Orbit Geometric Calibration and Performance. Remote Sensing, 6, 11127–11152. [Google Scholar]
- Tackett JL, & Di Girolamo L (2009). Enhanced aerosol backscatter adjacent to tropical trade wind clouds revealed by satellite-based lidar. Geophysical Research Letters, 36. [Google Scholar]
- Tanre D, Herman M, & Deschamps P (1981). Influence of the background contribution upon space measurements of ground reflectance. Applied Optics, 20, 3676–3684. [DOI] [PubMed] [Google Scholar]
- Teillet P, Barker J, Markham B, Irish R, Fedosejevs G, & Storey J (2001). Radiometric cross-calibration of the Landsat-7 ETM+ and Landsat-5 TM sensors based on tandem data sets. Remote Sensing of Environment, 78, 39–54. [Google Scholar]
- Trenberth KE, Anthes RA, Belward A, Brown O, Habermann T, Karl TR, Running S, Ryan B, Tanner M & Wielicki B (2013). Challenges of a sustained climate observing system in “Climate Science for Serving Society: Research, Modeling and Prediction Priorities. Asrar GR and Hurrell JW, Eds. Springer, 484 p. [Google Scholar]
- Trishchenko AP, Cihlar J, & Li Z (2002). Effects of spectral response function on surface reflectance and NDVI measured with moderate resolution satellite sensors. Remote Sensing of Environment, 81(1), 1–18. [Google Scholar]
- Tucker CJ, Pinzon JE, Brown ME, Slayback DA, Pak EW, Mahoney R, Vermote EF, & El Saleous N (2005). An extended AVHRR 8-km NDVI dataset compatible with MODIS and SPOT vegetation NDVI data. International Journal of Remote Sensing, 26, 4485–4498. [Google Scholar]
- USGS, Landsat Data Continuity Mission Level 1 (L1) Data Format Control Book (DFCB), LDCM-DFCB-004, Version 6.0, USGS EROS, 2012, Sioux Falls, USA, url: http://landsat.usgs.gov/documents/LDCM-DFCB-004.pdf [Google Scholar]
- USGS, Landsat 8 (L8) Data Users Handbook, 2015, LSDS-1574, Version 1.0, USGS EROS, 2015, Sioux Falls, USA, url: https://landsat.usgs.gov/documents/Landsat8DataUsersHandbook.pdf [Google Scholar]
- Ustin SL, Roberts DA, Pinzon J, Jacquemoud S, Gardner M, Scheer G, Castaneda CM, & Palacios-Orueta A (1998). Estimating canopy water content of chaparral shrubs using optical methods. Remote Sensing of Environment, 65, 280–291. [Google Scholar]
- Vermote EF, Tanré D, Deuze J-L, Herman M, & Morcette J-J (1997). Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Transactions on Geoscience and Remote Sensing, 35, 675–686. [Google Scholar]
- Vermote EF, & Roy DP (2002). Land surface hot-spot observed by MODIS over Central Africa. International Journal of Remote Sensing, 23, 2141–2143. [Google Scholar]
- Vermote EF, El Saleous NZ, Justice CO (2002). Atmospheric correction of MODIS data in the visible to middle infrared: first results. Remote Sensing of Environment, 83, 97–111. [Google Scholar]
- Vermote EF and Kotchenova S, Atmospheric correction for the monitoring of land surfaces, Journal of Geophysical Research, 113 (2008), p. D23S90. [Google Scholar]
- Vermote EF, Justice CO, Claverie M, Franch B (2015). Analysis of the performance of the Landsat 8/OLI land surface reflectance product, Remote Sensing of Environment. Submitted. WWW1, http://landsathandbook.gsfc.nasa.gov/inst_cal/prog_sect8_2.html, Landsat 7 Science Data User Handbook, Chapter 8 Pre-Launch, Last accessed May 4th 2015. [Google Scholar]
- WWW2, http://landsat.gsfc.nasa.gov/?p=5779, Landsat 8 Pre-launch OLI Performance Last accessed May 4th 2015.
- Zhang HK and Roy DP, (2015) Computationally inexpensive Landsat 8 Operational Land Imager (OLI) pansharpening, Remote Sensing. Submitted. [Google Scholar]
- Zhang HK, Roy DP, Kovalskyy V, (2015) Optimal solar geometry definition for global Landsat time series bi-directional reflectance normalization, IEEE Transactions on Geoscience and Remote Sensing. In Press. [Google Scholar]
- Zhu Z, & Woodcock CE (2014). Continuous change detection and classification of land cover using all available Landsat data. Remote Sensing of Environment, 144, 152–171. [Google Scholar]