Abstract
As a key variable in the climate system, soil moisture (SM) plays a central role in the earth’s terrestrial water, energy, and biogeochemical cycles through its coupling with surface latent heat flux (LH). Despite the need to accurately represent SM/LH coupling in earth system models, we currently lack quantitative, observation-based, and unbiased estimates of its strength. Here, we utilize the triple collocation (TC) approach introduced in Crow et al. (2015) to SM and LH products obtained from multiple satellite remote sensing platforms and land surface models (LSMs) to obtain unbiased global maps of SM/LH coupling strength. Results demonstrate that, relative to coupling strength estimates acquired directly from remote sensing-based datasets, the application of TC generally enhances estimates of warm-season SM/LH coupling, especially in the western United States, the Sahel, Central Asia, and Australia. However, relative to triple collocation estimates, LSMs (still) over-predict SM/LH coupling strength along transitional climate regimes between wet and dry climates, such as the central Great Plains of North America, India, and coastal Australia. Specific climate zones with biased relations in LSMs are identified to geographically focus the re-examination of LSM parameterizations. TC-based coupling strength estimates are robust to our choice of LSM contributing SM and LH products to the TC analysis. Given their robustness, TC-based coupling strength estimates can serve as an objective benchmark for investigating model predicted SM/LH coupling.
Plain Language Summary
Physical models describing land-atmosphere coupling have been developed to help better understand the impact of local, regional, and global-scale climate on weather and the water cycle. However, verifying the accuracy of these models is challenging over sparsely instrumented areas. Here, the strength of land-atmosphere coupling between soil moisture and terrestrial evapotranspiration is examined by combining multiple global-scale remote sensing and modeling products into a unified analysis. This analysis is unique in that it can be conducted globally and is unbiased by the presence of random errors in the remote sensing products. As such it provides the first robust estimate of the degree to which soil moisture and evapotranspiration are linked. Results show strong soil moisture/evapotranspiration coupling over the Western United States, the African Sahel, Central Asia, and Australia. However, they also demonstrate that most existing models are still over-predicting this coupling along transitional regions between wet and dry climates (like the Central Great Plains of North America, India, and coastal Australia). This work will help improve the representation of land-atmosphere coupling in models used to obtain future climate projections.
1. Introduction
Soil moisture (SM), through its direct limiting effect on surface latent heat flux (LH), modulates feedbacks between the land surface and the lower atmosphere (Koster et al., 2004; Guo et al., 2006; Jung et al., 2010; Combe et al., 2016). For regions with a strong causal relationship between SM and surface LH, this coupling can significantly affect terrestrial water, energy, and biochemical cycles in a changing climate (Seneviratne et al., 2010, 2013). Despite the widespread application of land surface models (LSMs) to conceptually diagnose this coupling relationship (Van den Hurk et al., 2011), there is no clear consensus on the true strength of terrestrial SM/LH coupling across the globe. Moreover, global observation-based quantification and validation of this relationship within LSMs have not yet been attempted (Dirmeyer et al., 2006a, 2009, 2018; Best et al., 2015).
The limiting effect of SM on LH is generally characterized as a first-order causal relationship within LSMs (Dirmeyer et al., 2006b). Validation practices of a model’s ability to characterize this coupling are commonly based on sampling mutual information proxies (e.g., correlation coefficient or the coupling index proposed by Dirmeyer et al., 2011) acquired from collocated SM and LH time series observations (Dirmeyer et al., 2009, 2018; Loew et al., 2017). However, these proxies are usually biased low due to the existence of random measurement errors in any instrument-based observation (i.e., remotely-sensed retrievals or ground measurements) (Crow et al., 2015; Findell et al., 2015) and scale representative differences between local observations and a (coarser-scale) modeling grid (Dirmeyer et al., 2018). Therefore, unbiased, observation-based estimates of SM/LH coupling strength are difficult to acquire.
Recent progress in triple collocation (TC) analysis (McColl et al., 2014; Gruber et al., 2016a) offers a strategy for deriving unbiased estimates of SM/LH coupling strength. Specifically, if triplets of LH and SM can be obtained from mutually independent sources, TC-based approaches allow us to estimate the variance of random errors affecting all three estimates of both LH and SM. This information, in turn, can be used to compensate sampled estimates of SM/LH coupling strength for the (degrading) impact of these errors on sampled correlations between SM and LH.
Using collocated SM and LH estimates obtained from ground measurements, remote sensing (RS) and a LSM, Crow et al. (2015) provided a proof-of-concept for the robust estimation of the SM/LH coupling strength via TC analysis. However, Crow et al. (2015) focused only on a handful of sites across the United States where long-term, high-quality, ground-based SM and LH measurements are available. Moving from their site-based approach to a continuous global investigation requires the simultaneous availability of two satellite-based products for SM and LH that are sufficiently independent for a TC analysis. Fortunately, recent advances in remotely-sensed SM using passive and active microwave sensors (Kumar et al., 2018) and RS-based LH using satellite-based land surface temperature (LST) products obtained from both thermal-infrared and microwave sensors (Anderson et al., 2011; Holmes et al., 2018) provide such an opportunity.
Bolstered by this newly developed TC method, and the simultaneous availability of remotely-sensed SM and LH datasets from multiple independent sources, this work seeks to obtain unbiased global estimates of terrestrial SM/LH coupling strength. Section 2 reviews the TC approach previously developed by Crow et al. (2015) as well as the RS- and LSM-based datasets used to construct the data triplets required by this approach. Results are presented in Section 3 and discussed in Section 4. Main conclusions are then summarized in Section 5.
2. Method and Datasets
2.1. Triple Collocation-based Coupling Strength Metric
For geophysical variables with at least three independent estimates, the mutually uncorrelated random error variances contained within these estimates can be determined through the triple collocation (TC) method (Stoffelen, 1998; McColl et al., 2014; Gruber et al., 2016a). This approach assumes each of the three estimates (Xi) follows a linear error model:
| (1) |
where α and β are temporally-constant additive and multiplicative biases, and ε is zero-mean random error which is independent of the truth T, i.e., error orthogonality. Based on these assumptions, the variances and the covariances for the three datasets can be written as:
| (2) |
| (3) |
where i, j ∈ [1, 2, 3], and the operators Cov[·] and Var[·] denote the covariance and temporal variance, respectively. In TC applications, the three datasets are usually assumed to have mutually independent errors and therefore Cov[εi, εj] = 0 when i ≠ j. Thus, from (2) and (3), the true signal variance (using one dataset as a reference) and random error variances of each dataset can be derived as:
| (4) |
| (5) |
where i, j, k ∈ [1, 2, 3] and i ≠ j ≠ k. Here, Xi is chosen as the reference to obtain the true signal variance Var[T]i.
Instead of estimating the random error variance of an unknown signal observed by three datasets as described above, Crow et al. (2015) extended TC to estimate the coupling strength between two different geophysical variables, namely SM and LH. The basic assumptions are same as in classic TC, that is, all measurements are linearly related to their corresponding true values
| (6) |
| (7) |
where α and β represent additive and multiplicative systematic errors of each dataset with regard to the (unknown) truth True, ε denotes zero-mean random error with temporally constant variance, and A and B represent three independent estimates of SM and LH, respectively. By further assuming the mutual independence of random errors ε within each triplet and the orthogonality of all errors with respect to its respective truth, the coefficient of determination R2 between two different geophysical variables can be solved as:
| (8) |
where i ≠ j ≠ k and l ≠ m ≠ n. The advantage of (8), as opposed to the direct sampling of R2 between any two SM and LH products, is that (8) is unbiased in the presence of random observational errors. Therefore, it provides a means for estimating true coupling strength between SM and LH using error-prone data (e.g., remote-sensing retrievals of SMA and LHB). A more detailed derivation for (8) can be found in Crow et al. (2015).
Note that an arbitrary “reference pair” of SMi and LHl products is applied within the numerator of (8). If all such pairings are free from cross-correlated estimation errors (Cov[εi, εl] = 0), the use of any single pair should not bias correlation results. Thus, considering all possible combinations of SMi and LHl from each corresponding triplet, nine estimates of R2[SMTrue, LHTrue]i,l can be obtained in total from (8). However, certain reference pairs may possess correlated LH and SM errors, specifically when both SMi and LHl are obtained from the same LSM. Therefore, a robust final estimate of R2[SMTrue, LHTrue] can be achieved by taking the median of results obtained from reference pairs deemed to include mutually independent SM and LH errors. The reference pairs used here are fully described below in Section 2.5.
In real-case applications, Crow et al. (2015) acquired their SM and LH triplets from mutually independent ground-, RS- and LSM-based sources. However, this strategy limited the geographic extent of their approach to only a handful of heavily instrumented sites in the United States. Therefore, a key challenge is substituting new remotely-sensed sources of LH and SM estimates into the analysis (to eliminate Crow et al. (2015)’s reliance on ground data) without violating the error independence assumption on which TC is based. More detailed explanations are included in Section 3.1 and the impact of potential violation of assumptions will be discussed in Section 4.1.
2.2. Remotely-sensed Soil Moisture Datasets
Given that the physical mechanism for retrieving SM using active scatterometer versus passive radiometer varies considerably, simultaneous SM retrievals acquired from both active and passive microwave sensors, in combination with LSM estimates, are commonly utilized together in TC applications (Draper et al., 2013; Su et al., 2014; Gruber et al., 2016a).
Here, global passive microwave (PMW) SM retrievals were obtained from the European Space Agency (ESA) Climate Change Initiative (CCI) product version 03.2 (Dorigo et al., 2017; Dorigo et al., 2018) between 1978 and 2015 at 0.25° spatial resolution (https://www.esa-landcover-cci.org/). This product was generated using a rigorous blending scheme that combines all Level 2 SM retrievals from available sensors into a (single) weighted optimal estimate using their corresponding error variances (Gruber et al., 2017). All PMW SM retrievals were derived via the same Land Parameter Retrieval Model (LPRM, Owe et al., 2008) that interprets brightness temperature measurements of several sensors. From 2007 onwards, this record includes: the Advanced Microwave Scanning Radiometer-Earth Observing System (AMSR-E) on board the NASA EOS Aqua satellite (Njoku et al., 2003), WindSat on board the Coriolis satellite (Parinussa et al., 2012), the Microwave Imaging Radiometer using Aperture Synthesis (MIRAS) on board Soil Moisture and Ocean Salinity (SMOS) mission (Kerr et al., 2010), and AMSR2 on board Global Change Observation Mission-Water (GCOM-W1) (Parinussa et al., 2015). Considering that more isothermal conditions in near-surface temperature profiles benefit the retrieval of surface soil moisture from passive microwave sensors, only night-time or early-morning retrievals were used in the merged ESA CCI-PASSIVE product (Liu et al., 2012). Note that the quality flags associated with the SM retrievals from each individual sensor were considered to screen for frozen soil conditions and dense vegetation (where the frequency dependent vegetation optical depth values >0.8 indicate that the canopy is too opaque for interpretation of the soil emission). The merged ESA CCI-PASSIVE SM product has been found to be superior to any single-sensor product (Dorigo et al., 2017).
Scatterometer-based SM retrievals were acquired using the Vienna University of Technology (TU-Wien) change detection algorithm (Naeimi et al., 2009) to C-band (5.255 GHz) Advanced SCATterometer (ASCAT) radar instrument on board the ESA MetOp satellite. The Level 2 SM product can be accessed from the EUropean organization for the exploitation of METerological SATellites (EUMETSAT) Satellite Application Facility on Support to Operational Hydrology and Water Management (H-SAF) website (http://hsaf.meteoam.it/soil-moisture.php). This product has a spatial resolution of 25×25 km with a grid spacing of 12.5 km and was resampled onto a regular 0.25° grid using an inverse-distance-weighted-averaging approach. Active microwave (AMW) SM retrievals from both overpasses at 9:30 a.m./p.m. local solar time were averaged into a daily product from January 2007 onwards. Retrievals were also filtered for frozen soil conditions based on auxiliary flag information.
2.3. Remote Sensing-based Latent Heat Flux Datasets
Diagnostic algorithms are commonly implemented for the derivation of LH estimates from RS data using LST derived from thermal infrared (TIR) imagery. Using the core framework of the two-source energy balance algorithm, LH retrievals can be derived from the Atmosphere Land Exchange Inverse (ALEXI) model using TIR-based LST from both geostationary and polar-orbiting satellite sensors. Here, continuous weekly ALEXI-TIR LH retrievals were derived at a global spatial resolution of 0.05° from 2003 to 2013 using clear-sky LST retrievals acquired from the Moderate Resolution Imaging Spectroradiometer (MODIS) TIR sensor. For additional details, see Hain and Anderson (2017). Hereinafter, this TIR-based approach will be referred to as the “ALEXI-TIR” algorithm.
LST can also be derived via passive microwave observations — opening up the possibility for deriving a new source of RS-based LH estimates. To this end, Holmes et al. (2015) re-constructed the LST diurnal cycle based on Ka-band brightness temperature observations acquired from a constellation of microwave satellites, including AMSR-E, AMSR-2, and WindSat. This new source of diurnal LST information was then used to run the ALEXI energy balance model to generate MW-based LH estimates at 0.25° global spatial resolution (Holmes et al., 2018). Hereinafter, this MW-based approach will be referred to as the “ALEXI-MW” algorithm.
Meteorological inputs for both the ALEXI-TIR and ALEXI-MW algorithms were acquired from the National Centers for Environmental Prediction (NCEP) Climate Forecast System Reanalysis (CFSR) and CFS-v2 product (Saha et al., 2010; 2014). Surface albedo and leaf area index were extracted from MODIS MOD43C and MOD15A products, respectively. Note that the most recent global ALEXI-TIR and ALEXI-MW LH products are at a weekly temporal resolution from 2003 to 2013. Recent comparisons of ALEXI-TIR and ALEXI-MW products against in-situ Fluxnet measurements demonstrated satisfactory accuracies in both products (Holmes et al., 2018). Thus, continuous weekly ALEXI-TIR and ALEXI-MW products were used without further masking.
Despite the application of an identical ALEXI modeling framework, LST inputs for ALEXI-TIR and ALEXI-MW (i.e., their key input) are derived from distinct spectral regimes with statistically independent error characteristics (Li et al., 2006). Therefore, our assumption is that LH estimates derived from different spectral bands will be mutually independent and are therefore suitable for application within the same TC triplet. Additional support for this assumption will be presented below in Section 3.1.
2.4. Land Surface Models
The Global Land Data Assimilation System (GLDAS) is designed to produce global fields of terrestrial water and energy fluxes and storages by incorporating various satellite and ground-based observations into offline simulations of advanced LSMs (Rodell et al., 2004), including Noah version 3.3 (Chen et al., 1996, Ek et al., 2003), Community Land Model (CLM) version 2.0 (Dai et al., 2003), Catchment Land Surface Model (CLSM) F2.5 (Koster et al., 2000), and the Variable Infiltration Capacity (VIC) (Liang et al., 1994) model run in water balance mode. From year 2001 onwards, the meteorological forcing datasets of GLDAS-1 and GLDAS-2 are mainly combined from National Oceanic and Atmosphere Administration (NOAA)/Global Data Assimilation System atmospheric analysis fields, the spatially and temporally disaggregated NOAA Climate Precipitation Center Merged Analysis of Precipitation (CMAP) and Global Precipitation Climatology Project (GPCP) precipitation fields. Additionally, radiation fields are derived using the Air Force Weather Agency’s AGRicultural METeorological modeling system (Rodell et al., 2004). GLDAS-2 Noah and CLSM simulations were run at a spatial resolution of 0.25°, and GLDAS-1 CLM and VIC models were at 1°.
Here, each pair of SM and LH fluxes from different LSM simulations was individually averaged from 3-hourly model simulations to daily values. Note that soil layer depths vary across LSMs. In particular, soil moisture estimates from the top first layer were extracted for Noah, VIC and CLSM using their 0–0.1, 0–0.1 and 0–0.02 m soil layers, respectively. For CLM, the top three soil layers were averaged to a total depth of 0–0.091 m.
2.5. Data Pre- and Post-processing
Before estimating SM/LH coupling strength, both RS- and LSM-based fluxes were pre-processed with consideration of their native spatial, temporal and vertical resolutions (listed in Table 1). First, all RS-based SM and LH retrievals were spatially resampled onto a regular 0.25° grid, and 1.00° LSM-based fluxes were spatially downscaled onto the same 0.25° grid. Second, due to their limited soil penetration capability, remotely-sensed SM retrievals depict a shallower vertical depth support than LSM-based SM estimations, usually on the order of 0 – 5 cm. Here, the exponential filtering approach developed by Albergel et al. (2008) was applied to effectively increase the vertical representation of daily RS-based SM time series by dampening its high-frequency signals. The key time scale parameter required by the filter was assumed to be temporally constant and tuned for each 0.25° grid using the Noah first layer (0–0.1 m) SM product as a comparison dataset. Finally, as mentioned above, the most recent global ALEXI-TIR and ALEXI-MW LH products are weekly summations. As a result, all RS- and LSM-based SM and LH fluxes were averaged from daily to weekly values after the aforementioned processing. Constrained by the temporal coverage of RS-based SM and LH retrievals, our analysis focused on the period 2007 to 2013.
Table 1.
Basic information for SM and LH used in the analysis.
| Product Name | Key Sources | Spatial Resolution | Temporal Resolution | Temporal Range |
|---|---|---|---|---|
| PMW SM (ESA CCI PASSIVE) | AMSR-E LPRM SM AMSR-2 LPRM SM SMOS LPRM SM | 0.25° | Daily | 1978–2015 |
| AMW SM (EUMETSAT) | ASCAT TU-Wien SM | 25 km | Daily | 2007 onwards |
| ALEXI-TIR | MODIS LST | 0.05° | Weekly | 2003–2013 |
| ALEXI-MW | MW-LST (Section 2.3) | 0.25° | Weekly | 2003–2013 |
| GLDAS-2.1 NOAH | GDAS, GPCP, AGRMET (Section 2.4) | 0.25° | 3-hourly | 2000 onwards |
| GLDAS-1 VIC | GDAS, GPCP, AGRMET | 1.0° | 3-hourly | 1979 onwards |
| GLDAS-1 CLM | GDAS, GPCP, AGRMET | 1.0° | 3-hourly | 1979 onwards |
| GLDAS-2.0 CLSM | Princeton Meteorological Forcing | 0.25° | Daily | 1948–2014 |
Following Crow et al. (2015), time series of SM and LH products were transformed into temporal ranks before applying (8), which yields coefficients of determination in Spearman rank space. As long as the relationship between SM and LH remains monotonically increasing, these coefficients will not be impacted by nonlinearity in functional dependence of LH on SM. In addition, given the limited number of weeks (maximum 364) in which all SM and LH data were simultaneously available from January 2007 to December 2013, the coupling strength metric obtained from (8) was applied for all possible combinations of SM/LH reference pairs to reduce sampling uncertainty. In total, eight different estimates of R2[SMTrue, LHTrue]i,l can be acquired: 1) SMPMW/LHTIR, 2) SMPMW/LHMW, 3) SMPMW/LHLSM, 4) SMAMW/LHTIR, 5) SMAMW/LHMW, 6) SMAMW/LHLSM, 7) SMLSM/LHTIR, and 8) SMLSM/LHMW. This list couples all possible SM/LH combinations with the notable exception of SMLSM/LHLSM since error cross-correlation is expected in SM and LH products generated by the same LSM. Subsequently, the median of all eight estimates was utilized as the robust estimate (Huber, 2011) of true SM/LH coupling strength R2[SMTrueLHTrue]. Uncertainty due to limited temporal sampling was quantified via a 500-member boot-strapping analysis (Efron and Tibshirani, 1994). Each median replicate was obtained by sampling half of the original sample size with replacement for all eight reference pairs. The standard deviation of boot-strapped replicates was then used to characterize the sampling error.
Only warm-season SM/LH coupling results were considered in the analysis. This required differential seasonal filtering in various latitude bands which was empirically defined to be comparable with other similar climate studies (Dirmeyer, 2011; Phillips and Klein, 2014; Seneviratne et al., 2013; Teuling et al., 2005). For tropical regions (23.25° N to 23.25° S), all 12 months were included. In the subtropics (23.25° N to 35° N and 23.25° S to 35° S), results were based on either May–October data (in the Northern Hemisphere) or November–April data (in the Southern Hemisphere). In temperate zones (>35° N and >35 ° S), results were based on June-July-August data (in the Northern Hemisphere) or December-January-February data (in the Southern Hemisphere). Global analyses were conducted for both original and anomaly time series data. The latter was obtained by subtracting a fixed (2007–2013) seasonal climatology calculated by taking the mean (across the entire 7-year data record) of all SM or LH estimates within a 13-week moving window centered on a particular week of the year.
3. Results
Our global investigation of SM/LH coupling strength is based on weekly RS and LSM time series data aggregated over each 0.25° grid. For each grid, at least 80 collocated samples were required for applying (8). TC generally requires a minimum level of mutual cross-correlation between products in each triplet to yield stable results. Therefore, a minimum Spearman rank coefficient of determination (R2) of 0.03 [−] was required for all pairwise combinations within both the SM and LH triplets. Pixels not passing this cross-correlation threshold were masked from the analysis. This threshold was determined as a compromise between maintaining sufficient global coverage and filtering non-physical results (Crow et al., 2015). As described above, all global results were based on the period 2007–2013 and the (latitude-dependent) seasonal masking described in Section 2.5.
3.1. Verification at AmeriFlux Tower Sites
The central consideration in applying TC is confidence in the mutual independence of the three estimates selected to comprise the SM and LH triplets. Our two RS-based LH products (ALEXI-TIR and ALEXI-MW) are formulated from the same two-source energy balance model. Therefore, concerns about the mutual independence of their errors are warranted. Similar cross-dependence concerns exist for RS-based SM products acquired from passive and active microwave approaches.
Therefore, to test the validity of using two different RS products within the same triplet, we replicated the AmeriFlux tower-based results in Crow et al. (2015) via the substitution of ground-based SM and LH observations with comparable RS-based products. That is, the flux tower-based LH is replaced with ALEXI-MW LH estimates and ground-based SM is replaced with SM derived from ASCAT observations. If cross-correlation exists within the two RS-based LH products (ALEXI-MW and ALEXI-TIR) or within the two RS-based SM products (ASCAT and CCI-PASSIVE), these substitutions should be associated with systematic changes in TC-based correlations acquired via (8).
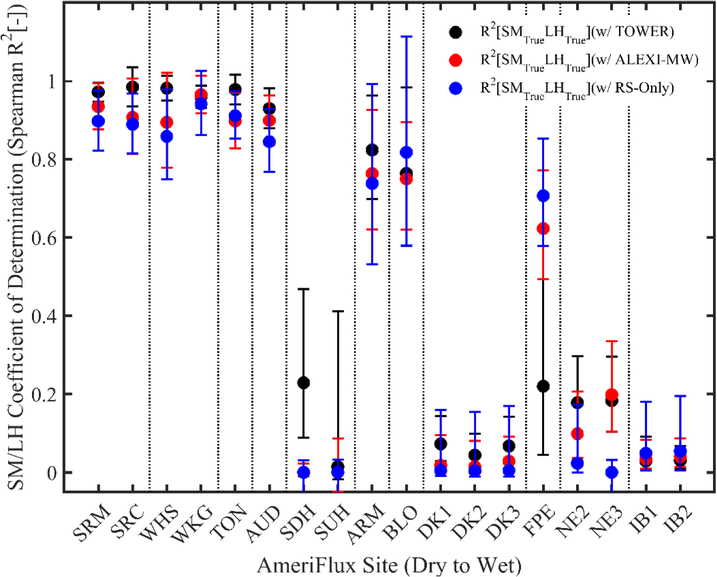
Results from this sensitivity analysis are shown in Figure 1. Note that the black bars plot the same TC estimates as Figure 1 in Crow et al. (2015). By bringing the RS-based ALEXI-MW into the LH triplet (in red), generally consistent TC results in Figure 1 can be obtained with and without the use of flux tower-based LH observations. Likewise, replacing the ground-based SM with ASCAT retrievals (in blue) does not qualitatively change TC results over the AmeriFlux sites. Slightly larger discrepancies are found at the FPE site where TC results derived using ground measurements (black bar) have a higher level of uncertainty than results derived using only model and RS data. This is likely due to the elimination of spatial representative errors (between local-scale ground-based observation and coarse-scale RS- and model-based data) when ground-based observations are not utilized.
Figure 1.
TC-based SM/LH coupling strength estimates acquired from a variety of sources over a set of AmeriFlux sites (see Appendix B). Black symbols (“TOWER”) replicate earlier results in Crow et al. (2015) based on using ground/tower-based SM and LH observations (plus Noah SM, Noah LH, PMW SM, and ALEXI-TIR LH) to complete the triplet. Red symbols (“ALEXI-MW”) capture the impact of using ALEXI-MW LH in place of flux tower observations. Blue symbols (“RS-Only”) capture the impact of further replacing ground-based SM observations with AMW SM retrievals (thus eliminating all dependence on ground-based observations). The consistency demonstrates the applicability of selected RS-based SM and LH in place of ground-based data for TC analysis.
This consistency in TC results suggests that, despite their use of the same retrieval algorithm framework, differences in the LST inputs used to force ALEXI-TIR and ALEXI-MW LH are profound enough that their LH retrievals can be considered effectively independent for TC applications. Therefore, it is appropriate to utilize ALEXI-MW as another source of RS-based LH for the global investigation of SM/LH coupling. Furthermore, the simultaneous use of active and passive-based SM retrievals in the same triplet does not appear to be problematic in the application of (8). Additional discussion on the impact of any residual error cross-correlation existing between RS-based LH and SM products on the TC estimates is provided below in Section 4.1.
3.2. Robustness to Land Surface Model Variations
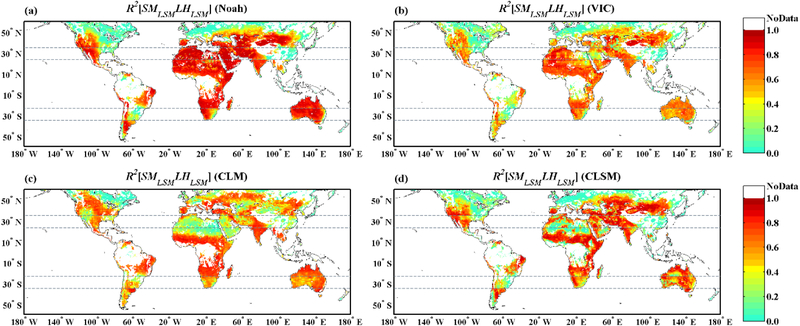
Another important diagnostic for TC results is robustness to variations in the LSM-based estimates used to construct the data product triplet. Due to variations in the processes and parameterization schemes embedded in LSMs, different models exhibit large discrepancies in the degree of direct SM/LH coupling they predict (see Figure 2). Among the four LSMs considered here, the Noah model (Figure 2a) has the strongest warm-season SM/LH coupling with a global mean and median R2[SMLSMLHLSM] of 0.53 [−] and 0.70 [−], respectively. On the contrary, SM and LH coupling is relatively weaker in the VIC model which has a global mean R2[SMLSMLHLSM] of 0.45 [−] and median of 0.54 [−]. Notice that the spatial patterns of SM/LH coupling strength also vary across LSMs. Both Noah (Figure 2a) and VIC (Figure 2b) have shown strong coupling (> 0.5 [−]) between SM and LH over arid regions, such as the Sahara and Central Australia. In contrast, R2[SMLSMLHLSM] results for CLM (Figure 2c) and CLSM (Figure 2d) suggest moderate to marginal SM/LH coupling in these areas. Differences in the degree of SM/LH coupling strength across LSMs are also observed over western United States, South America, and the Arabian Peninsula. Overall, various LSMs predict distinct magnitudes and spatial patterns in coupling strength.
Figure 2.
Variations of predicted warm-season SM/LH coupling strength between the LSMs: (a) Noah, (b) VIC, (c) CLM, and (d) CLSM. Parallel lines at different latitudes indicate the delineation of tropical, sub-tropical and temperate zones for defining the warm-season period. White land grid cells indicate regions with insufficient RS-based retrievals for comparison (“NoData” in legend).
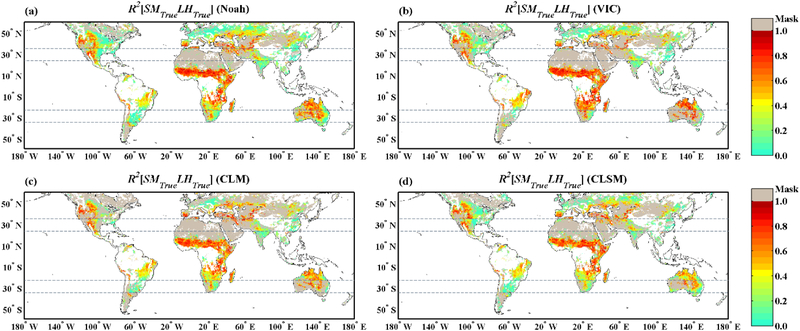
While these LSM differences are prominent, TC results acquired from (8) should, in theory, be insensitive to our choice of a particular LSM to provide the third member of the data product triplet. To examine the robustness of TC-based SM/LH coupling estimates against various models, SM and LH products from four LSMs have been individually applied in (8) and results are shown in Figure 3. As noted above, grids with low mutual correlation (R2[−] < 0.03 [−]) among either SM or LH triplets are masked. The TC estimates derived with different LSMs dataset yield generally consistent magnitudes of SM/LH coupling strength. In addition, all four cases in Figure 3 illustrate a strikingly similar spatial distribution of areas with enhanced SM/LH coupling. Based on TC estimates, strong coupling between SM and LH are observed over Africa, western North America, the Cerrado region of Brazil, Central Asia, and Australia except for coastal regions with high vegetation density.
Figure 3.
TC-based estimates of warm-season SM/LH coupling strength with LSM SM and LH datasets obtained from the (a) Noah, (b) VIC, (c) CLM, and (d) CLSM LSMs. The generally consistent magnitudes and agreement in spatial patterns demonstrate the robustness of TC results with respect to LSM model choice.
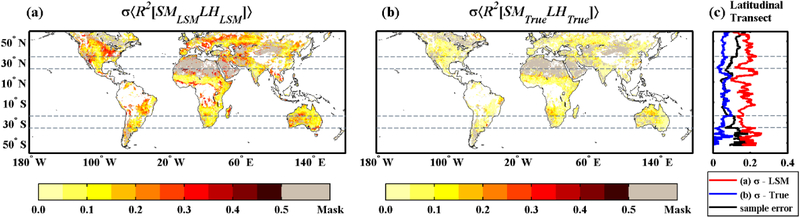
Figure 4 shows the variations of direct cross-correlation and TC-based estimates of SM/LH coupling across LSMs. Prior to application of TC, different parameterization schemes in LSMs lead to distinct patterns and magnitudes of coupling strength, and thus large inter-model spread for correlation results (σ < R2[SMLSMLHLSM] >) in Figure 4a. However, TC-based coupling strength estimates are generally robust to the choice of LSM and exhibit much lower inter-model spread (σ < R2[SMTrueLHTrue] >), as shown in Figure 4b. The differences in inter-model spreads are compared along the latitudinal transect in Figure 4c, showing consistency in TC estimates across LSMs. In addition, the temporal sampling errors are estimated through boot-strapping analysis as described in Section 2.5. From Figure 4c, the remaining variability in TC estimates (blue line) has a comparable magnitude with respect to the standard deviation (1-sigma) of estimated sampling error (black line). This suggests that residual LSM-to-LSM variations remaining in TC results can largely be attributed to inadequate temporal sampling. This lack of bias associated with the use of varying LSMs lends credibility to our interpretation of (8) as an unbiased reflection of true SM/LH coupling strength. Therefore, based on encouraging verification results in Figures 1–4, we will use (8) below to critique levels of SM/LH coupling predicted by LSMs and observed by remotely-sensed SM and RS-based LH products.
Figure 4.
Inter-model variations (expressed as standard deviations) in warm-season SM/LH coupling strength across different (a) LSMs and (b) TC-based estimates with independent LSM as input. Mean standard deviations along the latitudinal transect are show in (c), as well as the 1-sigma sampling error (black line) obtained from a boot-strapping analysis.
3.3. Global Coupling Strength Between Soil Moisture and Latent Heat Flux
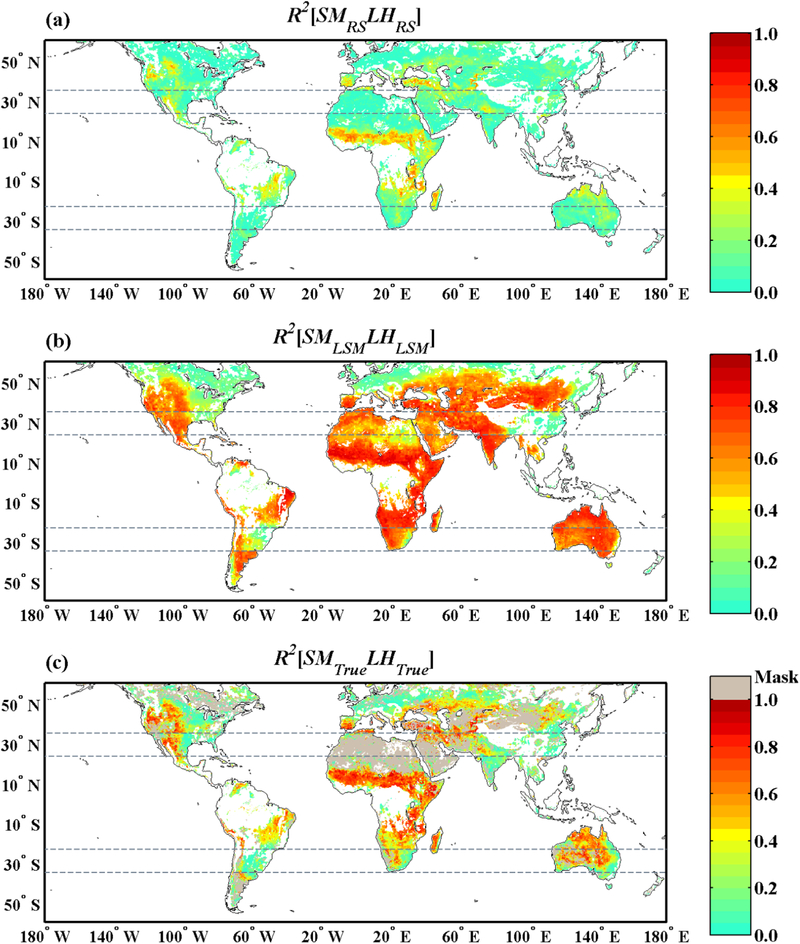
SM/LH coupling strength can be directly derived from RS-only datasets (without any TC calculations). Figure 5a shows averaged RS-based estimates (R2[SMRSLHRS]) from SM/LH RS combinations, i.e., CCI-PASSIVE/ALEXI-TIR, CCI-PASSIVE/ALEXI-MW, ASCAT/ALEXI-TIR, ASCAT/ALEXI-MW of remotely-sensed SM and RS-based LH retrievals. Meanwhile, averaged R2[SMLSMLHLSM] across all four LSMs is shown in Figure 5b. Globally, the R2[SMRSLHRS] estimates sampled from RS data are generally smaller than 0.4 [−] except for Central Africa. On the contrary, the LSMs predict much higher levels of coupling (R2[SMLSMLHLSM] > 0.6 [−]) over the Africa, the Arabian Peninsula, western Asia, Australia, western North America, and parts of the South America. Comparing RS results in Figure 5a with LSM results in Figure 5b, large discrepancies exist over both arid and transitional regions, where the partition of energy fluxes strongly depends on the soil wetness. Moreover, these significant discrepancies in the estimated magnitudes of SM/LH coupling strength are mostly due to LSM intrinsic coupling being much higher than RS-predicted coupling.
Figure 5.
Global mean estimates of warm-season SM/LH coupling derived from (a) RS-based products, (b) LSMs, and (c) TC-based estimates.
There are two possibilities for explaining this difference. First, LSMs may systematically over-represent the levels of coupling. However, considering the random measurement errors which degrade the accuracy of RS products (Holmes et al., 2018; Sorensson et al., 2018), a second possibility is that elevated levels of retrieval noise in RS retrievals are causing them to systematically underestimate true levels of coupling (Findell et al., 2015).
As was shown by Crow et al. (2015), TC can be used to distinguish between these two possibilities. In particular, the TC-based approach in (8) corrects for the impact of random errors in observations and provides an unbiased estimate that is unaffected by either noise in the RS retrievals or systematic errors in LSM estimates (see Figure 4). Accordingly, a true coupling estimation can be acquired with the simultaneous availability of SM and LH triplets. Arithmetically averaged TC-based coupling estimates (R2[SMTrueLHTrue]) across all four LSMs are shown in Figure 5c. Grey shading reflects the masking of grid cells with insufficient mutual correlations among SM or LH products (see above).
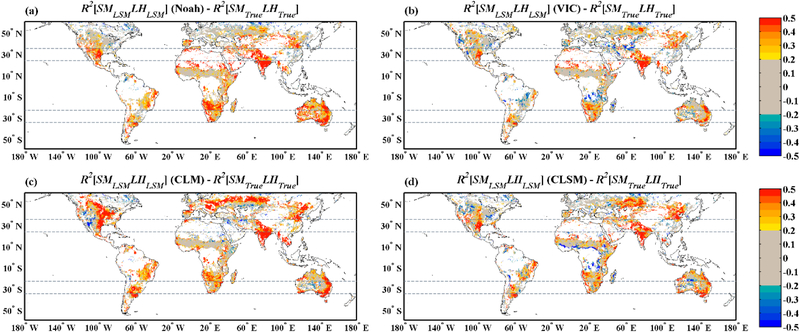
Overall, the LSMs appear to predict somewhat more SM/LH coupling in Figure 5b than TC-based estimates of true coupling strength in Figure 5c. However, there are strong regional variations in these differences and, as shown above in Figure 2 and Figure 4a, strong LSM-to-LSM variations are not reflected in Figure 5b. Therefore, direct comparisons between model predicted and TC estimated coupling strengths are needed to identify regional biases in LSM SM/LH coupling predictions. To this end, Figure 6 plots the global distribution of differences between TC-based (R2[SMTrueLHTrue]) and LSM-based (R2[SMLSMLHLSM]) coupling results individually for each LSM. All differences within the 2-sigma confidence interval of R2[SMTrueLHTrue], which has a global averaged standard deviation (obtained via the boot-strapping analysis) of 0.10 [−], have been masked in Figure 6. Therefore, the map indicates regions where LSM SM/LH predictions are significantly different than comparable TC estimates of true coupling strength.
Figure 6.
Differences of warm-season SM/LH coupling strength between model predictions and TC-based estimates for the (a) Noah, (b) VIC, (c) CLM, and (d) CLSM LSMs. Grids within the 2-sigma confidence interval are masked (see grey shading).
Different LSMs demonstrate distinct spatial patterns of over-/under-coupling relative to our TC baseline. Generally, more over-coupling is found in Noah and CLM than in VIC and CLSM. Comparing Noah and TC-based coupling estimates in Figure 6a, Noah appears to over-predict SM/LH coupling strength (relative to TC) over arid and low-vegetated zones, including the: Sahara Desert, Arabian Desert, Thar Desert in Indian, Kalahari Desert in South Africa, Chihuahuan Desert in North Mexico, and arid areas of Central Australia. In addition, Noah also over-predicts coupling in India and within the Cerrado region of Brazil. Marginal under-couplings are found in northeastern North America and northern Russia.
However, this over-coupling is not universal. In contrast, extensive under-coupling is noted in CLM. Most noticeably, bias in CLM SM/LH coupling appears to have a relationship with underlying vegetation and climate conditions (Figure 6c). Specifically, over-coupling is primarily found in heavily-vegetated humid regions, while under-coupling is seen in arid or semi-arid areas with less SM and sparser vegetation coverage (e.g., the western United States, Central Asia, and Central Australia). Likewise, VIC (Figure 6b) under-couples SM and LH for certain regions with moderate vegetation density (e.g., eastern North America, the Cerrado region of Brazil, and Central Africa). As shown in Figure 6d, CLSM predicts generally similar pattern with VIC except for relatively less SM/LH coupling over the transitional wet/dry climate zone (near 10° N) in Central Africa.
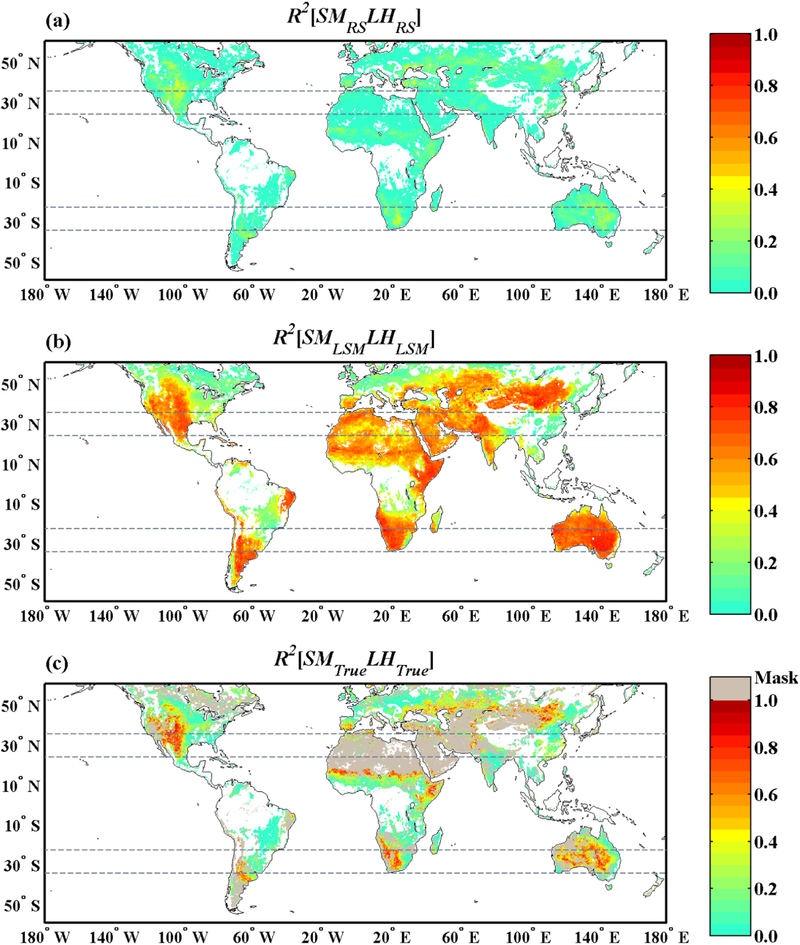
In TC applications, strong seasonality has been shown to produce non-robust TC results (Chen et al., 2016). Therefore, we also re-applied (8) to SM and LH anomaly time series. Anomalies are calculated by subtracting out the long-term seasonal climatology as described in Section 2.5. Results are shown in Figure 7. As expected, without the strong seasonal variations in water availability and insolation, the overall coupling strength of SM/LH (Figure 7) decreases when compared to Figure 5. However, the LSMs still generally predict more coupling than RS-based estimates. Moreover, the TC-based (anomaly) coupling strength estimates (Figure 7c) are generally much closer to LSM-based predictions (Figure 7b) than RS-based results. Regions with strong SM/LH coupling are distributed mainly over transitional zones and semi-arid regions where LSMs also predict similar spatial patterns.
Figure 7.
Same as Figure 5 but for SM and LH anomaly time series.
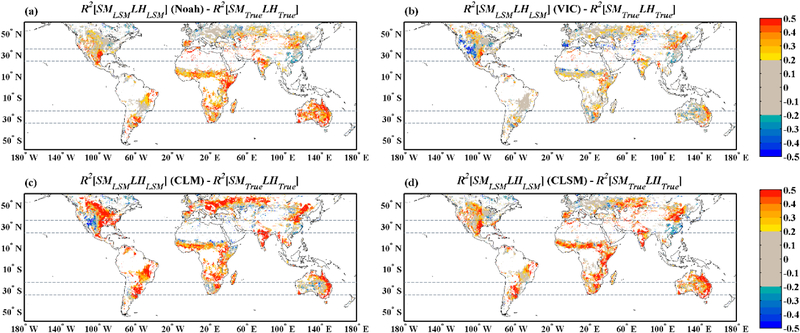
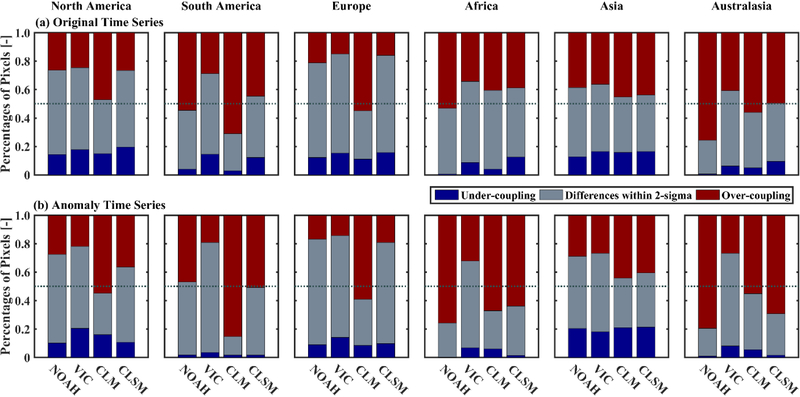
Comparing the baseline TC-based and various LSMs predicted estimates of SM/LH coupling strength, similar spatial tendencies (with regard to over- versus under-coupling in LSMs) are found for both the anomaly (Figure 8) and original time series (Figure 6). For the anomaly analysis, Noah, CLM, and CLSM generally overestimate the coupling across the globe, among which CLM has the most prominent over-coupled relations. On the other hand, both VIC and CLM underestimate the coupling over western United States and Central Australia. In eastern China, all four LSMs systematically predict less SM/LH coupling. Therefore, taken as a whole, the original (Figure 6) and anomaly (Figure 8) time series analyses demonstrate consistent results with regard to LSM SM/LH coupling bias. Percentages of pixels with over-coupling and under-coupling in various LSMs are summarized for six continents in Figure 9.
Figure 8.
Same as Figure 6 but for SM and LH anomaly time series.
Figure 9.
Percentages of pixels with SM/LH over-coupling (dark red) and under-coupling (dark blue) in LSMs’ predictions as compared to the TC-based estimates for six continental regions. Results are based on both (a) original and (b) anomaly time series of SM and LH. Percentages of pixels with (non-significant) differences between LSM- and TC-based coupling strength estimates within a 2-sigma confidence interval are in gray.
3.4. Climate Zone Analysis
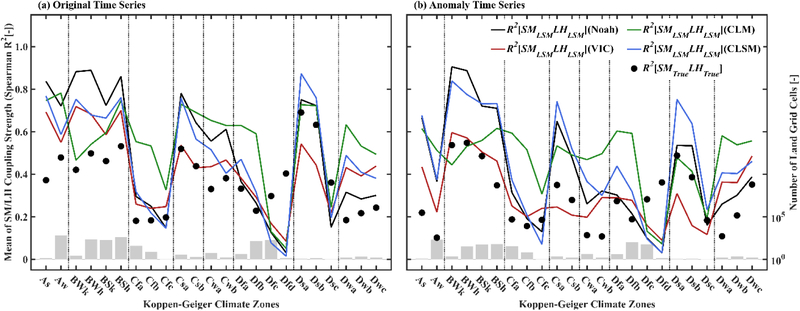
It is also potentially useful to examine the performance of LSMs as a function of climate zone. To this end, LSM- and TC-based coupling estimates from both the original and anomaly time series are grouped based on their Köppen-Geiger climate zone (Kottek et al., 2006) classification. Detailed descriptions of each climate zone index are included in Table 2. Mean values of R2[−] for each climate category are then sorted from high to low mean annual air temperature in Figure 10. Climate zones containing less than 100 grid cells (in which TC estimates are available) are omitted.
Table 2.
Explanations for climate classification index (adopted from Kottek et al. (2006)).
| Main Climate | Precipitation | Temperature |
|---|---|---|
| A: equatorial | W: Desert | h: hot arid |
| B: arid | S: Steppe | k: cold arid |
| C: warm temperate | f: fully humid | a: hot summer |
| D: continental | s: summer dry | b: warm summer |
| E: polar | w: winter dry | c: cool summer |
| m: monsoonal | d: extremely continental | |
| F polar frost | ||
| T polar tundra |
Figure 10.
Aggregated mean values of warm-season SM/LH coupling strength for various Köppen-Geiger climate zones based on both (a) original and (b) anomaly time series analysis. Grey bars (and right vertical axis) indicate the number of grids with valid TC results.
Although LSM- and TC-based coupling estimates differ in exact absolute values, the general trends with regard to different climate zones are consistent. All LSMs predict relatively strong coupling between SM and LH over tropical (As and Aw) and arid (BWk, BWh, BSk, and BSh) climate zones in Figure 10a. For warm temperate climate zones, the coupling of SM/LH significantly increases with the reduced soil wetness from fully humid (Cf) to summer dry (Cs) and winter dry (Cw) conditions. This tendency also exists for colder continental climate zones from Df to Ds and Dw, except for Dsc where summer is usually dry (limited soil water availability) and cool (low temperature). For climate zones with comparable precipitation conditions, SM/LH coupling generally decreases with reduced summer maximum air temperature from Dsa (hot summer) to Dsb(warm summer) and Dsc (cold summer). Moving from the original to anomaly time series (Figure 10b), one exception is found for tropical savannah climate zone where LSMs predict less anomaly coupling.
When compared against the robust TC-based results (in black circles), LSMs slightly overestimate the coupling over tropical arid and semi-arid climate zones, including As (equatorial savannah with dry summer), Aw (equatorial savannah with dry winter), BW (cold arid desert), and BS (hot arid desert). Noah, VIC, and CLSM predict a relatively accurate coupling for regions with adequate precipitation, such as Cf and Df. By contrast, CLM generally predicts more coupling than TC analysis for these climate zones. On the other hand, VIC is the only one (out of four LSMs) to under-represent the coupling over Ds (continental climate with dry summer). In addition, LSMs are systematically over-coupled for Dw (continental dry winter) climate zones.
4. Discussion
Over the past two decades, various ground-based observational networks of land surface fluxes and meteorological states have been established for the validation of RS-based retrievals and model-based simulations (Dorigo et al., 2011; Baldocchi et al., 2001). However, these networks are generally located in either North America or Europe and therefore capture a relatively limited range of land surface and climatic conditions for global investigations. In addition, the spatial scale differences between point-scale ground measurement and grid-averaged RS product or model simulation can imperil the accuracy of coupling estimates acquired from point-scale ground observations. Note that the spatial representative mismatch across measurements can be partially alleviated by using various remotely-sensed products with comparable spatial resolutions for global LSMs. Nevertheless, random measurement errors can still induce bias into the sampled correlation between observed variables (Crow et al., 2015). Recently, using an aggregated surface flux dataset FLUXNET2015, Dirmeyer et al. (2018) explored both the atmospheric leg (sensible heat flux/lifting condensation level) and terrestrial leg (soil moisture/latent heat flux) of land-atmosphere coupling across offline/coupled LSMs and multiple reanalysis products. Their results suggested a potentially over-coupled relationship between SM and LH across LSMs. However, their analysis was confined by both the limited geographical extent of the FLUXNET sites and the strong scale contrast between these point-scale observations and coarse-scale LSM grids. Therefore, an unbiased (and spatially extensive) estimate of the true coupling of two geophysical variables is needed to eliminate both spatial scale differences and compensate for the biasing impact of random measurement errors.
RS-based products are usually subject to random errors originated from instrument sensitivity, sensor calibration, retrieval physics and parameterization (Congalton, 1991). Traditional pairwise correlation calculations that ignore random errors may not be appropriate for characterizing the relationship between two variables. For example, the direct use of RS-based estimates substantially under-predicts SM/LH coupling strength (Figure 5a and 7a). A naïve interpretation of this results would suggest that LSMs strongly over-couple SM and LH over almost all regions of the world (see Figure 5b and 7b). However, when explicitly accounting for the random measurement errors via a TC analysis, a significantly larger value of true SM/LH coupling (Figure 5c and 7c) is obtained as compared to underlying RS-based estimates (Figure 5a and 7a).
Consequently, the diagnosis of LSM coupling biases becomes much more complex and geographically variable. Among the four LSMs considered here, VIC turns out to be generally accurate in describing the relationship between SM and LH (Figure 6b and 8b). Nevertheless, certain regional biases of both over- and under-coupling are still observed in LSMs with respect to TC results (see Figure 6 and Figure 8) due to imperfect model physics. In summary, it is important to consider the impact of random errors in RS products when applying canonical statistical measures (e.g. correlation coefficient, root-mean-square-error) to evaluate or benchmark LSMs. The application of (8) is recommended for related applications, especially when multiple RS products are available.
4.1. Impact of Cross-correlated Error
A critical issue when applying the TC approach in (8) is the potential for mutual error dependency among data members in each triplet, specifically for the LH triplet containing both ALEXI-TIR and ALEXI-MW products and the SM triplet containing both AMW and PMW retrievals. Previous studies indeed suggest that error cross-correlation also exists for AMW and PMW SM retrievals (Gruber et al., 2016b; Chen et al., 2016). Our analysis of cross-correlation at AmeriFlux tower sites indicates that differences in LST inputs for ALEXI-TIR and ALEXI-MW LH products or retrieval processes (and spectral regimes) for AMW and PMW SM products appear to be sufficient for ensuring error independence and the confident application of TC. However, moving from a handful of sites to global analysis, the existence of residual non-zero error cross-correlation among LH or SM products may not be negligible and its possible effect on estimates of coupling strength needs to be discussed.
Appendix A provides a detailed description of the impact of potentially neglected error cross-correlation on TC-based coupling estimates derived via (8). Analytical derivations show that positive error cross-correlation between two datasets in the triplet would negatively bias the estimated true signal variance when using the third independent member as the reference. Thus, in the case of cross-correlated ALEXI-TIR and ALEXI-MW LH errors, a positively-biased estimate of SM/LH coupling strength would be obtained by utilizing a LSM-based LH product as a reference. In contrast, if either ALEXI-TIR or ALEXI-MW LH is used as the reference, the derived estimate can be negatively-biased. Therefore, cross-correlated errors in RS-based LH products would increase the spread in coupling strength estimates acquired across all possible reference pairs. A similar effect would accompany the presence of correlated errors in ASCAT (AMW) and CCI-PASSIVE (PMW) SM products (see Appendix A for details).
As described in Section 2.5, the sensitivity of our final TC-based coupling results to this spread is minimized here through our use of a median operator to summarize a single result from across all eight possible reference pair choices. Specifically, four out of the eight reference pairs are based on either LSM-based LH or SM products (as described in Section 2.5) and can potentially lead to biased higher estimates of SM/LH coupling strength in (8). On the contrary, the other four (biased lower) estimates are obtained using RS-based products as references (see Appendix A). This suggests that our approach should be reasonably robust to the presence of error cross-correlation in either RS-based LH and SM products. Note that this interpretation is supported by earlier results shown in Figure 1.
4.2. Implications for Land-atmosphere Coupling
Under all circumstances, our results consistently indicate that the random observational errors in RS-based products greatly complicate their application for benchmarking LSM coupling results. However, by using the robust TC estimates derived in part from RS products (Figure 5c and Figure 7c), regions with over- or under-coupled relationship across different LSMs can be identified (Figure 6 and Figure 8). The spatial extent and distribution of over-coupled predictions are comparably similar among various LSMs over the globe, especially for Noah, CLM, and CLSM. Interestingly, all four LSMs tend to over-predict SM/LH coupling over the central Great Plains of North America, the Sahel, India, and coastal Australia (Figure 6 and 8). These regions are commonly known as “hot-spots” of strong land-atmosphere coupling (Koster et al., 2004). Benchmarking the performance of LSMs over these hot-spot regions is of vital importance for seasonal weather and climate forecasting. On the other hand, all four LSMs tend to slightly under-represent the SM/LH coupling relationship in China. VIC and CLM generally under-predict the coupling over less intense hot-spots regions, including western North America, Central Asia, and Central Australia.
When coupled with climate models, bias in the LSM’s SM/LH coupling strength can affect the surface partitioning of sensible and latent heat fluxes and thus water and energy interactions along the land-atmosphere interface. This can result in biased predictions of extreme event frequencies, such as heatwaves and droughts (Ukkola et al., 2016a, 2016b). Note that different LSMs vary in process representation of soil surface-subsurface hydrology, groundwater storage, and plant water components (Egea et al., 2011). It is therefore critical to pinpoint the exact processes that contribute to the unrealistic characterization of water and energy exchanges in LSMs. However, this is beyond the scope of this work and will be addressed in our forthcoming work by exploring various processes and parameterization schemes in the modular Noah-MP model (Niu et al., 2011).
5. Conclusions
Based on the simultaneous availability of multiple SM and LH products from satellite and LSMs, this work provides an unbiased estimate of SM/LH coupling strength at the global scale. In particular, the TC strategy of Crow et al. (2015) is applied globally, for the first time, to compensate for the impact of random observational errors on sampled correlation statistics — an effect which is commonly neglected. This allows us to obtain quasi-global maps of unbiased SM/LH coupling strength estimates for comparisons against comparable LSM predictions.
Using the TC-based robust estimate, several important conclusions can be drawn. First, it is found that with the existence of random measurement errors, RS-based coupling strength estimates are prone to large negative biases and thus insufficient for directly benchmarking the true SM/LH coupling relationship. Past studies using ground-based measurements are likely to subject to the same limitations (Dirmeyer et al., 2018; Ukkola et al., 2016b). By contrast, the TC-based approach in (8) provides a means for compensating for this effect. When observational errors are properly accounted for, significantly higher levels of true SM/LH coupling strength relative to RS-based estimates (Figure 5 and 7) are obtained. Regions with strong SM/LH coupling are found over western Northern America, the Sahel, Central Asia and Australia. Relative to TC-based results, regional areas of over- or under-coupling in LSMs are identified.
Overall, results are consistent with Dirmeyer et al. (2018) in indicating that LSMs generally predict over-coupling. However, large regional and LSM-to-LSM variations are also observed. For example, CLM appears to be under-coupled in semi-arid areas and over-coupled in heavily-vegetated humid regions. In addition, areas of over-coupling appear to be concentrated in regions of globe with strong land-atmosphere coupling. Such identification of regional biases can guide subsequent efforts to improve LSM physics and/or parameterizations. Note that TC-based coupling strength estimates are generally robust to the choice of a particular LSM to provide the third (SM or LH) member of each triplet. Moreover, both the original and anomaly time series analyses yield overall consistent results, lending credibility to our conclusions.
One obvious limitation here is our focus on a set of relatively dated LSM versions provided by the GLDAS-1 project. This is particularly for CLM which has evolved from CLM 2.0 (applied in GLDAS-1 and thus examined here) to CLM 4.5 with some fundamental changes. Future work with more recent LSM versions is clearly needed. Likewise, a daily-scale SM/LH coupling analysis would be preferable relative to the weekly time-scale used here. Expected enhancements to ALEXI LH products should make this possible in the near future. Improvement to ALEXI LH products are also expected via the inclusion of Clouds and Earth’s Radiant Energy Systems (CERES) meteorological forcing datasets (Wielicki et al., 1996; https://ceres.larc.nasa.gov/).
In contrast to previous research focusing on the use of ground-based measurements (Ukkola et al., 2016b; Dirmeyer et al., 2006a; 2018) or multi-model cross-comparison (Best et al., 2015; Haughton et al., 2016), our results are primarily constructed from multiple independent RS-based observations and model products (free of spatial representativeness differences) and yield an objective benchmark for LSM coupling strength estimates. More importantly, this analysis provides quasi-global results that are not restricted to sparse flux tower locations. As a result, climate zones with either over- or under-coupled SM/LH relations in LSMs are readily identified and can be prioritized for future LSM improvement and multi-model comparison experiments, such as the Land Surface, Snow and Soil moisture Model Intercomparison Project (LS3MIP; Van den Hurk et al., 2016) conducted as part of the sixth phase of the Coupled Model Intercomparison Project (CMIP6; Eyring et al., 2016). Moreover, the TC-based coupling metric can also be utilized for analyzing other coupled geophysical variables when its prerequisites are satisfied. For example, the relationship between SM and subsequent (or antecedent) precipitation (Guillod et al., 2015; Tuttle and Salvucci, 2016) or SM and maximum summertime air temperature (Miralles et al., 2012).
Key Points:
Multiple sources of remote sensing-based soil moisture and latent heat flux products are integrated via triple collocation
Global observation-based estimates of coupling strength between surface soil moisture and latent heat flux are obtained
Land surface models overestimate the strength of this coupling along transitional climate regimes
Acknowledgments
This work was supported by the grant 17-TASNPP17–0095 funded by the NASA Science of Terra, Aqua, and Suomi NPP program. The used GLDAS data are available from the NASA Goddard Earth Sciences Data and Information Services Center (GES DISC) (https://hydro1.gesdisc.eosdis.nasa.gov/data/GLDAS/). The ESA CCI PASSIVE soil moisture product is from http://dx.doi.org/10.5285/d2eea061026240eb8a2f9cc64a691338, and ASCAT data are available from EUMETSAT’s H-SAF data portal (http://hsaf.meteoam.it/soil-moisture.php). In-situ AmeriFlux data can be obtained from http://ameriflux.lbl.gov/. The global ALEXI-TIR and ALEXI-MW LH data products are available upon request.
Appendix A
The accuracy of any TC-based estimate depends strongly on the validity of the error independence assumption. In the presence of non-zero error cross-correlation (Gruber et al., 2016b), direct usage of (4) and (8) can lead to biased estimates. Specifically, if there only exists positive error cross-correlation between dataset Xj and Xk (Cov[εj, εk] > 0, Cov[εi, ε] = 0, and Cov[εi, εk] = 0), the estimated true signal variance Var[T]i using dataset Xi as the reference can be biased low with regard to actual variance of true signal Var[T]
| (A1) |
Instead, when using dataset Xj or Xk as the reference, the estimated true signal variance Var[T]j or Var[T]k are positively biased
| (A2) |
Therefore, the estimated coefficient of determination R2[SMTrue, LHTrue]i,l derived from (8) becomes biased high when SM dataset SMi and/or LH dataset LHl are chosen as the reference
| (A3) |
where Cov[εj, εk] and/or Cov[εm, εn] are (positive) non-zero cross-correlated errors between SMj and SMk and/or LHm and LHn. By contrast, in the case of SMj/LHm is chosen as the reference pair, the estimated coefficient of determination R2[SMTrue, LHTrue]j,m will be biased low
| (A4) |
Analogous biases also exist for the reference pairs of SMj/LHn, SMk/LHm, and SMk/LHn.
Here, eight reference pairs are utilized to obtain estimates of SM/LH coupling strength using (8). Concerning the potential positive cross-correlated errors between ALEXI-TIR and ALEXI-MW LH products and/or ASCAT and CCI-PASSIVE SM products, four reference pairs —using LSM SM or LH as a reference— tend to produce positively biased estimates (A3), i.e., SMPMW/LHLSM, SMAMW/LHLSM, SMLSM/LHTIR, SMLSM/LHMW. Instead, the other four estimates are biased lower (A4) using reference pairs of SMPMW/LHTIR, SMPMW/LHMW, SMAMW/LHTIR, and SMAMW/LHMW. Therefore, the existence of error cross-correlation will tend to increase the spread of coupling strength estimates acquired from eight reference pairs. Nevertheless, given that it is obtained via a median operator (applied to all eight possible reference choices), final TC-based coupling estimates should be relatively robust to this tendency.
Appendix B
Table B1.
Basic attributes of a set of AmeriFlux sites used here and Crow et al. (2015).
| Abbreviation | AmeriFlux Site | Latitude/Lo ngitude |
|---|---|---|
| SRM | Santa Rita Mesquite | 31.821°/−110.866° |
| SRC | Santa Rita Creosote | 31.908°/−110.840° |
| WHS | Lucky Hills | 31.744°/−110.052° |
| WKG | Kendall Grasslands | 31.737°/−109.942° |
| TON | Tonzi Ranch | 38.432°/−120.966° |
| AUD | Audubon Grasslands | 31.591°/−110.509° |
| SDH | Sand Hills Dry Valley | 42.069°/−101.407° |
| SUH | Sand Hills Upland Dune | 42.066°/−101.367° |
| ARM | ARM-CART | 36.606°/−97.489° |
| BLO | Blodgett Forest | 38.895°/−120.633° |
| DK1 | Duke Open Field | 35.971°/−79.093° |
| DK2 | Duke Hardwoods | 35.974°/−79.100° |
| DK3 | Duke Pine | 35.978°/−79.094° |
| FPE | Fort Peck | 48.308°/−105.102° |
| NE2 | Mead Irrigated | 41.164°/−96.470° |
| NE3 | Mead Rainfed | 41.180°/−96.440° |
| IB1 | Fermi Agricultural | 41.859°/−88.223° |
| IB2 | Fermi Prairie | 41.841°/−88.241° |
References
- Albergel C, Rüdiger C, Pellarin T, Calvet JC, Fritz N, Froissard F, Suquia D, Petitpa A, Piguet B, and Martin E (2008), From near-surface to root-zone soil moisture using an exponential filter: an assessment of the method based on in-situ observations and model simulations, Hydrol. Earth Syst. Sci, 12, 1323–1337, doi: 10.5194/hess-12-1323-2008. [DOI] [Google Scholar]
- Anderson MC, Kustas WP, Norman JM, Hain CR, Mecikalski JR, Schultz L, González-Dugo MP, Cammalleri C, d’Urso G, Pimstein A, and Gao F (2011), Mapping daily evapotranspiration at field to global scales using geostationary and polar orbiting satellite imagery, Hydrol. Earth Syst. Sci, 15, 223–239, doi: 10.5194/hess-15-223-2011. [DOI] [Google Scholar]
- Baldocchi D, Falge E, Gu L, Olson R, Hollinger D, Running S, Anthoni P, Bernhofer C, Davis K, Evans R, Fuentes J, Goldstein A, Katul G, Law B, Lee X, Malhi Y, Meyers T, Munger W, Oechel W, Paw KT, Pilegaard UK, Schmid HP, Valentini R, Verma S, Vesala T, Wilson K, and Wofsy S (2001), FLUXNET: A new tool to study the temporal and spatial variability of ecosystem–scale carbon dioxide, water vapor, and energy flux densities, Bull. Amer. Meteor. Soc, 82, 2415–2434, doi:. [DOI] [Google Scholar]
- Best MJ, Abramowitz G, Johnson H, Pitman A, Balsamo G, Boone A, Cuntz M, Decharme B, Dirmeyer P, Dong J, Ek M, Guo Z, Haverd V, van den Hurk BJ, Nearing GS, Pak B, Peters-Lidard C, Santanello JA, Stevens L, and Vuichard N (2015), The plumbing of land surface models: benchmarking model performance, J. Hydrometeor, 16, 1425–1442, doi: 10.1175/JHM-D-14-0158.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen F, Mitchell K, Schaake J, Xue YK, Pan HL, Koren V, Duan QY, Ek M, and Betts A (1996), Modeling of land surface evaporation by four schemes and comparison with FIFE observations, J. Geophys. Res, 101(D3), 7251–7268, doi: 10.1029/95JD02165. [DOI] [Google Scholar]
- Chen F, Crow WT, Colliander A Cosh MH, Jackson TJ, Bindlish R, Reichle RH, Chan SK, Bosch DD, Starks PJ, and Goodrich DC (2016), Application of triple collocation in ground-based validation of Soil Moisture Active/Passive (SMAP) level 2 data products, IEEE J. Sel. Topics Appl. Earth Observ. Remote Sens, 99, 1–14, doi: 10.1109/JSTARS.2016.2569998. [DOI] [Google Scholar]
- Combe M, de Arellano JV-G, Ouwersloot HG, and Peters W (2016), Plant water-stress parameterization determines the strength of land-atmosphere coupling, Agric. For. Meteorol, 217, 61–73, doi: 10.1016/j.agrformet.2015.11.006 [DOI] [Google Scholar]
- Congalton RG (1991), Remote sensing and geographic information system data integration: error sources and research issues, Photogramm. Eng. Remote Sensing, 57(6), 677–687. [Google Scholar]
- Crow WT, Lei F, Hain C, Anderson MC, Scott RL, Billesbach D, and Arkebauer T (2015), Robust estimates of soil moisture and latent heat flux coupling strength obtained from triple collocation, Geophys. Res. Lett, 42(20), 8415–8423, doi: 10.1002/2015GL065929. [DOI] [Google Scholar]
- Dai Y, Zeng X, Dickinson RE, Baker I, Bonan GB, Bosilovich MG, Denning AS, Dirmeyer PA, Houser PR, Niu G, and Oleson KW (2003), The common land model, Bull. Am. Meteorol. Soc, 84, 1013–1023, doi: 10.1175/BAMS-84-8-1013. [DOI] [Google Scholar]
- Dirmeyer P (2011), The terrestrial segment of soil moisture-climate coupling, Geophys. Res. Lett, 38, L16702, doi: 10.1029/2011GL048268. [DOI] [Google Scholar]
- Dirmeyer PA, Koster RD, and Guo Z (2006a), Do global models properly represent the feedback between land and atmosphere?, J. Hydrometeor, 7(6), 1177–1198, doi: 10.1175/JHM532.1. [DOI] [Google Scholar]
- Dirmeyer PA, Gao X, Zhao M, Guo Z, Oki T, and Hanasaki N (2006b), GSWP-2: Multimodel analysis and implications for our perception of the land surface, Bull. Amer. Meteor. Soc, 87(10), 1381–1398, doi: 10.1175/BAMS-87-10-1381. [DOI] [Google Scholar]
- Dirmeyer PA, Schlosser CA, and Brubaker KL (2009), Precipitation, recycling, and land memory: An integrated analysis, J. Hydrometeor, 10(1), 278–288, doi: 10.1175/2008JHM1016.1. [DOI] [Google Scholar]
- Dirmeyer PA, Chen L, Wu J, Shin C-S, Huang B, Cash BA, Bosilovich MG, Mahanama S, Koster RD, Santanello JA, Ek MB, Balsamo G, Dutra E, and Lawrence DM (2018), Verification of Land–Atmosphere Coupling in Forecast Models, Reanalyses, and Land Surface Models Using Flux Site Observations, J. Hydrometeor, 19(2), 375–392, doi: 10.1175/JHM-D-17-0152.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dorigo WA, Wagner W, Hohensinn R, Hahn S, Paulik C, Xaver A, Gruber A, Drusch M, Mecklenburg S, van Oevelen P, Robock A, and Jackson T (2011), The International Soil Moisture Network: a data hosting facility for global in situ soil moisture measurements, Hydrol. Earth Syst. Sci, 15(5), 1675–1698, doi: 10.5194/hess-15-1675-2011. [DOI] [Google Scholar]
- Dorigo W; Wagner W, Gruber A, Scanlon T, Hahn S, Kidd R, Paulik C, Reimer C, van der Schalie R, and de Jeu R (2018), ESA Soil Moisture Climate Change Initiative (Soil_Moisture_cci): Version 03.2 data collection. Centre for Environmental Data Analysis, 29 June 2018, doi: 10.5285/d2eea061026240eb8a2f9cc64a691338. [DOI] [Google Scholar]
- Dorigo W, Wagner W, Albergel C, Albrecht F, Balsamo G, Brocca L, Chung D, Ertl M, Forkel M, Gruber A, Haas E, Hamer PD, Hirschi M, Ikonen J, de Jeu R, Kidd R, Lahoz W, Liu YY, and Lecomte P (2017), ESA CCI Soil Moisture for improved Earth system understanding: state-of-the art and future directions, Remote Sens. Environ, 203, 185–215, doi: 10.1016/j.rse.2017.07.001. [DOI] [Google Scholar]
- Draper C, Reichle R, de Jeu R, Naeimi V, Parinussa R, and Wagner W (2013), Estimating root mean square errors in remotely sensed soil moisture over continental scale domains, Remote Sens. Environ, 137, 288–298, doi: 10.1016/j.rse.2013.06.013. [DOI] [Google Scholar]
- Efron B and Tibshirani RJ (1994), The bootstrap estimate of standard error In An Introduction to the Bootstrap, 1st ed; Chapman and Hall/CRC: Boca Raton, FL, USA; pp. 45–49. [Google Scholar]
- Egea G, Verhoef A, and Vidale PL (2011), Towards an improved and more flexible representation of water stress in coupled photosynthesis–stomatal conductance models, Agric. For. Meteorol, 151(10), 1370–1384, doi: 10.1016/j.agrformet.2011.05.019. [DOI] [Google Scholar]
- Ek MB, Mitchell KE, Lin Y, Rogers E, Grunmann P, Koren V, Gayno G, and Tarpley JD (2003), Implementation of Noah land surface model advances in the National Centers for Environmental Prediction operational mesoscale Eta model, J. Geophys. Res, 108(D22), 8851, doi: 10.1029/2002JD003296. [DOI] [Google Scholar]
- Eyring V, Bony S, Meehl GA, Senior CA, Stevens B, Stouffer RJ, and Taylor KE (2016), Overview of the Coupled Model Intercomparison Project Phase 6 (CMIP6) experimental design and organization, Geosci Model Dev, 9, 1937–1958, doi: 10.5194/gmd-9-1937-2016. [DOI] [Google Scholar]
- Findell KL, Gentine P, Lintner BR, and Guillod BP (2015), Data length requirements for observational estimates of land–atmosphere coupling strength, J. Hydrometeor, 16(4), 1615–1635, doi: 10.1175/JHM-D-14-0131.1. [DOI] [Google Scholar]
- Gruber A, Dorigo WA, Crow W, and Wagner W (2017), Triple Collocation-Based Merging of Satellite Soil Moisture Retrievals, IEEE Trans. Geosci. Remote Sens, 55(12), 6780–6792, doi: 10.1109/TGRS.2017.2734070. [DOI] [Google Scholar]
- Gruber A, Su C-H, Zwieback S, Crow W, Dorigo W, and Wagner W (2016a), Recent advances in (soil moisture) triple collocation analysis, Int. J. Appl. Earth Obs. Geoinf, 45, 200–211, doi: 10.1016/j.jag.2015.09.002. [DOI] [Google Scholar]
- Gruber A, Su CH, Crow W, Zwieback S, Dorigo W, and Wagner W (2016b), Estimating error cross-correlations in soil moisture data sets using extended collocation analysis, J. Geophys. Res: Atmos, 121(3), 1208–1219, doi: 10.1002/2015JD024027. [DOI] [Google Scholar]
- Guillod BP, Orlowsky B, Miralles DG, Teuling AJ, and Seneviratne SI (2015), Reconciling spatial and temporal soil moisture effects on afternoon rainfall, Nat. Commun, 6, 6443, doi: 10.1038/ncomms7443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Guo Z, Dirmeyer PA, Koster RD, Sud YC, Bonan G, Oleson KW, Chan E, Verseghy D, Cox P, Gordon CT, McGregor JL, Kanae S, Kowalczyk E, Lawrence D, Liu P, Mocko D, Lu C, Mitchell K, Malyshev S, McAvaney B, Oki T, Yamada T, Pitman A, Taylor CM, Vasic R, and Xue Y(2006), GLACE: the global land–atmosphere coupling experiment. Part II: analysis, J. Hydrometeor, 7(4), 611–625, doi: 10.1175/JHM511.1. [DOI] [Google Scholar]
- Miralles DG, van den Berg MJ, Teuling AJ, and de Jeu RAM (2012), Soil moisture-temperature coupling: A multiscale observational analysis, Geophys. Res. Lett, 39(21), L21707, doi: 10.1029/2012GL053703. [DOI] [Google Scholar]
- Hain CR and Anderson MC (2017), Estimating morning change in land surface temperature from MODIS day/night observations: Applications for surface energy balance modeling, Geophys. Res. Lett, 44(19), 9723–9733, doi: 10.1002/2017GL074952. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haughton N, Abramowitz G, Pitman AJ, Or D, Best MJ, Johnson HR, Balsamo G, Boone A, Cuntz M, Decharme B, and Dirmeyer PA (2016), The plumbing of land surface models: Is poor performance a result of methodology or data quality?, J. Hydrometeor, 17(6), pp.1705–1723, doi: 10.1175/JHM-D-15-0171.1. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes TRH, Hain CR, Crow WT, Anderson MC, and Kustas WP (2018), Microwave implementation of two-source energy balance approach for estimating evapotranspiration, Hydrol. Earth Syst. Sci, 22(2), 1351–1369, doi: 10.5194/hess-22-1351-2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Holmes TRH, Crow WT, Hain CR, Anderson M, and Kustas WP (2015), Diurnal temperature cycle as observed by thermal infrared and microwave radiometers, Remote Sens. Environ, 158, 110–125, doi: 10.1016/j.rse.2014.10.031. [DOI] [Google Scholar]
- Huber PJ (2011), Robust statistics, In International Encyclopedia of Statistical Science, pp. 1248–1251, Springer. [Google Scholar]
- Jung M, Reichstein M, Ciais P, Seneviratne SI, Sheffield J, Goulden ML, Bonan G, Cescatti A, Chen J, De Jeu R, et al. (2010), Recent decline in the global land evapotranspiration trend due to limited moisture supply, Nature, 467, 951–954, doi: 10.1038/nature09396. [DOI] [PubMed] [Google Scholar]
- Kerr YH, Waldteufel P, Wigneron JP, Delwart S, Cabot F, Boutin J, Escorihuela MJ, Font J, Reul N, Gruhier C, and Juglea SE (2010), The SMOS mission: New tool for monitoring key elements of the global water cycle, Proc. IEEE, 98(5), 666–687, doi: 10.1109/JPROC.2010.2043032. [DOI] [Google Scholar]
- Koster RD, Suarez MJ, Ducharne A, Stieglitz M, and Kumar P (2000), A catchment-based approach to modeling land surface processes in a general circulation model: 1. Model structure, J. Geophys. Res: Atmos, 105(D20), 24809–24822, doi: 10.1029/2000JD900327. [DOI] [Google Scholar]
- Koster RD, Dirmeyer PA, Guo Z, Bonan G, Chan E, Cox P, Gordon CT, Kanae S, Kowalczyk E, Lawrence D, et al. (2004), Regions of strong coupling between soil moisture and precipitation, Science, 305(5687), 1138–1140, doi: 10.1126/science.1100217. [DOI] [PubMed] [Google Scholar]
- Kottek M, Grieser J, Beck C, Rudolf B, and Rubel F (2006), World map of the Köppen-Geiger climate classification updated. Meteorologische Zeitschrift, 15(3), 259–263, doi: 10.1127/0941-2948/2006/0130. [DOI] [Google Scholar]
- Kumar SV, Dirmeyer PA, Peters-Lidard CD, Bindlish R, and Bolten J (2018), Information theoretic evaluation of satellite soil moisture retrievals, Remote Sens. Environ, 204, 392–400, doi: 10.1016/j.rse.2017.10.016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li F, Kustas WP, Anderson MC, Jackson TJ, Bindlish R, and Prueger JH (2006), Comparing the utility of microwave and thermal remote-sensing constraints in two-source modeling over an agricultural landscape, Remote Sens. Environ, 101, 315–329, doi: 10.1016/j.rse.2006.01.001. [DOI] [Google Scholar]
- Liang X, Lettenmaier D, Wood EF, and Burges SJ (1994), A simple hydrologically based model of land surface water and energy fluxes for GSMs, J. Geophys. Res, 99(D7), 14,415–14,428, doi: 10.1029/94JD00483. [DOI] [Google Scholar]
- Loew A, Bell W, Brocca L, Bulgin CE, Burdanowitz J, Calbet X, Donner RV, Ghent D, Gruber A, and Kaminski T (2017), Validation practices for satellite based earth observation data across communities, Rev. Geophys, 55(3), doi: 10.1002/2017RG000562. [DOI] [Google Scholar]
- Liu YY, Dorigo WA, Parinussa RM, de Jeu RA, Wagner W, McCabe MF, P Evans J, and van Dijk AIJN (2012), Trend-preserving blending of passive and active microwave soil moisture retrievals, Remote Sens. Environ, 123, 280–297, doi: 10.1016/j.rse.2012.03.014. [DOI] [Google Scholar]
- McColl KA, Vogelzang J, Konings AG, Entekhabi D, Piles M, and Stoffelen A (2014), Extended triple collocation: Estimating errors and correlation coefficients with respect to an unknown target, Geophys. Res. Lett, 41(17), 6229–6236, doi: 10.1002/2014GL061322. [DOI] [Google Scholar]
- Naeimi V, Scipal K, Bartalis Z, Hasenauer S, and Wagner W (2009), An improved soil moisture retrieval algorithm for ERS and METOP scatterometer observations, IEEE Trans. Geosci. Remote Sens, 47(7), 1999–2013, doi: 10.1109/TGRS.2008.2011617. [DOI] [Google Scholar]
- Niu GY, Yang ZL, Mitchell KE, Chen F, Ek MB, Barlage M, Kumar A, Manning K, Niyogi D, Rosero E, Tewari M, and Xia Y (2011), The community Noah land surface model with multiparameterization options (Noah-MP): 1. Model description and evaluation with local-scale measurements, J. Geophys. Res: Atmos, 116(D12), doi: 10.1029/2010JD015139. [DOI] [Google Scholar]
- Njoku EG, Jackson TJ, Lakshmi V, Chan TK, and Nghiem SV (2003), Soil moisture retrieval from AMSR-E, IEEE Trans. Geosci. Remote Sens, 41(2), 215–229, doi: 10.1109/TGRS.2002.808243. [DOI] [Google Scholar]
- Owe M, de Jeu R, and Holmes T (2008), Multisensor historical climatology of satellite-derived global land surface moisture, J. Geophys. Res: Earth Surf, 113(F1), doi: 10.1029/2007JF000769. [DOI] [Google Scholar]
- Parinussa RM, Holmes TRH, and de Jeu RAM (2012), Soil moisture retrievals from the WindSat spaceborne polarimetric microwave radiometer, IEEE Trans. Geosci. Remote Sens, 50(7), 2683–2694, doi: 10.1109/TGRS.2011.2174643. [DOI] [Google Scholar]
- Parinussa RM, Holmes TR, Wanders N, Dorigo WA, and de Jeu RAM (2015), A preliminary study toward consistent soil moisture from AMSR2, J. Hydrometeor, 16(2), 932–947, doi: 10.1175/JHM-D-13-0200.1. [DOI] [Google Scholar]
- Phillips TJ and Klein SA (2014), Land-atmosphere coupling manifested in warm-season observations on the U.S. southern great plains, J. Geophys. Res.: Atmos, 119(2), 509–528, doi: 10.1002/2013JD020492. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rodell M, Houser PR, Jambor U, Gottschalck J, Mitchell K, Meng C, Arsenault K, Cosgrove B, Radakovich J, Bosilovich M, Entin JK, Walker JP, Lohmann D, and Toll D (2004), The global land data assimilation system, Bull. Amer. Meteor. Soc, 85(3), 381–394, doi: 10.1175/BAMS-85-3-381. [DOI] [Google Scholar]
- Saha S, Moorthi S, Pan H-L, Wu X, Wang J, Nadiga S, Tripp P, Kistler R, Woollen J, Behringer D, et al. (2010), The NCEP climate forecast system reanalysis, Bull. Amer. Meteor. Soc, 91(8), 1015–1058, doi: 10.1175/2010BAMS3001.1. [DOI] [Google Scholar]
- Saha S, Moorthi S, Wu X, Wang J, Nadiga S, Tripp P, Behringer D, Hou YT, Chuang H.-y., Iredell M, Ek M, Meng J, Yang R, Mendez MP, van den Dool H, Zhang Q, Wang W, Chen M, and Becker E (2014), The NCEP climate forecast system version 2, J. Clim, 27(6), 2185–2208, doi: 10.1175/JCLI-D-12-00823.1. [DOI] [Google Scholar]
- Seneviratne SI, Corti T, Davin EL, Hirschi M, Jaeger EB, Lehner I, Orlowsky B, and Teuling AJ (2010), Investigating soil moisture–climate interactions in a changing climate: A review, Earth Sci. Rev, 99(3), 125–161, doi: 10.1016/j.earscirev.2010.02.004. [DOI] [Google Scholar]
- Seneviratne SI, Wilhelm M, Stanelle T, Hurk B, Hagemann S, Berg A, Cheruy F, Higgins ME, Meier A, Brovkin V, et al. (2013), Impact of soil moisture-climate feedbacks on CMIP5 projections: First results from the GLACE-CMIP5 experiment, Geophys. Res. Lett, 40(19), 5212–5217, doi: 10.1002/grl.50956. [DOI] [Google Scholar]
- Sörensson AA, and Ruscica RC (2018), Intercomparison and Uncertainty Assessment of Nine Evapotranspiration Estimates Over South America, Water Resour. Res, 54(4), 2891–2908, doi: 10.1002/2017WR021682. [DOI] [Google Scholar]
- Stoffelen A (1998), Toward the true near-surface wind speed: Error modeling and calibration using triple collocation, J. Geophys. Res.: Oceans (1978–2012), 103(C4), 7755–7766, doi: 10.1029/97JC03180. [DOI] [Google Scholar]
- Su CH, Ryu D, Crow WT, and Western AW (2014), Beyond triple collocation: Applications to soil moisture monitoring, J. Geophys. Res.: Atmos, 119(11), 6419–6439, doi: 10.1002/2013JD021043. [DOI] [Google Scholar]
- Teuling AJ, Uijlenhoet R, and Troch PA (2005), On bimodality in warm season soil moisture observations, Geophys. Res. Lett, 32, L13402, doi: 10.1029/2005GL023223. [DOI] [Google Scholar]
- Tuttle S and Salvucci G (2016), Empirical evidence of contrasting soil moisture-precipitation feedbacks across the United States, Science, 352(6287), 825–828, doi: 10.1126/science.aaa7185. [DOI] [PubMed] [Google Scholar]
- Ukkola A, De Kauwe M, Pitman A, Best M, Abramowitz G, Haverd V, Decker M, and Haughton N (2016), Land surface models systematically overestimate the intensity, duration and magnitude of seasonal-scale evaporative droughts, Environ. Res. Lett, 11(10), 104012. [Google Scholar]
- Ukkola AM, Pitman AJ, and De Kauwe MG, Abramowitz G, Kala J, and Wang Y-P(2016), Modelling evapotranspiration during precipitation deficits: identifying critical processes in a land surface model, Hydrol. Earth Syst. Sci, 20(6), 2403–2419, doi: 10.5194/hess-20-2403-2016. [DOI] [Google Scholar]
- Van den Hurk B, Best M, Dirmeyer P, Pitman A, Polcher J, and Santanello J (2011), Acceleration of land surface model development over a decade of GLASS, Bull. Amer. Meteor. Soc, 92(12), 1593–1600, doi: 10.1175/BAMS-D-11-00007.1. [DOI] [Google Scholar]
- Van den Hurk B, Kim H, Krinner G, Seneviratne SI, Derksen C, Oki T, Douville H, Colin J, Ducharne A, Cheruy F, Viovy N, et al. (2016), LS3MIP (v1.0) contribution to CMIP6: the Land Surface, Snow and Soil moisture Model Intercomparison Porject-aims, setup and expected outcome, Geosci Model Dev, 9, 2809–2832, doi: 10.5194/gmd-9-2809-2016. [DOI] [Google Scholar]
- Wielicki BA, Barkstrom BR, Harrison EF, Lee III RB, L Smith G, and Cooper JE (1996), Clouds and the Earth’s Radiant Energy System (CERES): An earth observing system experiment, Bull. Amer. Meteor. Soc, 77(5), 853–868, doi:. [DOI] [Google Scholar]