Evidence of Unlimited-Capacity Surface Completion

Abstract

Capacity limitations of perceptual surface completion were assessed using a simultaneous–sequential method. Observers searched among multiple surfaces requiring perceptual completion in front of other objects (modal completion) or behind other objects (amodal completion). In the simultaneous condition, all surfaces were presented at once, whereas in the sequential condition, they appeared in subsets of 2 at a time. For both modal and amodal surface completion, performance was as good in the simultaneous condition as in the sequential condition, indicating that surface completion unfolds independently for multiple surfaces across the visual field (i.e., has unlimited capacity). We confirmed this was due to the formation of surfaces defined by the pacmen inducers, and not simply to the detection of individual features of the pacmen inducers. These results provide evidence that surface-completion processes can be engaged and unfold independently for multiple surfaces across the visual field. In other words, surface completion can occur through unlimited-capacity processes. These results contribute to a developing understanding of capacity limitations in perceptual processing more generally.

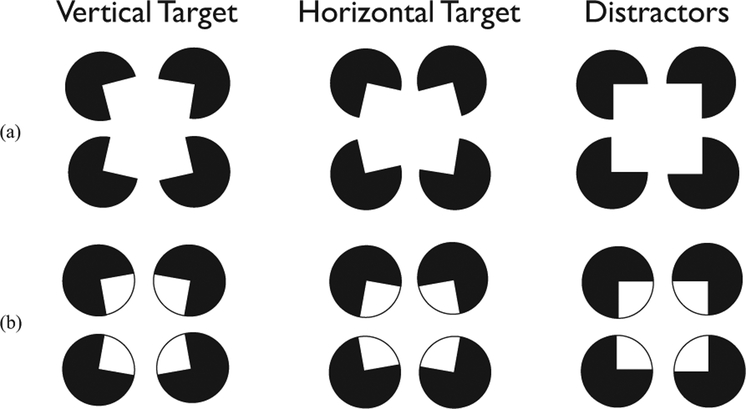
The world consists of objects in three dimensions, making it unusual to view surfaces that are unobstructed by other surfaces. In some cases, the alignment of explicit edges and matched features gives rise to the appearance of a surface that is occluding other surfaces (i.e., is between the observer and the other surface). The apparent white square in front of four black disks in Figure 1a illustrates this kind of surface completion, which is known as modal completion (Kanizsa, 1955, 1979). In other cases, the alignment of edges can give rise to the representation of a completed surface behind an occluding object, though the occluded surface is not perceived directly. The apparent white square viewed through four apertures in Figure 1b illustrates this kind of surface completion, which is known as amodal completion (e.g., Anderson, Singh, & Fleming, 2002; Ringach & Shapley, 1996). Critically, for both types of surface completion, there are no local stimulus correlates in the retinal image to the completed parts of the surface.

Figure 1.

In Experiment 1, targets and distractors were modally completed surfaces (a). In Experiment 2, targets and distractors were amodally completed surfaces (b).

Surface representation is recognized as a fundamental aspect of visual processing (Gibson, 1979; Marr, 1982; Nakayama, He, & Shimojo, 1995). Theories differ, however, whether the initial establishment of surface representations depends on limited-capacity processes or whether it can occur entirely through unlimited-capacity processes. Unlimited-capacity processes are those that unfold independently for multiple stimuli. Limited-capacity processes are ones that become less effective for a given stimulus as they are engaged by more stimuli. Limited-capacity processes may be serial (i.e., only one stimulus can be processed at a time); this is an extreme of limited capacity. However, limited-capacity processes can also be parallel; multiple stimuli may be processed simultaneously, but they are processed less effectively than when processed alone. The terms limited versus unlimited are indicators of dependence or independence of processing, respectively, rather than amount of processing.

Many theories maintain that only processes that extract basic feature information (e.g., orientation, luminance contrast, color) are unlimited-capacity processes. According to these theories, processes that combine, or otherwise transform, feature representations to allow for object recognition and other functions are limited-capacity processes (e.g., Biederman, 1987; Treisman & Gelade, 1980; Wolfe, Cave, & Franzel, 1989). Others have argued that at least some more complex representations, such as conjunctions of features and shape information, can be established through unlimited-capacity processes (e.g., Davis & Driver, 1994; Rensink & Enns, 1995, 1998; Mordkoff & Danek, 2011).

Herein, we focused on the establishment of surface representations. One reason for this focus is that the assertion that only feature extraction is achieved through unlimited-capacity processes predicts that surface completion will show evidence of engaging limited-capacity processes. This follows because there are no local stimulus correlates (i.e., something defined by features) in the retinal image that corresponds to the surfaces that are perceived. Surface completion, therefore, requires processing beyond feature extraction. Asking whether surface completion requires limited-capacity processes can therefore test this assertion. A related reason for the focus of this study derives from a view put forward by Nakayama et al. (1995), which states that surfaces, not features, are the primary representations of visual perception out of which more complex representations are formed (see Nakayama et al., 1995, for a review). As such, surfaces are likely to be extracted through processes that unfold independently across the visual field, that is, through unlimited-capacity processes. Evidence of unlimited-capacity surface completion would therefore be consistent with this view, and would be inconsistent with the view that only features are primary representations.

To test whether surface completion can be achieved through unlimited-capacity processes, we used a version of the simultaneous–sequential method (Eriksen & Spencer, 1969; Shiffrin & Gardner, 1972) that was used by Scharff, Palmer, and Moore (2011a) to demonstrate, in part, that contrast detection is unlimited capacity. The simultaneous–sequential method minimizes concerns that are associated with other methods that have been used to assess capacity limitations, such as measuring the effects of increasing the number of stimuli (i.e., set size; e.g., Davis & Driver, 1994; Grabowecky & Treisman, 1989; Li, Cave, & Wolfe, 2008) or measuring the effects of dual over single tasks. Both of these other methods can be problematic, because various aspects of task difficulty—separate from capacity limitations—can contribute to the measured effects (Duncan, 1980; Eckstein, Thomas, Palmer, & Shimozaki, 2000; Huang & Pashler, 2005; Palmer, 1994; Pashler, 1998; Shaw, 1984; Townsend, 1990; Wolfe, 2003). Differences in the number of decisions that must be made across conditions is an example. The simultaneous–sequential method overcomes these concerns by equating both the number of tasks that must be done (always a single task) and the number of stimuli to be processed across conditions. Critically, the total amount of exposure time for any given stimulus is also equated across conditions. What varies is how many stimuli must be processed at the same time, all of them (simultaneous condition) or only subsets of them (sequential). Finally, exposure time is relatively brief and/or stimulus quality is relatively poor in order to ensure that there is an advantage to be gained in the sequential condition, assuming that processing is limited capacity. Unlimited-capacity processing predicts no difference in performance between the simultaneous and sequential conditions. This follows because, if a process is an unlimited-capacity process, then, barring physical interference, it should make no difference how many stimuli must be processed at any given time. In contrast, limited-capacity processing predicts an advantage for sequential over simultaneous presentation, because processing capacity will be divided across fewer stimuli in the sequential condition than in the simultaneous condition at any given time.

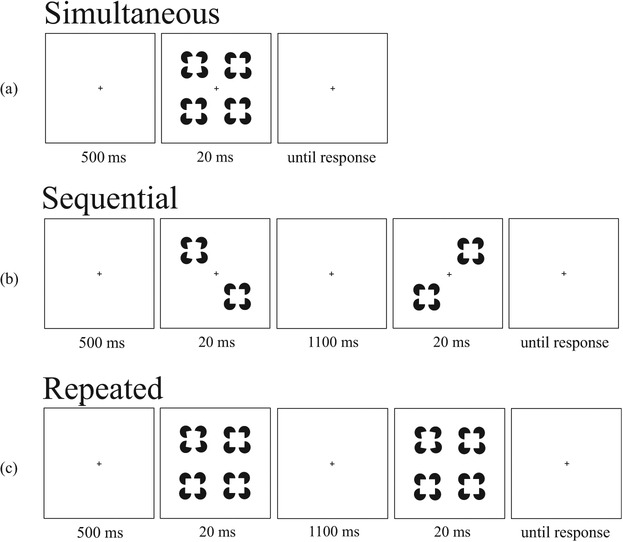
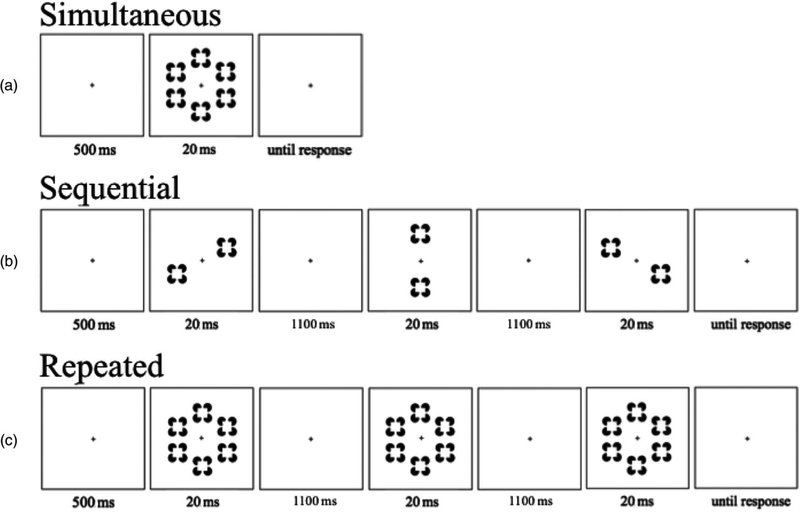
In our study, observers searched for a single target surface among a set of three distractor surfaces (see Figure 1). The target was elongated, either horizontally or vertically, by rotating the pacmen inducers (Ringach & Shapley, 1996). The distractors were square. Surfaces were defined either on the basis of modal completion (Experiment 1) or amodal completion (Experiment 2). Thus, to do this task, surface completion must occur. In the simultaneous condition, all search items were presented at the same time (see Figure 2a). In the sequential condition, the same search items were presented in subsets of two, one subset at a time (see Figure 2b). Notice that any given surface was available for exactly the same amount of time across these two conditions. Following Scharff et al. (2011a), we included a repeated condition, which was the same as the simultaneous condition, except that the whole display was repeated a second time, thereby providing twice the amount of time available to sample the stimulus (see Figure 2c). Observing an advantage in the repeated condition over the simultaneous condition is critical to the logic. It ensures that there was an advantage to be gained through more processing time and, therefore, if no difference in performance occurs between the simultaneous and the sequential conditions, it is not because the timing was such that all stimuli could be processed regardless of capacity limitations. The repeated condition also allows for a test of a specific version of limited capacity. If completion processes are extremely limited capacity, such that only a fixed amount of information (e.g., a single surface) can be processed at one time (i.e., it is fixed capacity), then the sequential condition may be as good as the repeated condition (see Scharff et al., 2011a, for a formal account of these predictions).

Figure 2.

On each trial, observers saw four surfaces (one target, three distractors) and reported whether the orientation of the target surface was “horizontal” or “vertical.” In this example, the target is vertical and located in the upper left. Stimuli were presented in the following three conditions. In the simultaneous condition, all four search items are presented at once (a). In the sequential condition, the same search items are presented, but divided into subsets of two across sequential frames (b). In the repeated condition, all four search items are presented across sequential frames in the same configuration (c).

Experiments 1 and 2: Testing the Processing Capacity Limitations of Modal and Amodal Surface Completion

Method

Observers.

Ten observers from the University of Iowa were tested in each of the first two experiments (Experiment 1: two men, eight women, age range: 20–43 years; Experiment 2: two men, eight women, age range: 19–43 years). All were volunteers from within the laboratory. Two of the coauthors participated in the experiment while the remaining observers were naive as to the purpose of the study. All observers reported normal or corrected-to-normal visual acuity and color vision.

Equipment.

Stimuli were displayed on a flat-screen CRT monitor (19-inch ViewSonic G90fB) controlled by a Macintosh Pro (Mac OS X) with a 512MB NVIDEA GeForce 8800 GT graphics card (1024 × 768 pixels, viewing distance = 65 cm, horizontal refresh rate = 100 Hz). Stimuli were generated using the Psychophysics Toolbox, Version 3.0.8 (Brainard, 1997; Pelli, 1997) for MATLAB, Version 7.5 (The MathWorks, Natick, MA). Observers were seated in a height-adjustable chair in front of the display, and used an adjustable chin rest to maintain a constant distance from the monitor.

Stimuli.

Displays consisted of 16 black (4 cd/m²) pacmen inducers (1.2° in diameter with a 90° segment) presented on a gray (71 cd/m²) background. Each inducer was 1.2° in diameter with a 90° segment (“mouth”) removed. The inducers were configured to give rise to the perception of four surfaces centered 3.1° from fixation. The shape of the surfaces (i.e., square, horizontal, or vertical) was manipulated by the angle rotation of the pacmen inducers (Kanizsa, 1955, 1979; Ringach & Shapley, 1996). No rotation of the inducers produced a square distractor, while a 6° angle of rotation in the appropriate directions produced a curvilinear rectangle that was oriented either horizontally or vertically.

The pacman closest to fixation was 1.8° away, and the pacman furthest from fixation was 4.9° away. The surfaces were separated horizontally and vertically by 1.6° measured edge-to-edge. To support amodal completion in Experiment 2, a black arc was drawn across the open segment of the inducers. The addition of these arcs removed the subjective square, which biased the implied surfaces to be seen through apertures (Anderson et al., 2002; Ringach & Shapley, 1996).

Task.

The task was to find and report whether the curvilinear item (the target) was horizontal or vertical by pressing the “F” or “J” key, respectively. Observers were instructed to maintain central fixation and to respond as accurately as possible.

Procedure.

Observers completed eight 45-min sessions on separate days. Each of the eight sessions consisted of 288 experimental trials divided into six blocks (96 observations per condition). The first two sessions were considered practice and served to familiarize participants to the task. All practice sessions were excluded from the data analysis. This resulted in 576 observations per display per observer.

Trials began with a centrally located black fixation cross (0.8° × 0.8°) for 500 ms. In the simultaneous condition, this was followed by the four surfaces for 20 ms, and then a blank screen until response. In the sequential condition, fixation was followed by two surfaces for 20 ms presented along either the positive or the negative diagonal, a blank interstimulus interval (ISI) of 1,100 ms, the other two surfaces for 20 ms presented along the opposite diagonal, and a blank screen until response. The repeated condition was the same as the sequential condition, except that all four surfaces appeared in both of the two 20 ms displays. Written feedback was given in the form of words “correct” or “incorrect” at fixation following each response. The next trial automatically began 1,000 ms after the presentation of feedback.

Display condition (simultaneous, sequential, repeated), target type (horizontal, vertical), and target position (upper-left, upper-right, lower-left, lower-right) were randomly mixed within blocks of trials and appeared equally often. Which of the two diagonally opposite positions were presented first in the sequential display was constant for a given observer, but varied across observers. The purpose of this was to eliminate uncertainty of presentation positions.

Results

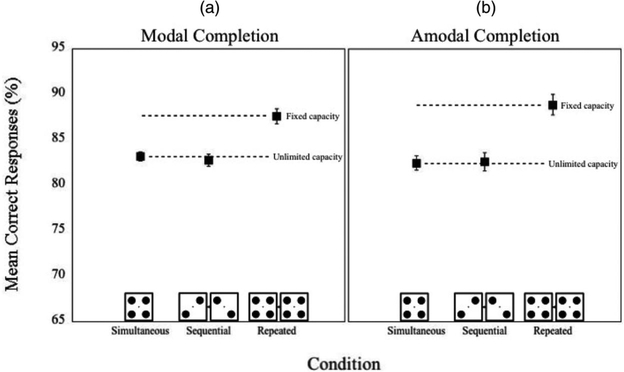
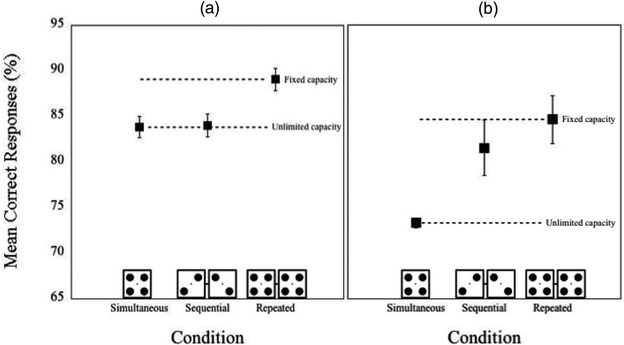
The results of Experiment 1 were consistent with an unlimited-capacity modal of surface completion. Figure 3a shows the mean percent correct as a function of condition collapsed across observers for Experiment 1. Overall, there was a significant effect of display condition, F(2, 18) = 16.25, p < .001, mean square error (MSE) = 4.44, ${\eta }_{\text{p}}^2=0.64$. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (82.8%) than in the simultaneous condition (83.1%), t(9) = 0.55, ns; however, accuracy was significantly greater in the repeated condition (87.6%) compared with the sequential condition, t(9) = 4.26, p < .01.

Figure 3.

Mean correct responses as a function of display collapsed across observers in Experiments 1 and 2. We found equal performance across the simultaneous and sequential conditions, and a reliable advantage in the repeated condition. This suggests that both modal (a) and amodal (b) surface completion engage only unlimited-capacity processes. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Morey, 2008).

The results of Experiment 2, summarized in Figure 3b, were also consistent with unlimited-capacity surface completion, in this case, amodal completion. Again, there was a significant effect of display condition, F(2, 18) = 14.21, p < .001, MSE = 9.48, ${\eta }_{\text{p}}^2=0.61$. Accuracy was not reliably greater in the sequential condition (82.6%) than in the simultaneous condition (82.4%), t(9) = 0.13, ns. Accuracy was significantly greater in the repeated condition (88.9%) than in the sequential condition, t(9) = 3.93, p < .01.

A critical assumption of the simultaneous–sequential method is that the conditions differ only with respect to when the stimuli are processed. However, in the simultaneous condition, the target always appeared in the “first” frame because there was only one frame, whereas, in the sequential condition, the target could appear in either the first or the second frame. This difference could provide an advantage to the simultaneous condition due to memory differences across the two conditions. To assess this, we compared performance in the sequential condition for trials in which the target appeared in the first and second frames. No reliable differences were observed, Experiment 1: 82.2% (first frame) versus 83.5% (second frame), t(9) = 0.38, ns; Experiment 2: 80.7% (first frame) versus 84.6% (second frame), t(9) = 1.29, ns.

In summary, we found evidence of unlimited-capacity processing when we used stimuli that supported both modal and amodal surface completion. Furthermore, the reliable difference in performance for repeated over sequential conditions ensures that there was an advantage to be gained through more processing time. The repeated advantage also demonstrates that these experiments had the power to detect a fixed-capacity limit.

Experiment 3: Target Identification Depends on Forming a Surface Representation

The similar performance across the simultaneous and sequential conditions in Experiments 1 and 2 was taken as evidence that both modal and amodal surface completion can be done entirely through unlimited-capacity processes. It is possible, however, that the task could be done based on simple features. Specifically, the horizontal and vertical targets differed with respect to the edge curvature of the local pacmen inducers, in addition to the global orientation defined by the emerging surface (Ringach & Shapley, 1996). A concern, therefore, is that observers adopted the strategy simply to search for particular angles of local pacmen inducers that defined the horizontal and vertical targets (see Figure 1) and could report “horizontal” versus “vertical” without depending on surface completion. What looks like evidence of unlimited-capacity surface completion, therefore, might instead reflect unlimited-capacity feature detection.

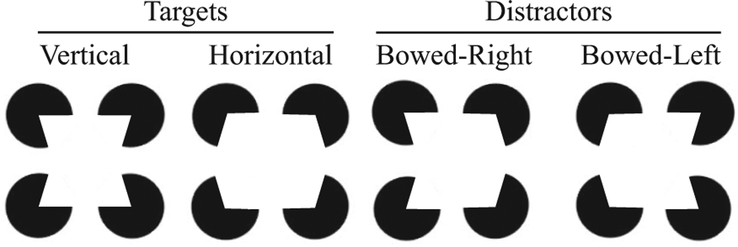
Experiment 3 was conducted to address this possibility. We prevented observers from using local pacmen angles by changing the displays and the task such that any single pacman was uninformative with regard to target identity (see Figure 4). The wedges of the pacmen mouths were increased or decreased from the original 90° to form a new set of targets and distractors. Specifically, they were increased from 90° to 105° to create an illusory surface of a horizontally elongated target or decreased from 90° to 75° to create a vertically elongated surface. One of these targets was randomly chosen and presented among three distractor surfaces. Distractors contained both types of increased-from-90° or decreased-from-90° angle types, producing surfaces that appeared to bow left or bow right. Because the target and distractors within each display contained identical angle types, it was not possible to perform the task on the basis of any single inducer.

Figure 4.

Target and distractor surfaces used in Experiments 3. Observers searched for a vertically or a horizontally elongated target among three distractor items. Bowed-left or bowed-right distractor items were chosen randomly on a trial-to-trial basis to occupy the remaining three locations. These stimuli eliminate a potential strategy to use the angle of single pacmen inducers to perform the task because targets and distractors are 50% identical.

Method

The methods were the same as in Experiment 1, with the following exceptions.

Observers.

Six observers participated in this experiment (one man, five women, age range: 21–44 years). All were volunteers from within the laboratory, and reported normal or corrected-to-normal visual acuity and color vision. All observers were naive to the purpose of the experiment prior to being tested, except for the two coauthors.

Stimuli.

The mouths of the pacmen inducers were either increased or decreased from 90° by 15° to create acute or obtuse angles. The vertical target was composed of all acute inducer angles, while the horizontal target was composed of all obtuse inducer angles. Of the four inducers that formed each distractor surface, two had acute and two had obtuse angles (see Figure 4). Acute angles appeared either on the left or the right side of each distractor surface, forming the perception of surfaces that either bowed right or bowed left, respectively. Which distractor appeared (i.e., bowed left or bowed right) in the remaining three locations was chosen randomly trial-to-trial.

Observers completed eight 45-min sessions on separate days. Excluding two practice sessions, this resulted in 576 observations per display per observer.

Task.

Observers searched for either a vertically or a horizontally elongated target among three distractor items. Observers reported which one of two targets was present by pressing “F” or “J” on the computer keyboard. Instructions emphasized to maintain central fixation and to respond as accurately as possible without trying to make responses quickly.

Results

The results of Experiment 3 were consistent with unlimited-capacity processing. Figure 5a shows the mean percent correct as a function of condition collapsed across observers. Overall, there was a significant effect of display condition, F(2, 10) = 5.91, p < .05, MSE = 8.93, ${\eta }_{\text{p}}^2=0.54$. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (84.0%) than in the simultaneous condition (83.9%), t(5) = 0.08, ns; however, accuracy was significantly greater in the repeated condition (89.1%) compared with the sequential condition, t(5) = 2.89, p < .05.

Figure 5.

Mean correct responses as a function of display collapsed across observers in Experiment 3. Evidence consistent with unlimited capacity was obtained for surfaces that could not be discriminated on the basis of single pacmen inducers (a). Evidence of fixed capacity was obtained when either the top or bottom half of each surface from Figure 4 was removed and participants were forced to complete the task by using the relative angle position of two inducers (b). Based on the results of these control experiments, we concluded that observers in Experiments 1 and 2 used a surface representation to perform the task and not the position of either single inducers or the relative alignment of a couple inducers. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Morey, 2008).

For sequential trials, performance did not differ reliably when the target appeared in the first frame (84.7%) compared with the second frame (83.3%), t(5) = 0.31, ns, indicating that targets presented first did not suffer from more memory loss than targets presented closer in time to response.

In summary, we found evidence of unlimited-capacity processing even when observers could not complete the task on the basis of individual inducers.

Although unlikely, it is possible that observers in this control experiment still bypassed searching among surfaces, completing the task instead by searching through the relative orientation of two pacmen angles from either the top half or bottom half of each surface-forming group. To rule out this concern, we conducted a follow-up experiment in which we removed either the bottom two (lower left, lower right) or the top two (top left, top right) pacmen from each surface. This forced observers to use only one half of the display to do the task. If this experiment fails to produce evidence of unlimited-capacity processing, we can safely conclude that the unlimited-capacity processing observed in Experiment 3 was not caused by observers relying on only part of the display.

The follow-up experiment yielded evidence of fixed-capacity processing. Figure 5b shows the mean percent correct as a function of condition collapsed across observers. There was a significant effect of display condition, F(2, 6) = 6.82, p < .05, MSE = 20.066, ${\eta }_{\text{p}}^2=0.70$. As predicted by fixed-capacity processing, accuracy was not reliably greater in the sequential condition (81.5%) than in the repeated condition (84.6%), t(3) = 1.05, ns; however, accuracy was significantly lower in the simultaneous condition (73.3%) compared with the repeated condition, t(3) = 6.491, p < .01. For sequential trials, targets presented first (85.7%) did not suffer from more memory loss than targets presented closer in time to response (77.3%), t(3) = 1.396, ns. This result strengthens our case that strategies that involve isolating the orientation of the local pacmen inducers did not drive our unlimited capacity finding in previous experiments. Thus, participants must have formed a surface representation. Further, this follow-up to our control experiment demonstrates that it is possible to obtain evidence of limited capacity using the simultaneous–sequential method.

Experiment 4: Generalizing From Four Surfaces to Six Surfaces

In a fourth experiment, we generalized the results from the previous experiments by extending the total number of surfaces from four to six. A concern with the simultaneous–sequential method is that if too many stimuli are used, there can be differences due to sensory interference, such as masking or crowding, between the simultaneous and sequential conditions that do not reflect differences in the process in question. However, to demonstrate the generality of the unlimited-capacity finding for surface completion, we increased the total number of surfaces from four to six. A total of six modally defined surfaces were presented in the simultaneous condition, whereas three sets of two modally defined surfaces were presented, one subset at a time, in the sequential condition.

Method

The methods were the same as in Experiment 1, with the following exceptions.

Observers.

Four observers participated in this experiment (one man, three women, age range: 21–46 years). All were volunteers from within the laboratory and reported normal or corrected-to-normal visual acuity and color vision. All observers were naive to the purpose of the experiment prior to being tested, except for two coauthors.

Stimuli.

Example stimuli are shown in Figure 6. Twenty-four black pacmen inducers were configured to give rise to the perception of six surfaces arranged along an imaginary circle around fixation. Each inducer was 1.2° in diameter with a 90° segment removed. The centers of the implied surfaces were 4.0° from fixation. The pacman closest to fixation was 2.2° away, and the pacman furthest from fixation was 5.3° away. The surfaces were separated horizontally and vertically by 0.9° measured edge-to-edge. Note that each additional surface increased the number of items in the display by four. For this reason, it is difficult to increase the display size beyond six without introducing factors unrelated to surface processing, such as sensory interference and crowding.

Figure 6.

On each trial, observers saw six surfaces (one target, five distractors) and reported whether the orientation of the target surface was “horizontal” or “vertical.” In this example, the target is vertical and located in the upper right. Stimuli were presented in the following three conditions. In the simultaneous display, all six search items were presented at once (a). In the sequential display, the same search items were presented, but divided into subsets of two across three sequential frames (b). In the repeated display, all six items were presented in the same configuration across three sequential frames (c).

Procedure.

In simultaneous displays, six stimuli—a single target and five distractors—were presented in the same frame for 20 ms. In sequential displays, the six stimuli were presented two at a time in diagonally opposite positions for 20 ms, separated by a blank frame of 1,100 ms. The order in which the diagonals were presented was fixed for a given observer, but counterbalanced across observers. In repeated displays, all six items were presented in the same configuration across three sequential displays, which provided three chances to find the target.

As before, the shape of the surfaces (i.e., square, horizontal, or vertical) was manipulated by the angle rotation of the pacmen inducers (Ringach & Shapley, 1996). No rotation of the inducers produced a square distractor, while a 6° angle of rotation in the appropriate directions produced a curvilinear rectangle that was oriented either horizontally or vertically. Each session consisted of 216 trials divided into six blocks (72 observations per condition).

Task.

Observers searched for either a vertically or a horizontally elongated target among five distractor items. Observers reported which one of two targets was present by pressing “F” or “J” on the computer keyboard. Instructions emphasized to maintain central fixation and to respond as accurately as possible without trying to make responses quickly.

Results

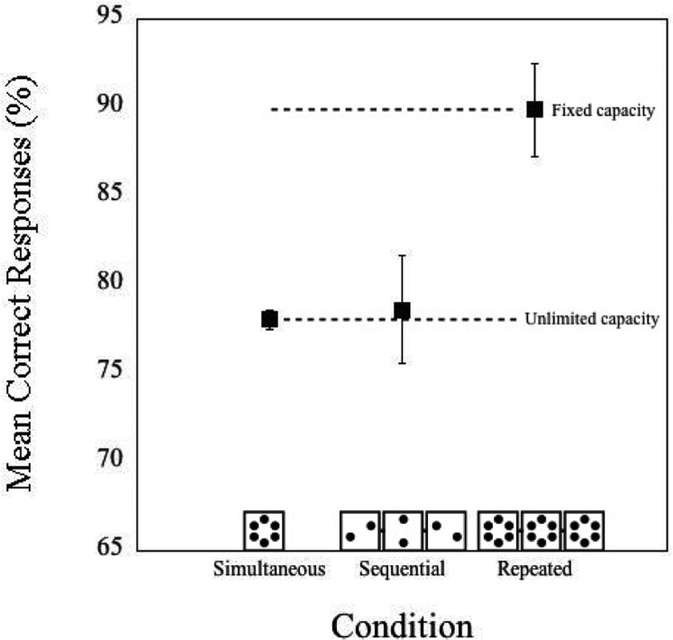
The results of Experiment 4 were consistent with unlimited-capacity processing. Figure 7 shows the mean percent correct as a function of condition collapsed across observers. Overall, there was a significant effect of display condition, F(2, 6) = 8.10, p = .02, MSE = 22.02, ${\eta }_{\text{p}}^2=0.73$. As predicted by unlimited-capacity processing, accuracy was not reliably greater in the sequential condition (78.6%) than in the simultaneous condition (78.0%), t(3) = 0.18, ns; however, accuracy in the repeated condition was significantly higher than in the sequential condition (89.9%), t(3) = 3.572, p < .05.

Figure 7.

Mean correct responses as a function of display collapsed across observers in Experiment 4. We demonstrated the generality of unlimited-capacity surface processing by showing equal performance across the simultaneous and sequential conditions, even for six stimuli. Error bars are within-subject 95% confidence intervals (Cousineau, 2005; Morey, 2008).

We compared performance within sequential trials when the target was presented in the first frame and when the target was presented in the third frame. We found that performance across both frames were statistically equal, 77.1% (first frame) versus 78.8% (third frame), t(3) = 0.22, ns, suggesting that targets presented first did not suffer from more memory loss than targets presented closer in time to response.

In summary, we found evidence of unlimited-capacity processing. Participants searched through two surfaces at a given time just as accurately as they searched through six surfaces at once. These results demonstrate the generality of the unlimited-capacity finding when more than four surfaces require representation.

General Discussion

Applying the simultaneous–sequential method to whether surface completion can occur through unlimited-capacity processes, we found evidence that it can. Observers were able to process up to six surfaces that required perceptual completion simultaneously just as well as they were able to process them in subsets of two sequentially. This is the hallmark pattern of unlimited-capacity processing (Shiffrin & Gardner, 1972).

These findings are consistent with previous claims that surface completion is spatially parallel and that it occurs early within the stream of visual information processing (Davis & Driver, 1994; Gurnsey, Humphrey, & Kapitan, 1992; He & Nakayama, 1992; Kimchi & Peterson, 2008; Moore, Elsinger, & Lleras, 2001; Peterhans & von der Heydt, 1991; Rensink & Enns, 1995, 1998; von der Heydt, Zhou, & Friedman, 2003). The surfaces in this study must have been processed in parallel because the alternative—serial processing—is an extreme form of limited-capacity processing, and no evidence was observed for any kind of limited-capacity processing. The current findings are consistent with claims that surface completion occurs early within the stream of visual information processing, insofar as late processing tends to be limited capacity. Finally, a specific version of the hypothesis that surface representations are established in parallel and early within the stream of visual information processing is the assertion of Nakayama et al. (1995) that surfaces are the primary visual representations, rather than features. The current results lend further credence to that view in that they show that surface representations, like feature representations, can be established through unlimited-capacity processes.

The application of the simultaneous–sequential method to surface completion also contributes to a developing picture of capacity limitations in perceptual processing more generally. An early application of the extended version of this method (i.e., inclusion of the repeated condition) compared contrast discrimination and word categorization because these two tasks were, on the surface, expected to have extremely different capacity limitations (Scharff et al., 2011a). Confirming this expectation, contrast discrimination yielded results that were consistent with unlimited-capacity processing, whereas word categorization yielded results that were consistent not just with limited capacity, but with fixed-capacity processing, something that is predicted by serial models of reading (e.g., Rayner & Posnansky, 1978). Thus, these two tasks—contrast discrimination and word categorization—constitute extreme conditions, representing unlimited-capacity processing, on the one hand, and maximally limited-capacity (i.e., fixed-capacity) processing, on the other. In contrast to word categorization, Shiffrin and Gardner (1972) had found evidence of unlimited-capacity letter identification. Together, the results indicate that at some point in processing, between letter identification and word categorization, a severe processing limitation ensues.

Returning to nonverbal stimuli, another study applied the extended simultaneous–sequential method to object categorization (e.g., photographs of foxes vs. deer) and found, like word categorization, evidence of fixed-capacity processing (Scharff, Palmer, & Moore, 2011b). It is possible that the severe processing limitation is related to accessing semantic representations, something that word and picture categorization have in common. The hypothesis that semantic access is the only severe processing limitation, however, can be rejected on the basis of another study in which the method was applied to an abstract shape-identification task. Three-dimensional meaningless shapes—made out of Lego blocks, foam blocks, or crumpled paper—were photographed from different points of view, and observers had to categorize a given picture as being of a particular target object (Scharff, Palmer, & Moore, 2013). This task, which required minimal semantic categorization, yielded evidence of fixed-capacity processing. The difficulty with this shape task does not seem to be related to the processing of abstract stimuli in general because Huang, Pashler, and Junge (2004) found evidence using the simultaneous–sequential method of unlimited-capacity symmetry detection when the patterns were abstract formations of dots.

Taken as a whole, this body of work using the simultaneous–sequential method is consistent with at least two general hypotheses of capacity limitations in perceptual processing. One is that there are two fixed-capacity limitations in perceptual processing, one involving word processing and the other involving object formation. The other is that the fixed-capacity limitation in word categorization and shape categorization are caused by a common limitation in perceptual-unit formation. This is essentially a generalized characterization of object formation to include verbal stimuli as well. None of the evidence to date can discriminate between these two hypotheses, though parsimony argues in favor of the latter. Notice that both hypotheses suggest an analogical, if not a deeper, comparison between the verbal tasks and object-perception tasks: letters are to words as surfaces are to objects.

Finally, we end with a discussion of the contrast between processing capacity (the degree to which a process can be engaged independently by multiple stimuli; Broadbent, 1958; Estes & Taylor, 1964; Rumelhart, 1970; Shiffrin & Gardner, 1972) and storage capacity (the amount of information that can be maintained in memory; Alvarez & Cavanagh, 2004; Awh, Barton, & Vogel, 2007; Luck & Vogel, 1997). Many recent studies have investigated the storage capacity of visual working memory. In an initial article, Luck and Vogel (1997) used a simple change-detection method to estimate whether observers were able to hold approximately three stimuli in visual working memory. This study led to a flurry of follow-up studies asking questions about the nature of this capacity limitation, such as whether it is limited by the number of objects that can be held or the degree of precision with which stimuli can be remembered, or both. Because estimates of storage capacity from these studies tend to be on the order of 2.5 to four items (see Brady, Konkle, & Alvarez, 2011, for a review), one might criticize the use of the simultaneous–sequential method with conditions that vary from two-at-a-time presentations (sequential) to four-at-a-time presentations (simultaneous) because both two and four fall within the range of most people’s “capacity.” It is critical to remember, however, that the simultaneous–sequential method is assessing processing independence versus dependence, not storage capacity. If stimulus presentation conditions are such that performance is limited by how much information can be extracted from the display (e.g., because stimuli are presented briefly), then limited-capacity processing predicts a difference between simultaneous versus sequential even for one versus two items. Two versus four has been used to minimize contamination from differences in eye movements across conditions, but the logic is identical. We extended our conditions to six items to demonstrate generality, but it is important to note that the logic does not depend on this extension. Finally, if equal performance across the simultaneous and sequential conditions resulted from the system’s ability to store four items at a glance, despite the processing mechanisms those stimuli engage, then evidence of limited capacity with only four items should rarely, if ever, occur. Yet there are examples of limited-capacity processing using the simultaneous–sequential method in which the simultaneous condition includes only four items, such as in tasks requiring shape identification, spatial configuration, object categorization, and word categorization (Huang & Pashler, 2005; Scharff et al., 2011a, 2011b, 2013). We conclude that the extended version of the simultaneous-sequential method is sensitive to detect limitations in processing capacity where they exist, even with the presentation of only four items. Using this method, we find that surface completion engages only unlimited-capacity processes.