Limited influence of perceptual organization on the precision of attentional control

Abstract

The role of perceptual organization in the precision of attentional control was assessed in three experiments. Observers viewed circular arrays of disks that varied in density. One disk was cued, directing attention to that disk. A series of tones then indicated shifts of attention to the next disk that was of the same color (Experiments 1 and 2) or on the same depth plane (Experiment 3). In the homogeneous condition, all of the disks were the same color (Experiments 1 and 2) or on the same depth plane (Experiment 3). In the heterogeneous condition, the disks alternated in color (Experiments 1 and 2) or stereoscopically defined depth (Experiment 3). If the observers were able to limit attention to disks within a group, the effective density of the displays in the heterogeneous conditions should have been one half that in the homogeneous conditions. There was little evidence that the observers could do this, indicating a limited role of perceptual organization in the precision of attentional control.

Researchers have made use of a variety of metaphors to guide discussion of the mechanisms underlying visual attention (for reviews, see Cave & Bichot, 1999; Fernandez-Duque & Johnson, 1999). Perhaps the most prevalent is that attention is a spotlight into which some information falls and other information does not (e.g., Posner, 1980; Posner, Snyder, & Davidson, 1980; cf. Cave & Bichot, 1999). Metaphors other than the attentional spotlight, however, have been used frequently as well. These include attention as a zoom lens (e.g., Eriksen & St. James, 1986; Eriksen & Yeh, 1985), attention as a gradient filter (e.g., LaBerge & Brown, 1989), and attention as a nonlinear filter (e.g., Cutzu & Tsotsos, 2003; Tsotsos et al., 1995). Common to all of these metaphors is the characterization that some information in the retinal image is processed differently than other information and that there is an active selection process that is controlled, at least in part, by the observer. Questions arise then concerning what factors determine what information is selected and what the limitations of the selection process are.

The present article is concerned with limitations of the spatial extent of the selection process and, in particular, the extent to which the organization of a visual scene can influence the spatial extent of selection. The spatial extent of attention has been investigated using a variety of methods. For example, the flankers task (e.g., Eriksen & Hoffman, 1972) requires observers to report the identity of a stimulus at one location (the target) while ignoring the identity of nearby stimuli (the flankers). If the flankers are too close to the target, observers’ responses tend to be systematically influenced by the identity of the flankers. This is taken as evidence that the spatial extent of attention cannot be reduced to the size of that separation. Using this method, Eriksen and Hoffman estimated the minimal spatial extent of selection to be about 1° of visual angle; flankers that were separated from the target by more than that had no influence on responses to the target. Other researchers, using spatial cuing combined with probe detection and related methods, proposed a gradient area of selection extending as much as 19° from a cued location (e.g., Downing & Pinker, 1985; Henderson & Macquistan, 1993; LaBerge & Brown, 1986). Still others, using methods involving many distractors and, sometimes, multiple targets separated by variable distances, have suggested that the area of selection has a facilitatory-center–inhibitory-surround profile with a spatial extent that is as large as 6° and as small as 1° (e.g., Bahcall & Kowler, 1999; Cutzu & Tsotsos, 2003; Mounts, 2000a, 2000b; Steinman, Steinman, & Lehmkuhle, 1995). Finally, some researchers have suggested that the spatial extent and shape of attentional selection varies with the task and with the properties of the stimuli (e.g., Eriksen & St. James, 1986; Juola, Bouwhuis, Cooper, & Warner, 1991; LaBerge & Brown, 1986), as well as their location within the visual field (e.g., S. He, Cavanagh, & Intriligator, 1996, 1997; Sagi & Julesz, 1986).

In this context of a heterogeneity of approaches and findings, Intriligator and Cavanagh (2001) introduced a new method designed specifically for measuring the spatial extent of attention. In this task, which we will refer to as the attentional walk task, observers are shown arrays of identical disks, similar to those shown in Figure 1, that vary in density and eccentricity. Observers fixate the central point, and a short time later, one of the disks briefly changes color, indicating that attention should be shifted to that disk without moving fixation. After the presentation of this cue, a series of instructions is given directing the observer to shift attention one disk to the left or the right of the currently attended disk (e.g., “left,” “right,” “left,” “left,” etc.). At the end of a five- to seven-step series of commands, a single disk changed color and served as a probe. The task is to indicate whether or not the final probe disk marks the point where the attentional walk ended. The logic of this task is that if the minimal size of the selection window—a construct referred to as attentional resolution by S. He et al. (1997)—is coarser than the distance between the disks, observers will be unable to reliably select one disk over an adjacent disk in response to the shift commands and will, therefore, be unable to reliably perform the walk task. The highest density within which observers are still able to reliably report the endpoint of an attentional walk would then give an estimate of the attentional resolution for a specific experimental setting (e.g., the eccentricity of the array and where within the visual field the walk occurred).

Figure 1.

Example of attentional walk displays used in the heterogeneous condition in Experiment 1. Participants were asked to shift their attention to disks of only one color while fixating the center disk. In the heterogeneous condition (shown here), this meant shifting attention to every other item. In the homogeneous condition (not shown), in which all the disks were the same color, this meant shifting attention to adjacent items.

Using the attentional walk task, Intriligator and Cavanagh (2001) showed that there is a broad range of display densities for which observers can perceive that there are individual items without difficulties, yet cannot conduct a reliable attentional walk. Thus, there is a notable dissociation between attentional resolution and spatial acuity. This dissociation has been cited frequently as reflecting something like a minimal window size or grain size of selection that is distinct from the limitations of acuity that are determined by early vision mechanisms.

In several recent articles (Moore, Lanagan-Leitzel, Chen, Halterman, & Fine, 2007; Moore, Lanagan-Leitzel, & Fine, 2008), we have presented evidence that the attentional walk task reflects limitations on the precision with which attention can be targeted, rather than (only) a minimal size of the attentional selection area. If we adopt the spotlight metaphor for expository purposes, the distinction between a limited minimal size for attentional selection and limited precision of attentional localization is like the distinction between the smallest diameter to which a spotlight can be reduced and the spatial reliability with which the center of the spotlight—however large or small it may be—can be moved from one location to another. The spotlight can be quite small but controlled with a hand that trembles, or it can be quite large and controlled with a stable hand. Thus, the two limitations of mechanism and process are in principle orthogonal, although they may induce conflated limitations on performance within tasks such as the walk task. Distinguishing between the different limitations may require more formal approaches, where performance is considered across a broader range of conditions and quantitative predictions can be made on the basis of specific psychophysical models of the alternative mechanisms (see J. Palmer & Moore, in press, for an initial attempt at this).

In the present study, we asked whether the perceptual organization of the scene can influence the precision with which attention can be targeted, as measured with the attentional walk task. In an earlier study (Moore et al., 2007), we showed that performance in the attentional walk task is better when the array in which the attentional walk occurs consists of heterogeneously colored disks than when it consists of identical (gray) disks. Note that this would not be expected if the walk task reflected only limitations of attentional resolution. If attention could not be allocated selectively to an individual item in the array, color could not be reliably associated with a particular item and could in turn, therefore, provide no guidance of attention to a particular item. If it is assumed that the limitations on performance in the walk task reflect limitations on the precision with which attention can be controlled, more distinct items apparently allow for more stable control. Does this advantage derive merely from local distinctiveness, or does it reflect attention being allocated within a scene that is perceptually organized and whose heterogeneity provides increased opportunity to represent items as distinct objects or targets for attentional focus? If the walk task reflects attention being allocated within an organized representation of the scene, perhaps performance can be facilitated even more through strategic changes in the organization of the scene. For example, if every other item in the array were red and the rest were green, perhaps one could conduct an attentional walk from red item to red item, thereby effectively halving the density of the display. If, however, performance in the walk task does not reflect attention being allocated within an organized representation of the display but, instead, depends only on the local (image level) distinctiveness of items, then, although there may be some advantage for the organized display over a completely homogeneous array, similar to that found by Moore et al. (2007), it is unlikely that it would effectively halve the display density.

EXPERIMENT 1

In Experiment 1, we tested whether alternating the color/luminance of disks within an array would allow observers to conduct an attentional walk among disks of one color and effectively reduce the density of the array by one half. Arrays with densities of 12, 24, and 48 disks per array were used. The disks either were all the same color (red or green; homogeneous displays) or alternated red and green (heterogeneous displays). The task was to move attention, in response to shift commands, from the current disk to the next disk of the same color. For heterogeneous arrays, this involved movements of attention that skipped over one item with each shift of attention.

The hypothesis was that attentional walks occur within perceptually organized representations and that the reason heterogeneity of surface features facilitated attentional walks in the previous study (Moore et al., 2007) was that it provided an opportunity to represent individual items as distinct objects and, therefore, as targets for attention. The strongest version of this hypothesis would predict that in the present experiment, performance with 48-disk heterogeneous arrays should be as good as performance with 24-disk homogeneous arrays. Similarly, performance with 24-disk heterogeneous arrays should be as good as performance with 12-disk homogeneous arrays. This follows because heterogeneous arrays should be perceptually organized into two interleaved arrays (one red and one green), each with half the number of disks. Therefore, if attentional walks occur within perceptually organized representations, observers should conduct their attentional walks within one of these half-density arrays. To the extent that this strong hypothesis did not hold, either because heterogeneity of surface features provided merely local distinctiveness or because the observers could not reliably limit attention to the relevant organized group, performance in the heterogeneous condition should resemble that in the homogeneous condition.

Method

Participants.

Sixteen observers (mean age, 24.4 years; 13 female, 3 male) completed the experiment. All the participants were naive as to the purpose of the experiment and were paid for their participation. They reported normal or corrected-to-normal visual acuity and color vision. The same 16 observers participated in Experiment 2 as well. Order of participation was counterbalanced across participants.

Apparatus.

The experiment was controlled by an IBM-compatible PC driving an 18-in. color CRT monitor at a spatial resolution of 1,024 × 768 pixels, with a refresh rate of 85 Hz. Stimulus creation and trial events were controlled with MATLAB (Version 6.5, Release 13; MathWorks, Natick, MA) software in combination with the Psychophysics Toolbox (Version 2.54) extensions (Brainard, 1997; Pelli, 1997). Viewing distance was fixed at 65 cm, using a chin- and headrest.

Stimuli.

As depicted in Figure 1, displays consisted of circular arrays of disks (0.71° in diameter) presented on a dark background (5.48 cd/m²). The arrays consisted of 12, 24, or 48 disks that were distributed evenly around a central white fixation dot (0.44° in diameter) on an imaginary circle with a radius of 6.96° (measured from fixation to the center of the disks). All of the disks were white (111.5 cd/m²) in the fixation displays. The cue indicating the start disk was a brief blinking (300 msec) of one of the disks, during which it expanded to 0.91° in diameter. During the attentional walk part of the trial, the disks were either all red or all green (homogeneous) or were alternating red and green (heterogeneous). For the response displays, the disks changed to colored disks. Colors were chosen pseudorandomly from among five different colors (red, green, light blue, purple, and dark blue), with the constraints that the two disks to either side of the target disk (on which the attentional walk should end) each had a different color and no two adjacent disks in the array had the same color. Luminance values for the different colors were 23.8 cd/m² (red), 69.6 cd/m² (green), 79.4 cd/m² (light blue), 37.8 cd/m² (purple), and 15.1 cd/m² (dark blue). In addition, the response display included an array of five rectangles at the bottom of the screen, one in each of the five colors making up the response array, which served as a menu for indicating the color of the target disk. Each rectangle was 2.38° high and 6.08° wide. The response menu was presented 10.37° below the center of the response array, centered vertically with it. Short beeps (computer’s default beep at medium volume) were used to indicate each walk step. The experiment was conducted with the room lights put to a low setting.

Task.

The participants were asked to remain fixated on the central fixation marker throughout the trial. The task was to shift attention to the cued disk in the array and then, if a series of tones occurred (multiple-step condition), to shift attention clockwise/counterclockwise following each tone from the current disk to the next similarly colored (red or green) disk in the display. When the series of tones ended, the array changed to a response array, and the observers reported the color of the disk on which the attentional walk had ended by clicking on the appropriate rectangle in the response menu. On some trials (zero-step condition), no tones occurred following the cue. Instead, the cue display was followed immediately by the response array. The task was the same: indicate the color of the currently attended disk (i.e., the cued disk in this case).

Design.

A 2 (display type: homogeneous or heterogeneous) × 3 (density: 12, 24, or 48) × 2 (walk type: zero step or multiple step) within-subjects design was used. Twenty percent of the trials were zero-step trials, and 80% were multiple-step trials. The color of the disks in the homogeneous displays and of those disks on which walks occurred in the heterogeneous displays was fixed as red or green for a given participant and was counterbalanced across participants. Walk direction was also fixed as clockwise or counterclockwise for a given participant and was counterbalanced across participants. Display type, density, and walk type were mixed within blocks of trials. Each observer participated in one experimental session of ten 30-trial blocks. The first block served as practice and was excluded from the analysis. Trials on which the mouse click was outside of the response menu were repeated. This resulted in a total of 9 zero-step observations and 36 multiple-step observations for each display and density condition for each participant.

Procedure.

At the beginning of the session, a set of written instructions describing the task was presented on the computer screen. After reading the instructions, the observers completed 10 experimental blocks, which took about 75 min, including breaks. Breaks were provided every 30 trials. The observers were encouraged to rest as much as they needed to during these breaks. The observers continued the experiment following a break by pressing a button on the keyboard.

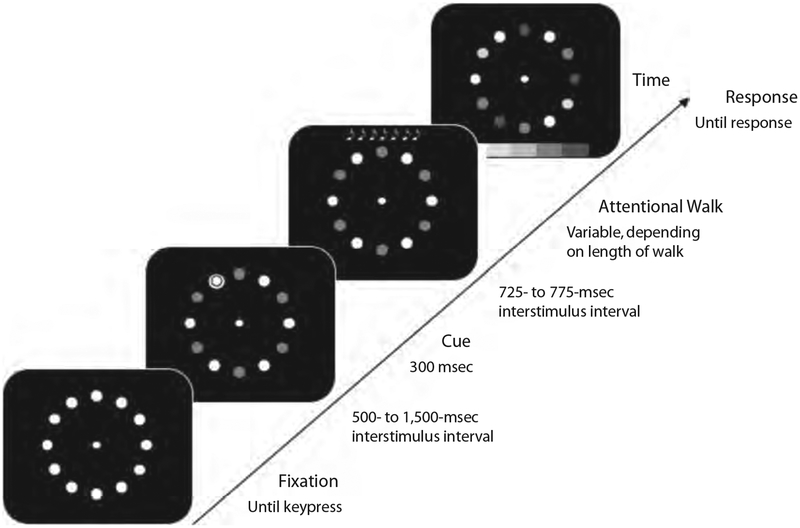
Trial events are illustrated in Figure 2. Each trial began with the presentation of the fixation dot, surrounded by an array of white disks. Instructions emphasized that the observers should remain fixated throughout the trial. The participants initiated a trial by fixating and pressing the left mouse button to indicate that they were ready to start the trial. As soon as the buttonpress was detected, the disks changed color: Either all the disks were one color (homogeneous condition), or red and green disks alternated (heterogeneous condition). After an interstimulus interval (ISI) of a randomly chosen value in the range between 500 and 1,500 msec, one of the disks blinked for 300 msec to indicate the starting point of the attentional walk. After a variable ISI of 725, 750, or 775 msec, either the response display was presented (in the zero-step condition), or a series of beeps (six, seven, eight, or nine beeps, randomly chosen) indicated the attentional walk (in the multiple-step condition). Every beep was separated from the next beep by an ISI, randomly chosen, of 725, 750, or 775 msec. One thousand milliseconds after the final beep, all the disks changed color (i.e., the response display was presented), and the response menu appeared at the bottom of the screen. The response display remained visible until a mouse keypress was registered or for 10 sec if no response occurred. When the wrong response was given, the message “Incorrect response” was displayed at the center of the display; when the mouse click was outside of the menu area, the message “Outside response area” was presented. The participants clicked the mouse to continue to the next trial. After presentation of the blank screen for 1,000 msec, the initial fixation display was shown, and the next trial started whenever the participant pressed the mouse key.

Figure 2.

Illustration of the basic trial sequence in all three experiments. After the participants indicated that they were fixating the center, a cue appeared that defined the starting point of the attentional walk. During the walk, the participants shifted their attention from disk to disk according to a series of beeps. At the end of the trial, the participants indicated the color of the disk that their attention had shifted to after the last beep by clicking on the response field of the same color (for illustration purposes, here indicated in different gray levels) with the mouse.

Results and Discussion

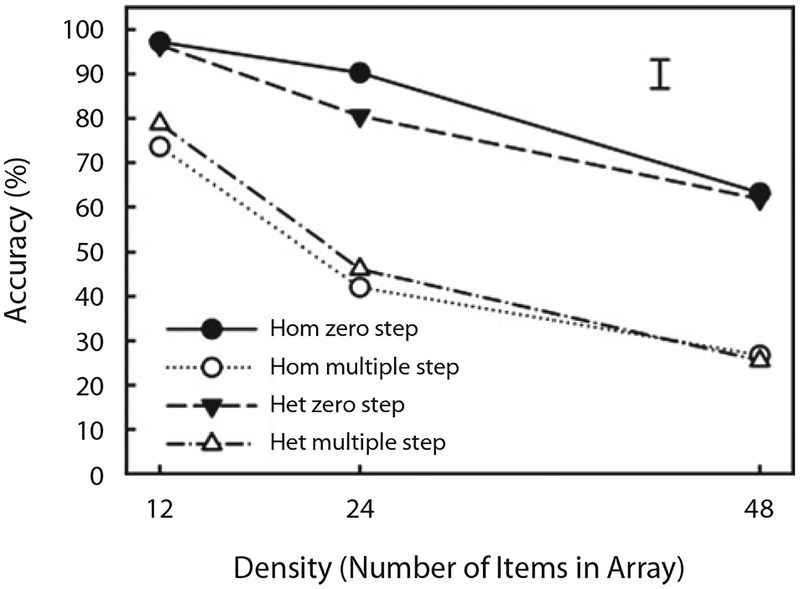
Figure 3 shows mean accuracy as a function of density, display type, and walk type in Experiment 1.¹ Mean accuracies for individual observers were submitted to a 2 (display type: homogeneous or heterogeneous) × 3 (density: 12, 24, or 48) × 2 (walk type: zero step or multiple step) ANOVA. Alpha was set at .05 for this and all the subsequent analyses. Whenever appropriate, p values were Greenhouse–Geisser corrected to adjust for violations of the sphericity assumption. There were reliable main effects of walk type [F(1,15) = 125.54, p < .001] and density [F(2,30) = 137.31, p < .001], but there was no reliable effect of display type [F(1,15) = 0.11, n.s.]. In addition, there was a significant interaction between walk type and density [F(2,30) = 14.01, p < .001]. Thus, consistent with the usual findings in the attentional walk task, accuracy decreased with increasing density and did so significantly more in the multiple-step condition, in which an attentional walk had to be done, than in the zero-step control condition, in which no walk occurred. As can be seen by the similarity of the two multiple-step functions in Figure 3, however, there was no evidence that the observers were able to limit their walks to the array of the relevant color.

Figure 3.

Mean accuracy shown as a function of density (number of items in the display), display type (homogeneous [Hom] and heterogeneous [Het]), and walk type (zero-step control and multiple-step attentional walk) in Experiment 1. The error bar corresponds to two times the standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

To reinforce this apparent lack of an effect of display type on walk performance, we performed separate 2 (display type) × 3 (density) ANOVAs for the zero- and multiple-step conditions separately. There were reliable main effects of density in both cases [zero step, F(2,30) = 94.57, p < .001; multiple step, F(2,30) = 86.91, p < .001] but no effect of display type in either case [zero step, F(1,15) = 1.60, n.s.; multiple step, F(1,15) = 2.77, n.s.] and no interaction between display type and density in either case [zero step, F(2,30) = 1.22, n.s.; multiple step, F(2,30) = 1.54, n.s.].

Although overall performance suggests that the observers were limited in their ability to selectively shift attention only to items of the relevant color, the specific pattern of errors that the participants made does suggest that there was some influence of perceptual organization on performance in the attentional walk task. Figure 4 shows the probability of reporting the color of a given disk as a function of the distance of that disk relative to the target (one or two positions away from the target). Thus, these are all error trials, but they represent specific types of errors: those trials on which the attentional walk apparently landed one item away from the target location or those on which it apparently landed two items away from the target location. As can be seen in Figure 4, the pattern of errors in the multiple-step condition (bottom panel) is very different from that in the zero-step condition (upper panel). Whereas, in the zero-step condition, virtually no responses corresponded to the color of the item that was two positions away from the target, in the multiple-step condition, a much greater proportion of responses corresponded to the item two positions away. Moreover, this difference was greater for the heterogeneous condition than for the homogeneous condition. This pattern indicates that when the observers’ attentional walks went bad, they tended to end up two items away more often in the heterogeneous condition than they did in the homogeneous condition. If the arrays were perceptually grouped by color, and attentional walks were conducted within one of the grouped arrays, two items away physically in the heterogeneous condition corresponded to one item away in the grouped representation (i.e., it was the next item of the like color in the array). Thus, this pattern of errors suggests that the attentional walk task may have occurred, at least sometimes, within a grouped representation.

Figure 4.

Mean probability of reporting the color of a given disk shown as a function of the disk’s distance from the target disk for Experiment 1. The upper graph shows the percentage of trials on which an item was reported as a function of density (number of items in the display) and display type (homogeneous [hom] and heterogeneous [het]) in the zero-step condition. The lower graph shows the same for the multiple-step condition. The error bar corresponds to two times the standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

This pattern of errors was confirmed by the statistics. Participant data were submitted to a 2 (item position: one away or two away) × 2 (display type) × 3 (density) × 2 (walk type) ANOVA. Of special interest for our question, there was a main effect of item position [F(1,15) = 94.03, p < .001], as well as a reliable three-way interaction between item position, display type, and walk type [F(1,15) = 12.37, p < .05]. A separate 2 (item position) × 2 (display type) × 3 (density) ANOVA was therefore conducted for the multiple-step condition. Again focusing on the relevant analysis only, there was a reliable main effect of item position [F(1,15) = 24.09, p < .001], as well as a significant interaction between item position and display type [F(1,15) = 24.24, p < .001], confirming that more responses corresponded to one position away (16.7%) than to two positions away (9.6%) in the homogeneous display (as is typical in these tasks; see Moore et al., 2007), whereas almost exactly the same proportions of responses were given at the two positions (12.3% vs. 12.6%) in the heterogeneous displays, something that is unusual, since most errors in the walk task are one-away errors.

EXPERIMENT 2

It is possible that the color cue used in Experiment 1 was an insufficiently powerful grouping cue and that this is why the observers were unable to use it to organize the displays and limit their attentional walks to the relevant subset of items. It is possible, for example, that the regular spacing of the items caused the whole circular array to be the dominant perceptual organization, rather than the interleaved red and green subsets of items. In Experiment 2, we sought to strengthen the grouping of like-colored items by adding connecting arcs for the same colors/luminances of the disks, so that the red and green disks were now grouped not only by color/luminance, but also by uniform connectedness (see Figure 5). According to the analysis offered by S. Palmer and Rock (1994), adding uniform connectedness should be powerful support for perceptually organizing these displays into two separate arrays within which, in principle, an attentional walk could be executed.

Figure 5.

Example of an attentional walk display in the heterogeneous (left) and homogeneous (right) conditions in Experiment 2. Participants were asked to shift their attention within disks of only one color while fixating the center disk. In the heterogeneous condition, this meant shifting attention to every other item. In the homogeneous condition, this meant shifting attention to adjacent items.

Method

The method was the same as that in Experiment 1, except where noted.

Participants.

The same 16 observers who completed Experiment 1 participated in this experiment.

Apparatus.

Experiment 2 was controlled by a different IBM-compatible PC connected to the same color CRT monitor with a spatial resolution of 1,024 × 768 pixels and a refresh rate of 85 Hz. Stimuli were presented using MATLAB (Version 7.0.1, Release 14; MathWorks) and the new Psychophysics Toolbox (Version 3.0.8) extensions (Brainard, 1997; Pelli, 1997). Viewing distance was fixed at 65 cm using a chin- and headrest.

Stimuli.

The displays were the same as those used in Experiment 1, except that in the walk displays, arcs of 0.1° thickness connected same-colored disks. These connections between disks were either convex for a given color, forming a flower-like form for that color, or concave for a given color, forming a star-like form for that color (see Figure 5). In the homogeneous conditions, all the arcs were either concave or convex, randomly chosen on a given trial. In the heterogeneous condition, concave arcs connected one subset of colors, whereas convex arcs connected the other subset. Which color was connected by which type of arc was chosen randomly.

Task.

The task was the same as that in Experiment 1.

Design.

A 2 (display type: homogeneous or heterogeneous) × 4 (density: 12, 18, 24, or 36) × 2 (walk type: zero step or multiple step) within-subjects design was used. We used a slightly different set of densities in Experiment 2 than in Experiment 1 because the displays of density 48 seemed to be too dense, on the basis of both informal observation and the relatively low performance even on zero-step displays for densities of 48 in Experiment 1. Each block in Experiment 2 consisted of 40 trials. Each observer participated in one experimental session of eight blocks (plus one practice block, not included in the data analysis), resulting in 8 zero-step observations and 32 multiple-step observations in each display and density condition for each participant.

Procedure.

The general procedure and specific trial sequence were the same as those in Experiment 1.

Results and Discussion

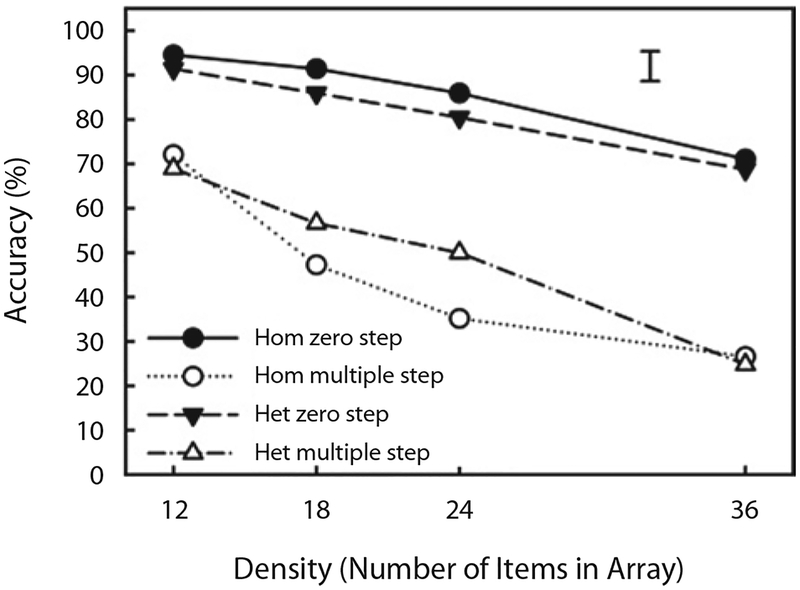
Figure 6 shows mean accuracy as a function of density, display type, and walk type. Mean accuracies for individual observers were submitted to a 2 (display type: homogeneous or heterogeneous) × 4 (density: 12, 18, 24, or 36) × 2 (walk type: single step or multiple step) ANOVA. As in Experiment 1, there were reliable main effects of density [F(3,45) = 63.34, p < .001] and walk type [F(1,15) = 154.98, p < .001], but there was no main effect of display type [F(1,15) = 0.05, n.s.]. The interaction between walk type and density was significant [F(3,45) = 7.71, p < .001]. Unlike in Experiment 1, there was also a significant interaction between display type and walk type [F(1,15) = 10.13, p < .05].

Figure 6.

Mean accuracy shown as a function of density (number of items in the display), display type (homogeneous [Hom] and heterogeneous [Het]), and walk type (zero-step control and multiple-step attentional walk) in Experiment 2. The error bar corresponds to two times the standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

Separate 2 (display type) × 4 (density) ANOVAs for the zero- and multiple-step conditions revealed that the effect of display type was reliable in the zero-step condition [F(1,15) = 4.73, p < .05]. The observers were a little more accurate for the homogeneous display (85.7%) than for the heterogeneous display (81.6%) when they had to report only the cued item. Most important for the question of whether the observers’ attentional walks were influenced by the perceptual organization of the displays, however, are the analyses of the multiple-step condition. Here, unlike in Experiment 1, although the main effect of display type was not quite reliable [F(1,15) = 3.88, p < .07], there was a reliable interaction between display type and density [F(3,45) = 8.79, p < .001]. This interaction seems to have been driven by the two medium-density conditions in which performance was 9% and 15% better in the heterogeneous condition than in the homogeneous condition for the density 18 and density 24 conditions [t(15) = 2.74, p < .05, and t(15) = 3.78, p < .01, respectively]. No other comparisons were reliable.

As in Experiment 1, the specific pattern of errors that the participants made also suggests that there was some influence of perceptual organization on performance in the attentional walk task. Figure 7 shows the probability of reporting the color of a given disk as a function of the distance of that disk relative to the target (one or two positions away from the target). Again, these are all error trials; they represent just specific types of errors. There were more errors overall in the multiple-step condition than in the zero-step condition. In the zero-step condition, errors tended to be one-away errors, rather than two-away errors, regardless of whether the displays were homogeneous or heterogeneous. In the multiple-step condition, however, there was a greater tendency to make two-away errors in the heterogeneous multiple-step condition than in the homogeneous multiple-step condition—the pattern that would be expected if attentional walks were being limited to the relevant set of items.

Figure 7.

Mean probability of reporting the color of a given disk shown as a function of the disk’s distance from the target disk in Experiment 2. The upper graph shows the percentage of trials on which an item was reported as a function of density (number of items in the display) and display type (homogeneous and heterogeneous) in the zero-step condition. The lower graph shows the same for the multiple-step condition. The error bar corresponds to two times the standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

Analyses confirmed this overall pattern. The individual participant data were submitted to a 2 (item position: one away or two away) × 2 (display type) × 4 (density) × 2 (walk type) ANOVA. Reporting just the relevant analysis, there was a significant main effect of item position [F(1,15) = 117.59, p < .001]. In addition, the three-way interaction between item position, display type, and walk type was reliable [F(1,15) = 15.29, p < .001]. Most critical for the question of whether attentional walks were limited to the relevant set of items, a separate 2 (item position) × 2 (display type) × 4 (density) analysis for the multiple-step condition revealed, as in Experiment 1, a reliable main effect only of position [F(1,15) = 46.55, p < .001], as well as a significant interaction between item position and display type [F(1,15) = 12.22, p < .01]. More error responses were made corresponding to the identity of the item one position away from the target (18.5%) than corresponding to the identity of the item two positions away (8.9%) in the homogeneous display. However, as in Experiment 1, this pattern was different for the heterogeneous display. Here, errors were nearly equally likely to correspond to the item one position away and to the item two positions away (13.1% vs. 11.8% for the one-away and two-away conditions, respectively).

In summary, adding uniform connectedness as a grouping cue to color/luminance did increase the influence of perceptual organization on performance in an attentional walk task, relative to the task with color/luminance only (Experiment 1). Nonetheless, the improvement was far less than would have been expected if the observers had been able to limit their attentional walks to a single subset of colors in the heterogeneous display. Had that been the case, performance in the multiple-step density 36 heterogeneous condition would have been as good as that in the multiple-step density 18 homogeneous condition, which it was not [t(15) = 3.80, p < .01], and performance in the multiple-step density 24 heterogeneous condition would have been as good as that in the multiple-step density 12 homogeneous condition, which it was not [t(15) = 5.36, p < .001]. Moreover, there would have been almost exclusively two-away errors for the heterogeneous displays. Clearly, these patterns were not attained. Given the presumed power of uniform connectedness as a grouping principle (S. Palmer & Rock, 1994; S. E. Watson & Kramer, 1999), these results suggest that perceptual organization has limited influence on attentional walks within dense displays of items. Nonetheless, some influence of perceptual organization was apparent.

EXPERIMENT 3

In the final experiment, we introduced what was intended to be a still stronger form of perceptual organization in order to push the question of whether attentional walks can be limited to the relevant set of items. In particular, we used stereoscopic displays to introduce retinal disparities that caused the two groups of items within the arrays to appear at distinct depth planes and, therefore, appear to be sitting on two distinct surfaces. Surfaces have been shown to be especially powerful in supporting the selective allocation of attention (Z. J. He & Nakayama, 1992, 1995; Marrara & Moore, 2000; McLeod, Driver, & Crisp, 1988; Nakayama & He, 1996; Nakayama, He, & Shimojo, 1995). If observers cannot limit performance in their attentional walks to one surface or the other, where items at alternating depth planes are presented, it would suggest strongly that the guidance of attention in this task is influenced by image-level characteristics and does not occur, entirely, within a scene-based (i.e., perceptually organized) representation. This would be a significant observation, given that so many other attentional tasks have been shown to be based on scene-based representations (e.g., Baylis & Driver, 1993; Driver & Baylis, 1989; Egly, Driver, & Rafal, 1994; Z. J. He & Nakayama, 1992, 1995).

Method

The experiment was conducted at the Leibniz Research Center for Working Environment and Human Factors (Germany). Except where noted, the method was the same as those in the other two experiments.

Participants.

Sixteen observers (mean age, 22.1 years; 6 female, 10 male) completed this experiment. They were paid volunteers from the Dortmund community. All reported normal or corrected-to-normal visual acuity and color vision. Eight additional observers had to be excluded. Three failed to pass a custom stereovision test, 3 felt incapable of performing the task and the experiment was terminated after the first block, and 2 observers did not have any observations left in certain conditions after removing trials with eye movements (see below for details).

Apparatus.

The stimuli were presented on a 21-in. color CRT monitor (resolution, 1,024 × 768 pixels; refresh rate, 120 Hz) that was driven by a Quadro FX 3000 graphics card (NVIDIA Inc., Santa Clara, CA). A CrystalEyes 3 stereo display system (StereoGraphics Inc., San Rafael, CA) was used to simulate depth. This system allows for the presentation of separate left- and right-eye images through liquid-crystal shutter glasses. The presentation rate was synchronized with the monitor and set at 60 Hz per eye. The experiment was controlled by an IBM-compatible PC that ran software written in C/C ++ using OpenGL. Viewing distance was fixed at 52 cm using a chin- and headrest.

Eye movements were recorded with an electrooculogram (EOG), using Ag/AgCl electrodes placed on the outer canthi of eyes for horizontal (h) EOGs and infra- and supraorbitally in line with the pupil of the left eye for vertical (v) EOGs. The BrainVision Recorder software (Version 1.03; BrainProducts Inc., Munich) was used to record the EOG signals. This program ran on a second PC that was connected to a BrainVision Quickamp amplifier (BrainProducts Inc.). The sampling rate was set to 250 Hz, and the signal was low-pass filtered (120 Hz) and stored for further analysis. The resolution of an EOG is such that eye position can be determined within ±1.5°–2° (e.g., Joyce, Gorodnitsky, King, & Kutas, 2002; Young & Sheena, 1975). Given the eccentricity of the stimuli employed here (~7°), this resolution was sufficient to detect the presence of eye movements away from fixation.

Stimuli.

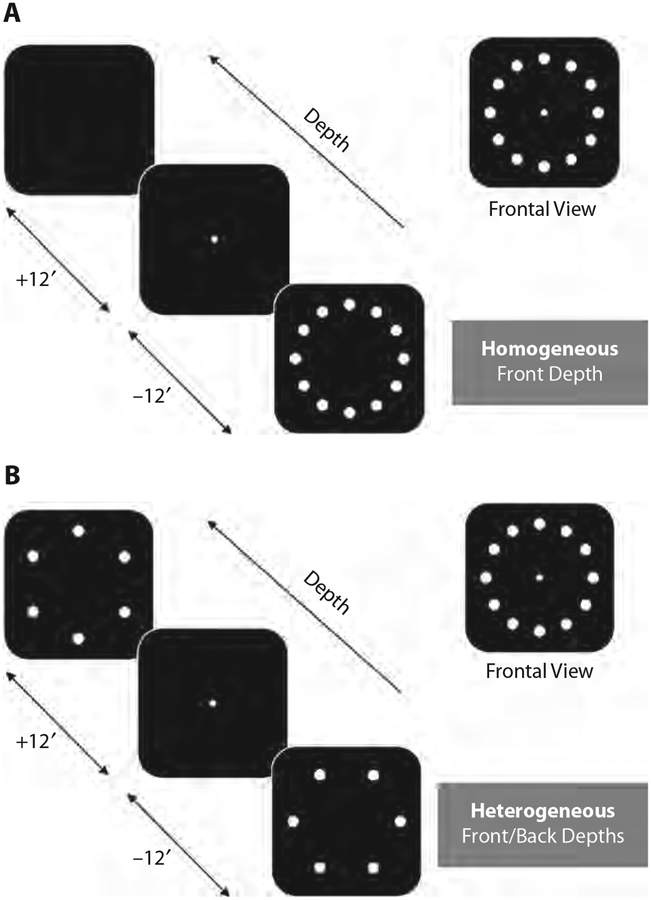
Displays consisted of circular arrays of identical white (153 cd/m²) disks presented on a dark background (2.30 cd/m²). Stimuli sizes and eccentricities were the same as in the other two experiments, except that the diameter of the disks was slightly increased to 0.72°. The fixation display and response display were always presented at the horopter (intermediate depth), which was at the depth of the monitor. Figure 8 illustrates how the homogeneous and heterogeneous walk displays were designed. In the homogeneous condition, all of the disks in the walk display were presented either in the front or in the back, relative to the horopter, whereas in the heterogeneous condition, every second disk was presented in the front plane and the other disks were presented in the back plane, resulting in the perception of two rings of dots at two depth planes. The crossed and uncrossed binocular disparities used for the front and back depth planes corresponded to −12 and +12 arc min, respectively.

Figure 8.

Example of attentional walk displays in the homogeneous (A) and heterogeneous (B) conditions in Experiment 3. Participants were asked to shift their attention on disks of only one depth while fixating the center disk.

Task.

The task was basically the same as that in Experiments 1 and 2. Instead of moving attention to a certain color, the participants had to move their attention to a certain depth plane.

Design.

A 2 (display type: homogeneous or heterogeneous) × 4 (density: 10, 14, 20, or 28) × 2 (walk type: zero step or multiple step) within-subjects design was used. Pilot studies indicated that the participants were unable to do the attentional “depth” walk for the same densities as those used in Experiment 2. We therefore adapted the densities and used 10, 14, 20, and 28 items. The direction (clockwise, counterclockwise) and depth (front, back) of the attentional walks were counterbalanced across participants. The observers participated in two experimental sessions of 10 blocks. The first 3 blocks of the first session and the first block of the second session were considered as practice and were discarded. Each block contained 40 trials which consisted of 1 (20%) zero-step and 4 (80%) multiple-step trials for each of the eight display type × density combinations. This resulted in a total of 16 zero-step and 64 multiple-step trials for each condition and observer (after removing the practice blocks). The number of trials per condition was increased, as compared with the previous experiments, because trials containing eye movements were determined offline by visually inspecting the hEOG and vEOG traces. An average of 44.27% of the trials had to be eliminated due to eye movements.

Procedure.

Each observer completed two 2.5-h sessions on subsequent days. At the beginning of the first session, the TNO Stereo Test was administered to ensure that the observers had normal depth perception. All the observers passed this test (mean stereoacuity = 0.72 arc min). Then the EOG electrodes were applied, and the eye movement recordings were calibrated. Written instructions were also provided, in which it was emphasized that the participants should maintain fixation throughout a trial.

Given that the TNO test measures stereoacuity only for (para-) foveal vision, the observers were also administered a custom stereovision test that measured depth perception under the same peripheral vision conditions as those used in the actual experiment. This involved presenting the observers with high-density (28-item) heterogeneous displays in which all the items in one depth plane were green in color and all the items in the other depth plane were red in color. The task was to report the depth at which the green items were presented by pressing the “v” keyboard key for front and the “h” key for back. It was stressed to the participants that they should respond as accurately as possible and take as much time as needed to do so. There were two blocks of 32 trials each. Half of the trials contained green items at the front depth, and the other half contained green items at the back depth (presented in a pseudorandom order). To familiarize the participants with the displays, they were presented for 20 sec in the first block and then for only 500 msec in the second block to help reduce the probability of eye movements. The entire first block and the first 5 trials of the second block were considered as practice and were eliminated. For the remaining trials, 90% accuracy was set as criterion performance. As was noted above, 3 observers failed to reach this criterion.

For the experimental blocks, the trial sequence was identical to that in Experiments 1 and 2 with the exception that instead of changing color from the fixation to the walk display, the disks changed in depth plane: In the homogeneous condition, all the disks moved from the horopter to either the front or the back plane, whereas in the heterogeneous condition, one half of the disks moved to the front and the other half moved to the back. For the response display, all the disks moved back to the horopter (intermediate depth) and were pseudorandomly colored, as in the previous experiments. The “blinking” of the cued disk was achieved by unrendering and rendering it every 50 msec (for 300 msec), instead of having it expand and contract. Another minor difference was that only mouse clicks within the response menu were accepted when the response display was shown. Finally, occasions for breaks were given halfway through a block (i.e., after 20 trials) and at the end of a block, encouraging the observers to use them to relax.

Results and Discussion

Figure 9 shows mean accuracy as a function of density, display type, and walk type. Mean accuracies for individual observers were submitted to a 2 (display type: homogeneous or heterogeneous) × 4 (density: 10, 14, 20, or 28) × 2 (walk type: single step or multiple step) ANOVA. As in Experiments 1 and 2, there were reliable main effects of walk type [F(1,15) = 42.72, p < .001] and density [F(3,45) = 87.75, p < .001], but there was no main effect of display type [F(1,15) = 2.82, n.s.]. The interaction between walk type and density was also significant [F(3,45) = 22.27, p < .001], as were the display type × walk type interaction [F(1,15) = 10.43, p < .01] and the three-way interaction [F(3,45) = 4.59, p < .05].

Figure 9.

Mean accuracy shown as a function of density (number of items in the display), display type (homogeneous [Hom] and heterogeneous [Het]), and walk type (zero-step control and multiple-step attentional walk) for Experiment 3. The error bar corresponds to two times standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

Separate 2 (display type) × 4 (density) ANOVAs for the zero- and multiple-step conditions were performed. For the zero-step condition, only the main effect of density reached significance [F(3,45) = 33.21, p < .001]. For the multiple-step condition, there were significant main effects of display type [F(1,15) = 8.05, p < .05] and density [F(3,45) = 67.46, p < .001], as well as a significant display type × density interaction [F(3,45) = 3.25, p < .05], as in Experiment 2. This interaction seems to have been driven by the density 20 condition, in which performance was 15% [t(15) = 2.84, p < .05] better in the heterogeneous condition than in the homogeneous condition.

As in both Experiments 1 and 2, the specific pattern of errors revealed some influence of perceptual organization on performance. Figure 10 shows the probability of reporting the color of a given disk as a function of the distance of that disk relative to the target (one or two positions away from the target). Again, these are all error trials; they represent just specific types of errors. There were again more errors overall in the multiple-step condition than in the zero-step condition. In the zero-step condition, errors tended to be one-away errors, rather than two-away errors, regardless of whether the displays were homogeneous or heterogeneous. In the multiple-step condition, however, the dominance of one-away errors was less in the heterogeneous condition (15.0% one-away vs. 13.4% two-away) than in the homogeneous condition (26.1% one-away vs. 8.7% one-away).

Figure 10.

Mean probability of reporting the color of a given disk shown as a function of the disk’s distance from the target disk for Experiment 3. The upper graph shows the percentage of trials on which an item was reported as a function of density (number of items in the display) and display type (homogeneous [hom] and heterogeneous [het]) in the zero-step condition. The lower graph shows the same for the multiple-step condition. The error bar corresponds to two times the standard error, computed in the way suggested by Loftus and Masson (1994) for multifactor within-subjects designs.

This pattern was confirmed by the analysis, in which participant data were submitted to a 2 (item position: one-away or two-away) × 2 (display type) × 4 (density) × 2 (walk type) ANOVA. Of relevance to the present analysis, there was a significant main effect of item position [F(1,15) = 76.82, p < .001] and a significant item position × display type × walk type interaction [F(1,15) = 27.79, p < .001]. Therefore, a separate 2 (item position) × 2 (display type) × 4 (density) ANOVA was conducted for the multiple-step condition. Again, restricting ourselves to the critical effects, there was, as in the previous experiments, a reliable main effect of item position [F(1,15) = 40.02, p < .001], as well as significant interactions between item position and display type [F(1,15) = 20.26, p < .001] and item position and density [F(3,45) = 7.28, p < .01].

In summary, separating relevant and irrelevant subsets of items on distinct surfaces improved attentional walk performance, but as in Experiment 2, the improvement was far less than would have been expected if the observers had been able to limit their attentional walks to a relevant subset of items in the heterogeneous display. Had that been the case, performance in the multiple-step density 28 heterogeneous condition would have been as good as that in the multiple-step density 14 homogeneous condition, which it was not [t(15) = 6.55, p < .001], and performance in the multiple-step density 20 heterogeneous condition would have been as good as that in the multiple-step density 10 homogeneous condition, which it was not [t(15) = 6.52, p < .001]. There also would have been almost exclusively two-away errors for the heterogeneous displays.

In a final analysis, we considered the possibility that the ability to limit attentional walks to a given surface might depend on which surface one is trying to limit it to. In particular, limiting attention to the front surface, where there were no items “between” the observer and the relevant surface, might have been easier than limiting it to the back surface, where there were items on a surface that was “between” the observer and the relevant surface (Downing & Pinker, 1985; Tipper, Lortie, & Baylis, 1992). To provide some insight into this possibility, we looked at performance separately for those observers whose walks were limited to the front surface versus the back surface. Performance was closer to that predicted by an effective halving of the density when the attentional walks were limited to items in the front surface than when the attentional walks were limited to items in the back surface. This pattern did not achieve statistical significance in post hoc analyses. However, given that the relevant source of variance was an interaction that included a between-subjects variable and, thus, was not as powerful as the within-subjects comparisons that have been discussed throughout the article, the apparent trend seems worth noting.

GENERAL DISCUSSION

This study was concerned with the question of what impact perceptual organization has on people’s ability to shift attention within cluttered displays, as assessed with the attentional walk task (Intriligator & Cavanagh, 2001). The motivating question was whether observers can limit the allocation of attention exclusively to specific perceptually organized subsets of dense displays. For example, if items in an array alternate in color/luminance, can observers limit their attentional walks to one of the subsets of items on the basis of grouping by similarity and, in the extreme, reduce the effective density by half?

Experiment 1 addressed this question using arrays of items that alternated by color/luminance or not. The participants were instructed to make their attentional shifts during their walks to the next item of a given color. This experiment yielded little evidence that the observers were able to functionally eliminate the irrelevant items from the alternating displays and reduce density by one half. In Experiments 2 and 3, different cues were used in an effort to strengthen the organization of items into the relevant and irrelevant subsets. Specifically, Experiment 2 added the cue of uniform connectedness (S. Palmer & Rock, 1994) to the color/luminance grouping cue in Experiment 1. Uniform connectedness is widely held to have a foundational status as a perceptual grouping cue (e.g., Hecht & Vecera, 2007; Matsukura & Vecera, 2006; S. Palmer & Rock, 1994; S. E. Watson & Kramer, 1999). Given that fact, we reasoned, it would be especially likely to support the limitation of attention to a given group of items in the array. Experiment 3 presented the different subsets of items on different stereoscopically defined surfaces, a cue that has been shown to be powerful in guiding attention in other contexts, such as visual search (Z. J. He & Nakayama, 1992) and cuing (Z. J. He & Nakayama, 1995; Marrara & Moore, 2000). The results from Experiments 2 and 3 showed that the observers were able to use the organization cues in Experiments 2 and 3 more than in Experiment 1. The improvement in performance, however, was well below that which would be expected if they were essentially parsing the display into relevant and irrelevant items and functionally reducing density by half.

On the face of it, these findings seem to conflict with those in several of the existing literatures. First consider visual search. Performance in visual search tasks can be improved by defining relevant subsets of items on the basis of stimulus characteristics such as color (e.g., Egeth, Virzi, & Garbart, 1984; Kaptein, Theeuwes, & van der Heijden, 1995; Moore & Egeth, 1998), temporal synchrony (Jiang, Chun, & Marks, 2002; D. G. Watson & Humphreys, 1997), surface (Z. J. He & Nakayama, 1992; Moore, Elsinger, & Lleras, 2001), and common motion (McLeod et al., 1988). Why, then, were the advantages of grouped arrays so limited in the present study in which attentional walks were investigated? There are two important differences between standard visual search tasks and attentional walk tasks that could account for this apparent conflict. First, visual search displays are rarely as dense as those in which attentional walks become difficult. Second, shifts of attention in the attentional walk task are forced to be serial, and which specific items must be attended for a given shift is fixed. In contrast, although visual search may sometimes be serial, it certainly is not always serial, and the order in which items are checked is not fixed. Given these differences, advantages due to organizational factors in visual search may derive from strategies for guiding the search process in terms of which items should be considered. In contrast, the primary limiting factor in the attentional walk task is not which items to attend, but the ability to select one specific item, rather than another, reliably.

The other literature with which these findings may appear to conflict is the object-based attention literature, in which robust effects of perceptual grouping on the allocation of attention have been found (e.g., Baylis & Driver, 1992; Chen, 1998; Driver & Baylis, 1989; Egly et al., 1994; Kramer & Jacobson, 1991; Moore & Fulton, 2005; Moore, Yantis, & Vaughan, 1998; Vecera & Farah, 1994). Those effects tend to be within-object advantages—that is, information that is part of a selected object or group is processed better than information that is part of another object or group. For the attentional walk task, this “advantage” would be a disadvantage, because the task requires that individual items within the group be selected distinctly from each other. Thus, the relative ineffectiveness of cues such as common color and uniform connectedness on the allocation of attention in the attentional walk task might derive from an inability to both unify a group of items and then individuate them, without losing the unification.

Finally, a recent alternative view of selection, introduced by Huang and Pashler (2007), is particularly relevant to the question addressed in the present study. The foundational hypothesis of this view, which they refer to as the Boolean map model of attention, is that visual information can be parsed into two regions along a given dimension, such as color. Thus, if red is the selection criterion, displays are parsed into red and not red, and only the selected aspect of the display is apprehended. Note that the selection would define two regions whether there were only red and green items in the display or whether there were red, green, blue, and yellow items in the display. The parsing is binary: red versus not red. This idea can account for a large number of phenomena and data patterns within the attention literature. With regard to the present study, one can ask why observers did not parse the displays in Experiment 1, for example, into red and not-red components and functionally reduce the density of the displays by one half. An explanation similar to that regarding object-based attention applies here. Although it may have been possible to select just the red items, in accord with the Boolean map idea, the task then was to shift attention within that subset of items. Extending the Boolean map idea, it would be necessary to attentionally parse the display further in terms of this item and not this item in order to successfully navigate the display in response to the shift commands. This further step may disrupt the original red and not-red parsing, or the further parsing may be costly.

In summary, these results indicate that although perceptual organization can play a role in how attention is shifted and controlled within a densely cluttered visual field, that role is limited. In particular, organization does not seem to allow observers to reliably limit their walks to one group or another. Instead, we suggest that the main benefit of the grouping cues may be that they increase the heterogeneity of the display, which in turn facilitates individuation of the items. This would be essentially the same advantage as that observed with displays that were heterogeneous but could not be organized into distinct groups, in Moore et al. (2007).