Increased error-correction leads to both higher levels of variability and adaptation

Elisabeth B Knelange; Joan López-Moliner

doi:10.1371/journal.pone.0227913

. 2020 Feb 4;15(2):e0227913. doi: 10.1371/journal.pone.0227913

Increased error-correction leads to both higher levels of variability and adaptation

Elisabeth B Knelange ¹, Joan López-Moliner ^1,^*

Editor: Welber Marinovic²

PMCID: PMC6999875 PMID: 32017774

Abstract

In order to intercept moving objects, we need to predict the spatiotemporal features of the motion of both the object and our hand. Our errors can result in updates of these predictions to benefit interceptions in the future (adaptation). Recent studies claim that task-relevant variability in baseline performance can help adapt to perturbations, because initial variability helps explore the spatial demands of the task. In this study, we examined whether this relationship is also found in interception (temporal domain) by looking at the link between the variability of hand-movement speed during baseline trials, and the adaptation to a temporal perturbation. 17 subjects performed an interception task on a graphic tablet with a stylus. A target moved from left to right or vice versa, with varying speed across trials. Participants were instructed to intercept this target with a straight forward movement of their hand. Their movements were represented by a cursor that was displayed on a screen above the tablet. To prevent online corrections we blocked the hand from view, and a part of the cursor’s trajectory was occluded. After a baseline phase of 80 trials, a temporal delay of 100 ms was introduced to the cursor representing the hand (adaptation phase: 80 trials). This delay initially caused participants to miss the target, but they quickly accounted for these errors by adapting to most of the delay of the cursor. We found that variability in baseline movement velocity is a good predictor of temporal adaptation (defined as a combination of the rate of change and the asymptotic level of change after a perturbation), with higher variability during baseline being associated with better adaptation. However, cross-correlation results suggest that the increased variability is the result of increased error correction, rather than exploration.

Introduction

The human race is remarkably skilled in timing tasks like catching or hitting a ball [1, 2]. However, large inter-individual differences can be observed when it comes to these skills. To become successful at ball sports, a person needs to be able to accurately account for continuous changes in both the environment and their own body. To this end, we can use sensory feedback to guide our movement [3]. However, sensory feedback from our movements is processed by our brain with a delay that can reach up to about 150 ms [4–6]. This can lead to unstable movements, because corrections to errors are initiated with a delay. In order to not only rely on sensory feedback and select appropriate motor commands, we are thought to be able to predict the sensory consequences of these motor commands. Studies have shown that our brain maintains an internal forward model that holds the predictions regarding the sensory consequences [7, 8]. However, the outcome of a motor command can change due to systematic disturbances like fatigue in the muscles [9]. Accurate timing of our motor commands in a dynamic world requires continuous evaluation and updating of the predicted consequences of these motor commands [10]. This can be done by evaluating the difference between the actual and the predicted sensory consequences of a motor command (the prediction error [7, 11]). However, prediction errors do not always stem from incorrect motor commands. Noise can come from different stages of the sensorimotor process [12, 13]. Different types of noise associated with neural processes like movement planning [14–18] or execution [19–21] cause variability. In addition, trial-to-trial variability in the outcome of the movement can be caused by inaccurate estimates of the task requirements [22] and disturbances from the outside world [23]. Errors caused by these types of noise do not necessarily require updates of the internal model.

Updating the forward model is generally thought to be done by decreasing the prediction error over time (error-based learning) [24, 25]. Dominant theories in the field of motor control suggest that error correction is an optimal process [26, 27]. The amount of error correction depends on the reliability of the predicted sensory consequences and the reliability of the received sensory consequences [28]. However, in situations in which error feedback is unavailable or uninformative, the environment needs to be explored in order to find and exploit the most beneficial solution. This type of process is called reinforcement learning [29, 30]. It can also be beneficial in situations where the average end-point error is zero, but the movement is still updated in order to become more efficient [31]. Reinforcement learning, specifically exploration, usually leads to enhanced variability in the explored dimension of the behavior. Furthermore, research suggest that the nervous system could actively regulate this process when needed [32]. For this reason, we hereafter use exploration strategies to refer to the active process of learning through exploration. Some studies have found that reinforcement learning could also accelerate learning in error-based learning tasks [32]. More specifically, a benefit of task-specific baseline variability in adaptation during spatial perturbation paradigms has been found. This means that even if sensory feedback is available to the participant, more variability in the task-specific dimension could facilitate learning. It is thought that the brain has a memory of previously encountered errors [33]. Similarly, it has been proposed that predicted (future) errors might activate learned weights for motor primitives (neural mechanism that coordinate a set of movements rather than independent movements), which could elevate learning [34]. In line with this idea, reinforcement learning could lead to more experience with different movement errors and facilitate correcting future errors [35]. However, the idea that increased variability leads to better adaptation has been questioned by other studies claiming that variability originates from the different types of noise coming from motor control processes, which can have either positive, neutral or negative effects on adaptation [13].

Thus, the role of variability on adaptation is still under debate. The main question remains, can variability caused by exploration strategies directly benefit the updating of the forward model of a motor command, or are the two merely a result of error correction strategies? So far, the main focus of these studies has been the role of spatial and force-field perturbations. However, as large delays are inherent to the sensorimotor system and to contemporary electronic devices, temporal perturbation tasks have given great insights into adaptation in this domain [36–39]. It therefore is valuable to examine if task-specific variability in temporal features of movement can predict adaptation to these delays. Temporal perturbations (delays) require humans to identify a new temporal relationship between the motor command and the sensory consequences. The effect of delays on the spatial prediction error is increased with higher movement speeds (i.e. moving faster increases the gap between hand and delayed feedback), while lower speeds have less effect on the size of the prediction error. Variability in movement speed can therefore help to explore this temporal relationship, and benefit the examination of newly introduced delays. If exploration itself provides a benefit in adaptation, we do not expect the movement speed to be systematically related to previously encountered errors. However, a recent study by [40] found that error correction strategies could explain differences of the learning rate in a balancing task. If error correction rather than exploration is the main benefit for adaptation, higher rates of error correction are to be expected throughout the baseline for people that adapt more. The aim of the study was to examine if higher baseline movement speed variability can predict adaptation in a temporal timing task. As we found a positive relationship, we followed up this analysis by examining if this relationship was the result of exploratory behavior, or if higher variability might be the result of increased error correction.

Materials and methods

Participants

20 students of the university of Barcelona (20.3 ±SD 2.3 years; 15 female) participated in the experiment. All participants gave written consent. In order to be eligible for inclusion, participants’ vision and hearing needed to be normal or corrected to normal, and they needed to be free from movement restrictions or problems. The study was part of a program that has been approved by The University of Barcelona Bioethics Committee (CBUB) (Insitutional review board IRB 00003099) and was conducted in accordance to the Declaration of Helsinki.

Apparatus

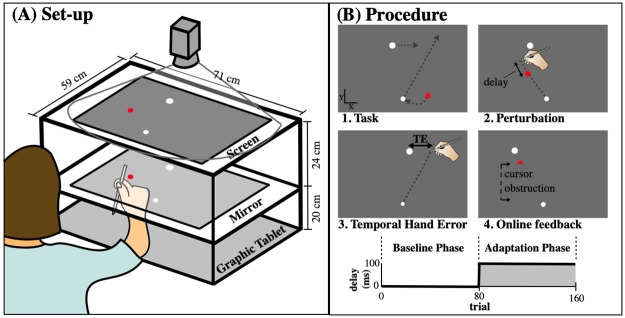
The setup of the experiment is shown in Fig 1A. Participants were seated in front of a graphic tablet (Calcomp Drawing Tablet III 24240), which recorded the movements of a hand-held stylus that the participants used in the experiments. A half-silvered upward facing mirror was located above the graphic tablet. Above the mirror, a projector displayed an image of the task onto a horizontal back-projection screen, at a frame rate of 72 Hz and a resolution of 800 by 600 pixels. The participant could see the reflection of this image in the mirror. The hand and the hand-held stylus were blocked from view by the mirror. A Macintosh Pro 2.6-GHz Quad-Core computer recorded the position of the stylus at 125 Hz and controlled the projected image. We calibrated the setup by aligning the position of the stylus with the location of five projected dots. This calibration allowed us to accurately display a cursor that represented the location of the stylus above the graphic tablet. The projected background was black (depicted as gray in Fig 1A). The feedback had a systematic delay of approximately 40 ms with relation to the hand movement. This value was determined before the start of the study with an interception task (similar to the one described below), in which we compared the stylus position and the target location on trials in which participants indicated they had hit the target. The system delay will have been corrected for in all of the future display and analysis of the data.

Task

Fig 1 shows the setup and the procedure for the experiment. The goal of the task was to intercept a target (white dot) on the screen with the cursor (red dot), that followed the movement of the hand. In order to start a trial, the participant had to move the cursor to the starting position (Fig 1B-1). A high-pitched sound marked the start of the trial. Randomly across trials, the target would move from left to right or vice versa at one of 3 different speeds (17.5, 22.5 or 27.5 cm/s). The three different speeds were used to prevent participants from learning were to intercept at what time, without taking the movement of the target into account. The target path was +20 cm in the y-direction from the starting position. Participants were instructed to intercept the target with a smooth straight movement, and to end their movement well beyond the target’s trajectory line. There were no points rewarded, only when the center of the cursor hit the target, an acoustic signal would sound.

After the explanation of the task and a familiarization phase of 10 trials, the experiment started. The experiment consisted of a baseline phase followed by an adaptation phase. During the baseline phase of 80 trials, no additional delays were added to the system. During the adaptation phase, the cursor movement was delayed with an additional 100 ms compared to the hand movement (Fig 1B-2). As participants could not see their own hand, they were unaware of these additional delays. This was verified by verbal confirmation at the end of the experiment.

To discourage online corrections we blocked the cursor’s path from view between 0.5 and 16 cm (see Fig 1B-4) along the y-axis from the starting location. During the baseline this led to an average of 126 ms (95% bootstrapped CI [124-128 ms]) visibility of the cursor before it would reach the trajectory line. As a result, participants could see the cursor cross the target’s trajectory line, but online corrections were minimized.

Analysis of responses

The data was prepared for analysis with the aid of the R-program [41]. In order to account for any deficient recordings and missing data, the raw position data for the hand and cursor in the x and y direction were interpolated by steps of 0.008 s and filtered with a bidirectional Butterworth filter (cut-off = 6Hz, sampling rate = 125 Hz). The velocity and acceleration of the hand were computed by calculating the first and second order derivatives of the filtered position data with respect to time. The derivatives were calculated for each time point by dividing the change in position by the change in time over the past two time points (average Δt = 0.016s).

Of the 20 participants, one was excluded from the study due to recording issues with the graphic tablet. For the remaining 19 participants (3040 trials), we inspected the movement speed during the movement before the target’s trajectory line was reached. As we had instructed participants to move through the target’s trajectory line, we discarded trials in which subjects moved through it with very low speeds (v < 20 cm/s). Two other participants were removed from the study because the systematically failed to comply with these instructions of the task (in >25% of their trials). For the 17 included participants we removed the trials in which this was the case (2.1% of the remaining trials discarded).

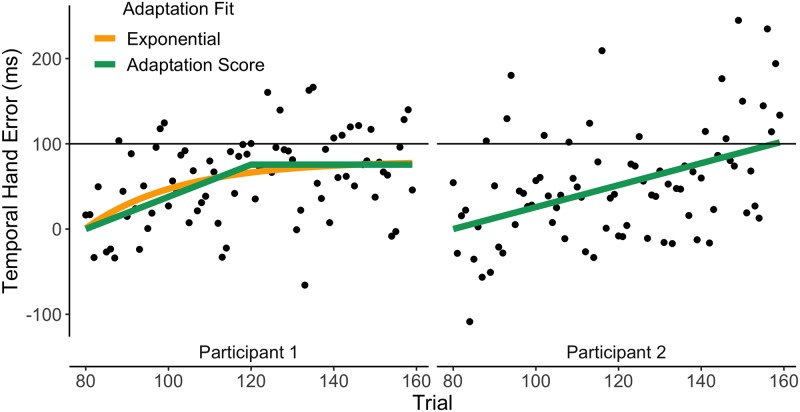
We calculated the Temporal Hand Error (TE) on each trial. TE was defined as the temporal difference between the hand and the target reaching the same point on the target’s trajectory line (Fig 1B-3). The TE was baseline-corrected by subtracting the average TE of the last 30 baseline trials for each participant in order to make sure any biases within subjects were removed. Positive values denoted the hand leading the target and negative values denoted the hand lagging behind the target. In order to hit the target when a temporal perturbation was applied, subjects would have to start leading the target with their hand. The TE was used to calculate the Adaptation Score for each participant. The Adaptation Score was calculated by fitting a two-state line through the TE data points of the adaptation phase (see Fig 2), with intercept 0. The slope (a) and asymptote (b) that resulted in a minimum residuals were each first normalized across subjects and then summed. The Adaptation Score gave us the ability to reward both speed and final level of adaptation. High values of the score meant that participants were relatively fast and had more complete levels of adaptation. Low values meant that participants adapted slowly and incomplete. Although we had the possibility to analyze slope and asymptote separately (to see if speed or final level of adaptation was affected differently) we only had a few participants with higher slopes, which made this analysis more difficult (see Table 1). We therefore decided only to focus on the Adaptation Score.

Fig 2 — The dots represent the moving averages (window = 4 trials) of two example participants. In order to calculate the Adaptation Score, the slope (a) and asymptote (b) were normalized across subjects and then summed for each participant. For P1 we were able to fit an exponential function, while for P2 the adaptation an exponential could not be fit.

Table 1. Pre-normalized slopes (a) and Asympotes (b) and adaptation scores for all the subjects.

a (unnormalized)	b (unnormalized)	Adaptation Score
7.1	86	-0.298
3.3	70	-1.49
8.8	70	-1.03
1.1	110	0.503
7.9	64	-1.42
34.3	76	1.33
1.2	100	0.266
1.3	112	0.684
3.7	75	1.49
7.5	82	-0.465
7.3	73	-0.991
3.4	72	1.08
1.3	113	1.67
1.2	110	0.611
1.9	76	-1.28
2.7	77	-1.15
0.90	109	0.492

Open in a new tab

Adaptation is often quantified by fitting the exponential function (exp(−τ ⋅ trial)) and calculating the time constant τ of this function. However, our pilot data showed we could not fit this function for each participant, as some participants adapted in a non-exponential way. There were 11 participants for which we were able to calculate the exponential function. In order to verify our method of quantifying adaptation, we compared τ of this exponential to our Adaptation Score and confirmed our main finding (see below) using τ instead of the Adaptation Score.

Movement onset was calculated according to algorithm A as proposed by [42] on the tangential velocity of the hand (tolerance range = 10%). The average movement speed (Mv) between the time of movement onset and the crossing of the target’s trajectory line was calculated. We also calculated the absolute movement angle (Ma) from the y-axis, calculated between movement onset and movement onset + 200 ms.

In order to identify the relationship between different kinematic variables and Temporal Hand Error, we analyzed the relationship between Mv, Ma, movement time (T), absolute target velocity (tv), (σ^Mv)²- group (LOW = 0; HIGH = 1) and their interactions on TE. We did this with a LASSO Regression for both the baseline and adaptation phase (lambda = 0.6). LASSO Regression can be used with multicollinear variables. We calculated bootstrapped confidence intervals (95%). LASSO regression includes a penalization. Confidence intervals can therefore only provide information about the variability regarding β for each predictor, but they should be interpreted with caution when it comes to the significance of the predictors.

Additionally, we performed another analysis with this technique in order to verify the respective contributions of movement speed variability ((σ^Mv)²) and movement angle ((σ^Ma)²) and their interaction on the Adaptation Score. As expected with regards to our hypothesis, we found the only included predictor of the Adaptation Score to be the (σ^Mv)² (see Results). The remainder of our analysis was therefore focused on the role of Mv on Adaptation.

The correlation between Mv variability across baseline trials ((σ^Mv)²) and the Adaptation Score was calculated using the rcorr- function from the Hmisc-package [43]. We used Spearman, in addition to Pearson, because Spearman (based on ranks) captures monotonic relation better than Pearson (which requires linear relations). We also calculated this relationship for τ calculated for the 11 participants that showed exponential adaptation curves.

We examined if the predictive capacity of (σ^Mv)² was due to the sequential effects of the TE on Mv by dividing the participants in a LOW (n = 9) and HIGH (n = 8) (σ^Mv)² group based on the size of their movement speed variability. In order to verify if there were group differences in variances for Mv and TE, we did F-tests on the results from the baseline phase (var.test-function for R). As we suspected that the benefit of (σ^Mv)² came from error correction rather than exploration, we expected sequential effects of TE_t on Mv_t+1. The sequential effects can show us if the error on one trial had an effect on the movement speed of consecutive trials. We verified this idea in two different ways: First, we fit a linear mixed model (lmer-function of the lme4-package [44] that examined the slopes of the HIGH and LOW (σ^Mv)² group, with subject as a nested random effect. We found significant effect for the HIGH (σ^Mv)² group, indicating that movement speed was used to account for previous encountered errors. In order to examine this effect in more detail, we calculated the cross correlation (ccf-function for R) between the TE and Mv for lag 0 through 3 for each subject individually to capture the corrective pattern. This way we could examine the effects of the movement speed on the error (lag 0) and the effect of the error on the movement speed over the next 3 trials (lag 1-3). In order to decrease the effect of any auto-correlation or common trends within the time-series we prewhitened the TE and Mv for each participant with the prewhiten-function of the psd-package. Bootstrapped confidence intervals (95%) were calculated. The results were correlated with the individual Adaptation Score results, in order to examine if sequential effects of TE on Mv could predict differences in adaptation.

Results

We first analyzed the behavior or participants within a trial for both phase 1 and 2 (see Table 2). A negative TE denoted being late, and a positive TE denoted being early. Both phases included (σ^Mv)²-group and movement time (T) as predictors of TE. Larger movement times led to a more negative TE. The HIGH (σ^Mv)² group had on average more positive TE. None of the other main effects were included as predictors, although there seemed to be some small interaction effects. As movement time was one of the main predictors of error, it is likely that participants use Mv to account for errors. However, another way to account for errors is by varying the movement angle (Ma). We found a significant correlation between Mv and Ma (R = 0.62, p < 0.001), and (σ^Mv)² and (σ^Ma)² (R = 0.67, p < 0.005). The results of the LASSO Regression (λ = 0.37) showed us that only (σ^Mv)² was a significant predictor of the Adaptation Score (β = 0.01; 95% CI[0.008–0.020]), while (σ^Ma)² and (σ^Ma)² ⋅ (σ^Mv)² were dropped. The remainder of the analysis will therefore only focus on Mv.

Table 2. Predictors for temporal hand error within a trial for Phase 1 and 2.

λ = 0.6 for both models. As LASSO regression includes a penalization, caution is required when interpreting Confidence Intervals.

Predictor	Phase 1 β [95%CI]	Phase 2 β [95%CI]
Ma	⋅	⋅
Mv	⋅	⋅
tv	⋅	⋅
HIGH (σ^Mv)²	4.74 [0.24–9.48]	13.44 [10.55–26.88]
T	-18.36[-36.72–(-5.52)]	-1.87[-11.68–7.43]
Ma ⋅ Mv	-0.0016 [-0.0060–(-0.00073)]	-0.011 [-0.021–(-0.0072)]
Ma ⋅ tv	-0.0026 [-0.0087–0.0049]	⋅
Ma ⋅ HIGH (σ^Mv)²	⋅	⋅
Ma ⋅ T	0.40 [0.090–1.04]	2.15 [1.38–4.30]
Mv ⋅ tv	⋅	⋅
Mv ⋅ HIGH (σ^Mv)²	0.035[-0.156–0.070]	⋅
Mv ⋅ T	-1.67 [-3.09–(-0.69)]	-1.28 [-2.57–(-0.72)]
tv ⋅ HIGH (σ^Mv)²	0.15 [0.02–0.35]	0.35[0.20–0.70]
tv ⋅ T	-0.47 [-0.93–(-0.34)]	-0.70[-1.25–(-0.58)]
HIGH (σ^Mv)² ⋅ T	⋅	⋅

Open in a new tab

The experiment was designed to study the relationship between (σ^Mv)² and the Adaptation score. Fig 2 shows two example subjects and their responses during the experiment. Participants showed various degrees of adaptation. Adaptation scores varied between -1.49 and +1.67 (Table 1).

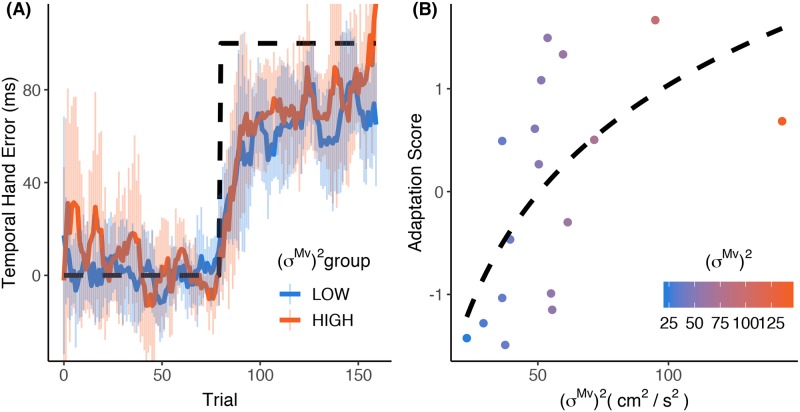
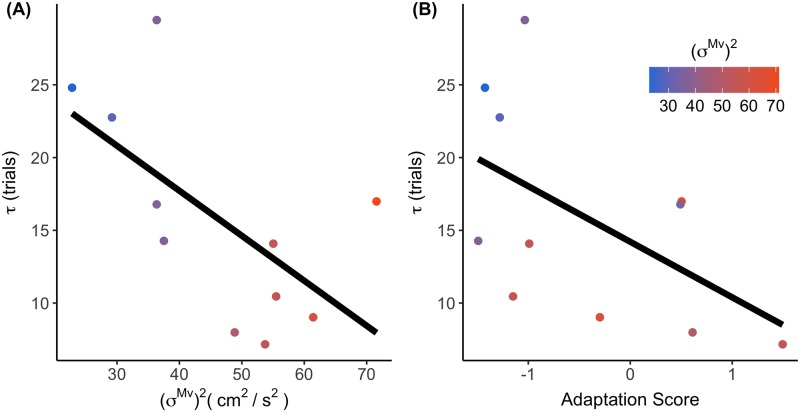
Fig 3A displays the moving average (window = 4 trials) of TE throughout the task. The blue line shows the mean of the nine participants with below-average (σ^Mv)², and the orange line depicts the mean of the eight participants with above-average (σ^Mv)². The spread around these lines represent the standard deviation of the data across subjects. When the temporal perturbation of 100 ms is introduced, subjects account for this delay by reaching the target’s trajectory earlier with their hand in relation to the target. This is depicted by a more positive TE in Fig 3. Upon visual inspection there seemed to be a slightly faster adaptation for the HIGH group than for the LOW group (see Fig 3B). In order to verify this notion, we calculated an adaptation score for each participant. We found a significant correlation between (σ^Mv)² and the adaptation score (Pearson r = 0.51, p = 0.037). We found an even higher Spearman correlation (r = 0.61, p = 0.009), indicating that the relationship might be better described by a logarithmic curve (dashed line in Fig 3B). These findings imply that there is a strong positive relationship between (σ^Mv)² and the adaptation. We confirmed this result by finding a negative correlation between (σ^Mv)² and τ (r = -0.63, p = 0.038) (Fig 4A). This was as expected, as the Adaptation Score had a negative (albeit not significant) correlation with τ as calculated by the exponential (r = -0.54, p = 0.088) (Fig 4B).

Fig 4 — A. The relation between movement speed variability and τ of the exponential function. B. The relationship between the Adaptation Score and τ of the exponential function.

As expected, the F-test revealed a significant difference between the HIGH and LOW variability groups in baseline Mv (F(1, 1315) = 2.5, p < 0.001). However, no differences were found for TE (F(1,1315) = 1.1, p = 0.35). This is important because it ensures that differences in sequential effects that are found between groups are not the result of differences in errors that were made.

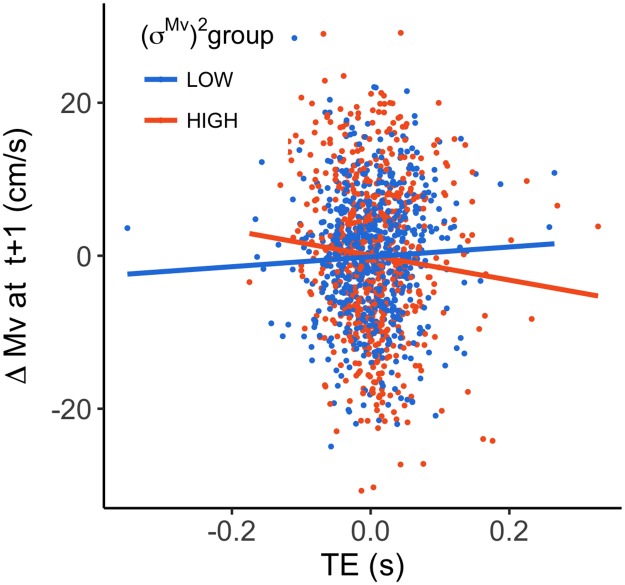
We examined the relationship between the TE on a certain trial, and the change in Mv on the next trial for participants in the HIGH and in the LOW (σ^Mv)² group (see Fig 5). The mixed linear model revealed that, when the error was zero, neither of the groups significantly changed their Mv (p = 0.69 (LOW); p = 0.59 (HIGH)). The effect of TE on the next trial’s Mv was significant for the HIGH (σ^Mv)² group (slope = -15.9 cm/s²; p = 0.02). The LOW (σ^Mv)² group did not show a significant effect (slope = 6.3 cm/s²; p = 0.68). The ANOVA revealed a significant difference between groups (F(1, 1263) = 5.2, p = 0.02). This suggests that participants with a higher (σ^Mv)² increased their speed when encountering a negative error and vice versa, while the participants with lower (σ^Mv)² did not.

Fig 5 — Dots represent individual trials for subjects within the HIGH (orange) and LOW (blue) (σ^Mv)² group. The lines indicate the predicted slope of the model.

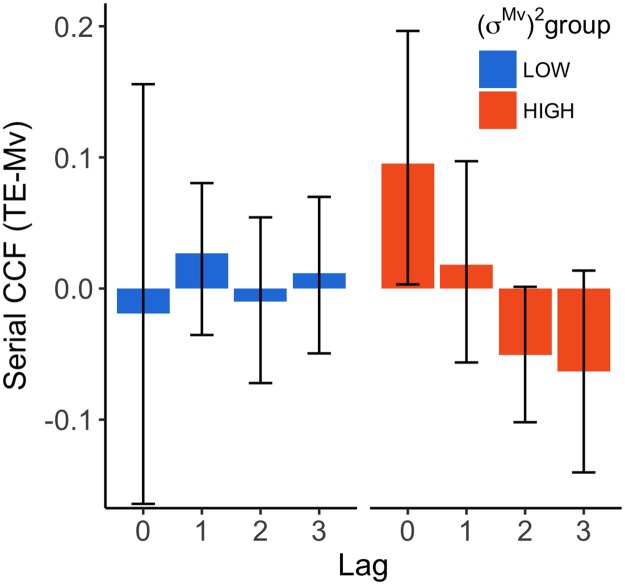
In order to examine if this difference can predict adaptation on an individual level, we calculated the cross correlation (ccf) between Mv at different t+lag and TE (Fig 6). A negative ccf indicates that a negative error (arriving too late) leads to increased velocities, and a more positive error (earlier) leads to decreased velocities. Consequently, a positive ccf indicates the opposite (negative error → decreased velocities; positive error → increased velocities). In congruence with Fig 6, participants with higher (σ^Mv)² scores seemed to have a trend towards more negative ccfs, while the participants with low (σ^Mv)² scores had ccfs near zero. The high (σ^Mv)² group showed a positive ccf(0) (i.e. the cross correlation between Mv and TE within a trial). Slower hand movements led to more negative TE and fast hand movement to positive TE. It shows that for this group there is some dependency of the TE on the Mv within a trial.

Fig 6 — The serial ccf for lag 0-3 for the HIGH (orange) and LOW (blue) (σ^Mv)² groups. The error bars represent the 95% bootstrapped confidence intervals.

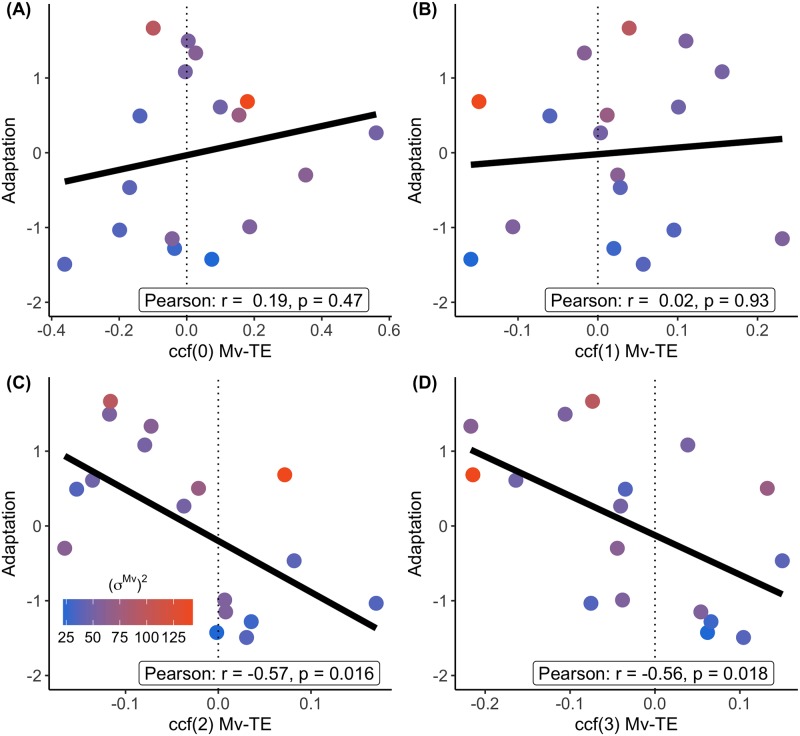
To see if this difference could explain the differences in adaptation, we calculated the correlation between the different lags and the Adaptation Score (Fig 7). The correlation between Mv and TE within a trial (lag0), i.e. how the Mv affected the TE, seemed to not be able to explain differences in adaptation. Although there is also no correlation for ccf(1), the lag2 and lag3 ccf seem to predict the Adaptation Score in this experiment. This suggests that errors might not be corrected right away, or only partially from trial to trial.

Fig 7 — The ccf is shown for lags 0-3 (A-D). The color of the data-points (blue-orange) indicates the size of the (σ^Mv)². The dotted line indicates a ccf of zero.

Discussion

This study found a positive relationship between variability of movement speed during the baseline phase, and the adaptation to a temporal perturbation. Our results indicate that this variability might be a result of error correction strategies, rather than exploration. Participants that corrected their movement velocity after encountering an error on average adapted more than participants who did not. To our knowledge, we are the first ones to reveal such a relationship in temporal adaptation.

The role of noise in adaptation has recently received a lot of attention. A study by Wu et al. [32] suggested that there might be a positive influence of variability on adaptation through reinforcement learning, revealed by an increased baseline variability for fast adapters. In line with these results, we found a benefit of increased baseline variability on the adaptation for temporal perturbations. However, our results suggest that participants with higher variability use their velocity more as a way to correct for errors. Our results are therefore more in line with the idea that motor noise from different types of processes can have either a positive, negative or neutral effect on adaptation [13]. Two types of noise that are relevant for adaptation are sensory noise and motor noise. Sensory noise can influence adaptation by influencing the uncertainty of the error [22, 45]. More sensory noise can lead to higher variability. However, error correction actually decreases with more uncertain sensory information. It is therefore unlikely that sensory noise was the source of the increased adaptation. Motor noise can roughly be divided into planning noise and execution noise [16]. A recent study by Vliet et al. [46] found that execution noise correlated negatively with adaptation rate, while planning noise revealed the opposite trend. Execution noise increases the uncertainty of the feedback that is received. Contrarily, more noise in the planning process can lead to more uncertain forward predictions, with a higher rate of error correction as a result. In the current study, we did not measure noise in the system directly. We therefore cannot determine the direct effect of planning noise and/or execution noise on the adaptation. However, it has been suggested that planning noise, in the form of stochastic resonance, could have a positive effect on signal detection by enhancing sub-threshold signals to supra-threshold [47–49]. Enhanced error-detection could lead to more error correction. Our results are in line with the idea that higher planning noise could increase the reliance on error feedback and lead to larger trial-to-trial corrections [46].

The question remains: why did we find a positive relationship between baseline variability and adaptation, while many other studies did not [13, 50–53]? It is likely that differences in design, such as variability measure or feedback provided, trigger variations in the accumulation of the different types of noise. In this study, we defined the average movement speed as an indicator of task-relevant variability, instead of the movement speed at the moment of interception, or the error at interception. We theorized that movement velocity would provide the richest information about the temporal contingencies of the sensorimotor system, and therefore could be more beneficial for exploration. By averaging the movement speed on each trial we believe to have filtered out a large part of the execution noise. This could have highlighted the effect of planning noise on adaptation. Similarly, Wu et al. [32] calculated the variability of deflection of a rewarded hand path throughout the movement, while He et al. [13] looked at the endpoint error. It is likely that endpoint error is more susceptible to execution noise. On the other hand, Dhawale et al. [54] suggested in a recent review that differences in results between studies might be inherent to differences in feedback. In Wu et al. [32], feedback was absent during the baseline, which may have led to an accumulation of planning noise (drift) that could not be corrected trial-to-trial [55]. In He et al. [13], feedback was provided throughout the movement, which means the variability measure might be dominated by execution noise. In the current study, we did provide error feedback in the baseline, which might be taken as evidence against the latter idea. However, these ideas together support the hypothesis that experimental designs that promote planning noise over execution noise are more likely to reveal a positive relationship between variability and adaptation.

Next, we need to consider the effect of generalization on the results. The term generalization refers to how the mapping between action and consequence generalizes to other tasks and target speeds. Research has shown that generalization of temporal perturbations is limited to tasks that are very similar to the learned task [39]. We used three different target speeds in two directions in this study. Some participants might had a better generalization from one speed to the other than others. It is possible that at the moment the perturbation was applied, some participants were able to generalize the changing consequences better for all target speeds and, as a result, adapt faster. For generalization to have an effect on our results there would need to be a relationship between movement speed variability and generalization. More variable people might develop broader tuning curves, and as a result adapt faster. We think this idea is captured well within the notion of exploration that is part of our original hypothesis: higher variability due to exploration might broaden the brain’s knowledge on the temporal contingencies over a broader range of target speeds and situations. Unfortunately our current dataset cannot give a definitive answer to the question of generalization.

Throughout the study, we mainly focused on how participants change their movement speed from trial-to-trial. However, in this task subjects were free to change their interception location or movement angle and onset time in order to account for prediction errors. This leads to a variety of strategies that participants can use to perform the task and correct for errors. These strategies are not independent of the target speed, nor independent of each other. For example, faster targets can lead to faster movements, earlier onset times and/or to broader hitting positions [56–58]. Furthermore, we found a correlation between the movement angle and the movement speed. These interconnections between movement features make it challenging to examine the participants’ strategies. However, it has been proposed that, in order to successfully hit a target, people benefit more from estimating the time it takes to reach the target’s trajectory, followed by fine-tuning the point of interception throughout the movement (online correction), as opposed to estimating when the target will reach the interception location [2]. As a result, errors are likely attributed to incorrect estimations of the time it takes to reach the target’s trajectory, rather than an incorrect estimations of interception location. As online correction was discouraged in our experiment, the reliance on error correction through changing the predicted temporal features of the movement was enhanced even further. During this experiment, successful participants used their movement speed as a control agent for trial-to-trial error correction in interception, and to a lesser extend their interception location or movement angle. This does not mean that low adapters do not have useful strategies of error correction. However, if the source of an error is temporal, using movement speed as a corrective strategy can be beneficial. Vice versa, if an error is spatial, corrections in movement angle would be more favorable. It is therefore possible that the difference in adaptation is rooted in the interpretation of the error.

Ccf(0) seemed to be slightly higher in the high variability group compared to the low variability group. This shows that participants with higher variability had a higher cross-correlation between the speed of movement and the temporal hand error in the same trial. This suggests that the temporal hand errors that participants with higher variability make are more dependent on the movement speed. This is not a surprising feature, given that more variability can more easily reveal a dependency of the temporal hand error on the movement speed. Another reason why ccf(0) is higher in the HIGH variability group is that participants with more dependency of temporal hand error on movement speed use their movement speed more as a way to correct for error and as a result, adapt more. We need to consider the possibility that this positive ccf(0) could have had an effect on the negative ccfs found in later lags. When a slow hand movement is made and a negative error occurs, it is more likely that the next movement will be faster. This therefore can lead to negative ccfs in consecutive lags. However, these differences in ccf(0) were not able to explain differences in adaptation. Therefore it seems unlikely that dependencies between Mv and TE within a trial alone could have explained more negative ccfs for consecutive lags.

To conclude, we found a correlation between movement speed variability and adaptation to a temporal perturbation. Further analysis of this relationship indicated that this is likely the result of error correction strategies that also benefited the adaptation, although the results are not conclusive. More research is needed to examine the contributions of movement speed, interception location and movement angle and the differences between temporal and spatial perturbations. Furthermore, it would be interesting to know how these error correction strategies are related to different types of noise and how the how the brain regulates these processes.

Acknowledgments

We would like to thank Cristina de la Malla and Björn Jörges for their stimulating discussion and help evaluating the manuscript.

Data Availability

The data can be found in the OSF repository: DOI 10.17605/OSF.IO/BF7SE.

Funding Statement

This work is part of the PACE project, which received funding from the European Union’s Horizon 2020 research and innovation programme under the Marie Sklodowska-Curie grant agreement No 642961. We also received funding from grant PSI2017-83493-R of AEI/FEDER, UE. There were no commercial relationships. The funders had no role in study design, data collection and analysis, decision to publish, or preparation of the manuscript.

References

1. Regan D. Visual factors in hitting and catching. J Sports Sci. 1997;15(6):533–58. 10.1080/026404197366985 [DOI] [PubMed] [Google Scholar]
2. Brenner E, Smeets JBJ. How people achieve their amazing temporal precision in interception. J Vis. 2015;15(3). 10.1167/15.3.8 [DOI] [PubMed] [Google Scholar]
3. Adams JA. A closed-loop theory of motor learning. J Mot Behav. 1971;3(2):111–49. 10.1080/00222895.1971.10734898 [DOI] [PubMed] [Google Scholar]
4. Miall RC, Weir DJ, Wolpert DM, Stein JF. Is the cerebellum a smith predictor? J Mot Behav. 1993;25(3):203–16. 10.1080/00222895.1993.9942050 [DOI] [PubMed] [Google Scholar]
5. López-Moliner J, Brenner E, Louw S, Smeets JBJ. Catching a gently thrown ball. Exp Brain Res. 2010;206(4):409–17. 10.1007/s00221-010-2421-1 [DOI] [PubMed] [Google Scholar]
6. López-Moliner J, Keil MS. People favour imperfect catching by assuming a stable world. PLoS One. 2012;7(4):e35705 10.1371/journal.pone.0035705 [DOI] [PMC free article] [PubMed] [Google Scholar]
7. Jordan MI, Rumelhart DE. Forward models: Supervised learning with a distal teacher. Cognitive science. 1992;16(3):307–354. 10.1207/s15516709cog1603_1 [DOI] [Google Scholar]
8. Wolpert DM, Miall RC. Forward Models for Physiological Motor Control. Neural Netw. 1996;9(8):1265–1279. 10.1016/s0893-6080(96)00035-4 [DOI] [PubMed] [Google Scholar]
9. Zhou S, Carey MF, Snow RJ, Lawson DL, Morrison WE. Effects of muscle fatigue and temperature on electromechanical delay. Electromyogr Clin Neurophysiol. 1998;38(2):67–73. [PubMed] [Google Scholar]
10. Wei K, Körding K. Relevance of error: what drives motor adaptation? J Neurophysiol. 2009;101(2):655–64. 10.1152/jn.90545.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]
11. Huang VS, Haith A, Mazzoni P, Krakauer JW. Rethinking motor learning and savings in adaptation paradigms: model-free memory for successful actions combines with internal models. Neuron. 2011;70(4):787–801. 10.1016/j.neuron.2011.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]
12. Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nature reviews neuroscience. 2008;9(4):292 10.1038/nrn2258 [DOI] [PMC free article] [PubMed] [Google Scholar]
13. He K, Liang Y, Abdollahi F, Fisher Bittmann M, Kording K, Wei K. The Statistical Determinants of the Speed of Motor Learning. PLoS Comput Biol. 2016;12(9):e1005023 10.1371/journal.pcbi.1005023 [DOI] [PMC free article] [PubMed] [Google Scholar]
14. Churchland MM, Afshar A, Shenoy KV. A central source of movement variability. Neuron. 2006;52(6):1085–96. 10.1016/j.neuron.2006.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]
15. Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV. Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci. 2006;26(14):3697–712. 10.1523/JNEUROSCI.3762-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
16. van Beers RJ. Motor learning is optimally tuned to the properties of motor noise. Neuron. 2009;63(3):406–17. 10.1016/j.neuron.2009.06.025 [DOI] [PubMed] [Google Scholar]
17. Chaisanguanthum KS, Shen HH, Sabes PN. Motor variability arises from a slow random walk in neural state. J Neurosci. 2014;34(36):12071–80. 10.1523/JNEUROSCI.3001-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]
18. Haar S, Donchin O, Dinstein I. Individual Movement Variability Magnitudes Are Explained by Cortical Neural Variability. J Neurosci. 2017;37(37):9076–9085. 10.1523/JNEUROSCI.1650-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]
19. Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394(6695):780–4. 10.1038/29528 [DOI] [PubMed] [Google Scholar]
20. Jones KE, Hamilton AF, Wolpert DM. Sources of signal-dependent noise during isometric force production. J Neurophysiol. 2002;88(3):1533–44. 10.1152/jn.2002.88.3.1533 [DOI] [PubMed] [Google Scholar]
21. van Beers RJ, Haggard P, Wolpert DM. The role of execution noise in movement variability. J Neurophysiol. 2004;91(2):1050–63. 10.1152/jn.00652.2003 [DOI] [PubMed] [Google Scholar]
22. Osborne LC, Lisberger SG, Bialek W. A sensory source for motor variation. Nature. 2005;437(7057):412–6. 10.1038/nature03961 [DOI] [PMC free article] [PubMed] [Google Scholar]
23. Tan H, Wade C, Brown P. Post-Movement Beta Activity in Sensorimotor Cortex Indexes Confidence in the Estimations from Internal Models. J Neurosci. 2016;36(5):1516–28. 10.1523/JNEUROSCI.3204-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]
24. Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci. 2006;26(14):3642–5. 10.1523/JNEUROSCI.5317-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]
25. Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci. 2010;33:89–108. 10.1146/annurev-neuro-060909-153135 [DOI] [PubMed] [Google Scholar]
26. Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427(6971):244–7. 10.1038/nature02169 [DOI] [PubMed] [Google Scholar]
27. Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5(11):1226–35. 10.1038/nn963 [DOI] [PubMed] [Google Scholar]
28. Wei K, Körding K. Uncertainty of feedback and state estimation determines the speed of motor adaptation. Front Comput Neurosci. 2010;4:11 10.3389/fncom.2010.00011 [DOI] [PMC free article] [PubMed] [Google Scholar]
29. Kaelbling LP, Littman ML, Moore AW. Reinforcement learning: A survey. Journal of artificial intelligence research. 1996;4:237–285. 10.1613/jair.301 [DOI] [Google Scholar]
30. Sutton RS, Barto AG, et al. Introduction to reinforcement learning. vol. 135 MIT press; Cambridge; 1998. [Google Scholar]
31. Wolpert DM, Diedrichsen J, Flanagan JR. Principles of sensorimotor learning. Nat Rev Neurosci. 2011;12(12):739–51. 10.1038/nrn3112 [DOI] [PubMed] [Google Scholar]
32. Wu HG, Miyamoto YR, Gonzalez Castro LN, Ölveczky BP, Smith MA. Temporal structure of motor variability is dynamically regulated and predicts motor learning ability. Nat Neurosci. 2014;17(2):312–21. 10.1038/nn.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]
33. Herzfeld DJ, Vaswani PA, Marko MK, Shadmehr R. A memory of errors in sensorimotor learning. Science. 2014;345(6202):1349–53. 10.1126/science.1253138 [DOI] [PMC free article] [PubMed] [Google Scholar]
34. Takiyama K, Hirashima M, Nozaki D. Prospective errors determine motor learning Nat Commun. 2015;6: 5925 10.1038/ncomms6925 [DOI] [PMC free article] [PubMed] [Google Scholar]
35. Herzfeld DJ, Shadmehr R. Motor variability is not noise, but grist for the learning mill. Nat Neurosci. 2014;17(2):149–50. 10.1038/nn.3633 [DOI] [PubMed] [Google Scholar]
36. Vercher JL, Gauthier GM. Oculo-manual coordination control: ocular and manual tracking of visual targets with delayed visual feedback of the hand motion. Exp Brain Res. 1992;90(3):599–609. 10.1007/bf00230944 [DOI] [PubMed] [Google Scholar]
37. Cunningham DW, Billock VA, Tsou BH. Sensorimotor adaptation to violations of temporal contiguity. Psychol Sci. 2001;12(6):532–5. 10.1111/1467-9280.d01-17 [DOI] [PubMed] [Google Scholar]
38. de la Malla C, López-Moliner J, Brenner E. Seeing the last part of a hitting movement is enough to adapt to a temporal delay. J Vis. 2012;12(10). 10.1167/12.10.4 [DOI] [PubMed] [Google Scholar]
39. de la Malla C, López-Moliner J, Brenner E. Dealing with delays does not transfer across sensorimotor tasks. J Vis. 2014;14(12). 10.1167/14.12.8 [DOI] [PubMed] [Google Scholar]
40. Barbado-Murillo D, Caballero Sánchez C, Moreside J, Vera-García FJ, Moreno FJ. Can the structure of motor variability predict learning rate? J Exp Psychol Hum Percept Perform. 2017;43(3):596–607. 10.1037/xhp0000303 [DOI] [PubMed] [Google Scholar]
41.R Core Team. R: A Language and Environment for Statistical Computing; 2013. Available from: http://www.R-project.org/.
42. Teasdale N, Bard C, Fleury M, Young DE, Proteau L. Determining movement onsets from temporal series. J Mot Behav. 1993;25(2):97–106. 10.1080/00222895.1993.9941644 [DOI] [PubMed] [Google Scholar]
43.Harrell Jr FE. Hmisc: Harrell Miscellaneous; 2018. Available from: https://CRAN.R-project.org/package=Hmisc.
44. Bates D, Mächler M, Bolker B, Walker S. Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software. 2015;67(1):1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]
45. Knelange EB, López-Moliner J. Decreased Temporal Sensorimotor Adaptation Due to Perturbation-Induced Measurement Noise. Front Hum Neurosci. 2019;13:46 10.3389/fnhum.2019.00046 [DOI] [PMC free article] [PubMed] [Google Scholar]
46. van der Vliet R, Frens MA, de Vreede L, Jonker ZD, Ribbers GM, Selles RW, et al. Individual Differences in Motor Noise and Adaptation Rate Are Optimally Related. eNeuro. 2018;5(4). 10.1523/ENEURO.0170-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]
47. Stacey WC, Durand DM. Stochastic resonance improves signal detection in hippocampal CA1 neurons. J Neurophysiol. 2000;83(3):1394–402. 10.1152/jn.2000.83.3.1394 [DOI] [PubMed] [Google Scholar]
48. Hänggi P. Stochastic resonance in biology. How noise can enhance detection of weak signals and help improve biological information processing. Chemphyschem. 2002;3(3):285–90. [DOI] [PubMed] [Google Scholar]
49. van der Groen O, Tang MF, Wenderoth N, Mattingley JB. Stochastic resonance enhances the rate of evidence accumulation during combined brain stimulation and perceptual decision-making. PLoS Comput Biol. 2018;14(7):e1006301 10.1371/journal.pcbi.1006301 [DOI] [PMC free article] [PubMed] [Google Scholar]
50. Mattar AAG, Ostry DJ. Generalization of dynamics learning across changes in movement amplitude. J Neurophysiol. 2010;104(1):426–38. 10.1152/jn.00886.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]
51. Ostry DJ, Darainy M, Mattar AAG, Wong J, Gribble PL. Somatosensory plasticity and motor learning. J Neurosci. 2010;30(15):5384–93. 10.1523/JNEUROSCI.4571-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]
52. Vahdat S, Darainy M, Milner TE, Ostry DJ. Functionally specific changes in resting-state sensorimotor networks after motor learning. J Neurosci. 2011;31(47):16907–15. 10.1523/JNEUROSCI.2737-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]
53. Fernandes HL, Stevenson IH, Kording KP. Generalization of stochastic visuomotor rotations. PLoS One. 2012;7(8):e43016 10.1371/journal.pone.0043016 [DOI] [PMC free article] [PubMed] [Google Scholar]
54. Dhawale AK, Smith MA, Ölveczky BP. The Role of Variability in Motor Learning. Annu Rev Neurosci. 2017;40:479–498. 10.1146/annurev-neuro-072116-031548 [DOI] [PMC free article] [PubMed] [Google Scholar]
55. van Beers RJ, van der Meer Y, Veerman RM. What autocorrelation tells us about motor variability: insights from dart throwing. PLoS One. 2013;8(5):e64332 10.1371/journal.pone.0064332 [DOI] [PMC free article] [PubMed] [Google Scholar]
56. Bairstow PJ. Analysis of hand movement to moving targets. Human Movement Science. 1987;6(3):205–231. 10.1016/0167-9457(87)90013-3 [DOI] [Google Scholar]
57. Brouwer AM, Brenner E, Smeets JB. Hitting moving objects. The dependency of hand velocity on the speed of the target. Exp Brain Res. 2000;133(2):242–8. 10.1007/s002210000371 [DOI] [PubMed] [Google Scholar]
58. Brouwer AM, Brenner E, Smeets JBJ. Hitting moving objects: is target speed used in guiding the hand? Exp Brain Res. 2002;143(2):198–211. 10.1007/s00221-001-0980-x [DOI] [PubMed] [Google Scholar]

PLoS One. doi: 10.1371/journal.pone.0227913.r001

Decision Letter 0

Welber Marinovic

7 Aug 2019

PONE-D-19-18039

Increased error-correction leads to both higher levels of variability and adaptation

PLOS ONE

Dear Dr. López-Moliner,

Thank you for submitting your manuscript to PLOS ONE. After careful consideration, we feel that it has merit but does not fully meet PLOS ONE’s publication criteria as it currently stands. Therefore, we invite you to submit a revised version of the manuscript that addresses the points raised during the review process.

==============================

The manuscript has been reviewed by two expert academic reviewers in your area of research. I share their assessment that this is an interesting topic of investigation looking at how individual differences in people's behaviour may predict later adaptation. Although I do invite a revision of the submitted work, the reviewers also highlighted significant issues with data analysis that required considerable work. I hope you may be able to address the reviewers concerns with data analysis convincingly.

==============================

We would appreciate receiving your revised manuscript by Sep 21 2019 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

To enhance the reproducibility of your results, we recommend that if applicable you deposit your laboratory protocols in protocols.io, where a protocol can be assigned its own identifier (DOI) such that it can be cited independently in the future. For instructions see: http://journals.plos.org/plosone/s/submission-guidelines#loc-laboratory-protocols

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

Please note while forming your response, if your article is accepted, you may have the opportunity to make the peer review history publicly available. The record will include editor decision letters (with reviews) and your responses to reviewer comments. If eligible, we will contact you to opt in or out.

We look forward to receiving your revised manuscript.

Kind regards,

Welber Marinovic

Academic Editor

PLOS ONE

Journal Requirements:

When submitting your revision, we need you to address these additional requirements.

Please ensure that your manuscript meets PLOS ONE's style requirements, including those for file naming. The PLOS ONE style templates can be found at

http://www.journals.plos.org/plosone/s/file?id=wjVg/PLOSOne_formatting_sample_main_body.pdf and http://www.journals.plos.org/plosone/s/file?id=ba62/PLOSOne_formatting_sample_title_authors_affiliations.pdf

1. Thank you for including your ethics statement: All participants gave written consent. Their vision and hearing were normal or corrected to normal, and no movement restrictions or problems were reported. The study was part of a program that has been approved by the local ethics committee and was conducted in accordance to the Declaration of Helsinki.

Please amend your current ethics statement to include the full name of the ethics committee/institutional review board(s) that approved your specific study

Once you have amended this/these statement(s) in the Methods section of the manuscript, please add the same text to the “Ethics Statement” field of the submission form (via “Edit Submission”).

For additional information about PLOS ONE ethical requirements for human subjects research, please refer to http://journals.plos.org/plosone/s/submission-guidelines#loc-human-subjects-research.

2. Please provide more information regarding the setting (e.g. locations, relevant dates, periods of recruitment, data collection) as well as the sources, methods and criteria of participants' selection.

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. Is the manuscript technically sound, and do the data support the conclusions?

The manuscript must describe a technically sound piece of scientific research with data that supports the conclusions. Experiments must have been conducted rigorously, with appropriate controls, replication, and sample sizes. The conclusions must be drawn appropriately based on the data presented.

Reviewer #1: No

Reviewer #2: Yes

**********

2. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: No

Reviewer #2: No

**********

3. Have the authors made all data underlying the findings in their manuscript fully available?

The PLOS Data policy requires authors to make all data underlying the findings described in their manuscript fully available without restriction, with rare exception (please refer to the Data Availability Statement in the manuscript PDF file). The data should be provided as part of the manuscript or its supporting information, or deposited to a public repository. For example, in addition to summary statistics, the data points behind means, medians and variance measures should be available. If there are restrictions on publicly sharing data—e.g. participant privacy or use of data from a third party—those must be specified.

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Is the manuscript presented in an intelligible fashion and written in standard English?

PLOS ONE does not copyedit accepted manuscripts, so the language in submitted articles must be clear, correct, and unambiguous. Any typographical or grammatical errors should be corrected at revision, so please note any specific errors here.

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Review Comments to the Author

Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Reviewer #1: The authors investigated how movement variability is related to motor adaptation in the temporal domain. Although the motivation of the study and the target-intersection task sound interesting, I cannot agree with the validity of the analysis in the current paper. Please respond to the following questions carefully.

In sum, I was interested in the target-intersecting task, but I cannot be favorable for almost all the results.

Major

1) Even under assuming straight pen trajectories, this task is redundant. That is, subjects can choose the pair of initial movement angle and movement velocity to achieve the task. The authors should investigate how the pair is modified depending on perturbation and task set; however, they investigated only movement velocity. These missing analyses can hide significant findings inherent in this interesting experiment. Without the analysis of the movement angle, it is not worth to discuss their results.

2) In the adaptation, we can assume a simple state-space model, Mv(t+1) = lambda*Mv(t) + eta*(TE(t)+zeta(t)) + xi(t), where lambda is forgetting rate, eta is learning rate, xi(t) is motor noise, and zeta(t) is sensory noise to perceive TE(t). Under this equation, it is self-evident that the larger sigma_MV results in faster learning, because a high magnitude of xi(t)+eta*zeta(t) (i.e., sigma_MV) is nearly equivalent to high learning rate. Please mention clearly that the current results are not mere results of high sensory noise.

3) I wonder how generalization affected the results. Because the authors used three different speeds for target motions, they need to coednsider how the adaptation in one speed can be generalized to other speeds. Another possibility was the participants with small \\sigma_MV showed little generalization compared to those with large \\sigma_MV.

4) Please discuss slope and asymptote separately. Why did the authors sum those values to quantify Adaptation Score?

5) Despite the clarity of Fig. 3B (if the Adaptation Score were a valid value to quantify adaptation), Figs. 4-6 do not seem meaninful. The reason is the small correlation in Fig.3, cross-correlation that does not seem to be significantly different from 0 in Fig. 4, and low correlations in Fig.5. In Figs. 3 and 5, it seems impossible to predict one variable based on the other.

Reviewer #2: The authors examine the relationship between variability in hand movement speed during baseline and the adaptation to a temporal perturbation of sensory feedback (delay). They find that baseline variability is a good predictor of adaptation expressed as a summary score including the rate at asymptote level of adaptation. The authors argue that the increased baseline variability seen in ‘good adapters’ is not due to exploration, but rather to increased correction of errors in previous trials.

The source and relevance of motor variability, and the explanation of individual differences in motor learning, are critical issues in the field of motor control and learning. The authors provide important novel insights into the role of exploration and variability in motor learning. The experiment is well designed, and the paper is generally well written and concise.

My main comment is that the analyses of the relation between variability and adaptation should be more clearly explained and motivated. How/why were the particular analyses performed? Why was the adaptation score calculated this way? What is meant by sequential effects? How were the participants divided into groups? Why was the linear model fitted to the group data, and the cross-correlation performed per participant? Why are both a Pearson and a Spearman correlation reported; how exactly are variability and adaptation related? Why do some analyses test differences between groups, while other analyses focus on correlation of baseline temporal variability with other measures?

Another important point is that the term ‘exploration’ should be clearly defined. Is this an actively controlled (or deliberate) process, or an automatic, implicit process? The term ‘exploration strategies’ (used by the authors) makes me think that it is a deliberate process, but I am not sure this is what the authors mean.

Minor comments

Introduction

Lines 4-18. I understand what the authors are saying here but the reasoning is a little confusing. They first argue that we need sensory feedback, and then say that sensory feedback is too slow for corrections and we thus need an internal model. It might be helpful to distinguish between immediate corrections and adjustment to changes. In addition, we also need to predict the trajectory of the ball if we’re intercepting a moving object and rely on sensory feedback. Please clarify this paragraph.

L 22. “… neural variability”. If the authors refer to execution noise as well as planning noise, please remove ‘neural’.

L 30-31. “In situations in which error feedback is not clear…” I think ‘not available’ would be the correct term here. If not, please explain what is meant by ‘not clear’.

L 33-35. “It can also be beneficial …. in the explored dimension of the behaviour”. It’s not clear to me what this means, please expand.

L 36-38. Since the Wu et al paper is a main motivation for the current study, I think it would be helpful to expand the description of their findings a little bit.

L 42-45. It is not clear to me how exploration strategies could directly benefit the updating of the forward model, please clarify. And what is the potential role of variability from other sources than exploration?

Methods

Fig 1B. Display 4 is missing a title. It is unclear what the figure below the 4 displays belongs to.

L 92-93. What was the size of the target and the cursor?

L 109-110. 0.5 cm from where?

Fig 2 - legend. The word ‘summarized’ should be ‘summed’.

General. Were the results collapsed for the different target speeds?

Results

L 177. “There seems to be a slightly faster adaptation for the HIGH group than for the LOW group.” This is not clear to me from figure 3A. Was the slope or asymptote level of adaptation different between groups?

Fig 4. I would just like to note that I don’t find this figure particularly convincing. From the scatter, it looks like there is no relationship in either of the groups.

L 206-207. Shouldn’t the lag zero correlation be positive for both groups?

Fig 5. What do the error bars represent?

L 213-214. A word is missing in this sentence.

Discussion

Could the authors speculate about the origin of differences in error correction? For example, do people have differences in error sensitivity? Is the mechanism similar to differences in adaptation rate resulting from differences in error size or different levels of uncertainty of sensory feedback?

**********

6. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

[NOTE: If reviewer comments were submitted as an attachment file, they will be attached to this email and accessible via the submission site. Please log into your account, locate the manuscript record, and check for the action link "View Attachments". If this link does not appear, there are no attachment files to be viewed.]

While revising your submission, please upload your figure files to the Preflight Analysis and Conversion Engine (PACE) digital diagnostic tool, https://pacev2.apexcovantage.com/. PACE helps ensure that figures meet PLOS requirements. To use PACE, you must first register as a user. Registration is free. Then, login and navigate to the UPLOAD tab, where you will find detailed instructions on how to use the tool. If you encounter any issues or have any questions when using PACE, please email us at figures@plos.org. Please note that Supporting Information files do not need this step.

PLoS One. 2020 Feb 4;15(2):e0227913. doi: 10.1371/journal.pone.0227913.r002

Author response to Decision Letter 0

23 Oct 2019

Dear editor and reviewers,

Thank you very much for spending time and effort improving this manuscript. It has been a very useful process. The response to the Reviewers PDF file contains all the answers and also some figures that cannot be included here. I refer you to this file for these figures.

Response to the reviewers:

The authors would like to thank the reviewers for their insightful comments on our manuscript. We have carefully evaluated each of their responses and concerns. We also thank the reviewers and editor for their patience and extending the deadline for our re-submission. Each of the comments will be evaluated separately below.

Reviewer 1

The authors investigated how movement variability is related to motor adaptation in the temporal domain. Although the motivation of the study and the target-intersection task sound interesting, I cannot agree with the validity of the analysis in the current paper. Please respond to the following questions carefully. In sum, I was interested in the target-intersecting task, but I cannot be favorable for almost all the results.

ANSWER: Dear reviewer 1, Thank you very much for your evaluation. The points that were brought up have proven very useful to us when improving our manuscript. We hope that we have clearly understood your concerns and that you are satisﬁed with our answers and corrections.

1. Even under assuming straight pen trajectories, this task is redundant. That is, subjects can choose the pair of initial movement angle and movement velocity to achieve the task. The authors should investigate how the pair is modiﬁed depending on perturbation and task set; however, they investigated only movement velocity. These missing analyses can hide signiﬁcant ﬁndings inherent in this interesting experiment. Without the analysis of the movement angle, it is not worth to discuss their results.

ANSWER: We acknowledge that interception location plays a role when evaluating the movements of our participants. Variability in movement speed and aiming angle are correlated in our data (see ﬁgure 1 PDF). The reason why only movement speed was analyzed was because of the hypothesis that was the base of the research. As previous research had claimed exploration (and as a result variability) could beneﬁt error-based learning, our hypothesis followed this same rhetoric. We assumed that theoretically it would make more sense that exploration of movement speed would beneﬁt temporal adaptation over exploration in the movement angle, (and movement angle might beneﬁt spatial adaptation more). However, we realize that this assumption might blind us from other behavior that could have beneﬁted adaptation. In order to get more information on this idea we have modeled Partial Least Squares Regression (PLS) on the adaptation scores with absolute movement angle variability σ-Ma and movement speed variability σ-Mv as predictors. This PLS can give us information on the contribution of diﬀerent correlated predictors on a dependent variable.

AdaptationScore = 1.27 · σMv + 0.56 · σMa − 1.33 · (σMv · σMa )

This relationship in itself is very interesting, because together a larger part of the Adaptation Score can be explained than by just the σ-Mv. It indicates that both σ-Mv and σ-Ma have a positive main eﬀect on the Adaptation Score, but that either high or low values in both negatively aﬀects this relationship. However, of these predictors, only for σ-Mv the estimated (bootstrapped) 95% conﬁdence intervals that are diﬀerent from zero (see ﬁgure 2), indicating that only σ-Mv has a signiﬁcant eﬀect on the Adaptation Score. We therefore believe that our initial assumption, in which we stated that speciﬁcally movement speed is beneﬁcial for temporal adaptation, is not violated. However, we understand that other readers might have these same questions, which is why we have added the results of the above mentioned PLS to the manuscript and discussed its implications further in the discussion section.

2. In the adaptation, we can assume a simple state-space model,

Mv(t + 1) = λ ∗ Mv(t) + η ∗ (TE(t) + ζ(t)) + xi(t)

where lambda is forgetting rate, eta is learning rate, xi(t) is motor noise, and zeta(t) is sensory noise to perceive TE(t). Under this equation, it is self-evident that the larger σ Mv results in faster learning, because a high magnitude of xi(t) + eta ∗ zeta(t) (i.e., σ Mv ) is nearly equivalent to high learning rate. Please mention clearly that the current results are not mere results of high sensory noise.

ANSWER: One important way in which adaptation can be modeled is with a state space model. Another way it can be modelled is with a Bayesian tool, for example a Kalman ﬁlter. The reason that these Bayesian of models are used is that learning from errors is often thought to be optimal. More uncertain feedback (due to sensory and/or motor noise) leads to smaller error updates. Although higher sensory noise generally leads to more variability in movement outcome, we would not expect learning rate to be higher because of it. Furthermore, assuming that zeta would be gaussian noise with mean of zero, we are not sure if the error would always be perceived as larger and therefore updates would be larger. The measure of error (TE) in our task is 1 dimensional. This means that the noise could have decreased the perceived error just as likely as it could have increased it, which means on average increased correction of the error is not expected. We have extended the text about noise in the discussion a bit to also cover sensory noise.

3. I wonder how generalization aﬀected the results. Because the authors used three diﬀerent speeds for target motions, they need to coednsider how the adaptation in one speed can be generalized to other speeds. Another possibility was the participants with small σMv showed little generalization compared to those with large σMv .

ANSWER: The three diﬀerent speeds were used to prevent participants from learning were to intercept at what time, without taking the movement of the target into account. Given the size of the dataset, we cannot be sure if the diﬀerent speeds have an eﬀect on the results. Some participants might have larger generalization than others (with the term generalization referring to how the mapping between action and consequence generalizes to other tasks/speeds). It is possible that at the moment the perturbation was applied, the broadly generalizing participants were able to generalize the changing consequences better for all target speeds and adapt faster as a result. However, higher generalization would not directly lead to more variable movement speed during the baseline.

On the other hand, increased movement speed variability might in itself lead to more generalization (as proposed by the reviewer’s second suggestion). Hence, more variable people might develop broader tuning curves, and as a result adapt faster. We think this idea is captured well within the notion of exploration that is part of our original hypothesis. Research has shown that generalisation temporal perturbations is limited only to tasks that are very similar to the learned task (de la Malla et al, 2014). Higher variability due to exploration might broaden the brains knowledge on the temporal contingencies over a broader range of target speeds and situations. Unfortunately our current dataset cannot give a clear answer to the question of generalization. As discussed in manuscript, we suspect the variability is a result of error correction rather than exploration. However, we understand that others might have the same question and have therefore dedicated a section to it in the discussion.

4. Please discuss slope and asymptote separately. Why did the authors sum those values to quantify Adaptation Score?

ANSWER: Adaptation is often calculated by ﬁtting an exponential function on the data and calculating the Time Constant (TC) of this best-ﬁt. A smaller TC indicates better adaptation. This method assumes that adaptation takes place according to an exponential function. We aimed at another way of calculating adaptation, as during pilot studies we were not able to calculate this ﬁt for each participant, indicating that not each participants adaptation can be quantiﬁed this way (See ﬁgure 3 PDF). We opted for an Adaptation Score (AS) that could be determined for each participant so that we could also account for the participants that had less typical types of adaptation, for example more linear. The reason we normalised and summed the two in order to calculate the AS is because both slope and asymptote determine the quality of the adaptation. Very low levels of adaptation (asymptote, b) might be achieved with a slope (a) that is steep, while a higher level of adaptation might be achieved with a low slope. It is the participants that have both fast (slope) and high (asymptote) adaptation that have high AS, while slow and low adaptation would lead to low AS. Although we are unsure if this is the best way of quantifying the adaptation, we have found that (for the participants we were able to calculate the TC of the exponential for; n=11), the TC was negatively correlated with the AS (albeit not signiﬁcantly; R = - 0.54; p = 0.088). This indicates that the AS can replace TC as a measure of adaptation. Figure 4 below shows how the AS and TC are related. When we use the TC instead of the AS to correlate the relationship between σMv and adaptation, we ﬁnd a signiﬁcantly negative correlation (R = -0.63, p = 0.038), providing more evidence that our measure of adaptation yields similar results to the more standard ones. We have added these results to the manuscript.

5. Despite the clarity of Fig. 3B (if the Adaptation Score were a valid value to quantify adaptation), Figs. 4-6 do not seem meaninful. The reason is the small correlation in Fig.3, cross-correlation that does not seem to be signiﬁcantly diﬀerent from 0 in Fig. 4, and low correlations in Fig.5. In Figs. 3 and 5, it seems impossible to predict one variable based on the other.

ANSWER: We acknowledge that we have not reached a deﬁning answer to the question of what the reason behind the variabilityadaptation relationship is. The data hints towards increased variability being due to the use of movement speed in order to correct for error. We aimed to convey the idea that the results regarding the cause of the relationship are non-conclusive, however we might not have fully succeeded. We will state more clearly that further research is needed to ﬁnd more conclusive answers.

References:

de la Malla, C., Lopez-Moliner, J., & Brenner, E. (2014). Dealing with delays does not transfer across sensorimotor tasks. Journal of vision, 14(12), 8-8.

Reviewer 2:

The authors examine the relationship between variability in hand movement speed during baseline and the adaptation to a temporal perturbation of sensory feedback (delay). They ﬁnd that baseline variability is a good predictor of adaptation expressed as a summary score including the rate at asymptote level of adaptation. The authors argue that the increased baseline variability seen in good adapters is not due to exploration, but rather to increased correction of errors in previous trials.

The source and relevance of motor variability, and the explanation of individual diﬀerences in motor learning, are critical issues in the ﬁeld of motor control and learning. The authors provide important novel insights into the role of exploration and variability in motor learning. The experiment is well designed, and the paper is generally well written and concise.

ANSWER: Dear reviewer 2, thank you for your kind words and your suggestions. We found them very valuable when rewriting the manuscript. We hope to have answered your questions and concerns to your satisfaction.

1. My main comment is that the analyses of the relation between variability and adaptation should be more clearly explained and motivated. How/why were the particular analyses performed? Why was the adaptation score calculated this way? What is meant by sequential eﬀects? How were the participants divided into groups? Why was the linear model ﬁtted to the group data, and the cross-correlation performed per participant? Why are both a Pearson and a Spearman correlation reported; how exactly are variability and adaptation related? Why do some analyses test diﬀerences between groups, while other analyses focus on correlation of baseline temporal variability with other measures?

ANSWER: We have expanded the methods section to more clearly to account for the uncertainties and questions of the reviewer. In summary, we have added the use of an exponential function, more widely used in adaptation, and found a correlation with our score (see Fig 3 and 4). Once we have shown this correlation, we keep our score because, unlike the exponential function, we were able to ﬁt our score to all subjects. Concerning the use of the ccf, it only makes sense to apply to individual data, since averaging would factor out the individual corrective patters. This analysis has been done in the spatial domain (see van Beers, 2009). While the lmm can capture individual variability in the random structure of the model. We used Spearman, in addition to Pearson, because Spearman (based on ranks) captures monotonic relation better than Pearson (which requires linear relations). We have rewritten the methods to motivate our choices more clearly.

2. Another important point is that the term exploration should be clearly deﬁned. Is this an actively controlled (or deliberate) process, or an automatic, implicit process? The term exploration strategies (used by the authors) makes me think that it is a deliberate process, but I am not sure this is what the authors mean. This part could indeed use some clariﬁcation. ANSWER: The process is thought to be actively controlled. We have rewritten the section (note that Q6 is incorporated in this section as well).

3. Lines 4-18. I understand what the authors are saying here but the reasoning is a little confusing. They ﬁrst argue that we need sensory feedback, and then say that sensory feedback is too slow for corrections and we thus need an internal model. It might be helpful to distinguish between immediate corrections and adjustment to changes. In addition, we also need to predict the trajectory of the ball if were intercepting a moving object and rely on sensory feedback. Please clarify this paragraph. ANSWER: Agreed: we have rewritten the paragraph.

4. L 22. neural variability. If the authors refer to execution noise as well as planning noise, please remove neural. ANSWER: Corrected

5. L 30-31. In situations in which error feedback is not clear I think not available would be the correct term here. If not, please explain what is meant by not clear. ANSWER: Corrected to ”unavailable or uninformative”

6. L 33-35. It can also be beneﬁcial . in the explored dimension of the behaviour. Its not clear to me what this means, please expand. ANSWER: Changed in order to increase clarity.

7. L 36-38. Since the Wu et al paper is a main motivation for the current study, I think it would be helpful to expand the description of their ﬁndings a little bit. ANSWER: Expanded

8. L 42-45. It is not clear to me how exploration strategies could directly beneﬁt the updating of the forward model, please clarify. And what is the potential role of variability from other sources than exploration? ANSWER: Exploration strategies can help us learn about the outcome of our motor commands. When we explore more, we get richer information about the relationship between the motor commands and its sensory outcome. We have expanded our explanation of exploration. We also added some more information about other forms of noise, like sensory noise.

9. Fig 1B. Display 4 is missing a title. It is unclear what the ﬁgure below the 4 displays belongs to. ANSWER: Corrected

10. L 92-93. What was the size of the target and the cursor? ANSWER: Added

11. L 109-110. 0.5 cm from where? ANSWER: Added

12. Fig 2 - legend. The word summarized should be summed. ANSWER: Corrected

13. Were the results collapsed for the diﬀerent target speeds? ANSWER: We indeed did not look at the diﬀerences in target speed. Target speed was one of 3 speeds leftwards or rightwards random. We chose diﬀerent target speeds so that the participants could not just learn a speciﬁc location and time to intercept at each trial. However, our dataset is not large enough to do the analysis for diﬀerent. However, in accordance with the comments of reviewer 1 (Q3), we elaborated about the use of the diﬀerent speeds and its aﬀect on generalization in the discussion.

14. L 177. There seems to be a slightly faster adaptation for the HIGH group than for the LOW group. This is not clear to me from ﬁgure 3A. Was the slope or asymptote level of adaptation diﬀerent between groups? ANSWER: This indeed was initially only visual inspection and was after veriﬁed with the Adaptation score. We rewrote this section.

15. Fig 4. I would just like to note that I dont ﬁnd this ﬁgure particularly convincing. From the scatter, it looks like there is no relationship in either of the groups. ANSWER: We acknowledge that we have not reached a deﬁning answer to the question of what the reason behind the variabilityadaptation relationship is. The data hints towards increased variability being due to the use of movement speed in order to correct for error. We aimed to convey the idea that the results regarding the cause of the relationship are exploratory, however we might not have fully succeeded. We will state more clearly that the data of the second part is exploratory and should be aimed to be reproduced in future studies.

16. L 206-207. Shouldnt the lag zero correlation be positive for both groups? ANSWER: Lag zero cross correlation was more positive in the HIGH variability group. The HIGH variability group moved in more variable speeds and it might be that the relationship between movement speed and error might therefore more easily revealed. It could also mean that the HIGH variability group had a stronger relationship between movement speed and error, they were more likely to use movement speed as a correction mechanism in future. We expanded this part in the discussion a bit further.

17. Fig 5. What do the error bars represent? ANSWER: Error bars represent the 95% bootstrapped conﬁdence intervals. We have now added this in the ﬁgure description as well.

18. L 213-214. A word is missing in this sentence. ANSWER: Corrected

19. Could the authors speculate about the origin of diﬀerences in error correction? For example, do people have diﬀerences in error sensitivity? Is the mechanism similar to diﬀerences in adaptation rate resulting from diﬀerences in error size or diﬀerent levels of uncertainty of sensory feedback?

ANSWER: One of the mentioned mechanisms in the Discussion is a possible diﬀerence in planning noise, which might lead to more uncertain predicted sensory feedback (hence more correction of error) or enhance the detection of errors. We expanded a bit on that topic and added the role of sensory noise. We also included a part about a possible role of generalization on error correction and the idea that error can be interpreted as having a more spatial or more temporal origin.

Attachment

Submitted filename: Response to Reviewers.pdf

Click here for additional data file.^{(720.7KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0227913.r003

Decision Letter 1

Welber Marinovic

19 Nov 2019

PONE-D-19-18039R1

Increased error-correction leads to both higher levels of variability and adaptation

PLOS ONE

Dear Dr. López-Moliner,

==============================

The two expert reviewers agree that the paper has merit but had some final comments that I would like to see addressed as much as possible in a revised manuscript. The comments/requests are relatively minor and I believe that I will be able to reach a final decision without additional input from the reviewers.

==============================

We would appreciate receiving your revised manuscript by Jan 03 2020 11:59PM. When you are ready to submit your revision, log on to https://www.editorialmanager.com/pone/ and select the 'Submissions Needing Revision' folder to locate your manuscript file.

If you would like to make changes to your financial disclosure, please include your updated statement in your cover letter.

Please include the following items when submitting your revised manuscript:

A rebuttal letter that responds to each point raised by the academic editor and reviewer(s). This letter should be uploaded as separate file and labeled 'Response to Reviewers'.
A marked-up copy of your manuscript that highlights changes made to the original version. This file should be uploaded as separate file and labeled 'Revised Manuscript with Track Changes'.
An unmarked version of your revised paper without tracked changes. This file should be uploaded as separate file and labeled 'Manuscript'.

We look forward to receiving your revised manuscript.

Kind regards,

Welber Marinovic

Academic Editor

PLOS ONE

[Note: HTML markup is below. Please do not edit.]

Reviewers' comments:

Reviewer's Responses to Questions

Comments to the Author

1. If the authors have adequately addressed your comments raised in a previous round of review and you feel that this manuscript is now acceptable for publication, you may indicate that here to bypass the “Comments to the Author” section, enter your conflict of interest statement in the “Confidential to Editor” section, and submit your "Accept" recommendation.

Reviewer #1: All comments have been addressed

Reviewer #2: (No Response)

**********

2. Is the manuscript technically sound, and do the data support the conclusions?

Reviewer #1: Yes

Reviewer #2: Yes

**********

3. Has the statistical analysis been performed appropriately and rigorously?

Reviewer #1: Yes

Reviewer #2: Yes

**********

4. Have the authors made all data underlying the findings in their manuscript fully available?

Reviewer #1: Yes

Reviewer #2: Yes

**********

5. Is the manuscript presented in an intelligible fashion and written in standard English?

Reviewer #1: Yes

Reviewer #2: Yes

**********

6. Review Comments to the Author

Reviewer #1: The authors revised their manuscript carefully. Although they missed discussing the effects of generalization, their citing paper can support to interpret the effects of generalization to some extent (but not wholly, of course). I have now a positive attitude towards the acceptance of this manuscript after responding to the following comments. I have two more comments about the PLS, the evaluation of the adaptation score, and discussion.

In the analysis of PLS, they considered only a simple second-order interaction of ma and mv. I guess that the TE can be affected by mv*T*sin(ma) under the assumption of the constant velocity through the movement time T (although this assumption is probably wrong). It should be investigated the more appropriate relation between adaptation score and some kinematic variables.

2) In l.72-76, they mentioned that the history of error of future error could affect adaptation. Why not consider the influence of predicted error on motor adaptation [2]? Because we cannot be sure what kind of information affects motor adaptation, we should keep our scope broad.

ref:

[1] Furuki D & Takiyama K, 2019, Decomposing motion that changes over time into task-relevant and task-irrelevant components in a data-driven manner: application to motor adaptation in whole-body

movements, Sci Rep

[2] Takiyama K, Hirashima M, Nozaki D, 2015, Prospective errors determine motor learning, Nat Comm

Reviewer #2: I am happy with most of the changes that the authors made. However, I do have a few more comments, as outlined below. Line numbers refer to the manuscript with tracked changes.

Line 214-223. After reading the comment of the other reviewer on the redundancy of the task, I understand why the authors performed this analysis, but this analysis is not clearly motivated in the paper. (I also think that in its current form this analysis will not mitigate the concern of the other reviewer, but I will leave this up to the other reviewer. I’d be happy to explain more if needed).

It would also be useful to explain the relationship between Mv and Ma in more detail than mentioning that there is a correlation. Have the authors verified whether this relation is independent of target speed?

Line 257. “Adaptation scores varied between -1.49 and +1.67.” Since the scores are normalized these numbers don’t provide much information. It would be useful to have an overview of the (unnormalized) slopes, asymptotes and adaptation scores for all participants. It would also be useful to provide some information about the goodness of fit for the two-state lines.

Figure 2 + 4. The y-axis of these figures is labelled ‘Temporal Error (ms)’. This might be confusing as it suggests that the error increases during the adaptation phase (rather than going towards zero). In addition, it seems that the numbers on the y-axis of the revised Fig 2 are seconds instead of ms.

**********

7. PLOS authors have the option to publish the peer review history of their article (what does this mean?). If published, this will include your full peer review and any attached files.

If you choose “no”, your identity will remain anonymous but your review may still be made public.

Do you want your identity to be public for this peer review? For information about this choice, including consent withdrawal, please see our Privacy Policy.

Reviewer #1: No

Reviewer #2: No

PLoS One. 2020 Feb 4;15(2):e0227913. doi: 10.1371/journal.pone.0227913.r004

Author response to Decision Letter 1

2 Jan 2020

Review Comments to the Author  Please use the space provided to explain your answers to the questions above. You may also include additional comments for the author, including concerns about dual publication, research ethics, or publication ethics. (Please upload your review as an attachment if it exceeds 20,000 characters)

Dear reviewer, thank you for your comments. Below you can find the answers to other points raised. We hope we have sufficiently satisfied your concerns.

 1) Although I understand that they want to focus on the adaptation score, the temporal error (TE) is a more direct measure of adaptation without any post-hoc calculation of such as variability. Although I understand the difficulty of calculating the relation among TE, movement angle (ma), and movement velocity (mv), recent studies enable us to evaluate the relation using a data-driven technique [1]. Further, it is possible to calculate the task-relevant and task-irrelevant variabilities with the technique. It should be better to discuss the relation between task-relevant variability and adaptation score after clarifying the relation among TE, ma, and mv.In the analysis of PLS, they considered only a simple second-order interaction of ma and mv. I guess that the TE can be affected by mv*T*sin(ma) under the assumption of the constant velocity through the movement time T (although this assumption is probably wrong). It should be investigated the more appropriate relation between adaptation score and some kinematic variables.

We agree with the suggestion to check the relationship between different kinematic variables and TE. We used a LASSO regression to analyse explanatory predictors (similar to the Ridge regression in the suggested literature). This showed us that the movement time was one of the main predictors of Temporal error. We already saw that To not exhaust the reader with too many different types of analyses we have also changed the PLS to a LASSO regression to see the relationship between sigma_mv, sigma_ma and adaptation.  2) In l.72-76, they mentioned that the history of error of future error could affect adaptation. Why not consider the influence of predicted error on motor adaptation [2]? Because we cannot be sure what kind of information affects motor adaptation, we should keep our scope broad.

 We agree with the reviewers comment and have added some information about prospective errors in the introduction.

ref: [1] Furuki D & Takiyama K, 2019, Decomposing motion that changes over time into task-relevant and task-irrelevant components in a data-driven manner: application to motor adaptation in whole-body movements, Sci Rep [2] Takiyama K, Hirashima M, Nozaki D, 2015, Prospective errors determine motor learning, Nat Comm  Reviewer #2: I am happy with most of the changes that the authors made. However, I do have a few more comments, as outlined below. Line numbers refer to the manuscript with tracked changes. Dear reviewer, thank you very much for your further comments. We hope we have satisfied your final notes.

  Line 195-197. “The slope (a) and asymptote (b) that resulted in a minimum residuals were first normalized across subjects and then summed.” I realized that the question that I asked in the previous round, “Why was the adaptation score calculated this way?”, was rather vague. I am happy that the authors clarified why they used this score rather than the time constant of an exponential function. However, I also meant to ask whether the authors expected variability to influence both the slope and the asymptote of adaptation? What was the reason for summing the slope and asymptote, rather than treating them as individual variables? Although we were interested to see if there was a difference, we did not have a specific prediction. Rather we tried to find a replacement for the more commonly used exponential function. We chose to sum the two because summing them leads to an Adaptation Score that represents fast and high levels of adaptation with high scores, and slow and low levels of adaptation with low scores. Anything in between can either mean an interplay between the slope and intercept. In some previous literature the focus was put on speed of adaptation to benefit from exploration strategies. Looking at the individual slopes and asymptotes we unfortunately cannot make up any distinct effect. This might also be because we had only a few participants with higher slopes. We have added an overview of the slopes and asymptotes.

 This analysis makes me wonder about the strategies that participants used. Were most participants fairly stereotyped in where they would intercept the target? The figure showing the Mv and Ma variability correlations seems to suggest that most participants had a fairly low variance in Ma, but some participants have a rather high variance.It would also be useful to explain the relationship between Mv and Ma in more detail than mentioning that there is a correlation. Have the authors verified whether this relation is independent of target speed? We have added a Lasso regression analysis to look at how TE was affected by different kinematic variables, among others: target speed, Mv and Ma.

 See above

Attachment

Submitted filename: Response_Reviewers.pdf

Click here for additional data file.^{(43.7KB, pdf)}

PLoS One. doi: 10.1371/journal.pone.0227913.r005

Decision Letter 2

Welber Marinovic

3 Jan 2020

Increased error-correction leads to both higher levels of variability and adaptation

PONE-D-19-18039R2

Dear Dr. López-Moliner,

We are pleased to inform you that your manuscript has been judged scientifically suitable for publication and will be formally accepted for publication once it complies with all outstanding technical requirements.

Within one week, you will receive an e-mail containing information on the amendments required prior to publication. When all required modifications have been addressed, you will receive a formal acceptance letter and your manuscript will proceed to our production department and be scheduled for publication.

Shortly after the formal acceptance letter is sent, an invoice for payment will follow. To ensure an efficient production and billing process, please log into Editorial Manager at https://www.editorialmanager.com/pone/, click the "Update My Information" link at the top of the page, and update your user information. If you have any billing related questions, please contact our Author Billing department directly at authorbilling@plos.org.

If your institution or institutions have a press office, please notify them about your upcoming paper to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, you must inform our press team as soon as possible and no later than 48 hours after receiving the formal acceptance. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information, please contact onepress@plos.org.

With kind regards,

Welber Marinovic

Academic Editor

PLOS ONE

Additional Editor Comments (optional):

Reviewers' comments:

PLoS One. doi: 10.1371/journal.pone.0227913.r006

Acceptance letter

Welber Marinovic

8 Jan 2020

PONE-D-19-18039R2

Increased error-correction leads to both higher levels of 2 variability and adaptation

Dear Dr. López-Moliner:

I am pleased to inform you that your manuscript has been deemed suitable for publication in PLOS ONE. Congratulations! Your manuscript is now with our production department.

If your institution or institutions have a press office, please notify them about your upcoming paper at this point, to enable them to help maximize its impact. If they will be preparing press materials for this manuscript, please inform our press team within the next 48 hours. Your manuscript will remain under strict press embargo until 2 pm Eastern Time on the date of publication. For more information please contact onepress@plos.org.

For any other questions or concerns, please email plosone@plos.org.

Thank you for submitting your work to PLOS ONE.

With kind regards,

PLOS ONE Editorial Office Staff

on behalf of

Dr. Welber Marinovic

Academic Editor

PLOS ONE

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Attachment

Submitted filename: Response to Reviewers.pdf

Click here for additional data file.^{(720.7KB, pdf)}

Attachment

Submitted filename: Response_Reviewers.pdf

Click here for additional data file.^{(43.7KB, pdf)}

Data Availability Statement

The data can be found in the OSF repository: DOI 10.17605/OSF.IO/BF7SE.

[pone.0227913.ref001] 1. Regan D. Visual factors in hitting and catching. J Sports Sci. 1997;15(6):533–58. 10.1080/026404197366985 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref002] 2. Brenner E, Smeets JBJ. How people achieve their amazing temporal precision in interception. J Vis. 2015;15(3). 10.1167/15.3.8 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref003] 3. Adams JA. A closed-loop theory of motor learning. J Mot Behav. 1971;3(2):111–49. 10.1080/00222895.1971.10734898 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref004] 4. Miall RC, Weir DJ, Wolpert DM, Stein JF. Is the cerebellum a smith predictor? J Mot Behav. 1993;25(3):203–16. 10.1080/00222895.1993.9942050 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref005] 5. López-Moliner J, Brenner E, Louw S, Smeets JBJ. Catching a gently thrown ball. Exp Brain Res. 2010;206(4):409–17. 10.1007/s00221-010-2421-1 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref006] 6. López-Moliner J, Keil MS. People favour imperfect catching by assuming a stable world. PLoS One. 2012;7(4):e35705 10.1371/journal.pone.0035705 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref007] 7. Jordan MI, Rumelhart DE. Forward models: Supervised learning with a distal teacher. Cognitive science. 1992;16(3):307–354. 10.1207/s15516709cog1603_1 [DOI] [Google Scholar]

[pone.0227913.ref008] 8. Wolpert DM, Miall RC. Forward Models for Physiological Motor Control. Neural Netw. 1996;9(8):1265–1279. 10.1016/s0893-6080(96)00035-4 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref009] 9. Zhou S, Carey MF, Snow RJ, Lawson DL, Morrison WE. Effects of muscle fatigue and temperature on electromechanical delay. Electromyogr Clin Neurophysiol. 1998;38(2):67–73. [PubMed] [Google Scholar]

[pone.0227913.ref010] 10. Wei K, Körding K. Relevance of error: what drives motor adaptation? J Neurophysiol. 2009;101(2):655–64. 10.1152/jn.90545.2008 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref011] 11. Huang VS, Haith A, Mazzoni P, Krakauer JW. Rethinking motor learning and savings in adaptation paradigms: model-free memory for successful actions combines with internal models. Neuron. 2011;70(4):787–801. 10.1016/j.neuron.2011.04.012 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref012] 12. Faisal AA, Selen LP, Wolpert DM. Noise in the nervous system. Nature reviews neuroscience. 2008;9(4):292 10.1038/nrn2258 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref013] 13. He K, Liang Y, Abdollahi F, Fisher Bittmann M, Kording K, Wei K. The Statistical Determinants of the Speed of Motor Learning. PLoS Comput Biol. 2016;12(9):e1005023 10.1371/journal.pcbi.1005023 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref014] 14. Churchland MM, Afshar A, Shenoy KV. A central source of movement variability. Neuron. 2006;52(6):1085–96. 10.1016/j.neuron.2006.10.034 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref015] 15. Churchland MM, Yu BM, Ryu SI, Santhanam G, Shenoy KV. Neural variability in premotor cortex provides a signature of motor preparation. J Neurosci. 2006;26(14):3697–712. 10.1523/JNEUROSCI.3762-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref016] 16. van Beers RJ. Motor learning is optimally tuned to the properties of motor noise. Neuron. 2009;63(3):406–17. 10.1016/j.neuron.2009.06.025 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref017] 17. Chaisanguanthum KS, Shen HH, Sabes PN. Motor variability arises from a slow random walk in neural state. J Neurosci. 2014;34(36):12071–80. 10.1523/JNEUROSCI.3001-13.2014 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref018] 18. Haar S, Donchin O, Dinstein I. Individual Movement Variability Magnitudes Are Explained by Cortical Neural Variability. J Neurosci. 2017;37(37):9076–9085. 10.1523/JNEUROSCI.1650-17.2017 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref019] 19. Harris CM, Wolpert DM. Signal-dependent noise determines motor planning. Nature. 1998;394(6695):780–4. 10.1038/29528 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref020] 20. Jones KE, Hamilton AF, Wolpert DM. Sources of signal-dependent noise during isometric force production. J Neurophysiol. 2002;88(3):1533–44. 10.1152/jn.2002.88.3.1533 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref021] 21. van Beers RJ, Haggard P, Wolpert DM. The role of execution noise in movement variability. J Neurophysiol. 2004;91(2):1050–63. 10.1152/jn.00652.2003 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref022] 22. Osborne LC, Lisberger SG, Bialek W. A sensory source for motor variation. Nature. 2005;437(7057):412–6. 10.1038/nature03961 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref023] 23. Tan H, Wade C, Brown P. Post-Movement Beta Activity in Sensorimotor Cortex Indexes Confidence in the Estimations from Internal Models. J Neurosci. 2016;36(5):1516–28. 10.1523/JNEUROSCI.3204-15.2016 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref024] 24. Mazzoni P, Krakauer JW. An implicit plan overrides an explicit strategy during visuomotor adaptation. J Neurosci. 2006;26(14):3642–5. 10.1523/JNEUROSCI.5317-05.2006 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref025] 25. Shadmehr R, Smith MA, Krakauer JW. Error correction, sensory prediction, and adaptation in motor control. Annu Rev Neurosci. 2010;33:89–108. 10.1146/annurev-neuro-060909-153135 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref026] 26. Körding KP, Wolpert DM. Bayesian integration in sensorimotor learning. Nature. 2004;427(6971):244–7. 10.1038/nature02169 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref027] 27. Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5(11):1226–35. 10.1038/nn963 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref028] 28. Wei K, Körding K. Uncertainty of feedback and state estimation determines the speed of motor adaptation. Front Comput Neurosci. 2010;4:11 10.3389/fncom.2010.00011 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref029] 29. Kaelbling LP, Littman ML, Moore AW. Reinforcement learning: A survey. Journal of artificial intelligence research. 1996;4:237–285. 10.1613/jair.301 [DOI] [Google Scholar]

[pone.0227913.ref030] 30. Sutton RS, Barto AG, et al. Introduction to reinforcement learning. vol. 135 MIT press; Cambridge; 1998. [Google Scholar]

[pone.0227913.ref031] 31. Wolpert DM, Diedrichsen J, Flanagan JR. Principles of sensorimotor learning. Nat Rev Neurosci. 2011;12(12):739–51. 10.1038/nrn3112 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref032] 32. Wu HG, Miyamoto YR, Gonzalez Castro LN, Ölveczky BP, Smith MA. Temporal structure of motor variability is dynamically regulated and predicts motor learning ability. Nat Neurosci. 2014;17(2):312–21. 10.1038/nn.3616 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref033] 33. Herzfeld DJ, Vaswani PA, Marko MK, Shadmehr R. A memory of errors in sensorimotor learning. Science. 2014;345(6202):1349–53. 10.1126/science.1253138 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref034] 34. Takiyama K, Hirashima M, Nozaki D. Prospective errors determine motor learning Nat Commun. 2015;6: 5925 10.1038/ncomms6925 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref035] 35. Herzfeld DJ, Shadmehr R. Motor variability is not noise, but grist for the learning mill. Nat Neurosci. 2014;17(2):149–50. 10.1038/nn.3633 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref036] 36. Vercher JL, Gauthier GM. Oculo-manual coordination control: ocular and manual tracking of visual targets with delayed visual feedback of the hand motion. Exp Brain Res. 1992;90(3):599–609. 10.1007/bf00230944 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref037] 37. Cunningham DW, Billock VA, Tsou BH. Sensorimotor adaptation to violations of temporal contiguity. Psychol Sci. 2001;12(6):532–5. 10.1111/1467-9280.d01-17 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref038] 38. de la Malla C, López-Moliner J, Brenner E. Seeing the last part of a hitting movement is enough to adapt to a temporal delay. J Vis. 2012;12(10). 10.1167/12.10.4 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref039] 39. de la Malla C, López-Moliner J, Brenner E. Dealing with delays does not transfer across sensorimotor tasks. J Vis. 2014;14(12). 10.1167/14.12.8 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref040] 40. Barbado-Murillo D, Caballero Sánchez C, Moreside J, Vera-García FJ, Moreno FJ. Can the structure of motor variability predict learning rate? J Exp Psychol Hum Percept Perform. 2017;43(3):596–607. 10.1037/xhp0000303 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref041] 41.R Core Team. R: A Language and Environment for Statistical Computing; 2013. Available from: http://www.R-project.org/.

[pone.0227913.ref042] 42. Teasdale N, Bard C, Fleury M, Young DE, Proteau L. Determining movement onsets from temporal series. J Mot Behav. 1993;25(2):97–106. 10.1080/00222895.1993.9941644 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref043] 43.Harrell Jr FE. Hmisc: Harrell Miscellaneous; 2018. Available from: https://CRAN.R-project.org/package=Hmisc.

[pone.0227913.ref044] 44. Bates D, Mächler M, Bolker B, Walker S. Fitting Linear Mixed-Effects Models Using lme4. Journal of Statistical Software. 2015;67(1):1–48. 10.18637/jss.v067.i01 [DOI] [Google Scholar]

[pone.0227913.ref045] 45. Knelange EB, López-Moliner J. Decreased Temporal Sensorimotor Adaptation Due to Perturbation-Induced Measurement Noise. Front Hum Neurosci. 2019;13:46 10.3389/fnhum.2019.00046 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref046] 46. van der Vliet R, Frens MA, de Vreede L, Jonker ZD, Ribbers GM, Selles RW, et al. Individual Differences in Motor Noise and Adaptation Rate Are Optimally Related. eNeuro. 2018;5(4). 10.1523/ENEURO.0170-18.2018 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref047] 47. Stacey WC, Durand DM. Stochastic resonance improves signal detection in hippocampal CA1 neurons. J Neurophysiol. 2000;83(3):1394–402. 10.1152/jn.2000.83.3.1394 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref048] 48. Hänggi P. Stochastic resonance in biology. How noise can enhance detection of weak signals and help improve biological information processing. Chemphyschem. 2002;3(3):285–90. [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref049] 49. van der Groen O, Tang MF, Wenderoth N, Mattingley JB. Stochastic resonance enhances the rate of evidence accumulation during combined brain stimulation and perceptual decision-making. PLoS Comput Biol. 2018;14(7):e1006301 10.1371/journal.pcbi.1006301 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref050] 50. Mattar AAG, Ostry DJ. Generalization of dynamics learning across changes in movement amplitude. J Neurophysiol. 2010;104(1):426–38. 10.1152/jn.00886.2009 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref051] 51. Ostry DJ, Darainy M, Mattar AAG, Wong J, Gribble PL. Somatosensory plasticity and motor learning. J Neurosci. 2010;30(15):5384–93. 10.1523/JNEUROSCI.4571-09.2010 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref052] 52. Vahdat S, Darainy M, Milner TE, Ostry DJ. Functionally specific changes in resting-state sensorimotor networks after motor learning. J Neurosci. 2011;31(47):16907–15. 10.1523/JNEUROSCI.2737-11.2011 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref053] 53. Fernandes HL, Stevenson IH, Kording KP. Generalization of stochastic visuomotor rotations. PLoS One. 2012;7(8):e43016 10.1371/journal.pone.0043016 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref054] 54. Dhawale AK, Smith MA, Ölveczky BP. The Role of Variability in Motor Learning. Annu Rev Neurosci. 2017;40:479–498. 10.1146/annurev-neuro-072116-031548 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref055] 55. van Beers RJ, van der Meer Y, Veerman RM. What autocorrelation tells us about motor variability: insights from dart throwing. PLoS One. 2013;8(5):e64332 10.1371/journal.pone.0064332 [DOI] [PMC free article] [PubMed] [Google Scholar]

[pone.0227913.ref056] 56. Bairstow PJ. Analysis of hand movement to moving targets. Human Movement Science. 1987;6(3):205–231. 10.1016/0167-9457(87)90013-3 [DOI] [Google Scholar]

[pone.0227913.ref057] 57. Brouwer AM, Brenner E, Smeets JB. Hitting moving objects. The dependency of hand velocity on the speed of the target. Exp Brain Res. 2000;133(2):242–8. 10.1007/s002210000371 [DOI] [PubMed] [Google Scholar]

[pone.0227913.ref058] 58. Brouwer AM, Brenner E, Smeets JBJ. Hitting moving objects: is target speed used in guiding the hand? Exp Brain Res. 2002;143(2):198–211. 10.1007/s00221-001-0980-x [DOI] [PubMed] [Google Scholar]

PERMALINK

Increased error-correction leads to both higher levels of variability and adaptation

Elisabeth B Knelange

Joan López-Moliner

Roles

Abstract

Introduction

Materials and methods

Participants

Apparatus

Fig 1. Set-up and procedure.

Task

Analysis of responses

Fig 2. Adaptation score examples.

Table 1. Pre-normalized slopes (a) and Asympotes (b) and adaptation scores for all the subjects.

Results

Table 2. Predictors for temporal hand error within a trial for Phase 1 and 2.

Fig 3. The relationship between (σMv)2 and adaptation score.

Fig 4. Verification of the adaptation score.

Fig 5. The relationship between the baseline TE on trial t-1 and the subsequent change in Mvel.

Fig 6. Serial ccf for each (σMv)2 group.

Fig 7. The relationship between the ccf score and the adaptation score.

Discussion

Acknowledgments

Data Availability

Funding Statement

References

Decision Letter 0

Welber Marinovic

Roles

Author response to Decision Letter 0

Decision Letter 1

Welber Marinovic

Roles

Author response to Decision Letter 1

Decision Letter 2

Welber Marinovic

Roles

Acceptance letter

Welber Marinovic

Roles

Associated Data

Supplementary Materials

Data Availability Statement

ACTIONS

PERMALINK

RESOURCES

Similar articles

Cited by other articles

Links to NCBI Databases

Fig 3. The relationship between (σ^Mv)² and adaptation score.

Fig 6. Serial ccf for each (σ^Mv)² group.