The association of grey matter volume and cortical complexity with individual differences in children’s arithmetic fluency

Abstract

Only a small amount of studies have looked at the structural neural correlates of children’s arithmetic. Furthermore, these studies mainly implemented voxel-based morphometry, which only takes the volume of regions into account, without looking at other structural properties. The current study aimed to contribute knowledge on which brain regions are important for children’s arithmetic on a structural level, by not only implementing voxel-based morphometry, but also cortical complexity analyses, based on the fractal dimension index. This complexity measure describes a characteristic of surface shape. Data of 43 typically developing 9-10 year-olds were analyzed. All children were asked to take part in two test sessions: behavioral data collection and MRI data acquisition. For data analysis, mean values for volume and cortical complexity were estimated within regions of interest (ROIs) and extracted for further analysis. The selected ROIs were based on regions found to be related to children’s mathematical abilities in previous research. Results point towards associations between arithmetic fluency and the volume of the right fusiform gyrus, as well as the cortical complexity of the left postcentral gyrus, right insular sulcus, and left lateral orbital sulcus. Remarkably, no significant associations were observed between the children’s arithmetic fluency and the volume or cortical complexity of typically arithmetic-associated parietal regions, such as the superior parietal lobe, intraparietal sulcus, or angular gyrus. Accordingly, the current study highlights the importance of structural characteristics of brain regions other than these typically arithmetic-associated parietal regions for children’s arithmetic fluency.

1. Introduction

Arithmetic, or the ability to add, subtract, multiply or divide numbers, is an essential skill for further mathematical development (Kilpatrick et al., 2001), with a ubiquitous role in daily life, especially for children. Over the past few years, many neuroimaging studies have aimed to unravel the neural basis of children’s arithmetic, but have mainly focused on functional neural aspects (Arsalidou et al., 2018, for a meta-analysis; Peters and De Smedt, 2018, for a review). The amount of studies looking at the structural neural correlates of children’s arithmetic is scarce (e.g., Evans et al., 2015; Isaacs et al., 2001; Price et al., 2016). The current study aims to contribute knowledge on which brain regions are important for children’s arithmetic on a structural level, by not only implementing voxel-based morphometry, but also cortical complexity analyses, based on the fractal dimension index (Yotter et al., 2011). Furthermore this study focuses on children of a small age range, to minimize maturational confounds. Because our main interest was in the neural basis of fluency in arithmetic, a key competence in children’s mathematical development as well as the hallmark feature of children with learning disorders in mathematics, such as dyscalculia, we investigate children who are at a point in development where a lot of arithmetic knowledge has already been automatized (i.e., 9-10 year-olds, all 4th graders). Doing so, we will focus on all neural regions that were previously found to be both structurally and/or functionally related to children’s mathematical abilities (Arsalidou et al., 2018; Peters and De Smedt, 2018).

In children, accumulating evidence of functional magnetic resonance imaging (fMRI) research points towards an arithmetic brain network involving a large set of interconnected areas, including frontal (i.e., ventrolateral prefrontal cortex, important for attentional control processes, and dorsolateral prefrontal cortex, important for procedural memory, working memory, and cognitive control), parietal (i.e., inferior and superior parietal lobes, involved in the processing of number magnitude, cardinality, and numerical quantity), occipito-temporal (responsible for decoding the visual form of numbers), and medial-temporal (i.e., hippocampus, linked to linked to episodic and semantic long-term memory systems) regions. Though this network shows some similarities to the network observed in adults (Menon, 2015), children’s arithmetic network is different (Arsalidou et al., 2018, for a meta-analysis; Peters and De Smedt, 2018, for a review), as overall less involvement of the superior parietal lobe is observed, along with larger involvement of the hippocampus, occipito-temporal, and prefrontal medial regions.

Only a small amount of studies have looked at the structural neural correlates of children’s arithmetic. The few studies that did study these structural correlates (see Peters and De Smedt, 2018, for an overview) mainly implemented voxel-based morphometry, which typically uses T1-weighted volumetric MRI scans and performs statistical tests across voxels to identify volume differences between groups. Accordingly, a series of t-tests can be performed at every voxel to identify differences in patterns of regional anatomy between groups of subjects (Whitwell, 2009). Using this method of data analysis, some structural imaging studies have compared groups of children who differed in their level of arithmetic skill (Isaacs et al., 2001; Ranpura et al., 2013; Rotzer et al., 2008; Rykhlevskaia et al., 2009). The first study reporting such data was Isaacs et al. (2001), who performed whole-brain voxel-based morphometry analyses on 24 adolescents born preterm at 30 weeks gestation or less, but without any neurological disabilities, comparing those with and without difficulties in arithmetic calculation. Doing so, the study observed reduced grey matter volume in the left intraparietal sulcus for the children with a deficit in calculation ability, suggesting an involvement of the volume of the intraparietal sulcus in the processing of number magnitude. Subsequent studies then similarly aimed to investigate differences between children with dyscalculia, which is a specific neurodevelopmental learning disorder characterized by difficulties in calculation which cannot be explained by intellectual disabilities, uncorrected sensory problems, mental or neurological disorders or inadequate instruction (American Psychiatric Association, 2013), and typically developing children. For example, a study by Rotzer et al. (2008) compared 12 9-year-old children with developmental dyscalculia to 12 age-matched controls and observed reduced grey matter volume for the children with dyscalculia in the right posterior parietal cortex (including the right intraparietal sulcus), the anterior cingulum, the left inferior frontal gyrus, and the bilateral middle frontal gyrus. A later study by Rykhlevskaia et al. (2009) investigated 24 7- to 9-year-old children with developmental dyscalculia, and compared them to a group of typically developing children matched on age, gender, intelligence, reading abilities and working memory capacity. This study also revealed reduced grey matter volume for the children with dyscalculia in the superior parietal lobule (again including the right intraparietal sulcus), but also in the bilateral fusiform gyrus, parahippocampal gyrus and right anterior temporal cortex. Finally, a study by Ranpura et al. (2013) investigated volumetric differences between 11 8- to 14-year-old children with dyscalculia, and typically developing children, the results of which again pointed towards reduced grey matter volume in the right parietal cortex for children with dyscalculia, as well as volumetric reductions in the right occipital, fusiform and parahippocampal gyri. In all, these studies consistently showed that poor arithmetic performance is accompanied by less volume in (mostly right-hemispheric) parietal grey matter. Agreeing with critiques on the exclusive bias towards only focusing on the parietal cortex (Fias et al., 2013), these studies also highlight the critical importance of regions outside of the parietal cortex for children’s arithmetic.

The group comparison method of the studies reviewed above, however, is limited, as it only allows for categorical comparisons of, for example, clinical or atypical groups of children to typically developing peers. Within voxel-based morphometry, however, it is possible to perform regression analyses across voxels to assess neuroanatomical correlates of cognitive or behavioral skills, thus applying a more dimensional approach (Whitwell, 2009). Doing so, the structural correlates of arithmetic can also be examined within a typically developing population. Surprisingly few studies, however, have examined this association between grey matter and arithmetic in typically developing children. A study by Li et al. (2013) revealed that, in 59 9- to 11-year-old Chinese children, individual differences in scores on the arithmetic subtest of the WISC-RC were significantly and positively correlated with the grey matter volume in the left intraparietal sulcus. This study, however, did apply a region of interest approach and thus only looked at the bilateral intraparietal sulci, possibly missing associations with other cortical regions. Using a longitudinal design, Evans et al. (2015) investigated whether grey matter volume in early childhood (43 children, 7- to 9-year-olds) was predictive of outcomes in numerical abilities (based on the Numerical Operations subscale of the WIAT-II) six years later. The study reported that grey matter volumes of various parts of the arithmetic network (i.e., posterior parietal cortex, ventral occipito-temporal cortex, and prefrontal cortex) predicted the growth in arithmetic across primary school, however, the volume of these observed regions at time 1 was not correlated with mathematical skill at the same point in time. Price et al. (2016) also investigated the relation between grey matter volume and math competence (based on the Woodcock–Johnson III Tests of Achievement) over one year in a sample of 50 6- to 8-year-olds. Their whole-brain voxel-based morphometry results showed that grey matter volume in the left intraparietal sulcus at the end of the 1st grade was related to math competence at the end of the 2nd grade. Grey matter volume of the intraparietal sulcus, however, did not change over that year, but was still correlated with math competence at the end of 2nd grade. When correlating volume to a specific arithmetic subtest (i.e. Woodcock-Johnson Calculation), however, this observed association with the intraparietal sulcus was also a lot weaker for year 1 and did not survive multiple comparisons in year 2. Finally, Supekar et al. (2013) had a group of 3rd graders (24 children, 8-9 years-old) follow an 8 week math tutoring program that focused on efficient counting and fact retrieval, in between two structural scanning sessions. They observed that the volume of the right hippocampus, a region linked to episodic and semantic long-term memory, and not the intraparietal sulcus, predicted the learning gains of the one-on-one tutoring sessions, with larger hippocampal volumes before the intervention predicting larger intervention gains, confirming the role of the hippocampus in arithmetic fact retrieval.

All of the studies above confirm that the grey matter volume of different neural regions (e.g., superior parietal lobe, intraparietal sulcus, inferior and middle frontal gyrus, fusiform gyrus, hippocampus) is associated with individual differences in arithmetic performance. These studies, however, often merged data across wide age ranges (e.g., 8–14 years old), which might lead to the over-interpretation of associations between differences in volume and differences in mathematical development, as results might still be affected by maturational confounds. To minimize such maturational confounds, samples with small age-ranges are necessary to clearly define brain regions of the arithmetic network for which grey matter volume is correlated to arithmetic fluency at a certain point in development. Some of these studies (e.g., Li et al., 2013) also implemented a region of interest approach, only looking at the parietal cortex and possibly missing possible associations with the volume of other brain regions. Other studies, however, used a longitudinal design (Evans et al., 2015) in which the volume of brain regions was associated to growth in arithmetic skill, but not to arithmetic skill at the same point in time.

New techniques for structural data analysis have also arisen over the past years, allowing the study of structural brain differences to go beyond looking at volume alone. For example, surface-based morphometry has numerous advantages over the use of volumetric data, as it has been shown that the implementation of brain surface meshes for spatial registration increases the accuracy of brain registration compared to mere volume-based registration (Desai et al., 2005). Accordingly, additional metrics of cortical structure are applicable. One such metric is cortical complexity, which quantifies the spatial frequency of gyrification and fissuration of the brain surface (Luders et al., 2004), and is most commonly measured through the use of a gyrification index, defined as the ratio of the inner surface size to the outer surface size of an outer hull. However, gyrification analyses have certain shortcomings, such as that the gyrification metric depends on how the outer hull is defined, on the normalization of the brain to reduce the effect of brain size, and on noise in the surface reconstruction, which could artificially inflate the surface area without corresponding to the actual anatomy. These shortcomings can be resolved by quantifying cortical complexity through the fractal dimensionality index (Yotter et al., 2011).

The fractal dimensionality index was originally designed to quantify the structure of fractals (Kiselev et al., 2003), but can describe a characteristic of the surface shape (see Yotter et al., 2011 for an in depth description of how brain complexity is measured), without relying on the definition of an outer hull (Lopes and Betrouni, 2009). In this sense, cortical complexity does not directly measure the intuitive meaning of the word complexity, such as the surface being more detailed. A fractal is a structure that is self-similar across a range of scales, making the complexity analysis correspond to how space-filling the fractal surface is. As such, regions with high fractal dimensionality values generally appear to be more periodically spaced (e.g., like a sine wave with regular peaks and troughs). This may be because the more periodically spaced structures also tend to fill more space over the range of scales examined for derivation of complexity values (Yotter et al., 2011).

Fractal dimensionality analyses have successfully been implemented in studies comparing patient groups, such as individuals with Alzheimer’s disease (e.g., Ruiz de Miras et al., 2017) or Williams syndrome (e.g., Thompson et al., 2005), to controls, demonstrating a decline in fractal dimensionality in these group comparisons. Moreover, being sensitive to other differences in grey matter structure that are not indexed by volume or cortical thickness, cortical complexity has also been used to study age and gender related differences in brain structure (Luders et al., 2004; Madan and Kensinger, 2016), and, most notably, to study differences in cognitive function (King et al., 2010; Im et al., 2006; Mustafa et al., 2012; Sandu et al., 2014). For example, Im et al. (2006) observed positive correlations between whole-brain fractal dimensionality and both IQ and years of education, implying a link between higher cortical complexity and higher cognitive functioning. Noteworthy, however, was that the correlations with education were slightly stronger than those with IQ, indicating a possible influence of education-related development on cortical complexity. King et al. (2010) even found that fractal dimensionality correlated more strongly with scores on a cognitive battery compared to measures of cortical thickness and gyrification. A study by Mustafa et al. (2012) observed that seniors with greater whole-brain white matter complexity had higher fluid intelligence scores and less evidence of age-related cognitive decline. Sandu et al. (2014) observed that decreases in late life cortical complexity are associated with declines in information processing speed, auditory-verbal learning, and reasoning, again indicating a link between higher cortical complexity and better cognitive function. Cortical complexity analyses have not yet been used in children’s mathematical cognition, but the studies above support the use of cortical complexity through fractal dimensionality as a sensitive metric for capturing relations between brain structure and cognitive function. Their implementation within the field of mathematical cognition could thus provide interesting insights into children’s arithmetic brain network.

Against this background, the first aim of the current study is to use voxel-based morphometry to study how structural differences in brain anatomy relate to differences in typically developing 9- to 10-year-old children’s arithmetic fluency. Secondly, as general associations have previously been observed between better cognitive function and increased cortical complexity, we also aim to examine if specific associations between arithmetic fluency and the cortical complexity of regions in children’s arithmetic brain network can be found. Specifically, based on the existing literature, we expect to observe structural associations with children’s arithmetic fluency in the intraparietal sulcus, given its clear relevance to arithmetic (e.g., Arsalidou et al., 2018; Menon, 2015; Peters and De Smedt, 2018), but also in the bilateral temporal lobe and inferior parietal (angular and supramarginal gyrus) lobes, given their association with children’s arithmetic fact retrieval, and therefore with arithmetic fluency (Polspoel et al., 2017). While doing these analyses, we will implement a region of interest (ROI) approach based on the neural regions that were previously found to be both structurally and/or functionally related to children’s mathematical abilities (Arsalidou et al., 2018; Peters and De Smedt, 2018). To the best of our knowledge, this study is the first to go beyond voxel-based morphometry analyses by investigating such associations through fractal dimensionality.

2. Methods

2.1. Participants

For the current study, data of 50 typically developing Flemish 4th graders were collected, yet data of 3 children were discarded due to technical acquisition problems (n = 1), excessive motion (n = 1), or problems during standardized testing (n = 1), and data of 4 more children were discarded after data quality control (see below for more details). Of the remaining 43 participants (ages 9 to 10; M = 9.68 years, SD = 0.34) 23 were boys, 20 were girls, and 8 children were left-handed. No participants had a history of learning difficulties, or neurological or psychiatric disorders. All participants were recruited via the elementary school they attended, in the surrounding area of the university, and were given a financial compensation for their participation. Written informed consent was obtained from a parent or legal guardian of each participating child. The study was approved by the Medical Ethical Committee of the University of Leuven (S59167).

Each child was asked to take part in two test sessions. During the first session, behavioral data were collected through various standardized measures. The second session included the acquisition of the MRI data, and always followed the first session by two to three weeks (M = 19.54 days, SD = 6.34). This MRI acquisition session also contained the collection of diffusion (Polspoel et al., 2019) and functional data (Polspoel et al., 2017) that have been reported elsewhere. Only the T1-data and their association with the general standardized tests are reported in the current study.

2.2. Standardized assessment

The standardized assessment session consisted of the evaluation of arithmetic (i.e., our main variable of interest), reading (i.e., to check the specificity of our results to arithmetic), and intelligence and motor reaction time (i.e., as control variables). To measure children’s arithmetic competence, the Tempo Test Arithmetic (TTA; de Vos, 1992) was used. This standardized arithmetic test, which is similar to the Math Fluency subtest of the Woodcock-Johnson III tests of Achievement (Woodcock et al., 2003), is very sensitive to individual differences in arithmetic fluency. The TTA contains five columns of arithmetic items: one column per operation and a fifth column with mixed operations. Each column starts with single digit items and increases in difficulty. Participants get 1 min per column to write down as many correct answers as possible. As the current sample included a small age range, all participating children were part of the same norm group, and thus the raw scores (i.e., the sum of the amount of correctly answered items in each column) were used for statistical analysis.

Reading was assessed through tests that are similar in their conceptualization as the TTA, as they are timed tests as well: the One Minute Test (OMT; Brus and Voeten, 1979) and the Klepel (Van den Bos et al., 1994), which respectively measure the reading of words and pseudowords. Both the OMT and Klepel consist of 116 words, but for the OMT, the children get 1 min to correctly read aloud as many words as possible, while for the Klepel, the time limit is set to 2 min, and the children read aloud pseudowords. Again, raw scores (i.e., the amount of correctly read words) were used for statistical analysis.

Next, the WISC-III-NL Block Design and Vocabulary subtests were used to measure intellectual ability, as measures of performance and verbal IQ, respectively (Wechsler, 2005). For intellectual ability, norm scores were used for the statistical analyses. Finally, to measure motor reaction time, participants had to indicate which of two figures (always a circle, triangle, square, star, or heart; one on the left, one on the right) presented on a computer screen was filled in white by, as quickly as possible, pressing the corresponding key. Accuracy and reaction time were recorded for each trial, yet, as ceiling levels were reached for accuracy, only reaction time was used for the subsequent analyses (De Smedt and Boets, 2010).

2.3. MRI data acquisition

MRI scanning was performed with a Philips Ingenia 3.0T CX MRI scanner with a SENSE 32-channel head-coil, located at the Department of Radiology of the University Hospital in Leuven, Belgium. Wash cloths were used to stabilize the children’s heads and consequently minimize head motion. The anatomical T1 images were acquired with the following sequence: 0.98 × 0.98 × 1.2 mm voxel size, 256 × 256 acquisition matrix, 8° flip angle, TE 4.6 ms, 250 × 250 × 218 mm field of view (approximately 8 min of scanning time). As part of data collection for different studies (e.g., Polspoel et al., 2017; Polspoel et al., 2019), the scanning session also included four functional MRI runs of 5 min, and a diffusion MRI run of 12 min, leading to a total scanning time of approximately 40 min.

All preprocessing was done with the Computational Anatomy Toolbox (CAT12) within the Statistical Parametric Mapping software package for Matlab (SPM12, Wellcome Department of Cognitive Neurology, London), following the standard processing pipeline within the CAT12 software. First, preprocessing included segmentation of the anatomical images; both grey matter and surface estimations were calculated. Next, data quality and sample homogeneity were tested through the Mahalanobis distance (De Maesschalck et al., 2000; Gaser, 2018). This is a combination of weighted overall image quality, which is a measure of noise and spatial resolution before preprocessing, and mean correlation, which is a measure of the homogeneity of the data and thus the quality after preprocessing. Data of four subjects were discarded, as their Mahalanobis distance was larger than two standard deviations of the sample average. Finally, spatial smoothing was performed with 8 mm (voxel-based morphometry) and 20 mm (cortical complexity) FWHM Gaussian smoothing kernels (Gaser, 2018).

2.4. Selection of ROIs

ROIs for statistical analyses were selected from the available atlases in the CAT12 software package (i.e., the Hammers and lpba40 atlases for voxel-based morphometry; the aparc.a2009s atlas for cortical complexity). The selected ROIs were whole anatomical regions found to be related to children’s mathematical abilities in previous, both structural and functional, research (Arsalidou et al., 2018; Peters and De Smedt, 2018). After preprocessing, mean values for volume and cortical complexity were estimated within each ROI and extracted for further analysis. An overview of the selected ROIs can be found in Table 1.

Table 1. Overview of selected ROIs for the voxel-based morphometry and cortical complexity analyses.

	Frontal	Parietal	Temporal	Occipital
Voxel-based morphometry	Orbito Front Gyr	Postcentral Gyr	Ant Med Temp Lobe	Fusiform Gyr
	Inf Front Gyr	Inf Par Lobe	Fusiform Gyr	Lingual Gyr
	Mid Front Gyr	Sup Par Lobe	Inf Mid Temp Gyr	Lat Occ Lobe
	Sup Front Gyr	Angular Gyr	Sup Temp Gyr
	Ant Cingulate Gyr	Supramarginal Gyr	Post Temp Lobe
	Precentral Gyr	Insular Cortex	Insular Cortex
	Insular Cortex		Hippocampus
Cortical complexity	Orbital Sulc/Gyr	Postcentral Sulc/Gyr	Inf Temp Sulc/Gyr	Ant Occ Sulc
	Inf Front Sulc/Gyr	Inf Par Lobe	Mid Temp Gyr	Inf Occ Gyr & Sulc
	Mid Front Sulc/Gyr	Sup Par Lobe	Sup Temp Sulc/Gyr	Par-Occ Sulc
	Sup Front Sulc/Gyr	Angular Gyr	Med Occ-Temp Sulc	Med Occ-Temp Sulc
	Ant Cingulate Gyr	Supramarginal Gyr	Lat Occ-Temp Sulc	Lat Occ-Temp Sulc
	Precentral Sulc/Gyr	Intraparietal Sulc	Insular Sulcus/Cortex	Lingual Sulc/Gyr
	Insular Sulc/Cortex	Precuneus	Parahippocampal Gyr	Fusiform Gyr
		Par-Occ Sulcus	Fusiform Gyr
		Insular Sulc/Cortex

Note: Sup = Superior; Inf = Inferior; Ant = Anterior; Post = Posterior; Mid = Middle; Med = Medial; Lat = Lateral; Front = Frontal; Par = Parietal; Temp = Temporal; Occ = Occipital; Gyr = Gyrus; Sulc = Sulcus. All ROIs were looked at bilaterally.

2.5. Statistical analyses

For statistical analyses, the JASP software package (JASP Team, 2017) was used to calculate Pearson correlations and their corresponding Bayes Factors between the results of the TTA and the extracted mean values of the ROIs. The Bayesian approach has the advantage to quantify the evidence that data provide for one hypothesis over another (Andraszewicz et al., 2015). Accordingly, Bayes factors (BF₁₀) of 1, 1–3, 3–10, 10–30, 30–100, or > 100 respectively point towards no, anecdotal, substantial, strong, very strong, or decisive evidence for the hypothesis of an association between two variables (Jeffreys, 1961). The results of the frequentist approach to statistical testing are also reported. For these analyses, the Bonferroni method of controlling for multiple comparisons (p = Target Alpha Level/number of ROIs; p = .05/42 = 0.001 for voxel-based morphometry and p = .05/78 = 0.0006 for cortical complexity) was implemented. Partial correlations were also calculated with IQ and motor reaction time simultaneously added as control variables. To test the specificity of the results, the significant correlations were also calculated with our reading measure as to check whether any observed associations with arithmetic are also observed with another symbolic academic skill (i.e., reading), measured in a similar, timed, way.

3. Results

3.1. Behavioral results

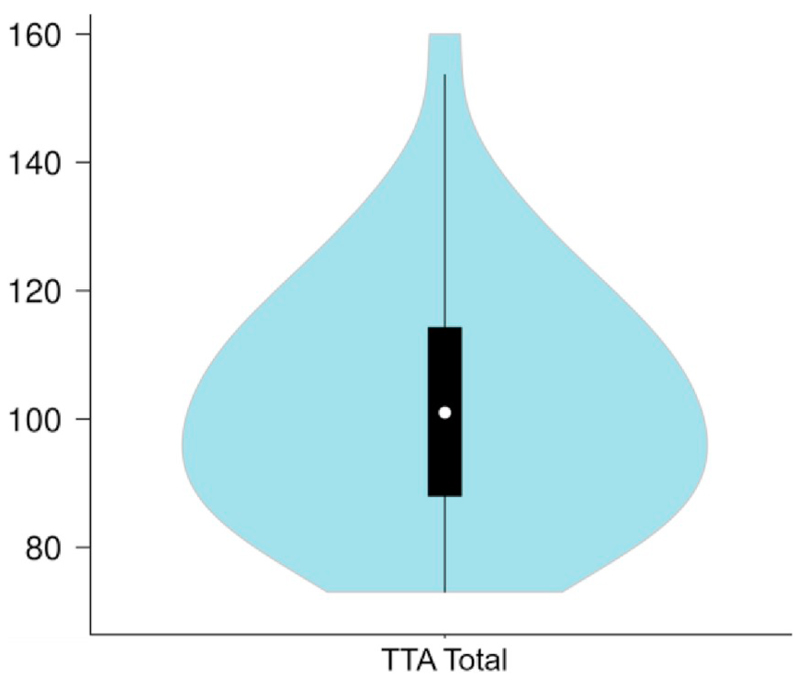
Descriptive statistics of arithmetic, reading, intellectual ability (all in standardized scores), and motor reaction time can be found in Table 2. This table demonstrates that our sample shows proper variation and has means close to the expected population averages. As the results of the different columns of the TTA highly correlated with each other, ranging from r = 0.616 to r = 0.818, only the raw total scores were used for analysis (M = 102.12, SD = 19.01, Min = 73, Max = 160). The distribution of these raw total scores can be found in a violin plot in Fig. 1. Important to note is that, even though the minimum score for some of the tasks was low, none of the participating children had been diagnosed with any type of learning disorder or intellectual disability.

Table 2. Descriptive statistics of the behavioral assessment.

	Mean	SD	Minimum	Maximum
Arithmetic – TTA Total	5.54	2.82	1	10
Block Design	10.86	3.21	6	19
Vocabulary	11.64	2.16	7	16
Reading	9.80	2.59	2.5	16.50
Motor Reaction Time	487.9	107.7	350.1	840.6

Note: The scores for arithmetic, intellectual ability, and reading are standardized scores. The scores on the arithmetic test are standardized as M = 5, SD = 2, with a maximum of 10. The scores on the intelligence and reading tests are standardized as M = 10, SD=3, with a maximum of 19. The scores for motor reaction time are raw scores displaying the average reaction time.

Fig. 1.

Violin plot displaying the distribution of the raw total scores of the TTA.

To check for possible gender differences, we performed a one-way ANOVA on the raw total score of the TTA, with gender as a grouping variable. This analysis revealed a significant difference, with boys showing better performance, however, the Bayes factor (BF₁₀) for this analysis pointed towards anecdotal evidence at best (F(1, 41) = 4.546, BF₁₀ = 1.776, p = .039). Furthermore, when adding motor reaction time as a covariate to this analysis, this significant difference disappeared as well (F(1, 40) = 2.291, BF₁₀ = 1.776, p = .138).

3.2. Voxel-based morphometry

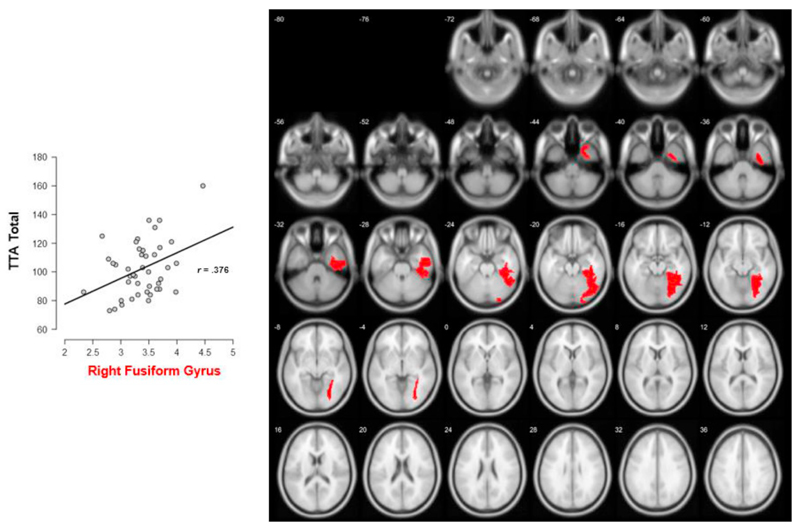
Results of the voxel-based morphometry analyses only point towards statistical significance (p < .05) and substantial evidence (BF₁₀ > 3) for an association between arithmetic fluency and the right fusiform gyrus (r = 0.376; BF₁₀ = 3.760; p = .013). A visualization on transverse slices and a scatterplot of this correlation can be found in Fig. 2. Due to the high amount of ROIs under study, the results using a frequentist approach to statistics did not survive after controlling for multiple comparisons. However, Bayesian statistics are affected less by this multiple comparison problem (Dienes, 2011), and still point towards substantial evidence for an association between arithmetic and the volume of the right fusiform gyrus. A one-way ANOVA on the volume of the fusiform gyrus also revealed no significant differences between boys and girls (F(1, 41) = 2.805, BF₁₀ = 0.911, p = .102), and the observed correlation between the fusiform gyrus and arithmetic remained significant when controlling for gender.

Fig. 2.

Transverse slices and scatterplot with fit line of the correlation between the total score of the TTA and the volume of the right fusiform gyrus.

Remarkably, no significant associations were observed between the children’s arithmetic fluency and the volume of previously observed, typically arithmetic-associated parietal regions (i.e., superior parietal lobe, angular gyrus and supramarginal gyrus). Furthermore, the Bayes factors (BF₁₀) for the correlations of the TTA with the volume of these regions were consistently below 1, pointing towards, albeit not necessarily substantial, more evidence for the null hypothesis of no association between these parietal regions and arithmetic fluency. These results can be found in Table 3.

Table 3. Correlations between arithmetic fluency and typically arithmetic-associated parietal regions for the voxel-based morphometry analyses.

		L SPL	R SPL	L AG	R AG	L SMG	R SMG
TTA Total	r	.046	.191	.171	.098	.099	.113
	BF10	0.198	0.395	0.340	0.229	0.231	0.244
	p	.767	.219	.272	.533	.526	.472

Note: SPL = Superior Parietal Lobe; AG = Angular Gyrus; SMG = Supramarginal Gyrus; L = Left; R = Right. The used atlases only consider voxel-based morphometry possible on gyri, hence the absence of the intraparietal sulcus in this analysis, yet all typically arithmetic-associated areas that surround the intraparietal sulcus (i.e., postcentral gyrus, superior parietal lobe, angular gyrus, and supramarginal gyrus) were included. The critical p-values for Bonferonni correction for multiple comparisons is p < .001.

These voxel-based morphometry analyses were also performed without the 8 left handed participants of our sample, which led to the same results, as at least substantial evidence for an association was observed between the total score of the TTA and the volume of the right fusiform gyrus (r = 0.413; BF₁₀ = 3.914; p = .014), but not for any other ROI.

Finally, to assess the specificity of our results, correlations were calculated with our reading measure, yet no substantial evidence or statistical significance (r = 0.231, BF₁₀ = 0.555, p = .136) was observed for the correlations between reading and the right fusiform gyrus.

3.3. Cortical complexity

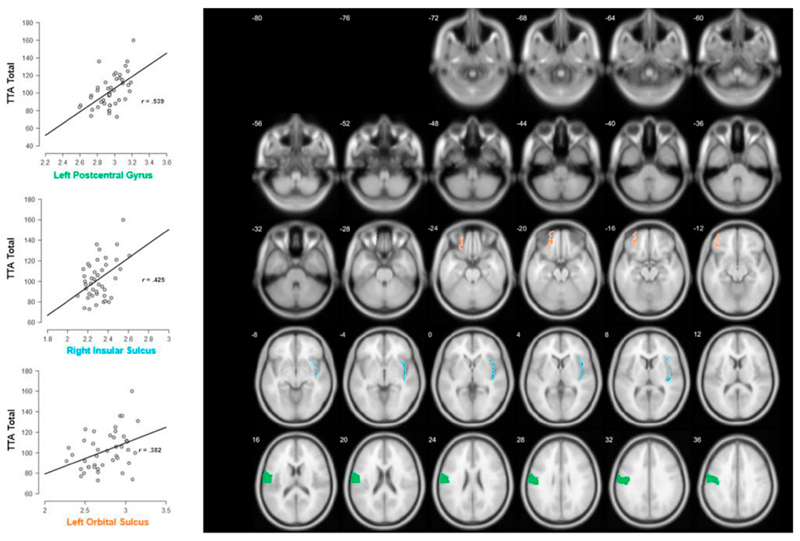
For the cortical complexity analyses, statistical significance (p < .05) and substantial evidence (BF₁₀ > 3) was observed for associations with the left postcentral gyrus (r = 0.539; BF₁₀ = 155.773; p < .001), right insular sulcus (r = 0.425; BF₁₀ = 9.388; p = .005), and left orbital sulcus (r = 0.382; BF₁₀ = 4.183; p = .011). Visualizations on transverse slices and scatterplots of these correlations are displayed in Fig. 3. These observed correlations remained significant when simultaneously controlling for intellectual ability and motor reaction time. Due to our stringent control for multiple comparisons, only the results for the left postcentral gyrus survived after controlling for multiple comparisons. A one-way ANOVA on the cortical complexity of these three regions also revealed no significant differences between boys and girls (left postcentral gyrus: F(1, 41) = 0.040, BF₁₀ = 0.306, p = .842; right insular sulcus: F(1, 41) = 2.300, BF₁₀ = 0.749, p = .137; left orbital sulcus: F(1, 41) = 0.273, BF₁₀ = 0.336, p = .604), and the observed correlations with arithmetic remained significant when controlling for gender.

Fig. 3.

Transverse slices and scatterplots with fit lines of the correlations between the total score of the TTA and the cortical complexity of the left postcentral gyrus, right insular sulcus, and left orbital sulcus.

For the cortical complexity analyses as well, no substantial evidence was observed for associations between the children’s arithmetic fluency and typically arithmetic-associated parietal regions (i.e., the intraparietal sulcus, superior parietal lobe, angular gyrus and supramarginal gyrus). The Bayes factors (BF₁₀) for these correlations were consistently below 1 (except for the left angular gyrus), again pointing towards more evidence for the null hypothesis of no association between the variables. These results can be found in Table 4.

Table 4. Correlations between arithmetic fluency and typically arithmetic-associated parietal regions for the cortical complexity analyses.

		L SPL	R SPL	L AG	R AG	L SPL	R SPL	L IPS	R IPS
TTA Total	r	-.086	-.168	.291	-.120	-.077	.229	.136	.070
	BF10	0.220	0.334	1.073	0.253	0.214	0.544	0.274	0.209
	p	.581	.280	.059	.442	.140	.581	.384	.655

Note: SPL = Superior Parietal Lobe; AG = Angular Gyrus; SMG = Supramarginal Gyrus; IPS = Intraparietal Sulcus. The critical p-values for Bonferonni correction for multiple comparisons is p < .0006.

These cortical complexity analyses were also performed without the left handed participants of the research sample. This again led to the same results, as at least substantial evidence for an association was observed between the total score of the TTA and the cortical complexity of the left postcentral gyrus (r = 0.528; BF₁₀ = 34.203; p = .001), right insular sulcus (r = 0.405; BF₁₀ = 3.466; p = .016), and left orbital sulcus (r = 0.417; BF₁₀ = 4.140; p = .013), but not for any other ROI.

When calculating the correlations with our reading measure, strong evidence was observed for an association between reading and the left lateral orbital sulcus (r = 0.471, BF₁₀ = 26, p = .001), suggesting that the associations with the left orbital sulcus are not specific to arithmetic. No substantial evidence (BF₁₀ > 3) was found for an association with any of the other ROIs found to be associated with arithmetic fluency (left postcentral gyrus: r = 0.306, BF₁₀ = 1.309, p = .046; right insular sulcus: r = 0.224, BF₁₀ = 0.520, p = .149).

4. Discussion

Previous studies on the structural neural correlates of children’s arithmetic have used voxel-based morphometry to highlight an association between arithmetic and grey matter volume in the superior parietal lobe, including the intraparietal sulcus, as well as other brain regions outside of the parietal cortex, such as the inferior and middle frontal gyrus, the fusiform gyrus and the hippocampus (Evans et al., 2015; Isaacs et al., 2001; Li et al., 2013; Price et al., 2016; Ranpura et al., 2013; Rotzer et al., 2008; Rykhlevskaia et al., 2009; Supekar et al., 2013). These existing studies, however, often compared groups of children who strongly differed in their level of arithmetic skill (e.g. dyscalculia vs. typically developing children), used research samples with wide age ranges, not fully eliminating possible maturational confounds, and were limited to voxel-based morphometry, which only takes the volume of brain structures into account, disregarding other structural properties. The current study focused on typically developing children of a narrow age range, at a point in development where a lot of arithmetic knowledge has already been automatized, and aimed to move beyond voxel-based morphometry analyses by implementing surface-based morphometry analyses to correlate with 9- to 10-year-old children’s arithmetic fluency, focusing on cortical complexity through fractal dimensionality. This cortical complexity looks at differences in the shape rather than the size of cortical structures, and is a sensitive metric for capturing relations between brain structure and cognitive function (King et al., 2010; Im et al., 2006; Madan and Kensinger, 2016; Mustafa et al., 2012; Sandu et al., 2014). Consequently, as general associations have previously been observed between cognitive function and cortical complexity, the current study aimed to examine if specific associations between arithmetic and the cortical complexity of regions in children’s arithmetic brain network were to be found. Taken together, the current study thus aimed to provide a more comprehensive depiction of the structural neural correlates of children’s arithmetic.

The results of the voxel-based morphometry analyses point towards positive correlations between arithmetic and the right fusiform gyrus. These results, however, must be interpreted with caution as, even though the Bayesian analysis indicated substantial evidence for an association of the fusiform gyrus with children’s arithmetic, the frequentist results did not remain significant after controlling for multiple comparisons. Nevertheless, the finding aligns with previous research, as the volume of the fusiform gyrus had already been related to children’s arithmetic in a study by Rykhlevskaia et al. (2009), who observed reduced volume of the fusiform gyrus for children with developmental dyscalculia in comparison to their typically developing peers. Furthermore, previous diffusion MRI research (e.g., Polspoel et al., 2019; Rykhlevskaia et al., 2009) has indicated the right inferior longitudinal fasciculus, which connects the occipital lobe to the anterior part of temporal lobe, including the fusiform gyrus, as a crucial white matter tract for children’s arithmetic fluency, again emphasizing the importance of the fusiform gyrus within children’s arithmetic (Pinheiro-Chagas et al., 2018). In fMRI research in adults, ventral visual stream areas, including the fusiform gyrus, are also found to be consistently co-activated with the intraparietal sulcus across a wide range of numerical tasks (Arsalidou and Taylor, 2011), with functional responses which increase with arithmetic complexity (Keller and Menon, 2009; Menon, 2015; Pinheiro-Chagas et al., 2018; Rickard et al., 2000; Rosenberg-Lee et al., 2009; Wu et al., 2009; Zago et al., 2001). Being part of the inferior temporal cortex, the fusiform gyrus probably plays an important role in the encoding of complex visual stimuli (i.e., orthographic processing, or the recognition and discrimination of number-letter strings; Allison et al., 1999; Binder et al., 2006; Milner and Goodale, 2008).

The observation of an association with the right fusiform gyrus rather than the left might be explained through the Theory of Constructive Operators (e.g., Pascual-Leone, 1970; Pascual-Leone and Johnson, 2005; Arsalidou and Pascual-Leone, 2016), which states that the right hemisphere is more involved in the processing of automatized schemes, whereas the left hemisphere is more involved in tasks that are not yet automatized, for which children need a larger mental-attentional capacity. Because the recognition of Arabic numerals is already fairly automatized in the children of the present sample, this might explain why the right rather than the left fusiform gyrus was correlated with individual differences in arithmetic. More recently, however, it has also been suggested that the inferior temporal cortex may have a role of early identification of problem difficulty, beyond mere digit recognition (Pinheiro-Chagas et al., 2018). Accordingly, even though the voxel-based morphometry results of the current study must be interpreted with caution, this result is in line with previous research and emphasizes the relevance of the right fusiform gyrus in children’s arithmetic.

Next, the results of our fractal dimension analyses mainly point towards positive correlations between children’s arithmetic and cortical complexity in the left postcentral gyrus, indicating that children with higher cortical complexity in this region have higher arithmetic fluency skills. The postcentral gyrus is adjacent to the superior parietal lobe and lies in continuity with the intraparietal sulcus, whose roles within the representation and manipulation of numerical quantity and arithmetic in general have been clearly established (Arsalidou et al., 2018; Menon, 2015; Peters and De Smedt, 2018). Consequently, cortical complexity in the postcentral gyrus might become important as the region acts as an extension of, and might affect or be affected by its adjacent arithmetic-related regions. Previously, activation in the postcentral gyrus itself was mainly observed during grasping tasks (Simon et al., 2002), but postcentral activations have also been linked to the use of arithmetic strategies, such as subvocalization and finger counting, as the region corresponds to somatotopic regions responsible for lips, mouth, fingers, and hands (Kesler et al., 2006). Furthermore, the postcentral gyrus has also been discussed as being important for number tasks in children (Arsalidou et al., 2018), as, in both adults and children, activation in the right inferior parietal cortex (including the intraparietal sulcus and the postcentral gyrus) has been related to nonsymbolic numerical and spatial processing (Kaufmann et al., 2008). The current structural imaging study can only but speculate on the function of this postcentral region. Further research investigating the region’s exact role within arithmetic is necessary.

Our results also displayed positive correlations between the cortical complexity of the right insular cortex (more specifically the right insular sulcus) and children’s arithmetic. Due to the stringency of our correction, this result did not remain statistically significant after controlling for multiple comparisons, yet a Bayes Factor (BF₁₀) close to 10 was observed, suggesting strong evidence for an association between both variables. Structural associations between the right insula and children’s arithmetic have been observed in a study by Han et al. (2013), who used deformation-based morphometry (based on the application of non-linear registration procedures to spatially normalize one brain to another one, where deformations then provide information about the type and localization of structural differences between the brains, which can be used for data analysis; Gaser et al., 2001) to study anatomical variations between the brains of 10-year-olds with and without mathematical difficulties. The insula has also often been observed in studies on numerical cognition (Arsalidou and Taylor, 2011), but its exact function in arithmetic is still unclear, as it is not typically discussed as part of mathematical problem solving models (Arsalidou et al., 2018). Over all, the insula is known for directing attentional resources and decision-making (Arsalidou and Taylor, 2011; Menon, 2015; Supekar and Menon, 2012), but this structure has also been implicated in emotional processing (Damasio et al., 2000) and speech-motor function (Fox et al., 2001). As such, the insula may be involved in intrinsically motivated behaviors (Arsalidou et al., 2018). The right insula in particular has also been identified as a key ROI in specific phobias, including mathematics anxiety (Lyons and Beilock, 2012). More specifically, these authors observed that the higher one’s math anxiety is, the more increases in activity in regions such as the bilateral dorso-posterior insula (which are associated with visceral threat detection and the experience of pain itself) can be observed (Lyons and Beilock, 2012). As a result, disturbances in cognitive/emotional processes such as motivation or anxiety could lead to disruptions in the normal course of procedures, and consequently interrupt the processes of solving calculation problems (Han et al., 2013). As the current study, however, did not collect measures for emotional processing, further research is needed to further investigate the insula’s role within children’s arithmetic.

The fractal dimensionality analyses also indicate the left orbital sulcus as being related to children’s arithmetic, yet, due to this result not surviving controlling for multiple comparisons and the Bayes Factor only pointing towards substantial evidence at best, it must be interpreted with caution. This result, however, does agree with previous research, as structural differences in the left orbitofrontal cortex were also observed in the study by Han et al. (2013) between children with and without mathematical difficulties. Similar to the insular cortex, the orbitofrontal cortex is associated with attention, decision-making, and executive function. Consequently, the function of this region is most likely not arithmetic-specific. Our data align with this, as significant correlations were also observed between the fractal dimensionality of the left lateral orbital sulcus and our reading measure, which points to a domain-general rather than arithmetic-specific finding.

Surprisingly, no substantial evidence was observed for associations between the volume or cortical complexity of the previously reported parietal regions related to number processing and arithmetic, i.e., the superior and inferior parietal lobes, including the intraparietal sulcus (Evans et al., 2015; Isaacs et al., 2001; Li et al., 2013; Price et al., 2016; Ranpura et al., 2013; Rotzer et al., 2008). Even more, the Bayes Factors (BF₁₀) for these correlational analyses were consistently below 1, pointing towards evidence in favor of the null hypothesis of no association between the volume or cortical complexity of these regions and the children’s arithmetic fluency, although this evidence was not always substantial. This absence of structural associations (in both volume and cortical complexity) of parietal regions and arithmetic was recently also found by Moreau et al. (2019), who studied group differences in brain structures in adults with dyslexia, dyscalculia, both disorders, and controls. This study revealed no evidence for structural differences in the parietal cortex between these groups of individuals, who differed in their mathematical abilities.

The discrepancy between the current data (as well as those of Moreau et al., 2019) and the other available literature that found associations between (inferior) parietal cortex and arithmetic, which led to our hypotheses, however, could be due to a variety of reasons. First, it is possible that the importance of the intraparietal sulcus (at least on a structural level) mainly becomes apparent when comparing children with extremely low arithmetic fluency or developmental dyscalculia to typically developing peers (Ranpura et al., 2013; Rotzer et al., 2008; Rykhlevskaia et al., 2009), which was not the case for the present sample.

Second, differences between the current findings and previous work might also be due to the implementation of different tasks for arithmetic assessment across studies. Our assessment of arithmetic (TTA; de Vos, 1992) is primarily focused around arithmetic fluency, as it is a timed task in which each column mainly contains single-digit items. This means that performance is likely to be determined by children’s knowledge of arithmetic facts. The fact that our results thus reflect associations with fluency-related arithmetic processes, such as arithmetic fact retrieval, could also explain the absence of associations with the intraparietal sulci and superior parietal lobes. Developmental fMRI studies, including training studies, have shown that these latter structures of the arithmetic network are more related to procedural calculation strategies, which require number magnitude processing, rather than automatized fact retrieval, which is more likely to be related to brain activity in temporo-parietal and (medial) temporal lobe areas (e.g. Peters and De Smedt, 2018, for a review).

Third, our results also differ from the study by Price et al. (2016), who found that grey matter volume in the left intraparietal sulcus at the end of first grade predicts arithmetic achievement at the end of second grade in typically developing children. As the children in the study by Price et al. (2016) were first graders (6- to 8-year-olds), they were at the beginning of their arithmetic development where procedural calculation strategies (such as counting) are much more dominant than fact retrieval to solve arithmetic problems. The absence of associations with the volume of the intraparietal sulcus in the current study might thus also reflect an effect of maturation, implying that the volume of the intraparietal sulcus is mainly relevant in earlier stages of typical arithmetic development, where procedural calculation strategies (such as counting) are used a lot more than fact retrieval to solve arithmetic problems. This in turn also emphasizes the need for studying specific age groups in small age ranges, as during this short period of time a lot of important developments within arithmetic occur, which are associated with different brain regions. Against this background, studies that include wide age ranges (e.g., Ranpura et al., 2013), should be interpreted with caution.

Fourth, studies that reported correlations between the intraparietal sulcus and arithmetic have often restricted their analyses to the inferior parietal cortex (Li et al., 2013), but did not investigate at a whole brain level if and how other regions correlated with individual differences in arithmetic. It is thus plausible that brain regions outside of the parietal cortex, as were observed in the current study, would have correlated with arithmetic, if a bilateral intraparietal sulcus mask had not been used. Given these results, the current study thus emphasizes the importance of neural regions outside of the parietal cortex for children’s arithmetic fluency, as has been previously emphasized (Fias et al., 2013; Peters and De Smedt, 2018).

Finally, associations between children’s arithmetic and the volume of the intraparietal sulcus have also been reported in a longitudinal context (Evans et al., 2015). The study by Evans et al. (2015), for example, also observed relations with the volume of posterior parietal regions, but only found these associations when trying to predict arithmetic skill across six years of development, and did not observe them at the same point time in time. As these associations were thus only found longitudinally, our cross-sectional results are consistent with this study.

Using the fractal dimensionality analyses within children’s arithmetic, the current study also shines light on the implementation of structural MRI research that takes into account the shape of structures, to better capture individual differences in the organization of cortical regions and their association with behavior. A limitation of the current study, however, does lie in the fact that, because of the implemented atlases and how some of the cortical regions are defined therein (e.g., the fusiform gyrus), whole anatomical regions were used as ROIs, instead of subdivisions of those regions, possibly introducing additional variance into our data. As the cortical complexity analyses become more fine-grained, future studies would be advised to implement such subdivisions, in order to get more fine-grained insights into individual differences in the organization of cortical regions and how they relate to children’s arithmetic. There is also a need for future studies to investigate how these measures of cortical complexity specifically relate to brain function and other cognitive outcomes.

The current study was also conducted with a research sample of only 9- to 10-year-olds, to minimize maturational confounds. Such narrow-aged studies are critical as merging data across wide age ranges, even though statistically controlled for, might lead to over-interpretations of associations between differences in grey mater volume/structure and differences in mathematical development. Accordingly, we feel it is crucial to emphasize the need for similar studies in children of different ages, such as first or second graders, who are at the beginning of their arithmetic development, or children in secondary school, who have reached a more advanced level of arithmetic. As previous research (Im et al., 2006) also observed stronger associations of cortical complexity to years of education than to IQ, indicating a possible influence of education-related development on cortical complexity, and keeping in mind (educational-based) neural plasticity, studies with a longitudinal follow-up throughout educational development are also deemed necessary to understand the direction of observed associations between cortical complexity and cognitive function, as well as to pinpoint when in development these associations start to emerge.

Finally, we would like to stress the necessity of similar research (i.e., research that moves beyond looking at volume for studying the structural correlates of arithmetic), not just across age groups, but in atypical populations, such as math-gifted children, or children with developmental dyscalculia, as this could deliver additional insights into the neural development of their mathematical skills.