Skip to main content
PMC home page
Research logoLink to Research
. 2020 Jan 24;2020:8151059. doi: 10.34133/2020/8151059

Manipulation of Band Degeneracy and Lattice Strain for Extraordinary PbTe Thermoelectrics

Yixuan Wu 1, Pengfei Nan 2, Zhiwei Chen 1, Zezhu Zeng 3, Siqi Lin 1, Xinyue Zhang 1, Hongliang Dong 4, Zhiqiang Chen 4, Hongkai Gu 4,5, Wen Li 1, Yue Chen 3, Binghui Ge 2,✉, Yanzhong Pei 1,✉
PMCID: PMC7000992  PMID: 32025663

Abstract

Maximizing band degeneracy and minimizing phonon relaxation time are proven to be successful for advancing thermoelectrics. Alloying with monotellurides has been known to be an effective approach for converging the valence bands of PbTe for electronic improvements, while the lattice thermal conductivity of the materials remains available room for being further reduced. It is recently revealed that the broadening of phonon dispersion measures the strength of phonon scattering, and lattice dislocations are particularly effective sources for such broadening through lattice strain fluctuations. In this work, a fine control of MnTe and EuTe alloying enables a significant increase in density of electron states near the valence band edge of PbTe due to involvement of multiple transporting bands, while the creation of dense in-grain dislocations leads to an effective broadening in phonon dispersion for reduced phonon lifetime due to the large strain fluctuations of dislocations as confirmed by synchrotron X-ray diffraction. The synergy of both electronic and thermal improvements successfully leads the average thermoelectric figure of merit to be higher than that ever reported for p-type PbTe at working temperatures.

1. Introduction

Driven by energy crisis and the resultant environmental issues, interests in advancing clean energy technologies have grown rapidly in this century. Based on either Seebeck or Peltier effect, thermoelectrics have important applications in energy harvesting, refrigeration, and thermal sensing, due to the capability of a direct conversion between heat and electricity [1–3]. To enable a widespread application, the conversion efficiency needs to be maximized, which requires thermoelectric materials to have a high figure of merit zT = S2σT/(κE + κL). In details, S, σ, T, κE, and κL are the Seebeck coefficient, electrical conductivity, absolute temperature, and electronic and lattice components of the thermal conductivity, respectively [4].

Ideally, zT can be maximized when both electronic transport properties and lattice thermal conductivity are fully optimized [5–7]. However, critical electronic parameters determining zT, including S, σ, and κE, are strongly intercorrelated, leading to the difficulty of improving zT through an individual manipulation of a certain parameter. A great deal of efforts have been devoted to decoupling these parameters for an effective enhancement in power factor S2σ, and successful strategies are typified by engineering the band structure for a high band degeneracy [8–11], a low electron inertial mass [12], and a weak charge scattering [13], which has been demonstrated in various thermoelectrics [4, 14–19].

Alternatively, a minimization in lattice thermal conductivity (κL) has led to great zT enhancements as well, which can be realized either by strengthening the scattering of phonons [20–23] in known materials or by exploring new materials with a intrinsically low κL [24]. For the former aspect of phonon scattering, it is recently revealed that the essence can be attributed to the broadening of phonon dispersion. The ideal phonon dispersion (frequency versus wave vector) is a curve called the “ground state” at 0 K. In fact, due to the existence of anharmonic lattice vibrations at finite temperatures in real materials, the resultant dynamic interatomic-force-constant fluctuations would lead the phonon dispersion to show frequency fluctuations around the “ground state,” which equivalently leads to a widening of the phonon dispersion “curve.” In addition to inherent lattice anharmonicity, various defects [4, 25] could induce fluctuations in atomic mass and/or in interaction force constant for a further broadening [26–29]. For the latter case of intrinsically low κL, demonstrated strategies include a strong lattice anharmonicity [30, 31], a low sound velocity [32] in loosely bonded materials with heavy and diffusive species [33, 34], and a low fraction of acoustic phonons [35] enabled in a complex crystal structure [36–38].

These approaches have been frequently proven to be successful for advancing thermoelectrics, especially in p-type IV-VI compounds [16, 39–47]. Manipulation of the energy offset between the light valence band (L) and the heavy valence band (Σ) via alloying enables charge carriers to be transported by many band valleys (band degeneracy) for an increase in σ without explicitly reducing S [48]. With years of exploration, effective alloying species for converging the valence bands of conventional PbTe thermoelectrics at desired temperatures are found to be monotellurides including MnTe [49], MgTe [50], CdTe [51], YbTe [52], EuTe [53], SrTe [54], and SnTe [55]. These alloys have shown greatly enhanced zT, yet the lattice thermal conductivity seems not to be all simultaneously minimized by the alloying process [49, 51, 56].

It is therefore motivated that a synergic approach on minimizing κL by various defects for a further enhancement in zT [57–62]. Since all these defects would introduce fluctuations in atomic mass and/or in lattice strain [27, 28, 63, 64], both of which would lead to fluctuations in phonon frequency at a given wave vector (i.e. broadening in phonon dispersion) [26]. This accelerates phonons to relax back to its equilibrium states (from the “excited states” to the widened “ground states”) since available frequencies are much more diversified in a broadened phonon dispersion [65]. Efforts have been often devoted on 0D point defects [28, 66–68] and 2D boundary interfaces [2, 69–74] for minimizing κL, which are, respectively, considered to be effective sources for scattering phonons with high and low frequencies [25, 75, 76]. Recently developed technique for introducing in-grain dislocations in IV-VI thermoelectrics is particularly interesting, not only because the resultant 1D defects are effective for scattering phonons with midrange frequencies [22, 77–80] but also dislocations could enable a reduction in κL nearly at no expense of a reduction in carrier mobility [26].

In order to maximize the thermoelectric performance of p-type PbTe, this work focuses on a full optimization of valence band convergence by alloying with EuTe and MnTe. Simultaneously, Na-doping is used to ensure not only a sufficiently high dislocation density for a maximization in lattice strain fluctuations but also a high enough carrier concentration. The well-improved electronic performance enabled by converged valence bands and the significantly reduced κL due to dislocations induced lattice strain fluctuations, synergistically lead to an extraordinary thermoelectric performance.

2. Results and Discussions

The details on synthesis, characterization, transport property measurements, and band structure calculations are given in the Supporting Information. X-ray diffraction (including synchrotron X-ray) was used to characterize the phase compositions and to estimate the lattice parameters. As shown in , observable diffraction peaks can be well indexed to the rock salt structure of PbTe. The lattice parameter decreases linearly with the increase of MnTe concentration, which can be understood by the smaller size of Mn as compared to that of Pb. The carrier concentration of NayEu0.03Mn0.03Pb0.94-yTe saturates at y > 3% (), indicating a Na solubility at this nominal concentration.

2.1. Electronic Transport Properties

PbTe alloying with EuTe and MnTe have been proven to effectively converge the valence bands and increase the band gap of PbTe [49, 53]. Previous work further indicated that the thermoelectric performance optimized at a concentration of ~3% EuTe alloying [53] or a concentration of ~4% MnTe alloying [49]. Importantly, an increase of Na-doping in PbTe-3%EuTe alloys is found to enable a controllable transition of dominant types of defect form 0D substitutions to 1D in-grain dislocations and then to 2D interfaces induced by nanoprecipitation [53]. According to these results, this work focuses on PbTe-3%EuTe alloys as the parent material with further MnTe alloying and Na doping for optimizing both the band structure, carrier concentration, and microstructure.

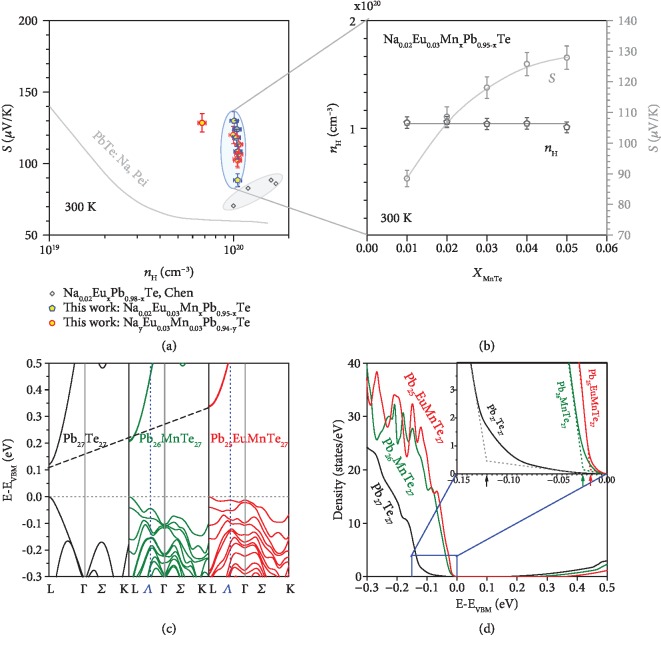
Figure 1(a) shows the room temperature carrier concentration-dependent Seebeck coefficient for various series of PbTe alloys from this work and literature [53, 56]. It is shown that further alloying with MnTe in this work indeed leads to a further increase in the Seebeck coefficient. In more details, an increase of MnTe-alloying concentration does not lead to an observable change in carrier concentration when a > 2% Na doping is used, but the Seebeck coefficient continuously increases (Figure 1(b)).

Figure 1.

Figure 1

Open in a new tab

Room temperature Seebeck coefficient (S) versus Hall carrier concentration (nH) for various series of PbTe alloys from this work and literatures [53, 56] (a) and MnTe-alloying concentration-dependent Seebeck coefficient and Hall carrier concentration at room temperature (b) for Na0.02Eu0.03MnxPb0.95-xTe synthesized in this work. Calculated band structures (c) and density of states (d) of Pb27Te27, Pb26MnTe27 and Pb25EuMnTe27 with a setting of valence band maximum (VBM) at 0 eV.

This could be understood by the MnTe-alloying which induced further optimization in the valence band structure, as evidenced from the band structure calculations shown in Figures 1(c) and 1(d). The details on density functional theory (DFT) calculations are given in the supplementary. It is seen that the valence band maximum (VBM) and the conduction band minimum (CBM) locate at L point for Pb27Te27, Pb26MnTe27 and Pb25EuMnTe27. In addition, the direct band gap at L increases due to MnTe and EuTe alloying [53]. Furthermore, MnTe and EuTe alloying [53] effectively reduces the energy offsets between the valence bands, leading to an involvement near the VBM of many bands for charge transport. Therefore, a superior electronic performance can be expected in these PbTe-EuTe-MnTe alloys. It should be noted that a supercell is needed to simulate the doping systems, and a back-folding technique is used for all the materials including pristine PbTe to enable a self-consistent comparison on DOS change due to doping. Similarly, an involvement of multiple transporting valence bands has been observed as well in SnTe heavily alloyed with MgTe [81].

The density of states (DOS) for Pb27Te27, Pb26MnTe27, and Pb25EuMnTe27 are shown in Figure 1(d). It is seen that the DOS near the valence band edge increases with MnTe and EuTe alloying. This indicates that alloying with EuTe and MnTe are indeed helpful for converging possibly transporting valence bands for maximizing the Seebeck coefficient. The increase in density of state due to MnTe and EuTe alloying can further be confirmed by optical measurements ( and ), where the inertial effective mass determined by the Lyden method [82] shows a similar increase with increasing MnTe alloying at a given carrier concentration of ~1.05 × 1020 cm−3. This helps understand the reduction in mobility observed (Figure 2(d)), in addition to charge scattering due to defects. The 3% MnTe and EuTe alloying are focused in this work, because these contents of 3% are the optimized ones to achieve the highest electronic properties in PbTe-MnTe and PbTe-EuTe solid solutions, according to previous works [49, 53].

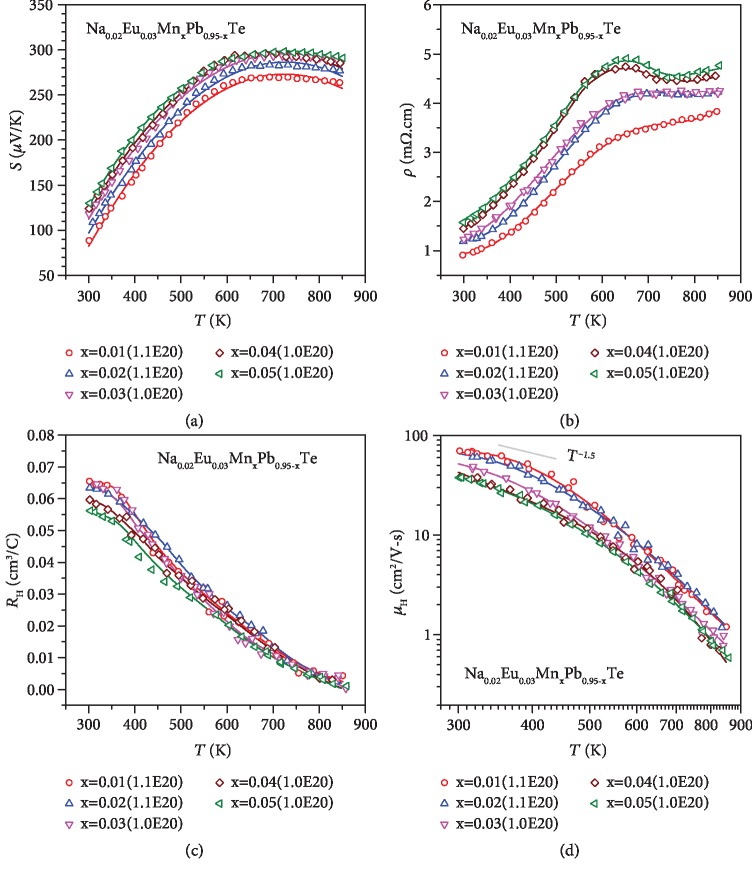
Figure 2.

Figure 2

Open in a new tab

Temperature-dependent Seebeck coefficient (a), resistivity (b), Hall coefficient (c), and Hall mobility (d) for Na0.02Eu0.03MnxPb0.95-xTe.

The detailed temperature-dependent electronic transport properties including the Seebeck coefficient, resistivity, Hall coefficient, and Hall mobility for Na0.02MnxPb0.98-xTe (x ≤ 0.05) and NayEu0.03Mn0.03Pb0.94-yTe (y ≤ 0.05) are shown in Figures 2 and 3, respectively. In pristine p-type PbTe, the Hall coefficient peaks at about 450 K [83], which can be a rough indication of valence band convergence. In this work, such a peaking in Hall coefficient is not observable, which corresponds to well-converged valence bands in the entire temperature range. Temperature-dependent Hall mobility all show an unchanged dominant carrier scattering by acoustic phonons.

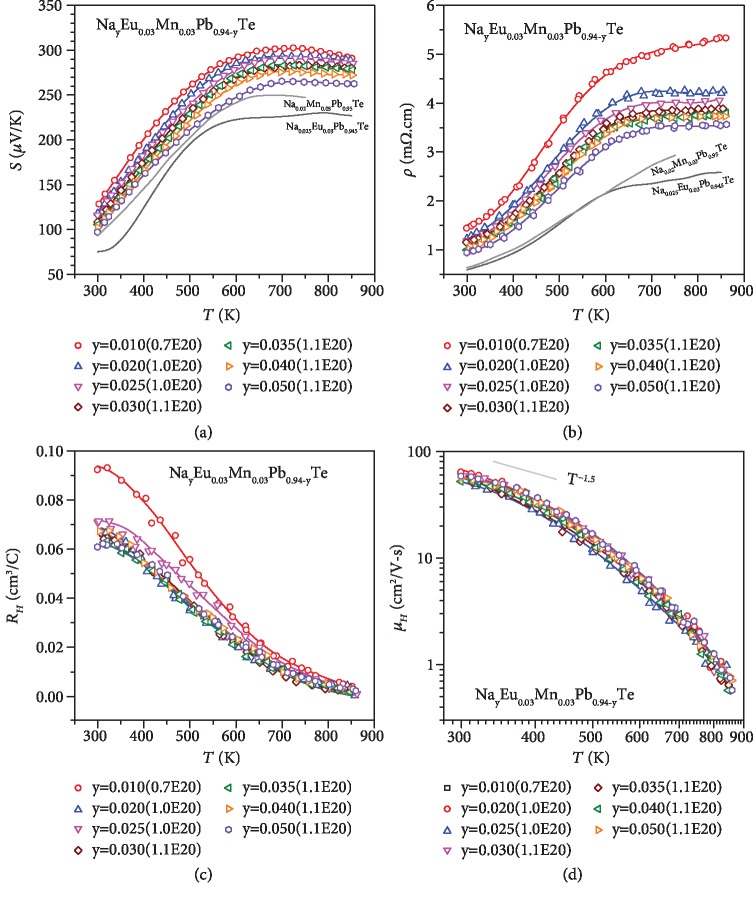
Figure 3.

Figure 3

Open in a new tab

Temperature-dependent Seebeck coefficient (a), resistivity (b), Hall coefficient (c), and Hall mobility (d) for NayEu0.03Mn0.03Pb0.94-yTe, with a comparison to literature results [49, 53].

2.2. Thermal Transport Properties

A full enhancement in performance relies largely on a minimization in lattice thermal conductivity (κL). Phonon transport is essentially determined by the phonon dispersion and its broadening. In addition to inherent phonon scattering due to lattice anharmonicity, various defects could create mass and strain fluctuations [28, 64] for broadening phonon dispersion [27]. Such broadening leads to a shortening in phonon relaxation time for a reduced κL. Without an explicit variation in composition, as the case here that a ~3%MnTe+3%EuTe alloying is focused on because of its capability for well-converged valence bands, manipulation of lattice strain fluctuation becomes an important avenue for reducing κL further.

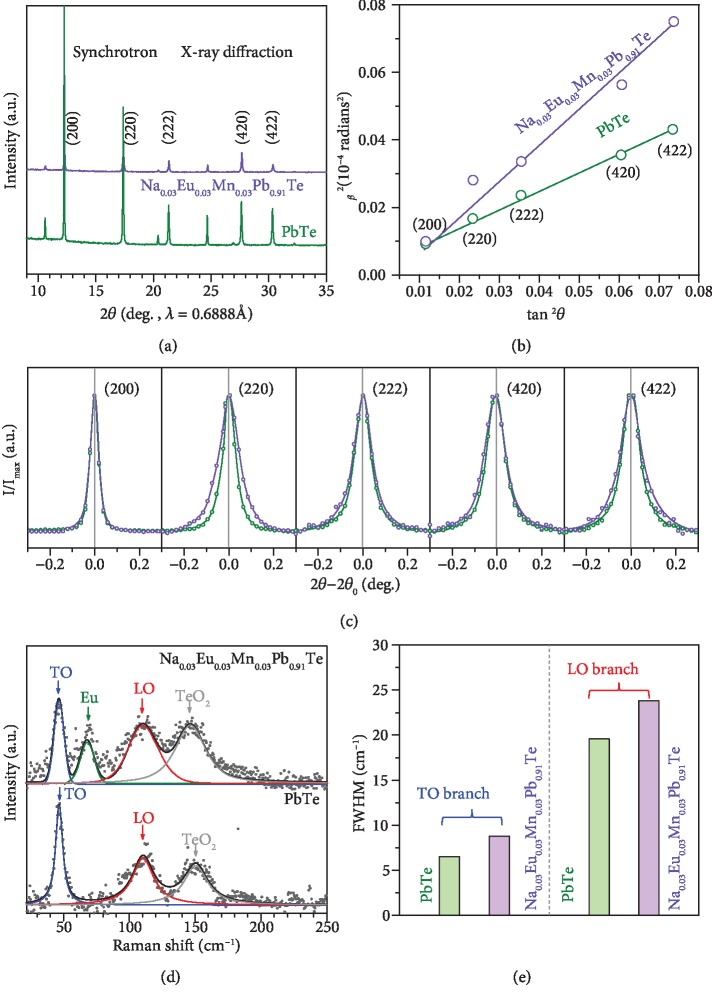
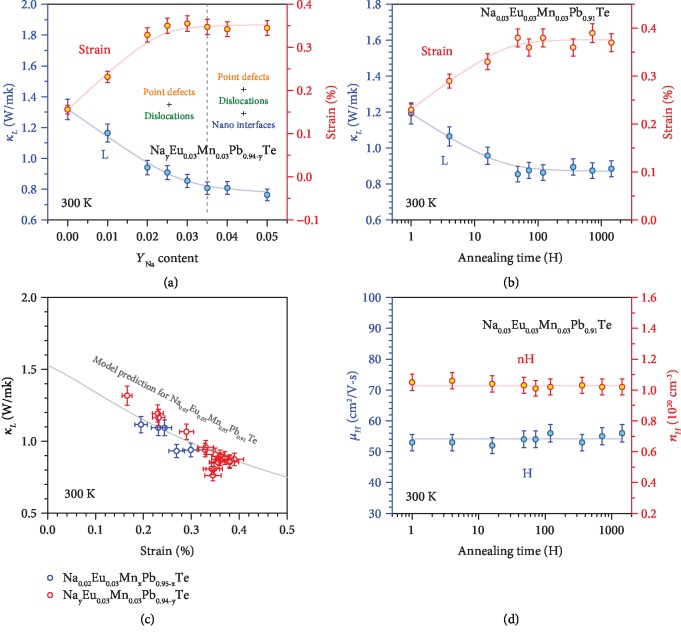
Theoretically, lattice strain fluctuations would cause the broadening of phonon dispersion due to the local expansion and compression. Therefore, X-ray diffraction and Raman scattering techniques are the macroscopic, convenient, and reliable methods to determine the lattice strains and phonon dispersion broadening. Once lattice strain fluctuations exist, a broadening and a reduction in intensity of XRD peaks will be observed [84]. The details on lattice strain estimation from X-ray diffraction are given in the supplementary. shows the synchrotron X-ray diffraction patterns, Figure 4(b) shows the corresponding strain analyses for PbTe and Na0.03Eu0.03Mn0.03Pb0.91Te with detailed broadening of diffraction peaks (Figure 4(c)). β in Figure 4(b) is the “full width at half maximum” of the intense diffraction peaks and θ is the Bragg angle. A much larger slope for Na0.03Eu0.03Mn0.03Pb0.91Te corresponds to the larger lattice stain fluctuations induced by dislocation as will be discussed below.

Figure 4.

Figure 4

Open in a new tab

Synchrotron X-ray diffraction patterns (a), strain analysis (b), detailed broadening of diffraction peaks (c), Raman spectrum with Lorentzian deconvolutions (d), and the resulting Raman peak broadening (e) for pristine PbTe and Na0.03Eu0.03Mn0.03Pb0.91Te at room temperature.

Furthermore, lattice strain fluctuations could result in local symmetry breaking of the ideal rock-salt structure of PbTe, which further leads the optical modes at Brillouin zone center including pristine PbTe to be first-order Raman active [85]. The broadening in Raman peaks of both transverse optical (TO) and longitudinal optical (LO) modes at Γ point enables a direct indication of the broadening in phonon dispersion due to lattice strain fluctuations [86]. To estimate the positions of active modes induced by impurities (Eu, Mn, and Na), an extended linear diatomic-chain model is utilized for estimating the frequencies of the local modes [87]. As shown in Figure 4, Raman peaks at about 47 cm−1, 74 cm−1, 108 cm−1, and 150 cm−1, respectively, correspond to the TO modes, Eu impurity, LO modes, and TeO2 [86, 88]. The solid curves show the deconvolution using a Lorentzian approximation. It should be noted that it is difficult to distinguish the peaks of Mn2+ at ~99 cm−1 and Na+ at ~142 cm−1 because of the possible overlapping with those of LO at 108 cm−1 and TeO2 at ~148 cm−1. Similar to literature Raman results of PbTe materials [89, 90], broadening of Raman peak of TO and LO modes can be observed in this work, which confirms the existence of lattice strains and the strain-induced force constant fluctuations leading to a broadening in the phonon dispersion. Similar Raman peak broadening due to existence of lattice strains are frequently observed in many semiconductors [91–93].

Microscopically, scanning transmission electron microscopy (STEM) is used to reveal the origin of lattice strains. As shown in Figure 5, very dense in-grain dislocations are observable in Na0.03Eu0.03Mn0.03Pb0.91Te. To analyze the lattice strain induced by dislocations, typical high-magnification STEM images are focused. Based on a geometric phase analysis (GPA), which is a semiquantitative lattice image-processing approach, spatially distributed strain fields can be mapped (Figure 5(d)). It can be seen that both tensile and compressive strains concentrated around the dislocations are as large as a few percentages, which enables a large average strain fluctuation of ~0.4% in the entire material of Na0.03Eu0.03Mn0.03Pb0.91Te according to the X-ray diffraction (Figure 6(a)). As shown in Figures 5, , it is interesting that a further increase of Na-doping concentration leads to a coexistence of both dense dislocations and Pb-poor nanoprecipitates, where the heterogeneous precipitates are confirmed by electron diffraction and energy dispersion spectrum (EDS) analyses (). Similar to literature results, the average lattice strains saturate at y ≥ 3% in NayEu0.03Mn0.03Pb0.94-yTe alloys (Figure 6(a)), indicating that nanoprecipitates do not introduce significant lattice strain fluctuations [80].

Figure 5.

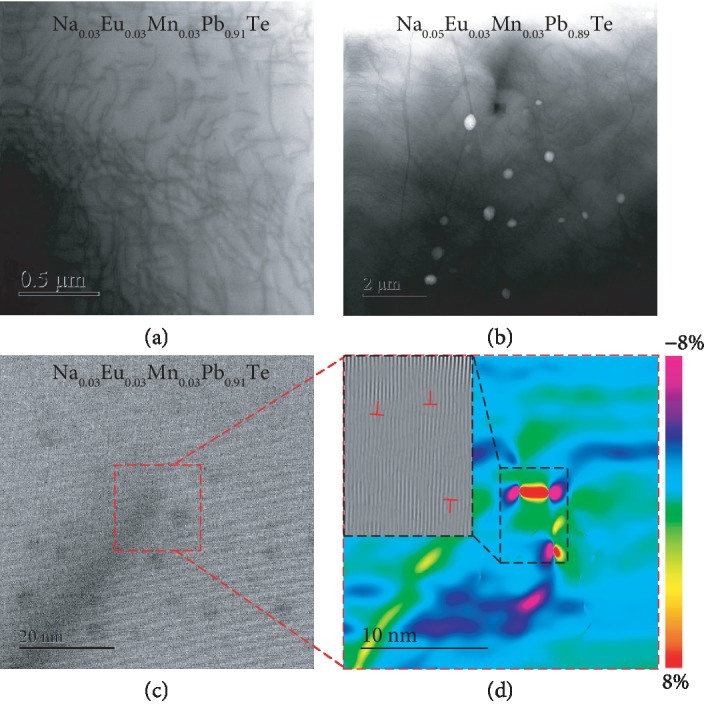
Figure 5

Open in a new tab

Low-magnification STEM images for Na0.03Eu0.03Mn0.03Pb0.91Te (a) and Na0.05Eu0.03Mn0.03Pb0.89Te (b), showing dense dislocations and a few nanoprecipitates (white spots). High-magnification STEM image (c) and the corresponding strain mappings (d) for Na0.03Eu0.03Mn0.03Pb0.91Te. Both samples are annealed at 900 K for 48 hours to reach the dislocation equilibrium.

Figure 6.

Figure 6

Open in a new tab

Composition-dependent lattice strains and lattice thermal conductivity (κL) for NayEu0.03Mn0.03Pb0.94-yTe with a 48-hour annealing at 900 K (a); annealing time-dependent lattice strain (at 900 K), and κL for Na0.03Eu0.03Mn0.03Pb0.91Te (b); lattice strain-dependent κL with a comparison to model prediction for Na0.03Eu0.03Mn0.03Pb0.92Te (c); and annealing time-dependent Hall mobility and carrier concentration (d) for Na0.03Eu0.03Mn0.03Pb0.91Te.

A direct observation of dislocation formation and movement is generally challenging, and it is believed that clustering of vacancies is important for these processes. Na doping in this work leads to a high hole concentration of ~1020 cm−3, which could promote the formation of oppositely charged anion vacancies due to charge compensation. Driven by thermodynamics and dynamics such as annealing at high temperatures, clustering/collapsing of vacancies and dislocation climb could lead to the formation and multiplication for dense dislocations at equilibrium [22, 53]. A control experiment in Na0.03Eu0.03Mn0.03Pb0.91Te with different annealing durations at 900 K enables an observation of dislocation equilibrium taking a few dozen hours, as indicated by the saturation in lattice strain in long-term (≥48 hours) annealed samples (Figure 6(b)). Interestingly, these in-grain dislocations are found to be sable up to at least 2 months at the annealing temperature of 900 K, and the underlying mechanism deserves a further study.

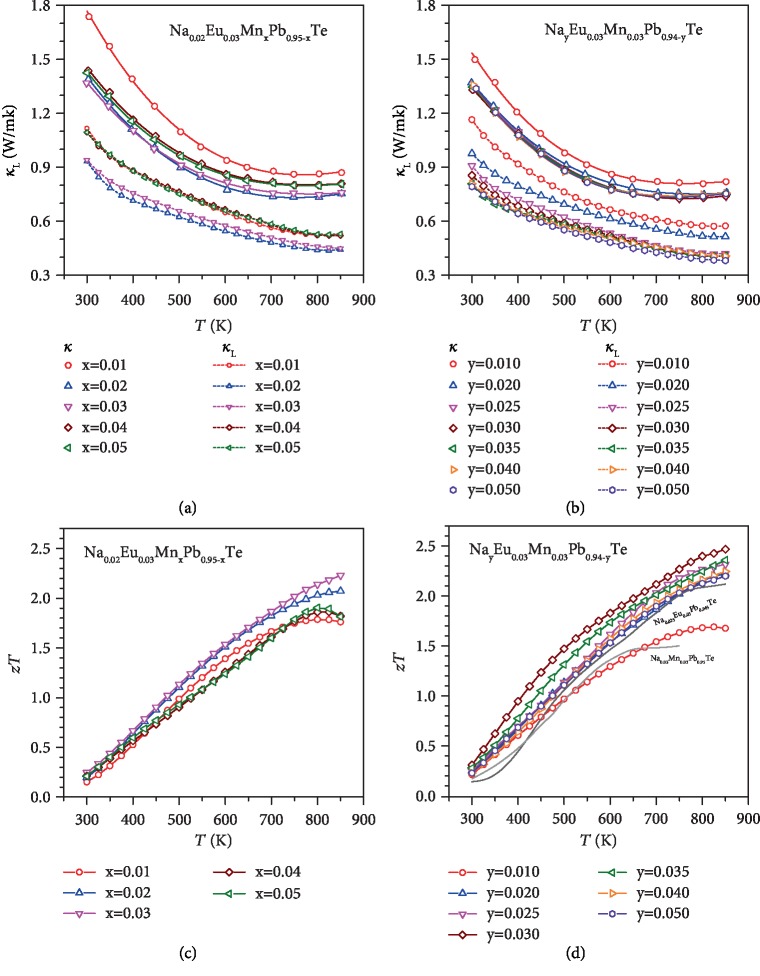
Most importantly, both the increase and saturation in lattice strain for Na0.03Eu0.03Mn0.03Pb0.91Te consistently lead to the decrease and saturation in lattice thermal conductivity (Figures 6(a) and 6(b)). Lattice thermal conductivity (κL) is estimated through subtracting the electronic contribution according to Wiedemann–Franz law (κE = LT/ρ) from total thermal conductivity, where L is the Lorenz factor determined via a single parabolic band (SPB) model with acoustic scattering (Figures 2(d) and 3(d)). With a nearly unchanged sound velocity due to alloying and doping (), the increase in lattice strains is found to indeed take the major responsibility for the decrease in κL, which can further be predicted by κL modeling without any fitting parameters (Figure 6(c)). Details on κL modeling are given in the supplementary (). κL as low as 0.8 W/m-K at room temperature is one of the lowest ever reported for p-PbTe.

Interestingly, the carrier mobility, carrier concentration, and Seebeck coefficient are found to be nearly unchanged with the variation of lattice strain fluctuations for Na0.03Eu0.03Mn0.03Pb0.91Te (Figure 6(d)), although κL decreases significantly. The well-maintained mobility in materials with strains can be understood by the high dielectric constant of PbTe and the relatively high temperature range involved in this work, both of which significantly weaken the charge scattering by electrostatic fields of dislocations [26]. Such a nearly independent κL reduction induced by strain engineering would enable an effective approach for enhancing PbTe thermoelectrics.

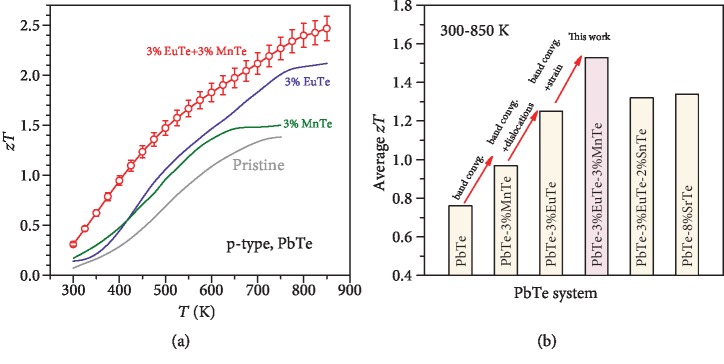
Synergy of superior electronic performance guaranteed by the well-converged valence bands and minimal lattice thermal conductivity (Figures 7(a) and 7(b)) enabled by dislocation-induced lattice strains, successfully leads to a realization of extraordinary zT (Figures 7(c) and 7(d)). It should be noted that the slight increase in κL at T > 750 is due to the bipolar effect as seen from Figure 3. Figure 8 shows the evolution of zT enhancements due to the beneficial effects of band convergence and dislocation-induced lattice strains. It is interesting to note that the average zT within 300-850 K of ~1.5 realized in this work is actually higher than that ever reported for p-type PbTe thermoelectrics. Furthermore, the high zT is found to be highly reproducible ().

Figure 7.

Figure 7

Open in a new tab

Temperature-dependent total and lattice thermal conductivity (a, b) and thermoelectric figure of merit (c, d) for Na0.02Eu0.03MnxPb0.95-xTe (a, c) and NayEu0.03Mn0.03Pb0.94-yTe (b, d).

Figure 8.

Figure 8

Open in a new tab

Temperature-dependent thermoelectric figure of merit (with the standard deviation of 12 measurements) and its average within 300-850 K in optimally doped PbTe alloys, with a comparison to literature results [26, 49, 53, 54, 56].

3. Summary

This work demonstrates the effectivity of MnTe and EuTe coalloying for maximizing the valence band degeneracy as well as of dislocation-induced lattice strains for minimizing phonon relaxation time of PbTe. The resultant synergy of both electronic and thermal approaches successfully leads to a breakthrough in thermoelectric efficiency. It is shown that dislocation-induced lattice strains enable a nearly independent reduction in lattice thermal conductivity, which could in principle open new possibilities for advancing PbTe and similar thermoelectrics.

Acknowledgments

This work is supported by the National Key Research and Development Program of China (2018YFB0703600), the National Natural Science Foundation of China (Grant Nos. 51861145305 and 51772215), the Fundamental Research Funds for Science and Technology Innovation Plan of Shanghai (18JC1414600), and the Fok Ying Tung Education Foundation (Grant No. 20170072210001). ZZ and YC are grateful for the financial support from RGC under project numbers 17200017 and 17300018, and the research computing facilities offered by ITS, HKU. The authors thank BL14B1 (Shanghai Synchrotron Radiation Facility) for the SR-XRD experiments.

Contributor Information

Binghui Ge, Email: bhge@ahu.edu.cn.

Yanzhong Pei, Email: yanzhong@tongji.edu.cn.

Conflicts of Interest

There are no conflicts to declare.

Authors' Contributions

Y.P. conceptualized the study. Y.W. and Z.C did the experiments. P.N. and B.G. characterized TEM. Z.Z. and Y.C calculated the DFT. H.D., Z.C., and H.G characterized the synchrotron X-ray. Y.P., W.L., and B.G helped in the discussion of the study. All the authors wrote and revised the manuscript.

Supplementary Materials

Supplementary Materials

Materials and Methods: Table S1: parameters used for the modeling. Figure S1: XRD patterns (a-c) and lattice parameters (d-e) for Na0.02Eu0.03MnxPb0.95-xTe (a, d), NayEu0.03Mn0.03Pb0.94-yTe (b, e), and Na0.03Eu0.03Mn0.03Pb0.91Te (c, f) with different annealing time. Figure S2: normalized optical absorption coefficient for Na0.02Eu0.03MnxPb0.95-xTe (a) and NayEu0.03Mn0.03Pb0.94-yTe (b) at room temperature. Table S2: room temperature Hall carrier concentration (nH), inertial effective mass (mI∗), plasma energy, and density (g/cm3) for Na0.02Eu0.03MnxPb0.95-xTe, and NayEu0.03Mn0.03Pb0.94-yTe. Figure S3: TEM images and EDS composition mappings for Na0.03Eu0.03Mn0.03Pb0.91Te. Figure S4: low-magnification STEM images (a) and high-magnification STEM image(b), electron diffraction patterns(c), and EDS composition mappings (d-i) for Na0.05Eu0.03Mn0.03Pb0.89Te, indicating the coexistence of both dense dislocations and nanoprecipitates. Figure S5: MnTe (a) and NaTe (b) content-dependent sound velocity for Na0.02Eu0.03MnxPb0.95-xTe and NayEu0.03Mn0.03Pb0.94-yTe at room temperature. Figure S6: repeated measurements for the high-zT composition Na0.03Eu0.03Mn0.03Pb0.91Te showing highly reproducible and stable thermoelectric properties.

Click here for additional data file. (2.3MB, pdf)

References

  • 1.Bell L. E. Cooling, heating, generating power, and recovering waste heat with thermoelectric systems. Science. 2008;321(5895):1457–1461. doi: 10.1126/science.1158899. [DOI] [PubMed] [Google Scholar]
  • 2.Mori T. Novel principles and nanostructuring methods for enhanced thermoelectrics. Small. 2017;13(45):p. 1702013. doi: 10.1002/smll.201702013. [DOI] [PubMed] [Google Scholar]
  • 3.Liu W., Hu J., Zhang S., Deng M., Han C. G., Liu Y. New trends, strategies and opportunities in thermoelectric materials: a perspective. Materials Today Physics. 2017;1:50–60. doi: 10.1016/j.mtphys.2017.06.001. [DOI] [Google Scholar]
  • 4.Zhu T., Liu Y., Fu C., Heremans J. P., Snyder J. G., Zhao X. Compromise and synergy in high-efficiency thermoelectric materials. Advanced Materials. 2017;29(14) doi: 10.1002/adma.201605884. [DOI] [PubMed] [Google Scholar]
  • 5.Snyder G. J., Toberer E. S. Complex thermoelectric materials. Nature Materials. 2008;7(2):105–114. doi: 10.1038/nmat2090. [DOI] [PubMed] [Google Scholar]
  • 6.Xiao C., Li Z., Li K., Huang P., Xie Y. Decoupling interrelated parameters for designing high performance thermoelectric materials. Accounts of Chemical Research. 2014;47(4):1287–1295. doi: 10.1021/ar400290f. [DOI] [PubMed] [Google Scholar]
  • 7.Mao J., Liu Z., Zhou J., et al. Advances in thermoelectrics. Advances in Physics. 2018;67(2):69–147. doi: 10.1080/00018732.2018.1551715. [DOI] [Google Scholar]
  • 8.Pei Y., Shi X., LaLonde A., Wang H., Chen L., Snyder G. J. Convergence of electronic bands for high performance bulk thermoelectrics. Nature. 2011;473(7345):66–69. doi: 10.1038/nature09996. [DOI] [PubMed] [Google Scholar]
  • 9.Kim H. S., Heinz N. A., Gibbs Z. M., Tang Y., Kang S. D., Snyder G. J. High thermoelectric performance in (Bi0.25Sb0.75)2Te3 due to band convergence and improved by carrier concentration control. Materials Today. 2017;20(8):452–459. doi: 10.1016/j.mattod.2017.02.007. [DOI] [Google Scholar]
  • 10.Pei Y., Wang H., Snyder G. J. Band engineering of thermoelectric materials. Advanced Materials. 2012;24(46):6125–6135. doi: 10.1002/adma.201202919. [DOI] [PubMed] [Google Scholar]
  • 11.Lin S., Li W., Chen Z., Shen J., Ge B., Pei Y. Tellurium as a high-performance elemental thermoelectric. Nature Communications. 2016;7(1) doi: 10.1038/ncomms10287. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 12.Pei Y., LaLonde A. D., Wang H., Snyder G. J. Low effective mass leading to high thermoelectric performance. Energy & Environmental Science. 2012;5(7):p. 7963. doi: 10.1039/c2ee21536e. [DOI] [Google Scholar]
  • 13.Wang H., Pei Y., LaLonde A. D., Snyder G. J. Weak electron-phonon coupling contributing to high thermoelectric performance in n-type PbSe. Proceedings of the National Academy of Sciences of the United States of America. 2012;109(25):9705–9709. doi: 10.1073/pnas.1111419109. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 14.Shuai J., Geng H., Lan Y., et al. Higher thermoelectric performance of Zintl phases (Eu0.5Yb0.5)1-xCaxMg2Bi2 by band engineering and strain fluctuation. Proceedings of the National Academy of Sciences. 2016;113(29):E4125–E4132. doi: 10.1073/pnas.1608794113. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 15.Liu W., Tan X., Yin K., et al. Convergence of conduction bands as a means of enhancing thermoelectric performance ofn-TypeMg2Si1−xSnxSolid solutions. Physical Review Letters. 2012;108(16) doi: 10.1103/PhysRevLett.108.166601. [DOI] [PubMed] [Google Scholar]
  • 16.Li W., Chen Z., Lin S., et al. Band and scattering tuning for high performance thermoelectric Sn1− _x_ Mn _x_ Te alloys. Journal of Materiomics. 2015;1(4):307–315. doi: 10.1016/j.jmat.2015.09.001. [DOI] [Google Scholar]
  • 17.Zhou X., Yan Y., Lu X., et al. Routes for high-performance thermoelectric materials. Materials Today. 2018;21(9):974–988. doi: 10.1016/j.mattod.2018.03.039. [DOI] [Google Scholar]
  • 18.Shuai J., Mao J., Song S., Zhang Q., Chen G., Ren Z. Recent progress and future challenges on thermoelectric Zintl materials. Materials Today Physics. 2017;1:74–95. doi: 10.1016/j.mtphys.2017.06.003. [DOI] [Google Scholar]
  • 19.Mao J., Wu Y., Song S., et al. Anomalous electrical conductivity of n-type Te-doped Mg3.2Sb1.5Bi0.5. Materials Today Physics. 2017;3:1–6. doi: 10.1016/j.mtphys.2017.08.001. [DOI] [Google Scholar]
  • 20.Zhou C., Lee Y. K., Cha J., et al. Defect engineering for high-performance n-type PbSe thermoelectrics. Journal of the American Chemical Society. 2018;140(29):9282–9290. doi: 10.1021/jacs.8b05741. [DOI] [PubMed] [Google Scholar]
  • 21.Mao J., Shuai J., Song S., et al. Manipulation of ionized impurity scattering for achieving high thermoelectric performance in n-type Mg3Sb2-based materials. Proceedings of the National Academy of Sciences. 2017;114(40):10548–10553. doi: 10.1073/pnas.1711725114. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 22.Chen Z., Ge B., Li W., et al. Vacancy-induced dislocations within grains for high-performance PbSe thermoelectrics. Nature Communications. 2017;8 doi: 10.1038/ncomms13828. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 23.Li J., Chen Z., Zhang X., et al. Simultaneous optimization of carrier concentration and alloy scattering for ultrahigh performance GeTe thermoelectrics. Advancement of Science. 2017;4(12) doi: 10.1002/advs.201700341. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 24.Li W., Lin S., Zhang X., Chen Z., Xu X., Pei Y. Thermoelectric properties of Cu2SnSe4with intrinsic vacancy. Chemistry of Materials. 2016;28(17):6227–6232. doi: 10.1021/acs.chemmater.6b02416. [DOI] [Google Scholar]
  • 25.Chen Z., Zhang X., Pei Y. Manipulation of phonon transport in thermoelectrics. Advanced Materials. 2018;30(17) doi: 10.1002/adma.201705617. [DOI] [PubMed] [Google Scholar]
  • 26.Wu Y., Chen Z., Nan P., et al.  Lattice Strain Advances Thermoelectrics. Joule. 2019;3(5):1276–1288. doi: 10.1016/j.joule.2019.02.008. [DOI] [Google Scholar]
  • 27.Cowley R. A. Anharmonic crystals. Reports on Progress in Physics. 1968;31(1):123–166. doi: 10.1088/0034-4885/31/1/303. [DOI] [Google Scholar]
  • 28.Klemens P. G. The scattering of low-frequency lattice waves by static imperfections. Proceedings of the Physical Society. 1955;A68:1113–1128. [Google Scholar]
  • 29.Urban J. J. Anharmonic Convergence: Tuning Two Dials on Phonons for High _zT_ in _p_ -type PbTe. Joule. 2019;3(5):1180–1181. doi: 10.1016/j.joule.2019.04.014. [DOI] [Google Scholar]
  • 30.Morelli D. T., Jovovic V., Heremans J. P. Intrinsically minimal thermal conductivity in CubicI−V−VI2Semiconductors. Physical Review Letters. 2008;101(3) doi: 10.1103/PhysRevLett.101.035901. [DOI] [PubMed] [Google Scholar]
  • 31.Li C. W., Hong J., May A. F., et al. Orbitally driven giant phonon anharmonicity in SnSe. Nature Physics. 2015;11(12):1063–1069. doi: 10.1038/nphys3492. [DOI] [Google Scholar]
  • 32.Li W., Lin S., Ge B., Yang J., Zhang W., Pei Y. Low sound velocity contributing to the high thermoelectric performance of Ag8SnSe6. Advancement of Science. 2016;3(11) doi: 10.1002/advs.201600196. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 33.Liu H., Shi X., Xu F., et al. Copper ion liquid-like thermoelectrics. Nature Materials. 2012;11(5):422–425. doi: 10.1038/nmat3273. [DOI] [PubMed] [Google Scholar]
  • 34.Wu Y., Li W., Faghaninia A., et al. Promising thermoelectric performance in van der Waals layered SnSe2. Materials Today Physics. 2017;3:127–136. doi: 10.1016/j.mtphys.2017.10.001. [DOI] [Google Scholar]
  • 35.Lin S., Li W., Li S., et al. High thermoelectric performance of Ag9GaSe6 enabled by low cutoff frequency of acoustic phonons. Joule. 2017;1(4):816–830. doi: 10.1016/j.joule.2017.09.006. [DOI] [Google Scholar]
  • 36.Snyder G. J., Christensen M., Nishibori E., Caillat T., Iversen B. B. Disordered zinc in Zn4Sb3 with phonon-glass and electron-crystal thermoelectric properties. Nature Materials. 2004;3(7):458–463. doi: 10.1038/nmat1154. [DOI] [PubMed] [Google Scholar]
  • 37.Li W., Lin S., Weiss M., et al. Crystal structure induced ultralow lattice thermal conductivity in thermoelectric Ag9AlSe6. Advanced Energy Materials. 2018;8(18) doi: 10.1002/aenm.201800030. [DOI] [Google Scholar]
  • 38.Zhang X., Chen Z., Lin S., Zhou B., Gao B., Pei Y. Promising thermoelectric Ag5−δTe3with intrinsic low lattice thermal conductivity. ACS Energy Letters. 2017;2(10):2470–2477. doi: 10.1021/acsenergylett.7b00813. [DOI] [Google Scholar]
  • 39.Luo J., You L., Zhang J., et al. Enhanced average thermoelectric figure of merit of the PbTe-SrTe-MnTe alloy. ACS Applied Materials & Interfaces. 2017;9(10):8729–8736. doi: 10.1021/acsami.6b16060. [DOI] [PubMed] [Google Scholar]
  • 40.Manettas A., Santos R., Ferreres X. R., Aminorroaya Yamini S. Thermoelectric performance of single phase p-type quaternary (PbTe)0.65–x(PbSe)0.35(PbS)xAlloys. ACS Applied Energy Materials. 2018;1(5):1898–1903. doi: 10.1021/acsaem.7b00174. [DOI] [Google Scholar]
  • 41.Li W., Wu Y., Lin S., et al. Advances in environment-friendly SnTe thermoelectrics. ACS Energy Letters. 2017;2(10):2349–2355. doi: 10.1021/acsenergylett.7b00658. [DOI] [Google Scholar]
  • 42.Skipetrov E. P., Zvereva E. A., Volkova O. S., Slyn'ko E. I., Mousalitin A. M. On Fermi level pinning in lead telluride based alloys doped with mixed valence impurities. Materials Science and Engineering: B. 2002;91-92:416–420. doi: 10.1016/S0921-5107(01)01029-7. [DOI] [Google Scholar]
  • 43.LaLonde A. D., Pei Y., Wang H., Jeffrey Snyder G. Lead telluride alloy thermoelectrics. Materials Today. 2011;14(11):526–532. doi: 10.1016/S1369-7021(11)70278-4. [DOI] [Google Scholar]
  • 44.Li J., Zhang X., Lin S., Chen Z., Pei Y. Realizing the high thermoelectric performance of GeTe by Sb-doping and Se-alloying. Chemistry of Materials. 2016;29:605–611. [Google Scholar]
  • 45.Li J., Zhang X., Chen Z., et al. Low-symmetry rhombohedral GeTe thermoelectrics. Joule. 2018;2(5):976–987. doi: 10.1016/j.joule.2018.02.016. [DOI] [Google Scholar]
  • 46.Takagiwa Y., Pei Y., Pomrehn G., Snyder G. J. Dopants effect on the band structure of PbTe thermoelectric material. Applied Physics Letters. 2012;101(9):p. 092102. doi: 10.1063/1.4748363. [DOI] [Google Scholar]
  • 47.Bu Z., Li W., Li J., et al. Dilute Cu2Te-alloying enables extraordinary performance of r-GeTe thermoelectrics. Materials Today Physics. 2019;9:p. 100096. doi: 10.1016/j.mtphys.2019.100096. [DOI] [Google Scholar]
  • 48.Zhang X., Pei Y. Manipulation of charge transport in thermoelectrics. npj Quantum Materials. 2017;2(1) doi: 10.1038/s41535-017-0071-2. [DOI] [Google Scholar]
  • 49.Pei Y., Wang H., Gibbs Z. M., LaLonde A. D., Snyder G. J. Thermopower enhancement in Pb1− _x_ Mn _x_ Te alloys and its effect on thermoelectric efficiency. NPG Asia Materials. 2012;4(9):p. e28. doi: 10.1038/am.2012.52. [DOI] [Google Scholar]
  • 50.Ohta M., Biswas K., Lo S. H., et al. Enhancement of thermoelectric figure of merit by the insertion of MgTe nanostructures in p-type PbTe doped with Na2Te. Advanced Energy Materials. 2012;2(9):1117–1123. doi: 10.1002/aenm.201100756. [DOI] [Google Scholar]
  • 51.Pei Y., LaLonde A. D., Heinz N. A., Snyder G. J. High thermoelectric figure of merit in PbTe alloys demonstrated in PbTe–CdTe. Advanced Energy Materials. 2012;2(6):670–675. doi: 10.1002/aenm.201100770. [DOI] [Google Scholar]
  • 52.Jian Z., Chen Z., Li W., Yang J., Zhang W., Pei Y. Significant band engineering effect of YbTe for high performance thermoelectric PbTe. Journal of Materials Chemistry C. 2015;3(48):12410–12417. doi: 10.1039/C5TC03068D. [DOI] [Google Scholar]
  • 53.Chen Z., Jian Z., Li W., et al. Lattice dislocations enhancing thermoelectric PbTe in addition to band convergence. Advanced Materials. 2017;29(23) doi: 10.1002/adma.201606768. [DOI] [PubMed] [Google Scholar]
  • 54.Tan G., Shi F., Hao S., et al. Non-equilibrium processing leads to record high thermoelectric figure of merit in PbTe-SrTe. Nature Communications. 2016;7(1) doi: 10.1038/ncomms12167. [DOI] [PMC free article] [PubMed] [Google Scholar]
  • 55.Albany H. J., Ocio M. Electrical properties and band structure in Pb1-xSnxTe. Le Journal de Physique Colloques. 1968;29(C4):C4-125–C4-128. doi: 10.1051/jphyscol:1968417. [DOI] [Google Scholar]
  • 56.Pei Y., LaLonde A., Iwanaga S., Snyder G. J. High thermoelectric figure of merit in heavy hole dominated PbTe. Energy & Environmental Science. 2011;4(6):2085–2089. doi: 10.1039/c0ee00456a. [DOI] [Google Scholar]
  • 57.Zhao L. D., Wu H. J., Hao S. Q., et al. All-scale hierarchical thermoelectrics: MgTe in PbTe facilitates valence band convergence and suppresses bipolar thermal transport for high performance. Energy & Environmental Science. 2013;6(11):3346–3355. doi: 10.1039/c3ee42187b. [DOI] [Google Scholar]
  • 58.Ahn K., Biswas K., He J., Chung I., Dravid V., Kanatzidis M. G. Enhanced thermoelectric properties of p-type nanostructured PbTe–MTe (M = Cd, Hg) materials. Energy & Environmental Science. 2013;6(5):p. 1529. doi: 10.1039/c3ee40482j. [DOI] [Google Scholar]
  • 59.Pei Y., Lensch-Falk J., Toberer E. S., Medlin D. L., Snyder G. J. High thermoelectric performance in PbTe due to large nanoscale Ag2Te precipitates and La doping. Advanced Functional Materials. 2011;21(2):241–249. doi: 10.1002/adfm.201000878. [DOI] [Google Scholar]
  • 60.Androulakis J., Todorov I., He J., Chung D. Y., Dravid V., Kanatzidis M. Thermoelectrics from abundant chemical elements: high-performance nanostructured PbSe–PbS. Journal of the American Chemical Society. 2011;133(28):10920–10927. doi: 10.1021/ja203022c. [DOI] [PubMed] [Google Scholar]
  • 61.Gelbstein Y., Dado B., Ben-Yehuda O., Sadia Y., Dashevsky Z., Dariel M. P. High Thermoelectric Figure of Merit and Nanostructuring in Bulkp-type Gex(SnyPb1−y)1−xTe alloys Following a spinodal decomposition Reaction†. Chemistry of Materials. 2010;22(3):1054–1058. doi: 10.1021/cm902009t. [DOI] [Google Scholar]
  • 62.Ahn K., Han M. K., He J., et al. Exploring Resonance Levels and Nanostructuring in the PbTe-CdTe System and Enhancement of the Thermoelectric Figure of Merit. Journal of the American Chemical Society. 2010;132(14):5227–5235. doi: 10.1021/ja910762q. [DOI] [PubMed] [Google Scholar]
  • 63.Yang J. Theory of thermal conductivity. Springer; 2004. [Google Scholar]
  • 64.Gelbstein Y., Dashevsky Z., Dariel M. P. Highly efficient bismuth telluride doped p-type Pb0.13Ge0.87Te for thermoelectric applications. physica status solidi (RRL) – Rapid Research Letters. 2007;1(6):232–234. doi: 10.1002/pssr.200701160. [DOI] [Google Scholar]
  • 65.Chen Z., Zhang X., Lin S., Chen L., Pei Y. Rationalizing phonon dispersion for lattice thermal conductivity of solids. National Science Review. 2018;5(6):888–894. doi: 10.1093/nsr/nwy097. [DOI] [Google Scholar]
  • 66.Zaitsev V. K., Fedorov M. I., Gurieva E. A., et al. Highly effectiveMg2Si1−xSnxthermoelectrics. Physical Review B. 2006;74(4) doi: 10.1103/PhysRevB.74.045207. [DOI] [Google Scholar]
  • 67.Pei Y., Zheng L., Li W., et al. Interstitial point defect scattering contributing to high thermoelectric performance in SnTe. Advanced Electronic Materials. 2016;2(6) doi: 10.1002/aelm.201600019. [DOI] [Google Scholar]
  • 68.Mao J., Wu Y., Song S., et al. Defect engineering for realizing high thermoelectric performance in n-type Mg3Sb2-based materials. ACS Energy Letters. 2017;2(10):2245–2250. doi: 10.1021/acsenergylett.7b00742. [DOI] [Google Scholar]
  • 69.Joshi G., Lee H., Lan Y., et al. Enhanced thermoelectric figure-of-merit in nanostructured p-type silicon germanium bulk alloys. Nano Letters. 2008;8(12):4670–4674. doi: 10.1021/nl8026795. [DOI] [PubMed] [Google Scholar]
  • 70.Hsu K. F., Loo S., Guo F., et al. Cubic AgPbmSbTe2+m: bulk thermoelectric materials with high figure of merit. Science. 2004;303(5659):818–821. doi: 10.1126/science.1092963. [DOI] [PubMed] [Google Scholar]
  • 71.Biswas K., He J., Blum I. D., et al. High-performance bulk thermoelectrics with all-scale hierarchical architectures. Nature. 2012;489(7416):414–418. doi: 10.1038/nature11439. [DOI] [PubMed] [Google Scholar]
  • 72.Poudel B., Hao Q., Ma Y., et al. High-thermoelectric performance of nanostructured bismuth antimony telluride bulk alloys. Science. 2008;320(5876):634–638. doi: 10.1126/science.1156446. [DOI] [PubMed] [Google Scholar]
  • 73.Klemens P. G. Thermal conductivity and lattice vibrational modes. Solid State Physics. 1958;7:1–98. doi: 10.1016/S0081-1947(08)60551-2. [DOI] [Google Scholar]
  • 74.Pei Y., May A. F., Snyder G. J. Self-tuning the carrier concentration of PbTe/Ag2Te composites with excess Ag for high thermoelectric performance. Advanced Energy Materials. 2011;1(2):291–296. doi: 10.1002/aenm.201000072. [DOI] [Google Scholar]
  • 75.Ohno S., Aydemir U., Amsler M., et al. Achieving zT > 1 in inexpensive Zintl phase Ca9Zn4+xSb9by phase boundary mapping. Advanced Functional Materials. 2017;27(20) doi: 10.1002/adfm.201606361. [DOI] [Google Scholar]
  • 76.Wang H., Wang J., Cao X., Snyder G. J. Thermoelectric alloys between PbSe and PbS with effective thermal conductivity reduction and high figure of merit. Journal of Materials Chemistry A. 2014;2 [Google Scholar]
  • 77.Kim S. I., Lee K. H., Mun H. A., et al. Dense dislocation arrays embedded in grain boundaries for high-performance bulk thermoelectrics. Science. 2015;348(6230):109–114. doi: 10.1126/science.aaa4166. [DOI] [PubMed] [Google Scholar]
  • 78.Xin J., Wu H., Liu X., Zhu T., Yu G., Zhao X. Mg vacancy and dislocation strains as strong phonon scatterers in Mg2Si1−xSbx thermoelectric materials. Nano Energy. 2017;34:428–436. doi: 10.1016/j.nanoen.2017.03.012. [DOI] [Google Scholar]
  • 79.Carruthers P. Scattering of phonons by elastic strain fields and the thermal resistance of dislocations. Physics Review. 1959;114(4):995–1001. doi: 10.1103/PhysRev.114.995. [DOI] [Google Scholar]
  • 80.Hanus R., Agne M. T., Rettie A. J. E., et al. Lattice softening significantly reduces thermal conductivity and leads to high thermoelectric efficiency. Advanced Materials. 2019;31(21):p. 1900108. doi: 10.1002/adma.201900108. [DOI] [PubMed] [Google Scholar]
  • 81.Tang J., Yao Z., Chen Z., et al. Maximization of transporting bands for high-performance SnTe alloy thermoelectrics. Materials Today Physics. 2019;9:p. 100091. doi: 10.1016/j.mtphys.2019.03.005. [DOI] [Google Scholar]
  • 82.Lyden H. A. Measurement of the conductivity effective mass in semiconductors using infrared reflection. Physics Review. 1964;134(4A):A1106–A1112. doi: 10.1103/PhysRev.134.A1106. [DOI] [Google Scholar]
  • 83.Ravich Y. I., Efimova B. A., Smirnov I. A. Semiconducting Lead Chalcogenides. Monographs in Semiconductor Physics v. 5. New York: Plenum Press; 1970. [Google Scholar]
  • 84.Williamson G. K., Hall W. H. Die verbreiterung der roentgeninterferenzlinien von aluminium- und wolframspaenen. Acta metallurgica. 1953;1(1):22–31. doi: 10.1016/0001-6160(53)90006-6. [DOI] [Google Scholar]
  • 85.Cowley R. The theory of Raman scattering from crystals. Proceedings of the Physical Society. 1964;84(2):281–296. doi: 10.1088/0370-1328/84/2/311. [DOI] [Google Scholar]
  • 86.Ravich I. I. Semiconducting Lead Chalcogenides. Vol. 5. Springer Science & Business Media; 2013. [Google Scholar]
  • 87.Lucovsky G., Brodsky M. H., Burstein E. Extension of a linear diatomic-chain model for the calculation of local-mode frequencies in real crystals. Physical Review B. 1970;2(8):3295–3302. doi: 10.1103/PhysRevB.2.3295. [DOI] [Google Scholar]
  • 88.Pine A. S., Dresselhaus G. Raman scattering in paratellurite, TeO2. Physical Review B. 1972;5(10):4087–4093. doi: 10.1103/PhysRevB.5.4087. [DOI] [Google Scholar]
  • 89.Romčević N., Trajić J., Romčević M., Golubović A., Nikolić S., Nikiforov V. N. Raman spectroscopy of PbTe1− _x_ S _x_ alloys. Journal of Alloys and Compounds. 2005;387(1-2):24–31. doi: 10.1016/j.jallcom.2004.06.059. [DOI] [Google Scholar]
  • 90.Baleva M., Momtchilova M. Raman modes of the GeS-type orthorhombic phase of PbTe. Physical Review B. 1994;50(20):15056–15062. doi: 10.1103/PhysRevB.50.15056. [DOI] [PubMed] [Google Scholar]
  • 91.Nootz G., Schulte A., Chernyak L., et al. Correlations between spatially resolved Raman shifts and dislocation density in GaN films. Applied Physics Letters. 2002;80(8):1355–1357. doi: 10.1063/1.1449523. [DOI] [Google Scholar]
  • 92.Falkovsky L. A., Bluet J. M., Camassel J. Strain relaxation at the3C−SiC/Siinterface: Raman scattering experiments. Physical Review B. 1998;57(18):11283–11294. doi: 10.1103/PhysRevB.57.11283. [DOI] [Google Scholar]
  • 93.Miyagawa H., Kamiya D., Sato C., Ikegami K. Strain measurement for Raman-inactive substrates with PbO thin films using Raman coating method. Journal of Materials Science. 1999;34(1):105–110. doi: 10.1023/A:1004421826443. [DOI] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supplementary Materials

Materials and Methods: Table S1: parameters used for the modeling. Figure S1: XRD patterns (a-c) and lattice parameters (d-e) for Na0.02Eu0.03MnxPb0.95-xTe (a, d), NayEu0.03Mn0.03Pb0.94-yTe (b, e), and Na0.03Eu0.03Mn0.03Pb0.91Te (c, f) with different annealing time. Figure S2: normalized optical absorption coefficient for Na0.02Eu0.03MnxPb0.95-xTe (a) and NayEu0.03Mn0.03Pb0.94-yTe (b) at room temperature. Table S2: room temperature Hall carrier concentration (nH), inertial effective mass (mI∗), plasma energy, and density (g/cm3) for Na0.02Eu0.03MnxPb0.95-xTe, and NayEu0.03Mn0.03Pb0.94-yTe. Figure S3: TEM images and EDS composition mappings for Na0.03Eu0.03Mn0.03Pb0.91Te. Figure S4: low-magnification STEM images (a) and high-magnification STEM image(b), electron diffraction patterns(c), and EDS composition mappings (d-i) for Na0.05Eu0.03Mn0.03Pb0.89Te, indicating the coexistence of both dense dislocations and nanoprecipitates. Figure S5: MnTe (a) and NaTe (b) content-dependent sound velocity for Na0.02Eu0.03MnxPb0.95-xTe and NayEu0.03Mn0.03Pb0.94-yTe at room temperature. Figure S6: repeated measurements for the high-zT composition Na0.03Eu0.03Mn0.03Pb0.91Te showing highly reproducible and stable thermoelectric properties.

Click here for additional data file. (2.3MB, pdf)

Articles from Research are provided here courtesy of American Association for the Advancement of Science (AAAS) and Science and Technology Review Publishing House

RESOURCES