Optimising treatment decision rules through generated effect modifiers: a precision medicine tutorial

Summary

This tutorial introduces recent developments in precision medicine for estimating treatment decision rules. The objective of these developments is to advance personalised healthcare by identifying an optimal treatment option for each individual patient based on each patient's characteristics. The methods detailed in this tutorial define composite variables from the patient measures that can be viewed as ‘biosignatures’ for differential treatment response, which we have termed ‘generated effect modifiers’. In contrast to most machine learning approaches to precision medicine, these biosignatures are derived from linear and non-linear regression models and thus have the advantage of easy visualisation and ready interpretation. The methods are illustrated using examples from randomised clinical trials.

Background

Personalised medicine refers to making treatment decisions based on each individual patient's characteristics. This is in contrast to the ‘one treatment fits all’ approach that is predicated on an assumption that one treatment is better than any other for every patient. Precision medicine is a term, similar to personalised medicine, related to prevention and treatment of disease that takes into account each person's genetics and other biological phenotypes, environment and lifestyle. Traditional randomised clinical trials (RCTs) compare two or more treatments with respect to the average outcome in a target population and typically lead to a recommendation that all individuals in the target population be assigned the treatment that was shown to be more efficacious on average. The target populations are usually defined by some demographic characteristics, such as age groups or by clinical features, such as chronicity or age at onset of the condition. In mental health, there is a very high degree of heterogeneity even within these targeted subpopulations in terms of treatment outcome. As a result, the standard approach to treatment in psychiatry can be an inefficient cycle of prescribing treatments via trial-and-error, resulting in a patient's prolonged suffering.

The goal of personalised medicine is to reduce this inefficiency and improve patient care by tailoring treatment decisions based on each individual patient's characteristics. To refine treatment decision-making, researchers have tried to characterise subgroups of patients in RCTs who tended to respond well to one treatment but not as well to other treatments in the study. Such characteristics are termed treatment ‘effect modifiers’ or just ‘moderators’. Among different approaches for finding effect modifiers, the most popular is based on linear regression modelling, in which the outcome is regressed on the treatment indicator, a specific patient characteristic (such as severity of symptoms, age, duration of illness) and the treatment-by-characteristic interaction. A significant interaction term would suggest that the relative benefit of one treatment versus the another depends on the value of that characteristic. Such a characteristic is then considered an effect modifier because an individual patient's benefit from one treatment versus another treatment depends on the patient's characteristic score. Effect modifiers inform the treatment decision for each specific patient, thus personalising the decision.

Challenges in psychiatry

The search for effect modifiers has a long history in mental health research, yet currently there is no reliable way of matching each patient to his/her optimal treatment for depression or other psychiatric conditions. One reason is that most baseline measures typically have small moderating effects and, individually, they contribute little to inform optimal treatment decisions. Given p baseline characteristics, the popular regression approach to personalised medicine involving all p predictor-by-treatment interactions becomes unwieldy, unstable and difficult to interpret when p is moderate to large.

Another reason for the lack of progress in personalised medicine in psychiatry is that the information clinicians conventionally use, assessed through medical history, psychological and clinical examination, is either not relevant or not precise enough. In the past few decades, the understanding of biological mechanisms underlying mental disorders has grown and these advances may lead to more finely tuned and better performing patient-tailored treatment decisions. Precision psychiatry capitalises on progress in technology that allows characterising patient's behaviour, environment, genetics and brain biology in detail unattainable even a few years ago. These new sources of complex and high-dimensional data are a promising new direction for advancing mental health research and practice. In the era of precision psychiatry, identifying treatment effect modifiers among the massive amount of patient information requires more complex analytic methodologies than those used in traditional research.

Use of a regression-based approach

In this paper we present a parsimonious alternative to the conventional linear regression models for finding effect modifiers. The approach we describe here can provide interpretable results in terms of a specially constructed composite predictor, which we term a generated effect modifier (GEM). In efficacy studies, after the primary analysis of treatment efficacy has been performed, the usual practice is to seek individual effect modifiers (single patient baseline characteristics) with the ultimate goal of informing treatment decisions, for example Brotman et al¹ and Markowitz et al.² When no single variable has a strong modifying effect, the GEM approach provides an appealing alternative.

Some recent advances in precision medicine are based on machine learning algorithms, including support vector machines for example Zhao et al³ and Song et al⁴ and tree-based methods for example Laber & Zhao.⁵ In this tutorial, we focus instead on regression-based approaches, which can provide treatment decision rules (TDRs) that are both effective and readily interpretable.

We present the framework used in deriving optimal TDRs and define optimality criteria. We consider the most common case of modelling the outcome using a classical linear model and we show how to combine multiple predictors into a single GEM. The linear GEM approach is then generalised to accommodate non-linear relationships between an outcome and an effect modifier. These precision psychiatry methods are then illustrated using examples from mental health research.

Method

Notation and introductory example

We begin with an example, which motivates the methodology presented in this tutorial, while introducing the notation and terminology used in the area of optimal treatment decisions. Brotman et al¹ performed an RCT to evaluate the effects of an early childhood intervention called ParentCorps in comparison with pre-kindergarten (pre-K) education as usual on learning, behaviour and health outcomes. The trial involves randomisation of elementary schools in socioeconomically disadvantaged neighbourhoods, in which a majority of students were born to families who recently immigrated to the USA. All 12 schools had pre-K programmes and were randomised either to ParentCorps or to pre-K education as usual. ParentCorps is a preventive intervention that aims to increase parental involvement in early learning, and to promote positive behaviour support and effective behaviour management in the home and classroom through parallel behavioural strategies for parents and teachers. The goal of the intervention is to mitigate the negative influence of poverty on children's development, thus resulting in long-term benefits on academic achievement, mental and physical health.

The purpose of this study was to identify and characterise the students for whom ParentCorps is most effective with respect to academic achievement using a set of baseline characteristics (or covariates). Using conventional regression notation, we will denote the baseline characteristics by x's and the outcome by y. In this example, we take the outcome to be y = end-of-kindergarten reading achievement as assessed by testers (masked to intervention status), using a nationally normed (mean 100, s.d. = 15) psychometrically sound measure of academic achievement. This example has six baseline characteristics: x₁ = conduct problems, x₂ = defiance, x₃ = emotion understanding, x₄ = school readiness, x₅ = pre-academic skills and x₆ = academic problems. In general, it will be convenient to denote the of set baseline characteristics by a single vector x, with p elements, where p is the number of baseline characteristics. Note, that vectors are denoted with bold symbols to distinguish them from individual variables or other elements of a vector. In the ParentCorps example x = (x₁, x₂, …, x_p)′, p = 6. We will use the variable A to denote the treatment options, usually coded as A = 0 and A = 1 in the case of two treatments. In the ParentCorps example, we have A = 1 for ParentCorps and A = 0 for the control. Given a vector x of baseline characteristics, a TDR is simply a function of the baseline characteristics d(x) that assigns a specific treatment A = 0 or A = 1 to patients with those characteristics. The goal is to determine a treatment decision function d that will recommend one of these treatments for any patient. Thus, if d(x) = 1 for a patient with characteristics x, s/he is expected to benefit more from Treatment A = 1 than if Treatment A = 0 had been assigned instead. We wish to determine the function d that will have some optimality properties.

Optimal TDRs

To compare different TDRs, we need to be able to measure them using some quantitative evaluation metric. One useful measure for a decision rule d is the ‘value’, which we denote by V(d). The value of a decision rule is defined as the average of the outcome y that would result if all patients in the entire target population were to be treated according to the decision function d. Here we consider outcome variables y that are continuous, and assume, for the sake of discussion, that higher values of y are preferred. The ‘optimal treatment decision’ is the one that, when applied to the target population, has the largest value.

From a statistical learning point of view, the goal is to determine a treatment decision function d that maximises the value. The value of a treatment decision function can be estimated from observed data. A common method of estimating the value of a TDR is the inverse probability weighted estimator (IPWE), see, for example Robins et al⁶ and Zhang et al.⁷ The IPWE of the value of a TDR is simply a (weighted) average of outcomes y of the patients whose assigned treatment coincides with the treatment recommended by the TDR. The weights are defined by the inverse of the probability of being assigned to that treatment, i.e. the patients' propensity for receiving a given treatment. When treatments are randomly assigned in a study, these propensities are fixed by design, for example for a two-arm RCT with 1:1 randomisation for treatment assignments, the probability that any participant receives any treatment is ½ in this case, the value of a TDR is estimated by the (unweighted) average of the outcomes of patients whose assigned treatment coincides with the treatment recommended by the TDR.

When two treatments are available, one trivial TDR is simply d(x) = 0, i.e., assign all patients to receive treatment A = 0, regardless of their covariates x. Alternatively, the rule d(x) = 1 would dictate that all patients receive treatment A = 1 regardless of x. Such rules would result from a ‘one size fits all’ treatment strategy. The goal of traditional RCTs is to evaluate the values of these two simple TDRs, to compare them and to recommend the use of the one that has higher value. Our goal is to improve upon the performance of both of these two trivial rules by constructing a TDR that intelligently incorporates patient information x in making treatment decisions.

Effect modifiers in a linear regression model

Perhaps the most straightforward approach to incorporating patient features into a TDR is through linear regression. If there is just one numerical characteristic (or predictor) x₁ to be investigated as a potential modifier of the treatment effect in a study with two treatments, we might posit the linear regression model

model 1

In this model, we note that β₁ represents the effect of x₁ that is common for both treatment groups, and β₂ represents the treatment (A) effect when x₁ = 0, sometimes referred to as a main effect of A. A part of model (1) that is useful for patient-specific treatment selections is the interaction term β₃A*x₁. A non-zero interaction term coefficient β₃ would indicate that x₁ is a treatment effect modifier, in which case x₁ should be used in any TDR. For a patient with a given level x₁ of the covariate, the expected outcome under treatment A = 0 is β₀ + β₁x₁, while that under treatment A = 1 is β₀ + β₁x₁ + β₂ + β₃x₁, and therefore the difference between these outcomes is β₂ + β₃x₁. The optimal treatment decision based on model (1) is simple: provided that higher scores on the outcome are preferred, if β₂ + β₃x₁ > 0, treatment A = 1 will be better for the patient, and if β₂ + β₃x₁ < 0, then treatment A = 0 will be better (if lower scores on the outcome are better, the opposite treatment decision is optimal). As the outcome under the two treatments is the same when β₂ + β₃x₁ = 0, in this case the decision might be based on other considerations, for example, prescribe the treatment with fewer side-effects or that is easier to comply with.

GEMs

With multiple characteristics, x₁, x₂, …, x_p, TDRs can be estimated using more complex multiple regression models that include all such variables and also their interactions with the treatment indicator. Such models, however, quickly become unstable and less interpretable as the number of predictors increases. An appealing and parsimonious regression approach to constructing TDRs is to form a composite variable, which we define to be a linear combination of the predictors. Given a vector of p predictors x = (x₁, …, x_p)′, we consider linear combinations of the predictors z = α′x = α₁x₁ + · · · + α_px_p, where α is a p-dimensional vector α = (α₁, …, α_p)′. We call the composite variable z a GEM.

Modelling the outcome in terms of a GEM for each treatment group provides a parsimonious approach to constructing a TDR and the GEM can be thought of as a biosignature for treatment response. The GEM can then be used in the simple linear regression model (1) to determine an easily interpreted TDR. This can be accomplished using a simple linear regression by replacing x₁ in (1) by the GEM z and determining the subsequent decision rule based on z.

Note, that in many psychiatric and psychological studies, treatment differences may go undetected by standard clinical trials analytic tools, because of high variability in the outcome that is unrelated to treatment differences. Differences between treatment effects may only become evident when treatment effect modifiers are introduced that separate the outcome variability related to differences in treatment effects from the variance unrelated to these effects. It is quite possible that the two treatments might be equally effective on average, but each one might be preferred for a different subset of patients. From clinical trials data, identifying subgroups of patients with differential treatment response classes (for example responder and non-responder classes) can often be achieved through a latent class or latent growth analysis,^8–11 by identifying biomarkers related to these response classes from patients' baseline predictors, or based on clustering.¹² In contrast, the GEM utilises an underlying outcome model of form (1), with the focus of estimating a composite treatment effect modifier z from baseline predictors. Using methods for tailoring/personalised medicine requires modelling individual treatment differences targeting subgroups with heterogeneous treatment effect. The model of form (1) allows computing individual treatment differences and constructing individual treatment rules, as functions of a biomarker signature z, efficiently utilising information on patient's characteristics. The GEM is an interpretable approach to discovering treatment effects heterogeneity, and thus, helps to identify and characterise subgroups of patients that will benefit from one but not the other of the treatment options and vice versa.

The challenge in constructing a GEM is to find the coefficient vector α that can lead to a good TDR. A natural choice for GEM coefficients α, in terms of moderator analysis, is to maximise the statistical significance of the interaction effects (assessed via an F-test) since differential treatment effects are quantified by interactions. The GEM coefficients α can be obtained by maximising an F-ratio statistic (i.e. minimising its corresponding P-value) whose numerator and denominator can be expressed in terms of matrices of covariance characterising the between- and within-group variations in the relationships between the p predictors and the outcomes for the two treatment groups. The vector of GEM coefficients α is then given by the leading eigenvector based on a product involving the numerator and denominator matrices (technical details are given in Petkova et al¹³).

As the GEM seeks the linear combination that minimises the P-value for the interaction term (i.e. maximising the associated F-ratio statistic), this will inflate type I (i.e. false positive) error rates; a remedy for this error inflation is to use a permutation approach to adjust the interaction P-value in the GEM model. The software for fitting a GEM model in R¹⁴ is available in the package pirate.¹⁵ The permutation algorithm for computing the interaction P-value is also implemented in this package.

Effect modifiers in non-linear models

Although linear models are extensively used because of their simplicity of fitting and interpretation, frequently, there is no reason to believe that the outcome will depend linearly on any such GEM. By considering non-linear relationships, the additional flexibility in the resulting TDRs may improve their performance. The linear GEM approach (see the GEMs subsection above) can be extended to accommodate non-linear associations.

Non-parametric regression, for example Green & Silverman,¹⁶ is a flexible approach useful when parametric regression models (for example linear or quadratic) do not adequately explain the relationship between the outcome y and the predictors x. An attractive semi-parametric approach to modelling non-linear relationships is the single-index model,^17,18 in which the outcome y is modelled as a non-linear link function g( · ) of a parametric (linear) combination of predictors z = α′x = α₁x₁ + · · · + α_px_p via y = g(α′x) + ε, where the shape of the function g( · ) and the coefficients α are determined by the data. We proposed in Park et al¹⁹ a parsimonious single-index model approach as a non-linear generalisation of the linear GEM approach (outlined in the GEMs subsection above). The model in Park et al¹⁹ is called a single-index model with multiple-links (SIMML), modelling the outcome for each treatment using a common GEM z = α′x (the single index) via a non-parametric link function for each treatment (the multiple links). For two treatments, the model would look like this:

where μ(x) represents a main effect of x, common for both treatments. Interaction effects between the treatment variable A and the GEM z = α′x are determined by the distinct shapes of the non-linear link functions g₀(z) and g₁(z). The corresponding TDR is to assign treatment 1 if g₁(z) > g₀(z) and assign treatment 0 otherwise (see Fig. 2 in the Results section for illustration).

Fig. 2.

The relationship between the derived single index z = α'x and change in depression severity for placebo (dark green curve) and the drug (light green curve) treatment.

The grey areas around the curves indicate the 95% confidence bands. The dashed vertical line indicates the cut-off point on the single index, above which a patient benefits from the drug. GEM, generated effect modifier.

The GEM coefficients of linear combination α are estimated iteratively, repeating two steps:

1. for a given vector of coefficients α, non-parametric regression techniques (for example, B-splines),²⁰ are used to estimate g₀(·) and g₁(·) (and any working model, for example, a linear model, can be assumed for the function μ(·)); and

2. for given treatment-specific link functions g₀(·) and g₁(·), the coefficients α are estimated via a weighted least-squares method based on a linear approximation of the treatment-specific link functions.

The iteration between these two steps continue until convergence. The SIMML can be fit using R¹⁴ code available in the package simml.²¹

Results

We now illustrate the application of these GEM approaches using the ParentCorps intervention described above and a study of treatments for people with major depressive disorder.

ParentCorps intervention example

In Brotman et al,¹ the authors show that based on standard efficacy analyses, with respect to reading achievement, the intervention is effective on average, over and above gains achieved from attending a pre-K education-as-usual programme. Within an at-risk population (children living in socioeconomically disadvantaged neighbourhoods), children who enter pre-K without being ‘school ready’ are at further risk for academic underachievement. Children with high levels of behavioural dysregulation (for example with conduct problems or children that are defiant), low levels of social-emotional skills (for example low emotion understanding and an unengaged approach to learning) and limited pre-academic skills (for example letter recognition, basic math concepts) are at an additional risk for underachievement. According to the theory of change, the intervention might be most beneficial for children with any or a combination of these characteristics.

In this study, there were complete data for all child predictors and the reading achievement outcome for 753 students, 370 from schools randomised to ParentCorps and 383 from control schools. We standardise the predictors to have mean zero and unit variance (see Table 1 for the mean and the standard deviation of each predictor before standardisation). Although this standardisation is not a requirement for this modelling approach, standardising allows ready interpretation of the relative importance of each individual predictor in describing the differential treatment responses.

Table 1.

Potential correlates of the efficacy of the ParentCorps intervention with respect to academic achievement

	Meana	s.d.a		Regression coefficientc
			Interaction,b P	A = 0	A = 1	Estimatedd α
Conduct problems	0.40	0.66	0.497	0.68	−0.33	−0.13
Defiance	0.25	0.42	0.115	−2.40	2.12	0.82
Emotion understanding	1.17	0.46	0.936	0.50	0.93	0.34
School readiness	0.32	0.45	0.693	−0.45	−0.22	−0.07
Pre-academic skills	99.4	12.9	0.660	5.17	−1.66	−0.70
Academic problems	0.46	0.77	0.512	−3.06	0.05	0.10

a. The means and standard deviations of the variables (prior to standardisation).

b. P-values for the interaction covariate-by-treatment term from model (1).

c. Regression coefficients from models with all six variables as predictors for treatment A = 1 (ParentCorps) and A = 0 (control).

d. The estimated coefficients of the GEM for the standardised variables (mean 0 and standard deviation 1).

First, we fit individual models (1) separately for each of the p = 6 risk factors including treatment assignment (ParentCorps (A = 1) versus control (A = 0)) and interaction. Table 1 gives the P-values of the F-test for significance of the interaction terms for these potential modifiers of ParentCorps treatment effect. None of the interaction terms were significant at the 0.05 level. Second, we fit a full unrestricted linear regression model with all predictors and their interactions with treatment 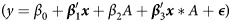and a reduced model without the interactions 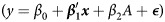. An F-test for significance of the full set of interactions indicated that there was not a significant interaction effect (F_(6,739) = 1.26, P = 0.274). The regression coefficients associated with from the full model for the two treatment groups, i.e., β₁ for A = 0 and β₁ + β₃ for A = 1, are given in columns 4 and 5 in Table 1, respectively. Technically, these are the same coefficients that would be obtained if we regressed the outcome on all six predictors using separate regression models for each treatment group.

Next, the coefficients of the linear combination α for the GEM criteria were estimated (last column of Table 1). Based on the permutation testing approach to control type I error rates (described in the GEMs subsection above), the resulting GEM has a statistically significant interaction with the treatment indicator (P = 0.003). The relative importance of each predictor in terms of characterising the heterogeneous treatment responses can be judged by the relative magnitude of the GEM coefficients (see Table 1). We note that the GEM highlights the importance of defiance and pre-school academic skills.

The relationship between the GEM and the outcome for the two intervention conditions is shown in Fig. 1. The cut-off point on the linear combination of predictors (i.e. the GEM) above which a child would benefit from the experimental intervention is −1.26. It is clear from the figure that TDR based on this GEM variable z = α′x excludes from treatment only a small proportion of children (to the left of the vertical line at −1.26). This analysis and the resulting figure can also be used to determine the cut-off point(s) on the GEM where the differences between the two treatments are considered statistically significant – for this, the point where the confidence bands for the two regression lines stop overlapping could be considered as an approximation; here this point is around GEM = –0.5. Of course, statistical significance depends heavily on the sample size and might not correspond to clinical significance. We use clinical significance below, when we illustrate the use of the GEM methodology for making practical decisions.

Fig. 1.

The relationship between the derived generated effect modifier (GEM) and reading achievement outcome for ParentCorps (light green) and pre-kindergarten as usual (dark green) interventions.

The grey areas around the lines indicate the 95% confidence bands. The dashed vertical grey vertical line (at GEM = –1.26) indicates the cut-off point on the linear combination of predictors above which a child would benefit from the experimental intervention. The dotted vertical grey line (at GEM = 1.8) indicates the cut-off point on the GEM, above which the benefit from the ParentCorps is of magnitude of at least 15 points, i.e., 1 s.d. of the outcome measure.

The value of the TDR based on the GEM, estimated using the IPWE, is 111.9 (95% CI 109.7–112.8). For comparison, the estimated value of the policy of providing everyone with the ParentCorps intervention, obtained by averaging the outcomes of students randomised to the intervention schools is 111.2 (95% CI 110.0–112.4), whereas the value of the decision to give no one the intervention is 108.4 (95% CI 107.1–109.7). The confidence intervals suggest that there is no difference in value using either the GEM-based decision rule or the rule that assigns ParentCorps to all pre-K students. The GEM-based TDR could not be expected to result in a value higher than the policy of providing the ParentCorps programme to everyone, as no student could be reasonably expected to do worse with ParentCorps compared with standard pre-K. The results from this analysis, however, allow the identification of children who would benefit most from the programme. Specifically, children whose GEM value is greater than –1.26 (indicated by the dashed grey vertical line in Fig. 1) can be expected to have a better outcome under ParentCorps compared with the usual pre-K programme and the degree of this benefit as a result of the intervention becomes quite substantial for larger values of GEM. For example, children whose GEM score exceeds 1.8 (the dotted grey vertical line of Fig. 1) are predicted to have more than a 15-point (or 1 s.d.) improvement in academic achievement because of the intervention. Thus, the GEM can be used to determine a threshold (for example, a 1 s.d. improvement) to guide schools' administrations in spending resources for motivating parents to participate in the ParentCorps meetings, lectures and other activities, as parents' participation is essential for the success of this intervention.

The data and the R¹⁴ code for this example are provided in supplementary Files 1 and 2 available at https://doi.org/10.1192/bjo.2019.85.

Depression study example

The previous subsection illustrated an application of the linear GEM to develop a TDR. This subsection illustrates the advantage of the SIMML in allowing non-linear flexibility in developing a TDR. We illustrate the GEM methodology using data from an 8-week RCT for the treatment of depression comparing a selective serotonin reuptake inhibitor (SSRI) antidepressant drug (A = 1) to a placebo (A = 0). The goal of the study is to identify baseline characteristics that are associated with differential response to the antidepressant versus placebo. The investigators defined ‘biosignature’ as a combination of patient measures that constitutes a moderator of the treatment effect. In this example, n = 88 participants were randomised to placebo and n = 78 were randomised to an SSRI drug. The outcome measure was defined as the change score from baseline to week 8 (y = week 0 – week 8) on the Hamilton Rating Scale for Depression (HRSD). High values of HRSD indicate higher depression severity and thus positive change score indicates a reduction in depression severity. Baseline clinical characteristics include: x₁ = age; x₂ = severity of depressive symptoms measured by the HRSD at baseline; x₃ = logarithm of duration (in month) of the current major depressive episode; and x₄ = age at onset of first major depressive episode. In addition to these standard clinical assessments, patients underwent neuropsychiatric testing at baseline to assess psychomotor slowing, working memory, reaction time (RT) and cognitive control (for example post-error recovery), as these behavioural characteristics are believed to correspond to biological phenotypes related to response to antidepressants.²² These neuropsychiatric measures include: x₅ = (A not B) RT-negative; x₆ = (A not B) RT-non-negative; x₇ =(A not B) RT-all; x₈ = (A not B) RT-total correct;²³ x₉ = median choice RT CRT;²⁴ x₁₀ = word fluency WF;²⁵ x₁₁ = flanker accuracy; x₁₂ = flanker RT; x₁₃ = post conflict adjustment.²⁶ All baseline covariates are standardised to have mean 0 and unit variance.

For this example, we employ the non-linear variant of the GEM methodology by applying the SIMML model from the Effect modifiers in non-linear model subsection above. Based on bootstrap confidence intervals for the coefficients of the linear combination α, only 4 of the original 13 covariates were retained to form the GEM, in which the associated 95% bootstrap confidence intervals obtained from 200 bootstrap replications do not include 0's: age, symptom severity, log(duration of major depressive episode) and flanker RT. The results of fitting the non-linear GEM are illustrated in Fig. 2.

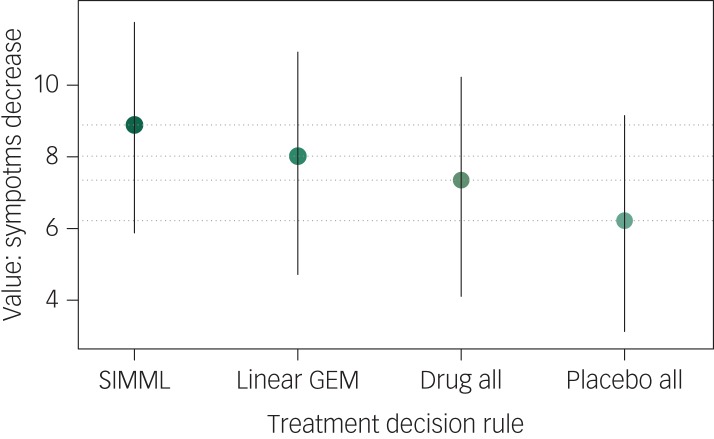
The value of the TDR based on SIMML is 8.89 (95% CI 5.88–11.75). The value of the TDR based on the linear GEM is 8.02 (95% CI 4.72–10.92), suggesting that the non-linear flexibility of the SIMML approach can lead to TDRs that provide better individual outcomes on average. For comparison, the standard TDR to treat everyone with the drug has a value of 7.35 (95% CI 4.11–10.22) and the TDR to treat everyone with placebo has a value of 6.22 (95% CI 3.13–9.15), see Fig. 3. Here, the wide 95% confidence intervals, resulting from the small sample sizes in this example, indicate that all pairwise differences between the values of the TDRs are non-significant. Still, the difference between the values of the two trivial TDRs (to treat everyone with drug versus to treat everyone with placebo, difference of 1.13) is smaller in magnitude than the difference between the value of the SIMML-based TDR and the decision to treat everyone with the drug (difference of 1.54). This means that patient-tailored antidepressant assignment, compared with the standard TDR of assigning antidepressants to everyone, can result in a benefit of magnitude similar to the average benefit of the antidepressant compared with placebo. This observation highlights the potential of making treatment decisions based on individual patient characteristics for improving public health.

Fig. 3.

Values of the treatment decision rules based on the non-linear (single-index model with multiple-links (SIMML)) and linear generated effect modifier approaches, and the two trivial treatment decisions to treat everyone with the antidepressant (Drug all) or with placebo (Placebo all) with 95% confidence intervals.

The data and the R¹⁴ code for this example are provided in supplementary Files 3 and 4.

Discussion

This tutorial has summarised an approach to precision medicine for the development of optimal TDRs based on individual patient's characteristics. The method for estimating TDRs described here is one of many recently proposed in the literature. Research on precision medicine has flourished with methods on using clinical and biological markers to guide the development of patient-tailored treatment decisions, see Zhao et al,³ Song et al,⁴ Zhang et al,⁷ Cai et al,²⁷ Qian & Murphy,²⁸ Wang et al²⁹ and Benkeser et al.³⁰ among many others. Misspecification of the models for the outcome under different treatments, which can lead to suboptimal TDRs, is among the major concerns stimulating the new developments. This has led to the proliferation of machine learning approaches. However, machine learning approaches typically require data-sets with very large numbers of patients (in the thousands), which are not common in mental health research. The flexibility offered by the non-linear GEM based on the SIMML provides some protection with regard to model misspecification.

Recommendations

Still, the performance of the TDRs depends on the unknown true relationship between the observed patient characteristics and the outcome under different treatments and in particular, the covariates that contribute to the differential response to treatment. Our recommendation is to employ more than one method and to compare the TDRs with respect to their estimated values. Of course, any TDR must be subsequently validated in properly designed studies. An appropriate design of a validation study would be a three-arm RCT, where the experimental treatment, the control treatment and treatment assignment according to the investigated TDR are compared.

A frequently asked question is one about sample size necessary to develop good TDRs. At this time, there are no established rules for computing required sample sizes. As noted above, machine learning methods typically require sample sizes in the thousands. Parametric methodologies, such as those discussed in this tutorial, are more efficient and thus, can provide reliable results with smaller samples. Still, it is well known that the sample sizes necessary to detect an overall treatment effect with traditional linear models are, usually, sufficient to detect only large interactions between the treatment and a baseline covariate, while individual covariates typically have only small effects as treatment effect modifiers, especially in mental health research. In addition, adjustment for multiple testing when more than a single covariate is investigated, would reduce the efficiency of any procedure that relies on individual tests for the baseline covariates. This point of view highlights the advantages of the proposed GEM methodology.

Confirmatory versus discovery research

However, we want to make the following important distinction between the traditional efficacy analysis of clinical trials and analyses for developing TDRs. In the traditional efficacy analysis, one compares the two treatments and then proceeds to investigate whether any baseline characteristics is a treatment effect modifier. Such investigations are formulated and planned in the classic hypotheses testing framework, with strict rules about qualifying the findings as significant or not, and with corresponding interpretation of the results. In contrast, the search for optimal TDRs is, in essence, a process of discovery, which means that formal hypotheses testing is used only at the validation stage, for example when a TDR is compared in a three-arm study against the two competing treatments (such as experimental and a control), as mentioned above. In the TDR development stage, the goal is to obtain a decision function that performs better than assigning everyone to one or other of the two competing treatments. In the discovery process, one might employ the hypotheses testing framework, as we did in the ParentCorps intervention example results section above via the permutation test for the GEM or in the depression example above, where we selected 4 of the 13 possible covariates based on bootstrap confidence intervals. Cross-validation with external data-sets or splitting the available data-set, when adequate external data are not available, is a much more appropriate analytic technique for developing TDRs than classic statistical tests. The development of a TDR goes through internal validation and external validation (possibly on multiple external data-sets) before investigators are confident enough to test the TDR in an RCT and ultimately deploy it in clinical practice.

The GEM method presented in this tutorial can be useful for discovery of treatment effect modifiers in clinical trials. We presented two illustrations in which the standard approach of testing for effect modification one-by-one all individual covariates using model (1) did not yield any potential individual biomarkers. Jointly including all covariates and their interactions with treatment did not provide evidence for effect modification either, although a significant heterogeneity in the outcome was observed in those cases. The simplicity of application, visualisation and interpretation of the GEM method makes it an appealing tool among the various methodologies for developing personalised TDRs.

As medical technology continues to evolve, producing increasingly complex data modalities, research in precision medicine must continue in order to accommodate these advances and make optimal use of the available information. One such avenue is the development of TDRs that can incorporate predictors that are not only scalars (such as symptoms severity or response time on a given task), but also more complex data objects, such as images or time series of measurements. This is particularly relevant in psychiatry where neuroimaging and electroencephalogram measures are frequently collected to characterise the structural and functional integrity of the brain. The dominant practice of summarising neuroimaging data with the averages in specific brain regions can lead to inefficiencies in the TDRs using such data as potential biomarkers. Recent progress has been made using functional data analysis³¹ approaches to estimate TDRs in a regression context with functional predictors.^32–35 Through the optimal use of data, these functional data approaches may be able to discover features in the complex data that are strongly related to differential effects of treatment.

Funding

This work was supported by NIMH grants R01 MH099003 and K01 MH113850.