Combining Supervised and Unsupervised Learning for Improved miRNA Target Prediction

Abstract

MicroRNAs (miRNAs) are short non-coding RNAs which bind to mRNAs and regulate their expression. MiRNAs have been found to be associated with initiation and progression of many complex diseases. Investigating miRNAs and their targets can thus help develop new therapies by designing anti-miRNA oligonucleotides. While existing computational approaches can predict miRNA targets, these predictions have low accuracy. In this paper, we propose a two-step approach to refine the results of sequence-based prediction algorithms. The first step, which is based on our previous work, uses an ensemble learning approach that combines multiple existing methods. The second step utilizes support vector machine (SVM) classifiers in one- and two-class modes to infer miRNA-mRNA interactions based on both binding features, as well as network features extracted from gene regulatory network. Experimental results using two real data sets from TCGA indicate that the use of two-class SVM classification significantly improves the precision of miRNA-mRNA prediction.

1. Introduction

Recent studies have proven the role of non-coding RNA molecules, specifically miRNAs, in many diseases such as cancers. MiRNAs bind to mRNAs with partial sequence complementarity, resulting in cleavage of mRNAs or inhibiting translation of mRNAs to proteins. Due to the partial complementarity of binding sites, several miRNAs can bind to, or target, one mRNA and one miRNA can target several mRNAs. Advanced genetic therapeutic approaches to control expression of genes, such as designing Anti-miRNAs Oligonucleotides (AMOs), confirm the benefits of identifying miRNA targets [1].

Predicting miRNAs targets is a challenging problem. The difficulty arises from the partial complementarity of miRNA and mRNA sequences: The degree of complementarity between sequences that is required to conclude that a given miRNA targets a specific mRNA is unclear. Nonetheless, sequence complementarity has been used extensively in sequence-based methods of predicting miRNA targets [2–4]. The main drawback of these methods is their low precision, i.e. low number of experimentally validated interactions among all possible interactions. In order to improve sequence-based target predictions, various computational methods have been developed based on additional information, such as sequence features. For instance, RNAhybrid [5] and miRanda [6] have taken the accessibility of target sites as well as conservation into account. Although some of their predicted interactions have been later verified in laboratory, these methods still suffer from low precision.

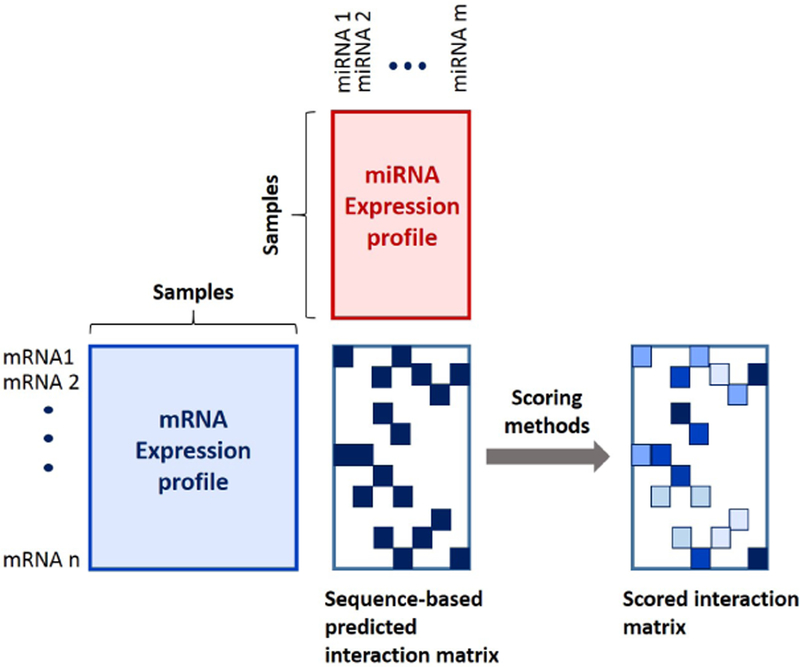
Advances in microarray technology has empowered researchers to concurrently measure expression levels of miRNAs and mRNAs in samples. This has resulted in a new class of methods that utilizes both expression profiles, as well as sequence-based predictions for improved precisions. The workflow of these methods is depicted in Figure 1. Almost all of these methods use machine learning techniques to circumvent the challenges of miRNA target prediction [7–17]. Typically, these methods can be categorized in two large groups: unsupervised and supervised learning methods. Briefly, unsupervised learning methods are applicable in settings, where no labeled responses are available. On the other hand, supervised learning methods require labeled training data.

Figure 1:

Refinement of sequence-based predicted interactions using concurrent miRNA and mRNA expression profiles.

Methods based on correlation and mutual information (MI) are the simplest approaches for miRNA target prediction [7–9]. In correlation-based approaches, miRNA-mRNA associations are evaluated using Pearson and/or Spearman correlation. Then, given the expected inverse relationship between expressions of miRNAs and their targets, interactions with large negative correlations are considered as targets [7,8]. Since correlation only captures linear associations between variables, correlation-based approaches may not be suitable in miRNA target prediction, where non-linear associations may be abundant. MI, which is an information theoretic measure that quantifies the amount of shared information between two variables, has thus been proposed as an alternative to correlation-based methods [9]. MI captures non-linear relationships in addition to linear relationships; however, it is a non-negative measure. As a result, the direction of association between miRNA and mRNA expression cannot be determined based on MI. Regularization methods based on the LASSO [18] form another class of unsupervised learning methods. Lasso-mir [10] and TaLasso [11] are two examples of such methods. Both of them use LASSO to identify association between miRNAs and mRNAs given concurrent miRNA and mRNA expression profiles, as well as sequence-based predicted targets. The difference between these two methods is that TaLasso tries to solve the convex problem considering non-positivity of coefficients as a constraint while lasso-mir does not consider such a constraint. Bayesian methods have also been used in unsupervised miRNA target prediction. These methods, which directly account for the uncertainty of prediction specifications include the method of [19], which learns the structure of miRNAs and mRNAs regulatory network from concurrent expression profiles without considering sequence-based predicted targets. Another example of Bayesian approach for miRNA target prediction is GenMiR++ [20, 21]. In contrast to [19], GenMiR++ utilizes predicted miRNA-mRNA interactions by the other methods and scores miRNA-mRNA pairs according to the contribution of miRNA expression to explain mRNA expression, given the expression of all other miRNAs.

In the light of increasing the number of experimentally validated interactions, a number of supervised learning methods have recently been developed for predicting miRNA targets. These methods formulate the miRNA target prediction as a classification problem. They extract features from validated miRNA-mRNA duplexes and use them to train a classification model, that is used to predict the status of unknown miRNA-mRNA interactions [12–17]. As an example, Target-Miner [15] applies SVM to identify miRNA-mRNA interactions based on the extracted context features, e.g., the frequency of single bases, from miRNA-target duplexes. NBmiRTar [16] and miREE [17] are other examples of such tools; they utilize the structural features of miRNAs-mRNAs duplexes, such as number of bases unpaired in the seed region, position in the Untranslated Region (UTR) site, and duplex minimum free energy, to build a predictive model. Clearly, the performance of these supervised methods depends directly on the quality and quantity of training data sets used to build the predictive model. Another related, but different supervised learning approach is the SMILE method [22]; while the above methods use validated miRNA-mRNA duplex features, SMILE uses outcomes of different target prediction methods to create the training data and then, uses an SVM model to predict the status of unknown interactions based on its predicted status in other methods. A major challenge in the application of supervised learning methods, including those mentioned above, is the unavailability of negative examples, i.e. miRNA-mRNA pairs that are known to not interact with each other. To address this challenge, [23] has applied a one-class, or unary, classification approach to identify miRAN-mRNA interactions based on structural and sequence features of miRNAs. One-class classification can be useful in settings where training data from the second class is imperfect [24], which is the case in miRNA target prediction.

In light of existing methods, the present study aims to improve the precision of miRNA target prediction using a two-step procedure. The first step, which is based on our previous work [25], utilizes miRNA and mRNA expression profiles to refine the predicted interactions from different methods by using a consensus unsupervised learning approach. The second step uses features of the predicted miRNA-mRNA interactions to develop a supervised learning approach based on an SVM model, in order to refine the interactions from the first step.

To build our SVM, we consider two different sets of features, including target site biding features and gene-gene network features. The gene-gene network is composed of genes involved in miRNA-mRNA interactions and is constructed based on gene expression profiles. Although several researches have confirmed the usefulness of target site binding features in identifying true miRNA-mRNA interactions, the usefulness of gene network features in this task has not been carefully investigated. In this study, we investigate whether information from the gene interaction network, and in particular connectivity patterns in the network, improve the accuracy of miRNAs target prediction. Finally, we also compare unary and binary classification models. In the case of unary classification, we only use validated miRNA-mRNA interactions to train the model and test it on either validated and non-validated interactions. In the case of binary classification, given the paucity of information on non-occurring miRNA-mRNA interactions that comprise negative examples, we follow the existing proposals for extracting negative examples from data; see Section 2.4 for details. By comparing unary and binary classification methods, we then investigate the extent to which the use of negative examples in two-class supervised learning can improve the prediction of miRNA-mRNA interactions.

Figure 2 gives an overview of the data and methods used in this paper. The data set used to build the predictive models is depicted in Figure 2(a): Each row of this data corresponds to a single of mRNA-miRNA pair; the blue and purple columns show ‘binding’ and ‘network’ features; the last column, ‘val flag’ shows the status of interaction as validated or non-validated interaction. Figure 2(b) gives an overview of to the proposed predictive modeling approach. Briefly, miRNA-mRNA interactions learned using the unsupervised learning step are used as ‘test’ data, while the remaining interactions are used as ‘training’ data. Prior to building predictive models, Principle Component Analysis (PCA) is used to refine the network features (see Section 2.4 for additional details). Three predictive models based on only binding features, only network features, and both are then built and compared. All experiments in this paper have been performed on two real data sets on Testicular Germ Cell Tumor (TGCT) and Kidney Renal Clear Cell Carcinoma (KIRC), downloaded from The Cancer Genome Atlas (TCGA) database¹.

Figure 2:

(a) Schematic of the data set used to train and test SVM models. The data consists of two groups of features: blue columns show binding features and purple columns show weighted network features, (b) Overview of the proposed predictive modeling approach.

The rest of the paper paper is organized as follows: in Section 2, we discuss the data sets used in this article and present our method in details. Experimental results are presented in Section 3. The findings of the paper are discussed in Section 4.

2. Materials and Methods

2.1. Data Pre-processing

We downloaded matched miRNA and mRNA RNASeq files (level 3.0) for TGCT and KIRC from TCGA database as read_counts. Level 3.0 data from TCGA have been carefully checked for quality and preprocessed². Hence, according to [26], additional data pre-processing is not required. However, prior to our analysis, we normalized the read_counts across each samples, by replacing each read_count with (read_count – min_count)/(max_count min_count), where min_count and max_count refer to the minimum and maximum read count in each sample. We then performed log₂-transformation on (read_counts + 1). The resulting data matrices for miRNA and mRNA were of dimensions [1046 × 156] and [20531 × 156] for TGCT and [1046 × 248] and [20531 × 248] for KIRC, respectively—the first dimension in the above matrices corresponds to miRNAs and mRNAs, and the second dimension corresponds to the matched samples.

2.2. Unsupervised Learning and Extracting Binding Features

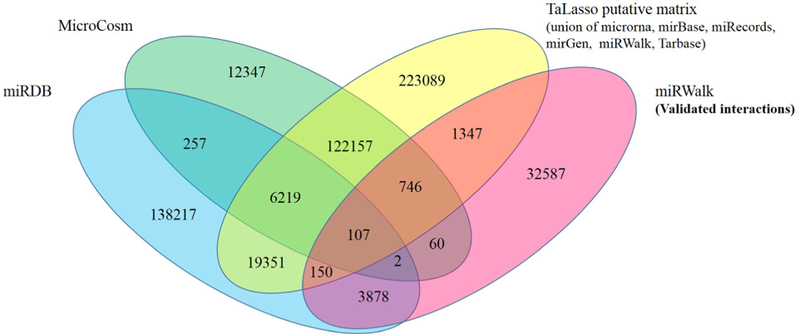
The sequence-based predicted interaction matrix was constructed from the union of putative interaction matrices from TaLasso³, MicroCosm v5.0⁴, and miRDB v5.0 [27] for both cancers. The TaLasso putative interaction matrix itself is a union of six other predictions from MicroRNA [28], mirBase [29], miRecords [30], miRGen [31], miRWalk [32], and Tarbase [33]. We also downloaded the most recent validated interaction data from miRWalk 2.0 [32]. Both putative and validated interaction matrices are binary matrices. Overall, there were 12,137 genes and 751 miRNAs in the union of all predicted interactions. The Venn diagram in Figure 3 shows the number of common interactions between various predictions.

Figure 3:

Venn diagram of predicted and validated interactions downloaded from various databases.

In addition to interactions, we also downloaded “Good mirSVR score, Conserved miRNA” and “Good mirSVR score, Non-conserved miRNA” target site predictions from MicroRNA database [28]. These data sets contain binding features for each target site including:

• Conservation score – This score measures the evolutionary conservation of sequence blocks across multiple vertebrates using a phylogenetic hidden Markov model, to filter out less conserved predicted target sites [34].

• Alignment score – The miRNA-mRNA alignment score is computed based on the maximum number of matched base pairs, e.g., C:G pairs, between miRNA and mRNA sequences [35].

• Energy – The minimum free energy measures the strength/stability of the miRNA-mRNA binding. This measures is usually negative with lower values indicating more stable bindings [36].

• mirSVR score – This score [37] is based on a weighted sum of multiple features, including base pairing at the seed region and 3′ end of the miRNA, A/U (Adenine/Uracil) composition near the target sites and secondary structure accessibility, and relative position of the target site in the UTR and conservation score.

When more than one target site existed for a specific interaction, the average score across all target sites was calculated and assigned to the interaction. The resulting data set contains 2,949,269 interactions between 19,796 mRNAs and 1,100 miRNAs. We refer to this data set as the binding data.

In addition to the binding data, our method requires both expression data for miRNAs and mRNAs (measured using RNAseq), as well as the set of putative interactions. Upon collecting these data sets, miRNAs and mRNAs that are common among all three data were used to develop our predictive model. Moreover, miRNAs that did not target any mRNAs were removed from the data sets. Similarly, mRNAs that were not targeted by any miRNAs were also removed. Table 1 shows the number of interactions, mRNAs, and miRNAs in the final data set.

Table 1:

Data characteristics.

Data type	Interactions	Validated int.	Non-validated int.	miRNAs	mRNAs
TGCT	30209	1142	29067	195	7828
KIRC	29023	1134	27889	185	7717

Similar to our previous work [25], TaLasso and GenMiR++ were used to primitively refine/reduce the sequence-based predicted interactions. Binding features for the SVM classifiers — blue columns in Figure 2(a) — were then defined based on the refined sequence-based interactions.

2.3. Feature Extraction From Gene Regulatory Network

Gene regulatory networks (GRN) represent how genes interact with each other to govern various biological processes. Nodes in a GRN represent genes and edges depict the relationships between genes. Among the many methods for constructing GRN based on gene expression profiles, here we use ARACNE [38] and WGCNA [39].

ARACNE

In this approach, the presence of an edge between a pair of genes is determined based on the magnitude of the mutual information (MI) for their gene expression levels, regardless of other genes.

ARACNE is implemented in the Bioconductor package minet [40], aracne() function. The output of aracne() is a pruned MI matrix, with nonzero entries for edges of the network. The number of edges in the estimated network can be (partially) controlled using the threshold ε: for each triplet of nodes (i, j, k), the weakest edge, say (i, j), is removed if its weight is below min{(w_ik), (w_jk)} − ε. In this study, we set ε = 0.01.

WGCNA

In this approach, a weighted correlation network based on gene expression profiles is used to reconstruct the gene regulatory network. The weighted correlation is calculated as:

$$\mathit{\text{ad}}{\mathit{\text{j}}}_{ij}={\left|cor\left(x_i,x_j\right)\right|}^{\beta },$$ (1)

for a tuning parameter β ≥ 1. The weighted network amplifies higher correlations values at the expense of lower correlations. WGCNA is implemented in the R-package WGCNA [39], where a weighted matrix is obtained from the adjacency() function. To obtain a network, we apply threshold 0.3 and 0.35 for KIRC and TGCT data, respectively. We have determined these thresholds such that the resulting networks each have a single large connected component.

After constructing the GRN, the following network features for each node/gene and network were calculated using igraph R-package [41]:

• Degree (f_N1) – Degree counts the number of connected edges to each node. In biological networks, the nodes with high degree nodes are more likely to be important/essential nodes in the network.

• Hub score (f_N2) – The hub scores of the nodes are defined as the principal eigenvector of A*t(A), where A is the adjacency matrix of the network.

• Page rank score (f_N3) – The so-called Google page rank, is related to the procedure of ranking web pages by Google search engine. It scores each node based on page rank of the connected node. In this regard, nodes that link to i and have high page rank score, are given more weight; conversely, nodes that link to i, but link to a lot of other nodes in general, are given less weight.

• Betweenness (f_N4) – Betweenness for a node is defined by the number of shortest paths going through that node.

• Closeness (f_N5) – The closeness centrality of a node is defined by the inverse of the average length of the shortest paths to/from all the other nodes in the graph. In the other words, it measures how many steps are required to access every other node from a given node.

• Eccentricity (f_N6) – The eccentricity of a node is its shortest path distance from the farthest other node in the graph.

• Alpha Centrality (f_N7) – The alpha centrality measure can be considered as a generalization of eigenvector centrality. The alpha centrality of the nodes in a graph is defined as the solution, in x, of the following matrix equation:

  $$x=\alpha A^{T}x+e={\left(I-\alpha A^T\right)}^{-1}e,$$ (2)

  where A is the adjacency matrix of the graph, I is identity matrix, e is the vector of exogenous sources of status of the nodes, and α is the relative importance of the endogenous versus exogenous factors.

• Bonacich’s power centrality (f_N8) – It is de fined by C_BP (α, β) = α(I – βA)⁻¹A1, where β is an attenuation parameter (set here by exponent) and A is the graph adjacency matrix. The coefficient α acts as a scaling parameter, and is set here such that the sum of squared scores is equal to the number of nodes. Interpretively, the power of a node is directly dependent on the power of its neighbors.

Given the above features, gene i is characterizes by a vector of network features as:

$$\mathit{\text{NetFeat}}\left(g_i\right)=\left[f_{N1},f_{N2},\dots ,f_{N8}\right].$$

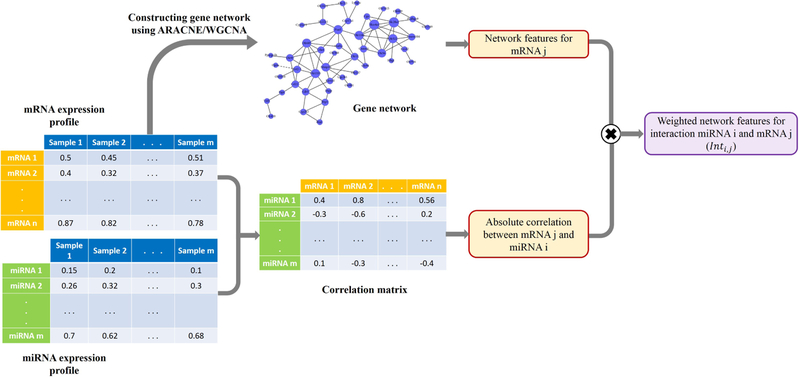
Note that the extracted features concern only genes/mRNAs, and not miRNA-mRNA interactions. To obtain interaction-specific features, absolute values of correlation between expression levels of miRNA i and mRNA j were used to form a weighted sum of network features for their interaction, d_ij:

$$\begin{gathered} \mathit{\text{NetFeat}}\left(d_{ij}\right)=\left|w_{ij}\right|\times \mathit{\text{NetFeat}}\left(g_j\right) \\ \text{where}{w}_{ij}=\text{cor}(\mathit{\text{expr}}(i),\mathit{\text{expr}}(j)); \end{gathered}$$ (3)

here, expr(i) and expr(j) are expression levels of miRNA i and gene j.

Figure 4 shows the steps for calculating network features. These features are depicted in the purple columns of figure 2(a).

Figure 4:

Extracting network features and assigning them to interactions obtained from union of top n interactions in TaLasso and GenMiR++.

2.4. Training and Test Data Preparation

To apply the proposed SVM classifiers, the full learning data, including both binding and network features, was divided into training and test data. Figure 2(b) illustrates the procedure, from obtaining binding data and network features to constructing the full learning data and dividing it to training and test parts. To this end, the union of n top ranked interactions obtained by TaLasso and GenMiR++ were considered as test data and the remaining interactions in the data were used for training. The selection of top n ranked interactions as test data creates a more challenging learning task, which is appropriate for the validation of our method. As mentioned before, SVM was used in two modes, namely, two-class (binary) and one-class (unary). Binary SVM uses both positive and negative examples, whereas only positive examples are used in unary SVM.

For both unary and binary SVM models, validated interactions in the training data constitute the positive examples. However, obtaining negative examples for binary SVM in our context is a challenging task. In the context of miRNA target prediction, negative examples correspond to miRNA-mRNA pairs which are known not to interact with each other. Unfortunately, such information is not available. Thus, various methods for generating negative examples have been proposed, including methods based on random sequences [14, 16]. Recently, Yu et al. [22] have shown that negative examples are likely interactions which are not been predicted by multiple prediction tools. Following this proposal, among all interactions obtained from the nine databases in Section 2.2, interactions which have been predicted by only one method were considered as negative examples. Since the number of validated interactions in training data, N_υal, was much less than the number of non-validated interactions, N_nval, down-sampling was used to the balance the number of positive and negative examples in the training data. More specifically, a total of N_υal non-validated examples were randomly chosen from the entire set of non-validated examples and were used to train the predictive model.

We then performed a pair-wise correlation analysis to discern patterns of correlation of network features in the training data. The analysis revealed that some of network features were correlated with each other. We thus used PCA to extract new orthogonal network features that capture information in the original network features. To this end, using the proportion of variance explained (PVE), the number of principle components (PCs) was determined such that the selected PC’s explain 90% of the variability in the original data. The projection of the original network features onto the space of principal components was then used to represent this information.

2.5. Supervised Learning and the Evaluation of Feature Contributions

Unary and binary SVM classifiers with Radial Basis Function (RBF) kernel, were fit using the e1071 R-package [42]. Three versions of each SVM classifier were used to identify miRNA-mRNA interactions, by considering (a) only binding features, (b) only network features, and (c) both sets of features. Figure 2(b) illustrates the various steps for preparing training and test data used in our analysis. To assess the performance of classifiers, 10-fold Cross-Validation (CV) on training data was performed, then the trained models were applied on test data in order to calculate precision and the Area Under the ROC Curve (AUC).

In addition to predicting miRNA-mRNA interactions, we used a logistic regression model to assess the predictive power of each group of features, namely, binding features and network features. To this end, we trained the model using the training data and obtained p-values for each feature.

3. Results

Figure 5(a) shows the number of shared interactions between validated miRNA-mRNA interactions and the top n ranked interactions identified by TaLasso and GenMiR++ for n ∈ {100, 200, … , 1000} in the TGCT data; Figure 5(b) shows the same result in the KIRC data. An enrichment analyses similar to that used in our previous work [25] indicates that for both methods and data sets, the identified interactions across all values of n ∈ {100, 200, … , 1000} differ significantly from randomly selected interactions (p-value ≤ 0.01). Details of the enrichment analysis are described in the Appendix A.

Figure 5:

(a) and (b) The number of validated interactions among top-ranked identified interactions by TaLasso and GenMiR++ in TGCT and KIRC data, (c) and (d) Shared interactions identified by TaLasso and GenMiR++ in TGCT and KIRC data.

Figure 5(c) shows the number of shared interactions between TaLasso and GenMiR++, as well as the number of validated interactions among them for TGCT data; Figure 5(d) shows the same result for the KIRC data. It can be seen that ~60% of the top n predicted interactions are shared by both methods. It is worth noting that despite apparent similarity of curves in (a) and (b), the growth rates of the two curves in (c) and (d) are rather different. This difference underscores the low precision of both estimation methods. Given these findings, and following our previous work [25], we use a consensus approach and consider the common top n interactions in both methods.

3.1. Feature Extraction from Gene Regulatory Network

Gene regulatory networks for both TGCT and KIRC were constructed using both ARACNE and WGCNA based on mRNA expression profiles. Table 2 shows characteristics of the constructed networks for TGCT and KIRC data. It includes the number of nodes (genes), edges, and summary statistics of the degree distributions, including minimum, maximum, first and third quartile, mean, and median. It can be seen that the networks constructed by ARACNE are connected (number of clusters is one), whereas the networks constructed by WGCNA are disconnected and have more edges than those constructed by ARACNE.

Table 2:

Characteristics of gene regulatory networks of TGCT and KIRC data constructed using ARACNE and WGCNA.

Data type	Method	Node	Edge	#Clust.	Mindeg	1stQu.deg	Mediandeg	Meandeg	3rdQu.deg	Maxdeg
TGCT	ARACNE	7828	30784	1	1	4	6	7.865	8	4377
KIRC	ARACNE	7717	35290	1	1	4	6	9.146	9	1807
TGCT	WGCNA	7828	362132	2854	0	0	4	92.52	68	1436
KIRC	WGCNA	7717	100984	3592	0	0	1	26.17	20	597

Next, the network features discussed in Section 2.3 were calculated for each network. To explore the relationship between these features, pair-wise correlation between them were calculated (Figure 6). The figure shows that in all four networks there are strong correlations between (degree and page rank score), (alpha centrality and power centrality), and (eccentricity and closeness). It is worth noting that while the correlation between eccentricity and closeness is negative in ARACNE networks, it is positive in WGCNA networks. In addition, there are strong correlation between (degree and betweenness) and (page rank score and betweenness) in the networks constructed using ARACNE, whereas there are no such such correlation in the networks constructed by WGCNA; this latter difference is due to the presence of multiple connected components in WGCNA networks. In order to assign gene-specific network features to miRNA-mRNA interactions, the correlation between miRNA and mRNA expression profiles were calculated and the absolute values were used as weights for network features.

Figure 6:

Correlation between network features; (a) TGCT network from ARACNE; (b) KIRC network from ARACNE; (c) TGCT network from WGCNA; (d) KIRC network from WGCNA.

Given the high correlation in network features, PCA was used to reduce the dimension and extract the relevant information from network features. Figure 7 shows cumulative PVE plots of ARACNE and WGCNA networks for TGCT and KIRC data sets. Given these results, a cutoff of 90% was used to select the number of PCs which capture at least 90% of variation in the network features from the training data. The network features in training and test data were then projected into the space of PCs in order to obtain lower-dimensional summaries for use in the SVM models discussed in the next section.

Figure 7:

Cumulative proportion of variance explained. (a) Network constructed by ARACNE, TGCT data; (b) Network constructed by ARACNE, KIRC data, (c) Network constructed by WGCNA, TGCT data; (d) Network constructed by WGCNA, KIRC data.

3.2. Supervised Learning: SVM Classification

Binary and unary SVMs were used to predict miRNA-mRNA interactions. While the test data for these two classifiers were the same, the training data were different. For binary SVM, the training data comprised both positive and negative examples, whereas for unary SVM, the training data only included positive examples.

For both SVM models and for n ∈ {100, 200, … , 1000}, we used the top n ranked interactions identified by GenMiR++ or TaLasso as test data. For binary SVM, we down-sampled node-pairs with no interactions to create a balanced training data set. Only validated interactions were used as positive examples for unary SVM.

Binary and unary SVM models with RBF kernel in the setting of 10-fold CV were trained for each n ∈ {100, 200, … , 1000} and three groups of features including only binding features, only network features, and all of the features.

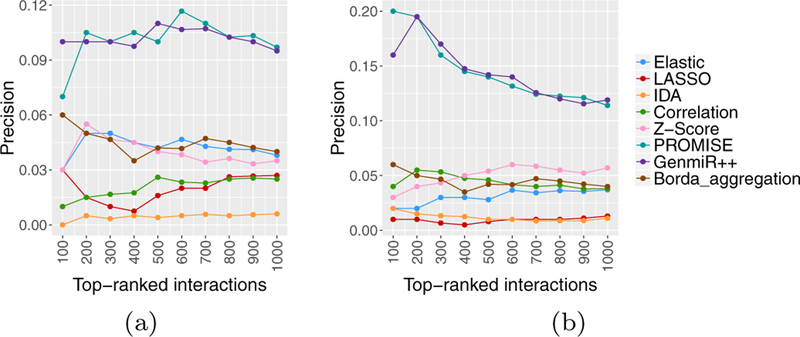
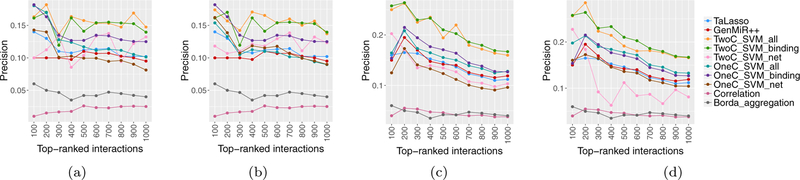
To assess the performance of the SVM models, we compared them with TaLasso, GenMiR++, miRNA-mRNA prediction based on the Pearson correlation (considering only negative coefficients), and the ensemble method of Le et al. [43], named Borda aggregation⁵. The Borda aggregation method first finds differentially expressed mRNAs and miRNAs; it then applies eight miRNA-mRNA prediction methods, including Pearson, IDA, MIC, Lasso, Elastic, Z-score, ProMISe, and GenMiR++ on matched miRNA and mRNA expression data. In the last step, it aggregates the results from top 5 methods for identifying interactions using the Borda count election method. Given the unavailability of ‘normal’ samples in our data sets, we were not able to identifying differentially expressed miRNAs and mRNAs. Thus, to apply the Borda aggregation method to our data, we ran each of the link prediction methods on all miRNAs and mRNAs pairs (instead of those corresponding to differentially active pairs). This resulted in considerably higher computational complexity, and as a result, we did not obtain any results for the MIC method. Figure 8 shows the precision of the individual and aggregate method for both TGCT and KIRC data.

Figure 8:

Precision of individual methods as well as integrated result, (a) TGCT data, (b) KIRC data.

To improve the miRNA-mRNA predictions from Borda, among the 7 prediction methods used in Borda, we aggregated the predictions of top 5 methods for the KIRC data, namely, Pearson, Elastic, Z-score, ProMISe, and GenMiR++ and the predictions of top 4 methods for the TGCT data, namely Elastic, Z-score, ProMISe, and GenMiR++.

Figure 9 compares the precision of different variants of our proposed method with precision of TaLasso, GenMiR++, Pearson correlation and Borda integration. These plots clearly indicate that, in all experiments, the proposed supervised methods clearly outperform correlation and Borda integration. Comparing the supervised methods, it can be seen that the binary SVM classifiers trained with all features, TwoC_SVM_all, and trained with only binding features, TwoC_SVM_binding, are superior to the other methods. Following TwoC_SVM_all and TwoC_SVM_binding, OneC_SVM_binding has the largest precision in both data sets. However, OneC_SVM_all is clearly worse than OneC_SVM_binding, whereas the corresponding binary SVM models trained have similar precisions. Moreover, in both data sets, OneC_SVM_net has the worst performance, and is even worse than TaLasso and GenMiR++. Finally the performance of TwoC_SVM_net appears to be most variable in different data sets and different network reconstructions. In general, compared to TaLasso and GenMiR++, TwoC_SVM_all/TwoC_SVM_binding have higher precision in identifying validated miRNA-mRNA interactions; the improvement is from 30% to 50% in the two data sets. In addition, in both data sets, differences between precisions of TwoC_SVM_binding and TwoC_SVM_all are somewhat negligible. Finally, it can be seen that for the most part, binary SVMs work better than unary SVMs for all groups of features. This superiority can be attributed to the impact of using the negative examples.

Figure 9:

Comparison of Precisions of the proposed methods with competing approaches. (a) TGCT network from ARACNE; (b) TGCT network from WGCNA; (c) KIRC network from ARACNE; (d) KIRC network from WGCNA.

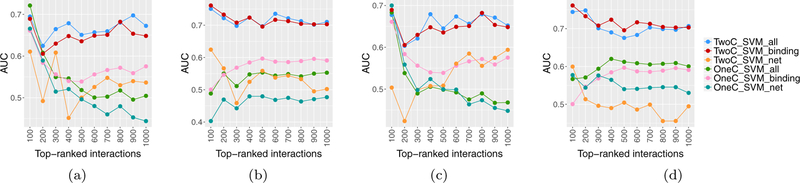
To better assess the performance of miRNA-mRNA prediction methods, we also calculated the area under the ROC curves (AUC) over the test data. (The ROC curves are presented in the Appendix B.) AUCs for TGCT and KIRC data sets are shown in Figure 10. It can be seen that in TGCT data, AUC values for TwoC_SVM_all are slightly better than TwoC_SVM_binding; however, in the KIRC data, the results from these two methods are mixed.

Figure 10:

Obtained AUC values of SVM classifiers. (a) Network constructed by ARACNE, TGCT data; (b) Network constructed by ARACNE, KIRC data, (c) Network constructed by WGCNA, TGCT data; (d) Network constructed by WGCNA, KIRC data.

3.3. Effects of Different Types of Features on Discriminating Validated and Non-validated Interactions

Motivated by the results from the previous section, in this section we examine the predictive power of each group of features is in discriminating validated miRNA-mRNA interactions.

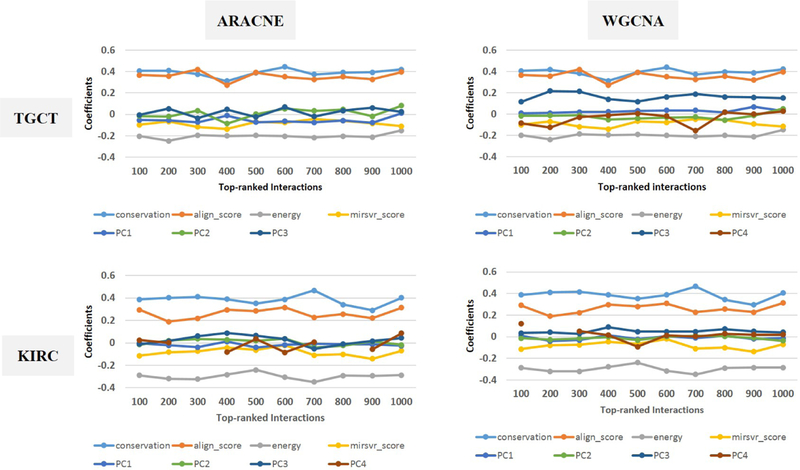
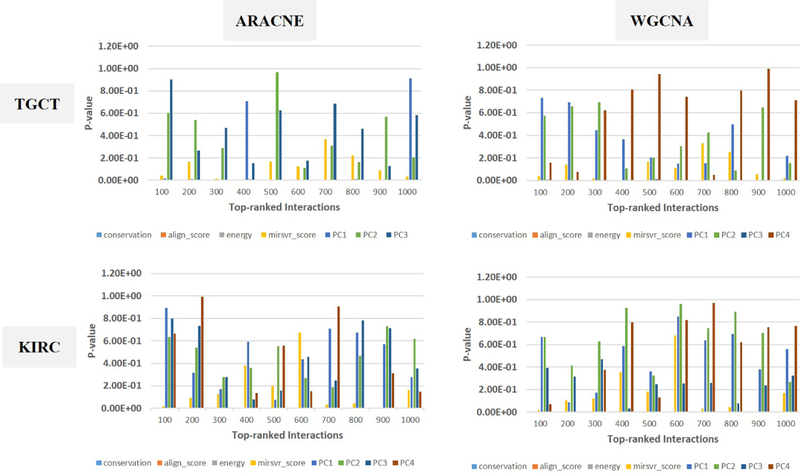
Figures 11 and 12 show results of tests based on logistic regression to examine the predictive power of each group of features. It can be seen that, with the exception of mirSVR score, other network features (i.e., those starting with ‘PC’) have very small coefficients (Figure 11) with non-significant p-values (Figure 12) compared to binding features. These results suggest that in presence of target site binding features, network features do not contribute to improve discrimination of validated interactions. In the other words, the connectivity patterns of genes considered here do not help identify miRNA-mRNA interactions. Note that discontinuities of curves in Figure 11, e.g. for KIRC and ARACNE, correspond to cases where PC4 is not represented in the 300 top-ranked interactions. In this case, only the first three PCs have been used in the prediction model. The corresponding p-values are also not shown in Figure 12.

Figure 11:

Coefficients corresponding to each feature in the logistic regression model.

Figure 12:

p-values corresponding to coefficients of logistic regression model.

4. Discussion

We examined whether a new prediction method utilizing both unsupervised and supervised approaches could improve the accuracy of miRNA target prediction. Our unsupervised learning method uses an ensemble approach, and combines results of two well-known miRNA target prediction algorithms that utilize expression profiles. Our supervised learning methods utilize additional features of binding sites and genetic networks. To assess the utility of negative examples in miRNA target prediction, we trained both unary and binary SVM classifiers using these features and compared their performances. The results indicate that our proposed method can boost the precision of miRNA target prediction up to 50%. This improved precision narrows down the primitive predicted interactions and reduces the time and cost required to validate interactions through laboratory experiments. Identification of such interactions can lead to design of novel AMOs that can control the expression of target genes and can be used for therapeutic purposes.

By comparing binary and unary SVMs we also showed how the construction of the training set can affect the results of classification. In all our settings, binary classification gave better predictions than unary classification. Finally, we also tested the predictive impact of binding and network features on binary classification results using a test based on logistic regression. The results show regardless of the construction method, genetic network features do not contribute to binary classifiers beyond what is achieved using binding features.

Two possible extensions of the proposed method may improve the performance and reliability of miRNA target prediction. First, here we utilized a limited number of binding and network features. Adding new features of miRNA-mRNA interactions, may improve the prediction performance. Second, our unsupervised learning step uses a consensus learning method based only on two existing methods. However, the accuracy and reliability of consensus methods can be improved by expanding the set of learning methods used [44, 45]. It may thus be beneficial to include additional miRNA-mRNA interaction learning methods in the proposed consensus learning approach.

Biographies

Nafiseh Sedaghat received the B.S. degree in computer engineering from Ferdowsi University of Mashhad, Iran, in 2003 and the MS degree in computer engineering specialized in artificial intelligence from Islamic Azad University, Mashhad branch, Iran, in 2010. She has started her PhD study in artificial intelligence in 2010 in Iran University of Science and Technology (IUST), Iran, in 2010. In 2014, she has attended in Department of Biostatistics, University of Washington, WA, USA, for 7 months as an intern. Her research interests include analysis of biological data and biological networks, e.g. gene networks and miRNA-mRNA interactions.

Mahmood Fathy received the B.S. degree in electronics from Iran University of Science and Technology (IUST), Tehran, Iran, in 1984, the M.S. degree in computer architecture from Bradford University, U.K., in 1987, and the Ph.D. degree in image processing computer architecture from the University of Manchester Institute of Science and Technology, U.K., in 1991. Currently, he is a faculty member of Department of Computer Engineering at IUST. His research interests include the quality of service in computer networks, image and video processing, as well as machine learning applications in bioinformatics.

Mohammad-Hossein Modarressi, M.D. Ph.D., is a professor of Human Genetics at Tehran University of Medical Sciences. His work focuses specifically on the genes and miRNAs are involved in testis (spermatogenesis) and Cancer. He is a scientific member of National biosafety council and Medical Genetics Board of Iran. Prof. Modarressi is Vice-Chancellor for Research and Technology in Science and Research Branch of Islamic Azad University. Genome-Nilou Medical Diagnostic Laboratory in Iran has been founded by him.

Ali Shojaie is an Associate Professor of Biostatistics and Adjunct Associate Professor of Statistics at the University of Washington. Dr. Shojaie’s research lies in the intersection of machine learning for high-dimensions data, statistical network analysis, and applications in biology and social sciences. Dr. Shojaie’s team develops methods for network-based analysis of diverse “omics” data, as well as inference procedures for high-dimensional models.