Methods for Accommodating Nonproportional Hazards in Clinical Trials: Ready for the Primary Analysis?

INTRODUCTION

Evaluation of new anticancer therapies in randomized clinical trials (RCTs) is typically based on comparing a new treatment with a standard one, using a time-to-event end point such as overall survival or progression-free survival (PFS). Although the statistical framework underlying the design of these RCTs is centered on formal testing of a treatment effect, methods for estimation (quantification) of the treatment benefit are also specified. Currently, log-rank statistical tests and/or proportional hazards models are commonly used for the trial design and primary analysis. These methods are optimized for treatment effects that do not change substantially over time (the proportional hazard assumption).

Introduction of immunotherapeutic agents with potentially delayed treatment effects has renewed interest in statistical methods that can better accommodate general departures from proportional hazards and, particularly, a delayed treatment effect. This has led to considerable attention in, and some controversy about, appropriate statistical methodology for comparing survival curves, as demonstrated by the comments and replies on trial reports^1-24 and at a Duke–US Food and Drug Administration workshop²⁵ that offered alternatives to the standard log-rank/hazard-ratio methodology. While these new methods could be useful, as outlined in comprehensive reviews,^26-30 we offer a caution about some of these methods’ limitations in translating statistical evidence into clinical evidence, both for formal treatment-effect hypothesis testing and for estimation (when used for the primary analysis).

TESTING TREATMENT EFFECTS

The two most commonly discussed treatment-effect testing approaches developed to be sensitive to departures from the proportional hazards assumption are based on weighted log-rank tests and restricted mean survival times (RMSTs). Weighted log-rank tests allow one to give more weight to emphasize a particular part of the survival curve, in contrast to the standard log-rank test, which weights all parts of the survival curves equally. For example, one of the first weighted log-rank tests, the generalized Wilcoxon test,^31,32 gives more weight to the early portions of the survival curve and thus is sometimes recommended for situations in which the treatment effect may dissipate over time.³³ In addition to the early-emphasis Wilcoxon test $(G^{1,0}$), the general family of weighted log-rank tests³⁴ includes the standard log-rank test and a late-emphasis test ($G^{0,1}$), which gives more weight to the later portions of the survival curves. Accordingly, the late-emphasis test has been suggested for situations in which the treatment effect potentially may be delayed.^26,35

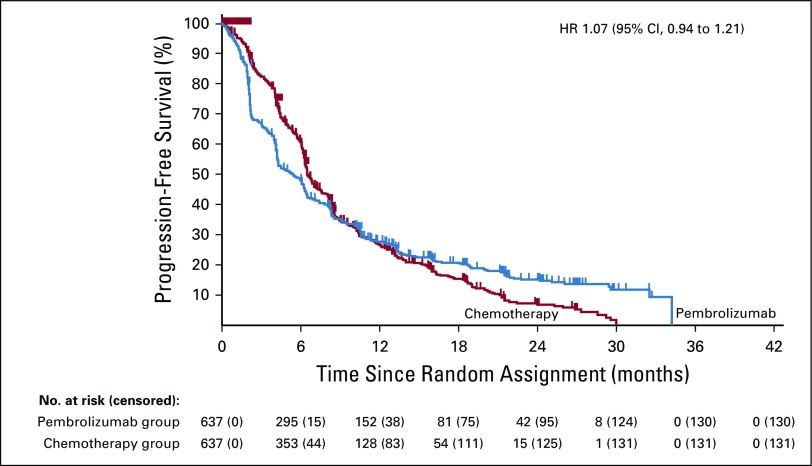
As an example, consider the PFS curves from the KEYNOTE-042 trial³⁶ (Fig 1), which compared pembrolizumab with chemotherapy in first-line, metastatic non–small-cell lung cancer. This is a good example for evaluating alternative methods, because the observed survival curves cross, implying nonproportional hazards. The standard log-rank test is not significant with a hazard ratio (HR) estimate of 1.07. Using the late-emphasis test in this immunotherapy setting allows one to focus the comparison of the separation in the tails of the PFS curves, rejecting the null hypothesis in favor of pembrolizumab with a one-sided P < .0001 (individual patient data are reconstructed³⁷ from Fig 1). The drawback with this approach, however, is that if the treatment effect is not delayed, then using the late-emphasis test will result in a considerable loss of power as compared with the standard log-rank test. Moreover, because it down-weights the early events, the late-emphasis test does not properly account for existence of early harm, potentially leading to clinically incorrect conclusions. For example, it is possible to have the experimental-arm survival curve always below the control-arm curve but with the late-emphasis test rejecting the null hypothesis in favor of the experimental-treatment arm (Fig A1).

FIG 1.

Progression-free survival curves for patients with non–small-cell lung cancer in the KEYNOTE-042 trial for the PD-L1 TPS 1% or greater population. This is Figure 3C from Mok et al.³⁶ The individual patient data were reconstructed by digitizing the progression-free survival curves using WebPlotDigitizer (https://automeris.io/WebPlotDigitizer/) and then using the algorithm from Guyot et al.³⁷ All statistical tests presented in this paper were done using these reconstructed data. HR, hazard ratio.

To avoid the potential loss of power with using the late-emphasis test, numerous versatile testing procedures have been developed that involve multiple weighted log-rank tests.^38-40 For example, Karrison⁴⁰ suggested using the maximum of the log-rank, early-emphasis, and late-emphasis tests as the test statistic. However, as noted by Karrison,⁴⁰ these tests can reject the null hypothesis both in favor of the experimental treatment and in favor of control treatment on the same data. Indeed, when applied to KEYNOTE-042^36,37 to test the superiority of pembrolizumab, the maximum test rejects the null hypothesis in favor of pembrolizumab (one-sided P < .0001); at the same time, when applied to the same data to test the superiority of chemotherapy, the maximum test rejects the null hypothesis in favor of chemotherapy (one-sided P < .0001). The same result is obtained from the Max-Combo test,²⁵ which additionally includes a test (G^1,1) that gives more weight to the middle portion of the survival curves. This is an unfortunate situation, given that there would not appear to be any clinically meaningful overall advantage established for either arm. (Note that although the curves suggest a potential subpopulation that may benefit from pembrolizumab, this subpopulation needs to be prospectively identified to improve treatment.)

The other commonly discussed approach to accommodate nonproportional hazards is the RMST, which graphically corresponds to the area under the Kaplan-Meier curve over a specified time.τ.^41-44 An RMST test is based on the area between the experimental arm and the control arm Kaplan-Meier curves up to time τ: the larger the area, the greater the treatment effect. Although there is no proportional hazards assumption required for this analysis, it does have the major limitation that the area between the curves is only calculated up to a specified time τ, and the statistical significance of the results depends on the chosen τ.^16,22 For example, in comments^1,6,8,12,21 on trial reports published in Journal of Clinical Oncology that suggested using the RMST, the chosen τs were 15, 21, 24, 45, 48 and 108 months. Because the selection of τ in these comments appears to be based on the observed Kaplan-Meier curves, the statistical significance quoted for the RMST is potentially exaggerated if the τs were chosen to maximize the statistical significance. On the other hand, prospectively selecting τ before the study starts can be challenging because of the uncertainties about what the survival curves will look like, and a poor choice could result in dramatically reduced power.

To address the difficulty of choosing τ for the RMST methodology, versatile RMST methods have been developed to allow choosing from a range of τ values to maximize the observed treatment-arm difference while accounting for this data-driven choice of τ in the calculation of the P value.^29,45 Although these methods will produce a valid P value in terms of type 1 error, they have the same flaw as the versatile weighted log-rank tests: They can sometimes yield a statistically significant result that is clinically meaningless by focusing exclusively on a particular part of the survival curves. For example, application of a versatile RMST procedure⁴⁵ to KEYNOTE-042 data (Fig 1)^36,37 rejects the null hypothesis that the curves are equal in favor of chemotherapy, with a one-sided P < .0001; this is because the procedure intentionally selects the chemotherapy-arm advantage in the first 8 months as the most statistically relevant portion of the curves.

Modern definitive (ie, phase III) RCTs follow a set of design and conduct practices (eg, prespecification of a primary outcome, formal interim analysis plans, sample size with sufficient power against clinically meaningful alternatives) that ensure a statistically significant result will correspond to a clinically significant result (with few exceptions).⁴⁶ Thus, one should be cautious about abandoning the log-rank test in favor of tests that can squeeze out more statistically significant results from observations that have no clinical significance. In specific situations where the clinical interest focuses on a specific aspect of the survival curves, an appropriate test should be used regardless of whether there are proportional hazards. For example, in RTOG-0534,⁴⁷ for patients with prostate cancer with an increasing prostate-specific antigen level after prostatectomy, the primary end point was the freedom from biochemical progression at 5 years, because it was thought that short-term delays in progression were not as clinically relevant as long-term freedom from progression. In other situations in which it is known that the intervention cannot affect early events, a weighted log-rank test that down-weights early events may also be appropriate. Examples include some screening trials (eg, National Lung Screening Trial⁴⁸) and prevention trials (eg, Women’s Heath Trial).⁴⁹

ESTIMATION OF TREATMENT EFFECTS

Even with proportional hazards, the HR is not a particularly intuitive measure of treatment effect. (The exception is when the survival curves are approximately exponential in shape, in which case the HR is the ratio of the control and experimental arm medians.) RMST-based approaches are among several possible summary measures that may complement the estimated HR.³⁰ However, contrary to its proponents,^28,50,51 we find it lacking as a particularly insightful summary of the clinical benefit of an experimental treatment. First, although mathematically well defined, the notion of a restricted mean has no common-sense interpretation: What is the clinical interpretation of “the mean survival time to some prespecified time point [τ]”⁵⁰? Second, use of RMST for estimation requires prespecification of τ, which can dramatically change the value of the estimated treatment effect. For example, consider an RCT in which 70% of patients in the control arm and 90% of those in the experimental arm are cured at 2 years (and the curves are approximately exponential up to 2 years): the RMST difference is 2.6, 5, and 7.4 months when τ is 2, 3, and 4 years, respectively. Given these changing values, it is not clear how the approach elucidates the clinical impact of the 20% increase in cure rates.

As with other summary measures, the RMST value without the context of the survival curves could be misleading about clinical significance of the experimental treatment. For example, consider a trial in which metronomic chemotherapy was compared with placebo in progressive pediatric malignant solid tumors.⁵² No significant improvement was reported for the metronomic therapy, with median PFS of 49 and 46 days in the experimental and control arms, respectively (HR, 0.69; 95% CI, 0.47 to 1.03; log-rank P = .07). An RMST reanalysis¹⁰ reported a 0.8-month difference in PFS RMST (2.4 v 1.6 months for the metronomic and placebo arms, respectively), which was statistically significant (P = .02). Fang et al¹⁰ concluded that their RMST analysis “provided a more clinically meaningful interpretation of the treatment effect.” Given absence of any clinically meaningful differences in the observed PFS curves,⁵² one would have to agree with Pramanik et al¹¹ that regardless of the statistical significance, “this meager difference between mean survivals may remain clinically unimportant.”

In another example, a trial evaluating the efficacy of neratinib after trastuzumab-based adjuvant therapy in early-stage HER2-positive breast cancer⁵³ reported a disease-free survival HR of 0.67 (log-rank P = .0091). In their reanalysis, Hasegawa et al⁴ noted that the observed HR of 0.67 corresponds to just a 0.5-month improvement in RMST disease-free survival (from 23.0 to 23.5 months) and suggested that this improvement was of “debatable advantage.” In response, Chan et al⁵ noted that the RMST analysis used a τ of 24 months. This implies that the maximum possible RMST is 24 months (which would be if all experimental patients were cured), so the maximum possible improvement in RMST is 1.0 month (from the 23-month RMST observed in the control arm). Therefore, the observed 0.5-month improvement in the neratinib arm represents 50% of the maximum possible effect (ie, everybody is cured)—an improvement that would seem of clinical significance.

Kaplan-Meier curves (with CIs) for the experimental and control arms of an RCT offer a comprehensive display of the experimental-arm effectiveness. Trying to reduce these curves to a single summary of treatment benefit is challenging. Although the clinical utility of an estimator is somewhat in the eyes of the beholder, we are unimpressed by the RMST ability to consistently capture the magnitude of clinical benefit across clinical settings.

To our knowledge, the use of HRs and log-rank tests as primary analysis tools has not impeded the development, testing, and acceptance of effective oncologic therapies (eg, the checkpoint inhibitors). When there are concerns about delayed treatment effects and/or long-term cures, log-rank–based designs with slightly inflated sample size (10%),⁵⁴ additional follow-up,²⁷ and modified interim futility analyses^27,55 can provide robust power. Methods for accommodating nonproportional hazards such as RMST, weighted log-rank tests, and others^56-59 can be useful secondary analyses because it is often difficult to have a single summary measure to accurately reflect the totality of clinical effect. However, before abandoning log-rank test–based primary analyses of definitive RCTs, we will need to see more convincing evidence of how these alternative methods can improve development of effective cancer therapies.

APPENDIX

FIG A1.

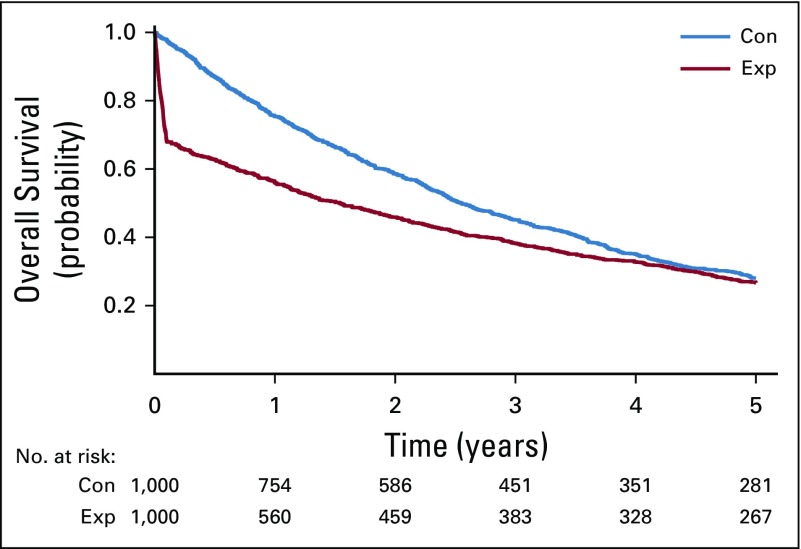
An example of a hypothetical randomized clinical trial where the survival curve for an experimental arm (red line) is always below the control arm curve (blue line) yet the late-emphasis test (G^0,1) rejects the null hypothesis in favor of the experimental arm with one-sided p-value of 0.0046. The trial data were generated assuming 1000 patients per arm with instant accrual and 5 years of follow-up; in the control arm survival was assumed to follow an exponential distribution with constant hazard of 0.25, in the experimental arm survival was assumed to follow a piecewise exponential distribution with a hazard of 4 in the first 1.2 months and a hazard of 0.19 after the first 1.2 months.

AUTHOR CONTRIBUTIONS

Conception and design: All authors

Financial support: All authors

Provision of study material or patients: All authors

Collection and assembly of data: All authors

Data analysis and interpretation: All authors

Manuscript writing: All authors

Final approval of manuscript: All authors

Accountable for all aspects of the work: All authors

AUTHORS' DISCLOSURES OF POTENTIAL CONFLICTS OF INTEREST

Methods for Accommodating Nonproportional Hazards in Clinical Trials: Ready for the Primary Analysis?

The following represents disclosure information provided by authors of this manuscript. All relationships are considered compensated unless otherwise noted. Relationships are self-held unless noted. I = Immediate Family Member, Inst = My Institution. Relationships may not relate to the subject matter of this manuscript. For more information about ASCO's conflict of interest policy, please refer to www.asco.org/rwc or ascopubs.org/jco/site/ifc.

Open Payments is a public database containing information reported by companies about payments made to US-licensed physicians (Open Payments).

No potential conflicts of interest were reported.