Single-cell activity tracking reveals that orbitofrontal neurons acquire and maintain a long-term memory to guide behavioral adaptation

Abstract

Learning to predict rewards based on environmental cues is essential for survival. The orbitofrontal cortex (OFC) contributes to such learning, by conveying reward-related information to brain areas such as the ventral tegmental area (VTA). Despite this, how cue-reward memory representations form in individual OFC neurons and are modified based on new information is unknown. To address this, using in vivo 2-photon calcium imaging in mice, we tracked the response evolution of thousands of OFC output neurons, including those projecting to VTA, through multiple days and stages of cue-reward learning. Collectively, we show that OFC contains several functional clusters of neurons distinctly encoding cue-reward memory representations, with only select responses routed downstream to VTA. Surprisingly, these representations were stably maintained by the same neurons even after extinction of the cue-reward pairing, and supported behavioral learning and memory. Thus, OFC neuronal activity represents a long-term cue-reward associative memory to support behavioral adaptation.

Animals can learn and remember multiple features of cue-reward associations such as the specific type of reward predicted by a cue (e.g. banana or apple), the probability of receiving that reward given the cue, the magnitude of the reward, the delay to the reward, the average value of the cue given its associated reward, and/or the state-space¹ of the cue-reward association (i.e. the set of rules governing the association; e.g. the cue predicts the reward only in a specific context). Multiple such representations have been associated with the OFC^2–5 and perhaps for this reason, cross-species studies have implicated the OFC in a wide array of functions, including reversal learning^6,7, contingent learning^8,9, value representation^3,6,8,10,11, state representation^1,12,13, uncertainty/confidence estimation^14,15, reward seeking^16,17, imagination of unexperienced outcomes^18,19, and more. Nevertheless, how representations of distinct features of a cue-reward association evolve during learning within individual OFC neurons, and, whether these representations provide a long-term memory of the association at a single-neuron and population level even after changes in the original association, are unknown.

Investigating these questions requires overcoming two major technical challenges in recording neuronal activity. First, to study response evolution during learning and subsequent maintenance of learned responses, it is essential to longitudinally track the activity of the same set of neurons across days of behavioral learning and/or performance. Second, to address whether unique subpopulations acquire distinct memory representations, it is important to sufficiently sample such heterogeneity by recording from large numbers of neurons, including projection-defined subpopulations. For instance, while it is thought that OFC mediates learning by conveying cue-reward information to VTA—a critical regulator of learning containing neural correlates of reward prediction error²⁰—it is unknown whether select representations within OFC output neurons are relayed to VTA. Thus, in order to longitudinally track activity in large numbers of neurons, including projection-defined ones, we used two-photon calcium imaging²¹. We did so during a discriminative Pavlovian trace conditioning task that requires both within-trial memory of a previously presented cue during the trace interval, and long-term memory of learned cue-reward associations. This task is ideal to investigate the aforementioned questions as it can be learned quickly by mice, thereby allowing longitudinal tracking of neurons during and after learning²².

Such large-scale longitudinal recording, along with unsupervised approaches for classification of response patterns, allowed us to demonstrate that putative OFC projection neurons contain distinct functionally-identifiable subpopulations with different response types, and that select associative information is conveyed by direct projections from OFC to VTA. The large-scale longitudinal tracking further allowed us to evaluate OFC neuronal response dynamics during different phases of learning, including a phase in which the cue-reward association was experimentally extinguished. This revealed that OFC subpopulations convey a long-term memory of the original cue-reward association even after it is changed, both at individual neuronal and population level. Additional experiments showed that encoding in some clusters was consistent with the forward and reverse probability of state transitions between a cue and reward, and that they collectively support learning and memory.

Results

Distinct clusters of OFC neurons represent a learned cue-reward association

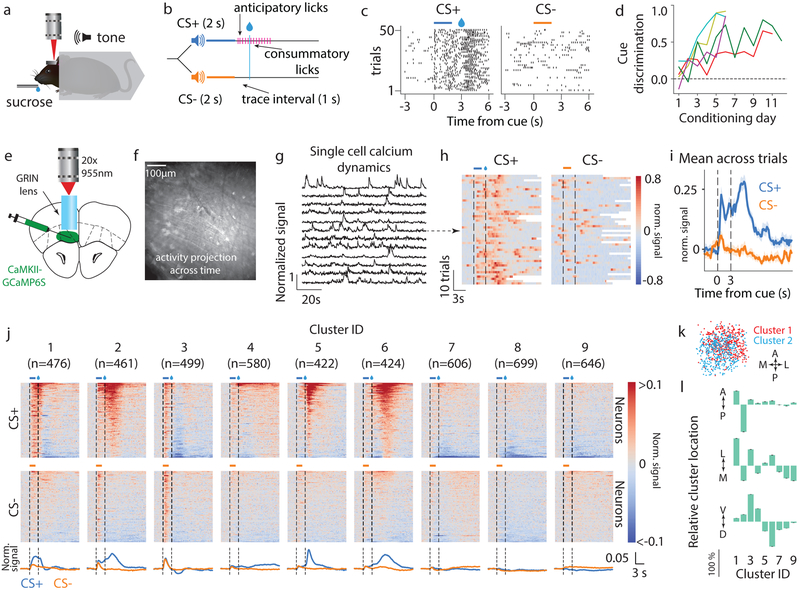
We trained mice on a Pavlovian cue-reward association task (Fig 1a–c). Mice learned to lick in response to an auditory conditioned stimulus (CS+) predicting sucrose reward, but not another stimulus (CS-) predicting no reward (Fig 1d)²². Importantly, there was a one second trace interval following the offset of these stimuli/cues until reward delivery (CS+ trials) or omission (CS- trials). This period allowed us to measure responses indicative of the cue-reward association after termination of the sensory stimulus. Throughout learning, we imaged calcium dynamics from putative OFC output neurons in the medial sub-region of OFC (containing medial and ventral orbital; labeled vmOFC henceforth)²³. These neurons expressed the fluorescent calcium indicator GCaMP6S via viral transduction (AAVdj-CaMKIIα-GCaMP6S)²⁴ (Fig 1e–i, Supplementary Video 1). We were able to validate ex vivo that the fluorescent dynamics of GCaMP6S-expressing neurons allow decoding of spiking activity (Supplementary Fig 1). After learning, the activity of individual neurons generally showed considerable trial-to-trial variability and heterogeneous time-locked responses to cues, which were not merely due to the lick responses previously reported in OFC (Supplementary Fig S2)²⁵. To obtain an unbiased evaluation of the heterogeneity in responses across the population, we used an unsupervised clustering algorithm¹⁵ to group the average CS+ and CS- triggered peri-stimulus time histograms (PSTH) of all recorded neurons after behavioral learning (n=4813 from n=5 mice, Supplementary Fig 3). This approach revealed 9 clusters of neurons based on responses (Fig 1j, Supplementary Fig 3). Each of these 9 clusters was generally separable in a high-dimensional principal component space from every other cluster (Supplementary Fig 4), supporting the idea that functionally distinct cell types differentially encode cue-reward response dynamics.

Fig. 1. vmOFC CaMKIIα-expressing (OFC-CaMKII) neurons display heterogeneous response profiles reflecting cue, reward, and associative information following behavioral acquisition.

a. Headfixed Pavlovian conditioning, b. Task schematic, c. Example behavioral session from a trained animal showing anticipatory licking to CS+ but not CS-. d. Evolution of behavioral discrimination between cues (Methods) for 5 individual mice from whom imaging data were acquired. e. Schematic of imaging, f. Example standard deviation projection of activity across time from a trained animal. g. Example calcium dynamics showing normalized fluorescence signal (Methods). h. Example neuron’s (arrow) normalized fluorescence signal aligned to cue (peristimulus time histogram, or PSTH) with trials sorted by delay to first lick (see Supplementary Fig 2 for licking behavior and more example neurons). White bars indicate start of next trial. i. PSTH showing mean normalized signal across n=50 trials. Shaded region is standard error of the mean. Please note that we show PSTHs only to provide a visualization of raw data, and not as a directly analyzable signal (Methods). j. Classification of neurons into 9 response clusters based on their trial-averaged activity after animals were trained (Methods, Supplementary Fig 3, 4). PSTHs of individual neurons are shown and sorted on the y-axis. Bottom traces represent population average within each cluster. Clusters are ordered by mean activity between cue and reward. k. Relative spatial location across field of view for two example clusters (A: anterior, P: posterior, M: medial, L: lateral, Methods). l. Relative percentage shift in the mean location of a cluster with respect to the mean of all neurons, normalized to the cluster with the maximum shift along each cardinal axis (D: dorsal, V: ventral, raw data in Supplementary Fig 3e). Error bars represent standard error of the mean. Statistical results are in Supplementary Table 1 for all figures.

The responses of clusters 2, 5 and 6 qualitatively replicate prior studies showing elevated responses to rewarded cues compared to unrewarded cues, and positive reward responses^10,26–29. The slight negative CS+ responses of clusters 7, 8 and 9 are consistent with additional prior observations of negative responses to rewarded cues^16,29. Nevertheless, we also observed other unique response patterns. For instance, cluster 1 showed a large selective positive response to CS+ throughout the cue-reward delay, but also a suppression after reward delivery. Clusters 2 and 3 showed largely similar responses to CS+ and CS- immediately after cue presentation. Cluster 3 also showed non-selective trace interval response and a large negative reward response. Lastly, cluster 4 showed sustained positive responses following reward that distinguished between CS+ and CS- trials. Overall, these findings suggest that there are separable and unique clusters of neurons based on their response patterns and that they may have unique roles in learning and memory. Consistent with this, the mean spatial locations of these clusters were statistically distinct along all three cardinal axes (Fig 1k,l, p<10⁻¹⁰, n=4460 neurons, see Supplementary Table 1 for a compilation of all statistical results in the manuscript, including all statistical details). For instance, clusters that typically responded with an increase in activity during CS+ were found to be more ventral within vmOFC, whereas clusters with lower activity or suppression during CS+ were found to be more dorsal (Fig 1l).

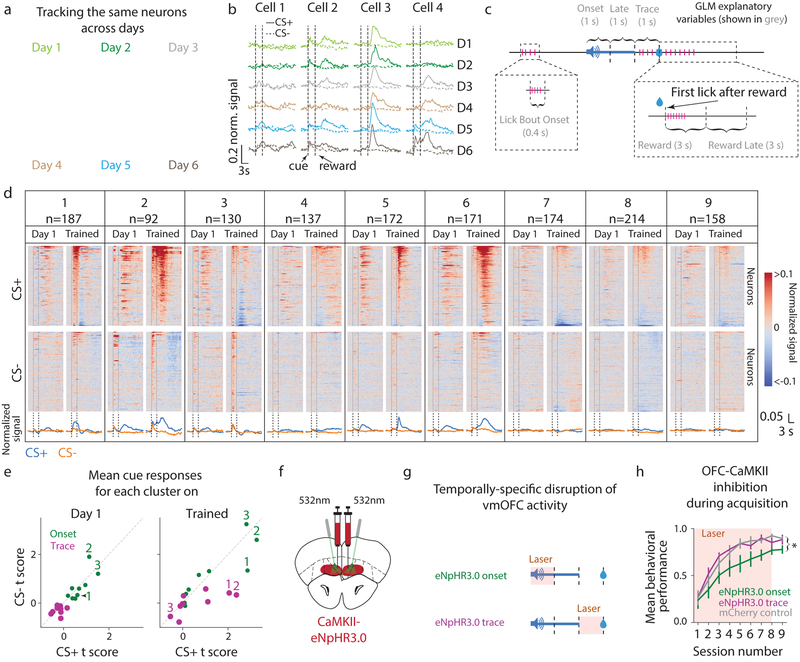
While these results suggest the presence of distinct subpopulations of vmOFC output neurons, whether these responses arise during the course of learning or exist prior to learning is unknown. To investigate this, we compared responses from the same longitudinally-tracked neurons before and after learning (n=1435 tracked from n=5 mice, Fig 2a, b, Supplementary Video 2). To quantify neuronal responses, we deconvolved fluorescence traces to remove changes in fluorescence due to the slow dynamics of the calcium indicator³⁰ (Supplementary Fig 5). To account for cue, licking, and reward-related activity, we then used a multiple linear regression/general linear model (GLM) fit of deconvolved fluorescence (Fig 2c, Supplementary Fig 5, Methods). The responses of all clusters of neurons (defined based on responses after acquisition) were largely similar to each other prior to acquisition, both during the “cue onset” period (a label to define a one second time period after cue onset) and the trace interval (Fig 2d, e, Supplementary Fig 6). After learning, cue onset responses, especially of clusters 2 and 3, remained similar to both CS+ and CS-, whereas trace responses of most clusters evolved distinct responses to CS+ and CS-. We will henceforth refer to neural activity that does not distinguish between a cue associated with a reward and another cue that is not associated with a reward as “cue-reward association-insensitive” or in short, “association-insensitive”. We will also label activity that distinguishes between these cues as “cue-reward associative”, or in short, “associative”. Thus, some vmOFC neurons, especially those in clusters 2 and 3 but not 1, convey association-insensitive information during the cue onset period. Further, vmOFC neurons across most clusters evolved trace responses reflecting associative information.

Fig. 2. vmOFC neuronal activity exhibits cue onset responses, and evolves responses reflecting cue-reward associations during behavioral acquisition.

a. Activity projection images from one animal (yellow in Fig 1d) showing that the same cells can be tracked across days. b. Example neurons’ PSTH around cues shown for every day of behavior from naïve to trained (CS+ solid, CS- dashed) c. Schematic of the epochs analyzed using a GLM (Methods) fit to individual neurons’ deconvolved fluorescence. d. PSTHs on Day 1 and Trained, recorded from all longitudinally-tracked neurons. Neurons are sorted by their responses on Trained, with the same ordering maintained on Day 1. e. Mean GLM t scores (Methods) of responses across a cluster to CS+ and CS- during the onset (1 s after cue onset) or trace period. Three example clusters are labeled. It is possible that GLM estimates are biased against detecting suppression in activity (Supplementary Fig 1c) f. Schematic of optogenetic experiment to target OFC-CaMKII neurons. g. Schematic for temporally-specific disruption of vmOFC activity during either the cue onset or the trace interval epochs. h. Behavioral acquisition of reward seeking to CS+ while OFC-CaMKII neurons are inhibited during the cue onset or trace period, or in control animals without opsin expression (Methods). Inhibition during the cue onset period suppressed learning, but not expression of learned behavior (Supplementary Fig 7) Measure of center is the mean and error bars represent standard error of the mean. * represents p<0.05 (see Supplementary Table 1 for exact p values, sample sizes and tests).

In order to test whether inhibition of these temporally-specific activity patterns degrades behavioral acquisition, we optogenetically inhibited CaMKIIα-expressing vmOFC neurons within either the cue onset or trace periods during behavioral acquisition (Fig 2f–h). Interestingly, we found that optogenetic inhibition during the cue onset period, but not trace interval, blunted initial behavioral acquisition, with neither manipulation affecting behavioral performance after acquisition (Supplementary Fig 7). The optogenetic effect on behavioral acquisition may be either due to a disruption of association-insensitive cue onset responses such as in clusters 2 and 3 or associative cue onset responses of cluster 1. During the cue onset period, association-insensitive responses of clusters 2 and 3 contributed much more to the variance in activity (32.1% and 37.1% respectively) than cluster 1 (19.3%) (Supplementary Fig 6). Though this suggests that association-insensitive responses of clusters 2 and 3 contributed more to the optogenetic effect, directly testing between these hypotheses is currently technically infeasible. Thus, we decided to characterize the nature of these distinct responses (association-insensitive or associative) using projection-specific imaging and longitudinal tracking of these clusters.

Cue-reward associative, but not cue, information is relayed to VTA

OFC is thought to play a role in behavioral learning primarily through its interactions with the VTA dopaminergic system^31,32. Accordingly, prior studies have shown that inactivating lateral OFC disrupts encoding in VTA dopaminergic neurons^31,33, and that independently inactivating OFC or the VTA, or cross-hemispherically inactivating both, is sufficient to disrupt learning based on unexpected outcomes³⁴. However, OFC activity could influence VTA dopaminergic activity either through direct projections or indirectly through regions such as the nucleus accumbens³¹. Thus, whether direct projection neurons from OFC to VTA convey learning-related signals is unknown.

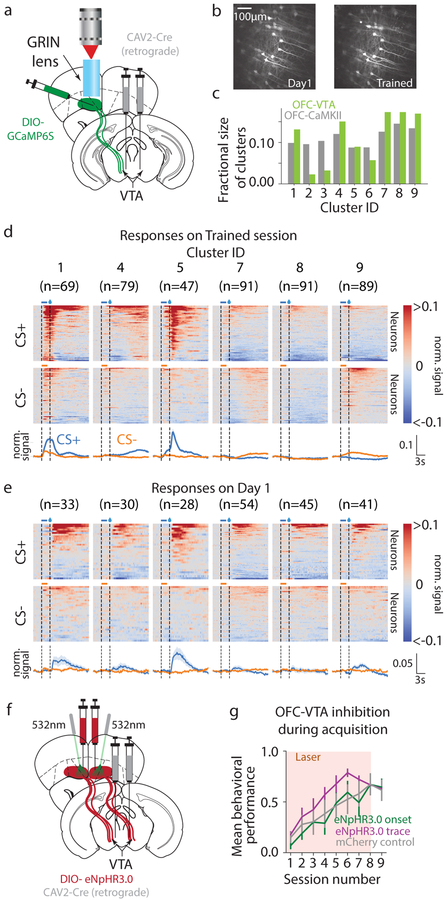
To test this, we investigated functional encoding in vmOFC neurons projecting to VTA (OFC-VTA) (Fig 3a, b, Supplementary Video 3, Methods, n=526 VTA projecting neurons from n=7 mice). OFC-VTA neurons largely comprised 6 to 7 clusters from the larger OFC-CaMKII population (Fig 3c, Methods). Anatomical studies suggested that OFC-VTA neurons were enriched more dorsally (deeper layers) in vmOFC (Supplementary Fig 8), consistent with the fact that the two clusters considerably impoverished in OFC-VTA neurons (clusters 2 and 3) were found ventrally in the OFC-CaMKII population (Fig 1l). These clusters were unique as they showed large association-insensitive cue onset responses (Fig 1j, Fig 2d, e). Thus, large association-insensitive cue onset responses are not present in the VTA-projecting population, as is especially clear from their absence on Day 1 of acquisition (Fig 3d, e, n=250 tracked VTA projecting neurons from n=7 mice, Supplementary Video 4).

Fig. 3. OFC-VTA neurons convey information selective to cue-reward associations.

a. Schematic of imaging experiment to record from vmOFC neurons projecting to VTA (OFC-VTA). b. Example activity projection maps of OFC-VTA cells on Day 1 and Trained. c. Fraction of neurons per cluster in OFC-VTA compared to OFC-CaMKII population. We restricted further analysis to those clusters in which we could identify at least 2 cells on average per animal in the imaging plane tracked over learning, which also excluded cluster 6 d. PSTHs during Trained session showing responses of clusters. e. PSTHs of neurons in these clusters on Day 1, showing the absence of cue onset responses. f. Schematic of optogenetic experiment to target OFC-VTA neurons. g. Behavioral acquisition of reward seeking to CS+ during inhibition of OFC-VTA neurons showed no effect during cue onset or trace periods. Reduced behavioral performance of all groups compared to OFC-CaMKII group is likely due to a difference in age (Methods). Measure of center is the mean and error bars represent standard error of the mean.

Since association-insensitive cue onset responses, especially in clusters 2 and 3, are absent in OFC-VTA neurons, but associative responses, including from cluster 1, are present, this presented an opportunity to test which of these responses mediate behavioral acquisition. We found that optogenetic inhibition of OFC-VTA neurons did not causally influence behavioral acquisition during the cue onset period (Fig 3f, g). Further, this manipulation also did not affect reward seeking after learning (Supplementary Fig 7). Hence, activity conveying associative, but not association-insensitive cue information, is routed to VTA, with this activity not contributing to behavioral acquisition or reward seeking.

Evolution of OFC associative responses generally lag behavioral acquisition

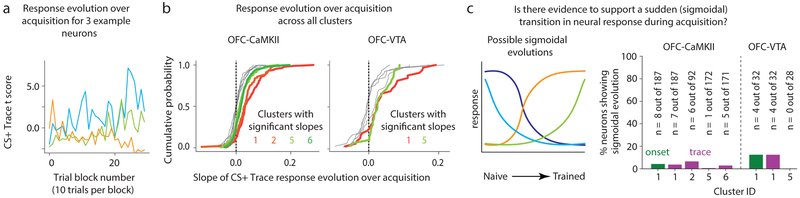
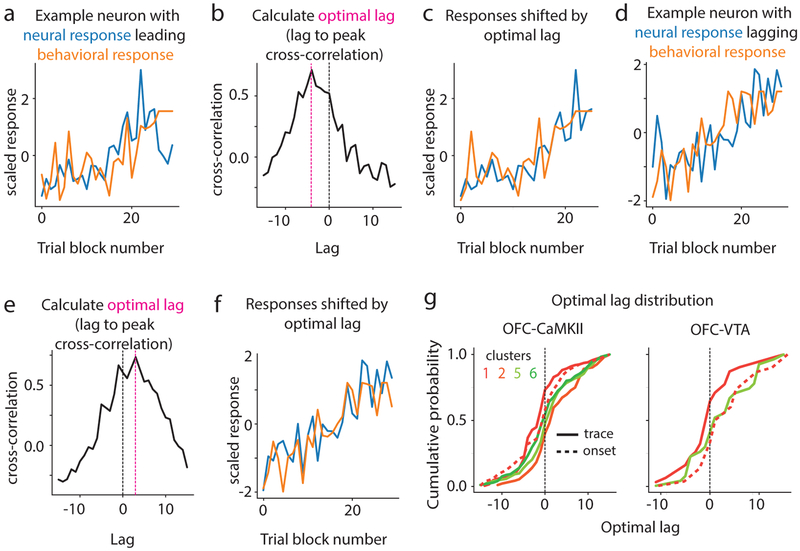
Associative responses reflect a cue-reward memory. Yet, whether these memory representations arise before or after behavioral acquisition is unknown. We addressed this question by focusing on clusters that showed significant change in their CS+ trace encoding during acquisition (labeled “learning-related clusters”), which we identified as clusters 1, 2, 5 and 6 in OFC-CaMKII neurons, and clusters 1 and 5 in OFC-VTA neurons (Fig 4a,b). Since cluster 1 showed evolution of associative responses also during the cue onset period (Fig 2), we investigated this evolution as well. By eye, the responses of most recorded neurons appeared to evolve gradually during acquisition without sudden transitions (examples shown in Fig 4a), which was confirmed quantitatively (Fig 4c, Methods). Therefore, we used a cross-correlation analysis to address whether response evolution for each neuron occurred earlier or later than the evolution of anticipatory licking across trial blocks (Fig 5a–f, Methods). A negative optimal cross-correlation lag meant that neural response evolution led, i.e. was earlier than, behavioral evolution and vice-versa. The distribution of lags for all neurons within a cluster for the learning-related clusters revealed that the trace interval response of cluster 1 led behavioral evolution whereas other clusters lagged behavior (Fig 5g). While this result is consistent with the hypothesis that associative activity of cluster 1 contributes to behavioral acquisition, inhibition of activity during the trace interval (which also contained these associative responses) did not slow behavioral acquisition (Fig 2h). Though inhibition during the cue onset period did indeed disrupt behavioral acquisition (Fig 2h), associative cue onset responses of cluster 1 did not significantly lead behavior. These results showed remarkable consistency between OFC-CaMKII and OFC-VTA neurons (Supplementary Fig 9). Thus, associative cue onset responses of cluster 1 likely do not support behavioral acquisition. Interestingly, we found that even reward responses reflected cue-reward memory, as these responses changed after learning (e.g. Fig 2d), with cluster-specific time courses of evolution (Supplementary Fig 9). Collectively, these results demonstrate unique learning dynamics for different vmOFC neuronal clusters, with most responses lagging behavior.

Fig. 4. Acquisition of associative responses is gradual and not sudden.

a. The CS+ trace GLM t score of 3 example neurons over trial blocks (~10 CS+ trials per block) of behavioral acquisition for three example neurons. Visually, it is apparent that these show gradual changes over acquisition. The slope of the best-fit line to these changes was used to quantify neuronal learning. b. The distribution of slopes of CS+ trace response evolution over acquisition for all neurons within a cluster for both OFC-CaMKII and OFC-VTA neurons. Clusters 1, 2, 5 and 6, and cluster 1 and 5 were found to have significant mean slope for the OFC-CaMKII and OFC-VTA neurons, respectively (“learning-related clusters”, see text). c. We tested whether there was sufficient support to claim a sigmoidal (sudden) transition in neural responses across behavioral acquisition. The left panel shows possible shapes for neuronal response evolution that are consistent with a sigmoidal model as opposed to a linear (gradual) model. The right panel shows the percentage of neurons with considerable support for sigmoidal evolution (Methods), showing that very few neurons had response evolution consistent with a sudden transition in responses. CS+ cue onset responses of cluster 1 were also analyzed since these contained associative information (see text).

Fig. 5. Different time courses of learning across clusters.

a. Behavioral evolution and the neural response evolution of an example neuron whose response evolution leads behavior. b. Cross-correlation analysis showing that peak cross-correlation is at a negative optimal lag, i.e. with neural response leading behavior. c. Behavioral and neural response evolution shifted by the optimal lag, showing high correlation. d-e. Same as a-c but for a neuron whose evolution lags behavior (positive optimal lag). g. Distribution of optimal lags for neurons within a cluster for the learning-related clusters of OFC-CaMKII and OFC-VTA neurons. Trace interval response of cluster 1 shows a significant negative mean lag, but no other response, including cue onset response of cluster 1, shows significant negative lag.

OFC neurons form distinct memory representations across clusters

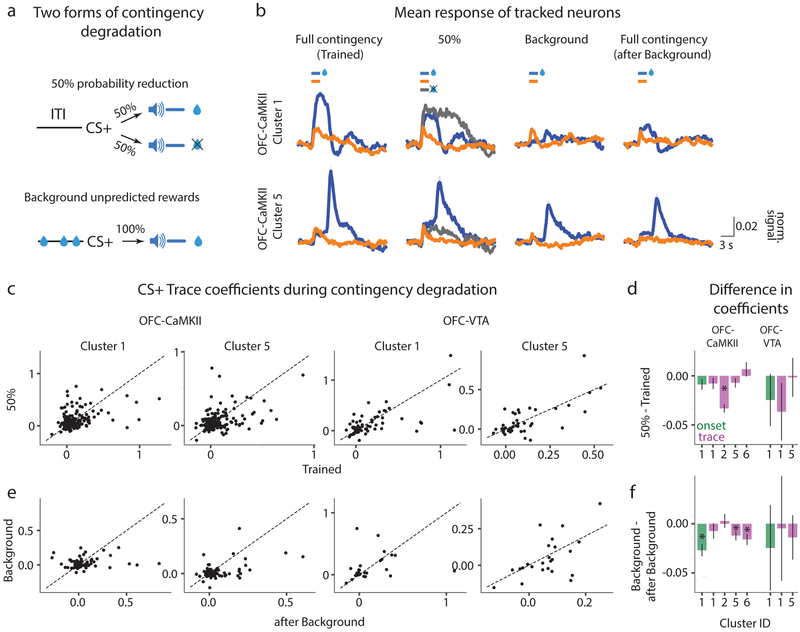
The above results raise a fundamental question: what do vmOFC associative responses represent? They could in principle represent the identity of reward predicted by CS+, magnitude, delay to or probability of the expected reward, or the value of CS+. In order to test for these representations, we performed two manipulations that degraded the contingency of the cue-reward association (Fig 6a). In one, we reduced the probability of reward delivery to 50% after CS+ presentation (50% session). This degradation affected the probability of the expected reward and the value of the cue, but not the identity, magnitude or delay of the expected reward. In the other, we maintained the probability of reward delivery at 100%, but introduced random unpredictable rewards during the inter-trial interval (background reward delivery session, henceforth “Background” session)^35,36. In these sessions, an average of 148 +/− 22 (standard deviation) rewards were unpredictable, while 60 were predictable, thereby making only 1 in 3.5 rewards predictable by the cue. Thus, this degradation changed the value of the cue with respect to the inter-trial interval, but did not affect the identity, magnitude, delay to or probability of expected reward.

Fig. 6. Differential sensitivities of clusters to two forms of contingency degradation.

a. The CS+-reward contingency was degraded in two ways. In one, the probability of reward was reduced to 50%. In the other, all features of the association including probability (100%), magnitude and delay of the reward were held constant, but random unpredictable rewards were delivered during the intertrial interval (Methods). b. Average PSTH across all neurons within a cluster for OFC-CaMKII clusters 1 (n=178 neurons tracked across all sessions) and 5 (n=168 neurons tracked across all sessions; shading is 95% confidence interval, see Supplementary Fig 14 for individual neuronal PSTHs from all learning-related clusters). These show the considerable reduction in CS+ responses in the Background session, which recovers in the after Background session (Methods). c. The GLM coefficients (see Methods) for every tracked neuron between the Trained and 50% session from clusters 1 and 5 for both OFC-CaMKII and OFC-VTA neurons. d. Average difference in GLM coefficients between 50% and the Trained sessions for both OFC-CaMKII and OFC-VTA learning-related clusters. e, f. Same as c and d for comparison between Background and after Background sessions. For d and f, measure of center is the mean and error bars represent standard error of the mean. * represents p<0.05 (see Supplementary Table 1 for exact p values, sample sizes and tests). See Supplementary Fig 10 for results from all clusters.

If the signals encoded in vmOFC generally represent reward probability given the cue, the encoding strength of all learning-related clusters should reduce in the 50% session. Instead, only cluster 2 showed reduction in associative encoding (Fig 6b–d, Supplementary Fig 10). Further, if the signals encoded in vmOFC indeed represented reward probability or other value-related features of this association such as the expectation, magnitude or delay of the reward given the cue, the Background session should not produce any changes in the encoding strength. Instead, all learning-related clusters except 2 showed significant recovery in encoding strength following the Background session (Fig 6b, e, f, Supplementary Fig 10, see Methods for rationale of experimental design). Thus, cue-reward associative responses in vmOFC clusters 1, 5 and 6, do not encode features such as probability, expectation, magnitude or delay of the reward, given the cue. Additional analyses, including of the reward receipt and omission responses, also showed that these responses are unlikely to represent value (Supplementary Fig 11) or prediction error (Supplementary Fig 12). Thus, associative encoding in clusters 1, 5 and 6 is not consistent with commonly assumed memory representations regarding cue-reward associations (see Discussion).

OFC memory representations show long-term maintenance after behavioral extinction

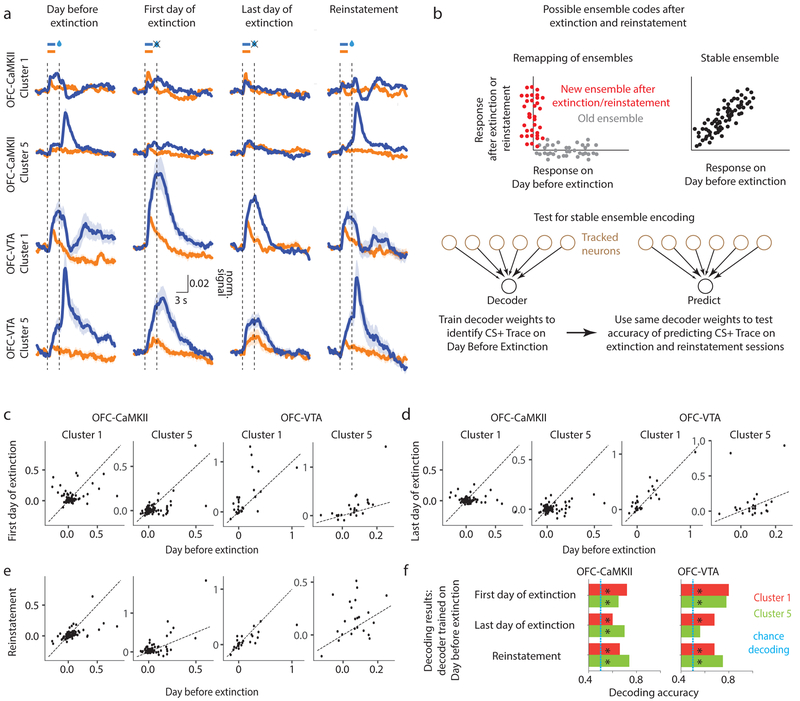
The insensitivity of some clusters to partial reinforcement in the 50% session raised the intriguing possibility that they might stably represent learned information even when the reward probability is extinguished to 0%. The average PSTHs across all neurons within a cluster suggested that the mean encoding might indeed be stable after extinction, especially in OFC-VTA neurons (Fig 7a). Decades of research show that extinction of a learned association is due to new neural learning, instead of unlearning³⁷. Accordingly, some neurons become selectively active only during/after extinction or subsequent reinstatement^38,39. A schematic of such new extinction learning is shown in Fig 7b (“Remapping of ensembles”), which results in stability of responses at the population-level, but not the single-neuron level. On the other hand, a long-term memory representation of the original cue-reward association would be stable both at the population and single-neuron level (Fig 7b, “Stable ensemble”). PSTHs for longitudinally-tracked neurons suggested that there might indeed be such a long-term memory correlate in OFC-VTA neurons (Supplementary Fig 13). To the best of our knowledge, such a direct correlate of a long-term cue-reward memory reflected in the activity of individual neurons has not previously been observed.

Fig. 7. Learned associative information is stably maintained after extinction, especially in OFC-VTA neurons.

a. Average PSTH of all neurons within a cluster (shading is 95% confidence interval) is shown for Day before extinction (same as “after Background” in Fig 6b), First day of extinction, Last day of extinction and Reinstatement (see Supplementary Fig 13 for PSTHs of individual neurons from all learning-related clusters). The magnitude of the CS+ trace interval responses is high even after extinction and reinstatement, especially for OFC-VTA clusters. n=(178, 168, 27, 23) tracked neurons across all sessions were included for clusters 1 and 5 from OFC-CaMKII and clusters 1 and 5 from OFC-VTA neurons. b. (Top) Schematic for two possible ensemble codes during extinction with each dot representing the response of a neuron. In one, there is a remapping of ensembles, such that a new ensemble represents the CS+-reward association after extinction. In the other, there is a stable ensemble representing the association after extinction. (Bottom) Test for stable ensemble coding by checking whether a stable decoder trained on Day before extinction can predict CS+ trace responses on a given trial after extinction and reinstatement (Methods). c-e. Scatter plot of CS+ trace coefficients on Day before extinction versus First day of extinction (c), Last day of extinction (d), and Reinstatement (e). f. Results of decoding on the extinction and reinstatement sessions for clusters 1 and 5 in OFC-CaMKII and OFC-VTA neurons (see Supplementary Fig 13 for all clusters, as well as behavior during extinction). Cross-validated accuracies for the Day before extinction were 0.83 for OFC-CaMKII clusters 1 and 5, and 0.76 and 0.85 respectively for OFC-VTA clusters 1 and 5. Measure of center is the mean. * represents p<0.05 (see Supplementary Table 1 for exact p values, sample sizes and tests).

In order to quantitatively test for stability of encoding, we first trained a decoder to decode CS+ trace responses on the Day before extinction using neurons tracked across extinction and reinstatement, and tested if the same decoder was able to predict CS+ trials on the other sessions (Fig 7c, Methods). If the same population of neurons could significantly decode CS+ trace responses on these test sessions, it would show that a stable ensemble represents cue information after extinction. This was indeed the case for the learning-related clusters (Fig 7c–f, Supplementary Fig 13). After excluding animals relatively resistant to extinction (Supplementary Fig 13) to rule out apparent stable encoding due to lack of extinction learning, we found that cluster 2 no longer showed significant decoding, but clusters 1, 5 and 6 did. This is consistent with the earlier result that only cluster 2 (impoverished in OFC-VTA) is sensitive to probability reduction (Fig 6d). Therefore, OFC-VTA neurons encode a long-term cue-reward memory even after behavioral extinction of the original association.

Reward and associative encoding in OFC-VTA neurons guide behavioral adaptation

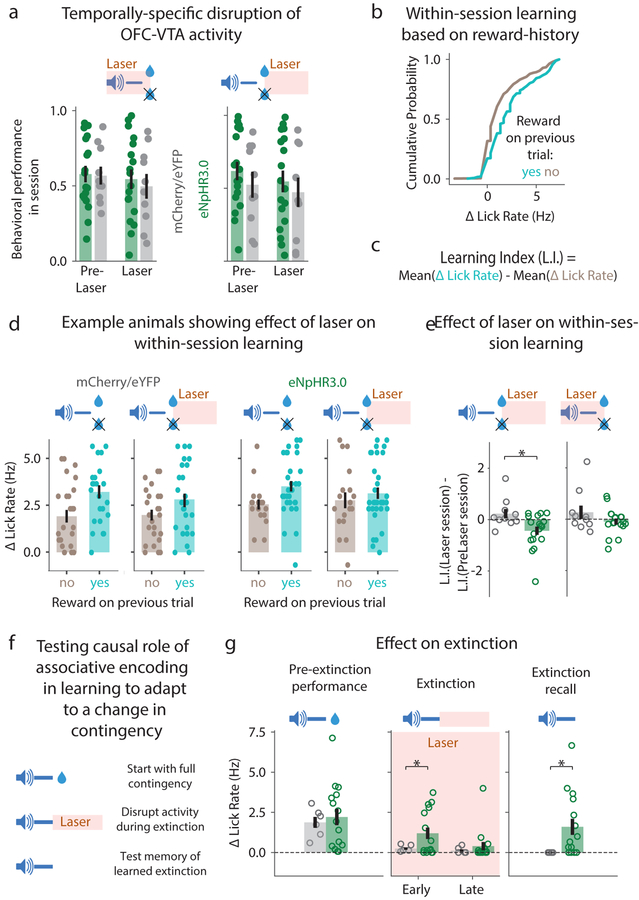
Despite shedding some light on neural representations, the above experiments did not resolve the functional role of associative and reward encoding in OFC-VTA neurons. To address this, we optogenetically inhibited OFC-VTA activity during a) the cue-reward delay after behavioral acquisition (Supplementary Fig 7), b) cue-reward delay after 50% probability reduction (Fig 8a), and c) reward consumption period after 50% probability reduction (Fig 8a). None of these manipulations produced any effect on reward seeking. Since earlier results also showed no effect on acquisition (Fig 3g), we hypothesized that OFC-VTA neurons may instead mediate behavioral adaptation to changes in learned associations.

Fig. 8. OFC-VTA reward and trace interval responses contribute to behavioral updating.

a. Disruption of OFC-VTA activity during either the cue-reward delay or the reward consumption period (3 s after reward delivery) had no effect on behavioral performance as measured by baseline-subtracted anticipatory licking Measure of center is the mean and error bars represent standard error of the mean for all panels in the figure. * represents p<0.05 (see Supplementary Table 1 for exact p values, sample sizes and tests) for all panels in the figure. b. Distribution of baseline-subtracted lick rates on a given trial of the 50% session across all OFC-VTA imaging animals, split by whether the previous trial was rewarded or unrewarded (see Supplementary Fig 11 for OFC-CaMKII animals). c. Calculation of a within-session Learning Index. d. Example control (mCherry/eYFP) or experimental (eNpHR3.0) animals showing baseline-subtracted lick rates across n=50 trials split by reward history on both a pre-laser and a laser session. This shows a disruption of within-session learning due to laser in the experimental, but not the control animal. e. Change in Learning Index due to laser for the population of experimental and control mice. Laser was tested during both reward consumption and the cue-reward delay. f. Schematic for testing the role of OFC-VTA activity after cue offset on extinction learning and memory. g. Baseline-subtracted lick rates show faster extinction learning for controls compared to experimental mice (Methods). Baseline subtracted lick rate on the first trial of a subsequent extinction session in the absence of laser (extinction recall) shows degradation of extinction memory in OFC-VTA inhibition animals.

We first tested whether OFC-VTA neurons mediate within-session learning in the 50% probability sessions, as mice showed more baseline-subtracted anticipatory licking on a given trial when the previous trial was rewarded (Fig 8b). This presumably reflects updating of estimated probability of reinforcement on a trial-by-trial basis. We quantified this learning using a Learning Index measuring the difference in mean licking based on previous trial outcome (Fig 8c). In individual animals, we observed that within-session learning was reduced when OFC-VTA activity was inhibited following reward delivery/omission, but not in control animals (Fig 8d). Across the population of mice tested, within-session learning was disrupted by OFC-VTA inhibition during the reward period, but not the cue period (Fig 8e). Thus, OFC-VTA reward, but not cue, encoding contributes to trial-by-trial behavioral updating based on previous reward outcome.

Since OFC-VTA cue encoding remained stable even after extinction (Fig 7), we further hypothesized that it controls extinction learning and memory. In order to test an effect on extinction learning, we inhibited OFC-VTA activity after cue offset while mice underwent behavioral extinction (Fig 8f). Mice receiving OFC-VTA inhibition showed slower learning of extinction, but eventually learned extinction within a session (Fig 8g). In order to test an effect on extinction memory, we tested behavioral performance on a subsequent extinction retrieval session without OFC-VTA inhibition. Despite OFC-VTA inhibited mice learning extinction by the end of the extinction session, their behavioral memory of extinction was degraded on the extinction retrieval session (Fig 8g). Hence, stable maintenance of OFC-VTA activity contributes to both extinction learning and memory.

Discussion

Historically, studies of OFC have looked for neural correlates of associative encoding by conducting per-neuron statistical tests of a priori hypotheses^26,29. Instead, the large-scale recording undertaken here allowed us to perform an unsupervised clustering of vmOFC neurons based on their responses, which could be validated with longitudinal activity tracking. Tracking of the same neurons allowed us to demonstrate that the same clusters showed similar response profiles on multiple different sessions after acquisition, even after changes to the learned association (Supplementary Fig 14). Such stability of cluster responses, combined with projection-specificity of clusters, demonstrates the presence of distinct functionally-identifiable neuronal subpopulations within vmOFC. Longitudinal tracking further allowed us to demonstrate stability of responses even after behavioral extinction. To the best of our knowledge, this is the first finding of neuronal activity reflective of a long-term memory of a previously learned cue-reward association after extinction, anywhere in the brain. Next, we discuss each important finding within the context of the existing literature on OFC function.

OFC cue onset responses support behavioral acquisition

Prior studies observed no effect of OFC lesion or chronic inactivation on Pavlovian acquisition^40,41. However, it is possible that this apparent lack of effect may be due to compensation by other brain regions, since rapid optogenetic inhibition has revealed regions involved in behavioral control that produce no behavioral effect when lesioned or chronically inactivated⁴². Thus, we tested the role of vmOFC activity in behavioral acquisition using rapid and reversible optogenetic inhibition. Indeed, we found that inhibition of cue onset activity in OFC-CaMKII, but not OFC-VTA neurons, degraded behavioral acquisition. Though the lack of effect due to OFC-VTA inhibition could technically be due to incomplete inhibition, this is unlikely as OFC-VTA inhibition was sufficient to cause deficits in two other types of learning (Fig 8).

The cue onset period, during which OFC-CaMKII activity supports acquisition, contained association-insensitive responses of clusters 2 and 3, and associative responses of cluster 1. Directly testing which of association-insensitive or associative responses mediate the observed behavioral effect is currently technically infeasible as it requires selective bilateral manipulation of individual functionally-identified clusters in a deep brain area. Nevertheless, some aspects of our data favor the hypothesis that behavioral acquisition is mediated by association-insensitive, and not associative responses. First, OFC-VTA neurons, despite containing the associative responses of cluster 1, do not support behavioral acquisition. Second, association-insensitive responses together contributed ~3.5 times the variance in cue onset activity compared to associative responses. Third, while association-insensitive responses are present prior to behavioral acquisition, associative cue onset responses of cluster 1 did not lead behavioral acquisition. Four, only activity during the cue onset period (containing association-insensitive and associative responses), but not the trace interval (containing associative responses), supports behavioral acquisition. Thus, the parsimonious explanation of our findings is that association-insensitive responses of clusters 2 and 3 contribute to behavioral acquisition.

It may be surprising that cue-reward association-insensitive responses might still mediate the acquisition of behavior reflecting these associations. Yet, animals must learn about both CS+ and CS-: one predicts reward, whereas the other predicts no reward. Therefore, these association-insensitive cue onset responses may reflect attentional/salience signals that are known to gate behavioral learning⁴³, possibly relayed by basal forebrain inputs⁴⁴ or sensory cortices³.

Despite parsimony favoring association-insensitive responses supporting behavioral acquisition, we cannot rule out a non-VTA-projecting subset of cluster 1 neurons controlling behavioral acquisition. For these reasons, a direct test between these hypotheses will need to be conducted in the future by manipulating individual functionally-identified clusters⁴⁵. These issues highlight the immense need in the field for careful interpretations and future deconstruction of behavioral deficits resulting from bulk neuronal activity manipulation.

vmOFC responses are stable after learning

Typically, neuronal recording studies do not longitudinally track the activity of the same neurons across multiple days. Such recording is important to assess whether a given activity pattern within individual neurons reflects a single-cell and population-level correlate of memory. Our data show that learned information is stably maintained by vmOFC neurons after learning, even after contingency changes (Supplementary Fig 14). These results are superficially in contrast with observations suggesting instability (i.e. not perfect stability) in individual posterior parietal neuronal encoding during stable behavior after learning⁴⁶. However, without knowing what fraction of neurons in any given brain region control behavior, relative instability may just be an indication of a small subset of stably-responding neurons controlling behavior, with activity of the remaining ones varying randomly. The presence of these distinct stably maintained memory representations raises an important question: what features of the cue-reward association are conveyed in these representations? To address this, we longitudinally tracked the same vmOFC neurons across different contingency changes after learning.

What do vmOFC memory representations encode?

Sensitivity of vmOFC encoding to background unpredictable rewards in clusters 1, 5 and 6 demonstrates that encoding in these clusters cannot simply reflect probability, magnitude, expectation or delay of the reward following the cue. Nevertheless, could it reflect value or desirability⁵? The reduction in associative responses due to random unpredicted rewards may reflect a reduction in desirability of sucrose due to temporary satiety. However, this is unlikely as mice lick to consume sucrose equally vigorously during the Background, Trained or 50% sessions (Supplementary Fig 15), showing that animals do not devalue the reward paired with CS+. Thus, this procedure is different from the more commonly used devaluation procedure⁵, and hence, these results are not consistent with a simple encoding of desirability.

Another possibility is that encoding in these clusters represents the value of a cue computed with reference to a reward rate prior to the cue, as proposed by the Training-Integrated Maximized Estimation of Reinforcement Rate (TIMERR) theory⁴⁷. This theory qualitatively fits reward seeking behavior during CS+ and CS- trials in Background and 50% sessions (Supplementary Fig 15). However, since OFC clusters encode associations stably despite reduction in reward probability to 50% or 0% (clusters 1, 5 and 6), or are not affected by the presence of unpredictable rewards (cluster 2), and since they do not show trial-by-trial updating of responses based on reward history (Supplementary Fig 10), it is unlikely that these clusters encode value as proposed by TIMERR. Though, we cannot rule out activities of individual neurons being correlated with value-related quantities.

What feature of the cue-reward association might then be represented by these clusters? Associative encoding in cluster 2 is consistent with a representation of reward probability given a cue, as its activity is sensitive to this probability but not the presence of unpredictable rewards; though this should be quantitatively tested using multiple reward probabilities. However, encoding in clusters 1, 5 and 6 is inconsistent with this probability. One intriguing possibility is that these clusters may represent the likelihood that a reward is preceded by a given cue (i.e. p(cue|reward)) instead of the posterior probability that a reward is delivered after the cue (i.e. p(reward|cue)). The likelihood will only be updated upon reward receipt and will be unchanged in the 50% session as all rewards are preceded by the cue. It will also be much lower in the Background session as unpredicted rewards, which outnumber the predicted rewards, are not preceded by the cue. Perhaps most intriguingly, this quantity would not be updated after extinction due to the absence of rewards, thereby providing a long-term memory of the original association.

Representing the likelihood that a reward is preceded by a cue, i.e. p(cue|reward), is advantageous not just because it could act as a long-term memory, but also because it provides a computationally efficient teaching signal for learning the probability of reward given a cue, i.e. p(reward|cue). This is because learning p(cue|reward) requires update only when rewards are received, which are ethologically much sparser than cues. This learning is much more efficient than directly learning p(reward|cue), which requires update on every sensory cue. Once learned, p(cue|reward) can be inverted using Bayes’ rule to estimate p(reward|cue). In any case, as we did not manipulate reward magnitudes, these probabilities might reflect an underlying reward rate instead of pure probabilities of state transitions.

Specific memory representations are conveyed by vmOFC to VTA

Among the learning-related clusters representing associative information, clusters 1, 5 and 6, but not 2, project to VTA. This suggests that information contained in these neurons (consistent with p(cue|reward)) could influence learning in VTA dopaminergic neurons. Consistent with this, long time-scale inactivation of OFC reduces cue responses in putative VTA dopaminergic neurons³³. However, since cue responses of VTA dopaminergic neurons are sensitive to the probability of reward given the cue⁴⁸, OFC-VTA responses likely undergo a Bayesian inversion before affecting dopaminergic neuronal activity. Alternatively, cluster 2 might affect VTA dopaminergic activity via indirect projections.

An influential idea about OFC-VTA communication is that OFC conveys the important states/variables relevant to represent the current task structure to VTA¹. Such OFC signaling is thought to be especially useful for behavior during states that are partially observable, i.e. not explicitly signaled within the environment¹³. Some aspects of our data fit with this hypothesis. For instance, since our task is a trace conditioning paradigm, there is a memory period (trace interval) during which both CS+ and CS- trials are indistinguishable without remembering which cue was previously presented. Consistent with the state representation hypothesis, neural recordings during the trace interval evolve to distinguish between CS+ and CS- trials, implying access to this memory. Further, even vmOFC reward responses convey partially observable aspects of the task. For instance, reward response of cluster 1, positive early in learning (Fig 2 and Supplementary Fig 6b), becomes negative once the reward is fully predicted by an earlier cue (Fig 2, Supplementary Fig 6b and Fig 6b: rewarded trials minus unrewarded trials). This suggests that the state of reward receipt is distinguished depending on whether or not it was predicted by a temporally-distant past cue. This negative reward response might cancel out a positive reward response from elsewhere to produce the classic reward prediction error correlate in VTA dopaminergic neurons⁴⁸.

Despite this, some key aspects of our data are inconsistent with the state-space hypothesis of OFC. First, inhibition of either OFC-CaMKII or OFC-VTA neurons during the trace interval—a memory period—does not impair Pavlovian reward seeking, despite this requiring representation of partially observable states (Fig 8a, Supplementary Fig 7). Additional data are also not consistent with the strict form of the hypothesis since OFC-VTA neurons do not represent cue states prior to learning (Fig 3e). Of course, one could argue that state representation in vmOFC is useful only once the task is well-learned. However, associative activity in clusters 1, 5 and 6 that project to VTA, is sensitive to the presence of unpredictable rewards in the intertrial interval despite all other aspects of the task remaining unchanged. Indeed, animals could use the same state space to learn that the intertrial interval now has higher value and that in relation to the intertrial interval, CS+ now has a lower value. Therefore, a simple encoding of state space is not consistent with these data. Instead, as discussed earlier, a parsimonious account is that OFC conveys the backward probability of cue to reward state transitions to VTA (i.e. p(cue|reward)).

Importantly, this proposed function of OFC-VTA neurons is sufficient to explain the deficits observed in extinction learning and memory due to OFC-VTA optogenetic inactivation. Without a signaling of p(cue|reward) by OFC-VTA neurons, animals would not learn that the reason for the lack of rewards during extinction is specifically because p(reward|cue) is now zero. Instead, animals might learn through compensatory mechanisms that p(reward) is zero, thereby causing behavioral extinction. On the extinction recall day, the estimate of p(reward|cue) is still high, and could control behavior, thereby resulting in an apparent deficit of extinction memory. In simple terms, p(cue|reward) provides a credit assignment signal to relate changes in reward probability specifically to the cue. This interpretation is consistent with a previously observed deficit in appropriate action-reward contingency learning following OFC lesions⁹. It is also consistent with a prior study showing a hierarchical effect of lateral OFC inactivation on reversal learning⁴⁹. Interestingly, it was previously hypothesized that lateral OFC encodes a template of the old association to update behavior after changes in the association²⁸. However, this hypothesis was not borne out in lateral OFC neuronal recordings during reversal learning²⁹. Our results demonstrate that vmOFC neurons directly projecting to VTA do indeed maintain a correlate of the memory of the old association after extinction.

Conclusion

Studying the neuronal network basis of learning and memory requires studying evolution of responses in the same neurons throughout these processes. Due to technical challenges, such a feat has been difficult in deep brain areas⁵⁰. Here, in a simple yet interesting behavioral task, we showed that subpopulations of OFC neurons represent a long-term memory of multiple features of cue-reward associations. Despite the simplicity of the task used, we found dramatic complexity in OFC neuronal encoding. The complexity of information encoding within vmOFC is almost definitely higher than that found here. Thus, these results open up the possibility that the dazzling complexity of OFC function may result from distinct neuronal subpopulations within OFC contributing to distinct functions. Future studies investigating the function of functionally-identified neuronal subpopulations could isolate individual functions to individual subpopulations, and map out activity transformations occurring within and outside OFC. Future studies could also investigate whether OFC contains long-term memory representations for cue-drug of abuse associations and their role in cue-induced reinstatement of drug seeking. Overall, the present findings advance a powerful approach to investigate such fundamental questions.

Methods

Subjects and Surgery:

All experimental procedures were approved by the Institutional Animal Care and Use Committee of the University of North Carolina and accorded with the Guide for the Care and Use of Laboratory Animals (National Institutes of Health). Adult male C57BL/6J mice (Jackson Laboratories, 6–8 weeks, 20–30 g) were group housed with littermates, acclimatized to the animal housing facility and handled by the experimenter until surgery. Stereotactic (David Kopf Instruments) survival surgeries were performed under sterile conditions. The general surgical protocol has been described previously^22,51. Animals were anesthetized during surgery. Induction was carried out by using 5% isoflurane mixed with pure oxygen (1 L/min) for thirty seconds or so, after which anesthesia was maintained using 0.6–1.5% isoflurane. Animal respiratory rate was monitored intermittently by the surgeon to ensure appropriate depth of anesthesia. The animals were also placed on a heating pad to ensure proper thermal regulation. Pre-operative buprenorphine (0.1 mg/kg in saline, Buprenex) treatment was given for analgesia. Dryness of eyes was prevented by using an eye ointment (Akorn). 2% lidocaine was topically applied on the scalp prior to incision. Subcutaneous injection of sterile saline (0.3 mL 0.9% NaCl in water) was given prophylactically to prevent dehydration. Details of viral injection, lens and optic fiber implantation are provided below in the 2-photon imaging and optogenetics sections. A custom made stainless steel ring (5 mm ID, 11 mm OD, 2–3 mm height) was implanted on the skull for headfixation, which was stabilized with skullscrews and dental cement. Following surgery, animals received acetaminophen (Tylenol, 1 mg/mL in water) in their drinking water for 3 days. Animals were given at least 21 days (and often, many more) with ad libitum access to food and water to recover from surgery. Following recovery, animals were water deprived to reach 85–90% of their pre-deprivation weight and maintained in a state of water deprivation for the duration of behavioral experiments. Animals were weighed and handled daily to monitor their health. In rare instances when weight fell below 80%, we restored water access and slowly re-introduced water deprivation. The amount of water given daily was often around 0.6 mL but was varied based on the daily weight of each animal. A total of 83 (12 imaging, 65 optogenetics, 4 patch-clamp electrophysiology, 2 anatomy) mice were used in this study.

Head-fixed behavior:

Head-fixed behavior was done similar to a previous paper²², with the only difference that the inter-trial interval was exponentially distributed with a mean of 30 s. Following recovery and sufficient time for fluorescence/opsin expression, the mice were water deprived. Mice were habituated to head fixation for at least 3 days prior to behavioral sessions. After the weights stabilized around 85–90% of pre-deprivation weight, mice were trained to lick for sucrose in a custom-designed headfixed behavior set up (by VMKN) with software written in MATLAB and hardware control achieved using MATLAB and Arduino. In these sessions, mice were delivered drops of sucrose (10% in water, ~2.5 μL) according to a truncated Poisson process with mean interval of 12 s and maximum interval of 90 s. The sessions continued until 100 drops were delivered and thus, lasted 20 minutes on an average. Mice were considered trained to lick if they licked at least 950–1000 times over the entire session and completed at least two sessions. Once this part of the training was complete, mice were run on a Pavlovian conditioning task. Mice received one of two possible auditory tones (3 kHz pulsing tone or 12 kHz constant tone, 75–80 dB) that lasted for 2 seconds. A second after the cues turned off, the mice received a reward to one of the tones (designated CS+), whereas the other tone resulted in no reward (designated CS-). The identity of a tone as CS+ or CS- was counterbalanced across mice in all experiments. The cues were presented in a pseudorandom order and in equal proportion until a total of 100 trials (cue presentations) were completed. The intertrial interval between two consecutive presentations of the cues was drawn from a truncated exponential distribution with mean of 30 s and a maximum of 90 s, with an additional 6 s constant delay. Anticipatory licking (Fig 1c) seen in animals was an indication of cue-triggered reward expectation. Thus, a behavioral readout of learning could be obtained by calculating the change in average lick rate during the cue (3 s after cue onset) and the baseline before the cue (1 s). However, this measure is sensitive to outlier trials in which the animal may have shown a lot of licks. Thus, to get a better measure of reliability of licking induced by a cue, we calculated a score based on the area under a Receiver Operating Characteristic curve (auROC) formed by the distributions of lick rates to the cue versus the baseline across trials. This score was scaled to get a measure of reward seeking to a cue (Fig 2h, Fig 3g) defined as 2×auROC(cue v. baseline)-1, such that lick rates at baseline levels produced a behavioral performance score of zero and perfect discrimination between cue licking and baseline licking would be a score of 1. In cases in which the discrimination of behavioral performance between the two cues was of interest, cue discrimination (Fig 1e) was measured as the twice the area under a Receiver Operating Characteristic curve (auROC) formed by the distributions between the baseline subtracted lick rates to CS+ versus CS- minus 1. Defined thus, cue discrimination is equal to zero when animals are licking at an equal rate for both cues. If cue discrimination was found to be larger than 0.4 on at least 2 consecutive sessions or larger than 0.7, animals were considered trained. See below for specific details on imaging or optogenetic experiments.

2-photon microscopy:

Calcium activity of neurons was imaged using 2-photon microscopy by expressing a calcium indicator (GCaMP6S) in cells of interest. This was done using a viral approach. For studying putative pyramidal neurons, we injected AAVdj-CaMKIIα-GCaMP6S (~5×10¹² infectious units per mL, UNC Vector Core, 1:6 diluted in saline) in vmOFC (n=5 mice). For studying cells in vmOFC projecting to VTA, we injected AAVdj-EF1α-DIO-GCaMP6S (~3×10¹² infectious units per mL, UNC Vector Core, full strength) in vmOFC (n=7 mice). Two injections of 500 nL each were performed (+2.5 mm AP, −1.1 mm ML, −2.3 mm DV and +2.9 mm AP, −1 mm ML, −2.3 mm DV from bregma). These coordinates were lateral compared to the coordinate for the lens implantation (+2.5 mm AP, −0.75 mm ML, −2.2 mm DV from bregma). Lens (1 mm diameter GRIN lens, GLP1040 Inscopix) insertion followed a previously described protocol⁵¹. In one animal, we implanted both a 1.8 mm stainless steel sleeve (optical cannula) around the lens, and the lens. This animal was excluded from analysis of the relative spatial location of cells. For the study of vmOFC cells projecting to VTA, we also bilaterally injected a retrogradely transported Canine Adenovirus 2 expressing Cre recombinase (CAV2-Cre, ~6×10¹² infectious units per mL, Institut de Génétique Moléculaire de Montpellier) in the VTA (−3.2 mm AP, +/−0.6 mm ML, −4.5 mm DV from bregma, 500 nL). A minimum of 6 weeks was given for proper virus expression in the OFC-CaMKII group and at least 8 weeks was given for the OFC-VTA group prior to commencement of imaging during Pavlovian conditioning.

We used the Olympus Fluoview FVMPE-RS 2-photon microscope. We used a resonant scanner (30 Hz frame rate acquisition) and performed an online averaging of 6 times to get an effective frame rate of 5 Hz. This was done to minimize size of recorded files as we had negligible motion artifacts. A GaAsP-PMT with adjustable voltage, gain and offset was used, along with a green filter cube. We also used a long working distance 20x air objective that is specifically optimized for infrared wavelengths (Olympus, LCPLN20XIR, 0.45 NA, 8.3 mm WD) and imaged with a 955 nm laser (SpectraPhysics, ~100 fs pulse width) with automated alignment. The animals were placed on a 3-axis rotating stage to precisely align the surface of the GRIN lens to be perpendicular to the light path, such that the entire circumference of the lens is crisply in focus (within 1–2 μm). We noted down the goniometer readings and ensured that the mouse is placed in the head-fixing apparatus in the same angle for all imaging days. We then selected the imaging plane with respect to the surface of the lens, which could be done to within 1–2 μm. This procedure was followed every day and considerably improved the ability to image the exact same plane day after day. The imaging acquisition was triggered by a custom Arduino code right before the start of a behavioral session, and a TTL output of every frame was sent as an input to the Arduino to keep timestamps on a common scale. The imaging acquisition was triggered off at the end of the behavioral session (~ one hour).

In every mouse, one z-plane was imaged throughout acquisition so that the same cells could be tracked through learning. After mice were trained, other z-planes were also imaged (one per session) to get a measure of the total functional heterogeneity in the network. A total of 2–6 z-planes per mouse were imaged in the OFC-CaMKII group, whereas 1–3 z-planes were imaged in the OFC-VTA group. The z-planes were estimated to be at least 50 μm apart from each other. Once all the z-planes were imaged in a trained animal, these planes were again imaged after the probability of reward was reduced to 50%. Once these sessions were completed, mice were trained back on a 100% reward contingency to return to pre-50% levels of performance. We also ran sessions with unpredicted rewards mixed in with predicted rewards (Background). In the Background sessions, there were 148 +/− 22 (standard deviation) unpredicted rewards during the ITI and 60 fixed rewards (session contained 60 CS+ and 60 CS- trials). There was a minimum delay of 6 s between the last unpredictable reward in an ITI and the next cue. This was to reliably separate potential lick or consumption responses from the next cue response. After Background sessions, the original 100% contingency was re-introduced. Animals showed consistent performance across all 100% contingency sessions, given enough time to adapt after changes (1–3 sessions). Since we generally did not image activity on the behavioral training session prior to the Background session, we quantified the change in responses due to the presence of background rewards by quantifying the recovery in activity following the Background session. Once mice performed at a trained level in the 100% contingency sessions, we extinguished the cue-reward pairing by delivering both cues in the absence of reward (extinction). The extinction session was maintained for 2–3 sessions. The last day of extinction was analyzed to test the effect of extinction on the network encoding of behavioral variables. Following extinction, a reinstatement session was run in which the CS+-reward contingency was reintroduced at 100%. All animals resumed reward seeking within 5–10 trials during reinstatement.

Imaging data analysis:

The Olympus OIR files collected during imaging through Olympus FluoView (FV1200) were exported as tif files. Each session was split into multiple tif files so as to limit the size of each to 4 GB. These tif files were then combined offline to an HDF5 format using a custom code. These HDF5 files were then motion corrected in the x-y plane using a hidden Markov model (SIMA v1.3⁵²). We had found that the imaging plane showed very little z movement in vmOFC (<5 μm based on a random sample of sessions). Following motion correction, regions of interest (ROIs) were manually annotated (explained below) using ImageJ on the standard deviation projection of activity across time. These ROIs were imported into SIMA and then used for signal extraction. A custom code added neuropil correction to the SIMA signal extraction (described below). Motion correction, signal extraction, and neuropil correction were all implemented on remote Amazon Web Services (AWS) EC2 machines using a custom launch code that is now available as part of the SIMA master code (excluding neuropil correction). Running analysis on AWS was significantly faster (up to 25 times) than on local machines as we could analyze multiple files simultaneously.

Two steps from the above pipeline are worth explaining in a bit more detail. Manual annotation of ROIs was done by drawing a polygon around each cell using ImageJ. As imaging of cells in vmOFC often contained apical dendrites of cells in the imaging plane (unlike surface cortical imaging), we had to take care to exclude these dendrites from the analysis of somatic activity. In many cases, small dendritic segments could be clearly resolved as overlapping with parts of somatic ROIs and in this case, only a part of the somatic ROI was drawn that did not overlap with any resolvable structures. This was also done in case of cell-to-cell overlap. Since this procedure is likely to still retain significant contribution due to unresolved neuropil, we performed neuropil correction. Neuropil correction was done by first calculating a neuropil signal around each ROI. This was done by calculating a weighted sum of all recorded pixels excluding those falling within a 15-pixel (~17 μm) radius of all ROIs. The weight for any pixel was calculated using a Gaussian function centered on the ROI of interest with a radius of 50 pixels (~45 μm). These parameters were obtained after a systematic search of the parameter space in a small subset of sessions and visually comparing the obtained fluorescence traces against the raw videos. The results in the manuscript are robust against large variation in these parameters. Once the neuropil signal was calculated for every ROI, a correction of this signal was done by subtracting 0.8 multiplied by this signal from the raw calcium trace of the ROI. The factor 0.8 was found to generally accord with what was seen by eye. For a few sessions in which we compared this general procedure with results obtained from another package (Suite2p⁵³), we found that a neuropil subtraction coefficient close to 0.8 provided good correspondence in results and was approximately the average correction coefficient calculated in Suite2p. Since neuropil subtraction can produce negative values for the calcium signals of cells on some frames, instead of calculating a ΔF/F normalization where the denominator could sometimes be really low, producing spuriously high values, we normalized fluorescence signals (Fig 1g–j, Fig 3d, e) as the ratio (F-F_median)/(F_max-F_min). This normalized signal was zero for the median value of the fluorescence, which was close to the baseline level of fluorescence for most cells as calcium transients were sparse, high amplitude events. This scaling ensured that the high amplitude calcium transients were always positive and less than 1. The closer the maximum normalized signal was to 1, the closer the median value of fluorescence was to the minimum value of fluorescence, i.e. the higher the signal-to-noise ratio. This scaling was done only to obtain comparable normalized fluorescence signals across ROIs for visualization and does not affect analysis of responses to behavioral events (see below).

Once a normalized fluorescence signal was calculated as above, we aligned every cell’s activity to the cue (3 s before cue to 17 s after cue) to visualize cue-locked activity of the cell (Fig 1i). Any overlap with consecutive trials was removed from this matrix (coded as ‘nan’). We then calculated the peristimulus time histogram (PSTH) of the cell as the average across all trials (Fig 1i, j). We did not analyze the PSTHs directly as a measure of cue or reward response. This is primarily because fluorescence measurements from neurons are only a proxy for underlying neural activity as they result from an interaction between the neural activity and dynamics of the calcium indicator. Due to the slow time course of decay but fast onset of GCaMP6s²⁴, fluorescence measured at any given moment could be due to activity at that moment or activity seconds ago. A further caveat of using PSTHs to infer cue responses is that due to the averaging of all trials, potential changes in neural activity due to motor confounds from licking are not separated from cue responses. For these reasons, the PSTHs calculated here are only used for visualization and as input for the clustering analysis, representing temporal response patterns of neurons.

We performed clustering analysis on the PSTH of all ROIs to test if there were any functional clusters. This is an unbiased means to evaluate the heterogeneity in response patterns. We largely followed the methodology presented elsewhere¹⁵. In our case, we were interested in the time course of activity to both CS+ and CS- cues. We used 100 frames (20 s) measured around each cue, resulting in a 200-dimensional dataset in total (Supplementary Fig 3). The PSTH for CS+ and CS- were appended to create a 200-column vector of data points for each cell. We first reduced the dimensionality of this data using principal component analysis (PCA) (Supplementary Fig 3). To select the number of principal components, we used the standard method of finding a bend in the plot of the variance explained per principal component—the scree plot (Supplementary Fig 3). As can be seen from the plot, beyond the number of chosen principal components (n=8), there was minimal variability explained per principal component. After this, the data were projected onto the lower dimensional subspace formed by the principal components. These data were the input to the clustering algorithm. Considering that even our reduced dimensionality data were eight dimensional, we used spectral clustering as it has previously been argued to produce stable results in higher dimensional data sets¹⁵. We further found that the optimal silhouette score for spectral clustering was better than for other clustering methods such as k-means or hierarchical clustering. The clustering was performed using the Scikit-learn function sklearn. cluster. Spectralclustering with the affinity matrix calculated using a k-nearest neighbor connectivity matrix. The number of nearest neighbors was varied by a factor of 40. The number of clusters was also varied systematically. The best parameters were chosen by maximizing the silhouette score over a grid search over parameters. After the best parameters were found, we estimated the stability of our results across trials by subsampling various fractions of trials and calculating the Adjusted Rand Index (ARI). For each fraction chosen, we found better than chance (ARI=0) reliability in clustering. Thus, the clustering results were generally stable across trials, but did reflect the considerable trial-to-trial variability in responses. There were many neurons within each cluster in each of the imaging mice. In order to classify neurons in vmOFC projecting to VTA into the clusters identified within the OFC-CaMKII population, we used a linear support vector classifier (Scikit-learn) to classify each OFC-VTA cell’s PSTH based on the mean PSTH per cluster from OFC-CaMKII.

Once clustering was performed, neurons were assigned the corresponding cluster label. So, if the neuron was imaged on another day, its cluster index determined from the clustering on the trained data was used. To register ROIs across days, we used manual registration due to the high amount of structural resolution in the imaging data. Structural annotation of ROIs limited the dropout of cells on intermittent days due to low activity, when compared to functional detection of ROIs.

To analyze neural activity, we first deconvolved the calcium transients to remove fluorescence changes purely due to the calcium indicator. This was done using OASIS with a first order autoregressive model with L1 penalty³⁰. Deconvolved spikes using this method were found to reliably represent true spiking activity in cells ex vivo when firing was sparse. However, when neurons were made to fire at a high baseline firing rate (8 Hz), pauses in firing were not detected properly (Supplementary Fig 1). This means that suppression of firing is likely to be underrepresented in the inferred spikes. It was for this reason that we decided to do clustering of cells prior to deconvolution as otherwise, the error in deconvolution might have been propagated to clustering as well. To make the deconvolved signals comparable across neurons, we also divided it by the estimated noise in the signal, as provided by OASIS.

To calculate average change in activity caused by the various behavioral variables, we used a General Linear Model (GLM) framework instead of a PSTH approach, which is confounded by variable action timings with respect to cue. Since we were primarily interested in obtaining interpretable measures of responses to behavioral variables, we defined explanatory variables as spanning multiple frames with respect to the variables. Thus, we did not use a time-varying kernel approach, which would have provided better model fits but would require conversion to an average coefficient for interpretable response measures. The explanatory variables were defined as shown in Fig 2c for sessions with full contingency. We also included the frame number since the start of the session as an additional variable in the model to account for potential instability in responses over time. Each explanatory variable (other than frame number) was coded as 0 on every frame except for the frames in which they were present, in which case, their value was coded as 1. Thus, the coefficient of response to an explanatory variable measures the average change attributable to the presence of that variable, while controlling for other variables. For measuring an action response, we tried two approaches: one in which responses locked to lick bout onsets were calculated over a 400 ms window and another in which responses to lick count per frame was calculated. We defined a lick bout onset as the first lick in a set of licks (possibly containing one lick) separated by interlick intervals less than 500 ms²⁵. We found that the lick bout onset model was consistently, but slightly better than the lick count model on a random selection of sessions and thus, used this model for all data analysis. This is also consistent with a previous study on lick responses in OFC demonstrating that lick responses are primarily to lick bout onsets instead of individual licks²⁵. We also tested whether the first lick after the cue could capture lick related responses and found that this was not the case for the few sessions we tested (an example session is shown in Supplementary Fig 2). Thus, we did not investigate this model further. For the 50% probability sessions, we also added Reward Omission and Reward terms (0–3 s after the first lick after omission or reward respectively), along with Reward Omission Late and Reward Late terms (3–6 s after the first lick after omission or reward respectively). In addition to these, we also included an interaction term measuring the effect of trial reward history (i.e. whether the previous trial was rewarded or not) on the responses to cue, reward and omission (Supplementary Fig 11). The GLM equation was thus as shown below.

$$dF(t)=d{F}_0+{\beta }_{lickonset}{I}_{lickonset}(t)+\sum _{event}{\beta }_{event}{I}_{event}(t)+{\beta }_{drift}t+\sum _{History}\sum _{event}{\beta }_{History:event}{I}_{event}(t)History(t)+\epsilon$$

where dF(t) represents deconvolved fluorescence on frame t. β’s represent the coefficients, I’s represent indicator variables corresponding to either lick onsets or other events such as cue onset, cue late, cue trace, reward, reward late, reward omission, and reward omission late. These indicator variables were coded 0 or 1 depending on the time periods defined above. The second to last term corresponds to an interaction between trial reward history (defined above) and these events. Finally, ε corresponds to the error term (see below).

The GLM was solved using least squares regression. This is because on a subset of sessions, we attempted generalized linear model approaches with inverse Gaussian and gamma distributions and found that these provided considerably worse fits than a model assuming normality. Thus, we used an ordinary least squares approach for the GLM used in this paper. The coefficients returned by the GLM were converted to a t score by dividing by the estimated standard error so as to create a normalized response. The t score measures the reliability of the response rather than the magnitude, which is much more susceptible to outlier trials. Thus, for standard analyses, we used t scores (Fig 2–5), though we show that analyses using coefficients produce similar results (Supplementary Fig 15). Nevertheless, since t scores are also dependent on the number of trials, when we compared variables across sessions with this change (Background sessions have 120 trials, while other sessions have 100), we used the coefficients themselves instead of the t scores (Fig 6, 7). Since we were primarily interested in using the GLM to obtain interpretable response measures to behavioral variables and not predictive accuracy, we did not conduct cross-validation of the model to compare models with or without the inclusion of variables. If predictive accuracy is of interest, a time-varying kernel approach would be an important addition to our model to fit time course of activity within a trial.

To test whether neuronal response evolution fitted a sigmoidal or linear model better, we fitted the neuronal response with a 4-parameter sigmoidal model $response=\frac{p_0}{{\left(1+e^{-p_1.trialblock}\right)}^{p_2}}+p_3$, where response is the CS+ trace response (GLM t score is shown in Fig 4 but results with coefficients look similar), trialblock is the trial block number (5 trial blocks per session of 50 CS+ trials), and p₀, p₁, p₂ and p₃ are the parameters. We assumed normal errors for both the sigmoidal and linear models (with slope and intercept). Least-squares fitting in this case is mathematically equivalent to maximum likelihood estimation. Hence, we used the optimize.curve_fit function in Scipy for this purpose. The lower bounds for the parameters were (−∞, 0, 0, −∞) and upper bounds were (∞, ∞, ∞, ∞). We found that the least squares fitting sometimes approached a sub-optimal local minimum based on the initialization of p₁. Thus, we tested 10 logarithmically-spaced possible initial values for p₁, viz. 10⁰, 10¹,…, 10⁹. We picked the solution with the lowest mean squared error. We then calculated the Akaike Information Criterion⁵⁴ for both the sigmoidal and linear models as

$$AIC=2k+n\text{ln}(MRSS)+\frac{2k(k+1)}{n-k-1}$$

, where k is the number of parameters, n is the number of trial blocks, MRSS is the mean residual sum of squares for the model. This is corrected for small samples.

We considered an AIC score of sigmoidal model being less than 6 below AIC score of the linear model as showing considerable support for the sigmoidal model, given the nested nature of the two models. This corresponds to a relative likelihood of the sigmoidal model of 95.3%⁵⁴.

We ran the cross-correlation analysis using the correlate() function of Numpy. In order to calculate the normalized cross-correlation, if n corresponded to the neural signal and b the behavioral signal, we first normalized these by $n=\frac{n-\langle n\rangle }{{\sigma }_n{l}_n}$ and $b=\frac{b-\langle b\rangle }{{\sigma }_b}$, where 〈 〉 corresponds to the mean, σ the standard deviation and l_n, the length of n (i.e. number of trial blocks). This normalization ensured that the cross-correlation remained between −1 and +1. The optimal lag (Fig 5) was calculated as the lag of peak cross-correlation.

We ran the decoding analysis (Fig 7c) using the fluorescence signal on individual trials from longitudinally-tracked neurons. We focused on trace interval responses for these analyses since cue onset responses might reflect sensory responses in addition to associative information (e.g. in cluster 2). We tested whether we could correctly identify the CS+ trace interval response versus the baseline response right before CS+ (1 s). This was to test if the CS+ trace encoding of neurons remained stable across sessions. We used a linear support vector classifier from Scikitlearn (SVC function with a linear kernel). This classifier was trained on a reference session (Day before extinction in Fig 7 and Trained in Supplementary Fig 14) and the same classifier was used to test prediction accuracy on other sessions. For training, we ran a 10-fold cross-validated grid search (using the GridSearchCV function). γ and C for the classifier were tested between 10⁻², 10⁻¹, …, 10². The decoder with the best cross-validation accuracy was used as the optimal decoder on the reference session. The prediction accuracy on the test session was calculated using the score method of the classifier. The null distribution for the accuracy was calculated as the accuracy when the true trial labels (CS+ versus baseline) were compared against randomly permuted versions of the labels. 1000 shuffles were performed. The one-tailed p value (clear a priori hypothesis that prediction accuracy is higher than null) was calculated as the percentile at which the true accuracy lay. Benjamini-Hochberg correction was used to correct p values for multiple comparisons between the different test sessions for each cluster.

In order to decode reward seeking behavior during acquisition from the GLM t scores (Supplementary Fig 6c, d), we used ridge regression, as implemented in Scikitlearn. This was implemented using a leave-one-out cross-validation scheme per animal. Thus, in order to predict the behavior on the n^th day of acquisition for one animal, we trained a ridge regression model on the cue response t scores (Onset, Late and Trace) of all tracked neurons on every other day. This model was then used to predict a behavioral performance score (auROC of cue versus baseline lick rates) on the n^th day. The goodness of fit of the regression was calculated for each animal as the R² defined by 1-sum of squares around model/sum of squares around mean of data. Note that defined in this way, R² can be arbitrarily negative if the mean of the model does not capture the mean of the data. To get a single measure of how well the regression performed across all animals, we pooled the true and predicted performance from all animals since there was no systematic deviation of the mean performance between animals, at least for CS+ decoding. A regression between the ground truth and the prediction in this case provided a measure of how well the decoding algorithm performed across all animals. The weights of the regression plotted in Supplementary Fig 6c, d were those that predicted behavioral performance on the day with the most accurate cross-validated prediction.

Estimating anatomical coordinates of imaged neurons

In order to estimate the relative location of cells with respect to each other, our primary intent was to calculate a single spatial map across animals by adjusting for the different lens placements. To do so, we first calculated the placement of the center of the lens for each mouse. To get an approximation for the linear optical properties of the GRIN lens, we imaged fluorescent beads in agarose gel with and without lens. We then aligned frames which corresponded to the exact same pattern of beads between the images obtained with and without the lens. Using the spatial positions of these frames, we estimated the transformation between object distance and image distance. This was corrected for the refractive index of the tissue (assumed to be the same as sea water, 1.38). We also similarly estimated the transverse magnification, which was negative (inverted image). The above procedure was only done for one GRIN lens and hence, we do not know how much variability exists across lenses. Since our primary intent was simply to align the fields of view across mice, we used these to transform each field of view onto a single relative spatial map based on the center of the lens in each animal, and do not specify absolute spatial locations of cells.

Testing for differences in Pearson’s correlation between different pairs of sessions:

The stability of neural encoding across sessions can be evaluated by testing whether activity is correlated between sessions (Supplementary Fig 14), with the caveat that non-responsive neurons may contribute to this correlation. The primary hypotheses we were testing were: is there significant correlation in neuronal responses after learning, and, is this correlation higher than seen prior to learning?

Thus, it was decided that for comparisons of correlations between session pairs, the relevant tests would be against the Day before Trained → Trained correlation, as shown in Supplementary Fig 14c. In principle, every possible pair of comparisons could have been conducted. However, comparisons other than those shown in the figure were not of interest. Thus, the multiple comparisons correction was performed only across the 5 comparisons of interest.

In order to test for difference in correlation, we treated non-overlapping pairs of sessions (e.g. Day 1 → Day 2 against Day before Trained → Trained) as independent. Overlapping pairs of sessions (e.g. Day 1 → Trained against Day before Trained → Trained) were treated as dependent measures. For the independent comparisons, we tested for significant difference in Pearson r’s by employing Fisher’s r to z transformation⁵⁵. For the dependent comparisons, we used Steiger’s test⁵⁶.

Optogenetics:

We followed our previously established protocol for conducting behavioral optogenetics studies⁵⁷. Briefly, wild type mice in the OFC-CaMKII group were injected with AAV5-CaMKIIα-eNpHR3.0-mCherry (n=20 mice, ~ 4×10¹² infections units/mL) or AAV2-CaMKIIα-eNpHR3.0-eYFP (n=3 mice, ~ 2×10¹² infections units/mL) for inhibition of cells. Control animals in this group were injected with AAV5-CaMKIIα-mCherry (n=11 mice, ~ 4×10¹² infections units/mL). The vmOFC injection coordinates were (+2.6 mm AP, +/−0.83 mm ML, −2.39 mm DV) from bregma at a 10 degree angle. In all animals, there was considerable expression of the virus. The expression was limited to the ventral and medial parts of OFC, with no expression in the lateral part of OFC or infralimbic cortex. While there was expression in the rostral prelimbic cortex in some mice, the optic fiber was further ventral, preventing light from being focused on to the rostral prelimbic cortex. For the OFC-VTA group, we injected AAV5-EF1α-DIO-eNpHR3.0-mCherry (n=15 mice, ~4×10¹² infectious units/mL) or AAV5-EF1α-DIO-eNpHR3.0-eYFP (n=4 mice, ~8×10¹² infections units/mL) in vmOFC, and CAV2-Cre (~6×10¹² infectious units per mL) in VTA. Control animals in this group were injected with AAV5-EF1α-DIO-mCherry (n=7 mice, ~4×10¹² infectious units/mL) or AAV5-EF1α-DIO-eYFP (n=4 mice, ~6×10¹² infectious units per mL) in vmOFC and CAV2-Cre in VTA. The VTA injection coordinates were (−3.2 mm AP, +/−0.6 mm ML, −4.5 mm DV) from bregma. All injection volumes were 500nL bilaterally. In all of the above cases, the optic fibers were placed bilaterally in vmOFC at (+2.6 mm AP, +/−0.83 mm ML, −1.89 mm DV) at 10-degree angles from bregma. All animals received 532 nm laser delivered at 10 mW power at the fiber tip. In all experiments, laser was delivered on every CS+ and CS- trial for each session. We waited at least 3 weeks after OFC-CaMKII surgeries and 6 weeks after OFC-VTA surgeries to ensure sufficient virus expression. Within each experiment, all groups were age-matched. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those typically used in the field.

The experiment with inhibition of cells during initial learning was done for both OFC-CaMKII and OFC-VTA groups (Fig 2g, h, Fig 3f, g). The experiment during initial learning addressed whether inhibition of cells during either the first second after cue onset (cue onset group) or the one second trace interval (trace group) produced any effect on initial learning. The numbers of animals ran on the acquisition experiment were 11 cue onset, 12 trace and 11 controls for OFC-CaMKII, and 8 cue onset, 7 trace and 7 controls for OFC-VTA. Controls were counterbalanced across experiments to either receive inhibition during the cue onset period or the trace period and were pooled. Every animal was run with laser present on the first 8 conditioning days. The 9^th conditioning day was run without laser to test if the laser caused any significant change in the expression of behavior, which was also tested after learning. Behavioral performance for either cue was measured as the auROC between the two distributions formed by mean lick rate during the cue (3 s) versus baseline (1 s).

Optogenetics analysis:

We had decided a priori that in order to test the rate of initial learning (Fig 2h, Fig 3g), we would test performance on the first day that the group that attains highest peak performance reaches stable performance. This was to ensure that a statistically significant effect on behavioral acquisition is due to an effect during learning instead of an effect after learning is established. More specifically, this test would separate the following two scenarios: 1) differences between groups arising only after all groups reach peak performance (i.e. an effect after learning), and 2) differences between groups arising before any group reaches peak performance (i.e. an effect during learning). To identify the test day as described above, we fit a sigmoid function to the behavioral evolution and identified the day that it reached 99% of the plateau level. For OFC-CaMKII, this was day 7.05 for the control group and for the OFC-VTA group, this was day 6.80 for the trace interval group. Since these were fractional, to be conservative, we averaged the performance for the two days surrounding the threshold for each animal and performed pairwise comparisons between the cue onset group and the control, as well as the trace and the control group. These two comparisons were corrected for multiple comparisons using the Benjamini-Hochberg false discovery rate correction. Each test was performed by using a bootstrapping procedure to calculate a sampling distribution of the difference in means between two groups. The bootstrapping was done by resampling with replacement from animals, and within each animal, from trials. In order to calculate the expected distribution under the null hypothesis of equal means, the above sampling distribution was shifted to have zero mean and then the 2-tailed p value of the test was found by calculating twice the percentile of the observed difference.

One potential caveat exists for the analysis procedure described above. In principle, it is possible that the difference between the groups occurs by chance on the test sessions. In this case, the difference is not due to any patterned difference in acquisition but due to a chance difference on the test day. Thus, if the previous test (i.e. on the day that the best group reached peak performance) produced a statistically significant result, we performed an additional test to check for a patterned difference. To test for any patterned difference, we first calculated the difference in mean performance for each experimental group (cue onset and cue trace) from the control group for each session. We then tested if the set of per-session differences excluding the test sessions has a mean significantly different from zero. We then corrected for the multiple comparisons resulting from comparisons for both experimental groups.

One of the OFC-VTA control animals died after the initial learning and hence, this animal was not included for any further experiment. After the acquisition experiment, we first gave animals a break of a few days prior to running further experiments. We next tested if inhibition produced any effect on the expression of a learned behavior. In order to perform these experiments, we trained all groups of animals to the same level. After equivalent performance level was reached for all groups, we ran one session with laser presented on all trials during the session and compared performance to the previous session without laser for each animal. We ran two separate experiments for laser timings: one with the 1 second cue onset-trace-control laser experiment (for both CS+ and CS-) and another with laser during the 3 second period between cue onset and reward time (for both CS+ and CS-) (Supplementary Fig 7). We found no difference in performance due to the presence of laser in any case on the expression of learned behavior. The expression test was run at 100% probability for OFC-VTA and 50% for OFC-CaMKII. The numbers of animals run for this test were 7 cue onset, 8 trace and 7 controls for OFC-CaMKII; 15 experimental animals and 7 controls for inhibition during the full 3 second delay; 8 cue onset, 7 trace and 6 controls for the OFC-VTA group; and 18 experimental and 10 control animals for inhibition during the full 3 second period.

For the OFC-VTA group, in addition to the acquisition and expression experiments described above, we also tested if the trial-by-trial adaptation of reward seeking causally depended on the signaling of reward within OFC-VTA neurons. Since we did not observe trial-by-trial adaptation of CS+ trace interval responses (Supplementary Fig 11), we hypothesized that a functional role of OFC-VTA neurons, if any, in driving trial-by-trial adaptation would be restricted to the reward consumption period. Thus, we ran two separate experiments: one with inhibition during 3 s from cue onset (as a control) and another during 3 s from reward delivery or omission (Fig 8a). In order to test trial-by-trial adaptation in reward seeking, we calculated the net lick rate over baseline for trials in which the previous trial was rewarded minus the same measure for trials in which the previous trial was unrewarded (Fig 8c). The effect of laser on this measure of trial-by-trial adaptation (Learning Index) was then calculated by subtracting the Learning Index on the laser session and the previous session without laser (Fig 8e). This change from the pre-laser session was compared between the experimental and control groups. The comparison was done using a Welch’s t test so as to not assume homoscedasticity. 18 experimental animals and 10 control animals were run for this test.

Lastly, we tested the effect of inhibition of OFC-VTA neurons on extinction of a learned cue-reward pairing. Prior to running extinction, we ensured that every animal maintained high cue discrimination (> 0.4, i.e. auROC > 0.7) for at least two sessions on a 100% contingency. On the day of running extinction, we first ran a pre-extinction session of 50 trials (25 CS+ and 25 CS-) at 100% contingency to ensure that animals maintained high performance on the day. This performance level was equal for all groups (Fig 8g). During extinction (0% probability of reward), laser was presented for four seconds after cue offset. Since learning about extinction could not have happened until after the first trial, we defined the early extinction period as the next 5 trials. Late extinction was defined as the last 5 trials. After the extinction session, we ran another extinction session on the next day without laser. On this session, the amount of anticipatory licking on the first trial provided a measure for how much the animals recalled extinction. If animals licked at high levels during the first trial, it suggests a deficit in the memory of having learned the extinction contingency. A total of 15 experimental animals and 6 control animals were run on the extinction test.

Patch-clamp electrophysiology:

Whole-cell recordings of GCaMP6S-expressing neurons were performed 5–6 weeks after microinjections of AAVdj-CaMKII-GCaMP6S into each hemisphere of vmOFC (500 nL/side). Following surgery, mice were anesthetized with pentobarbital (50 mg/kg) and perfused with ice-cold (0–2 °C) sucrose cutting solution composed of the following in mM: 119 NaCl, 1.0 NaH₂P0₄, 4.9 MgCl₂, 0.1 CaCl₂, 26.2 NaHCO₃, 1.25 glucose (305–310 mOsm). Following perfusion, brains were removed within one minute, and coronal sections containing vmOFC (300 μm thick) were taken using a vibrating blade (Leica, VT 1200). Sections were then incubated in artificial cerebral spinal fluid (aCSF; 32 °C) containing the following in mM: 119 NaCl, 2.5 KCl, 1.0 NaH₂P0₄, 1.3 MgCl₂, 2.5 CaCl₂, 26.2 NaHCO₃, 15 glucose (305–310 mOsm). After one or more hours of recovery, slices were constantly perfused with aCSF and visualized using differential interference contrast through a 40x water-immersion objective mounted on an upright microscope (Olympus BX51WI). Whole-cell recordings were obtained using borosilicate pipettes (3–6 MΩ) back-filled with internal solution containing the following in mM: 130 K-gluconate, 10 KCl, 10 HEPES, 10 EGTA, 2 MgCl₂, 2 ATP, 0.2 GTP (pH 7.35; 285 mOsm).

Current-clamp recordings were obtained from GCaMP6S-expressing neurons to determine how calcium dynamics in vmOFC neurons correlated with action potential frequency. First, to determine how induction of action potentials from a quiescent state affected GCaMP6S fluorescence, neurons were held below resting membrane potential (−70 mV), and 4 spike trains of 1, 2, 4, and 8 action potentials were evoked in pseudorandom sequences (1 per neuron, 4 total sequences) using 2 ms, 2 nA depolarizing pulses (20 Hz). Each spike train was separated by 100, 500, 1000, or 5000 ms (all 4 timing configurations per neuron), resulting in 16 distinct protocols, which allowed us to identify how different spiking patterns might influence the dynamics of our recorded GCaMP6S signals. Next, we determined how changes in activity in tonically-firing vmOFC neurons might influence the calcium dynamics of those cells. Neurons were held below resting membrane potential (−70 mV), but baseline action potentials were evoked using the 2 ms, 2 nA depolarizing pulses (8 Hz). During this tonic firing, a short period of inhibition was introduced, wherein no spiking was enforced for 3 seconds. In addition, after another period of tonic firing (8 Hz), we elevated the enforced spike rate (16 Hz) for 1 second. Electrophysiological data acquisition occurred at 10 kHz sampling rate through a MultiClamp 700B amplifier connected to a Digidata 1440A digitizer (Molecular Devices). Data were analyzed using Clampfit 10.3 (Molecular Devices). GCaMP6S fluorescence dynamics was visualized using a mercury lamp (Olympus, U-RFL-T) and microscope-mounted camera (QImaging, optiMOS). Imaging data were acquired through Micro-Manager software, and extracted through hand-drawn regions of interest for each recorded neuron using ImageJ.

Retrograde tracing:

Retrograde tracing allowed us to identify the anatomical location and organization of OFC-VTA neurons (Supplementary Fig 8). Mice were injected with retrogradely-trafficked viruses encoding eYFP or tdTomato (AAV2retro-hSyn-eYFP; ~2×10¹² infectious units/mL; AAV2retro-CAG-tdTomato; ~2×10¹² infectious units/mL) into the VTA (500 nL/side; AP: −3.20 mm, ML: +/−0.60 mm, DV: −4.50 mm from bregma). Five weeks following surgery, mice were sacrificed for histology (n=2), and a student blind to all experiments counted the number of eYFP or tdTomato expressing neurons in vmOFC. Next, the anatomical location of each cell was measured using ImageJ.

Confocal microscopy:

Histological images were captured using a 20x air objective on a confocal microscope (model 710) with ZEN 2011 software (Carl Zeiss, Germany). Laser wavelengths and power intensities were optimized for each section and fluorophore. Tiled scans were stitched online and z-stacks were taken at 1 μm. The resulting stack was then averaged across all sections resulting in a maximum intensity projection, which was then presented or analyzed without further processing in ImageJ.

Data filtering and potential biases in data collection:

Mice were randomly selected for each of the experimental condition prior to surgery. As much as possible, littermates were used as controls for each optogenetic experiment. The experimenter was not blind to the virus injections. In the OFC-CaMKII optogenetic inhibition study (34 mice total), mice had to be run in three separate cohorts as it was practically infeasible to run more than 12 animals at a time due to a limitation on the number of behavioral boxes. These cohorts showed similar behavior and hence, were pooled for data analysis. In the OFC-VTA experiments, we expected experimental results to be less variable as the imaging data showed reduced heterogeneity across neurons (fewer clusters). Thus, we decided to run the experiments in a total of 23 mice. In this case, all animals were run in a single cohort as we added additional behavioral boxes. The order of running animals on any given day was generally fixed for a given animal but the animals run simultaneously across boxes were counterbalanced across each group for every experiment. Each experimental group was also counterbalanced between behavioral boxes. Every animal was given a supplemental water amount in addition to a behavioral session based on the requirement to maintain stable weight. This was done immediately after the session. This additional amount was different depending on the season during which the experiment was conducted (varying between ~0.3–0.9 mL on an average) but was similar across experimental and control groups within a cohort. The only mice excluded during the study were those in which experiments could not be conducted properly, either due to death or damage to the optic fiber prior to or during experiments, or incorrect delivery of light due to faulty patch cable connection.

Please check the “Life Sciences Reporting Summary” for a compilation of important details regarding the experimental and analytical pipeline.