Abstract
Multisite phosphorylation is an important mechanism of post-translational control of protein kinases. The effects of combinations of possible phosphorylation states on protein kinase activity are difficult to study experimentally because of challenges in isolating a particular phosphorylation state; surprising little effort on this topic has been expended in computational studies. To understand the effects of multisite phosphorylation on the plant protein kinase brassinosteroid insensitive 1-associated kinase 1 (BAK1) conformational ensemble, we performed Gaussian accelerated molecular dynamics simulations on eight BAK1 mod-forms involving phosphorylation of the four activation-loop threonine residues and binding of ATP-Mg2+. We find that unphosphorylated BAK1 transitions into an inactive conformation with a “cracked” activation loop and with the αC helix swung away from the active site. T450 phosphorylation can prevent the activation loop from cracking and keep the αC helix in an active-like conformation, whereas phosphorylation of T455 only slightly stabilizes the activation loop. There is a general trend of reduced flexibility in interlobe motion with increased phosphorylation. Interestingly, the αC helix is destabilized when the activation loop is fully phosphorylated but is again stabilized with ATP-Mg2+ bound. Our results provide insight into the mechanism of phosphorylation-controlled BAK1 activation while at the same time represent the first, to our knowledge, comprehensive, comparative study of the effects of combinatorial phosphorylation states on protein kinase conformational dynamics.
Significance
Protein kinases are regulated through post-translational phosphorylation, serving as a control switch for catalytic activity. Often, protein kinases are regulated by multiple phosphorylation sites, which can have nonadditive effects on catalytic activity. However, the relationship between phosphorylation state and function is difficult to study experimentally and has not been extensively explored. Using molecular dynamics simulations, we study how different phosphorylation states impact the stability of the active-like conformation of an important plant protein kinase, brassinosteroid insensitive 1-associated kinase 1 (BAK1). We find that a single phosphorylation site is largely responsible for stabilizing the active-like state, although other phosphorylation sites play a smaller role in influencing BAK1 dynamics. Together with previous experimental evidence, this suggests that several phosphorylation sites influence BAK1 function through a different mechanism.
Introduction
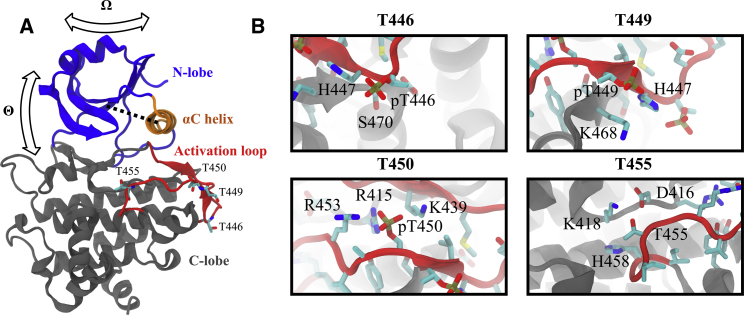
Protein kinases play the role of switches in the molecular circuitry of eukaryotic cells (1). Their ability to be switched on or off by phosphorylation while at the same time catalyzing phosphorylation of other proteins, often other protein kinases, allows for complex dynamics of a propagated signal at the cost of free energy (2,3). The central role of protein kinases in eukaryotic signaling pathways has driven intense research efforts to understand the structural basis of their phosphorylation-controlled activity. From this work, a number of structural features have been identified, which can be used to tell whether a particular protein kinase conformation is inactive, despite the diversity of protein kinase activation mechanisms (4, 5, 6). These features include (Fig. 1) proximal positioning of the αC helix with respect to the remainder of the N-lobe, stabilization of the activation loop in a conformation lying flat on the C-lobe, positioning of the DFG-motif-phenylalanine residue outside of the ATP-binding pocket (commonly called the DFG-in conformation), and binding of an ATP-Mg2+ complex. The absence of any one of these features signifies a likely inactive protein kinase, although formation of all features is no guarantee of activity. When the problem of interest is purely one of classification, automatic approaches based in machine learning can be used to identify active and inactive protein kinase conformations (7,8).
Figure 1.
(A) A crystal structure of the BAK1 kinase domain in an active-like conformation (PDB: 3TL8 (20), chain A). The structure is coarsely partitioned into important regions of note for our analysis and color coded in a manner consistent throughout this article. The four threonine phosphorylation sites on the BAK1 activation loop are shown. The interlobe opening angle and twisting angle as well as the αC helix to N-lobe β-sheet distance are shown. (B) Close-up views of the four threonine phosphorylation sites on the BAK1 activation loop and nearby residues are shown. The threonine residues are phosphorylated as in the crystal structure. This figure was produced using VMD 1.9.2 (30) and Inkscape 0.91 (46). To see this figure in color, go online.
A number of experimental and computational studies have sought to understand how phosphorylation alters the structural ensembles, and consequently the phosphotransferase activity, of protein kinases. Dual phosphorylation of human ERK2 kinase has been shown to cause a conformational change in the activation loop (9,10) and promote interlobe dynamics (11). Kuzmanic et al. (12) used metadynamics simulations to study the effects of dual phosphorylation, ATP, and Mg2+ binding and substrate binding on the p38α protein kinase free energy landscape, finding that dual phosphorylation is insufficient for activation. Although ATP-Mg2+ binding further stabilized the active-like conformations, the presence of all factors was found to be necessary for stabilization of the active-like conformation. We note that the presence of ATP and Mg2+ is necessary for a kinase to be functionally active, and we refer to conformations with the characteristics of the active state but without ATP and Mg2+ bound as active like. Ruff et al. (13) used spectroscopic methods coupled with molecular dynamics (MD) simulations to study the activation of Aurora kinase A, finding that phosphorylation of a single site stabilizes an active conformation of the activation loop within the DFG-in ensemble. Although these and other studies (14) have provided physical insight into phosphorylation-induced activation of protein kinases, very little work has focused on understanding the relationships between the combinatorial space of phosphorylation sites and protein kinase activation. Such relationships are important to understand because mappings of phosphorylation state to function, from rheostat-like behavior in which phosphotransfer activity is proportional to the number of phosphorylated sites to epistatic mappings with nonlinear relationships between phosphorylation sites and function, have significant consequences on signaling network dynamics (2,15).
Brassinosteroid insensitive 1-associated kinase 1 (BAK1) is a leucine-rich repeat (LRR) receptor-like kinase (RLK) responsible for initiation of several growth and immune signaling pathways in plants (16,17). BAK1 acts as a coreceptor to a number of other LRR-RLKs with larger LRR domains, associating with its coreceptors upon ligand binding and subsequently triggering either unidirectional or bidirectional phosphorylation of the intracellular kinase domains (16, 17, 18, 19). Although a great deal of effort has gone into understanding the signaling pathways in which BAK1 is involved, the physicochemical basis of BAK1 activation through phosphorylation remains unclear, although crystal structures of the BAK1 kinase domain (Fig. S1) have provided important clues (20,21) and our computational work has explored BAK1 kinase domain conformational dynamics (22, 23, 24).
Previously, Wang et al. (25) used a combination of in vitro kinase activity assays and mass spectrometry to explore the effects of mutating BAK1 phosphorylation sites on its activity toward a number of its LRR-RLK substrates. Their study revealed differential phosphorylation of LRR-RLK targets by BAK1 in vitro with different BAK1 phosphorylation patterns produced through mutations. Their results suggest that at least for phosphorylation of the other kinase domains tested, the BAK1 activation-loop residues T450 and T455 are the most important phosphorylation sites, followed by T446 and T449 and subsequently S290 and T312. These results raise the possibility that the phosphorylation pattern of BAK1 controls its specificity toward its many substrates, further supported by evidence that distinct sets of phosphorylation sites control BAK1 activity within brassinosteroid and immune signaling pathways (26). Other results from kinase activity assays using a peptide substrate found that a T455A mutation of BAK1, preventing T455 phosphorylation, had the largest effect on BAK1 activity, whereas mutation of the other three activation-loop threonine residues (T446, T449, T450) had less of an effect (27).
The experimental study of the mapping from phosphorylation states to protein conformational ensembles, and consequently function, are greatly complicated by difficulties in isolating specific phosphorylation states. On the other hand, all-atom computational models have no such difficulty while revealing physicochemical details underlying the behavior of a protein and thus present an attractive avenue for studying post-translational control of protein kinase function. In our view, a complete explanation of the mechanisms of protein kinase phosphorylation-controlled activity and specificity would require exploration of changes in the phosphotransfer reaction itself through quantum mechanics/molecular mechanics simulations, the BAK1 conformational ensemble through classical MD simulations, and the thermodynamics and kinetics of BAK1-substrate association through biased and/or coarse-grained MD. In this study, we focus on the second of these levels of biomolecular dynamics, exploring the impact of seven phosphorylation states constructed from the four threonine phosphorylation sites on the activation loop of BAK1, as well as the presence of ATP in the binding pocket on the conformational ensemble of BAK1. We used Gaussian accelerated MD (GAMD) simulations (28) to efficiently explore the conformational space of each mod-form without the need to define any collective variables on which to perform enhanced sampling.
Given the conserved structural features of protein kinases necessary for catalysis of phosphotransfer reactions (4), we compare the free energy landscapes over these features across all eight mod-forms, a term coined to generally describe modification states of proteins (29), to gain insight into how phosphorylation of BAK1 activation-loop residues individually and collectively affects the conformational aspect of BAK1 activation. We find that the activation loop of the unphosphorylated BAK1 kinase domain “cracks” and forms what is likely an inactive conformation. Phosphorylation of T450 alone, which is surrounded by positive residues in crystal structures (20,21), can prevent activation-loop cracking and hold the BAK1 activation loop in a largely active-like conformation. Phosphorylation of the four activation-loop threonine residues appears to additively reduce interlobe angular flexibility, in which the presence of ATP in the ATP-binding pocket ultimately promotes a more closed conformation. The αC helix is able to swing outward in the unphosphorylated state, whereas it appears unable to do so in the presence of any phosphorylation state we have examined. Additionally, the αC helix appears to remain largely intact except when all four activation-loop threonine residues are phosphorylated and ATP is not present.
Our results suggest that phosphorylation of T450 is the most important factor for controlling the features of activation that we have examined and provide an expanded structural basis for the primary importance of T450 and T455 phosphorylation in BAK1 activation. More generally, our study represents, to our knowledge, the first investigation of the relationship between combinatorial multisite phosphorylation in protein kinases and their conformational ensembles, revealing structural details underlying post-translational control of an important protein kinase.
Methods
System setup
All systems were set up using the psfgen plugin within VMD (30). The CHARMM 36 force field (31) was used for protein atoms. The protein atoms of the core BAK1 kinase domain were taken from a crystal structure (Protein Data Bank, PDB: 3TL8, chain A (20)), and all phosphoryl group atoms were removed. The desired phosphoryl groups for each system were added within psfgen, along with hydrogen atoms. The BAK1 structure was then solvated in a box of TIP3P (32) water molecules so that the edges of the box were 10 Å from any protein atom. Cl− and Na+ ions were added to neutralize each system and bring the salt concentration to ∼150 Mm. To add ATP and Mg2+ to BAK1, a PKA crystal structure (PDB: 4HPU (33)) containing AMP-PNP and two associated Mg2+ ions was aligned to BAK1 (PDB: 3TL8, chain A) using the MultiSeq VMD plugin (34), and the resulting AMP-PNP and Mg2+ coordinates were used to place ATP and Mg2+ into the BAK1 ATP-binding pocket. The ParmEd tool within AmberTools 18 (35) was used to convert X-PLOR format structure and topology files into Amber format.
Simulation details
All simulations were run in Amber18 (35) with a time step of 2 fs and with hydrogen-containing bonds constrained using the SHAKE algorithm (36). All production runs were maintained at constant temperature of 300 K using a Langevin thermostat with a coupling time constant of 2 ps and at a constant pressure of 1 bar using a Berendsen barostat with a τ of 1 ps. The particle mesh Ewald method (37) was used to treat electrostatics, and a cutoff of 10 Å was used for nonbonded interactions. Frames were saved to trajectory files every 10 ps.
All systems were subjected to energy minimization. For each of the eight systems, we initiated 10 independent simulations starting from the equilibration step and following the same procedure from then on. Each replicate was equilibrated for 20 ns and then run for an additional 26 ns to collect statistics for determination of GAMD (38) parameters. Using these parameters, independently estimated for each replicate, we ran 500 ns of GAMD simulations for each replicate, amounting to 5 μs of aggregate simulation time for each system.
Definitions of collective variables
N-lobe to C-lobe angles
We defined two angles between the BAK1 N-lobe and C-lobe to monitor twisting and bivalve-like opening motions. We defined the N-lobe β-sheet using the backbone atoms of residues 302–307, 313–319, and 360–364, and we defined the αE-helix using the backbone atoms of residues 388–406. For both sets of atoms in each frame, we calculated the inertia tensor:
| (1) |
where N is the number of atoms, is the mass of atom i, is the Cartesian coordinate column vector of atom i, and E is the identity tensor. Diagonalizing I yields
| (2) |
where the columns of Q contain the principal axes of rotation and is a diagonal matrix of the moments of inertia. We use the principal axis with the smallest corresponding moment of inertia to define the axis of the BAK1 N-lobe β-sheet, roughly parallel to the backbone in the sheet, and the helical axis of the αE-helix. We call these axes and , respectively. We note that one must take care to ensure that each axis has a consistent direction, related by multiplication by −1. A third vector in the C-lobe was defined by taking the center of mass of backbone atoms of residues 388–391 at one end of the αE-helix and of backbone atoms of residues 483–487 in the adjacent αF-helix, and calculating . The vectors and were used to define a C-lobe plane with a normal vector:
| (3) |
and the projection of onto the C-lobe plane was defined as . Then, the opening angle can be defined as
| (4) |
and the twisting angle can be defined as
| (5) |
Other collective variables
To measure its helical content, the αC helix was defined as residues 324–339. Helical content was measured according to the definition in the NAMD collective variable-based calculations manual (39). The activation loop was defined as residues 437–459, and the C-lobe excluding the activation loop, defined as residues 368–436 and residues 460–576, was used to align BAK1 to the crystal structure. The root mean-square deviation (RMSD) of the activation loop in each frame compared to the crystal structure was then measured. Swinging of the αC helix was described by the distance between the centers of mass of the previously chosen sets of atoms defining the αC helix and the N-lobe β-sheet . The DFG flip CV was defined as the distance between L404 α-carbon and C4 of the F435 side chain minus the distance between D416 α-carbon and C4 of the F435 side chain.
Unbiased PMFs from GAMD
We used the multistate Bennett acceptance ratio (MBAR) (40) to reweight samples from GAMD simulations. The MBAR estimator provides estimates of relative free energies and their covariance across different thermodynamic states. Using these relative free energy estimates, one can estimate unbiased potentials of mean force (PMFs) from samples produced by biased MD simulations, as in the case of GAMD. All MBAR analysis was done using pymbar 3.0.4 (41).
Typically, when using MBAR, PMFs are estimated through expectations using reweighted samples:
| (6) |
where is a function taking a value of 1 if x falls into bin i and 0 otherwise. To produce smooth PMFs, we instead use Gaussian basis functions:
| (7) |
where is the variable vector of interest, and σ is the bandwidth of the basis functions. In our analysis, . We assume zero local covariance between variables. The unbiased probability density is then estimated as an MBAR expectation value as follows:
| (8) |
where is the function mapping the full configuration of a frame to the collective variable vector . We estimate the PMF as follows:
| (9) |
subtracting an estimate of from each .
RMSFs
The root mean-square fluctuations (RMSFs) of BAK1 α-carbons were estimated from MD simulations by first aligning all frames to the crystal structure α-carbons and calculating α-carbon displacements according to
| (10) |
where is the coordinate vector for the α-carbon of residue i at time t, and is the coordinate vector of the same residue α-carbon in the crystal structure. The RMSF of α-carbons were then obtained according to
| (11) |
where the ensemble averages were estimated in the unbiased ensemble using MBAR.
General analysis
The structural alignment shown in Fig. S1 was performed using MultiSeq (34) within VMD 1.9.3. A large portion of analysis in Python was done using Jupyter Notebooks (42).
Results
A “canonical” inactive conformation of the BAK1 kinase domain
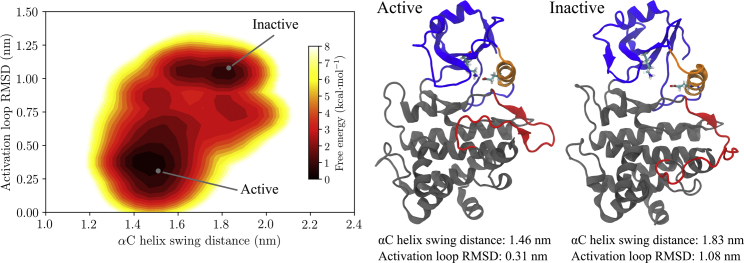
In GAMD simulations of the unphosphorylated BAK1 kinase domain, BAK1 underwent conformational changes into structures displaying classic characteristics of an inactive kinase domain (Fig. 2). The αC helix was able to swing away from the N-lobe into a metastable state with an αC helix to N-lobe β-sheet distance of around 1.8 nm in contrast to 1.5 nm in active-like conformations. The activation loop also underwent a conformational change, “cracking” in half into a far more open structure with an overall RMSD from the crystal structure of around 1.0 nm. This apparently metastable, inactive state is only accessible from the active-like state when the activation loop first begins to crack, followed by swinging of the αC helix.
Figure 2.
Left, the free energy landscape over αC-helix swinging distance and activation-loop RMSD to a crystal structure (PDB: 3TL8 (20), chain A) for the unphosphorylated BAK1 kinase domain. The locations of the two structures shown on the right, taken from trajectories, are indicated. The right section shows structures from simulations representing the metastable active-like and inactive free energy basins. Note the cracking of the activation loop and swinging of the αC helix away from the rest of the N-lobe in the inactive structure. Additionally, the αC helix in the inactive structure has partially unfolded. This figure was produced using VMD 1.9.2 (30), Matplotlib 1.5 (47), and Inkscape 0.91 (46). To see this figure in color, go online.
There was no flip from the DFG-in to DFG-out conformation (Fig. S18) in unphosphorylated BAK1 nor in any mod-form, as indicated by the purely negative values of the DFG flip CV defined in the Methods. However, the same DFG flip CV reveals a conformational change in the catalytic loop of unphosphorylated BAK1 (Fig. S18 A). The higher stability of conformations with DFG flip CVs less than −0.5 in unphosphorylated and pT455 BAK1 results from a flip of the catalytic loop away from the active site (Fig. S19), resulting in a greater distance between D416 and F435. This catalytic loop conformational change constitutes further movement from the active-like BAK1 structure in both the unphosphorylated and pT455 proteins.
Phosphorylation, especially of T450, stabilizes the active-like conformation
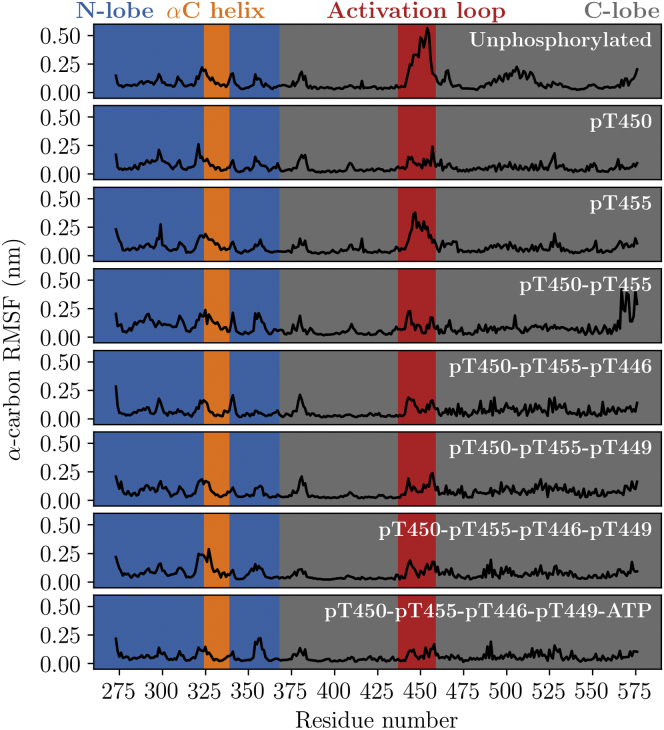
We calculated the RMSF of the BAK1 α-carbons in each mod-form to evaluate the effects of phosphorylation and ATP binding on overall backbone fluctuations. The BAK1 activation loop had large RMSF values in the unphosphorylated state (Fig. 3), indicating a high degree of structural motion. In comparison, the RMSF of the activation loop and the region from residues 475–525 is greatly reduced in the pT450 state, in addition to every other state in which T450 is phosphorylated. Although the RMSF of the activation loop is slightly reduced in the pT455 state as compared to the unphosphorylated state, the pT455 state has a higher RMSF in this region in comparison to all other states. These results suggest that phosphorylation of T450 may be critical for stabilizing the activation loop. Very little difference in the RMSF of the αC helix is apparent across all mod-forms.
Figure 3.
α-carbon RMSF of the BAK1 kinase domain for each mod-form calculated from GAMD simulations, reweighted using MBAR. Phosphorylation of T450 reduces the large activation-loop fluctuations seen in the unphosphorylated state, whereas phosphorylation of T455 is insufficient for activation-loop stabilization. This figure was produced using Matplotlib 1.5 (47). To see this figure in color, go online.
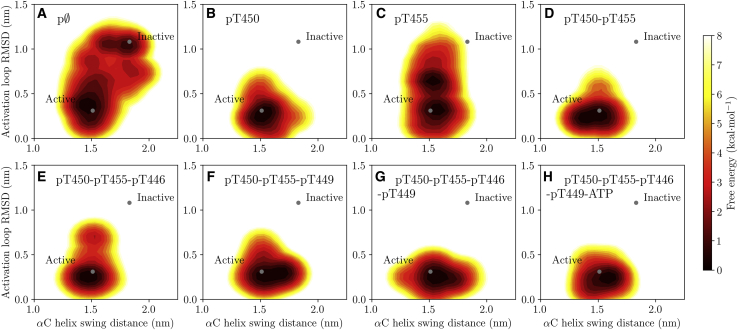
To further examine the effects of mod-form on activation-loop dynamics and αC-helix motion, we calculated PMFs over the αC-helix swing distance and activation-loop RMSD to a crystal structure (PDB: 3TL8 (20), chain A), both as described in the Methods. In agreement with our RMSF calculations, the BAK1 activation loop is able to explore a large range of conformations in the unphosphorylated state, as indicated by free energy minima at activation-loop RMSDs of 0.4 and 1.0 nm (Fig. 4 A). At the same time, the αC helix can swing out into its inactive conformation but only after the activation loop has changed conformation. Phosphorylation of T450 eliminates the second inactive minimum and stabilizes the activation loop at an RMSD of around 0.25 nm (Fig. 4 B). Phosphorylation of T455 alone appears to stabilize the activation loop to a small extent as compared to the unphosphorylated state (Fig. 4 C), again yielding two minima in the PMF, although the second minimum is shifted down to an activation-loop RMSD of around 0.6 nm. All other mod-form RMSD PMFs are similar to that of the pT450 state, although in the pT450-pT455-pT446 state, a second minimum in the PMF is evident, 2–3 kcalmol−1 less stable than the active-like state. In all mod-forms with any degree of phosphorylation, BAK1 exists in a single free energy basin in terms of αC-helix swinging distance. Overall, there appears to be a trend toward a larger swinging distance with more phosphorylation.
Figure 4.
PMFs over the BAK1 αC helix to N-lobe β-sheet center of mass distance and activation-loop RMSD with respect to a crystal structure (PDB: 3TL8 (20), chain A). The notation pϕ is used as shorthand for the unphosphorylated BAK1 kinase domain. The PMFs were calculated from GAMD simulations, reweighted using MBAR. This figure was produced using Matplotlib 1.5 (47). To see this figure in color, go online.
We evaluated the convergence of each PMF with sampling time (Figs. S2–S9), finding that all PMFs except for that of unphosphorylated BAK1 appear to have converged. However, the time series plots of unphosphorylated BAK1 in Figs. S2–S9 indicate that the large structural fluctuations implied by the corresponding PMF are not due to a single aberrant trajectory but reflect the behavior of several of the 10 trajectories. Additionally, we examined the effects of different bandwidths in the Gaussian basis functions used to estimate each PMF (Figs. S10–S17), finding no significant qualitative differences in the PMFs when using different bandwidths.
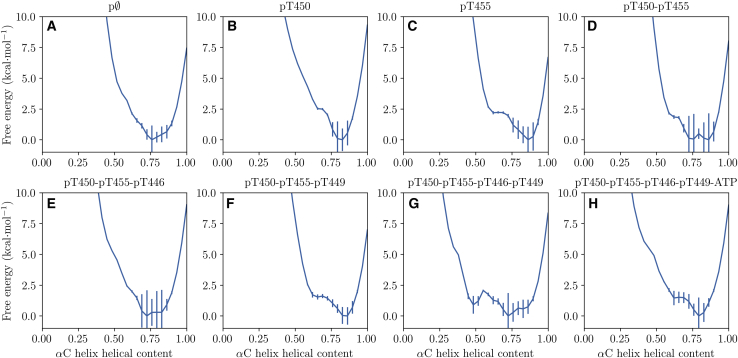
In previous work, we found local unfolding in the BAK1 αC helix (22,23). In all mod-forms simulated here, there was a certain degree of local αC-helix unfolding at its N-terminal end. However, for most mod-forms the αC helix remained stable at around 75% helical content (Fig. 5). Interestingly, when the BAK1 activation loop is fully phosphorylated but ATP is not present, a partially unfolded αC helix becomes more favorable (Fig. 5 G). Binding of ATP and Mg2+ appears to again promote a stable αC helix at 75% helical content (Fig. 5 H). The presence of local unfolding of the αC helix is in part consistent with previous results (22), even though in this case we do not consider phosphorylation of T324 adjacent to the αC helix and we observe a relatively stable αC helix once ATP and Mg2+ are bound.
Figure 5.
PMFs over the BAK1 αC-helix helical content. The notation pϕ is used as shorthand for the unphosphorylated BAK1 kinase domain. The PMFs were calculated from GAMD simulations, reweighted using MBAR, and error bars are MBAR standard deviations. This figure was produced using Matplotlib 1.5 (47). To see this figure in color, go online.
Additionally, phosphorylation of BAK1 constrains interlobe dynamics in our simulations. In unphosphorylated BAK1, the opening and twisting angles span larger ranges than in any other mod-form (Fig. S20). Two free energy minima exist in unphosphorylated BAK1, where the minimum with Ω ≈ 75° and 5° corresponds to a conformation with a largely open conformation. In contrast, when the BAK1 activation loop is fully phosphorylated and ATP and Mg2+ are bound, the N-lobe β-sheet is stabilized at an angle of around 60° and the N-lobe takes a slightly positive opening angle, likely as a result of accommodating ATP (Fig. S20 H).
Phosphosite contact probabilities
To better understand the physical mechanism through which phosphorylation affects BAK1 dynamics, we calculated MBAR reweighted contact probabilities for each of the activation-loop threonine residues with all other protein residues, using a cutoff distance of 0.4 nm and considering the minimum distance between pairs of heavy atoms.
Aside from its neighboring residues, the T446 side chain largely does not form any strong contacts (Fig. S21). In several mod-forms, T446 is in contact with one or both M441 and M551, both unlikely to be because of any direct interactions between T446 and either residue. Similarly, the T449 side chain does not maintain contact with many residues (Fig. S21), except for K468, regardless of whether T449 is phosphorylated, and R415 and K439. The fact that T449 is in contact with R415, K439, and L329 only in the unphosphorylated and pT455 mod-forms suggests that these contacts may form because of activation-loop fluctuations.
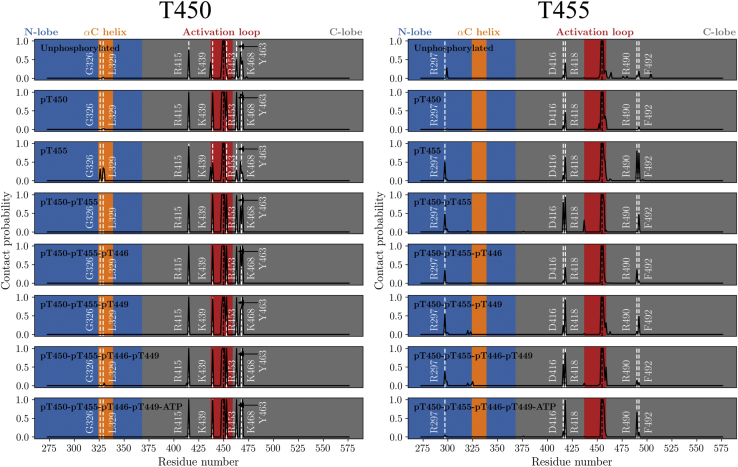
As in crystal structures (Fig. 1; (20,21)), T450 contacts R415, K439, Y463, and K468 in the active-like activation-loop conformation (Fig. 6). It is precisely these interactions between pT450 and the positively charged R415, K439, and K468 that are likely to be responsible for the ability of T450 to stabilize the activation loop in an active-like conformation, as suggested by the reduced contact probabilities in the unphosphorylated and pT455 mod-forms. It is clear from the T450 contact probabilities that phosphorylation of T450 itself is alone responsible for promoting these interactions, as in the pT455 state, the T450 contacts are far less often formed, whereas at the same time, the T450 contact probabilities in the pT450 state are essentially identical to all other mod-forms containing a phosphorylated T450.
Figure 6.
Contact probabilities for BAK1 T450 and T455 in each mod-form, reweighted using MBAR. The black dotted lines represent the reference threonine residue, whereas the white dotted lines denote contacting residues of interest. This figure was produced using Matplotlib 1.5 (47). To see this figure in color, go online.
Finally, the contacts of T455 indicate that T455 phosphorylation directly plays some role in influencing the interlobe dynamics by interacting with R297 on the N-lobe (Fig. 6). This contact is weak in the unphosphorylated state but is only absent in the pT450 and ATP-bound state, possibly because of the increased opening angle induced by ATP and Mg2+ binding (Fig. S20). Phosphorylation of T455 appears to promote interaction with R418, potentially explaining how T455 phosphorylation plays a role in weakly stabilizing the activation loop.
Discussion
We have described the effects of seven phosphorylation patterns (including the null, unphosphorylated, pattern) and ATP binding on the conformational dynamics of the BAK1 kinase domain. We have identified what may be a canonical, metastable inactive BAK1 kinase domain conformation, characterized by activation-loop cracking. This activation-loop conformational change is reminiscent of human ERK2 kinase, which takes on a similarly cracked activation-loop conformation when unphosphorylated (9), while taking on an active-like conformation when doubly phosphorylated (10). From our simulations, it appears that phosphorylation of T450 is most important for maintaining an active-like activation-loop conformation, whereas T455 phosphorylation may play a role in further stabilizing the activation loop. All examined phosphorylation states promote proximal positioning of the αC helix to the remainder of the N-lobe as compared to the unphosphorylated state, where the αC helix can swing into an inactive conformation only after a conformational change in the activation loop.
It is difficult to make comparisons with the available experimental data in a meaningful way because of the combination of means through which phosphorylation of a residue could influence the activity of BAK1 toward a given target. Purely in terms of BAK1 conformational dynamics, the T450 phosphorylation site appears to be most important for stabilizing a crystal-structure-like conformation. Phosphorylation of T455 appears to be of secondary importance, significantly stabilizing the activation loop only when T450 is also phosphorylated. From our results, T446 and T449 phosphorylation does not appear to significantly contribute toward stabilizing an active-like BAK1 conformation. By mutating BAK1 phosphorylation sites to alanine and examining the amount of phosphorylated substrate in vitro, several groups have found that T450 and T455 are likely the most functionally important sites, whereas T446 and T449 are less important because of the smaller effect of their mutation to alanine on substrate phosphorylation levels (25,27). However, it is unclear whether mutation of T455 has a larger effect than mutation of T450 (27) or if mutation of either has a similar effect, although this likely depends on the substrate.
As mentioned in the Introduction, we specifically focused on the effects of phosphorylation and ATP binding on the BAK1 kinase domain conformational dynamics, neglecting the possible effects of these changes to BAK1 on the catalyzed phosphotransfer reaction itself and on association with substrates. Although phosphorylation of T446 and T449 does not appear to affect BAK1 conformational dynamics significantly, it is possible that pT446 and pT449 play an important role in recognition of specific BAK1 substrates. Similarly, pT450 and pT455 may play some role in association with substrates or may alter the free energy landscape associated with phosphotransfer from ATP to the substrate. Both of these possibilities require future investigation.
For any BAK1 conformation to be active, ATP and Mg2+ must be bound. Ideally, we would have simulated each BAK1 phosphorylation state with and without ATP bound. However, we chose to examine ATP-bound BAK1 when all four activation-loop sites were phosphorylated to reduce the number of simulations required. We based this choice on the reasoning that mutation of any one of the activation-loop phosphorylation sites reduces BAK1 activity (25,27) so that it is reasonable to assume that pT450-pT455-pT446-pT449 BAK1 is a minimally phosphorylated, fully active kinase when ATP is bound.
It is important to note that as with any MD simulations of proteins, the total amount of sampling we have done is likely inadequate to completely describe the global conformational dynamics of the BAK1 kinase domain relevant to its biological function, even with the GAMD boost potentials applied. Although examples of estimated activation-loop timescales in other protein kinases are available, for example, in human Src kinase (43), it is difficult to know a priori how BAK1 activation-loop timescales will compare. Given the hierarchical structure of protein free energy landscapes (44,45), we could continue to simulate BAK1 on longer timescales while continuing to observe new behaviors with slower associated kinetics to no end. Still, it is likely that the behavior we have observed is relevant to dynamics in the local region of conformational space around the crystal structure, where all αC-helix swing distance and activation-loop RMSD PMFs appear locally converged with the exception of unphosphorylated BAK1 (Figs. S2–S9). Even though this unphosphorylated BAK1 PMF does not appear to be fully converged, the large fluctuations observed in several independent trajectories (Fig. S2) support the qualitative conclusions of this article.
One final factor influencing our results that must be discussed is our choice of starting crystal structure. Of the six available structures of the BAK1 kinase domain (Fig. S1), we chose chain A of PDB: 3TL8 (20). This structure, along with the three other chains of PDB: 3TL8, was acquired with the bacterial protein AvrPtoB bound to BAK1, inhibiting its kinase activity. The remaining two structures (21) are not bound to AvrPtoB. Although all six structures are similar (Fig. S1), with similar structural features indicating active-like conformations (Fig. S22), the structures corresponding to PDB: 3UIM and 3ULZ have partially disordered and thus partially resolved αC helices. We chose PDB: 3TL8 chain A because its highly ordered αC helix more closely resembles that of an idealized active-like protein kinase once the inhibiting AvrPtoB protein is removed. We also note that PDB: 3UIM and 3ULZ differ from all chains of PDB: 3TL8 slightly in the activation-loop conformation. It is likely that choosing PDB: 3UIM or 3ULZ as our starting structure would impact our results, but we believe that choosing a more active-like structure that did not require local structure prediction was the best possible option.
Author Contributions
A.S.M. and D.S. designed the research. A.S.M. performed the research and wrote the manuscript with input from D.S.
Editor: Alan Grossfield.
Footnotes
Supporting Material can be found online at https://doi.org/10.1016/j.bpj.2019.12.026.
Supporting Material
References
- 1.Bray D. Protein molecules as computational elements in living cells. Nature. 1995;376:307–312. doi: 10.1038/376307a0. [DOI] [PubMed] [Google Scholar]
- 2.Tyson J.J., Chen K.C., Novak B. Sniffers, buzzers, toggles and blinkers: dynamics of regulatory and signaling pathways in the cell. Curr. Opin. Cell Biol. 2003;15:221–231. doi: 10.1016/s0955-0674(03)00017-6. [DOI] [PubMed] [Google Scholar]
- 3.Kholodenko B.N. Cell-signalling dynamics in time and space. Nat. Rev. Mol. Cell Biol. 2006;7:165–176. doi: 10.1038/nrm1838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Taylor S.S., Kornev A.P. Protein kinases: evolution of dynamic regulatory proteins. Trends Biochem. Sci. 2011;36:65–77. doi: 10.1016/j.tibs.2010.09.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Taylor S.S., Keshwani M.M., Kornev A.P. Evolution of the eukaryotic protein kinases as dynamic molecular switches. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2012;367:2517–2528. doi: 10.1098/rstb.2012.0054. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Endicott J.A., Noble M.E., Johnson L.N. The structural basis for control of eukaryotic protein kinases. Annu. Rev. Biochem. 2012;81:587–613. doi: 10.1146/annurev-biochem-052410-090317. [DOI] [PubMed] [Google Scholar]
- 7.McSkimming D.I., Rasheed K., Kannan N. Classifying kinase conformations using a machine learning approach. BMC Bioinformatics. 2017;18:86. doi: 10.1186/s12859-017-1506-2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 8.Modi V., Dunbrack R.L., Jr. Defining a new nomenclature for the structures of active and inactive kinases. Proc. Natl. Acad. Sci. USA. 2019;116:6818–6827. doi: 10.1073/pnas.1814279116. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Zhang F., Strand A., Goldsmith E.J. Atomic structure of the MAP kinase ERK2 at 2.3 A resolution. Nature. 1994;367:704–711. doi: 10.1038/367704a0. [DOI] [PubMed] [Google Scholar]
- 10.Canagarajah B.J., Khokhlatchev A., Goldsmith E.J. Activation mechanism of the MAP kinase ERK2 by dual phosphorylation. Cell. 1997;90:859–869. doi: 10.1016/s0092-8674(00)80351-7. [DOI] [PubMed] [Google Scholar]
- 11.Xiao Y., Lee T., Ahn N.G. Phosphorylation releases constraints to domain motion in ERK2. Proc. Natl. Acad. Sci. USA. 2014;111:2506–2511. doi: 10.1073/pnas.1318899111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Kuzmanic A., Sutto L., Orozco M. Changes in the free-energy landscape of p38α MAP kinase through its canonical activation and binding events as studied by enhanced molecular dynamics simulations. eLife. 2017;6:e22175. doi: 10.7554/eLife.22175. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Ruff E.F., Muretta J.M., Levinson N.M. A dynamic mechanism for allosteric activation of Aurora kinase A by activation loop phosphorylation. eLife. 2018;7:e32766. doi: 10.7554/eLife.32766. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Barr D., Oashi T., van der Vaart A. Importance of domain closure for the autoactivation of ERK2. Biochemistry. 2011;50:8038–8048. doi: 10.1021/bi200503a. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Ferrell J.E., Jr., Ha S.H. Ultrasensitivity part II: multisite phosphorylation, stoichiometric inhibitors, and positive feedback. Trends Biochem. Sci. 2014;39:556–569. doi: 10.1016/j.tibs.2014.09.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 16.Chinchilla D., Shan L., Kemmerling B. One for all: the receptor-associated kinase BAK1. Trends Plant Sci. 2009;14:535–541. doi: 10.1016/j.tplants.2009.08.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Liebrand T.W., van den Burg H.A., Joosten M.H. Two for all: receptor-associated kinases SOBIR1 and BAK1. Trends Plant Sci. 2014;19:123–132. doi: 10.1016/j.tplants.2013.10.003. [DOI] [PubMed] [Google Scholar]
- 18.Macho A.P., Zipfel C. Plant PRRs and the activation of innate immune signaling. Mol. Cell. 2014;54:263–272. doi: 10.1016/j.molcel.2014.03.028. [DOI] [PubMed] [Google Scholar]
- 19.Belkhadir Y., Jaillais Y. The molecular circuitry of brassinosteroid signaling. New Phytol. 2015;206:522–540. doi: 10.1111/nph.13269. [DOI] [PubMed] [Google Scholar]
- 20.Cheng W., Munkvold K.R., Chai J. Structural analysis of Pseudomonas syringae AvrPtoB bound to host BAK1 reveals two similar kinase-interacting domains in a type III Effector. Cell Host Microbe. 2011;10:616–626. doi: 10.1016/j.chom.2011.10.013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yan L., Ma Y., Lou Z. Structural basis for the impact of phosphorylation on the activation of plant receptor-like kinase BAK1. Cell Res. 2012;22:1304–1308. doi: 10.1038/cr.2012.74. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Moffett A.S., Bender K.W., Shukla D. Molecular dynamics simulations reveal the conformational dynamics of Arabidopsis thaliana BRI1 and BAK1 receptor-like kinases. J. Biol. Chem. 2017;292:12643–12652. doi: 10.1074/jbc.M117.792762. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 23.Moffett A.S., Bender K.W., Shukla D. Allosteric control of a plant receptor kinase through S-glutathionylation. Biophys. J. 2017;113:2354–2363. doi: 10.1016/j.bpj.2017.08.059. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Moffett A.S., Shukla D. Using molecular simulation to explore the nanoscale dynamics of the plant kinome. Biochem. J. 2018;475:905–921. doi: 10.1042/BCJ20170299. [DOI] [PubMed] [Google Scholar]
- 25.Wang Y., Li Z., Shui W. Assessment of BAK1 activity in different plant receptor-like kinase complexes by quantitative profiling of phosphorylation patterns. J. Proteomics. 2014;108:484–493. doi: 10.1016/j.jprot.2014.06.009. [DOI] [PubMed] [Google Scholar]
- 26.Perraki A., DeFalco T.A., Zipfel C. Phosphocode-dependent functional dichotomy of a common co-receptor in plant signalling. Nature. 2018;561:248–252. doi: 10.1038/s41586-018-0471-x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 27.Wang X., Kota U., Clouse S.D. Sequential transphosphorylation of the BRI1/BAK1 receptor kinase complex impacts early events in brassinosteroid signaling. Dev. Cell. 2008;15:220–235. doi: 10.1016/j.devcel.2008.06.011. [DOI] [PubMed] [Google Scholar]
- 28.Miao Y., Sinko W., McCammon J.A. Improved reweighting of accelerated molecular dynamics simulations for free energy calculation. J. Chem. Theory Comput. 2014;10:2677–2689. doi: 10.1021/ct500090q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Prabakaran S., Lippens G., Gunawardena J. Post-translational modification: nature’s escape from genetic imprisonment and the basis for dynamic information encoding. Wiley Interdiscip. Rev. Syst. Biol. Med. 2012;4:565–583. doi: 10.1002/wsbm.1185. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 30.Humphrey W., Dalke A., Schulten K. VMD: visual molecular dynamics. J. Mol. Graph. 1996;14:33–38, 27–28. doi: 10.1016/0263-7855(96)00018-5. [DOI] [PubMed] [Google Scholar]
- 31.Huang J., MacKerell A.D., Jr. CHARMM36 all-atom additive protein force field: validation based on comparison to NMR data. J. Comput. Chem. 2013;34:2135–2145. doi: 10.1002/jcc.23354. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 32.Jorgensen W.L., Chandrasekhar J., Klein M.L. Comparison of simple potential functions for simulating liquid water. J. Chem. Phys. 1983;79:926–935. [Google Scholar]
- 33.Bastidas A.C., Deal M.S., Taylor S.S. Phosphoryl transfer by protein kinase A is captured in a crystal lattice. J. Am. Chem. Soc. 2013;135:4788–4798. doi: 10.1021/ja312237q. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Roberts E., Eargle J., Luthey-Schulten Z. MultiSeq: unifying sequence and structure data for evolutionary analysis. BMC Bioinformatics. 2006;7:382. doi: 10.1186/1471-2105-7-382. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Case D.A., Ben-Shalom I.Y., Kollman P.A. University of California; San Francisco: 2018. AMBER 2018. [Google Scholar]
- 36.Miyamoto S., Kollman K.A. SETTLE: an analytical version of the SHAKE and RATTLE algorithm for rigid water models. J. Comput. Chem. 1992;13:952–962. [Google Scholar]
- 37.Darden T., York D., Pedersen L. Particle mesh Ewald: an N log(N) method for Ewald sums in large systems. J. Chem. Phys. 1993;98:10089–10092. [Google Scholar]
- 38.Miao Y., Feher V.A., McCammon J.A. Gaussian accelerated molecular dynamics: unconstrained enhanced sampling and free energy calculation. J. Chem. Theory Comput. 2015;11:3584–3595. doi: 10.1021/acs.jctc.5b00436. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Phillips J.C., Braun R., Schulten K. Scalable molecular dynamics with NAMD. J. Comput. Chem. 2005;26:1781–1802. doi: 10.1002/jcc.20289. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Shirts M.R., Chodera J.D. Statistically optimal analysis of samples from multiple equilibrium states. J. Chem. Phys. 2008;129:124105. doi: 10.1063/1.2978177. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 41.Beauchamp K.A., Chodera J.D., Shirts M.R. pymbar 3.0.4 (Chodera Lab) https://github.com/choderalab/pymbar
- 42.Kluyver T., Ragan-Kelley B., Willing C., Jupyter Development Team . Jupyter Notebooks-a publishing format for reproducible computational workflows. In: Loizides F., Schmidt B., editors. Positioning and Power in Academic Publishing: Players, Agents and Agendas. IOS press; 2016. pp. 87–90. [Google Scholar]
- 43.Shukla D., Meng Y., Pande V.S. Activation pathway of Src kinase reveals intermediate states as targets for drug design. Nat. Commun. 2014;5:3397. doi: 10.1038/ncomms4397. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Hu X., Hong L., Smith J.C. The dynamics of single protein molecules is non-equilibrium and self-similar over thirteen decades in time. Nat. Phys. 2016;12:171–174. [Google Scholar]
- 45.Ye W., Götz M., Sönnichsen C. Conformational dynamics of a single protein monitored for 24 h at video rate. Nano Lett. 2018;18:6633–6637. doi: 10.1021/acs.nanolett.8b03342. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 46.Inkscape Project Team . Free Software Foundation; 1991. Inkscape 0.91.http://inkscape.org [Google Scholar]
- 47.Hunter J.D. Matplotlib: a 2D graphics environment. Comput. Sci. Eng. 2007;9:90–95. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.