BATCAVE: calling somatic mutations with a tumor- and site-specific prior

Abstract

Detecting somatic mutations withins tumors is key to understanding treatment resistance, patient prognosis and tumor evolution. Mutations at low allelic frequency, those present in only a small portion of tumor cells, are particularly difficult to detect. Many algorithms have been developed to detect such mutations, but none models a key aspect of tumor biology. Namely, every tumor has its own profile of mutation types that it tends to generate. We present BATCAVE (Bayesian Analysis Tools for Context-Aware Variant Evaluation), an algorithm that first learns the individual tumor mutational profile and mutation rate then uses them in a prior for evaluating potential mutations. We also present an R implementation of the algorithm, built on the popular caller MuTect. Using simulations, we show that adding the BATCAVE algorithm to MuTect improves variant detection. It also improves the calibration of posterior probabilities, enabling more principled tradeoff between precision and recall. We also show that BATCAVE performs well on real data. Our implementation is computationally inexpensive and straightforward to incorporate into existing MuTect pipelines. More broadly, the algorithm can be added to other variant callers, and it can be extended to include additional biological features that affect mutation generation.

INTRODUCTION

Cancer develops through the accumulation of somatic mutations and clonal selection of cells with mutations that confer an advantage. Understanding the evolutionary history of a tumor, including the mutations that drive its growth, the genetic diversity within it and the accumulation of new mutations, requires accurate variant identification, particularly at low variant allele frequency (1–4). Accurate variant calling is also critical for optimizing the treatment of individual patients’ disease (5–9). Low frequency mutations challenge current variant calling methods, because their signature in the data is difficult to distinguish from the noise introduced by Next Generation Sequencing (NGS), and this challenge increases with sequencing depth.

Many methods have been developed for calling somatic mutations from NGS data. The earliest widely used somatic variant callers developed specifically for tumors, MuTect1 (10) and Varscan2 (11), used a combination of heuristic filtering and a model of sequencing errors to identify and score potential variants and set a threshold score designed to balance sensitivity and specificity. Subsequent research gave rise to a number of alternate strategies, including haplotype-based calling (12), joint genotype analysis (SomaticSniper (13), JointSNVMix2 (14), Seurat (15), CaVEMan (16) and MuClone (17)), allele frequency-based analysis (Strelka2 (18), LoFreq (19), EBCall (20), deepSNV (21), LoLoPicker (22), and MuSE (23)), and ensemble and deep learning methods (MutationSeq (5), BAYSIC (24), SomaticSeq (25) and SNooPer (26)). These methods vary in their complexity and specific focus. But they all implicitly or explicitly assume that the rate of mutation is uniform across the genome.

The mutational processes that generate single nucleotide variants in tumors do not act uniformly across the genome. If fact, even the processes of spontaneous mutation that are active in all somatic tissues depend sensitively on local nucleotide context (27–29). Additional mutational processes are active in tumors, due to mutagen exposure or defects in DNA maintenance and repair, and these processes are also sensitive to local nucleotide context (30–34). The specific mutational processes active in a particular tumor generate its unique mutation profile, and differences within and between tumor types are pronounced (35–39). For example, the mutation profiles differ substantially among the three breast tumors illustrated in Figure 1B–D.

Figure 1.

Real tumor mutation profiles. In each panel, the x-axis corresponds to each of the 96 possible mutation types, and the y-axis is the proportion of total mutations of each type. (A) The observed mutation profile of an acute myeloid leukemia used in our real data analysis (52). (B) The observed mutation profile of a breast tumor used in our real data analysis (4). (C and D) The observed mutation profiles of two additional breast tumors (53).

Here we present an enhanced variant-calling algorithm that uses the biology of each individual tumor’s mutation profile to improve identification of low allelic frequency mutations. Our BATCAVE algorithm first estimates the tumor’s mutation profile and mutation rate using high-confidence variants and then uses them as a prior when calling other variants. Our R implementation of the algorithm, batcaver, takes output from the MuTect variant caller as input and returns the posterior probability that a site is variant for every site observed by MuTect. Using both simulated and real data, we show that the addition of a mutation profile prior to MuTect produces a superior variant caller. Our algorithm is simple and computationally inexpensive, and it can be integrated into numerous other variant callers. Broad adoption of our approach will enable more confident study of low allelic frequency mutations in tumors in both research and clinical settings.

MATERIALS AND METHODS

Somatic variant calling probability model

At every site in the genome with non-zero coverage, Next Generation Sequencing produces a vector 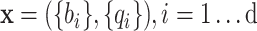of base calls b and their associated quality scores q, where d is local read depth. Variant callers use the data to choose between competing hypotheses:

(1)

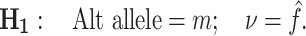(2)

Here m is any of the three possible alternate non-reference bases and ν is the variant allele frequency. The maximum likelihood estimate of ν is simply , the number of variant reads divided by the local read depth. The posterior probability of a given hypothesis, P(m, ν), is the product of the likelihood of the data given that hypothesis and the prior probability of that hypothesis. Assuming that reads are independent, this is

(3)

where f_{m, ν}(x_i) is the probability model for reads, and p(m, ν) is the prior.

Assuming that the identity of the alternate allele and its allele frequency are independent and that ν is uniformly distributed, equation (3) becomes

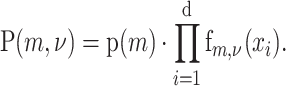(4)

The focus of BATCAVE is to provide a tumor- and site-specific estimate of the prior probability of mutation p(m).

Site-specific prior probability of mutation

The probability that we have denoted p(m) in equation (4) is more precisely the joint probability that a mutation has occurred M and that it was to allele m, which we denote p(m, M). But p(m, M) is not uniform across the genome. Rather it depends on the local genomic context C, so its full form is p(m, M|C) (40). Assuming that m and M are independent conditional on the genomic context, p(m, M∣C) = p(m∣C)p(M∣C), which we can use Bayes’ theorem to further decompose as

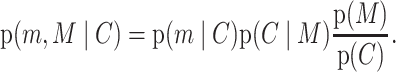(5)

We next show how to estimate the quantities in equation (5).

Estimation of the mutation profile

Many aspects of genomic architecture can affect the somatic mutation rate at multiple scales (40). Here we focus on a small-scale feature, the trinucleotide context, which is known to strongly affect the prior probability of single-nucleotide mutation (27–29). The trinucleotide context of a genomic site consists of the identity of the reference base and the 3’ and 5’ flanking bases. There are six classes of base substitution: C>A, C>G, C>T, T>A, T>C, T>G (all referred to by the pyrimidine of the mutated Watson-Crick pair). This results in a total of 32 (4 × 2 × 4) reference contexts and 3 alternate bases per reference base. Indexing by the c = {1…32} contexts and by the m = {1…3} alternate bases, we have 96 possible substitution types S_{m, c}. equation (5) is then

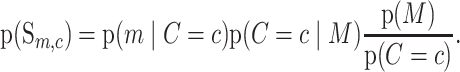(6)

The first two terms on the right-hand side can be estimated from the observed mutation profile (Figure 1).

We model the observed mutation profile S as multinomial with parameter . Each element of represents the expected proportion of mutations that are to allele m and in context c. In a tumor with many high-confidence observed mutations, could be estimated directly from the observed mutation profile S. But in practice many entries in would then have zero weight. We thus model the distribution of S as Dirichlet-multinomial with pseudo-count hyper-parameter ,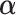

(7)

In BATCAVE we use the symmetric non-informative hyper-parameter 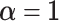, so a priori mutation is equally likely to any allele and in any context.

To estimate , we identify a subset of high confidence variants, based on an initial calculation of their likelihood given the data. These are variants for which the evidence in the read data overwhelms any reasonable value of the site-specific prior probability of mutation. Let D be the set of high confidence variant calls, which we define as those having posterior odds >10 to 1 without the site-specific prior and s ∈ D be the substitution type of each mutation in D. The posterior distribution of is then 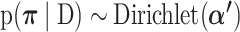where

(8)

andI is the indicator function. Returning to Equation (6), given that a mutation has occurred, the posterior probability it occurred in context c is

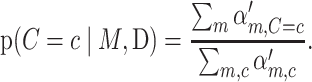(9)

The posterior probability of mutation to allele m given that a mutation has occurred in context C = c is then

(10)

The prior probability of each particular trinucleotide context p(C = c) is computed simply as the proportion of sequenced trinucleotide contexts that have context c. The R implementation of BATCAVE ships with pre-computed tables for both human whole exomes and whole genomes.

Estimation of the mutation rate

The final piece of Equation (6) is p(M), the prior probability of mutation, which we specify as the per-base per-division mutation rate μ. In an exponentially growing and neutrally evolving tumor, branching process calculations (3) show that the expected total number of mutations M_tot between two allele frequencies (f_min, f_max) is

(11)

The number of bases N is 3 · 10⁹ for a whole genome and 3 · 10⁷ for a whole exome. The quantity μ/β is the effective mutation rate, where β is the fraction of cell divisions that lead to two surviving lineages. We make the simplifying assumption that there is no cell death (β = 1), so we somewhat over-estimate μ. We then estimate μ by counting observed high-confidence mutations between allele frequencies f_min and f_max. Sample contamination by normal cells can result in underestimation of tumor mutation allele frequencies. To account for this, our implementation of BATCAVE takes as input an estimated sample purity p_ur. All estimated allele frequencies are then multiplied by a factor of 1/p_ur before being used in equation (11). We set f_max to be the largest allele frequency in D, but we must choose f_min conservatively, depending on sequencing depth. In the R implementation of BATCAVE, f_min and p_ur are free parameters. For this paper, we set f_min = 0.05, because we are working at high depth. For our simulated data analyses, we set p_ur = 1, and for our real data analyses, we set p_ur to the estimated purity.

Likelihood function

The current implementation of BATCAVE builds on MuTect, because MuTect reports the log ratio of the likelihood functions for the null and alternative hypotheses (Equation 1) as TLOD (MuTect1) or t_lod_fstar (MuTect2). We used MuTect 1.1.7 for all analyses in this paper, so we have

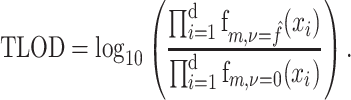(12)

The log posterior odds is the log likelihood ratio (TLOD) plus the log prior odds, so the posterior odds in favor of the alternate hypothesis for a given substitution type is

(13)

Here p(S_{m, c}) is the prior probability of a substitution of type S_{m, c}, as described in equation (6) and specified in equations (9)–(11). When comparing our posterior odds to those of MuTect, we assume a uniform per-base probability of mutation of 3 · 10⁻⁶ (10), so

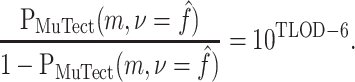(14)

Implementation

We have implemented the BATCAVE algorithm as an R package called batcaver. The package leverages the Bioconductor packages BSgenome (41), GenomicAlignments (42), VariantAnnotation (43), and SomaticSignatures (44) for fast and memory-efficient variant annotation and genomic context identification. Reference sequences are specified as BSgenome objects, allowing efficient access to genomic context information.

An assumption of the BATCAVE algorithm is that the mutation profile of low-confidence mutations is similar to that of the high-confidence mutations from which the prior is inferred. To test this assumption, batcaver performs a statistical hypothesis test comparing these two mutation profiles (45). If the two profiles differ at a significance threshold of α = 0.05, batcaver issues a warning and outputs the profiles.

Tumor simulations

We used a neutral branching process with no death and μ = 3 · 10⁻⁶ to simulate realistic distributions of mutation frequencies. Tumors were simulated with three different mutation profiles composed of COSMIC mutation signatures (version 2) (46). Each simulated profile includes COSMIC signature 1, which is found in nearly all tumors and is associated with spontaneous cytosine deamination. The ‘Concentrated’ profile (Figure 2A) is an equal combination of COSMIC signatures 1, 7,and 11, which has a large percentage of C > T substitutions such as are often seen in cancers caused by UV exposure (47). The ‘Intermediate’ profile (Figure 2B) is an equal combination of COSMIC signatures 1, 4 and 5, which has been associated with tobacco carcinogens and is representative of some lung cancers (47). The ‘Diffuse’ profile (Figure 2C) is an equal combination of COSMIC signatures 1, 3, and 5, which has been associated with inactivating germline mutations in the BRCA1/2 genes leading to a deficiency in DNA double strand break repair (32). Simulated variants were sampled from a combination of the Cancer Genome Atlas (TCGA) and Pan-Cancer Analysis of Whole Genomes (PCAWG) databases, which include mutations found in all types of cancer. Whole genome (100× depth) and whole exome (500X depth) reads were simulated from the GRCh38 reference genome using VarSim (48) and aligned with BWA (49), both with default parameters. Variants were inserted to create tumors with BAMSurgeon with default parameters (50) and called with MuTect 1.1.7 (10) with the following parameters:

Figure 2.

Simulated tumor mutation profiles. As in Figure 1, in each panel the x-axis corresponds to each of the 96 possible mutation types, and the y-axis is the proportion of total mutations of each type. (A) A mutation profile used for simulating tumors, made up of equal proportions of COSMIC mutation signatures 1, 7 and 11. (B) Equal proportions of signatures 1, 4 and 5. (C) Equal proportions of signatures 1, 3 and 5.

java -Xmx24g -jar $MUTECT_JAR –analysis_type MuTect –reference_sequence $ref_path –dbsnp $db_snp –enable_extended_output –fraction_contamination 0.00 –tumor_f_pretest 0.00 –initial_tumor_lod -10.00 –required_maximum_alt_allele_mapping_quality_score 1 –input_file:normal $tmp_normal –input_file:tumor $tmp_tumor –out $out_path/$chr.txt –coverage_file $out_path/$chr.cov.

Variants identified by MuTect are labeled as to whether they pass all filters, fail to pass only the the evidence threshold tlod_f_star filter, or fail to pass any other filter. Variants that passed all filters or failed only tlod_f_star were then passed to BATCAVE for prior estimation and rescoring.

Calibration metric

To quantify the difference in calibration between MuTect and BATCAVE, we used the Integrated Calibration Index (51). Briefly, a loess-smoothed regression was fit by regressing the binary (True=1, False=0) true variant classification against the reported posterior probability for both MuTect and BATCAVE. For a perfectly calibrated caller, the regression fit would be the diagonal line y = x. The Integrated Calibration Index is a weighted average of the absolute distance between the calibration curve and the diagonal line of perfect calibration.

Real data

We analyzed two real datasets, one from an acute myeloid leukemia (AML) (52) and one from a multi-region sequencing experiment in breast cancer (4). We downloaded the normal and primary whole-genome AML tumor bam files from dbGaP accession number phs000159.v8.p4. Griffith et al. generated a platinum set of variant calls for this tumor (52), which we used for our true positive dataset. We downloaded the normal and tumor whole-exome breast cancer bam files from NCBI Sequence Read Archive accession SRP070662. Griffith et al. estimated the purity of their primary sample to be 90.7%, and we used this value for tumor purity in batcaver. Shi et al. generated a gold set of variant calls for each tumor region sequenced (4), which we used for our true positive dataset. For these multi-region data, we analyzed the three biological replicates from each of six tumors (Table 1), running BATCAVE separately on each of the eighteen samples, and we combined results to generate precision-recall curves. Shi et al. estimated sample purities of between 26 and 80%, and we used these estimates in batcaver. We called variants using Mutect 1.1.7 as in our simulations, except that both these datasets were originally aligned to GRCh37, so we used that reference.

Table 1.

Variant calling metrics for all datasets

			AUROC		AUPRC		ICI
Scenario	Mutation profile	μ (estimated)	MuTect	BATCAVE	MuTect	BATCAVE	MuTect	BATCAVE
100× whole genome	Concentrated	3.6e-7	0.987	0.993	0.972	0.975	0.117	0.287
100× whole genome	Intermediate	3.2e-7	0.987	0.989	0.972	0.973	0.118	0.214
100× whole genome	Diffuse	3.2e-7	0.988	0.989	0.971	0.973	0.120	0.219
500× whole exome	Concentrated	3.6e-7	0.848	0.929	0.674	0.758	0.138	0.109
500× whole exome	Intermediate	3.6e-7	0.847	0.881	0.677	0.706	0.108	0.112
500× whole exome	Diffuse	3.6e-7	0.850	0.873	0.676	0.698	0.105	0.116
real AML (52)	Actual	3.6e-8			0.996	0.988
real breast (4)	Actual	6.6e-7			0.972	0.968

μ = per-base mutation rate, AUROC/AUPRC = Area Under Receiver Operating Characteristic/Precision-Recall Curve, ICI = Integrated Calibration Index. Smaller values of ICI are superior.

RESULTS

We implemented BATCAVE as a post-call variant evaluation algorithm to be used with MuTect (Versions 1.1.7 or >2.0) (10). BATCAVE extracts the log-likelihood ratio for each potential variant site from the MuTect output, and then it uses that ratio to separate the potential sites into high and low confidence groups. The mutation profile and mutation rate are estimated from the high confidence sites, and the posterior probability of mutation is then recomputed for all sites. The BATCAVE algorithm is inexpensive, processing 22 000 variants per second on a typical desktop computer, which corresponds to roughly 100 s to process a 500× exome and 2000 s for a 100× whole genome.

To test the performance of BATCAVE, we generated six different tumor/normal pairs, corresponding to 100X whole genomes and 500X whole exomes for three different mutation profiles. The three mutation profiles were chosen to resemble a melanoma (concentrated), a lung cancer (intermediate), and a BRCA-driven breast cancer (diffuse) (Figure 2). We also tested BATCAVE using two real cancer datasets, a whole-genome Acute Myeloid Leukemia (AML) (52) and a whole-exome multi-region breast cancer (4). In both, deep sequencing and variant validation were performed with the specific purpose of evaluating tumor variant calling pipelines. Because our focus is on evaluating the statistical calling model, we computed all test metrics using only those potential variants that passed MuTect’s heuristic filters and entered the statistical model.

Tests using simulated data

To improve variant identification, the context-dependent prior probability of mutation must converge to an accurate representation of the data generating distribution within the set of high-confidence mutations. When applied to simulated data, the prior converged within a few hundred mutations (Figure 3), and the batcaver package emits a warning if there are fewer than 500 high-confidence mutations. For comparison, in our simulated datasets the number of high-confidence mutations ranged between 1500 and 5000, and in the real AML we test on it is over 17 000 (52).

Figure 3.

Convergence of the mutational prior to the data generating distribution. Plotted is the Kullback–Leibler divergence between the simulated and estimated profiles versus number of incorporated mutations for whole exomes. Convergence for whole genomes is similar.

We assessed classification performance using the areas under both the receiver operating characteristic and the precision-recall curves, because the classes are unbalanced (∼5 to 1 ratio of false to true variants in our simulated data). By both metrics BATCAVE outperforms MuTect (Figure 4A-B, Supplementary Figure S1A-B and Table 1). The extent of the performance difference is dependent on both the sequencing depth and the concentration of the mutation profile. Deeper sequencing and more concentrated mutation profiles increase the performance advantage of BATCAVE.

Figure 4.

Variant-calling performance on simulated and real data. Throughout, MuTect results are plotted with gray lines and BATCAVE results with black lines. (A) Precision-recall curves and (B) receiver operating characteristic curves for different mutation profiles. (C and D) Calibration plots. Shaded regions show distributions of posterior probabilities for true positive variants, and smooth lines show loess-smoothed relationships, from which the Integrated Calibration Index is calculated. For a perfectly calibrated caller, those curves would match the dashed y=x line. (E and F) Precision-recall curves for real data in which substantial mutation validation was performed (4,52).

For all simulated tumors, the estimated mutation rate was ∼3 · 10⁻⁷ (Table 1), which is lower than the simulated rate of 3 · 10⁻⁶. This is likely due to restrictions within BAMSurgeon, such as sequencing depth and quality, that prevent 100% of simulated variants from being inserted into the reads.

We also assessed calibration, the likelihood that a potential variant with a given posterior probability is actually a true variant. We measured overall calibration performance using the Integrated Calibration Index (ICI) (51), which integrates the difference between predicted and observed probabilities, weighted by the density of the predicted probabilities. This metric is particularly useful in our case, because the density of posterior probabilities is bi-modal (Figure 4C-D and Supplementary Figure S1C-D). A large fraction of true negative variants have posterior probabilities less than 10⁻⁴, far below any meaningful threshold, so we evaluated calibration only on potential variants with posterior probability >0.01. For these potential variants, BATCAVE tends to increase posterior probabilities of low probability but true variants (density curves in Figures 4C-D and Supplementary Figure S1C-D) while decreasing probabilities of low probability but false variants. For 500× exomes, the calibration of BATCAVE is better than MuTect across the full spectrum of posterior probabilities (Figure 4 and Table 1). For 100× whole genomes, the calibration of BATCAVE is slightly worse (Supplementary Figure S1 and Table 1), likely because there are few low probability true positive variants in tumors sequenced to 100× depth. As with the other metrics, the advantage of BATCAVE increases with the concentration of the mutation profile and the sequencing depth.

In practice, variant callers are typically used with a threshold score above which a variant is called. The user’s choice of threshold ideally meets their need to balance precision and recall; accurate posterior probability estimates enable an informed choice. For posterior probability thresholds between 60 and 90%, the precision of BATCAVE calls is similar to the chosen threshold (Figure 5 and Supplementary Figure S2). For this range of thresholds, however, the posterior probabilities from MuTect poorly predict precision (Figure 5 and Supplementary Figure S2). For any posterior probability threshold above 70%, MuTect has a false positive rate of roughly 8%, whereas BATCAVE has a false positive rate that decreases as the threshold increases. The cost of MuTect’s compressed range of posterior probabilities is recall; at any posterior probability threshold BATCAVE has recall better than MuTect. Consequently, BATCAVE posterior probabilities are more informative than MuTect’s with regard to choosing a calling threshold.

Figure 5.

Posterior probability calibration for realistic calling thresholds, for 500× exomes. Plotted is precision and recall for variants identified using various realistic posterior probability thresholds. At these thresholds, the precision of BATCAVE is much closer to the given threshold than MuTect, no matter the concentration of the mutation profile.

Tests using real tumor data

We tested BATCAVE using two datasets for which deep sequencing and variant validation were performed with the express purpose of evaluating tumor variant calling pipelines, yielding high quality true and false positive data (4,52). However, only variants called by at least one variant caller were validated. As a result, there are no validated true or false negative calls, so we considered only precision-recall comparisons for these data.

Griffith et al. sequenced the whole genome of an acute myeloid leukemia (AML) primary tumor to a depth of >360× and used targeted sequencing to validate nearly 200 000 mutations (52). We estimated a per-base mutation rate for this tumor of 3.6 × 10⁻⁸, which is consistent with previous estimates of AML mutation rates (3,52). For this tumor, the mutation profiles of high- and low-confidence mutations differ (p ∼ 10⁻¹²). The low-confidence mutation profile contains additional spikes of mutations corresponding to five substitution types (Supplementary Figure S3). Nevertheless, for both MuTect and BATCAVE, the precision-recall curve is almost perfect for the validated variants (0.988 and 0.996 area under the curve) (Figure 4E and Table 1).

Shi et al. performed multi-region whole exome sequencing on six individual breast tumors to a mean target sequencing depth of 160× and validated all variants identified by three different variant calling pipelines (4). We estimated an average per-base mutation rate for these tumor regions of 6.6 × 10⁻⁷, which is consistent with observed mutation rates for breast cancers (53) and with the low number of validated somatic mutations. For the validated variants, MuTect and BATCAVE yielded almost identical precision-recall curves (Figure 4F and Table 1)

DISCUSSION

BATCAVE is an algorithm that leverages the biology of individual tumor mutation profiles to improve identification of low allelic frequency somatic variants. Our implementation is built on MuTect, one of the most widely used somatic variant callers. BATCAVE improves on the classification accuracy of MuTect in synthetic data (Figure 4A–D, Supplementary Figure S1 and Table 1) across the entire range of recall and specificity. Moreover, BATCAVE is better calibrated than MuTect at relevant posterior probability thresholds (Figure 5 and Supplementary Figure S2), allowing researchers and clinicians to make informed choices about the trade-off between precision and recall. For real data, testing on validated calls shows that BATCAVE does not degrade performance for variants that are relatively easy to identify (Figure 4E-F and Table 1). The BATCAVE algorithm can thus be included in a wide variety of sequencing pipelines.

We evaluated BATCAVE with simulated tumors with three different mutation profiles and two real tumors. The simulated diffuse and intermediate profiles (Figure 2A and B) represent baseline profiles of lung and breast tumors, respectively. And the concentrated profile (Figure 2C) represents a tumor driven by a particular mutational process, such as UV exposure. But mutational profiles are highly heterogeneous, so concentrated profiles can be found in any tumor type (e.g. Figure 1C). The two real datasets we considered are among the few for which extensive validation of variant calls has been performed (4,52). They happen, however, to have diffuse mutation profiles (Figure 1A and B), which reduces the expected advantage of BATCAVE over MuTect (Table 1). A more fundamental challenge of using these real data for testing callers is that only a subset of potential variants are validated. This subset tends to be relatively easy to call, so both MuTect and BATCAVE have almost perfect precision and recall for variants that pass heuristic filters (Figure 4 and Table 1). Moreover, few true negative sites are validated, so specificity and calibration are impossible to calculate. Deep sequencing experiments that validate random samples of uncalled potential variants would give much-needed insight into the differences among statistical models in variant calling.

The improved calibration of BATCAVE posterior probabilities compared to MuTect provides several advantages. In practice, called variants are often manually reviewed to further reduce false positives (54). Improved calibration enables users to focus review on the most questionable variants. In the clinic, identified variants act as biomarkers for susceptibility to targeted drugs (55). Well-calibrated posterior probabilities facilitate the use of probabilistic risk models in the choice of treatment (56), rather than an all or nothing approach. For research purposes, the International Cancer Genome Consortium recommends that catalogs of somatic mutations target a precision of 95% and a recall of 80% (57). Achieving this goal while minimizing cost demands well-calibrated posterior probabilities.

Our current implementation of BATCAVE is as a post-calling algorithm for MuTect, but the algorithm is broadly applicable. We chose to build BATCAVE off MuTect because MuTect is widely used, has state-of-the-art sensitivity and specificity, and includes numerous heuristic filters and alignment adjustments that reduce the prevalence of sequencing errors in results (10,52). But the mutational prior can be incorporated into almost any caller with an underlying probabilistic model. For example, Strelka2 computes a joint posterior probability over tumor and normal genotypes, assuming a constant somatic mutation probability at each genomic site (18). Replacing that constant probability with a mutational prior would require a more complicated manipulation of the quality scores output by Strelka than for MuTect, but it is conceptually straightforward.

Following MuTect (10), BATCAVE assumes a uniform prior on the variant allele frequency. In general, low-frequency variants are expected to be more common than high-frequency variants. Nevertheless, the uniform frequency prior is appropriate when the goal is to make the best call possible at each potential variant site. By favoring low-frequency and thus typically low-evidence variants, a nonuniform prior would increase the false positive rate. Note however, that if the goal were not to best identify individual variants, but rather to best estimate the distribution of variant allele frequencies within the tumor, then a nonuniform frequency prior would be appropriate (58).

To estimate the tumor mutation rate, BATCAVE uses a model of the distribution of variant allele frequencies generated during exponential growth (equation 11). Mutations that change copy number might distort the empirical allele frequency distribution, biasing the estimate. But substantially biasing the estimate would require copy number changes in a large number of genomic regions. Nevertheless, a potential extension of the BATCAVE algorithm would be to incorporate external copy number calls in order to adjust allele frequencies before estimating the mutation rate.

Sequencing multiple regions of the same tumor is of growing interest for understanding tumor heterogeneity and evolution (59). In fact, the breast cancer data we analyze came from a multi-region study (4). We called variants independently across samples, because MuTect only considers a single sample at a time. But calling variants jointly across samples could substantially increase sensitivity. In the future, the BATCAVE algorithm could be integrated into a multi-sample caller such as MultiSNV (60). In that case, an optimal implementation would likely exploit the relationship between mutational priors in related samples.

The BATCAVE algorithm is computationally inexpensive; our current implementation adds 1 s per 22 000 variants evaluated to a standard GATK best-practices variant calling pipeline. The majority of the computational cost is associated with extracting the trinucleotide context for each potential variant site from the reference genome. Since most callers are already walking the reference genome during the calling process, extracting the trinucleotide context simultaneously would virtually eliminate the computational cost of implementing a mutational prior.

The BATCAVE algorithm incorporates genomic context into the probabilistic model for variant calling. Our current implementation focuses on trinucleotide context, which is known to have a large effect on local mutation rates (61,62). There are, however, many other aspects of genomic context that can affect local mutation rates (40), including replication timing (63), expression level (64) and chromatin organization (65). Some of these, such as replication timing and chromatin organization, could be incorporated into the BATCAVE mutational prior using the empirical distribution of mutations in the human germline (66). Others, such as expression level, could be tumor-specific, but would require information not available in the variant calls to compute. In the long run, we believe that incorporating more tumor biology into variant calling models will continue to improve performance.

BATCAVE divides the data into two classes: high- and low-confidence variants. The high-confidence variants are used to estimate the mutational prior and mutation rate, which are then used to improve the calling of low-confidence variants. Statistically, this is an empirical Bayesian approach (67), in which the high and low-confidence variants are treated as parallel experiments (68,69). In general, high-confidence variants tend to have relatively high allelic frequencies, and consequently tend to have arisen early in tumor development.

An implicit assumption of BATCAVE is that the mutational process does not change between high- and low-confidence variants, implying that the mutational profile of the tumor is temporally constant. Recent studies have found differences in mutational profiles among variants of different allelic frequencies (70), and although in general those differences are relatively small, they can be significant in some cases. Our batcaver software warns the user if the high- and low-confidence mutational profiles are statistically different. It also outputs those profiles, so the user can assess whether the difference will substantially affect their results. A potential extension of the BATCAVE algorithm is to process potential variants in order of descending allelic frequency and to update the estimated mutational prior as the algorithm proceeds. This approach might increase sensitivity to low-frequency variants generated by recently arisen mutational processes, at the cost of potentially increasing sensitivity to patterns of sequencing error.

Our results show that adding a mutational prior substantially improves probabilistic variant calling, particularly for tumors with concentrated profiles. Improved variant calling increases the benefit-to-cost ratio of deep sequencing in both research and clinical applications. Moreover, BATCAVE proves to be a better calibrated caller than vanilla MuTect (Figure 5). Different users will prefer different tradeoffs in terms of precision and recall, which can be more accurately made with BATCAVE. Our R implementation, batcaver, can be easily incorporated into any MuTect-based pipeline, and the mutational profile algorithm can be incorporated into many other callers.

SOFTWARE AVAILABILITY

The batcaver R package can be downloaded or installed from http://github.com/bmannakee/batcaver. The version of batcaver used to generate results and all analysis code have been preserved on Zenodo https://doi.org/10.5281/zenodo.3471715. Python code used to generate simulated tumors has been preserved on Zenodo https://doi.org/10.5281/zenodo.3471741

SUPPLEMENTARY DATA

Supplementary Data are available at NARGAB Online.

FUNDING

National Science Foundation via Graduate Research Fellowship Award [DGE-1143953 to B.K.M.]; National Institute of General Medical Sciences of the National Institutes of Health [R01GM127348 to R.N.G.].

Conflict of interest statement. None declared.