Assessing Spatiotemporal and Functional Organization of Mitochondrial Networks

Abstract

The functional and spatiotemporal organization of mitochondrial redox signaling networks can be studied in detail in cardiac myocytes and neurons by assessing the time-resolved signaling traits of their individual mitochondrial components. Perturbations of the mitochondrial network through oxidative stress can lead to coordinated, cluster-bound behavior in the form of synchronized limit-cycle oscillations of mitochondrial inner membrane potentials. These oscillations are facilitated by both structural coupling through changes in the local redox balance and signaling microdomains and functional coupling that is yet poorly understood. Thus, quantifiable measures of both coupling mechanisms, local dynamic mitochondrial coupling constants and functional clustering coefficients, are likely to offer valuable information on mitochondrial network organization. We provide step-by-step methodologies on how to acquire and assess these measures for inner membrane potential fluorescence fluctuations in laser-scanning two-photon microscope recordings of cardiac myocytes and neurons, that can be applied to other tissues as well.

1. Introduction

Mitochondria contribute to a wide range of cellular processes such as metabolic pathway control, ATP production, cellular homeostasis and apoptosis, redox oxidation and oxidative phosphorylation, β-oxidation of fatty acids, and calcium signaling. Their role as intracellular hubs that influence, control, and interfere with cellular functions implicates them in many diseases and disorders, e.g., cardiovascular and neurological pathologies [1–3].

There are numerous methodologies to measure mitochondrial activity, many of them linked to mitochondrial signals that are generated by changes in the local redox or pH environment [3–5]. These signals enable mitochondrial regulation of specific enzymes, transcription processes, and communication with other mitochondria [2, 6, 7]. In fact, mitochondria may produce changes of their inner membrane shape [8] or potential [9] in response to external stimuli that alter the local redox status like oxidative stress, thiol-oxidizing substances (diamide), or substrate deprivation [10–13].

A well-studied example appears in mitochondrial inner membrane potential oscillations in cardiac myocytes where mitochondria form a lattice-like, cell-wide network of densely packed organelles to facilitate cardiac energy demand and supply [11]. These oscillations typically commence with a local perturbation of the mitochondrial redox environment and can be reliably reproduced by a focalized laser flash that depolarizes the inner membrane potential, ΔΨ_m, of a small fraction of mitochondria [14]. The stress-associated increase of locally confined reactive oxygen species (ROS) is sensed by mitochondrial inner membrane anion channels that may open to release ROS when ROS levels surpass a critical threshold [11, 14, 15].This autocatalytic or ROS-induced ROS release (RIRR) mechanism is controlled by ROS scavenging processes so that, in a confined environment, a cyclical activation of RIRR can lead to local mitochondrial ΔΨ_m oscillations [14, 16, 17]. However, depending on the gradient and distribution of intracellular ROS densities, ROS-sensitive mitochondrial inner membrane potential channels, and availability of ROS scavenging molecules, ΔΨ_m oscillations may not be restricted to the initial nucleus of mitochondria with a perturbed redox environment, but can expand to the whole cell by destabilizing ΔΨ_m of neighboring mitochondria such that a wave of ΔΨ_m depolarization transcends through the myocyte [18]. This process is also coordinated by electrochemical coupling at inter-mitochondrial junctions [8]. Typically, the experimentally observed myocyte-wide ΔΨ_m oscillations are mainly sustained by a cluster of synchronously oscillating mitochondria distributed over the whole myocyte, which we call a spanning cluster [18]. Spanning clusters emerge when intracellular ROS values in a sufficiently large volume of the myocyte approach a critical threshold, a phenomenon that can be linked to percolation theory [12, 13, 18]. There is evidence, however, that not all mitochondria participate in synchronized ΔΨ_m oscillations: some mitochondria oscillate with different frequencies, some do not oscillate at all, and others oscillate only temporarily, i.e., they may leave the cluster due to an exhaustion of ROS defense mechanisms [19, 20]. In addition, of those mitochondria that oscillate with different frequencies, some may lock to a common oscillatory mode to form a smaller synchronized cluster that coexists next to the spanning cluster. Since network mitochondria are structurally and functionally coupled through a plentitude of local and global mitochondrial ROS balance mechanisms, naturally, these processes are nonstationary and interdependent. Inter-mitochondrial coupling is further influenced by the interplay of mitochondria with other intracellular organelles (e.g., myofilaments or sarcoplasmic reticulum [21]), by mitochondrial functional heterogeneity [22, 23], and generally by any other intracellular, intercellular, and extracellular regulatory mechanism that exerts an influence on mitochondrial function. Mitochondrial structural heterogeneity adds to the complexity of the mitochondrial network [24, 25]. The observed mitochondrial ΔΨ_m oscillations therefore reveal changing frequencies and amplitudes [19, 20], as does the size and growth of synchronized mitochondrial clusters; however, the mere presence of synchronized oscillations suggests a strong influence of local coupling in the mitochondrial network [26]. Furthermore, an experimentally observed inverse relation between size and frequency of synchronized clusters indicates that large clusters take longer to equilibrate their inter-mitochondrial coupling mechanisms and, thus, possess a lower common frequency than smaller clusters [20, 26]. A large cluster of synchronously oscillating mitochondria usually features a decrease in ΔΨ_m amplitudes over time, which is accompanied by a decelerated cluster growth, indicating an exhaustion of ROS scavenging mechanisms and, therefore, is a sign of impending cell death. Measures of inter-mitochondrial coupling or functional network properties can thus provide important information about the network’s response to perturbations and may be used to simulate large mitochondrial oscillator networks.

Recent modeling efforts of mitochondrial network behavior have shown that a reaction-diffusion model built on biochemical exchange rates for mitochondrial matrix constituents (calcium, NADH, ADP, Krebs cycle intermediates) and mitochondrial inner membrane potential physiology (including the RIRR mechanism) correctly predicts limit-cycle ΔΨ_m oscillations [16, 27]. However, increasingly deterministic models of mitochondrial networks that include various forms of regulation and control on mitochondrial behavior, including functional and structural coupling of mitochondria within the network or with other (extra-)cellular organelles, biochemical pathways, as well as diffusion dynamics or fluxes of relevant biomolecules, need enormous computational resources. A more efficient approach is the introduction of stochastic noise in the description of individual mitochondrial signals [26]. The application of stochasticity in cardiac mitochondrial networks is justified for strong links between network components [28]. Based on an extension of the Kuramoto model of coupled oscillators [29, 30], stochastic differential equations for the mitochondrial ΔΨ_m oscillation phase can be utilized to assign to every mitochondrion m a time-dependent coupling constant K_m(t) (of local mean-field type, see below) to quantify its coupling to the nearest mitochondrial neighbors [26]. The model uses the observed drift of mitochondrial frequencies toward a local mean frequency described as stochastic Ornstein-Uhlenbeck frequencies [31]. It shows larger inter-mitochondrial coupling in smaller clusters at the early stages of myocyte-wide ΔΨ_m oscillations, suggesting a strong effect of local coupling [26, 32]; also, see a discussion of coupling dynamics in mitochondrial frequency clusters [33].

The concept of a cluster of mitochondria with similar frequencies does not presume a spatially contiguous ensemble of mitochondria. In fact, some mitochondria may connect to the common oscillatory mode of a large cluster of synchronously oscillating mitochondria, although they are too distant from any cluster mitochondrion to experience local coupling. In analogy to functional networks of communicating neurons [34], such functional relations were recently examined for the network of mitochondrial oscillators [35]. They allow the quantification of a topological clustering coefficient that provides a measure of functional connectedness between mitochondrial oscillators. The analysis of functional clustering is not restricted to mitochondria from one major cluster of synchronously oscillating mitochondria, but involves all oscillating mitochondria. Briefly, functional clustering of mitochondrion m is a measure of the topological connections between all topological neighbors of m. Understanding of the dynamic changes in functional clustering provides valuable clues about the network’s spatiotemporal organization in exploring the connectedness between mitochondria that cannot be explained by immediate (structural) coupling effects. It could be shown that functional clustering in mitochondrial networks is significantly higher than that in equivalent random networks [35]; this result supports the notion of a functional-structural unity in mitochondrial unity in mitochondrial networks [36].

Below we provide a detailed description of experimental and computational methods to assess mitochondrial spatiotemporal organization for the stress-induced cardiac myocyte mitochondrial inner membrane potential oscillations. Specifically, we present point-by-point procedural methodologies based on findings and results [19, 20, 26, 35] for the extraction of individual mitochondrial ΔΨ_m signals and identification of nearest neighbors (Subheading 3.1–Subheading 3.4), the extraction of time-dependent frequency content for each mitochondrial ΔΨ_m signal using wavelet analysis (Subheading 3.5), the identification of a major cluster of synchronously oscillating mitochondria and its frequency and cluster size analysis (Subheading 3.6), the analysis of local cluster coherence (Subheading 3.7), the analysis of propagation of mitochondrial signals following the onset of myocyte-wide oscillations (Subheading 3.8), the analysis of functional connectedness and functional mitochondrial clustering (Subheading 3.9), and the determination of local inter-mitochondrial coupling (Subheading 3.10).

2. Materials

2.1. Sets of Mitochondrial Signals

The assessment of the mitochondrial networks’ spatiotemporal properties relies on time-resolved recordings of mitochondrial signals in an entire mitochondrial population. Naturally, in these recordings, mitochondrial signals must be associated with or arise from the single organelle level, i.e., they can be linked to mitochondrial metabolic pathway products, mitochondrial respiration, mitochondrial membrane channel signaling molecules, and/or mitochondrial membrane potential. The recordings also need to have a sufficiently high spatial resolution of ideally less than 500 nm to allow a differentiation of individual mitochondria. A further prerequisite is an adequate temporal resolution that captures dynamic changes in mitochondrial signals and signaling. For mitochondrial redox signaling or membrane potential fluctuations, the image sampling period is ideally less than 5 s [3, 20].

A well-studied example are mitochondrial inner membrane potentials in isolated cardiac myocytes: they can be marked with the fluorescence dyes tetramethylrhodamine-ethyl ester or methyl ester (TMRE or TMRM, hereafter referred to as TMRE) and measured with a laser-scanning two-photon microscope [13, 14]. Such mitochondrial signals can be recorded with sufficient temporal resolution to visualize ΔΨ_m oscillations (see also Fig. 1). Other examples of time-resolved measurements of mitochondrial signaling within mitochondrial networks include the assessment of mitochondrial redox and mitochondrial matrix pH dynamics in mice intercostal axons and neuromuscular junctions [7] or cell cultures [37], stress-induced pulsing of mitochondrial membrane potentials in Arabidopsis [38], or in vivo mitochondrial superoxide signals for mouse skeletal muscle and sciatic nerve [39].

Fig. 1.

Mitochondrial oscillations in a cardiac mitochondrial network. (a) Two-photon image of a TMRE-fluorescent guinea pig cardiac myocyte (upper panel) and with an overlaid grid that captures single mitochondria (lower panel), e.g., the yellow mitochondrion in the upper right corner of the cell. (b) TMRE intensity plot of the marked mitochondrion in (a) and the corresponding absolute squared wavelet transform (lower panel). The selected mitochondrion shows oscillations that range between 20 and 40 mHz. (c) Frequency distribution maps obtained from a different cardiac myocyte. The upper panel shows the mean mitochondrial oscillation frequency, averaged over all mitochondria, as a function of time. The lower panel shows maps of frequency distributions during two time-points (indicated in red in the upper panel). Missing pixels were interpolated. Most mitochondria oscillate with frequencies between 14 and 16 mHz while a small cluster in the right corner of the cell shows a strong increase in oscillation frequency during the two time-points between (Adapted from Fig. 1 in [26], with permission from ref. 26. Copyright 2015)

A transition of the mitochondrial network into myocyte-wide synchronized ΔΨ_m oscillations could be measured ex vivo in freshly isolated adult guinea pig ventricular myocytes [14], but also in cellular structures of intact heart tissue of guinea pigs [40] and in vivo in rat glandular cells [41], demonstrating that mitochondrial ΔΨ_m oscillations can prevail in a superordinate cellular network that contains additional control mechanisms, e.g., through intercellular gap junctions.

Every imaging methodology requires its own biological specimen, solutions, mitochondrial markers, and imaging protocols [3, 7, 14, 20, 26, 37–41]. However, since our group mostly worked with mitochondrial inner membrane potential signals from isolated cardiomyocyte experiments, we provide here a brief list of necessary materials to perform this specific experiment:

1. Materials for the Isolation of Cardiac Myocytes.

   • Enzymatically dispersed adult guinea pig ventricular myocytes (see also [9]).
   • Dulbecco’s modified Eagle’s medium (10–013, Mediatech, Inc. Herndon, VA).
   • Laminin-coated Petri dishes.
   • 5% CO₂ incubator.
   • Tyrode’s solution containing 140 mM NaCL, 5 mM KCl, 1 mM MgCl₂, 10 mM HEPES, and 1 mM CaCl₂, with a pH = 7.5 (adjusted with NaOH), supplemented with
   • 10 mM glucose (or other substrates such as pyruvate, lactate, or β-hydroxybutyrate; see [26]).
   • Upright epifluorescence microscope (BX61W1; Olympus, Waltham, MA).
   • 100 μM TMRE stock solution.
2. Materials for Image Acquisition.

   • Multiphoton laser scanning fluorescence system: Fluoview FV1000 MPE (Olympus) and a DeepSee ultrafast laser (Spectra Physics, Santa Clara, CA).

2.2. Software to Process the Mitochondrial Signals

Any imaging processing program, raster graphics editor, and technical computing software may be adequate for signal processing and network analysis; however, we used the following programs:

• ImageJ v1.38q or later, including the image stabilizer plug-in for ImageJ [42].

• Adobe Photoshop CS4 or later.

• Matlab v7.1.0.246 or later.

• OriginPro 8 SR0 v8.0724 or later.

3. Methods

3.1. Studies in Isolated Cardiac Myocytes

We briefly describe the mitochondrial network imaging protocol, and we provide an example for the acquisition of mitochondrial signals in isolated cardiomyocytes; more detailed protocols can be found in [9, 14]:

1. Load the freshly isolated cardiac myocytes with 25 nM TMRE for 20–30 min in a thermostatically controlled flow chamber (at 37 C) that is mounted on the stage of an upright epifluorescence microscope.

2. Washout the dye by perfusing the cardiac myocytes with Tyrode solution supplemented with 10 mM glucose (or other substrates) and 1 mM Ca²⁺ for 2–3 min. Visualize the myocytes with an objective 40×/1.0 W MP.

3. Record images using the multiphoton laser scanning fluorescence microscope (Fluoview FV 1000 MPE) with excitation at 740 nm and the red emission of TMRE collected at 605 nm using a 578–630 nm band-pass filter.

4. Trigger mitochondrial inner membrane oscillations with a localized (5 × 5 μm²) laser flash.

3.2. Image Processing

1. For each stack of recorded images, use the ImageJ image stabilizer plug-in to minimize movement effects of the cardiac myocyte and the mitochondrial network.

2. For each stack of stabilized images, identify the onset of mitochondrial inner membrane potential oscillations (or an equivalent onset or relevant signal change for other types of experiments that involve mitochondrial signals/signaling), as the first image where the mean TMRE fluorescence intensity drops by more than 10% with respect to the averaged mean TMRE intensity of the previous images.

3. Identify the smallest period l of all TMRE oscillations that comprise a significant amount of the mitochondrial network (usually more than 30% of the network’s mitochondria).

4. Arrange the images after the first significant TMRE intensity drop (see step 2) in intervals of l.

5. Average all images in each interval.

3.3. Extract Individual Mitochondrial Signals

1. Use a maximum-intensity averaged image from the set of images resulting from Subheading 3.2, step 5 (above) as a template, and upload it into a raster graphics editor program to manually draw grid lines around each mitochondrion on a pixel-by-pixel basis for each separate image (layer) (see Note 1).

2. Save the grid image as a binary image.

3. Allocate a numerical identifier for each grid mesh, i.e., for each mitochondrion (e.g., using the function bwlabel in Matlab).

4. Average the TMRE intensity in each grid mesh across every time-point to obtain a mean intensity for each mitochondrion, at every time-point of the recording. This last step produces the individual mitochondrial inner membrane potential time series signals.

3.4. Identification of Nearest Neighbors

1. Determine the “center of gravity” for each mitochondrial grid mesh.

2. For every mitochondrion m, determine all mitochondria other than m for which the connection between their centers of gravity by a straight line crosses exactly one grid line. Save their numerical identifiers as the nearest neighbors of m.

3.5. Wavelet Analysis of Individual Mitochondrial Signals

The wavelet transform of a time series signal provides a measure of the frequency content of the signal at a specific time-point [43, 44]. This is especially useful if one probes signals with time-varying (dynamic) frequency content, as is the case in mitochondrial oscillations during oxidative stress [19, 20, 26].

1. Normalize each mitochondrial time series signal by its standard deviation and pad the number of recorded images with zeros to the next higher power of 2. This will accelerate the ensuing computation and prevent a wraparound from the end of the time series to the beginning.

2. 1. Apply the wavelet transform to each mitochondrial signal: Matlab possesses a built-in wavelet toolbox; however, there are also wavelet software packages for other computational platforms [45].
   2. Specific parameters for the mother wavelet should be adapted to the observed dynamic changes of the signal. For the continuous analysis of mitochondrial signals we recommend the Morlet wavelet (as opposed to other wavelet forms such as the Mexican hat wavelet or the Paul wavelet) for its higher frequency resolution.
   3. Choose fixed wavelet scales to adequately sample all relevant frequencies that are present in the mitochondrial signal. It is convenient to choose the smallest resolvable scale as s₀ = 4 dt (dt being the sampling period), corresponding to at least four data points needed to adequately resolve one oscillation, and thus, to a maximum frequency of f_max = s₀⁻¹. Larger scales s_k should be chosen as s_k = s₀ 2^{k dk}, where k = 0,1,…K, with K = log₂ T / s₀)/dk, recording time T, and dk = 0.1–0.25, leading to at least four subscales within each scale. This oversampling is necessary to obtain adequate frequency information in between the scales. The largest scale can be constrained further by excluding very long periods that surpass 10% of the longest visible period L of a synchronized mitochondrial oscillation, thus setting a minimum frequency of f_min (1.1 L)⁻¹. This procedure helps avoid time-consuming =computation by focusing on the relevant frequencies.

3. Determine the wavelet power spectrum at each time-point by taking the squared absolute value of the wavelet transform.

4. Interpolate the wavelet power spectrum to a frequency resolution of 0.1 mHz.

5. Determine the frequency with the maximum wavelet power in the interpolated wavelet power spectrum from step 4, at each time-point (for each mitochondrion). This provides the time-resolved frequency for an individual mitochondrion.

3.6. Major Mitochondrial Frequency Clusters and Frequency Cluster Size Analysis

The major mitochondrial frequency cluster determines the cluster of (oscillating) mitochondria with similar frequency content at a specific time-point t (see also Fig. 2a in [20]).

Fig. 2.

Propagation of mitochondrial oxidation events in axons and neuromuscular junctions. (a) Mitochondrial redox event propagation in a triangularis sterni explant axon of a Thy1-mito-Grx1-roGFP2 mice after nerve crush injury. The signal propagates from left to right and indicates clustered oxidation (see also [3, 7]). (b) Propagation of mitochondrial matrix pH events in a triangularis sterni explant neuromuscular junction of mice injected with recombinant adeno-associated virus particles (rAAV-1/2-mito-SypHer; for details see [7]). Mitochondrial signal propagation is more fragmented and prolonged (Adapted from Figs. 3 and 5 in [7], with permission from ref. 7. Copyright 2016)

1. Determine the distribution histogram (over a frequency resolution of 1/dt) of mitochondrial frequencies at each time-point t.

2. Determine the maximum (peak) of each histogram, P_max(t), and its associated frequency, ν_max(t), that corresponds to the major mitochondrial frequency.

3. Identify all mitochondria that contribute to P_max(t).

4. Identify mitochondria in a peak that is directly adjacent to P_max(t), P_a(t), with a peak magnitude of at least 10% of the magnitude of P_max(t).

5. Determine the mean (TMRE) signal S_max(t) from mitochondria that belong to P_max(t).

6. Determine the mean (TMRE) signal S_a(t) from mitochondria that belong to P_a(t).

7. Within a window of 1.1 [ν_max(t)]⁻¹ around time-point t, find the correlation coefficient c_a of the signals S_max and S_a.

8. Add the mitochondria in P_a(t) to P_max(t) if c_a 0.95 (corresponding to at least 95% correlation of the signals).

9. Repeat steps 4–8 until you reach a P_a(t) with c_a < 0.95 for frequencies both higher and lower than ν_max(t).

10. Determine all mitochondria that do not belong to P_max(t).

11. For each mitochondrion m of the mitochondria in step 10, determine the correlation coefficient c_m of its (TMRE) signal with the mean (TMRE) signal of the mitochondria in P_max(t) within a window of 1.1 [ν_max(t)]⁻¹. If c_m ≥ 0.95, include mitochondrion m in the cluster of mitochondria that form P_max(t).

12. Assign a cluster frequency at time-point t being the mean frequency from all mitochondria in P_max(t).

13. Determine the (normalized) space occupied by the cluster mitochondria at time-point t by adding the sizes of each mitochondrion in P_max(t) and dividing by the size of the myocyte area.

14. In analogy to step 13, one may obtain a relative cluster size by dividing the number of mitochondria in P_max(t) by the total number of mitochondria.

15. Determine the time-dependent mean cluster frequency as the averaged frequency from the wavelet frequencies at time-point t for all mitochondria belonging to the major cluster.

16. For the analysis of the relation between cluster frequency and size, produce a graph where you insert the values from step 15 (x-axis) and step 13 or 14 (y-axis) for all time-points, in analogy to Fig. 2c, d in [20].

3.7. Local Cluster Coherence Analysis

A complementary analysis to investigate the temporal and spatial properties of a major mitochondrial cluster can be achieved by determining the coherence of each of the cluster mitochondria with its nearest neighbors. A coherence analysis of two (oscillating) signals is sensitive to both a change in phase relationships and a change in power [46]. For two signals S_A and S_B, it results from the quotient of absolute squared cross-spectrum between S_A and S_B and the product of the auto-spectra of S_A and S_B. Coherence levels range between zero and one.

1. At each time-point t, create a window W around t of size 1.1 L (see Subheading 3.5, step 2c).

2. Choose a frequency band; a convenient frequency band for mitochondrial oscillations under oxidative stress ranges from 0 to 100 mHz.

3. Choose the number of sampling points for the discrete fast Fourier transform that is being used for the coherence analysis; a convenient choice is 2¹¹ sampling points that, for the frequency band in step 1, lead to (2¹¹/2) + 1 segments or approximately 0.1 mHz per segment.

4. Choose a Hanning window of size W/8.

5. Choose an overlap of 50% between segments.

6. A convenient method to determine the coherence between two mitochondrial signals is then provided by Matlab’s mscohere function with the parameters given in steps 1–5.

7. Determine the mean coherence at time-point t for each cluster mitochondrion m as the average coherence of m with all its nearest neighbors within the window W.

8. To compare the coherence of cluster mitochondria and non-cluster mitochondria, the procedure in steps 1–7 can be repeated for all non-cluster mitochondria (see also Fig. 3 in [20]) (see Note 2).

9. To allow for comparison among different recordings, the time-resolved coherence values should be normalized in time through linear interpolation at a resolution that is equal or smaller than the smallest recorded sampling period.

Fig. 3.

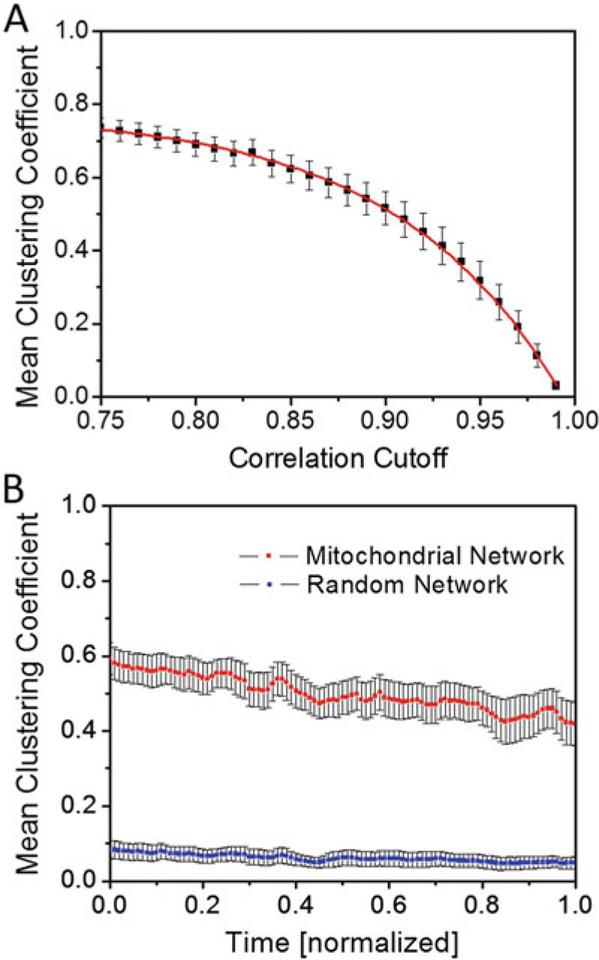
Functional mitochondrial clustering. (a) Time- and myocyte-averaged mean clustering coefficient for different cutoffs of the correlation coefficient that defines the threshold for functional connectedness. The red curve was fitted with the function f(x) = a∙exp.(−x/b) + c (a = −7.81∙10⁻⁶ ± 1.33∙10⁻⁶, b = −8.64∙10⁻² 0.13∙10⁻², c = 77.65∙10⁻² ± 0.35∙10⁻²; see also [35]). The 50% value of the mean clustering coefficient is approximately crossed at a correlation cutoff of 0.9, which approximately coincides with the median derivative value of the fitted curve. (b) Mean clustering coefficient for a correlation cutoff of 0.9, averaged over nine different glucose-perfused cardiac myocytes (red line; for details see [35]) and for equivalent random networks that are built on the same set of vertices and number of links (blue line). (Reprinted with permission from ref. 35. Copyright 2014)

3.8. Propagation of Mitochondrial Signals

Properties of a propagating mitochondrial signal, in the myocyte or axon, can be measured with isochronal maps that are created with reference to the onset of the mitochondrial signal changes (see also Fig. 2 for an isochronal map of axonal mitochondria in Thy1-mito-Grx1-roGFP2 mice triangularis sterni explants [7]). Isochronal maps provide information not only about the signal’s propagating velocity but also about the synchronization properties of the mitochondrial network; for example, propagation of the mitochondrial inner membrane potential depolarization may arise from a nucleus of already synchronized mitochondria [18, 20].

1. Determine the first signal change in a mitochondrion’s signal by marking the onset of the signal change (see also Subheading 3.2, step 2), t₁, and the first signal maximum or minimum thereafter, t₂.

2. From all time-points in the interval [t₁, t₂], exclude the 10% of time-points whose signal value is closest to that at t₁ and the 10% of time-points whose signal value is closest to the signal value at t₂.

3. Determine the earliest, t_I, and latest, t_E, of the remaining time-points.

4. Take the arithmetic mean of t_I and t_E as the mitochondrial signal change reference point, t_S, and repeat steps 1–3 for all mitochondria.

5. Of all mitochondrial reference points t_S, use the earliest one as reference point and create a color-interpolated isochronal map over all t_S values.

3.9. Functional Connectedness and Functional Mitochondrial Clustering

The mitochondrial network’s functional characteristics can be further studied using a recently proposed methodology [34] that is based on the correlation of mitochondrial signals [35]. This procedure acknowledges the fact that some mitochondria from the network may form a spanning cluster of synchronously oscillating mitochondria at different cellular positions that do not necessarily have close spatial proximity [13, 18, 20]. Mitochondria in these spatially non-contiguous clusters, however, may oscillate in synchrony, and there may be several of such spanning clusters hidden in the myocyte. This property constitutes the main difference with respect to the major mitochondrial frequency clusters (see above) that only consider one (major) cluster of similarly oscillating mitochondria.

1. At each time-point t, create a window W around t of size 1.1 L (see Subheading 3.5, step 2c).

2. For each pair of mitochondria, determine the cross-correlation coefficient c_p of their respective signals, in W. If coefficient c_p 0.9, allocate a (undirected) link between both mitochondria. This correlation coefficient cutoff value is arbitrary; however, it may be chosen based on the behavior of the clustering coefficient (see below and Fig. 3a): the clustering coefficients reach a plateau for lower correlation cutoff values and drop to zero for correlation cutoff values that approach 1. One may therefore reasonably assume an intermediate correlation cutoff at the point where the curve of clustering coefficients versus correlation coefficients reaches its median derivative value (Fig. 3a). This procedure generates a dynamic functional topology of the mitochondrial network.

3. For each mitochondrion m, determine the set N of mitochondria that are topologically connected to m, according to 2.

4. Determine the number of mitochondria in N, m_N, and the number of topological connections between all mitochondria in N, D_N.

5. Determine the clustering coefficient for mitochondrion m at time t as C_m(t) = 2 D_N/(m_N(m_N–1)) (see also [35]).

6. Determine the mean clustering coefficient of the whole network at time-point t as C(t) = (1/M) Σ_m C_m(t), where m represents the number of mitochondria in the network.

7. The functional network must be tested against a random network (see Fig. 3b). Construct the random network having the same number of network mitochondria, M, with the Erdös-Rényi model [47]: randomly assign m_N(t) links to each mitochondrion m at time-point t, where m_N(t) corresponds to the number of topologically connected mitochondria to m at t, obtained from the functional analysis in steps 2–4.

3.10. Local Inter-Mitochondrial Coupling

In contrast to functional properties of the mitochondrial network that may connect distant mitochondria, inter-mitochondrial coupling between nearest neighbors provides a measure for local network properties. Local coupling of oscillating mitochondria can be probed using a stochastic phase model of coupled oscillators with drifting frequencies [26]. The model is based on the Kuramoto model for weakly coupled circadian oscillators [29]; however, instead of assigning one overall coupling constant for the whole network, the stochastic phase model assigns time-dependent coupling constants for each mitochondrion [31]. We provide a step-by-step algorithm to determine these coupling constants, as described in [26]. For a short description of the relevant model parameters and functions, see Table 1.

Table 1.

Table of used symbols and parameters

Symbol	Description
ΔΨm	Inner mitochondrial membrane potential
dt	Sampling period of signal
T	Recording time of signal
s0	Smallest wavelet scale for wavelet analysis
l	Smallest period of a synchronized mitochondrial oscillation during a signal recording
L	Longest period of a synchronized mitochondrial oscillation during a signal recording
Pmax(t)	Maximum peak of mitochondrial frequency histogram at time t
cm, ca, cn	Correlation coefficients
W	Running window for cluster coherence analysis and topological analysis
mN	Number of mitochondria in the network N
dN	Number of topological connections between all mitochondria in the network N
Cm(t)	Clustering coefficient of mitochondrion m at time t
C(t)	Mean network clustering coefficient
M	Number of network mitochondria
Rm(t)	Local order parameter in the stochastic phase model for mitochondrion m
Ψm(t)	Local mean-field phase in the stochastic phase model for mitochondrion m
ϕm(t)	Phase of mitochondrion m
ωm(t)	Intrinsic frequency of mitochondrion m
vm(t)	Mean frequency for mitochondrion m, corresponds to the wavelet frequency
σm	Standard variation of nm(t)
ζ	Random number drawn from a distribution with zero mean and variance sm2
γ	Decay rate parameter for the Ornstein-Uhlenbeck frequencies
λ	Optimization parameter for Tikhonov regularization
Km(t)	Coupling constant for mitochondrion m
s(t)	Normalized intensity signal for the mitochondrial network

1. For each mitochondrion, determine the dynamic mitochondrial phase from the mitochondrial wavelet frequency, ν_m(t), as follows:

   • Determine the phase ϕ_m(t) of mitochondrion m from the wavelet transform at time t using the inverse tangent of the quotient of the imaginary and real part of the wavelet transform (atan2 in Matlab).
   • Determine the differential dϕ_m(t)/dt as the difference of consecutive phase values divided by the sampling period.
   • Apply a median filter of order 1.1 L (medfilt1 in Matlab), to account for frequency changes at the turning point of phase cycles.
   • Use linear interpolation of phase changes between the nearest positive values, to interpolate over negative values (see Note 3).

2. For each mitochondrion m at time-point t, sum the respective phases of the nearest neighbors of m, ϕ^(m)_n(t), as Σ_n exp(2πi ϕ^(m)_n(t)) and divide by the number of nearest neighbors (see also Eq. (2) in [26]).

3. Determine the local order parameter R_m(t) as the absolute value of the result in step 2.

4. Determine the local phase angle Ψ_m(t) of the result in step 2.

5. Determine the phase sum P_m(t) = R_m(t)sin(2π[Ψ_m(t)− ϕ_m(t)]), which is part of the coupling term in the phase differential equation, Eq. (3) in [26].

6. Determine the parameter σ_m as the standard deviation of the dynamic wavelet frequency of mitochondrion m.

7. For each mitochondrion m, create a Gaussian distribution with zero mean and variance σ_m².

8. Use an initial random phase value ω_m(0) from a distribution with mean ν_m(dt) and variance σ_m²

9. Update the intrinsic phase ω_m(t) with the equation

   $$\begin{gathered} {\omega }_m(t+dt)={\omega }_m(t)\text{exp}(-\gamma \cdot dt)+{\nu }_m(t)[1-\text{exp}(-\gamma \cdot dt)] \\ +\text{Sqrt}(1-\text{exp}(-2\gamma \cdot dt))\zeta , \end{gathered}$$

   where, for cardiac myocytes with substrate perfusion, γ ≈ 0.07 [26], and ζ a random number drawn from the distribution in step 7 (see also Eq. (1) of the supplementary information in [26]) (see Note 4).

10. Determine the time-points t_z for which the phase sum P_m(t) (step 5) has a sign shift (from negative to positive or vice versa).

11. At each time-point t, determine the coupling constant

    $$\left[{\nu }_m(t)-{\omega }_m(t)\right]/P_m(t)$$

    from the update equation in step 9 (see also Eq. (3) in the supplementary information in [26]). If this quotient is smaller than zero, repeat the analysis with a new random number from step 9 until the quotient becomes positive.

    Perform at least 10 10 runs (better 10 100, as used in [26]) for ten different random initial phase values in step 8 and for ten different runs through the update phases in step 9 (with a different random number ζ at each time-point). Average the resulting coupling constants, K_m(t), over all runs and starting points.

    • if P_m(t) is close to zero, determine the parameter λ for Tikhonov regularization from the minimization of the function f(λ) = √(1 + 1/λ) √(r₁^T(λ) r₀(λ)) on the interval [M/100, 100 M] with M = || P_m || / T , and (here we use vector notation for vector elements corresponding to time-points and 1_T to the unit vector of size T), see also [26, 48]:

      $$\begin{gathered} x_0={\left[P_m{}^2+\lambda 1_T\right]}^{-1}{P}_m{}^T\left[{\nu }_m-{\omega }_m\right], \\ {r}_0(\lambda )=\left[{\nu }_m(t)-{\omega }_m(t)\right]-P_m{x}_0, \\ {x}_1={\left[P_m{}^2+\lambda 1_T\right]}^{-1}{P}_m{}^T{r}_0+x_0, \\ {r}_1(\lambda )=\left[{\nu }_m(t)-{\omega }_m(t)\right]-P_m{x}_1. \end{gathered}$$

      As a starting value one may choose λ_i = || P_m || / √(T). A convenient optimization function is provided by fminsearch in Matlab. If the optimization does not converge, set λ to the lower bound λ = M/100.

    • For the optimized parameter λ, apply a median filter (medfilt1 in Matlab with order 1.1 P) on the coupling constants [P_m^T + λ 1_T]⁻¹ P_m^T [ν_m−ω_m].

    • Average over all runs and starting points as above to determine K_m(t).

12. The forward model can be tested by determining the update phases ϕ_m(t) directly from the equation

    $$\text{d}{\varphi }_m(t)/\text{d}t={\omega }_m(t)+K_m(t)P_m(t),$$
    with updated intrinsic frequencies ω_m(t) as above. The (normalized) mitochondrial network signal s(t) is then constructed as

    $$s(t)=(1/M){\Sigma }_m\text{cos}\left({\varphi }_m(t)\right),$$

    where the sum runs over all mitochondria divided by the total number of mitochondria, M.

4. Notes

1. When drawing the grid to separate individual mitochondria in Subheading 3.3, step 1, the overlay image of the averaged images can sometimes be very blurry due to insufficient movement stabilization with the ImageJ image stabilizer plugin in Subheading 3.2, step 1. It is then best to only focus on the averaged image closest to the onset of myocyte-wide synchronized mitochondrial depolarizations.

2. The “non-cluster” coherence in Subheading 3.7, step 8 can be higher than the coherence of the major frequency cluster. This may be due to a minority of spatially close mitochondria that oscillate in a highly coherent fashion but with a frequency or phase difference that is largely different to those mitochondria in the major cluster.

3. It often occurs that, for some time-points, a few mitochondria do not show any signal changes apart from noise; however, they are still assigned a wavelet frequency which is usually either the upper or lower cutoff frequency. To eliminate these mitochondria from the model calculations in Subheading 3.10, one may exclude, at every time-point, all mitochondria with values at the cutoff frequencies.

4. The optimal decay rate parameter γ in Subheading 3.10, step 9, if not known, should be determined with an error estimation in a forward model that matches the averaged signal of all network mitochondria (Subheading 3.10, step 12) over many γ values (see also Fig. S6 in the supplementary information in [26]). A convenient choice is to take increasing γ values as multiples of 0.01 s⁻¹ in the interval [0 s⁻¹,1 s⁻¹]. Typically, increasing γ values approach an asymptotic (constant) error value (that accounts for the deviation between the forward model and the averaged mitochondrial network signal); the optimal decay rate parameter may then be chosen as the first γ whose error value is within 1% of the asymptotic error value.